Operation State Identification Method for Converter Transformers Based on Vibration Detection Technology and Deep Belief Network Optimization Algorithm
Abstract
1. Introduction
2. Vibration Mechanism and Signal Measurement of Converter Transformers
2.1. Vibration Mechanism of Converter Transformers
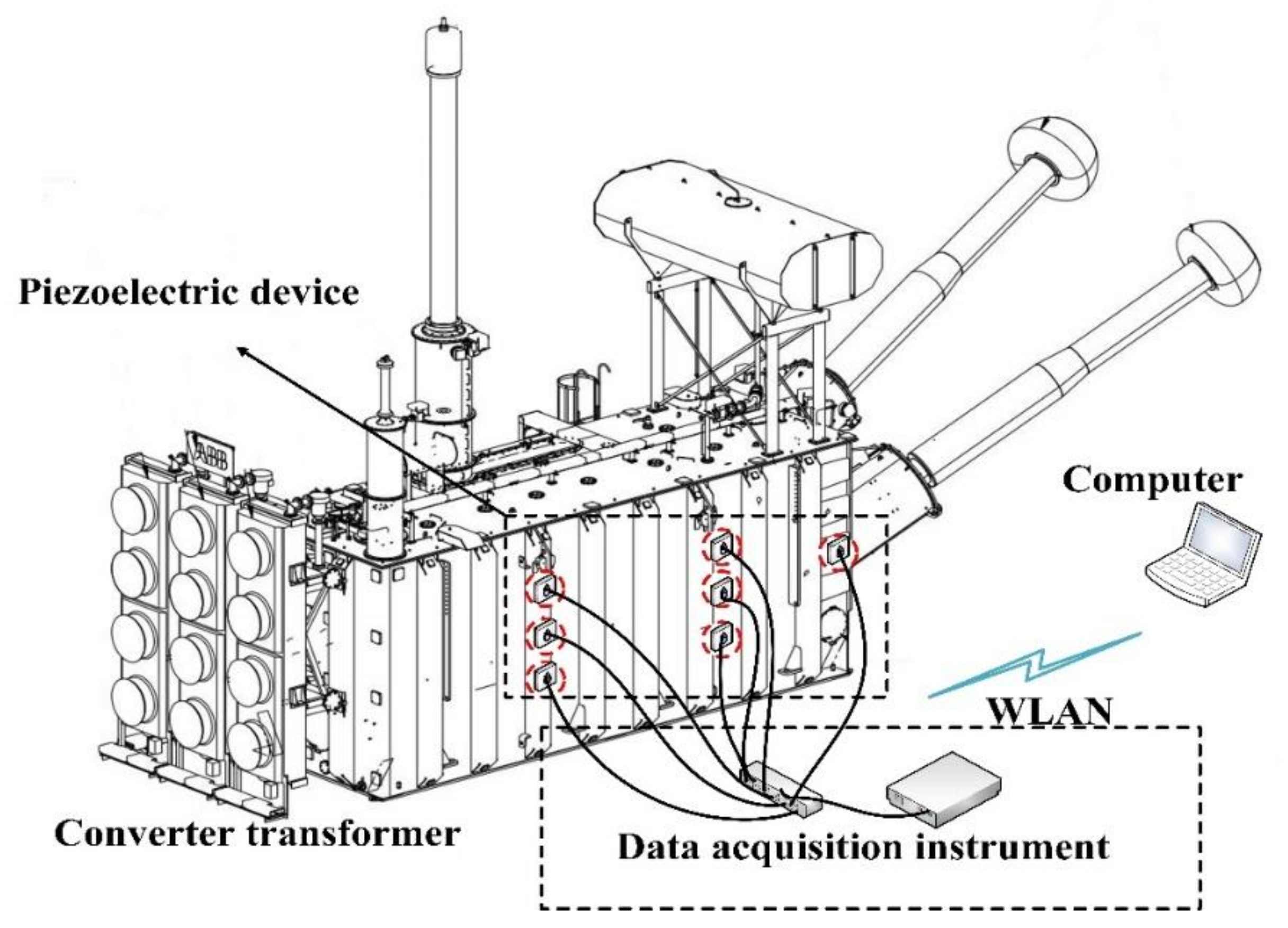
2.2. Signal Measurement of the Converter Transformer
- (1)
- Several piezoelectric devices are arranged on the measurement tank surface to obtain the vibration signals from the tank surface. The piezoelectric actuator is used to suppress the periodic noise generated by physical contact when the piezoelectric device is affixed to the tank wall, and the piezoelectric vibration sensor is used to output the collected vibration signal.
- (2)
- Vibration signals are amplified by the integrated circuits inside the sensors, and the output signals from the sensors are transmitted to a high-precision distributed data acquisition instrument through cables;
- (3)
- Analog signals are converted into digital signals through a digital–analog converter; digital signals are transmitted to a computer through a local area network.
2.3. Data Source
3. Characteristic Analysis of the Vibration Signal
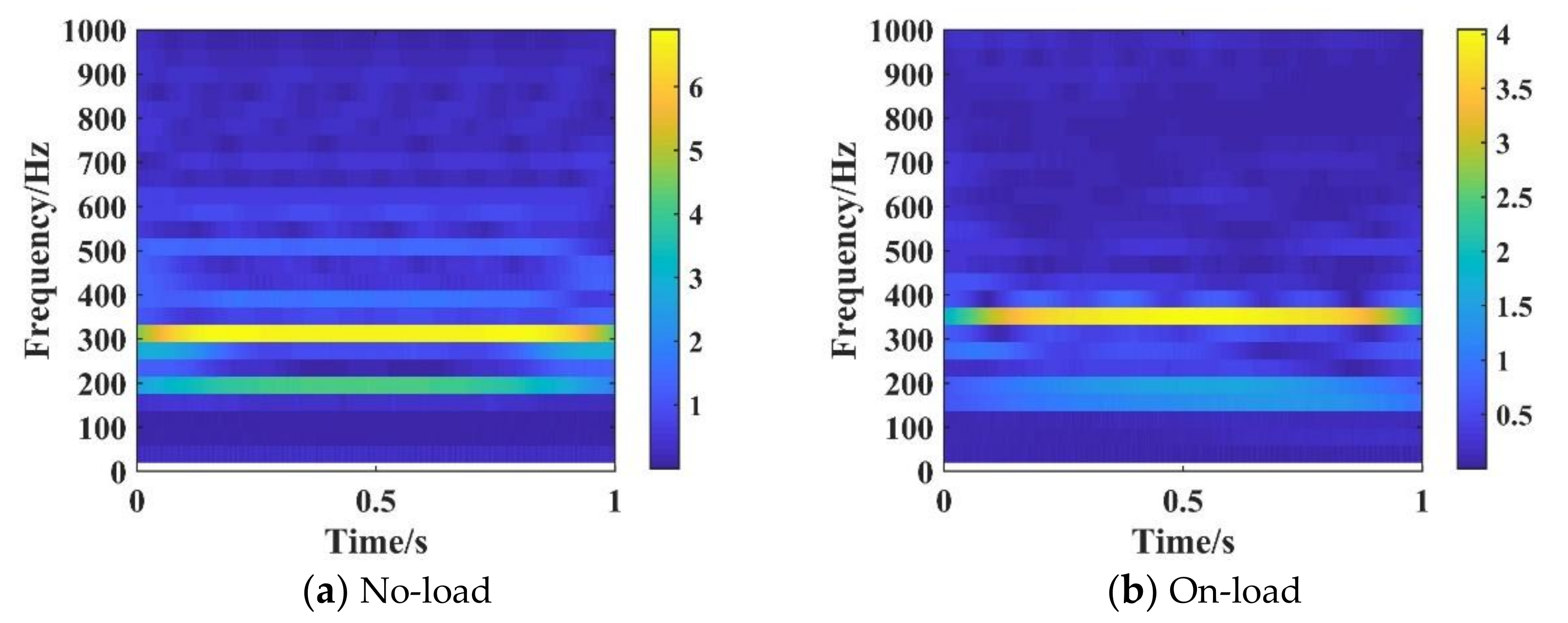
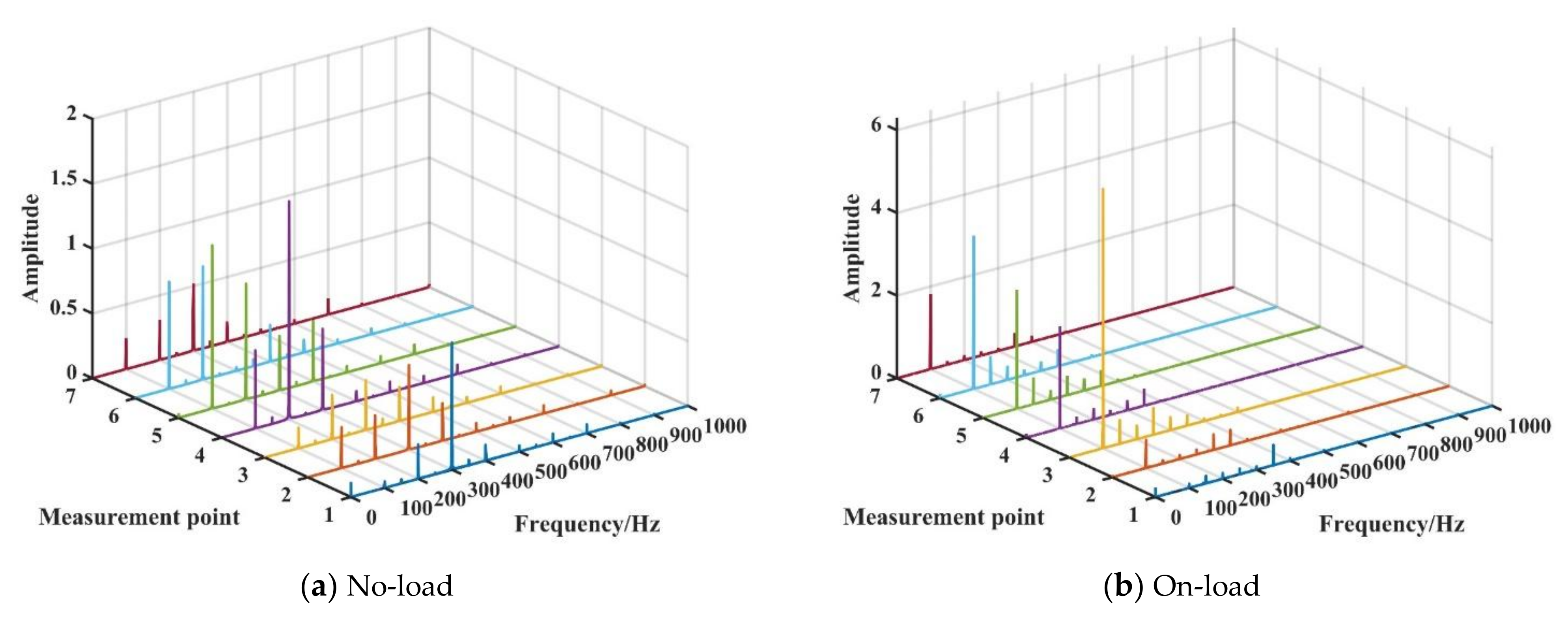
3.1. Time-Frequency Characteristics of Vibration Signals
3.2. Construction of Eigenvectors
3.2.1. Fast Fourier Transform (FFT)
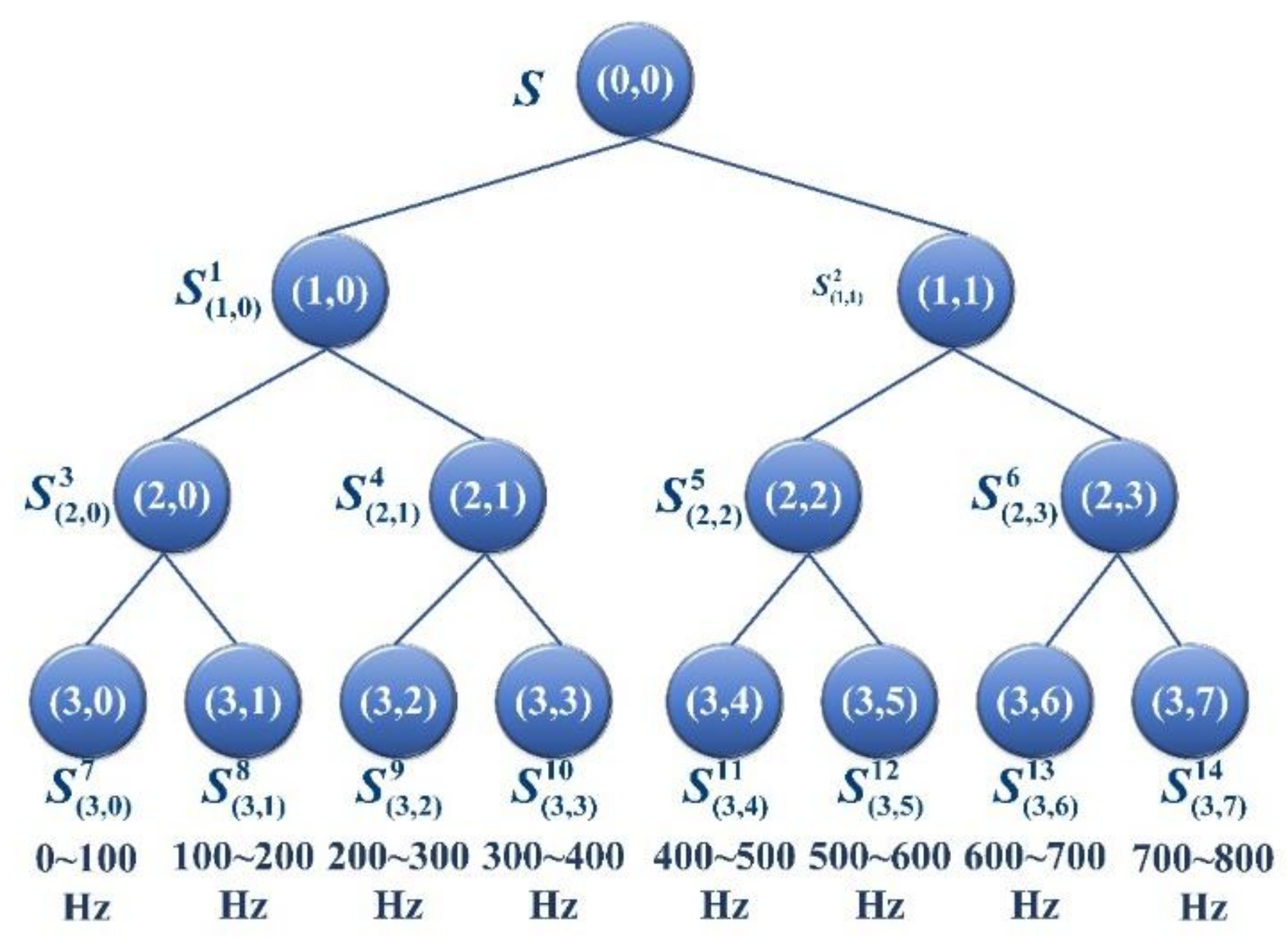
3.2.2. Wavelet Packet Decomposition (WPD)
3.2.3. Time Domain Indexes (TDI)
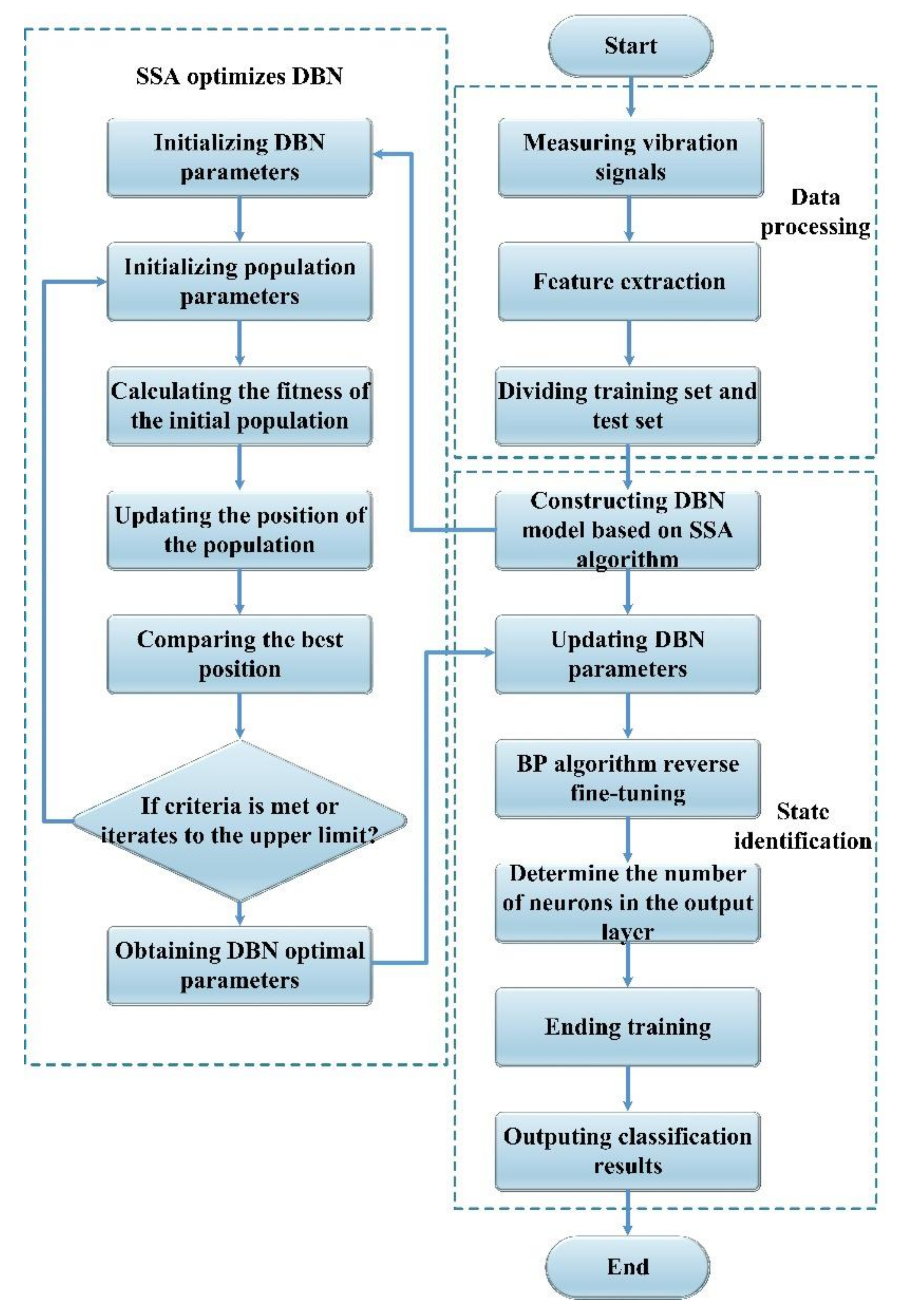
4. Deep Belief Network Optimization Algorithm
4.1. Deep Belief Network (DBN)
4.1.1. Restricted Boltzmann Machine (RBM)
4.1.2. Network Structure
4.2. Sparrow Search Algorithm (SSA)
4.2.1. Principle of the Algorithm
4.2.2. Mathematical Model of the Algorithm
4.2.3. Optimization Process of DBN
5. Experimental Verification
5.1. Experiment in the No-Load State
5.2. Experiment in the On-Load State
5.3. Validation on Extended Data Sets
5.3.1. Validation of Classification Accuracy
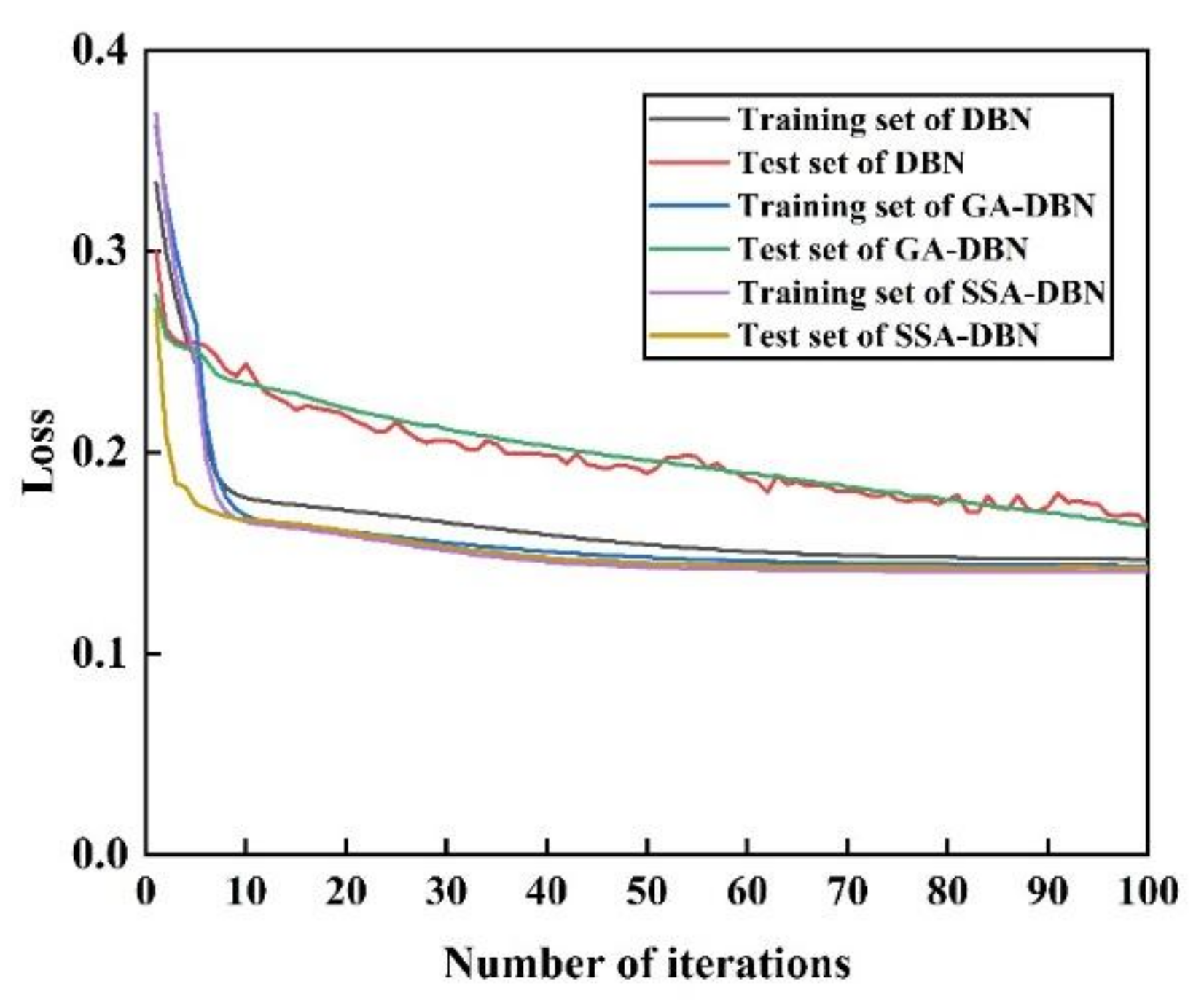
5.3.2. Fitting Effect Validation
6. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Experiment | Classification Algorithms | Optimal Parameters | Other Parameters (max) |
|---|---|---|---|
| No-load state | ELM | Number of hidden layer nodes: 5 Activation function: sigmoid | Number of hidden layer nodes: 4 Activation function: sigmoid |
| SVM | Penalty factor: 0.3 Radius of Gamma function: 0.05 Stop training error: 1 × 10−3 | Penalty factor: 0.2 Radius of Gamma function: 0.02 Stop training error: 1 × 10−3 | |
| BPNN | Network structure: 32 The learning rate: 0.1 | Network structure: 25 The learning rate: 0.1 | |
| DBN | Number of hidden layer nodes: 13,5 Learning rate: 0.14 Momentum factor: 0.9 Maximum number of iterations: 100 | Number of hidden layer nodes: 15,5 Learning rate: 0.16 Momentum factor: 0.87 Maximum number of iterations: 100 | |
| GA-DBN | Number of hidden layer nodes: 13,4 Learning rate: 0.18 Momentum factor: 0.84 Maximum number of iterations: 100 | Number of hidden layer nodes: 12,4 Learning rate: 0.20 Momentum factor: 0.76 Maximum number of iterations: 100 | |
| SSA-DBN | Number of hidden layer nodes: 13,5 Learning rate: 0.21 Momentum factor: 0.89 Maximum number of iterations: 100 | Number of hidden layer nodes: 11,8 Learning rate: 0.27 Momentum factor: 0.87 Maximum number of iterations: 100 | |
| On-load state | ELM | Number of hidden layer nodes: 5 Activation function: sigmoid | Number of hidden layer nodes: 3,8 Activation function: sigmoid |
| SVM | Penalty factor: 0.5 Radius of Gamma function: 0.2 Stop training error: 1 × 10−3 | Penalty factor: 0.4 Radius of Gamma function: 0.1 Stop training error: 1 × 10−3 | |
| BPNN | Number of hidden layer nodes: 15 The learning rate: 0.1 | Number of hidden layer nodes: 8 The learning rate: 0.1 | |
| DBN | Number of hidden layer nodes: 15,5 Learning rate: 0.16 Momentum factor: 0.76 Maximum number of iterations: 100 | Number of hidden layer nodes: 9,3 Learning rate: 0.15 Momentum factor: 0.53 Maximum number of iterations: 100 | |
| GA-DBN | Number of hidden layer nodes: 13,2 Learning rate: 0.14 Momentum factor: 0.88 Maximum number of iterations: 100 | Number of hidden layer nodes: 12,6 Learning rate: 0.13 Momentum factor: 0.85 Maximum number of iterations: 100 | |
| SSA-DBN | Number of hidden layer nodes: 10,3 Learning rate: 0.25 Momentum factor: 0.9 Maximum number of iterations: 100 | Number of hidden layer nodes: 12,4 Learning rate: 0.27 Momentum factor: 0.88 Maximum number of iterations: 100 | |
| Extended dataset | ELM | Number of hidden layer nodes: 5 Activation function: sigmoid | Number of hidden layer nodes: 4 Activation function: sigmoid |
| SVM | Penalty factor: 0.8 Radius of Gamma function: 0.02 Stop training error: 1 × 10−3 | Penalty factor: 0.2 Radius of Gamma function: 0.02 Stop training error: 1 × 10−3 | |
| BPNN | Number of hidden layer nodes: 50 The learning rate: 0.1 | Number of hidden layer nodes: 25 The learning rate: 0.1 | |
| DBN | Number of hidden layer nodes: 13,5 Learning rate: 0.1 Momentum factor: 0.5 Maximum number of iterations: 100 | Number of hidden layer nodes: 15,5 Learning rate: 0.16 Momentum factor: 0.87 Maximum number of iterations: 100 | |
| GA-DBN | Number of hidden layer nodes: 8,4 Learning rate: 0.1 Momentum factor: 0.5 Maximum number of iterations: 100 | Number of hidden layer nodes: 12,4 Learning rate: 0.20 Momentum factor: 0.76 Maximum number of iterations: 100 | |
| SSA-DBN | Number of hidden layer nodes: 13,5 Learning rate: 0.1 Momentum factor: 0.9 Maximum number of iterations: 100 | Number of hidden layer nodes: [11,8] Learning rate: 0.27 Momentum factor: 0.87 Maximum number of iterations: 100 |
| Feature Extraction Method | Classification Algorithms | Accuracy of the Training set (%) [Optimal Parameters/ Other Parameters (Max)] | Accuracy of the Test Set (%) [Optimal Parameters/ Other Parameters (Max)] |
|---|---|---|---|
| FFT | ELM | 76.6071/75.5357 | 77.5000/76.2500 |
| SVM | 91.9643/91.2500 | 100.0000/91.2500 | |
| BPNN | 73.5714/71.7857 | 75.0000/67.5000 | |
| DBN | 87.5000/87.2314 | 87.5000/82.5000 | |
| GA-DBN | 90.8929/89.1071 | 93.7500/86.2500 | |
| SSA-DBN | 91.7857/90.3571 | 100.0000/92.5000 | |
| WPD | ELM | 83.7500/82.5000 | 55.0000/50.0000 |
| SVM | 89.8214/89.2857 | 62.5000/51.2500 | |
| BPNN | 75.0000/73.5714 | 50.0000/41.2500 | |
| DBN | 85.7143/84.1071 | 78.7500/71.2500 | |
| GA-DBN | 79.4643/79.2857 | 87.5000/83.7500 | |
| SSA-DBN | 82.5000/81.9643 | 86.2500/81.2500 | |
| TDI | ELM | 77.6786/77.5000 | 31.2500/25.0000 |
| SVM | 80.3571/80.0000 | 50.0000/43.7500 | |
| BPNN | 83.9286/83.0357 | 37.0000/32.50000 | |
| DBN | 94.4643/93.0357 | 62.5000/50.0000 | |
| GA-DBN | 88.0357/86.6071 | 62.5000/51.2500 | |
| SSA-DBN | 90.3571/90.1786 | 70.0000/68.7500 | |
| FFT + WPD + TDI | ELM | 96.4286/94.6429 | 87.5000/81.2500 |
| SVM | 95.3571/94.4643 | 87.5000/80.0000 | |
| BPNN | 96.6071/95.5357 | 85.0000/72.5000 | |
| DBN | 100.0000/99.6429 | 91.2500/90.0000 | |
| GA-DBN | 100.0000/99.1071 | 92.5000/90.0000 | |
| SSA-DBN | 100.0000/98.7500 | 100.0000/97.5000 |
| Feature Extraction Method | Classification Algorithms | Accuracy of the Training Set (%) [Optimal Parameters/ Other Parameters (Max)] | Accuracy of the Test Set (%) [Optimal Parameters/ Other Parameters (Max)] |
|---|---|---|---|
| FFT | ELM | 67.1429/65.7143 | 70.0000/65.0000 |
| SVM | 69.6429/68.5714 | 67.5000/61.2500 | |
| BPNN | 81.4286/81.0714 | 80.0000/73.7500 | |
| DBN | 81.4286/80.1786 | 85.0000/73.7500 | |
| GA-DBN | 83.9286/82.6786 | 85.0000/77.5000 | |
| SSA-DBN | 82.5000/81.2500 | 87.5000/82.5000 | |
| WPD | ELM | 77.1429/76.6071 | 80.0000/76.2500 |
| SVM | 89.2857/89.1071 | 87.5000/83.7500 | |
| BPNN | 87.8571/87.5000 | 85.0000/78.7500 | |
| DBN | 82.1429/81.4286 | 90.0000/88.7500 | |
| GA-DBN | 95.7143/95.3571 | 92.5000/80.0000 | |
| SSA-DBN | 92.5000/91.4286 | 95.0000/91.2500 | |
| TDI | ELM | 62.8571/62.1429 | 77.5000/75.0000 |
| SVM | 75.3571/74.1071 | 82.5000/80.0000 | |
| BPNN | 86.0714/85.8929 | 85.0000/72.5000 | |
| DBN | 88.2143/87.8571 | 90.0000/85.0000 | |
| GA-DBN | 86.4286/84.6429 | 95.0000/87.5000 | |
| SSA-DBN | 90.3571/90.0000 | 100.0000/90.0000 | |
| FFT + WPD + TDI | ELM | 74.2857/73.5714 | 82.5000/77.5000 |
| SVM | 88.5714/87.3214 | 95.0000/88.7500 | |
| BPNN | 88.5714/87.5000 | 90.0000/80.0000 | |
| DBN | 98.9286/97.3214 | 97.5000/96.2500 | |
| GA-DBN | 97.8571/96.0714 | 100.0000/95.0000 | |
| SSA-DBN | 99.2857/97.5000 | 100.0000/95.0000 |
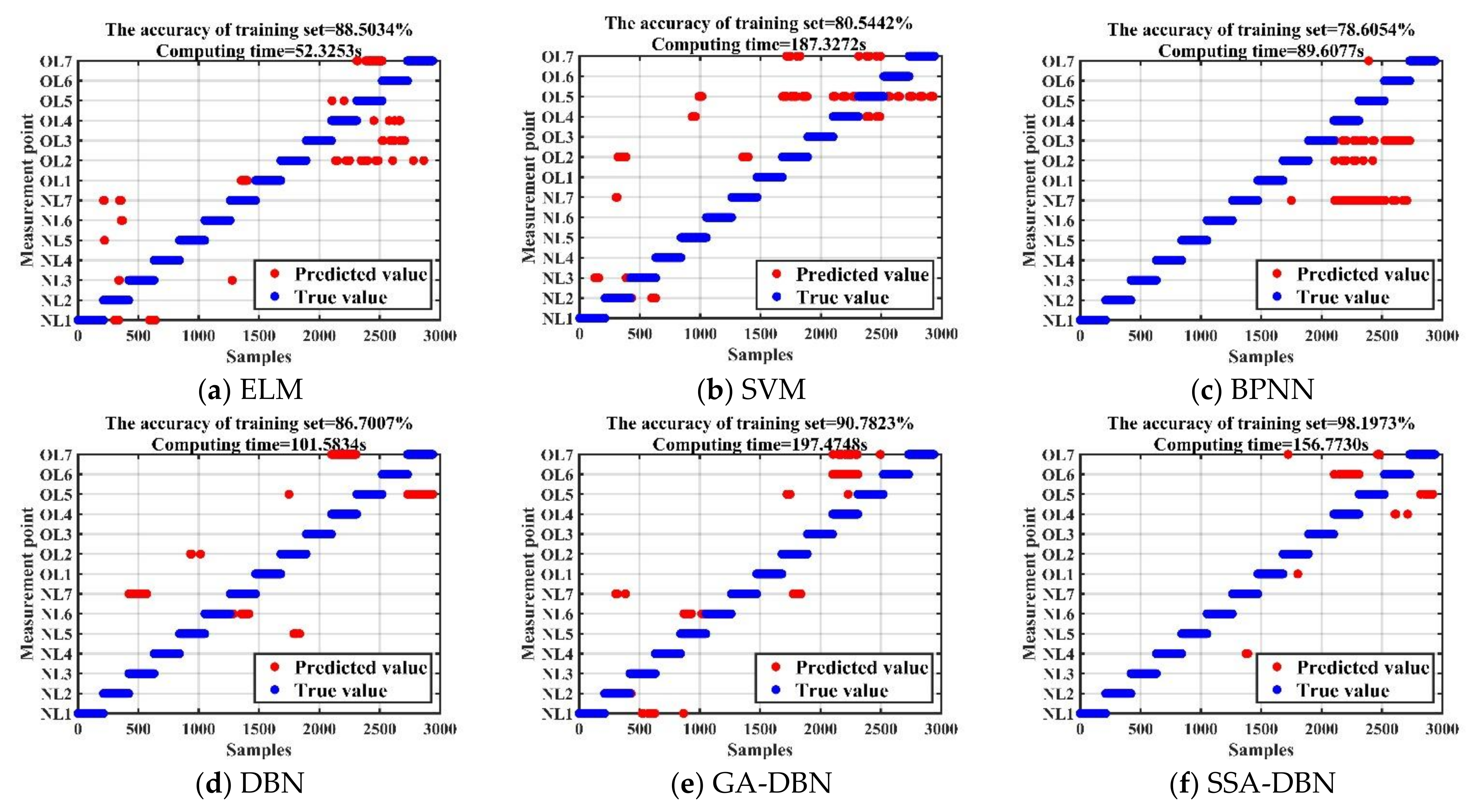
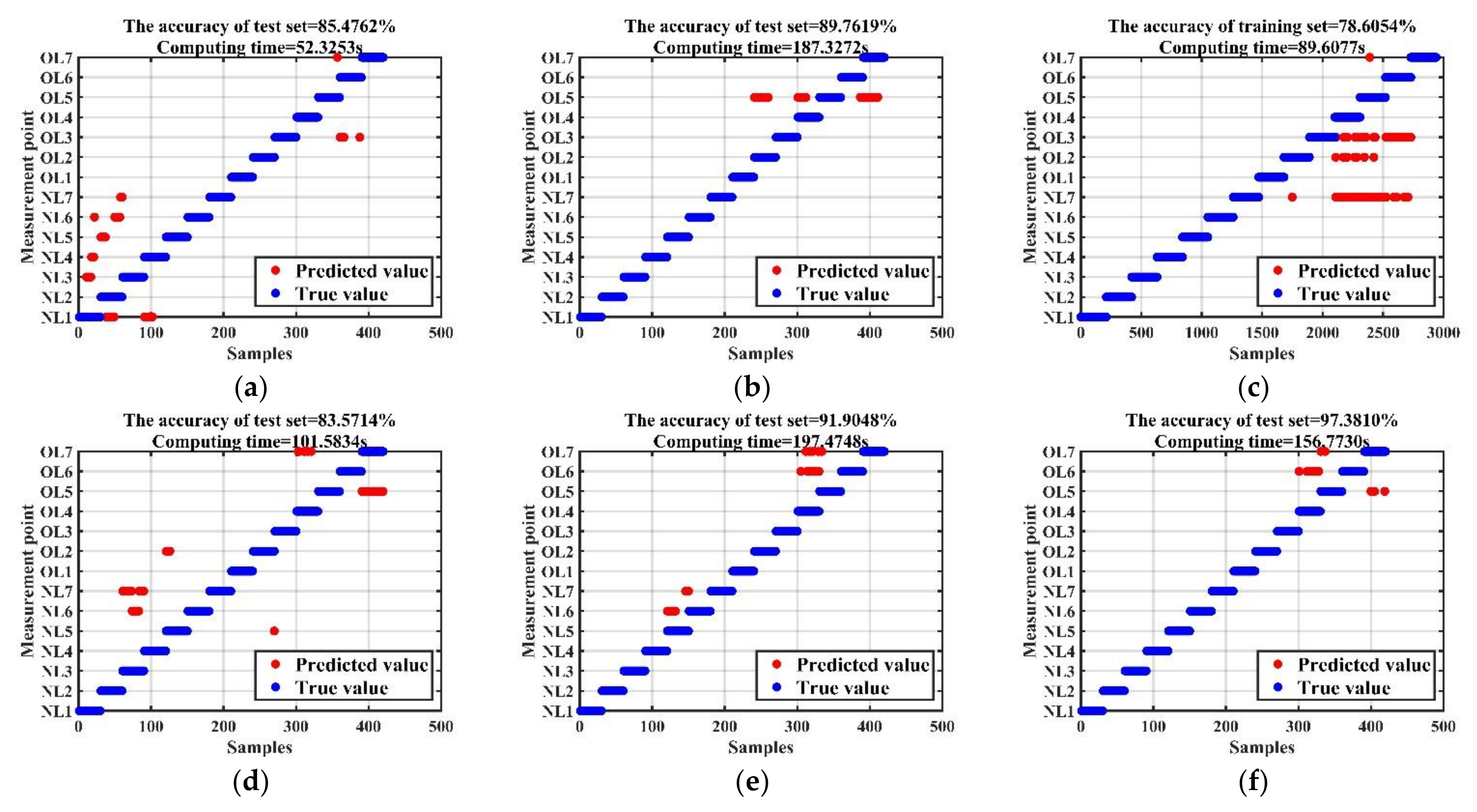
| Feature Extraction Method | Classification Algorithms | Accuracy of the Training Set (%) [Optimal Parameters/ Other Parameters (Max)] | Accuracy of the Test Set (%) [Optimal Parameters/ Other Parameters (Max)] |
|---|---|---|---|
| FFT + WPD + TDI | ELM | 88.5034/87.6531 | 85.4762/82.3810 |
| SVM | 80.5442/78.0612 | 89.7619/85.9524 | |
| BPNN | 78.6054/75.4762 | 89.6077/86.1905 | |
| DBN | 86.7007/83.7415 | 83.5714/79.0476 | |
| GA-DBN | 90.7823/88.0952 | 91.9048/87.3810 | |
| SSA-DBN | 98.1973/97.2449 | 97.3810/96.1905 |
References
- Bhuvaneswari, G.; Mahanta, B. Analysis of converter transformer failure in HVDC systems and possible solutions. IEEE Trans. Power Deliv. 2009, 24, 814–821. [Google Scholar] [CrossRef]
- Lin, X.; Lu, J.; Tian, Q.; Weng, H.; Li, Z.; Tong, C.; Li, M.; Sun, J.; Yang, D. Abnormal operation behavior analysis and countermeasures on the differential protection of converter transformer. Int. J. Electr. Power Energy Syst. 2015, 64, 516–525. [Google Scholar] [CrossRef]
- Londhe, S.S.; Bachawad, M.R. Review of harmonic losses in HVDC converter transformer: Its causes and mitigation techniques. In Proceedings of the Innovations in Power and Advanced Computing Technologies (i-PACT), Vellore, India, 21–22 April 2017; pp. 1–5. [Google Scholar]
- Zhang, X.; Huang, R.; Zhou, D.; Wang, F. In Vibration Monitoring of Converter Transformer by Simplified permutation Entropy. In Proceedings of the 2018 Chinese Automation Congress (CAC), Xi’an, China, 30 November–2 December 2018; pp. 864–869. [Google Scholar]
- Bagheri, M.; Naderi, M.S.; Blackburn, T. Advanced transformer winding deformation diagnosis: Moving from off-line to on-line. IEEE Trans. Dielectr. Electr. Insul. 2012, 19, 1860–1870. [Google Scholar] [CrossRef]
- Akhavanhejazi, M.; Gharehpetian, G.B.; Faraji-Dana, R.; Moradi, G.; Mohammadi, M.; Alehoseini, H.A. A new on-line monitoring method of transformer winding axial displacement based on measurement of scattering parameters and decision tree. Expert Syst. Appl. 2011, 38, 8886–8893. [Google Scholar] [CrossRef]
- Fan, J.; Wang, F.; Sun, Q.; Bin, F.; Ye, H.; Liu, Y. An online monitoring system for oil immersed power transformer based on SOFC detector with a new quantification approach. IEEE Sens. J. 2017, 17, 6662–6671. [Google Scholar] [CrossRef]
- Fan, J.; Fu, C.; Yin, H.; Wang, Y.; Jiang, Q. Power transformer condition assessment based on online monitor with SOFC chromatographic detector. Electr. Power Energy Syst. 2020, 118, 105805–105812. [Google Scholar] [CrossRef]
- Hejazi, M.; Gharehpetian, G.; Moradi, G.; Alehosseini, H.; Mohammadi, M. Online monitoring of transformer winding axial displacement and its extent using scattering parameters and k-nearest neighbour method. IET Gener. Transm. Distrib. 2011, 5, 824–832. [Google Scholar] [CrossRef]
- Joshi, P.; Kulkarni, S. A novel approach for on-line deformation diagnostics of transformer windings. In Proceedings of the IEEE PES General Meeting, Providence, RI, USA, 25–29 July 2010; pp. 1–6. [Google Scholar]
- Tang, L.; Luo, R.; Deng, M.; Su, J. Study of partial discharge localization using ultrasonics in power transformer based on particle swarm optimization. IEEE Trans. Dielectr. Electr. Insul. 2008, 15, 492–495. [Google Scholar]
- Hu, G.; Zhang, L.; Wu, X.; Correia, D.; He, W. Detecting the capacity of distribution transformer based on an on-line method. In Proceedings of the 2011 Asia-Pacific Power and Energy Engineering Conference, Xi’an, China, 25–28 March 2011; pp. 1–4. [Google Scholar]
- Palani, A.; Santhi, S.; Gopalakrishna, S.; Jayashankar, V. Real-time techniques to measure winding displacement in transformers during short-circuit tests. IEEE Trans. Power Deliv. 2008, 23, 726–732. [Google Scholar] [CrossRef]
- De Rybel, T.; Singh, A.; Vandermaar, J.A.; Wang, M.; Marti, J.R.; Srivastava, K.D. Apparatus for online power transformer winding monitoring using bushing tap injection. IEEE Trans. Power Deliv. 2009, 24, 996–1003. [Google Scholar] [CrossRef]
- Hong, K.; Huang, H.; Zhou, J. Winding condition assessment of power transformers based on vibration correlation. IEEE Trans. Power Deliv. 2014, 30, 1735–1742. [Google Scholar] [CrossRef]
- García, B.; Burgos, J.C.; Alonso, Á. Winding deformations detection in power transformers by tank vibrations monitoring. Electr. Power Syst. Res. 2005, 74, 129–138. [Google Scholar] [CrossRef]
- García, B.; Burgos, J.C.; Alonso, Á. Transformer tank vibration modeling as a method of detecting winding deformations-part I: Theoretical foundation. IEEE Trans. Power Deliv. 2005, 21, 157–163. [Google Scholar] [CrossRef]
- García, B.; Burgos, J.C.; Alonso, Á. Transformer tank vibration modeling as a method of detecting winding deformations-part II: Experimental verification. IEEE Trans. Power Deliv. 2005, 21, 164–169. [Google Scholar] [CrossRef]
- Zhang, F.; Ji, S.; Shi, Y.; Ren, F.; Zhan, C.; Zhu, L. Comprehensive vibration generation model of transformer winding under load current. IET Gener. Transm. Distrib. 2019, 13, 1563–1571. [Google Scholar] [CrossRef]
- Zhang, F.; Ji, S.; Ma, H.; Saha, T.K. Operational Modal Analysis of Transformer Windings. IEEE Trans. Power Deliv. 2020, 35, 1285–1298. [Google Scholar] [CrossRef]
- Zhou, H.; Hong, K.; Huang, H.; Zhou, J. Transformer winding fault detection by vibration analysis methods. Appl. Acoust. 2016, 114, 136–146. [Google Scholar] [CrossRef]
- Zhang, P.; Li, L.; Cheng, Z.; Tian, C.; Han, Y. Study on Vibration of Iron Core of Transformer and Reactor Based on Maxwell Stress and Anisotropic Magnetostriction. IEEE Trans. Magn. 2019, 55. [Google Scholar] [CrossRef]
- Khan, I.; Xu, Y.; Kar, S.; Chow, M.; Bhattacharjee, W. Compressive Sensing and Morphology Singular Entropy-Based Real-Time Secondary Voltage Control of Multiarea Power Systems. IEEE Trans. Ind. Inform. 2019, 15, 3796–3807. [Google Scholar] [CrossRef]
- Ji, S.; Luo, Y.; Li, Y. Research on extraction technique of transformer core fundamental frequency vibration based on OLCM. IEEE Trans. Power Deliv. 2006, 21, 1981–1988. [Google Scholar]
- Geng, C.; Wang, F.; Zhang, J.; Jin, Z. Modal parameters identification of power transformer winding based on improved empirical mode decomposition method. Electr. Power Syst. Res. 2014, 108, 331–339. [Google Scholar] [CrossRef]
- Borucki, S. Diagnosis of technical condition of power transformers based on the analysis of vibroacoustic signals measured in transient operating conditions. IEEE Trans. Power Deliv. 2012, 27, 670–676. [Google Scholar] [CrossRef]
- Zhao, M.; Xu, G. Feature extraction of power transformer vibration signals based on empirical wavelet transform and multiscale entropy. IET Sci. Meas. Technol. 2017, 12, 63–71. [Google Scholar] [CrossRef]
- Hong, K.; Wang, L.; Xu, S. A variational mode decomposition approach for degradation assessment of power transformer windings. IEEE Trans. Instrum. Meas. 2018, 68, 1221–1229. [Google Scholar] [CrossRef]
- Cao, C.; Xu, B.; Li, X. Monitoring Method on Loosened State and Deformational Fault of Transformer Winding Based on Vibration and Reactance Information. IEEE Access 2020, 8, 215479–215492. [Google Scholar] [CrossRef]
- Ghanizadeh, A.J.; Gharehpetian, G.B. ANN and cross-correlation based features for discrimination between electrical and mechanical defects and their localization in transformer winding. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 2374–2382. [Google Scholar] [CrossRef]
- Shah, A.M.; Bhalja, B.R. Discrimination between internal faults and other disturbances in transformer using the support vector machine-based protection scheme. IEEE Trans. Power Deliv. 2013, 28, 1508–1515. [Google Scholar] [CrossRef]
- Raichura, M.B.; Chothani, N.G.; Patel, D.D. Identification of internal fault against external abnormalities in power transformer using hierarchical ensemble extreme learning machine technique. IET Sci. Meas. Technol. 2019, 14, 111–121. [Google Scholar] [CrossRef]
- Shah, A.M.; Bhalja, B.R. Transmission; Distribution, Fault discrimination scheme for power transformer using random forest technique. IET Gener. Transm. Distrib. 2016, 10, 1431–1439. [Google Scholar] [CrossRef]
- Kartojo, I.H.; Wang, Y.B.; Zhang, G.J. Partial Discharge Defect Recognition in Power Transformer using Random Forest. In Proceedings of the 2019 IEEE 20th International Conference on Dielectric Liquids (ICDL), Roma, Italy, 15 August 2019; pp. 1–4. [Google Scholar]
- Dai, J.; Song, H.; Sheng, G.; Jiang, X. Dissolved gas analysis of insulating oil for power transformer fault diagnosis with deep belief network. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 2828–2835. [Google Scholar] [CrossRef]
- Liang, Y.; Xu, Y.Y.; Wan, X.S.; Li, Y.; Liu, N.; Zhang, G.J. Dissolved gas analysis of transformer oil based on deep belief networks. In Proceedings of the 2018 12th International Conference on the Properties and Applications of Dielectric Materials (ICPADM), Xi’an, China, 20–24 May 2018; pp. 825–828. [Google Scholar]
- Deng, H.B.; Hu, J.; Wang, X.S.; Yu, M. In Transformer fault diagnosis based on massive vibration data. In Proceedings of the 2019 Chinese Control And Decision Conference (CCDC), Nanchang, China, 12 September 2019; pp. 4586–4591. [Google Scholar]
- Hong, K.; Huang, H.; Zhou, J.; Shen, Y. A method of real-time fault diagnosis for power transformers based on vibration analysis. Meas. Sci. Technol. 2015, 26, 115011–115021. [Google Scholar] [CrossRef]
- Cao, C.; Xu, J.; Lin, X.; Li, X. State diagnosis method of transformer winding deformation based on fusing vibration and reactance parameters. IET Electr. Power Appl. 2019, 14, 818–826. [Google Scholar]
- Zhang, B.; Zhao, D.; Wang, F.; Shi, K.; Zhao, Z. Research on mechanical fault diagnosis method of power transformer winding. J. Eng. 2019, 16, 2096–2101. [Google Scholar]
- Zollanvari, A.; Kunanbayev, K.; Bitaghsir, S.A.; Bagheri, M. Transformer Fault Prognosis Using Deep Recurrent Neural Network Over Vibration Signals. IEEE Trans. Instrum. Meas. 2020, 70. [Google Scholar] [CrossRef]
- Hong, K.; Lin, G. State classification of transformers using nonlinear dynamic analysis and Hidden Markov models. Measurement 2019, 147, 106851–106860. [Google Scholar] [CrossRef]
- Zhang, F.; Ji, S.; Shi, Y.; Zhan, C.; Zhu, L. Investigation on vibration source and transmission characteristics in power transformers. Appl. Acoust. 2019, 151, 99–112. [Google Scholar] [CrossRef]
- Shao, P.; Luo, L.; Li, Y.; Rehtanz, C. Electromagnetic vibration analysis of the winding of a new HVDC converter transformer. IEEE Trans. Power Deliv. 2011, 27, 123–130. [Google Scholar] [CrossRef]
- Xu, J.; Zhou, J.; Yang, Y. Research on vibration and noise characteristic of converter transformer under DC bias. In Proceedings of the 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 1–5. [Google Scholar]
- Liu, C.; Jin, M.; Tian, H.; Zhou, X.; Zhao, Y.; Chen, W. Converter transformer vibration analysis for ±800KV Fengxian HVDC substation. In Proceedings of the 2016 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Chengdu, China, 29 December 2016; pp. 1–3. [Google Scholar]
- Secic, A.; Krpan, M.; Kuzle, I. Vibro-Acoustic Methods in the Condition Assessment of Power Transformers, A. Survey. IEEE Access 2019, 7, 83915–83931. [Google Scholar] [CrossRef]
- Zou, L.; Guo, Y.; Liu, H.; Zhang, L.; Zhao, T. A Method of Abnormal States Detection Based on Adaptive Extraction of Transformer Vibro-Acoustic Signals. Energies 2017, 10, 12. [Google Scholar] [CrossRef]
- Hu, Y.; Zheng, J.; Huang, H. Experimental Research on Power Transformer Vibration Distribution under Different Winding Defect Conditions. Electronics 2019, 8, 842. [Google Scholar] [CrossRef]
- Bagheri, M.; Zollanvari, A.; Nezhivenko, S. Transformer fault condition prognosis using vibration signals over cloud environment. IEEE Access 2018, 6, 9862–9874. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, Y.; Zhang, R.; Jiang, P.; Dong, Z.J.; Liu, G.; Ahmed, S. Novel Transformer Fault Identification Optimization Method Based on Mathematical Statistics. Mathematics 2019, 7, 288. [Google Scholar] [CrossRef]
- Huerta-Rosales, J.R.; Granados-Lieberman, D.; Amezquita-Sanchez, J.P.; Camarena-Martinez, D.; Valtierra-Rodriguez, M. Vibration Signal Processing-Based Detection of Short-Circuited Turns in Transformers: A Nonlinear Mode Decomposition Approach. Mathematics 2020, 8, 575. [Google Scholar] [CrossRef]
- Cheng, Q.; Zhao, Z.; Tang, C.; Qian, G.; Islam, S. Diagnostic of transformer winding deformation fault types using continuous wavelet transform of pulse response. Measurement 2019, 140, 197–206. [Google Scholar] [CrossRef]
- Chan, J.C.; Ma, H.; Saha, T.K. Time-frequency sparsity map on automatic partial discharge sources separation for power transformer condition assessment. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 2271–2283. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.-W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Hinton, G.E. Training products of experts by minimizing contrastive divergence. Neural Comput. 2002, 14, 1771–1800. [Google Scholar] [CrossRef] [PubMed]
- Larochelle, H.; Erhan, D.; Courville, A.; Bergstra, J.; Bengio, Y. An empirical evaluation of deep architectures on problems with many factors of variation. In Proceedings of the 24th international conference on Machine learning, New York, NY, USA, 20–24 June 2007; pp. 473–480. [Google Scholar]
- Xue, J.; Shen, B.J.S.S.; Engineering, C. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control. Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]




| Parameters | Value | |
|---|---|---|
| Type | ZZDFPZ-480000/500-400 | |
| Rated capacity | 480,000 kVA | |
| Voltage combination | kV | |
| Connection group | Ii0 | |
| Rated current | 1583.6/3408 A | |
| Rated frequency | 50 Hz | |
| Cooling mode | ODAF | |
| Insulation level (terminal of grid side) | 1.1 | SI/LI/LIC/AC 1175/1550/1705/680 kV |
| 1.2 | LI/AC 185/95 kV | |
| 2.1 | SI/LI/LIC/AC/DC/PR 1050/1300/1430/441/624/ 520/+240/−520 kV | |
| 2.2 | ||
| Type | Index | Parameters |
|---|---|---|
| IEPE piezoelectric acceleration sensor | Frequency response | 1 Hz~50 kHz |
| Range | 100 m/s2 | |
| Sensitivity | <10 mV/mos−2 | |
| Working temperature | −40 °C~120 °C | |
| PSt150/4/7 VS9 piezoelectric actuator | Nominal stroke | 9 μm ± 10% |
| Stiffness | 25 N/μm ± 20% | |
| Electrostatic capacity | 0.17 μF ± 20% | |
| Push/Pull | 20 N | |
| DH5902N data acquisition instrument | Sampling frequency | 20 kHz |
| Dynamic range | >100 dB | |
| Flatness of frequency response | ±1 dB | |
| Error | ±1 dB |
| Operation State | Voltages | Sample Number of Training Set | Sample Number of Test Set |
|---|---|---|---|
| No-load | 112.7 kV | 70 | 10 |
| 126.0 kV | 70 | 10 | |
| 140.9 kV | 70 | 10 | |
| 150.0 kV | 70 | 10 | |
| 152.0 kV | 70 | 10 | |
| 154.0 kV | 70 | 10 | |
| 154.9 kV | 70 | 10 | |
| 155.0 kV | 70 | 10 |
| Feature Extraction Method | Classification Algorithms | Accuracy of the Training Set (%) | Accuracy of the Test Set (%) | Computing Time (s) | Time Required for One Interation (s) |
|---|---|---|---|---|---|
| FFT | ELM | 76.6071 | 77.5000 | 40.7840 | 0.4078 |
| SVM | 91.9643 | 100.0000 | 42.0014 | 0.4200 | |
| BPNN | 73.5714 | 75.0000 | 25.7155 | 0.2572 | |
| DBN | 87.5000 | 87.5000 | 31.8840 | 0.3188 | |
| GA-DBN | 90.8929 | 93.7500 | 37.6975 | 0.3770 | |
| SSA-DBN | 91.7857 | 100.0000 | 34.2250 | 0.3423 | |
| WPD | ELM | 83.7500 | 55.0000 | 48.3214 | 0.4832 |
| SVM | 89.8214 | 62.5000 | 43.0044 | 0.4300 | |
| BPNN | 75.0000 | 50.0000 | 28.6184 | 0.2862 | |
| DBN | 85.7143 | 78.7500 | 31.1120 | 0.3111 | |
| GA-DBN | 79.4643 | 87.5000 | 38.0587 | 0.3806 | |
| SSA-DBN | 82.5000 | 86.2500 | 33.5362 | 0.3354 | |
| TDI | ELM | 77.6786 | 31.2500 | 38.2154 | 0.3822 |
| SVM | 80.3571 | 50.0000 | 50.3827 | 0.5038 | |
| BPNN | 83.9286 | 37.0000 | 29.1303 | 0.2913 | |
| DBN | 94.4643 | 62.5000 | 30.1976 | 0.3020 | |
| GA-DBN | 88.0357 | 62.5000 | 37.4445 | 0.3744 | |
| SSA-DBN | 90.3571 | 70.0000 | 35.0705 | 0.3507 | |
| FFT + WPD + TDI | ELM | 96.4286 | 87.5000 | 38.2773 | 0.3828 |
| SVM | 95.3571 | 87.5000 | 44.8157 | 0.4482 | |
| BPNN | 96.6071 | 85.0000 | 30.2692 | 0.3027 | |
| DBN | 100.0000 | 91.2500 | 33.4748 | 0.3347 | |
| GA-DBN | 100.0000 | 92.5000 | 41.5972 | 0.4160 | |
| SSA-DBN | 100.0000 | 100.0000 | 38.0185 | 0.3802 |
| Operation State | Currents | Sample Number of Training Set | Sample Number of Test Set |
|---|---|---|---|
| On-load | 1130 A | 70 | 10 |
| 1470 A | 70 | 10 | |
| 1910 A | 70 | 10 | |
| 1920 A | 70 | 10 |
| Feature Extraction Method | Classification Algorithms | Accuracy of the Training Set (%) | Accuracy of the Test Set (%) | Computing Time (s) | Time required for One Iteration (s) |
|---|---|---|---|---|---|
| FFT | ELM | 67.1429 | 70.0000 | 40.6442 | 0.4064 |
| SVM | 69.6429 | 67.5000 | 44.4661 | 0.4447 | |
| BPNN | 81.4286 | 80.0000 | 56.2929 | 0.5630 | |
| DBN | 81.4286 | 85.0000 | 32.0962 | 0.3210 | |
| GA-DBN | 83.9286 | 85.0000 | 40.9089 | 0.4091 | |
| SSA-DBN | 82.5000 | 87.5000 | 26.5524 | 0.2655 | |
| WPD | ELM | 77.1429 | 80.0000 | 50.2813 | 0.5028 |
| SVM | 89.2857 | 87.5000 | 46.2522 | 0.4625 | |
| BPNN | 87.8571 | 85.0000 | 64.3886 | 0.6439 | |
| DBN | 82.1429 | 90.0000 | 32.3561 | 0.3236 | |
| GA-DBN | 95.7143 | 92.5000 | 40.4619 | 0.4046 | |
| SSA-DBN | 92.5000 | 95.0000 | 28.2966 | 0.2830 | |
| TDI | ELM | 62.8571 | 77.5000 | 38.4253 | 0.3843 |
| SVM | 75.3571 | 82.5000 | 45.1797 | 0.4518 | |
| BPNN | 86.0714 | 85.0000 | 67.6195 | 0.6762 | |
| DBN | 88.2143 | 90.0000 | 32.3176 | 0.3232 | |
| GA-DBN | 86.4286 | 95.0000 | 37.0466 | 0.3705 | |
| SSA-DBN | 90.3571 | 100.0000 | 27.1930 | 0.2719 | |
| FFT + WPD + TDI | ELM | 74.2857 | 82.5000 | 38.9372 | 0.3894 |
| SVM | 88.5714 | 95.0000 | 45.0065 | 0.4501 | |
| BPNN | 88.5714 | 90.0000 | 68.1634 | 0.6816 | |
| DBN | 98.9286 | 97.5000 | 35.6022 | 0.3560 | |
| GA-DBN | 97.8571 | 100.0000 | 40.1203 | 0.4012 | |
| SSA-DBN | 99.2857 | 100.0000 | 31.4603 | 0.3146 |
| Operation State | Measurement Points | Sample Number of Training Set | Sample Number of Test Set |
|---|---|---|---|
| No-load | NL1 | 210 | 30 |
| NL2 | 210 | 30 | |
| NL3 | 210 | 30 | |
| NL4 | 210 | 30 | |
| NL5 | 210 | 30 | |
| NL6 | 210 | 30 | |
| NL7 | 210 | 30 | |
| On-load | OL1 | 210 | 30 |
| OL2 | 210 | 30 | |
| OL3 | 210 | 30 | |
| OL4 | 210 | 30 | |
| OL5 | 210 | 30 | |
| OL6 | 210 | 30 | |
| OL7 | 210 | 30 |
| Algorithms | Time Required for One Iteration (s) |
|---|---|
| DBN | 1.0158 |
| GA-DBN | 1.9747 |
| SSA-DBN | 1.5677 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Zhang, Z.; Xiao, R.; Jiang, P.; Dong, Z.; Deng, J. Operation State Identification Method for Converter Transformers Based on Vibration Detection Technology and Deep Belief Network Optimization Algorithm. Actuators 2021, 10, 56. https://doi.org/10.3390/act10030056
Wu Y, Zhang Z, Xiao R, Jiang P, Dong Z, Deng J. Operation State Identification Method for Converter Transformers Based on Vibration Detection Technology and Deep Belief Network Optimization Algorithm. Actuators. 2021; 10(3):56. https://doi.org/10.3390/act10030056
Chicago/Turabian StyleWu, Yongye, Zhanlong Zhang, Rui Xiao, Peiyu Jiang, Zijian Dong, and Jun Deng. 2021. "Operation State Identification Method for Converter Transformers Based on Vibration Detection Technology and Deep Belief Network Optimization Algorithm" Actuators 10, no. 3: 56. https://doi.org/10.3390/act10030056
APA StyleWu, Y., Zhang, Z., Xiao, R., Jiang, P., Dong, Z., & Deng, J. (2021). Operation State Identification Method for Converter Transformers Based on Vibration Detection Technology and Deep Belief Network Optimization Algorithm. Actuators, 10(3), 56. https://doi.org/10.3390/act10030056







