Actuator Fault Tolerant Control of Variable Cycle Engine Using Sliding Mode Control Scheme
Abstract
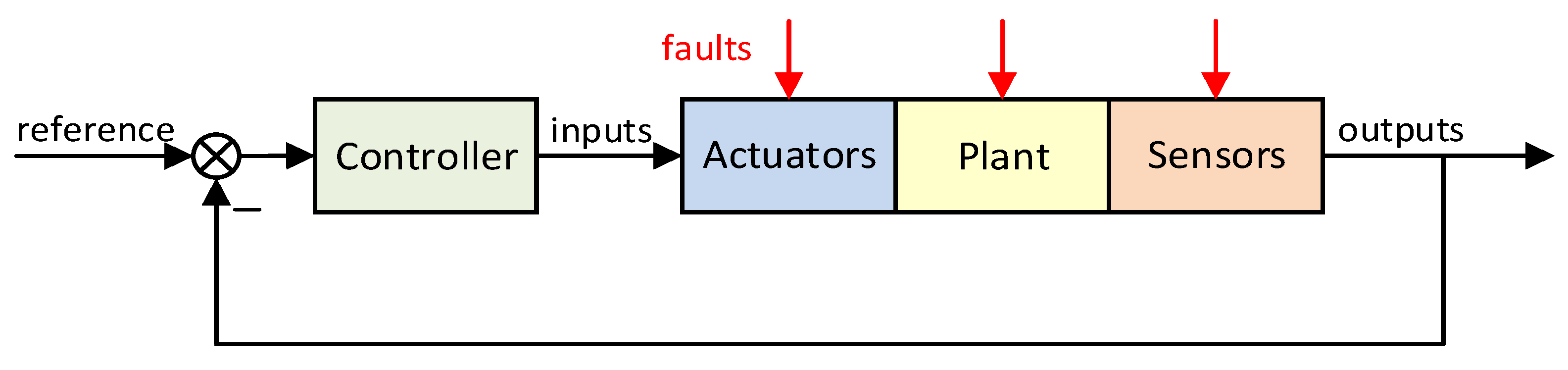
1. Introduction
2. Actuator Fault Tolerant Control Design
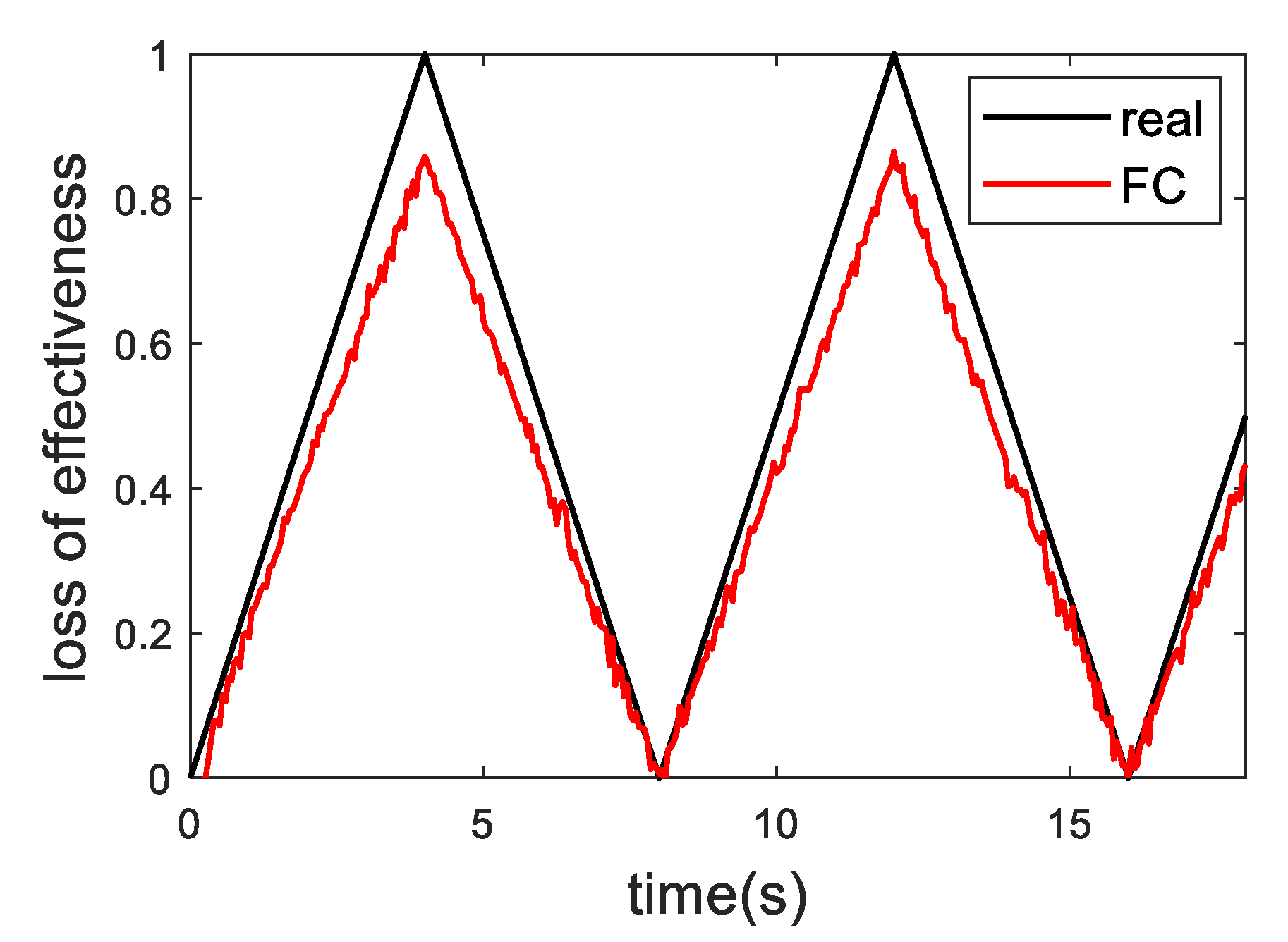
2.1. Fault Reconstruction
2.2. Fault Tolerant Control
- (1)
- If one of the two cases has a solution, the other one will also.
- (2)
- The two cases have the same control effect on the system.
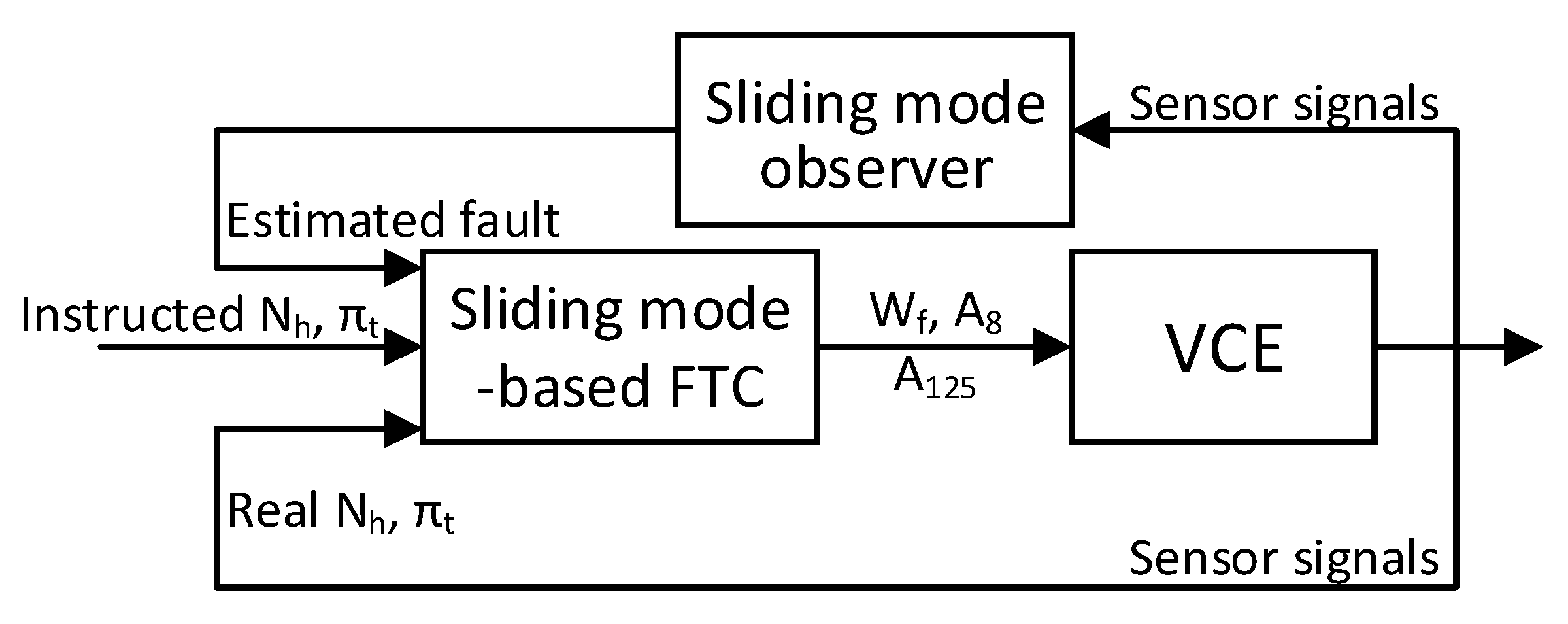
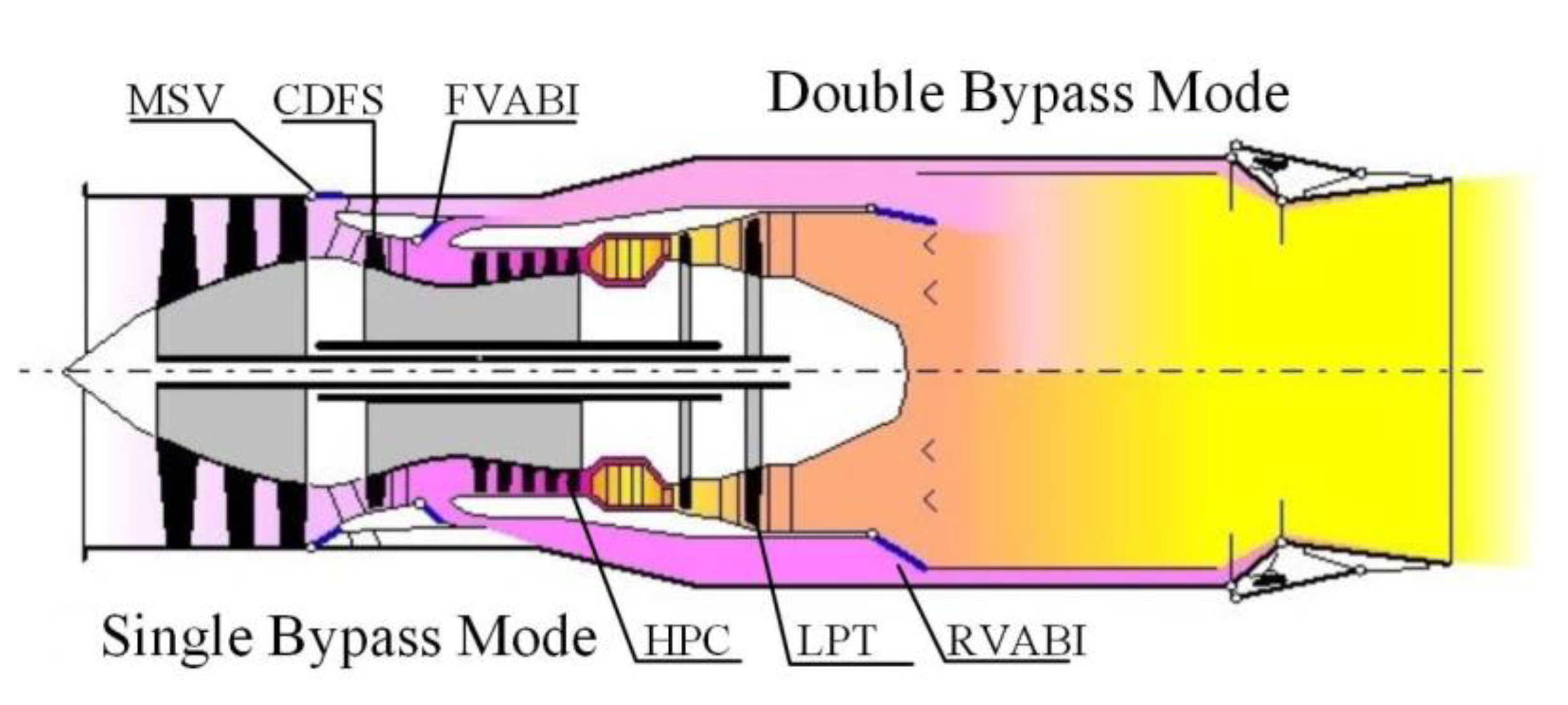
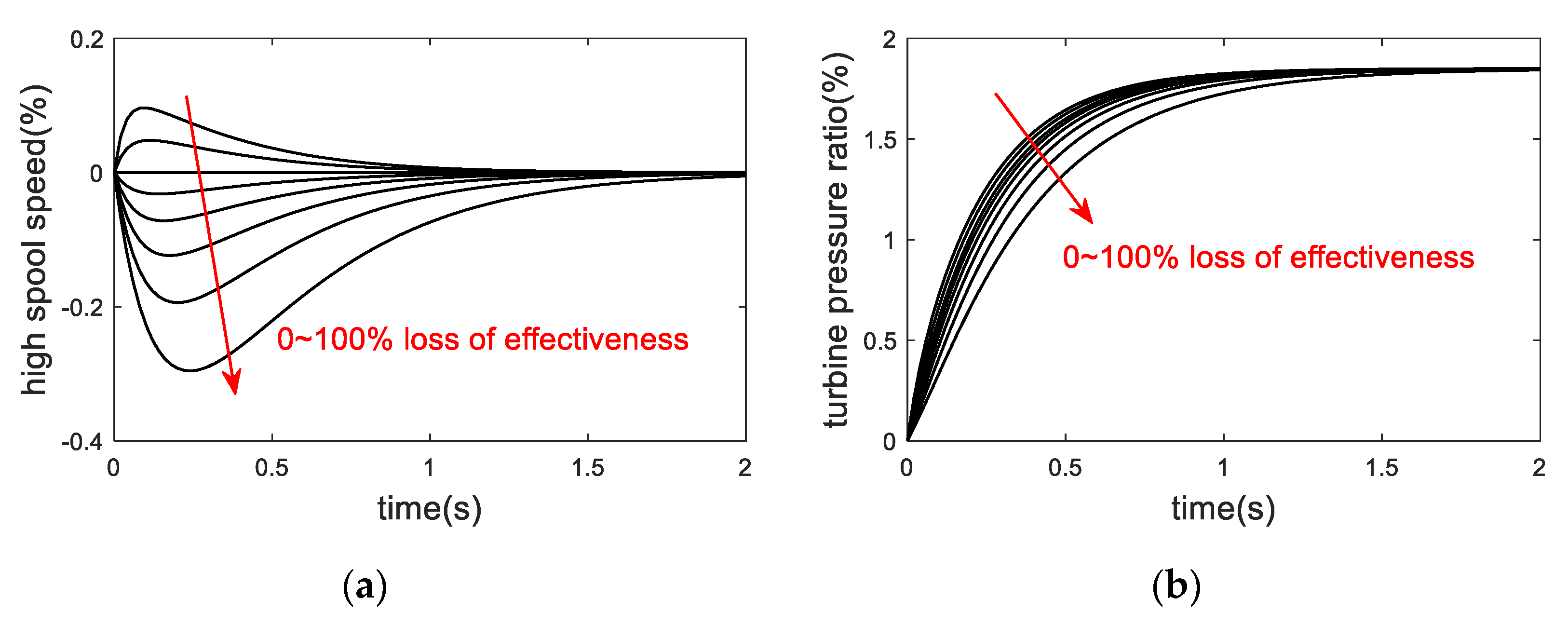
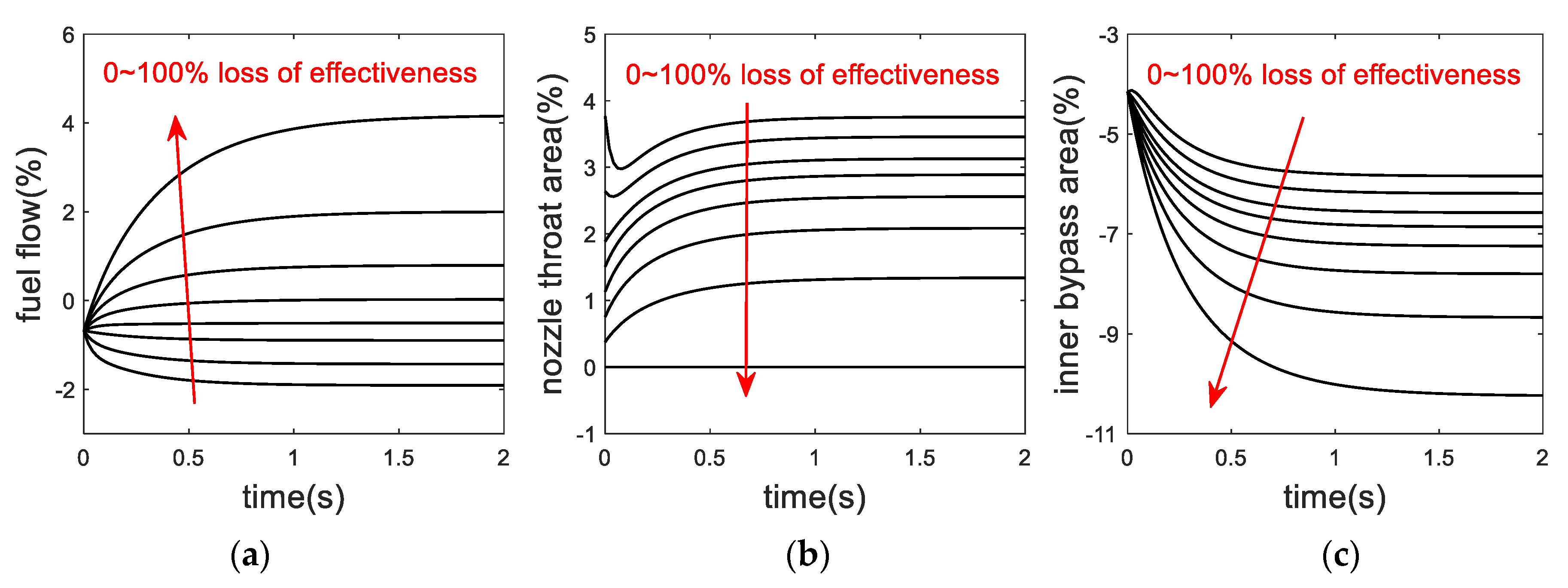
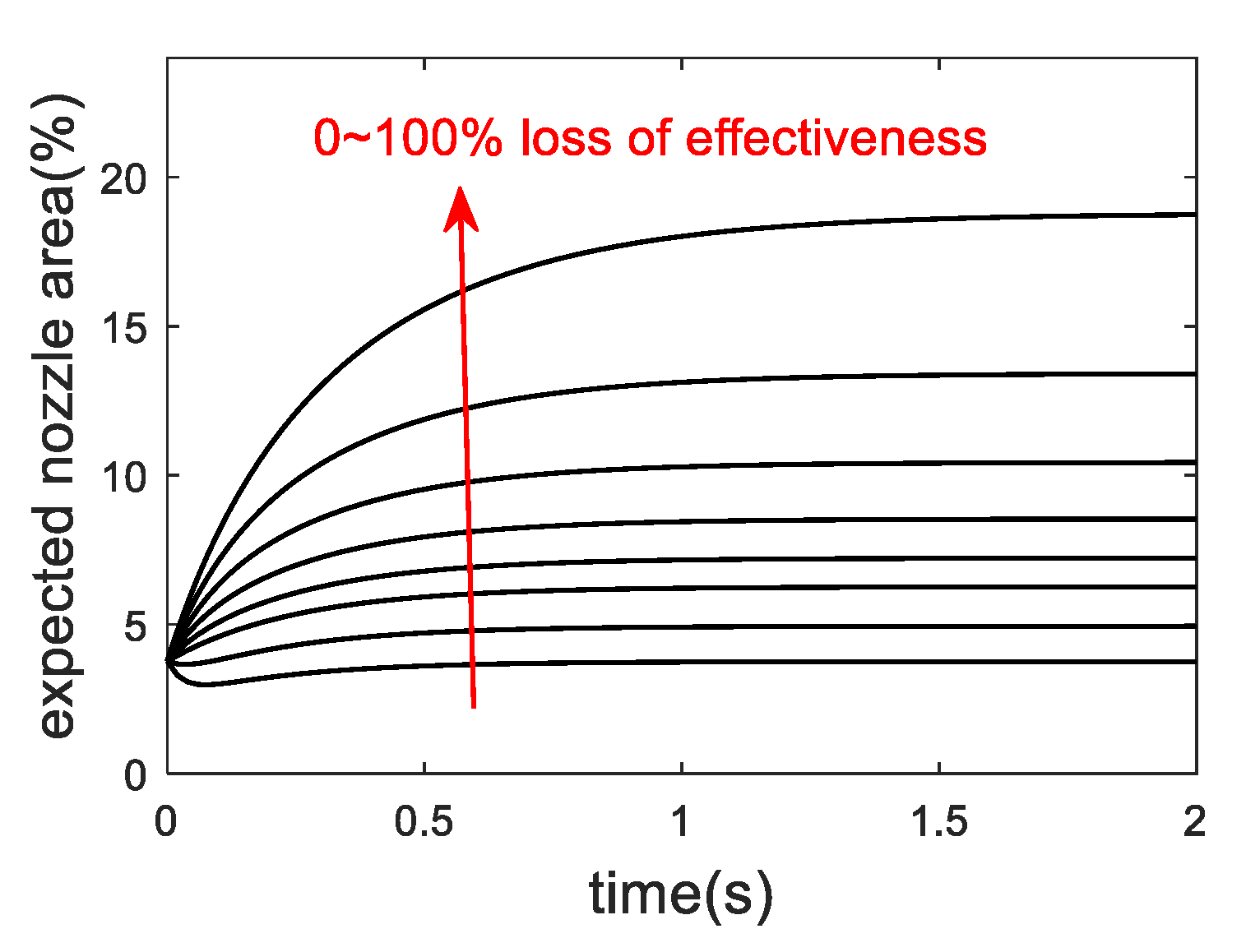
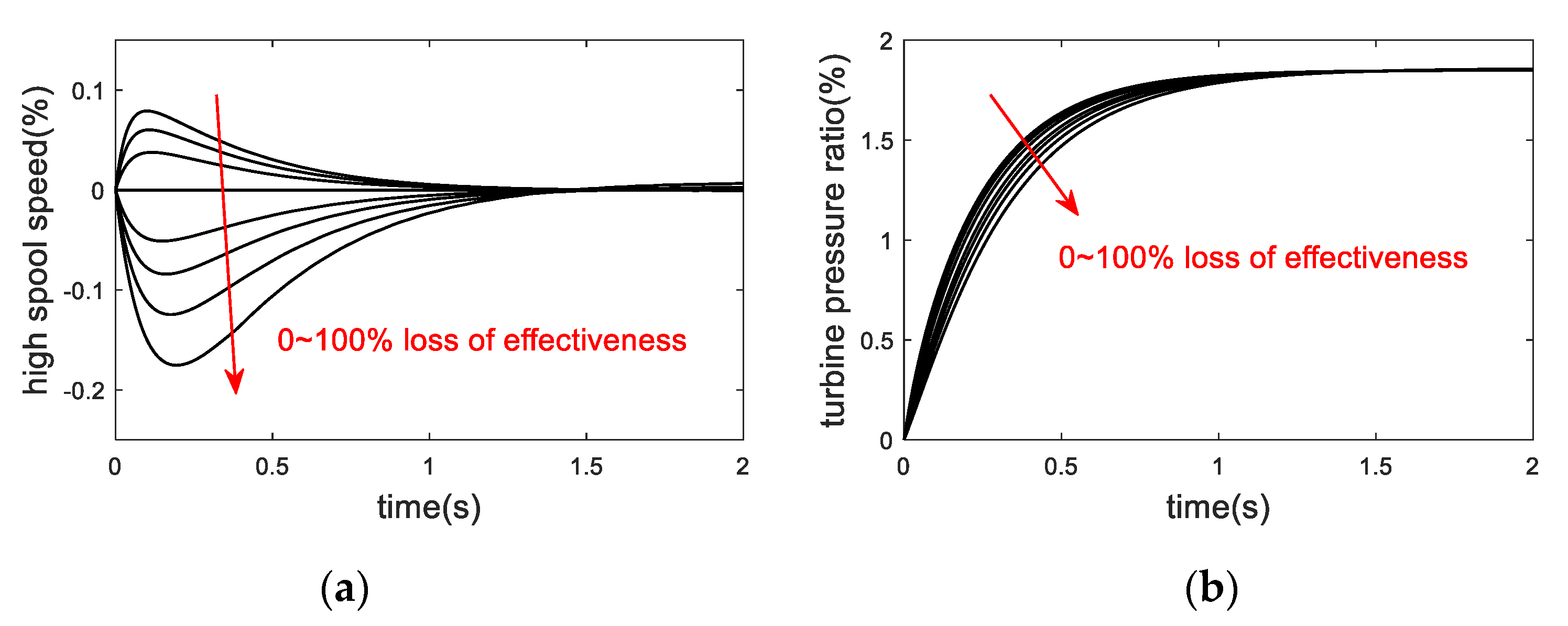
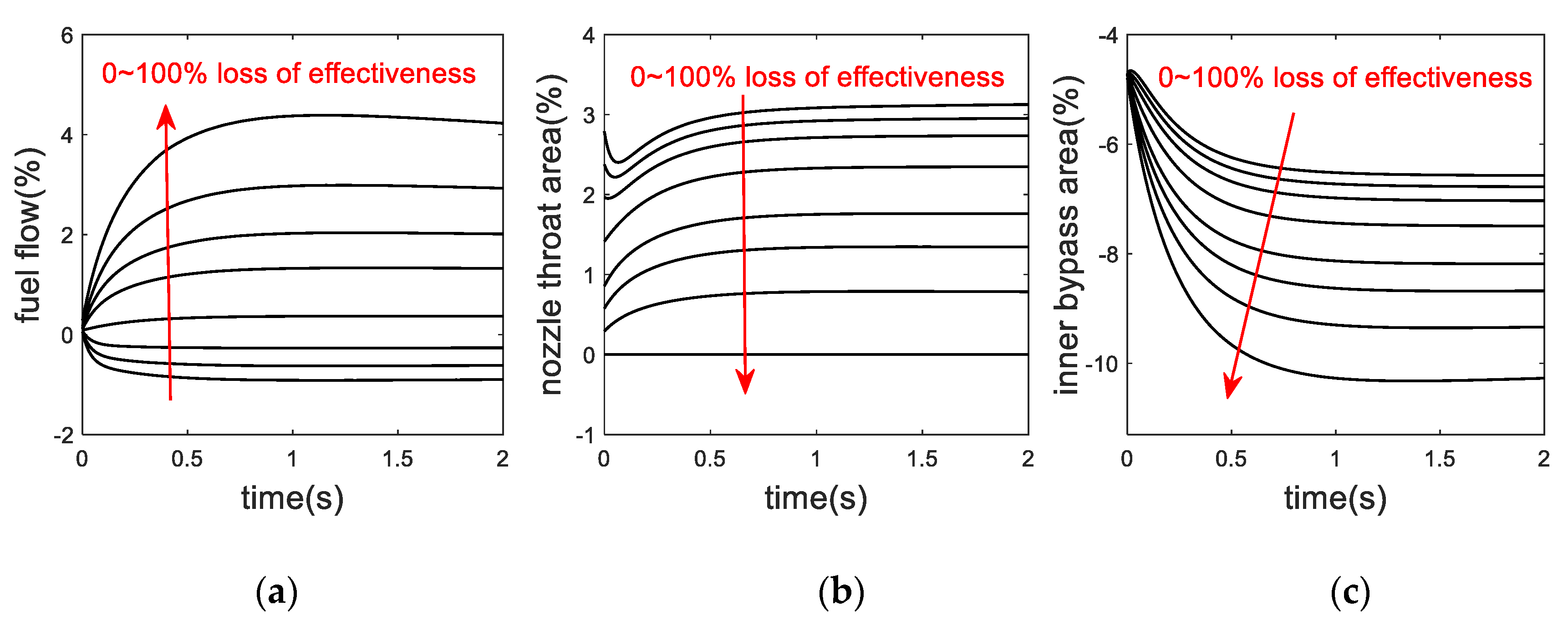
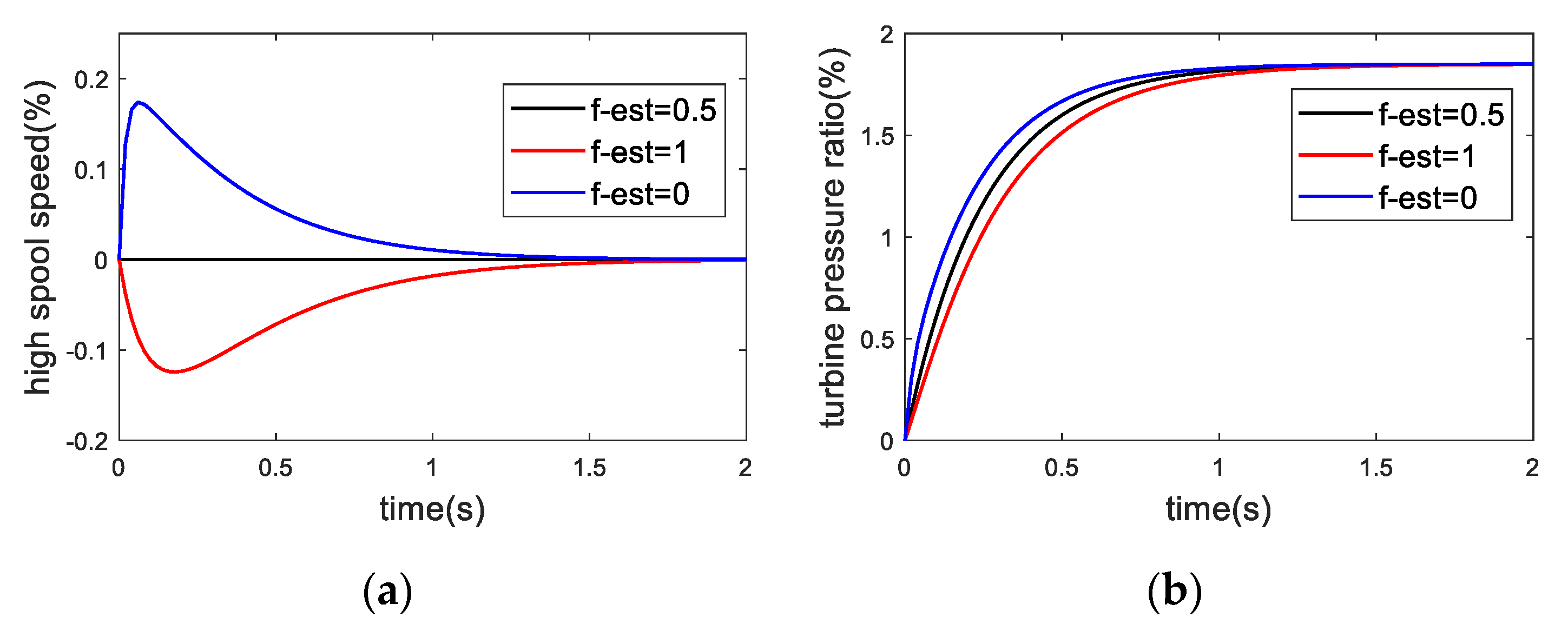
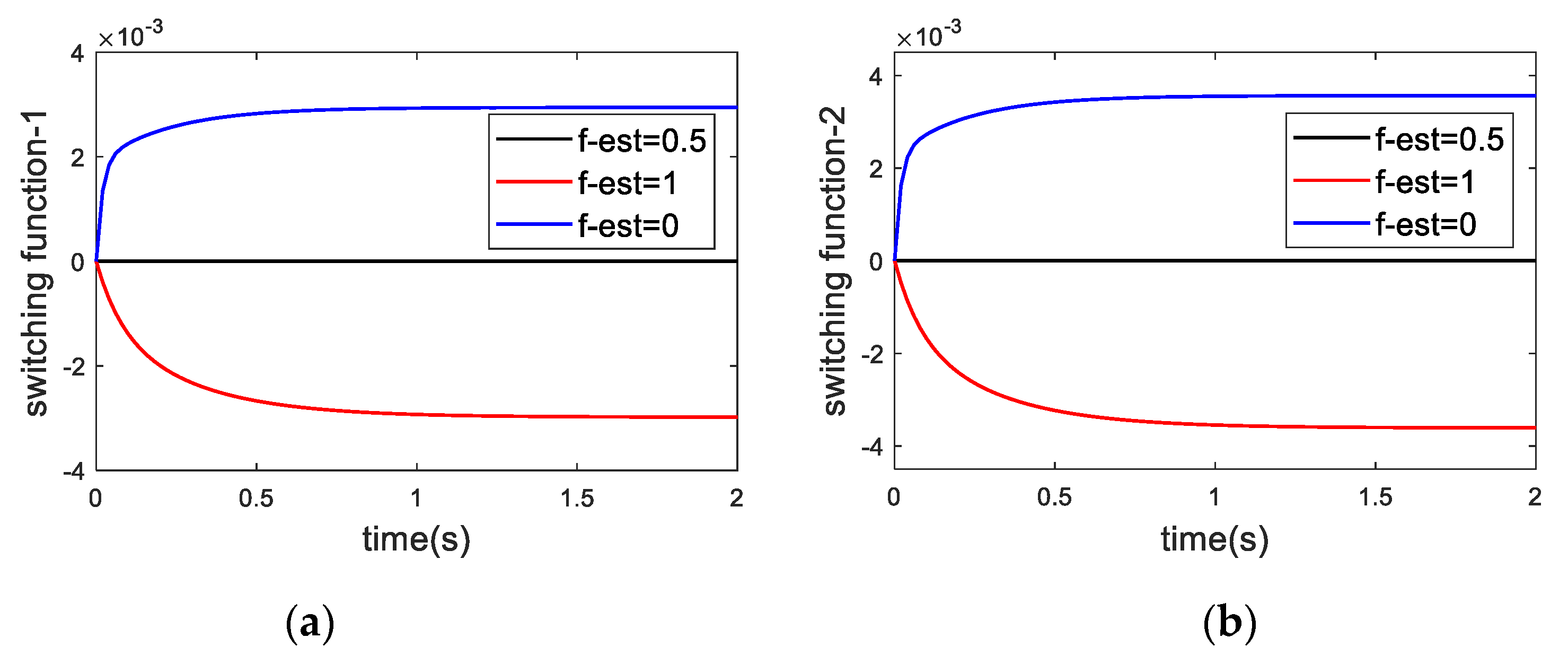
3. FTC Application in VCE
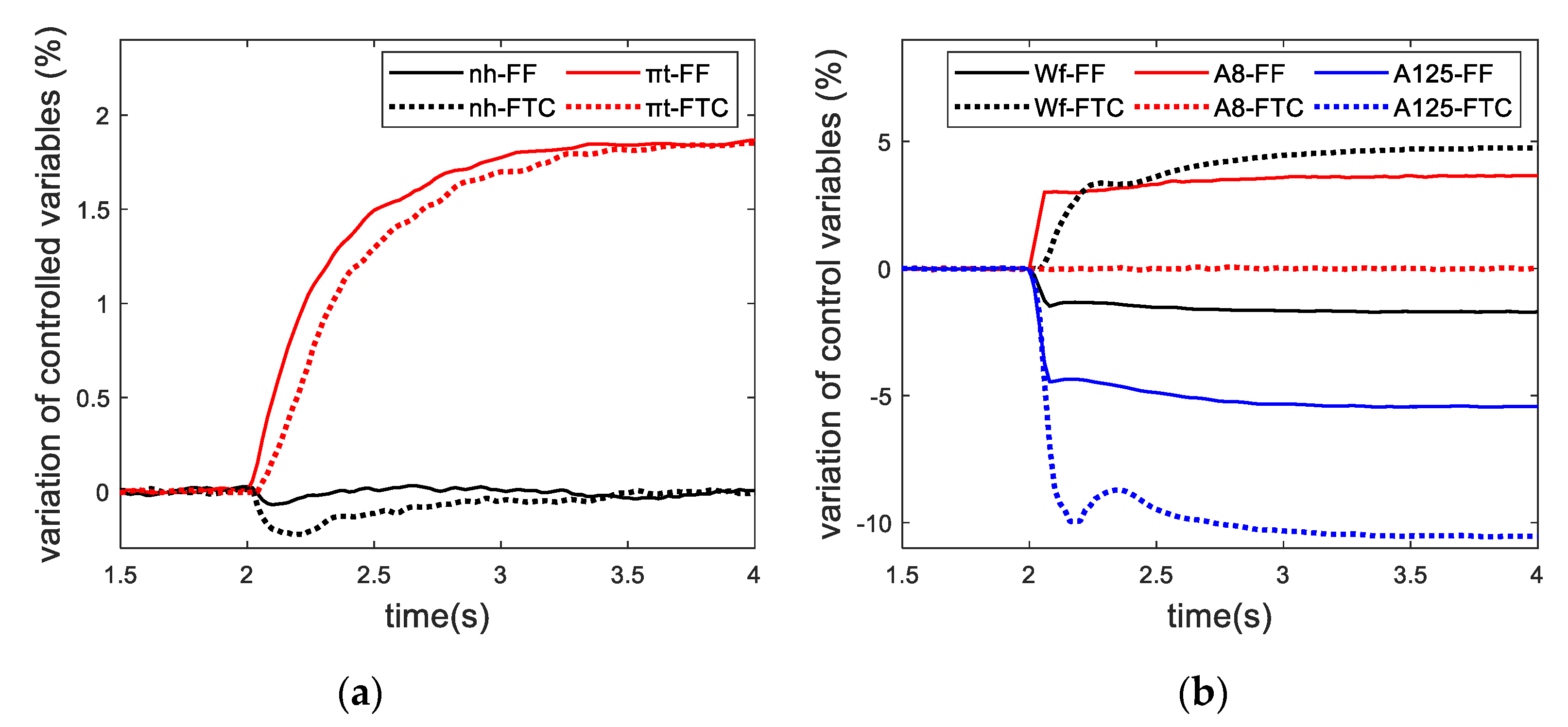
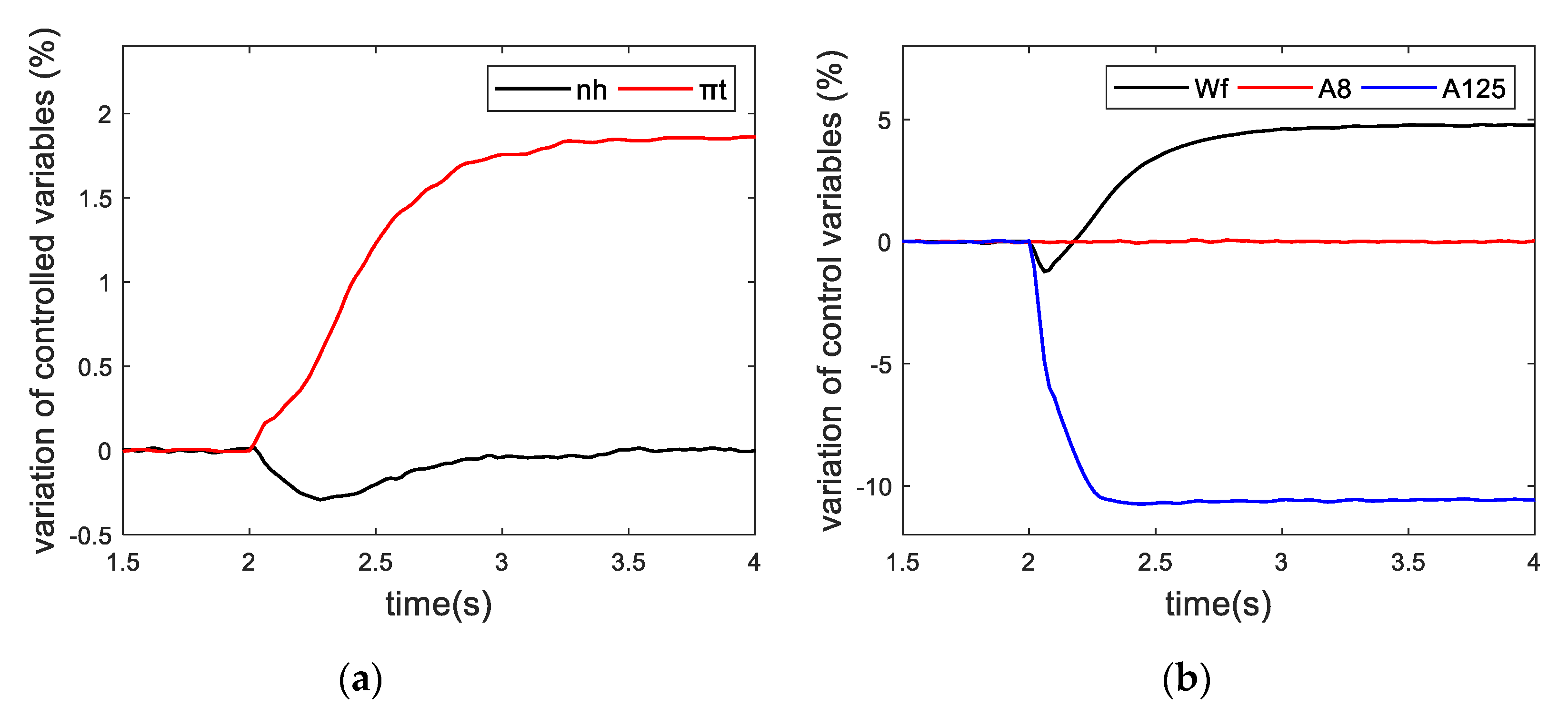
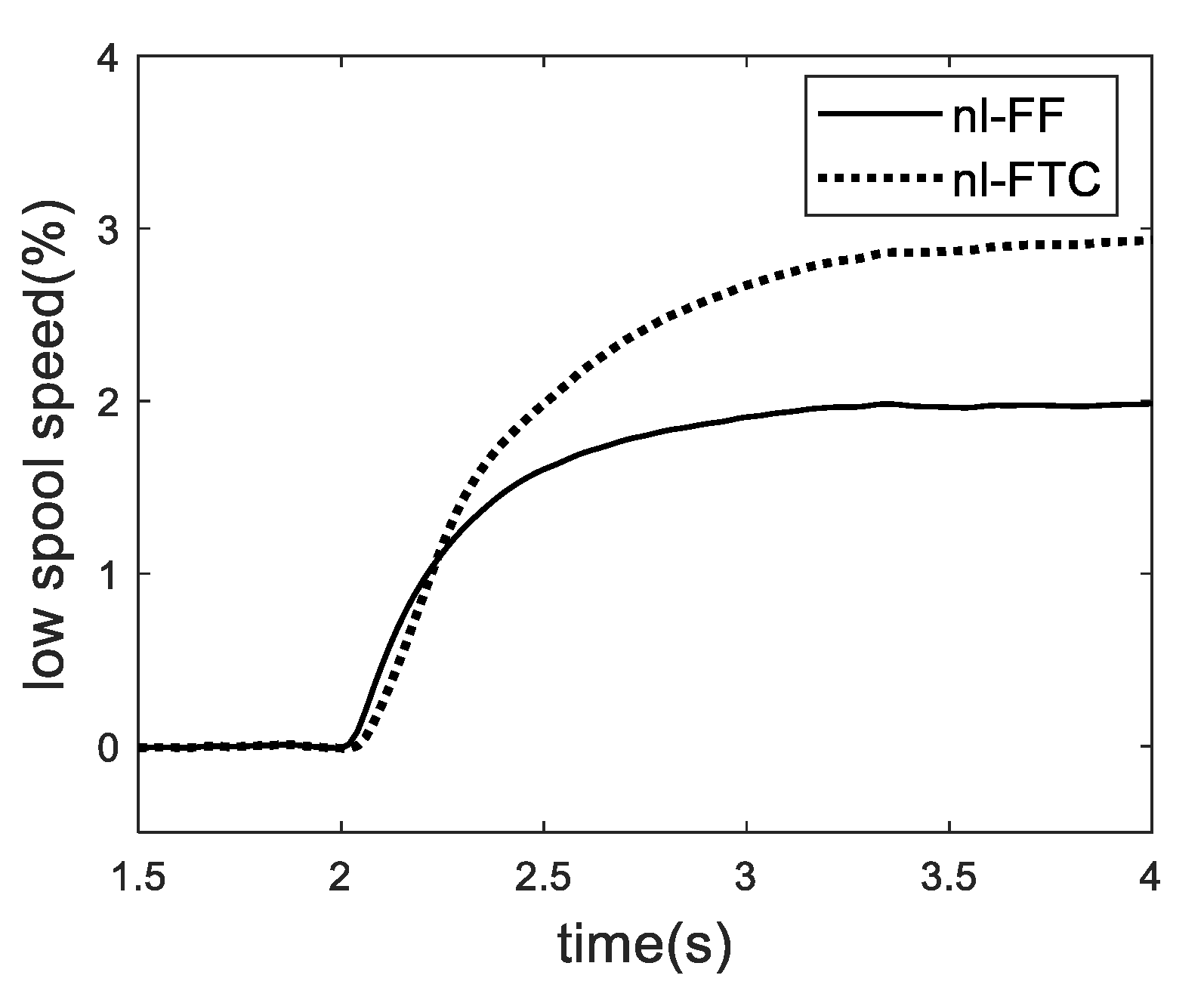
4. Hardware-in-The-Loop Test
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Edwards, C.; Lombaerts, T.; Smaili, H. Fault Tolerant Flight Control. Lecture Notes in Control and Information Sciences; Springer: Berlin, Germany, 2010; Volume 399, 560p. [Google Scholar]
- Zhang, Y.; Jiang, J. Bibliographical review on reconfigurable fault-tolerant control systems. Annu. Rev. Control. 2008, 32, 229–252. [Google Scholar] [CrossRef]
- Rausch, R.; Viassolo, D.; Kumar, A.; Goebel, K.; Eklund, N.; Brunell, B.; Bonanni, P. Towards in-flight detection and accommodation of faults in aircraft engines. In Proceedings of the AIAA 1st Intelligent Systems Technical Conference, Chicago, IL, USA, 20–22 September 2004; p. 6463. [Google Scholar]
- Nyulászi, L.; Andoga, R.; Butka, P.; Főző, L.; Kovacs, R.; Moravec, T. Fault detection and isolation of an aircraft turbojet engine using a multi-sensor network and multiple model approach. Acta Polytech. Hung. 2018, 15, 189–209. [Google Scholar]
- Huang, X.H. Sensor fault diagnosis and reconstruction of engine control system based on auto-associative neural network. Chin. J. Aeronaut. 2004, 17, 23–27. [Google Scholar] [CrossRef]
- Litt, J.S.; Parker, K.I.; Chatterjee, S. Adaptive Gas Turbine Engine Control for Deterioration Compensation Due to Aging. NASA/TM-2003-212607. 2003. Available online: https://archive.org/details/nasa_techdoc_20040001041 (accessed on 10 December 2020).
- Turso, J.; Litt, J. Intelligent, Robust Control of Deteriorated Turbofan Engines via Linear Parameter Varing Quadratic Lyapunov Function Design. In Proceedings of the AIAA 1st Intelligent Systems Technical Conference, Chicago, IL, USA, 20–22 September 2004; pp. 678–691. [Google Scholar]
- Zaccaria, V.; Ferrari, M.L.; Kyprianidis, K. Adaptive Control of Microgas Turbine for Engine Degradation Compensation. J. Eng. Gas Turbines Power 2020, 142, 041012. [Google Scholar] [CrossRef]
- Kawatsu, K.; Tsutsumi, S.; Hirabayashi, M.; Sato, D. Model-based fault diagnostics in an electromechanical actuator of reusable liquid rocket engine. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 1624. [Google Scholar]
- Wang, R.; Liu, M.; Ma, Y. Fault estimation for aero-engine LPV systems based on LFT. Asian J. Control 2021, 23, 351–361. [Google Scholar] [CrossRef]
- Musgrave, J.L.; Guo, T.H.; Wong, E.; Duyar, A. Real-time accommodation of actuator faults on a reusable rocket engine. IEEE Trans. Control. Syst. Technol. 1997, 5, 100–109. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Y.; Rysdyk, R.; Kwan, C.; Xu, R. An intelligent hierarchical approach to actuator fault diagnosis and accommodation. In Proceedings of the 2006 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2006. [Google Scholar]
- Boskovic, J.D.; Jackson, J.A.; Mehra, R.K.; Nguyen, N.T. Multiple-model adaptive fault-tolerant control of a planetary lander. J. Guid. Control Dyn. 2009, 32, 1812–1826. [Google Scholar] [CrossRef]
- Habibi, H.; Nohooji, H.R.; Howard, I. Backstepping Nussbaum gain dynamic surface control for a class of input and state constrained systems with actuator faults. Inf. Sci. 2019, 482, 27–46. [Google Scholar] [CrossRef]
- Chen, H.; Zhou, J.; Zhou, M.; Zhao, B. Nussbaum gain adaptive control scheme for moving mass reentry hypersonic vehicle with actuator saturation. Aerosp. Sci. Technol. 2019, 91, 357–371. [Google Scholar] [CrossRef]
- Ahmed Ali, S.; Guermouche, M.; Langlois, N. Fault-tolerant control based super-twisting algorithm for the diesel engine air path subject to loss-of-effectiveness and additive actuator faults. Appl. Math. Model. 2015, 39, 4309–4329. [Google Scholar] [CrossRef]
- Trinh, H.A.; Truong, H.V.A.; Ahn, K.K. Fault Estimation and Fault-Tolerant Control for the Pump-Controlled Electrohydraulic System. Actuators 2020, 9, 132. [Google Scholar] [CrossRef]
- Shin, D.; Moon, G.; Kim, Y. Design of reconfigurable flight control system using adaptive sliding mode control: Actuator fault. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2005, 219, 321–328. [Google Scholar] [CrossRef]
- Alwi, H.; Edwards, C. Fault tolerant control using sliding modes with on-line control allocation. Automatica 2008, 44, 1859–1866. [Google Scholar] [CrossRef]
- Chen, L.; Edwards, C.; Alwi, H.; Sato, M. Flight evaluation of a sliding mode online control allocation scheme for fault tolerant control. Automatica 2020, 114, 108829. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, Y. An adaptive fault-tolerant sliding mode control allocation scheme for multirotor helicopter subject to simultaneous actuator faults. IEEE Trans. Ind. Electron. 2018, 65, 4227–4236. [Google Scholar] [CrossRef]
- Patel, H.R.; Wilson, D. Parametric Cycle Analysis of Adaptive Cycle Engine. In Proceedings of the 2018 Joint Propulsion Conference, Cincinnati, OH, USA, 9–11 July 2018; p. 4521. [Google Scholar]
- Palman, M.; Leizeronok, B.; Cukurel, B. Mission Analysis and Operational Optimization of Adaptive Cycle Microturbofan Engine in Surveillance and Firefighting Scenarios. J. Eng. Gas Turbines Power 2019, 141, 011010. [Google Scholar] [CrossRef]
- Bringhenti, C.; Barbosa, J.R. Methodology for gas turbine performance improvement using variable-geometry compressors and turbines. Proc. Inst. Mech. Eng. Part A J. Power Energy 2004, 218, 541–549. [Google Scholar] [CrossRef]
- Simmons, R.J. Design and Control of a Variable Geometry Turbofan with and Independently Modulated Third Stream. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 2009. [Google Scholar]
- Edwards, C.; Spurgeon, S.K.; Patton, R.J. Sliding mode observers for fault detection and isolation. Automatica 2000, 36, 541–553. [Google Scholar] [CrossRef]
- Tan, C.P. Sliding Mode Observers for Fault Detection and Isolation. Ph.D. Thesis, University of Leicester, Leicester, UK, 2002. [Google Scholar]
- HäRkegåRd, O.; Glad, S.T. Resolving actuator redundancy—Optimal control vs. control allocation. Automatica 2005, 41, 137–144. [Google Scholar] [CrossRef]
- Farkas, B.; Wegner, S.A. Variations on Barbălat’s Lemma. Am. Math. Mon. 2016, 123, 825–830. [Google Scholar] [CrossRef]
- Kurzke, J. GasTurb—The Gas Turbine Performance Simulation Program; GasTurb GmbH: Aachen, Germany, 2012. [Google Scholar]
- Salehi, A.; Montazeri-Gh, M. Design and HIL-based verification of the fuel control unit for a gas turbine engine. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2020, 234, 1460–1470. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhao, Z.; Zhang, T. A mimicking technique of back pressure in the hardware-in-the-loop simulation of a fuel control unit. Simulation 2020, 96, 375–385. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, Y.; Zhang, T.; Lin, Z.; Zhao, Z.; Zhang, X. Actuator Fault Tolerant Control of Variable Cycle Engine Using Sliding Mode Control Scheme. Actuators 2021, 10, 24. https://doi.org/10.3390/act10020024
Yuan Y, Zhang T, Lin Z, Zhao Z, Zhang X. Actuator Fault Tolerant Control of Variable Cycle Engine Using Sliding Mode Control Scheme. Actuators. 2021; 10(2):24. https://doi.org/10.3390/act10020024
Chicago/Turabian StyleYuan, Yuan, Tianhong Zhang, Zhonglin Lin, Zhiwen Zhao, and Xinglong Zhang. 2021. "Actuator Fault Tolerant Control of Variable Cycle Engine Using Sliding Mode Control Scheme" Actuators 10, no. 2: 24. https://doi.org/10.3390/act10020024
APA StyleYuan, Y., Zhang, T., Lin, Z., Zhao, Z., & Zhang, X. (2021). Actuator Fault Tolerant Control of Variable Cycle Engine Using Sliding Mode Control Scheme. Actuators, 10(2), 24. https://doi.org/10.3390/act10020024




