Design of a Low-Frequency Harmonic Rotary Piezoelectric Actuator

Abstract

Piezoelectric actuators usually operate under a high frequency driving signal. Here we report a harmonic rotating piezoelectric actuator by coupling a harmonic wave generator and a friction rotor, in which the actuator can be actuated by a low-frequency sinusoidal signal with positive bias. The harmonic wave is generated by a two-stage magnifying mechanism consisting of a displacement amplifier and a harmonic rod. Applying piezoelectricity theory, the actuator’s output characteristic equations are deduced. What is more, the output characteristics of piezoelectric actuators are tested with the established experimental system. Results show that the generated harmonic displacements can drive the actuator to work normally at a driving voltage of larger than 90 V and the maximum total harmonic displacement of the piezoelectric actuator comes up to 427.6 μm under the driving voltage of 150 V. Meanwhile, the error between the measured and calculated values of the harmonic displacement is less than 7%. Furthermore, the rotational speed of the piezoelectric actuator reaches 5.45 rpm/min at 150 V voltage and 5 Hz driving frequency.

1. Introduction

Piezoelectric actuators use the inverse piezoelectric effect to convert electrical energy into mechanical energy or mechanical motion. Due to the advantages of its simple structure, light weight and fast response, piezoelectric actuators have been used in Micro Electro Mechanical Systems (MEMS), micro-robots, bioengineering and medical sciences, as well as fluid drive and vibration and noise control fields. Therefore, the research on piezoelectric drive technology has great economic and social value.

Numerous achievements in piezoelectric actuating have been obtained. Acosta [1] made use of idealized piezoelectric sensors to achieve photoacoustic imaging. Using the method of matched asymptotic expansions and the basic constitutive relations for piezoelectricity, the mathematical model for piezoelectric transducers was established. Through the proposed model, a better imaging effect is obtained. Wang et al. [2] designed a non-resonant stepping type bolt-clamped piezoelectric actuator. The proposed piezoelectric actuator was operated under a clamping and driving mechanism by using two longitudinal-bending transducers. Under 400 V_p-p voltages and 1 Hz signal drive, the average step distance was about 10.8 μm. When the load mass is 1.47 kg, the actuator can obtain a velocity of 1.42 μm/s. Applying four rotating traveling wave piezoelectric actuators, Hamamoto et al. [3] designed an aircraft similar to a dragonfly. Tomoaki [4] designed and manufactured a super-miniature piezoelectric motor with a stator volume of 1 mm³, which became one of the smallest piezoelectric motors in the world. In the motor, the stator consists of a metallic cube with a through-hole and piezoelectric elements adhered to its sides. The torque and speed were measured experimentally. Ho et al. [5] proposed a spiral driven piezoelectric motor, which is driven by four piezoelectric stacks and operates in double shear mode, with a transmission speed of 2.137 mm/s. In addition, Shi et al. [6] proposed a cyclic multi-degree-of-freedom piezoelectric ultrasonic motor continuously driven by four legs. The test results showed that the maximum output torque and maximum speed of the motor were 0.118 Nm and 55 rpm/min, respectively. Zeng et al. [7] designed and tested a new type of piezoelectric micromotor driven by asymmetric inertia impact. The resolution of this micromotor is 0.02 μm and the maximum load is 1 kg under the drive of 100 V voltage and 35 Hz. What is more, actuating with ’33’ electromechanical coupling mode, a surface-bondable multilayer piezoelectric actuator [8] was developed. Mazeika et al. [9] designed a multimodal piezoelectric traveling wave actuator with a cylindrical stator. The proposed actuator is clamped at the bottom and driven by a four-phase difference of pi/2 electric signals. Experimental results show the actuator can generate a 115 rpm/min rotation speed under constant initial conditions. Based on magnetostrictive material with simultaneous vibration, a rotating piezoelectric actuator with simultaneous vibration in the longitudinal direction was developed by Titsch et al. [10]. It was shown that the magnetic field and its frequency affect the amplitude of the piezoelectric actuator. Moreover, Ostasevicius et al. [11] used the piezoelectric actuator for separation and purification of biological microparticles.

Furthermore, many achievements have been made in the sensor and control of piezoelectric actuators. Liu et al. [12] investigated the monolithic piezoelectric control of soliton microcombs. By monolithically integrating piezoelectric actuators on ultralow-loss photonic circuits, soliton microcombs—a spectrum of sharp lines over a range of optical frequencies—can be modulated at high speeds with megahertz bandwidths. Zhu et al. [13] studied a piezoelectrically actuated fast tool servo (FTS) for the diamond turning of microstructured surfaces. Utilizing the newly developed FTS, two typical microstructured surfaces are ultra-precisely turned. Furthermore, the feasibility of this method is proven. As precision motion of the piezoelectric ultrasonic motor is severely affected by inherent friction, hysteresis nonlinearity and model uncertainties, Feng et al. [14] developed a novel integral terminal sliding-mode-based adaptive integral backstepping control to solve the precision problems. Using piezo response function and global optimization techniques, Sumit et al. [15] investigated the shape control optimization of the piezoelectric bimorph. A total of 28 piezoelectric actuators are used in the piezoelectric bimorph to generate the sinusoidal profile, elliptical profile and arbitrary deformation profile by the external load.

In the low-frequency driving field, there are also some piezoelectric applications. Nabavi et al. [16] proposed a piezoelectric MEMS vibration energy harvester that operates at a low resonant frequency of less than 200 Hz. By taking advantage of this efficient AI-based performance estimator, the harvested voltage can increase from 2.5 V to 3.4 V under 0.25 g excitation. To enhance the energy harvesting performance of low-frequency rotational motion, Mei et al. [17] proposed a quad-stable piezoelectric energy harvester. The experiments show that the quad-stable piezoelectric energy harvester with time-varying potential wells exhibits a wider operational frequency range (1–7 Hz) in rotational motion. Using liquid as an energy-capturing medium, Yang et al. [18] developed a piezoelectric vibration energy harvester, which can achieve ultralow frequency, low intensity and multidirectional vibration energy harvesting in a horizontal plane. The proposed harvester can generate 9.8 μW under an ultralow frequency of 2.6 Hz and a low intensity vibration excitation of 0.03 g. Modulated by an electromagnetic field, Xing et al. [19] proposed a low-frequency piezoelectric motor, which combines piezoelectric driving and magnetic modulation. Driven at a frequency of 3 Hz and a modulating voltage of 4.5 V, the output speed and torque are 0.1046 rad/min and 0.405 Nmm, respectively. Applying a piezoelectric torsional vibrator and the giant electrorheological fluid, a bidirectional non-contact rotary motor was developed by Qiu et al. [20]. At an excitation frequency of 118 Hz, the proposed motor generates 1.04 mNm torque when the electric field strength of 2 kV/mm with 30% duty cycle is applied to the giant electrorheological fluid. What is more, Barth [21] developed a harmonic micro motor that combined a harmonic drive gearbox and stack piezoactuators. The motor can realize low-speed motion and large output torque.

In addition to the above piezoelectric actuators, a variety of new rotary actuators and mechanisms based on different driving principles have appeared one after another. Yang et al. [22] presented a triboelectric micromotor coupled with a micromotor and a triboelectric nanogenerator; the proposed micromotor can be actuated by ultralow-frequency mechanical stimuli. With a sliding range of 50 mm at 0.1 Hz, the micromotor can start to rotate and reach over 1000 rpm/min at 0.8 Hz. The maximum operation efficiency of the triboelectric micromotor can reach 41%. For early detection of cardiovascular disease, Pullano et al. [23] proposed a novel passive device based on the triboelectric effect to evaluate pseudo impedance cardiography. The proposed device provides a novel monitoring approach opening a promising alternative for continuous and remote risk assessment.

Although many accomplishments have been made in the research of piezoelectric actuators, most of the research, however, has focused on intermediate- and high-frequency driving. The driving principle of the most traditional intermediate- and high-frequency piezoelectric actuators uses the stator resonance to produce the large amplitude, and then produces the motion with the rotor friction. What is more, most of the literature on low-frequency piezoelectric mechanisms are about piezoelectric energy acquisition devices. A few low-frequency piezoelectric actuators use electromagnetic clamping of the rotor or other principles to realize the motion between the stator and rotor. Therefore, the authors present a low-frequency harmonic rotating piezoelectric actuator. Compared with other piezoelectric actuators, the proposed actuator uses the harmonic friction drive between the harmonic rod and the rotor to transmit motion. At the same time, piezoelectric displacement amplifying the mechanism and harmonic rod are used to amplify the output displacement of piezoelectric stacks. Therefore, the end of the harmonic rod can generate a large enough displacement, and then generate a large displacement of the harmonic motion. In turn, it can drive the rotor to produce rotational motion.

The proposed motor has the advantages of simple structure, low output speed and low assembly precision. Only two piezoelectric stacks are used as driving sources to generate harmonic motion. Therefore, the actuator is easy to drive and control. At the same time, because the generated harmonics are not affected by the frequency, the proposed actuator can work under the drive of ultralow frequency and obtain ultralow speed rotation motion.

In this paper, the operating principle of the low-frequency harmonic rotating piezoelectric actuator is presented. The design process and driving parameters of the proposed piezoelectric actuator are analyzed. In addition, the actuator’s output characteristics are deduced. Using experimental equipment, the output characteristics of piezoelectric actuators were tested. The results lay the theoretical and experimental foundation for the improvement of the prototype of the low-frequency harmonic rotating piezoelectric actuator.

2. Driving Principle and Motion Analysis

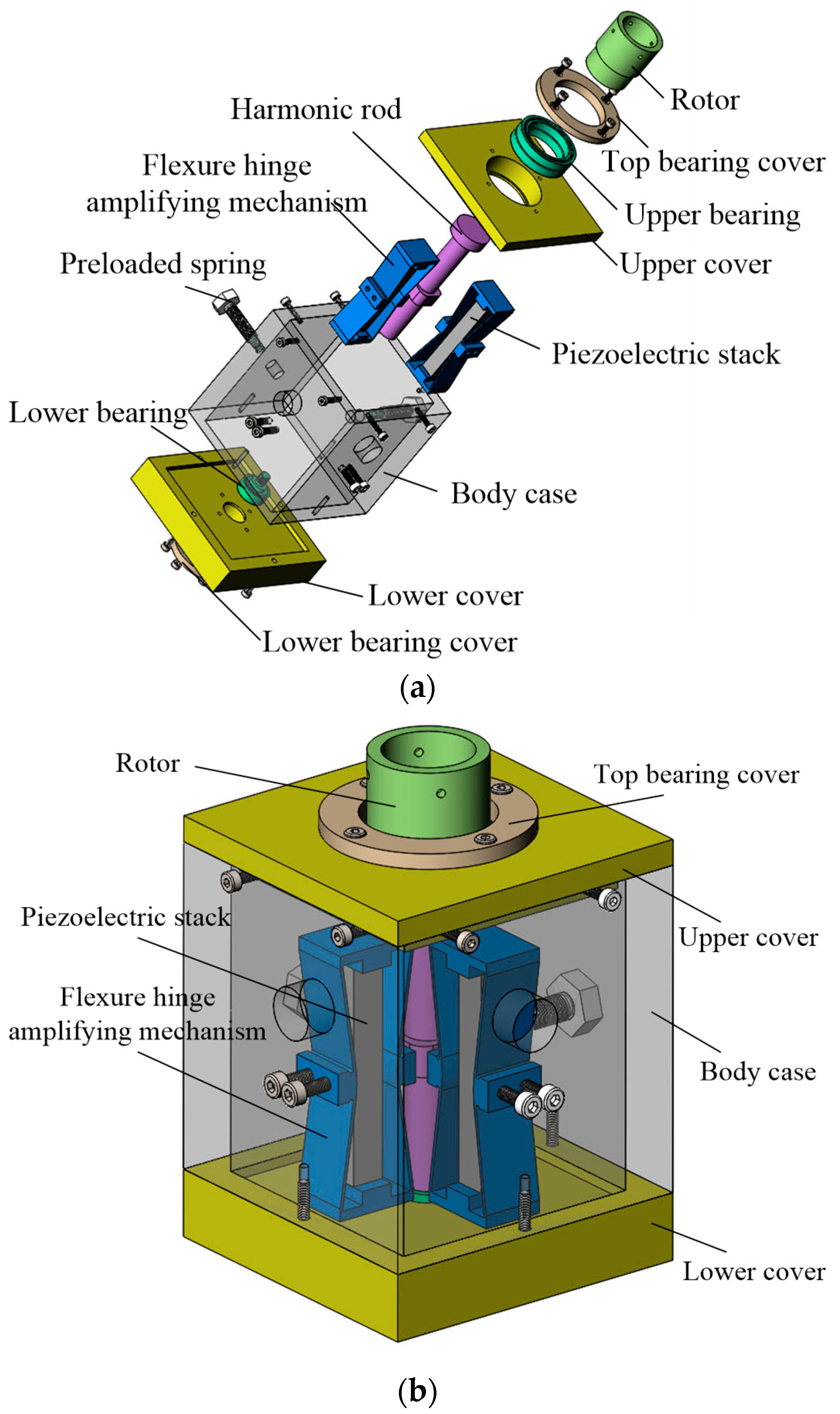
The proposed low frequency harmonic rotating piezoelectric actuator consists of a displacement amplification mechanism, motion output mechanism and auxiliary assembly mechanism. The displacement amplification mechanism includes piezoelectric stack and flexure hinge amplifying mechanism. The motion output mechanism is composed of a rotor and harmonic rod. Moreover, the auxiliary assembly mechanism includes a top bearing cover, upper bearing, upper cover, body case, lower bearing, threaded rod and preloaded spring, lower cover and lower bearing cover.

The driving principle of the proposed piezoelectric actuator is shown in Figure 1. The actuator is driven by two sinusoidal signals with 90 degrees of the phase difference. Driven by two signals, the piezoelectric stacks generate different degrees of elongation deformation. The deformation of piezoelectric stacks causes the deformation of the flexure hinge amplification mechanism. At the same time, the amount of deformation drives the harmonic rod to sway from left to right and from front to back. Under the action of a continuous signal, the harmonic rod generates a large displacement harmonic motion. Furthermore, under the action of harmonic force, friction motion between the harmonic rod and rotor is generated to drive rotor rotation.

The piezoelectric actuator presented in this paper is driven by a sinusoidal signal. The piezoelectric stack is easily damaged when it deforms in the negative direction, therefore, the positive signals are applied to the piezoelectric stack as a driving source. The equation of the driving signal curve can be expressed as:

$$\{\begin{array}{l}{U}_1\left(t\right)=\frac{1}{2}{U}_{\mathit{\text{p-p}}}\left[1+\sin \left(2\pi ft\right)\right]\\ U_2\left(t\right)=\frac{1}{2}{U}_{\mathit{\text{p-p}}}\left[1+\sin \left(2\pi ft+\frac{\pi }{2}\right)\right]\end{array}$$

(1)

where U_p-p and f are the peak-to-peak value and driving frequency of the driving signal, respectively.

When the piezoelectric stack works, it generates elastic deformation and its stress equation [24] is expressed as:

$$\{\begin{array}{l}{\epsilon }_{p1}=s_{33}\frac{P}{S_p}+\frac{1}{2h_p}{d}_{33}{U}_{\mathit{\text{p-p}}}\left[1+\sin \left(2\pi ft\right)\right]\\ {\epsilon }_{p2}=s_{33}\frac{P}{S_p}+\frac{1}{2h_p}{d}_{33}{U}_{\mathit{\text{p-p}}}\left[1+\sin \left(2\pi ft+\frac{\pi }{2}\right)\right]\end{array}$$

(2)

where P and s₃₃ are the preload and elastic flexibility coefficients of the piezoelectric stack, respectively; d₃₃, S_p and h_p are piezoelectric strain constant, sectional area and piezoelectric layer thickness of the piezoelectric stack, respectively.

Supposing the total length of the piezoelectric stack is l_np, and the number of ceramic layers in the piezoelectric stack is n, then l_np = nh_p. From the relationship between strain ε_p, total length l_np and total deformation δ_np, the following is obtained:

$$\{\begin{array}{l}{\delta }_{np1}=n\left(s_{33}{h}_p\frac{P}{S_p}+\frac{1}{2}{d}_{33}{U}_{\mathit{\text{p-p}}}\left[1+\sin \left(2\pi ft\right)\right]\right)\\ {\delta }_{np2}=n\left(s_{33}{h}_p\frac{P}{S_p}+\frac{1}{2}{d}_{33}{U}_{\mathit{\text{p-p}}}\left[1+\sin \left(2\pi ft+\frac{\pi }{2}\right)\right]\right)\end{array}$$

(3)

Figure 2 shows the deformation of displacement amplification mechanism. Here, O point is fixed end and O₁ point is free extension end. When the system is working, the two ends (points A and B) of the piezoelectric stack are stretched and deformed along the axis. The flexible arms, O₁C and O₁D, of the displacement amplification mechanism rotate slightly around points C and D. Thus, the free end O₁ produces an overhanging displacement.

The unilateral deformation of piezoelectric stack Δ_np can be written as:

$$\{\begin{array}{l}{\Delta }_{np1}=\frac{1}{2}{\delta }_{np1}\\ {\Delta }_{np2}=\frac{1}{2}{\delta }_{np2}\end{array}$$

(4)

According to the dimension relation in Figure 2, the length of the flexible arm can be written as:

$$\{\begin{array}{l}{l}_{d1}=\frac{\frac{1}{2}{l}_{np1}}{\cos \theta }=\frac{n{h}_{p1}}{2\cos \theta }\\ l_{d2}=\frac{\frac{1}{2}{l}_{np2}}{\cos \theta }=\frac{n{h}_{p2}}{2\cos \theta }\end{array}$$

(5)

where θ is the angle between the flexible arm and the horizontal.

The angle between the flexible arm and the horizontal changes after deformation, and its expression is:

$$\{\begin{array}{l}\cos {\varphi }_1=\frac{\frac{1}{2}{l}_{np1}+{\Delta }_{np1}}{l_{d1}}=\frac{\cos \theta \left(l_{np1}+2{\Delta }_{np1}\right)}{n{h}_{p1}}\\ \cos {\varphi }_2=\frac{\frac{1}{2}{l}_{np2}+{\Delta }_{np2}}{l_{d2}}=\frac{\cos \theta \left(l_{np2}+2{\Delta }_{np2}\right)}{n{h}_{p2}}\end{array}$$

(6)

Hence, the output displacement of the displacement amplification mechanism can be expressed by:

$$\{\begin{array}{l}{\delta }_{d1}=2l_{d1}\sin {\varphi }_1=\frac{n{l}_{p1}}{\cos \theta }\sin \left[\arccos \left(\frac{\cos \theta \left(l_{np1}+2{\Delta }_{np1}\right)}{n{l}_{p1}}\right)\right]\\ {\delta }_{d2}=2l_{d2}\sin {\varphi }_2=\frac{n{l}_{p2}}{\cos \theta }\sin \left[\arccos \left(\frac{\cos \theta \left(l_{np2}+2{\Delta }_{np2}\right)}{n{l}_{p2}}\right)\right]\end{array}$$

(7)

The output displacement of the displacement amplification mechanism is amplified by a two-order displacement through a harmonic rod. The relationship between the dimensions is shown in Figure 3, where l₁ and l₂ are two section lengths of the harmonic rod.

As seen in Figure 3, the displacement of the harmonic rod is proportional to the displacement of the displacement amplification mechanism. According to the triangle principle, the output displacement of the harmonic rod can be expressed by:

$$\{\begin{array}{l}{\delta }_{h1}=\frac{{\delta }_{d1}\left(l_1+l_2\right)}{l_1}\\ {\delta }_{h2}=\frac{{\delta }_{d2}\left(l_1+l_2\right)}{l_1}\end{array}$$

(8)

Furthermore, the total displacement is the sum of the displacement vectors in both directions, which can be expressed as:

$${\delta }_h=\sqrt{{\delta }_{h1}^2+{\delta }_{h2}^2}=\frac{l_1+l_2}{l_1}\sqrt{{\delta }_{d1}^2+{\delta }_{d2}^2}$$

(9)

To realize the continuous output of the rotor, the output displacement of the harmonic rod should be larger than its offset. Here, the harmonic offset is 0.2 mm. Hence, the relation between the output displacement of the harmonic rod and its offset is as follows:

$$\{\begin{array}{l}{\delta }_{h1}>{\Delta }_r\\ {\delta }_{h2}>{\Delta }_r\\ {\delta }_h>{\Delta }_r\end{array}$$

(10)

Through the above analysis, it is easy to determine the driving principle and motion law of a low-frequency rotating piezoelectric actuator. The structure of the low-frequency harmonic rotating piezoelectric actuator is presented in Figure 4, where the relationship between the components is clear. After two-stage displacement amplification, the proposed piezoelectric actuator obtained a large harmonic displacement to drive the rotor. To ensure the accuracy of harmonic generation and assembly precision, a movable upper cover was adopted. The gap between the rotor and the harmonic lever can be adjusted by adjusting the screws on the side. At the same time, two side-by-side bearings are used to ensure that the rotor is not deflected.

3. Simulation Analysis and Experimental Test

3.1. Output Displacement Analysis of Amplification Mechanism

The physical parameters of the piezoelectric stack are shown in

Table 1. Physical parameters of piezoelectric stack.

Parameters	Values
Piezoelectric strain constant d33 (pm/V)	635
Elastic flexibility coefficient s33 (μm2/N)	18
Sectional area of the piezoelectric stack Sp (mm2)	25
total length of the piezoelectric stack lnp (mm)	30
Density of the piezoelectric stack ρp (kg/m3)	7500
Young’s modulus of the piezoelectric stack Ep (GPa)	76.5
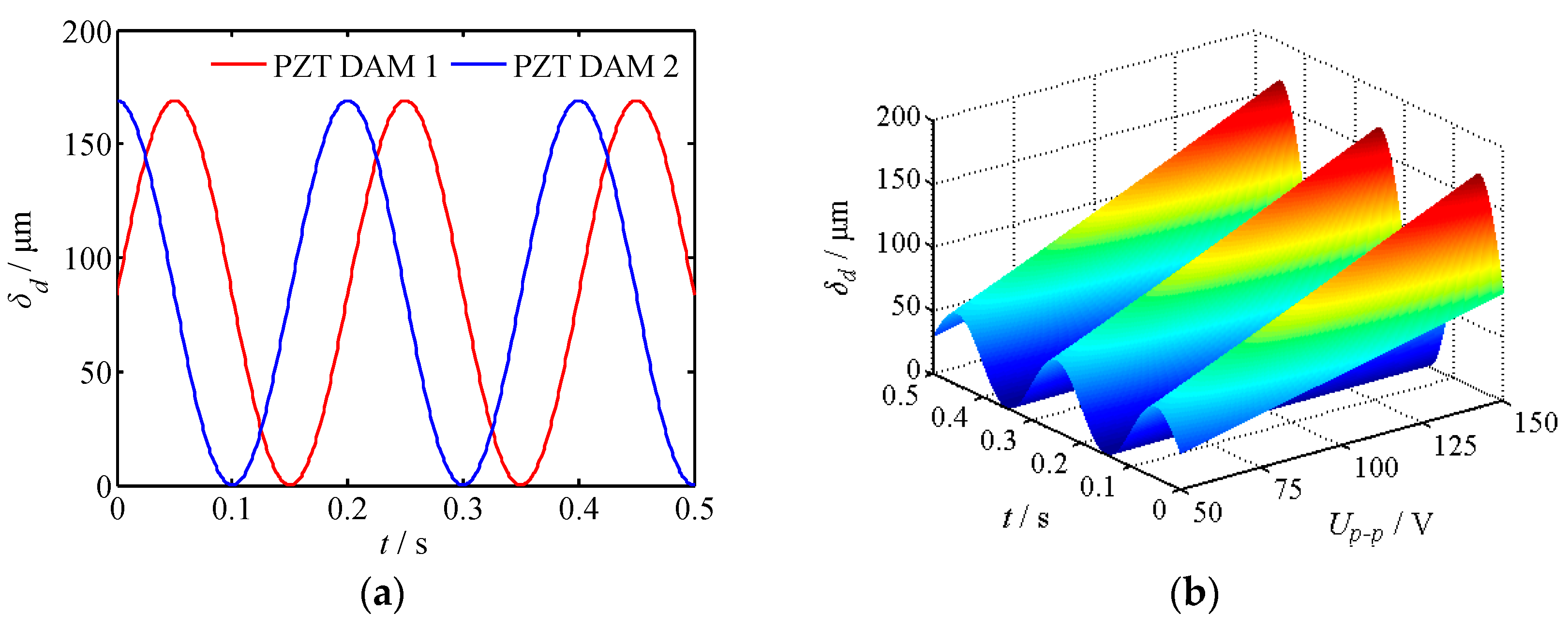
Poisson’s ratio of the piezoelectric stack νp	0.32

. Herein, the piezoelectric stack is provided by a signal generator with offset sinusoidal signals. Meanwhile, the piezoelectric driving power supply produced by Harbin Core Tomorrow Company is used to amplify the voltage of the driving signals. Substituting physical parameters of the piezoelectric stack into Equation (3), the output displacement curve of the piezoelectric displacement amplification mechanism can be obtained as shown in Figure 5, where the PZT DAM represents the Piezoelectric Displacement Amplification Mechanism (PZT DAM). From Figure 5, the following is obtained:

(1) When a sinusoidal driving signal is applied to the piezoelectric amplification mechanism, it produces a sinusoidal displacement change. The displacement phase between the two amplification mechanisms is still 90 degrees. In addition, the maximum output displacement of the two displacement amplification mechanisms is 169.1 μm under a driving voltage of 150 V.

(2) With the increase of driving voltage, the output displacement of piezoelectric displacement amplification mechanism increases in approximate linear proportion. As time goes on, it gives rise to a sinusoidal pattern.

At the same time, to verify the correctness of the theoretical calculation model, ANSYS finite element analysis software is used to carry out finite element simulation of the displacement amplification mechanism, which is presented in Figure 6. Here, Figure 6a shows mesh generation of the displacement amplification mechanism. The grid size is set by 0.5 mm. Hence, after mesh generation, the number of nodes and cells is 113,943 and 40,692, respectively.

The magnifying mechanism is made of steel; Young’s modulus and Poisson’s ratio are 210 GPa and 0.27, respectively. The yield strength of the material is 355 MPa and the density is 7850 kg/m³. However, Young’s modulus and Poisson’s ratio of the piezoelectric material are 76.5 GPa and 0.32, respectively. Meanwhile, the density of the piezoelectric material is 7500 kg/m³.

A fixed constraint is adopted at one end of the amplification mechanism, as shown in point O in Figure 2. As the selected piezoelectric stack can output a displacement of 30 μm, a displacement load of 30 μm is applied to both ends of the piezoelectric stack.

After finite element simulation, the deformation cloud diagram of the displacement amplification mechanism is shown in Figure 6b. From the figure, we see that the finite element simulation shows that the maximum output displacement of the displacement amplification mechanism is 163 μm. Hence, the error between the simulation value and the theoretical calculation value is 3.6%. The results indicate that the theoretical calculation model is reasonable.

Meanwhile, the output displacement experiment of piezoelectric displacement amplification mechanism is carried out to further verify the correctness of the theoretical calculation. The displacement amplification mechanisms and piezoelectric stacks for the experiment were manufactured by the Harbin Tiny Nano Company. Figure 7 presents the experimental test system for the piezoelectric displacement amplification mechanism. Here, the piezoelectric drive power supply adopts the three-channel power supply produced by the Harbin Core Tomorrow Company. The output displacement of the piezoelectric displacement amplifier is measured by LVDT inductance micro displacement measuring instrument. In addition, JUNTEK JDS-2900 signal generator was used to provide sinusoidal drive signals for the piezoelectric stacks. The experimental results of output displacement are shown in Figure 8, where Figure 8a–c represents the measured displacement of piezoelectric displacement amplification mechanisms 1 and 2, as well as the error between the measured value and the theoretical value, respectively. The experimental results indicate that:

(1) Compared with the theoretical calculation, the experimental curve of piezoelectric displacement amplification mechanism presents a weak nonlinear variation with the peak–peak voltage change. Driven by a 150 V voltage signal, the maximum output displacements of the two displacement amplification mechanisms are 166 μm and 163 μm, respectively.

(2) With the increase of voltage, the experimental error decreases first and then increases, and the error is the smallest when the voltage is 90–100 V. At the same time, the lower the voltage, the greater the error, therefore the lower voltage is not suitable for driving piezoelectric displacement amplification mechanism.

(3) When the voltage is within the range of 60–150 V, the output displacement error is within 5%. Within this voltage range, the error of displacement amplification mechanism 1 is smaller than that of amplification mechanism 2. At 150 V, the error between the output displacements of the two displacement amplifiers is 1.8%.

3.2. Harmonic Displacement Analysis

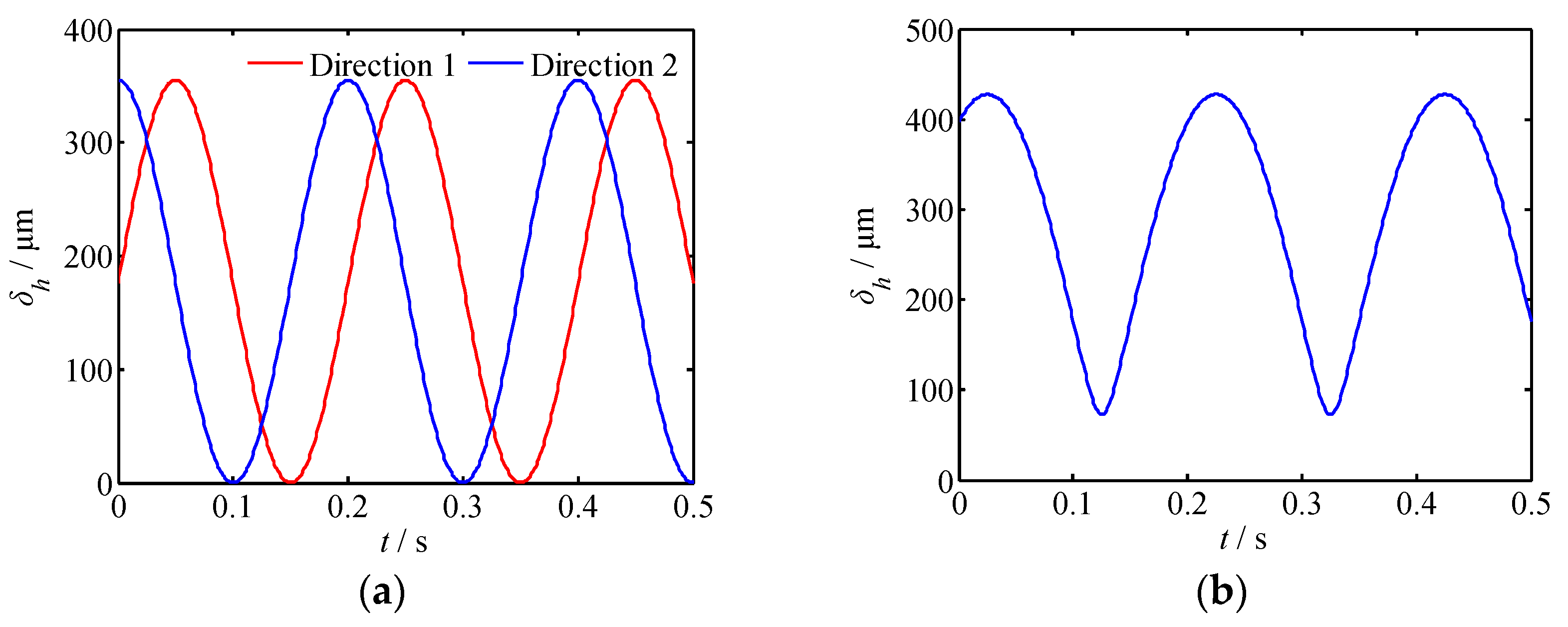
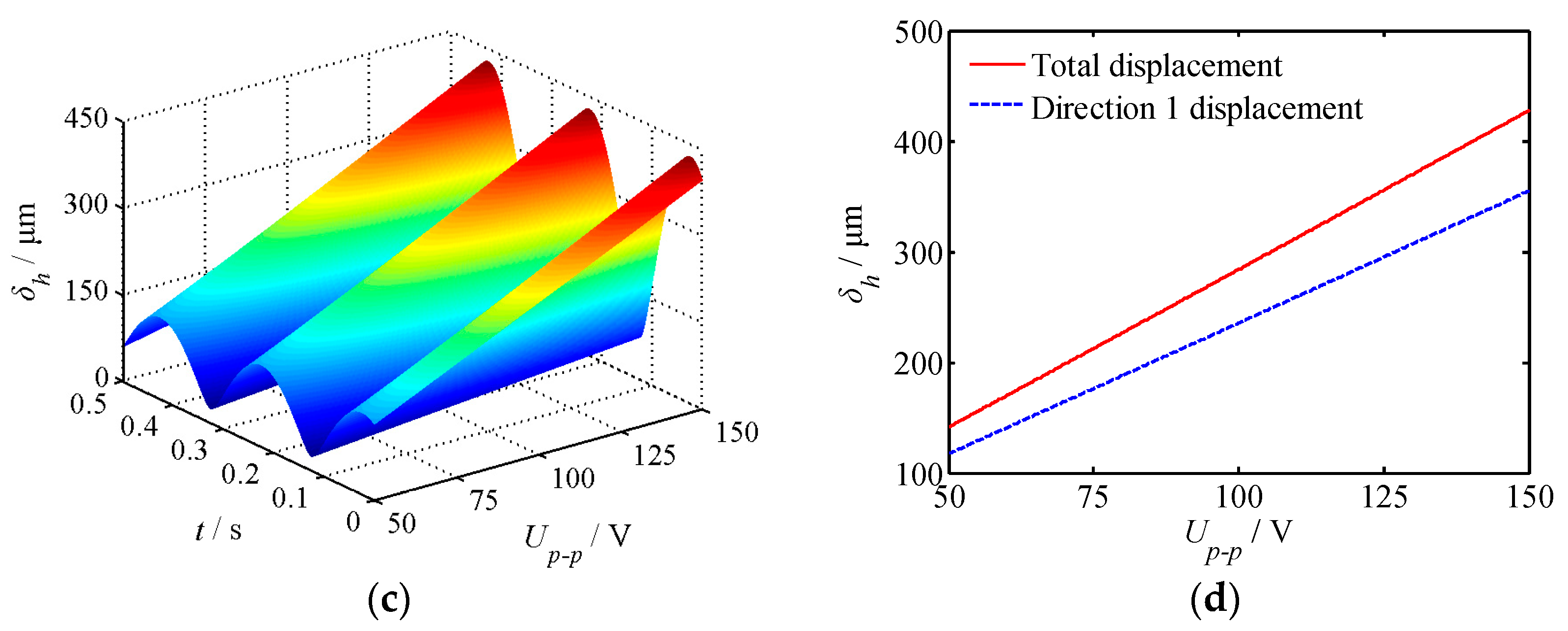
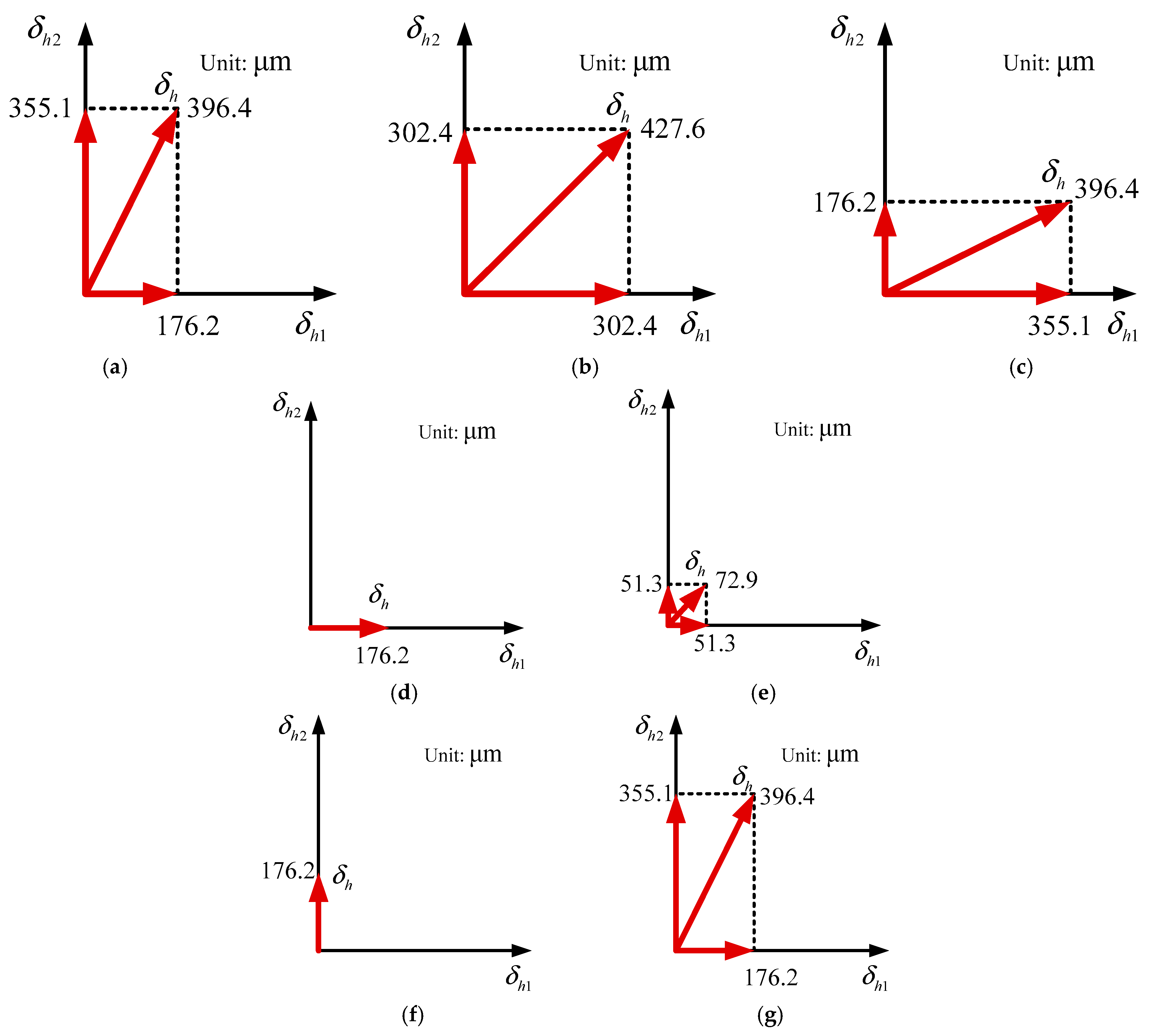
According to Equations (8) and (9), the harmonic displacement curves can be simulated as shown in Figure 9, where Figure 9a–d represents output harmonic displacement in both directions, total harmonic displacement, harmonic displacements that vary with time and voltage, comparison of total displacement and unidirectional displacement, respectively. In addition, the displacements at different moments in a certain period are also analyzed, which is presented in Figure 10. Here, a few special moments are selected for analysis, and T represents periodic time. From Figure 9 and Figure 10, it can be observed that:

(1) The harmonic displacements in both directions vary with time by sinusoidal curves; the phase difference is 90 degrees, which is the same as the input signal. The total displacement is approximately sinusoidal with time, and the frequency is the same as the input signal, but the phase is different. Herein, the total displacement is the superposition of the displacements in directions 1 and 2, and the phase difference of the displacement signals in the two directions is 90 degrees. Therefore, there is no case of both being 0, so the total displacement is always greater than 0 in Figure 9b.

(2) Under the driving voltage of 150 V, the maximum harmonic displacement in one direction is 355.1 μm, whereas the maximum total displacement is 427.6 μm. The maximum total displacement is 20.4% greater than the unidirectional maximum displacement.

(3) As the input peak–peak voltage increases, the total harmonic displacement and its single direction displacement increase approximately linearly.

(4) In a period, when t = 1/8 T, the total harmonic displacement is the maximum. When t = 1/4 T, the harmonic displacement in direction 1 is the maximum, whereas the largest value of direction 2 occurs at t = 0 or T. What is more, the minimum total displacement occurs at t = 5/8 T and the minimum value is 72.9 μm.

(5) When t =1/2 T and t = 3/4 T, the system outputs only one-directional displacement. The single directional displacement of direction 1 occurs at t = 1/2 T, with a value at 176.2 μm. While the single directional displacement of direction 2 occurs at t = 3/4 T, its value is still 176.2 μm. Meanwhile, when the total displacements take the maximum value and the minimum value, the corresponding displacements in two directions are equal.

(6) When the driving voltage is greater than 90 V, the harmonic displacement in all directions is greater than 200 μm, which can drive the proposed piezoelectric actuator to work normally.

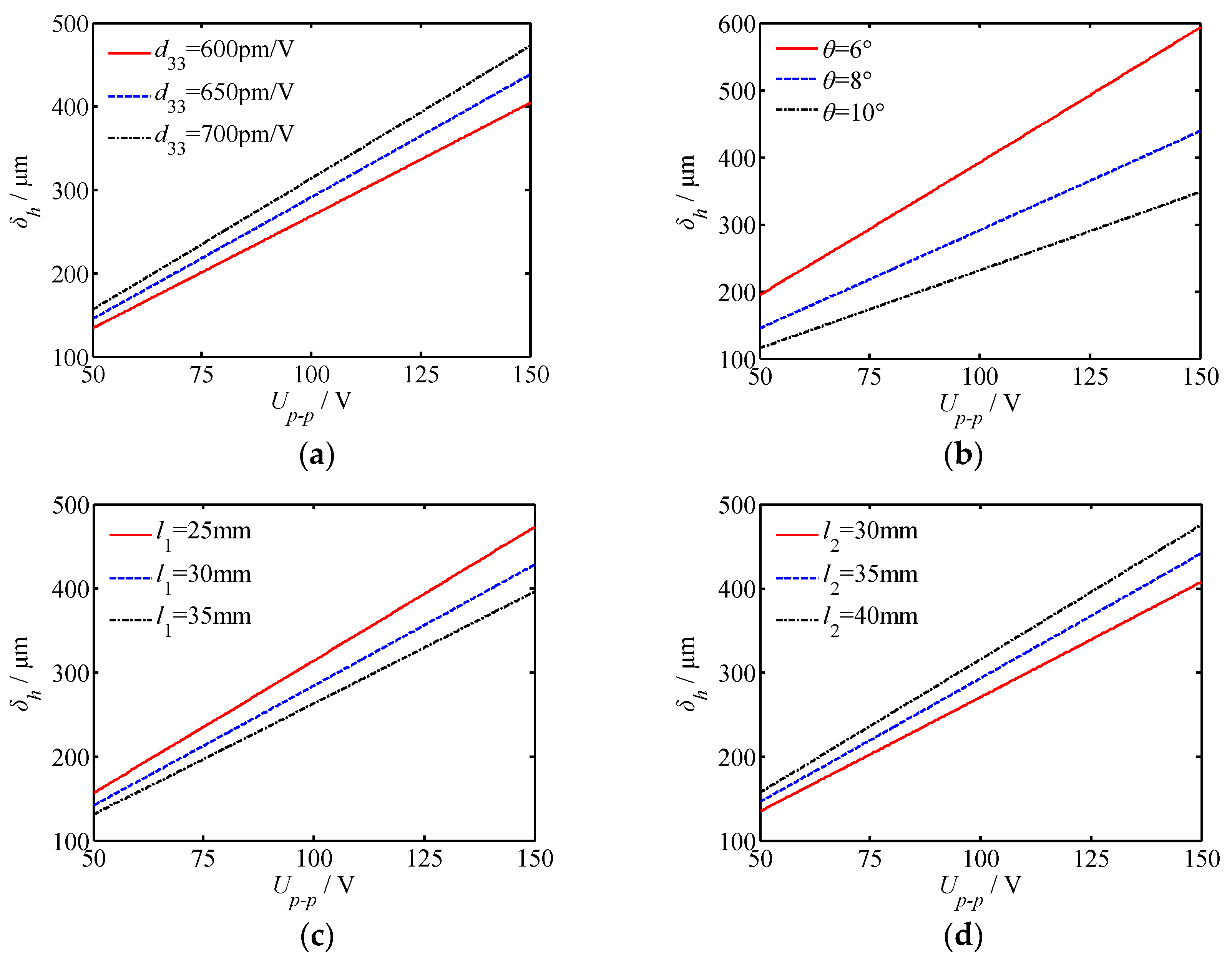
To investigate the influence of system parameters on harmonic displacement, the parameters’ piezoelectric strain constant d₃₃, the angle between the flexible arm and the horizontal θ and the length of harmonic rod l₁ and l₂ are selected as target parameters. The analysis results are shown in Figure 11. From the figure, we see that:

(1) The harmonic displacements change with the variation of d₃₃ and l₂ by the same rule. As d₃₃ and l₂ increase, the output displacements increase synchronously.

(2) The harmonic displacements are inversely proportional to the change of θ and l₁. Among them, the angle between the flexible arm and the horizontal of rotation has enormous influence on the output displacement.

Therefore, it is extremely important to set these parameters properly to improve the performance of the low-frequency harmonic rotary piezoelectric actuator.

To verify the correctness of the theoretical calculation of harmonic displacement, the harmonic displacement is tested experimentally. By using an LVDT inductance micrometer, the harmonic displacements in two directions are easily measured. Figure 12 shows the test results of harmonic displacement for the proposed piezoelectric actuator. The results indicate that:

(1) The measured value of harmonic displacement shows a nonlinear trend with peak–peak voltage change. This phenomenon is caused by the hysteresis effect of piezoelectricity of the piezoelectric material.

(2) The maximum error between theoretical calculations and experimental tests occurs at a driving voltage of 60 V and is 7.0%. When the driving voltage is larger than 80 V, the errors are stable and less than 3%. Hence, the reliability and accuracy of the theoretical model of the piezoelectric actuator are further verified.

Therefore, to minimize the experimental error, a relatively large driving voltage should be selected as far as possible when the piezoelectric actuator is driven.

3.3. Output Speed Test of the Prototype

In this article, the average measurement method is adopted to measure the rotating speed of the prototype. Under the condition of stable operation of the prototype, the average value of the measured speed N times within a certain time interval is the average speed of the system, and the expression can be written as:

$$n_{av}=\frac{1}{N}{\displaystyle \sum _{i=1}^N{n}_i},$$

(11)

where n_i is the rotational velocity measured at the i-th time.

An experimental prototype of the low-frequency harmonic rotating piezoelectric actuator is shown in Figure 13, where Figure 13a,b represents components and assembly of the machined prototype. Its experimental test scheme is presented in Figure 14. Driven by a continuous voltage signal, the prototype can run stably. Figure 15 shows the states of the piezoelectric actuator as it moves to different positions. Using the average measurement method, the rotational speed test results are shown in Figure 16. The results indicate that:

(1) When the frequency is constant, the piezoelectric actuator starts to rotate when the driving voltage reaches 90 V. With the increase of the driving voltage, the rotating speed first increases and then tends to a stable value. When the driving voltage is 150 V, the maximum rotating speed at 1 Hz, 3 Hz and 5 Hz can reach 1.88 rpm/min, 2.61 rpm/min and 5.45 rpm/min, respectively.

(2) When the driving voltage is constant, the output speed presents a nonlinear increase trend with the increase of driving frequency. At the same time, the experimental results show that the piezoelectric actuator operates smoothly under different driving frequencies.

The research results verify the feasibility of the proposed low-frequency harmonic piezoelectric actuator. Meanwhile, the investigation in this paper lays a theoretical and experimental foundation for the improvement of the piezoelectric actuator.

Compared with the harmonic piezoelectric motor developed by Barth [21], the proposed harmonic piezoelectric actuator in this paper just uses two 5 × 5 × 30 mm piezoelectric stacks as driving elements. Barth’s harmonic piezodrive motor actuates with eight 5 × 5 × 50 mm piezoelectric stacks. In addition, the harmonic gear used for reduction in Barth’s motor has high precision and is difficult to manufacture. In Ho’s research [5], a piezoelectric screw-driven motor operating in two shear vibration modes was developed. The stator structure of the screw-driven motor is formed by obliquely placing four piezoelectric actuators in a four-side hollowed cubic elastic body. In Ho’s motor, four piezoelectric stacks, 2 mm × 3 mm × 9 mm in size, are used as the driving source. The translational velocity of the motor is 1.174 mm/s with a 16 g mechanical load under 16 V peak voltage driving. Since the driving signals of the four piezoelectric stacks are different, it is difficult to drive and control the motors. At the same time, compared with the piezoelectric actuator proposed by the authors, the piezoelectric motor consumes more energy.

In Shi’s piezoelectric ultrasonic motor [6], a ring type composite stator with four driving feet uniformly arranged in the inner circumference of the ring stator is used to generate a specific combination of the A(0,5) axial bending modes and R(0,2) radial bending modes. The motor’s structure is relatively complex, and its maximum speed is 55 rpm/min. Since the ultrasonic motor is driven by resonance modes, its speed is not easy to adjust. The low-frequency piezoelectric actuator proposed by the authors not only reaches an ultralow speed, but also easily adjusts the speed by changing the driving frequency.

In addition, Xing’s low-frequency piezoelectric motor [19] combines piezoelectric driving and magnetic modulation together and transforms the reciprocating swing of the stator into step running of the rotor via the intermittent magnetic clamping between the rotor and stator. At a driving frequency of 3 Hz, it can output an ultralow speed of 0.66 rpm/min. Therefore, the motor has high innovation. Although the motor can output ultralow speed, the motor also has disadvantages; it is more complicated to drive and control because of its electromagnetic modulation. However, in the piezoelectric actuator proposed by the authors, only two piezoelectric stacks are used as the driving source. Therefore, its drive and control circuit is simple and easier to use.

Furthermore, Qiu’s non-contact rotary piezoelectric motor [20] uses a piezoelectric torsional vibrator and giant electrorheological fluid to generate rotational motion. At an excitation frequency of 118 Hz and electric field strength of 2.5 kV/mm, the motor generates a rotational speed of 6.28 rpm/min. This kind of motor introduces the giant electrorheological fluid into the piezoelectric motor, which has good innovation, but the structure and driving of the motor are too complicated to be of practical use. On the contrary, the piezoelectric actuator presented by the authors is simple in structure and easy to use.

Therefore, compared to other piezoelectric actuators, the piezoelectric actuator presented in this paper has the characteristics of reduced energy consumption, a simple structure, low manufacturing cost and is easy to control. As a result, the low-frequency harmonic rotating piezoelectric actuator has high application value.

4. Conclusions

In this paper, a low-frequency harmonic rotating piezoelectric actuator based on the harmonic friction principle is proposed. The operating principle of the low-frequency harmonic rotating piezoelectric actuator is presented. Using piezoelectricity and mathematics principle, the actuator’s output characteristic equations are deduced. With experimental equipment, the output characteristics of the piezoelectric actuators were tested. Results show that:

(1) The harmonic displacements produced by piezoelectric stacks can drive the proposed piezoelectric actuator to work normally when the driving voltage is larger than 90 V.

(2) The maximum total harmonic displacement of the piezoelectric actuator reaches 427.6 μm under the driving voltage of 150 V.

(3) The rotational speed of the piezoelectric actuator is 5.45 rpm/min under the driving voltage of 150 V at a frequency of 5 Hz.

(4) The error between the measured and calculated values of the harmonic displacement is less than 7%, which verifies the reliability of the theoretical model.

These results lay the theoretical and experimental foundation for the improvement of the prototype of the low-frequency harmonic rotating piezoelectric actuator.