Position Control of the Dielectric Elastomer Actuator Based on Fractional Derivatives in Modelling and Control
Abstract
:1. Introduction
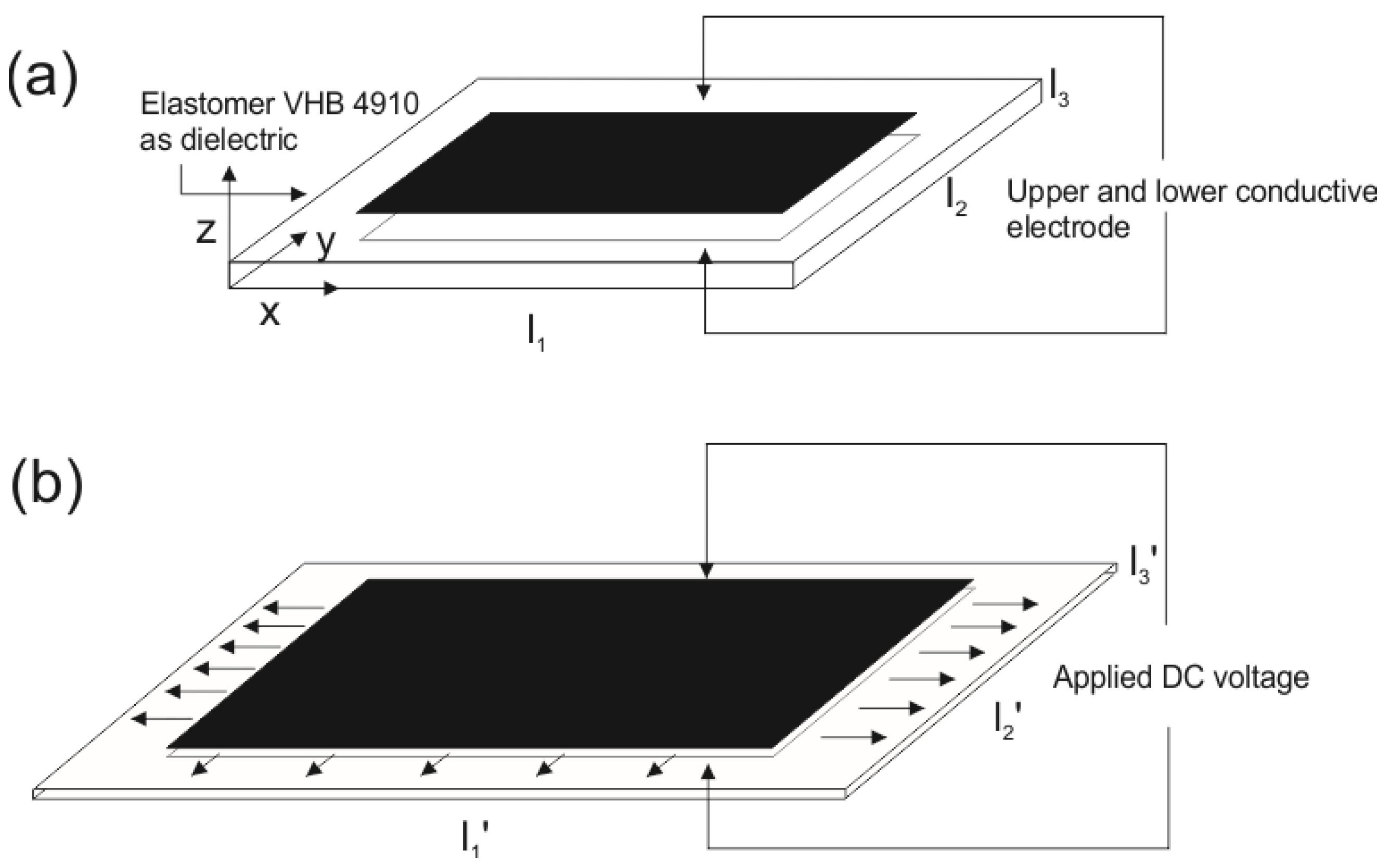
2. Materials and Methods
2.1. Using Fractional Calculus in Rheology and Control Theory
2.1.1. Fractional Calculus in Rheology
2.1.2. Fractional Calculus in Control Theory
2.2. Optimization of Parameters for the Controller by the Use of the FOMCON Toolbox in Matlab and Implementation of the Controller on a Microprocessor
Optimization of Parameters for the Controller
2.3. Continuous and Discrete Simulink Models of DEA
2.4. Implementation of on the DSP Microcontroller
3. Results
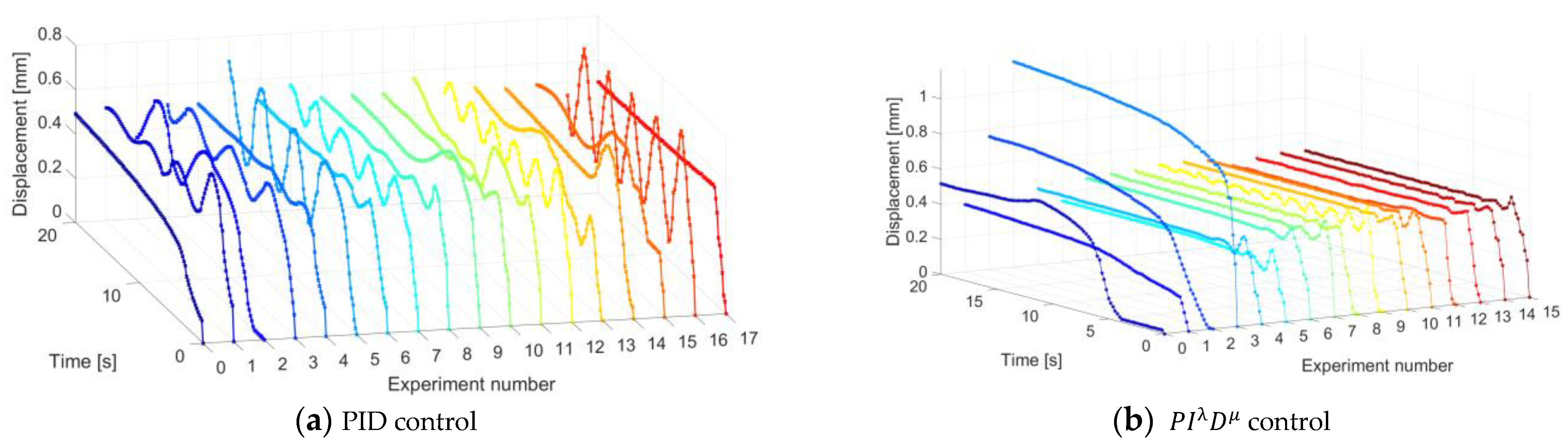
3.1. Step Responses of the Real DEA with PID and Control
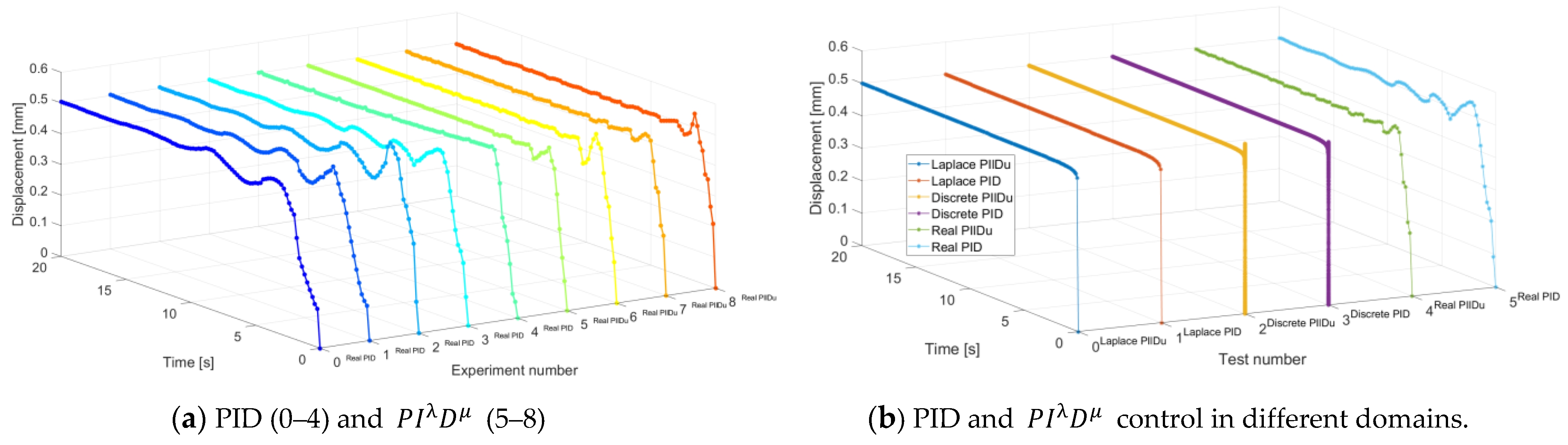
3.2. Comparing Results of Step Responses for Both Controllers and the Best Parameters in All Domains
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Biewener, A.; Patek, S. Animal Locomotion; OUP: Oxford, UK, 2018. [Google Scholar]
- Punning, A.; Kim, K.J.; Palmre, V.; Vidal, F.; Plesse, C.; Festin, N.; Maziz, A.; Asaka, K.; Sugino, T.; Alici, G.; et al. Ionic electroactive polymer artificial muscles in space applications. Sci. Rep. 2014, 4, 6913. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bar-Cohen, Y. Electroactive Polymer (EAP) Actuators as Artificial Muscles: Reality, Potential, and Challenges; SPIE Press: Bellingham, DC, USA, 2001. [Google Scholar]
- Leibniz, G.W. Mathematische Schiften; Georg Olms Verlagsbuchhandlung: Hildesheim, Germany, 1962. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999; Volume 198, p. 311. [Google Scholar]
- Zambrano-Serrano, E.; Muñoz-Pacheco, J.M.; Gómez-Pavón, L.C.; Luis-Ramos, A.; Chen, G. Synchronization in a fractional-order model of pancreatic β-cells. Eur. Phys. J. Spec. Top. 2018, 227, 907–919. [Google Scholar] [CrossRef]
- Jesus, M.M.-P.; Cornelio, P.-C.; Ernesto, Z.-S. The Effect of a Non-Local Fractional Operator in an Asymmetrical Glucose-Insulin Regulatory System: Analysis, Synchronization and Electronic Implementation. Symmetry 2020, 12, 1395. [Google Scholar]
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Tavazoei, M.S. Fractional order chaotic systems: History, achievements, applications, and future challenges. Eur. Phys. J. Spec. Top. 2020, 229, 887–904. [Google Scholar] [CrossRef]
- Mainardi, F.; Spada, G. Creep, relaxation and viscosity properties for basic fractional models in rheology. Eur. Phys. J. Spec. Top. 2011, 193, 133–160. [Google Scholar] [CrossRef] [Green Version]
- Caponetto, R.; Dongola, G.; Fortuna, L.; Petrá, I. Fractional Order Systems; World Scientific: Singapore, 2010; Volume 72. [Google Scholar]
- Petráš, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer: New York, NY, USA, 2011. [Google Scholar]
- Babič, M.; Vertechy, R.; Berselli, G.; Lenarčič, J.; Parenti Castelli, V.; Vassura, G. An electronic driver for improving the open and closed loop electro-mechanical response of Dielectric Elastomer actuators. Mechatronics 2010, 20, 201–212. [Google Scholar] [CrossRef]
- Sarban, R.; Jones, R. Physical Model-Based Active Vibration Control using a Dielectric Elastomer Actuator. J. Intell. Mater. Syst. Struct. 2012, 23, 473–483. [Google Scholar] [CrossRef]
- Li, Y.; Oh, I.; Chen, J.; Zhang, H.; Hu, Y. Nonlinear dynamic analysis and active control of visco-hyperelastic dielectric elastomer membrane. Int. J. Solids Struct. 2018, 152, 28–38. [Google Scholar] [CrossRef]
- Nguyen, C.; Vuong, N.; Kim, D.; Moon, H.; Koo, J.; Lee, Y.; Nam, J.-D.; Choi, H.R. Fabrication and Control of Rectilinear Artificial Muscle Actuator. Mechatron. IEEE/ASME Trans. 2011, 16, 167–176. [Google Scholar]
- Mustaza, S.M.; Lekakou, C.; Saaj, C.; Fras, J. Dynamic Modeling of Fiber-Reinforced Soft Manipulator: A Visco-Hyperelastic Material-Based Continuum Mechanics Approach. Soft Robot. 2019, 6, 305–317. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yeoh, O.H. Characterization of Elastic Properties of Carbon-Black-Filled Rubber Vulcanizates. Rubber Chem. Technol. 1990, 63, 792–805. [Google Scholar] [CrossRef]
- Cao, J.; Liang, W.; Ren, Q.; Gupta, U.; Chen, F.; Zhu, J. Modelling and Control of a Novel Soft Crawling Robot Based on a Dielectric Elastomer Actuator. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 1–9. [Google Scholar]
- Rizzello, G.; Naso, D.; York, A.; Seelecke, S. Modeling, Identification, and Control of a Dielectric Electro-Active Polymer Positioning System. IEEE Trans. Control Syst. Technol. 2015, 23, 632–643. [Google Scholar] [CrossRef]
- Rizzello, G.; Naso, D.; York, A.; Seelecke, S. Closed loop control of dielectric elastomer actuators based on self-sensing displacement feedback. Smart Mater. Struct. 2016, 25, 035034. [Google Scholar] [CrossRef]
- FOMCON. FOMCON Toolbox for Matlab. Available online: http://fomcon.net/ (accessed on 10 December 2020).
- Xue, D.; Chen, Y.; Atherton, D. Linear Feedback Control: Analysis and Design with MATLAB (Advances in Design and Control); Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2008. [Google Scholar]
- 3M™. 3M™ VHB™ Tape 4910. Available online: http://www.3m.com/3M/en_US/company-us/all-3m-products/~/3M-VHB-Tape-4910?N=5002385+3293242444&rt=rud (accessed on 24 July 2020).
- Conductive, B. Electric Paint. Available online: https://www.bareconductive.com/shop/electric-paint-50ml/ (accessed on 11 July 2020).
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models; Imperial College Press: London, UK, 2010; pp. 51–63. [Google Scholar]
- Lewandowski, R.; Chorążyczewski, B. Identification of the parameters of the Kelvin-Voigt and the Maxwell fractional models, used to modeling of viscoelastic dampers. Comput. Struct. 2010, 88, 1–17. [Google Scholar] [CrossRef]
- Diethelm, K. The Analysis of Fractional Differential Equations: An Application-Oriented Exposition Using Differential Operators of Caputo Type; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Timi, K.; Tomaž, V.; Janez, G.; Boštjan, R.; Karl, G. Parameters identification method for viscoelastic dielectric elastomer actuator materials using fractional derivatives. Mater. Res. Express 2018, 5, 075702. [Google Scholar]
- Karner, T.; Gotlih, J.; Razboršek, B.; Vuherer, T.; Berus, L.; Gotlih, K. Use of single and double fractional Kelvin-Voigt model on viscoelastic elastomer. Smart Mater. Struct. 2019, 29, 015006. [Google Scholar] [CrossRef]
- Monje, C.; Chen, Y.; Vinagre, B.; Xue, D.; Feliu, V. Fractional Order Systems and Control—Fundamentals and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Xue, D. FOFT Toolbox. Available online: https://www.mathworks.com/matlabcentral/fileexchange/60874-fotf-toolbox (accessed on 7 August 2020).
- Tepljakov, A. Fractional-Order Modeling and Control of Dynamic Systems; Springer International Publishing: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Karner, T.; Žefran, M.; Gotlih, K. Using Fractional Derivatives for Parameter Identification and Control of Dielectric Elastomer Actuators; Springer: Cham, Switzerland, 2019; pp. 2469–2479. [Google Scholar]
- Lewis, R.M.; Torczon, V.; Trosset, M.W. Direct search methods: Then and now. J. Comput. Appl. Math. 2000, 124, 191–207. [Google Scholar] [CrossRef] [Green Version]
- Sabatier, J.L.; Melchior, P.; Oustaloup, A. Fractional Order Differentiation and Robust Control Design: CRONE, H-infinity and Motion Control; Springer: Dordrecht, The Netherlands, 2015. [Google Scholar]
- Hackl, C.M.; Tang, H.-Y.; Lorenz, R.D.; Turng, L.-S.; Schroder, D. A Multidomain Model of Planar Electro-Active Polymer Actuators. IEEE Trans. Ind. Appl. 2005, 41, 1142–1148. [Google Scholar] [CrossRef]
- TMS320F28069M. Texas Instruments. Available online: http://www.ti.com/product/TMS320F28069M (accessed on 23 October 2020).
- Wenglor. YP05MGV80. Available online: https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&ved=2ahUKEwihnaWa0bbjAhXiB50JHWepBx0QFjAAegQIBhAC&url=http%3A%2F%2Fwww.shintron.com.tw%2Fproimages%2Ftakex%2Fwenglor%2FYP05MGV80.pdf&usg=AOvVaw0hZdH3GNiqDLpm9BclkSVw (accessed on 15 July 2020).
- Design, A. E1 Series 1 Watt. Available online: http://apowerdesign.com/products/E/E1/ (accessed on 23 October 2020).









| λ | μ | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Initial param. | 1 | 1 | 1 | 0.5 | 0.5 | ||||
| Optimal param. | 0 | 6.58 | 0.53 | 0.5 | 0.5 | 0.014 | 0.92 | 0 | |
| PID | Comp. parameters | 0 | 6.58 | 0.53 | 1 | 1 | 0.004 | 8.98 | 10.8 |
| Initial param. | 1 | 1 | 1 | 0.5 | 0.5 | ||||
| Optimal param. | 3.46 | 100 | 0.16 | 0.47 | 0.81 | 0.007 | 0.04 | 3 | |
| PID | Comp. parameters | 3.46 | 100 | 0.16 | 1 | 1 | 0.009 | 0.22 | 1.6 |
| Initial param. | 1 | 1 | 1 | 0.5 | 0.5 | ||||
| Optimal param. | 1 | 1 | 1 | 0.09 | 0.7 | 0.004 | 1.93 | 5 | |
| PID | Comp. parameters | 1 | 1 | 1 | 1 | 1 | 0.004 | 5.9 | 1.62 |
| Initial param. | 5.66 | 7.17 | 0.03 | 0.5 | 0.5 | ||||
| Optimal param. | 0 | 23.18 | 1.25 | 0.5 | 0.5 | 0.014 | 0.92 | 0 | |
| PID | Comp. parameters | 0 | 23.18 | 1.25 | 1 | 1 | 0.004 | 9.49 | 3.6 |
| Initial param. | 5.66 | 7.17 | 0.03 | 0.5 | 0.5 | ||||
| Optimal param. | 1.91 | 100 | 0.18 | 0.46 | 0.79 | 0.011 | 0.04 | 2.8 | |
| PID | Comp. parameters | 1.91 | 100 | 0.18 | 1 | 1 | 0.012 | 0.24 | 3 |
| Initial param. | 5.66 | 7.17 | 0.03 | 0.5 | 0.5 | ||||
| Optimal param. | 5.66 | 7.17 | 0.03 | 0.86 | 0.9 | 0.01 | 0.75 | 0 | |
| PID | Comp. parameters | 5.66 | 7.17 | 0.03 | 1 | 1 | 0.015 | 0.75 | 0 |
| averages | 0.010 | 0.77 | 1.16 | ||||||
| PID averages | 0.008 | 4.26 | 3.44 | ||||||
| Laplace TF | Simulink Contin. | Simulink Discrete | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| λ | μ | |||||||||||||
| PID | 0 | 6.58 | 0.53 | 1 | 1 | 0.004 | 8.98 | 10.8 | 0.38 | 9.9 | 47 | 0.38 | 9.6 | 68 |
| 0 | 6.58 | 0.53 | 0.5 | 0.5 | 0.014 | 0.92 | 0 | 0.014 | 1 | 28 | 0.014 | 0.85 | 15 | |
| PID | 3.46 | 100 | 0.16 | 1 | 1 | 0.009 | 0.22 | 1.6 | 0.04 | 0.42 | 30 | 0.04 | 0.42 | 30 |
| 3.46 | 100 | 0.16 | 0.47 | 0.81 | 0.007 | 0.04 | 3 | 0.01 | 0.12 | 46 | 0.01 | 0.12 | 43 | |
| PID | 1.91 | 100 | 0.18 | 1 | 1 | 0.092 | 0.24 | 3.10 | 0.05 | 0.75 | 48 | 0.050 | 0.75 | 48 |
| 1.91 | 100 | 0.18 | 0.46 | 0.79 | 0.008 | 0.04 | 2.80 | 0.010 | 0.11 | 45 | 0.010 | 0.11 | 42 | |
| PID | 5.66 | 7.17 | 0.03 | 1 | 1 | 0.011 | 0.75 | 0.00 | 0.05 | 0.36 | 1 | 0.05 | 0.35 | 1 |
| 5.66 | 7.17 | 0.03 | 0.86 | 0.9 | 0.01 | 0.75 | 0.50 | 0.02 | 0.30 | 0 | 0.02 | 0.31 | 1 | |
| PID | 1 | 1 | 1 | 1 | 1 | 0.004 | 5.9 | 1.62 | 1.24 | 8.20 | 20 | 1.24 | 8.20 | 20 |
| 1 | 1 | 1 | 0.09 | 0.7 | 0.004 | 1.93 | 5 | 0.35 | 8.42 | 1 | 0.48 | 2.56 | No. | |
| PID | 0 | 23.1 | 1.25 | 1 | 1 | 0.004 | 9.49 | 3.6 | 0.28 | 9.90 | 96 | 0.220 | 9.90 | 90 |
| 0 | 23.1 | 1.25 | 0.5 | 0.5 | 0.009 | 0.22 | 0 | 0.015 | 0.23 | 4 | 0.040 | 0.22 | 2 | |
| Exp. Number | R [%] | Steady-State Error | |||||
|---|---|---|---|---|---|---|---|
| 0 | 5.6 | 0.03 | 7.1 | 15.8 | 31.7 | 2.8 | No |
| 1 | 5.6 | 7.1 | 0.03 | 2 | 24.8 | 33.1 | No |
| 2 | 0 | 23.1 | 1.2 | 3.2 | No | 32.9 | Yes |
| 3 | 3.4 | 100 | 0.1 | 2.5 | No | 19.4 | Yes |
| 4 | 5.6 | 7.1 | 0.03 | 2.7 | 9.4 | 4.3 | No |
| 5 | 0 | 23.1 | 1.2 | 1.8 | No | 51.18 | Yes |
| 6 | 5.6 | 7.1 | 100 | 2.3 | 11 | 5 | No |
| 7 | 0.1 | 7.1 | 100 | 2.3 | No | 19.7 | Yes |
| 8 | 5.6 | 7.1 | 100 | 1.3 | 10.7 | 17.4 | No |
| 9 | 63 | 63 | 61 | 1.2 | 14.4 | 33.6 | No |
| 10 | 5.6 | 7.1 | 0.03 | 1.5 | 9.1 | 7.9 | No |
| 11 | 5.5 | 7.1 | 0.03 | 1.7 | No | 30.6 | Yes |
| 12 | 3.4 | 100 | 0.1 | 1.4 | No | 25.2 | Yes |
| 13 | 0 | 23.1 | 1.2 | 6.1 | 23.6 | 18 | No |
| 14 | 0 | 23.1 | 1.2 | 2.2 | 25.2 | 34.2 | Yes |
| 15 | 0 | 23.1 | 1.2 | 4.8 | 24.1 | 24.2 | No |
| 16 | 0 | 23.1 | 1.2 | 1.2 | No | 54.8 | Yes |
| 17 | 5.6 | 7.1 | 0.03 | 1.5 | 11.8 | 6 | No |
| Exp. | λ | μ | R [%] | Steady-State Error | |||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 3.4 | 100 | 0.16 | 0.47 | 0.81 | 2.7 | 33.6 | 13.4 | Yes |
| 1 | 1.9 | 100 | 0.18 | 0.46 | 0.79 | No | 40 | 0 | Yes |
| 2 | 5.6 | 7.1 | 0.03 | 0.86 | 0.9 | 2.7 | 40 | 54.7 | Yes |
| 3 | 5.6 | 7.1 | 0.03 | 0.86 | 0.9 | 1 | 40 | 146 | Yes |
| 4 | 5.6 | 7.1 | 0.03 | 0.86 | 0.9 | 1.2 | 40 | 0 | Yes |
| 5 | 1.91 | 100 | 0.18 | 0.47 | 0.81 | No | 10 | 0 | Yes |
| 6 | 5.6 | 7.1 | 0.03 | 0.98 | 0.9 | 1.4 | 25 | 0 | Yes |
| 7 | 5.6 | 23.1 | 0.03 | 0.86 | 0.9 | 1 | 30 | 0 | Yes |
| 8 | 0 | 23.1 | 0.03 | 0.5 | 0.5 | 1.1 | 10 | 0 | Yes |
| 9 | 0 | 23.1 | 1.2 | 0.5 | 0.5 | 1 | 25 | 14.2 | Yes |
| 10 | 0 | 23.1 | 1.2 | 0.5 | 0.5 | 1 | 4.2 | 2.2 | Yes |
| 11 | 5.6 | 7.1 | 0.03 | 0.86 | 0.9 | 1 | 7.4 | 5.4 | 1% |
| 12 | 5.6 | 7.1 | 0.03 | 0.9 | 0.9 | 1 | 15 | 0 | Yes |
| 13 | 5.6 | 7.1 | 0.03 | 0.6 | 0.9 | 1 | 15 | 0 | Yes |
| 14 | 5.6 | 7.1 | 0.03 | 0.6 | 0.8 | 1 | 5.8 | 0 | <1% |
| 15 | 5.6 | 7.1 | 0.03 | 0.5 | 0.9 | 1 | 4.3 | 9 | 1% |
| Exp. | λ | μ | Overshoot [%] | Steady-State Error | |||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 5.6 | 7.1 | 0.03 | 1 | 1 | 2.4 | 9.4 | 4.3 | No |
| 1 | 5.6 | 7.1 | 0.03 | 1 | 1 | 2.1 | 11 | 5 | No |
| 2 | 5.6 | 7.1 | 0.03 | 1 | 1 | 1.3 | 10.7 | 17.4 | No |
| 3 | 5.6 | 7.1 | 0.03 | 1 | 1 | 1.4 | 9.1 | 7.8 | No |
| 4 | 5.6 | 7.1 | 0.03 | 1 | 1 | 1.3 | 11.8 | 6 | No |
| 5 | 5.6 | 23.1 | 1.2 | 0.5 | 0.5 | 1 | 4.2 | 2.2 | No |
| 6 | 5.6 | 7.1 | 0.03 | 0.86 | 0.9 | 1 | 7.4 | 5.4 | 1% |
| 7 | 5.6 | 7.1 | 0.03 | 0.6 | 0.8 | 1 | 5.8 | 0.6 | <1% |
| 8 | 5.6 | 7.1 | 0.03 | 0.5 | 0.9 | 1.1 | 4.3 | 9 | 1% |
| Exp. | λ | μ | Overshoot [%] | Steady-State Error | |||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 5.6 | 7.1 | 0.03 | 0.8 | 0.9 | 0.12 | 0.41 | 0 | No |
| 1 | 5.6 | 7.1 | 0.03 | 1 | 1 | 0.13 | 0.44 | 0 | No |
| 2 | 5.6 | 7.1 | 0.03 | 0.868 | 0.9 | 0.09 | 0.44 | 5 | No |
| 3 | 5.6 | 7.1 | 0.03 | 1 | 1 | 0.09 | 0.68 | 3 | No |
| 4 | 5.6 | 7.1 | 0.03 | 0.6 | 0.8 | 1.13 | 5.84 | 0.6 | <1% |
| 5 | 5.6 | 7.1 | 0.03 | 1 | 1 | 1.54 | 9.14 | 7.8 | No |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karner, T.; Gotlih, J. Position Control of the Dielectric Elastomer Actuator Based on Fractional Derivatives in Modelling and Control. Actuators 2021, 10, 18. https://doi.org/10.3390/act10010018
Karner T, Gotlih J. Position Control of the Dielectric Elastomer Actuator Based on Fractional Derivatives in Modelling and Control. Actuators. 2021; 10(1):18. https://doi.org/10.3390/act10010018
Chicago/Turabian StyleKarner, Timi, and Janez Gotlih. 2021. "Position Control of the Dielectric Elastomer Actuator Based on Fractional Derivatives in Modelling and Control" Actuators 10, no. 1: 18. https://doi.org/10.3390/act10010018
APA StyleKarner, T., & Gotlih, J. (2021). Position Control of the Dielectric Elastomer Actuator Based on Fractional Derivatives in Modelling and Control. Actuators, 10(1), 18. https://doi.org/10.3390/act10010018






