Re-Examining the Public–Catholic School Gap in STEM Opportunity to Learn: New Evidence from HSLS

Abstract

This paper examines public–Catholic gap in STEM opportunity to learn in the US using Mahalanobis-distance matching and adjacent categories models. Consistent with prior studies, there are significant public–Catholic differences in math and science course sequence level and total credits earned. However, we find that these gaps are largely accounted for by selection processes among students of differing family background. Moreover, we find that the Catholic school advantage in STEM opportunity to learn differs by subject; Catholic school students are more likely to enroll in advanced math courses relative to middle-level courses, while their advantage in science is concentrated in the middle of the course-taking hierarchy.

1. Introduction

Examining differences in course taking across school sectors (i.e., public schools vs. Catholic schools) in the US provides insight into how differential access to selective schools affects opportunity to learn and may contribute to educational inequality. Bryk, Lee, and Holland’s classic book on Catholic schooling provided evidence that US Catholic school students took more numerous and more rigorous academic courses, compared with peers in public schools (Bryk et al. 1993; see also the 1985 special issue of Sociology of Education on this topic). Motivated in part by this sector disparity, beginning in the early 1990s, with a wave of standards-based reform policies, public schools started to develop and adopt new standards for high school course taking. Several studies examined the effectiveness of this series of policies on reducing the long-lasting school sector gap (e.g., Carbonaro and Covay 2010) and on improving students’ overall course-taking outcomes (e.g., Domina and Saldana 2012). Carbonaro and Covay (2010), for instance, argued that the private school advantage in course taking still existed in the 2000s, albeit at very small levels after accounting for student achievement differences across sector. Admission to private schools has become increasingly constrained in recent decades, with fewer students from poor or near-poor households, as well as one-parent households or households with only nonparental guardians, and those whose parents’ highest education level is equal to or less than a high school diploma enrolling in private schools (Cahalan and National Center for Education Statistics 2006; Wang et al. 2019). Thus, family background continues to interact with school-to-school differences in opportunity to learn to create educational inequality. The release of the High School Longitudinal Study (HSLS): 09 Transcript data in 2015 offers a new opportunity to re-examine the public–private gap in students’ STEM learning opportunities. With the help of HSLS:09, we, herein, investigate recent sector differences in STEM opportunity to learn using rigorous, fine-grained measures of course taking.

Standards-based school reforms aim to increasingly improve academic standards, enforce accountability, and pose higher graduation requirements for public school students. Evidence from the National Science Foundation (NSF) documents the effects of this set of policy initiatives. As of 2012, over 25 states have adopted “completing algebra II” as a high school graduation requirement for mathematics and “two years of science courses” for science (National Science Board (US) 2016). Considering higher level courses, the number of students who took at least one AP course approximately doubled from 2006 to 2016 (National Science Board (US) 2008, 2018; see also Chaney et al. (1997) for discussion of graduation requirements). This evidence highlights two important dimensions of students’ course taking, the number of academic courses taken, and the overall difficulty of coursework. Incorporating this dual emphasis, in this study, we analyze sector differences in the number of math and science courses taken in high school as well as course difficulty, measured by constructing a scale of math and science course sequence levels from 9th to 12th grade (Kelly 2004, 2009; Riegle-Crumb 2006; Stevenson et al. 1994).

To more clearly identify the effect of differences in academic press (Shouse 1996) across the school sector, as opposed to responsiveness to the achievement level of the student body and other selection mechanisms, we employ Mahalanobis-distance matching to examine sector differences in course taking among similar students in the HSLS:09. Similar students are identified by selection factors affecting the likelihood of attending Catholic school including family background variables, student demographic information, home learning environments, and prior learning experiences. Furthermore, we investigate the school sector gap at different levels of STEM course taking. Several studies argue that the school sector gap in math achievement gains are not equivalent across the spectrum of math skills (Carbonaro and Covay 2010; Hyde et al. 2008), with the Catholic school advantage concentrated in advanced math skills. This suggests that the standards-based reform movement may have different effects on the sector gap in higher-level courses than on overall course taking. Therefore, we examine the effect of Catholic school attendance on course-taking across different levels of the STEM course-taking hierarchy using adjacent categories models (Carbonaro and Covay 2010; Fullerton 2009).

Consequently, our research questions are as follow: (1) Are there public–Catholic differences in STEM course sequence level and/or the total amount of coursework taken? (2) Does family background and other non-school factors account for observed school sector differences in STEM course-taking outcomes? (3) Do sector differences in STEM course-taking outcomes differ across the course-taking hierarchy?

By exploring sector differences in STEM opportunity to learn using several specifications, our work not only provides insights on the specific dimensions of persisting school sector differences, but also points out the continuing need and potential to improve the rigor of course taking in public schools.

2. Background Literatures

2.1. High School STEM Learning: An Opportunity to Learn Perspective

Research on STEM education provides empirical evidence in understanding students’ pathway from early STEM experiences through the STEM workforce. High school math and science learning is critical in the development of students’ interests in STEM disciplines and entrance into STEM majors (Wang 2013), as high school learning experiences may enable students to create perceptions of themselves as STEM learners and to prepare themselves for post-secondary STEM learning (Mickelson et al. 2016; Riegle-Crumb and King 2010). One way to examine high school STEM learning is through the lens of math and science achievement (e.g., Crisp et al. 2009). However, in understanding the disparity in STEM learning outcomes between advantaged populations and underserved populations, achievement outcomes alone do not fully capture differences in schooling (e.g., Flores 2007; Martin 2009; Vanneman et al. 2009). Flores (2007), for instance, argued that studies solely focusing on achievement have rarely identified the root causes of achievement gaps. An alternative approach to examining disparities in learning outcomes is to focus on opportunity gaps, which highlight how structural and institutional inequalities may lead to achievement disparities (Martin 2009).

In general, the opportunity to learn perspective emphasizes the opportunity that students have been provided through schooling (Wilhelm et al. 2017). As one of the earliest studies on this topic, Sørenson and Hallinan (1977) conceptualized opportunity to learn (OTL) as an interactive mechanism, where characteristics of schooling and teaching moderate the role of ability and effort. In theory, this could mean that greater OTL exacerbates inequality, but explicitly compensatory processes are also in place in contemporary schools (Northrop 2017; Rowan et al. 2009), and the intensity of school relative to learning out-of-school is an important determinant of inequality (Downey and Condron 2016). More basically, the concept of opportunity to learn helps explain school-to-school differences in achievement growth (Montt 2011; Martin 2009). Within this framework, dimensions of schooling that affect learning include teacher characteristics and instructional quality (e.g., Kelly 2010; Kelly and Majerus 2011; Northrop and Kelly 2018; Minor et al. 2015); the degree of exposure to rigorous educational content (e.g., Hansen and Strietholt 2018; Northrop et al. 2019); and even basic physical resources and availability of learning materials and technology (e.g., Krashen et al. 2012).

Although there have been efforts to construct integrative measures of OTL (e.g., Bottia et al. 2018; Montt 2011), much research focuses on discrete educational processes and constructs that might be readily manipulated (Bottia et al. 2018). In this paper, we limit our instantiation of STEM opportunity to learn (OTL) to students’ exposure to rigorous math and science courses in high school. We also acknowledge that there are inherent differences between the degree of actual exposure to STEM courses and the underlying accessibility of STEM courses, as the selection and completion of high school math and science courses can be affected by both course availability (Tytler et al. 2008) and selection and placement mechanisms. Overall, the goal of this paper is to understand how entering a given school sector enables/constrains students’ richer experiences in STEM course taking.

2.2. Curricular Differentiation, and OTL across Countries

Curricular differentiation is a rational approach to tailoring instruction to better match students’ learning needs but may ultimately generate greater educational inequality especially at the secondary level (Gamoran and Mare 1989; Kelly 2019). Historically, the US school system stratified students into different levels of curriculum content based on their learning capacities and types of occupational preparation, which resulted in highly differentiated learning opportunities (Sørenson 1970; Spring 1976). Internationally, grouping students within a school based on level of ability and preparation is not the only means of exposing students to different course-taking experiences. Curricular differentiation can also occur across school type or geographic location (Montt 2011). For instance, Van Houtte and her colleagues studied within-school tracking (multilateral schools) and between-school tracking (categorial schools) in the Flemish (Belgium) school system and found that greater differences were associated with within-school tracking, in terms of students’ study involvement (Van Houtte and Stevens 2009) and self-esteem (Van Houtte et al. 2012). Hanushek and Wößmann (2006) also reported that sorting students based on test scores in the early years of schooling increased inequality with little effect on overall national scores.

2.3. Course-Taking, School Sector Gaps, and Standards-Based Reform

Since the 1980s, the debate over sector effects on students’ opportunity to learn have been informed by multiple large-scale longitudinal data collections in the US. Early studies reported that, compared to their public-school peers, Catholic school students took more academic courses, experienced higher achievement gains, and reported receiving higher quality instruction (Bryk et al. 1993; Coleman et al. 1982; Gamoran 1996; Hoffer 1997). For instance, in 1982, Catholic school students, on average, took approximately one additional year of academic math courses than public school students (Bryk et al. 1993). Catholic schools encourage students to take more academic courses by (1) assigning students into the academic track, (2) providing more academic and fewer elective courses, and (3) posing high graduation requirements (Bryk et al. 1993). In contrast, course enrollment in public schools of that era was described as akin to a “shopping mall” experience where students enrolled in courses based on their own inclinations with little oversight (Powell et al. 1985).

McDill et al. (1986) refer to this institutional-level emphasis on academic climate as academic press, meaning “a normative emphasis on academic excellence and conformity to specified academic standards.” Lee and Smith (1999) identified both internal and external factors that motivated a school to improve its academic press, including teachers’ expectations for student performance within schools, as well as externally imposed standards. As McDill et al. (1986) noted, the underlying rationale for higher standards included the argument that nationwide standards were not competitive when compared to educational systems internationally. Beginning in the 1990s, with a wave of standards-based school reform policies, policy groups started to develop higher curricular standards for instruction and learning (Department of Education (US) and Standards National Council on Education, and Testing 1992). As conceptualized in the opportunity to learn literature, improving instructional quality and exposing students to rigorous learning content are core tenants of standards-based reform (e.g., Minor et al. 2015; Montt 2011). Further, much of the standards-based reform movement adopted an explicit focus on reducing school-to-school differences in opportunity to learn (Minor et al. 2015).

In the wake of substantial standards-based school reform efforts, there is no doubt that public school students experience greater opportunity to learn, especially in terms of basic course-taking patterns and achievement growth (Domina and Saldana 2012; National Science Board (US) 2008, 2016, 2018). Domina and Saldana (2012) found that, over a two-decade period of change, the average high school graduate took approximately five more academic credits. Furthermore, US high school graduates took more advanced math credits from 1982 to 2004 as well. By 2004, approximately 43% of high school graduates earned credits in trigonometry or higher math courses whereas only 19% of high school graduates in the class of 1982 completed trigonometry or higher math courses (changes for public school students only are similar). However, improvements in the absolute mean level of course taking (i.e., a “rising tide” of course taking) do not necessarily mean that a decline in relative inequality between specific student groups will occur, even if all groups have experienced some improvement. For example, Domina et al. (2016) argue that during this period, socially advantaged groups created more advanced academic pathways, such as taking both Algebra and Geometry during eighth grade, to maintain their academic advantage.

Yet, given the generally widespread improvements in opportunity to learn for public school students occurring as a result of increased course-taking standards, we might expect to find a decline in the traditional Catholic school achievement advantage. Carbonaro (2003, 2006) reported that by the 1990s, public school students enjoyed similar achievement gains compared to their counterparts in private schools at the kindergarten and elementary level. However, in their more recent research using the Education Longitudinal Study (ELS), Carbonaro and Covay (2010) found that, at the high school level, private school students still took more academic math courses and thus enjoyed greater math achievement gains. Indeed, in the ELS data, the sector gaps in achievement growth that remain after accounting for selection processes are largely accounted for by differences in course-taking (Carbonaro and Covay 2010).

3. Methodology

3.1. Data

In this study, we use the High School Longitudinal Study of 2009 (HSLS:09) data from the US National Center of Educational Statistics (NCES). HSLS: 09 is a nationally representative longitudinal study of over 20,000 9th grade students from over 900 schools across the country beginning in 2009, with two waves of follow-up study in 2012 and 2016 (and a few minor updates in-between major follow-ups). The survey instruments include information from a student questionnaire, parent questionnaire, teacher questionnaire, and a school administrator questionnaire, with a specific focus on students’ STEM learning. HSLS:09 also features transcript data, which allow for full exploration of students’ course taking. Transcript data were collected in 2013–2014 and include course-taking records for each course that every student took during their high school study—there are over 1 million raw transcript records in HSLS. Approximately 70% of the transcript records are valid, containing course name, year/semester, credits and grade earned, and other identification information.

3.2. Dependent Variables

Two sets of dependent variables were developed to provide an overall picture of students’ course taking: Math and science course sequence levels, and the total credits earned. To capture students’ cumulative mathematics course taking, we assigned each student a unique Mathematic Course Sequence (MCS) code indicating the difficulty level of the combination of courses taken by the end of 12th grade. The MCS codes start with 1–less than algebra I and end with 9–calculus or higher, often based on identification of joint courses (e.g., Level 3 is Algebra I and Geometry). Students with higher MCS values have deeper and richer mathematic learning experiences than students with lower values. The full cumulative Mathematics Course Taking codes are shown in

Table 1. Cumulative Mathematic Course Sequence (MCS) Codes.

Mathematic Course Sequence (MCS)	Content
1	Less than Algebra I
2	Algebra I or Geometry, but not both
3	Algebra I and Geometry
4	Algebra I or Geometry, with at least one transition course
5	Algebra II
6	Algebra II with at least one math elective course
7	Algebra III or Trigonometry, but not both
8	Algebra III and Trigonometry
9	Calculus or higher

(see also Appendix A for a full description of the coding process).

Different in some respects from math courses, science courses vary in their disciplinary content (e.g., biology, chemistry, and physics, often referred to as the “big-three” in the popular press). Therefore, in addition to codes for sequential course difficulty/level (e.g., Biology I vs. Biology II), the Science Course Sequence (SCS) coding includes simple counts of disciplinary categories taken. The full cumulative Science Course Taking codes are shown in

Table 2. Cumulative Science Course Sequence (SCS) Codes.

Science Course Sequence (SCS)	Content
1	No big-three course (Physics, Chemistry, Biology)
2	One big-three course
3	Two big-threes without higher-level course
4	Three big-three without higher-level course
5	Two or three big-threes with at least one higher-level course

(see also Appendix B for a full description of the coding process).

Finally, the total number of mathematics and science course credits taken are also calculated. We investigate total credits earned rather than number of courses taken, because some courses are divided across multiple semesters/years, and not all courses are credit bearing.

3.3. Analytic Strategy

As a result of increased course-taking standards, we may expect to observe a decline in the advantage of Catholic school attendance in terms of OTL. In this article, we employ two analytical methods to examine the effect of Catholic school attendance on course taking in the era of standard-based reform. First, we use Mahalanobis-distance kernel matching to study sector effects on course taking in the context of selection bias (we use kmatch in Stata, see Jann (2017) for technical details and King and Nielsen (2019) for further discussion). Mahalanobis-distance matching is a general form of multivariate distance matching with the idea of creating a multivariate space of covariates X and matching based on the distance metric between observations (Diamond and Sekhon 2013). The multivariate distance between two observations, i and j has the form,

$$MD\left(X_i,X_j\right)=\sqrt{{\left(X_i-X_j\right)}^T{S}^{-1}\left(X_i-X_j\right)}$$

where S is the scaling matrix of X and X^T is the transpose matrix of X. As King and Nielsen (2019) argued, multivariate distance matching is more efficient, has less model dependence, and can improve balance relative to traditional covariate adjustment or propensity score matching. To find potential matches based on multivariate distance and determine the matching weights, we use a Kernel matching algorithm, which provides a non-parametric estimation of outcomes using Kernel weights. The Kernel weight is defined as (Frölich 2004),

$$W\left(i,j\right)=\frac{K(\varnothing )}{{\displaystyle \sum }K(\varnothing )}$$

where K() is the Kernel function, and $\varnothing$ is the matching quality function, given by:

$$\varnothing =\frac{M{D}_j-M{D}_i}{h_n}$$

where $h_n$ is the bandwidth of matching. Bandwidth selection was informed by checking the quality of covariate balance and was set to 1.2 after comparing different matching results. Selection factors affecting the likelihood of attending Catholic school include family background variables, student demographic information, home learning environments, and prior learning experiences. Description of all student-level covariates is provided in

Table 3. Descriptive statistics for student-level covariates.

	Sector Means (SE)
Student-Level Covariates	Catholic (n = 1851)	Public (n = 12,671)	Raw Difference
Took Algebra I before 9th grade (1 for yes)	0.30 (0.011)	0.27 (0.0038)	0.033 (0.011) **
Math Std. score at the start of 9th grade	54.71 (0.20)	50.67 (0.087)	4.04 (0.24) ***
Family SES	0.55 (0.017)	−0.045 (0.0064)	0.60 (0.018) ***
Middle school sector (1 for Private)	0.75 (0.0010)	0.022 (0.0012)	0.073 (0.005) ***
Frequency of reading science book before HS	2.22 (0.036)	2.19 (0.013)	0.030 (0.038)
Hispanic	0.15 (0.0083)	0.17 (0.0032)	−016 (0.009) ~
Gender (1 for male)	0.50 (0.012)	0.49 (0.0043)	0.016 (0.012)
Black	0.11 (0.014)	0.058 (0.0085)	0.053 (0.023) *
Asian	0.095 (0.014)	0.016 (0.0083)	0.079 (0.23) ***
Frequency of taking other courses with mother before HS	0.42 (0.036)	0.19 (0.016)	0.23 (0.046) ***
Frequency of participating math/science activity before HS	0.64 (0.026)	0.72 (0.011)	−0.082 (0.031) **
8th grade most advanced science course	2.35 (0.030)	2.07 (0.015)	0.28 (0.040) ***
8th grade most advanced math course	3.34 (0.032)	2.91 (0.017)	0.43 (0.046) ***
Frequency of using computer for learning before HS	2.23 (0.038)	2.16 (0.015)	0.069 (0.042) ~
Frequency of taking math courses with mother before HS	0.21 (0.041)	0.031 (0.017)	0.18 (0.048) ***
Frequency of taking science courses with mother before HS	0.43 (0.035)	0.24 (0.015)	0.19 (0.041) ***

^~p < 0.10. * p < 0.05. ** p < 0.01. *** p < 0.001.

. It is worthwhile to note that, as Altonji et al. (2005) suggest, we include middle school sector (private or public) as an important factor to address selection bias. Middle school sector is not directly measured in HSLS:09. Fortunately, the NCES School ID for 8th grade school attended is available and can be matched to School IDs in either the Common Core Data (CCD, a national database for all public elementary and secondary schools) or the Private School Universe Survey (PSS, a national representative survey on private elementary and secondary schools).

Then, using the extracted matched sample, we further control for school-level covariates (e.g., geographic regions, instructional resources, and racial composition) using regression methods (Stuart 2010). We use ordered logit regression models to estimate the effect of Catholic school attendance on student course-taking outcomes after controlling for school-level mediating effects. The logistic regressions take the form of:

$$logit\left[P\left(Y_i\le t\right)\right]={\beta }_0+{\beta }_1\left(Catholic\right)+\gamma X_i+\epsilon$$

where $t=1,2,\dots , M$, and $M$ is maximum value of the corresponding course sequence, ${\beta }_1$ is the effect of Catholic schools, $X_i$ is the vector of school level covariates, and standard errors are clustered by school ID.

Table 4. Descriptive statistics for school-level covariates.

	Sector Means (SE)
	Public (n = 12,671) a	Catholic (n = 1851)	Raw Difference
Require high-level Science courses b	0.091 (0.0025)	0.47 (0.012)	0.38 (0.0079) ***
Full-time teacher ratio	0.96 (0.00058)	0.88 (0.0032)	−0.081 (0.0020) ***
Mean math achievement	50.56 (0.040)	54.75 (0.096)	4.19 (0.11) ***
Mean SES	−0.050 (0.0031)	0.55 (0.067)	0.60 (0.0087) ***
Require high-level Math courses b	0.11 (0.0027)	0.51 (0.012)	0.40 (0.0084) ***
Offer advanced Physics courses b	0.44 (0.0043)	0.53 (0.012)	0.090 (0.012) ***
Offer advanced Chemistry courses b	0.59 (0.0043)	0.66 (0.011)	0.065 (0.012) ***
% of Hispanic students	13.90 (0.18)	9.69 (0.33)	−4.20 (0.49) ***
Offer Calculus courses b	0.74 (0.0038)	0.85 (0.0082)	0.11 (0.011) ***
Offer advanced Biology courses b	0.65 (0.0041)	0.70 (0.011)	0.043 (0.012) ***
% of Black students	13.23 (0.16)	8.92 (0.30)	−4.31 (0.43) ***
% of Asian students	3.23 (0.061)	4.93 (0.25)	1.70 (0.19) ***
% free lunch students	38.15 (0.20)	5.29 (0.34)	−32.86 (0.55) ***
Urbanicity
Suburb	0.36 (0.0042)	30 (0.011)	−0.57 (0.012) ***
Town	0.13 (0.0029)	0.14 (0.0081)	0.014 (0.0083) ~
Rural	0.28 (0.0039)	0.019 (0.0031)	−0.26 (0.010) ***
Block schedule	0.45 (0.0043)	0.19 (0.0091)	−0.26 (0.012) ***
Region
Midwest	0.24 (0.0037)	0.31 (0.011)	0.068 (0.011) ***
South	0.41 (0.0043)	0.33 (0.011)	−0.082 (0.012) ***
West	0.20 (0.0034)	0.091 (0.0066)	0.10 (0.0095) ***

^a Stand errors are in parenthesis. ^b 1 for offering or requiring corresponding courses. ^~ p < 0.10. * p < 0.05. ** p < 0.01. *** p < 0.001.

provides a description of all school-level covariates.

As an alternative to the main matching-based modeling strategy, we also employ more traditional covariate adjustment in a series of ordered logistic multilevel models. These models share a similar functional form,

$$\begin{gathered} Level1:logit\left[P\left(Y_{ij}\le t\right)\right]={\beta }_{0j}+{{\displaystyle \sum }}_{k=1}^{16}{\beta }_{kj}{X}_{ij}+{\gamma }_{ij}{\gamma }_{ij}~N\left(0,{\sigma }^2\right) \\ Level2:{\beta }_{0j}={\gamma }_{00}+{\gamma }_{01}Catholi{c}_j+{{\displaystyle \sum }}_{m=2}^{14}{\gamma }_{0m}{S}_j+{\mu }_{0j}{\mu }_{0j}~N\left(0,{\tau }_{00}\right) \\ {\beta }_{1j}={\gamma }_{10},\dots ,{\beta }_{mj}={\gamma }_{m0},\dots ,{\beta }_{16j}={\gamma }_{160} \end{gathered}$$

where $t=1,2,\dots , M$, and $M$ is maximum value of the corresponding course sequence, $X_{ij}$ are student-level covariates for student i in school j, ${\gamma }_{01}$ is the effect of Catholic schools, and $S_j$ are school-level covariates for school j. To compare ordered logistic regression coefficients across models, we explored both the KHB method (Kohler et al. 2011; see also Karlson et al. 2012) and linear probability model calculations to address the issues of confounding and re-scaling that arises in logistic model specifications. In the present data, when estimating the percentage reduction in the key sector effect due to mediation (i.e., the total effect of student background and other compositional variables in this study), calculations using the KHB and linear probability specification produce similar results. However, the KHB method was not developed specifically to address the scaling issue when comparing coefficients between matched and covariate adjusted models with different samples. Therefore, in the results section, we report results from linear probability model calculations.

As an extension of those models, we use adjacent categories models (see e.g., Fullerton 2009) to examine the effect of Catholic school attendance on course taking across the STEM course-taking hierarchy. We collapse the MCS and SCS course sequence codes into three tracking levels capturing major differences in course taking. Details on constructing an ordinal measure of course taking using information from the cumulative course sequence measure are shown in

Table 5. Constructing measures of course taking using information from the cumulative sequence of courses taken.

Math Course Sequence Level		Collapsed Level of Course Sequence b	Science Course Sequence Level		Collapsed Level of Course Sequence
1	Less than Algebra I	Low	1	No big-three a course	Low
2	Algebra I or Geometry, but not both		2	One big-three course
3	Algebra I and Geometry		3	Two big-threes without higher-level course	Middle
4	Algebra I or Geometry, with at least one transition course		4	Three big-three without higher-level course
5	Algebra II	Middle	5	Two or three big-threes with at least one higher-level course	High
6	Algebra II with at least one math elective course
7	Algebra III or Trigonometry, but not both	High
8	Algebra III and Trigonometry
9	Calculus or higher

^a Big-three includes biology, chemistry, and physics. ^b Collapsed qualitative categories are used in adjacent categories models.

.

Adjacent categories models share a similar functional form as the ordered logistic models but estimate the effect of Catholic school attendance more narrowly within pairs of adjacent categories.

4. Results

4.1. Descriptive Statistics

To examine the public–Catholic difference in terms of students’ cumulative Mathematic Course Sequence,

Table 6. Baseline difference in mathematic course sequence (MCS) between different school sectors and Chi square test (n = 14,522).

Mathematic Course Sequence (MCS)	Public School		Catholic School
	Frequency (Expected Frequency) a	Cumulative Frequency of a Given Level or Above	Frequency	Cumulative Frequency of a Given Level or Above
1 Less than Algebra I	181 (164.0)	12671 (100%)	7 (24.0)	1851 (100%
2 Algebra I or Geometry, but not both	1216 (1220.7)	12490 (98.6%)	183 (178.3)	1844 (99.6%)
3 Algebra I and Geometry	966 (876.9)	11274 (89.0%)	39 (128.1)	1661 (89.7%)
4 Algebra I or Geometry, with at least one transition course	460 (418.8)	10308 (81.4%)	20 (61.2)	1622 (87.6%)
5 Algebra II	2627 (2474.5)	9848 (77.7%)	209 (361.5)	1602 (86.5%)
6 Algebra II with at least one math elective course	990 (881.3)	7221 (57.0%)	20 (128.7)	1393 (75.3%)
7 Algebra III or Trigonometry, but not both	812 (821.1)	6231 (49.2%)	129 (119.9)	1373 (74.2%)
8 Algebra III and Trigonometry	2835 (3023.3)	5419 (42.8%)	630 (441.7)	1244 (67.2%)
9 Calculus or higher	2854 (2790.4)	2584 (20.4%)	614 (407.6)	614 (33.2%)
Total	12,671		1851

χ2(0.99, 8) = 508.26, p < 0.001. ^a Expected frequency under mathematical model of independence (part of the Chi-Square calculation).

presents a basic contingency table showing differences in course taking across school sectors both by cell frequency and cumulative frequency of a given level of course taking or higher.

The Chi-square (χ2) statistic provides a summary measure of association between sector and course taking using the raw cell frequency counts. As shown in Table 6, students from Catholic schools are more likely to take higher level math courses, χ2(0.99, 8) = 508.26, p < 0.001. For example, 74.2% of Catholic school students had attained an MCS level of 7 or above (algebra III or higher), compared to only 49.2% of public-school students. Likewise, students from Catholic schools are more likely to avoid low-level course combinations (e.g., equal or less than algebra II) than students from public schools (24.7% vs. 43.0% for category 5 or lower).

Table 7. Baseline difference in Science Course Sequence (SCS) between different school sectors and Chi square test (n = 14,522).

Mathematic Course Sequence (MCS)	Public School		Catholic School
	Frequency (Expected Frequency) a	Cumulative Frequency of a Given Level or Above	Frequency	Cumulative Frequency of a Given Level or Above
1 No big-three course	333 (306.9)	12,671 (100%)	18 (44.9)	1851 (100%)
2 One big-three course	1954 (1782.0)	12,338 (97.4%)	82 (260.3)	1833 (99.0%)
3 Two big-threes without higher-level course	4600 (4421.9)	10,384 (82.0%)	462 (645.9)	1751 (94.6%)
4 Three big-three without higher-level course	4697 (5021.4)	5784 (45.7%)	1069 (733.6)	1290 (69.7%)
5 Two or three big-threes with at least one higher-level course	1087 (1138.9)	1087 (8.6%)	220 (166.4)	220 (11.9%)
Total	12,671		1851

χ2(0.99, 4) = 418.31, p < 0.001. ^a Expected frequency under mathematical model of independence (part of the Chi-Square calculation).

presents analogous information for Science Course Sequences. As shown in Table 7, students from Catholic schools are more likely to take higher level science courses, χ2(0.99, 4) = 418.31, p < 0.001. For example, Catholic school students are more likely to experience all three important science disciplines (i.e., Biology, Chemistry, and Physics) than students from public schools (69.7% vs. 45.7% for category 4 or lower).

Overall, descriptive statistics for the dependent variables show a substantial baseline difference in course taking across school sectors. Catholic school students, in general, experience a higher difficulty level/rigor of course sequences in math and science. Public school students, on the other hand, experience reduced opportunity to learn, especially in terms of basic course-taking patterns, even with substantial standards-based school reform efforts.

4.2. Using Matching to Address Selection into Public and Catholic Schools

A total of 16 student-level covariates were used for matching to reduce selection bias. Selection factors affecting the likelihood of attending Catholic school include demographic information, prior achievement, features of the learning environment, and family SES. To evaluate the quality of matching, we compared covariates for the raw sample and matched sample in terms of their standardized mean difference and variance ratio. As shown in

Table 8. Balance check for matching (standard difference and variance ratio).

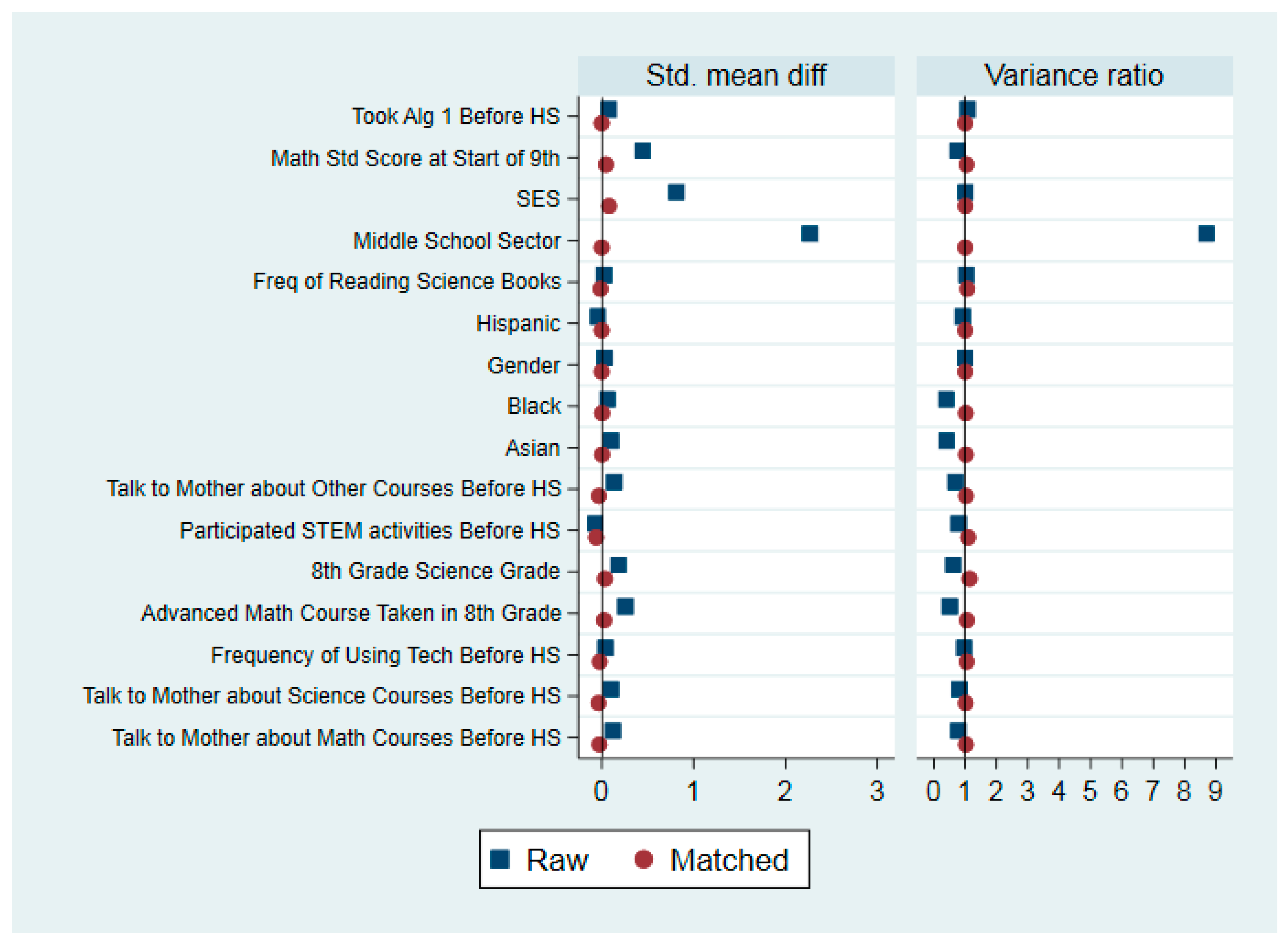
Balance Check for Standardized Mean Difference
Matching Covariates	Raw Sample (n = 14,522)			Matched Sample (n = 8199)
	Treated	Untreated	Std. DIff	Treated	Untreated	Std. Diff
Took Algebra I before 9th grade (1 for yes)	0.30	0.27	0.065	0.25	0.25	0.00
Math Std. score at the start of 9th grade	54.71	50.67	0.43	53.57	52.73	0.089
Family SES	0.55	−0.045	0.80	0.23	0.16	0.091
Middle school sector (1 for Private)	0.75	0.022	2.27	0.12	0.12	0.00
Frequency of reading science book before HS	2.22	2.19	0.023	2.25	2.27	−0.081
Hispanic	0.15	0.17	−0.057	0.097	0.097	0.00
Gender (1 for male)	1.50	1.49	0.026	1.50	1.50	0.00
Black	0.11	0.058	0.066	0.091	0.091	0.00
Asian	0.095	0.016	0.099	0.054	0.054	0.00
Frequency of taking other courses with mother before HS	0.42	0.19	0.13	0.62	0.60	0.012
Frequency of participating math/science activity before HS	0.64	0.72	−0.070	0.89	0.87	0.012
8th grade most advanced science course	2.35	2.07	0.19	2.23	2.24	−0.0096
8th grade most advanced math course	3.34	2.91	0.26	3.07	3.04	0.016
Frequency of using computer for learning before HS	2.23	2.16	0.038	2.36	2.33	0.021
Frequency of taking math courses with mother before HS	0.21	0.031	0.098	0.52	0.49	0.017
Frequency of taking science courses with mother before HS	0.43	0.24	0.12	0.60	0.58	0.015
Balance Check for Variance Ratio
Matching Covariates	Raw Sample (n = 14,522)			Matched Sample (n = 8199)
	Treated	Untreated	Var. Ratio	Treated	Untreated	Var. Ratio
Took Algebra I before 9th grade (1 for yes)	0.21	0.20	1.06	0.19	0.19	1.00
Math Std. score at the start of 9th grade	76.36	101.52	0.75	63.51	68.86	0.92
Family SES	0.55	0.55	1.01	0.41	0.44	0.93
Middle school sector (1 for Private)	0.19	0.022	8.55
Frequency of reading science book before HS	2.46	2.31	1.06	0.85	0.87	0.97
Hispanic	0.13	0.14	0.90	0.087	0.087	1.00
Gender (1 for male)	0.25	0.25	1.00	0.25	0.25	1.00
Black	0.39	0.96	0.41	0.11	0.10	1.00
Asian	0.38	0.92	0.41	0.073	0.073	1.01
Frequency of taking other courses with mother before HS	2.43	3.50	0.69	0.39	0.39	0.99
Frequency of participating math/science activity before HS	1.30	1.61	0.81	0.23	0.24	0.95
8th grade most advanced science course	1.75	2.78	0.63	0.42	0.43	0.98
8th grade most advanced math course	1.81	3.54	0.51	1.19	1.28	0.93
Frequency of using computer for learning before HS	2.78	2.80	0.99	1.03	1.05	0.98
Frequency of taking math courses with mother before HS	3.13	3.79	0.83	0.38	0.38	1.00
Frequency of taking science courses with mother before HS	2.19	2.78	0.79	0.35	0.36	0.99

, all covariates used for matching are well balanced. Figure 1 provides a visual summary of matching quality.

4.3. Effect of Catholic School Attendance on Course-Taking Outcomes

Table 9. Summary of the effect of Catholic schools on STEM course-taking outcomes.

	Math Course Sequence	Science Course Sequence	Total Math Credits	Total Science Credits
1 Unadjusted difference	0.73 (0.11) ***	0.71 (0.12) ***	0.24 (0.035) ***	0.49 (0.034) ***
2 Regression adjusted difference	−0.20 (0.16)	−0.11 (0.21)	−0.0041 (0.092)	0.020 (0.083)
Matched Sample
3 Unadjusted difference (ATE)	0.35 (0.081) ***	0.13 (0.034) **	0.024 (0.076)	0.17 (0.059) **
4 Regression adjusted: Matched sample	0.11 (0.078)	0.17 (0.08) *	0.016 (0.057)	−0.0025 (0.054)
Linear Model Calculation
5 Unadjusted difference	0.97 (0.059) ***	0.42 (0.022) ***
6 Regression adjusted for family background	0.31 (0.078) ***	0.22 (0.032) ***
7 Regression adjusted for family background and school-level covariates	0.26 (0.089) **	0.098 (0.036) **

^~p < 0.10. * p < 0.05. ** p < 0.01. *** p < 0.001.

reports estimates of the Catholic school effect on course taking using both traditional covariate adjustment methods, followed by matching estimators. The first row of Table 9 reports the raw logistic difference in course taking; this represents the simple observed differences from Table 1. In Row 2 we adjust for student- and school-level covariates. The third row of Table 9 reports the average treatment effects (ATE) in the logistic metric after matching. The last row of Table 9 is the estimated effect from an ordered logistic regression on the matched sample to further control school-level covariates.

As shown in the first row of Table 9, on average, for Catholic school students, the baseline odds of attaining a higher-level course sequence are approximately twice that of public school students ($e^{0.73}=2.08$ for math and $e^{0.71}=2.03$ for science, Table 9, Row 1). For total credits, there is approximately a one-quarter credit gap (0.24 from Table 9, Row 1) for math and a half credit gap (0.49 from Table 9, Row 1) for science.

Turning to the main results in Table 9, in the regression-adjusted matched sample (Table 9, Row 4), the Catholic school effect for math and science course taking using the course sequence level is much lower than the size of the baseline difference in Row 1. The odds of attaining a higher-level course sequence for Catholic school students are now estimated as 1.12 times and 1.19 times that of public school students for math and science course sequence, respectively, net of family background, other student-level non-school factors, and school-level covariates ($e^{0.12}=1.12$ for math and $e^{0.17}=1.19$ for science, Table 9, Row 4). To show the extent to which the sector course-taking differences remains unexplained, instead of comparing the coefficients from Table 9, Row 4 with Table 9, Row 1, we apply linear probability model calculations, which are more appropriate for assessing mediation (Table 9, Row 5 and Row 7). Linear probability model calculations shows that 73% of the sector effect on math course sequence and 76% of the sector effect on science course sequences is explained by family background, other student-level non-school factors, and school-level covariates, respectively, indicating that roughly one-quarter of the observed school sector difference still remains unexplained. The results from Rows 2–4 collectively indicate that, although we observe some discrepancy across models, some small sector differences in math and science course sequence level still remains, net of selection bias and school-level covariates. However, the effect on total math credits and science credits is near zero and not statistically significant (0.016 and −0.0025, respectively, Table 9, Row 4).

To further interrogate Research Question Two, we might also compare the average treatment effect (Table 9, Row 3) with the unadjusted difference (Table 9, Row 1). School-level covariates remain unadjusted in Row 3, so this comparison captures the extent to which family background and other non-school factors, operating only as individual-level effects and not compositionally, explains the sector course-taking difference. This may be useful as it is possible that the estimates in Row 4 over-adjust; that the adjustment for compositional effects inadvertently captures other school effects more intrinsically associated with school organizational functioning. In the unadjusted matched sample (Table 9, Row 3), the odds of attaining a higher-level course sequence for Catholic school students are 1.42 times and 1.14 times that of public school students for math and science course sequence, respectively, net of family background and other non-school factors ($e^{0.35}=1.42$ for math and $e^{0.13}=1.14$ for science, Table 9, Row 3). Linear probability model calculations (Table 9, Row 5 and Row 6) show that 68% of the sector effect on math course sequences and 47% of the sector effect on science course sequences is explained by family background and other non-school factors, respectively, indicating that roughly one-third to one-half of the observed Catholic school effect may be due to differences in academic press across sector. Turning to total credits taken, the estimated effect of Catholic school attendance on total science credits is approximately one-third of the raw difference ($0.17÷0.49=34.7\%$, Table 9, Row 3 and Row 1), while the effect on total math credits is near zero and not statistically significant (0.024, Table 9, Row 3).

Collectively, these results converge further in subsequent adjacent categories models where we are able to locate specific Catholic school course-taking advantages.

4.4. Adjacent Categories Model for Tracking

Table 10. Summary of the effect of Catholic schools on STEM course-taking outcomes within Adjacent track levels.

	Adjusted Difference with Logit Multilevel Model	Adjusted Difference with Logit Regression on Matched Sample
Math Course Sequence (Low vs. Middle)	−0.04 (0.028)	0.14 (0.32)
Math (Middle vs. High)	0.77 (0.23) ***	0.31 (0.14) *
Science (Low vs. Middle)	0.47 (0.26) ~	0.56 (0.24) *
Science (Middle vs. High)	0.036 (0.026)	0.027 (0.15)

^~p < 0.10. * p < 0.05. ** p < 0.01. *** p < 0.001.

reports estimates of the Catholic school effect in pairs of adjacent categories using model specifications from Table 10, Row 2 and 4.

As shown in Table 10, Catholic school attendance appears to have somewhat different effects on students’ math and science course taking. Catholic school attendance shows no significant advantage at the lower end of the math course-taking hierarchy. In contrast, at the upper end of the course-taking spectrum (i.e., Algebra II and above), Catholic school students have higher odds of attaining an advanced math sequence level. Considering the findings on science course taking in Table 10, Catholic school students have a statistically significant advantage at the lower-end of the course-taking spectrum but not at the upper-end. For example, Catholic school students have higher odds of taking at least two of the big three courses (e.g., biology and chemistry) vs. only one, but do not have a statistically significant advantage of taking a higher-level course beyond the big three (e.g., AP Chemistry).

5. Discussion

The central contribution of this paper is to re-examine classic insights from empirical studies (e.g., Bryk et al. 1993; Hallinan 1988) in the sociology of education that examine the social organization of schools. Schools provide access to curriculum and knowledge, ultimately shaping students’ educational attainment. Using recent nationally representative data and fine-grained measurement of student course taking, we examined differential access to rigorous STEM course taking in public and Catholic schools. Building on Bryk et al. (1993), Carbonaro and Covay (2010), Domina and Saldana (2012), Kelly (2009), and others, we identify significant sector differences in math and science course sequence level and total credits earned and conclude that these gaps are largely accounted for by selection processes among students of differing family background. Moreover, we find that the remaining Catholic school advantage in STEM opportunity to learn differs by subject.

Consistent with prior studies, we observe significant raw sector differences in course sequence level and total credits earned in unadjusted models (Table 6 and Table 7, and Table 9, Row 1). Although standards-based school reform has provided public school students with greater access to STEM courses (Domina and Saldana 2012), public students, on average, have not reached the overall difficulty level/rigor of the course sequences or even number of courses taken by Catholic school students.

Table 9, Row 4 reports the most completely adjusted models using Mahalanobis-distance kernel matching approach as well as adjustment for school composition covariates. We observe small sector differences in math and science course sequence net of family background and other non-school factors (0.11 and 0.17 from Table 9, Row 4) with roughly one-quarter of the observed difference remaining in linear probability model calculations, but essentially zero difference in total credits earned (0.016 and −0.0025, Table 9, Row 4). As an upper-bound alternative, Table 9, Row 3 reports that the analysis of the average treatment effect based on matching alone indicates that family background and other non-school factors account for approximately two-thirds of the observed differences in math course sequences (Table 9, Row 1 vs. Row 3 in the linear probability specification) and most of the observed differences in total math credits earned (Table 9, 0.24 from Row 1 and 0.024 from Row 3). For science courses, family background and other non-school factors account for roughly half of the observed differences in course sequences (Table 9, 0.71 from Row 1 and 0.13 from Row 3, with 47% as result of linear probability model calculations) and total credits earned (Table 9, 0.49 form Row 1 and 0.17 from Row 3), respectively. Any remaining Catholic school attendance advantage net of family background and other non-school effects is roughly one-third to one-half of the original Catholic school effect in these data. Overall, results from Mahalanobis-distance kernel matching approach indicates that family background and other non-school factors continue to play critical roles in exposing students to different opportunity to learn, but thereafter sector differences in course taking provide only a modest cumulative advantage to enrolled students.

More precise adjacent categories model specifications are able to locate specific Catholic school course-taking advantages. Catholic schools appear to have an advantage in lifting students to advanced math sequences who otherwise might enroll in mid-level courses, and to middle science sequence levels as opposed to low level science course-taking sequences (Table 10). Note that the mid-level math sequence in Table 5 represents Algebra II or equally rigorous electives. Our finding is consistent with the evidence that over 25 states have adopted “completing algebra II or equivalent courses” as a high school graduating requirement for mathematics (National Science Board (US) 2016), as public schools are not at any disadvantage in lifting students to mid-level sequence. This finding is also consistent with the fact that that standards-based reform targets students with course-taking experiences that do not support college enrollment. However, more recently, Minor et al. (2015) found that in responding to Algebra-for-All policy efforts (see e.g., Domina et al. 2015), some private schools implemented “double early access” to enable eighth grade students to complete both Algebra I and Geometry before the beginning of high school. This adjustment of curriculum structure by private schools increased inequality in learning opportunities across sector. It is also important to reiterate that Catholic school students have advantages in taking advanced math courses. Therefore, we believe that public schools should make efforts to bolster early exposure to some critical “gateway” math courses before 10th grade. Doing so will also benefit students with motivation and ability to have enough time to finish advanced math courses and potentially reduce the inequality in learning opportunities across sectors in the higher end of the course-taking hierarchy. Domina et al. (2019) also suggest that disadvantaged students should be provided with better access to high-achieving peers and more opportunities for skill building (see also Nomi and Raudenbush 2016).

For science course sequence levels, the Catholic school course-taking advantage is most obvious in exposing students to courses in multiple science disciplines. However, unlike the findings on math course sequence levels, Catholic schools do not appear to have any advantage in enrolling students in high-level science courses. Perhaps more so than prior research, this study highlights that both Catholic and public schools could better support students in taking high-level science courses. As described in Appendix B, we define higher-level science courses as comprehensive study of a specific disciplinary field with the pre- or co-requisite requirement of higher-level interdisciplinary knowledge (in most cases, a Calculus-level math course). A basic finding from Table 7 is that only approximately 10% of all students had experience with at least one higher-level science course. This is consistent with Teitelbaum’s (2003) finding that increasing basic course-taking requirements (e.g., requiring three years of science) does not necessarily “trickle up” into higher rates of advanced course taking. Therefore, our findings also suggest that additional supports, regardless of the type of school, are needed for students to pursue the rigorous STEM experiences.

Opportunity to learn continues to serve as a useful overall lens for examining private school advantages. Referencing the remaining advantage (Table 9, Row 4), Catholic schools do appear to provide students with greater exposure to rigorous academic courses, net of enrollment factors, and school-level covariates. Although here we have focused on curriculum structure, it is important to consider that variation in curriculum may itself be contingent not only on policy and the normative climate and ethos of the school (here, academic press), but also basic resources. As some early studies argued (e.g., Bryk et al. 1993), flexibility of budget and resource allocation may allow private schools to alter curriculum structures more easily, and even in that era there was a growing mandate for better STEM preparation.

This paper has several major limitations. First, consider the different patterns of Catholic course-taking advantage in math and science course taking. In these data, we are unable to uncover why the Catholic advantages are inherently different across disciplines. On the other hand, it is important to keep in mind that math and science achievement are interrelated, such that course taking in one-subject supports the other (Wang 2013). Thus, although located in different parts of the course-taking hierarchy, both gaps constitute a generalized gap in STEM opportunity to learn. Second, the present analysis contains only basic consideration of the timing of enrollment in critical courses. For example, Algebra is referred to as a “gateway” or “gatekeeper” to later academic performance and further enrollment in academic science courses, and we do include an indicator of enrollment in Algebra in middle school (Gamoran and Hannigan 2000; Nomi 2012). Yet, future research should more fully explore indicators of early exposure to critical math and science content. Third, our use of statistical matching methods is most robust if observed variables fully account for the difference in treatment and control individuals (Vandenberghe and Robin 2004). Here though, variables used in matching as controls for prior learning experiences are all measured at a single time point, the beginning of ninth grade, which suggests many of these are measured with some error or do not fully account for prior school experiences that might affect readiness for advanced course taking. Finally, course quality was not measured in this paper. The way we constructed course sequences uses only information from the standard course codes, leaving the concern that, for example, the quality of calculus instruction may vary across schools. Future studies may have direct observational measures of instruction (e.g., Hill et al. 2008), measures of assignment quality (Joyce et al. 2018), or other measures of instruction available.

Overall, it is encouraging to find that, consistent with prior research, sector differences in STEM course taking have narrowed in recent decades, and primarily reflect differences in the achievement composition of students enrolling in public and Catholic schools. However, non-trivial differences in STEM opportunity to learn remain across sector, and thus will continue to contribute to educational inequality.