Abstract
The current study spatially examines the local variability of robbery rates in the City of Saint Louis, Missouri using both census tract and block group data disaggregated and standardized to the 250- and 500-m raster grid spatial scale. The Spatial Lag Model (SLM) indicated measures of race and stability as globally influencing robbery rates. To explore these relationships further, Geographically Weighted Regression (GWR) was used to determine the local spatial variability. We found that the standardized census tract data appeared to be more powerful in the models, while standardized block group data were more precise. Similarly, the 250-m grid offered greater accuracy, while the 500-m grid was more robust. The GWR models explained the local varying spatial relationships between race and stability and robbery rates in St. Louis better than the global models. The local models indicated that social characteristics occurring at higher-order geographies may influence robbery rates in St. Louis.
1. Introduction
Analyzing crime can be accomplished by using different spatial techniques. Exploratory Spatial Data Analysis (ESDA) is a data-driven approach that incorporates quantitative techniques and visual outputs to expose spatial patterns and relationships (Anselin and Getis 1992). ESDA tools offer an opportunity to examine data for spatial outliers, trends, patterns, clustering, or relationships that indicate areas for further investigation (Anselin 1999). Different types of ESDA techniques are applied to explore specific spatial processes related to crime. Hotspot mapping methods are used to locate where crime concentrates or clusters in an area (Eck et al. 2005). These methods indicate where crimes may cluster in space but do not explain why they occur there (Caplan et al. 2012). Spatial autoregressive models account for spatial autocorrelation within models and indicate statistically significant global relationships (Anselin and Bera 1998), while Geographically Weighted Regression (GWR) models explore the local effects of explanatory variables on specific crimes in a study area (Fotheringham and Rogerson 2009).
The accuracy of spatial crime analysis is contingent on utilizing the appropriate spatial scale (Smith and Sandoval 2018). The size of a spatial scale is a fundamental component in determining existent spatial crime patterns, concentrations, clusters, or relationships (Anselin and Getis 1992). While a singular, perfect spatial scale to explore spatial crime may not exist, selecting one or many appropriate spatial scales is contingent on the specific research objectives or the extent of the study area (Tita and Radil 2010). Micro-level geographic scales are routinely used in spatial crime analysis as previous research suggests that crimes cluster at the smallest geographic units (Andresen and Malleson 2011; Braga et al. 2011; Brantingham and Brantingham 1999; Curman et al. 2015; Weisburd and Amram 2014; Weisburd et al. 2006, 2009, 2012).
The purpose of the current research is to use ESDA techniques to explore the locations of spatial clustering of robbery rates and to observe the global and local relationships of race and neighborhood stability with robbery rates, in the City of St. Louis, Missouri. Specifically, the American Community Survey (ACS) 2012 to 2016 five-year estimates data were collected at both the census tract and block group level and disaggregated to the 250- and 500-m raster grid level (Caplan et al. 2011, 2012; Kennedy et al. 2010, 2015; Barnum et al. 2017; Hart and Zandbergen 2014; He et al. 2018; Fitterer et al. 2015; Stucky and Ottensmann 2009; Dmowska and Stepinski 2014; Maimaitijiang et al. 2015; Patterson and Doyle 2009; Ratcliffe and McCullagh 1999; Drawve et al. 2016). With data standardized and spatial autocorrelation confirmed, the Spatial Lag Model (SLM) was applied to determine which independent variables had a global, significant relationship with robbery rates. Globally, percent African American and percent homeownership influenced robbery rates. To explore these relationships further, GWR was used to determine the local spatial variability of the relationships between percent African American and percent homeownership with robbery rates throughout St. Louis. Additionally, a Local Indicator of Spatial Association (LISA) analysis indicated small geographic clusters of robbery rates within the City of St. Louis.
The current study examines the following research questions: First, does census tract or block group data better explain the relationship between percent African American and robbery rates, and percent homeownership and robbery rates? We hypothesized that the census tract level of data provided a better explanation of the relationships between race and stability and robbery rates. Second, how do different spatial scales of standardized grid units influence the relationships between independent variables and robbery rates? We postulated that using different spatial scales of grids influenced each model’s level of explanatory power and precision. Third, how do the spatial relationships between race and robbery rates, and stability and robbery rates vary, locally in the City of St. Louis? We speculated that significant variations of the local spatial relationships between race or stability and robbery rates occurred throughout the city.
The current study adds to the spatial criminology literature in a few ways. First, evaluating the associated strength and influence of census tract and block group data in each model provides relevant information on utilizing data collected at different geographic scales. Second, disaggregating both census tract and block group data to standardized raster grids at the 250- and 500-m scale offers insight into how each standardized data scale operates at a micro-level. Third, the 250- and 500-m grids provide an additional micro-level spatial scale to explore crime spatially. Fourth, the City of St. Louis, with its declining population, high crime environment, and uneven development (Tighe and Ganning 2015), affords an opportunity to explore the forces shaping the spatial patterns of crime in a medium-sized, shrinking, Midwestern city. Lastly, the data for the research activity are recent, providing a modern snapshot to understand and model the current spatial crime environment.
1.1. Previous Research
1.1.1. Spatial Patterns and the Social Influence on Crime
Central to the analysis of crime and space is the social disorganization theory (Shaw and MacKay 1942). This theory suggests that the decay of social control in disadvantaged urban areas leads to an environment conducive to crime. Certain elements found in the disadvantaged and unequal areas, such as “demographic, economic, social, family disruption, and urbanization” (Andresen 2006, p. 489) are associated with higher crime. The individuals residing in disadvantaged areas are influenced by the social and cultural environment and are more inclined to participate in crime. With this, geographic crime patterns can be investigated and established in conjunction with socioeconomic variables.
The level of homeownership in an area may influence crime levels. John Hipp (2007) found that neighborhood crime declined with the increase in the number of homeowners. Similarly, in a longitudinal study conducted by Boggess and Hipp (2010), they observed that homeowners did not influence residential instability associated with higher crime levels in Los Angeles, California. While Xie and McDowall (2010) established that African Americans may be disproportionately precluded from owning homes; thus limiting the selection to dangerous or crime-ridden residential areas. The authors also suggest that the white population simply evades the disadvantaged neighborhoods which perpetuates homeownership disadvantages and results in residential segregation.
Different types of segregation in urban areas can contribute to increased crime. In examining the effect of income inequality on violent crime, Kang (2015) observed that economic segregation in urban neighborhoods significantly contributed to violent crime. Hipp (2011) also observed that in U.S. cities with increased inequality, greater economic segregation resulted in a substantial surge in crime levels. Racial segregation may also influence crime. Krivo et al. (2009) observed racial segregation as a crime generator in U.S. neighborhoods and cities. In their study, both African American and Latino populations that resided in the most deprived areas experienced disproportionately higher levels of crime, while white populations occupied more opulent areas with reduced crime. Feldmeyer (2010) found that when African American and Latino populations in California and New York experienced concentrated disadvantage and were segregated from white populations, homicides increased for both minority groups. While nationally, racial integration in U.S. cities has decreased violence and crime, the inclusion and integration of Hispanics with African American concentrated populations resulted in a decrease in African American homicides (Parker and Stansfield 2015). The same effect was not apparent when Hispanics were integrated with a white-dominated population. Parker and Stansfield (2015) also found that black homicides were not influenced by racial segregation, whereas white homicides were.
1.1.2. Local Spatial Variation in Crime
Crime research utilizing GWR for spatial analysis suggests that crime can be influenced differently across a study area; for example, violent crime in one neighborhood may be more influenced by certain explanatory factors than others in a study area (Zhang and Song 2014; Malczewski and Poetz 2005; Bunting et al. 2018; Cahill and Mulligan 2007). In researching the local spatial patterns of aggravated assault and larceny using census tracts in Miami-Dade County, Bunting et al. (2018) found significant variations in local associations between crime and socioeconomic variables. Specifically, poverty exerted a local and positive influence on aggravated assaults; aggravated assaults increased with greater levels of ethnic diversity, and residential burglary was locally influenced by housing characteristics. Similarly, Malczewski and Poetz (2005) observed varied, local spatial relationships between residential burglary and housing characteristics at the dissemination area level in London, Ontario. Another branch of literature explores local spatial relationships with alcohol outlets and violent crime. This collection suggests that specific types of alcohol outlets positively influence violent crime on a spatially varied level (Cameron et al. 2016; Wheeler and Waller 2009; Han and Gorman 2013).
The local variation of relationships between explanatory variables and crime may require different preventative policy or policing strategies to be applied throughout a study area (Malczewski and Poetz 2005). GWR becomes a valuable tool in identifying local areas within a city that may have varied social or economic environments that influence crime differently. Supporting this trend, Vilalta and Muggah (2016) used GWR to examine which theories of crime, social disorganization or institutional anomie, influenced Mexico City’s crime environment. The authors observed local spatial variation with variables representing the two different theories and their relationships with crime throughout Mexico City. GWR indicated some local areas that were more influenced by social disorganization features, while other local areas favored the institutional anomie theory. This increased local variation makes comprehensive policy and policing efforts to address crime for all municipalities less effective; thus, indicating the need for locally-tailored policing and policy formulation (Vilalta and Muggah 2016).
1.1.3. Spatial Scale
Since GWR provides a local measure of non-stationarity, small geographic scales are typically used with the technique for spatial crime research (Andresen and Malleson 2011; Braga et al. 2011; Brantingham and Brantingham 1999; Curman et al. 2015; Weisburd and Amram 2014; Weisburd et al. 2006, 2009, 2012). The smallest geographic scales provide more granularity to uncover local areas of spatial homogeneity and heterogeneity. The census tract (Cameron et al. 2016; Wheeler and Waller 2009; Bunting et al. 2018) and block group level geographies (Zhang and Song 2014; Han and Gorman 2013; Malczewski and Poetz 2005; Cahill and Mulligan 2007) are typically the smallest data units readily available and the most common spatial scales utilized in GWR analysis. The census boundaries are arbitrarily-derived geographic units; they are determined by obtaining a certain average population for each geographic unit area and do not coincide with other geographic boundaries, such as police, voting, or school districts (Bunch et al. 2018).
Raster grids or fishnets provide equally distributed, micro-level geographic areas to spatially analyze crime and associated explanatory factors. Using raster grids in spatial crime analysis to create micro-level geographic scales is a common and accepted methodology (Caplan et al. 2011, 2012; Kennedy et al. 2010, 2015; Barnum et al. 2017; Hart and Zandbergen 2014; He et al. 2018; Fitterer et al. 2015; Stucky and Ottensmann 2009; Dmowska and Stepinski 2014; Maimaitijiang et al. 2015; Patterson and Doyle 2009; Ratcliffe and McCullagh 1999; Drawve et al. 2016). Grid-based methods offer the ability to accurately capture the spatial crime environment considering very small geographic areas while also addressing the impacts associated with irregular polygons, such as the Modifiable Areal Unit Problem (MAUP) (Caplan et al. 2012) or topology constraints associated with defined geographies when utilizing spatial statistics (Grubesic 2006).
While scholars offer insights into the size of raster grids to be considered in spatial crime research (Chainey and Ratcliffe 2005; Caplan et al. 2011; Kennedy et al. 2010), the appropriate grid size can vary based on research objectives, the size of the study area, or even the ESDA or spatial statistical method utilized. Tita and Radil (2010) submit that a perfect, single geographic scale does not exist for any research activity. While micro-level geographies provide an increased level of granularity, higher-order geographies may still operate and influence spatial crime incidents and patterns.
RTM is a spatial risk model that utilizes a grid-based framework for determining the risk of crime based on selected explanatory variables, in geographic areas (Caplan et al. 2011, 2012; Kennedy et al. 2010, 2015; Barnum et al. 2017). RTM is a common methodology used in spatial crime analysis. While RTM and GWR are separate spatial methodologies, both interfaces require data inputs for dependent and independent variables. The quality and scale of the data used for the analysis may influence the results in both methods. Some of the user configurations of RTM include cell size, model type, and risk factor specifications. Although Caplan et al. (2013) provide default and suggested values for RTM selections, they may not be appropriate for all research projects. Varying the selections of configurations may produce contrasting results. The maximum spatial influence configuration allows users to determine the distance that the statistical tests will assess the identified risk factors, from a minimum of one block to a maximum of four blocks. This configuration requires consideration with the scale of data and grid cell size used in the analysis. Since RTM has a plethora of user configurations that could impact the level of risk identified in an area, several iterations utilizing different inputs may be required to obtain an accurate risk assessment.
Similar to RTM, the user configurations for GWR are sensitive. GWR users can also utilize raster grid-based units for a GWR analysis, although additional manipulation is required. The selected grid size also influences the spatial resolution of results; smaller grids are associated with finer local analysis and results. Other GWR user inputs include kernel model type, kernel type, bandwidth, bandwidth selection criteria, and other detailed specifications within those inputs. Kernel bandwidth, like the RTM maximum spatial variance configuration, determines the proximity and influence that observations are considered in the model. If the kernel bandwidth is configured too close, increased variance and decreased bias can result. The opposite effect occurs with kernel bandwidth that is too distant, resulting in decreased variance and increased bias (Vilalta 2013). Like RTM, GWR may require several user iterations with adjusted configurations to accurately represent observable relationships throughout space.
1.1.4. Hotspot Methodology
Hotspot methods are a suite of ESDA mapping tools that are commonly used to spatially analyze crime. Since crimes typically “concentrate at specific, select places” (Caplan et al. 2012, p. 245), hotspot techniques indicate where crime concentrations occur in a study area. These tools are relatively simple to execute and perform well at identifying and measuring areas of local and global spatial association. While hotspot mapping indicates crime concentrations with an associated significance level, they do not explain the factors contributing to the increased crime environment. Essentially, hotspot methods only consider the dependent variable and associated significance levels (Caplan et al. 2012). Also, choosing an appropriate geographic scale in hotspot analysis is important as variability and inaccuracies may result from using a geographic scale that is too large or small (Grubesic 2006). The spatial scale may also influence the sensitivity of hotspot methods in detecting outliers or subtle changes in values (Ord and Getis 1995; Anselin 1995; Lin and Lu 2006).
While several hotspot methods exist, two of the most commonly used hotspot methods in spatial crime analysis include the Getis-Ord Gi* statistic and Kernel Density Estimation (KDE). The Getis-Ord (local) Gi* statistic is a local measure of spatial autocorrelation that identifies statistically significant, spatially concentrated areas of high and low crime by comparing local to global averages (Kounadi and Leitner 2015). Frazier et al. (2013) applied the Getis-Ord Gi* methodology to analyze the relationship between dense clustering of demolition areas and high crime areas in the shrinking city of Buffalo, New York. Analyzing data over a five-year period, the authors found that crime shifted away from substantial demolition areas. Although the Getis-Ord Gi* indicated the variation of spatial crime patterns in conjunction with demolition, additional factors could have influenced the spatial patterns of crimes, such as new or increased policing efforts or variations in the socioeconomic environment. The Getis-Ord Gi* statistic, alone, would be unable to investigate the level of influence associated with these potential relationships.
Kernel Density Estimation (KDE) identifies crime hotspots and is typically available with major crime analysis software packages. KDE generates risk areas based on crime event locations. Using KDE for spatial crime analysis has its complexities, especially in selecting the appropriate kernel bandwidth. Parameter selections are important in providing the most accurate crime hotspot areas and increased predictive power of future crime locations. Hart and Zandbergen (2014) examined crimes in Arlington, Texas using KDE at various parameter settings. The variations in the interpolation method and bandwidth size influenced the prediction of future crime events, while the grid cell size did not have a discernible impact. The authors recommend using the quartic or triangular distribution, as these distributions increased predictive results. Additionally, smaller bandwidths were encouraged due to the decrease in predictive power associated larger bandwidths (Hart and Zandbergen 2014). Chainey (2013) examined the predictive power of crime using KDE while testing various parameter settings in Newcastle-upon-Tyne in North East England. Different grid cell sizes and kernel bandwidths were applied using the crimes of residential burglary and violent assaults. Similar to the findings of Hart and Zandbergen (2014), variations in the grid cell size did not improve predictions of future crime hotspots. The bandwidth size, however, considerably influenced the prediction of crime, with smaller bandwidths associated with improved accuracy (Chainey 2013).
2. Data
The data obtained for the current research study were derived from publicly available sources. Data for the dependent variable, robbery rates, were collected from the St. Louis Metropolitan Police Department (SLMPD) downloadable crime files. SLMPD publishes crime events monthly from 2008. There are some caveats associated with the data. First, the data are available by month for the past eleven years. The database captures violent crime events based on the reported date, not on the date of occurrence. For example, a robbery that occurred in January 2011 could be included in May 2011 data, creating the potential for inaccuracies in the data. Second, the geographic coordinates locating the violent crime event may be unavailable and are recorded as an approximate address or street intersection in the database. The address or intersection locations require conversion to geographic coordinates for analysis and increases the risk for error to enter the database and associated analysis. Table 1 indicates the number of robberies for each year (2012–2016), the number of robbery events that required additional location research, the number of robbery events that were unable to be located, and the total number of robberies used in the analysis.

Table 1.
Geospatial location of robbery events.
After the exclusion of robbery events that were unable to be geographically located, the robbery totals for analysis included 99% of the initial events, which provided a higher degree of accuracy in the analysis. The final dependent variable, robbery rate, used in the analysis included the number of robberies occurring in each grid, divided by the population of the corresponding grid, divided by five (the number of years in the study), and multiplied by 1000.
The independent variables in the study are derived from the ACS 5-year estimates (2012–2016). The independent variables were collected at both the census tract and block group geographic levels. Independent variables representing homeownership, unemployment, racial diversity, race, income inequality, and educational attainment were spatially tested, on a global level, for significance with the robbery rate. This yielded the percent African American and percent homeownership variables to assess local spatial variability with robbery rates. The percent African American independent variable was determined by dividing the population of African Americans alone by the total population; while the percent homeownership was owner occupied housing units divided by the occupied housing units.
The St. Louis municipal boundary and associated census tract and block group shapefiles were collected from the U.S. Census Bureau Tiger/Line shapefiles. The St. Louis municipal boundary served as the input feature to define the extent of a series of newly-created raster grid polygons. The raster grid polygons were created using two different spatial scales, 250-m and 500-m. This resulted in 2922,250-m grids and 777,500-m grids to serve as the geographic units in the study. The census tract geography typically has an average of 4000 people per unit, while the block group has an average of 1200 people per unit. In comparison, the 250-m raster grids had an average of 108 people per unit, while the 500-m grids had an average of 406 people per unit.
Using the gridded features as the geographic units in the analysis standardized the process of assessing different levels of spatial scale. This addressed potential issues caused by the variability associated with using common geographic units (Ren et al. 2017). Robbery events from 2012–2016 were spatially joined to the corresponding raster grid, for both the 250- and 500-m scale, that contained the event. This process resulted in the number of robberies completely contained in each respective raster grid, at both spatial scales. Based on the number of robbery events for each grid, a new field was created and the robbery rate for each grid was determined.
3. Methods
The process of spatial interpolation, using areal weighting, produced the values for the independent variables in each grid cell. Data at the census tract and block group level were obtained to establish the values of 250- and 500-m gridded units. The census tract and block group features and values were spatially intersected with the 250 and 500-m grids. The area was computed, summed, and joined for the resultant features. The area weight (area/sum of the area) and new independent variable grid value (independent variable*area weight) were calculated and spatially joined to the corresponding 250- or 500-m raster grid. See Equations (1) and (2).
Aw = Partial census tract or block group area weight
Ai = Individual area of each census tract or block group
At = Total area of the census tract or block group parts
Tv = Census tract or block group population
Ct = Census tract or block group total population
Aw = Partial census tract or block group area weight
This resulted in two sets of spatially interpolated values for independent variables; one derived from census tract data, available at the 250- and 500-m raster grid unit and the other obtained from block group data at the 250- and 500-m raster grid scale.
With the values of the dependent and independent variables determined, a LISA analysis was performed on the robbery rates to determine where the violent crime clustered in the city. The LISA analysis utilized queen continuity weighting when calculating a local value for each raster grid. The outcome produced LISA indices, clusters, and significance levels.
We began the analysis with an Ordinary Least Squares (OLS) regression model. See Equation (3). The dependent variable was the robbery rate and the independent variables were: (1) percent homeownership; (2) percent unemployment; (3) Theil racial diversity score; (4) Theil income inequality; (5) education attainment index; (6) percent white; and (7) percent African American. The terms and are the intercept and error term, respectively.
A Global Moran’s I analysis was performed on the OLS residuals to check for spatial autocorrelation. The Global Moran’s I considered neighboring polygons by using contiguity edges and corners, Euclidean distance, and weight by row (Wang and Arnold 2008). With spatial autocorrelation present among the OLS residuals of the 250- and 500-m grids for both census tract and block group data, the Spatial Lag Model (SLM) was performed to determine the most significant independent variables contributing to robbery rates in the City of St. Louis. The SLM corrects for spatial autocorrelation by including the values of the dependent variable in neighboring areas as an independent variable in the model (Anselin and Bera 1998). In the SLM is the spatial lag term for the robbery rate. Based on the results of the SLM, GWR was utilized to determine the local relationships between independent variables and robbery rates. Building on Equation (4), we developed two exploratory GWR models based on the coefficients that were theoretically significant: (1) a percent homeownership GWR model; and (2) a percent African American GWR model. In the general GWR model, represents a location and are the corresponding coordinates, and is percent homeownership or percent African American. The term ) is the estimated local coefficient and and are respectively the intercept and error term. See Equation (5).
The GWR models were used to determine how the spatial relationships between the independent variables of percent African American and percent homeownership and the dependent variable, robbery rates locally varied from global values across the City of St. Louis. GWR was also used to determine which geographic unit, the census tract or block group, provided a more robust explanation of data and relationships.
The GWR software requires user-input to calibrate the model. The calibration for the current study included a Gaussian kernel model type, an adaptive bi-square kernel type, a golden section search for bandwidth selection method, and the Akaike Information Criterion with Correction (AICc) for small sample sizes for bandwidth selection criteria. The Gaussian model type is typically used in modeling numeric values and spatial processes. The adaptive bi-square kernel type allows the kernel to vary based on the density of data points; high concentrations of data points result in a smaller bandwidth, while dispersed data points produce a larger bandwidth (Fotheringham and Rogerson 2009). The bi-square kernel also removes the influence of events beyond the selected bandwidth by weighting them with a zero weight (Bidanset and Lombard 2014). The golden section search for the bandwidth selection method provided the optimal bandwidth size in most cases. If the golden section search returned a warning message of “lower limit is selected,” a user-defined maximum and minimum number of nearest neighbors were entered based on the bandwidth results of previous iterations. The golden section search utilized the Akaike Information Criterion with correction for sample sizes (AICc) in evaluating model fit for optimal bandwidth selection (Nakaya et al. 2016).
4. Results
4.1. Descriptive Statistics
The descriptive statistics for census tract and block group data for both the 250- and 500-m grid scales are provided in Table 2. All the variables for each geographic data unit and grid-scale indicated the presence of spatial autocorrelation (p ≤ 0.001). The independent variables using the census tract data for both 250- and 500-m grids have comparable global Moran’s I, mean, standard deviation, minimum, and maximum values. The dependent variable showed some variation in the standard deviation and maximum values which can be attributed to the geographic space considered by the different-sized raster grids. Similar inferences can be drawn with the block group data and the 250- and 500-m grid scales.

Table 2.
Descriptive Statistics for Census Tract and Block Group Data at the 250- and 500-m Raster Grid Scale.
4.2. Analytical Models
4.2.1. Global Regression Models
The OLS residuals were tested for spatial autocorrelation using the Global Moran’s I. Spatial autocorrelation (p ≤ 0.001) was present for census tract and block group data in 250- and 500-m grids. See Table 2. Based on the presence of spatial autocorrelation in the OLS residuals, the Spatial Lag Model (SLM) was used to remove spatial autocorrelation from the model and to determine, globally, which independent variables explained robbery rates in the City of St. Louis. Using a maximum-likelihood estimation SLM, the census tract and block group data for 250- and 500-m grid models were analyzed. The percent African American independent variable at the block group data and 250-m grid level, significantly (p ≤ 0.05) influenced robbery rates for the City of St. Louis. The percent homeownership explanatory variable at the block group data and 500-m grid level, approached significance (p ≤ 0.10) to influence robbery rates across the study area. See Table 3. With global significance observed for percent African American and percent homeownership approaching significance, these two variables were selected to explore how each of their relationships varied, locally with robbery rates throughout the City of St. Louis.

Table 3.
Spatial Lag Model Results.
4.2.2. Spatial Clustering Models
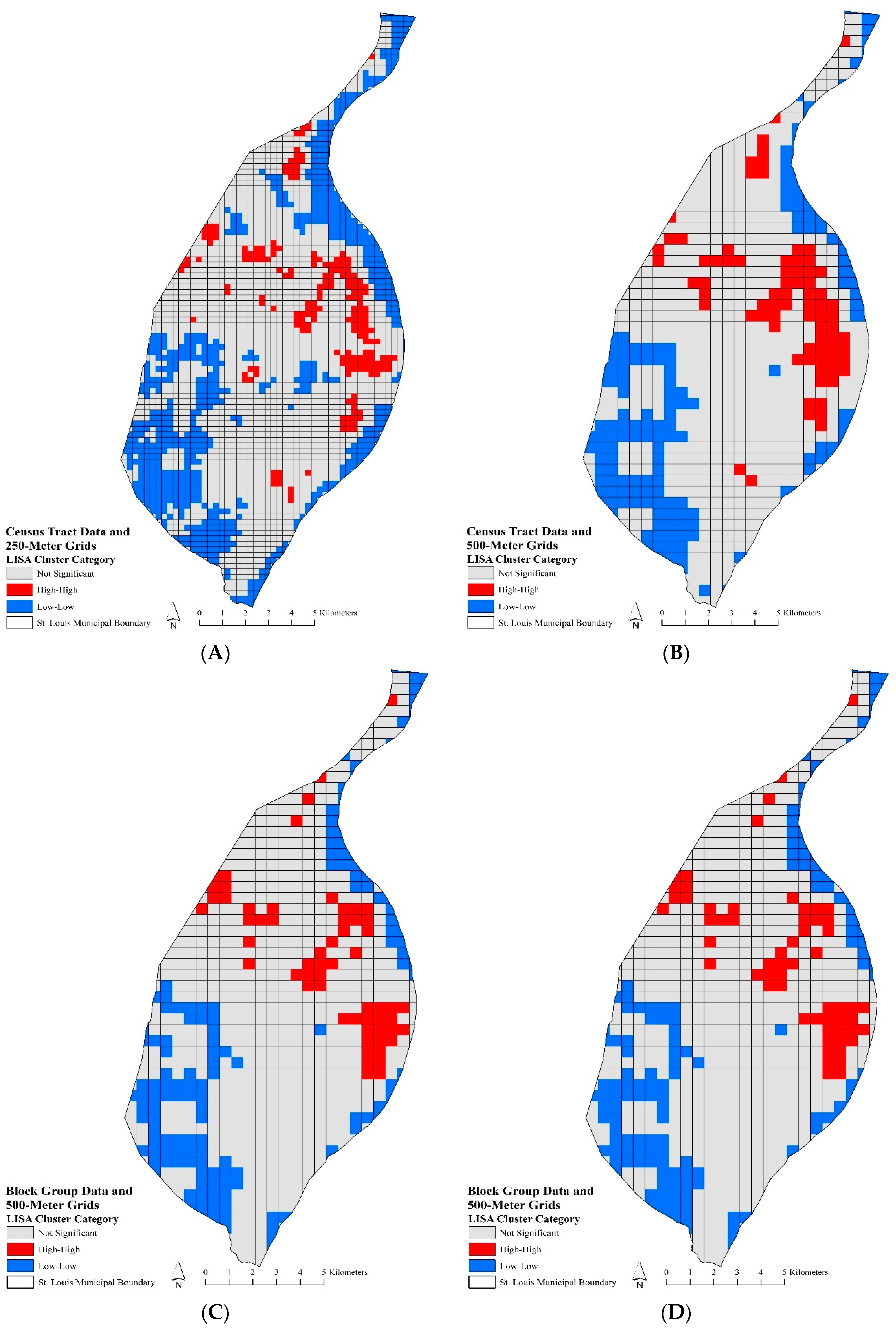
A LISA analysis indicated local hotspot and cold spot patterning of robbery rates in the City of St. Louis. Figure 1A–D depicts a LISA analysis for census tract and block group data at 250- and 500-m raster grids. The high-high LISA cluster category indicated robbery rate hotspots or areas with high spatial clustering, while the low-low LISA cluster category revealed cold spot or areas with low spatial clustering. In terms of Figure 1, both the significant hotspot and cold spot areas (p ≤ 0.05) for 250- and 500-m grid models were comparable. The 500-m grids for both census tract (Figure 1B) and block group data (Figure 1D) displayed generalized areas of hotspots and cold spots as compared to the detailed areas highlighted by the 250-m raster grids (Figure 1A,C). The smaller grid size offered greater precision in indicating micro-areas of significant spatial clustering of robbery rates in the City of St. Louis. The cold spot areas were found around the municipal boundary and the southwestern portion of the city. The hot spot areas were found in the heart of the city, primarily in the central eastern and northern parts. The block group data at the 500-m grid scale (Figure 1D) did not indicate the significant hotspot clustering found in the other models in the south-central portion of the city.
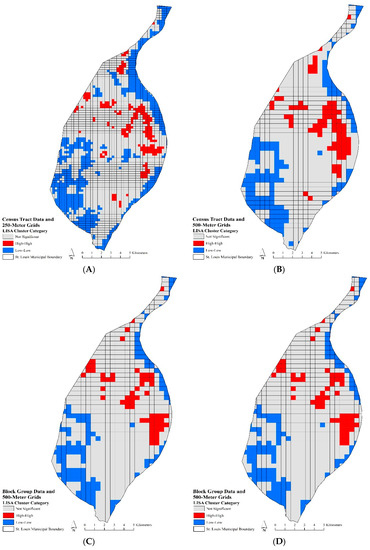
Figure 1.
Local Indicators of Spatial Association (LISA) analysis of census tract and block group data and 250- and 500-m grids. Red areas indicate hotspots, blue areas are cold spots, and gray areas are not significant. (A) census tract data and 500-m grids; (B) census tract data and 250-m grids; (C) block group data and 500-m grids; (D) block group data and 250-m grids.
4.2.3. Geographically Weighted Regression
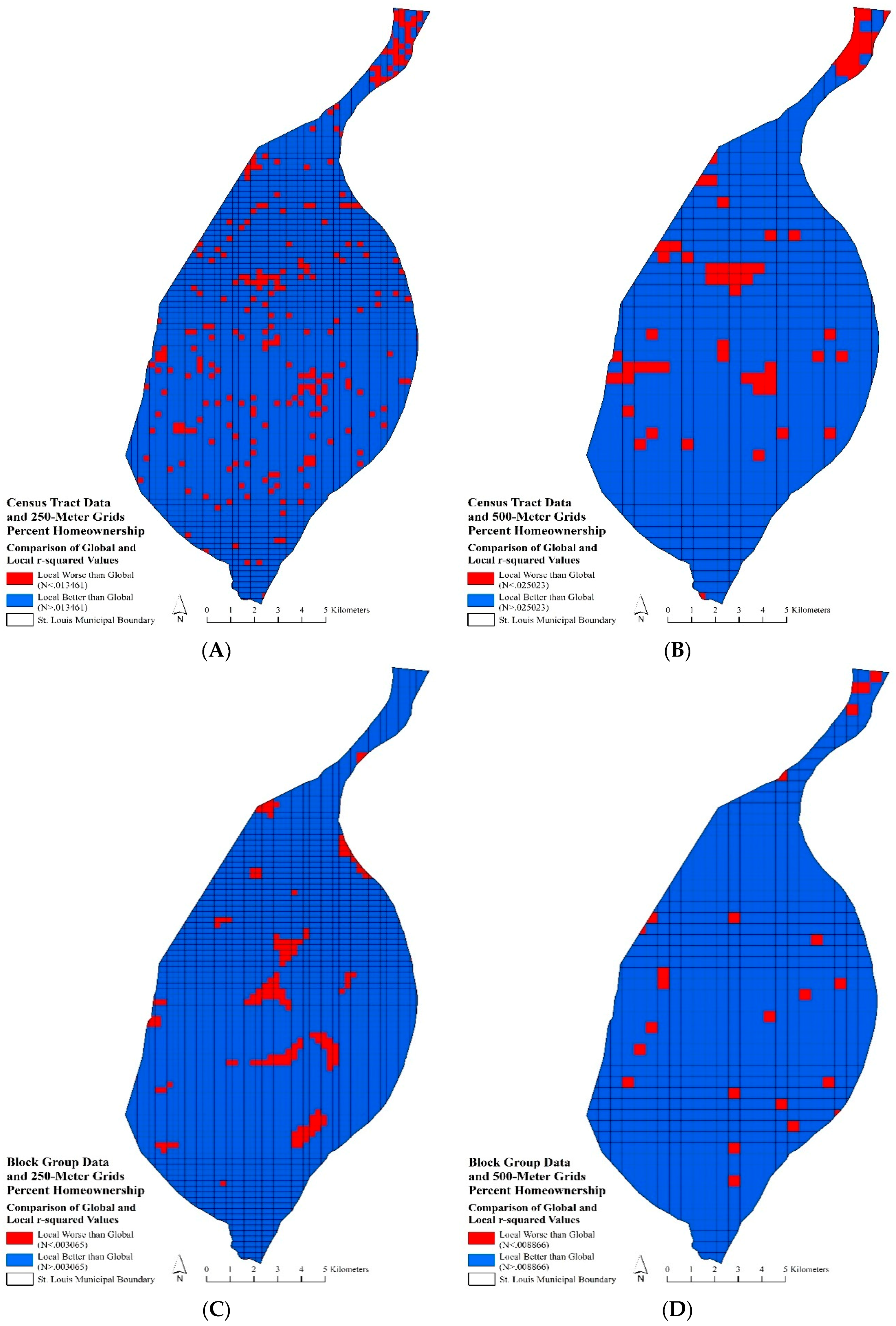
The results of the eight GWR models indicated local spatial variation in the relationships between percent African American and percent homeownership with the robbery rate, throughout the City of St. Louis. The GWR or local model r-squared values for each of the eight models were higher than the OLS models or global models. On average, the GWR models outperformed or explained more than the OLS models for both percent African American and percent homeownership with census tract and block group data at the 250- and 500-m grid scales. This indicated that OLS was unable to explain the local spatial variation of relationships between race or stability and robbery rates. Figure 2A–D indicated areas where local r-squared values were either higher or lower than the global r-squared values for the relationship between percent homeownership robbery rates. Figure 2A,B represent the global to local r-square comparison for percent homeownership using census tract data at the 250- and 500-m grid scales. Figure 2B indicated local model improvement over the global model, with 90% of the 500-m raster grids having higher local r-squared values than the global r-square value. The northern arm and a few small areas in the central portion of the city had lower local r-squared values than the global r-square. Percent homeownership using census tract data at the 250-m grid level (Figure 2A) showed more spatial variation in global to local model improvement. Similar patterns are apparent with both census tract data and 250- and 500-m grids. A scattered, degraded performance of the local model is readily apparent throughout the city; however, 92% of the 250-m raster grids saw an increase in local model performance. GWR produced improved local r-squared values for percent homeownership using block group data and 500-m grids, with 97% of the grids having a local r-squared value greater than the global r-squared value. The underperforming areas appeared in the northern arm and haphazardly scattered throughout the city (Figure 2D). In Figure 2C, local model underperformance appeared concentrated.
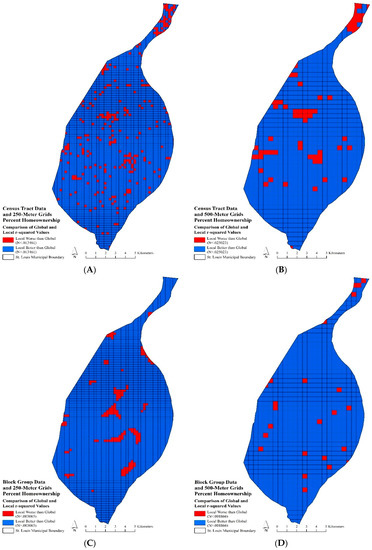
Figure 2.
Comparisons of global to local r-squared values throughout the study area. Blue grids indicate where the local model performs better than the global model, while the red grids indicate where the local model performs worse than the global model. (A) census tract data and 500-m grids; (B) block group data and 250-m grids; (C) block group data and 500-m grids; (D) block group data and 250-m grids.
The local relationship between percent African American and robbery rates indicated greater spatial variation than the relationship between percent homeownership and robbery rates. The census tract data and 500-m raster grid model had 76% of grids with r-squared values higher than the global r-squared value. Concentrated locations of lower than global, local r-squared values were apparent throughout the city. The census tract data at the 250-m grid model suggested a similar pattern with additional occurrences of lower-performing local models. The 250-m grids had a slight increase of raster grids (78%) with local r-squared values higher than global baseline r-squared value. The block group data with 250- and 500-m raster grid models displayed similar spatial variability in local r-squared values, with 75% of 500-m grids and 83% of 250-m grids having higher local r-squared values than the global baseline.
An examination of all eight models suggested that differences exist between utilizing census tract data and block group data and 250- and 500-m grids. First, both the global and local r-squared values are higher with the census tract data at the 500-m grid level in both the race and stability models (see Table 4). A degradation of global and local model explanation is apparent in comparing census tract data at the 500-m grids to the census tract data and block group data at the 250-m grids, for both race and stability models. The global and local r-squared values for census tract data at the 250-m grids and block group data at the 250- and 500-m grids have similar r-squared values, in both race and stability models. This may indicate that the process of spatial interpolation via areal weighting provided similar standardization of values for census tract data at the 250-m grid and block group data at the 250- and 500-m grids for both race and stability models. In comparing the Akaike Information Criterion (AIC) values for model quality, the 500-m grids had improved quality over the 250-m grids, indicated by lower global and local AIC values for the census tract and block group data in both race and stability models. Thus, the census tract data at the 500-m grid level appeared to be the most powerful in explaining the global and local relationships with race or stability and robbery rates. Although the census tract data and 500-m grid are more robust, the block group data and 250-m grid scale offered greater precision.

Table 4.
Global and Local Parameter Estimates for Geographically Weighted Regression Models.
In Table 4, the GWR range of coefficients was the greatest for census tract data and 500-m grids, with percent African American having a GWR range of 902.865 and percent homeownership having a GWR range of 311.316. This indicated that local coefficients for the census tract data at the 500-m grid scale had a large spread compared to the other data and grid models. The second highest spread of local coefficients appeared with block group data at the 250-m grid scale for both race and stability models. A greater GWR range is indicative of the local values being considered throughout the GWR model and can be seen in comparison with the range of OLS values, as they are very similar.
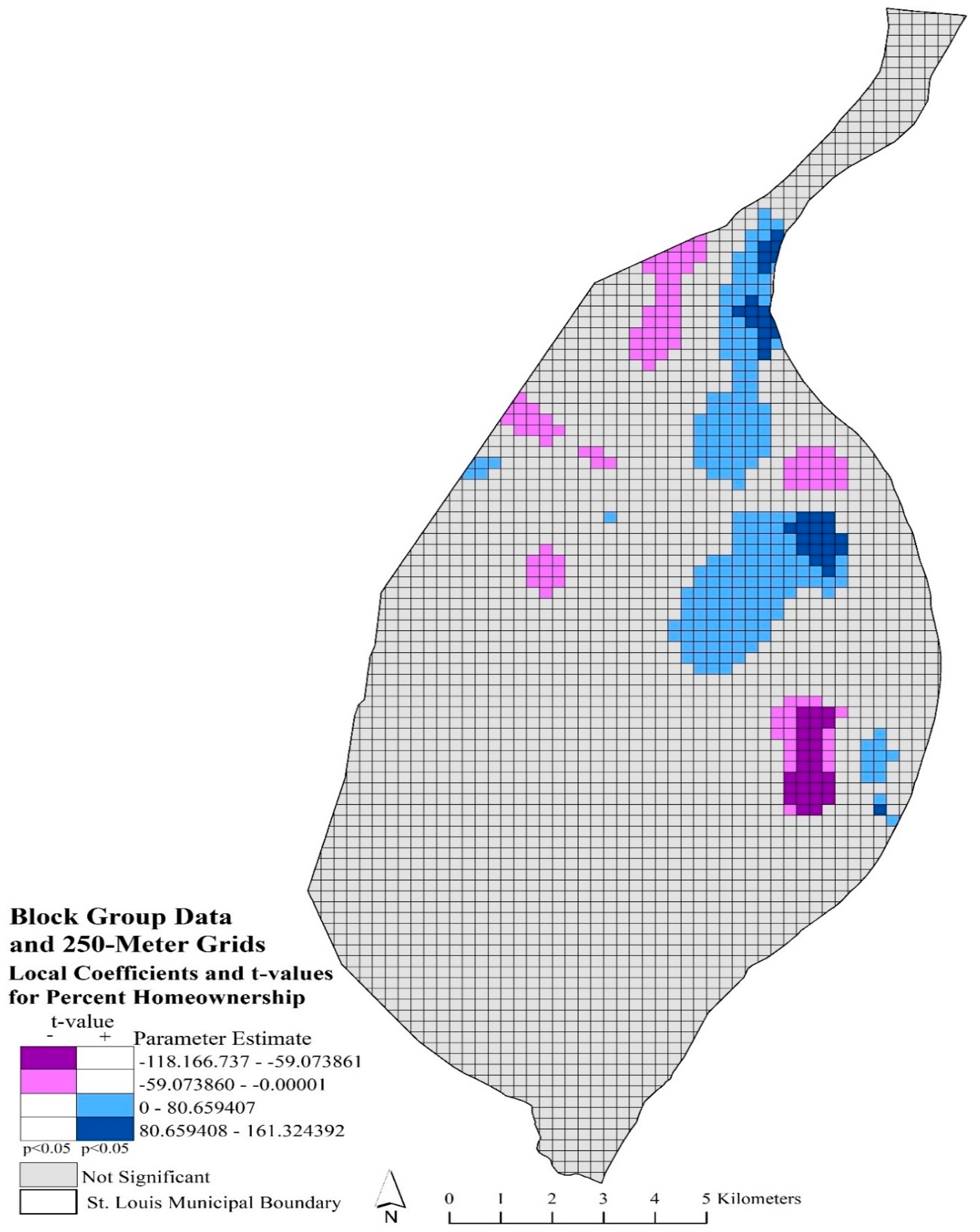
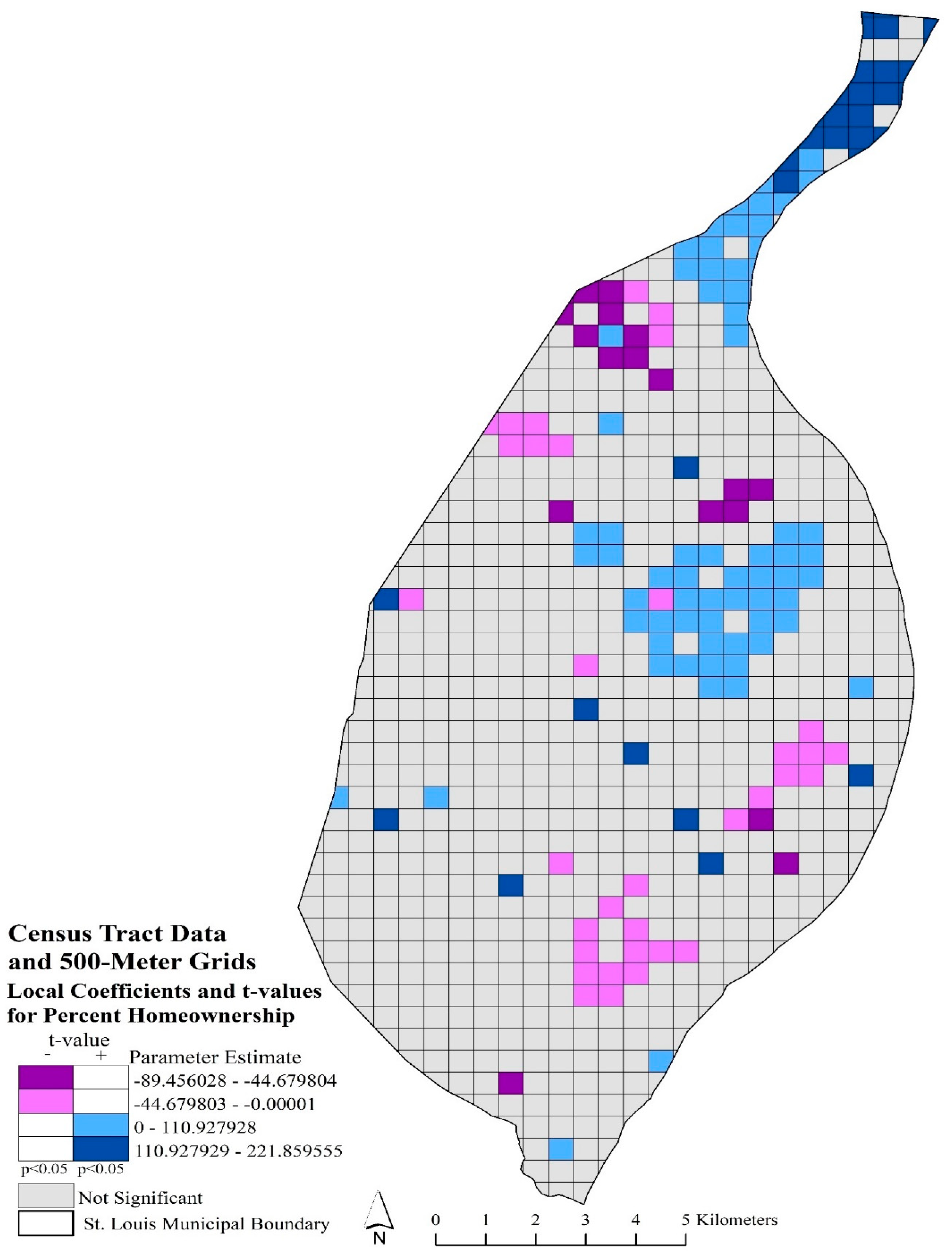
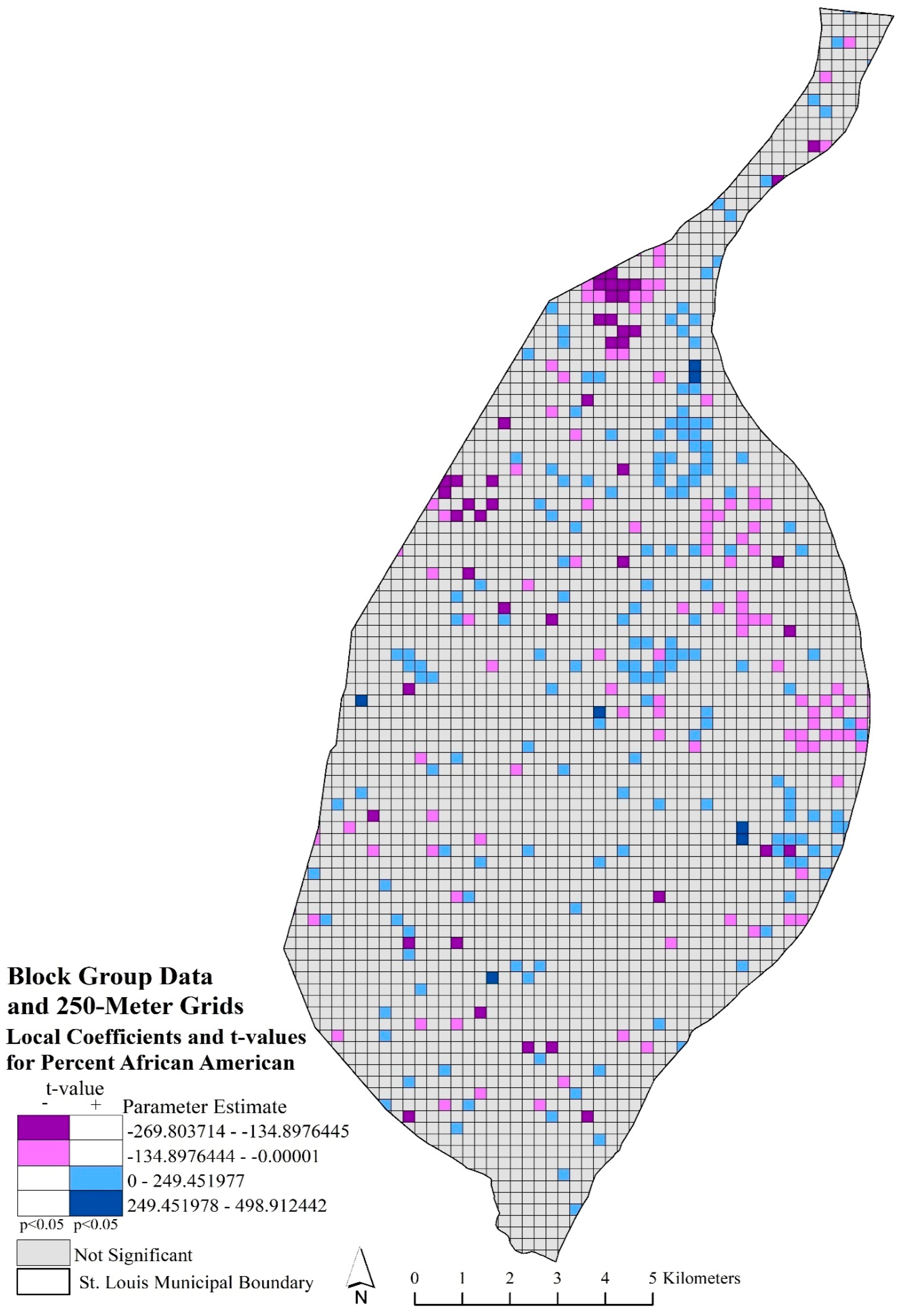
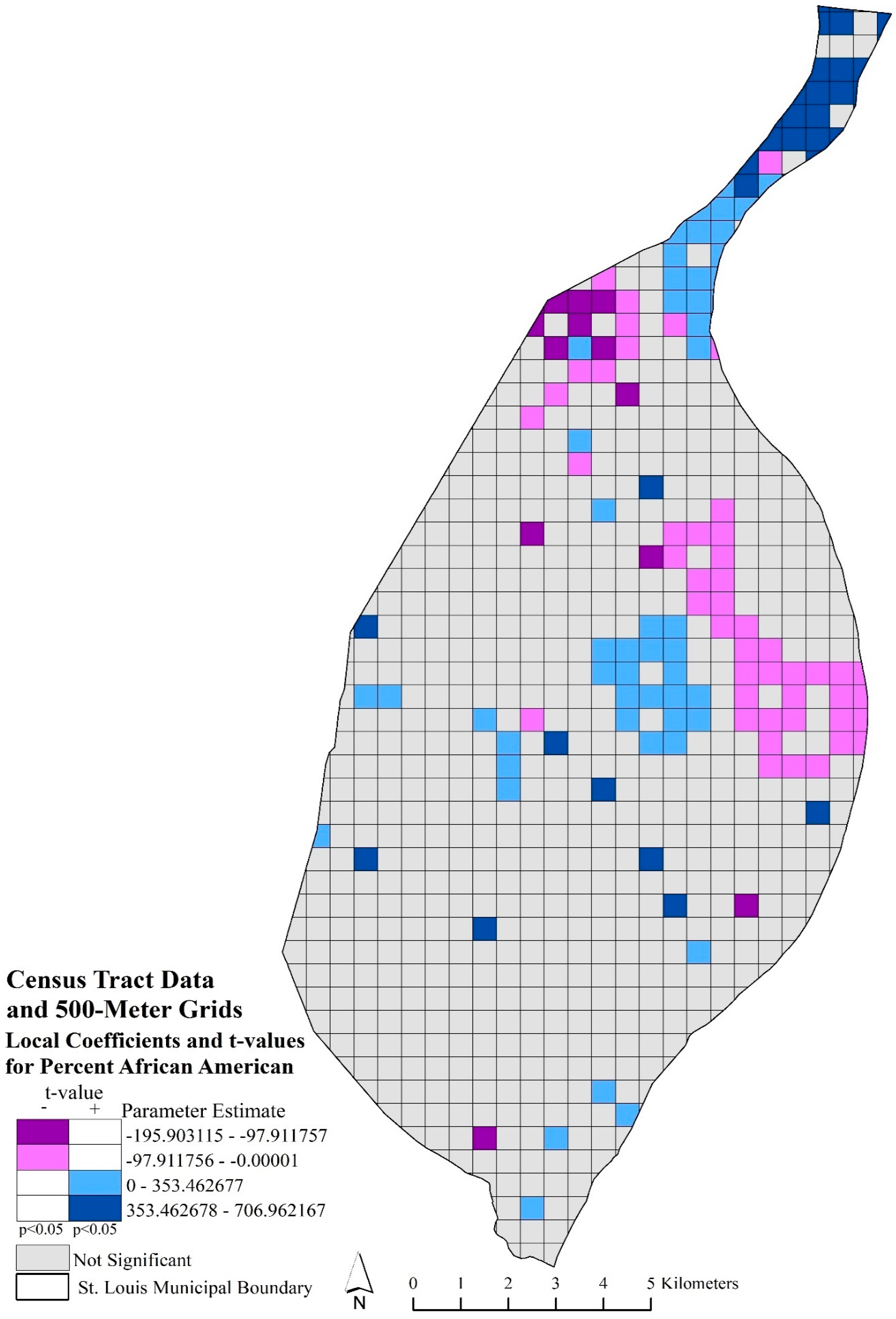
Bivariate maps depicting the spatial location of significant t-values (p < 0.05) and local parameter estimates are provided in Figure 3 and Figure 4. Displaying the local coefficients and significant t-values in a bivariate map provided the opportunity to interpret spatial nonstationary throughout the study area, while affording additional information on local, significant relationships (Mennis 2006). Figure 3 represents the local coefficients and significant t-values (p < 0.05) for percent homeownership using block group data and 250-m grids. The dark and light purple categories indicated where local parameter estimates, and significant t-values had a negative local relationship with robbery rates. These areas significantly (p < 0.05) indicated that lower homeownership rates were associated with a higher robbery rate. These areas are in the central and northern parts of the city. The dark and light blue areas depicted significant areas (p < 0.05) where higher rates of homeownership influenced a greater robbery rate. These areas are also located in the central and northern parts of the city. Figure 4 depicted local coefficients and significant t-values for percent homeownership with census tract data and 500-m grid model. In comparison with Figure 3, Figure 4 appeared more generalized and varied in significant local coefficients. Most of the northern arm of the city had significant positive local coefficients, while both Figure 3 and Figure 4 suggested that higher homeownership rates were associated with higher robbery rates in the central portion of the city. In Figure 4, southern portions of the city have significant negative local coefficients, which suggested that lower homeownership rates influenced robbery rates.
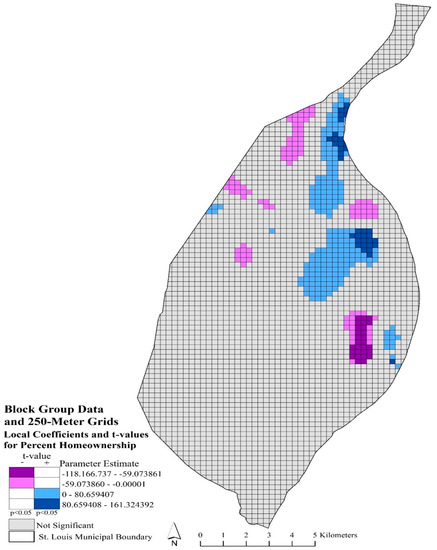
Figure 3.
Mapped percent homeownership local coefficients and significant t-values (p < 0.05) using block group data and 250-m grids. Purple grids indicated significant, negative coefficients; blue grids indicated significant, positive coefficients; and gray grids are not significant.
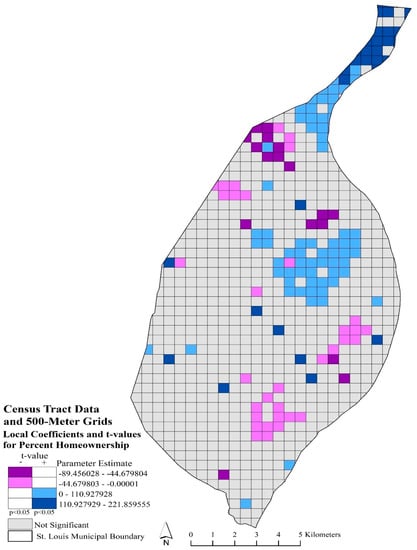
Figure 4.
Mapped percent homeownership local coefficients and significant t-values (p < 0.05) using census tract data and 500-m grids. Purple grids indicated significant, negative coefficients; blue grids indicated significant, positive coefficients; and gray grids are not significant.
Figure 5 depicted the local coefficients and significant t-values for percent African American using block group data and 250-m grids. The purple local areas depicted where a significant relationship occurred between the lower rate of African American population with a higher robbery rate. While the blue areas indicated where significant, increased rates of African American population and higher robbery rates occurred locally. These relationships were scattered throughout the study area, with only a few concentrated areas of significant negative relationships that occurred just before the northern arm and in the central eastern portions of the city and positive relationships in the north and west central and northeast portions of the city. Figure 6 represented the significant local coefficients for percent African American using census tract data and 500-m grids. A pronounced clustering of significant negative and positive local coefficients was apparent in the study area. The significant negative local relationships with percent African American and robbery rates occurred in the eastern part of city center, moving northwest, and southwest of the northern arm. The significant positive local relationships, percent African American and robbery rates, were found in the northern arm and in the center of the city.
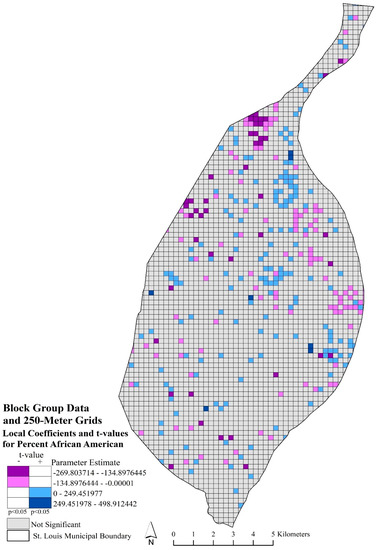
Figure 5.
Mapped percent African American local coefficients and significant t-values (p < 0.05) using block group data and 250-m grids. Purple grids indicated significant, negative coefficients; blue grids indicated significant, positive coefficients; and gray grids are not significant.
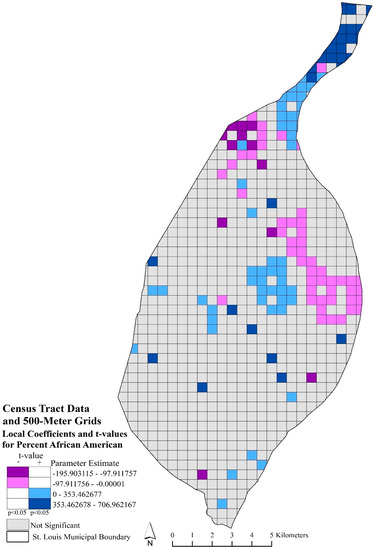
Figure 6.
Mapped percent African American local coefficients and significant t-values (p < 0.05) using census tract data and 500-m grids. Purple grids indicated significant, negative coefficients; blue grids indicated significant, positive coefficients; and gray grids are not significant.
These bivariate maps demonstrated that the spatial relationships between race or stability and robbery rates exhibited local spatial variation. These varied, local spatial relationships were not indicated in the global models, as the OLS statistical method assumed that spatial relationships remained the same throughout the study area. The GWR method indicated specific areas where relationships varied in the eight models we explored.
5. Discussion
This study explored three major research questions. First, does the census tract or block group data better explain the relationship between percent African American and robbery rates, and percent homeownership and robbery rates. We found that the standardized census tract data showed greater explanatory power in examining the local relationship between percent African American and percent homeownership and robbery rates. Second, how do different spatial scales of grids influence the relationships between independent variables and robbery rates. We observed that the larger (500-m grid) scale had higher explanatory power but lacked the precision of the smaller (250-m grid) scale. Last, how did the spatial relationships between race and robbery rates, and stability and robbery rates vary, locally in the City of St. Louis. We identified that the local spatial relationships between race or homeownership and robbery rates were varied, with the greatest variation found in the central portion of the city.
A LISA analysis indicated that robbery rates were spatially clustered in the City of St. Louis. Robbery rate hotspots were typically found in the north and east-central portions of the city, with some northwest tendencies. While the robbery rate cold spots were found around the city boundary and the southwestern part of the city. This analysis provided micro-spatial areas of increased robbery concentrations that can be focused on for preventative policing efforts.
With the presence of spatial autocorrelation in each of the models, the SLM globally-indicated that the independent variables of percent African American and percent homeownership had a significant relationship with robbery rates in St. Louis. Based on the global findings, GWR was used to explore how these relationships spatially varied, on a local level, across the study area.
The GWR analysis presented some important findings. The GWR models provided a better explanation of the local relationships between percent homeownership and the robbery rate as compared to the local relationships between percent African American and the robbery rate in St. Louis. The four models for percent African American had an average of 78% of grids with local r-squared values greater than the global r-squared value; while the four models for percent homeownership had an average of 93.25% of raster grids with local r-squared values greater than the global baseline. Local areas of homeownership or stability could be a more accurate indicator of robbery rates on a local level throughout the city while the local relationship between the percent African American population and robbery rates appeared to be less consistent.
GWR was also used to assess which scale of data, the census tract or block group, provided a better explanation of the selected independent variables and robbery rates in St. Louis. The block group data was collected at a finer spatial scale and offered greater spatial precision in analysis, but then presented as less powerful. For the 250- and 500-m grids, the 500-m grid was more powerful; however, the 250-m grid was more precise. In terms of the two spatial scales of data and two scales of micro-geographic units, larger geographies were associated with more robust models and smaller geographies offered greater spatial precision.
The bivariate maps that depicted significant t-values and parameter estimates indicated local spatial heterogeneity in all relationships of the eight GWR models. The results from the bivariate maps indicated that for some micro-areas in the city, other variables or higher order geographies could have influenced robbery rates. For example, for the percent homeownership with the block group data and 250-m grid scale model, clustered areas of significant and negative local coefficients of homeownership rates associated with higher robbery rates, this may suggest that other factors explain this relationship. For instance, potential factors may include a transient or renter population that could improve the explanation of robbery rates in a local area. Additionally, in the same model, concentrations of significant and positive percent homeownership local coefficients may suggest that a larger geographic scale, such as a culturally homogenous neighborhood, may be collectively influencing the robbery rate. Another possibility could be that the population residing in the area of increased robbery rates are not the same population committing the crimes and these local areas may provide spatial environment conducive to committing robbery (Brantingham and Brantingham 1993).
The global spatial regression models indicated percent African American and percent homeownership as significantly influencing robbery rates throughout the City of St. Louis and this finding correlated with St. Louis’ historical issue of residential segregation. St. Louis is one of the leading urban areas in the United States with extreme racial and residential segregation (Oliveri 2015). Deeply rooted racism in the early 1900s produced segregated neighborhoods, which influenced and perpetuated unfair home loan lending practices for several decades. The practice of redlining severely restricted housing for African Americans, which disproportionately inhibited economic growth and security associated with homeownership. The Fair Housing Act of 1968 made redlining illegal; however, the economic disadvantage and residential segregation remained (Purnell et al. 2018). A period of urban renewal backed by the federal government replaced several African American neighborhoods with commercial buildings and interstate developments (Johnson 2016). The affordable and vouchered housing made available to the displaced African American population, which was disproportionately poor and segregated, reinforced the racial and residential segregation in the city (Metzger 2014). White-flight to the surrounding suburban areas, especially to surrounding St. Louis County, resulted in the fortification of the racial divide (Purnell et al. 2018). St. Louis’ history of racial and residential segregation corresponded with the significant local spatial variation found for the percent African American population and percent homeownership’s influence on robbery rates. The varying degrees of and racial and residential segregation in St. Louis influence robbery differently throughout the city.
The current study has some limitations associated with GWR model configurations and the irregular size of the study area. Many user configurations can be applied and adjusted while using GWR to explore local spatial heterogeneity. Calibrating a GWR model can be an iterative process, with the kernel bandwidth as perhaps the most sensitive feature. Selecting the appropriate bandwidth is essential in accurately modeling local spatial relationships. Bandwidths that are too wide may not capture local spatial variation, while bandwidths that are too narrow may overrepresent local spatial variation (Yrigoyen et al. 2008).
The City of St. Louis has a municipal boundary that is irregular. The northern portion of the city is an isolated arm, bounded by St. Louis County to the west and the Mississippi River to the east. This part of the city is approximately 1.5 km (widest) and 6.5 km long and has a limited number of neighbors for configured bandwidths to consider in the GWR analysis. Due to this geographic limitation, future studies may consider the application of Conditional Geographically Weighted Regression (CGWR) (Leong and Yue 2017) or Multiscale Geographically Weighted Regression (MGWR) (Fotheringham et al. 2017), which allows bandwidths to vary and offers increased smoothing, may provide greater accuracy in the results to assess the relationships between the selected independent variables and robbery rates in this area.
The areal interpolation technique used in the current research also presents another limitation, an apparent trade-off between the scale of geography and data currency. The utilization of block and land parcel data assigned to raster grids would provide results at a smaller geographic scale and assign population to precise geographic areas associated with residential land use types. This methodological approach would result in more precise geography with outdated socioeconomic data (only available from the 2010 Decennial Census). The current research favored data currency for our methodological strategy. We utilized block group and census tract data from the ACS 5-year estimates (2012–2016) that coordinated with the existing crime patterns. While the limitations of these methodological approaches are considered, a multitude of geographic strategies exist to assign values to raster grids; all of which will inherently have limitations associated with user-defined criteria.
While the current study offered an explanatory analysis of spatial clustering and the global and local influencers of robbery rates using different geographic scales, future studies may consider applying a GWR methodology that allows for variations in bandwidths throughout the study area with each independent variable. This may provide greater accuracy in assessing local relationships. Although the relationships of percent African American and percent homeownership were indicated as globally significant with robbery rates from the SLM analysis and the subsequent local analysis, future research may consider how statistically insignificant independent variables at the global level, exert a potentially concentrated, statistically significant influence at the local level using different geographic scales. Comparing the results of characteristically similar cities or the same study area over two-different time periods may also yield interesting results.
Author Contributions
T.A.S. performed data curation, formal analysis, investigation, methodology, project administration, visualization, writing, reviewing, and editing. J.S.O.S. conceptualized, supervised, validated, reviewed, and edited the research.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Andresen, Martin. 2006. A spatial analysis of crime in Vancouver, British Columbia: A synthesis of social disorganization and routine activity theory. The Canadian Geographer 50: 487–502. [Google Scholar] [CrossRef]
- Andresen, Martin, and Nicolas Malleson. 2011. Testing the stability of crime patterns: Implications for theory and police. Journal of Research in Crime and Delinquency 48: 58–82. [Google Scholar] [CrossRef]
- Anselin, Luc. 1995. Local Indicators of Spatial Association-LISA. Geographical Analysis 27: 93–115. [Google Scholar] [CrossRef]
- Anselin, Luc. 1999. Interactive Techniques and Exploratory Spatial Data Analysis. In Geographical Information Systems: Principles, Techniques, Management and Applications. Edited by Paul Longley, Michael Goodchild, David Maguire and David Rhind. New York: Wiley, pp. 251–64. [Google Scholar]
- Anselin, Luc, and Anil Bera. 1998. Spatial Dependence in Linear Regression Models with an Introduction to Spatial Econometrics. In Handbook of Applied Economic Statistics. Edited by Aman Ullah and David Giles. New York: Marcel Dekker, pp. 237–89. [Google Scholar]
- Anselin, Luc, and Arthur Getis. 1992. Spatial statistical analysis and geographic information systems. The Annals of Regional Science 26: 19–33. [Google Scholar] [CrossRef]
- Barnum, Jeremy D., Joel M. Caplan, Leslie W. Kennedy, and Eric L. Piza. 2017. The crime kaleidoscope: A cross-jurisdictional analysis of place features and crime in three urban environments. Applied Geography 79: 203–11. [Google Scholar] [CrossRef]
- Bidanset, Paul, and John Lombard. 2014. The effect of kernel and bandwidth specification in geographically weighted regression models on the accuracy and uniformity of mass real estate appraisal. Journal of Property Tax Assessment & Administration 10: 5–14. [Google Scholar]
- Boggess, Lyndsay N., and John R. Hipp. 2010. Violent crime, residential instability and mobility: Does the relationship differ in minority neighborhoods? Journal of Quantitative Criminology 26: 351–70. [Google Scholar] [CrossRef]
- Braga, Anthony, David Hureau, and Andrew Papachristos. 2011. The relevance of micro places to citywide robbery trends: A longitudinal analysis of robbery incidents at street corners and block faces in Boston. Journal of Research in Crime and Delinquency 48: 7–32. [Google Scholar] [CrossRef]
- Brantingham, Patricia, and Paul Brantingham. 1993. Environment, Routine, and Situation: Toward a Pattern Theory of Crime. In Routine Activity and Rational Choice Advances in Criminological Theory. Edited by R. V. Clarke and M. Felson. New Brunswick: Transaction Publications, pp. 259–94. [Google Scholar]
- Brantingham, Paul, and Patricia Brantingham. 1999. Theoretical model of crime hot spot generation. Studies on Crime and Crime Prevention 8: 7–26. [Google Scholar]
- Bunch, Rick L., Christine Murray, Xiaoli Gao, and Eleazer D. Hunt. 2018. Geographic analysis of domestic violence incident locations and neighborhood level influences. International Journal of Applied Geospatial Research 9: 14–32. [Google Scholar] [CrossRef]
- Bunting, Ryan J., Oliver Yang Chang, Christopher Cowen, Richard Hankins, Staci Langston, Alexander Warner, Xiaxia Yang, Eric R. Louderback, and Shouraseni Sen Roy. 2018. Spatial patterns of larceny and aggravated assault in Miami–Dade County, 2007–2015. The Professional Geographer 70: 34–46. [Google Scholar] [CrossRef]
- Cahill, Meagan, and Gordon Mulligan. 2007. Using geographically weighted regression to explore local crime patterns. Social Science Computer Review 25: 174–93. [Google Scholar] [CrossRef]
- Cameron, Michael P., William Cochrane, Craig Gordon, and Michael Livingston. 2016. Alcohol outlet density and violence: A geographically weighted regression approach. Drug and Alcohol Review 35: 280–88. [Google Scholar] [CrossRef] [PubMed]
- Caplan, Joel M., Leslie W. Kennedy, and Joel Miller. 2011. Risk terrain modeling: Brokering criminological theory and GIS methods for crime forecasting. Justice Quarterly 28: 360–81. [Google Scholar] [CrossRef]
- Caplan, Joel M., Leslie W. Kennedy, and Eric L. Piza. 2012. Joint utility of event-dependent and environmental crime analysis techniques for violent crime forecasting. Crime & Delinquency 59: 243–70. [Google Scholar] [CrossRef]
- Caplan, Joel M., Leslie W. Kennedy, Eric Piza, and Jeremy Heffner. 2013. Risk Terrain Modelling Diagnostics Utility User Manual (Version 1). Newark: Rutgers Center on Public Security. [Google Scholar]
- Chainey, Spencer. 2013. Examining the influence of cell size and bandwidth size on kernel density estimation crim hotspot for predicting spatial patterns of crime. Bulletin of the Geographical Society of Liege 60: 7–19. [Google Scholar]
- Chainey, Spencer, and Jerry Ratcliffe. 2005. GIS and Crime Mapping. Chichester: Wiley. [Google Scholar]
- Curman, Andrea, Martin Andresen, and Paul Brantingham. 2015. Crime and place: A longitudinal examination of street segment patterns in Vancouver, BC. Journal of Quantitative Criminology 31: 127–47. [Google Scholar] [CrossRef]
- Dmowska, Anna, and Tomasz F. Stepinski. 2014. High resolution dasymetric model of U.S demographics with application to spatial distribution of racial diversity. Applied Geography 53: 417–26. [Google Scholar] [CrossRef]
- Drawve, Grant, Shaun A. Thomas, and Jeffery T. Walker. 2016. Bringing the physical environment back into neighborhood research: The utility of RTM for developing an aggregate neighborhood risk of crime measure. Journal of Criminal Justice 44: 21–29. [Google Scholar] [CrossRef]
- Eck, John, Spencer Chainey, James Cameron, Michael Leitner, and Ronald Wilson. 2005. Mapping Crime: Understanding hotspots; Washington, DC: U.S. Department of Justice Office of Justice Programs.
- Feldmeyer, Ben. 2010. The effects of racial/ethnic segregation on Latino and black homicide. The Sociological Quarterly 51: 600–23. [Google Scholar] [CrossRef]
- Fitterer, Jessica, Trisalyn Nelson, and Farouk Nathoo. 2015. Predictive crime mapping. Police Practice and Research 16: 121–35. [Google Scholar] [CrossRef]
- Fotheringham, A. Stewart, and Peter Rogerson. 2009. The SAGE Handbook of Spatial Analysis. London: SAGE Publications Ltd. [Google Scholar] [CrossRef]
- Fotheringham, A. Stewart, Wenbai Yang, and Wei Kang. 2017. Multiscale geographically weighted regression (MGWR). Annals of the American Association of Geographers 107: 1247–65. [Google Scholar] [CrossRef]
- Frazier, Amy E., Sharmistha Bagchi-Sen, and Jason Knight. 2013. The spatio-temporal impacts of demolition land use policy and crime in a shrinking city. Applied Geography 41: 55–64. [Google Scholar] [CrossRef]
- Grubesic, Tony H. 2006. On the application of fuzzy clustering for crime hot spot detection. Journal of Quantitative Criminology 22: 77–105. [Google Scholar] [CrossRef]
- Han, Daikwon, and Dennis Gorman. 2013. Exploring spatial associations between on-sale alcohol availability, neighborhood population characteristics, and violent crime in a geographically isolated city. Journal of Addiction 2013: 356152. [Google Scholar] [CrossRef] [PubMed]
- Hart, Timothy, and Paul Zandbergen. 2014. Kernel Density Estimation and Hotspot Mapping. Policing: An International Journal of Police Strategies & Management 37: 305–23. [Google Scholar] [CrossRef]
- He, Jinliao, Xianjin Huang, and Guangliang Xi. 2018. Measuring urban metrics of creativity using a Grid-Based geographically weighted regression model. Journal of Urban Planning and Development 144. [Google Scholar] [CrossRef]
- Hipp, John R. 2007. Income inequality, race, and place: Does the distribution of race and class within neighborhoods affect crime rates? Criminology 45: 665–98. [Google Scholar] [CrossRef]
- Hipp, John R. 2011. Spreading the wealth: The effect of the distribution of income and race/ethnicity across households and neighborhoods on city crime trajectories. Criminology 49: 631–65. [Google Scholar] [CrossRef]
- Johnson, Walter. 2016. What do we mean when we say, “structural racism”? Kalfou 3. [Google Scholar] [CrossRef]
- Kang, Songman. 2015. Inequality and crime revisited: Effects of local inequality and economic segregation on crime. Journal of Population Economics 29: 593–626. [Google Scholar] [CrossRef]
- Kennedy, Leslie W., Joel M. Caplan, and Eric Piza. 2010. Risk clusters, hotspots, and spatial intelligence: Risk terrain modeling as an algorithm for police resource allocation strategies. Journal of Quantitative Criminology 27: 339–62. [Google Scholar] [CrossRef]
- Kennedy, Leslie W., Joel M. Caplan, Eric L. Piza, and Henri Buccine-Schraeder. 2015. Vulnerability and exposure to crime: Applying risk terrain modeling to the study of assault in Chicago. Applied Spatial Analysis and Policy 9: 529–48. [Google Scholar] [CrossRef]
- Kounadi, Ourania, and Michael Leitner. 2015. Spatial information divergence: Using global and local indices to compare geographical masks applied to crime data. Transactions in GIS 19: 737–57. [Google Scholar] [CrossRef]
- Krivo, L., R. Peterson, and D. Kuhl. 2009. Segregation, racial structure, and neighborhood violent crime. American Journal of Sociology 114: 1765–802. [Google Scholar] [CrossRef]
- Leong, Yin-Yee, and Jack C. Yue. 2017. A modification to geographically weighted regression. International Journal of Health Geographics 16: 11. [Google Scholar] [CrossRef]
- Lin, Shing, and Yongmei Lu. 2006. Evaluating local non-stationarity when considering the spatial variation of large-scale autocorrelation. Transactions in GIS 10: 301–18. [Google Scholar] [CrossRef]
- Maimaitijiang, Maitiniyazi, Abduwasit Ghulam, J. S. Onésimo Sandoval, and Matthew Maimaitiyiming. 2015. Drivers of land cover and land use changes in St. Louis metropolitan area over the past 40 years characterized by remote sensing and census population data. International Journal of Applied Earth Observation and Geoinformation 35: 161–74. [Google Scholar] [CrossRef]
- Malczewski, Jacek, and Anneliese Poetz. 2005. Residential burglaries and neighborhood socioeconomic context in London, Ontario: Global and local regression analysis. The Professional Geographer 57: 516–29. [Google Scholar] [CrossRef]
- Mennis, Jeremy. 2006. Mapping the results of geographically weighted regression. The Cartographic Journal 43: 171–79. [Google Scholar] [CrossRef]
- Metzger, Molly W. 2014. Section 8 in the St. Louis region: Local opportunities to expand housing choice. Center for Social Development 14: 1–7. [Google Scholar]
- Nakaya, Tomoki, Martin Charlton, Jing Yao, and A. Stewart Fotheringham. 2016. GWR4.09 user manual: Windows application for geographically weighted regression modelling. Available online: http://manualslist.info/pdf/gwr409-user-manual-geodacenterorg.html (accessed on 30 October 2018).
- Oliveri, Rigel. 2015. Setting the stage for Ferguson: Housing discrimination and segregation in St. Louis. Missouri Law Review 80: 1053. [Google Scholar]
- Ord, John K., and Arthur Getis. 1995. Local spatial autocorrelation statistics: Distributional issues and an application. Geographical Analysis 27: 286–306. [Google Scholar] [CrossRef]
- Parker, Karen, and Richard Stansfield. 2015. The changing urban landscape: Interconnections between racial/ethnic segregation and exposure in the study of race-specific violence over time. American Journal of Public Health 105: 1795–805. [Google Scholar] [CrossRef] [PubMed]
- Patterson, Lauren A., and Martin W. Doyle. 2009. Assessing effectiveness of national flood policy through spatiotemporal monitoring of socioeconomic exposure. JAWRA Journal of the American Water Resources Association 45: 237–52. [Google Scholar] [CrossRef]
- Purnell, J., N. Cambria, and L. Brossart. 2018. Segregation in St. Louis: Dismantling the Divide. St. Louis: Washington University in St. Louis. [Google Scholar]
- Ratcliffe, Jerry, and Michael McCullagh. 1999. Burglary, victimization, and social deprivation. Crime Prevention and Community Safety 1: 37–46. [Google Scholar] [CrossRef]
- Ren, Hongyan, Lan Zheng, Qiaoxuan Li, Wu Yuan, and Liang Lu. 2017. Exploring determinants of spatial variations in the Dengue fever epidemic using geographically weighted regression model: A case study in the joint Guangzhou-Foshan area, China, 2014. International Journal of Environmental Research and Public Health 14: 1518. [Google Scholar] [CrossRef]
- Shaw, Clifford, and Henry MacKay. 1942. Juvenile Delinquency and Urban Areas: A Study of Rates of Delinquency in Relation to Differential Characteristics of Local Communities in American Cities. Chicago: University of Chicago Press. [Google Scholar]
- Smith, Tara A., and Juan. S. Onésimo Sandoval. 2018. A Spatial Analysis of Homicides in Saint Louis: The Importance of Scale. Spatial Demography. [Google Scholar] [CrossRef]
- Stucky, Thomas D., and John R. Ottensmann. 2009. Land use and violent crime. Criminology 47: 1223–64. [Google Scholar] [CrossRef]
- Tighe, J. Rosie, and Joanna P. Ganning. 2015. The divergent city: Unequal and uneven development in St. Louis. Urban Geography 36: 654–73. [Google Scholar] [CrossRef]
- Tita, George, and Steven Radil. 2010. Making space for theory: The challenges of theorizing space and place for spatial analysis in criminology. Journal of Quantitative Criminology 26: 467–79. [Google Scholar] [CrossRef]
- Vilalta, Carlos J. 2013. How exactly does place matter in crime analysis? Place, space, and spatial heterogeneity. Journal of Criminal Justice Education 24: 290–315. [Google Scholar] [CrossRef]
- Vilalta, Carlos, and Robert Muggah. 2016. What explains criminal violence in Mexico City? A test of two theories of crime. Stability: International Journal of Security & Development 5. [Google Scholar] [CrossRef]
- Wang, Fahui, and Martin T. Arnold. 2008. Localized income inequality, concentrated disadvantage and homicide. Applied Geography 28: 259–70. [Google Scholar] [CrossRef]
- Weisburd, David, and Shai Amram. 2014. The law of concentrations of crime at place: The case of Tel Aviv-Jaffa. Police Practice and Research 15: 101–14. [Google Scholar] [CrossRef]
- Weisburd, David, Shawn Bushway, Cynthia Lum, and Sue-Ming Yang. 2006. Trajectories of crime at place: A longitudinal study of street segments in the city of Seattle. Criminology 42: 283–322. [Google Scholar] [CrossRef]
- Weisburd, David, Nancy Morris, and Elizabeth Groff. 2009. Hot spots of juvenile crime: A longitudinal study of arrest incidents at street segments in Seattle, Washington. Journal of Quantitative Criminology 25. [Google Scholar] [CrossRef]
- Weisburd, David, Elizabeth Groff, and Sue-Ming Yang. 2012. The Criminology of Place: Street Segments and Our Understanding of the Crime Problem. New York: Oxford University Press. [Google Scholar]
- Wheeler, David C., and Lance A. Waller. 2009. Comparing spatially varying coefficient models: A case study examining violent crime rates and their relationships to alcohol outlets and illegal drug arrests. Journal of Geographical Systems 11: 1–22. [Google Scholar] [CrossRef]
- Xie, Min, and David McDowall. 2010. The Reproduction of Racial Inequality: How Crime Affects Housing Turnover. Criminology 48. [Google Scholar] [CrossRef]
- Yrigoyen, Coro Chasco, Isabel García Rodríguez, and José Vicéns Otero. 2008. Modelling spatial variations in household disposable income with geographically weighted regression. Estadística Españolal 50: 321–60. [Google Scholar]
- Zhang, Haifeng, and Wei Song. 2014. Addressing issues of spatial spillover effects and non-stationarity in analysis of residential burglary crime. GeoJournal 79: 89–102. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).