Interactions in Generalized Linear Models: Theoretical Issues and an Application to Personal Vote-Earning Attributes
Abstract
:1. Introduction
2. Interactions in Linear Models
3. Interactions in Generalized Linear Models
3.1. The Effect of the Link Function
3.2. Illustration of the Link Function Effect

3.3. Interpreting Interaction Effects in Generalized Linear Models
3.4. Reporting GLM Interaction Effects with First Differences
4. A Methodological Controversy in Political Science
5. Higher-Order Interactions
6. An Application to Personal Vote-Earning Attributes
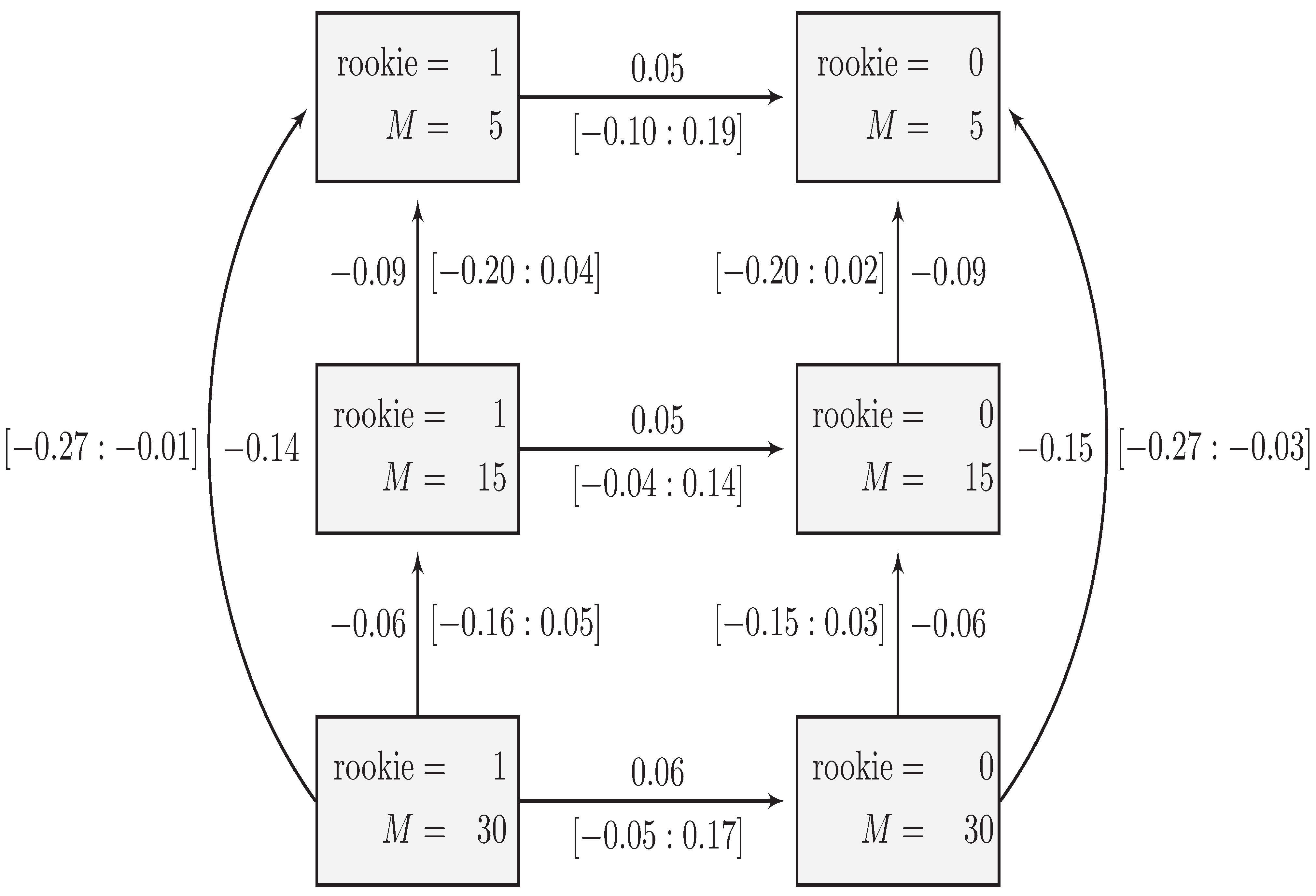
6.1. The First-order Interaction Model
| Model 1 | Model 2 | |||
|---|---|---|---|---|
| Estimate | Std. Error | Estimate | Std. Error | |
| Constant () | 0.74 | 0.14 | 0.69 | 0.18 |
| () | −0.49 | 0.11 | −0.50 | 0.14 |
| () | 0.63 | 0.29 | 0.33 | 0.39 |
| open () | −0.43 | 0.34 | −0.04 | 0.47 |
| rookie () | 0.11 | 0.26 | ||
| () | 0.02 | 0.20 | ||
| () | 0.36 | 0.56 | ||
| () | −0.50 | 0.64 | ||
| Null Deviance | 1493.6 on 1126 d.f. | 1473.3 on 1112 d.f. | ||
| Residual Deviance | 1471.7 on 1123 d.f. | 1448.2 on 1105 d.f. | ||
| AIC | 1479.7 | 1464.2 | ||
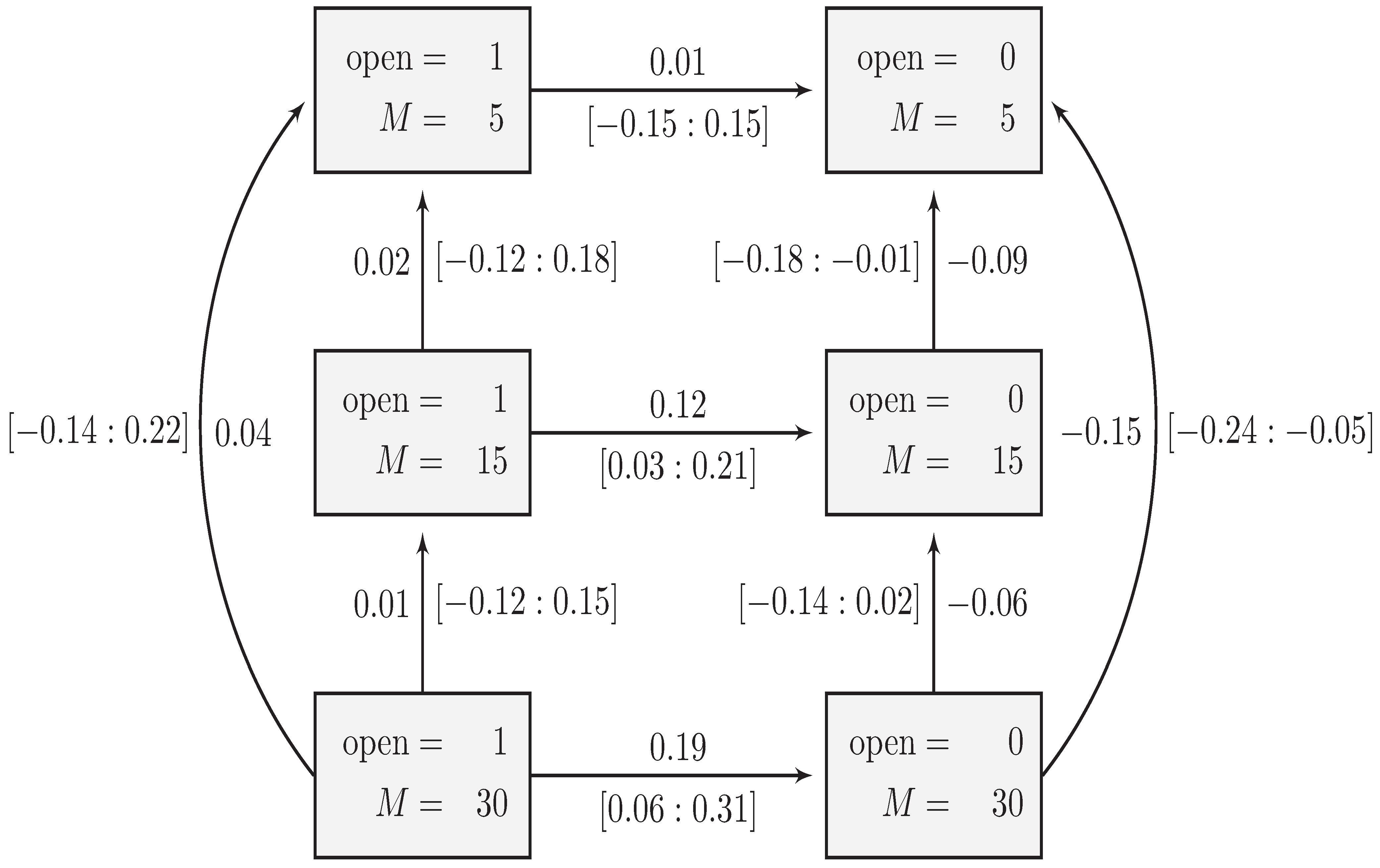
6.2. The Second-Order Interaction Model
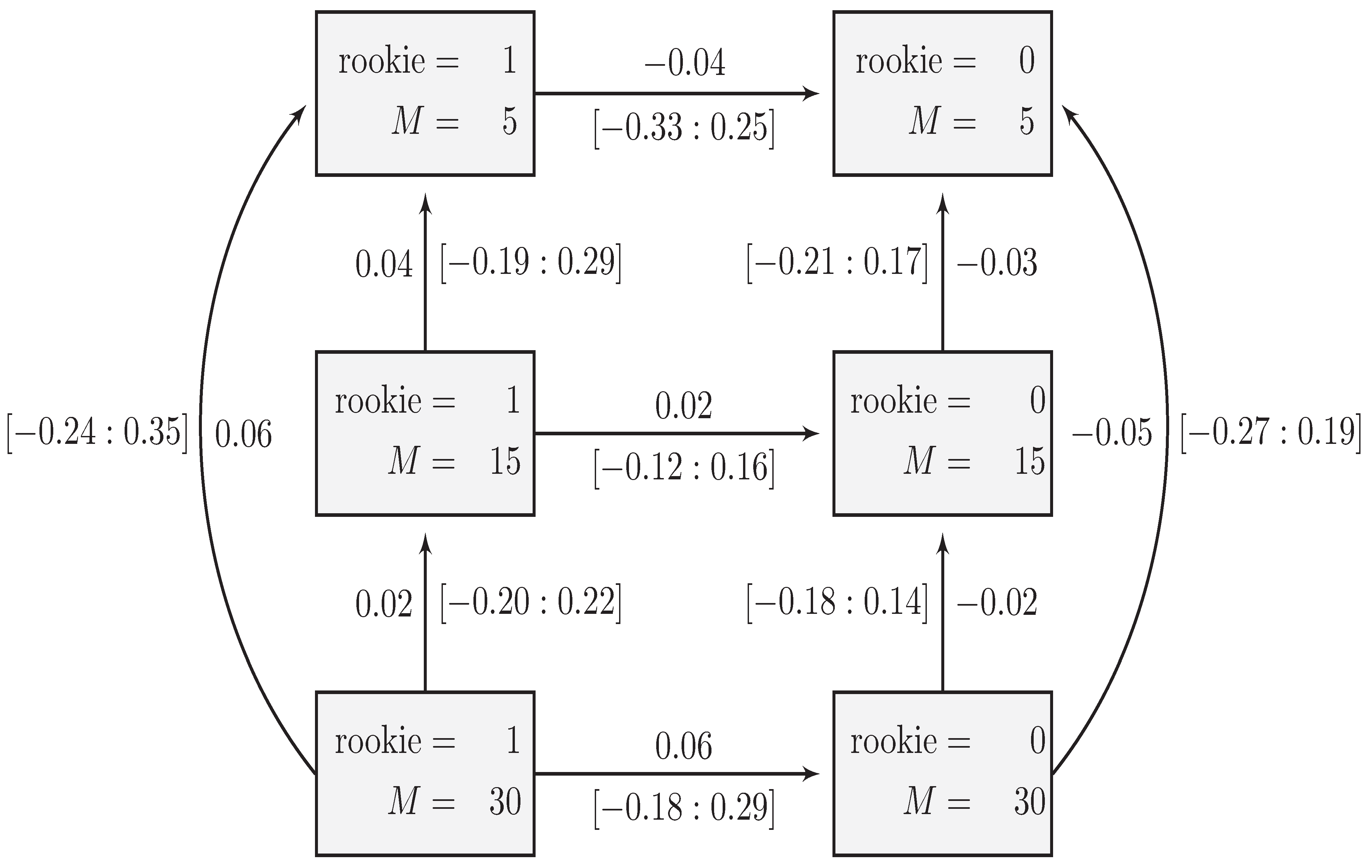
7. Conclusions
In summary, partial products of variables are correctly interpreted as interactions whatever their level of scaling, whether or not they are correlated, whether or not their means are zero, whether they are observational or experimental in origin, and whether single variables or sets of variables are at issue.
Acknowledgements
Conflict of Interest
References
- Robert J. Friedrich. “In Defense of Multiplicative Terms in Multiple Regression Equations.” American Journal of Political Science 26 (1982): 797–833. [Google Scholar] [CrossRef]
- William D. Berry, Jachueline H. R. Demritt, and Justin Esarey. “Testing for Interaction in Binary Logit and Probit Models: Is a Product Term Essential? ” American Journal of Political Science 54 (2010): 248–66. [Google Scholar] [CrossRef]
- Frances S. Berry, and William D. Berry. “Specifying a Model of State Policy Innovation.” American Political Science Review 85 (1991): 573–79. [Google Scholar] [CrossRef]
- William D. Berry. “Testing for Interaction in Models with Binary Dependent Variables.” Political Methodology Working Paper Archive. 1999. http://polmeth.wustl.edu/mediaDetail.php?docId=210.
- Howard Frant. “Specifying A Model of State Policy Innovation.” American Political Science Review 85 (1991): 571–73. [Google Scholar]
- Gary King. “Variance Specification in Event Count Models: From Restrictive Assumptions to a Generalized Estimator.” American Journal of Political Science 33 (1989): 762–84. [Google Scholar] [CrossRef]
- Thomas Brambor, William Roberts Clark, and Matt Golder. “Understanding Interaction Models: Improving Empirical Analyses.” Political Analysis 14 (2006): 63–82. [Google Scholar] [CrossRef]
- Cindy D. Kam, and Robert J. Franzese Jr. Modeling and Interpreting Interactive Hypotheses in Regression Analysis. Ann Arbor: University of Michigan Press, 2007. [Google Scholar]
- Jonathan Nagler. “Scobit: An Alternative Estimator to Logit and Probit.” American Journal of Political Science 38 (1994): 230–55. [Google Scholar] [CrossRef]
- Kim Fridkin Kahn, and Patrick J. Kenney. “A Model of Candidate Evaluations in Senate Elections: The Impact of Campaign Intensity.” The Journal of Politics. 59 (1997): 1173–205. [Google Scholar] [CrossRef]
- Dean Lacy, and Phillip Paolino. “Downsian Voting and the Separation of Powers.” American Journal of Political Science 42 (1998): 1180–99. [Google Scholar] [CrossRef]
- Bruce E. Moon, and William J. Dixon. “Politics, the State, and Basic Human Needs: A Cross-National Study.” American Journal of Political Science 29 (1985): 661–94. [Google Scholar] [CrossRef]
- William Roberts Clark, Michael J. Gilligan, and Matt Golder. “A Simple Multivariate Test for Asymmetric Hypotheses.” Political Analysis 14 (2006): 311–31. [Google Scholar] [CrossRef]
- R. A. Fisher, and W. A. Mackenzie. “Studies in Crop Variation. II. The Manurial Response of Different Potato Varieties.” Journal of the Agricultural Society 13 (1923): 311–20. [Google Scholar] [CrossRef]
- D. J. Finney. “Main Effects and Interactions.” Journal of the American Statistical Association 43 (1948): 566–71. [Google Scholar] [CrossRef] [PubMed]
- William H. Greene. Econometric Analysis. Upper Saddle River: Prentice Hall, 2003, Chapter 4. [Google Scholar]
- Ronald J. Wonnacott, and Thomas H. Wonnacott. Econometrics. New York: John Wiley & Sons, 1970. [Google Scholar]
- Paul D. Allison. “Testing for Interaction in Multiple Regression.” American Journal of Sociology 83 (1977): 144–53. [Google Scholar] [CrossRef]
- John Fox. Applied Regression Analysis, Linear Models, and Related Methods. Thousand Oaks: Sage, 1997, Chapter 14. [Google Scholar]
- George E. P. Box, and Norman R. Draper. Empirical Model-Building and Response Surfaces. Oxford: John Wiley & Sons, 1987. [Google Scholar]
- André I. Khuri, and John A. Cornell. Response Surfaces: Designs and Analyses. New York: Marcel Dekker, 1987. [Google Scholar]
- John A. Cornell, and Douglas C. Montgomery. “Fitting Models to Data: Interaction Versus Polynomial? Your Choice! ” Communications in Statistics–Theory and Methods 25 (1996): 2531–55. [Google Scholar] [CrossRef]
- J. A. Nelder. “A Reformulation of Linear Models.” (with discussion). Journal of the Royal Statistical Society, Series A 140 (1977): 48–76. [Google Scholar] [CrossRef]
- D. R. Cox. “Interaction.” International Statistical Review 52 (1984): 1–31. [Google Scholar] [CrossRef]
- Phillip Karl Wood, and Paul Games. “Rationale, Detection, and Implications of Interactions Between Independent Variables and Unmeasured Variables in Linear Models.” Multivariate Behavioral Research 25 (1990): 295–311. [Google Scholar] [CrossRef]
- James Jaccard, and Choi K. Wan. “Measurement Error in the Analysis of Interaction Effects between Continuous Predictors Using Multiple Regression: Multiple Indicator and Structural Equation Approaches.” Psychological Bulletin 117 (1995): 348–57. [Google Scholar] [CrossRef]
- Irva Hertz-Picciotto, Allan H. Smith, David Holtzman, Michael Lipsett, and George Alexeeff. “Synergism Between Occupational Arsenic Exposure and Smoking in the Induction of Lung Cancer.” Epidemiology 3 (1992): 23–31. [Google Scholar] [CrossRef] [PubMed]
- Susan F. Assmann, David W. Hosmer, Stanley Lemeshow, and Kenneth A. Mundt. “Confidence Intervals for Measures of Interaction.” Epidemiology 7 (1996): 286–90. [Google Scholar] [CrossRef] [PubMed]
- David W. Hosmer, and Stanley Lemeshow. “Confidence Interval Estimation of Interaction.” Epidemiology 3 (1992): 452–56. [Google Scholar] [CrossRef] [PubMed]
- Neil Pearce. “Analytical Implications of Epidemiological Concepts of Interaction.” International Journal of Epidemiology 18 (1989): 976–80. [Google Scholar] [CrossRef] [PubMed]
- Janet M. Box-Steffensmeier, and Christopher J. W. Zorn. “Duration Models and Proportional Hazards in Political Science.” American Journal of Political Science 45 (2001): 972–88. [Google Scholar] [CrossRef]
- Brad T. Gomez, and J. Matthew Wilson. “Political Sophistication and Economic Voting in the American Electorate: A Theory of Heterogeneous Attribution.” American Journal of Political Science 45 (2001): 899–914. [Google Scholar] [CrossRef]
- Diana Evans. “Oil PACs and Aggressive Contribution Strategies.” The Journal of Politics 50 (1988): 1047–56. [Google Scholar] [CrossRef]
- Jan E Leighley, and Arnold Vedlitz. “Race, Ethnicity, and Political Participation: Competing Models and Contrasting Explanations.” The Journal of Politics 61 (1999): 1092–114. [Google Scholar] [CrossRef]
- Dan Reiter, and Allan C. Stam III. “Democracy, War Initiation, and Victory.” American Political Science Review 92 (1998): 377–89. [Google Scholar] [CrossRef]
- Kenneth J. Rothman. Modern Epidemiology. Boston: Little Brown & Co., 1986. [Google Scholar]
- Ludwig Fahrmeir, and Gerhard Tutz. Multivariate Statistical Modelling Based on Generalized Linear Models. New York: Springer, 2001. [Google Scholar]
- P. McCullagh, and J. A. Nelder. Generalized Linear Models. New York: Chapman & Hall/CRC, 1989. [Google Scholar]
- Matthew S. Shugart, Melody E. Valdini, and Kati Suominen. “Looking for Locals: Voter Information Demands and Personal Vote-earning Attributes of Legislators under Proportional Representation.” American Journal of Political Science 49 (2005): 437–49. [Google Scholar] [CrossRef]
- Gary W. Cox. Making Votes Count: Strategic Coordination in the World’s Electoral Systems. New York: Cambridge University Press, 1997. [Google Scholar]
- John M. Carey, and Matthew S. Shugart. “Incentives to Cultivate a Personal Vote: A Rank Ordering of Electoral Formulas.” Electoral Studies 14 (1995): 417–39. [Google Scholar] [CrossRef]
- P. J. Green. “Iteratively Reweighted Least Squares for Maximum Likelihood Estimation, and some Robust and Resistant Alternatives.” Journal of the Royal Statistical Society, Series B 46 (1984): 149–92. [Google Scholar]
- Guido del Pino. “The Unifying Role of Iterative Generalized Least Squares in Statistical Algorithms.” Statistical Science 4 (1989): 394–408. [Google Scholar] [CrossRef]
- Gary King. Unifying Political Methodology. New York: Cambridge University Press, 1989. [Google Scholar]
- James Jaccard, Robert Turrisi, and Choi K. Wan. Interaction Effects in Multiple Regression. Thousand Oaks: Sage, 1990, p. 41. [Google Scholar]
- Neil H. Timm. Applied Multivariate Analysis. New York: Springer-Verlag New York, Inc., 2002. [Google Scholar]
- David Edwards. “Hierarchical Interaction Models.” Journal of the Royal Statistical Society, Series B 52 (1990): 3–20. [Google Scholar]
- Gary King, Michael Tomz, and Jason Wittenberg. “Making the Most of Statistical Analyses: Improving Interpretation and Presentation.” American Journal of Political Science 44 (2000): 341–55. [Google Scholar] [CrossRef]
- Jan de Leeuw. “Discussion of the Papers by Edwards, and Wermuth and Lauritzen.” Journal of the Royal Statistical Society, Series B 52 (1990): 21–50. [Google Scholar]
- Leo A. Goodman. “Interactions in Multidimensional Contingency Tables.” Annals of Mathematical Statistics 35 (1964): 632–46. [Google Scholar] [CrossRef]
- Leona S. Aiken, and Stephen G. West. Multiple Regression: Testing and Interpreting Interactions. Thousand Oaks: Sage, 1991. [Google Scholar]
- Ralph L. Rosnow, and Robert Rosenthal. “Definition and Interpretation of Interaction Effects.” Psychological Bulletin 105 (1989): 143–46. [Google Scholar] [CrossRef]
- Stephen E. Fienberg. The Analysis of Cross-classified Categorical Data. Cambridge: MIT Press, 1980. [Google Scholar]
- Henry Oliver Lancaster. The Chi-squared Distribution. New York: John Wiley & Sons, 1969. [Google Scholar]
- Poul Thyregod, and Henrik Spliid. “A Hypothesis of No Interaction in Factorial Experiments with a Binary Response.” Scandinavian Journal of Statistics 18 (1991): 197–209. [Google Scholar]
- Hiroyuki Uesaka. “Test for Interaction Between Treatment and Stratum with Ordinal Responses.” Biometrics 49 (1993): 123–29. [Google Scholar] [CrossRef] [PubMed]
- M. E. O’Neill. “The Distribution of Higher-Order Interactions in Contingency Tables.” Journal of the Royal Statistical Society, Series B 42 (1980): 357–65. [Google Scholar]
- Ralph L. Rosnow, and Robert Rosenthal. “If You’re Looking at the Cell Means, You’re Not Looking at Only the Interaction (Unless All Main Effects Are Zero).” Psychological Bulletin 110 (1991): 574–76. [Google Scholar] [CrossRef]
- G. Bingham Powell Jr. “Political Representation in Comparative Politics.” Annual Review of Political Science 7 (2004): 273–96. [Google Scholar] [CrossRef]
- Richard F. Fenno Jr. Home Style: House Members in Their Districts. Boston: Little Brown & Co., 1978. [Google Scholar]
- David R. Mayhew. Congress: The Electoral Connection. New Haven: Yale University Press, 1974. [Google Scholar]
- G. H. Freeman. “The Analysis and Interpretation of Interactions.” Statistician 12 (1985): 3–10. [Google Scholar] [CrossRef]
- John W. Tukey. “One Degree of Freedom for Non-Additivity.” Biometrics 5 (1949): 232–42. [Google Scholar] [CrossRef]
- Peter G. Moore, and John W. Tukey. “Query 112.” Biometrics 10 (1954): 562–68. [Google Scholar] [CrossRef]
- Jacob Cohen. “Partialed Products Are Interactions: Partialed Powers Are Curve Components.” Psychological Bulletin 85 (1978): 856–66. [Google Scholar] [CrossRef]
- 1Unfortunately, the term “main effect" is not very revealing or accurate. The coefficient for a non-multiplicative explanatory variable specification given by a variable that is specified as interacting with others, is the contribution for that variable at zero levels of all of the interacting variables. There is no mathematically implied primacy and a more accurate term would be “non-multiplicative” or “single contribution.” However, it seems unwarranted to try and change standard vernacular used by an overwhelming number of authors, dating from as far back as Fisher and Mackenzie [14] and Finney [15]. So this term will be used here.
- 2These models use algebraic forms where components such as exponents are estimated (and hence are different from standard polynomial regression, e.g., Fox ([19], S. 14.2)) in order to make local approximations to continuous, multidimensional response surfaces. For extended discussions, see Box and Draper [20], Khuri and Cornell [21], and Cornell and Montgomery [22].
- 3It is also interesting to note that when the multiplicative interaction term is highly correlated with one of the main effects, it is an indication that the other main effect is not varying much (consider the extreme case where one of the “variables” was the constant!).
- 4Sometimes this is exactly the case and perfectly appropriate. For instance, including gross domestic product (GDP) without separate terms for price and quantity in a model specification implies that price and quantity are important only when considered together. A reader would be quite confused to see price × quantity in this situation as if the constituent parts of GDP had some significance beyond their joint contribution but were not worthy of consideration as individual explanatory variables.
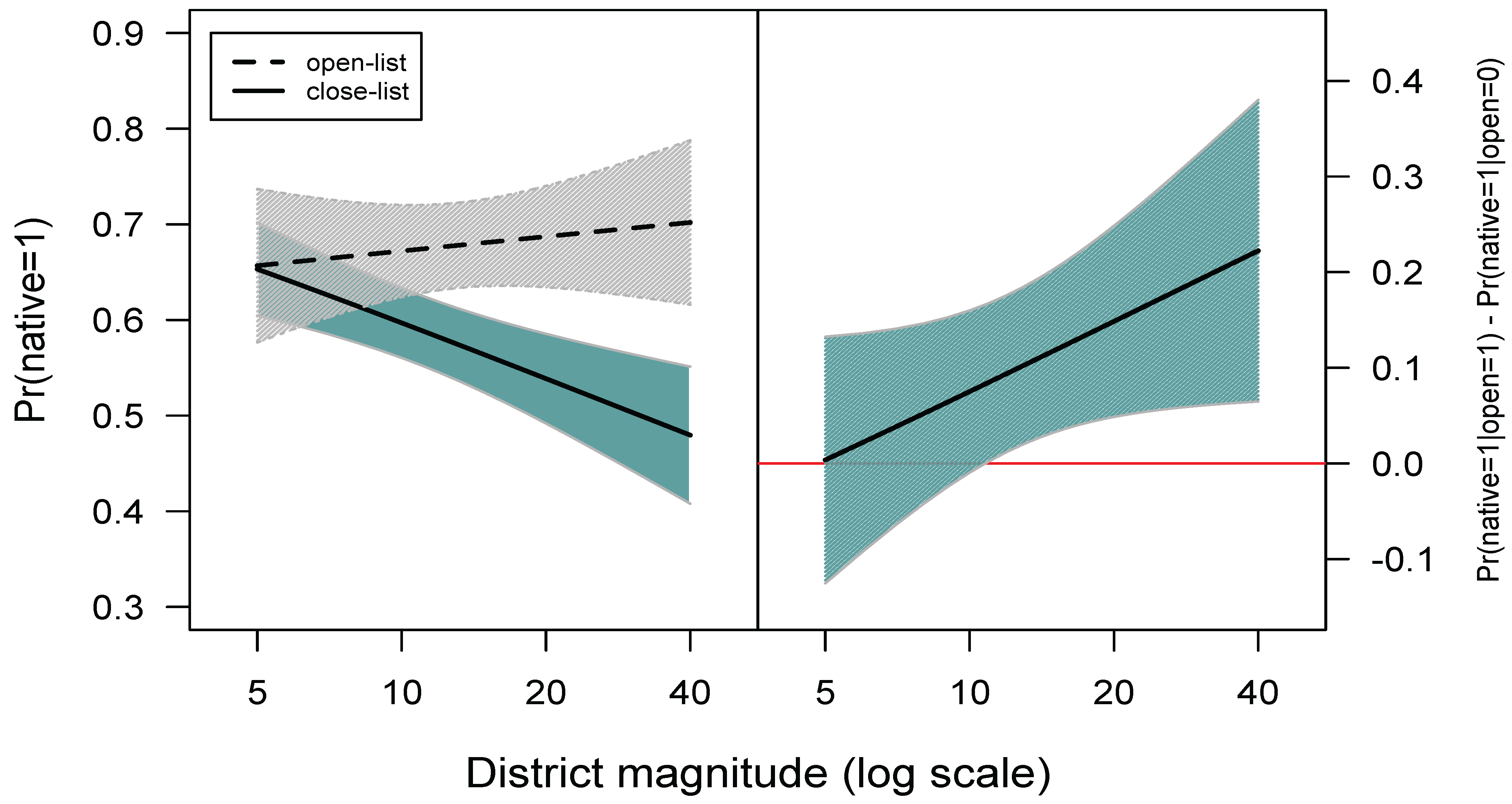
- 5Notice that, according to Carey [41] and Shugart et al. [39], list type and district magnitude interact to affect the incentive of the politicians to cultivate a personal vote and this interaction effect makes open lists and close lists influence PVEA in opposite directions. The hypothesized interaction effect between list type and district magnitude is different from the one introduced by the link function. Specifically, the interaction effect introduced through the link function only changes the magnitude of the main effect as can be seen below in Figure 1. However, adding an interaction term might change not only the magnitude but also the direction of the main effect. This is because the effect of the interaction term overwhelms the main effect as we show in Section 6. Therefore, the model presented in Equation (7) is not used to test the theoretical argument but only for the purpose of illustration.
- 6Since the complete effect of the explanatory variables specified as interacting in the model is conditional on the values of the other co-interacting specified variables, the associated standard error is as well. The derivation of the conditional standard errors for the simple case when there are only two explanatory variables is provided by Friedrich ([1], p. 810) and Jaccard et al. ([45], p. 27), and an abstract form is given in various textbooks, e.g., Timm [46].
- 7Freely distributed software for the calculation of conditional standard errors is available as an R package, and further technical derivations, replication data, as well as analyses of related specifications are available at the authors’ webpage.
- 8In their paper, Shugart et al. test for statistical significance of the difference between and , by means of a test, which is statistically significant at . Based on this result, they state that the effect of district magnitude matters for both list types and claim that the slopes for district magnitude in the two list types are statistically distinct from each other. However, the test does not tell us that is positive and statistically significant: the test only shows that is distinct from , which is a less important result.
- 9In fact, the lack of statistical significance of the effects for district magnitude can be observed in Figure 2 in Shugart et al.’s paper, which is reproduced in the left panel of Figure 2. To see that this is true, notice that the predicted probability for open list systems at a given district magnitude is always covered by the 95% confidence intervals within the given range of district magnitudes, which suggests that, in a magnitude range of 5 to 40, the estimated values of are not different from one another. This cannot be observed by only looking at individual coefficients.
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Tsai, T.-h.; Gill, J. Interactions in Generalized Linear Models: Theoretical Issues and an Application to Personal Vote-Earning Attributes. Soc. Sci. 2013, 2, 91-113. https://doi.org/10.3390/socsci2020091
Tsai T-h, Gill J. Interactions in Generalized Linear Models: Theoretical Issues and an Application to Personal Vote-Earning Attributes. Social Sciences. 2013; 2(2):91-113. https://doi.org/10.3390/socsci2020091
Chicago/Turabian StyleTsai, Tsung-han, and Jeff Gill. 2013. "Interactions in Generalized Linear Models: Theoretical Issues and an Application to Personal Vote-Earning Attributes" Social Sciences 2, no. 2: 91-113. https://doi.org/10.3390/socsci2020091
APA StyleTsai, T.-h., & Gill, J. (2013). Interactions in Generalized Linear Models: Theoretical Issues and an Application to Personal Vote-Earning Attributes. Social Sciences, 2(2), 91-113. https://doi.org/10.3390/socsci2020091




