Development of a CFD Model to Simulate Natural Ventilation in a Semi-Open Free-Stall Barn for Dairy Cows
Abstract
1. Introduction
2. Materials and Methods
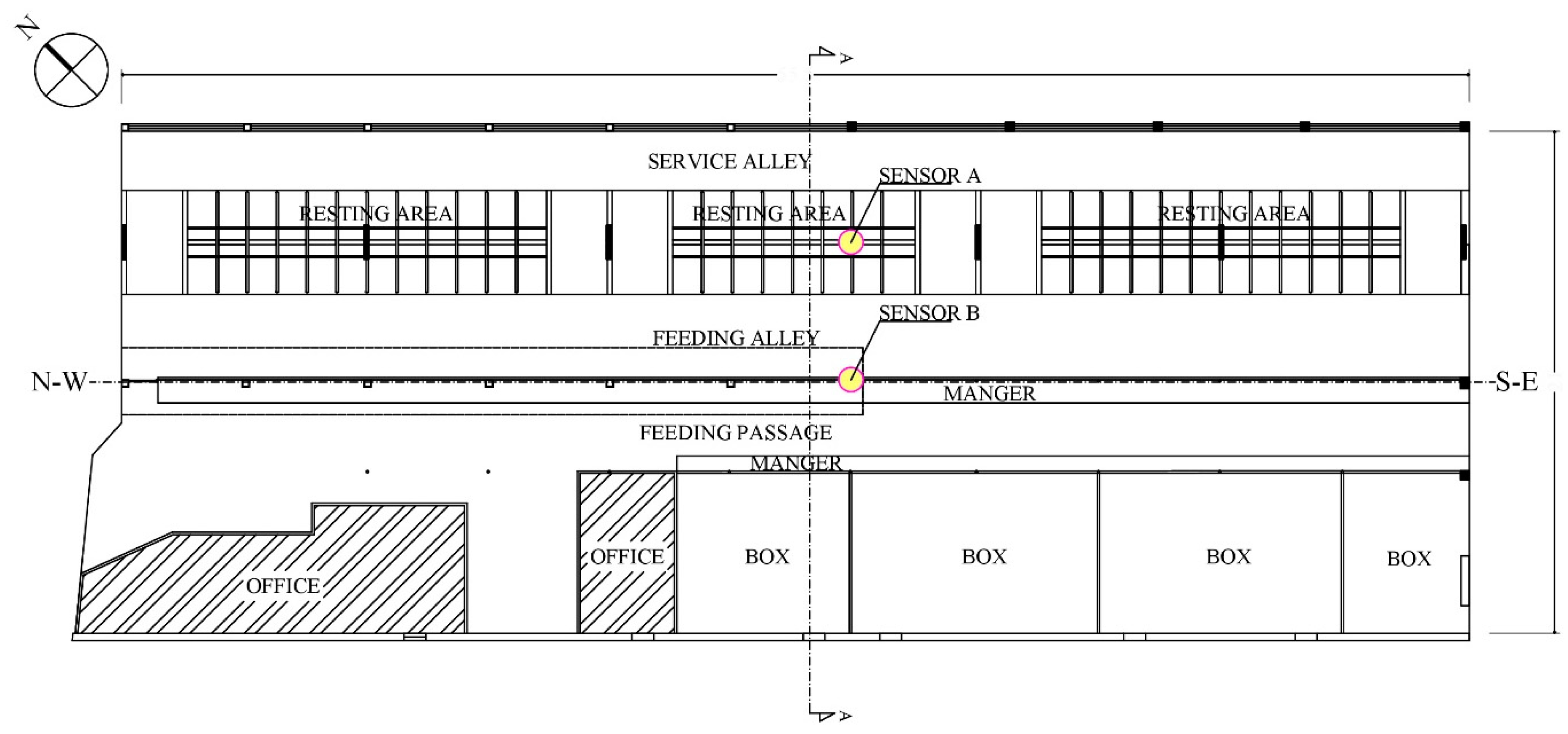
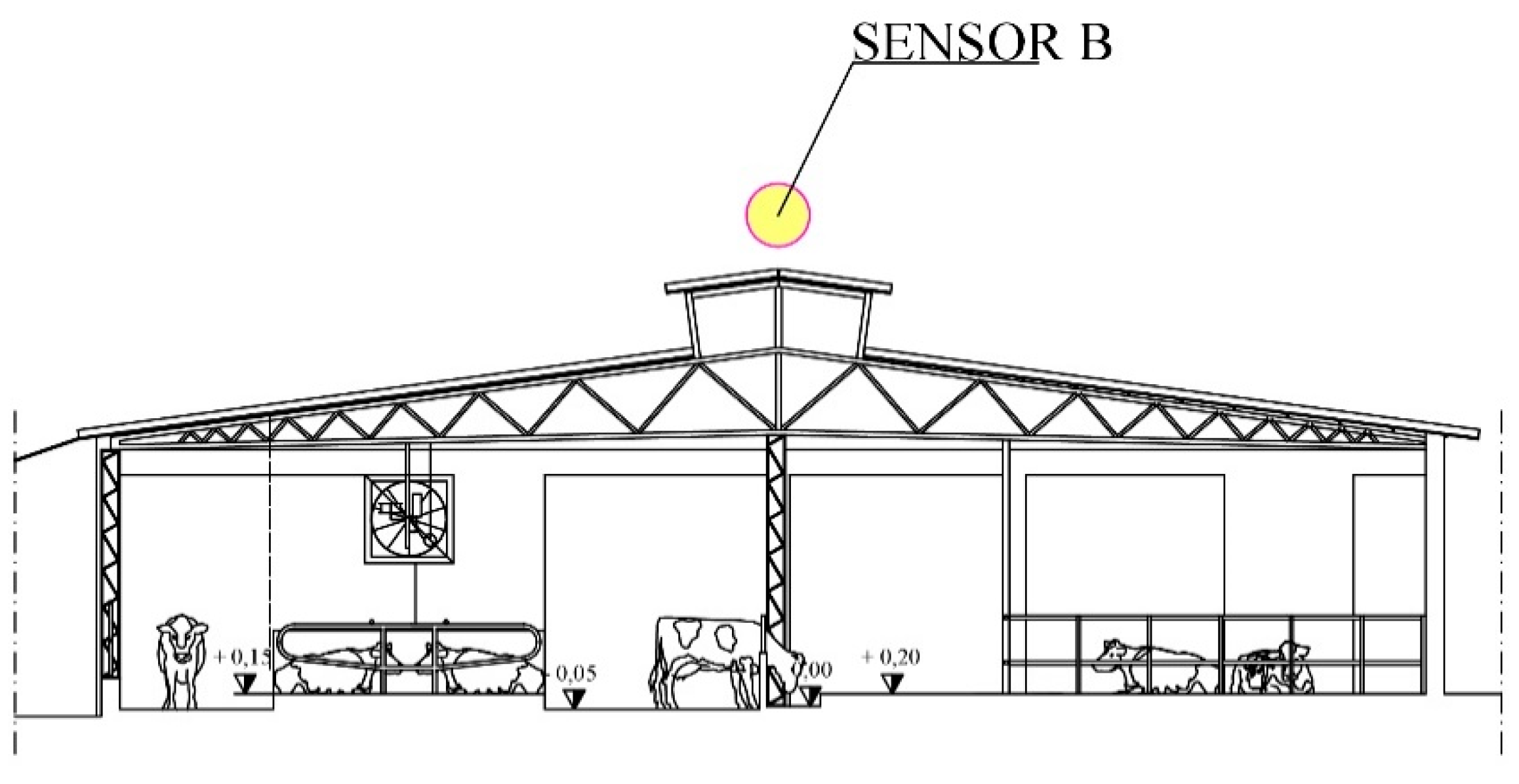
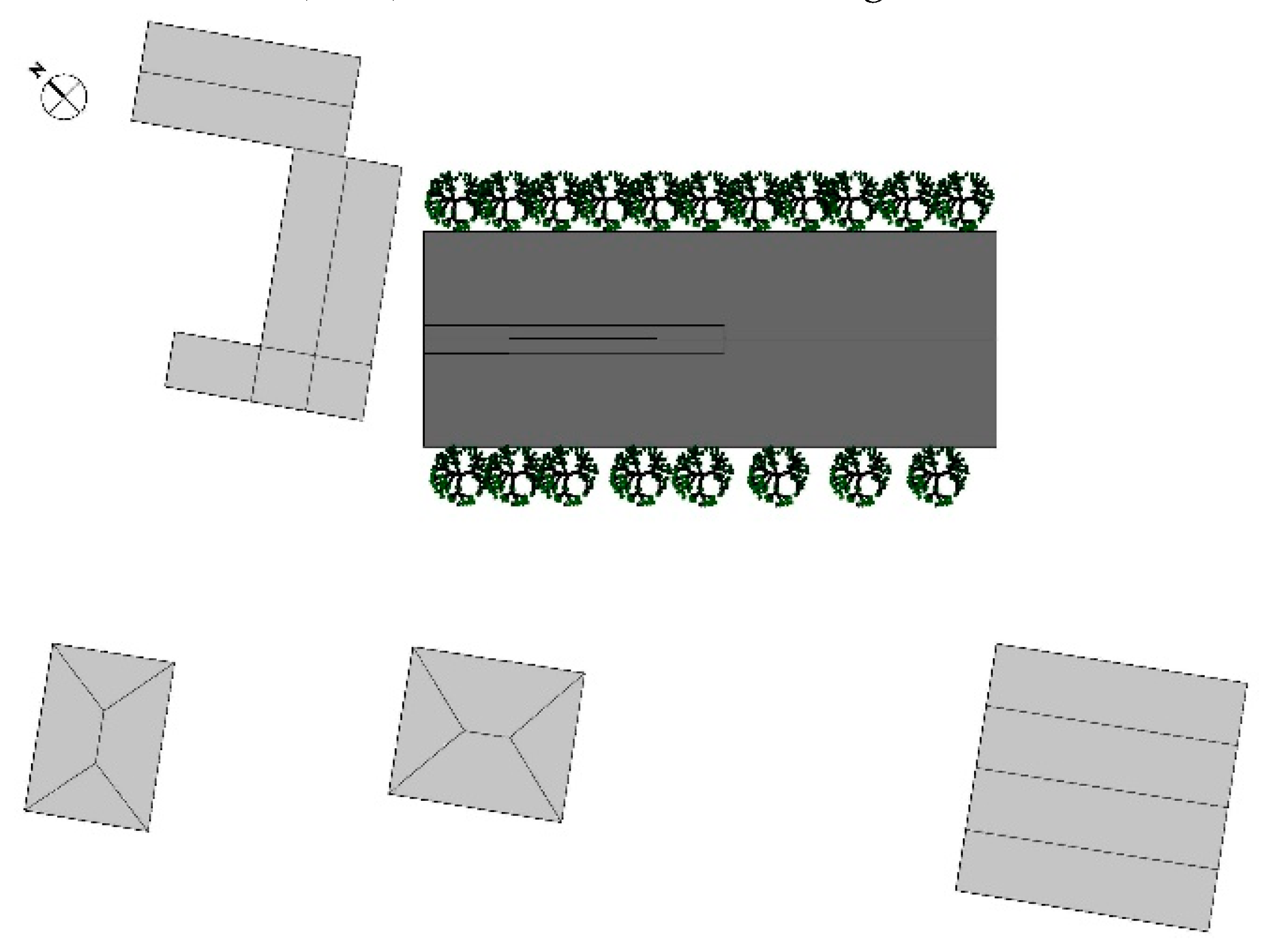
2.1. The Barn Under Study and Acquisition Data Systems
2.2. CFD Analysis
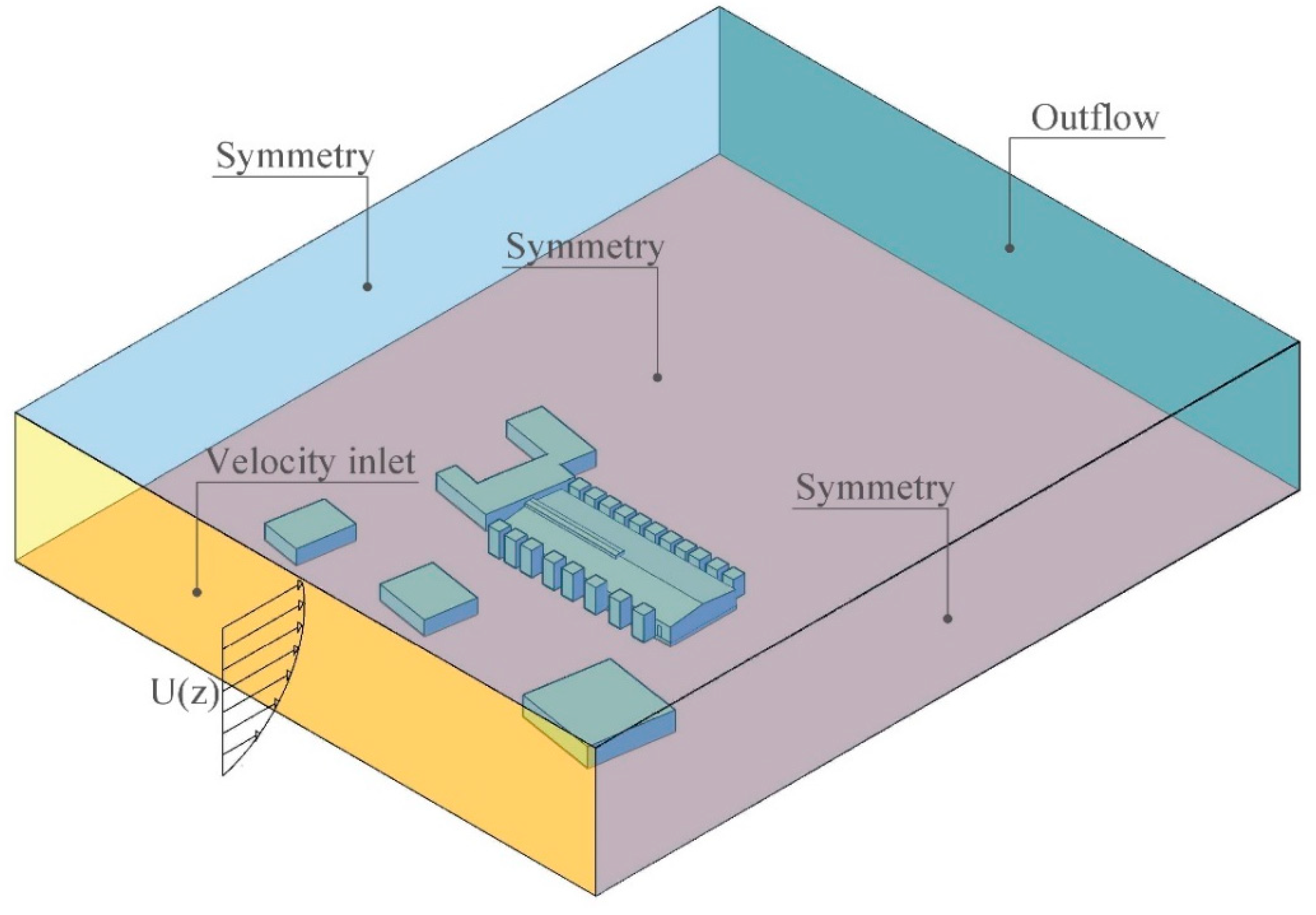
2.2.1. 3D Modelling
2.2.2. Mesh Characteristics and CFD Modelling
2.2.3. Mesh Sensitivity
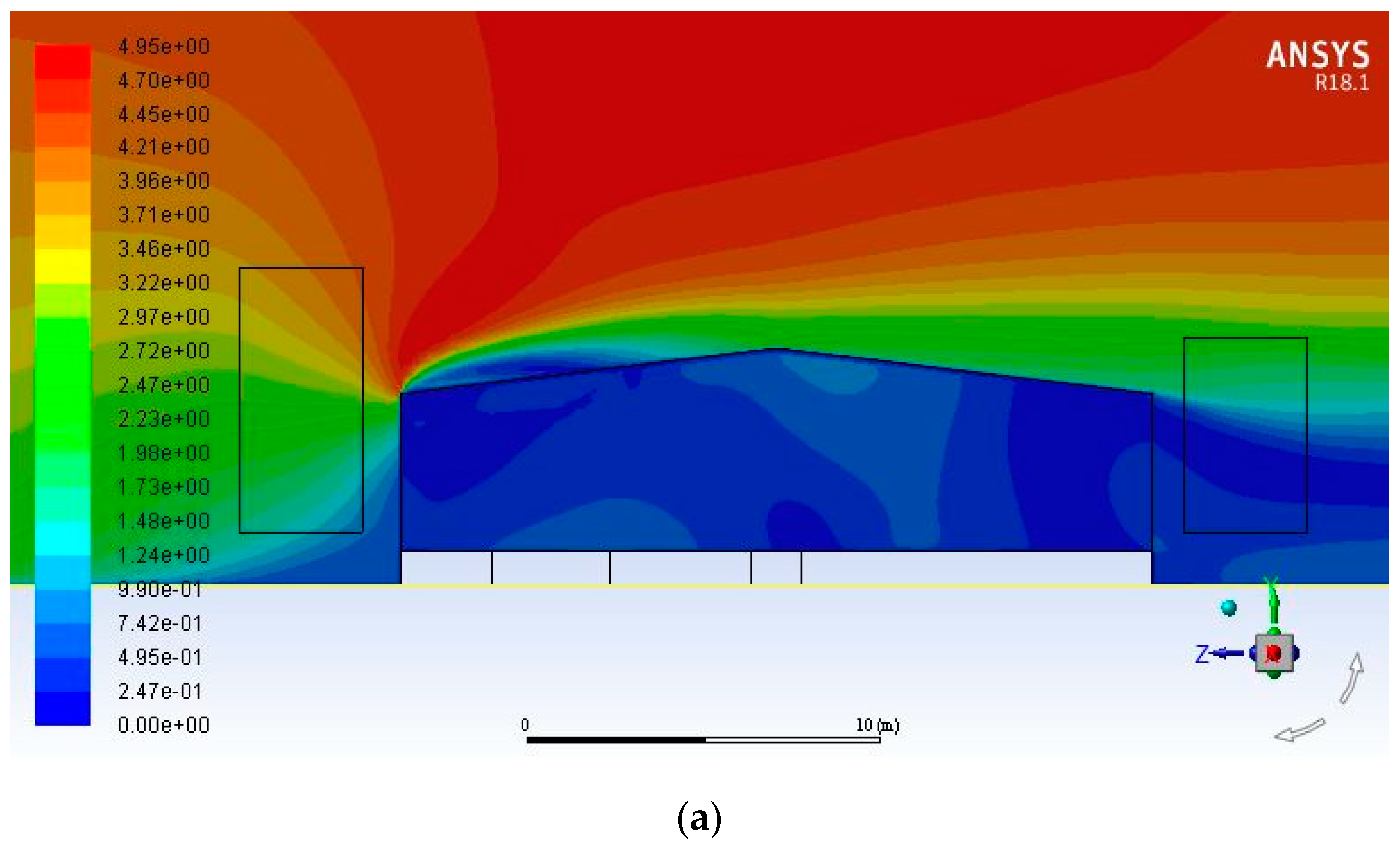
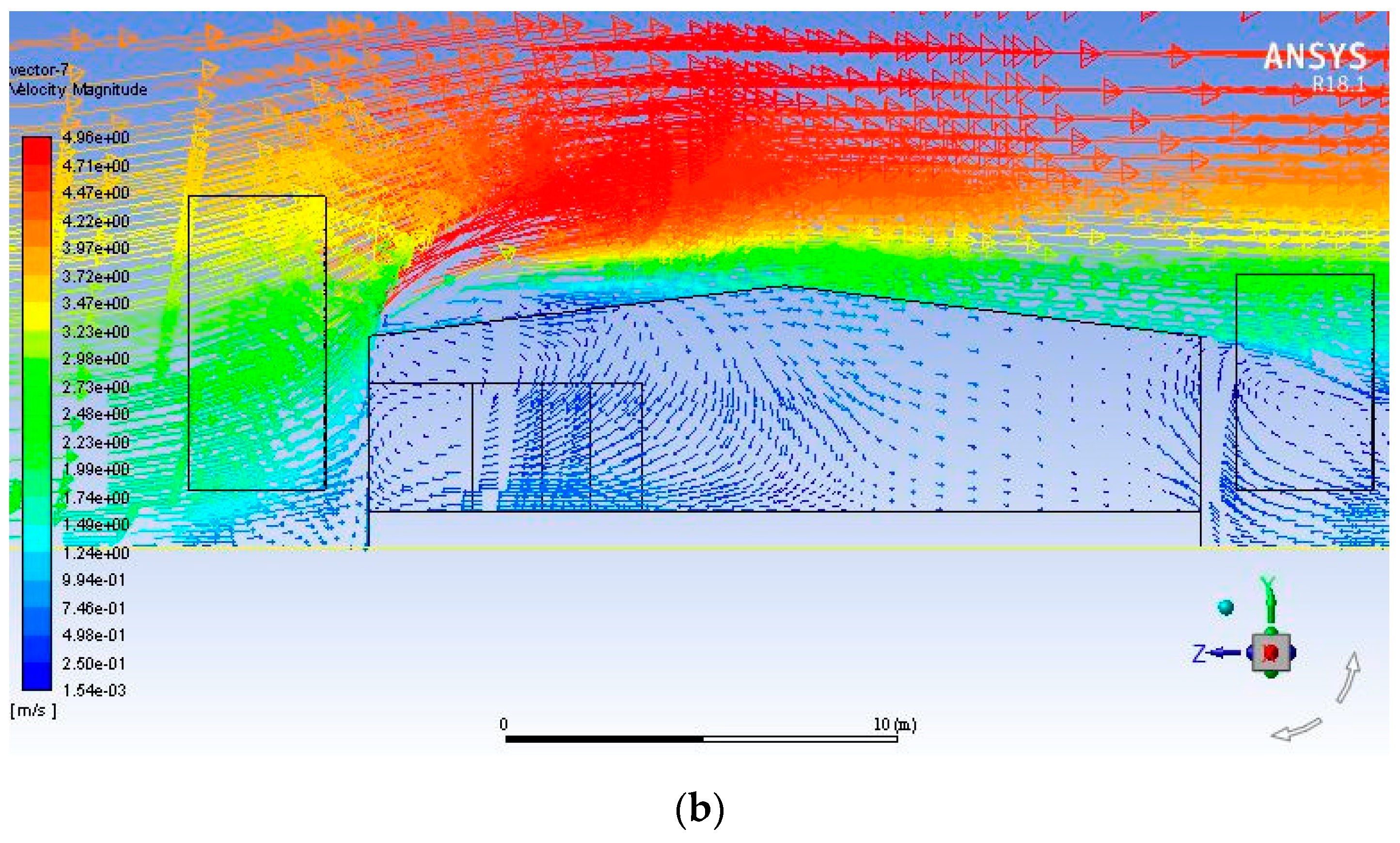
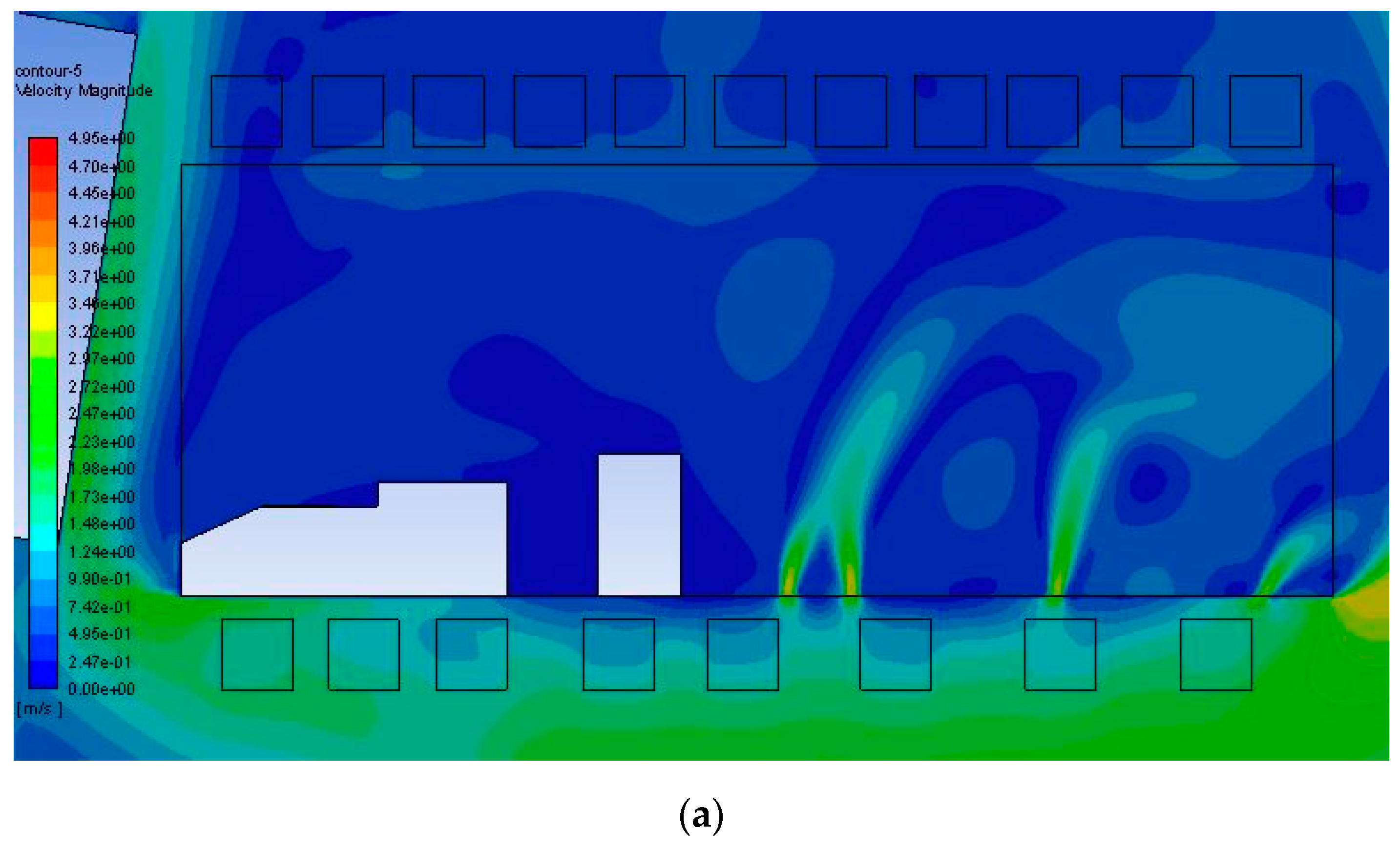
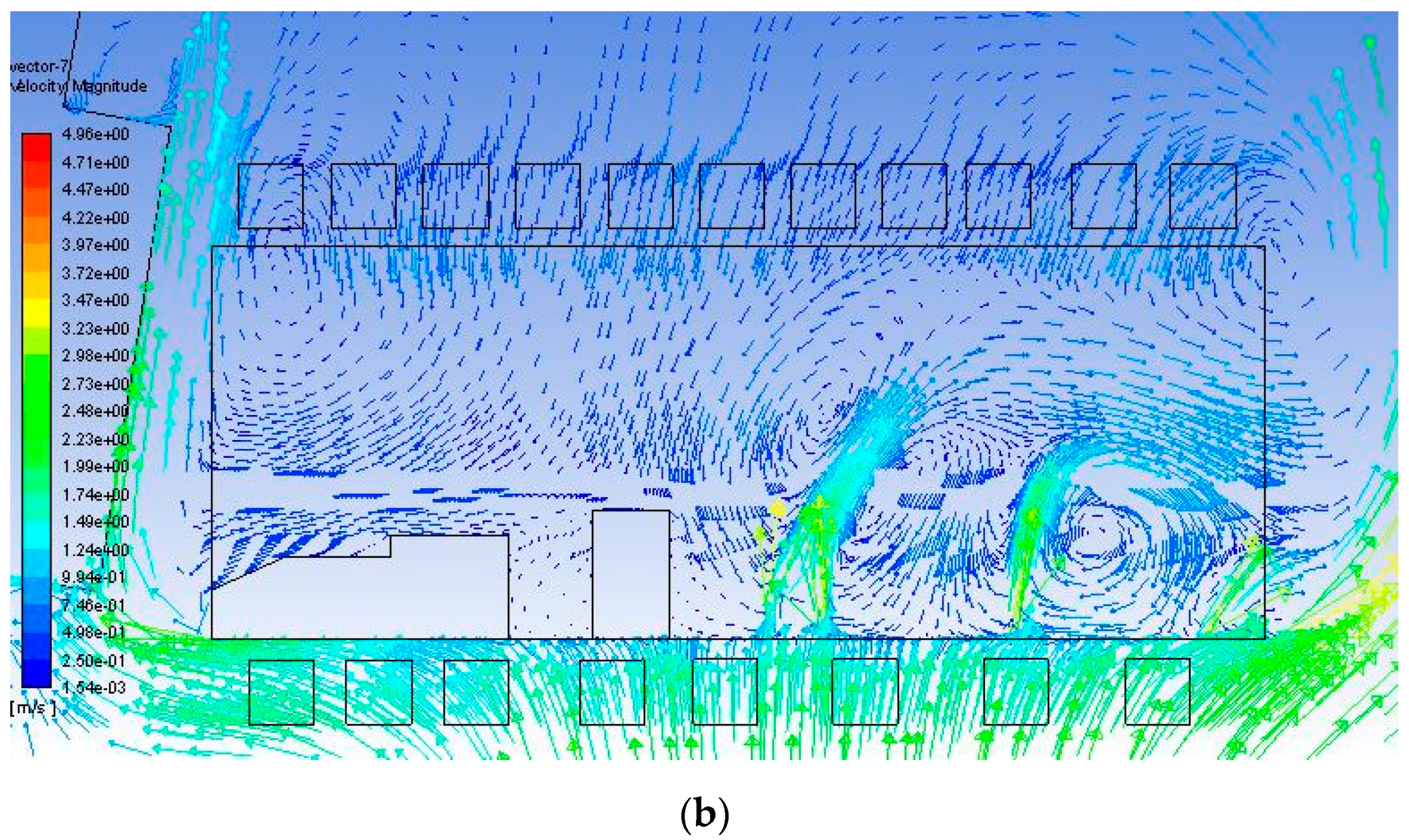
3. Results and Discussion
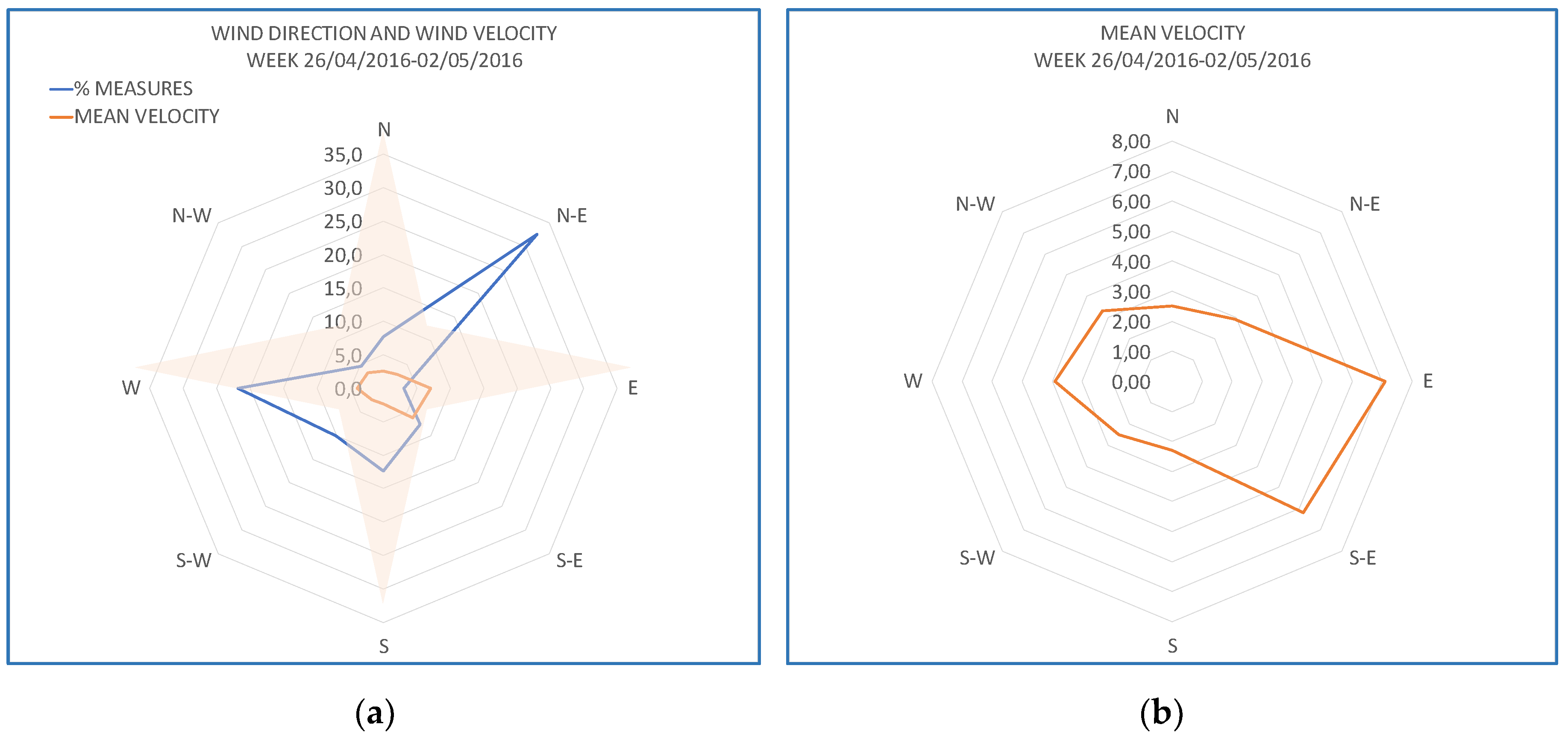
3.1. Setting of Model Parameters by Data Analyses
- A mean velocity Uref at reference height equal to 3.85 ms−1;
- A reference height Yref equal to 10 m;
- A power law exponent α equal to 0.14.
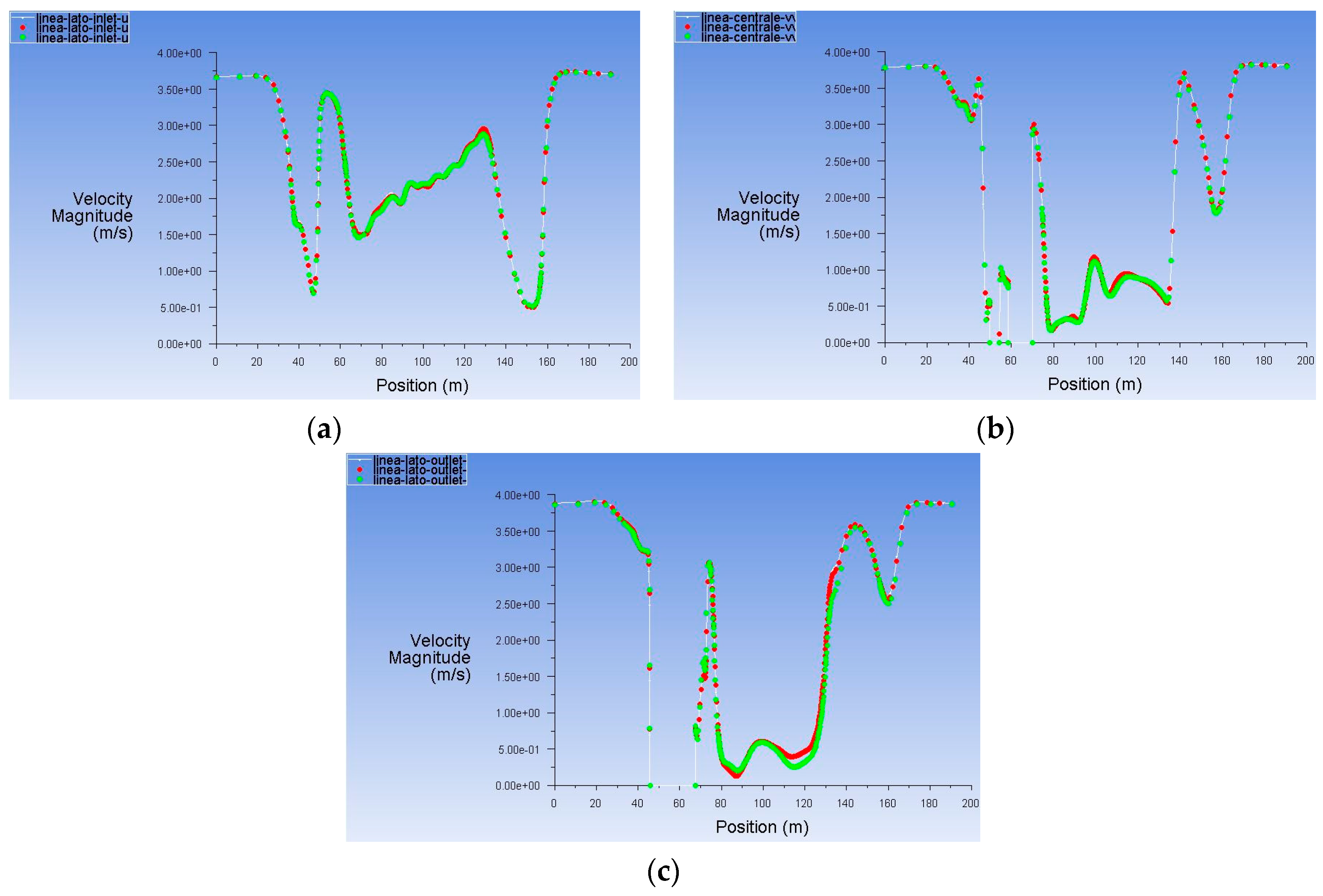
3.2. Validation of the Model
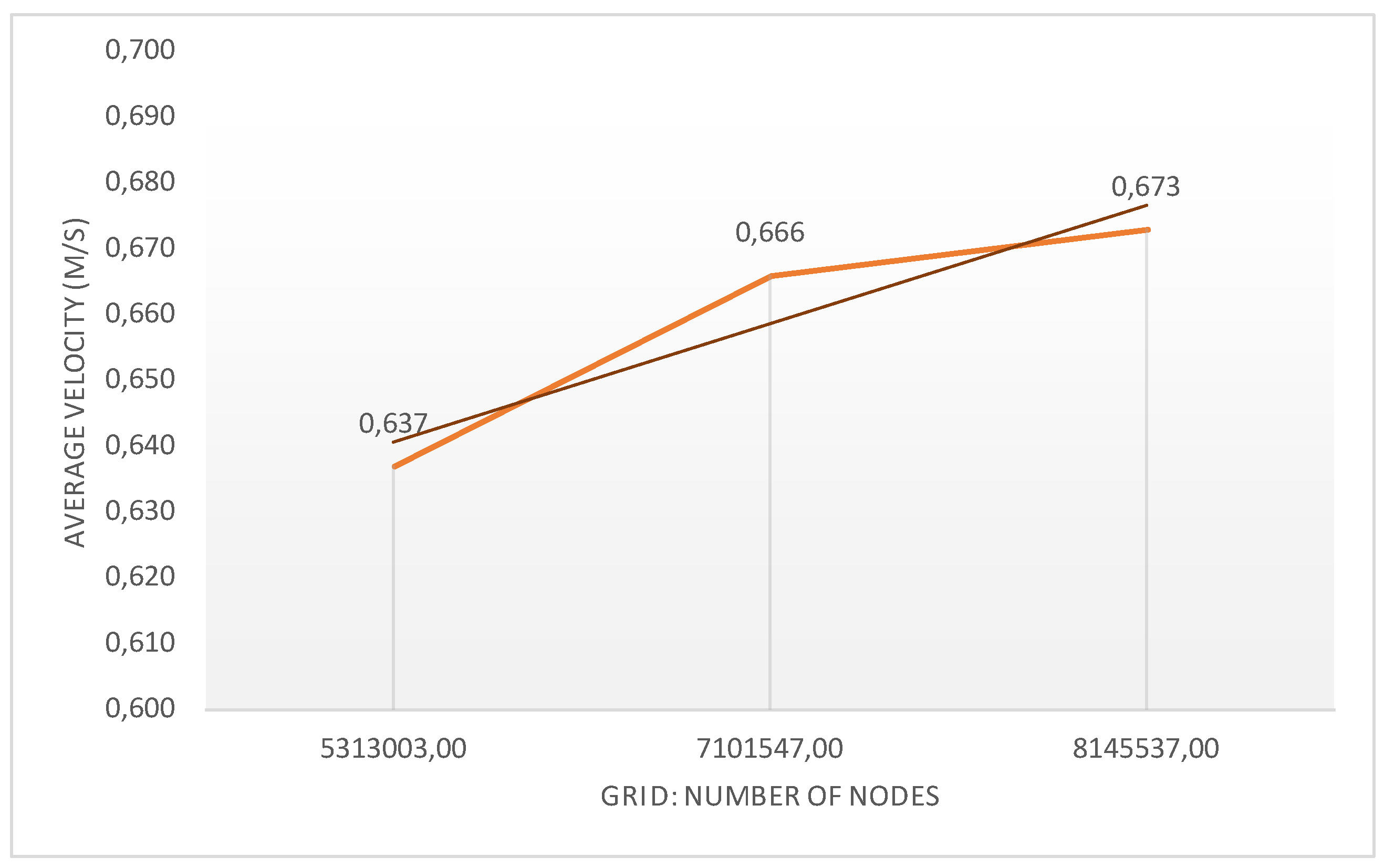
3.3. Mesh Sensitivity
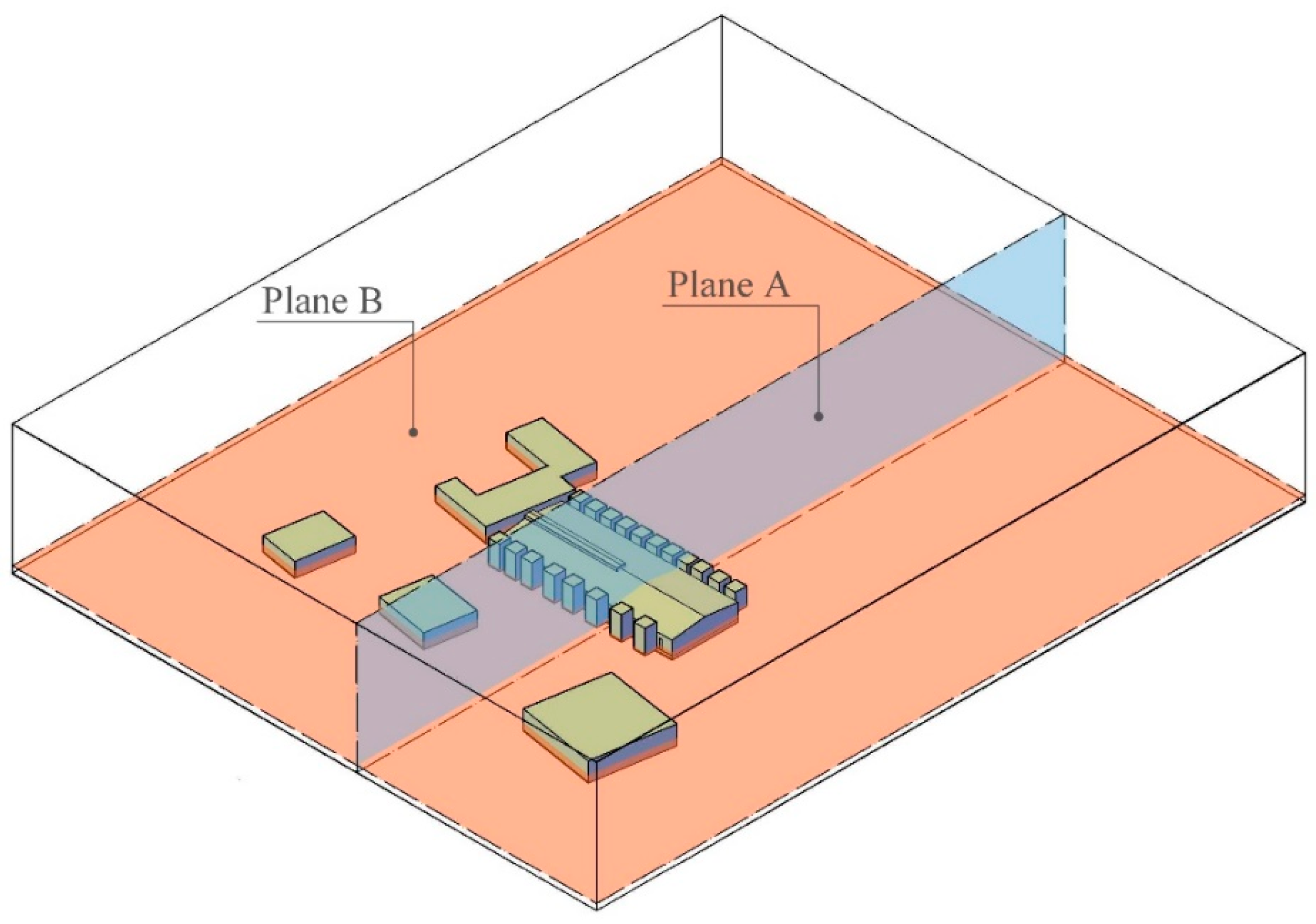
3.4. Study of Air Velocity Distribution in the Barn
4. Conclusions
- Know the air velocity in areas considered most sensitive for the presence of animals;
- Find, in a future research based on the results of this study, alternative design configurations, with the aim to discover the best condition for the well-being of users and animals.
Author Contributions
Funding
Conflicts of Interest
References
- Shen, X.; Zhang, G.; Wu, W.; Bjerg, B. Model-based control of natural ventilation in dairy buildings. Comput. Electron. Agric. 2013, 94, 47–57. [Google Scholar] [CrossRef]
- Rong, L.; Bjerg, B.; Batzanas, T.; Zhang, G. Mechanisms of natural ventilation in livestock buildings: Perspectives on past achievements and future challenges. Biosyst. Eng. 2016, 151, 200–217. [Google Scholar] [CrossRef]
- Zhiqiang, Z.; Mankibib, M.; Zoubirb, A. Review of natural ventilation models. Energy Procedia 2015, 78, 2700–2705. [Google Scholar]
- Wathes, C.M.; Charles, D.R. Air and Surface Hygiene. Livestock Housing; CAB International: Wallingford, OX, USA, 1994; pp. 123–148. [Google Scholar]
- Zhang, Y. Engineering control of dust in animal facilities. In Proceedings of the Dust Control in Animal Production Facilities, Proc. Congress, Aarhus, Denmark, 30 May–2 June 1999. [Google Scholar]
- Allocca, C.; Chen, Q.; Glicksman, L.R. Design analysis of single-sided natural ventilation. Energy Build. 2003, 35, 785–795. [Google Scholar] [CrossRef]
- Bournet, P.E.; Boulard, T. Effect of ventilator configuration on the distributed climate of greenhouses: A review of experimental and CFD studies. Comput. Electron. Agric. 2010, 94, 47–57. [Google Scholar] [CrossRef]
- Bjerg, B.; Cascone, G.; Lee, I.; Bartzanas, T.; Norton, T.; Hong, S.; Seo, I.; Banhazi, T.; Liberati, P.; Marucci, A.; et al. Modelling of ammonia emissions from naturally ventilated livestock buildings. Part 3: CFD modelling. Biosyst. Eng. 2013, 116, 259–275. [Google Scholar] [CrossRef]
- Down, M.J.; Foster, M.P.; McMahon, T.A. Experimental verification of a theory for ventilation of livestock buildings by natural convection. J. Agric. Eng. Res. 1990, 45, 269–279. [Google Scholar] [CrossRef]
- Bruce, J.M. Wind tunnel study: Suckler cow building. Farm Build. Prog. 1974, 38, 15–17. [Google Scholar]
- Bruce, J.M. Natural Ventilation-Its Role and Application in the Bio-Climatic Systems; Farm Building R&D Studies; Scottish Farm Buildings Investigation Unit: Aberdeen, Scotland, 1977. [Google Scholar]
- Bruce, J.M. Natural convection through openings and its application to cattle building ventilation. J. Agric. Eng. Res. 1978, 23, 151–167. [Google Scholar] [CrossRef]
- Bruce, J.M. Ventilation of a model livestock building by thermal buoyancy. Trans. Am. Soc. Agric. Eng. 1982, 25, 1724–1726. [Google Scholar] [CrossRef]
- Foster, M.P.; Down, M.J. Ventilation of livestock buildings by natural convection. J. Agric. Eng. Res. 1987, 37, 1–13. [Google Scholar] [CrossRef]
- Gürdil, G.A.K. Numerical simulation of natural ventilation rates in laying hen houses. J. Anim. Vet. Adv. 2009, 8, 624–629. [Google Scholar]
- Liberati, P.; Zappavigna, P.A. dynamic computer model for optimization of the internal climate in swine housing design. Trans. ASABE 2007, 50, 2179–2188. [Google Scholar] [CrossRef]
- Sapounas, A.; Dooren, H.J.C.; Smits, M.C.J. Natural Ventilation of Commercial Dairy Cow Houses: Simulating the Effect of Roof Shape Using CFD. In Proceedings of the 1st IS on CFD Applications in Agriculture, Valencia, Spain, 9–12 July 2012; pp. 221–228. [Google Scholar]
- Norton, T.; Grant, J.; Fallon, R.; Sun, D.W. Assessing the ventilation performance of a naturally ventilated livestock building with different eave opening conditions. Comput. Electron. Agric. 2010, 71, 7–21. [Google Scholar] [CrossRef]
- Seo, I.H.; Lee, I.B.; Moon, O.K.; Kim, H.T.; Hwang, H.S.; Hong, S.W.; Bitog, J.P.; Yoo, J.I.; Kwon, K.S.; Kim, Y.H.; et al. Improvement of the ventilation system of a naturally ventilated broiler house in the cold season using computational simulations. Biosyst. Eng. 2009, 104, 106–117. [Google Scholar] [CrossRef]
- Norton, T.; Grant, J.; Fallon, R.; Sun, D.W. Assessing the ventilation effectiveness of naturally ventilated livestock buildings under wind dominated conditions using computational fluid dynamics. Biosyst. Eng. 2009, 103, 78–99. [Google Scholar] [CrossRef]
- Wu, W.; Zhai, J.; Zhang, G.; Nielsen, P.V. Evaluation of methods for determining air exchange rate in a naturally ventilated dairy cattle building with large openings using computational fluid dynamics (CFD). Atmos. Environ. 2012, 63, 179–188. [Google Scholar] [CrossRef]
- Arcidiacono, C.; Porto, S.M.; Cascone, G. On ammonia concentrations in naturally ventilated dairy houses located in Sicily. Agric. Eng. Int. CIGR J. 2015, 294–309. [Google Scholar]
- Arcidiacono, C.; D’emilio, A. CFD analysis as a tool to improve air motion knowledge in dairy houses. Riv. Ing. Agrar. 2006, 1, 35–42. [Google Scholar]
- VDI 3783 Part 9. Environmental Meteorology—Prognostic Microscale Wind Field Models—Evaluation for Flow around Buildings and Obstacles; Beuth Verlag: Berlin, Germany, 2005.
- Franke, J.; Hellsten, A.; Schlünzen, H.; Carissimo, B. Best practice guideline for the CFD simulation of flows in the urban environment. In COST Action; European Cooperation in Science and Technology: Brussels, Belgium, 2007. [Google Scholar]
- Ramponi, R.; Blocken, B. CFD simulation of cross-ventilation for a generic isolated building: Impact of computational parameters. Build. Environ. 2012, 53, 34–48. [Google Scholar] [CrossRef]
- Di Sabatino, S.; Buccolieri, R.; Pulvirenti, B.; Britter, R. Simulations of pollutant dispersion within idealised. urban-type geometries with CFD and integral models. Atmos. Environ. 2007, 41, 8316–8329. [Google Scholar] [CrossRef]
- Horan, J.M.; Finn, D.P. Sensitivity of air change rates in a naturally ventilated atrium space subject to variations in external wind speed and direction. Energy Build. 2008, 40, 1577–1585. [Google Scholar] [CrossRef]
- Perén, J.I.; vah Hooff, T.; Leite, B.C.C.; Blocken, B. CFD analysis of cross-ventilation of a generic isolated building with asymmetric opening positions: Impact of roof angle and opening location. Build. Environ. 2015, 85, 263–276. [Google Scholar] [CrossRef]
- Montazeri, H.; Montazeri, F. CFD simulation of cross-ventilation in buildings using rooftop windcatchers: Impact of outlet openings. Renew. Energy 2018, 118, 502–520. [Google Scholar] [CrossRef]
- Gromke, C.; Buccolieri, R.; Di Sabatino, S.; Ruck, B. Dispersion study in a street canyon with tree planting by means of wind tunnel and numerical investigations-evaluation of CFD data with experimental data. Atmos. Environ. 2008, 42, 8640–8650. [Google Scholar] [CrossRef]
- Valenti, F.; Porto, S.; Tomasello, N.; Arcidiacono, C. Enhancing Heat Treatment Efficacy for Insect Pest Control: A Case Study of a CFD Application to Improve the Design and Structure of a Flour Mill. Buildings 2018, 8, 48. [Google Scholar] [CrossRef]
- Rong, L.; Nielsen, P.V.; Bjerg, B.; Zhang, G. Summary of best guidelines and validation of CFD modeling in livestock buildings to ensure prediction quality. Comput. Electron. Agric. 2016, 121, 180–190. [Google Scholar] [CrossRef]
- Norton, T.; Sun, D.W.; Grant, J.; Fallon, R.; Dodd, V. Applications of computational fluid dynamics (CFD) in the modelling and design of ventilation systems in the agricultural industry: A review. Bioresour. Technol. 2007, 98, 2386–2414. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Guo, L.; Maghirang, R.G. Numerical simulation of airflow and particle collection by vegetative barriers. Eng. Appl. Comput. Fluid Mech. 2012, 6, 110–122. [Google Scholar] [CrossRef]
- Barth, T.J.; Jespersen, D.C. The Design and Application of Upwind Schemes on Unstructured Meshes. In Proceedings of the AIAA 27th Aerospace Sciences Meeting, Reno, Nevada, 9–12 January 1989; Technical Report AIAA-89-0366; NASA Ames Research Center: Moffett Field, CA, USA, 1989. [Google Scholar]
- He, X.; Wang, J.; Guo, S.; Zhang, J.; Wei, B.; Sun, J.; Shu, S. Ventilation optimization of solar greenhouse with removable back walls based on CFD. Comput. Electron. Agric. 2018, 149, 16–25. [Google Scholar] [CrossRef]
- Dati SIAS. 2016. Available online: www.sias.regione.sicilia.it (accessed on 15 April 2018).
- Wieringa, J. Updating the Davenport roughness classification. J. Wind Eng. Ind. Aerodyn. 1992, 41, 357–358. [Google Scholar] [CrossRef]
- Sullivan, R.; Greeley, R. Comparison of aerodynamic roughness measured in a field experiment and in a wind tunnel simulation. J. Wind Eng. Ind. Aerodyn. 1993, 48, 25–50. [Google Scholar] [CrossRef]
- Schlichting, H. Boundary Layer Theory, 7th ed; McGraw-Hill: New York, NY, USA, 1979; pp. 578–595. [Google Scholar]
- Gan, C.; Salim, S. Numerical Analysis of Fluid-Structure Interaction between Wind Flow and Trees. In Proceedings of the World Congress on Engineering, London, UK, 2–4 July 2014. [Google Scholar]
- Jeanjean, A.P.R.; Hinchliffe, G.; McMullan, W.A.; Monks, P.S.; Leigh, R.J. A CFD study on the effectiveness of trees to disperse road traffic emissions at a city scale. Atmos. Environ. 2015, 120, 1–14. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, W.; Zhai, Z.; Chen, Q. Evaluation of various turbulence models in predicting airflow and turbulence in enclosed environments by CFD: Part-2—Comparison with experimental data from literature. HVAC R Res. 2007, 13, 871–886. [Google Scholar] [CrossRef]


| Sicilian Provinces | Number of Livestock Farms |
|---|---|
| Trapani | 170 |
| Palermo | 964 |
| Messina | 698 |
| Caltanissetta | 188 |
| Enna | 420 |
| Catania | 397 |
| Ragusa | 1472 |
| Syracuse | 569 |
| Number of Livestock Farms | ||||
|---|---|---|---|---|
| Sicilian Provinces | Cattles and Buffaloes Housing | Pigs Housing | Laying Hens Housing | Broilers Housing |
| Trapani | 113 | 9 | 65 | 13 |
| Palermo | 813 | 47 | 139 | 25 |
| Messina | 458 | 143 | 191 | 30 |
| Caltanissetta | 164 | 6 | 28 | 2 |
| Enna | 394 | 21 | 16 | 3 |
| Catania | 303 | 48 | 91 | 29 |
| Ragusa | 1389 | 159 | 60 | 19 |
| Syracuse | 535 | 52 | 38 | 6 |
| N. Simulation | Air Velocity at Weather Station (10 m height) (ms−1) | Air Velocity Outside the Barn (ms−1) (Sensor B) | Air velocity Inside the Barn (ms−1) (Sensor A) | ||||
|---|---|---|---|---|---|---|---|
| MEASURED | SIMULATED | RELATIVE ERROR % | MEASURED | SIMULATED | RELATIVE ERROR % | ||
| 1 (27/04-22:00) | 1.90 | 1.14 | 1.38 | 18.84 | 0.24 | 0.29 | 16.90 |
| 2 (28/04-02:00) | 2.90 | 1.83 | 2.08 | 13.02 | 0.40 | 0.45 | 12.31 |
| 3 (28/04-06:00) | 2.70 | 2.04 | 1.89 | 7.56 | 0.44 | 0.44 | 0.32 |
| 4 (28/04-07:00) | 2.70 | 1.96 | 1.89 | 3.64 | 0.46 | 0.44 | 5.00 |
| 5 (28/04-19:00) | 6.40 | 3.94 | 4.59 | 15.31 | 0.98 | 0.98 | 0.08 |
| 6 (28/04-20:00) | 6.00 | 3.43 | 4.31 | 22.82 | 0.79 | 0.91 | 14.70 |
| 7 (28/04-21:00) | 7.80 | 3.38 | 5.58 | 49.21 | 0.89 | 1.19 | 29.13 |
| 8 (28/04-22:00) | 7.90 | 4.51 | 5.66 | 22.65 | 1.07 | 1.20 | 11.36 |
| 9 (29/04-00:00) | 5.80 | 4.06 | 4.17 | 2.68 | 0.95 | 0.88 | 7.71 |
| 10(29/04-01:00) | 6.80 | 4.27 | 4.89 | 13.45 | 1.10 | 1.03 | 6.35 |
| 11(29/04-02:00) | 8.20 | 5.50 | 5.89 | 6.89 | 1.23 | 1.26 | 2.07 |
| 12(29/04-03:00) | 6.80 | 4.45 | 4.89 | 9.48 | 1.02 | 1.03 | 0.98 |
| 13(29/04-05:00 | 8.50 | 3.97 | 6.08 | 42.04 | 0.89 | 1.29 | 36.98 |
| 14(29/04-06:00) | 8.50 | 4.13 | 6.08 | 38.17 | 0.87 | 1.29 | 39.22 |
| 15(30/04-00:00) | 2.00 | 1.16 | 1.44 | 21.30 | 0.32 | 0.31 | 4.23 |
| 16(30/04-01:00) | 2.50 | 1.45 | 1.80 | 21.65 | 0.27 | 0.38 | 35.59 |
| 17(30/04-02:00) | 2.00 | 1.34 | 1.44 | 7.48 | 0.32 | 0.31 | 1.98 |
| 18(01/05-01:00) | 2.80 | 2.00 | 2.01 | 0.54 | 0.45 | 0.43 | 4.72 |
| 19(01/05-02:00) | 2.00 | 1.99 | 1.44 | 32.04 | 0.39 | 0.31 | 23.36 |
| 20(01/05-05:00) | 1.40 | 0.93 | 0.98 | 5.43 | 0.32 | 0.24 | 29.61 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tomasello, N.; Valenti, F.; Cascone, G.; Porto, S.M.C. Development of a CFD Model to Simulate Natural Ventilation in a Semi-Open Free-Stall Barn for Dairy Cows. Buildings 2019, 9, 183. https://doi.org/10.3390/buildings9080183
Tomasello N, Valenti F, Cascone G, Porto SMC. Development of a CFD Model to Simulate Natural Ventilation in a Semi-Open Free-Stall Barn for Dairy Cows. Buildings. 2019; 9(8):183. https://doi.org/10.3390/buildings9080183
Chicago/Turabian StyleTomasello, Nicoletta, Francesca Valenti, Giovanni Cascone, and Simona M. C. Porto. 2019. "Development of a CFD Model to Simulate Natural Ventilation in a Semi-Open Free-Stall Barn for Dairy Cows" Buildings 9, no. 8: 183. https://doi.org/10.3390/buildings9080183
APA StyleTomasello, N., Valenti, F., Cascone, G., & Porto, S. M. C. (2019). Development of a CFD Model to Simulate Natural Ventilation in a Semi-Open Free-Stall Barn for Dairy Cows. Buildings, 9(8), 183. https://doi.org/10.3390/buildings9080183






