Figure 1.
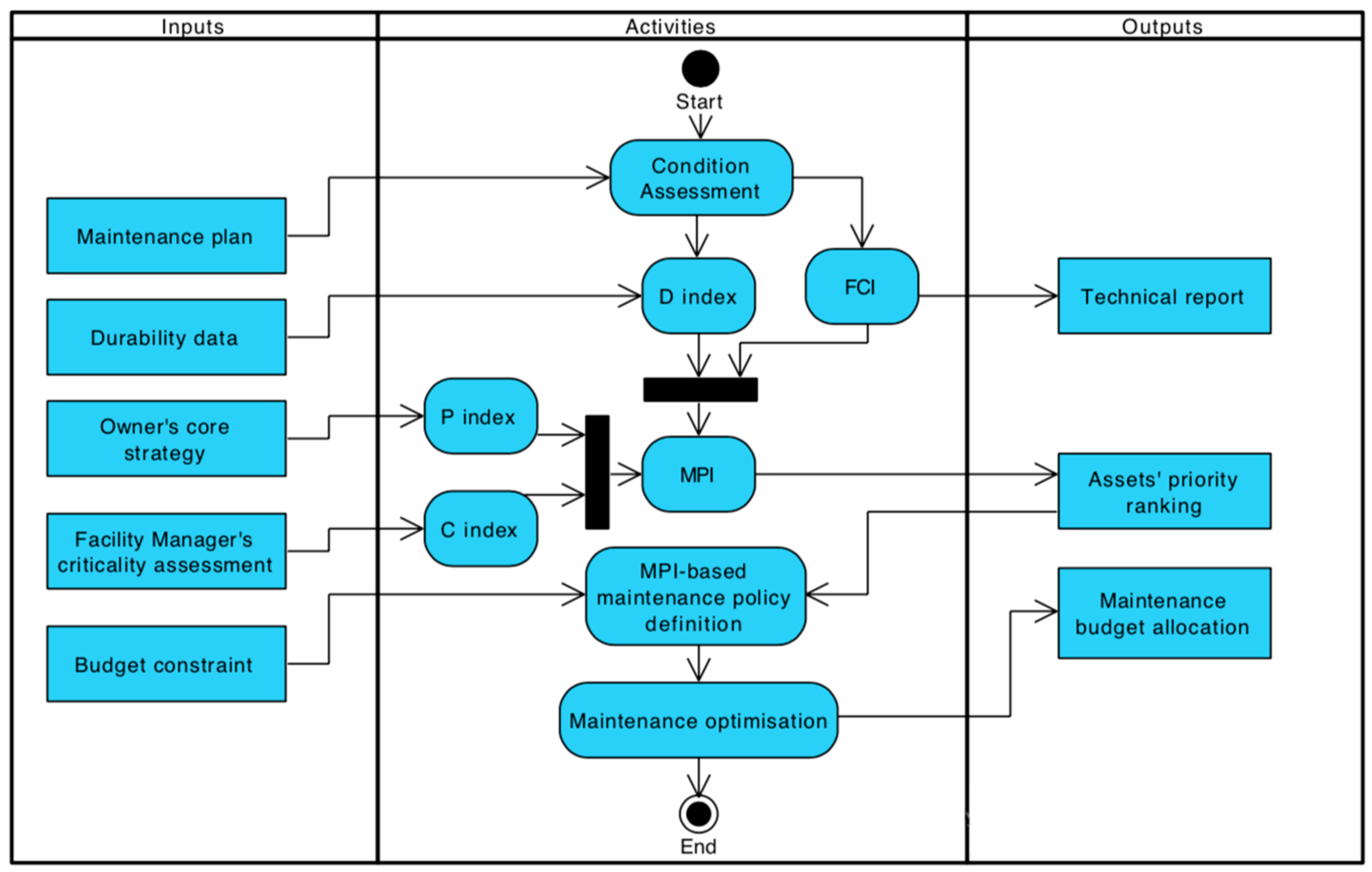
Process adopted for the development of the algorithm underpinning the Decision Support System (DSS).
Figure 1.
Process adopted for the development of the algorithm underpinning the Decision Support System (DSS).
Figure 2.
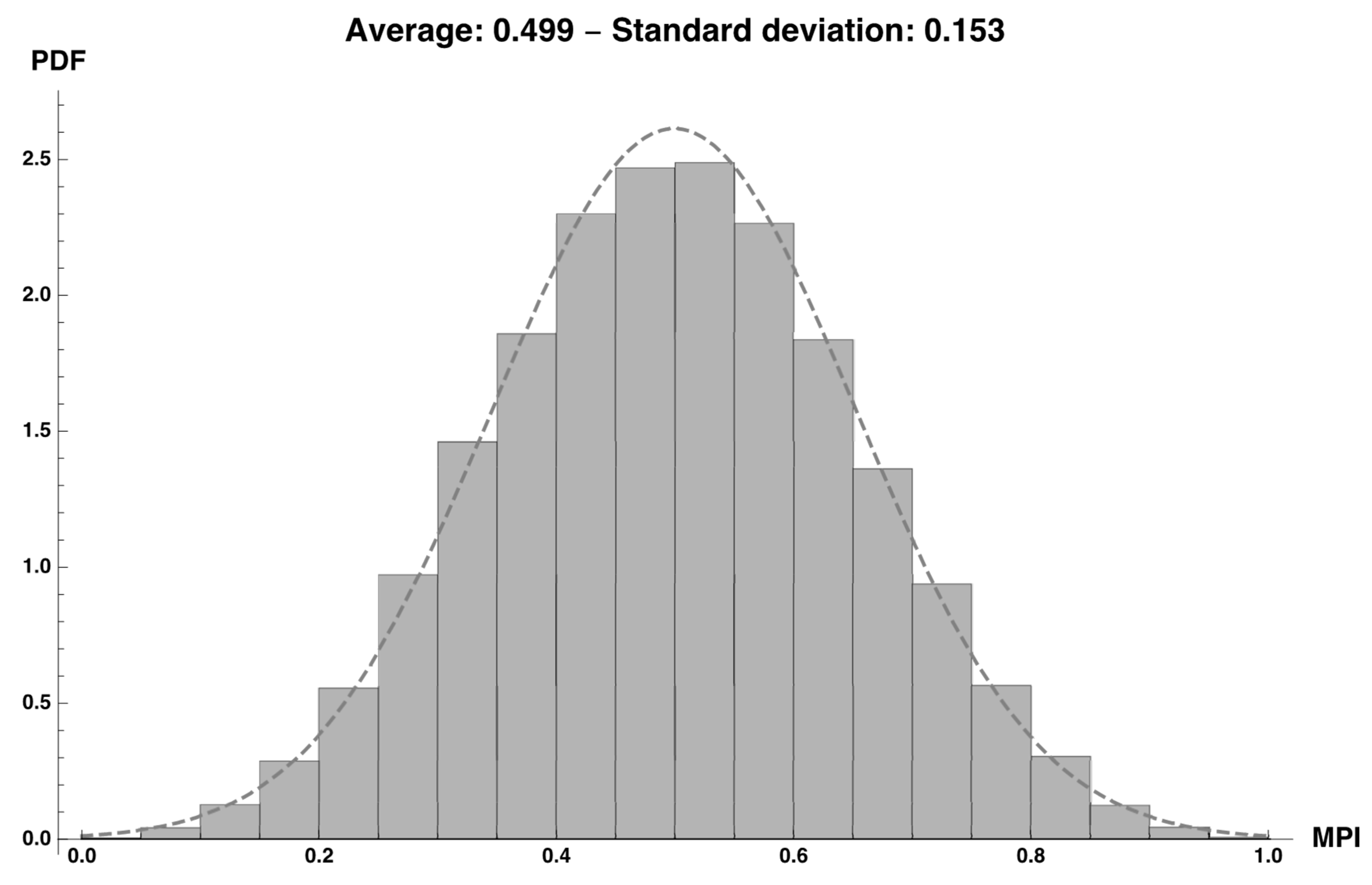
Results of the first of the five Montecarlo simulations compared to a Normal Distribution with the same average and standard deviation (Dashed line).
Figure 2.
Results of the first of the five Montecarlo simulations compared to a Normal Distribution with the same average and standard deviation (Dashed line).
Figure 3.
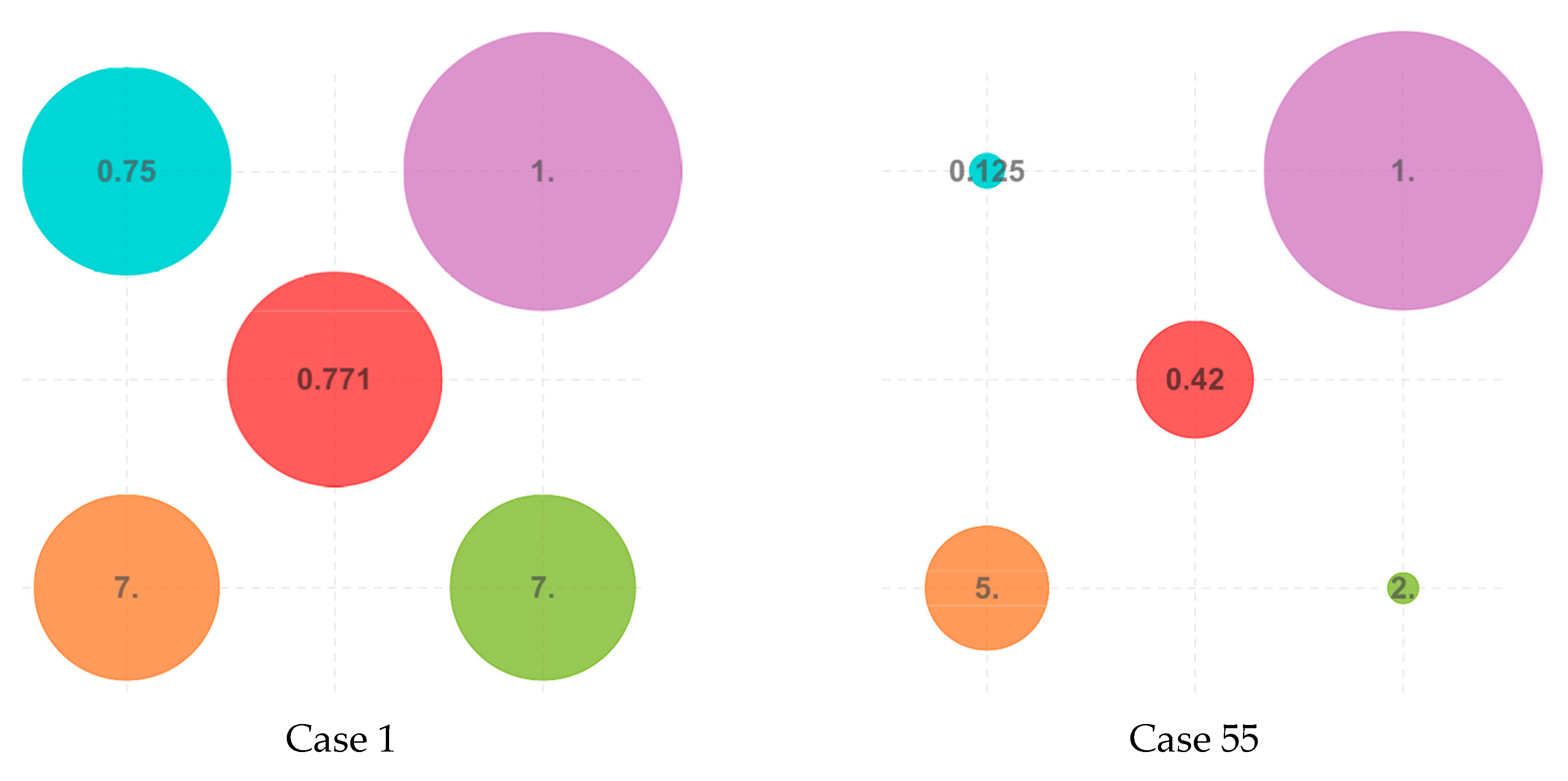
visualization of the combination of the four metrics composing the Maintenance Priority Index (MPI). The central circle represents the value of the Maintenance Priority Index (MPI).
Figure 3.
visualization of the combination of the four metrics composing the Maintenance Priority Index (MPI). The central circle represents the value of the Maintenance Priority Index (MPI).
Figure 4.
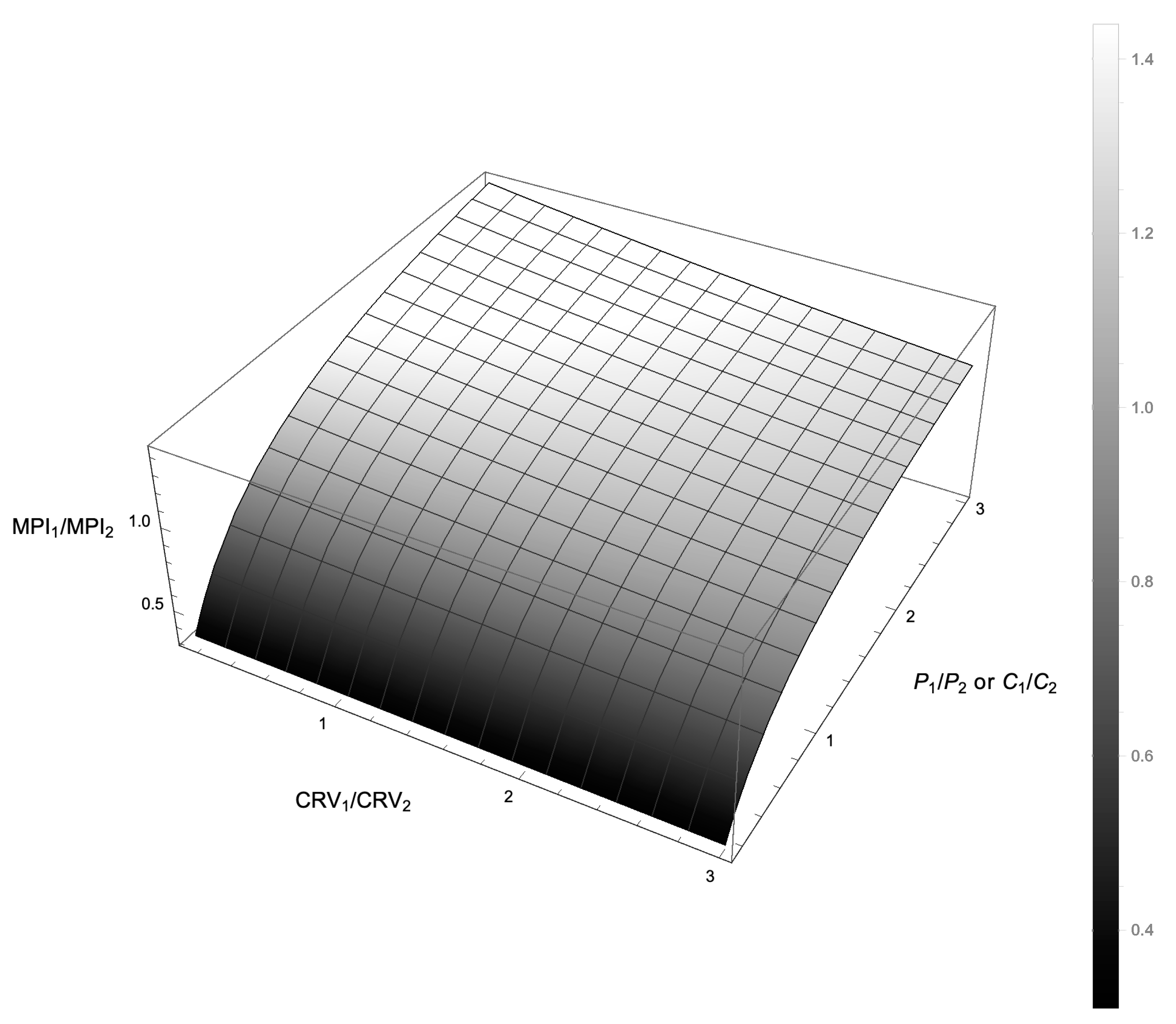
Ratio between the Maintenance Priority indexes (MPI) of two components according to the ratio of Current Replacement Values (CRV) and Priority index (or Criticality Index).
Figure 4.
Ratio between the Maintenance Priority indexes (MPI) of two components according to the ratio of Current Replacement Values (CRV) and Priority index (or Criticality Index).
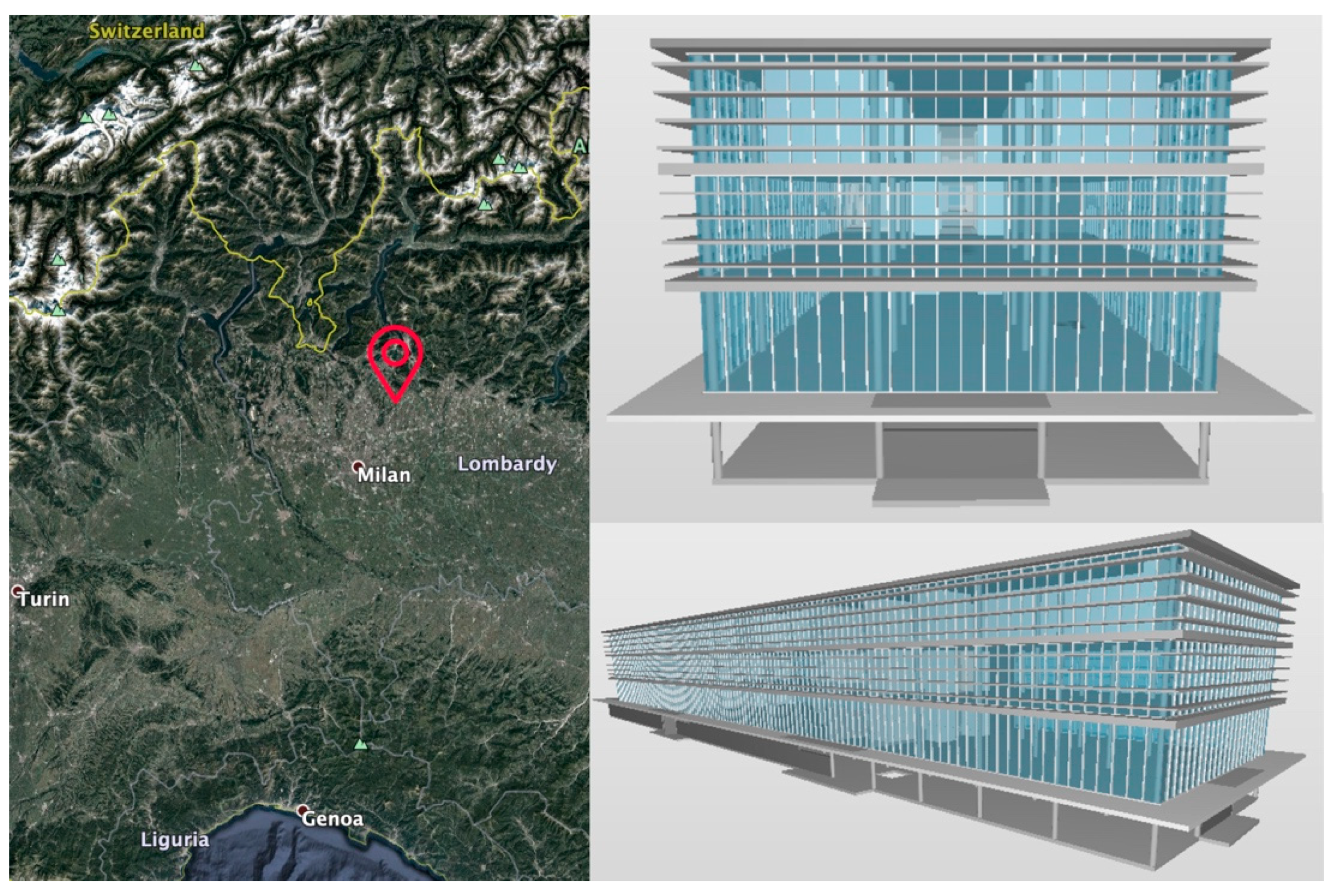
Figure 5.
location (left) and Building Information Model (BIM) model of the office building on which the Decision Support System (DSS) has been implemented.
Figure 5.
location (left) and Building Information Model (BIM) model of the office building on which the Decision Support System (DSS) has been implemented.
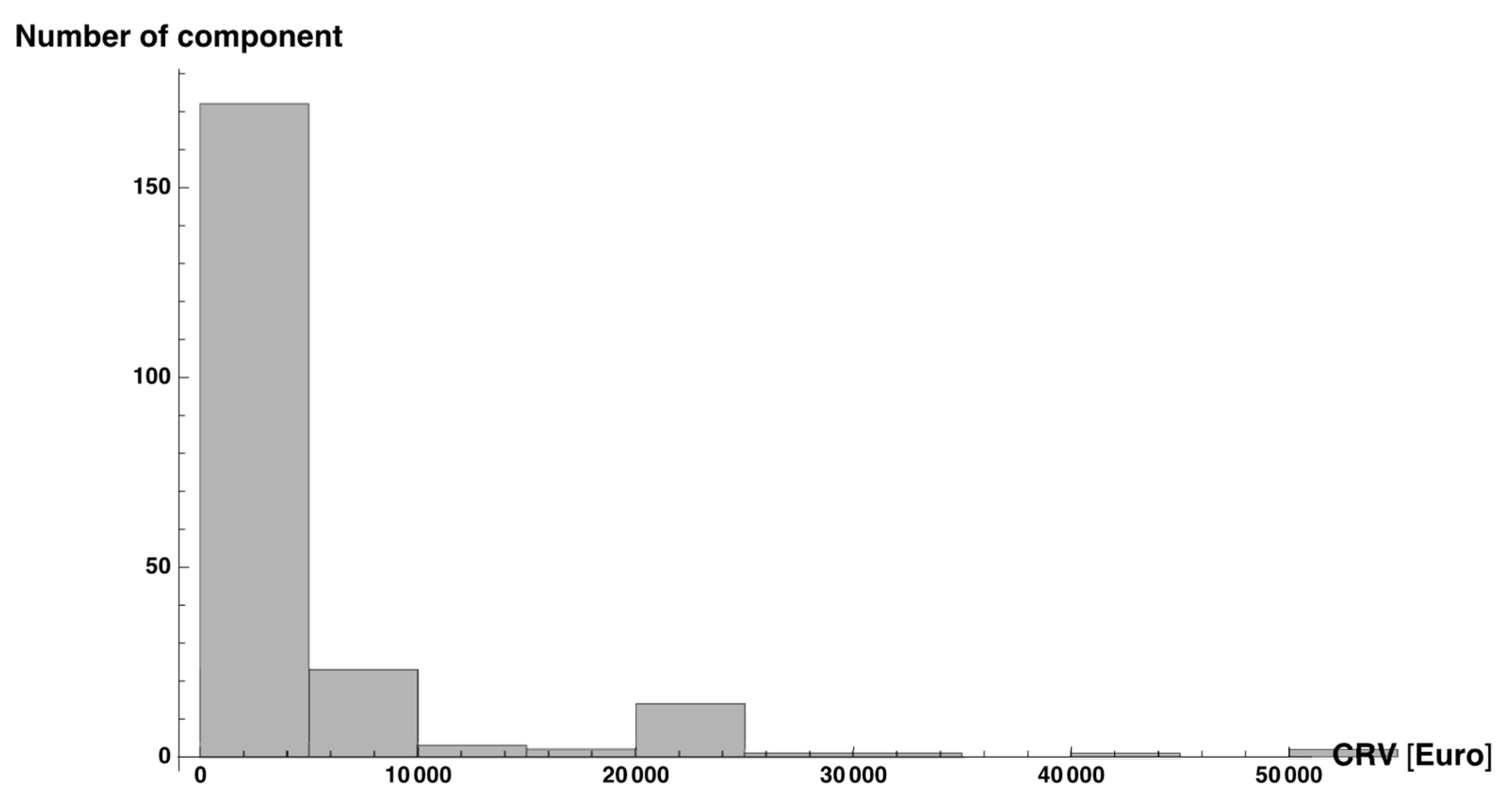
Figure 6.
Histogram of Current Replacement Value (CRV) for the components with Deferred Maintenance (DM) > 0. Most of the component have small CRV.
Figure 6.
Histogram of Current Replacement Value (CRV) for the components with Deferred Maintenance (DM) > 0. Most of the component have small CRV.
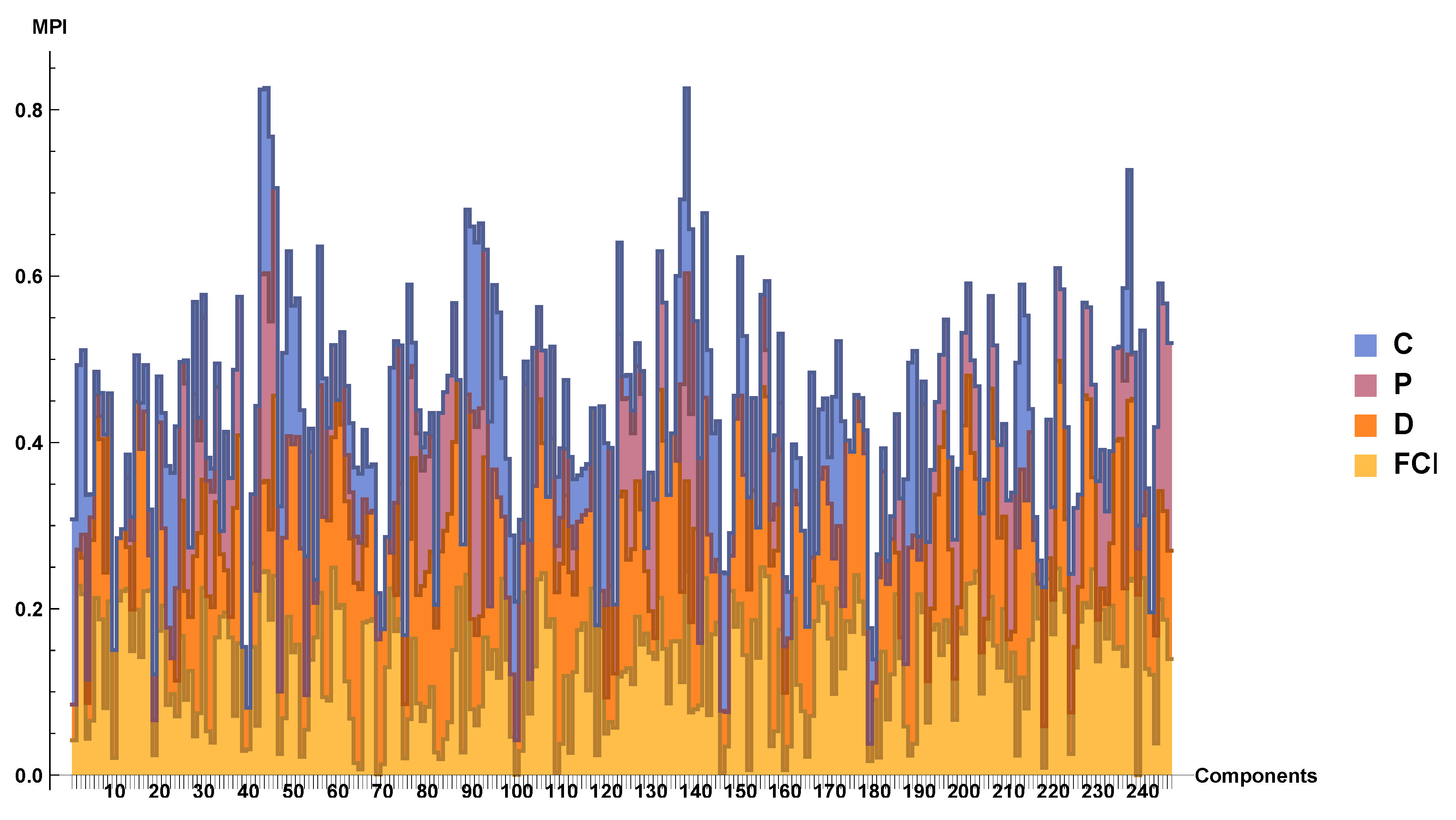
Figure 7.
Maintenance Priority Index (MPI) of the components with Deferred Maintenance (DM) > 0. The colors show how the Facility Condition Index (FCI), D index (measuring the age of the assets), P index (measuring the preference of the owner) and C index (measuring the criticality of each asset) contribute to the MPI of each component.
Figure 7.
Maintenance Priority Index (MPI) of the components with Deferred Maintenance (DM) > 0. The colors show how the Facility Condition Index (FCI), D index (measuring the age of the assets), P index (measuring the preference of the owner) and C index (measuring the criticality of each asset) contribute to the MPI of each component.
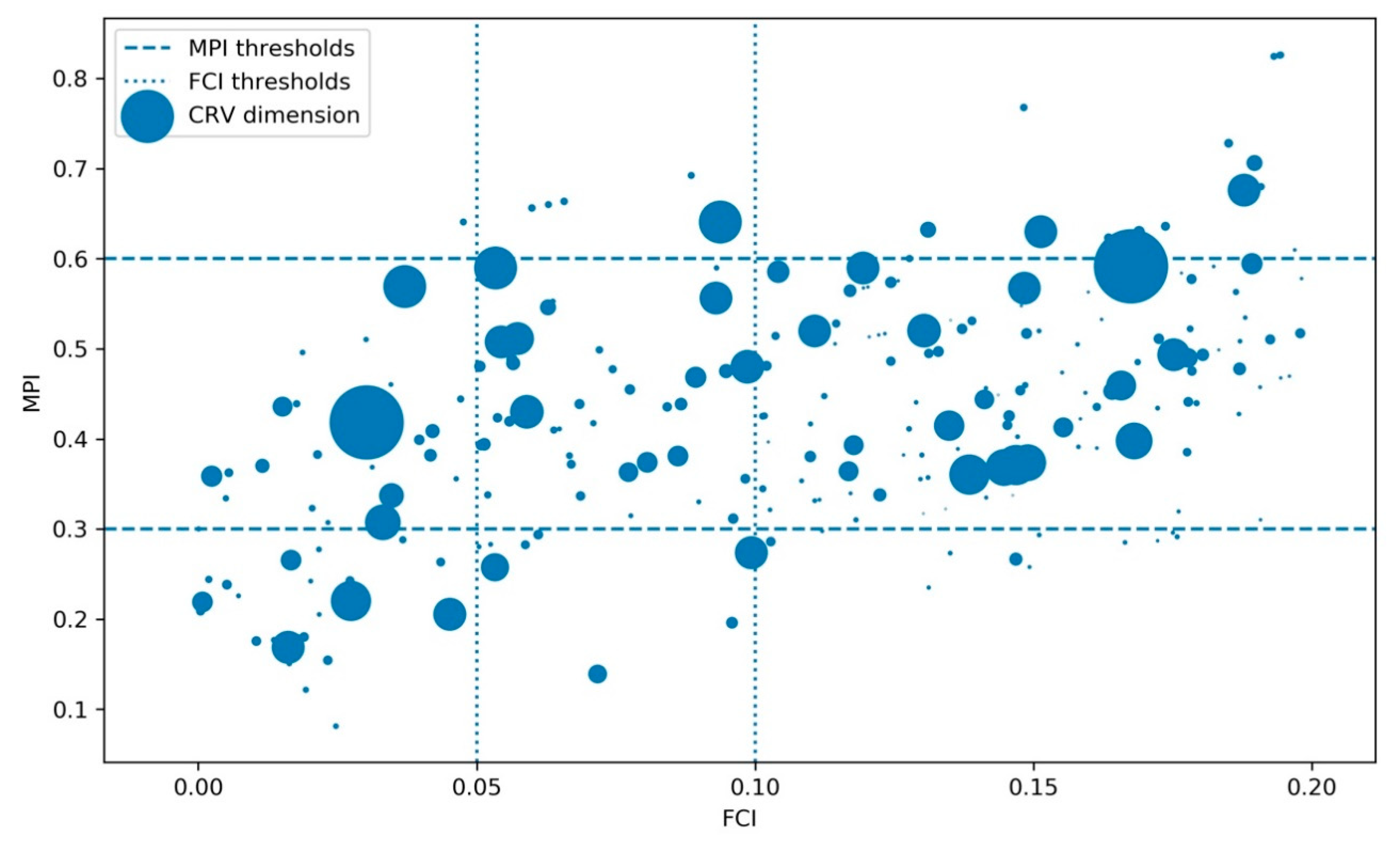
Figure 8.
Comparison between Facility Condition Index (FCI) and Maintenance Priority index (MPI) of the components and dimension of the Current Replacement Value (CRV).
Figure 8.
Comparison between Facility Condition Index (FCI) and Maintenance Priority index (MPI) of the components and dimension of the Current Replacement Value (CRV).
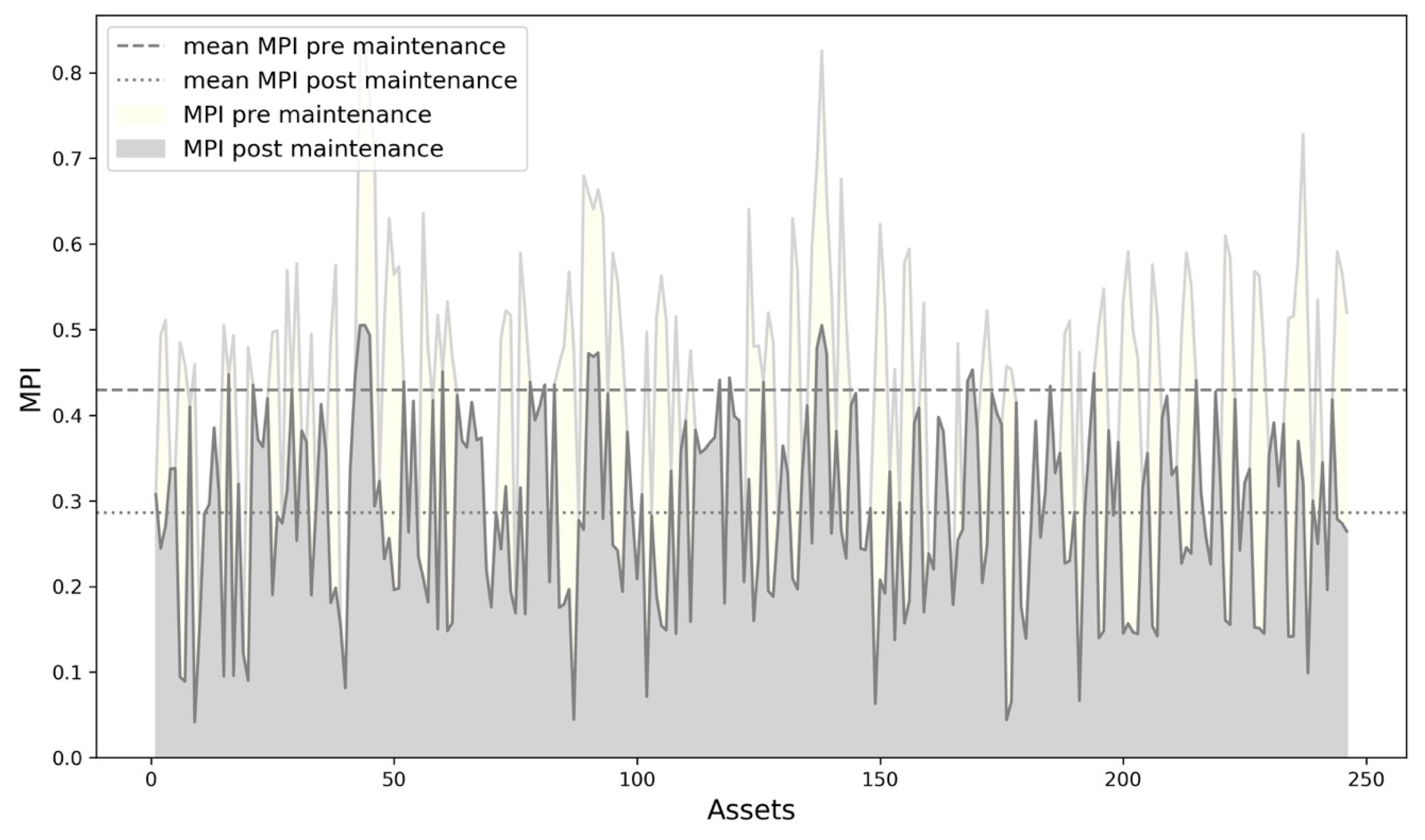
Figure 9.
Maintenance Priority Index (MPI) before (ivory) and after (light grey) maintenance. The dashed line is the average MPI after maintenance, the dotted one is the average MPI before maintenance.
Figure 9.
Maintenance Priority Index (MPI) before (ivory) and after (light grey) maintenance. The dashed line is the average MPI after maintenance, the dotted one is the average MPI before maintenance.
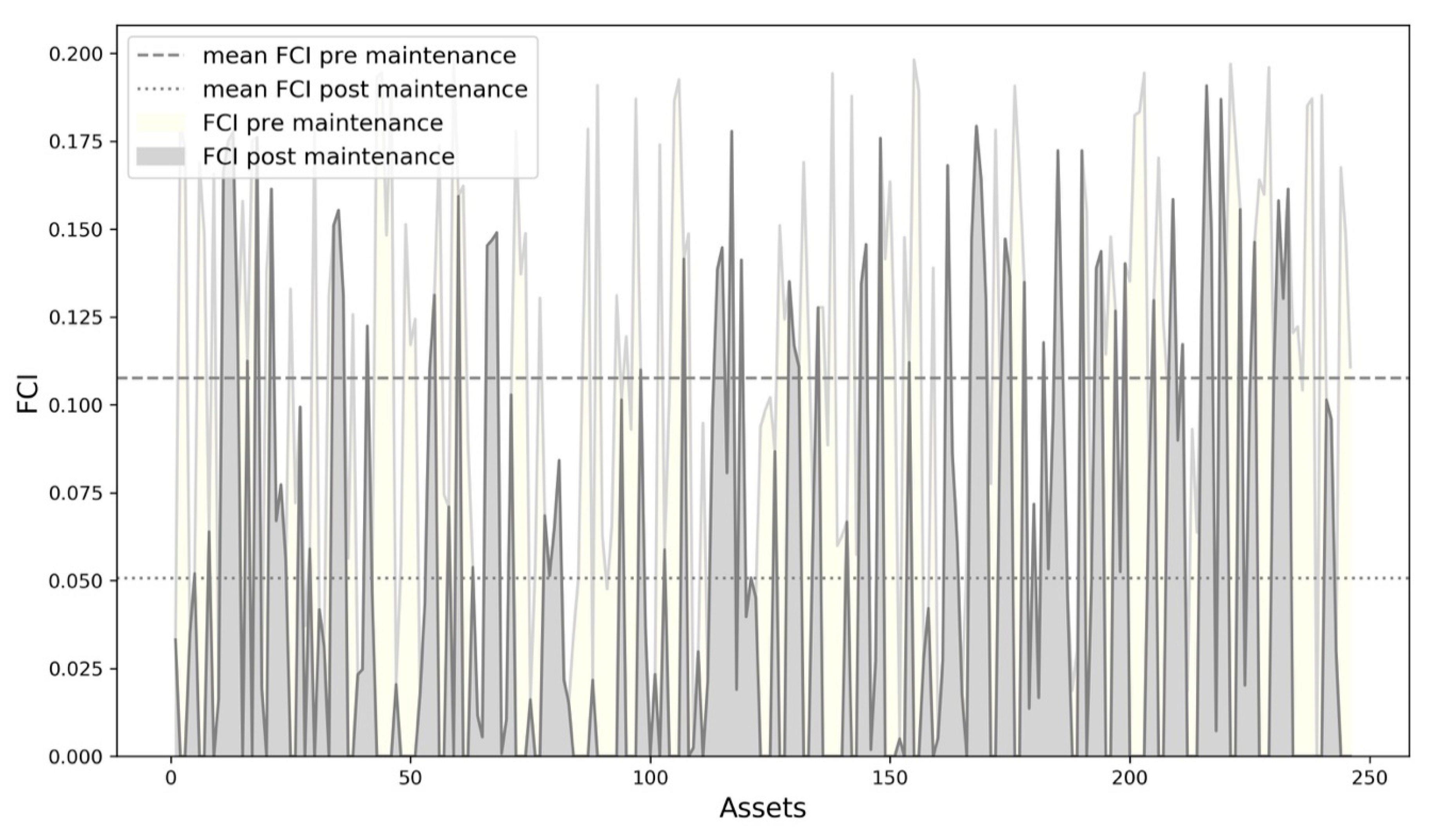
Figure 10.
Facility Condition Index (FCI) before (ivory) and after (light grey) maintenance. The dashed line is the average FCI after maintenance, the dotted one is the average FCI before maintenance.
Figure 10.
Facility Condition Index (FCI) before (ivory) and after (light grey) maintenance. The dashed line is the average FCI after maintenance, the dotted one is the average FCI before maintenance.
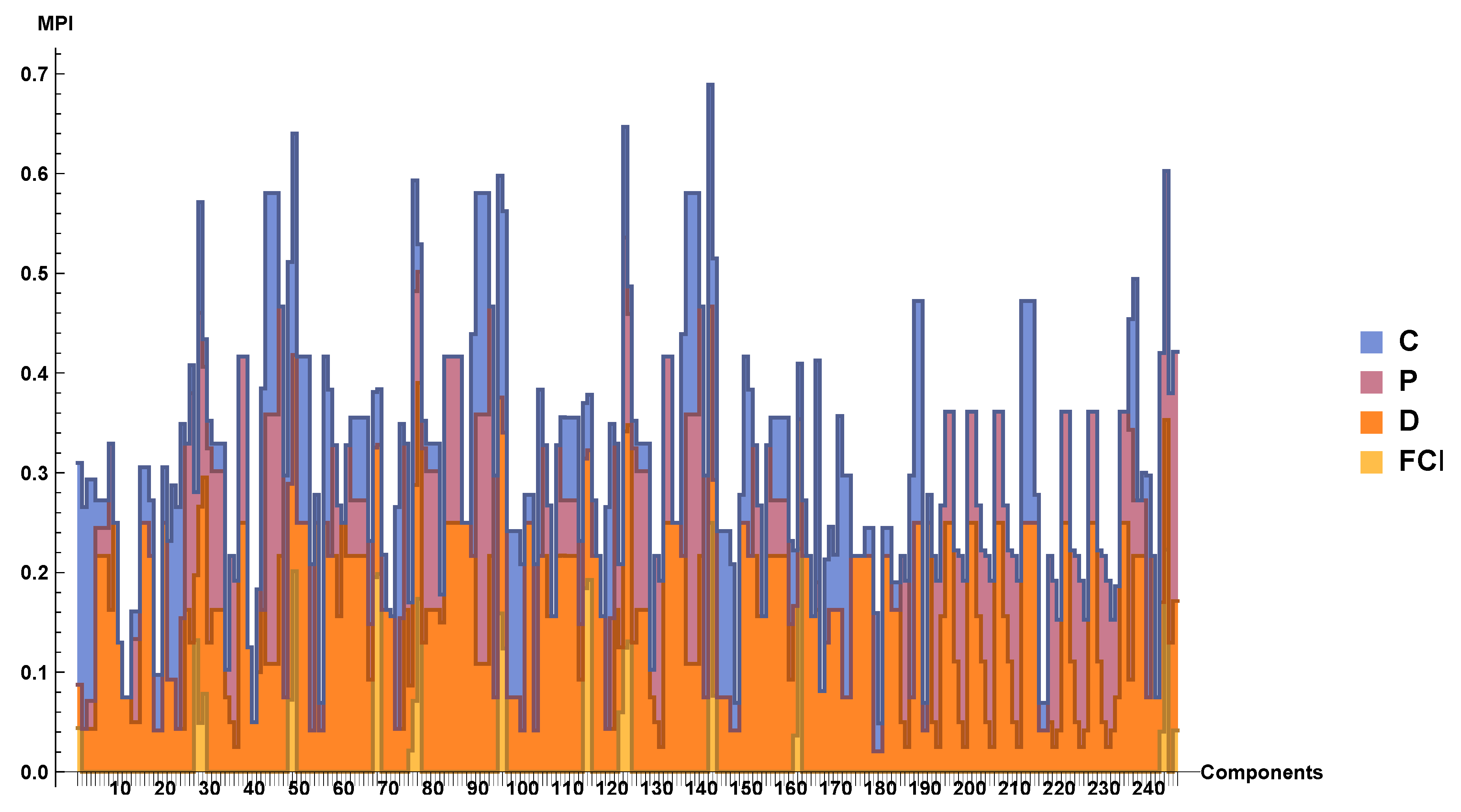
Figure 11.
Maintenance Priority Index (MPI) of the components after the maintenance. The colors show how the Facility Condition Index (FCI), D index (measuring the age of the assets), P index (measuring the preference of the owner) and C index (measuring the criticality of each asset) contribute to the MPI of each component.
Figure 11.
Maintenance Priority Index (MPI) of the components after the maintenance. The colors show how the Facility Condition Index (FCI), D index (measuring the age of the assets), P index (measuring the preference of the owner) and C index (measuring the criticality of each asset) contribute to the MPI of each component.
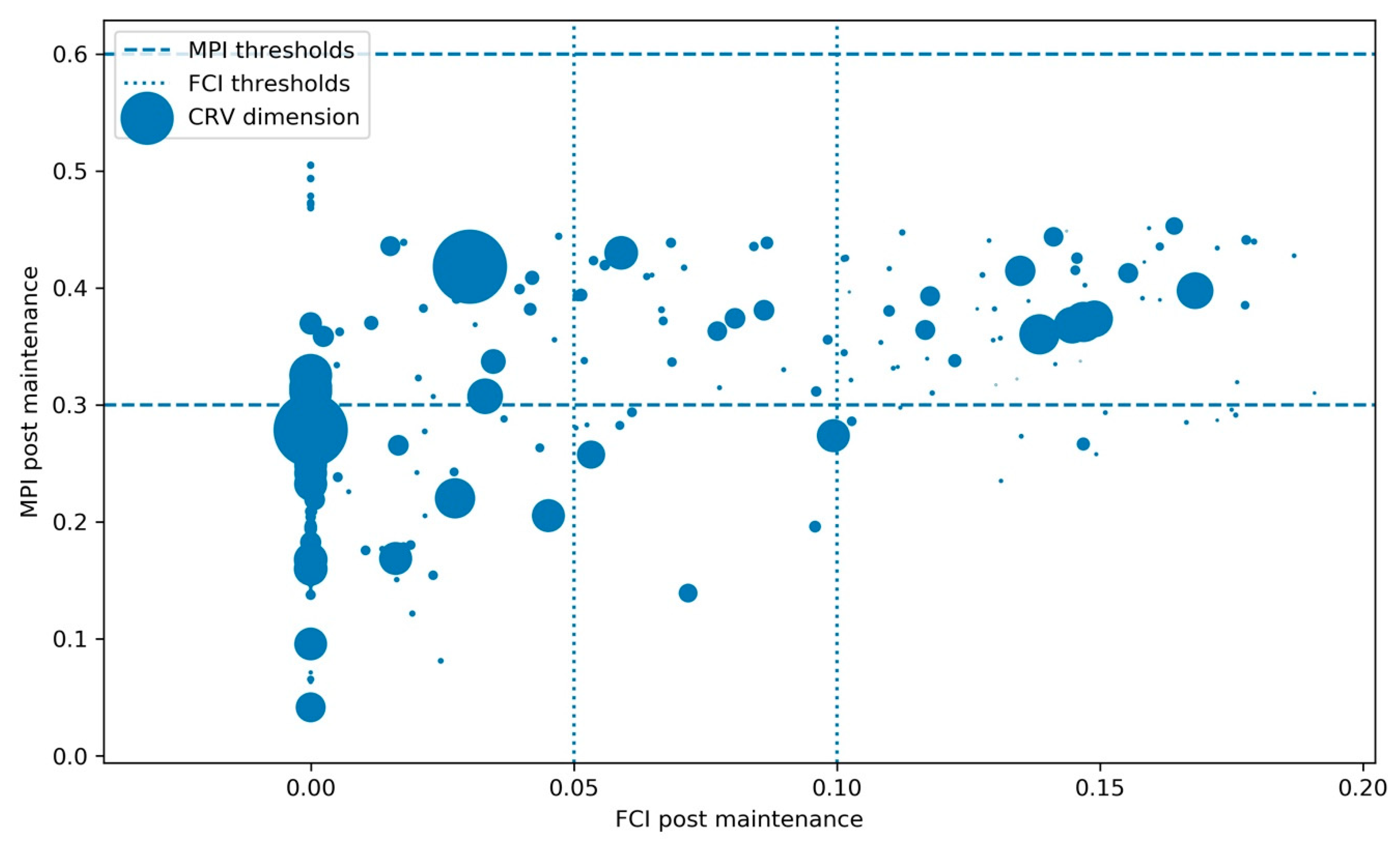
Figure 12.
Comparison between Facility Condition Index (FCI) and Maintenance Priority Index (MPI) of the components after maintenance.
Figure 12.
Comparison between Facility Condition Index (FCI) and Maintenance Priority Index (MPI) of the components after maintenance.
Figure 13.
Assets to be maintained (or not) according to different maintenance prioritization strategies (Facility Condition Index and Maintenance Priority Index computed after the Condition Assessment are shown).
Figure 13.
Assets to be maintained (or not) according to different maintenance prioritization strategies (Facility Condition Index and Maintenance Priority Index computed after the Condition Assessment are shown).
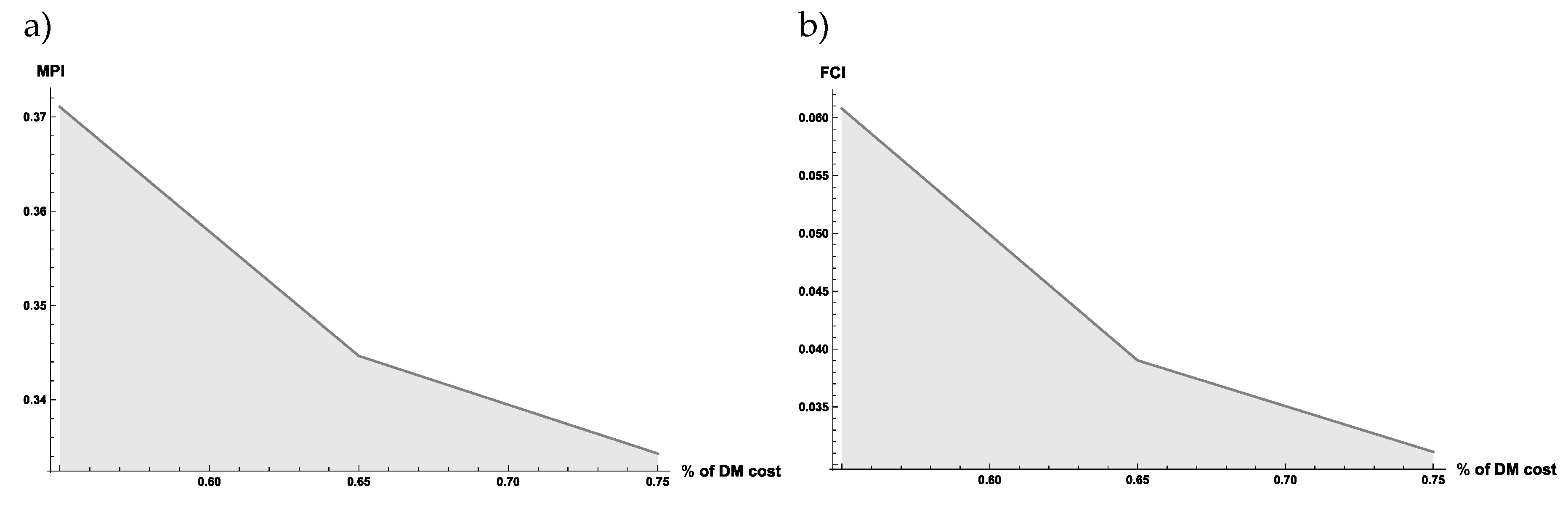
Figure 14.
Scenario analysis. How Maintenance Priority Index (MPI) (a) and Facility Condition Index (FCI) (b) change according to the budget constrain expressed in percentage of the Deferred Maintenance (DM) costs.
Figure 14.
Scenario analysis. How Maintenance Priority Index (MPI) (a) and Facility Condition Index (FCI) (b) change according to the budget constrain expressed in percentage of the Deferred Maintenance (DM) costs.
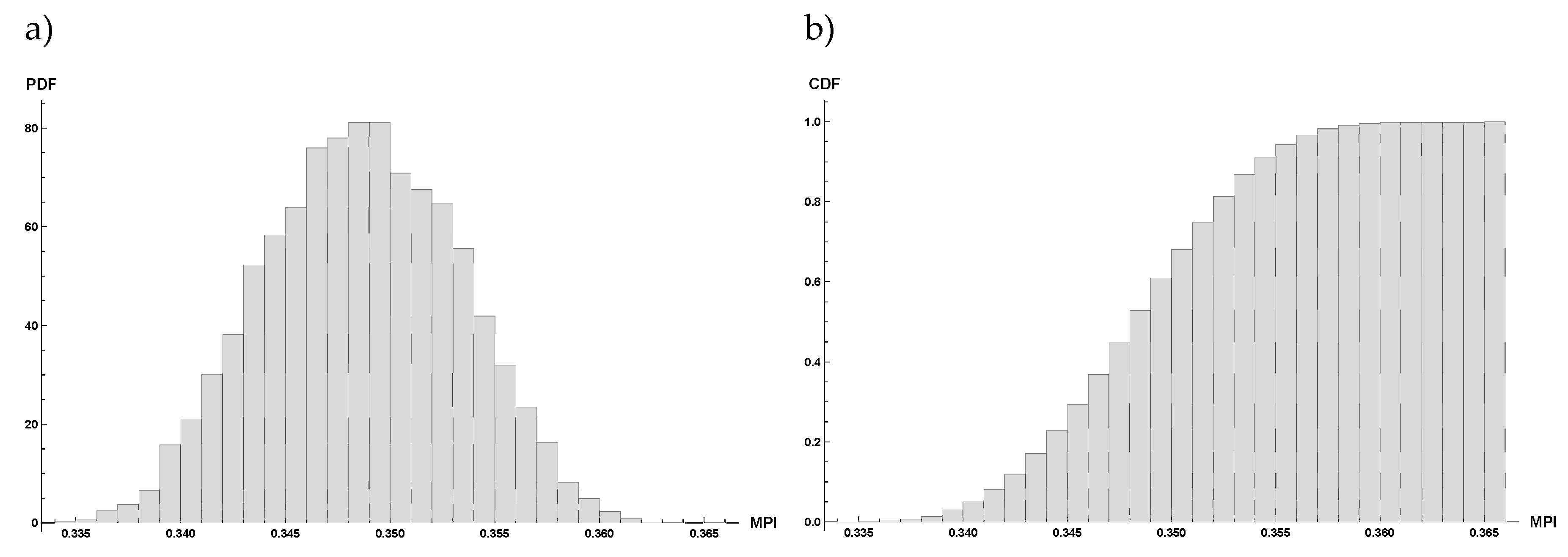
Figure 15.
Montecarlo simulation results. Probability (a) and Cumulative (b) density function of Maintenance Priority Index (MPI).
Figure 15.
Montecarlo simulation results. Probability (a) and Cumulative (b) density function of Maintenance Priority Index (MPI).
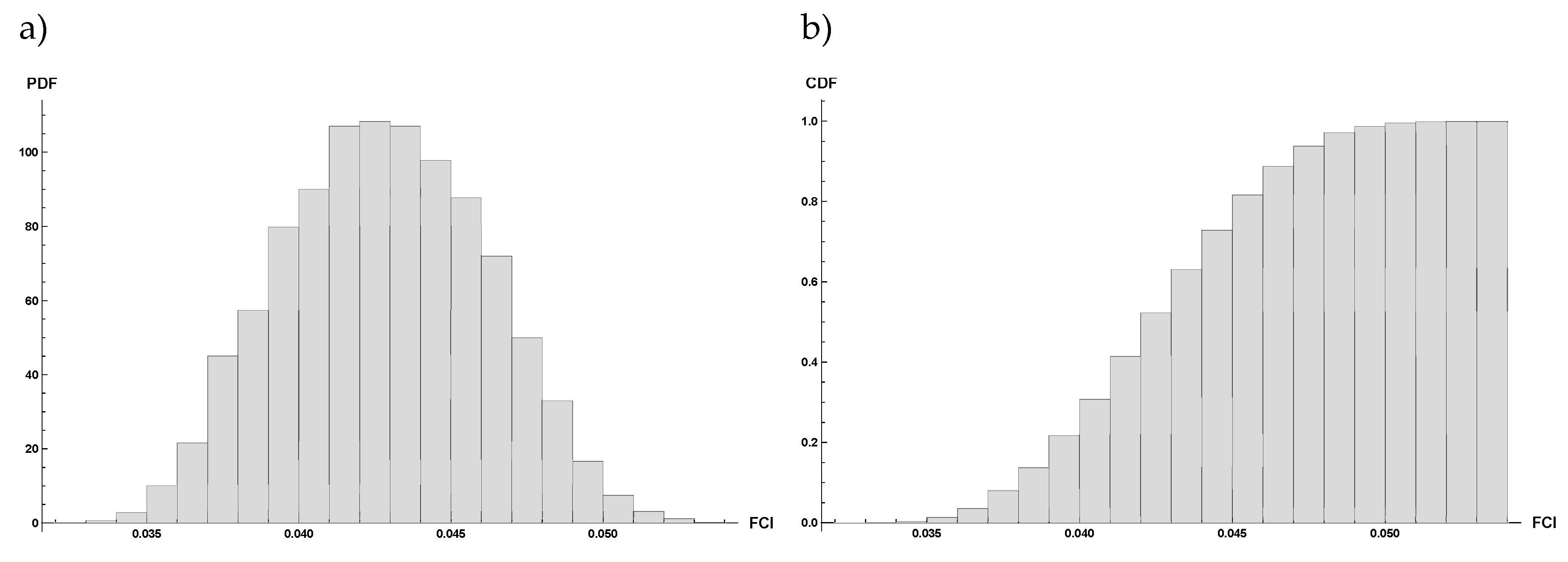
Figure 16.
Montecarlo simulation results. Probability (a) and Cumulative (b) density function of Facility Condition Index (FCI).
Figure 16.
Montecarlo simulation results. Probability (a) and Cumulative (b) density function of Facility Condition Index (FCI).
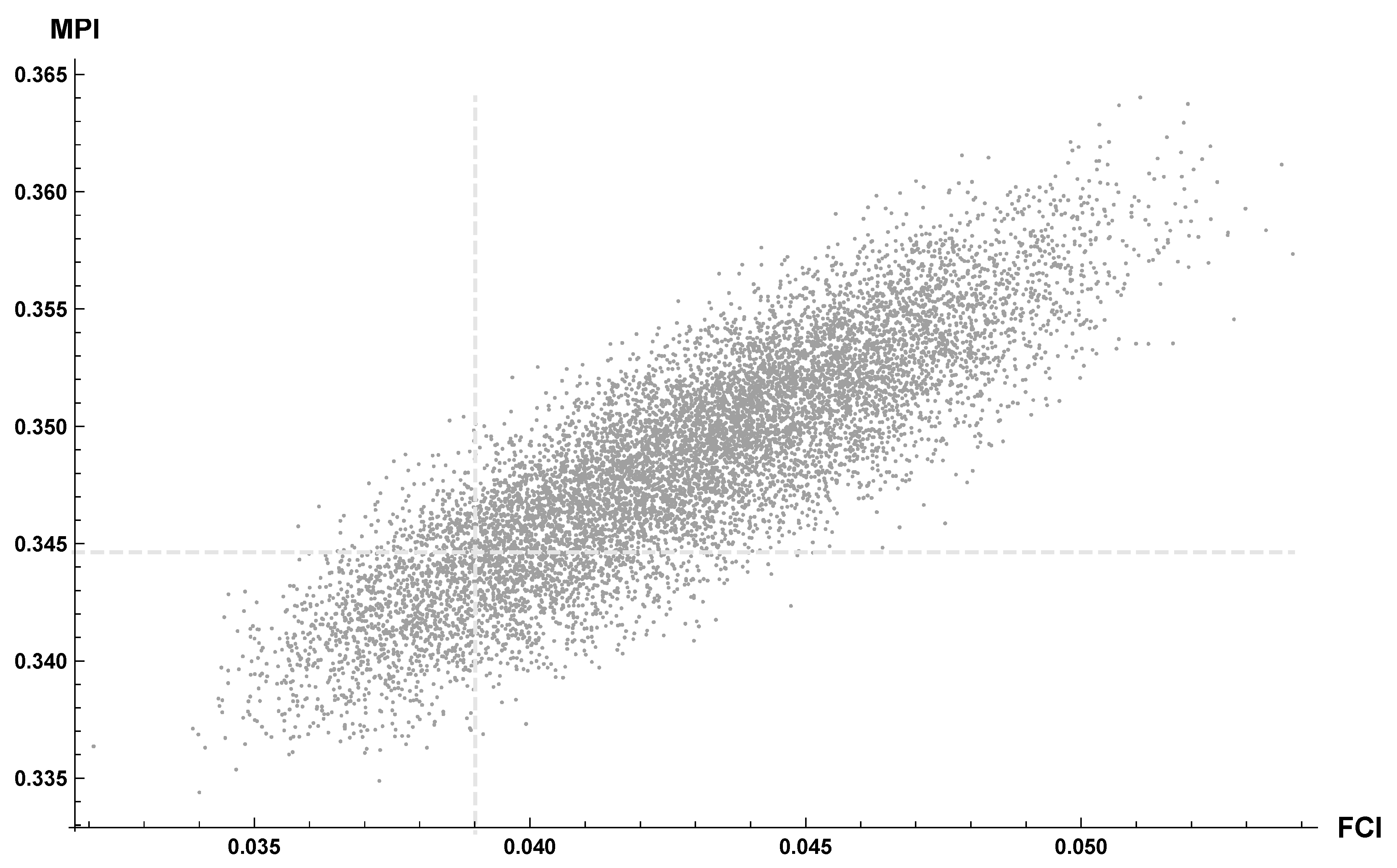
Figure 17.
Combination of Maintenance Priority Index (MPI) and Facility Condition Index (FCI) for each one of the 10,000 simulations compared to the deterministic Maintenance Priority Index (MPI) and Facility Condition Index (FCI) (dashed lines).
Figure 17.
Combination of Maintenance Priority Index (MPI) and Facility Condition Index (FCI) for each one of the 10,000 simulations compared to the deterministic Maintenance Priority Index (MPI) and Facility Condition Index (FCI) (dashed lines).
Table 1.
Severity classes adopted for the C* index. The classes are taken from the MIL-STD 1629(A) [
38].
Table 1.
Severity classes adopted for the C* index. The classes are taken from the MIL-STD 1629(A) [
38].
| Severity | Rank | Criteria |
|---|
| No effect | 1 | No effect on the product or subsequent processes |
| Very slight effect | 2 | Very slight effect on the product performance |
| Slight effect | 3 | Slight effect on the product performance |
| Minor effect | 4 | Fault does not require repair |
| Moderate effect | 5 | Fault on non-vital part requires repair |
| Significant effect | 6 | Product performance was degraded, but operable and safe. Non-vital part inoperable |
| Major effect | 7 | Major effect on process, repair on parts necessary. Subsystem inoperable |
| Extreme effect | 8 | Extreme effect on process, equipment damaged. Product inoperable but safe |
| Serious effect | 9 | Potential hazardous effect. |
| Hazardous effect | 10 | Hazardous effect |
Table 2.
Preference scale values.
Table 2.
Preference scale values.
| Preference | Rank |
|---|
| No impact on the business | 1 |
| Very slight impact | 2 |
| Slight impact | 3 |
| Minor impact on the business | 4 |
| Moderate impact | 5 |
| Significant impact | 6 |
| Major impact | 7 |
| High impact | 8 |
| Very high impact | 9 |
| Extremely high impact | 10 |
Table 3.
Results of the Montecarlo simulations.
Table 3.
Results of the Montecarlo simulations.
| MPI | Sim 1 | Sim 2 | Sim 3 | Sim 4 | Sim 5 |
|---|
| Mean | 0.499117 | 0.50098 | 0.499901 | 0.498664 | 0.500728 |
| Std. Dev. | 0.152626 | 0.152535 | 0.151193 | 0.152301 | 0.152611 |
Table 4.
Percentiles and Maintenance Priority Index (MPI) values.
Table 4.
Percentiles and Maintenance Priority Index (MPI) values.
| %tile | 5% | 10% | 15% | 20% | 25% | 30% | 35% | 40% | 45% | 50% |
| MPI | 0.2464 | 0.3011 | 0.3387 | 0.3681 | 0.3950 | 0.4197 | 0.4412 | 0.4608 | 0.4810 | 0.5007 |
| %tile | 55% | 60% | 65% | 70% | 75% | 80% | 85% | 90% | 95% | |
| MPI | 0.5206 | 0.5420 | 0.5621 | 0.5836 | 0.6065 | 0.6321 | 0.6620 | 0.6989 | 0.7508 |
Table 5.
Thresholds defined for the four metrics of the Decision Support System (DSS).
Table 5.
Thresholds defined for the four metrics of the Decision Support System (DSS).
| Metric | Good | Fair | Poor |
|---|
| FCI | FCI ≤ 5% | 5 < FCI < 10% | FCI > 10% |
| D | D ≤ 0.5 | 0.5 < D < 1 | D = 1 |
| P | P ≤ 3 | 3 < P ≤ 6 | P > 6 |
| C | C ≤ 3 | 3 < C ≤ 6 | C > 6 |
Table 6.
Reference values for the four metrics od the Decision Support System DSS.
Table 6.
Reference values for the four metrics od the Decision Support System DSS.
| Metric | Good | Fair | Poor |
|---|
| FCI | 2.5% | 7.5% | 15% |
| D | 0.25 | 0.75 | 1 |
| P | 2 | 5 | 7 |
| C | 2 | 5 | 7 |
Table 7.
Facility Condition Index (FCI) and scaled Facility Condition Index (FCI*) values adopted for the definition of the Maintenance Priority Index (MPI) thresholds.
Table 7.
Facility Condition Index (FCI) and scaled Facility Condition Index (FCI*) values adopted for the definition of the Maintenance Priority Index (MPI) thresholds.
| Parameters | Values |
|---|
| FCImin | 0 |
| FCI*min | 0 |
| FCImax | 0.2 |
| FCI*max | 0.75 |
Table 8.
Maintenance Priority Index (MPI) thresholds.
Table 8.
Maintenance Priority Index (MPI) thresholds.
| MPI Thresholds | Priority | Criteria |
|---|
| ≥ 0.6 | High | Maintain the asset as soon as possible |
| 0.3 > MPI > 0.6 | Medium | Maintain the asset if possible |
| MPI ≤ 0.3 | Low | No need for maintenance |
Table 9.
Variation of the Facility Condition Index (FCI) ratio and Maintenance Priority Index (MPI) ratio according to Current Replacement Value (CRV) ratio and Priority index (P) ratio.
Table 9.
Variation of the Facility Condition Index (FCI) ratio and Maintenance Priority Index (MPI) ratio according to Current Replacement Value (CRV) ratio and Priority index (P) ratio.
| Replacement Cost Ratio [CRV1/CRV2] | Priority Ratio [P1/P2] | |
|---|
| 0.4 | 0.6 | 0.8 | 1 | 1.2 | 1.4 | 1.6 |
|---|
| 0.5 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | FCI1/FCI2 |
| 0.66 | 0.82 | 0.94 | 1.03 | 1.11 | 1.16 | 1.21 | MPI1/MPI2 |
| 0.75 | 1.33 | 1.33 | 1.33 | 1.33 | 1.33 | 1.33 | 1.33 | FCI1/FCI2 |
| 0.65 | 0.81 | 0.93 | 1.02 | 1.09 | 1.14 | 1.19 | MPI1/MPI2 |
| 1 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | FCI1/FCI2 |
| 0.64 | 0.80 | 0.91 | 1.00 | 1.07 | 1.12 | 1.16 | MPI1/MPI2 |
| 1.25 | 0.80 | 0.80 | 0.80 | 0.80 | 0.80 | 0.80 | 0.80 | FCI1/FCI2 |
| 0.63 | 0.79 | 0.90 | 0.98 | 1.05 | 1.10 | 1.14 | MPI1/MPI2 |
| 1.5 | 0.67 | 0.67 | 0.67 | 0.67 | 0.67 | 0.67 | 0.67 | FCI1/FCI2 |
| 0.63 | 0.78 | 0.89 | 0.97 | 1.03 | 1.08 | 1.12 | MPI1/MPI2 |
| 1.75 | 0.57 | 0.57 | 0.57 | 0.57 | 0.57 | 0.57 | 0.57 | FCI1/FCI2 |
| 0.62 | 0.77 | 0.87 | 0.95 | 1.01 | 1.06 | 1.10 | MPI1/MPI2 |
Table 10.
Results of the Montecarlo simulation. Mean and standard deviation of Maintenance Priority Index (MPI) and Facility Condition Index (FCI) deterministic values obtained in the case study.
Table 10.
Results of the Montecarlo simulation. Mean and standard deviation of Maintenance Priority Index (MPI) and Facility Condition Index (FCI) deterministic values obtained in the case study.
| | Mean | Standard Deviation | Deterministic Values | % Difference Mean vs. Deterministic |
|---|
| MPI | 0.3486 | 0.0047 | 0.3446 | 1.16% |
| FCI | 0.0428 | 0.0034 | 0.0390 | 9.74% |
Table 11.
Results of the Montecarlo simulation. Maintenance Priority Index (MPI) and Facility Condition Index (FCI).
Table 11.
Results of the Montecarlo simulation. Maintenance Priority Index (MPI) and Facility Condition Index (FCI).
| p | 5% | 15% | 25% | 35% | 45% | 55% | 65% | 75% | 85% | 95% |
|---|
| MPI | 0.3408 | 0.3435 | 0.3452 | 0.3467 | 0.3480 | 0.3493 | 0.3506 | 0.3519 | 0.3536 | 0.3564 |
| FCI | 0.0373 | 0.0391 | 0.0403 | 0. 0414 | 0.0424 | 0.0433 | 0.0442 | 0.0452 | 0.0464 | 0.0483 |