Abstract
U-values of building elements are often determined using point measurements, where infrared imagery may be used to identify a suitable location for these measurements. Current methods identify that surface areas exhibiting a homogeneous temperature—away from regions of thermal bridging—can be used to obtain U-values. In doing so, however, the resulting U-value is assumed to represent that entire building element, contrary to the information given by the initial infrared inspection. This can be problematic when applying these measured U-values to models for predicting energy performance. Three techniques have been used to measure the U-values of external building elements of a full-scale replica of a pre-1920s U.K. home under controlled conditions: point measurements, using heat flux meters, and two variations of infrared thermography at high and low resolutions. U-values determined from each technique were used to calibrate a model of that building and predictions of the heat transfer coefficient, annual energy consumption, and fuel cost were made. Point measurements and low-resolution infrared thermography were found to represent a relatively small proportion of the overall U-value distribution. By propagating the variation of U-values found using high-resolution thermography, the predicted heat transfer coefficient (HTC) was found to vary between 183 W/K to 235 W/K (±12%). This also led to subsequent variations in the predictions for annual energy consumption for heating (between 4923 kWh and 5481 kWh, ±11%); and in the predicted cost of that energy consumption (between £227 and £281, ±24%). This variation is indicative of the sensitivity of energy simulations to sensor placement when carrying out point measurements for U-values.
Keywords:
building fabric; dwellings; heat flux; heat loss; in situ performance; IR thermography; U-value 1. Introduction
The domestic sector in the U.K. is responsible for 29% of the country’s overall energy consumption, second only to transport. Within the sector, around 80% of this energy consumption can be attributed to hot water and space heating [1]. Up to 40% of the U.K.’s housing is considered hard to treat (HTT) [2], meaning that it can be impractical or not economically beneficial to implement some forms of retrofitting to reduce heating demand. Of the anticipated total housing stock in 2050, around 70% of the stock has already been constructed [3], suggesting long life cycles for U.K. homes and slow replacement of the stock. Understanding the behaviour and performance of such HTT buildings is therefore key to realising the benefits of any applied energy saving measures.
Energy modelling is a useful tool in the arsenal of building energy performance prediction. The ability of a model to predict the heating demand of a building depends heavily on how the elements of that building are parameterised. It is important to ensure that the thermodynamic characteristics of building elements reflect those which are exhibited in situ. The parameters allocated to the elements that make up the outer envelope of a building are particularly important, as heat loss across this boundary is a dominant factor of the building’s overall heating demand.
U-values are described as a measure of heat loss through a building element, and can account for the variation in external conditions. U-values are calculated for building elements where the composition is known—i.e., the thickness and thermal conductivity of each layer of material—as stated in BR 443 [4]. Common structures have pre-calculated U-values listed in international standards, for example, CIBSE Guide A [5] and ISO 10456:2007 [6]. These standardised values are often used as a common reference point in the energy modelling of buildings and support a consistency of results.
1.1. The Performance Gap
Growing concern over the use of predetermined U-values in energy models is evident in a number of recent works. De Wilde [7] captures the concept of the “Performance Gap”, a discrepancy between the predictions and real energy performance of that building, from the design stage right through to post-occupancy. De Wilde discusses how discrepancies in the design stage are due to misinformation about performance targets, poor predictions of in-use performance, and poor specification of HVAC systems.
The stronger argument is recognized, however, that despite similarities in design against as-built building element composition, pre-calculated and standardised U-values simply do not represent the in-situ characteristics of those elements—the reasoning behind which can be diverse and depend on the context of the application.
Baker [8] compared the calculated and measured U-values for traditional buildings in Scotland. The heterogeneous composition of internal stone or limestone walls of these traditional buildings is recognised as an issue in modelling software, where these building elements are often not well represented. Baker goes on to discuss how assumed U-values used in modelling software are often conservative to account for this—an overestimation—resulting in underperformance in predictions. Taking a similar approach to Baker, Rye, and Scott [9] measured the U-value of 77 permutations of external walls, of both homogeneous and heterogeneous construction, for traditional buildings. They then compared these measured values to those assumed for reduced data standard assessment procedure (RdSAP) calculations [10]; these calculations are used to determine the energy performance/rating of existing buildings. Rye and Scott found that in 77% of cases, the assumed U-values were overestimated. The remaining cases were underestimated.
A later study [11] investigated the sensitivity of the standard assessment procedure (SAP) [10], to certain variables, including the U-value. The method applied by the SAP uses predetermined U-values in combination with additional building level data to determine an energy rating for domestic buildings, which is indicative of the energy performance of that building. Up to 75% of variance in the calculated energy rating (and inferred performance) was found, due to system efficiency, external wall U-value, and building geometry. It is also stated in [12] that predetermined U-values are likely to be inappropriate for energy certification and for the economic evaluation of retrofit. Their work indicates that assumed U-values in models are a large source of uncertainty when carrying out analysis of building energy performance. By taking realistic U-values into account, a reanalysis of annual domestic demand saw a reduction by up to 16%; this resulted in an increase of energy rating for over 20% of the study’s test cases.
There is growing evidence to indicate that there is often over-estimation of U-values within standard values, and therefore, a potential for inaccuracies in understanding the energy performance of the U.K.’s housing stock as a whole. Given that these data inform energy legislation and policy, as well as retrofit programmes, there is a strong case to re-evaluate the U-values used in modelling.
The performance gap phenomenon is not simply limited to the U.K.’s housing stock, however, and there is evidence of discrepancies between modelled and measured energy performance surface globally. In [13], discrepancies in the assumed thermal properties of wooden-framed buildings in Toronto, Canada were investigated. Assumed heat loss was largely impacted by the building’s wall-to-window ratio; additional framing used to support openings increasing the overall heat loss, resulting in an overestimation of performance. A further study on residential buildings during a retrofit project in Southern Germany highlighted the impact of the performance gap on such projects [14]. Incorrect assumptions of pre-retrofit building fabric and system performance were shown to give much more ambitious predictions of energy savings than was observed after the installation of retrofit. Further examples of the performance gap appearing in studies concerning older masonry in Italy [15] have also contributed to the mounting body of work that has identified discrepancies between assumed and actual fabric U-values.
Herrando et al. [16] extended the demonstration of the performance gap to industrial buildings. A study involving 21 faculty buildings at the University of Zaragoza (Spain) saw deviations in the overall energy consumption of up to 73% between the simulated and actual consumption. One final study [17] looked at the prediction of building performance in offices located in major Australian cities, identifying that assumptions not only concerning building fabric, but also occupant behavior and appliance and lighting usage encounter considerable variation, leading to a variation between real and simulated performance of up to 50%.
Demonstrated as a globally-recognised problem inherent with energy simulation tools, the importance of realising not only accurate but reliable and realistic inputs for these tools is stressed.
1.2. Model Calibration
To overcome the uncertainties attached to the performance gap, calibration techniques can be used to “fine-tune” models, using a number of different techniques.
Bayesian analysis is a probabilistic method used to calibrate models. Developed by Kennedy and O’Hagan [18], the technique has been applied in a number of studies [19,20,21,22,23]. Uncertainties within a model are defined into three categories: model output uncertainty, discrepancy between model outputs and measured data, and the uncertainty of measured data. Calibration seeks to find the closest match possible between measured and modelled outputs. To do this, calibration factors of each uncertainty are assigned with a pre-determined probability distribution, indicating the likelihood of that calibration factor delivering the closest match between the data. Throughout a series of data, this probability distribution is updated, until a final distribution is given for each of the calibration factors, that indicates the most probable value.
The process can be automated, and is found to be suitable for model calibration; however, an alternative technique that offers greater certainty is the deterministic approach. This method is investigated in [24,25,26] and involves a repetitive alteration of performance parameters, until the desired minimum discrepancy is found between measured and modelled results. Though claims are made in literature that this technique is superior to Bayesian calibration, the process is much more time-consuming.
A final calibration technique is offered by [27]. In this case, a purpose-built facility was used to measure the performance-determining parameters of a building (air permeability and U-values) under controlled conditions. On finding that assumed values in their modelling work did not match those measured in situ, model parameters were subsequently changed to the measured values. The study found that it was possible to reduce the performance gap of 18% to 2%.
1.3. Reliability of In-Situ Measurements
Collecting data from the field has a number of pragmatic and methodological challenges that can create problems for researchers and impact data collection and analysis [28]. At a more focused method level, in-situ measurement of U-values should only be seen as a point measurement in a particular period, being the duration of the measurement itself. The variation of U-values can happen in two vectors: spatial and across a period.
With any measurement will come error. U-value measurement even when carried out to the most recent international standard, ISO 9869 [29], has a significant expected error, with a global error in the methodology of around 14–28%. This figure should be kept in mind when expressing results and comparing studies. The breakdown of these errors is detailed in the standard, but examples of larger variation are items such as how the heat flux transducers are fixed to the wall, which can lead to errors of up to 17% when a suitable medium is not used between the sensor and the wall [30]. Differing methods of data analysis will lead to variations in the final outcome of the U-value result, such as when air temperature measures are used instead of surface temperature measurements.
Where moisture is present in elevated levels in measured elements, such as walls, it can cause the conductivity of the wall to be higher than predicted. When a masonry wall is subject to increased moisture levels, the conductivity can increase by over 100% when saturation point is reached. A modelled simulation of this effect is illustrated in Figure 1.
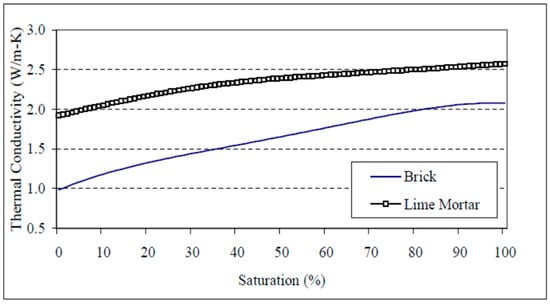
Figure 1.
Modelled thermal conductivity [31].
The presence of moisture within the hygroscopic materials of a building has a significant impact on the performance of that building. By omitting this effect when predicting energy performance, annual heat loss can be underestimated [32].
Many researchers have found variations across similar wall types, and discrepancies between the modelled and measured values of these walls. These discrepancies are often allocated to the variations in which the elements are constructed, such as materials, workmanship, and defects hidden from view, as well as issues such as air moving through an element, which will reduce the thermal performance of the element. An example of this is given in a recent study carried out at the Energy House on the subject of suspended timber floors. Significant variation was found across only one room, in which is a simple ventilated timber floor [33].
The observed U-values were found to be 0.56 ± 0.05 W/m2K far from the external walls (location 5), to 1.18 ± 0.11 W/m2K in the bay window area (location 14). This is illustrated in Figure 2, and provides a suitable example of the distribution of U-values in a single element. Researchers have found other examples of wide-ranging U-values across similar wall types, and even on the same sections of wall.
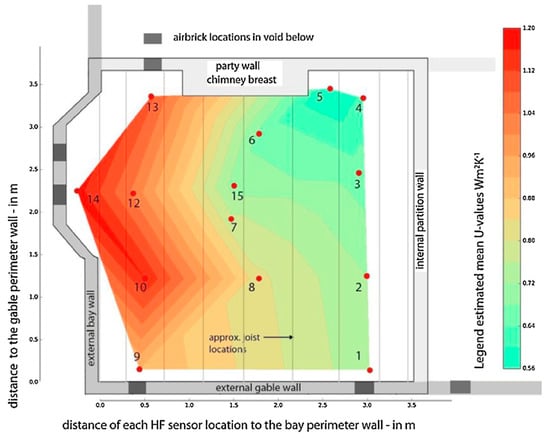
Figure 2.
Variation in U-value for a suspended timber floor [33].
A recent study carried out by the Building Research Establishment across a large sample of solid walls in the U.K. (n = 23) considered the use of four-point measurements on a single surface. A comparison of the average of measurements and the range of measured results revealed a variance of between 4% (an average of 1.68 W/m2K and a range of 0.07 W/m2K) and 73% (an average of 1.20 W/m2K and a range of 0.88 W/m2K) [34]. This illustrates that significant ranges might be expected in the simplest type of wall structures.
Internal and external variables can have a significant effect on U-value measurement outcomes [35]. Researchers have found that external variables, such as wind, precipitation, long wave radiation, and solar gain can have a major impact. As such, measurements may need to be adjusted for these environmental impacts, an example of this is the increased U-value found in vertical elements when affected by wind. The increased amount of air moving across the element caused a more rapid heat transfer, as the air layer surrounding the external face of the wall is stripped away. This causes the convective heat transfer coefficient of the elements external face to increase. Many studies have investigated the impact of wind on the convection coefficient—a function of windspeed—though each study demonstrated a difference in the impact [36,37,38,39]. Figure 2 presents an illustration of wind speed vs. change in convective heat transfer, quantifying the variation of the U-value in a suspended timber floor. The presence of air bricks around the perimeter was found to promote the increase of heat transfer through the floor, near to those locations, because of an increase in air flow.
This variation of point-measured U-values across single elements points to a question as to how we might more fully understand the distribution of U-values across an element and the wider building envelope. This led to the consideration of infrared thermography (IRT) for the determination of the fabric U-value to be used in the calibration of energy models.
1.4. Infrared Thermography
IRT has demonstrated its importance, not only for qualitative analysis of buildings with the inspection of heat loss and thermal defects [40,41], but also for quantitative analysis in the measurement of U-values. Lucchi [42] gave an extensive review of the application of IRT for building energy audits, identifying a common factor of difficulty in its field application.
Weather conditions have proven to be highly problematic when implicating short-term IRT [43,44,45], with effects of rain, solar incidence, and wind, leading to a distortion of data and bias in the results. Lucchi [42] goes on to discuss solutions to these problems can be sought by controlling these factors, in order to reduce the impact on the results; suggestions of limiting IRT measurements to dry days with low solar incidence, performing IRT during steady conditions, and the acquisition of compensation terms, are all made [44,45,46]
Further studies have also sought to perform IRT under controlled conditions, to eliminate the influence of weather, though on a much smaller scale than for whole buildings [47,48]. The following methodology section explores how, in this paper, the effects of weather have been mitigated, and the presence of controlled, steady-state conditions were used to reduce uncertainty and bias in the application of IRT for a whole dwelling.
2. Methodology
2.1. Infrared Thermography
The proposed method for understanding the distribution of U-values was IRT. The method was applied at high and low resolutions and compared with point U-values. This data was then applied to a dynamic model, in order to identify the impact of any variation on the predictive modelling of building energy performance.
IRT, as defined by BS ISO 18434-1:2008 [49], is the “Acquisition and analysis of thermal information from non-contact thermal imaging devices”. The thermal imaging device used throughout this work was the FLIR B425 camera; the collected thermal information was the internal surface temperatures for a whole dwelling. Table 1 lists the features of this piece of equipment.

Table 1.
FLIR B425 Equipment Features.
The dwelling considered for this study was the Energy House test facility at the University of Salford, a replica pre-1920s Victorian terrace home constructed within a climate-controlled chamber. The house is mostly unchanged from the original design, which considered a 222.5 mm solid brick wall with 13 mm dense gypsum plaster internally, single-glazed timber sash windows, suspended timber floors, and a 32° pitched roof. One change is the addition of 100 mm mineral wool insulation in the loft space. The building is considered a typical “two up, two down” home, meaning there are two habitable spaces on the ground floor (the living room and kitchen), and two habitable spaces on the first floor (each of the bedrooms). The building is also considered an end terrace, with the adjacent building conditioned to a fixed temperature to imitate occupancy (see [50] for a full description of the facility).
To capture the heat loss from the whole dwelling, IRT was carried out on the internal surfaces of the building envelope. This was carried out for the prominent rooms of the house: the living room, kitchen, master and second bedrooms. U-values calculated with this data were then used to inform calibrated models [27] for a prediction of the energy performance of the Energy House.
EN ISO 9869-1:2014 states that the U-value of a building element can be calculated using:
where Q is the heat flux through a surface (W/m2), Ti is the internal air temperature (K), and Te is the external air temperature (K). To apply this measurement to IRT, EN ISO 6946:2017 [51] says that the heat flux parameter can be separated into radiative and convective components:
where
This allows the calculation of the U-value with:
where ε, σ, and h are equation constants, Ts is the surface temperature (K), and Tref is the reflective temperature (K). Steady state conditions are required to uphold this equation; the benefit of using the Energy House test facility is that both internal and external conditions can be maintained with a high level of precision, creating quasi-steady state conditions.
While the surface temperature can be obtained within thermal images, the reflective temperature, a measure of the ambient temperature, must be determined separately. To do this, ISO 18434-1:2008 is applied. The standard states that the average temperature of a crumpled piece of reflective foil with an emissivity of 1 is equal to the reflective/ambient temperature. A piece of crumpled reflective foil was placed on each of the measured elements of the Energy House 4 h prior to image capture, and allowed to equilibrate with the surroundings. Images of these pieces of foil were captured before images of each wall were taken. Figure 3 shows an example of the foil used in situ within the research building.

Figure 3.
Crumpled foil used to determine reflective temperatures, fixed in situ under equilibrium with the affixed surface.
The pixels that make up thermal images contain discrete information on the surface temperature of the representative area. The information collected for each pixel was used to calculate the individual U-values of those pixels. Instead of taking point measurements using the heat flux method of ISO 9869-1:2014, thermal images can be used to generate a high-grain representation of U-value distribution across a surface.
Camera resolution limits the quantity of data captured for each measured element to the number of pixels in the image output. The distance between the camera and measured element can be increased to fit the whole surface into a single image; however, this leads to a loss of granularity in the collected data. A solution to this is to take multiple images of a single element and “stitch” them together—thus covering the entire element and retaining granularity. The one drawback of this approach is that for relatively large buildings, this process would be extremely time consuming.
For this study, low- and high-resolution IRT techniques were considered, where resolution here is defined as the number of pixels per measured element. Low-resolution IRT involves the capture of a single image per external wall, while high-resolution IRT uses multiple images stitched together. Images for low-resolution IRT were taken at the minimum focus distance of 0.4 m, while higher resolution images were taken from a distance of 1 m. This was to facilitate an increased capture area with minimal stitching (which causes error in overlaps), while retaining granularity of the data. Low-resolution images were limited to 76,800 pixels (per Table 1), while higher-resolution images use a minimum of 108,000 pixels (from the stitching of multiple photos).
2.2. Informed Modelling
Modal U-values for each surface were determined from each thermal image. This was done for both high- and low-resolution IRT; each measurement technique informed the re-calibration of the Energy House model, as shown in Figure 4.

Figure 4.
Model of the Energy House test facility in Designbuilder.
The study performed by [27] used point measurements of U-values, calculated using the average method of ISO 9869-1:2014. The positioning of sensors used in point measurements of U-values, however, does not allow for the full representation of the thermal performance of the building element under investigation.
To show the impact and variation of modelling results obtained using IRT, the same model as used in [24] was re-calibrated, using the calculated U-values from both low- and high-resolution imaging. The original calibration technique used the heat transfer coefficient (HTC) as a value against which models could be tested; this performance, indicating properties of the Energy House, was determined using a co-heating test [52].
The first step in reviewing the impact of IRT on predicted energy performance was to model the HTC using the average U-values calculated for each resolution. The HTC was modelled in Designbuilder, by considering steady-state conditions across the building envelope. For this model, the internal temperature is held at 18 °C, and the external temperature at 4.4 °C. This is done to ensure monodirectional heat flow through the building envelope, by imposing a temperature gradient of above 10 °C. Designbuilder automatically sizes the heating power required to maintain this temperature gradient, which is then used to calculate the HTC.
The next step was then to investigate the variation of predicted energy performance due to the variation in the U-value measurement. To do this, the Energy House model was adjusted, so that the U-values of the measured building elements reflected each peak represented by the U-value distributions. HTCs were then compared against the original calibrated HTC, which was measured in situ.
A final step reviewed the variance in dynamic simulation output as a result of the variance in the U-value found during this study. Annual simulations were performed on the Energy House model for each U-value variation. The simulation used weather data for Manchester, sourced from IWEC (International Weather for Energy Calculations), temperature control conditions from the Standard Assessment Procedure (SAP), and the default domestic occupancy schedules of Designbuilder, sourced from the U.K. National Calculation Methodology (UK NCM). Two key outputs of these simulations were used to analyse the variability of results—the consumption of energy for space heating and the resulting energy cost.
3. Results
3.1. Infrared Thermography Results
A number of different building elements were included in the IR measurement of the U-values. Core building elements of the Energy House—the external walls of the living room, kitchen, master and second bedrooms—were used for the final analysis.
The difference between low- and high-resolution imaging is demonstrated in Figure 5a,b. Both figures contain the total data used to interpret the U-value of the same building element—which in this case is the external wall of the living room. This is a masonry wall, a solid brick wall with a thickness of 222.5 mm and 13 mm of dense gypsum plaster.
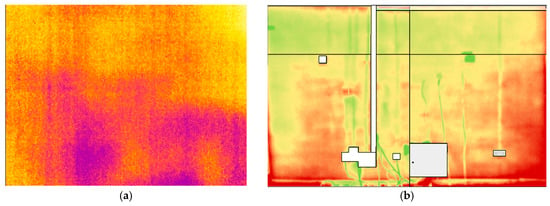
Figure 5.
(a) Low-resolution thermal image; (b) high-resolution thermal image (custom palette).
Individual pixels of all images were used to generate a pair of U-value matrices for each building element. These were then averaged to produce a mean U-value for the entire element. This process was carried out for a majority of the building elements making up the envelope of the Energy House; Figure 6 shows the resulting visualisation of U-values from the application of high-definition IRT to these building elements.
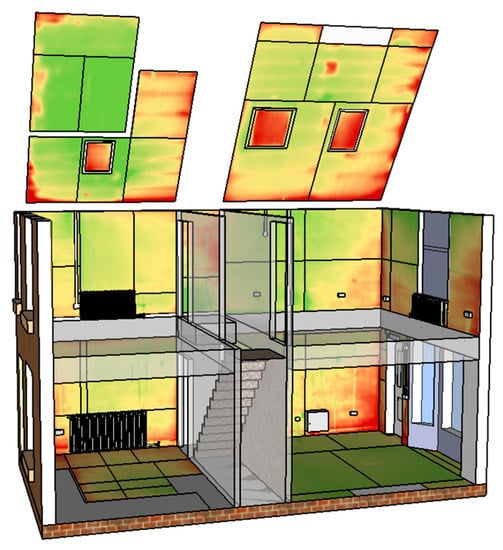
Figure 6.
Visualisation of the U-value distribution for components of the Energy House’s envelope, generated using high-resolution infrared thermography (IRT).
A comparison was made between the measured U-values (made using each of the measurement techniques) and the standardised U-values that are used in building performance assessment procedures (SAP, dynamic modelling, etc.). Table 2 lists the U-values for a solid wall construction as found in several standards; Table 3 then lists the U-values measured in situ using each of the chosen techniques. Note that for point measurements (ISO 9869-1:2014), three heat flux plates were used to measure each building element. Plates were fixed flush to the surface, using low tack tape in a vertical line. The average of all three measurements was taken for the final U-value, where data was collected for a minimum of 72 h.

Table 2.
Comparison of referenced U-values for solid walls.

Table 3.
Comparison of mean measured U-values for external walls of the energy house.
Table 2 shows a discrepancy between the assumed values of three standards; however, the greatest discrepancy is found when comparing these standard values to measured values from the Energy House. Point measurements made using ISO 9869-1:2014 provide similar U-values at all locations, with an average of 1.57 W/m2K. The same is seen for high-resolution IRT, which has an average of 1.52 W/m2K, but not for the low-resolution IRT. This results in a difference between measured and modelled U-values of up to 29%. Variation in U-value measurements also exists between the different measurement techniques. A variation of up to 25% was found to exist.
The largest variation was between two building elements of the low-resolution images and the remainder of the building elements. Low-resolution IRT was carried out without any prior heat flow information, to omit any bias toward homogeneous regions. On reflection, the location of the two higher U-values of Table 3 were from images taken within regions of higher heat flow, as indicated by the high-resolution data.
Distribution functions can be used to visualise the distribution of U-values over the surface of a building element. A normal distribution function can be applied to variables to determine the probability of its value, where the shape of the resulting distribution curve depends on the mean and standard deviation of the collected data. The total area under a distribution curve summates to a probability of 1, where each U-value is assigned a probability density at a certain point along the curve. A single value is assumed for point measurements, and so the distribution curve is simply a single line at that value, with a probability of 1. IRT returns a range of values informing U-value distributions, and so instead of a single line, a curve is produced, with varying probabilities of U-value measurement. Figure 7 shows the resulting normal distribution densities for low and high-resolution IRT, and compares these to measured and standardised U-values.
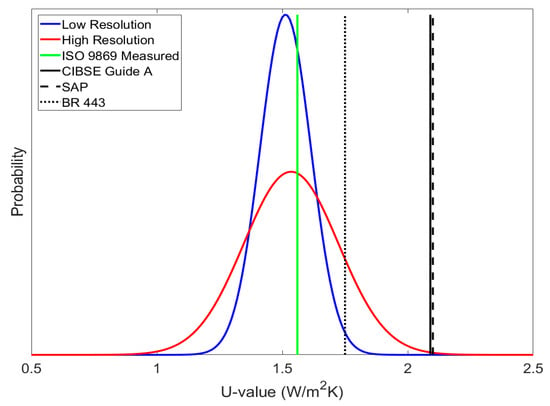
Figure 7.
Normal distribution density of U-values from IRT for the living room external wall, compared to a point measurement and standardised values.
The peaks of each distribution curve indicate the mean U-value around which they form; these mean U-values match those given in Table 3 for the living room (1.512 and 1.535 W/m2K for low and high-resolution, respectively). The shape of the curve indicates the probability of measuring a U-value on the element’s surface within the observed range. For a normal distribution, this probability peaks around the mean value, and falls away at the upper and lower boundaries. The distribution of the U-value was observed in Figure 5b; the green regions represent U-values tending toward the lower boundary, red regions represent the tendency towards the upper boundary, and the yellow/orange regions representing the most probable U-value found around the mean.
Figure 7 shows how high-resolution IRT produces a wide range of probability for U-value measurements of an element, and how low-resolution IRT and point measurements fall within this range. The implication of this is that further U-value measurements, be it point measurements or lower-resolution IRT, could fall anywhere within the wider range offered by high-resolution IRT, and that techniques collecting a reduced data sample do not fully represent the building element from which they are taken. Figure 8 shows the distributions for the master bedroom in the Energy House.
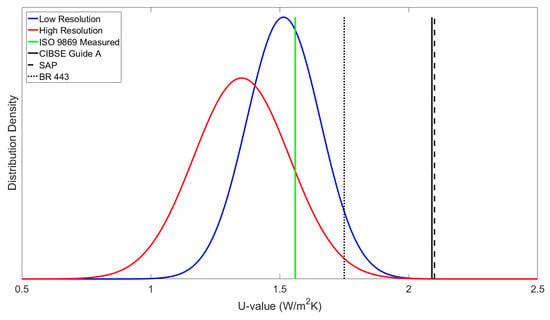
Figure 8.
Normal distribution density of U-values from IRT for the master bedroom external wall, compared to a point measurement and standardised values.
In Figure 8, the point measurement and low-resolution mean U-value still fall within the high-resolution range; however, now there is a shift towards the upper boundary. Upon review, this building element was found to have greater contrast between lower and higher U-values. Because of this, it is impractical to draw a conclusion about the mean around a single point; therefore, the distribution of U-values for this element does not follow a normal distribution. Instead, a distribution function representing a bimodal or multimodal distribution (variables with more than one mean value), can be called upon. One such function is the Epanechnikov Kernel distribution function, which was applied to the U-value data for the master bedroom, and shown in Figure 9.
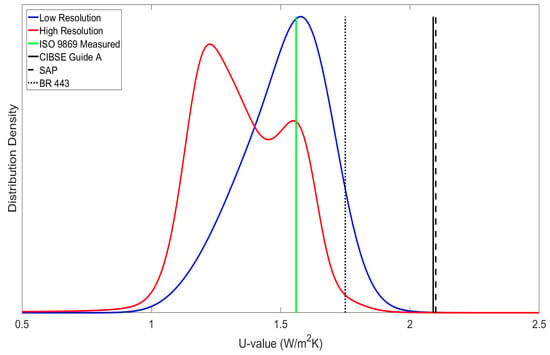
Figure 9.
Epanechnikov Kernel distribution density of U-values from IRT for the master bedroom external wall, compared to a point measurement and standardised values.
The kernel distribution identified two maxima in the distribution of the master bedroom, which relates to the contrasting heat loss through the wall. This bimodal distribution suggests that there are two prominent regions of heat loss, with a higher probability of taking lower point measurements (a mean of 1.23 W/m2K), and a lower probability of higher point measurements (1.56 W/m2K). Figure 9 indicates that the low-resolution image and the point measurements were both taken within a region with a higher U-value. This suggests that both techniques are susceptible to measurements that do not fully represent the building element. For a more realistic interpretation of U-value, the mean U-value of high-resolution IRT is proposed.
Note that kernel distribution functions are not used to represent all measurements. Only in scenarios where there is a high contrast in the U-value distribution will multi-nodal distributions occur. This was not found to be the case for low-resolution IRT in particular, nor for the majority of the high-resolution IRT; Figure 9 shows the most extreme case of bimodal U-value distribution.
Problems can arise when using these techniques in the field, where controlled conditions are not afforded and there are complications due climate conditions (e.g., moisture content and wind); in addition, occupant behaviour can occur, leading to an exaggeration of U-value heterogeneity. A wider range of probable U-values could be expected in the field due to this, meaning point measurements of the U-value receive greater probable variance. In this instance, knowledge of the full distribution of U-values can be essential.
To account for these influential factors, standardised U-values for types of building element are often overestimated [8,9,35], to cover the worst-case scenario. Under controlled conditions, the standardised U-values from BR 443, SAP and CIBSE are found towards the higher end of the U-value range; this means there is a low probability of making point measurements that match the BR 443 U-value, and a much lower probability that these measurements would match those from SAP and CIBSE. This is something which is observed for all external wall U-value measurements within the Energy House, indicating that standardised U-values can offer misinterpretation of a building’s true performance.
Poor representation of the thermal performance of a building’s fabric becomes particularly problematic when applied to predictive modelling. Accurate parameterisation of a building’s fabric is essential for carrying out dynamic energy analyses; however, standardised U-values are often called upon in modelling exercises, with SAP being a key example of this. The impact of using standardised parameters in modelling is that inaccuracy is propagated through to the predictions of those models.
The use of in-situ U-value measurements as a means of calibrating predictive models was tested by [27]. The calibration process demonstrated the possibility of improving the accuracy of predictive models to close the performance gap, a discrepancy observed between the modelled and actual performance of a building. The work in this paper suggests that further modelling accuracy could be obtained by using IRT and distribution densities, to determine U-values that more accurately represent the modelled building elements. This further addresses the measurement gap, a discrepancy between the measurement and the actual value of a variable. Although an improvement in accuracy is proposed with high-resolution IRT, U-value variation is inherently attached to the technique, and so modelling results are exposed to similar variation. A following modelling exercise investigates both accuracy and variation of modelling results, using each of the three techniques considered in this work.
3.2. Informed Modelling Results
A model of the Energy House (as described in [27]) was re-calibrated using the U-values calculated with data from each of the measurement techniques in this work. The average method from ISO 9869-1:2014 was used to calculate a U-value from heat flux density (point) measurements; data from both low and high-resolution thermal imaging were used to calculate a mean U-value around their distribution maxima. The standard deviations of each IRT data set were chosen as the upper and lower U-value range limits, which reflects the probable boundaries of successive U-value measurements using IRT on a similar building fabric. Each of the models was analysed both statically and dynamically. Static analysis was used to predict the global heat transfer coefficient (HTC) of the building, providing a comparison to the true HTC as a measure of accuracy. Dynamic analysis was used to predict annual gas consumption and fuel cost, and so demonstrate the variation in modelling results. Table 4 lists the results of static analyses, and the results of dynamic analyses are given in Table 5.

Table 4.
Static modelling results using U-values from point measurements, as well as low- and high-resolution IRT.

Table 5.
Dynamic modelling results using U-values from point measurements, as well as low- and high-resolution IRT.
Table 4 shows that all predicted HTC values are accurate; however, the closest to the measured HTC was the value predicted using the point measurements. Point measurements also offer the smallest deviation in results; superficially, this would indicate that the point measurement technique is the more favourable technique. In fact, the wide range of results found using IRT indicate that a similar variation should be expected when collecting point measurements, though this would depend on the positioning of sensors. Point measurements should not, then, be expected to offer a realistic mean U-value of a building element.
The uncertainty of results for both low- and high-resolution IRT is consistent. However, each technique offers a significantly different prediction of the HTC. Though the measured value falls within the bands of uncertainty, the variation in these results and their propagation through dynamic analysis is demonstrative of the substantial variation of the U-values that can be found in building elements, even under controlled conditions.
4. Conclusions
High-resolution IRT demonstrated a larger variation in U-values across building elements than was suggested by the reduced measurement techniques of low-resolution IRT or heat flow meter (HFM) point measurements. In some cases, high resolution IRT identified significant contrast in the heterogeneous heat flow through the Energy House building envelope, indicating that these contrasting regions can introduce bias into U-value measurements with smaller samples of data. While appearing superficially accurate, the accuracy of U-value point measurements can only be applied to surface areas exhibiting similar heat transfer properties; given the variation observed in high-resolution IRT, reduced sample measurements are then only representative of a proportion of any measured element.
Propagation of thermographic U-value measurements to informed modelling resulted in the maintenance of prediction accuracy for static analyses (HTC determination), but delivered a much lower precision. Results of dynamic simulations were then subject to a similar loss in precision and a larger variation in the prediction of those results (up to 11% variation in fuel consumption and up to 21% variation in fuel cost).
Limitations of IRT pertain to the conditions under which measurements are carried out, and also the complexity of the measured building. Measurements for this study were made in a controlled environment under quasi-steady-state conditions. Despite this, substantial U-value variation of single building elements was found when using high-resolution IRT. When transferring this technique into the field, external influences, such as solar radiation, occupancy, moisture content, etc., can have a profound impact on heat flow through a building’s envelope, the effects of which should be taken into careful consideration. This study also considered a relatively simple building with six conditioned spaces. High-resolution IRT proved to be time intensive; when larger, more complex buildings are considered, it may be more practical to resort to a more passive solution, such as the use of heat flow meters.
It is important therefore to recognize that significant variation in the U-values of building elements exists, and that this variation is propagated within predictive modelling. High-resolution IRT was identified as a technique to deliver a more representative parameterisation of building elements than point measurements; however, precision is inherently lost, and so greater variation in the prediction of building energy performance must be expected.
Two recommendations are made to further this work: investigation of the use of high-resolution IRT in the field, and the increase of data capture frequency for this technique. By considering the application of IRT under the influence of external factors, the feasibility of the technique in the field can be explored. Repeated high-resolution data capture over a period of time similar to the heat flux method could also be used. Successive revisions of the U-value distribution curves for building elements would then identify whether low-frequency data capture is sufficient, or whether variation in performance over time calls for a greater frequency of thermographic data collection.
Author Contributions
Alex Marshall conducted data analysis and wrote the paper. Johann Francou conducted the high-resolution IRT and carried out data analysis, Richard Fitton and Will Swan conceived the idea for the paper and contributed to the writing of it. Jacob Owen conducted the low-resolution IRT and carried out data analysis. Moaad Benjaber gave technical assistance in preparing and maintaining facility test conditions, and in the collection of data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- BEIS. Energy Consumption in the UK; The Department for Business, Energy and Industrial Strategy: London, UK, 2017.
- BRE. A Study of Hard to Treat Homes Using the English House Condition Survey; Defra and Energy Saving Trust: London, UK, 2008. [Google Scholar]
- SDC. ‘Stock Take’: Delivering Improvements in Existing Housing; Sustainable Development Commission: London, UK, 2006. [Google Scholar]
- BRE. BR 443 Conventions for U-Value Calculations; Building Research Establishment Press: London, UK, 2006. [Google Scholar]
- CIBSE. Guide A: Environmental Design; The Chartered Institute of Building Service Engineers: London, UK, 2006. [Google Scholar]
- ISO. BS ISO 10456:2007 Building Materials and Products, Hygrothermal Properties, Tabulated Design Values and Procedures for Determining Declared and Design Thermal Values; International Organization for Standardization: Geneva, Switzerland, 2007. [Google Scholar]
- De Wilde, P. The Gap between Predicted and Measured Energy Performance of Buildings: A Framework for Investigation. Autom. Constr. 2014, 41, 40–49. [Google Scholar] [CrossRef]
- Baker, P. U-Values and Traditional Buildings; Historic Scotland Conservation Group: Glasgow, UK, 2011. [Google Scholar]
- Rye, C.; Scott, C. The SPAB Research Report 1. U-Value Report; Society for the Protection of Ancient Buildings: London, UK, 2012. [Google Scholar]
- BRE. SAP: Standard Assessment Procedure; Building Research Establishment: London, UK, 2016. [Google Scholar]
- Stone, A.; Shipworth, D.; Biddulph, P.; Oreszczyn, T. Key Factors Determining the Energy Rating of Existing English Houses. Build. Res. Inf. 2014, 42, 725–738. [Google Scholar] [CrossRef]
- Li, F.G.; Smith, A.Z.P.; Biddulph, P.; Hamilton, I.G.; Lowe, R.; Mavrogianni, A.; Oikonomou, E.; Raslan, R.; Stamp, S.; Stone, A.; et al. Solid-wall U-values: Heat Flux Measurements Compared with Standard Assumptions. Build. Res. Inf. 2015, 43, 238–252. [Google Scholar] [CrossRef]
- Qasass, R.; Gorgolewski, M.; Ge, H. Timber Framing Factors in Toronto Residential House Construction. Archit. Sci. Rev. 2014, 57, 159–168. [Google Scholar] [CrossRef]
- Calì, D.; Osterhage, T.; Streblow, R.; Müller, D. Energy Performance Gap in Refurbished German Dwellings: Lesson Learned from a Field Test. Energy Build. 2016, 127, 1146–1158. [Google Scholar] [CrossRef]
- Lucchi, E. Thermal Transmittance of Historical Stone Masonries: A Comparison among Standard, Calculated and Measured Data. Energy Build. 2017, 151, 393–405. [Google Scholar] [CrossRef]
- Herrando, M.; Cambra, D.; Navarro, M.; de la Cruz, L.; Millán, G.; Zabalza, I. Energy Performance Certification of Faculty Buildings in Spain: The Gap between Esimated and Real Energy Consumption. Energy Conserv. Manag. 2016, 125, 141–153. [Google Scholar] [CrossRef]
- Daly, D.; Cooper, P.; Ma, Z. Understanding the Risks and Uncertainties Introduced by Common Assumptions in Energy Simulations for Australian Commercial Buildings. Energy Build. 2014, 75, 382–393. [Google Scholar] [CrossRef]
- Kennedy, M.C.; O’Hagan, A. Bayesian Calibration of Computer Models. J. R. Stat. Soc. A 2001, 63, 425–464. [Google Scholar] [CrossRef]
- Heo, Y.; Choudhary, R.; Augenbroe, G.A. Calibration of Building Energy Models for Retrofit Analysis under Uncertainty. Energy Build. 2012, 47, 550–560. [Google Scholar] [CrossRef]
- Manfren, M.; Aste, N.; Moshksar, R. Calibration and Uncertainty Analysis for Computer Models—A Meta-Model based Approach for Integrated Building Energy Simulation. Appl. Energy 2013, 103, 627–641. [Google Scholar] [CrossRef]
- Tian, W.; Yang, S.; Lu, Z.; Wei, S.; Pan, W.; Liu, Y. Identifying Informative Energy Data in Bayesian Calibration of Building Energy Models. Energy Build. 2016, 119, 363–376. [Google Scholar] [CrossRef]
- Li, Q.; Augenbroe, G.; Brown, J. Assessment of Linear Emulators in Lightweight Bayesian Calibration of Dynamic Building Energy Models for Parameter Estimation and Performance Prediction. Energy Build. 2016, 124, 194–202. [Google Scholar] [CrossRef]
- Chong, A.; Lam, K.P.; Pozzi, M.; Yang, J. Bayesian Calibration of Building Energy Models with Large Datasets. Energy Build. 2017, 154, 343–355. [Google Scholar] [CrossRef]
- Sun, J.; Reddy, T.A. Calibration of Building Energy Simulation Programs using the Analytic Optimization Approach. HVAC Res. 2006, 12, 177–196. [Google Scholar] [CrossRef]
- Pan, Y.; Huang, Z.; Wu, G. Calibrated Building Energy Simulation and its Application in a High-Rise Commercial Building in Shanghai. Energy Build. 2007, 39, 651–657. [Google Scholar] [CrossRef]
- Raftery, P.; Keane, M.; O’Donnell, J. Calibrating Whole Building Energy Models: An Evidence-Based Methodology. Energy Build. 2011, 43, 2356–2364. [Google Scholar] [CrossRef]
- Marshall, A.; Fitton, R.; Swan, W.; Farmer, D.; Johnston, D.; Benjaber, M.; Ji, Y. Domestic Building Fabric Performance: Closing the Gap between the In Situ Measured and Modelled Performance. Energy Build. 2017, 150, 307–317. [Google Scholar] [CrossRef]
- Swan, W.; Fitton, R.; Brown, P. A UK Practitioner View of Domestic Energy Performance Measurement. Proc. Inst. Civ. Eng. 2015, 168, 140–147. [Google Scholar] [CrossRef]
- ISO. BS ISO 9869-1:2014 Thermal Insulation—Building Elements—In Situ Measurement of Thermal Resistance and Thermal Transmittance—Calculation Methods; International Organization for Standardization: Geneva, Switzerland, 2014. [Google Scholar]
- Siviour, J.B.; Mcintyre, D.A. U-value Meters in Theory and Practice. Build. Serv. Eng. Res. Technol. 1982, 3, 61–69. [Google Scholar] [CrossRef]
- Mendes, N.; Winkelmann, F.C.; Lamberts, R.; Philippi, P.C. Moisture Effects on Conduction Loads. Energy Build. 2003, 35, 631–644. [Google Scholar] [CrossRef]
- Kraniotis, D.; Nore, K. Latent Heat Phenomena in Buildings and Potential Integration into Energy Balance. Procedia Environ. Sci. 2017, 38, 364–371. [Google Scholar] [CrossRef]
- Pelsmakers, S.; Fitton, R.; Biddulph, P.; Swan, W.; Croxford, B.; Stamp, S.; Calboli, F.C.F.; Shipworth, D.; Lowe, R.; Elwell, C.A. Heat-flow Variability of Suspended Timber Ground Floors: Implications for In Situ Heat-flux Measuring. Energy Build. 2017, 138, 396–405. [Google Scholar] [CrossRef][Green Version]
- Hulme, J.; Doran, S. In Situ Measurements of Wall U-Values in English Housing; Department for Energy and Climate Change: London, UK, 2014.
- Doran, S. DETR Framework Project Report: Field Investigations of the Thermal Performance of Construction Elements as Built; Building Research Establishment: London, UK, 2001. [Google Scholar]
- Lokmanhekim, M. Procedure for Determining Heating and Cooling Loads for Computerized Energy Calculations: Algorithms for Building Heat Transfer Subroutines; The American Society for Heating, Refrigerating and Air-Conditioning Engineers: New York, NY, USA, 1971. [Google Scholar]
- Ito, N. Field Experiment Study on the Convective Heat Transfer Coefficient on Exterior Surface of a Building. ASHRAE Trans. 1972, 78, 184–191. [Google Scholar]
- Sharples, S. Full-Scale Measurements of Convective Energy Losses from Exterior Building Surfaces. Build. Environ. 1984, 19, 31–39. [Google Scholar] [CrossRef]
- Nicol, K. The Energy Balance of an Exterior Window Surface, Inuvik. N.W.T., Canada. Build. Environ. 1977, 12, 215–219. [Google Scholar] [CrossRef]
- IEA (International Energy Agency). Annex 40: Commissioning of Building Heating, Ventilation and Air-Conditioning (HVAC) Systems for Improved Energy Performance; International Energy Agency: Paris, France, 2004. [Google Scholar]
- IEA (International Energy Agency). Annex 46: Holistic Assessment Tool-Kit on Energy Efficient Retrofit Measures for Government Buildings (EnERGo); International Energy Agency: Paris, France, 2010. [Google Scholar]
- Lucchi, E. Applications of the Infrared Thermography in the Energy Audit of Buildings: A Review. Renew. Sustain. Energy Rev. 2018, 82, 3077–3090. [Google Scholar] [CrossRef]
- Fokaides, P.A.; Kalogirou, S.A. Application of Infrared Thermography for the Determination of the Overall Heat Transfer Coefficient (U-Value) in Building Envelopes. Appl. Energy 2011, 88, 4358–4365. [Google Scholar] [CrossRef]
- Dall’O’, G.; Sarto, L.; Panza, A. Infrared Screening of Residential Buildings for Energy Audit Purposes: Results of a Field Test. Energies 2013, 6, 3859–3878. [Google Scholar] [CrossRef]
- Hoyano, A.; Asano, K.; Kanamaru, T. Analysis of the Sensible Heat Flux from the Exterior Surface of Buildings using Time Sequential Thermography. Atmos. Environ. 1999, 33, 3941–3951. [Google Scholar] [CrossRef]
- ISO. ISO 6781-3:2015 Performance of Buildings—Detection of Heat, Air and Moisture Irregularities in Buildings by Infrared Methods—Part 3: Qualifications of Equipment Operators, Data Analysts and Report Writers; International Organization for Standardization: Geneva, Switzerland, 2015. [Google Scholar]
- Nardi, I.; Paoletti, D.; Ambrosini, D.; de Rubeis, T.; Sfarra, S. U-value Assessment by Infrared Thermography: A Comparison of Different Calculation Methods in a Guarded Hot Box. Energy Build. 2016, 122, 211–221. [Google Scholar] [CrossRef]
- Ferreira, G.; Aranda, A.; Mainar-Toledo, M.D.; Zambrana, D. Experimental Analysis of the Infrared Thermography for the Thermal Characterization of a Building Envelope. Defect Diffus. Forum 2012, 326, 318–323. [Google Scholar] [CrossRef]
- ISO. ISO 18434-1:2008 Condition Monitoring and Diagnostics of Machines. Thermography Part 1: General Procedures; International Organization for Standardization: Geneva, Switzerland, 2008. [Google Scholar]
- Ji, Y.; Fitton, R.; Swan, W.; Webster, P. Assessing Overheating of the UK Existing Dwellings—A Case Study of Replica Victorian End Terrace House. Build. Environ. 2014, 77, 1–11. [Google Scholar] [CrossRef]
- ISO. BS EN ISO 6946:2017 Building Components and Building Elements—Thermal Resistance and Thermal Transmittance—Calculation Methods; International Organization for Standardization: Geneva, Switzerland, 2017. [Google Scholar]
- Johnston, D.; Miles-Shenton, D.; Farmer, D.; Wingfield, J. Whole House Heat Loss Test Method (Coheating); Leeds Metropolitan University: Leeds, UK, 2013. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).