Measuring and Interpreting Urban Externalities in Real-Estate Data: A Spatio-Temporal Difference-in-Differences (STDID) Estimator
Abstract
:1. Introduction
2. Measuring Urban Externalities with the Hedonic Pricing Model
2.1. The Hedonic Pricing Model
u = λWu + ε
2.2. Spatial Data Pooled over Time and Weights Matrices
ut = λSut + εt
3. Difference-in-Differences (DID) Estimator
3.1. Repeated-Sales (RS) Approach, or DID Estimator
Δyt = (αr − αs)ι + ΔXtβ + εt
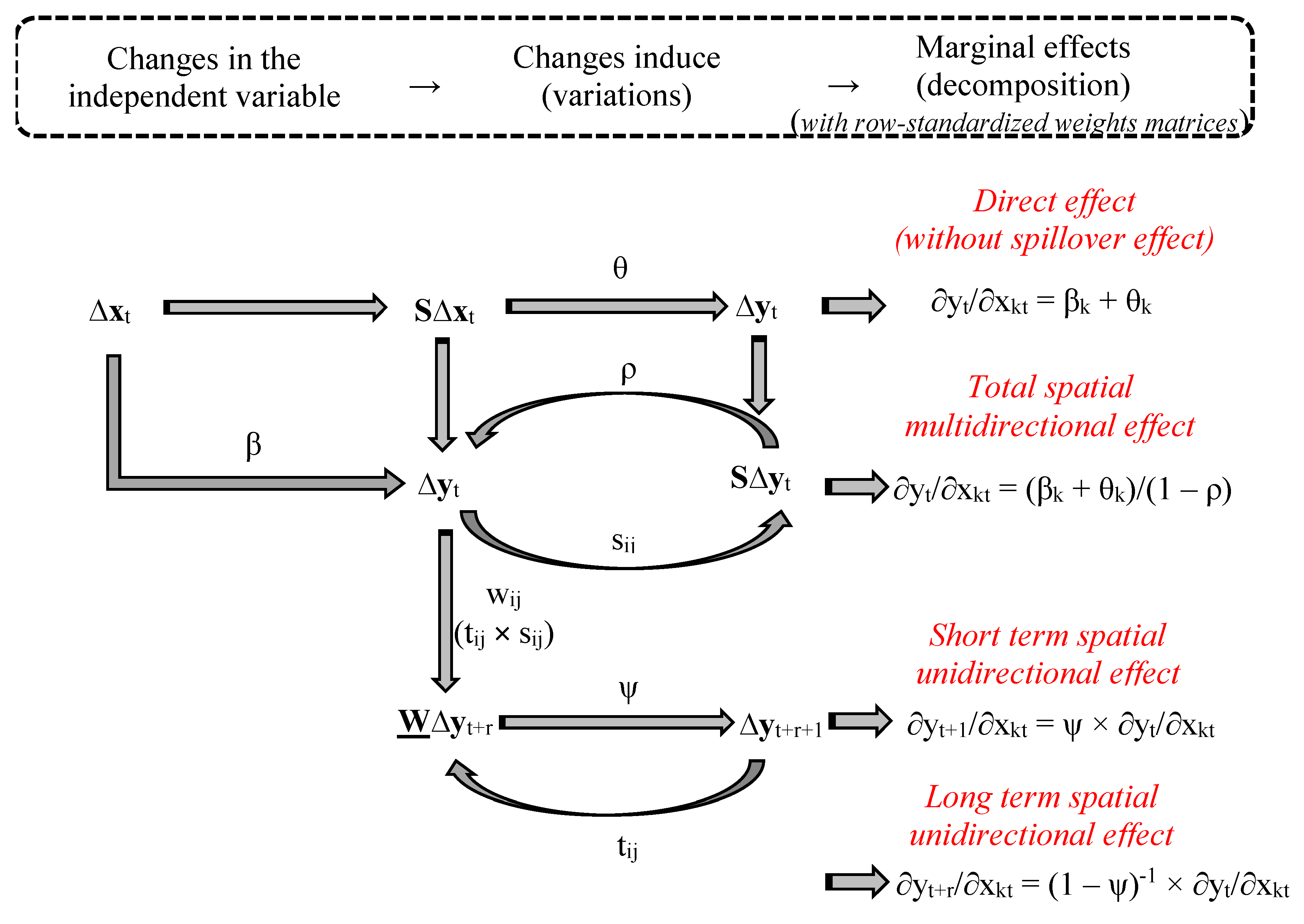
3.2. DID, SDID, STDID and Marginal Effects
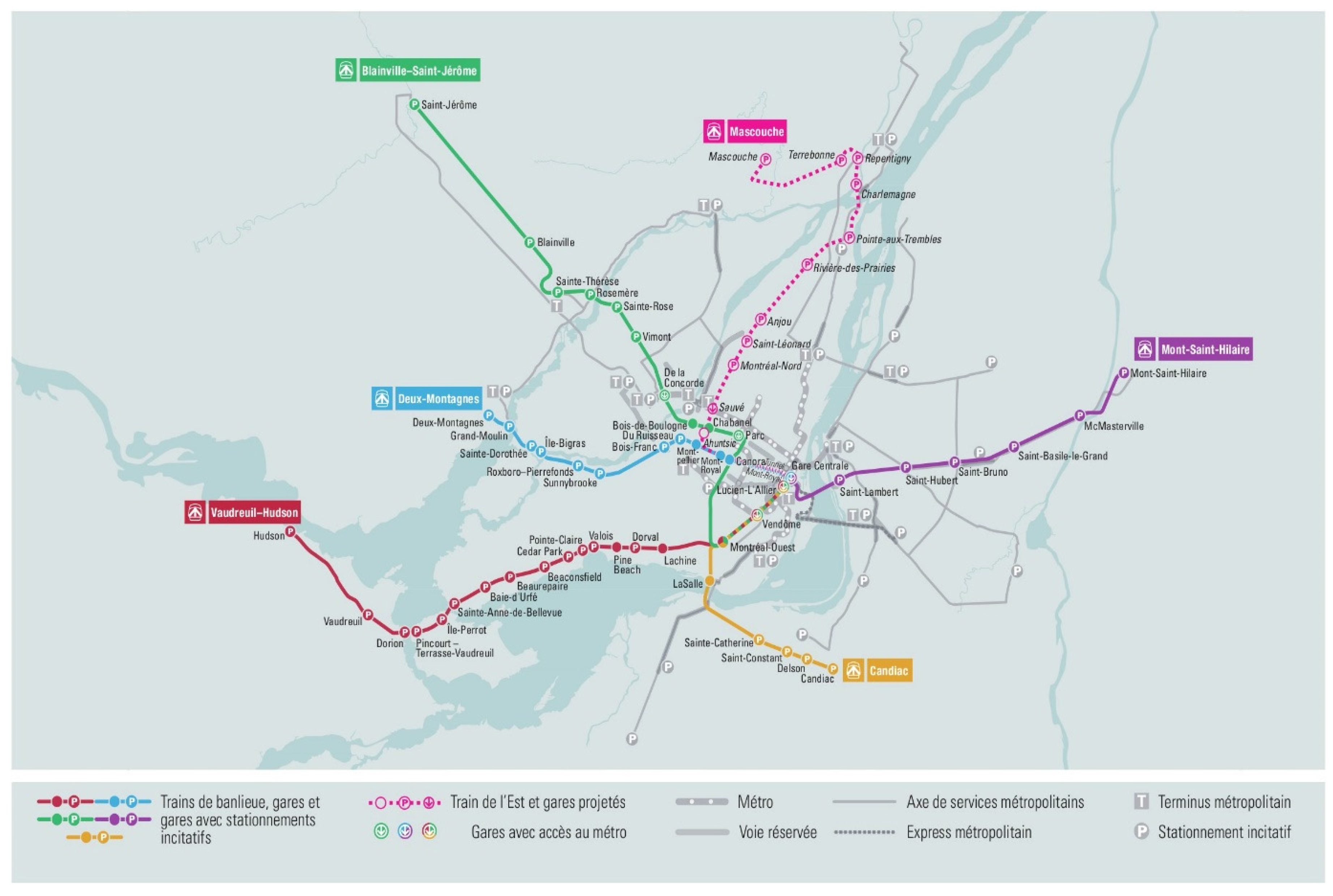
4. Empirical Investigation
4.1. Descriptive Statistics
4.2. Estimation Results
4.2.1. The South-East CRT Line
4.2.2. The North CRT Line
4.2.3. Calculating and Interpreting the Marginal Effect
4.3. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rosen, S. Hedonic Prices and Implicit Markets: Product Differentiation in Pure Competition. J. Political Econ. 1974, 82, 34–55. [Google Scholar] [CrossRef]
- Krige, D.G. Two-dimensional Weighted Moving Average Trend Surfaces for Ore Valuation. J. S. Afr. Inst. Min. Metall. 1966, 67, 13–38. [Google Scholar]
- Trigg, D.W.; Leach, A.G. Exponential Smoothing with an Adaptive Response Rate. J. Oper. Res. Soc. 1967, 18, 53–59. [Google Scholar] [CrossRef]
- Widrow, B.; Hoff, M.E. Adaptive Switching Circuits. In 1960 IRE WESCON Convention Record, Part 4; Institute of Radio Engineers: New York, NY, USA, 1960; pp. 96–104. [Google Scholar]
- Casetti, E. The Expension Method, Mathematical Modeling, and Spatial Econometrics. Int. Reg. Sci. Rev. 1997, 20, 9–33. [Google Scholar] [CrossRef]
- Casetti, E. Generating Models by Extension Method: Applications to Geographical Research. Geogr. Anal. 1972, 4, 81–91. [Google Scholar] [CrossRef]
- Cleveland, W.S.; Devlin, S.J. Locally Weighted Regression: An Approach to Regression Analysis by Local Fitting. J. Am. Stat. Assoc. 1988, 83, 596–610. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M.E. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships; Wiley: London, UK, 2002. [Google Scholar]
- Fotheringham, A.S.; Charlton, M.E.; Brunsdon, C. Geographically Weighted Regression: A Natural Evolution of the Expansion Method for Spatial Data Analysis. Environ. Plan. A 1998, 30, 1905–1927. [Google Scholar] [CrossRef]
- McMillen, D.P. One Hundred Fifty Years of Land Values in Chicago: A Nonparametric Approach. J. Urban Econ. 1996, 40, 100–124. [Google Scholar] [CrossRef]
- Ord, K. Estimation Methods for Models of Spatial Interaction. J. Am. Stat. Assoc. 1975, 70, 169–184. [Google Scholar] [CrossRef]
- Anselin, L. Spatial Econometrics: Methods and Models; Kluwer Academic: Dodrecht, The Netherlands, 1988. [Google Scholar]
- Dubin, R.A.; Pace, R.K.; Thibodeau, T.G. Spatial Autoregression Techniques for Real Estate Data. J. Real Estate Lit. 1999, 7, 79–96. [Google Scholar] [CrossRef]
- LeSage, J.P.; Pace, R.K. Advanced in Econometrics; Elsevier: Oxford, UK, 2004; Volume 18. [Google Scholar]
- Anselin, L.; Griffith, D.A. Do Spatial Effects Really Matter in Regression Analysis. Pap. Reg. Sci. Assoc. 1988, 65, 11–34. [Google Scholar] [CrossRef]
- LeSage, J.P.; Pace, R.K. Introduction to Spatial Econometrics; CRC Press: New York, NY, USA, 2009. [Google Scholar]
- LeSage, J.P. An Introduction to Spatial Econometrics. Revue D’économie Industrielle 2008, 123, 19–44. [Google Scholar] [CrossRef]
- LeSage, J.P. Pitfalls in Higher Order Model Extensions of Basic Spatial Regression Methodology. Rev. Reg. Stud. 2011, 41, 13–26. [Google Scholar]
- Overman, H.G. Making an Impact: Misreading, Misunderstanding, and Misrepresenting Research does Nothing to Improve the Quality of Public Debate Making. Environ. Plan. A 2014, 46, 2276–2282. [Google Scholar] [CrossRef]
- Corrado, L.; Fingleton, B. Where is the Economics in Spatial Econometrics? J. Reg. Sci. 2012, 52, 210–239. [Google Scholar] [CrossRef]
- Gibbons, S.; Overman, H.G. Mostly Pointless Spatial Econometrics? J. Reg. Sci. 2012, 52, 172–191. [Google Scholar] [CrossRef]
- LeSage, J.P.; Pace, R.K. The Biggest Myth in Spatial Econometrics. Econometrics 2014, 2, 217–249. [Google Scholar] [CrossRef]
- Thanos, S.; Dubé, J.; Legros, D. Putting Time into Space: Establishing the Coherence of Spatial Applications in the Housing Market. Reg. Sci. Urban Econ. 2016, 58, 78–88. [Google Scholar] [CrossRef]
- Dubé, J.; Legros, D. Spatial Econometrics Using Microdata; John Wiley & Sons: London, UK, 2014; p. 242. [Google Scholar]
- Dubé, J.; Legros, D. Dealing with Spatial Data Pooled over Time in Statistical Models. Lett. Spat. Resour. Sci. 2013, 6, 1–18. [Google Scholar] [CrossRef]
- Smith, T.E.; Wu, P. A Spatio-temporal Model of Housing Prices based on Individual Sales Transactions over Time. J. Geogr. Syst. 2009, 11, 333–355. [Google Scholar] [CrossRef]
- Pace, R.K.; Barry, R.; Clapp, J.M.; Rodriquez, M. Spatiotemporal Autoregressive Models of Neighborhood Effects. J. Real Estate Financ. Econ. 1998, 17, 15–33. [Google Scholar] [CrossRef]
- Dubé, J.; Legros, D. Spatial Econometrics and the Hedonic Pricing Model: What about the Temporal Dimension? J. Prop. Res. 2014, 31, 333–359. [Google Scholar] [CrossRef]
- Dubé, J.; Thériault, M.; Des Rosiers, F. Commuter Rail Accessibility and House Values: The Case of the Montréal South Shore, Canada, 1992–2009. Transp. Res. Part A 2013, 54, 49–66. [Google Scholar] [CrossRef]
- Dubé, J.; Des Rosiers, F.; Thériault, M.; Dib, P. Economic Impact of a Supply Change in Mass Transit in Urban Areas: A Canadian Example. Transp. Res. Part A 2011, 45, 46–62. [Google Scholar] [CrossRef]
- Dubé, J.; Legros, D.; Thériault, M.; Des Rosiers, F. A Spatial Difference-in-Differences Estimator to Evaluate the Effect of Change in Public Mass Transit Systems on House Prices. Transp. Res. Part B, 2014, 64, 24–40. [Google Scholar] [CrossRef]
- McMillen, D.P. Issues in spatial data analysis. J. Reg. Sci. 2010, 50, 119–141. [Google Scholar] [CrossRef]
- Greene, W.H. Econometric Analysis, 7th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2012. [Google Scholar]
- Wooldridge, J.M. Econometric Analysis of Cross Section and Panel Data; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Wooldridge, J.M. Introductory Econometrics: A Modern Approach; South-Western College Publishing: Cincinnati, OH, USA, 2000; p. 824. [Google Scholar]
- McMillen, D.P. Perspectives on Spatial Econometrics: Linear Smoothing with Structured Models. J. Reg. Sci. 2012, 52, 192–209. [Google Scholar] [CrossRef]
- LeSage, J.P. What Regional Scientists Need to Know about Spatial Econometrics. Rev. Reg. Stud. 2014, 44, 13–32. [Google Scholar] [CrossRef]
- Vega, S.H.; Elhorst, J.P. The SLX Model. J. Reg. Sci. 2015, 55, 339–363. [Google Scholar] [CrossRef]
- Abreu, M.; De Groot, H.L.F.; Florax, R.J.G.M. Space Growth: A Survey of Empirical Evidence Methods. Régions et Développement 2005, 21, 13–44. [Google Scholar] [CrossRef]
- Small, K.A.; Steimetz, S.S.C. Spatial Hedonics and the Willingness to Pay for Residential Amenities. J. Reg. Sci. 2012, 52, 635–647. [Google Scholar] [CrossRef]
- Steimetz, S.S.C. Spatial Multipliers in Hedonic Analysis: A Comment on “Spatial Hedonic Models of Airport Noise, Proximity, and Housing Prices”. J. Reg. Sci. 2010, 50, 995–998. [Google Scholar] [CrossRef]
- Kim, C.W.; Phipps, T.T.; Anselin, L. Measuring the Benefits of Air Quality Improvement: A Spatial Hedonic Approach. J. Environ. Econ. Manag. 2003, 45, 24–39. [Google Scholar] [CrossRef]
- Dubé, J.; Legros, D. Spatial Econometrics and Spatial Data Pooled over Time: Towards an Adapted Modelling Approach. J. Real Estate Lit. 2014, 22, 101–125. [Google Scholar]
- Dubé, J.; Legros, D. A Spatio-temporal Measure of Spatial Dependence: An Example Using Real Estate Data. Pap. Reg. Sci. 2013, 92, 19–30. [Google Scholar] [CrossRef]
- Bailey, M.J.; Muth, R.F.; Nourse, H.O. A Regression Method for Real Estate Price Index Construction. J. Am. Stat. Assoc. 1963, 58, 933–942. [Google Scholar] [CrossRef]
- Case, K.E.; Shiller, R.J. The Efficiency of the Market for Single-Family Homes. Am. Econ. Rev. 1989, 79, 125–137. [Google Scholar]
- Case, K.E.; Shiller, R.J. Prices of Single-Family Homes since 1970: New Indexes for Four Cities. N. Engl. Econ. Rev. 1987. [Google Scholar] [CrossRef]
- Clapp, J.; Giaccotto, C. Estimating Price Trends for Residential Property: A Comparison of Repeat Sale and Assessed Value Methods. J. Am. Stat. Assoc. 1992, 87, 300–306. [Google Scholar] [CrossRef]
- Ciuna, M.; De Ruggiero, M.; Salvo, F. Property Prices Index Numbers and Derived Indices. Prop. Manag. 2014, 32, 139–153. [Google Scholar]
- Heckman, J. Sample Selection Bias as a Specification Error. Econometrica 1979, 47, 153–161. [Google Scholar] [CrossRef]
- Heckman, J. The Common Structure of Statiscal Models Truncation, Sample Selection and Limited Dependent Variables and a Simple Estimator for Such Models. Ann. Econ. Soc. Meas. 1976, 5, 475–492. [Google Scholar]
- Gibbons, S.; Machin, S. Valuing School Quality, Better Transport, and Lower Crime: Evidence from House Prices. Oxf. Rev. Econ. Policy 2008, 24, 99–119. [Google Scholar] [CrossRef]
- Can, A.; Megbolugbe, I. Spatial Dependence and House Price Index Construction. J. Real Estate Financ. Econ. 1997, 14, 203–222. [Google Scholar] [CrossRef]
- Chagas, A.; Azzoni, C.; Almeida, A. A Spatial Difference-in-Differences Analysis to Measure the Sugarcane Producing Impact on Respiratory Health. In Proceedings of the European Regional Science Association, Lisbon, Portugal, 25–28 August 2015. [Google Scholar]
- Delgado, M.S.; Florax, F.J.G.M. Differnce-in-Differences Techniques for Spatial Data: Local Autocorrelation and Spatial Interaction. Econ. Lett. 2015, 137, 123–126. [Google Scholar] [CrossRef]
- Sunak, Y.; Madlener, R. Local Impact of Wind Farms on Property Values: A Spatial Difference-in-Differences Analysis. Internatl. Assoc. Energ. Econ. 2014. [Google Scholar] [CrossRef]
- Heckert, M. A Spatial Difference-in-Differences Approach to Studying the Effect of Greening Vacant Land on Property Values. Cityscape 2015, 17, 51–59. [Google Scholar]
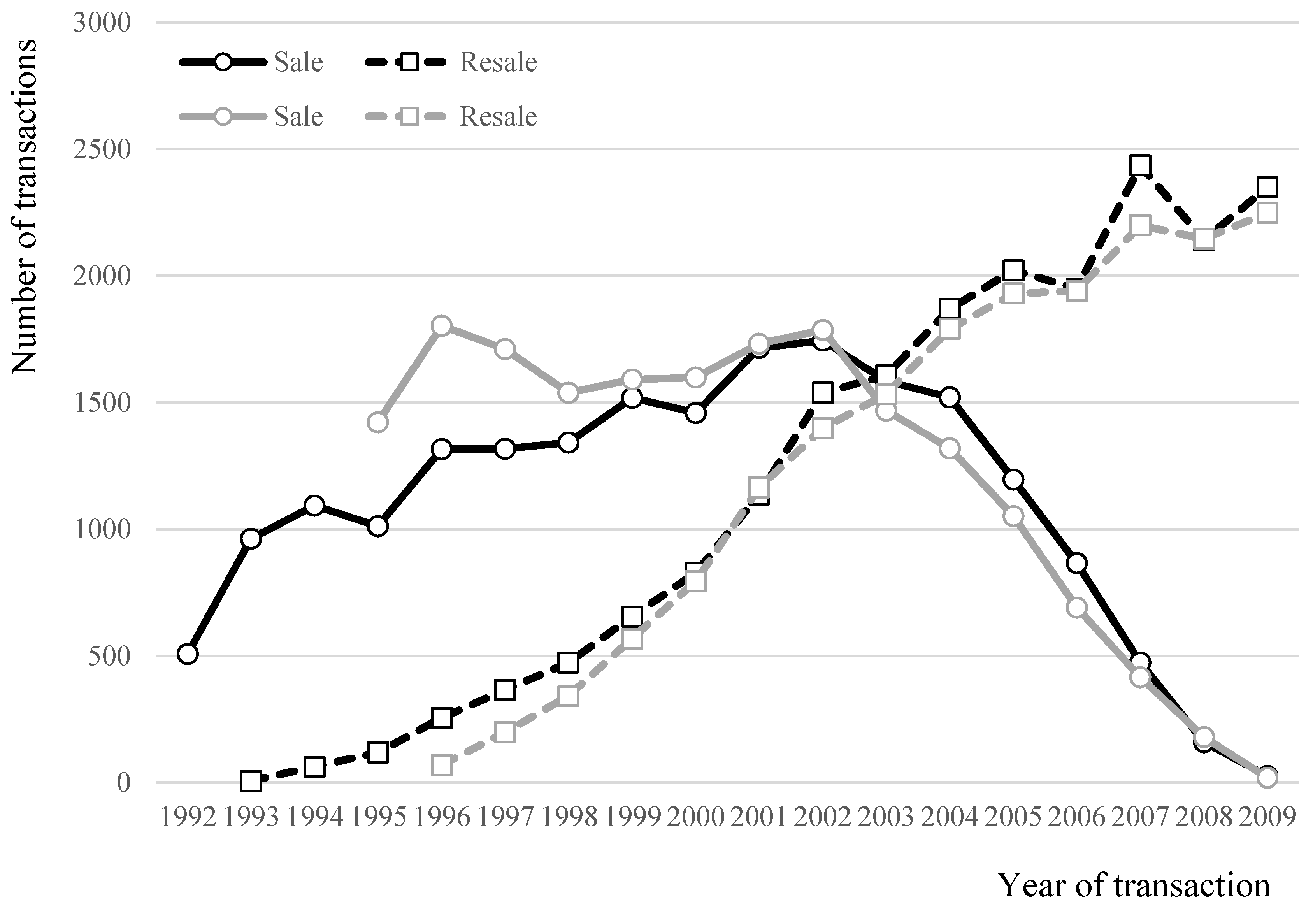

| Sale | |||||||||||||||
| Resale | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 |
| 1995 | |||||||||||||||
| 1996 | 57 | 11 | |||||||||||||
| 1997 | 117 | 68 | 13 | ||||||||||||
| 1998 | 126 | 141 | 60 | 15 | |||||||||||
| 1999 | 151 | 188 | 140 | 73 | 16 | ||||||||||
| 2000 | 149 | 200 | 193 | 151 | 87 | 15 | |||||||||
| 2001 | 160 | 212 | 226 | 198 | 204 | 143 | 22 | ||||||||
| 2002 | 136 | 204 | 188 | 220 | 252 | 209 | 161 | 28 | |||||||
| 2003 | 100 | 150 | 176 | 193 | 197 | 219 | 266 | 202 | 30 | ||||||
| 2004 | 90 | 132 | 159 | 138 | 193 | 234 | 288 | 297 | 216 | 43 | |||||
| 2005 | 82 | 123 | 139 | 147 | 178 | 190 | 257 | 298 | 257 | 217 | 42 | ||||
| 2006 | 64 | 118 | 120 | 104 | 131 | 137 | 216 | 308 | 268 | 286 | 159 | 29 | |||
| 2007 | 61 | 113 | 114 | 103 | 117 | 151 | 198 | 254 | 276 | 290 | 307 | 175 | 40 | ||
| 2008 | 70 | 75 | 96 | 103 | 120 | 162 | 149 | 192 | 227 | 248 | 297 | 230 | 146 | 31 | |
| 2009 | 58 | 67 | 87 | 93 | 95 | 139 | 175 | 206 | 194 | 235 | 246 | 257 | 229 | 148 | 19 |
| Sale | ||||||||||||||||||
| Resale | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 |
| 1992 | ||||||||||||||||||
| 1993 | 5 | 0 | ||||||||||||||||
| 1994 | 21 | 34 | 7 | |||||||||||||||
| 1995 | 32 | 56 | 29 | 1 | ||||||||||||||
| 1996 | 58 | 89 | 64 | 39 | 5 | |||||||||||||
| 1997 | 47 | 94 | 93 | 78 | 46 | 8 | ||||||||||||
| 1998 | 39 | 81 | 104 | 93 | 90 | 59 | 7 | |||||||||||
| 1999 | 39 | 79 | 119 | 89 | 138 | 111 | 69 | 11 | ||||||||||
| 2000 | 47 | 63 | 91 | 101 | 149 | 146 | 119 | 95 | 17 | |||||||||
| 2001 | 38 | 84 | 102 | 93 | 141 | 173 | 171 | 209 | 109 | 17 | ||||||||
| 2002 | 31 | 87 | 112 | 105 | 147 | 181 | 197 | 235 | 212 | 199 | 32 | |||||||
| 2003 | 43 | 64 | 81 | 74 | 125 | 114 | 163 | 198 | 217 | 264 | 216 | 48 | ||||||
| 2004 | 27 | 52 | 66 | 67 | 100 | 127 | 140 | 201 | 228 | 276 | 324 | 218 | 43 | |||||
| 2005 | 16 | 40 | 56 | 68 | 95 | 98 | 143 | 138 | 183 | 269 | 318 | 309 | 258 | 30 | ||||
| 2006 | 18 | 42 | 50 | 56 | 74 | 86 | 75 | 125 | 128 | 189 | 242 | 313 | 319 | 209 | 23 | |||
| 2007 | 20 | 40 | 48 | 51 | 91 | 78 | 112 | 109 | 168 | 188 | 247 | 284 | 362 | 369 | 228 | 40 | ||
| 2008 | 16 | 28 | 32 | 45 | 60 | 68 | 74 | 94 | 110 | 156 | 194 | 212 | 275 | 283 | 305 | 165 | 24 | |
| 2009 | 10 | 29 | 39 | 52 | 54 | 68 | 71 | 104 | 87 | 157 | 171 | 201 | 263 | 305 | 310 | 269 | 134 | 25 |
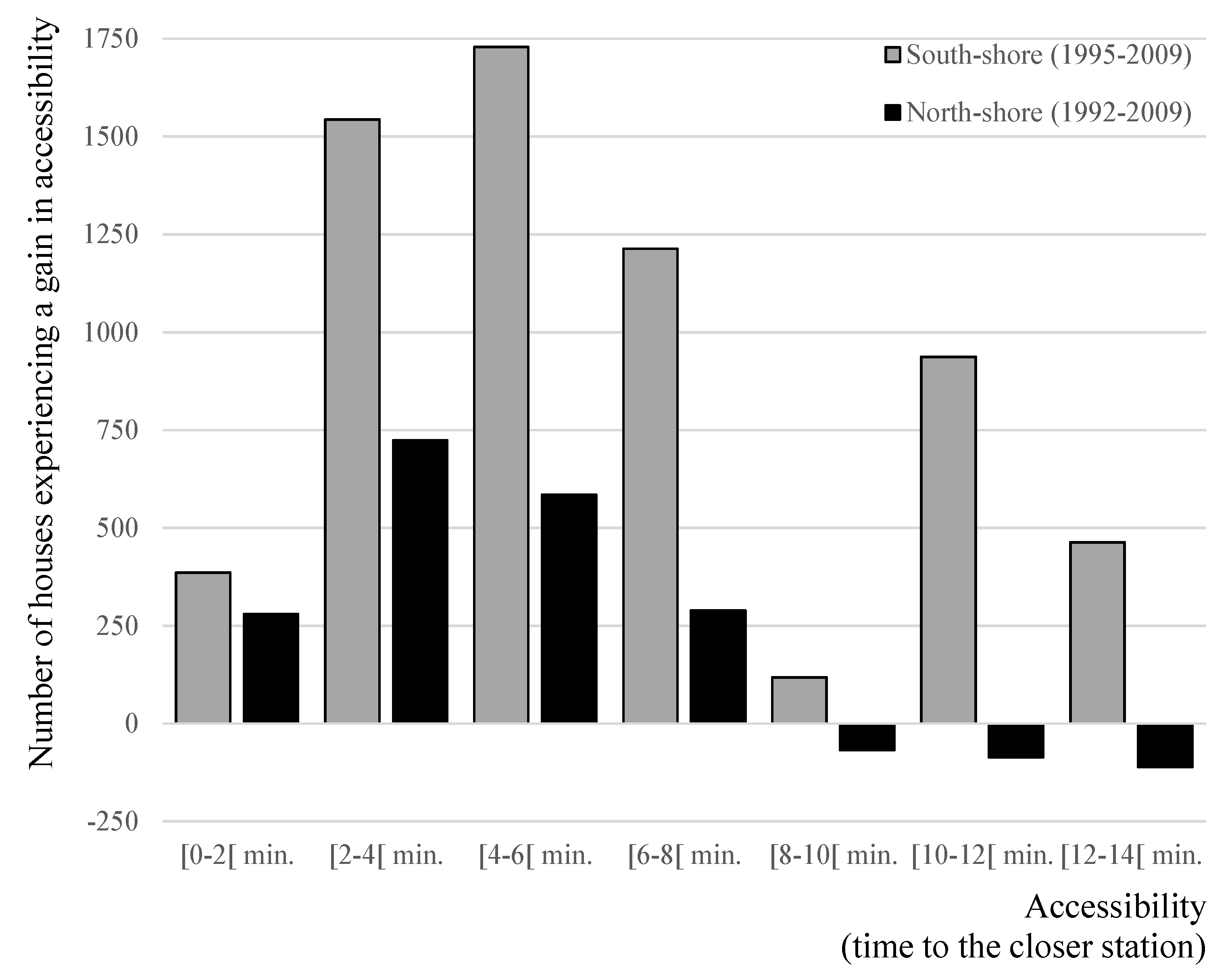
| ∆ Walking Distance | South | North |
|---|---|---|
| (0–500) m | 12 | 22 |
| (50–1000) m | 122 | 78 |
| (1000–1500) m | 424 | 198 |
| No improvement | 17,762 | 19,510 |
| Total | 18,320 | 19,808 |
| Models | DID Equation (17) | SDID Equation (19) | STDID Equation (22) | |||
|---|---|---|---|---|---|---|
| Variables | Coeff. | Sign. | Coeff. | Sign. | Coeff. | Sign. |
| ∆ Sale situation | ||||||
| Forclosure | −0.1468 | *** | −0.1473 | *** | −0.1474 | *** |
| Without legal warranty | −0.0792 | *** | −0.0778 | *** | −0.0776 | *** |
| Succession | −0.0898 | *** | −0.0824 | *** | −0.0816 | *** |
| Transfer | −0.0178 | *** | −0.0189 | *** | −0.0190 | *** |
| ∆ Walking distance | ||||||
| (0–500) m | 0.0573 | 0.0570 | 0.0578 | |||
| (500–1000) m | 0.0408 | * | 0.0379 | * | 0.0380 | * |
| (1000–1500) m | 0.0080 | 0.0076 | 0.0075 | |||
| ∆ Driving distance | ||||||
| (0–2) min. | 0.1743 | *** | 0.1773 | *** | 0.1774 | *** |
| (2–4) min. | 0.1199 | *** | 0.1179 | *** | 0.1177 | *** |
| (4–6) min. | 0.0528 | *** | 0.0517 | *** | 0.0519 | *** |
| (6–8) min. | −0.0148 | −0.0149 | −0.0145 | |||
| (8–10) min. | 0.0427 | *** | 0.0410 | ** | 0.0408 | ** |
| (10–12) min. | 0.0378 | ** | 0.0363 | 0.0361 | ||
| (12–14) min. | 0.0490 | 0.0514 | 0.0519 | |||
| (0–2) min. × distance to CBD | −0.0060 | *** | −0.0060 | *** | −0.0060 | *** |
| (2–4) min. × distance to CBD | −0.0034 | *** | −0.0033 | *** | −0.0033 | *** |
| (4–6) min. × distance to CBD | −0.0007 | * | −0.0007 | −0.0007 | ||
| (6–8) min. × distance to CBD | 0.0020 | *** | 0.0020 | *** | 0.0020 | *** |
| (8–10) min. × distance to CBD | −0.0012 | −0.0011 | −0.0011 | |||
| (10–12) min. × distance to CBD | −0.0011 | −0.0011 | −0.0010 | |||
| (12–14) min. × distance to CBD | −0.0016 | −0.0017 | −0.0017 | |||
| Temporal dummies variables | Yes | Yes | Yes | |||
| Dynamic spatial effect (ψ) | -- | -- | 0.0215 | *** | ||
| Multidirectional spatial effect (ρ) | -- | 0.0562 | *** | 0.0443 | *** | |
| R2 | 0.7371 | 0.7372 | 0.7373 | |||
| LL | 9540.08 | 9611.39 | 9619.98 | |||
| AIC | −18,920 | −19,058 | −19,074 | |||
| BIC | −18,294 | −18,417 | −18,425 | |||
| NT | 18,320 | 18,320 | 18,320 | |||
| Models | DID Equation (17) | SDID Equation (19) | STDID Equation (22) | |||
|---|---|---|---|---|---|---|
| Variables | Coeff. | Sign. | Coeff. | Sign. | Coeff. | Sign. |
| ∆ Sale situation | ||||||
| Forclosure | −0.1160 | *** | −0.1162 | *** | −0.1163 | *** |
| Without legal warranty | −0.0727 | *** | −0.0726 | *** | −0.0727 | *** |
| Succession | −0.0945 | *** | −0.0900 | *** | −0.0891 | *** |
| Transfer | −0.0177 | *** | −0.0185 | *** | −0.0186 | *** |
| ∆ Walking distance | ||||||
| (0–500) m | 0.0009 | 0.0024 | 0.0027 | |||
| (500–1000) m | −0.0182 | −0.0165 | −0.0170 | |||
| (1000–1500) m | −0.0035 | −0.0010 | −0.0009 | |||
| ∆ Driving distance | ||||||
| (0–2) min. | 0.1643 | ** | 0.1589 | *** | 0.1611 | *** |
| (2–4) min. | 0.0650 | * | 0.0633 | * | 0.0633 | * |
| (4–6) min. | 0.0431 | 0.0410 | 0.0390 | |||
| (6–8) min. | 0.0585 | 0.0553 | 0.0547 | |||
| (8–10) min. | 0.0228 | 0.0236 | 0.0230 | |||
| (10–12) min. | −0.0566 | −0.0562 | −0.0564 | |||
| (12–14) min. | 0.0018 | 0.0013 | 0.0016 | |||
| (0–2) min. × distance to CBD | −0.0026 | * | −0.0025 | ** | −0.0026 | ** |
| (2–4) min. × distance to CBD | −0.0012 | −0.0012 | −0.0012 | |||
| (4–6) min. × distance to CBD | −0.0007 | −0.0007 | −0.0006 | |||
| (6–8) min. × distance to CBD | −0.0009 | −0.0009 | −0.0009 | |||
| (8–10) min. × distance to CBD | −0.0004 | −0.0004 | −0.0004 | |||
| (10–12) min. × distance to CBD | 0,0016 | 0.0016 | * | 0.0016 | * | |
| (12–14) min. × distance to CBD | −0,0001 | −0.0001 | −0.0001 | |||
| Temporal dummies variables | Yes | Yes | Yes | |||
| Dynamic spatial effect (ψ) | -- | -- | 0.0139 | ** | ||
| Multidirectional spatial effect (ρ) | -- | 0.0342 | *** | 0.0273 | *** | |
| R2 | 0.7875 | 0.7875 | 0.7876 | |||
| LL | 13,126.78 | 13,162.83 | 13,167.93 | |||
| AIC | −26,072 | −26,140 | −26,148 | |||
| BIC | −25,353 | −25,406 | −25,406 | |||
| NT | 19,808 | 19,808 | 19,808 | |||
| Distances | [0–2[ min. ‡ | [2–4[ min. | [4–6[ min. | [6–8[ min. | [8–10[ min. |
|---|---|---|---|---|---|
| St-Lambert | |||||
| DID | 0.1445 | 0.1031 | 0.0492 | −0.0046 | 0.0368 |
| SDID | 0.1558 | 0.1073 | 0.0509 | −0.0051 | 0.0377 |
| STDID | 0.1574 | 0.1081 | 0.0517 | −0.0048 | 0.0379 |
| St-Hubert | |||||
| DID | 0.0850 | 0.0695 | 0.0419 | 0.0158 | 0.0249 |
| SDID | 0.0919 | 0.0720 | 0.0433 | 0.0162 | 0.0263 |
| STDID | 0.0929 | 0.0727 | 0.0439 | 0.0166 | 0.0265 |
| St-Bruno | |||||
| DID | 0.0553 | 0.0528 | 0.0383 | 0.0260 | 0.0190 |
| SDID | 0.0599 | 0.0544 | 0.0395 | 0.0269 | 0.0206 |
| STDID | 0.0607 | 0.0550 | 0.0400 | 0.0274 | 0.0208 |
| St-Basile-le-Grand | |||||
| DID | −0.0042 | 0.0192 | 0.0310 | 0.0464 | 0.0072 |
| SDID | −0.0041 | 0.0191 | 0.0318 | 0.0482 | 0.0091 |
| STDID | −0.0039 | 0.0196 | 0.0323 | 0.0488 | 0.0094 |
| McMasterville | |||||
| DID | −0.0340 | 0.0024 | 0.0274 | 0.0566 | 0.0013 |
| SDID | −0.0361 | 0.0015 | 0.0280 | 0.0589 | 0.0034 |
| STDID | −0.0361 | 0.0019 | 0.0284 | 0.0595 | 0.0037 |
| Mont-Saint-Hilaire | |||||
| DID | −0.0637 | −0.0144 | 0.0237 | 0.0668 | −0.0047 |
| SDID | −0.0681 | −0.0162 | 0.0242 | 0.0695 | −0.0023 |
| STDID | −0.0684 | −0.0158 | 0.0245 | 0.0702 | −0.0020 |
| Distances | [0–2[ min. ‡ | [2–4[ min. | [4–6[ min. | [6–8[ min. | [8–10[ min. |
|---|---|---|---|---|---|
| Rosemère | |||||
| DID | 0.0861 | 0.0283 | 0.0213 | 0.0302 | 0.0107 |
| SDID | 0.0864 | 0.0283 | 0.0213 | 0.0304 | 0.0106 |
| STDID | 0.0874 | 0.0285 | 0.0211 | 0.0302 | 0.0105 |
| Ste-Thérèse | |||||
| DID | 0.0731 | 0.0222 | 0.0176 | 0.0255 | 0.0086 |
| SDID | 0.0734 | 0.0221 | 0.0178 | 0.0259 | 0.0083 |
| STDID | 0.0740 | 0.0223 | 0.0178 | 0.0258 | 0.0082 |
| Blainville | |||||
| DID | 0.0601 | 0.0161 | 0.0140 | 0.0208 | 0.0066 |
| SDID | 0.0604 | 0.0159 | 0.0142 | 0.0215 | 0.0060 |
| STDID | 0.0606 | 0.0160 | 0.0146 | 0.0213 | 0.0060 |
| St-Jérôme | |||||
| DID | 0.0210 | −0.0022 | 0.0031 | 0.0067 | 0.0006 |
| SDID | 0.0213 | −0.0027 | 0.0037 | 0.0080 | −0.0009 |
| STDID | 0.0203 | −0.0027 | 0.0048 | 0.0079 | −0.0008 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dubé, J.; Legros, D.; Thériault, M.; Des Rosiers, F. Measuring and Interpreting Urban Externalities in Real-Estate Data: A Spatio-Temporal Difference-in-Differences (STDID) Estimator. Buildings 2017, 7, 51. https://doi.org/10.3390/buildings7020051
Dubé J, Legros D, Thériault M, Des Rosiers F. Measuring and Interpreting Urban Externalities in Real-Estate Data: A Spatio-Temporal Difference-in-Differences (STDID) Estimator. Buildings. 2017; 7(2):51. https://doi.org/10.3390/buildings7020051
Chicago/Turabian StyleDubé, Jean, Diègo Legros, Marius Thériault, and François Des Rosiers. 2017. "Measuring and Interpreting Urban Externalities in Real-Estate Data: A Spatio-Temporal Difference-in-Differences (STDID) Estimator" Buildings 7, no. 2: 51. https://doi.org/10.3390/buildings7020051
APA StyleDubé, J., Legros, D., Thériault, M., & Des Rosiers, F. (2017). Measuring and Interpreting Urban Externalities in Real-Estate Data: A Spatio-Temporal Difference-in-Differences (STDID) Estimator. Buildings, 7(2), 51. https://doi.org/10.3390/buildings7020051






