Using Genetic Algorithms for Real Estate Appraisals
Abstract
:1. Introduction
2. Targets and Research Design
3. A Brief Literature Review
4. Characteristics of Genetic Algorithms
- the space of solutions is complex, wide or its knowledge is very poor;
- the knowledge about a domain is poor or it is not possible to decode or restrict the space of solutions;
- traditional tools or techniques of mathematical analysis are unavailable.
- Control;
- Design;
- Simulation and identification;
- Planning;
- Classification, modelling and machine learning.
5. Case Study
- real estate rental price (monthly) expressed in euro (RERP);
- commercial area expressed in square meters (AREA);
- maintenance status (MAIN) expressed with a scores scale: 2 if the housing unit is in optimum conditions, 1 if maintenance status is good, 0 otherwise (mediocre status);
- number of floor level of housing unit (FLOOR).
- Area A: mean rental price up to € 1,700.00 (sequence: 1,0,0,0,0);
- Area B: mean rental price from € 1,700.00 to € 1,750.00 (sequence: 0,1,0,0,0);
- Area C: mean rental price from € 1,750.00 to € 1,800.00 (sequence: 0,0,1,0,0);
- Area D: mean rental price from € 1,800.00 to € 1,850.00 (sequence: 0,0,0,1,0);
- Area E: mean rental price over € 1,850.00 (sequence: 0,0,0,0,1).
- Solver: GA—Genetic Algorithm;
- Number of variables: 9;
- Population type: double vector;
- Population size: 45;
- Mutation: constraint dependent;
- Mutation: proportional scaling fitness function;
- Selection: selection function as stochastic uniform;
- Reproduction: elite count equal to 1, crossover fraction equal to 0.1;
- Crossover: heuristic function;
- Migration: both;
- Evaluate fitness and constraint functions: in serial;
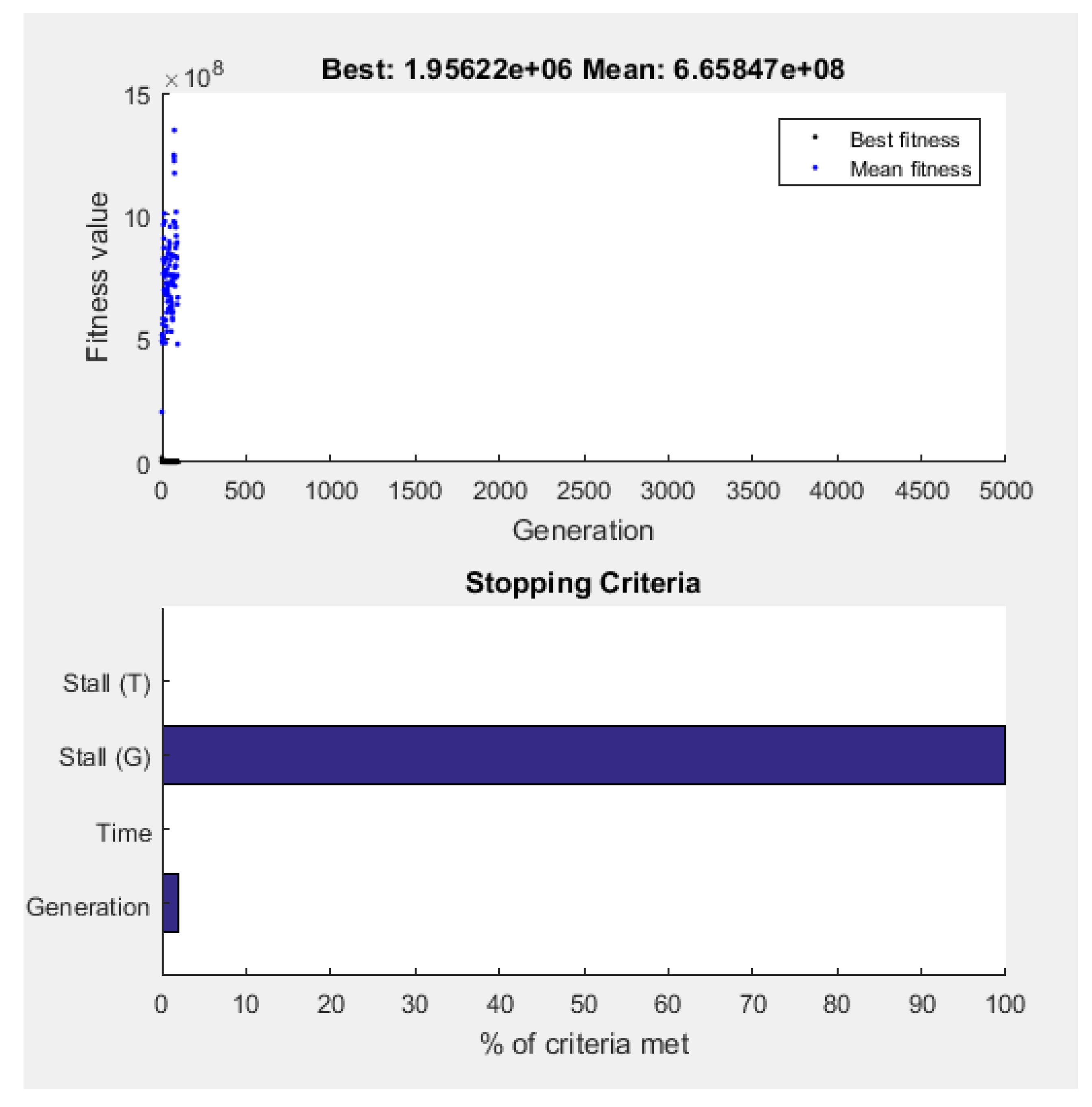
- Stopping criteria: maximum number of generations equal to 5,000;
- Plot function: best fitness, stopping.
- Variables “AREA”, “MAIN” and “FLOOR” are all positive, showing an increase in the real estate rental prices in correspondence of increasing amount of the respective real estate characteristics; this circumstance is in line with the normal dynamics of housing market;
- Housing units that fall in zones A and B are those who, according to the study previously conducted on the segmentation of real estate market for the urban area considered (which, remember, was done with a geoadditive model), have lower average prices; this fact is indirectly confirmed from data processing carried out with GA (housing units in zones A and B have the lower marginal prices);
- Housing units that fall in zone C are those who should have intermediate prices between the five different areas considered, but this circumstance is not detected in GA implementation; on the contrary, housing units in zone C have the higher marginal price;
- Housing units that fall in zones D and E are those who should have higher prices between the five different areas considered, but instead the GA implementation shows that housing units in zones D and E have negative marginal prices;
- The floor level variable (FLOOR) has an impact almost irrelevant on real estate rental prices (marginal price equal to €/month 0.90 for each additional floor level); in fact, compared to the average real estate rental price, this variable is about 0.13% in its average amount.
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Manganelli, B.; Morano, P. Estimating the market value of the building sites for homogeneous areas. Adv. Mater. Res. 2014, 869–870, 14–19. [Google Scholar]
- Manganelli, B. Real Estate Investing; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Del Giudice, V.; De Paola, P. Undivided real estate shares: Appraisal and interactions with capital markets. Appl. Mech. Mater. Trans. Tech. Pubbl. 2014, 584–586, 2522–2527. [Google Scholar] [CrossRef]
- Del Giudice, V.; De Paola, P. Spatial analysis of residential real estate rental market. In Advances in Automated Valuation Modeling; d’Amato, M., Kauko, T., Eds.; Studies in System, Decision and Control Series 86; Springer: Cham, Switzerland, 2017; pp. 155–162. [Google Scholar]
- Del Giudice, V.; De Paola, P.; Forte, F. The appraisal of office towers in bilateral monopoly’s market: Evidence from application of Newton’s physical laws to the Directional Centre of Naples. Int. J. Appl. Eng. Res. 2016, 11, 9455–9459. [Google Scholar]
- Del Giudice, V.; Evangelista, P.; De Paola, P.; Forte, F. Knowledge Management and Intellectual Capital in the Logistics Service Industry. In Proceedings of the International Conference on Knowledge Science, Engineering and Management (KSEM 2016), Passau, Germany, 5–7 October 2016. [Google Scholar]
- Del Giudice, V.; Manganelli, B.; De Paola, P. Depreciation Methods for Firm’S Assets, ICCSA 2016, Part III, Lecture Notes in Computer Science, 9788 (2016); Springer: Cham, Switzerland, 2016; pp. 214–227. [Google Scholar]
- Manganelli, B.; Del Giudice, V.; De Paola, P. Linear Programming in a Multi-Criteria Model for Real Estate Appraisal, ICCSA 2016, Part I, Lecture Notes in Computer Science, 9786 (2016); Springer: Cham, Switzerland, 2016; pp. 182–192. [Google Scholar]
- Del Giudice, V.; De Paola, P.; Manganelli, B. Spline Smoothing for Estimating Hedonic Housing Price Models, ICCSA 2015, Part III, Lecture Notes in Computer Science, 9157 (2015); Springer: Cham, Switzerland, 2015; pp. 210–219. [Google Scholar]
- Del Giudice, V.; De Paola, P. Geoadditive Models for Property Market. Appl. Mech. Mater. Trans. Tech. Pubbl. 2014, 584–586, 2505–2509. [Google Scholar] [CrossRef]
- Del Giudice, V.; De Paola, P. The effects of noise pollution produced by road traffic of Naples Beltway on residential real estate values. Appl. Mech. Mater. 2014, 587–589, 2176–2182. [Google Scholar] [CrossRef]
- Del Giudice, V.; De Paola, P.; Manganelli, B.; Forte, F. The monetary valuation of environmental externalities through the analysis of real estate prices. Sustainability 2017, 9, 229. [Google Scholar] [CrossRef]
- Del Giudice, V.; De Paola, P.; Cantisani, G.B. Rough Set Theory for real estate appraisals: An application to Directional District of Naples. Buildings 2017, 7, 12. [Google Scholar] [CrossRef]
- Tajani, F.; Morano, P.; Locurcio, M.; Torre, C.M. Data-driven techniques for mass appraisals. Applications to the residential market of the city of Bari (Italy). Int. J. Bus. Intell. Data Min. 2016, 11. [Google Scholar] [CrossRef]
- Morano, P.; Tajani, F.; Locurcio, M. GIS application and econometric analysis for the verification of the financial feasibility of roof-top wind turbines in the city of Bari (Italy). Renew. Sust. Energ. Rev. 2017, 70, 999–1010. [Google Scholar] [CrossRef]
- Morano, P.; Tajani, F. Bare ownership of residential properties: Insights on two segments of the Italian market. Int. J. Hous. Mark. Anal. 2016, 9, 376–399. [Google Scholar] [CrossRef]
- Goodman, A.C.; Thibodeau, T.G. Housing Market Segmentation. J. Hous. Econ. 1998, 7, 121–143. [Google Scholar] [CrossRef]
- Wiltshaw, D.G. A comment on methodology and valuation. J. Prop. Res. 1995, 12, 157–161. [Google Scholar]
- Ahn, J.J.; Lee, S.J.; Oh, K.J.; Kim, T.Y. Intelligent forecasting for financial time series subject to structural changes. Intell. Data Anal. 2009, 13, 151–163. [Google Scholar]
- Chen, W.S.; Du, Y.K. Using neural networks and data mining techniques for the financial distress prediction model. Expert Syst. Appl. 2009, 36, 4075–4086. [Google Scholar] [CrossRef]
- Dong, M.; Zhou, X.S. Knowledge discovery in corporate events by neural network rule extraction. Appl. Intell. 2008, 29, 129–137. [Google Scholar] [CrossRef]
- Lee, K.; Booth, D.; Alam, P. A comparison of supervised and unsupervised neural networks in predicting bankruptcy of Korean firms. Expert Syst. Appl. 2005, 29, 1–16. [Google Scholar] [CrossRef]
- Lu, C.J. Integrating independent component analysis-based denoising scheme with neural network for stock price prediction. Expert Syst. Appl. 2010, 37, 7056–7064. [Google Scholar] [CrossRef]
- Oh, K.J.; Han, I. Using change-point detection to support artificial neural networks for interest rates forecasting. Expert Syst. Appl. 2000, 19, 105–115. [Google Scholar] [CrossRef]
- Versace, M.; Bhatt, R.; Hinds, O.; Shiffer, M. Predicting the exchange traded fund DIA with a combination of genetic algorithms and neural networks. Expert Syst. Appl. 2004, 27, 417–425. [Google Scholar] [CrossRef]
- Dehghan, S.; Sattari, G.; Chehreh, C.S.; Aliabadi, M.A. Prediction of uniaxial compressive strength and modulus of elasticity for Travertine samples using regression and artificial neural networks. Min. Sci. Technol. 2010, 20, 41–46. [Google Scholar] [CrossRef]
- Hua, C. Residential construction demand forecasting using economic indicators: A comparative study of artificial neural networks and multiple regression. Constr. Manag. Econ. 1996, 14, 125–134. [Google Scholar] [CrossRef]
- Nguyen, N.; Cripps, A. Predicting Housing Value: A Comparison of Multiple Regression Analysis and Artificial Neural Networks. J. Real Estate Res. 2001, 22, 313–336. [Google Scholar]
- Worzala, E.; Lenk, M.; Silva, A. An Exploration of Neural Networks and Its Applicationto Real Estate Valuation. J. Real Estate Res. 1995, 10, 185–202. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley: Boston, MA, USA, 1989. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control and Artificial Intelligence; The MIT Press: Cambridge, MA, USA, 1975. [Google Scholar]
- Oh, K.J.; Kim, T.Y.; Min, S. Using genetic algorithm to support portfolio optimization for index fund management. Expert Syst. Appl. 2005, 28, 371–379. [Google Scholar] [CrossRef]
- Koza, J. Genetic Programming; The MIT Press: Cambridge, MA, USA, 1993. [Google Scholar]
- Wong, F.; Tan, C. Hybrid neural, genetic, and fuzzy systems. In Trading on the Edge; Deboeck, G.J., Ed.; Wiley: New York, NY, USA, 1994; pp. 243–261. [Google Scholar]
- Rechenberg, I. Evolutionsstrategie: Optimierung Technischer Systeme Nach Prinzipien der Biologischen Evolution; Frommann Holzboog: Stuttgart, Germany, 1973. [Google Scholar]
- Schwefel, H.P. Numerical Optimization of Computer Models; Wiley: New York, NY, USA, 1981. [Google Scholar]
- Fogel, L.J.; Owens, A.J.; Walsh, M.J. Artificial Intelligence through Simulated Evolution; Wiley: New York, NY, USA, 1966. [Google Scholar]
- Reed, P.; Minsker, B.S.; Goldberg, D.E. Designing a competent simple genetic algorithm for search and optimization. Water Resour. Res. 2000, 3612, 3757–3761. [Google Scholar] [CrossRef]
- Mitchell, M. An Introduction to Genetic Algorithms, 5th ed.; MIT Press: Cambridge, MA, USA; London, UK, 1999. [Google Scholar]
- Lertwachara, K. Selecting stocks using a Genetic Algorithm: A case of real estate investment trusts. Int. J. Comput. Internet Manag. 2007, 15, 20–31. [Google Scholar]
- Ahn, J.J.; Byun, H.W.; Oh, K.J.; Kim, T.Y. Using ridge regression with genetic algorithm to enhance real estate appraisal forecasting. Expert Syst. Appl. 2012, 39, 8369–8379. [Google Scholar] [CrossRef]
- Ma, H.; Chen, M.; Zhang, J. The prediction of real estate price index based on improved Neural Network Algorithm. Adv. Sci. Technol. Lett. 2015, 81, 10–15. [Google Scholar]
- Manganelli, B.; De Mare, G.; Nesticò, A. Using Genetic Algorithms in the housing market analysis. In Proceedings of the International Conference on Computational Science and Its Applications (ICCSA 2015), Banff, AB, Canada, 22–25 June 2015. [Google Scholar]
- De Mare, G.; Lenza, T.L.L.; Conte, R. Economic Evaluations using Genetic Algorithms to Determine the Territorial Impact Caused by High Speed Railways. Int. J. Soc. Educ. Econ. Manage. Eng. 2012, 6, 3313–3321. [Google Scholar]
- Nga, T.; Skitmoreb, M.; Wongc, K.F. Using genetic algorithms and linear regression analysis for private housing demand forecast. Build. Environ. 2008, 43, 1171–1184. [Google Scholar]
- Green, S.B. How many subjects does it take to do a regression analysis. Multivar. Behav. Res. 1991, 26, 499–510. [Google Scholar] [CrossRef] [PubMed]
- Marks, M.R. Two kinds of regression weights that are better than betas in crossed samples. Presented at the Meeting of the American Psychological Association, September 1966. [Google Scholar]
- Tabachnick, B.G.; Fidell, L.S. Using Multivariate Statistics, 6th ed.; Pearson: Boston, MA, USA, 2012. [Google Scholar]
- Harris, R.J.; Quade, D. The Minimally Important Difference Significant Criterion for Sample Size. J. Educ. Behav. Stat. 1992, 17, 27–49. [Google Scholar] [CrossRef]
- Schmidt, F.L. Statistical significance testing and cumulative knowledge in psychology: Implications for the training of researchers. Psychol. Methods 1996, 1, 115–129. [Google Scholar] [CrossRef]
- Harrell, F.E., Jr. Regression Modeling Strategies; Springer-Verlag: New York, NY, USA, 2001. [Google Scholar]
- Del Giudice, V. Estimo e Valutazione Economica dei Progetti; Paolo Loffredo Editore: Napoli, Italy, 2015. [Google Scholar]
- Narulaa, S.C.; Wellingtonb, J.F.; Lewisb, S.A. Valuating residential real estate using parametric programming. Eur. J. Oper. Res. 2012, 217, 120–128. [Google Scholar] [CrossRef]
- Kontrimasa, V.; Verikasb, A. The mass appraisal of the real estate by computational intelligence. Appl. Soft Comput. 2011, 11, 443–448. [Google Scholar] [CrossRef]
- Bourassa, S.C.; Cantoni, E.; Hoesli, M. Predicting house prices with spatial dependence: A comparison of alternative methods. J. Real Estate Res. 2010, 32, 139–159. [Google Scholar]
- Brooks, C.; Tsolacos, S. International evidence on the predictability of returns to securitized real estate assets: Econometric models versus neural networks. J. Prop. Res. 2003, 20, 133–155. [Google Scholar] [CrossRef]
- Chica-Olmo, J. Prediction of housing location price by a multivariate spatial method: Cokriging. J. Real Estate Res. 2007, 29, 92–114. [Google Scholar]
- Juan, Y.K.; Shin, S.G.; Perng, Y.H. Decision support for housing customization: A hybrid approach using case-based reasoning and genetic algorithm. Expert Syst. Appl. 2006, 31, 83–93. [Google Scholar] [CrossRef]
- Peterson, S.; Flanagan, A.B. Neural network hedonic pricing models in mass real estate appraisal. J. Real Estate Res. 2009, 31, 148–164. [Google Scholar]
- Rossini, P. Artificial neural networks versus multiple regression in the valuation of residential property. Aust. Land Econ. Rev. 1999, 3, 1–12. [Google Scholar]
- Wilson, I.D.; Paris, S.D.; Ware, J.A.; Jenkins, D.H. Residential property price time series forecasting with neural networks. Knowl.-Based Syst. 2002, 15, 335–341. [Google Scholar] [CrossRef]
- Del Giudice, V.; Manganelli, B.; De Paola, P. Hedonic Analysis of Housing Sales Prices with Semiparametric Methods. Int. J. Agric. Environ. Inf. Syst. 2017, 8, 65–77. [Google Scholar] [CrossRef]
- Del Giudice, V.; De Paola, P.; Cantisani, G.B. Valuation of Real Estate Investments through Fuzzy Logic. Buildings 2017, 7, 26. [Google Scholar] [CrossRef]
- Simonotti, M.; Salvo, F.; Ciuna, M.; De Ruggiero, M. Measurements of rationality for a scientific approach to the market-oriented methods. J. Real Estate Lit. 2016, 24, 403–427. [Google Scholar]
- Simonotti, M.; Salvo, F.; Ciuna, M. Multilevel methodology approach for the construction of real estate monthly index numbers. J. Real Estate Lit. 2014, 22, 281–302. [Google Scholar]
- Mahajan, R.; Kaur, G. Neural networks using genetic alghoritms. Int. J. Comput. Appl. 2013, 77, 6–11. [Google Scholar]
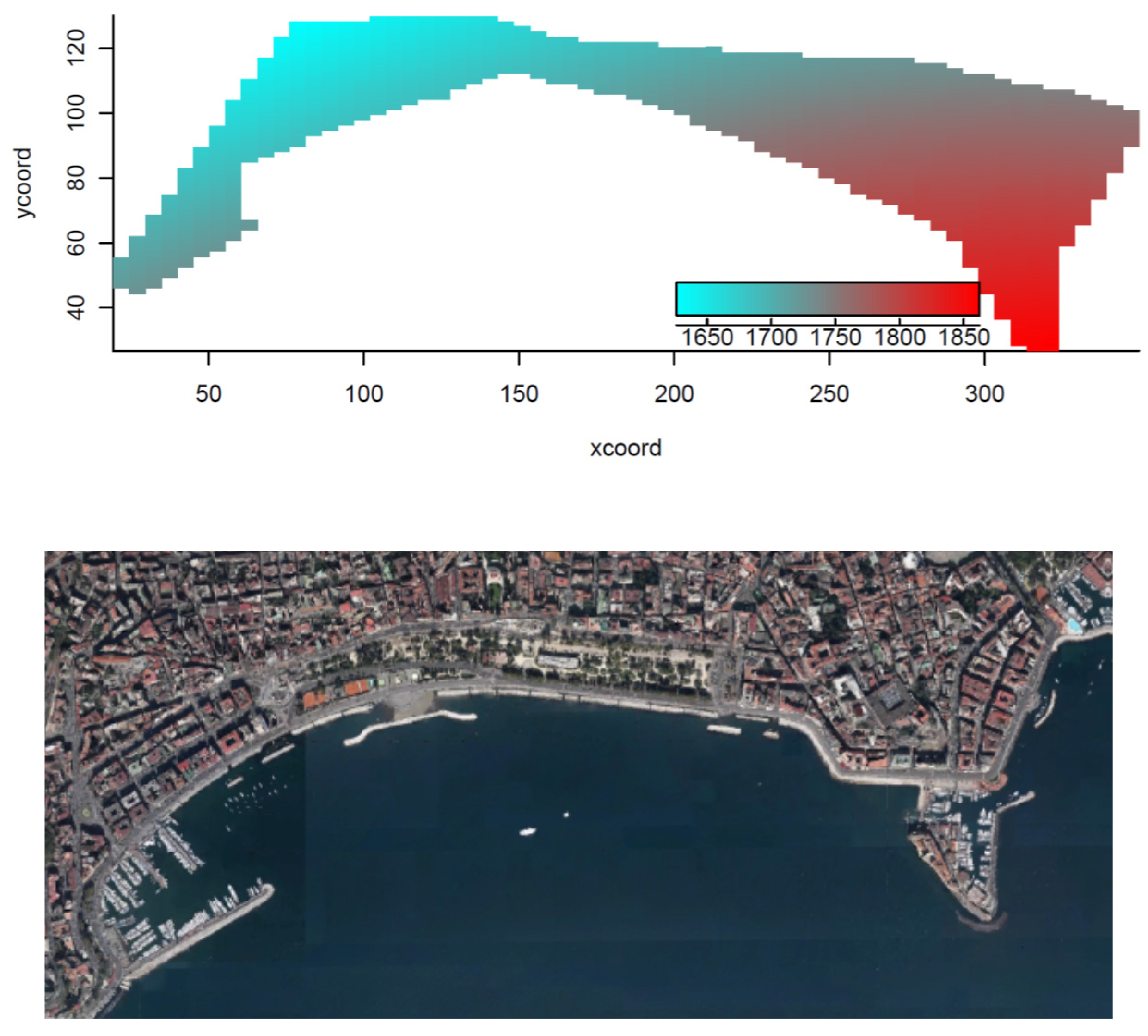
| Variable | Std. Dev. | Median | Mean | Min | Max |
|---|---|---|---|---|---|
| RERP | 6.000 | 963.51 | 1.692 | 400 | 6.000 |
| AREA | 71.29 | 100 | 122.311 | 30 | 460 |
| MAIN | 0.63 | 2 | 1.49 | 0 | 2 |
| FLOOR | 1.55 | 2 | 2.44 | 0 | 7 |
| Genetic Algoritms | ||
|---|---|---|
| b0 = −20.74 | bij | |
| Characteristics/Area | ||
| 1 | AREA | 13.21 |
| 2 | MAIN | 10.67 |
| 3 | FLOOR | 0.90 |
| 4 | A | 47.45 |
| 5 | B | 23.53 |
| 6 | C | 136.69 |
| 7 | D | −34.47 |
| 8 | E | −37.30 |
| Description | GA | MRA |
|---|---|---|
| Max overestimation (%) | 25.67% | 21.23% |
| Max underestimation (%) | 24.04% | 48.52% |
| Absolute average percentage error (%) | 10.62% | 11.50% |
| Number of overestimation in the sample (>15%) | 6 | 4 |
| Number of underestimation in the sample (<−15%) | 4 | 8 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Del Giudice, V.; De Paola, P.; Forte, F. Using Genetic Algorithms for Real Estate Appraisals. Buildings 2017, 7, 31. https://doi.org/10.3390/buildings7020031
Del Giudice V, De Paola P, Forte F. Using Genetic Algorithms for Real Estate Appraisals. Buildings. 2017; 7(2):31. https://doi.org/10.3390/buildings7020031
Chicago/Turabian StyleDel Giudice, Vincenzo, Pierfrancesco De Paola, and Fabiana Forte. 2017. "Using Genetic Algorithms for Real Estate Appraisals" Buildings 7, no. 2: 31. https://doi.org/10.3390/buildings7020031
APA StyleDel Giudice, V., De Paola, P., & Forte, F. (2017). Using Genetic Algorithms for Real Estate Appraisals. Buildings, 7(2), 31. https://doi.org/10.3390/buildings7020031







