Simulating Performance Risk for Lighting Retrofit Decisions
Abstract
:1. Introduction
2. Model Development
2.1. Model Structure
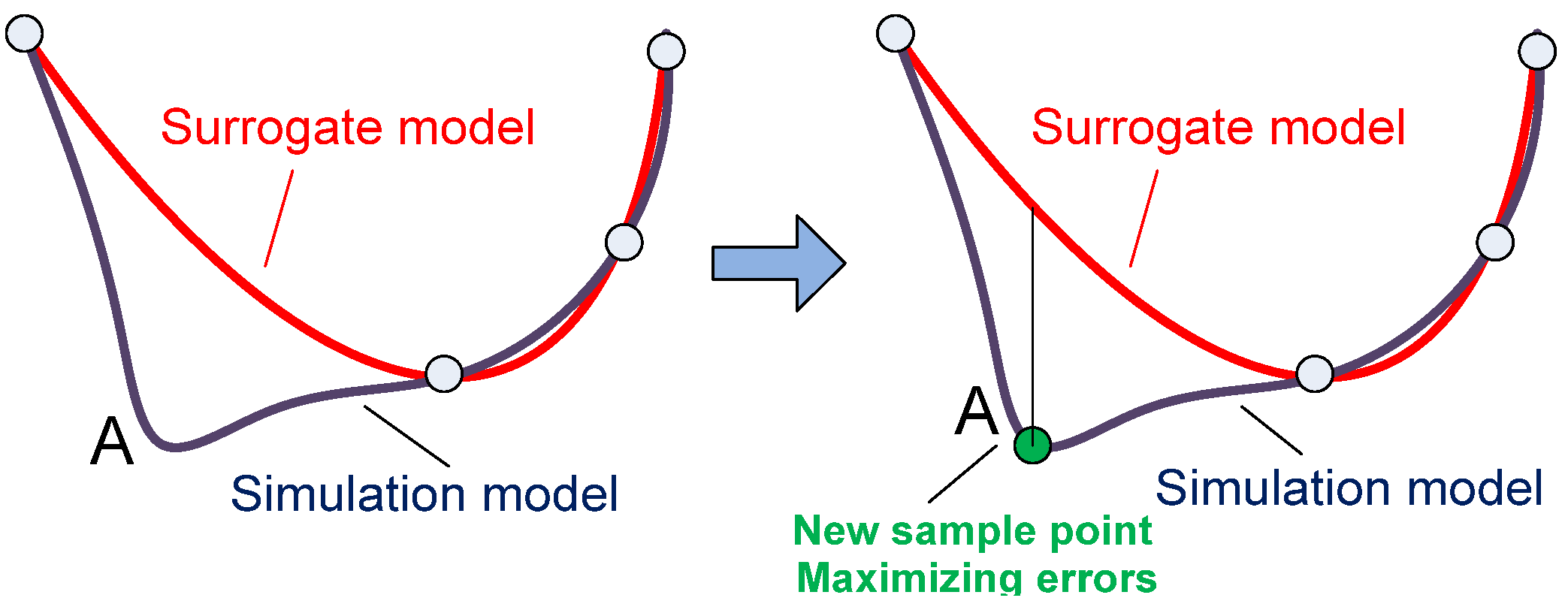
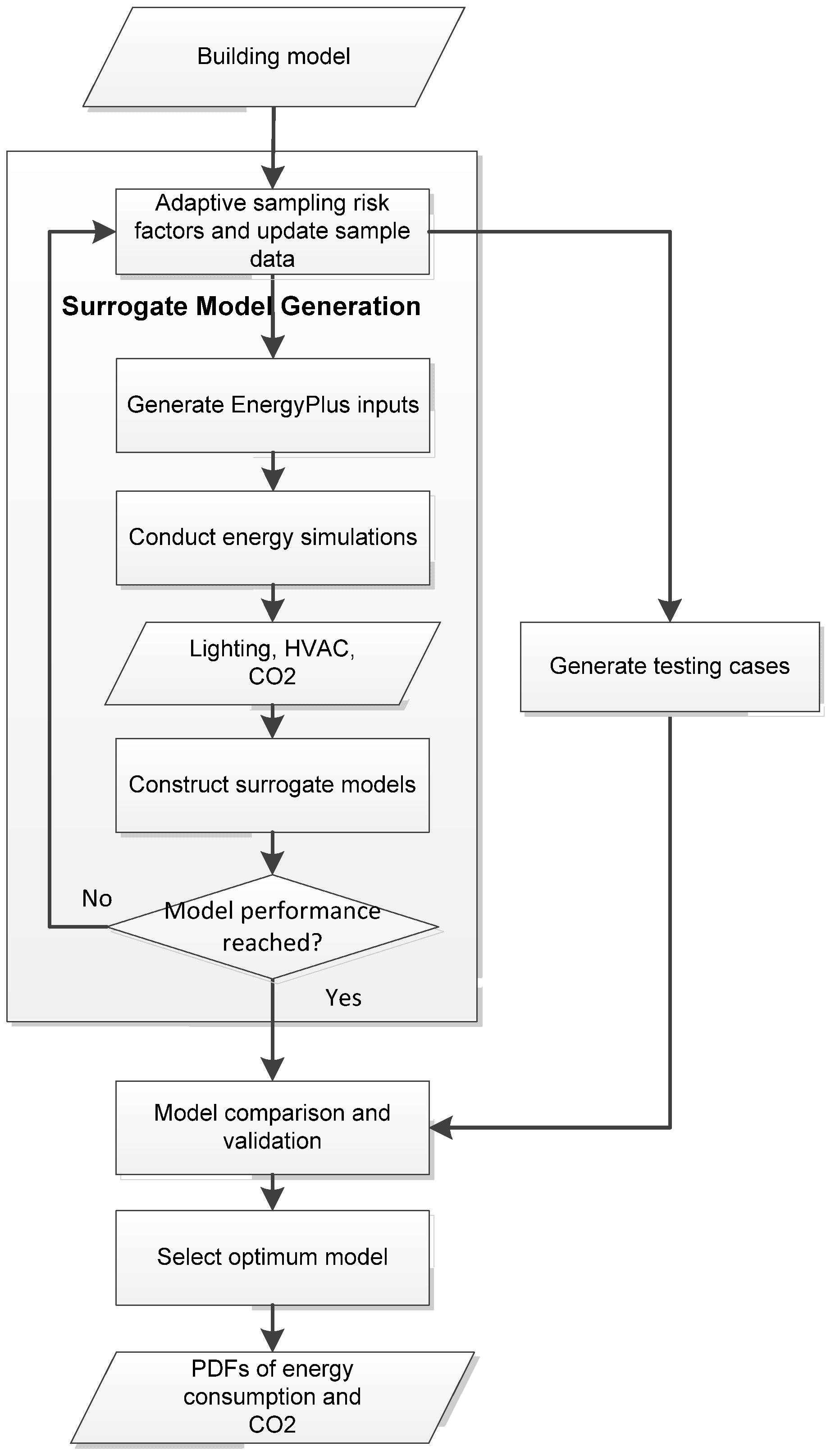
2.2. Risk Factor Sampling
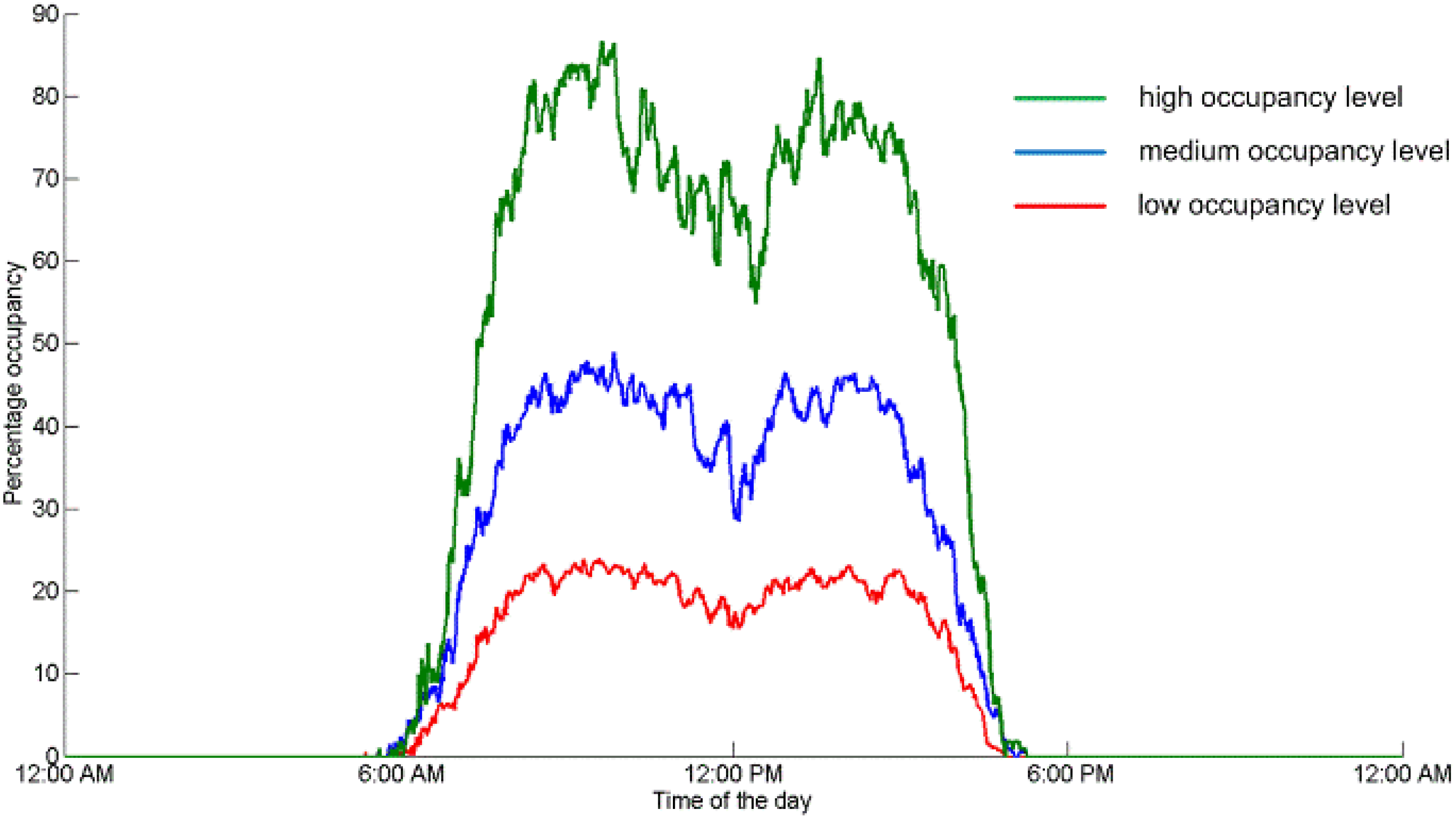
2.2.1. Occupancy Level
2.2.2. Lighting Control Strategies
- Manual Control: The lights are turned on in compliance with a pre-defined schedule. There is no automation in this process. A retrofitted building often uses this control strategy.
- Occupancy Control: This control strategy controls lighting on/off status based on the presence of occupants. In building simulation, a dynamic occupancy model can generate occupancy patterns that are used to simulate the occupant presence.
- Occupancy and Day-Lighting Control: This control strategy uses occupancy sensors to detect occupant presence and uses daylight sensors to measure daylight. Lights in perimeter zones dim in response to the daylight sensor readings. It is expected that more energy savings can be achieved while still maintaining desired luminance levels.
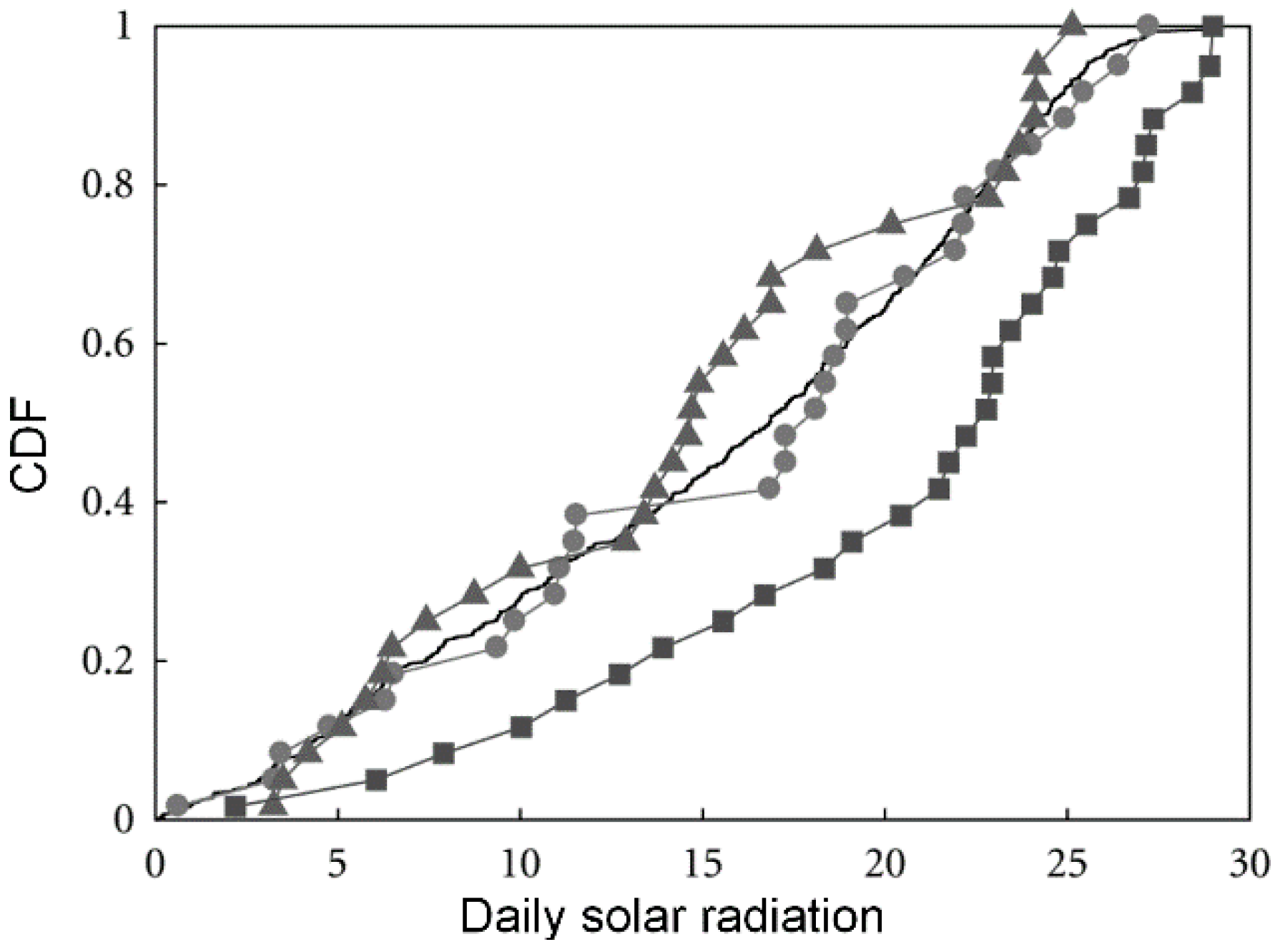
2.2.3. Weather Conditions

3. Case Study
3.1. Model Implementation
- Configuration File: This file defines the parameters of the surrogate model. For example, parameter of neural networks, and data sampling method (Latin hypercube sampling method) are used in this case study.
- Matlab Script/SUMO Tool: The tool calculates the objective function (i.e., lighting and HVAC energy consumption) from the output of EnergyPlus simulation. In the meantime, the tool calls the data generator to generate the sample for the next round simulation.
- Weather File Generator: Implemented in Python, it can dynamically produce the weather file by combing monthly actual weather data, given the probability from Matlab script.
- Occupancy Pattern Generator: Implemented in Matlab, it uses the stochastic occupancy model developed from collected office data [8].
- EnergyPlus Input File Generator: Implemented in Python, it reads risk factors, the reference building model template, and the control configuration file. The control configuration file defines the control strategy readable by EnergyPlus. The reference building model is modified from U.S. DOE reference model.
- EnergyPlus: In each iteration of the surrogate modeling process, the complete input file is fed into EnergyPlus. Parallel simulation uses a total of eight threads. The output file is processed by the SUMO tool.
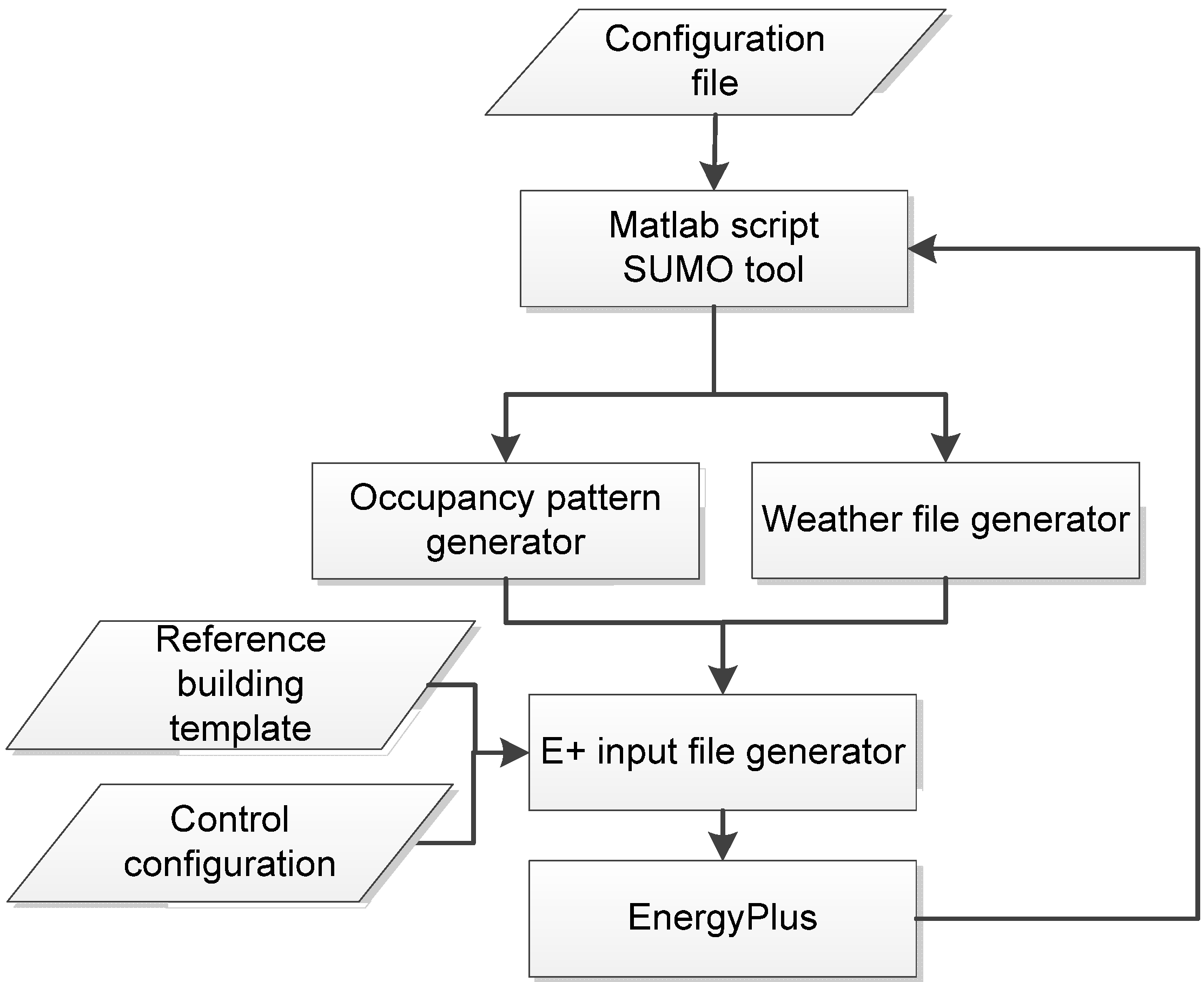
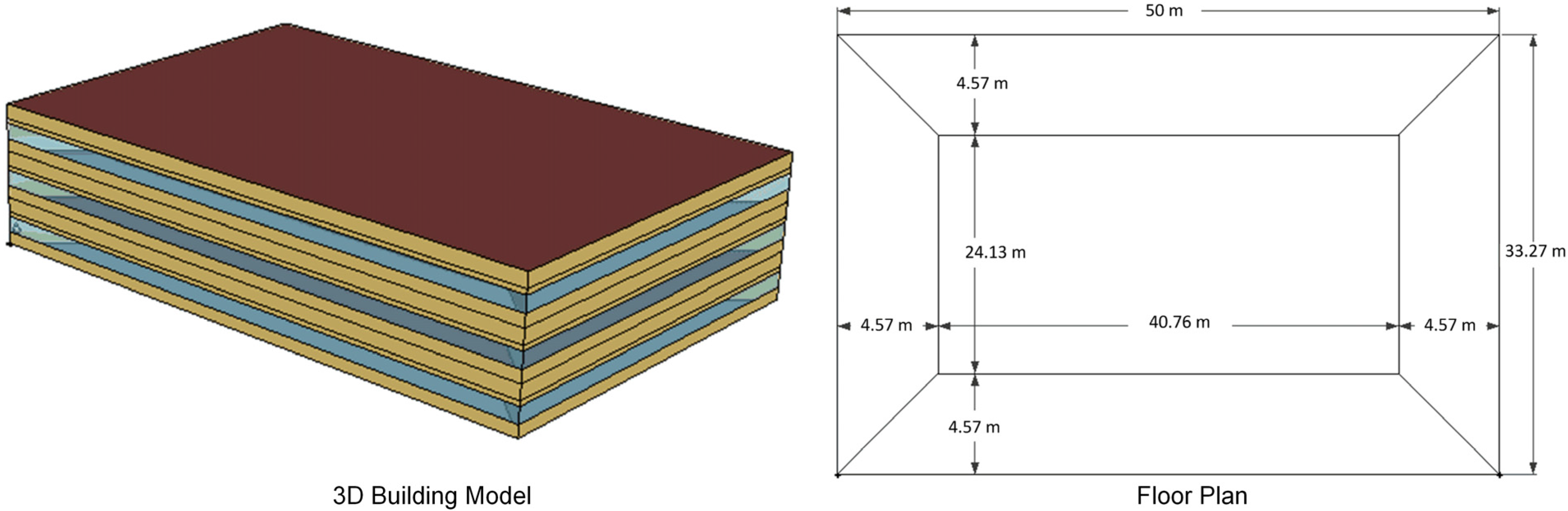
3.2. Building Model
- Envelope: The envelope thermal properties comply with ASHRAE Standard 90.1-1989 [25]. The exterior wall is set to steel frame walls. The window-to-wall ratio is set to 33.0%. The glass U-Factor is set to 3.354 W/m2-K and SHGC (Solar Heat Gain Coefficient) is set to 0.385.
- HVAC: Packaged multizone variable air volume system with plenum zones, gas furnace, and electric reheat. The fan efficiency is 0.59.
- Lighting Control: Manual control is used for the existing luminaire A. The luminaires are fully turned on when the first occupant arrives. They remain fully on until 6:30 p.m. or when the last occupant leaves the office, whichever is earlier. During the night (e.g., no occupants), a minimum of 10% of the existing luminaires are turned on. For retrofit luminaires automatic lighting control strategies are used: occupancy control, and occupancy + day-lighting control. The control information is stored in the control configuration file. During the night (e.g., no occupants), a minimum of 10% of the retrofit luminaires are turned on.
3.3. Risk Factor Sampling
- Lighting Control Strategy: Two control strategies are evaluated: occupancy control and occupancy + daylight control. Because the number of control strategies is limited (two in this case study), a surrogate model is developed for each type of control strategy and evaluated separately.
- Weather Condition: Three levels of weather and sky condition are generated: overcast (<30%), medium (30%–70%), and clear (>70%). A Gaussian distribution is used for each level with the standard deviation set to 20%. For example, when the sampled probability is 25%, then the sky condition is set to overcast. In each sample datum, the weather file generator will generate the corresponding weather file based on the probability value.
- Luminaire Input Wattage: The mean wattage is set to 11.52 W/m2 for retrofit luminaire and 13.83 W/m2 for the existing luminaire. The input wattage complies with Gaussian distribution with a standard deviation that is set to 5% of the mean value (i.e., standard deviation is set to 0.576 W/m2 for the retrofit luminaire and 0.69 W/m2 for the existing luminaire).
- Occupancy Level: The occupancy level is set to medium (e.g., mean peak occupancy level = 50% with a standard deviation of 10%), low (e.g., mean peak occupancy level = 30% with a standard deviation of 10%), or high (e.g., mean peak occupancy level = 80% with a standard deviation of 10%). Gaussian distribution is applied to each level. For example, if the occupancy level is set to medium (50%), a number of occupancy patterns are sampled using Gaussian distribution.
3.4. Results
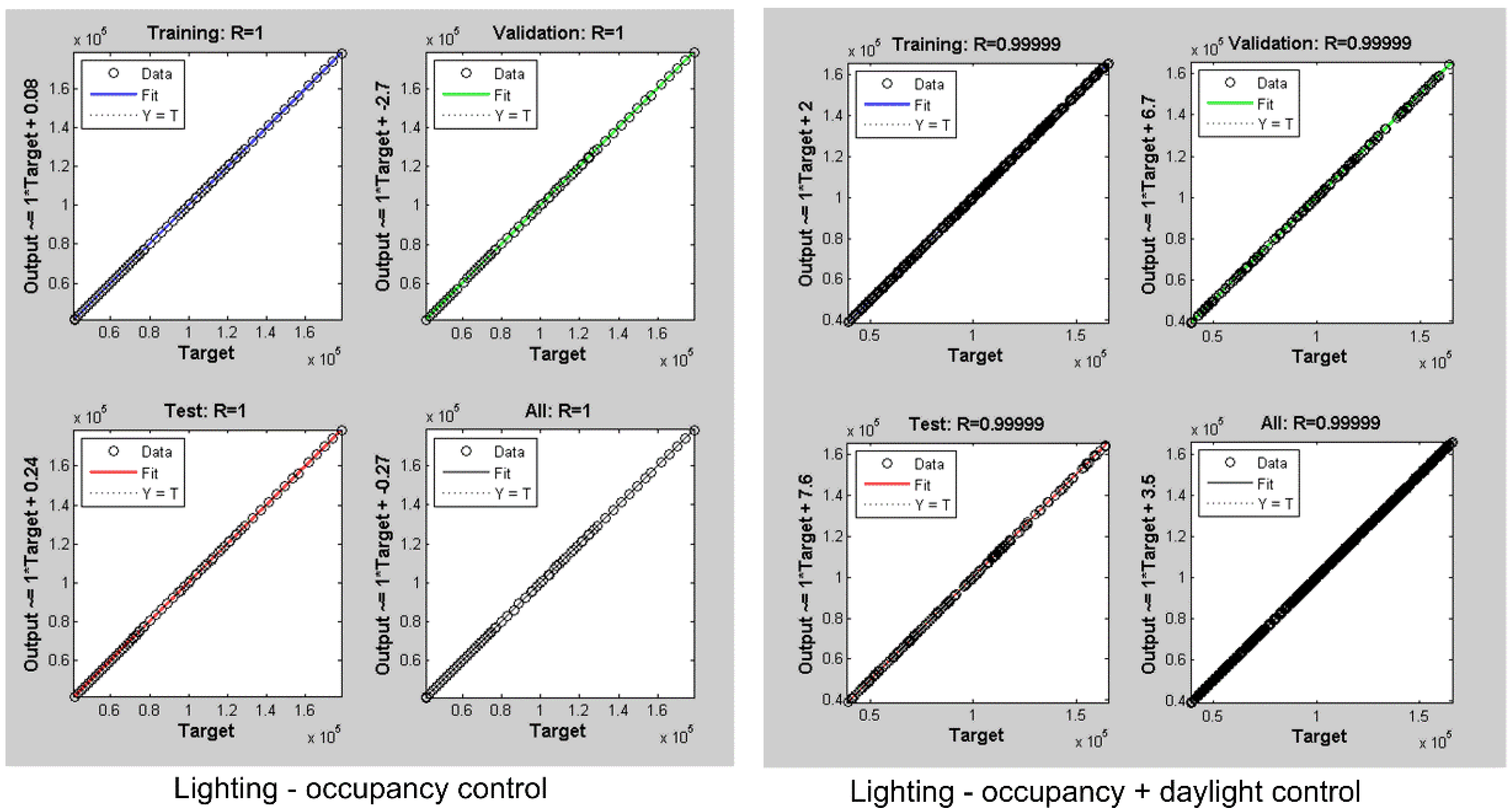
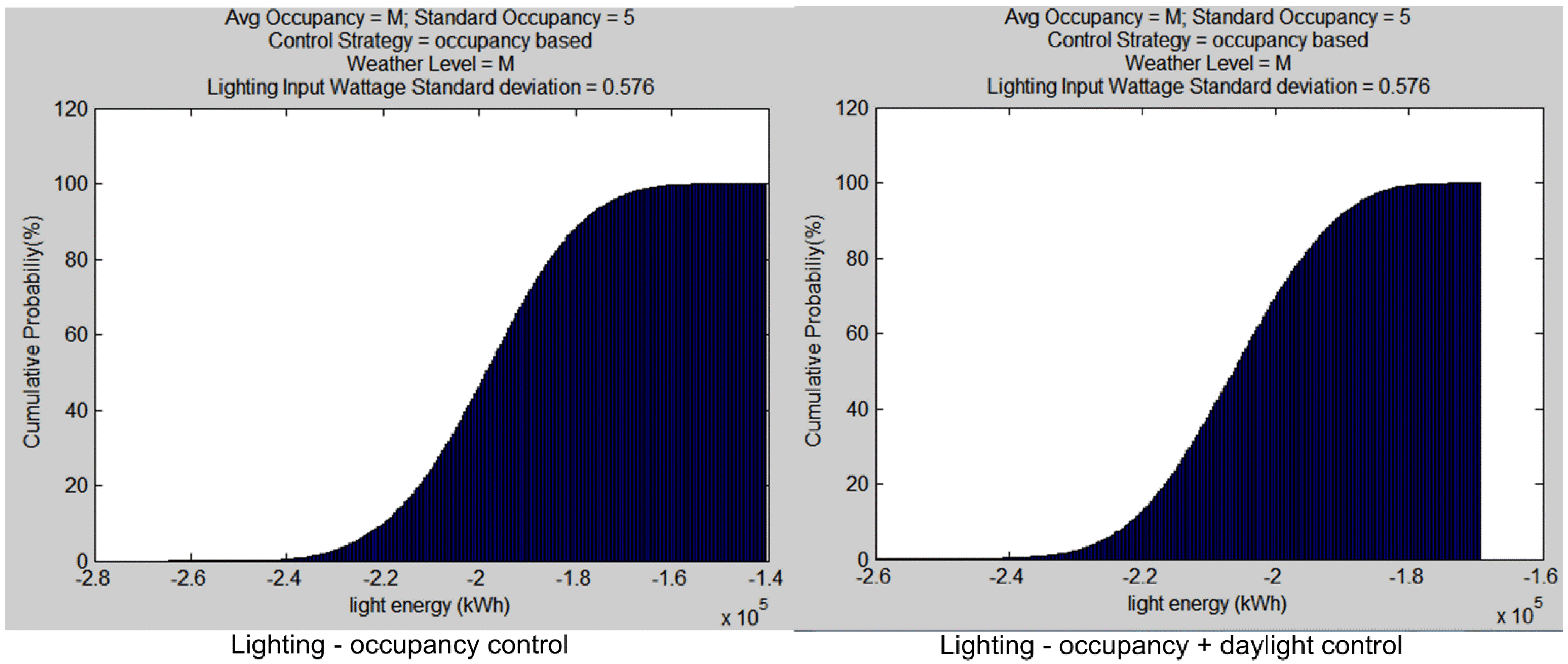
3.4.1. Lighting Energy Consumption

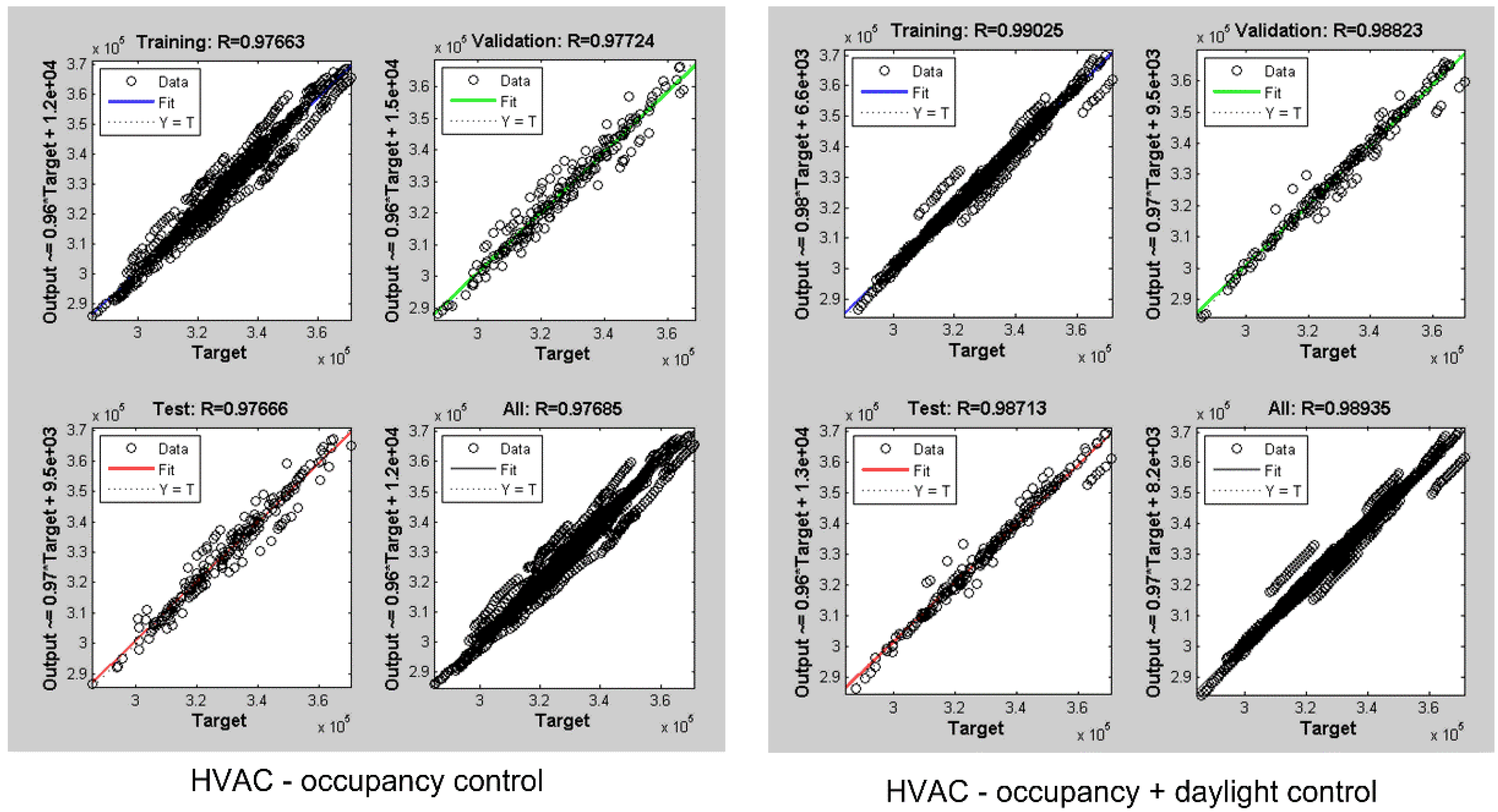
3.4.2. HVAC Energy Consumption
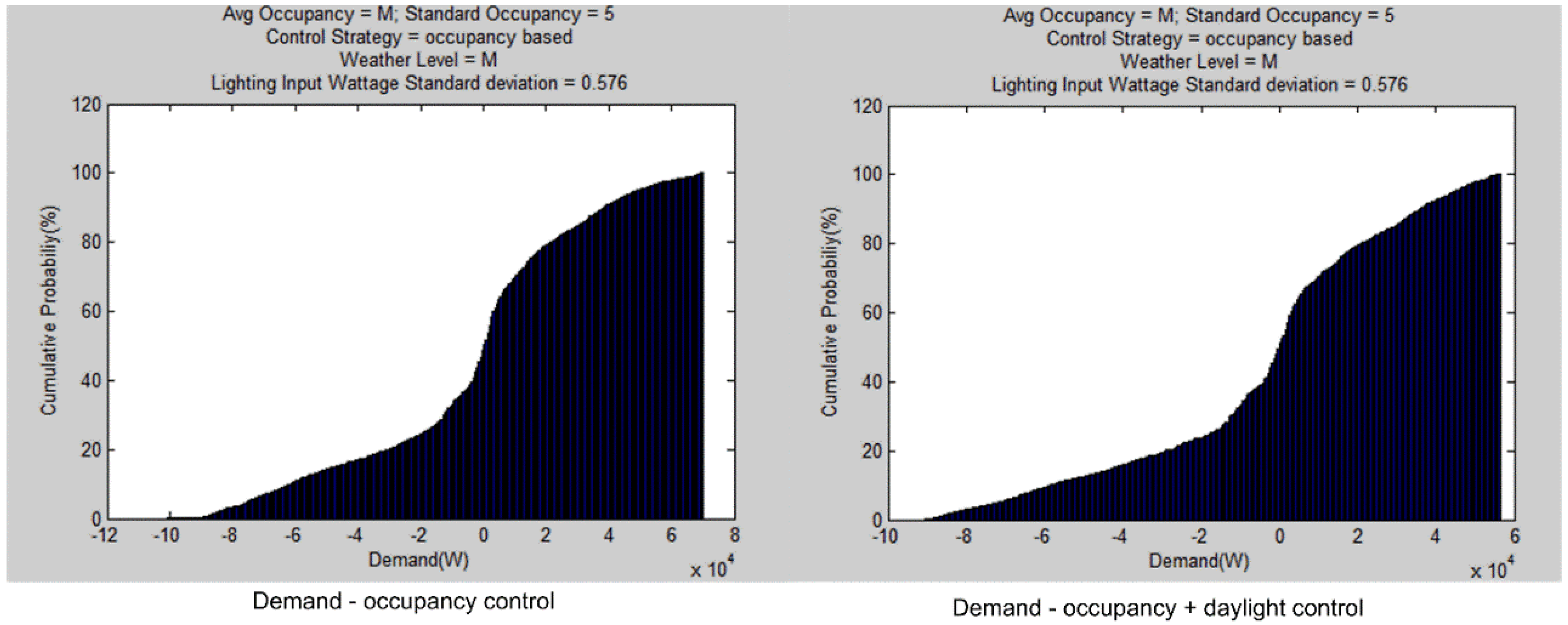
3.4.3. Electricity Demand
3.5. Discussion
- Lighting Energy Savings: Lighting has the largest energy savings. Both of the two control strategies have small standard deviation, indicating a lower risk.
- HVAC Energy Savings: HVAC energy savings is about 15% of the lighting energy savings. When the occupancy based control is used, the standard deviation is small. However, when the occupancy + daylight control is used, the standard deviation becomes much larger. This is caused by the dimming control of retrofit luminaire with a daylight control system. Thus, the risk level for HVAC energy savings becomes higher when the daylight control is used.
- Electricity Demand: The mean values for both control strategies are similar because the peak value of electricity is less sensitive to the luminaire dimming, and the peak value does not change too much even when using day-lighting control. The standard deviation is much larger. As stated in Section 3.4.3, using the retrofit luminaire with advanced lighting controls may not always reduce the electricity demand because the electricity demand of HVAC may increase. Another reason is that using an existing luminaire may generate more internal heat in winter, and help reduce the HVAC electricity demand. In a whole year, using a retrofit luminaire with advanced lighting controls can still help reduce the electricity demand by about 9 kW on average.
| Control | Lighting (MWh) | HVAC (MWh) | Demand (kW) | |||
|---|---|---|---|---|---|---|
| Occupancy | Occupancy + Daylight | Occupancy | Occupancy + Daylight | Occupancy | Occupancy + Daylight | |
| Mean | 201.5 | 208.0 | −30.6 | −31.2 | 9.3 | 9.4 |
| Standard deviation | 16.9 | 12.3 | 4.1 | 39.6 | 30.8 | 33.6 |
4. Conclusions
Acknowledgements
Author Contributions
Conflicts of Interest
References
- Heo, Y.; Choudhary, R.; Augenbroe, G.A. Calibration of building energy models for retrofit analysis under uncertainty. Energy Build. 2012, 47, 550–560. [Google Scholar] [CrossRef]
- Asadi, E.; da Silva, M.G.; Antunes, C.H.; Dias, L. Multi-objective optimization for building retrofit strategies: A model and an application. Energy Build. 2012, 44, 81. [Google Scholar] [CrossRef]
- Murray, S.N.; Walsh, B.P.; Kelliher, D.; O’Sullivan, D.T.J. Multi-variable optimization of thermal energy efficiency retrofitting of buildings using static modelling and genetic algorithms—A case study. Build. Environ. 2014, 75, 98–107. [Google Scholar] [CrossRef]
- Tian, W. A review of sensitivity analysis methods in building energy analysis. Renew. Sustain. Energy Rev. 2013, 20, 411–419. [Google Scholar] [CrossRef]
- Lam, J.C.; Wan, K.K.W.; Yang, L. Sensitivity analysis and energy conservation measures implications. Energy Convers. Manag. 2008, 49, 3170–3177. [Google Scholar] [CrossRef]
- Eisenhower, B.; O’Neill, Z.; Fonoberov, V.A.; Mezić, I. Uncertainty and sensitivity decomposition of building energy models. J. Build. Perform. Simul. 2012, 5, 171–184. [Google Scholar] [CrossRef]
- Shen, E.; Hu, J.; Patel, M. Comparison of Energy and Visual Comfort Performance of Independent and Integrated Lighting and Daylight Controls Strategies. In ACEEE Summer Study on Energy Efficiency in Industry; American Council for an Energy-Efficient Economy: New York, NY, USA, 2013. [Google Scholar]
- Shen, E.; Hu, J.; Patel, M. Energy and visual comfort analysis of lighting and daylight control strategies. Build. Environ. 2014, 78, 155–170. [Google Scholar] [CrossRef]
- Olbina, S.; Hu, J. Daylighting and thermal performance of automated split-controlled blinds. Build. Environ. 2012, 56, 127. [Google Scholar] [CrossRef]
- Reinhart, C.F.; Herkel, S. The simulation of annual daylight illuminance distributions—A state-of-the-art comparison of six RADIANCE-based methods. Energy Build. 2000, 32, 167–187. [Google Scholar] [CrossRef]
- Hu, J.; Olbina, S. Radiance-based Model for Optimal Selection of Window Systems. In Proceedings of the ASCE 2012 International Conference on Computing in Civil Engineering, Clearwater Beach, FL, USA, 17 June 2012.
- Hu, J.; Olbina, S. Simulation-based model for integrated daylighting system design. J. Comput. Civil Eng. 2013, 28. [Google Scholar] [CrossRef]
- Hu, J.; Olbina, S. Illuminance-based slat angle selection model for automated control of split blinds. Build. Environ. 2011, 46, 786–796. [Google Scholar] [CrossRef]
- Magnier, L.; Haghighat, F. Multiobjective optimization of building design using TRNSYS simulations, genetic algorithm, and artificial neural network. Build. Environ. 2010, 45, 739–746. [Google Scholar] [CrossRef]
- Hu, J.; Olbina, S. An Expert System Based on OpenStudio Platform for Evaluation of Daylighting System Design. In Proceedings of the ASCE International Workshop on Computing in Civil Engineering, Los Angeles, CA, USA, 23–25 June 2013; pp. 186–193.
- Gagne, J.M.L.; Andersen, M.; Norford, L.K. An interactive expert system for daylighting design exploration. Build. Environ. 2011, 46, 2351–2364. [Google Scholar] [CrossRef]
- Jentsch, M.F.; Bahaj, A.S.; James, P.A. Climate change future proofing of buildings—Generation and assessment of building simulation weather files. Energy Build. 2008, 40, 2148–2168. [Google Scholar] [CrossRef]
- Yun, G.Y.; Kim, H.; Kim, J.T. Effects of occupancy and lighting use patterns on lighting energy consumption. Energy Build. 2012, 46, 152–158. [Google Scholar] [CrossRef]
- Forrester, A.I.J.; Keane, A.J. Recent advances in surrogate-based optimization. Prog. Aerosp. Sci. 2009, 45, 50–79. [Google Scholar] [CrossRef]
- Neto, A.H.; Fiorelli, F.A.S. Comparison between detailed model simulation and artificial neural network for forecasting building energy consumption. Energy Build. 2008, 40, 2169–2176. [Google Scholar] [CrossRef]
- Wilcox, S.; Marion, W. Users Manual for TMY3 Data Sets; Technical Report NREL/TP-581-43156; National Renewable Energy Laboratory: Golden, CO, USA, 2008. [Google Scholar]
- Ebrahimpour, A.; Maerefat, M. A method for generation of typical meteorological year. Energy Convers. Manag. 2010, 51, 410–417. [Google Scholar] [CrossRef]
- SUMO Lab SUrrogate MOdeling (SUMO) Toolbox. Available online: http://www.sumo.intec.ugent.be/SUMO (accessed on 1 August 2013).
- U.S. Department of Energy Commericial Reference Buildings. Available online: http://energy.gov/eere/buildings/commercial-reference-buildings (accessed on 1 September 2013).
- American Society of Heating, Refrigerating and Air Conditioning, Inc (ASHREA). Energy Standard for New Buildings except Low-Rise Residential Buildings; ANSI/ASHRAE/IESNA Standard 90.1-1989; ASHREA: Atlanta, GA, USA, 1989. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, J.; Shen, E.; Gu, Y. Simulating Performance Risk for Lighting Retrofit Decisions. Buildings 2015, 5, 650-667. https://doi.org/10.3390/buildings5020650
Hu J, Shen E, Gu Y. Simulating Performance Risk for Lighting Retrofit Decisions. Buildings. 2015; 5(2):650-667. https://doi.org/10.3390/buildings5020650
Chicago/Turabian StyleHu, Jia, Eric Shen, and Yun Gu. 2015. "Simulating Performance Risk for Lighting Retrofit Decisions" Buildings 5, no. 2: 650-667. https://doi.org/10.3390/buildings5020650
APA StyleHu, J., Shen, E., & Gu, Y. (2015). Simulating Performance Risk for Lighting Retrofit Decisions. Buildings, 5(2), 650-667. https://doi.org/10.3390/buildings5020650






