Field Observation of Cooling Energy Savings Due to High-Reflectance Paints

Abstract

Cooling energy savings in a building with the roof coated with high-reflectance paint are examined. It is difficult to recognize such savings using the data observed hourly. Among the factors assumed to affect cooling energy load are: (1) internal heat generation, (2) set temperature, and (3) weather conditions. By analyzing the relationship between indoor-outdoor air temperature difference (averaged) and electric power consumption (integrated) of the air conditioner in the building over a day, the reduction in electric power consumption due to the use of a high-reflectance paint coating is estimated at approximately 72 Wh·m⁻²·day⁻¹.

1. Introduction

Nowadays, high-reflectance paint is gaining popularity in Japan for mitigating the heat island phenomenon. The method for evaluating high-reflectance paint is established in the Japanese Industrial Standards (JIS) [1,2]. Although the effect of such paint on the mitigation of the heat island phenomenon has been evaluated in many studies [3], few evaluate the cooling energy savings in a building actually coated with such paint, because such savings in a typical office or residential building with high thermal insulation performance are generally insignificant [4]. However, it cannot be ignored in a building with low thermal insulation performance, such as a factory, warehouse, or gymnasium. In this study, we analyzed the cooling energy savings due to the use of high-reflectance paint in a real building under use.

The cooling energy savings in a building brought about by the use of heat island mitigation technologies such as green wall, green roof, and high-reflectance paints have been studied by several researchers [5,6]. In these studies, the researchers conducted controlled experiments using the same two prefabricated houses without internal heat generation, to compare the difference in the energy consumption with or without heat island mitigation technologies under same weather conditions. However, building owners or managers require data on cooling energy savings caused by the high-reflectance paints in actual building sites.

Akbari et al. [7] analyzed cooling energy savings in real buildings under use in California, namely, a shop, school, and refrigerated warehouse. On the basis of the measurement results for summer, they concluded that the savings produced were 70, 42–48, and 57–81 Wh·m⁻²·day⁻¹, respectively. We have conducted similar experiments in Japan.

The introduction of high-reflectance paint to buildings without high thermal insulation performance, such as factories, warehouses, and gymnasia, is one of the energy saving measures. During implementation, it is necessary to analyze the effect of introducing the high-reflectance paint. In this study, we analyzed the cooling energy savings produced in a real building based on energy measurements.

2. Outline of Building and Measurement Case Study

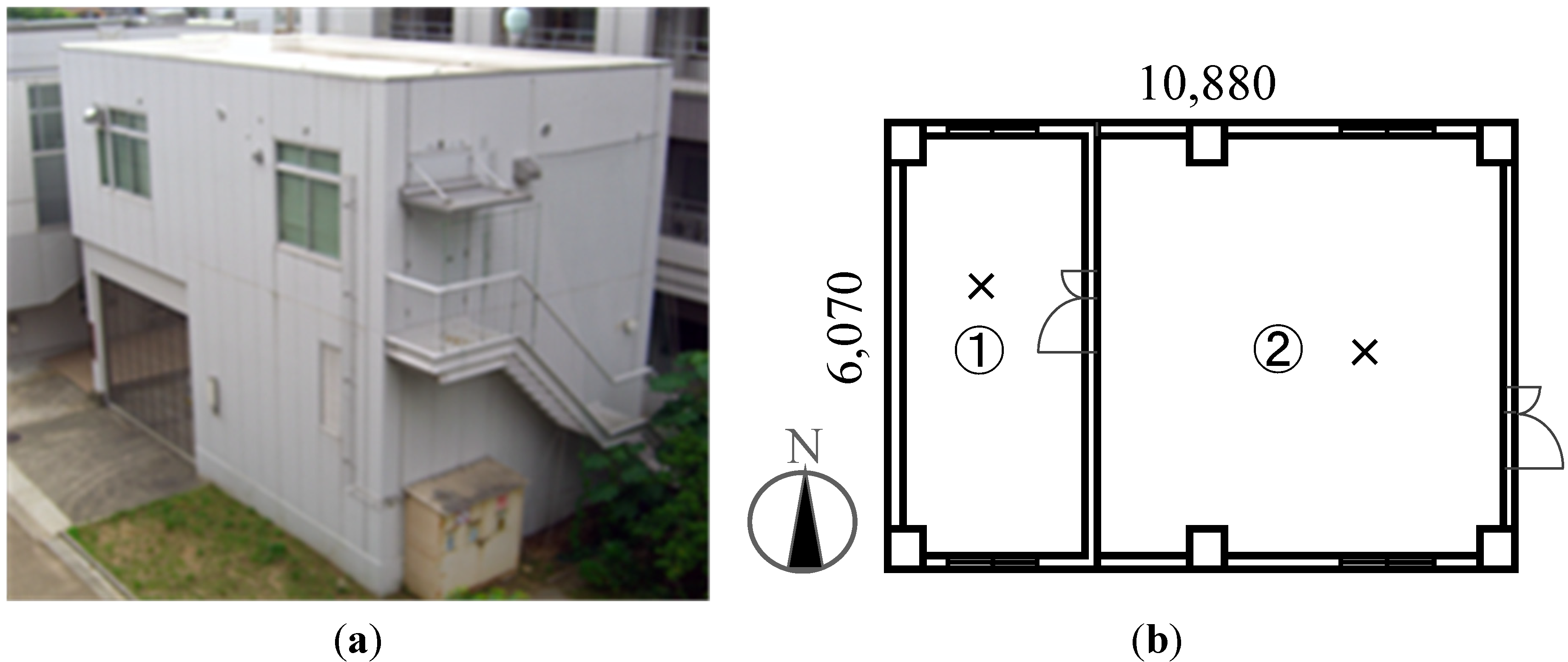
General office buildings have relatively higher ratio of window area and smaller ratio of roof area to the total envelope surface area. Moreover, they have significant internal heat generated from the appliances used in them, and so on. Therefore, the ratio of the cooling load owing to heat conduction from the roof to the total cooling load is low. In this study, the test building is a small (60 m²) two-story research building (with its first floor raised on pilotis) at Kobe University (see Figure 1 and Table 1). The test building is expected to offer significant potential for achieving cooling energy savings by deploying high-reflectance paint, owing to its small window area (15%) and large roof area (25%–30%) ratios to the total envelope surface area.

Figure 1. (a) Facade and (b) Plan (second floor) of test building (x: Measurement point in Figure 2).

Figure 1. (a) Facade and (b) Plan (second floor) of test building (x: Measurement point in Figure 2).

Table 1. Characteristics of objective rooms.

Room	Roof-to-Envelope Ratio	Wall-to-Envelope Ratio	Window-to-Envelope Ratio	Set Temperature
Room 1	20.7%	38.2%	5.3%	26 °C before 15:00, 8 August 2011 25 °C after 15:00, 8 August 2011 25 °C through 2012
Room 2	24.9%	36.8%	4.1%

Table 1. Characteristics of objective rooms.

Room	Roof-to-Envelope Ratio	Wall-to-Envelope Ratio	Window-to-Envelope Ratio	Set Temperature
Room 1	20.7%	38.2%	5.3%	26 °C before 15:00, 8 August 2011 25 °C after 15:00, 8 August 2011 25 °C through 2012
Room 2	24.9%	36.8%	4.1%

The experiment was conducted in rooms 1 and 2. The air conditioners in both rooms were continuously running for 24 h. The roof consists of a concrete slab (with 100 mm thickness) above the suspended ceiling (with 700 mm depth and 2730 mm height from the floor) without any heat insulating material. We measured the below and above surface temperatures of the slab and suspended ceiling, room temperature (at 1200 mm height), and power consumption of the air conditioners. The cross section of the point of measurement of temperature is shown in Figure 2. Waterproof membrane was installed on the slab. To avoid the influence of insolation, the roof surface temperature was measured using an infrared thermometer and those of the other elements were measured using a thermistor thermometer. The certificate cooling capacities of the air conditioners in rooms 1 and 2 are 7.1 and 14.5 kW, respectively. The power consumption was measured using a clamp-type power meter (HIOKI3168-98) at the power distribution panel. We obtained the temperature and power data at one-minute intervals, and averaged the temperature values and integrated the power consumption values over 10 min.

Figure 2. Cross section of temperature measurement points.

Figure 2. Cross section of temperature measurement points.

We conducted measurements for the periods, 12 July–26 September 2011 and 12 July–26 September 2012. High-reflectance paint was introduced on 2 August 2011. The cooling energy savings were evaluated by comparing the measurements before and after painting. The amount of horizontal solar radiation and average air temperature on typical summer days in Kobe are about 24–28 MJ·m⁻²·day⁻¹ and about 28 to 32 °C, respectively. The albedo of the objective paint is 86.9% (300–2500 nm wavelength according to JIS K 5602 [1]). The albedo measured by the pyranometer (which comprises white and black boards and measures solar radiation) was 16.9% before, 86.9% immediately after, and 76.1% after one year, of painting [8]. These are averaged values of the measurement results at three points on the roof surface (east, middle, and west).

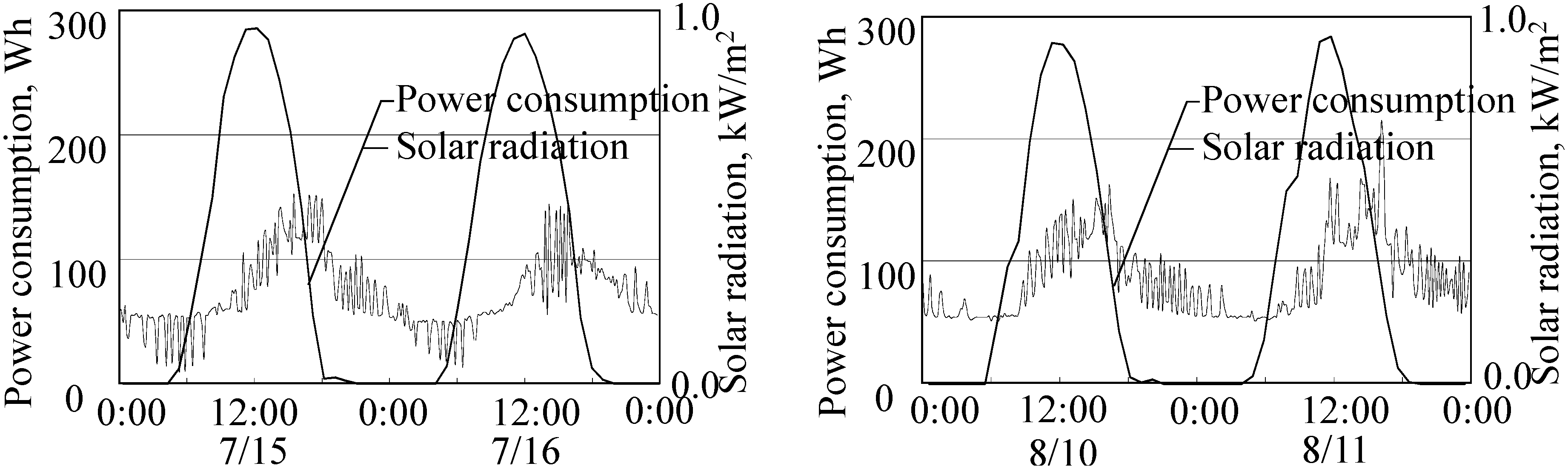
The results of temperature measurement under the slab, and above and under the suspended ceiling in room 1; the outdoor air temperature; and the solar radiation are shown in Figure 3. The temperature under the slab ranged from 40 to 27 °C and the maximum temperature was observed at around 18:00 owing to the thermal storage of the slab. The maximum temperature reduction on the roof surface was approximately 30 K after painting. The cooling energy consumption and solar radiation measurement results are shown in Figure 4. It is difficult to recognize the cooling energy savings by comparing the two values in a typical day even if the solar radiation values are similar to each other.

Figure 3. Measurement results for temperature under slab, and above and under suspended ceiling in room 1; outdoor air temperature; and solar radiation. left: Before painting; right: After painting.

Figure 3. Measurement results for temperature under slab, and above and under suspended ceiling in room 1; outdoor air temperature; and solar radiation. left: Before painting; right: After painting.

Figure 4. Measurement results for cooling energy consumption and solar radiation. left: Before painting; right: After painting.

Figure 4. Measurement results for cooling energy consumption and solar radiation. left: Before painting; right: After painting.

3. Method of Evaluating Cooling Energy Savings due to High-Reflectance Paint

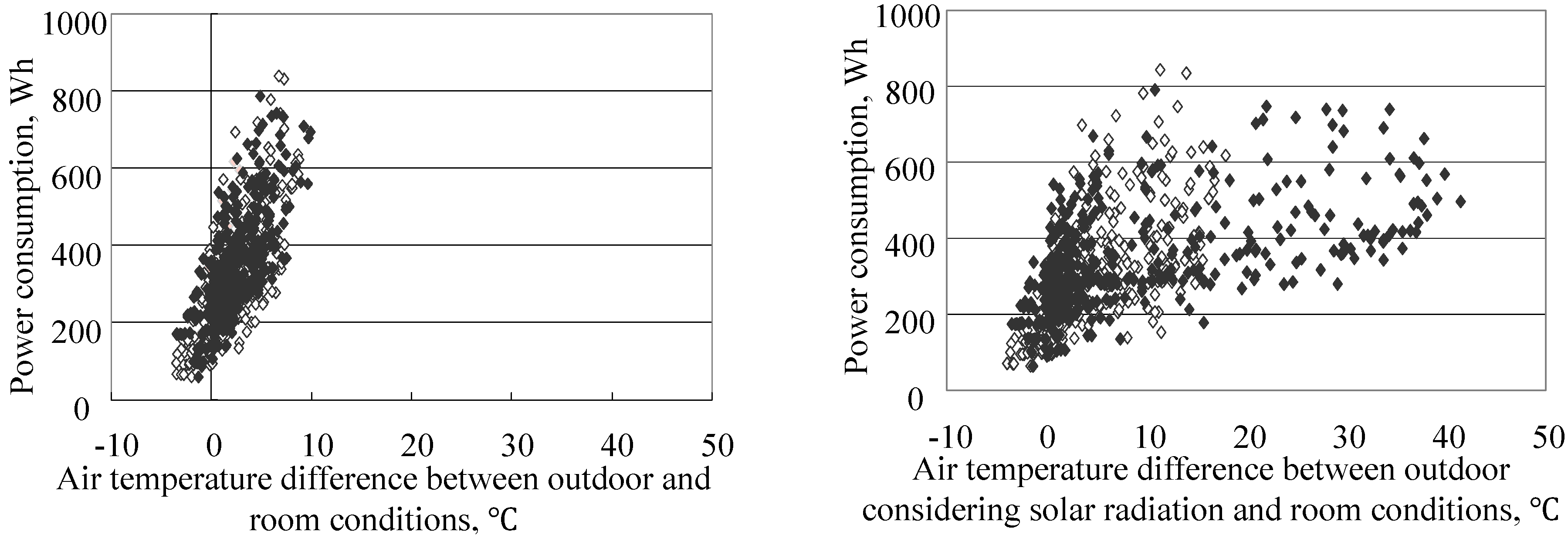
We analyzed the cooling energy savings by observing the difference in the cooling power consumption before and after painting. The hourly relationships between the outdoor-to-room air temperature difference and the cooling power consumption are shown in Figure 5. The black and white points represent the data before and after painting, respectively. Sol-air temperature is calculated by T_a + a × I/α, where T_a is air temperature (°C); a is solar absorptance (-); I is solar radiation (W/m²); α is convective heat transfer coefficient (W/m²/K). After painting, the sol–air temperature changes significantly (influenced by solar radiation) but the power consumption does not change as much. The air temperature difference is averaged and the power consumption is integrated over 1 h. Since the temperature under the slab reaches its maximum around the evening, it is difficult to recognize the relationship between the temperature difference of outdoor considering solar radiation and room conditions and power consumption using hourly data in the right of Figure 5.

Figure 5. Hourly relationship between outdoor-to-room air temperature difference and cooling power consumption. black: Before painting; white: After painting; left: Air temperature difference without considering solar radiation effect; right: Air temperature difference considering solar radiation effect.

Figure 5. Hourly relationship between outdoor-to-room air temperature difference and cooling power consumption. black: Before painting; white: After painting; left: Air temperature difference without considering solar radiation effect; right: Air temperature difference considering solar radiation effect.

We analyzed the relationship between the daily averaged outdoor-to-room air temperature difference and the daily integrated cooling power consumption by referring to the method of Akbari et al. [7]. The evaluation of cooling energy savings due to high-reflectance paint is mainly influenced by the following factors:

• internal heat generation;
• set temperature of the air conditioner;
• weather condition (air temperature, solar radiation).

As the object of this study is the evaluation of cooling energy savings in a real building under use, we did not instruct the room occupants on its use. Although the measurement results are affected by above three factors, the differences in the internal heat generation and the set temperature of air conditioner are not so large compared to those outlined in the reference method. In the test building, experimental devices such as constant temperature drying machine (1.4 kW, maximum use time: 5 h/day), mass spectrometer (2.8 kW, maximum use time: 10 h/day) are used irregularly by the day. The ratio of internal heat generation to total cooling load was estimated to be about 15% to 20% on average.

The cooling power consumption influenced by the internal heat generation, set temperature of the air conditioner, and weather condition is derived as follows:

E = A × I + B × ΔT + C

(1)

where E is the daily integrated cooling power consumption (Wh day⁻¹); I is the daily integrated solar radiation (Wh day⁻¹); ΔT is the difference between the daily averaged outdoor and room temperatures (in K); A is the coefficient related to absorptivity; B is the coefficient related to thermal conductance; and C is the internal heat generation. The cooling power consumption is directly proportional to these coefficients. As per the method, we should use the difference of enthalpy instead of ΔT since the power consumption includes the latent heat process, and consider the coefficient of performance of the air conditioner. However, in this study, we measured E, I, and ΔT and assumed that B and C do not change after painting. The influence of the set temperature of the air conditioner is reflected in ΔT, and that of the weather condition is reflected in ΔT and I. In the following chapter, we analyze the measurement results derived using Equation (1).

4. Examination of Cooling Energy Savings due to High-Reflectance Paint

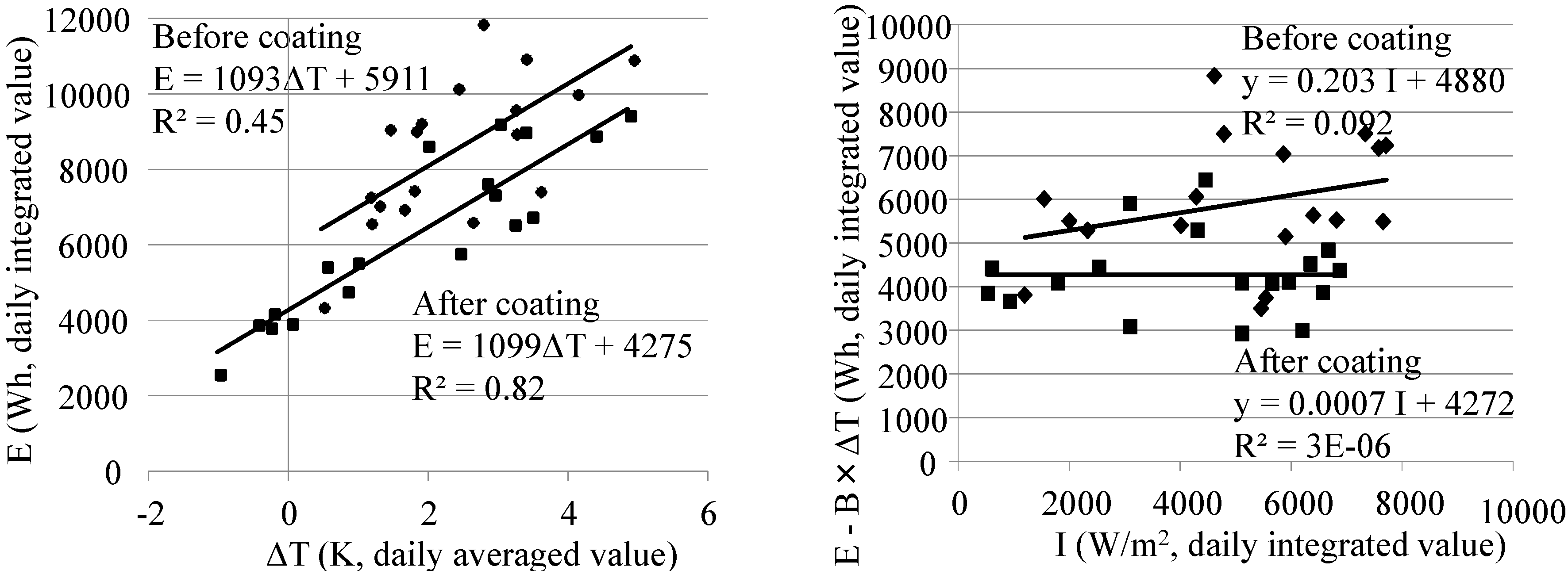
The daily relationship between the outdoor-to-room air temperature difference and the cooling power consumption is shown in the left of Figure 6. Since the slopes of the regression equations in both before- and after-painting cases are similar, it can be concluded that cooling power consumption is influenced by the outdoor air temperature. Additionally, it is influenced by the set temperature of the air conditioner, which was changed during the measurement period. The daily relationship between the solar radiation and the intercept of the regression equation (in the left of Figure 6) is shown in the right of Figure 6. Influences by ΔT and I are discussed respectively based on the left and right of Figure 6. The power consumption does not change after painting even when the daily integrated solar radiation value is high. When this factor is relatively higher, the cooling energy savings are about 1.6 kWh day⁻¹ (72 Wh m⁻² day⁻¹).

Figure 6. Relationship between (1) daily averaged outdoor-to-room air temperature difference and daily integrated cooling power consumption (left) and (2) daily integrated solar radiation and cooling consumption (right).

Figure 6. Relationship between (1) daily averaged outdoor-to-room air temperature difference and daily integrated cooling power consumption (left) and (2) daily integrated solar radiation and cooling consumption (right).

The value of B before painting is mostly the same as that after painting (in the left of Figure 6), and hence the influence of ΔT on power consumption is assumed to be similar before and after painting. The value of A after painting is nearly zero (in the right of Figure 6), and hence the influence of solar radiation on the cooling power consumption is assumed to be negligible after painting. Since internal heat generation was not controlled during measurement, the value of C is different before and after painting (in the right of Figure 6). Table 1 lists the characteristics of the objective rooms. Although the test building is actually in use, the analysis results have captured the approximate characteristics of its cooling energy consumption.

The regression equations of the cooling power consumption by air temperature difference between outdoors and rooms 1 and 2 are listed in Table 2 for three scenarios of painting: (1) before, (2) immediately after, and (3) one year after. The total cooling power consumption savings are divided by the respective floor areas (22.5 m² for room 1 and 43.5 m² for room 2) and expressed in the table. Since the slopes of the regression Equation (B) in the three scenarios are relatively similar in each room, the influence of ΔT on the cooling power consumption is similar in each room. For room 1, the values of B are almost similar for both immediately and one year after painting. However, the difference of energy savings between the immediately and one year after painting is not significant due to a little lower determination coefficient of each regression equation. The cooling energy savings in room 2 are lower than that in room 1. The ratio of internal heat generation to the total cooling load in room 2 is higher than that in room 1 because the former’s floor area is approximately twice the latter’s. Since the values of B for room 2 are lower than those for room 1, room 2 is not heavily influenced by the external weather condition.

Table 2. Regression equations for cooling power consumption due to air temperature difference between outdoor and room condition for the scenarios (1) before, (2) immediately after, and (3) one year after painting, in rooms 1 and 2.

Room	Condition	Regression Equation	Energy Savings
Room 1	Before painting *	E = 48.6 ΔT + 262.7 (R2 = 0.45)	72 Wh·m−2·day−1 91 Wh·m−2·day−1
	After painting **	E = 50.3 ΔT + 190.8 (R2 = 0.82)
	One year after painting ***	E = 48.0 ΔT + 171.6 (R2 = 0.82)
Room 2	Before painting *	E = 26.7 ΔT + 151.3 (R2 = 0.54	35 Wh·m−2·day−1 9 Wh·m−2·day−1
	After painting **	E= 27.6 ΔT + 116.6 (R2 = 0.60)
	One year after painting ***	E = 26.9 ΔT + 142.8 (R2 = 0.77)

* before painting: From 12 July to 31 July 2011; ** after painting: From 3 August to 26 September 2011; *** one year after painting: From 12 July to 26 September 2012.

Table 2. Regression equations for cooling power consumption due to air temperature difference between outdoor and room condition for the scenarios (1) before, (2) immediately after, and (3) one year after painting, in rooms 1 and 2.

Room	Condition	Regression Equation	Energy Savings
Room 1	Before painting *	E = 48.6 ΔT + 262.7 (R2 = 0.45)	72 Wh·m−2·day−1 91 Wh·m−2·day−1
	After painting **	E = 50.3 ΔT + 190.8 (R2 = 0.82)
	One year after painting ***	E = 48.0 ΔT + 171.6 (R2 = 0.82)
Room 2	Before painting *	E = 26.7 ΔT + 151.3 (R2 = 0.54	35 Wh·m−2·day−1 9 Wh·m−2·day−1
	After painting **	E= 27.6 ΔT + 116.6 (R2 = 0.60)
	One year after painting ***	E = 26.9 ΔT + 142.8 (R2 = 0.77)

* before painting: From 12 July to 31 July 2011; ** after painting: From 3 August to 26 September 2011; *** one year after painting: From 12 July to 26 September 2012.

5. Conclusions

In this study, we analyzed the cooling energy savings brought about by high-reflectance paint in a building actually under use, based on measured results. Considering the factors assumed to influence cooling energy load (namely, internal heat generation, set temperature of the air conditioner, and weather condition), we analyzed the relationship between (1) the daily integrated solar radiation and cooling power consumption values, and (2) the daily averaged outdoor-to-room temperature difference and cooling power consumption.

From (2), the cooling power consumption savings brought about by the high-reflectance paint were estimated at approximately 1.6 kWh day⁻¹ (72 Wh m⁻² day⁻¹). Similar results were confirmed one year after painting. However, the difference of energy savings between the immediately and one year after painting is not significant due to a little lower determination coefficient of each regression equation. Although the results measured in a building actually under use were considered, the approximate energy savings could be satisfactorily evaluated. However, when ΔT is relatively higher, the cooling power consumption tends to be significantly higher. Therefore, we may have to consider an improvement in the coefficient of performance of the air conditioner in such a case. In this study, the cooling energy saving effect by high-reflectance paint is mainly discussed. For example, reduction of mean radiation temperature by lowering the ceiling surface temperature should be evaluated in future study.