Group Effect on In-Plane Shear Performance in Wooden Nail Connections

Abstract

Cross-Laminated Timber (CLT) is ideal for tall timber structures but relies on environmentally concerning chemical adhesives. Nailed Cross-Laminated Timber (NCLT) offers a sustainable alternative by using densified wooden nails that form eco-friendly, adhesive-free bonds through lignin’s thermoplastic properties. However, significant uncertainties remain regarding the synergistic effects of multiple wooden nails. To address this, this study systematically analyzed the impact of the group effect on the mechanical performance of wooden nail joints. The results show that within the elastic range, the number of wooden nails has no significant effect on the elastic behavior of a structure. However, it is significantly positively correlated with both the joint yield load and yield displacement, enabling the accurate prediction of the structural yield point based on the number of wooden nails. With consistent nail arrangements, the group effect coefficient for the load-bearing capacity remains highly stable and shows no significant correlation with the number of nails. Additionally, an increase in the number of wooden nails significantly enhances the deformation resistance and structural stiffness, while having a minimal impact on ductility. This study reveals the linear additive nature of the group effect in wooden nails, providing important theoretical support for the design of NCLT.

1. Introduction

Timber structures are gradually evolving from low-rise to high-rise buildings due to their environmental and resource advantages. In this transition, Cross-Laminated Timber (CLT) has emerged as an ideal material for timber construction because of its superior performance. However, CLT relies heavily on petrochemical products (adhesives), which inevitably lead to issues such as environmental pollution and low recyclability. In contrast, Dowel Cross-Laminated Timber (DCLT) [1,2] addresses these concerns by utilizing wooden dowel connections. However, DCLT requires pre-drilling to achieve the accurate positioning of wooden dowel insertion points [3]. This high-precision but inefficient process elevates the production costs and time, posing challenges for the large-scale implementation of DCLT. With the advancement of wood modification technology, high-strength densified wooden nails [4] have achieved mechano-chemical synergistic bonding between wood components, enhancing connection performance while eliminating the need for pre-drilling. When combined with specialized driving equipment, this technology enables highly efficient continuous operation, significantly improving production efficiency and reducing construction costs. These developments provide new perspectives for environmentally friendly connection technologies.

Currently, studies have explored the use of densified wooden nails as an alternative to traditional dowels for timber-to-timber connections, leading to the development of Nailed Cross-Laminated Timber (NCLT) [5,6]. These densified wooden nails are made from hardwood that is impregnated with resin and compressed, providing significant advantages such as high density, high strength [7], corrosion resistance [8,9], and recyclability [10]. Additionally, when used in conjunction with an air gun machine [11], the processing of NCLT eliminates the need for pre-drilling, enabling continuous operations that effectively enhance production efficiency and mitigate the inefficiencies associated with DCLT manufacturing. As a result, this technology has garnered widespread attention in the European construction market.

Existing research has demonstrated that densified wooden nails exhibit superior withdrawal resistance. This phenomenon is attributed to the heat generated by friction as the nails are rapidly driven into the wood, melting the lignin. The melted lignin extrudes and accumulates on the surface of the nails, forming an adhesive layer upon solidification [12], which enhances the withdrawal strength [13]. A recent study has confirmed the validity of theoretical calculation models for the load-bearing capacity and stiffness of wooden nail joints under various stress conditions [14], providing essential theoretical support for the application of wooden nails as universal fasteners. Complementary to experimental approaches, finite element methods (FEMs) have been widely employed to analyze shear and tensile performance in timber connections, offering insights into the stress distribution and failure mechanisms under complex loading conditions [15]. Although the performance of wooden nails in shear-loaded structures is inferior to that of metal fasteners [9], increasing the number or diameter of wooden nails presents a viable strategy for optimizing structural performance when shear strength is a critical design criterion. Nonetheless, current studies mainly focus on the load-bearing performance of a single wooden nail [16,17], resulting in considerable uncertainty about the group effects of nails in multiple-nail timber-to-timber connections and their overall impact on structural performance.

In connections involving multiple fasteners, the load-bearing capacity of the combined fasteners is often less than the sum of the capacities of the single fasteners. This phenomenon is referred to as the group effect. Since the 1960s, equations [18,19,20] addressing the group effect in bolt connections have been gradually proposed, revealing an uneven load distribution among serially arranged fasteners, where the outermost fasteners bear the greatest load [21]. Furthermore, these theoretical equations are valid only within the elastic range [22]. Within this range, the load-bearing characteristics of multiple fastener connections are significantly affected by their arrangement and quantity [23,24,25,26]. To validate the effectiveness of nails in brittle and mixed failure modes, a closed-form analytical method [27,28,29] has been proposed, considering both the strength of the wood and the stiffness of the failure plane. This method can also be applied to the design of other small dowel fasteners. If a brittle failure mode can be effectively avoided and a single fastener, along with its arrangement, provide sufficient ductility for load redistribution, the overall load-bearing capacity of the structure can be calculated by summing the design values of the single fasteners [30].

The European standard Eurocode 5 (EC5) [31] and the American National Design Specification (NDS) [32] both account for local stress concentrations caused by densely arranged fasteners, adjusting the load-bearing capacity based on the effective number of fasteners (EC5) or the group action factor (NDS). Both standards emphasize the need for the mechanical coordination of fasteners across multiple shear planes, ensuring similar failure modes to prevent localized failure or premature collapse from misalignment. EC5 emphasizes geometric parameters and empirical formulas, adjusting the load-bearing capacity by calculating the effective number of fasteners (n_ef), focusing on the impact of the fastener arrangement and spacing. However, it does not account for fasteners perpendicular to the wood grain. In contrast, the NDS emphasizes the mechanical response of materials, highlighting the influence of material properties on multi-shear-plane structure behavior. The NDS adjusts the load-bearing capacity using a group effect coefficient (C_g) but only provides calculation methods for bolts and lag screws with diameters of between 6.35 mm and 25.4 mm.

The motivation for this study arose from the innovative concept of replacing adhesives and wooden dowels with wooden nails in CLT production to reduce the environmental impact and enhance recyclability [5]. An NCLT system with wooden nail connections consists of multiple discrete units, exhibiting typical discontinuous load transfer characteristics. However, existing research primarily focuses on continuous load-bearing media composed of multiple metal fasteners, making it difficult to accurately characterize the mechanical behavior of wooden nail groups. Furthermore, there is a lack of effective prediction and in-depth understanding of the failure evolution mechanisms of wooden nails in multiple discrete units. Therefore, this study aimed to examine the group effect in multi-nail connections in Cross-Laminated Timber, focusing particularly on how the nail number and arrangement affect the failure modes, yield characteristics, load-bearing capacity, slip modulus, and ductility. The objective was to provide scientific support for the wider application of NCLT in timber construction, advancing more efficient and sustainable design and construction practices.

2. Materials and Methods

2.1. Materials

The wooden nails selected for this study (LingoLoc^®, BECK Fastener Group, Mauerkirchen, Austria) were manufactured from European beech that had been impregnated with resin and subjected to unidirectional compression, achieving a density of 1280 ± 20 kg/m³ and an initial moisture content of 5.78 ± 0.21%. Other characteristics of the wooden nails are shown in

Table 1. Properties of wooden nails [12].

	Nail Properties
	Nominal length [mm]	45
	Nominal diameter [mm]	4.7
	Char. yield moment [N·mm]	2247
	Char. tensile capacity [N/mm2]	195.3
	Char. shear resistance [N]	527.4

. The timber boards used were Norway spruce (Picea abies (L.) H. Karst), with sectional dimensions of 90 mm × 25 mm and a density of 480 ± 10 kg/m³, along with an initial moisture content of 12.47 ± 0.16%. Prior to assembly, the timber boards were stored in a climate chamber maintained at a temperature of 20 °C and a relative humidity of 65% to ensure that their moisture content was controlled between 11% and 13%.

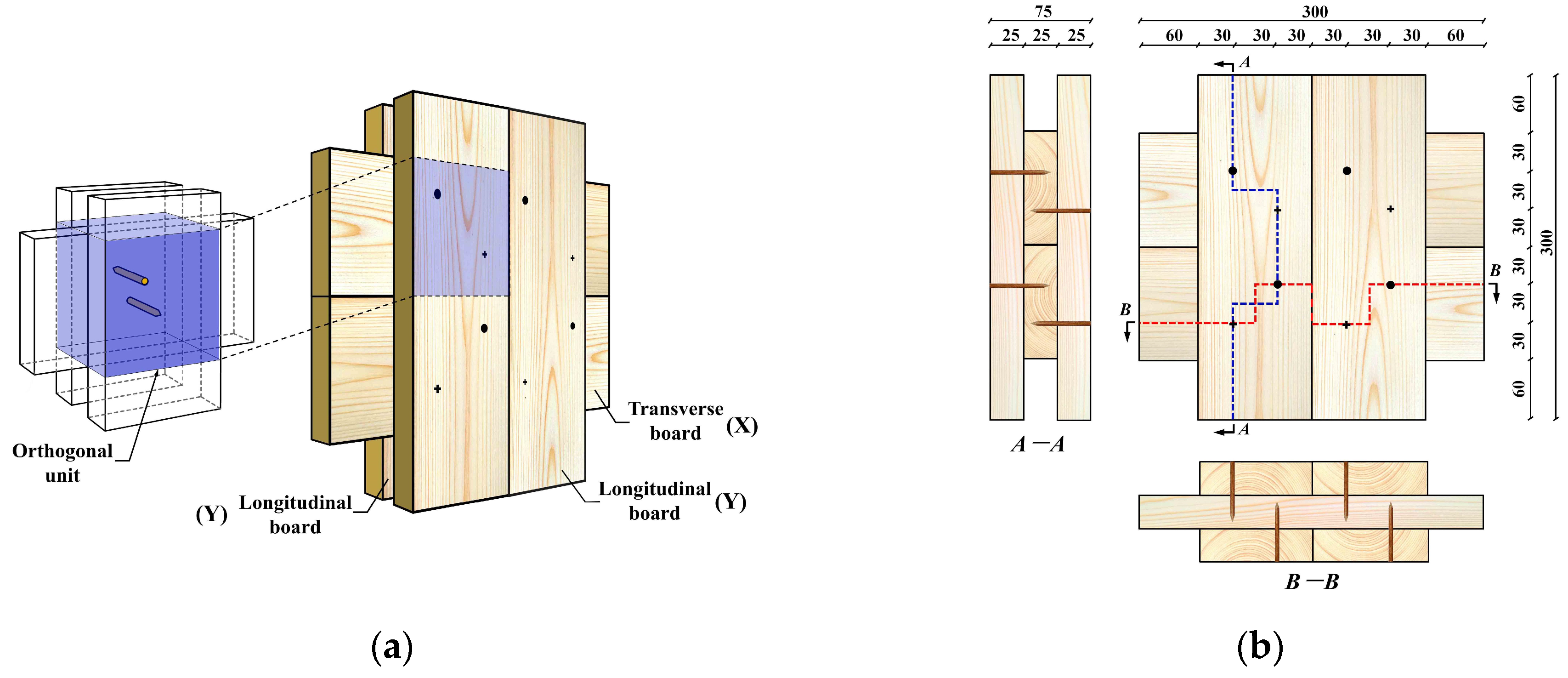
2.2. Specimens

The specimens consisted of three layers of orthogonal timber boards. Wooden nails were driven in with a specialized pneumatic nail gun (F60 CN15-PS90-H, FASCO S.R.L., Cadriano di Granarolo, Italy), set to an output pressure of 0.6 to 0.8 MPa. As shown in Figure 1a, the wooden nails were vertically driven into two adjacent orthogonal layers of the timber boards, ensuring that the tops of the nails were flush with the surface of the outer layer, while the tips penetrated approximately 75% of the thickness of the inner layer. The overlapping area was defined as one orthogonal unit, which consisted of two staggered wooden nails connecting the longitudinal and transverse boards. The symbols were defined as follows: The longitudinal board was denoted as Y, and the transverse board as X. In the front view of the specimen, if the observed number of longitudinal board was n and the number of transverse boards was m, the specimen was denoted as nYmX. For example, the specimen symbol for Figure 1a is 2Y2X, utilizing 8 wooden nails and comprising 4 orthogonal units. Figure 1b presents the specific parameters for the nail arrangement in the 2Y2X specimen, which are also applicable to other specimens. All specimen designs and their symbols are illustrated in Figure 2.

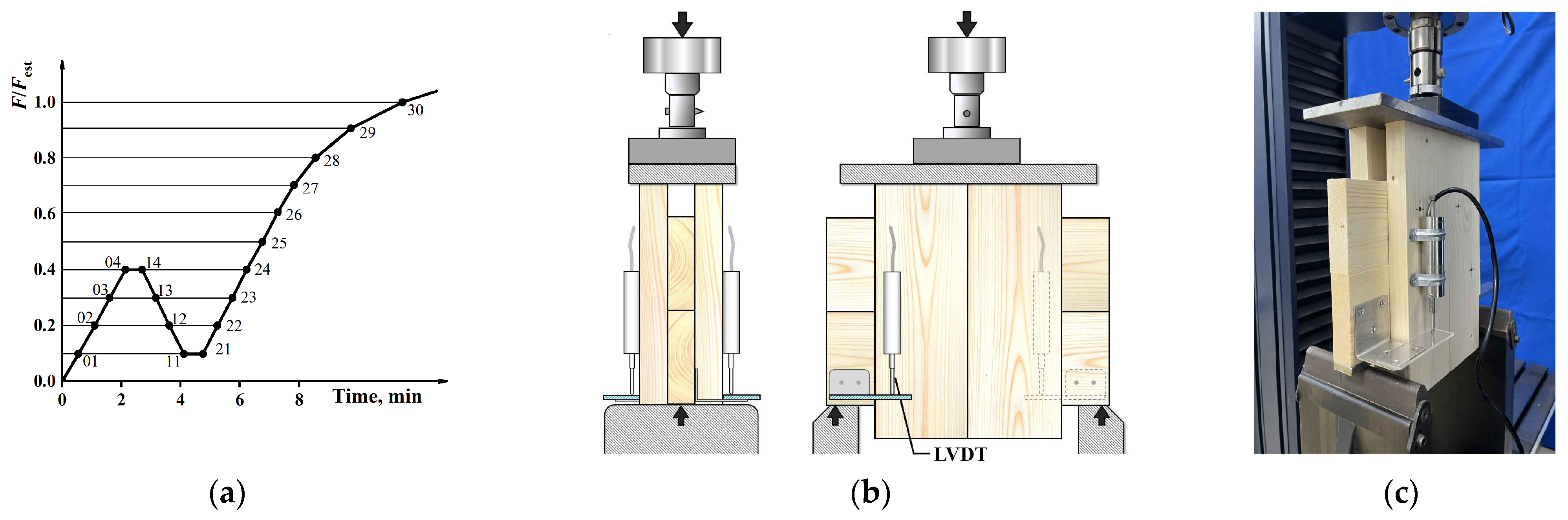
2.3. Testing Procedure and Loading Setup

As shown in Figure 3a, the loading procedure was conducted in accordance with the force control protocol outlined in EN 26891 [33]. The estimated maximum load F_est was defined as the average of the maximum loads F_max,i of various specimens of the same type. For each group of specimens, the estimated maximum load F_est was determined through testing, utilizing a constant loading rate of 0.5 mm/min. Verification was carried out to ensure the following conditions were met:

$$0.8F_{max,i}\le F_{est}\le 1.2F_{max,i}$$

(1)

The experiments adhered to the loading method outlined in EN 1380 [34], as shown in Figure 3b,c. A mechanical testing machine (UTM4304SLXY, SUNS CO., LTD, Shenzhen, China) with a capacity of 30 kN and a sampling frequency of 50 Hz was employed for the loading process. The relative displacement between the orthogonal laminated panels was measured using a YWC-50 strain gauge displacement sensor (LVDT) with a sampling frequency of 1 Hz and a measurement range of 50 mm. Each specimen type underwent 10 tests, yielding a total of 90 tests.

3. Results and Discussions

3.1. Load–Displacement Characteristics of Multi-Nail Joints

Figure 4 illustrates the load–displacement curves for all specimens, showcasing typical structural deformation behavior. During the initial loading phase, the joints experienced slight deformations due to adjustments in local contact surfaces, material compression, and the removal of minor irregularities. This deformation caused an irreversible small settlement (v_s), a characteristic widely recognized in natural materials [1]. As the load increased further, the joints transitioned into the elastic deformation phase. At lower loads, the initial slip (v_i) typically occurred at the connections, a parameter used to assess the initial stiffness of the joint and its responsiveness to small loads. Modifying the initial slip (v_i,mod) allows for a more accurate description of the stiffness characteristics. During subsequent unloading and reloading, the joints stayed within the elastic range, and the resulting slip is referred to as the elastic slip (v_e). This slip fully recovers to its original state after unloading, without causing permanent deformation. This parameter is commonly used to characterize the elastic response of connection joints and their resistance to deformation under reversible loads. According to EN 26891 [33], the formulas for calculating the modified initial slip (v_i,mod), settlement (v_s), and elastic slip (v_e) are as follows:

$$v_{i,mod}={\displaystyle \frac{4}{3}}\left(v_{04}-v_{01}\right)$$

(2)

$$v_s=v_i-v_{i,mod}$$

(3)

$$\begin{array}{c}{v}_e={\displaystyle \frac{2}{3}}\left(v_{14}+v_{24}-v_{11}-v_{21}\right)\end{array}$$

(4)

Figure 5 shows the slip within the elastic range for all specimens, along with the percentages of the settlement (v_s) and elastic slip (v_e) relative to the modified initial slip (v_i,mod). As the number of wooden nails in the specimens increased, both the overall slip and settlement also rose, indicating that a greater number of wooden nails led to larger local deformations and enhanced resistance to deformation. The mean percentages of the overall settlement (v_s) and elastic slip (v_e) relative to the modified initial slip (v_i,mod) were 30.62% and 71.28%, respectively, with coefficients of variation of 11.54% and 4.36%. This suggests that the elastic behavior of each specimen remained relatively stable within the elastic range, while the larger variability in settlement indicates uncertainties during the initial adjustments of contact surfaces and material compaction. The high proportion of elastic slip and the lower percentage of settlement further indicate that under load, the joints primarily exhibited elastic behavior, suggesting that most deformations were recoverable, with only a small portion being irreversible [35].

As the load increases, the joint transitions from the elastic to the plastic deformation phase, with the critical point being the yield point. The yield point defines the maximum elastic load the joint can sustain, reflecting its strength and deformability. This study defined the yield point using the Y&K method [36], as illustrated in Figure 6. The following steps were employed:

(1)

A secant line (Line I) was drawn between the load values of 0.1P_max and 0.4P_max, with its slope representing the initial stiffness K₀ of the joint;

(2)

A second secant line (Line II) was drawn between the load values of 0.4P_max and 0.9P_max;

(3)

Line II was translated until it was tangent to the curve, forming Line III;

(4)

The y-coordinate of the intersection of Line III and Line I represented the yield load P_y, while the corresponding x-coordinate indicated the yield displacement δ_y;

(5)

The load value of 0.8P_max was taken as the ultimate load P_u, with the corresponding x-coordinate as the ultimate displacement δ_u.

Figure 7 presents the analysis of the correlation between the number of wooden nails and the yield load and yield displacement of the joint. The results demonstrate a strong positive correlation between the number of wooden nails and both the yield load and yield displacement, indicating significant increases in these parameters with additional nails. Through linear regression analysis, this study further derived the regression equations for the yield point (Equations (5) and (6)), providing a clear mathematical model to quantify the impact of the number of wooden nails on the yield characteristics of the joint.

$$\begin{array}{c}{P}_y=218.31+697.64·n_{nail}\end{array}$$

(5)

$$\begin{array}{c}{\delta }_y=0.93+0.18·n_{nail}\end{array}$$

(6)

Upon reaching the yield point, the joint enters the plastic deformation region and continues to bear the load until its load-bearing capacity reaches its limit. At this stage, the strength of the connection no longer increases, and gradual failure initiates. This process is typically illustrated on the load–displacement curve by pronounced serrated fluctuations, reflecting the dynamic response of the structure during local failure and load redistribution. This phenomenon continues with ongoing load application until the structure ultimately collapses completely.

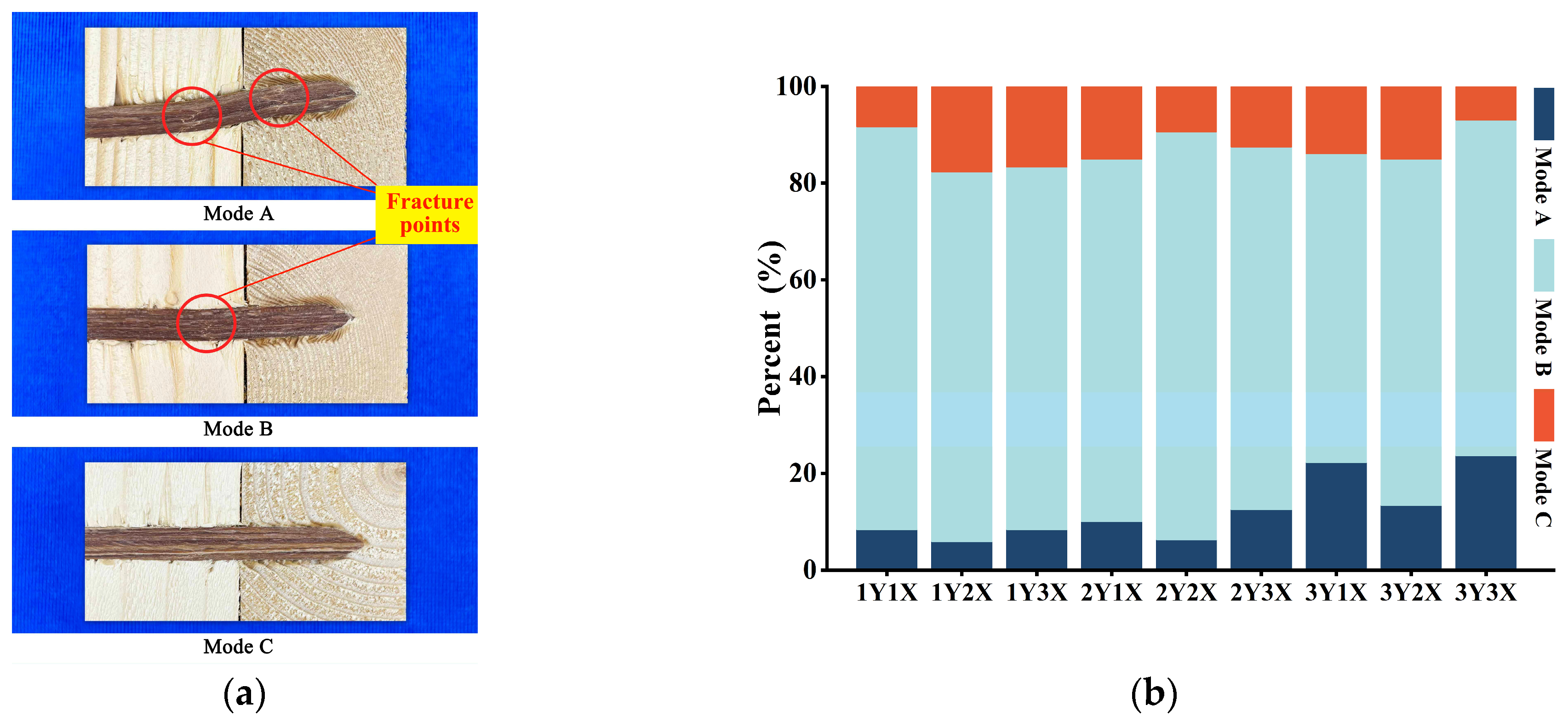
3.2. Failure Characteristics

Figure 8a illustrates the main deformation characteristics of the wooden nails in the grouped specimens, including two failure modes: two fracture points (Mode A), one fracture point (Mode B), and a no-fracture mode (Mode C). Previous studies indicated that fasteners arranged in series may experience an uneven load distribution, causing the outermost fastener to bear the greatest load, which leads to more severe damage [21]. Observations revealed that these three failure modes occurred randomly at various locations within individual specimens, without any discernible pattern.

Figure 8b shows the percentage of wooden nails exhibiting different modes across the specimens, with the average proportion of Mode B reaching 75%. This was attributed to the construction of the specimens, which consisted of multiple parallel boards instead of a single solid piece, resulting in a semi-independent and semi-connected characteristic among the orthogonal units. This unique configuration effectively distributed the load to each nail joint, resulting in a high degree of similarity in joint failure behavior. The diversity and randomness of nail failures may have stemmed from subtle differences in factors such as the fit between parallel boards, the compressive strength of the dowel holes, and the bending strength of the wooden nails.

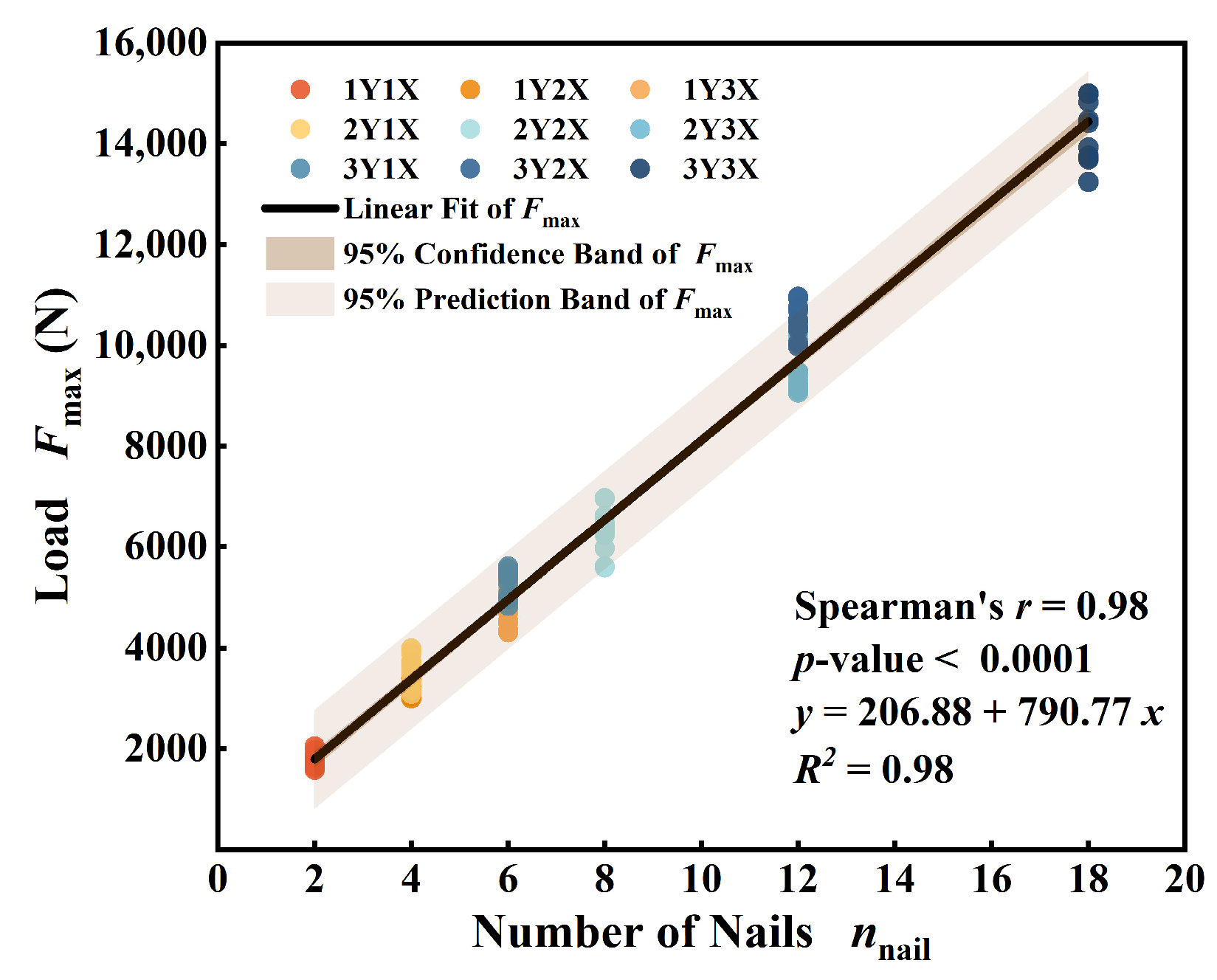
3.3. Maximum Load

In accordance with EN 26891 [33], the maximum load capacity of the structure was recorded, and the mean values are presented in

Table 2. Experimental results for maximum bearing load.

Symbol	1Y1X	1Y2X	1Y3X	2Y1X	2Y2X	2Y3X	3Y1X	3Y2X	3Y3X
Fmax [N]	1772.93	3144.4	4710.66	3528.08	6248.53	9422	5261.12	10,505.49	14,204.13
COV [%]	8.01	3.39	5.88	8.28	6.44	3.89	4.94	3.07	4.14
nef	2	4	6	4	8	12	6	12	18
Fmax/nnail [N]	886.47	786.1	785.11	882.02	781.07	785.17	876.85	875.46	789.12
Cg,load	1.00	0.89	0.89	0.99	0.88	0.89	0.99	0.99	0.89

. Figure 9 illustrates the results of the analysis of the correlation between the maximum load capacity of the joints and the number of wooden nails. The Spearman correlation analysis yielded a coefficient of 0.98, indicating a very strong positive correlation. Specifically, an increase in the number of wooden nails significantly enhanced the maximum load capacity of the joints. Further linear regression analysis produced the regression equation for these variables (see Equation (7)), with a goodness of fit of 0.98. This indicates that the equation accurately fits the experimental data. These results further confirm the significant impact of the number of wooden nails on the maximum load-bearing capacity of the joints and validate the reliability of the regression model in predicting the joint load capacity.

$$\begin{array}{c}{F}_{max}=206.88+790.77·n_{nail}\end{array}$$

(7)

In structures connected by multiple fasteners, the quantity and arrangement of the fasteners significantly influence the load-bearing capacity. According to the EC5 standard, for a row of fasteners arranged parallel to the grain, the effective load-bearing capacity standard value (F_v,ef,Rk) should be calculated using the following formula:

$$\begin{array}{c}{F}_{v,ef,RK}=n_{ef}·F_{v,RK}\end{array}$$

(8)

$$\begin{array}{c}{n}_{ef}=n^{k_{ef}}\end{array}$$

(9)

where F_v,ef,Rk is the effective load-bearing capacity standard value for fasteners arranged in a single row parallel to the grain, F_v,Rk is the load-bearing capacity standard value for each fastener aligned with the grain, n_ef is the effective number of fasteners in the row, n is the total number of fasteners in the row, and k_ef is the correction factor, with specific values provided in Table 8.1 of the EC5 standard.

The effective number of fasteners (n_ef) refers to the quantity of fasteners capable of effectively transmitting the load under specific design conditions. In a single row of n fasteners arranged parallel to the grain, if the fasteners are aligned perpendicularly to the grain and staggered with a spacing of at least 1d (where d is the fastener diameter), the effective number of fasteners (n_ef) should be used to evaluate the load-bearing capacity parallel to the grain. Otherwise, the effective number of fasteners should be calculated based on the single load-bearing capacity of each fastener. As shown in Figure 1 and Figure 2, the spacing between adjacent fasteners exceeded 14d. According to the provisions of EC5, the correction factor k_ef was set to 1, which allowed all fasteners to be regarded as effective in the load-bearing capacity calculation.

According to the provisions of the NDS, when using dowel-type fasteners with a diameter of less than 1/4 inch (6.35 mm), the group effect coefficient is set to 1.0. This indicates that for the wooden nails used in this study, which had a diameter of 4.7 mm, no additional adjustments to the group effect coefficient were necessary. Consequently, the overall load-bearing capacity of the joint could be directly calculated by summing the standard values of the single wooden nails.

Both EC5 and the NDS suggest that in the structures connected by multiple wooden nails in this study, all wooden nails could be considered effective, yielding a group effect coefficient (C_g,load) of 1.00. Table 2 displays the group effect coefficients derived from the experimental results. The results indicate that in one scenario, the group effect coefficient for the wooden nails remained stable at 0.99, closely aligning with the theoretical calculations from EC5 and the NDS. In another scenario, the group effect coefficient was approximately 0.89, representing a significant deviation from the theoretical value. Furthermore, among different specimens with the same number of wooden nails (e.g., 1Y2X and 2Y1X, 1Y3X and 3Y1X, 2Y3X and 3Y2X), notable differences in the group effect coefficients suggest that the quantity of wooden nails did not significantly affect the group effect coefficient. This phenomenon may have been due to variations in the arrangement of the wooden nails.

To examine the impact of the wooden nail arrangement on specimens’ load-bearing capacity, a significance analysis was conducted at the 0.05 confidence level using the average single-nail bearing capacity (Table 2), with the results presented in Figure 10. In the figure, “ns” represents p > 0.05, “**” represents p ≤ 0.01, and “***” represents p ≤ 0.001. Figure 10a illustrates a significant difference in the maximum load-bearing capacity among specimens with the same number of wooden nails. Specifically, structures with more nails arranged in rows than in columns exhibited a higher load-bearing capacity. Figure 10b further demonstrates the influence of the nail quantity in rows and columns on the single-nail load-bearing capacity. When the number of nails in rows exceeded that in columns (n_row > n_column), the average load-bearing capacity of a single nail was 880.20 N, resulting in a group effect coefficient (C_g,load) of 0.99 and a coefficient of variation (COV) of 0.57%, showing no significant differences. Similarly, when n_row ≤ n_column (except for in 1Y1X), the average load-bearing capacity was 785.31 N, resulting in a group effect coefficient (C_g,load) of 0.89 and a coefficient of variation (COV) of 0.33%, also showing no significant differences. These results suggest that when the nail arrangement was consistent (whether n_row > n_column or n_row ≤ n_column), the load-bearing capacity of a single nail remained stable. The stable group effect was due to the multilayered construction of NCLT, where semi-independent and semi-connected orthogonal units enable a uniform load distribution, maximizing the load-bearing capacity of each nail.

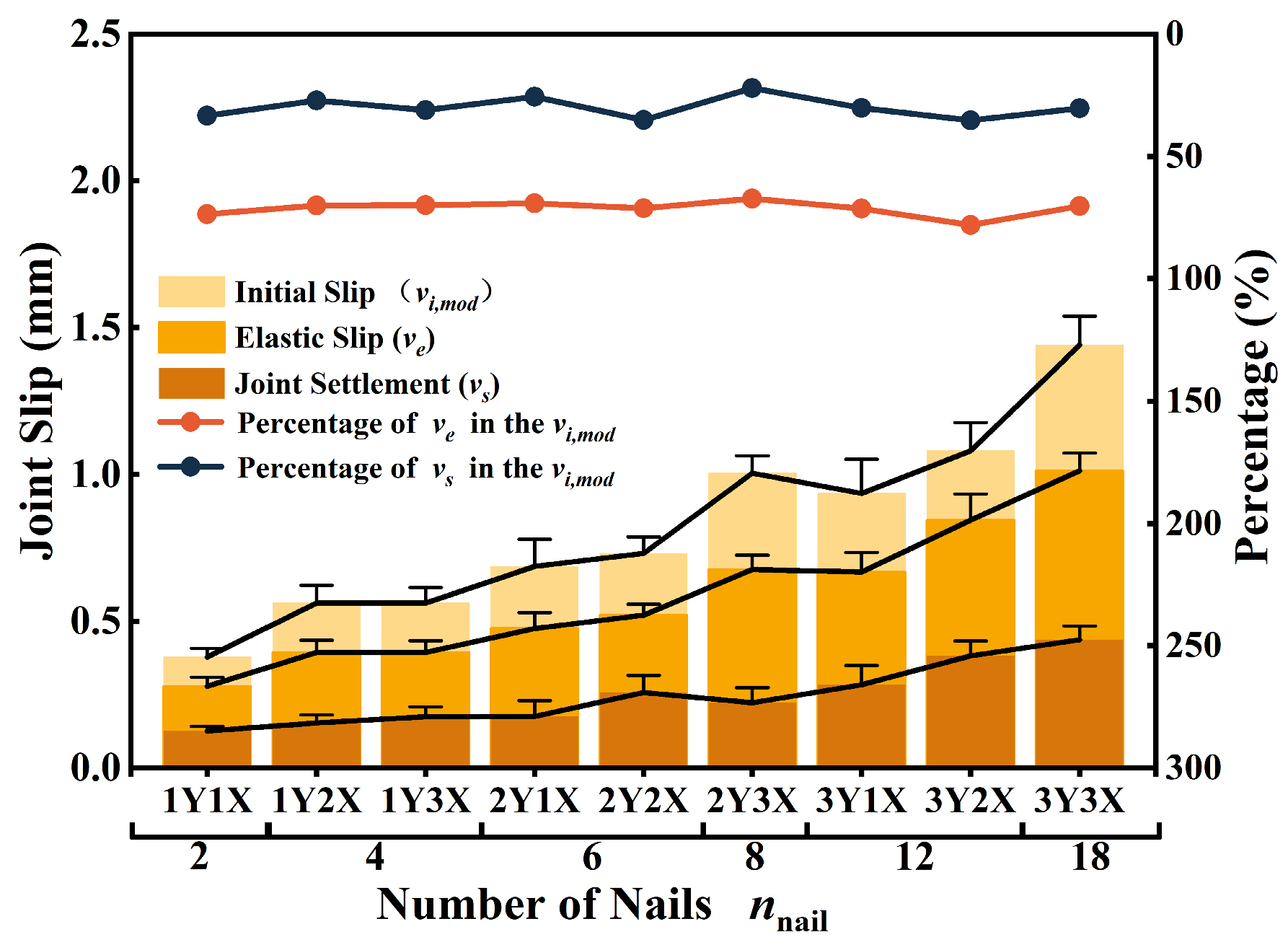
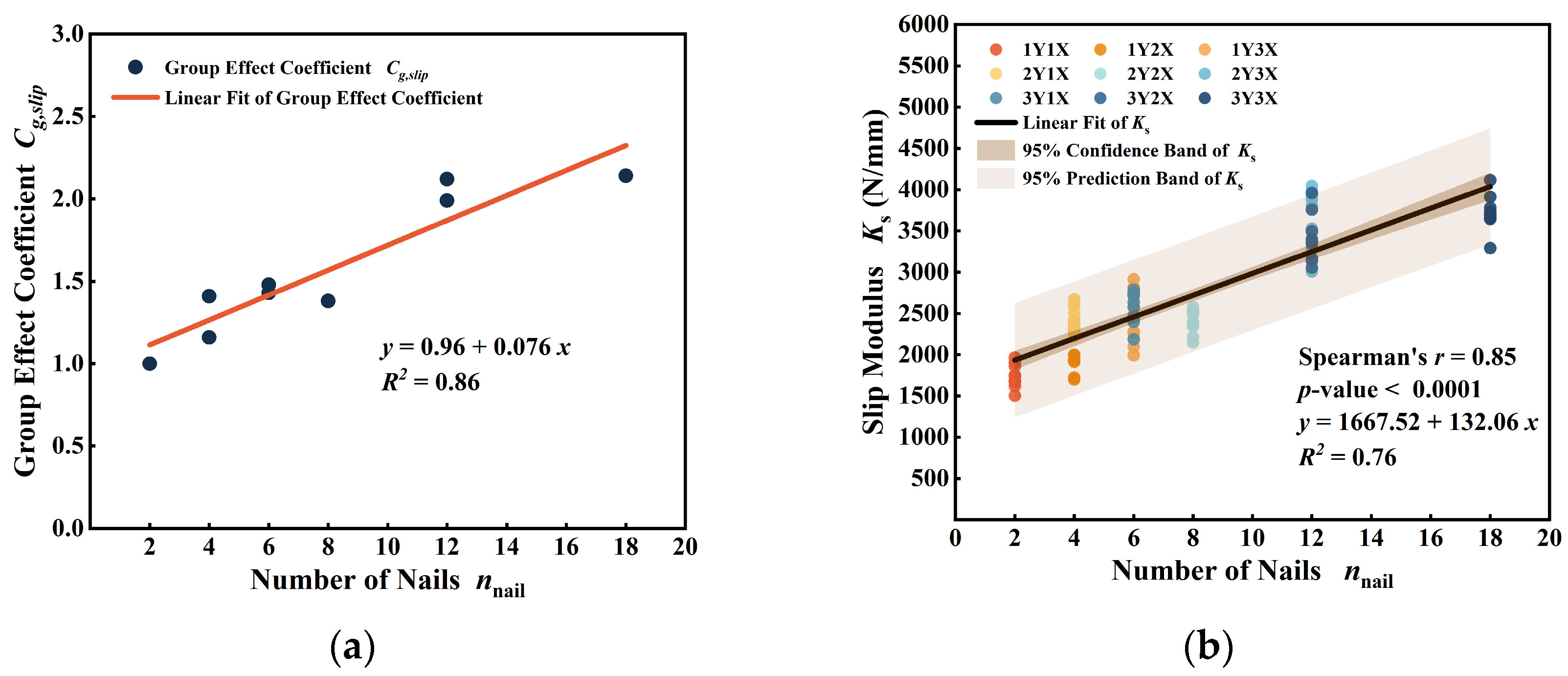
3.4. Slip Modulus

The slip modulus of the joints was calculated according to EN 26891 [33], as detailed in Equations (10) and (11).

$$\begin{array}{c}{K}_s={\displaystyle \frac{0.4F_{est}}{v_{i,mod}}}\end{array}$$

(10)

$$\begin{array}{c}{v}_{i,mod}={\displaystyle \frac{4}{3}}\left(v_{04}-v_{01}\right)\end{array}$$

(11)

where F_est is the mean pre-test load for each sample group, K_s is the initial stiffness, v_i,mod is the initial slip, v₀₄ is the slip corresponding to 0.4F_est, and v₀₁ is the slip at 0.1F_est.

In this study, the slip modulus of the dual node in a single orthogonal unit (K_s,1Y1X) served as the reference value. The group effect coefficient (C_g,slip) for each of the nine specimen groups was calculated as the ratio of their slip modulus (K_s,nYnX) to this reference, as shown in Equation (12).

Table 3. Calculation results for slip modulus.

Symbol	1Y1X	1Y2X	1Y3X	2Y1X	2Y2X	2Y3X	3Y1X	3Y2X	3Y3X
nnail	2	4	6	4	8	12	6	12	18
Ks [N/mm]	1737.69	2007.19	2484.45	2449.27	2397.1	3680.7	2571.34	3464.69	3717.07
COV [%]	8.01	10.81	12.88	6.04	5.79	11.57	7.43	9.47	5.64
Cg,slip	1.00	1.16	1.42	1.40	1.38	2.11	1.48	1.99	2.14

summarizes the slip modulus and corresponding group effect coefficients for all nine specimen groups.

$$\begin{array}{c}{C}_{g.slip}={\displaystyle \frac{K_{s,nPnA}}{K_{s,1P1A}}}\end{array}$$

(12)

As shown in Figure 11a, a linear regression analysis of the group effect coefficients for the nine specimen groups produced a regression equation (Equation (13)) with a goodness of fit (R²) of 0.86. This result indicates that the regression model provides a high degree of fit to the experimental data and accurately reflects the relationship between the group effect coefficient and the number of wooden nails. To further validate the regression model’s reliability, a Spearman correlation analysis was performed to assess the correlation between the group effect coefficient (C_g,slip) of the joint slip modulus and the number of nails (n_nail). The analysis revealed a strong positive correlation, with a Spearman correlation coefficient of 0.88 and a p-value below 0.002, confirming statistical significance.

$$\begin{array}{c}{C}_{g,slip}=0.96+0.076·n_{nail}\end{array}$$

(13)

The slip modulus of the overall structure could therefore be derived using Equations (10) and (11), as shown in Equation (14).

$$\begin{array}{c}{K}_{s,nPnA}=C_{g,slip}·K_{s,1P1A}·n_{nail}=1667.52+132.06·n_{nail}\end{array}$$

(14)

To further investigate the relationship between the number of wooden nails and the joint slip modulus, this study fitted the slip modulus equation (Equation (14)) to 90 experimental datasets (Figure 11b), resulting in a goodness of fit of 0.76. This indicates that the regression-based theoretical model exhibits high reliability and accuracy in predicting the slip modulus of joint connections with grouped wooden nails, effectively reflecting the group effect within the overall structure. Increasing the number of wooden nails significantly enhances the joint’s resistance to deformation, thereby improving the overall stiffness of the connection and illustrating the linear accumulation characteristic of the group effect.

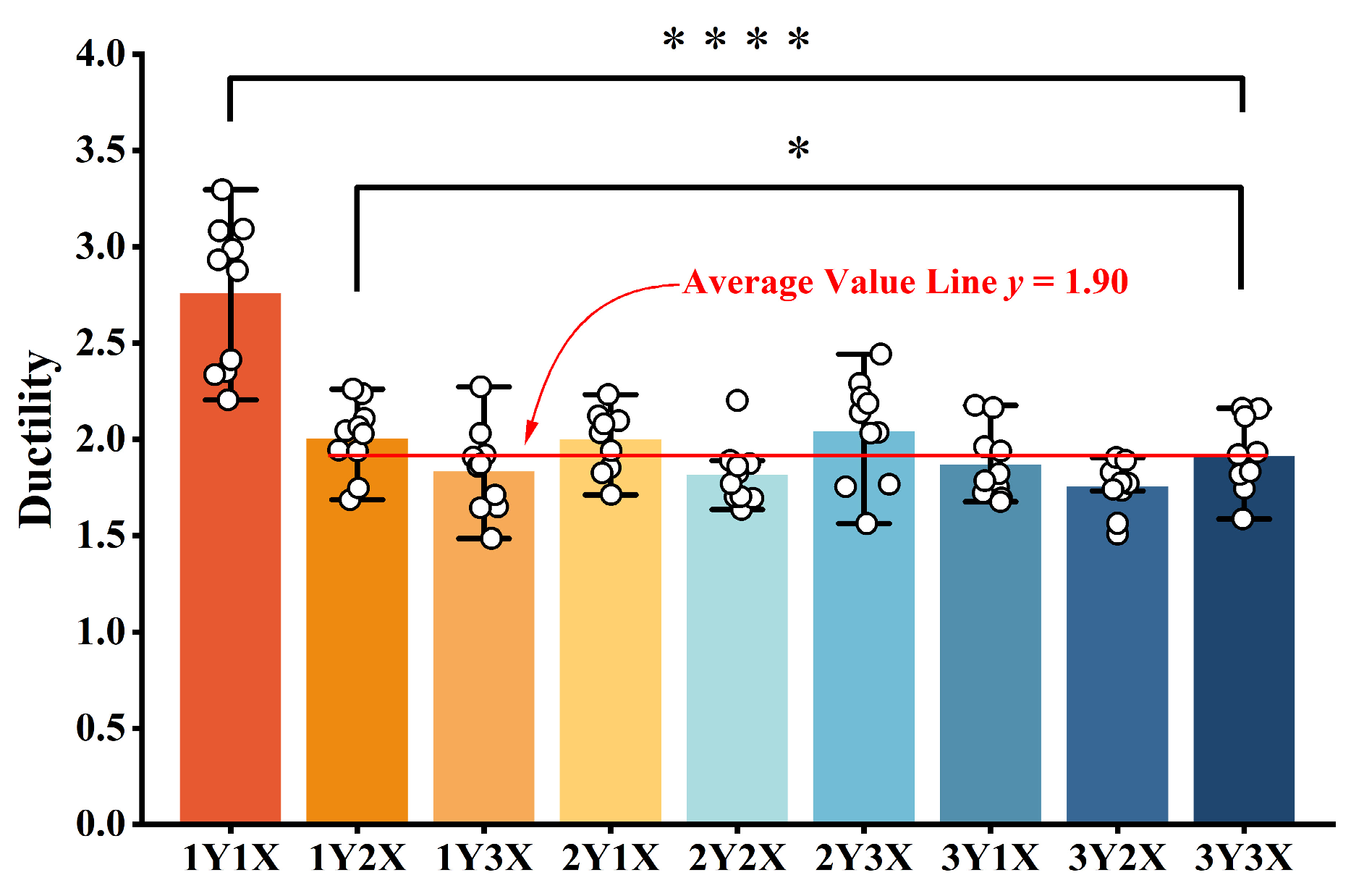
3.5. Ductility

According to EN 12512 [37], ductility is defined as the capacity of a joint to experience a substantial slip within the plastic range while maintaining strength. Ductility is quantified by the ratio of the ultimate slip to the yield slip, as outlined in Equation (15).

$$\begin{array}{c}D={\displaystyle \frac{{\delta }_u}{{\delta }_y}}\end{array}$$

(15)

Figure 12 demonstrates a highly significant difference in ductility between the 1Y1X specimen and other grouped connection specimens (p-value < 0.0,001). In the figure, single asterisks (*) represents p ≤ 0.05, and quadruple asterisks (****) represents p ≤ 0.0001. This suggests that the experimental results are unlikely to have resulted from random error and possess substantial statistical significance. Furthermore, with the exception of the 1Y1X specimen, the ductility of other grouped connection specimens showed significant differences (0.01 < p-value < 0.05), although these differences exhibited relatively weaker statistical significance. These findings suggest that the number and arrangement of wooden nails had a negligible impact on the ductility of the structure, which demonstrated stable performance. This stability was reflected in a mean ductility of 1.90 and a coefficient of variation (COV) of 9.88%, falling just below the threshold for low-variability systems as defined by the NDS (COV < 10%) [32]. Integrating the findings from Section 3.3, it is evident that in grouped specimens, the nail arrangement and single wooden nails provide adequate ductility for a uniform load distribution [27]. Consequently, the overall load-bearing capacity of a structure can be derived by summing the design values of the single nails.

The primary reason for the two distinct significance differences was the influence of the group effect on structural ductility. The 1Y1X specimen consisted of a single orthogonal unit, where two shear planes connected the principal and auxiliary materials through a single wooden nail joint. This configuration provided considerable rotational freedom between the longitudinal and transverse boards (Figure 13). During plastic deformation, this increased freedom facilitated a greater relative slip within the structure. Furthermore, the limited number of wooden nails and the localized connections meant that the slip phenomenon was not constrained by other units, leading to a pronounced ductility characteristic.

In contrast, the grouped connection specimens consisted of multiple orthogonal units that mutually constrained each other, thereby enhancing the overall structural integrity and local connection strength. However, this constraint simultaneously restricted the rotational degrees of freedom between units, effectively inhibiting free sliding during the plastic deformation stage. While such a constraint contributes to improved overall stiffness and stability, it also confines plastic deformation primarily to localized regions, consequently reducing the global ductility. Collectively, this mechanism elucidates the influence of group effects on ductility in discrete connection systems when nail groups work collaboratively, highlighting the need to carefully balance the local degrees of freedom and global constraints in design.

4. Conclusions

This study systematically analyzed the influence of the group effect on the yield point, load-bearing capacity, slip modulus, and ductility of wooden nail joints. The key conclusions derived from the experimental and regression analyses are as follows:

(1)

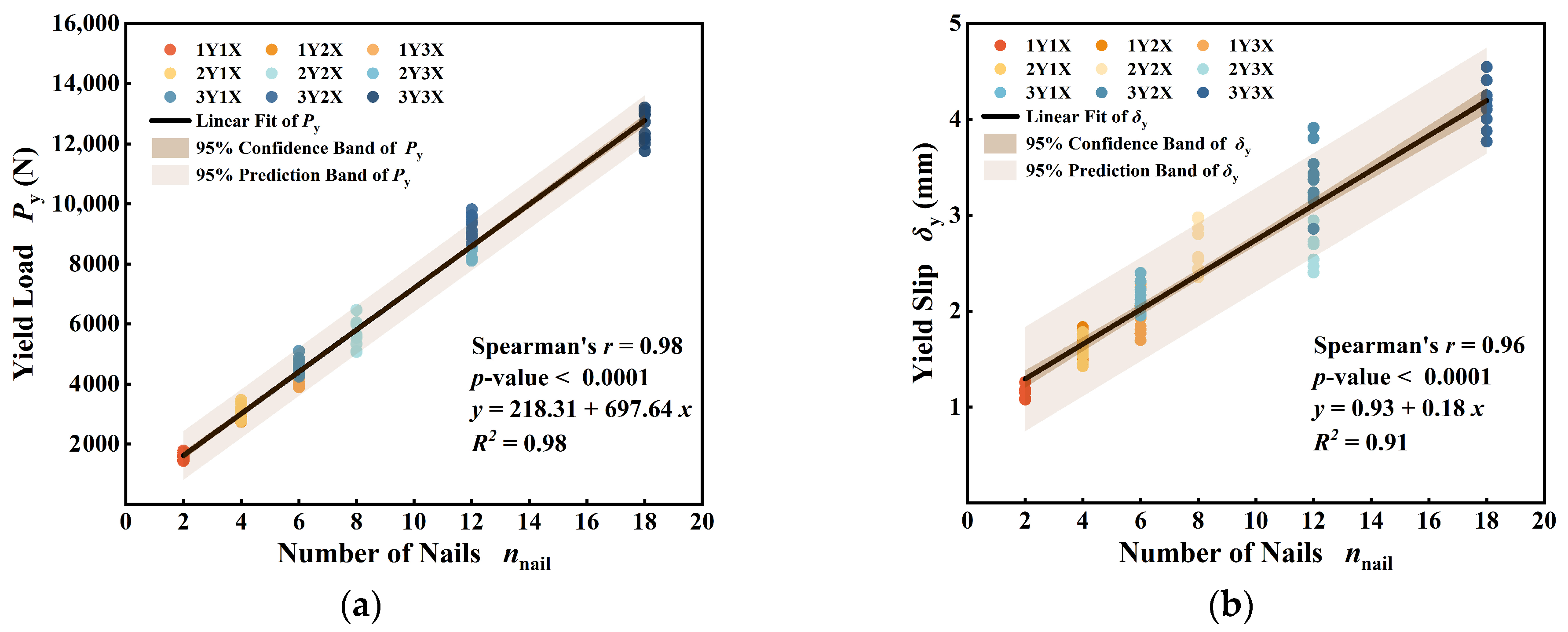
The number of wooden nails exhibits a significant positive correlation with both the yield load and yield displacement, enabling the effective prediction of the structural yield point. This relationship ensures the precise control of the yield load in the design of wooden structures.

(2)

The variations in material properties and assembly tightness due to the combination of multilayer boards lead to an uneven stress distribution at different joints. Consequently, the wooden nails experience varying degrees of failure, with failure modes exhibiting a random distribution.

(3)

The load-bearing capacity analysis revealed that a consistent arrangement of wooden nails results in a highly stable group effect coefficient, which demonstrates no significant correlation with the number of wooden nails. This stability enhances the predictability of wooden nail connections in NCLT design, thereby facilitating structural optimization and improving the overall reliability.

(4)

Spearman correlation analysis revealed a significant positive correlation between the number of wooden nails and the group effect coefficient of the joint slip modulus. Additionally, the theoretical model developed through regression analysis exhibits high accuracy in predicting the slip modulus of wooden nail group connections. An increase in the number of wooden nails effectively enhances the joint’s resistance to deformation and overall stiffness, illustrating the linear accumulation characteristic of the group effect.

(5)

Specimens composed of a single orthogonal unit exhibit greater rotational degrees of freedom, resulting in higher slip ductility. In contrast, group connections restrict the slip and rotational freedom through the mutual constraints of multiple orthogonal units. While this arrangement enhances the overall stiffness and stability of the structure, it results in relatively lower ductility, reflecting the suppressive effect of the group effect on structural deformation.

However, existing research still has the following limitations: (1) In discrete discontinuous media systems, the presence of spatial effects means that an increase in the load transfer hierarchy within the nailed layer can significantly impact the overall load-bearing performance of the structure. To accurately characterize the cooperative load-bearing mechanism of discontinuous transfer systems, it is necessary to introduce a discrete topology correction factor. (2) Current studies primarily expand the scale of wooden nails by increasing the number of discrete units (discontinuous transfer media) while keeping the number of nails within a single unit (continuous transfer media) constant. This critical factor has not yet been adequately explored, and classical theories, which are predominantly based on continuous transfer media, are not directly applicable to discontinuous systems.

Based on these findings, future research should focus on the performance degradation of NCLT discontinuous load transfer systems caused by hierarchical load transmission, incorporating a discrete topology correction factor to accurately describe the structural load-bearing characteristics. Additionally, considering that NCLT consists of multiple discrete units, where the nails within a single unit form a continuous transfer medium, it is essential to systematically investigate the group effect of nails within continuous media. This will help reveal the composite load transfer mechanism of NCLT, characterized by “global discontinuity–local continuity,” and provide new perspectives and methodologies for advancing the mechanics of discontinuous media.