Stability Analysis of Horizontal Layered Multi-Stage Fill Slope Based on Limit Equilibrium Method
Abstract
1. Introduction
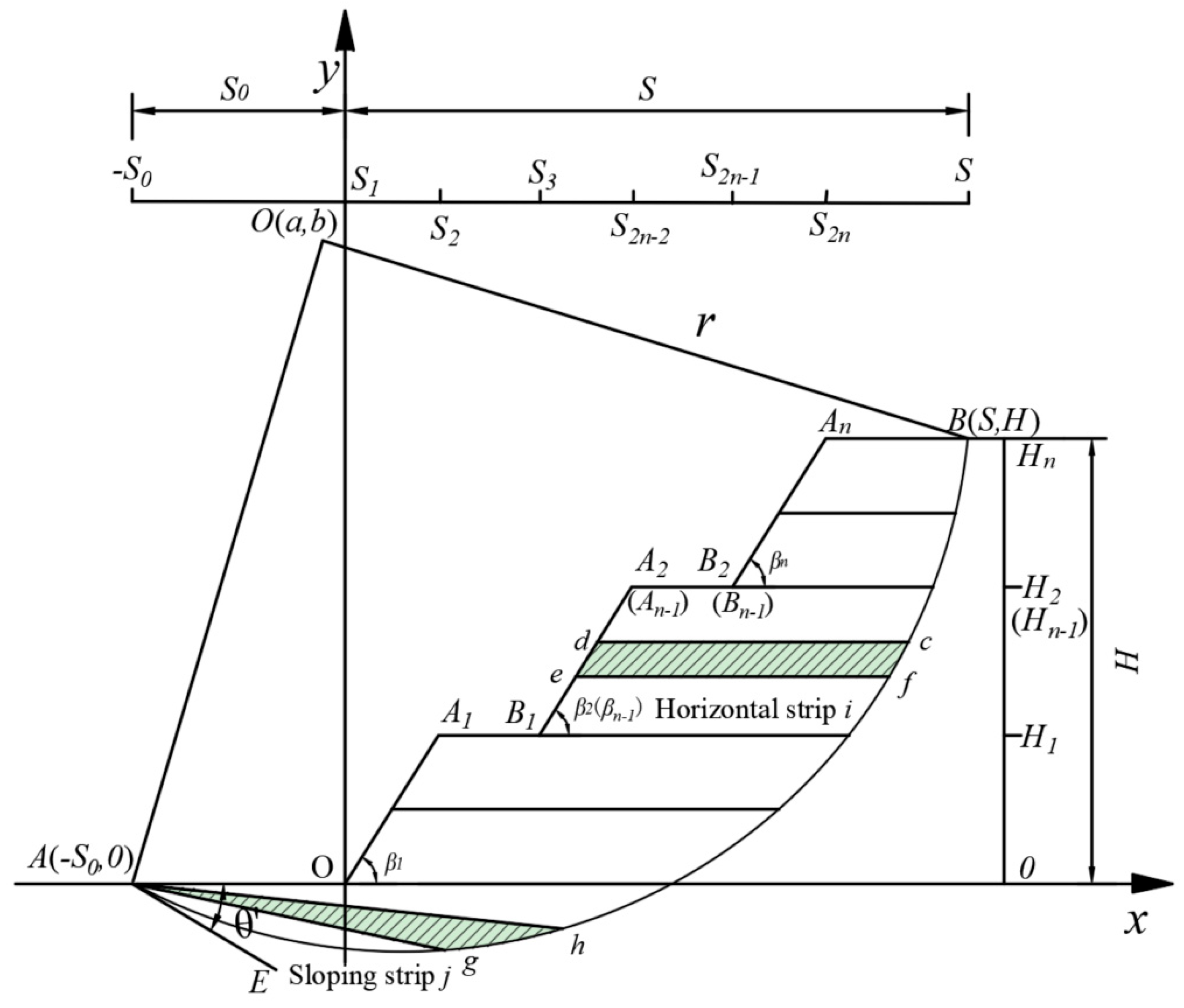
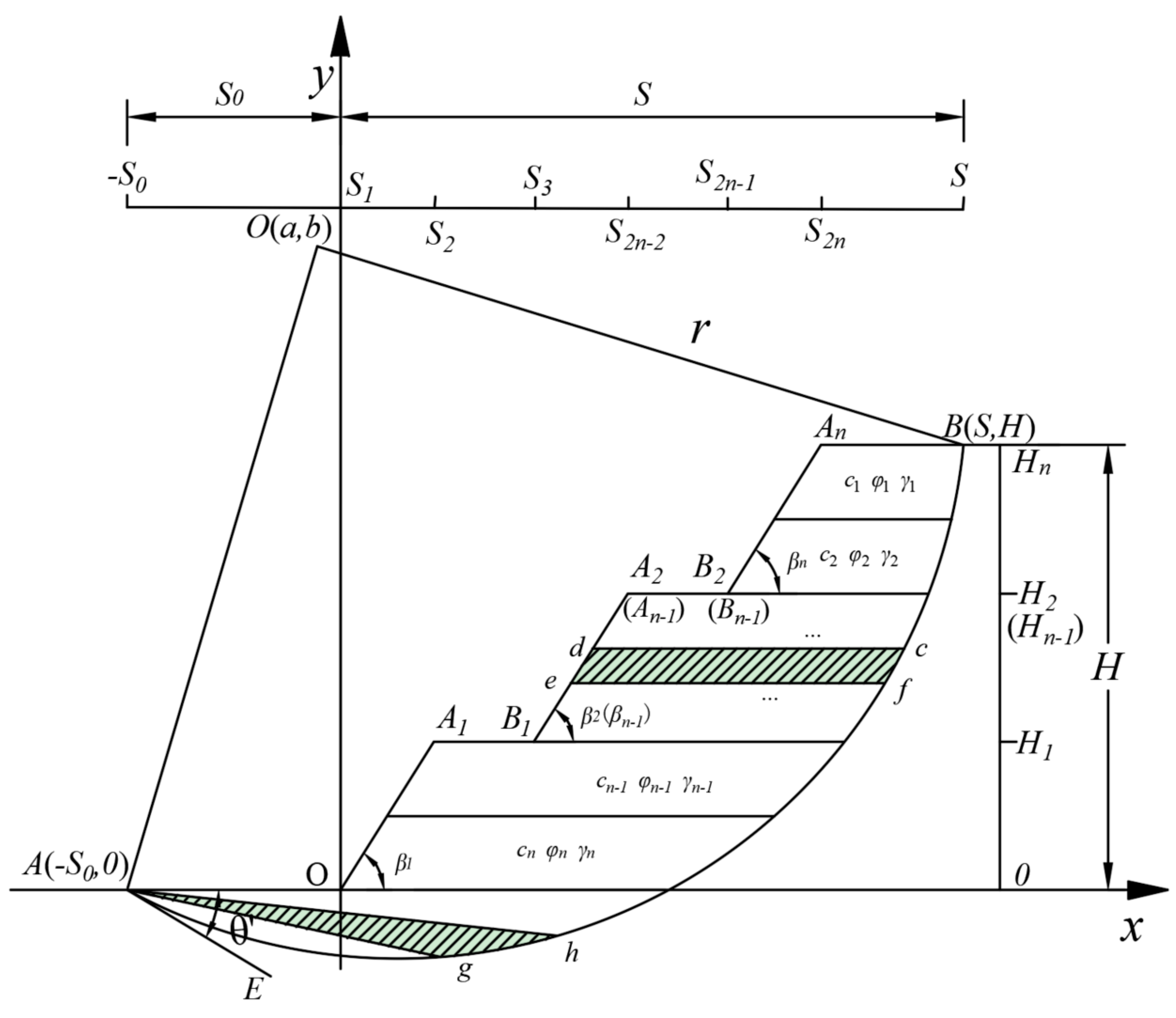
2. Basic Assumption of Sliding Soil and Stress Condition of Soil Strip
2.1. Basic Assumptions
- (1)
- The slope soil is an ideal rigid-plastic body;
- (2)
- The shear strength of slope soil complies with the Mohr–Coulomb criterion;
- (3)
- Ignore the interaction force between the soil strips taken;
- (4)
- The slope is a heterogeneous slope and the slip surface is an arc slip surface.
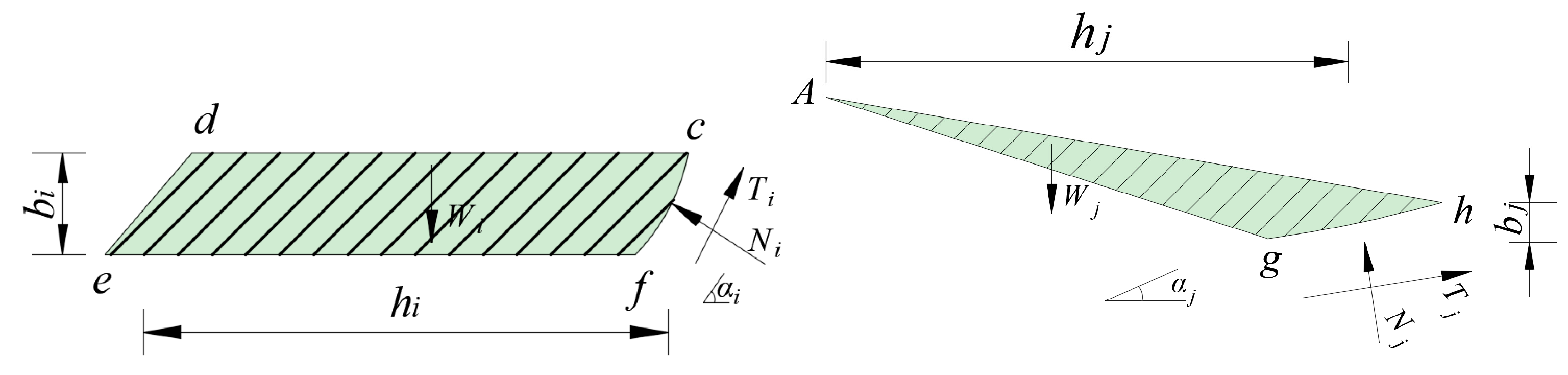
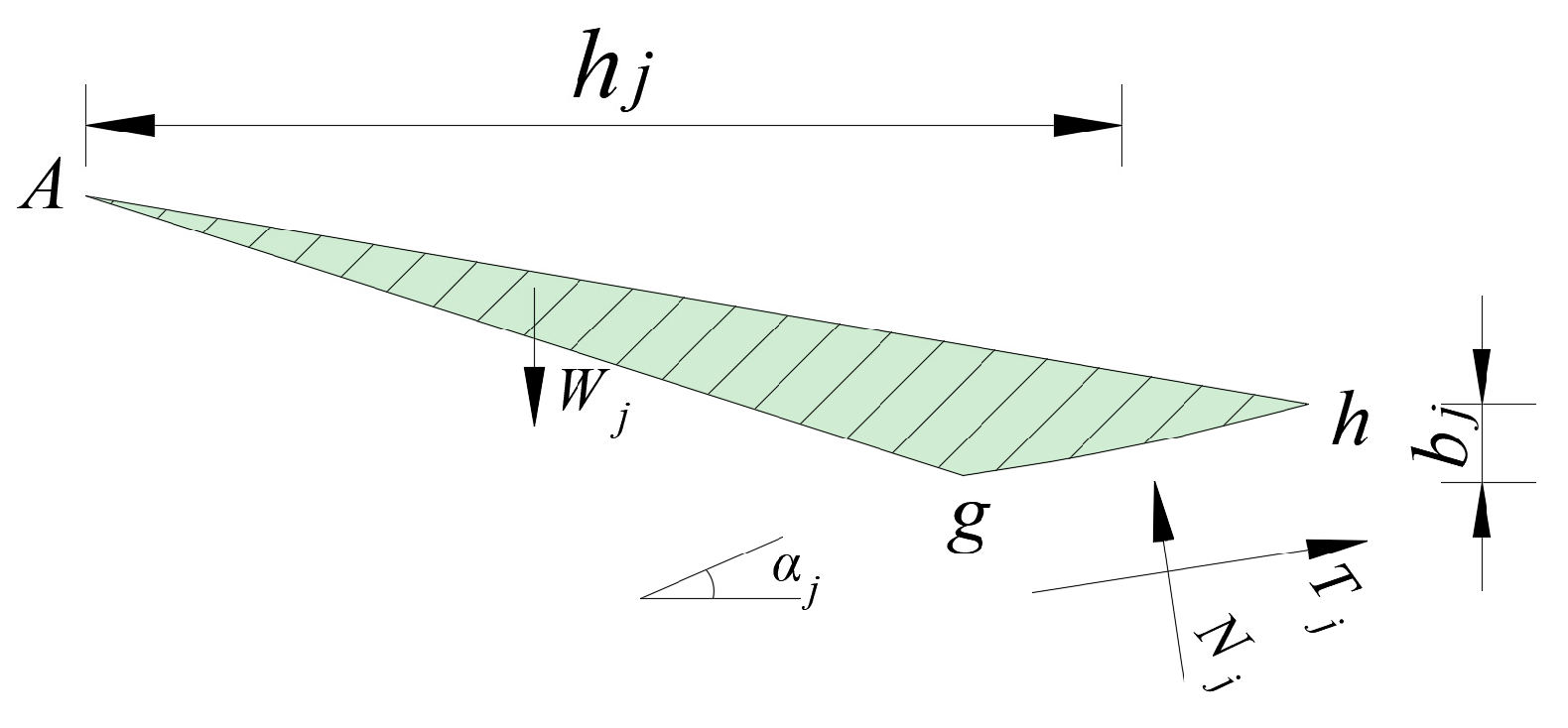
2.2. Stress Condition of Soil Strip
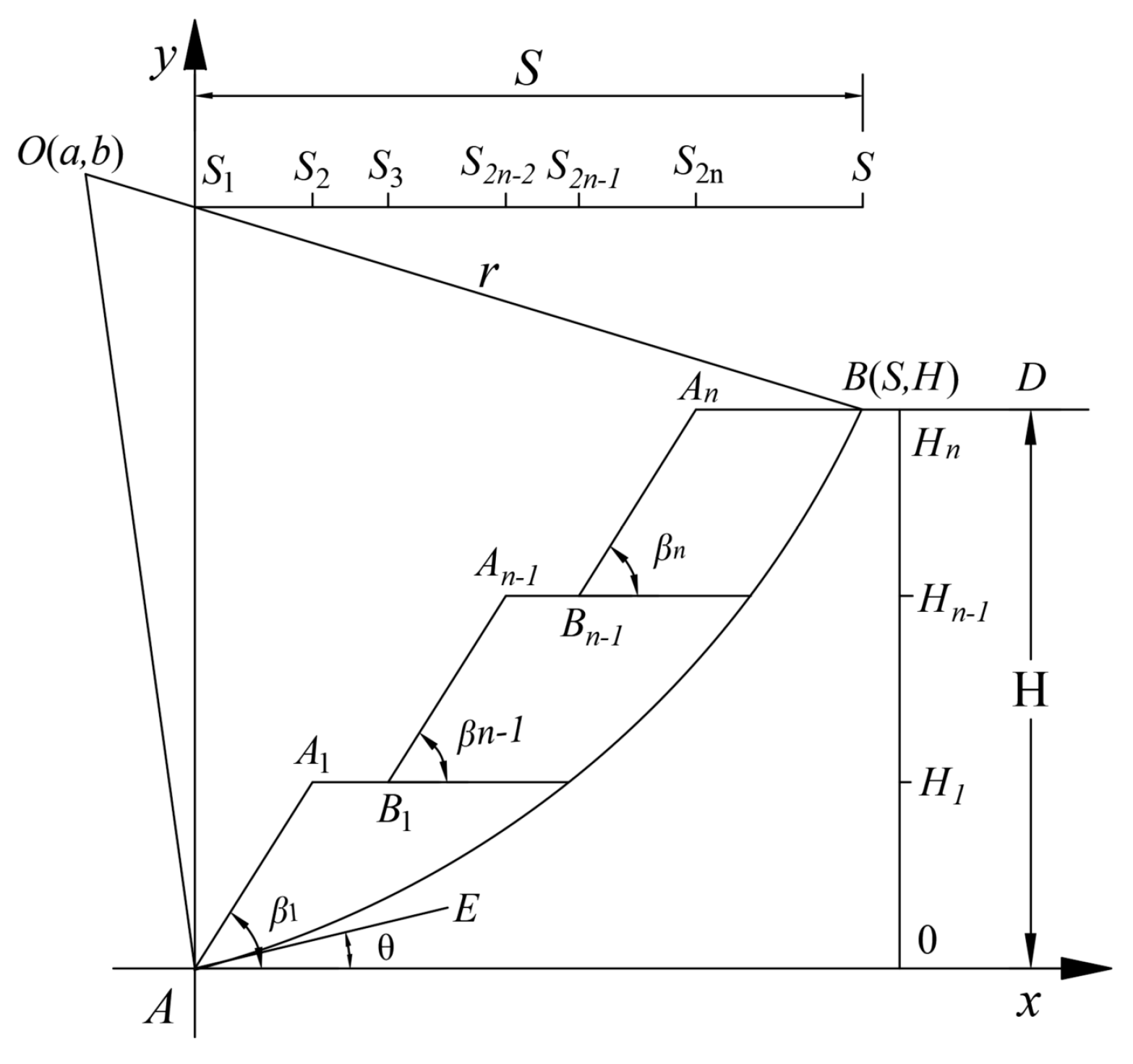
3. Stability Analysis of Multi-Stage Fill Slope Under Overall Failure Mechanism
3.1. Stability Analysis Under Circular Failure Mechanism of Slope Toe
3.1.1. Damage Mechanism
3.1.2. Stability Analysis
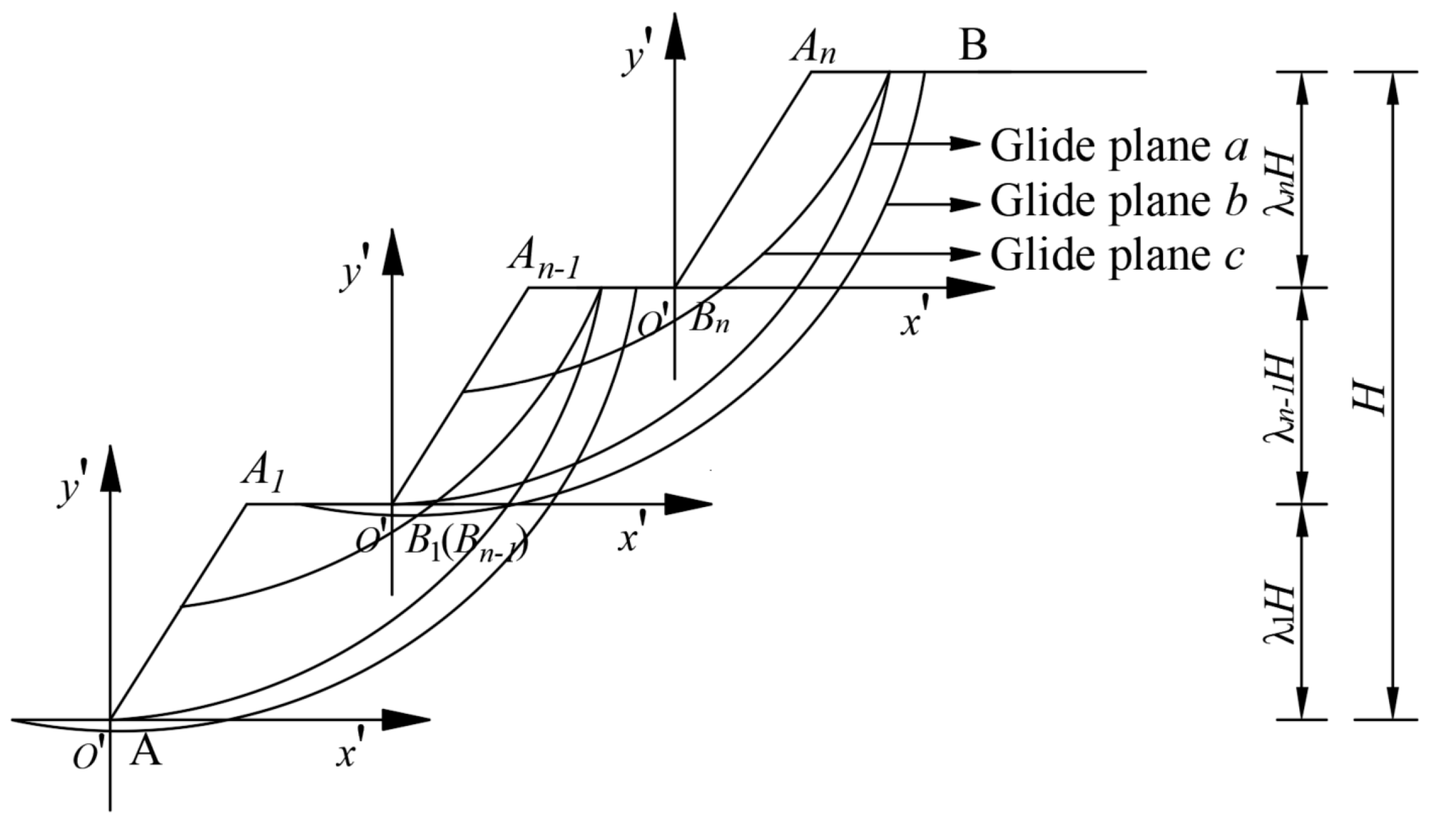
3.2. Stability Analysis Under the Mid-Point Circle Failure Mechanism
3.2.1. Failure Mechanism
3.2.2. Stability Analysis
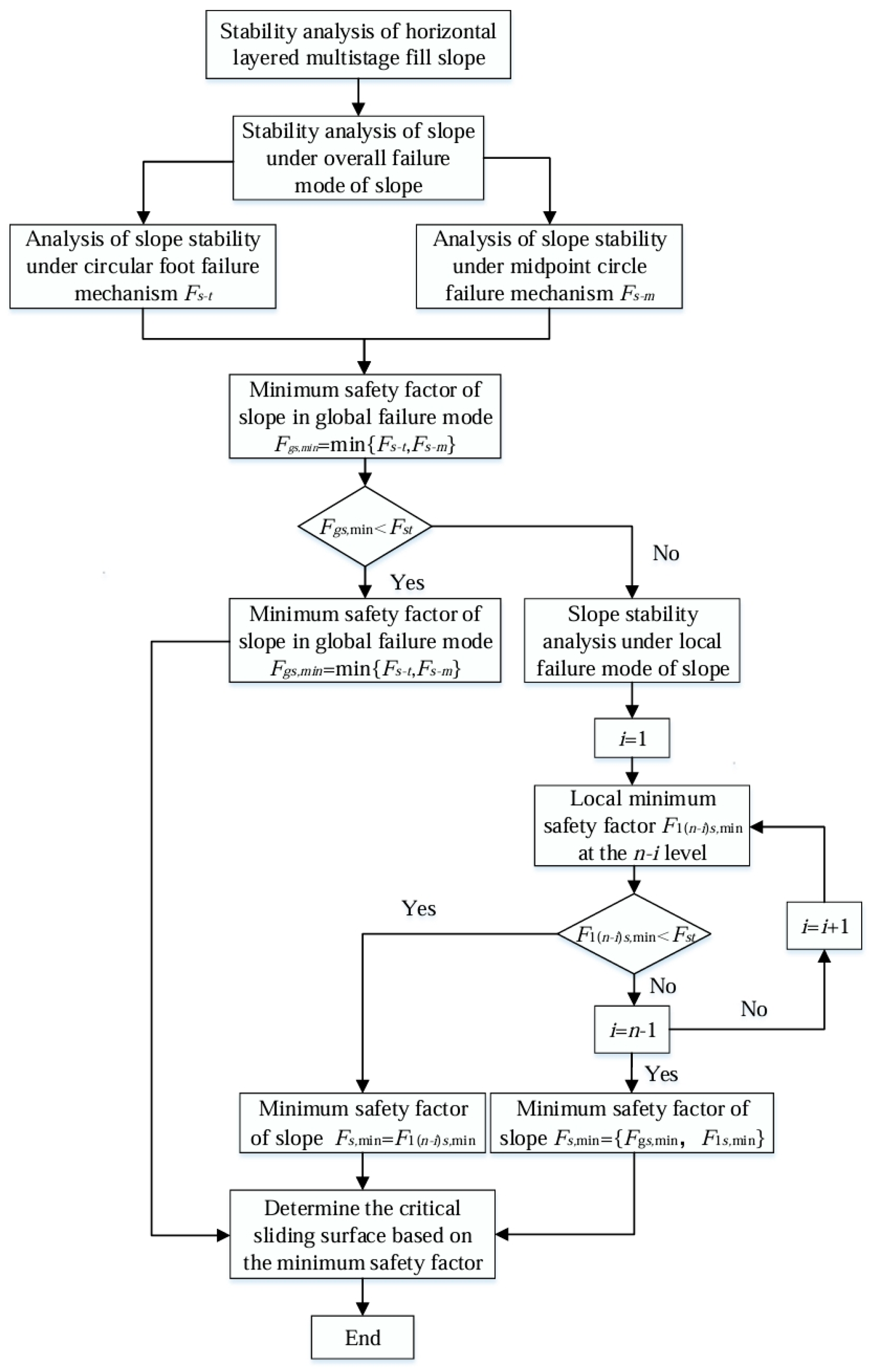
3.3. The Minimum Safety Factor of Multi-Stage Fill Slope Under the Overall Failure Mode
4. Stability Analysis of Multi-Stage Fill Slope Under Local Failure Mechanism
4.1. Slope Stability Analysis Under Local Single-Stage Failure Mode
4.1.1. Damage Mechanism
4.1.2. Stability Analysis
4.2. Slope Stability Analysis Under Local Multi-Stage Failure Mode
5. Multi-Stage Fill Slope Stability Analysis Process
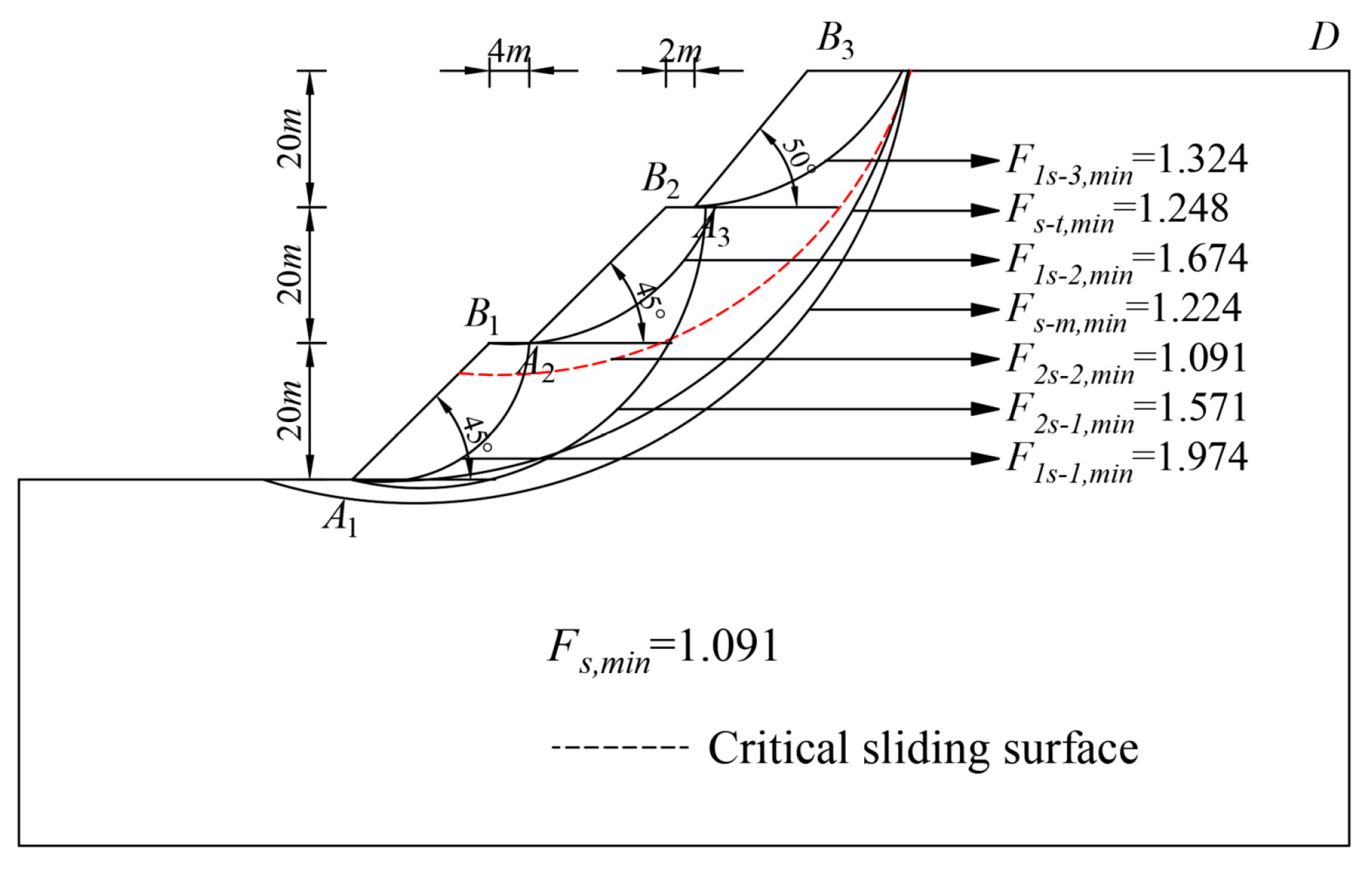
6. Example Verification
6.1. Example 1
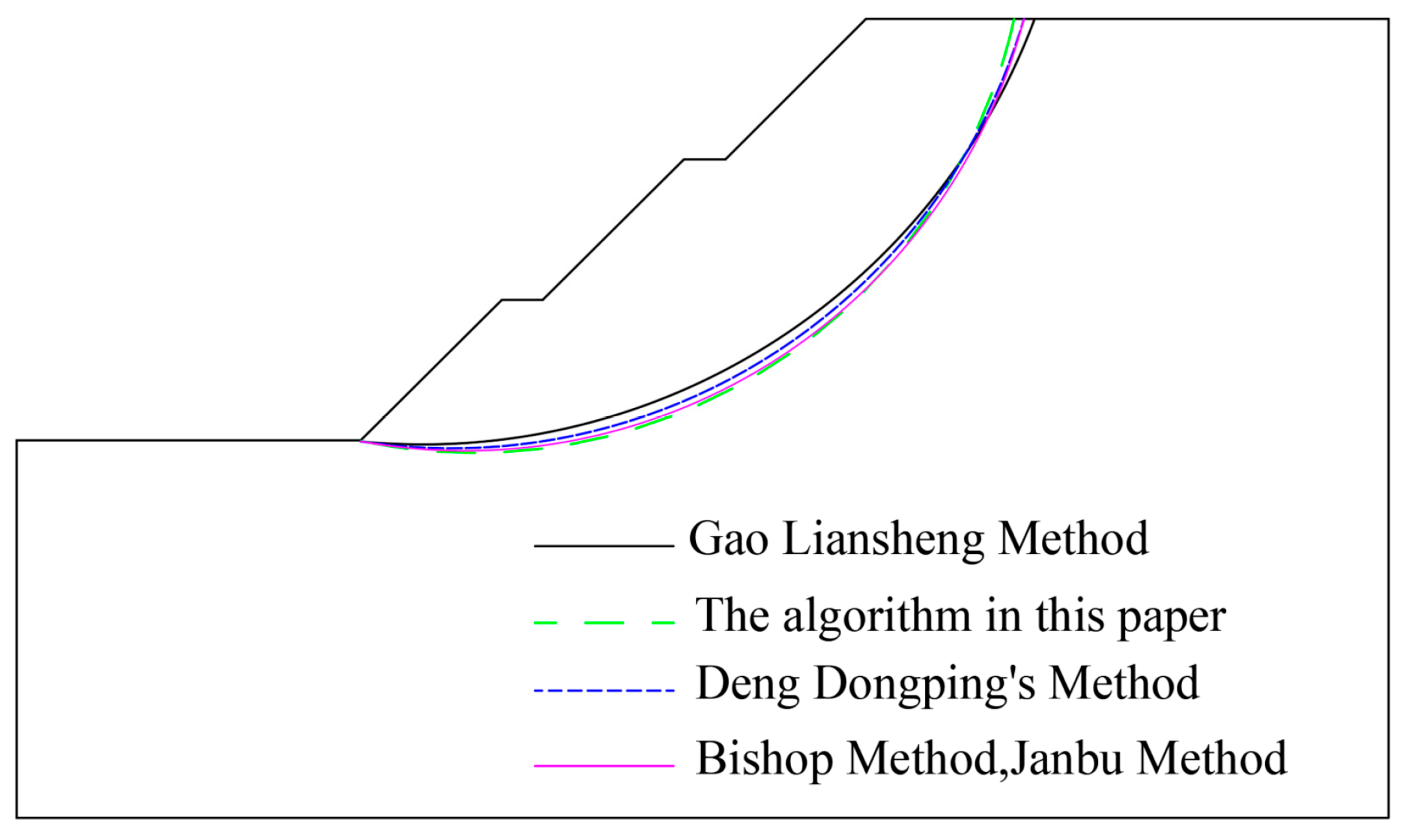
6.2. Example 2
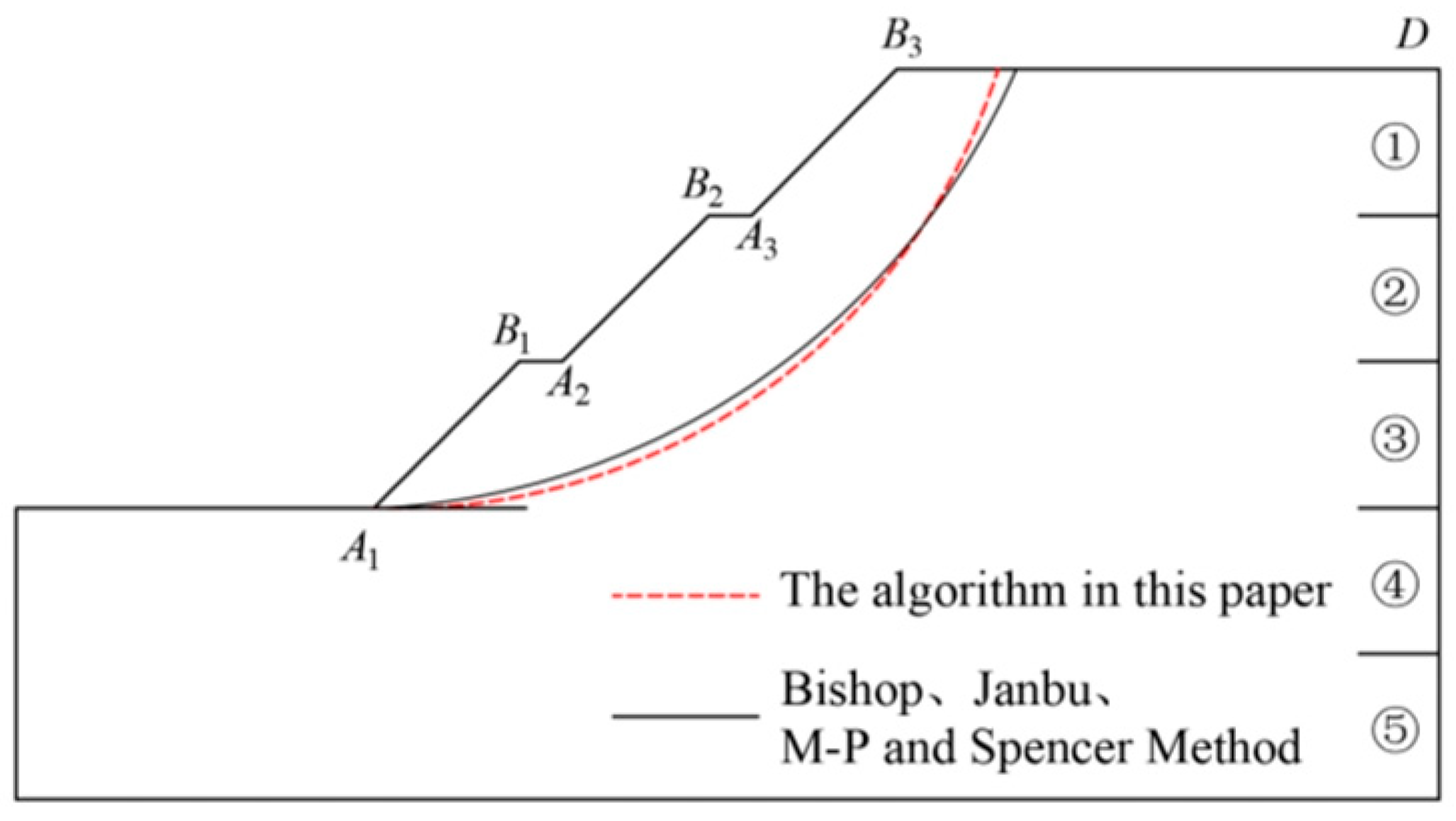
6.2.1. Algorithm in This Study
6.2.2. Traditional Strip Method
6.2.3. Comparative Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, Z.; Cheng, X. High Fill Slope Collapse: Stability Evaluation Based on Finite Element Limit Analyses. Transp. Geotech. 2024, 44, 101156. [Google Scholar]
- Mei, Y.; Zhou, D.; Hu, C.; Wang, X.; Zhang, Y.; Xiao, N.; Shi, W. Study on Deformation Characteristics of Loess Ultrahigh-Fill Slope Based on Large-Scale Undisturbed Soil Centrifugal Model Tests. Front. Earth Sci. 2022, 10, 848542. [Google Scholar]
- Jin, L.; Liao, Y. Upper Bound Analysis of Two-Layered Slopes Subjected to Seismic Excitations Using the Layer-Wise Summation Method. Buildings 2024, 14, 1990. [Google Scholar] [CrossRef]
- Zhang, F.; Jia, S.; Gao, Y. Stability Analysis of Cut-Fill and Deep Patch Unsaturated Slopes Under Steady Infiltration Conditions. Sci. China Technol. Sci. 2025, 68, 1120701. [Google Scholar]
- Wu, Y.; Zhou, X.; Liu, J. Long-Term Performance of the Water Infiltration and Stability of Fill Side Slope against Wetting in Expressways. Appl. Sci. 2022, 12, 5809. [Google Scholar] [CrossRef]
- Yao, Y.; Zhang, J.; Li, X.; Tu, Y.; Zhong, Z. The Stability of Slopes and Building Structures Using an Energy Visualization Procedure. Buildings 2024, 14, 3705. [Google Scholar] [CrossRef]
- Ren, Y.; Li, T.; Yang, L.; Wei, D.; Tang, J. Stability Analysis of Ultra-High-Steep Reinforced Soil-Filled Slopes Based on Centrifugal Model Tests and Numerical Calculation. Chin. J. Geotech. Eng. 2022, 44, 836–844. [Google Scholar]
- Ye, S.; Zhuang, Y.; Fang, G. Stability Factors and Deformation Law of Loess High Fill Slope. J. Lanzhou Univ. Technol. 2021, 47, 120–126. [Google Scholar]
- Liu, X.; Song, B.; Sun, Z.; Jiao, W. Critical Filling Height of Embankment over Soft Soil: A Three-Dimensional Upper-Bound Limit Analysis. Buildings 2025, 15, 395. [Google Scholar] [CrossRef]
- Renaud, V.; Al Heib, M.; Muller, R.; Burda, J. Long-Term Slope Stability of Abandoned Mine Lake—Numerical Modelling and Risk Assessment. Mater. Proc. 2021, 5, 88. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, C.; Zheng, W.; Wang, X.; Zhang, J. Analysis of the Stability of a High Fill Slope under Different Gradients and Precipitation Conditions. Appl Sci. 2024, 14, 7590. [Google Scholar] [CrossRef]
- Li, Z.; Sun, L.; Liu, L.; Guan, C. Research on Safety Evaluation Method of High-Fill Slope Considering Heterogeneity and Anisotropy. Bull. Eng. Geol. Environ. 2022, 81, 275. [Google Scholar]
- Amena, S. Analysis of the Stability of Reinforced Plastic Waste Treated Clay as Embankment Fill on Soft Soils. Adv. Civ. Eng. 2022, 2022, 1831970. [Google Scholar]
- Gong, W.; Zhang, X.; Pei, X.; Chen, L.; Jiang, R.; Sun, H.; Zhong, Y. Instability Modelling of Loess Fill Slope with Influence of Weak Zone of High and Steep Filling Interface. J. Eng. Geol. 2023, 31, 288–298. [Google Scholar]
- Yong, X.; Zhang, Y.; Hou, Y.; Han, B.; An, N.; Zhang, H.; Ma, Y. Stability of Loess High-Fill Slope Based on Monitored Soil Moisture Changes. Res. Cold Arid Reg. 2023, 15, 191–201. [Google Scholar]
- Yan, C.; Wang, H. Three-Dimensional Stability of Slopes with Cut-Fill Interface Based on Upper-Bound Limit Analysis. Chin. J. Geotech. Eng. 2024, 46, 174–181. [Google Scholar]
- Mostafaei, H.; Behnamfar, F.; Alembagheri, M. Nonlinear analysis of stability of rock wedges in the abutments of an arch dam due to seismic loading. Struct. Monit. Maint. 2020, 7, 295–317. [Google Scholar]
- Chen, X.; Zhou, Z.; Zhu, Y.; Pu, S.; Zhang, D.; Li, E. Evaluating Seismic Stability of Reinforced Soil Slopes Using the Limit Equilibrium Method: Influence of Geosynthetic Strength Indicators. Front. Phys. 2025, 12, 1526223. [Google Scholar]
- Fatehi, M.; Hosseinpour, I.; Jamshidi Chenari, R.; Payan, M.; Javankhoshdel, S. Deterministic Seismic Stability Analysis of Reinforced Slopes Using Pseudo-Static Approach. Iran. J. Sci. Technol. Trans. Civ. Eng. 2023, 47, 1025–1040. [Google Scholar]
- Zhang, F.; Jia, S.; Shu, S. Effects of Seismic Amplification on the 3D Stability of Fill Slopes in V-Shaped Valleys. Acta Geotech. 2024, 19, 3241–3255. [Google Scholar]
- Wang, X.; Yuan, Y.; Zhang, S. Reliability Analysis of Natural High Loess Slope and Backfill Slope in Northern Shanxi area. J. Xi’an Univ. Archit. Technol. 2021, 53, 665–672. [Google Scholar]
- Huang, A.; Ye, S. Sensitivity of High Fill Slope Stability Factors Under Seismic Conditions. Soil Mech. Found. Eng. 2020, 57, 356–363. [Google Scholar]








| Calculation Method | Center of a Circle (a,b) | Radius r/m | Safety Factor Fs,min |
|---|---|---|---|
| Bishop method | (22.564, 37.182) | 25.972 | 2.288 |
| Janbu method | (22.319, 37.408) | 25.884 | 2.107 |
| The algorithm in this paper | (22.385, 37.047) | 25.817 | 2.124 |
| Deng Dongping | - | - | 2.197 |
| Gao Liansheng | - | - | 2.072 |
| Soil Layer Numbering | |||
|---|---|---|---|
| ① Crushed stone | 27.6 | 38.5 | 20.2 |
| ② Sandy soil I | 27.0 | 28.0 | 19.0 |
| ③ Sandy soil II | 19.3 | 25.0 | 19.0 |
| ④ Silty clay I | 15.3 | 33.0 | 18.5 |
| ⑤ Silty clay II | 17.2 | 25.0 | 19.5 |
| Calculation Method | Center of a Circle (a,b) | Radius r/m | Safety Factor Fs,min |
|---|---|---|---|
| Bishop method | (89.28, 80.125) | 61.04 | 1.384 |
| Janbu method | (89.28, 80.125) | 61.04 | 1.297 |
| M-P method | (89.28, 80.125) | 61.04 | 1.395 |
| Spencer method | (89.28, 80.125) | 61.04 | 1.395 |
| Calculation Method | Safety Factor Fs,min | Minimum Relative Deviation of Safety Factor |
|---|---|---|
| The algorithm in this paper | 1.342 | - |
| Bishop method | 1.348 | −0.4% |
| Janbu method | 1.297 | 3.5% |
| M-P method | 1.395 | −3.8% |
| Spencer method | 1.395 | −3.8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Ye, S.; Qiu, M.; Ye, W.; Li, J. Stability Analysis of Horizontal Layered Multi-Stage Fill Slope Based on Limit Equilibrium Method. Buildings 2025, 15, 1105. https://doi.org/10.3390/buildings15071105
Li X, Ye S, Qiu M, Ye W, Li J. Stability Analysis of Horizontal Layered Multi-Stage Fill Slope Based on Limit Equilibrium Method. Buildings. 2025; 15(7):1105. https://doi.org/10.3390/buildings15071105
Chicago/Turabian StyleLi, Xiaohui, Shuaihua Ye, Manman Qiu, Weina Ye, and Jingbang Li. 2025. "Stability Analysis of Horizontal Layered Multi-Stage Fill Slope Based on Limit Equilibrium Method" Buildings 15, no. 7: 1105. https://doi.org/10.3390/buildings15071105
APA StyleLi, X., Ye, S., Qiu, M., Ye, W., & Li, J. (2025). Stability Analysis of Horizontal Layered Multi-Stage Fill Slope Based on Limit Equilibrium Method. Buildings, 15(7), 1105. https://doi.org/10.3390/buildings15071105





