Application of MASW, Microtremor, and Seismic Refraction Tests for Buildings in Vulnerable Communities

Abstract

The structural system is an essential component in engineering and architecture, determining the stability, strength, and functionality of buildings. This study addresses the integration of geophysical data obtained through techniques such as Multichannel Analysis of Surface Waves (MASW), microtremors, and seismic refraction in architectural and structural design, with special attention to its application in expanding urban areas and vulnerable communities. These methods allow for the characterization of the soil’s dynamic properties, identifying critical vibration periods that influence structural behavior, especially in sandy soils near rock outcrops up to 30 m deep. The discrepancy between soil vibration periods and structural periods can induce resonance phenomena, highlighting the need to incorporate geophysical analyses in the design to avoid structural failures. By using adapted equations, the dimensions of load-bearing elements like columns are optimized, considering stiffness, mass, and local seismic conditions. The results obtained through computational tools validate the effectiveness of this approach, ensuring safer and more sustainable designs. This study emphasizes the importance of merging geophysical and dynamic knowledge to optimize structural performance and promote resilience in complex geophysical environments. Incorporating soil vibration analysis not only improves building safety but also contributes to sustainable urban development, especially in regions prone to seismic events.

1. Introduction

The structural system is a crucial element in both engineering and architecture, playing a fundamental role in determining the stability, strength, and functionality of a structure [1]. The diversity of types and components that make up the structural configuration allows for a detailed analysis that highlights its relevance and contributions to the overall design of the structure [2]. This structural configuration encompasses a wide variety of types and components, each essential to ensuring the stability, strength, and functionality of the structure [3]. From load-bearing structures such as frames and shells to trusses and grids, the choice of configuration is based on the specific requirements of the project and its constraints. It is crucial to emphasize that the structural design of buildings is a time-consuming process, which can lead to suboptimal designs. Therefore, a meticulous and thoughtful selection of the structural configuration for each project is essential. However, with the assistance of graphics and an efficient structural simulator, optimal structural designs with reduced construction mass can be proposed [4]. By understanding the complexities of the structural configuration, it is possible to create innovative designs that withstand the test of structural displacement. This phenomenon refers to the lateral movement or displacement of a building or structure caused by external forces such as wind, earthquakes, or dynamic vibrational loads [5]. This phenomenon is a crucial factor in structural design, as excessive displacement can cause structural damage, discomfort for occupants, and even collapse in extreme cases. Therefore, structural engineering and displacement control play an essential role in ensuring the stability, accuracy, and safety of the systems involved [6]. Displacement control is a complex task that requires expertise in structural analysis and engineering. The factors that influence displacement control depend on design requirements, local building codes, and the nature of the structure itself. It is often necessary to conduct a thorough analysis, including computer simulations and structural calculations, to ensure effective displacement control in building designs [7]. It is important to note that displacement control techniques can vary depending on the specific application and context. The techniques mentioned above offer an overview of the different approaches used in various fields to manage and control displacement [8]. Following the magnitude ML = 6.0 earthquake in central Italy [9], Pescara del Tronto suffered severe damage and 48 fatalities, while Vezzano only experienced minor damage, despite being just 1.3 km away. The soil resonance in Pescara, with amplification in the 4–6 Hz range, exacerbated the damage, in contrast to Vezzano. Additionally, the better construction quality in Vezzano suggests lower seismic vulnerability, highlighting the importance of geotechnical and construction factors in seismic areas.

While previous studies have addressed seismic risk assessment and soil dynamics [10], there is a gap in the systematic integration of geophysical data, obtained through techniques such as MASW, microtremors, and seismic refraction, into architectural and structural design and their relationship with calculations to determine the sections of load-bearing elements such as columns, which are significant in terms of importance and failure levels [11]. This research addresses this gap by demonstrating how the combination of these methods can provide a detailed characterization of the soil’s dynamic properties, particularly in areas with high geological variability [12], unlike conventional approaches that often simplify soil conditions [13], as well as the need to consider specific soil vibrations to avoid structural resonance and optimize the seismic performance of buildings, thereby contributing to safer and more sustainable designs in complex geophysical environments, applied in a straightforward manner.

Seismic-resistant design is an ever-evolving field driven by the need to protect lives and minimize damage in seismically active environments. Previous research has established the critical importance of soil characterization in the analysis of the seismic response of structures [14]. Geophysical techniques, such as the Multichannel Analysis of Surface Waves (MASW) method and microtremor analysis, have proven to be effective tools for obtaining shear wave velocity profiles and estimating the fundamental period of the soil. In fact, seismic microzonation based on ambient noise [15] is a well-established practice for evaluating seismic hazard at the local level and classifying soil types according to standards such as Eurocode 8 [12].

However, current research can benefit from further exploration of the integration of geophysical data with structural design models to optimize both safety and efficiency [12]. While the importance of soil vibration periods is recognized [3], the existing literature does not sufficiently address how these data can be applied practically and economically in vulnerable communities where resources for construction and design are often limited. Furthermore, there is an opportunity to investigate how digital construction technologies, such as Building Information Modeling (BIM), could be integrated with geophysical test results to enhance the precision and effectiveness of seismic design [16].

This state-of-the-art review suggests that, while there are proven methodologies for soil characterization and seismic design, there remains a gap in the application of these methodologies in specific contexts, as well as in the integration of cutting-edge technologies to optimize the design process and improve the resilience of structures in vulnerable communities. Therefore, this study is justified by addressing this gap, demonstrating how the combination of geophysical methods, a detailed analysis of local seismicity, and the consideration of common construction practices in these communities can lead to safer and more sustainable designs.

To understand the soil dynamics and the vibrations it can withstand, we must consider the dynamic Poisson’s ratio in granular soils. This process allows us to obtain values for Poisson’s ratio in various types of soils [3]. Poisson’s ratio is a property that describes how a material deforms in response to an applied stress. In the case of granular soils, it refers to the relationship between lateral deformation and axial deformation when the soil is subjected to a dynamic load [17]. This process can significantly affect the behavior and response of the soil under different loads and conditions. Therefore, understanding and accurately determining this ratio is essential for designing and constructing structures and foundations safely and efficiently [18].

The vibration period of a structure is defined as the time it takes to complete a cycle of free oscillation after being displaced from its equilibrium position [19]. It is crucial to note that, from a dynamic perspective, it is preferable for the fundamental period of a building not to coincide with the dominant periods of seismic action to avoid dangerous resonances [20]. However, it has been found that lower vibration period values improve a building’s ability to dissipate energy during an earthquake [15]. Various studies have examined how structural configuration influences the vibration period. For example, it has been observed that the incorporation of rigid cores or shear walls reduces the period by increasing stiffness, while their absence leads to an increase in the period [21]. Additionally, structural systems with irregular floor plans may exhibit vibration modes with lower periods and less predictable directions compared to regular systems [15].

Microtremors are small ground vibrations caused by various sources, both natural and anthropogenic. These seismic waves have become a valuable tool for evaluating the dynamic characteristics and stability of building structures [11]. Microtremors typically involve high-frequency, low-amplitude ground movements generated by a variety of factors, including atmospheric pressure fluctuations, oceanic and atmospheric disturbances, and human activities. These vibrations contain valuable information about the subsurface and the structural characteristics of the built environment [22]. The study of a microtremor involves measuring and analyzing ground movement using seismometers and accelerometers placed at various locations around a building, capturing the unique response of the structure. The resulting data are processed and analyzed to extract valuable information [23]. A key application of microtremor analysis is the estimation of site amplification and the spectral characterization of microtremors at different locations. Specialized engineers can determine amplification factors at specific frequencies, which is crucial information for designing building structures that can withstand ground movements with varying frequencies [11].

In MASW tests, Rayleigh waves are used. It has been observed that when the wavelength is small, the phase velocity is influenced by the characteristics of the surface soil layers and extends to a depth equal to the wavelength. However, when the wavelength is greater, the phase velocity is also affected by the deeper layers of the soil strata [16]. If the waves are related to each other, they are considered dispersive. This characteristic exhibited by Rayleigh waves in non-uniform materials, as is often the case in soil deposits, forms the basis of several surface wave analysis methods. The first method developed for analyzing surface waves was known as SASW (Spectral Analysis of Surface Waves) [24]. Subsequently, the MASW (Multichannel Analysis of Surface Waves) method was developed [10] and ReMi (Refraction Microtremor) emerged. These surface wave evaluation techniques have advantages and disadvantages in terms of precision, detection range, ability to identify multiple layers, adaptability in noisy environments, speed of implementation, and cost [25].

The seismic refraction test (LS) is a geophysical technique used to investigate subsurface properties and determine the geological structure of a region [26]. This technique is based on the measurement and study of seismic vibrations that propagate through rock and soil layers [27]. In the context of infrastructure construction, seismic refraction is employed to assess soil bearing capacity and identify the presence of unstable or low-strength soil layers [28]. This information is particularly crucial in the planning of civil engineering projects such as the construction of bridges, roads, and buildings [29].

Poisson’s ratio ($v$) is a property that quantifies the lateral strain in relation to the longitudinal strain of a material subjected to a uniaxial load. This parameter describes the Poisson effect, a phenomenon by which a material tends to expand in directions perpendicular to the direction of compression (Figure 1a). In conventional concrete, $v$ typically ranges between 0.15 and 0.25 [30]. Poisson’s ratio is also influenced by ambient pressure and the quality of the rock in a rock mass (Equation (1)). In this context, it is relevant to consider the P-wave velocity ($V_p$, m/s) and the S-wave velocity ($V_s$, m/s) [31].

$$v={\displaystyle \frac{{(\frac{V_p}{V_s})}^2-2}{2{(\frac{V_p}{V_s})}^2-2}}$$

(1)

Young’s modulus (E) can be described as a mechanical property, also known as the modulus of elasticity. This property explains a material’s ability to undergo elastic deformations when subjected to an external force (Figure 1b). In this context, the shear modulus (G) and Poisson’s ratio (ν) are also relevant, leading to Equation (2) [32].

$$E=2G(1+v)$$

(2)

The shear modulus (G) is a measure of a material’s resistance to deformation due to shear or torsional stresses. It is defined as the ratio of the applied shear stress to the resulting angular deformation (Figure 1c). This modulus is also known as the shear modulus, transverse elasticity modulus, or tangential elasticity modulus. In this context, the material’s density (ρ) and the S-wave velocity (Vs, m/s) are also relevant, as seen in Equation (3) [33].

$$G=\rho V{s}^2$$

(3)

The bulk modulus (B) is defined as a material’s resistance to compression (Figure 1d). On the other hand, Poisson’s ratio (ν) describes how the change in shape is distributed in a material when subjected to a load, and Young’s modulus (E) measures the axial or longitudinal stiffness of a material (Equation (4)). It is important to emphasize that both Young’s modulus (E) and Poisson’s ratio (ν) are fundamental for understanding the material’s behavior under different loading conditions [32].

$$B={\displaystyle \frac{E}{3(1-2v)}}$$

(4)

The structural vibration period (Equation (4)) is a crucial parameter in seismic response. Its synchronization with the dominant frequency of the earthquake induces resonance, a risk that can be mitigated through optimal design of load-bearing element sections (walls, columns), which adjust lateral stiffness and control drifts according to standards such as ASCE 7-22 [34]. To determine the relationship between the sections of seismic-resistant elements (such as lateral drifts), the principal author has obtained key information from the analysis of the vibration period of a structure, which is critical for its response to seismic movements. The vibration period is defined as the time it takes for the structure to complete a cycle of movement. When this period coincides with the fundamental frequency of seismic movement, there is a high risk of resonance, which can trigger significant structural failures.

$$T=2\mathsf{\pi }\sqrt{{\displaystyle \frac{\mathrm{m}}{K}}}$$

(5)

Considering that the stiffness of a column is given by Equation (5):

$$K=12{\displaystyle \frac{\mathrm{E}\mathrm{I}}{{\mathrm{L}}^3}}=12{\displaystyle \frac{E\ast \frac{b\ast d^3}{12}}{{\mathrm{L}}^3}}={\displaystyle \frac{E\ast b\ast d^3}{{\mathrm{L}}^3}}$$

(6)

where

• E: Modulus of elasticity of the material;
• I: Moment of inertia of the column’s cross section;
• L: Height of the column;
• d: Width of the column;
• b: Length of the column.

Based on Equations (5) and (6), Equation (7) is derived, which allows the reinterpretation of the period T in terms of how the cross-sectional dimensions influence its behavior:

$$T=2\mathsf{\pi }\sqrt{{\displaystyle \frac{\mathrm{m}}{K}}}=2\mathsf{\pi }\sqrt{{\displaystyle \frac{\mathrm{m}}{\left(\frac{E\ast b\ast d^3}{{\mathrm{L}}^3}\right)}}}$$

(7)

Finally, by simplifying, we obtain Equation (8):

$$T=2\mathsf{\pi }\sqrt{{\displaystyle \frac{\mathrm{m}\ast {\mathrm{L}}^3}{E\ast b\ast d^3}}}$$

(8)

When b and/or d are increased:

• The numerator m⋅L³ tends to increase because the mass m is proportional to the cross-sectional area.
• The denominator E⋅b⋅d³ also increases.

It is important to note that the change in the denominator generally has a more pronounced effect, especially due to the d³ term present in the denominator. This suggests that the stiffness of the column increases more rapidly than the mass in relation to changes in the cross-sectional dimensions. Additionally, it clearly reveals that there is an inverse relationship between the size of the column’s cross section and its fundamental period: as the section increases, the period decreases. This implies that the column becomes stiffer and responds more quickly to dynamic forces. This behavior is crucial in structural design as it ensures that columns are adequate to support loads and resist movements during seismic events. Understanding how the geometry of structural elements’ cross sections is linked to their dynamic behavior is fundamental for seismic design. By integrating a detailed analysis of the area’s seismicity and optimizing structural design, it is possible to develop safer and more earthquake-resistant buildings. These considerations not only improve the safety of structures but also contribute to the advancement of engineering practices and urban development in earthquake-prone regions.

In structural design of buildings, structural integrity is based on three fundamental pillars: load resistance, appropriate material selection, and a systematic design process. Buildings must be designed to withstand both dead loads [35] (static and permanent) and live loads (dynamic and temporary) [36]. The choice of materials directly influences the strength and durability of key structural elements such as beams and columns [37].

The design process typically follows a sequential approach encompassing conceptual design, load analysis, structural analysis, and detailed system design [35]. Precision in these stages is significantly enhanced through the use of technologies such as Building Information Modeling (BIM) [36]. Adherence to local construction codes and regulations is a fundamental pillar to ensure safety and functionality [38]; structural design must also consider environmental factors, such as resistance to natural disasters like earthquakes and typhoons [35].

2. Materials and Methods

The microtremor method is primarily used to determine the fundamental period of a site and to evaluate the amplification of ground motion, both crucial aspects in seismic engineering. In this study, precise measurements were made using the Tektronix AFG1022 seismometers and accelerometers, manufactured by Tektronix, Inc. in Beaverton, Oregon, USA, which ensured an accuracy of ±1 ppm. To ensure the quality of the measurements, the system was calibrated with a Symmetricom 5071A cesium oscillator, manufactured by Microchip Technology Inc. in Chandler, AZ, USA, providing exceptional frequency stability, as shown in

Table 1. Microtremor acquisition parameters.

ID	Parameter	Description
T	Registration time	30 min
Lw	Spectral amplitude of ground motion	5, 7.5, 10, 15 and 20 s
Smax	Maximum lateral oscillation period of soil	1.9
Smin	Minimum amplitude of the seismic wave recorded	0.25
Tlta	Superior signal amplitude in a short period of time	30 s
Tsta	Lower signal amplitude in a short period of time	1 s

. For materials, a highly sensitive microtremor sensor was implemented, along with a digital seismograph to capture relevant data. For subsequent analysis, the Geopsy software version 2.0 was used, known for its effectiveness and accessibility within the scientific community. The methodology followed aligned with SESAME criteria recommendations, ensuring the validity and reliability of the collected data. During the sensor installation at the study site, special care was taken to ensure no external interferences could alter the measurements. Ground vibrations were recorded continuously for 30 min, which was essential to capture the natural and representative oscillations of the terrain. Subsequently, an H/V spectrum analysis was performed, involving the calculation of the ratio between the amplitudes of horizontal and vertical waves. This analysis was key to determining both the site’s fundamental period and the level of ground motion amplification. Finally, the obtained results were interpreted to assess how the site would respond to seismic events. This interpretation not only considered the measured data but also was enriched by accumulated experience in microtremor data processing, thereby generating more robust and applicable conclusions for the design of safe infrastructures. Upon completing this comprehensive process, resulting curves of fundamental periods offered a clear view of the terrain dynamics, crucial for preventing building damage during earthquakes.

The analysis of microtremors provides valuable information about the interaction between building structures and underlying soil layers [39]. The analysis of internal (P and S) and surface (Rayleigh and Love) waves is essential for understanding soil–structure interaction. These models allow for the characterization of dynamic soil properties and the evaluation of how shear and compression waves affect structural response. The integration of these models with geophysical techniques such as MASW and microtremors ensures a more accurate interpretation of the collected data. By examining the frequency and phase characteristics of microtremors, we can determine soil stiffness, damping properties, and potential resonances that may influence the dynamic response of structures [40]. Additionally, microtremor analysis is crucial in assessing soil liquefaction potential. Analyzing dominant frequencies and spectral ratios helps identify areas susceptible to liquefaction during earthquakes [41]. This information guides foundation design and contributes to mitigating soil failure risk [39]. Continuous monitoring of structural dynamic response allows for early detection of changes in integrity or performance. This early warning system facilitates timely interventions and maintenance, ensuring the safety and durability of structures [42].

The Multichannel Analysis of Surface Waves (MASW) method is commonly employed to obtain shear wave velocity (Vs) profiles of the subsurface, leveraging the dispersion phenomenon of surface waves. In this study, 24 vertical geophones were carefully arranged at a constant distance of 3 m apart. These instruments, along with a digital seismograph, enabled the continuous recording of both ambient vibrations and those induced by an impact source; in this case, a hammer. The geophone configuration was a crucial step, as their linear arrangement and equal spacing ensured effective coverage of the investigated area. During measurement, the ground vibrations were recorded over a specific time, capturing both natural microtremors and artificially generated waves. Specialized software was then used to analyze the dispersion of the surface waves. Programs like “Surface Wave Analysis Wizard” (Pickwin, version 3.14.) and “WaveEq” (Surface Wave Analysis, version 3.14) by Geometrics were employed to process and analyze the collected data. Through phase velocity versus frequency plots, dispersion curves were obtained, which, through an inversion process, allowed for the calculation of the shear wave velocity variation with depth. The interpretation of the resulting velocity profiles provided valuable information about the subsurface morphology, including the thickness and characteristics of different layers. Each recording of the S-wave, with a geophone interval of 2 m and a total of 24 geophones, was conducted using a 24-pound Comba-type seismic source. This source generated waves with a trigger of 0.2 s and a sampling interval of 0.5 ms, while the recording length was set to 2.0 s and the MASW line spanned 30 m. Finally, data stacking was performed based on the quality of the recordings, following the established protocols for the GEA24 seismograph by PASI (Turin, Italy). Overall, this methodological approach facilitated a detailed characterization of the subsurface structure and mechanical properties, essential for future engineering interventions and geotechnical studies, as shown in

Table 2. Equipment parameters MASW.

Parameter	Description
Device configuration	Linear
Seismograph	GEA24—PASI
Comba	24 Lb
Battery	12 V
Measurements	t, S-wave arrival time
Geophone interval	2.0 m
Total number of geophones	24 units
Geophone types	4.5 Hz vertical geophone.
Location of shot point	At 10% and 20% at the beginning and end of the line
Seismic source	24 Lb Comba
Trigger	0.2 s
Sampling interval	0.5 ms
Record length	2.0 s
Staking	According to the quality of the data
MASW lengths	30 m

.

When an impact occurs on the surface of a soil deposit, different types of waves are generated, both within the soil (compression and shear waves) and on the surface (mainly Rayleigh waves). Approximately 67% of the applied energy is transmitted as Rayleigh waves, 27% as shear waves, and 7% as compression waves [43]. Until recently, technology did not exist to monitor and analyze surface waves, so geophysical methods focused solely on recording and analyzing compression and shear waves. In a homogeneous soil, the Rayleigh wave propagates at a constant velocity, regardless of its wavelength. However, if there are layers with different properties in the soil, such as stiffness, density, or Poisson’s ratio, then the velocity of the Rayleigh wave will vary based on its wavelength.

Geophysical techniques that analyze surface waves benefit from the characteristic dispersion of these waves to identify soil properties. This factor is influenced by the way the site is stratified, particularly by the shear wave velocity profile. The interpretation of the seismic profile and the shear wave velocity values obtained through the MASW test are fundamental for this analysis. This methodology allows distinguishing the different layers and sublayers of the profile, according to Technical Standard E.030 [44].

Seismic refraction is a valuable technique used to unravel the elastic properties of the subsurface, specifically in terms of P-wave and S-wave velocities. This method not only allows for the identification of soil layer characteristics but also provides information about their thickness, which is fundamental for various applications in geology and engineering.

In conducting this study, specific materials were employed to facilitate the data collection process. Firstly, 24 vertical geophones with a sensitivity of 4.5 Hz were arranged linearly along the measurement area. Alongside them, a digital seismograph was used to record the seismic waves generated during the experiment. To generate these waves, an impact device, commonly a hammer, was applied to the ground surface at different points. The equipment installation was methodical: the geophones were placed in a straight line, spaced 5 m apart, ensuring adequate coverage of the study area. Once installed, wave generation was carried out by impacting the ground surface, allowing the geophones to capture the relevant seismic waves. During this process, the arrival times of the P-waves at each geophone were carefully recorded. The obtained data were stored in the seismograph for subsequent analysis.

To analyze the data, we employed SeisImager software, version 3.3, which greatly facilitated the processing of the recorded information. Using this software, we identified the first arrivals of the seismic waves and generated time–distance curves. Once the slopes for each seismic line were determined, we processed these data using DEEPSOIL v7 interpretation software to calculate the seismic velocities, as detailed in

Table 3. LS acquisition parameters.

Parameter	Description
Device configuration	Linear
Measurements	t, S-wave arrival time
Geophone interval	2.0 m
Total number of geophones	5.0 m
Geophone types	24 Db
Seismic source	0.2 s
Trigger	0.250 ms
Sampling interval	0.50 ms
Log length	24 Lb combo
Staking	According to data quality
LS lengths	120 m

, which outlines the parameters of the instruments used. This process relies on the principle that velocity increases with depth and remains constant within each layer, allowing us to calculate the wave velocities in the subsurface, thus providing valuable insights into the characteristics of the geological layers studied. It is worth noting that the LS seismic line was executed on a street with sandy soil.

The Nakamura method (H/V) was used to determine the response characteristics of the study area based on the analysis of Fourier spectra from recorded signals. The method relies on the relationship between the amplitude of the horizontal wave (H) and the amplitude of the vertical wave (V) in the frequency domain [12]. In this analysis, the first step is to calculate the amplitude spectrum for each seismic component: the two horizontal directions (H1 and H2) and the vertical (V). The amplitude spectrum shows us the magnitude of each frequency present in the signal. To obtain a more robust representation of the horizontal component, we combine H1 and H2 by calculating the square root of the sum of the squares of their amplitude spectra. This way, we achieve a more accurate and reliable picture of how the ground behaves in the horizontal direction during a seismic event, using computational programs to perform these calculations. The Nakamura method processing began with acquiring acceleration signals in three directions: two horizontal (X and Y) and one vertical (Z). Next, Fourier spectra were calculated for each of these signals. Once the Fourier spectra were obtained, the ratio between the horizontal wave amplitude and the vertical wave amplitude was calculated for each frequency [45]. This ratio is known as the H/V index. The H/V index provides information about the soil or structure response at different frequencies. A high H/V value indicates greater horizontal wave amplification compared to the vertical wave, which may signal the presence of specific resonances or vibration modes [12].

To properly interpret the results of the Nakamura method, it is essential to consider the geotechnical and structural context of the study site. Additionally, it is recommended to compare the obtained results with reference values or similar studies conducted in the same area [46]. The use of specialized computational tools for structural modeling and building analysis is a valuable resource. These tools offer a user-friendly interface, a wide range of analyses, and automatic design capabilities. They allow easy representation of the geometry of various structures and facilitate seismic evaluation [47]. Their use saves time and improves the quality of the structural design process, and to ensure consistency between the computational model and the numerical model, comparisons were made using experimental data and computational simulations. The results of the numerical model were validated through the tests conducted and the use of various computational programs, thus guaranteeing the accuracy and consistency of the results.

The Nakamura method (H/V) can be summarized as follows: three ambient vibration signals are recorded—the vertical component, the north–south component, and the east–west component. Fourier spectra are then calculated for each of these signals. The average Fourier spectra of the horizontal signals are divided by the Fourier spectrum of the vertical signal, resulting in a value for the fundamental period at the study point. In this particular case, measurements were taken for at least 30 min at each location to ensure sufficient time and avoid saturation from ambient noise that could affect the measurements. A sampling rate of 200 data points per second was used in ASCII recording format, without applying measurement filters during data acquisition.

3. Results

In the microtremor test, measurements were taken at a conveniently distributed point in the study area. The results of the H/V spectral ratio indicate that the fundamental period for short periods is T (0): 0.18 s, and for long periods, it is 1.03 s. The average H/V spectra from each sensor were analyzed, considering the mean value. The spectra exhibit a smooth peak shape, indicating that the amplitudes are less than two. The results suggest that the current terrain is classified as rigid soil. However, the presence of a colluvial deposit may lead to amplification at longer periods due to its depth and/or the free edge effect near the slope, as observed in Figure 2.

To carry out the MASW (Multichannel Analysis of Surface Waves) test, a linear array of 24 geophones is set up with a spacing of 3 m between them. A digital seismograph is used to record both ambient vibration (microtremors) and induced surface vibration (impacts, vehicular traffic, etc.), with wave frequencies generally exceeding 4.5 Hz. The goal is to achieve maximum precision in the arrival times of the seismic signal at each geophone and to reach the desired depth objectives; the color bands in Figure 2 represent the ratio between the amplitudes of horizontal and vertical waves (H/V) at different frequencies. These spectral characteristics are obtained through Fourier analysis of the recorded signals, using the Nakamura method.

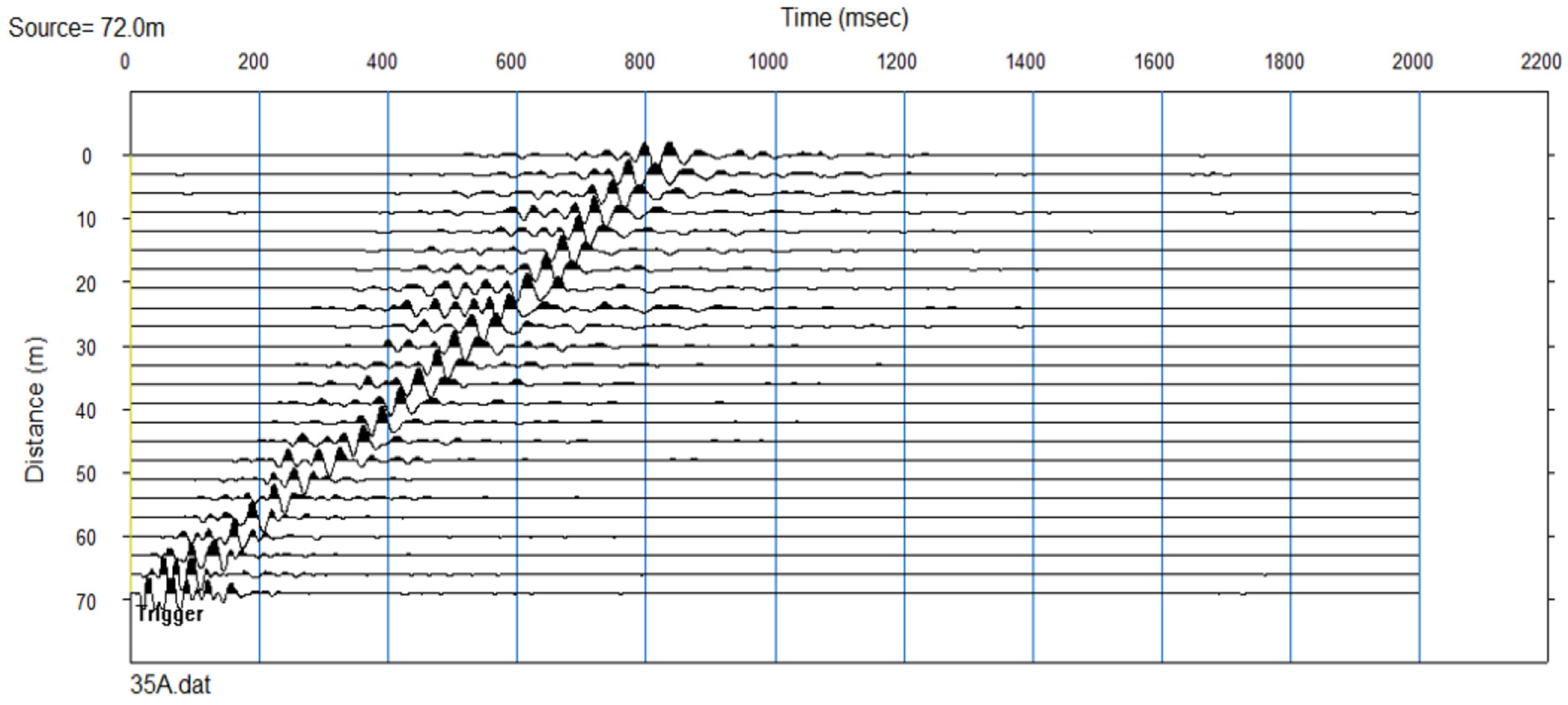
During the recording stage of surface waves, it is crucial to identify the ground roll or wave train. It is important to note that this involves capturing noise, and the dispersion properties of the noise can be used to infer properties near the elastic surface, as observed in Figure 3 and Figure 4. To understand the behavior of the shear wave signal (also known as the S-wave), we must recognize that it is hindered by the presence of other phases in the record. These phases are generated by energy movement in the subsurface and include refraction, reflection, diffraction, and surface waves such as Rayleigh and Love. Additionally, natural and environmental noise is also present.

According to the Technical Standard E.030 [44] of the National Building Regulations in Peru, which classifies soils based on the shear wave velocity Vs = 30 m/s, it has been determined that at this location, there is an S2 soil type, intermediate soils, and C soil. According to the European IBC 2015 [48], this classification indicates that the soil is either very dense or a soft rock when facing an earthquake. Therefore, the corresponding dynamic parameters were calculated for this MASW point.

During the investigation, Active Multichannel Analysis of Surface Waves (MASW) tests were also conducted at each of the studied locations. Using the obtained results, the average shear wave velocity Vs = 30 m/s was calculated, following the Norma E.030 [44], to determine the seismic properties of the soil based on one-dimensional shear wave profiles and their respective average velocities down to a depth of 30 m. The results indicate that the soil in the study area exhibits dynamic behavior of Type S2 (Intermediate Soils), as per the Norma E.030 [44], and Type C (Very Dense Soil or Soft Rock) according to the IBC 2015 [48], down to a depth of 30 m. In relation to the microtremor test results, it can be observed that the fundamental period of the site averages T0: 0.64 s for short periods, while for longer periods (>1.03 s), these values correspond to dense soils and/or soft rock.

The Horizontal to Vertical Spectral Ratio (HVSR) fundamental period is a measure used to analyze soil characteristics in response to seismic vibrations. It is obtained by comparing the amplitude of horizontal waves to vertical waves at a specific site. To analyze the HVSR fundamental period, techniques such as the Nakamura method are employed [49]. This method involves measuring and comparing the horizontal and vertical amplitude spectra of seismic waves recorded at a site. From these spectra, the fundamental period of the soil is determined, providing crucial information about its dynamic response and properties. This process allows for the analysis of seismic wave amplification or attenuation at a specific location, which is essential for designing safe structures and assessing seismic risk.

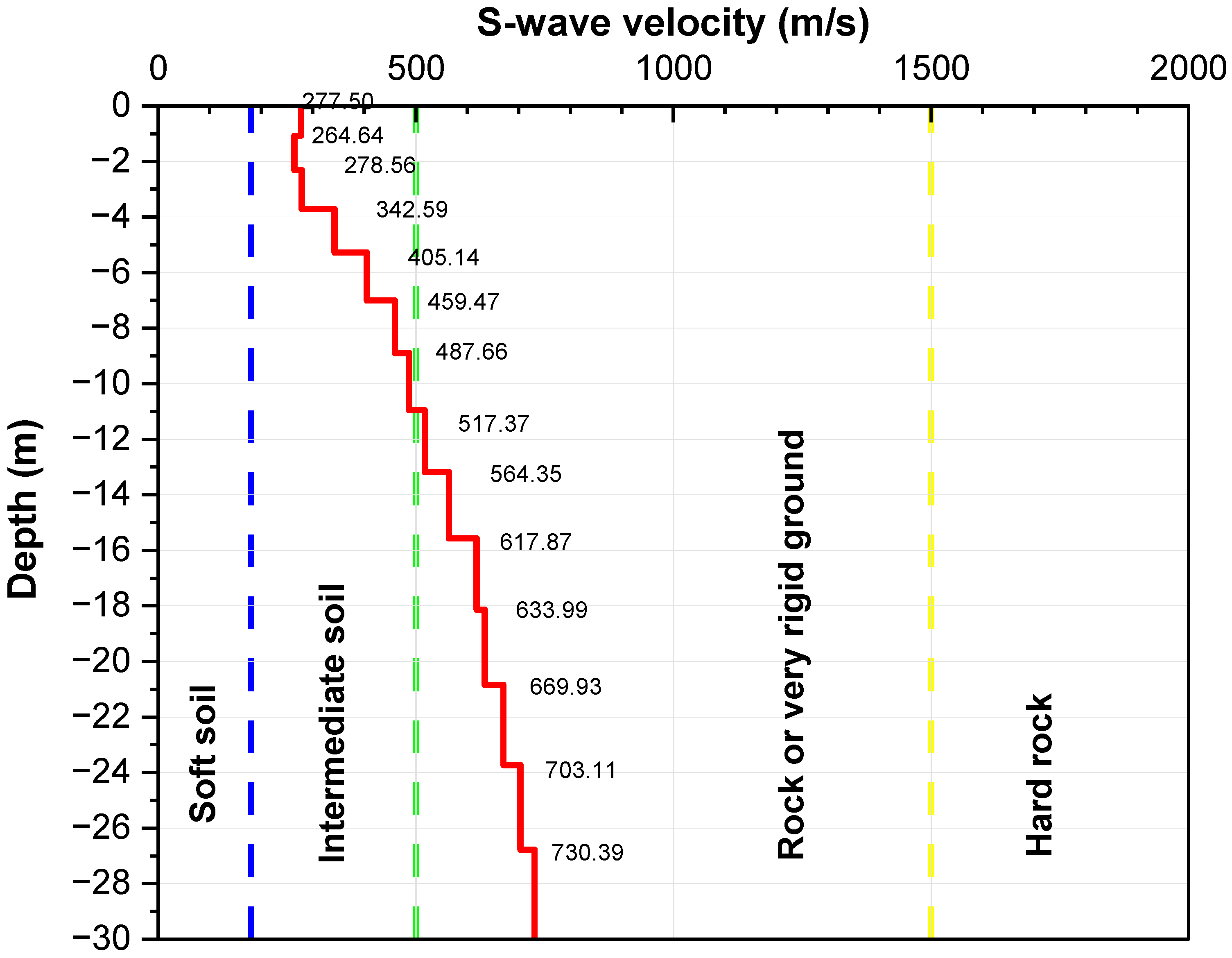
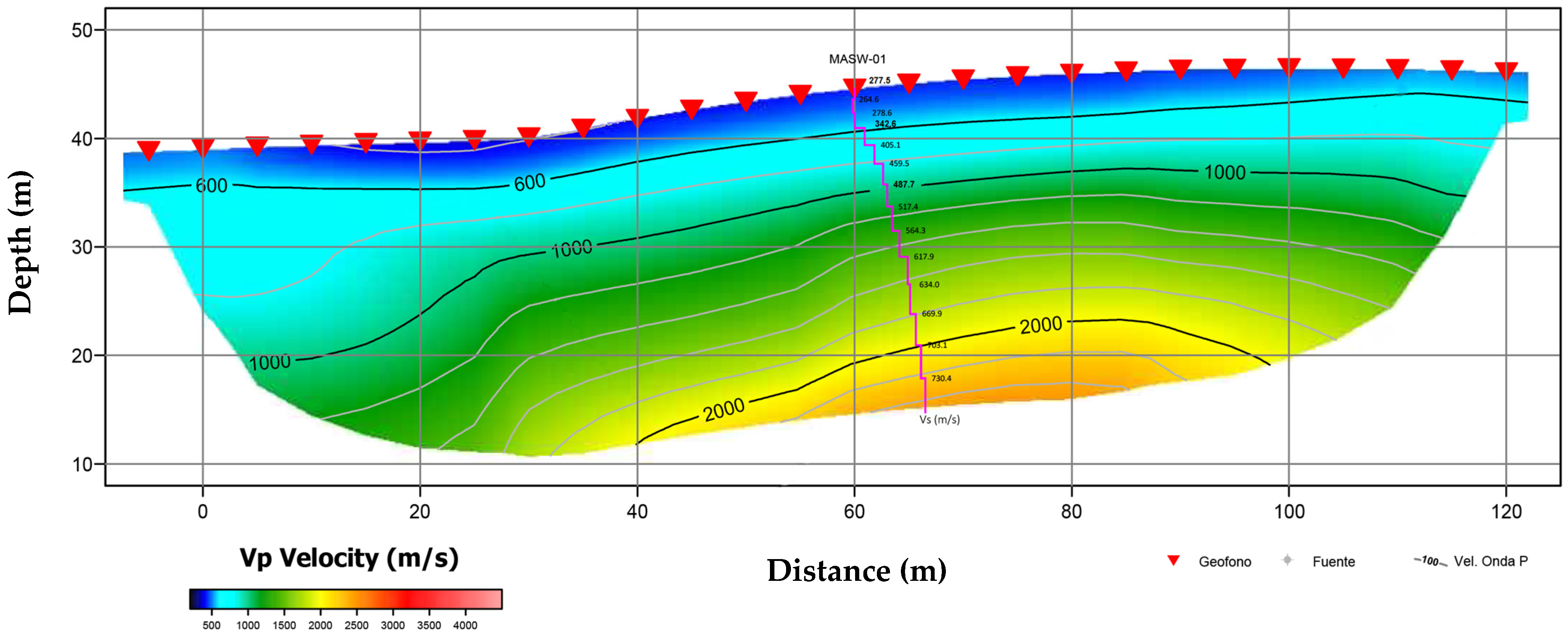
To perform the verification using the MASW test, we also utilized the software “Surface Wave Analysis Wizard” and “WaveEq (Surface Wave Analysis)”, both developed by Geometrics. These tools processed the 1D MASW records, allowing us to generate a Phase Velocity vs. Frequency graph and the dispersion curve (Figure 5). Subsequently, an inversion process was conducted to calculate the depth variation of the Shear Wave Velocity (Vs). The soil layers were defined based on these velocities (Vs), as illustrated in Figure 6.

Seismic refraction LS is a geophysical technique used to investigate subsurface properties and determine the geological structure of a region [26]. This method relies on measuring and analyzing seismic waves that propagate through rock and soil layers [27]. In the context of infrastructure construction, seismic refraction has been employed to assess soil bearing capacity and identify layers of unstable or low-strength soil [28]. This information is crucial for civil engineering projects such as bridge, road, and building construction [29]. The results obtained from seismic refraction along the section reveal the presence of four layers with varying P-wave velocities (Vp) (see Figure 7). The topmost layer has a Vp < 600 m/s and consists of colluvial material—angular to subangular gravels within a moderately dense silty or clayey matrix, covered by recent material. Below this, a layer with 600 < Vp < 1000 m/s is composed of gravel and fine silty sand covered by semicompacted residual soil, extending to a depth of 5 m. Subsequently, a layer with a velocity range of 1000 < Vp < 2000.0 m/s is identified. This layer comprises alluvial material (angular to subangular gravels and conglomerates) within a consolidated silty sand matrix, with a thickness ranging from 5 m to 22 m. Finally, underlying these layers is a Vp > 2000 m/s layer, consisting of consolidated conglomerate and/or hard rock.

Seismic design of buildings can be approached in various ways. One approach involves considering the stationary loads specified by applicable laws, but this may not guarantee appropriate seismic design [13]. Another approach is to design buildings based on elasticity analysis considering gravity, wind, and seismic effects [40]. Comparative analyses can determine the most effective and secure slab system for seismic scenarios, such as flat, ribbed, or conventional slabs [50]. Conducting comparative analyses can help determine the most effective and safe slab system for seismic scenarios, whether flat slabs, ribbed slabs, or conventional slabs. This type of analysis allows for the evaluation of how each slab system responds to seismic loads, identifying which offers better performance and safety in terms of strength, deformation, and energy absorption capacity [13]. For tall structures, estimating and specifying the lateral forces caused by seismic waves is crucial for designing structures that can withstand these forces [51]. In earthquake-prone areas, seismic retrofitting methods for masonry structures have been developed, including traditional and modern approaches using composite materials [52]. This research innovates in the seismic design of buildings by considering dynamic loads from different periods of seismic ground excitation, significantly impacting the design of constructions. The response of a structure to seismic forces depends both on the soil type and the structural characteristics [53]. The soil properties significantly influence the movement of the structural system as seismic waves pass through the soil layers [54]. The relationship between the predominant period of the soil and the fundamental period of the structure plays a crucial role in the damping reduction factors used in seismic design [55]. Additionally, the seismic loads acting on a structure largely depend on the local soil conditions, including the equivalent shear wave velocity and the predominant period of the building. Therefore, considering the different periods of seismic excitation is essential for designing earthquake-resistant buildings and ensuring adequate seismic performance.

By applying the theoretical basis and the adapted equation (Equation (7)), it is possible to simplify the calculation from load measurement (traditional method) to pre-dimension structural elements and optimize the design. This ensures that the proposed adapted equation not only meets structural requirements but also aesthetic ones, maximizing resistance to seismic movements. Once the soil vibration period is obtained through precise methods, such as Multichannel Analysis of Surface Waves (MASW) or the Nakamura method [56], techniques like HVSR fundamental period analysis are used. These results allow for the determination of the global dimensions of structural elements, as shown in the simplified formula for a square section, which can be extended to other geometries.

$$T=2\mathsf{\pi }\sqrt{{\displaystyle \frac{\mathrm{m}\ast {\mathrm{L}}^3}{E\ast b\ast d^3}}}=2\mathsf{\pi }\sqrt{{\displaystyle \frac{\mathrm{m}\ast {\mathrm{L}}^3}{E\ast d^4}}}$$

(9)

$$T^2=4{\mathsf{\pi }}^2{\displaystyle \frac{\mathrm{m}\ast {\mathrm{L}}^3}{E\ast d^4}}\cong d=\sqrt[4]{{\displaystyle \frac{4{\mathsf{\pi }}^2\mathrm{m}\ast {\mathrm{L}}^3}{E\ast T^2}}}$$

(10)

Using these equations, we can express the soil period and ensure that it does not coincide with the fundamental period of the structure to avoid resonance, which could have catastrophic consequences. By utilizing response spectra obtained from vibration periods, along with the type of buildings that may be more affected [57], the behavior of structures located near the epicenter, on hard soil or rock, can be analyzed. In these cases, the peak value of seismic movement occurs at high frequency or low period, around 0.3 s. This type of movement particularly affects low-rise buildings, which are the focus of this study. These structures, common in vulnerable communities (such as precarious housing and self-built constructions), are generally rigid and tend to vibrate with this natural period.

4. Discussion

When designing buildings to withstand ground vibration, several factors must be considered. These include the geological and soil engineering conditions at the affected foundation base [50]. The building or structure’s type and design also play a role, along with the vibration frequency, duration, and distance from the vibration source [58]. Material selection and foundation type are crucial factors [59]. Additionally, the flexibility of foundations and soil–structure interaction (SSI) must be taken into account [60,61]. The seismic response of a building is influenced by foundation flexibility and soil properties, varying based on soil stiffness, foundation depth, and building mass ratio. A comprehensive understanding of these factors is essential for designing buildings that can withstand ground vibrations [61].

The soil period has a significant impact on building design. Accurately defining soil movement during long periods (LPGM) is crucial for seismic design, especially in regions with limited seismic observations [62] An innovative method of LPGM simulation (Long Period Ground Motion) that includes probabilistic seismic hazard analysis (PSHA) is proposed, overcoming the limitations of methods based on empirical relationships. The robustness of the building and the risk to life and property are evaluated based on seismic threat analysis. The return period of the designed ground motions is not evident in building codes, making it difficult to assess the risk posed by buildings designed according to these codes [63]. Tall buildings near deep sedimentary layers may experience low-frequency ground movements over prolonged periods, which could cause damage and collapse [64]. The fundamental period of buildings is influenced by soil–structure interaction (SSI) effects, and current empirical expressions for predicting fundamental periods may yield incorrect results [65,66]. When the vibration periods of seismic waves closely align with the building’s inherent vibration period, resonance occurs, substantially increasing deformations, accelerations, and stresses in structural components [67].

Research on the seismic behavior of structures is subject to various limitations that require cautious interpretation of the results, considering that geographical generalization is restricted, given that geological and seismic conditions vary regionally [68], requiring complementary studies to apply the findings in other contexts (e.g., adaptation of soil characterization techniques and seismic analysis) [69].

Likewise, soil variability, including heterogeneity in stratigraphy and moisture, can influence geophysical tests, demanding exhaustive analyses to avoid erroneous conclusions [70]. Considering that measurement techniques such as MASW and microtremors have inherent limitations, such as susceptibility to environmental noise and possible underestimation of seismic effects, it is advisable to corroborate results with complementary methods. Seismic modeling, based on simplifying assumptions, also introduces uncertainty, requiring a critical evaluation of the validity of these assumptions [71].

It is recommended to restrict trafficability at the time of the test to avoid environmental noise that may disturb data collection, with the support of citizen security and municipal permission.

Variability in construction materials, influenced by quality and seismic response, demands on-site sampling to validate the effectiveness of design recommendations. Regulatory and cultural considerations are essential, as alignment with local regulations and cultural practices ensures the acceptance and implementation of interventions in vulnerable communities [72]. The research contributes to the field by demonstrating the effectiveness of combining geophysical methods such as MASW, microtremors, and seismic refraction to characterize the dynamic properties of the soil, crucial information for evaluating seismic load response and preventing structural resonance phenomena [67,68]. Additionally, Equation (9) is an innovative adaptation based on the approximation for resonance calculation, avoiding architectural design and then structural design.

The relevance of the study lies in its focus on areas of urban expansion and proximity to rock outcrops, where soil characteristics (especially sandy soils) can significantly influence structural behavior [73]. By determining the soil vibration periods using ambient vibration data, the research underscores the need to incorporate these findings into building design, thus optimizing structural performance and sustainability in complex geophysical environments [74]. Specifically, this work promotes a methodology that merges geophysical and dynamic knowledge, enabling the design of resilient structures that consider soil resistance and compressibility in foundation design [75]. The implementation of these geophysical techniques is essential for designing safer and more sustainable buildings in the face of seismic events, directly contributing to risk reduction in vulnerable communities [76].

The process of the proposal in this research begins by identifying the location and conducting geophysical tests to determine the soil period (Ts). Then, the initial column section is calculated using simplified equations, and the relationship between the structural period (T) and the section dimensions is analyzed. By adjusting these dimensions, their impact on stiffness and mass is evaluated, optimizing the design to avoid resonance. A seismic analysis is carried out and validated using advanced computational tools, ensuring regulatory compliance and resistance. Finally, detailed structural plans integrated into the architectural design are developed, guaranteeing a safe, functional project adapted to specific seismic conditions.

5. Conclusions

The conclusions of this study provide essential information on the tests necessary to determine soil vibration periods and their typology, which is fundamental for building design and seismic performance. The critical importance of linking the period of a structure with potential seismic movements in its environment is highlighted, considering this key aspect to ensure safety and structural integrity.

The vibration periods associated with sandy soils near rock outcrops, with a depth of up to 30 m, near vulnerable populations and urban expansion areas were analyzed, finding periods of 0.60 s. These geological characteristics influence structural behavior, as the fundamental period varies with the mass, stiffness, and height of the building, being essential to prevent structural resonance. It is suggested that determining soil vibration periods is crucial in building planning and should include considerations of construction type and soil conditions.

Data analysis methods based on ambient vibrations are effective tools for determining the fundamental period of structures, such as MASW, microtremors, and seismic refraction tests, which are useful for characterizing subsurface conditions and providing critical information for building design on intermediate soils [77]. These geophysical studies are vital for understanding subsurface characteristics and ensuring structural stability, integrating considerations of soil resistance and compressibility in foundation design [78].

Incorporating soil vibration analysis into architectural design is fundamental for creating safer, sustainable, and resilient buildings against seismic events. The integration of findings on vibration periods and their relationship with seismic activity offers multiple opportunities to improve the quality and safety of buildings [79]. Architects, by adopting a collaborative approach with structural engineers, should balance form, function [80], and resilience to design urban spaces that are not only aesthetically appealing but also capable of withstanding [81] the forces of nature [82].

This integration will allow for an architecture that values both aesthetics and safety, a crucial aspect in a world where seismic events are becoming more frequent and intense. The discrepancy between soil vibration periods and structural periods can induce resonance phenomena, underscoring the need to incorporate geophysical and dynamic knowledge into the design to optimize structural performance and ensure sustainability in complex geophysical environments.