Evolutionary Game Analysis of Construction Worker Safety Supervision Based on Complex Network
Abstract
1. Introduction
2. Literature Review
2.1. Study on Unsafe Behavior of Workers
2.2. Study on the Impact of Incentives and Disincentives on Workers
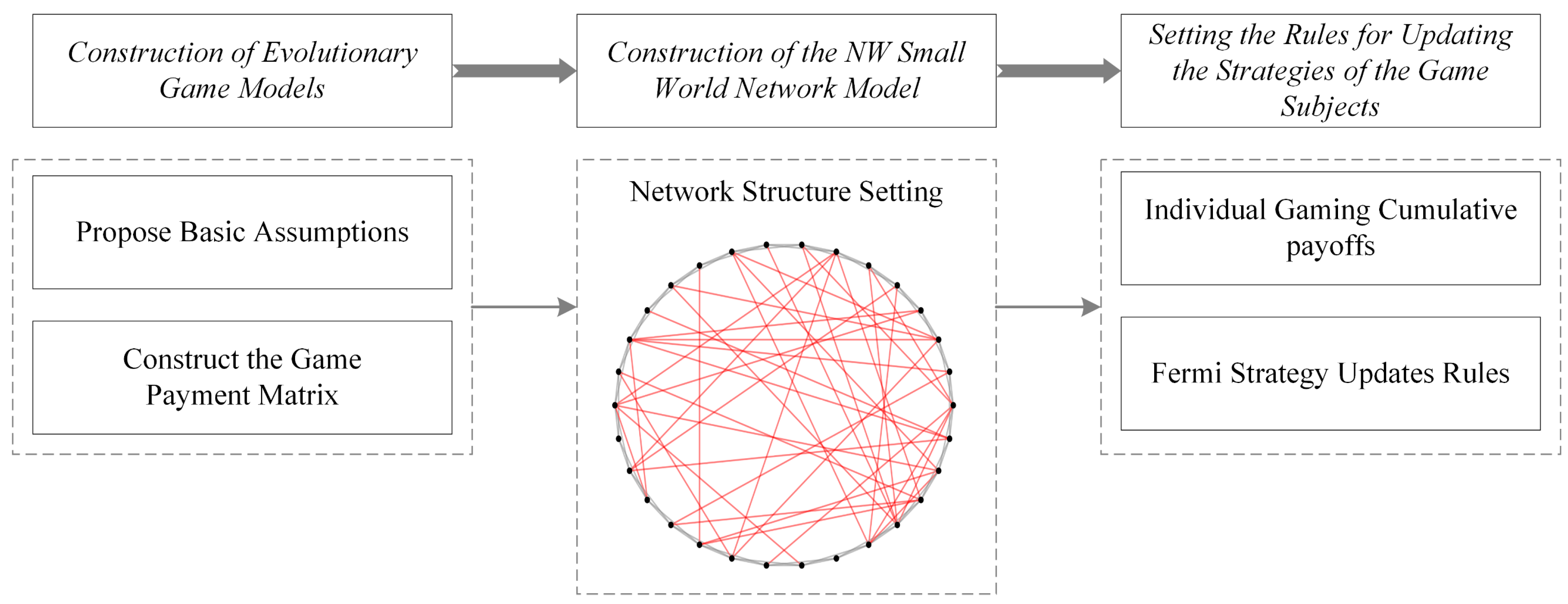
3. Model Building
3.1. Model Assumptions
3.2. Setting of the Network Structure
3.3. Selection of Strategy Update Rules
4. Numerical Simulation
4.1. Initial Parameter Setting
4.2. Impact of Reward and Penalty Mechanism
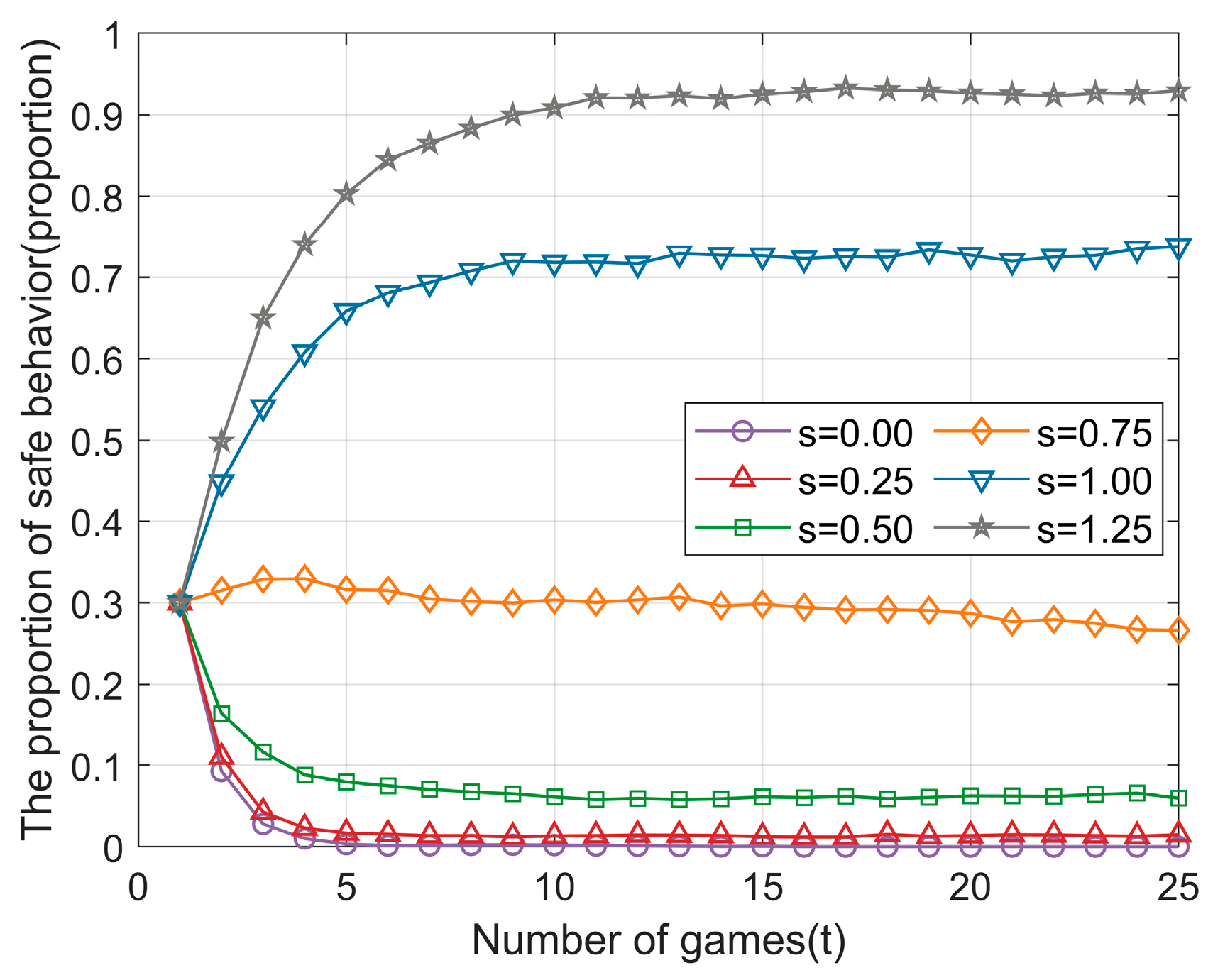
4.2.1. Reward Value for Safe Behavior
4.2.2. Penalty Value for Unsafe Behavior
4.2.3. Combination of Reward and Penalty
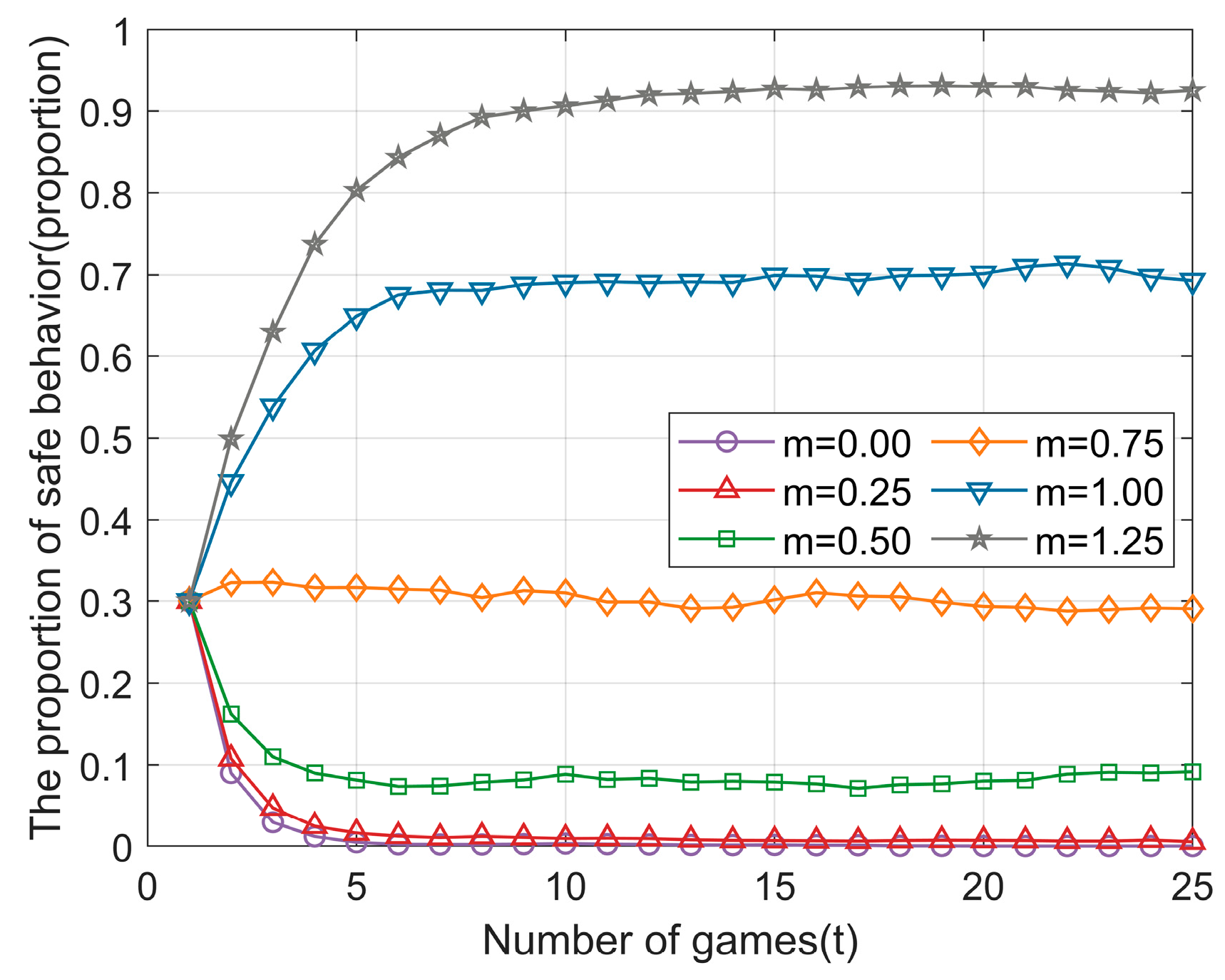
4.2.4. Supervisory Intensity of Safety Managers
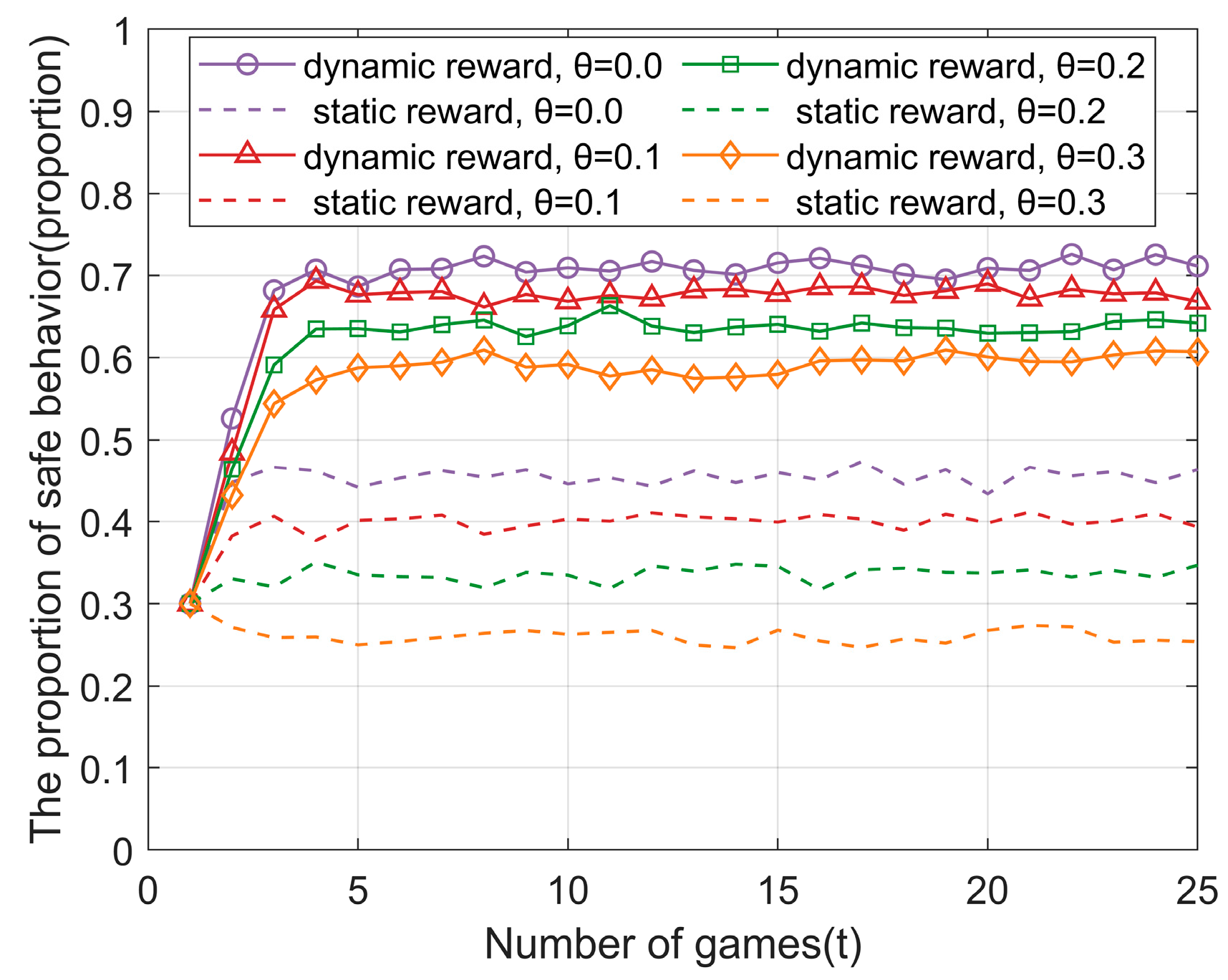
4.2.5. Spillover Effect and Dynamic Reward Systems
4.3. Sensitivity Analysis
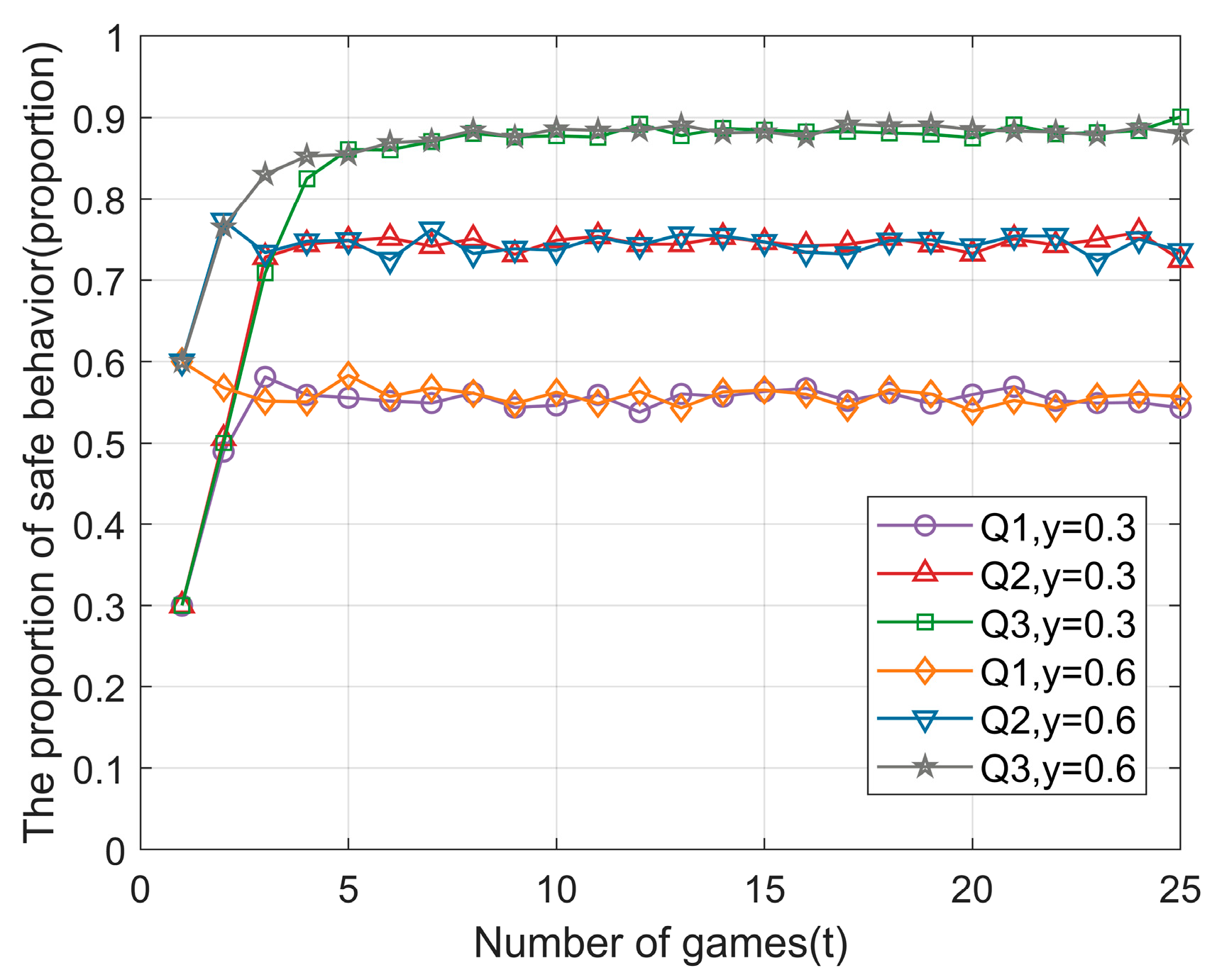
4.3.1. Initial Proportion
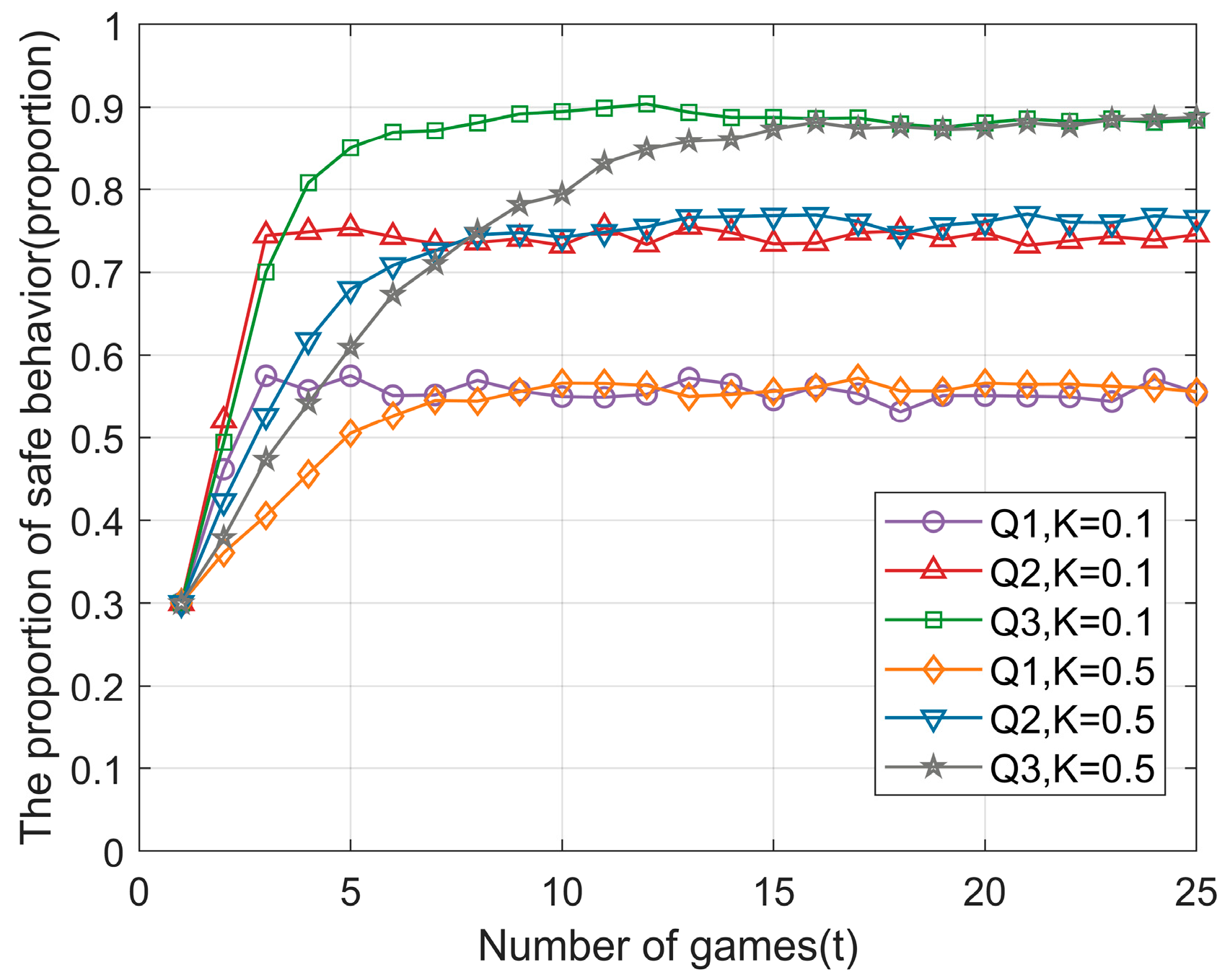
4.3.2. Network Structure
4.3.3. The Degree of Bounded Rationality
5. Discussion
5.1. Research Findings
5.2. Suggestions
- Establishing a reasonable reward and punishment mechanism is a crucial strategy for enhancing construction workers’ safe behavior. Specifically, rewarding safe behavior while penalizing unsafe behavior can effectively regulate workers’ actions. Appropriately increasing reward and penalty values can further boost workers’ motivation to choose safe behavior and improve the overall effectiveness of safety supervision.
- Regarding the implementation of this reward and punishment mechanism, a dynamic reward mechanism should be emphasized. This approach links rewards to the safe performance of the worker group, thereby enhancing the diffusion of safe behavior. Compared with static rewards, dynamic reward mechanisms can better encourage workers to maintain safe behavior over the long term and foster a positive reinforcement cycle. Regarding penalties, a blanket approach should be avoided, especially in scenarios with spillover effects. Efforts should be made to prevent situations where the entire team is penalized due to the unsafe behavior of individual workers. It is recommended to adopt a precise punishment strategy, ensuring that penalties are targeted at specific violators rather than innocent team members. This helps to maintain team stability while effectively restraining unsafe behavior.
- Regarding safety supervision, it is necessary to appropriately enhance the supervisory intensity of safety managers and increase the frequency of on-site inspections. The timely identification and penalization of unsafe behaviors can significantly improve the effectiveness of safety supervision. At the same time, considering the increasing adoption of information technology, modern supervision tools, such as IoT monitoring and smart safety helmets, should be actively integrated into safety management. This allows for the real-time monitoring of workers’ safety and a better understanding of the safety status of the worker group.
6. Conclusions and Prospect
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ministry of Housing and Urban-Rural Development, Department of Quality and Safety Supervision of Engineering Construction. Case Analysis of Construction Safety Accidents; China Architecture & Building Press: Beijing, China, 2019.
- Yuan, B.; Xu, S.; Chen, L.; Niu, M. How Do Psychological Cognition and Institutional Environment Affect the Unsafe Behavior of Construction Workers?—Research on fsQCA Method. Front. Psychol. 2022, 13, 875348. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Geng, X.; Wang, Y. Research on the Network Topology Characteristics of Unsafe Behavior Propagation in Coal Mine Group from the Perspective of Human Factors. Resour. Policy 2023, 85, 104020. [Google Scholar] [CrossRef]
- Sanni-Anibire, M.O.; Mahmoud, A.S.; Hassanain, M.A.; Salami, B.A. A Risk Assessment Approach for Enhancing Construction Safety Performance. Saf. Sci. 2020, 121, 15–29. [Google Scholar] [CrossRef]
- Ansori, N.; Widyanti, A.; Sutalaksana, I.Z. Decision Latitude, Supervisor Support, and Coworker Support in Small and Medium Enterprises (SMEs): A Psychosocial Exploratory Analysis to Enhance Safety Behavior. In Proceedings of the International Multi Conference of Engineers and Computer Scientists 2019 IMECS 2019, Hong Kong, 13–15 March 2019. [Google Scholar]
- Ghasemi, F.; Sari, M.; Yousefi, V.; Falsafi, R.; Tamošaitienė, J. Project Portfolio Risk Identification and Analysis, Considering Project Risk Interactions and Using Bayesian Networks. Sustainability 2018, 10, 1609. [Google Scholar] [CrossRef]
- Wang, H.-H.; Chen, J.-H.; Arifai, A.M.; Gheisari, M. Exploring Empirical Rules for Construction Accident Prevention Based on Unsafe Behaviors. Sustainability 2022, 14, 4058. [Google Scholar] [CrossRef]
- Li, H.; Lu, M.; Hsu, S.-C.; Gray, M.; Huang, T. Proactive Behavior-Based Safety Management for Construction Safety Improvement. Saf. Sci. 2015, 75, 107–117. [Google Scholar] [CrossRef]
- Meng, Q.; Liu, W.; Li, Z.; Hu, X. Influencing Factors, Mechanism and Prevention of Construction Workers’ Unsafe Behaviors: A Systematic Literature Review. Int. J. Environ. Res. Public. Health 2021, 18, 2644. [Google Scholar] [CrossRef]
- Chen, Y.; Lv, Y.; Chai, F.; Wang, X. Evolutionary Game Analysis of Unsafe Behavior of Construction Workers from the Perspective of Dynamic Incentives. Saf. Environ. Eng. 2020, 27, 197–203. [Google Scholar] [CrossRef]
- Zulkefli, F.A.; Ulang, N.M.; Baharum, F. Construction Health and Safety: Effectiveness of Safety Incentive Programme. SHS Web Conf. 2014, 11, 01012. [Google Scholar] [CrossRef]
- Guo, B.H.W.; Goh, Y.M.; Le Xin Wong, K. A System Dynamics View of a Behavior-Based Safety Program in the Construction Industry. Saf. Sci. 2018, 104, 202–215. [Google Scholar] [CrossRef]
- Ting, H.-I.; Lee, P.-C.; Chen, P.-C.; Chang, L.-M. An Adjusted Behavior-Based Safety Program with the Observation by Front-Line Workers for Mitigating Construction Accident Rate. J. Chin. Inst. Eng. 2020, 43, 37–46. [Google Scholar] [CrossRef]
- Shin, M.; Lee, H.-S.; Park, M.; Moon, M.; Han, S. A System Dynamics Approach for Modeling Construction Workers’ Safety Attitudes and Behaviors. Accid. Anal. Prev. 2014, 68, 95–105. [Google Scholar] [CrossRef] [PubMed]
- Haslam, R.A.; Hide, S.A.; Gibb, A.G.F.; Gyi, D.E.; Pavitt, T.; Atkinson, S.; Duff, A.R. Contributing Factors in Construction Accidents. Appl. Ergon. 2005, 36, 401–415. [Google Scholar] [CrossRef]
- Liu, S.; Tang, S. Research on contagion mechanism of unsafe behavior of construction workers based on CA. China Saf. Sci. J. 2023, 33, 24–31. [Google Scholar] [CrossRef]
- Ma, H.; Lv, H. Propagation Simulation of Unsafe Behavior of Construction Workers Under the Influence of Spatial Neighbors. J. Civ. Eng. Manag. 2022, 39, 86–91. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, H.; Guo, H.; Wu, Y.; Luo, Z. Causal Inference of Construction Safety Management Measures towards Workers’ Safety Behaviors: A Multidimensional Perspective. Saf. Sci. 2024, 172, 106432. [Google Scholar] [CrossRef]
- Wang, L.; Chai, W.; Sun, N.; Tong, R. Unlocking the Mechanism of Work Environment on Miners’ Unsafe Behaviors: A Meta-Analysis and System Dynamics. Resour. Policy 2024, 96, 105217. [Google Scholar] [CrossRef]
- Yang, X.; Sun, X.; Ren, G. Analysis of the Conscious Unsafe Behavior of Construction Workers in Multi-party Games. Saf. Secur. 2020, 41, 70–74. [Google Scholar] [CrossRef]
- Zhou, Q.; Fang, D. Mechanism of impact of safety climate on safety behavior in construction: An empirical study. China Civ. Eng. J. 2009, 42, 129–132. [Google Scholar]
- Yin, C.; Pang, Q.; Wang, K.; Zhang, X. Stochastic Evolution Game Analysis of Safety Behavior of Construction Workers in the Construction Industry Based on the Moran Process. Saf. Environ. Eng. 2023, 30, 73–80. [Google Scholar] [CrossRef]
- Li, L.; Cao, L.; Li, Y.; Wang, S.; Li, R.; Zhi, M. Game analysis of coal miners’ unsafe behaviors based on informal organization leadership. J. Xi’an Univ. Sci. Technol. 2022, 42, 1088–1095. [Google Scholar] [CrossRef]
- Fu, L.; Li, X.; Wang, X.; Li, M. Safety Risk Propagation in Complex Construction Projects: Insights from Metro Deep Foundation Pit Projects. Reliab. Eng. Syst. Saf. 2025, 257, 110858. [Google Scholar] [CrossRef]
- Cao, C.; Li, S.X.; Liu, T.X. A gift with thoughtfulness: A Field Experiment on Work Incentives. Games Econ. Behav. 2020, 124, 17–42. [Google Scholar] [CrossRef]
- Jiang, M.; Zhao, L. Tripartite evolutionary game analysis of production safety supervision under the reward and punishment mechanism. Ind. Saf. Environ. Prot. 2023, 49, 52–58. [Google Scholar]
- Jiao, P.; Zhang, S.; Zhao, X. Evolutionary game of safety supervision between government and road transport enterprises based on third-party. J. Chang. Univ. Nat. Sci. Ed. 2021, 41, 106–115. [Google Scholar] [CrossRef]
- Ye, G.; Yang, L.; Li, X.; Cao, H.; Zhang, Y. Study on the positive effect of rewards and punishments on the evolution of construction workers’ safety behavior. J. Saf. Environ. 2022, 22, 201–210. [Google Scholar] [CrossRef]
- Wang, D.; Guan, Y.; Jia, Q. Research on propagation path of construction workers’ unsafe behavior based on social network analysis. J. Saf. Sci. Technol. 2018, 14, 180–186. [Google Scholar]
- Zheng, B.; Wu, H.; Kuang, L.; Qin, J.; Du, W.; Wang, J.; Li, D. A Simple Model Clarifies the Complicated Relationships of Complex Networks. Sci. Rep. 2014, 4, 6197. [Google Scholar] [CrossRef]
- Zhou, D.; Han, Y.; Lu, J. Investigation and Characteristics Analysis on Construction Workers Group. Archit. Technol. 2016, 47, 182–185. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective Dynamics of ‘Small-World’ Networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Zhou, G.; Li, C.; Li, T.; Yang, Y.; Wang, C.; He, F.; Sun, J. Outer Synchronization Investigation between WS and NW Small-World Networks with Different Node Numbers. Phys. Stat. Mech. Its Appl. 2016, 457, 506–513. [Google Scholar] [CrossRef]
- Xie, F. Game Theory on Complex Networks; Tsinghua University Press: Beijing, China, 2016; ISBN 978-7-302-40262-6. [Google Scholar]
- Fan, R.; Dong, L.; Yang, W.; Sun, J. Study on the Optimal Supervision Strategy of Government Low-Carbon Subsidy and the Corresponding Efficiency and Stability in the Small-World Network Context. J. Clean. Prod. 2017, 168, 536–550. [Google Scholar] [CrossRef]
- Wang, G.; Li, Y.; Zuo, J.; Hu, W.; Nie, Q.; Lei, H. Who Drives Green Innovations? Characteristics and Policy Implications for Green Building Collaborative Innovation Networks in China. Renew. Sustain. Energy Rev. 2021, 143, 110875. [Google Scholar] [CrossRef]
- Shi, J.; Zheng, P.; Chang, D.; Xu, L. On the propagation manner of the miners’ reckless behaviors based on the so-called SEIMR model. J. Saf. Environ. 2021, 21, 1203–1211. [Google Scholar] [CrossRef]
- Yu, Z.; Zhou, G.H.; Yang, S.J. Subjective Game Analysis on the Behavior of Safety Management in the High-Risk-System Based on Prospect Theory. In Proceedings of the 2012 International Conference on Management Science & Engineering 19th Annual Conference Proceedings, Dallas, TX, USA, 20–22 September 2012. [Google Scholar]
- Zohar, D.; Erev, I. On the Difficulty of Promoting Workers’ Safety Behaviour: Overcoming the Underweighting of Routine Risks. Int. J. Risk Assess. Manag. 2006, 7, 122–136. [Google Scholar] [CrossRef]
- Qi, S.; Yao, M.; Cheng, J.; Chen, M.; Zhang, Y. Intervention Effect of Safety Incentives on Unsafe Behavior of Construction Workers with Herd Motivation. J. Saf. Sci. Technol. 2018, 14, 186–192. [Google Scholar] [CrossRef]
- Meng, Q.; Liu, Y.; Li, Z.; Wu, C. Dynamic Reward and Penalty Strategies of Green Building Construction Incentive: An Evolutionary Game Theory-Based Analysis. Environ. Sci. Pollut. Res. 2021, 28, 44902–44915. [Google Scholar] [CrossRef]
- Mei, Q.; Zhong, J.; Zhang, Q.; Liu, S. Evolutionary Path of Work Safety Strategies in Cluster’s Enterprises under Spillover Effect. J. Syst. Manag. 2018, 27, 40–49, 56. [Google Scholar]
- Fang, D.; Wu, C.; Wu, H. Impact of the Supervisor on Worker Safety Behavior in Construction Projects. J. Manag. Eng. 2015, 31, 04015001. [Google Scholar] [CrossRef]





| Safe Behavior | Unsafe Behavior | ||
|---|---|---|---|
| Safe behavior | |||
| Unsafe behavior | |||
| Safe Behavior | Unsafe Behavior | ||
|---|---|---|---|
| Safe behavior | R1 + s(1 + y) R1 + s(1 + y) | R1 + s(1 + y) − μθF R2 + s(1 − μ)(1 + y) − μm − εL | |
| Unsafe behavior | R2 + s(1 − μ)(1 + y) − μm − εL R1 + s(1 + y) − μθF | R2 − m − εL R2 − m − εL | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Cao, J.; Wu, Z.; Wei, Q. Evolutionary Game Analysis of Construction Worker Safety Supervision Based on Complex Network. Buildings 2025, 15, 907. https://doi.org/10.3390/buildings15060907
Zhang F, Cao J, Wu Z, Wei Q. Evolutionary Game Analysis of Construction Worker Safety Supervision Based on Complex Network. Buildings. 2025; 15(6):907. https://doi.org/10.3390/buildings15060907
Chicago/Turabian StyleZhang, Feilian, Jiawei Cao, Zhe Wu, and Qicheng Wei. 2025. "Evolutionary Game Analysis of Construction Worker Safety Supervision Based on Complex Network" Buildings 15, no. 6: 907. https://doi.org/10.3390/buildings15060907
APA StyleZhang, F., Cao, J., Wu, Z., & Wei, Q. (2025). Evolutionary Game Analysis of Construction Worker Safety Supervision Based on Complex Network. Buildings, 15(6), 907. https://doi.org/10.3390/buildings15060907






