Finite Element Modeling with Sensitivity and Parameter Variation Analysis of a Deep Excavation: From a Case Study
Abstract
1. Introduction
2. Materials and Methods
2.1. Case Study
2.2. Numerical Model
2.2.1. Soils and Structural Elements
2.2.2. Mesh
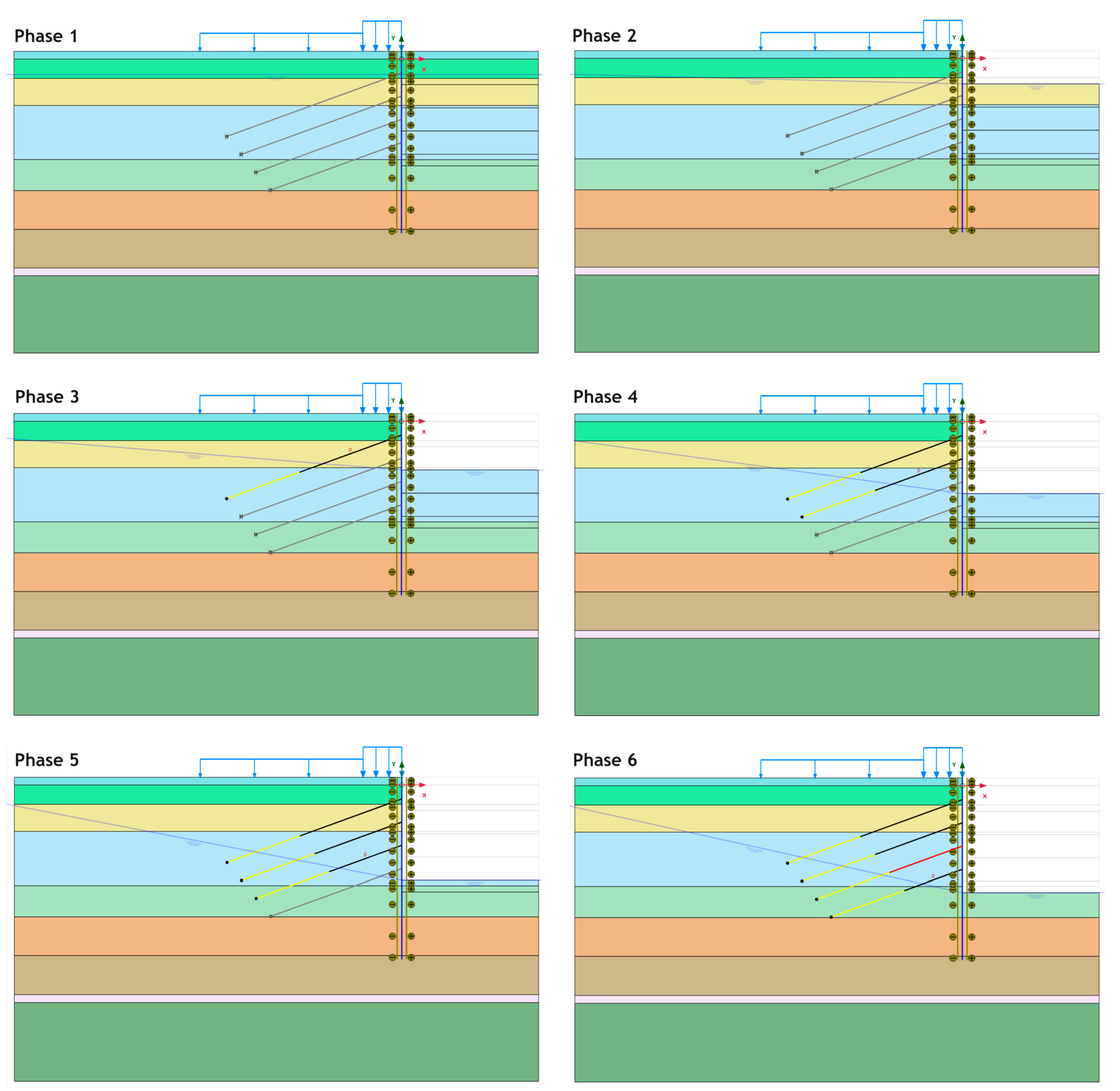
2.2.3. Excavation Phases
2.2.4. Sensitivity Analysis and Parameter Variation Analysis
3. Results and Discussions
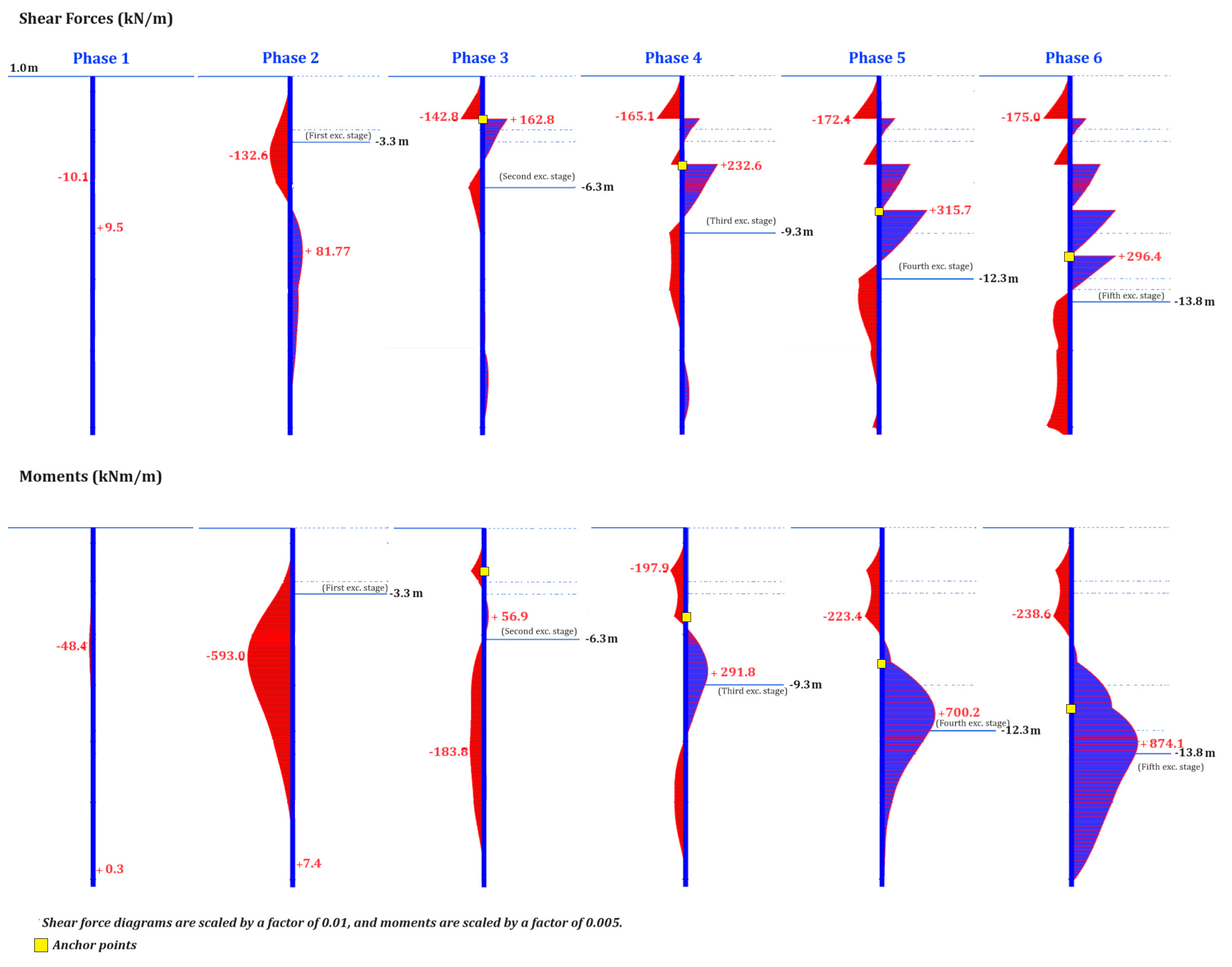
3.1. Numerical Model Results
3.2. Sensitivity Analysis and Parameter Variation
3.3. Comparison with the Case Study
4. Conclusions
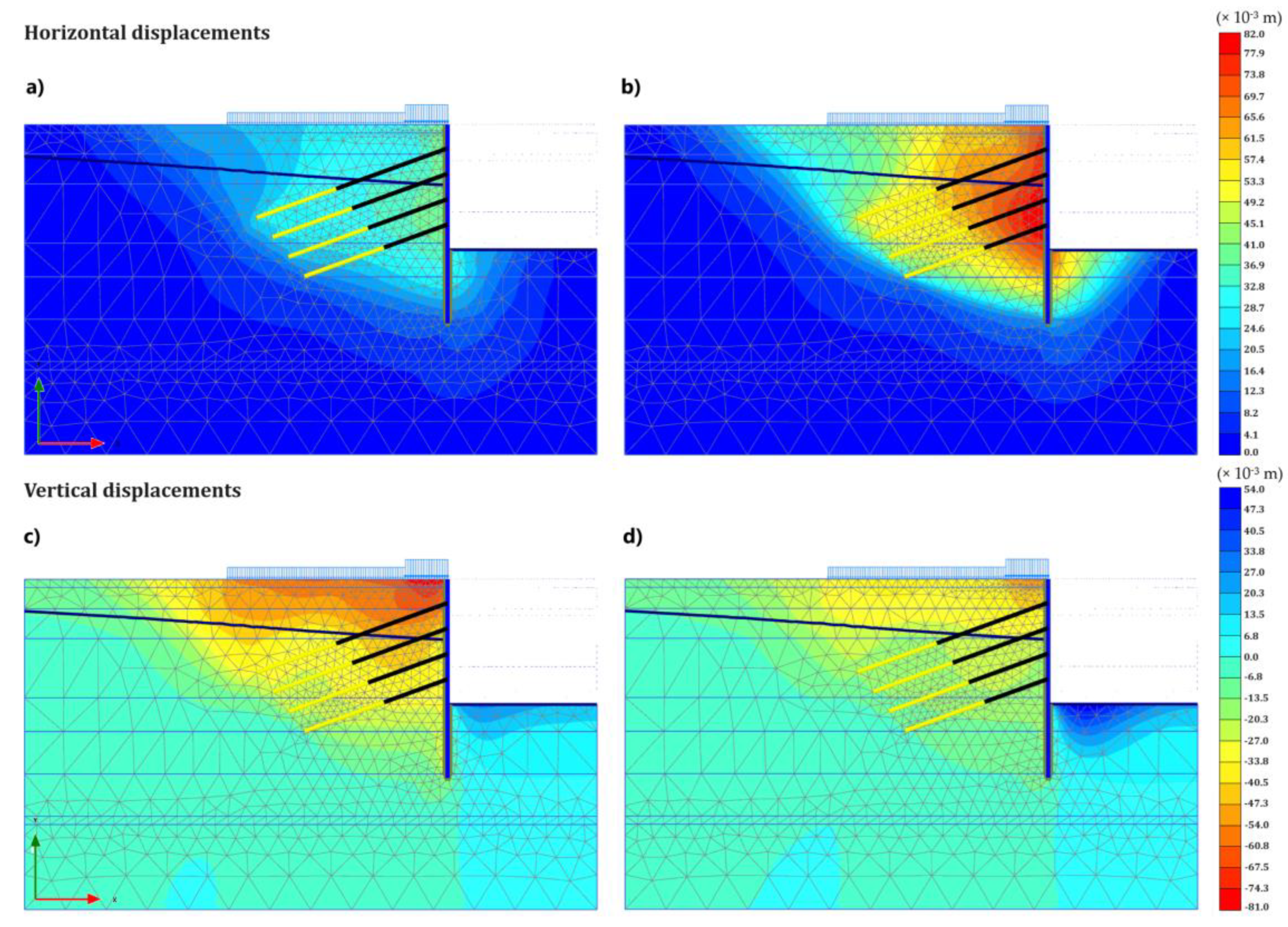
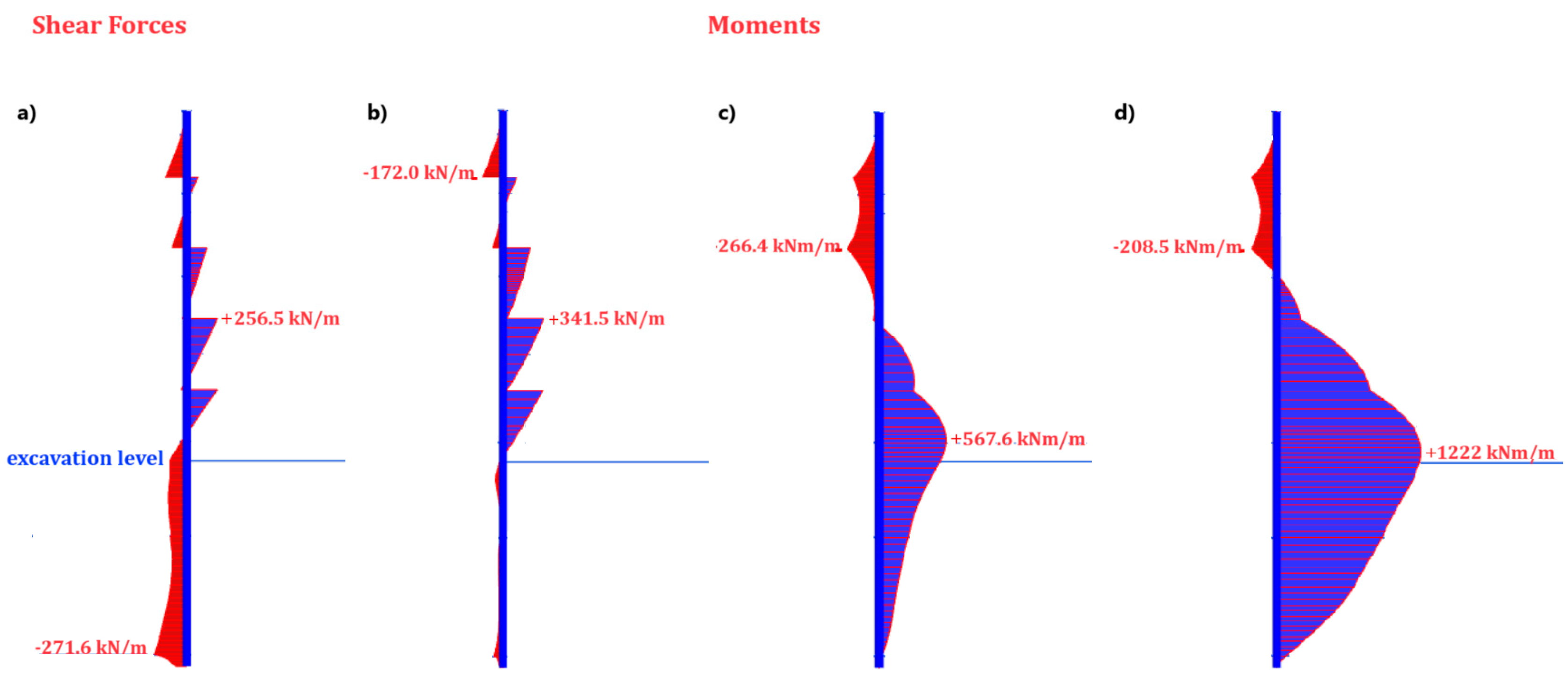
- Based on the numerical model, the lateral displacements are concentrated near the middle of the diaphragm wall, with the excavation base being critical for heave and the nearby structures most affected by the settlements. Internal force diagrams show that the shear forces and moments on the diaphragm wall may be reduced by anchors. Safety factor evaluations confirmed the deep excavation is safe.
- The sensitivity analysis revealed that variations in the elasticity moduli and shear strength parameters, such as cohesion and internal friction angle, are critical for deep excavations. Precise determination of the internal friction angle and cohesion is essential, though the influence of elasticity moduli on the excavation outcomes may be less significant.
- A parameter variation analysis, conducted on key features from the sensitivity analysis, identified the models with maximum (MaxDispl) and minimum (MinDispl) displacements out of 129 analyses. These models highlighted the safety margins of the design, revealing significant differences in the displacements and internal forces. A 3-unit variation in a few soil parameters was found to substantially impact the results.
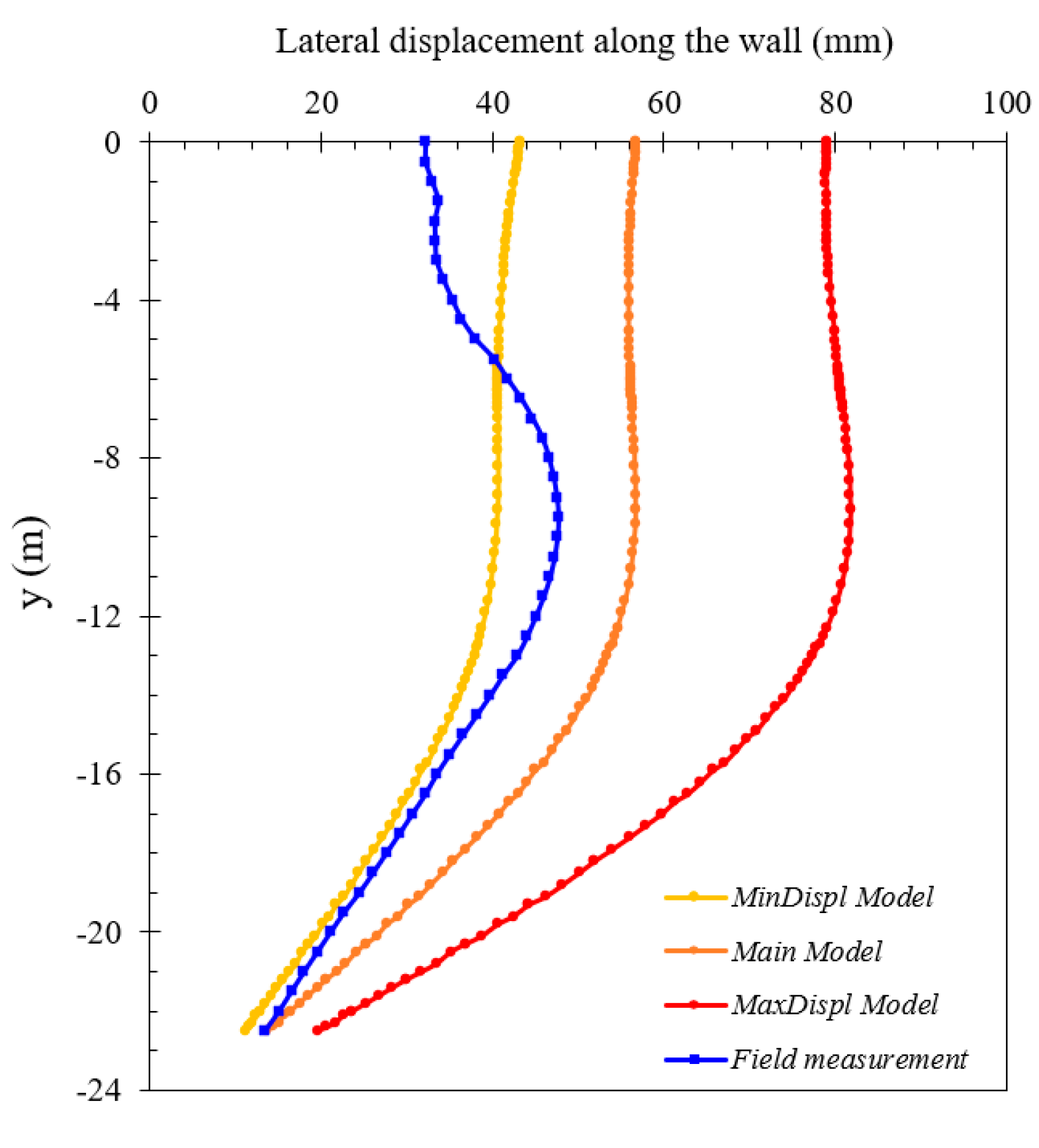
- The horizontal displacements of the wall from numerical models were compared with field measurements from the case study, showing consistency and confirming the model’s accuracy. The actual displacements fell between the MinDispl and the main model, but significant differences between the minimum, main, and maximum models highlighted the impact of varying material properties in projects.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FEM | Finite element method |
| SensiScores | Sensitivity scores |
| MaxDispl | Maximum displacement |
| MinDispl | Minimum displacement |
| UD | Undrained analysis |
| D | Drained analysis |
References
- Tan, Y.; Fan, D.; Lu, Y. Statistical analyses on a database of deep excavations in Shanghai soft clays in China from 1995–2018. Pract. Period. Struct. Des. Constr. 2022, 27, 04021067. [Google Scholar] [CrossRef]
- Van, N.D.; Kim, D.; Choo, Y. Nonlinear seismic performance of buildings considering deep excavation-soil-structure interaction. Bull. Earthq. Eng. 2024, 22, 5119–5145. [Google Scholar] [CrossRef]
- Peng, T.; Ren, D.; Kang, C.; Liu, H.; Xue, P.; Huang, H. Deformation characteristics of soft soil induced by deep excavation and its impact on adjacent tunnels: A case study in Shanghai. KSCE J. Civ. Eng. 2024, 28, 1715–1728. [Google Scholar] [CrossRef]
- Cui, X.; Li, Z.; He, H.; Liu, T.; Wang, J. Observed characterization of multi-level retaining structure for deep excavation of subway station. Urban Rail Transit 2024, 10, 89–106. [Google Scholar] [CrossRef]
- Liu, G.B.; Jiang, R.J.; Ng, C.W.; Hong, Y. Deformation characteristics of a 38 m deep excavation in soft clay. Can. Geotech. J. 2011, 48, 1817–1828. [Google Scholar] [CrossRef]
- Chen, R.P.; Lee, Z.C.; Chen, Y.M.; Ou, C.Y. Failure investigation at a collapsed deep excavation in very sensitive organic soft clay. J. Perform. Constr. Facil. 2015, 29, 04014078. [Google Scholar] [CrossRef]
- Bhatkar, T.; Barman, D.; Mandal, A.; Usmani, A. Prediction of behaviour of a deep excavation in soft soil: A case study. Int. J. Geotech. Eng. 2017, 11, 10–19. [Google Scholar] [CrossRef]
- Hu, J.; Ma, F. Failure investigation at a collapsed deep open cut slope excavation in soft clay. Geotech. Geol. Eng. 2018, 36, 665–683. [Google Scholar] [CrossRef]
- Ou, X.; Zhang, X.; Fu, J.; Zhang, C.; Zhou, X.; Feng, H. Cause investigation of large deformation of a deep excavation support system subjected to unsymmetrical surface loading. Eng. Fail. Anal. 2020, 107, 104202. [Google Scholar] [CrossRef]
- Zhou, F.; Zhou, P.; Li, J.; Lin, J.; Ge, T.; Deng, S.; Wang, Z. Deformation characteristics and failure evolution process of the existing metro station under unilateral deep excavation. Eng. Fail. Anal. 2022, 131, 105870. [Google Scholar] [CrossRef]
- Zhang, W.G.; Hu, X.Y.; Zhang, R.H.; Chen, C.X.; Li, Y.Q.; Ye, W.Y.; Chen, R.L. Numerical analysis of one-strut failure in deep braced excavation considering anisotropic clay behavior. J. Cent. South Univ. 2023, 30, 4168–4181. [Google Scholar] [CrossRef]
- Hsieh, P.G.; Ou, C.Y.; Liu, H.T. Basal heave analysis of excavations with consideration of anisotropic undrained strength of clay. Can. Geotech. J. 2008, 45, 788–799. [Google Scholar] [CrossRef]
- Do, T.N.; Ou, C.Y.; Chen, R.P. A study of failure mechanisms of deep excavations in soft clay using the finite element method. Comput. Geotech. 2016, 73, 153–163. [Google Scholar] [CrossRef]
- Goh, T.C.; Zhang, F.; Zhang, W.; Zhang, Y.; Liu, H. A simple estimation model for 3D braced excavation wall deflection. Comput. Geotech. 2017, 83, 106–113. [Google Scholar] [CrossRef]
- Wu, L.; Sun, J.; Tong, Y. Parametric sensitivity study of deep excavation in Singapore old alluvium formation. Adv. Civ. Eng. 2021, 2021, 8644288. [Google Scholar] [CrossRef]
- Dinakar, K.N.; Prasad, S.K. Behaviour of tie back sheet pile wall for deep excavation using PLAXIS. Int. J. Res. Eng. Technol. 2014, 3, 97–103. [Google Scholar] [CrossRef]
- Cui, K.; Défossez, P.; Richard, G. A new approach for modelling vertical stress distribution at the soil/tyre interface to predict the compaction of cultivated soils by using the PLAXIS code. Soil Tillage Res. 2007, 95, 277–287. [Google Scholar] [CrossRef]
- Babu, G.S.; Singh, V.P. Simulation of soil nail structures using PLAXIS 2D. Plaxis Bull. 2009, 25, 16–21. [Google Scholar]
- Hsiung, B.C.B.; Dao, S.D. Evaluation of constitutive soil models for predicting movements caused by a deep excavation in sands. Electron. J. Geotech. Eng. 2014, 19, 17325–17344. [Google Scholar]
- Bowers, J.T.; Webb, M.C.; Beaver, J.L. Soil parameters for design with the 3D PLAXIS hardening soil model. Transp. Res. Rec. 2019, 2673, 708–713. [Google Scholar] [CrossRef]
- Saleh, S.; Mohd Yunus, N.Z.; Ahmad, K.; Mat Said, K.N. Numerical simulation with hardening soil model parameters of marine clay obtained from conventional tests. SN Appl. Sci. 2021, 3, 156. [Google Scholar] [CrossRef]
- Arslan, E.; Kayaturk, D.; Durmus, M.R.; Bagca, I.; Imamoglu, T.; Sert, S. The role of utilizing load in different cases while numerical modeling of multi-story buildings on alluvial stratum: A comparison study. Arab. J. Sci. Eng. 2024, 49, 13845–13860. [Google Scholar] [CrossRef]
- Rao, S.S. The Finite Element Method in Engineering; Butterworth-Heinemann: London, UK, 2017. [Google Scholar]
- Wang, L.; Juang, C.H.; Atamturktur, S.; Gong, W.; Khoshnevisan, S.; Hsieh, H.S. Optimization of design of supported excavations in multi-layer strata. J. GeoEng. 2014, 9, 1–12. [Google Scholar] [CrossRef]
- Al-Ne’aimi, R.M.S.; Nasir, H.K. Numerical study of design parameters influencing anchored diaphragm walls for deep excavation. Innov. Infrastruct. Solut. 2023, 8, 301. [Google Scholar] [CrossRef]
- Santos, M.D.; Danziger, B.R.; Sieira, A.C. A case of numerical analysis of settlements due to excavation on nearby structures. In Proceedings of the 12th International Conference on International Association for Computer Methods and Advances in Geomechanics (IACMAG), Goa, India, 1–6 October 2008; pp. 3849–3857. [Google Scholar]
- Ou, C.Y. Finite element analysis of deep excavation problems. J. GeoEng. 2016, 11, 1–12. [Google Scholar] [CrossRef]
- Gaur, A.; Sahay, A. Comparison of different soil models for excavation using retaining walls. SSRG Int. J. Civ. Eng. 2017, 4, 43–48. [Google Scholar] [CrossRef]
- Pal, D.; Khan, A.K. Analysis of multivariate regression and deep excavation in expansive soil using PLAXIS 2D. In Geotechnical Characterization and Modelling; Gali, L., Latha, M.P., Ravi, R., Eds.; Lecture Notes in Civil Engineering; Springer: Singapore, 2020; Volume 85, p. 69. [Google Scholar] [CrossRef]
- Pak, A.; Maleki, J.; Aghakhani, N.; Yousefi, M. Numerical investigation of stability of deep excavations supported by soil-nailing method. Geomech. Geoeng. 2021, 16, 434–451. [Google Scholar] [CrossRef]
- Sang-To, T.; Hoang-Le, M.; Khatir, S.; Mirjalili, S.; Wahab, M.A.; Cuong-Le, T. Forecasting of excavation problems for high-rise buildings in Vietnam using planet optimization algorithm. Sci. Rep. 2021, 11, 23809. [Google Scholar] [CrossRef] [PubMed]
- Kog, Y.C.; Loh, K.K. Soil parameters of Kallang formation and old alluvium in Singapore for excavation study with Plaxis. Pract. Period. Struct. Des. Constr. 2022, 27, 04022006. [Google Scholar] [CrossRef]
- Büyükgökçe, F. Parametrical Analysis of Shoring Systems Exposed to Lateral Load in Deep Excavations. Master’s Thesis, Sakarya University, Sakarya, Türkiye, 2018. (In Turkish). [Google Scholar]
- Yalçın, G.; Uncuoğlu, E. The investigation of the single row anchored wall behaviour by numerical analysis studies. In Proceedings of the 8th International Geotechnical Symposium, İstanbul, Türkiye, 13–15 November 2019. [Google Scholar]
- Whitman, R.V. Organizing and evaluating uncertainty in geotechnical engineering. J. Geotech. Geoenviron. Eng. 2000, 126, 583–593. [Google Scholar] [CrossRef]
- Bentley Systems, Inc. Plaxis 2D, Version 2024; Bentley Systems, Inc.: Exton, PA, USA, 2024. [Google Scholar]
- Zhou, B.; Marshall, A.M.; Yu, H. The effect of relative density on settlement above tunnels in sand. In Proceedings of the International Symposium on Geomechanics from Micro to Macro, Nottingham, UK, 20–22 May 2014; pp. 127–139. [Google Scholar]
- Sert, S.; Önalp, A. Sensitivity and parameter variation analysis in excavation problems. In Proceedings of the 4th Geotechnical Symposium, Adana, Türkiye, 1–2 December 2011. (In Turkish). [Google Scholar]
- Aslan, V.; Yağcı, B. A parametric study for lateral displacement of cantilever diaphragm walls. AKU J. Sci. Eng. 2018, 18, 015601. (In Turkish) [Google Scholar] [CrossRef]
- Aslan, V.; Yağcı, B. Geotechnical modeling differences in the analysis of deep excavation support systems. J. BAUN Inst. Sci. Technol. 2018, 20, 514–526. (In Turkish) [Google Scholar] [CrossRef][Green Version]
- Borgh, R. Sensitivity Analysis of Numerical Models for Diaphragm Walls with Cross-Walls in Soft Soils. Master’s Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2018. [Google Scholar]
- Ganesh, K.M.; Ray, A.; Dagdi, D.; Rai, R.; Jaiswal, A. Sensitivity analysis of excavation support systems using numerical modelling. J. Inst. Eng. India Ser. D 2023, 105, 1127–1136. [Google Scholar] [CrossRef]
- Obrzud, R.F. On the use of the hardening soil small strain model in geotechnical practice. Numerics Geotech. Struct. 2010, 16, 1–17. [Google Scholar]
- Dey, A. Calibration of a PLAXIS finite element dynamic model: Effect of domain width and meshing schemes/AES. In Proceedings of the Third Indian Young Geotechnical Engineers Conference, Kochi, India, 15–17 December 2011; p. 127132. [Google Scholar]
- Sert, S.; Önalp, A.; Arel, E. The influence of soil parameter variations on numerical solutions. In Proceedings of the 13th National Congress on Soil Mechanics and Foundation Engineering, İstanbul, Türkiye, 1–2 October 2010. (In Turkish). [Google Scholar]
- Duncan, J.M. Factors of safety and reliability in geotechnical engineering. J. Geotech. Geoenviron. Eng. 2000, 126, 307–316. [Google Scholar] [CrossRef]
- The Design and Application Principles of Excavation Support Structures. Published in Türkiye’s Official Gazette on 18 December 2022. Available online: https://www.resmigazete.gov.tr/eskiler/2022/12/20221218-2.htm (accessed on 18 December 2022).
- Ranjan, H.S.; Rao, S. Analysis of the effect of anchor rod on the behavior of diaphragm wall using PLAXIS 3D. Aquat. Procedia 2015, 4, 240–247. [Google Scholar] [CrossRef]



| Symbol 1 | The Number of Soil Layer | Unit | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| - | Hardening Soil Small-Strain | - | ||||||||
| - | D | UD | D | UD | D | UD | D | UD | UD | - |
| γunsat/γsat | 18/19 | 18/19 | 19/20 | 19/20 | 20/21 | 19/20 | 21/22 | 19/20 | 20/21 | kN/m3 |
| E50ref | 12,000 | 8000 | 15,000 | 10,000 | 25,000 | 22,000 | 50,000 | 30,000 | 40,000 | kN/m2 |
| Eoedref | 12,000 | 8000 | 15,000 | 10,000 | 25,000 | 22,000 | 50,000 | 30,000 | 40,000 | kN/m2 |
| Eurref | 36,000 | 24,000 | 45,000 | 30,000 | 75,000 | 66,000 | 150,000 | 90,000 | 120,000 | kN/m2 |
| C′ref | 1 | 2 | 1 | 20 | 10 | 15 | 15 | 10 | 10 | kN/m2 |
| φ′ | 32 | 26 | 30 | 28 | 34 | 28 | 34 | 28 | 28 | ° |
| ψ | 3 | 0 | 0 | 0 | 4 | 0 | 4 | 0 | 0 | ° |
| G0ref | 38,600 | 38,000 | 39,600 | 64,000 | 101,200 | 113,000 | 112,000 | 123,000 | 152,000 | kN/m2 |
| K0nc | 0.47 | 0.56 | 0.50 | 0.53 | 0.44 | 0.53 | 0.44 | 0.53 | 0.53 | - |
| Rinter | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 | - |
| Parameter | Symbol | Wall | Anchor-Free Length | Anchor-Fixed Length | Unit |
|---|---|---|---|---|---|
| Model | - | Plate | Anchor | Geogrid | - |
| Material type | - | Elastic | Elastoplastic | Elastic | - |
| Axial stiffness | EA1 | 24,000,000 | 163,800 | 600,000 | kN/m |
| Bending stiffness | EI | 1,280,000 | - | - | kNm2/m |
| Poisson’s ratio | v | 0.15 | - | - | - |
| Dimensions | d | 0.8 | - | - | m |
| Spacing | Lspacing | - | 2 | 2 | m |
| Soil | E50ref & Eoedref (kN/m2) | Eurref (kN/m2) | φ′ (°) | C′ref (kN/m2) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Min | Ref | Max | Min | Ref | Max | Min | Ref | Max | Min | Ref | Max | |
| 1 | 10,800 | 12,000 | 13,200 | 32,400 | 36,000 | 39,600 | 29 | 32 | 35 | - | - | - |
| 2 | 7200 | 8000 | 8800 | 21,600 | 24,000 | 26,400 | 23 | 26 | 29 | - | - | - |
| 3 | 13,500 | 15,000 | 16,500 | 40,500 | 45,000 | 49,500 | 27 | 30 | 33 | - | - | - |
| 4 | 9000 | 10,000 | 11,000 | 27,000 | 30,000 | 33,000 | 25 | 28 | 31 | - | - | - |
| 5 | 22,500 | 25,000 | 27,500 | 67,500 | 75,000 | 82,500 | 31 | 34 | 37 | 7 | 10 | 13 |
| 6 | 19,800 | 22,000 | 24,200 | 59,400 | 66,000 | 72,600 | 25 | 28 | 31 | 12 | 15 | 18 |
| 7 | 45,000 | 50,000 | 55,000 | 135,000 | 150,000 | 165,000 | 31 | 34 | 37 | 12 | 15 | 18 |
| 8 | 27,000 | 30,000 | 33,000 | 81,000 | 90,000 | 99,000 | 25 | 28 | 31 | 7 | 10 | 13 |
| 9 | 36,000 | 40,000 | 44,000 | 108,000 | 120,000 | 132,000 | 25 | 28 | 31 | 7 | 10 | 13 |
| Soils | Thickness (m) | Sensitivity Score | ||||
|---|---|---|---|---|---|---|
| E50ref | Eoedref | Eurref | C′ | φ′ | ||
| 1-Fill | 1 | 0 | 1 | 1 | - | 1 |
| 2-Silty clay | 2.5 | 1 | 0 | 1 | - | 4 |
| 3-Silty sandy gravel | 3.5 | 2 | 1 | 1 | - | 12 |
| 4-Sandy clay | 7 | 0 | 1 | 2 | - | 8 |
| 5-Sandy clayey gravel | 4 | 1 | 0 | 0 | 9 | 8 |
| 6-Sandy clay | 5 | 1 | 1 | 2 | 7 | 18 |
| 7-Clayey sandy gravel | 5 | 1 | 1 | 0 | 3 | 9 |
| 8-Silty sandy clay | 1 | 0 | 0 | 0 | 0 | 0 |
| 9-Sandy clay | 10 | 0 | 0 | 0 | 3 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arslan, E.; Akmaz, E.; Çakır, U.F.; Öztürk, Ö.; Pir, H.; Acartürk, S.; Akça, N.Ç.; Karakuş, Y.; Sert, S. Finite Element Modeling with Sensitivity and Parameter Variation Analysis of a Deep Excavation: From a Case Study. Buildings 2025, 15, 658. https://doi.org/10.3390/buildings15050658
Arslan E, Akmaz E, Çakır UF, Öztürk Ö, Pir H, Acartürk S, Akça NÇ, Karakuş Y, Sert S. Finite Element Modeling with Sensitivity and Parameter Variation Analysis of a Deep Excavation: From a Case Study. Buildings. 2025; 15(5):658. https://doi.org/10.3390/buildings15050658
Chicago/Turabian StyleArslan, Eylem, Emre Akmaz, Utku Furkan Çakır, Özlem Öztürk, Hamza Pir, Sena Acartürk, Nisanur Çağlar Akça, Yasin Karakuş, and Sedat Sert. 2025. "Finite Element Modeling with Sensitivity and Parameter Variation Analysis of a Deep Excavation: From a Case Study" Buildings 15, no. 5: 658. https://doi.org/10.3390/buildings15050658
APA StyleArslan, E., Akmaz, E., Çakır, U. F., Öztürk, Ö., Pir, H., Acartürk, S., Akça, N. Ç., Karakuş, Y., & Sert, S. (2025). Finite Element Modeling with Sensitivity and Parameter Variation Analysis of a Deep Excavation: From a Case Study. Buildings, 15(5), 658. https://doi.org/10.3390/buildings15050658







