Abstract
This paper presents an innovative procedure for the stability assessment of masonry domes, aiming at simplifying the modelling and the computational stages of structural analysis. It exploits a macroscopic approach to discretise masonry, specifically using elastic bodies linked by nonlinear interfaces. The latter are made by axial and, when needed, tangential trusses—in turn characterised by an elastic perfectly plastic/brittle behaviour—which constitute the joints connecting homogenised elastic macroblocks. The objective is—by employing low-cost commercial Finite Element software—to predict the behaviour of a masonry curved structure up to failure, maintaining the computational complexity low and the approach accessible to a common user. The process enables not only the quantification of damage at failure but also the tracking of its evolution within the structure, by examining axial forces found in the trusses at each load step. The method allows the modelling of the response of any kind of masonry structure under imposed loads or displacements. Its efficacy is proven on a paradigmatic dome (Global Vipassana Pagoda, Mumbai, India) by comparing the results with limit analysis precedent studies. Finally, the major reliability of a 3D approach is demonstrated.
1. Introduction
Masonry monumental structures can exhibit a variety of structural weaknesses that can be induced by many concurring factors, the most important being the inability of the material to withstand tensile stresses, the peculiar geometry (vaults [1], domes [2], corbel arches, stairs [3], minarets [4], castles [5], mosques [6], etc.), the arrangement of the blocks, and the typology of the loads applied (gravity loads, seismic action, wind, blasts, impacts, etc.).
Within the previously mentioned open issues, the stability assessment of masonry domes subjected to gravity loads is a classic topic that dates from the seminal work by Durand-Claye (1880) [7], who extended the stability area method to vaults of revolution. Taking advantage of the symmetry, it is possible to limit the investigation to a single “lune”, defined as the part between two contiguous meridian planes forming a small angle, and which generates the dome by repetition.
Such an approach is nowadays considered classic, and works within Heyman’s hypotheses, i.e., assuming a material is unable to withstand tensile stresses and imposing the no-sliding condition. The higher complexity of the problem, when compared with the stability analysis of arches, is induced by the presence of meridian stresses, which help in increasing the load-carrying capacity and are always present in the compressed upper calotte. Conversely, in the lower part, cracks appear along meridians with the onset of positive normal stresses, an instance that induces the separation of contiguous lunes, which behave in the lower part as flying buttresses with tapered cross-sections [8].
In the last few decades, researchers have continued to focus on the stability assessment of domes, adopting a variety of different approaches, the most successful being (i) again, Durand-Claye’s method [7], (ii) thrust network analysis [9,10], (iii) Upper Bound Limit Analysis (UB-LA) [11,12], (iv) the utilisation of finite elements (FEs) with either material model exhibiting softening [13], or (v) behaviour with zero tensile resistance [14,15,16].
The approaches recalled above are characterised by manyfold limitations. For instance, approaches based on Durand-Claye’s method are exclusively manual. Consequently, the possibility of studying complex geometries and non-standard loading conditions is limited. Furthermore, there is the need to assume simplified hypotheses on the masonry behaviour (e.g., a vanishing tensile strength along meridians). On the contrary, thrust network analysis has been associated with computerised routines from the beginning, but uses the steps from Heyman’s hypotheses formulated for arches, thus exhibiting similar limitations. In particular, a quite relevant underestimation of the load-carrying capacity may be possible, with too-safe predictions not always suitable in common practices of assessment. UB-LA has also been used in combination with FEs [11,17], and it exhibits the potential for being sufficiently general to deal with complex geometries, different loading conditions, and more sophisticated material models (e.g., orthotropic). However, the accessibility in daily design is limited, because computerised limit analysis requires the formulation of either linear or nonlinear programming problems, which can be solved numerically by means of optimisation tools typically not available in commercial software. Furthermore, no information on displacements can be retrieved by such analyses, and this drawback pertains to all previously mentioned approaches, a limitation that fits poorly with the most recent trends in structural engineering, oriented towards the so-called displacement-based design. Speaking about commercial FE software, the scientific literature dealing with domes analysed via standard finite elements is more abundant [18,19,20], but the material models adopted are typically complex, requiring many mechanical and numerical parameters to be tuned, and therefore cannot be considered a viable alternative for a practitioner with an unspecific background in the field.
Having in mind to put at the disposal of the common user a numerical tool that requires (i) limited expertise and (ii) software equipped only with elastic 3D elements and trusses behaving in either an elasto-plastic or -fragile fashion (called, from now on, Cutoff Bars, CoBs), the authors have recently presented a procedure of analysis for masonry curved structures [21] that can provide—exclusively through meshes identical to those used in elasticity—an estimation of (i) collapse loads, (ii) failure mechanisms, and (iii) displacements, assuming any kind of geometry and loading condition and with a constitutive model that can be elasto-ductile or -fragile, and orthotropic. The numerical approach proposed belongs to the wide family of the so-called Elastic Body and Spring Methods (EBSMs), where masonry is modelled in bulk with elastic macroblocks, and nonlinearity is lumped at the edges of contiguous macroblocks, classically by means of the introduction of flexural and shear springs.
The authors intend to exploit this modelling approach for nonlinear static analyses for every kind of masonry assemblage and structural typology.
The specificity of the approach proposed allows considering the most relevant and commonly known properties of masonry, such as heterogeneity and nonlinearity [22]. Indeed, being a composite material, made by bonded or unbonded units, masonry is intrinsically heterogeneous [23,24]. The units are usually made of various materials like rubble or carved stones, blocks, (un)burnt clay bricks, or often a combination of them (mixed masonry). A heterogeneous modelling strategy can be adopted in EBSMs by simply matching the dimension of the macroblocks with that of the units. A more precise tracking of the nonlinear phenomena when compared with the Distinct Element Method DEM is straightforwardly obtainable by discretising the units with more finite elements. Furthermore, lumping nonlinearity at the interfaces between contiguous macroblocks gives the possibility to model masonry considering a variety of nonlinear material properties. For instance, a brittle behaviour in tension, a limited ductile/fragile compressive strength, and nonlinear sliding (in this latter case, shear cutoff bars are needed) are all features that can be suitably modelled. When a homogenised approach is needed, for instance, to reduce the computational burden, orthotropy can be reproduced, assigning different mechanical properties to interfaces aligned to parallels and meridians. Furthermore, limit analysis and No-Tension Material (NTM) results [25,26,27,28] can be also retraced, imposing an elastic–perfectly plastic behaviour to CoBs. Large-scale sensitivity analyses, carried out also assuming different material properties and models, are rapidly obtainable thanks to (i) the monoaxial nonlinear behaviour of the CoBs and (ii) the utilisation of robust and standard solvers already available in any low-cost FE software. In this regard, referring to the authors’ previous publications, the reader may notice that a better fitting of numerical curves to the experimental capacity is obtainable when a Small-Tension Material (STM) is assumed. In particular, instead of using joint elements in compression only, elastic–perfectly plastic joints with limited tensile strength are typically used to model the possible residual strength of masonry [21,29].
The paper applies such a specific EBSM modelling strategy to assess the stability of a paradigmatic and complex case study, namely the Global Vipassana Pagoda (GVP), a meditation space located in Mumbai, India (Figure 1). The GVP is geometrically characterised by high complexity, being the result of the superposition of three domes: the first segmental, the intermediate catenary, and the upper one conical. The problem is also of paramount practical importance, considering the large span of the segmental dome of about 85 m. The huge internal room of the lower dome and the hollow space of the other domes make the Pagoda a peculiar example imported from Burmese architecture. Indeed, while the Shwedagon Pagoda, Myanmar is a solid stupa (the traditional Indian Buddhist reliquary), the GVP hollow space is designed to host meditators. The Shwedagon Pagoda was the archetype from which the GVP was copied. This is an expression of gratitude to Myanmar for the preservation of the Vipassana practice [30,31]. Figure 1a reports a comparison between the two architectural typologies by means of a schematical cross-section.

Figure 1.
(a) Scheme comparing the cross-sections of a traditional Burmese stupa and the Global Vipassana Pagoda typology. (b) General outer view of the Global Vipassana Pagoda with one of the authors and (c) particular of the external skin.
The GVP has been previously studied by Varma and co-workers in [32] with a method blending FEs and thrust line analysis, in which a FE axisymmetric model meshed with three noded elements was proposed and where the vanishing tensile strength was enforced by repeating iteratively elastic analyses with an orthotropic material. The most recent publication about the GVP is by Aita et al. [33], in which the structural assessment under gravity loads was performed by LA and the method of stability area [7,34,35], but focusing exclusively on the segmental dome.
The designers of the GVP exploited the double-curvature, axisymmetric domes, assembling stone blocks, specifically designed with a unique shape to avoid sliding, and clay bricks. Aside from architectural considerations, specifically carved stone blocks together with the dome curvature allowed building the GVP domes with no centring, contrarily to in situ cast concrete, which requires massive formworks. The materials exploited and the layering result in the structure being made of mixed masonry [36]. From a modelling point of view, some ways to homogenise mixed masonry exist, which proved to be able to closely reproduce its actual behaviour [37,38]. The method exploited here has been demonstrated to work well even for the GVP. Homogenising the whole cross-section allows, with a few input parameters, to rapidly provide information at collapse comparable with data coming from LA [21], with the non-negligible advantage that information on displacements is also available. This is done because perfect adherence is considered between one layer and the next (in wall stratigraphy), and no perceptible difference in the behaviour is measurable. In the EBSM used in this case, the homogenised properties are assigned to macroblocks linked by ad hoc joints made of unidimensional elements.
Analyses are carried out under the progressive application of the self-weight, probably the pivotal parameter that secures stability, to provide a safety index of the structure, intended as the ratio between the applied self-weight making the structure collapse, and the real one. A comparison between the real dome geometry and the same cross-section modelled as if it were a barrel vault reveals how much higher the strength of a dome is, and how crucial it is to model the exact geometry in double-curvature masonry structures.
2. The Global Vipassana Pagoda
The Global Vipassana Pagoda (GVP) is a massive masonry structure covering the largest meditation hall in the world [30]. The structure results from the superposition of three domes and the addition of an auxiliary spherical segment located between the first and second dome from the ground (Figure 2). The spherical segmental dome has a diameter of 85.15 m at ground level and is 26.27 m tall internally. The second dome from the ground is a catenary with a height equal to 33.26 m, whereas the top one is conical, 22.19 m tall. The total height on the external side is 89.93 m from the zero level. The addition of an auxiliary dome makes the outer shape similar to a bell, whereas the buttressing mass placed at the extrados of the segmental dome confers to the external perimeter an octagonal shape. On each side of the octagon, a door allows entering the meditation hall.
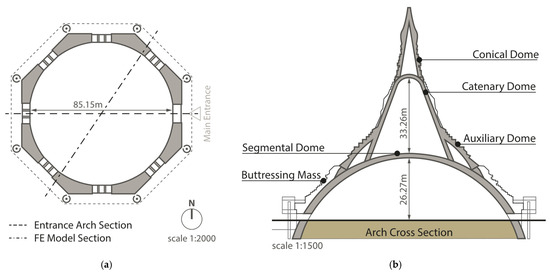
Figure 2.
(a) Plan and (b) shorter section of the Global Vipassana Pagoda.
Thanks to the massive structure and the shape of the stones, the dome was constructed without centring (Figure 3a,b). Jodhpur stone blocks for the segmental dome were carved in a specific shape, designed to prevent sliding (Figure 3c).

Figure 3.
Phases of the construction process without centring for (a) the segmental dome and (b) the catenary and auxiliary domes, with the considerable thickness of the wall layers. A couple of bricks are highlighted to give an idea of the dimensions. (c) The shape of the carved Jodhpur stones for the wall layers is designed to prevent sliding and facilitate the assemblage.
The external structure of the domes was erected in stone blocks [39], whereas the internal layers were built in brick and rubble masonry [30]. The mortar adopted was a traditional lime-Surkhi (a sort of pozzolanic mortar), with good strength (up to 5 MPa) and adhesiveness [40].
The global behaviour will be addressed in the following subsections. The objective is the evaluation of the load-carrying capacity under the self-weight of the structure. After having properly modelled the structure, capacity curves will be plotted, referring to a point in the intrados of the segmental dome. The following subsections will delve into the details of the analysis process conducted by EBSM.
2.1. Structural Modelling
The present numerical strategy belongs to the wide macro-modelling family [6], namely, blocks and mortar are not considered separately, and, hence, interfaces should be regarded exclusively as elements where masonry nonlinearity is lumped [21]. In principle, the approach proposed is also perfectly suited for micro-modelling, but due to the complexity of the texture, and the huge geometric dimensions of the structure, the computational burden required would not justify such a detailed investigation.
Commercial FEM software (Straus7 release R3.1.3, Academic license owner ICT Politecnico di Milano) was used to model the GVP. Once an axisymmetric section of the structure was taken, a 10°-wide fuse and a corresponding vault of 1 m were extruded in a cylindrical and a cartesian reference system, respectively. Then, boundary conditions were set, and the mechanical properties for the macroblocks and the interfaces were assigned (see the ranges in Table 1).

Table 1.
General mechanical properties of materials.
In reality, there are also hooping pre-stressed RC beams at the base of the pagoda, designed to secure an extra resistance to the possible horizontal spreading of the springing.
By good approximation, the role played by such structural elements can be taken into consideration by simply imposing a zero-radial displacement of all the base nodes. Furthermore, no monitoring of their state is possible, and, given the past infiltration issues, their life span is not easily predictable. The analyses also neglect the buttressing mass, thus considering the thinnest structural thickness in the worst-case scenario.
In the following subsections, the 3D analysis will be presented in detail. Then, a 2D analysis will be reported to demonstrate the minor usability for such great structures, unless under the infinite compressive strength hypothesis. Eventually, a comparison between the two methods is drawn.
2.1.1. 3D Case
For the 3D analysis of the GVP, the model was configured as in Figure 4. This case is an axisymmetric problem [43,44] in which no force is imposed along the angle θ, but the meridian joint shall respond to the outward displacement of the slice by hoop tensile strength. The relationship between the fuse and the rest of the dome should be considered. Indeed, the boundary conditions have been set to:
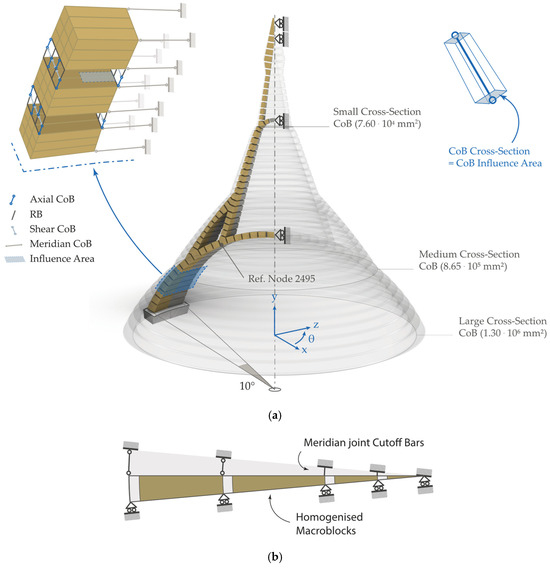
Figure 4.
(a) 3D view of the GVP model with the analysed slice enlightened and separated into two halves, 5° each: the macroblocks and the meridian joint fuses. Enlargement of the macroblocks’ discretisation with the joint construction on the upper left, and the assignment of the CoB cross-section on the right side. (b) Top view scheme of the boundary conditions applied to the slice modelled.
- Tie the slice in the hoop direction, as happens in a real domical structure (meridian cutoff bars, CoBs);
- Consider the mutual action of a fuse against the axisymmetric one (rollers);
- Assume the impossibility of sliding at the springing and fixed joints.
As anticipated, the macroblocks of the heterogeneous model are connected by parallel joints constructed by rigid beams and axial and tangential springs [21,29]. The CoBs are assigned with different tensile strengths to perform a sensitivity analysis.
2.1.2. 3D Case: NLSA Results
Nonlinear static analyses were run to check the stability under the self-weight of the structure. The step density has been increased in the last increments, close to the plateau of the capacity curve, to make the results more accurate and facilitate convergence. The solver took a variable amount of time depending on the mechanical properties of the cutoff bars, which were the only parameters changing from one simulation to the other. Table 2 collects information about the time needed for the nonlinear analyses performed. The reader may note a much shorter computational time for the fc = inf. case.

Table 2.
The computational time for the NLSA on the 3D model of the GVP against various combinations of CoB mechanical properties.
The resulting capacity is represented in the curves of Figure 5 (limited compressive strength) and Figure 6 (infinite compressive strength). The curves refer to the node highlighted in Figure 4a, chosen because it is located in the area of major vertical displacement (due to the intensity of the superimposed loads). Keeping the compressive strength of the joint springs constant and varying the tensile strength, a small variation is noticed between the solutions. As can be observed, the most sensible variation is obtained by raising the meridian joint tensile resistance.

Figure 5.
Sensitivity analysis on the GVP model under different hypotheses on tensile resistance of joint CoBs.
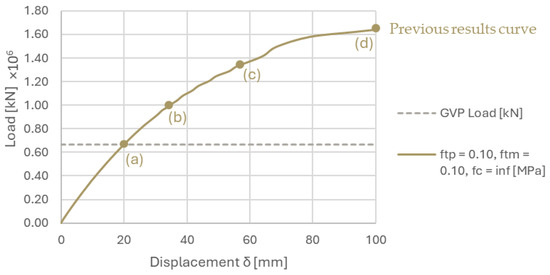
Figure 6.
The capacity curve of the Global Vipassana Pagoda with joint springs under the hypothesis of infinite compressive resistance concerning the self-weight of the bare structure (no buttressing). The capacity curve comes from the study started in Gandolfi et al., 2024 [45]. The reference points, from (a)–(d), are related to the deformed shapes of Figure 7.
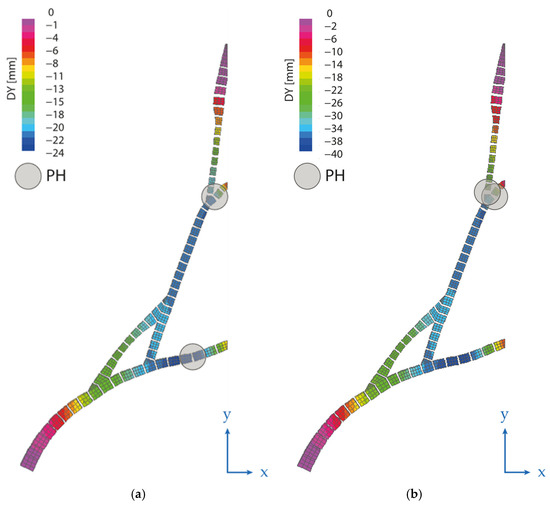
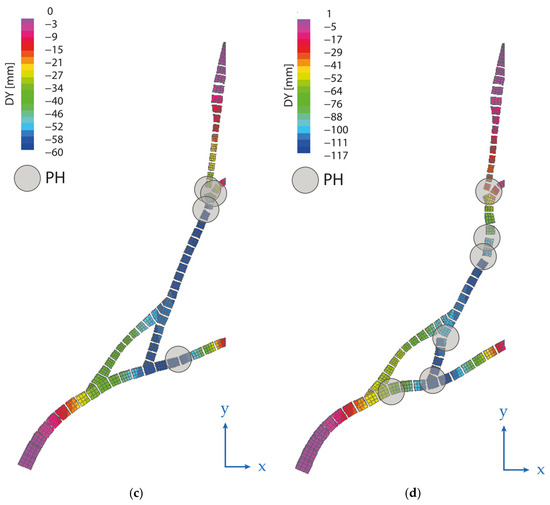
Figure 7.
Deformed shape relative to the vertical displacement (DY) of the GVP 3D model: (a) 21st Step, 6.65·105 kN (self-weight), (b) 29th step, 9.98·105 kN (1.5 times the self-weight), (c) 37th step, 1.33·106 kN (twice the self-weight), and (d) 42nd step, 1.66·106 kN (2.5 times the self-weight). The progressive formation of plastic hinges is identified through the steps.
Assuming the hypothesis of infinite compression resistance, the structural model shows far more capacity, so some more consideration is needed. In Figure 6, the pushdown curve of the GVP is plotted as a refined version of the one in the authors’ preliminary study [45]. Four meaningful steps pointed out in Figure 6 are related to the deformed shapes visible in Figure 7. In the same picture, the temporal development of plastic hinges is highlighted by the analysis of vertical displacement (DY) of the four steps.
2.1.3. 2D Case or the Equivalent Vault
In the bi-dimensional case, an equivalent vault for the GVP is analysed, and the related load-carrying capacity is derived. The model is explained with the schemes of Figure 8. For the details about the modelling procedure for the joint, the reader is referred to [46], which is specific to 2D cases. The following Boundary Conditions (BCs) are applied so to ensure the vault-like behaviour:
- The leaning against the other half for symmetry conditions and the constraint for rotation is set with a double pendulum;
- The theoretical impossibility of sliding at the springing is represented by fixed nodes.
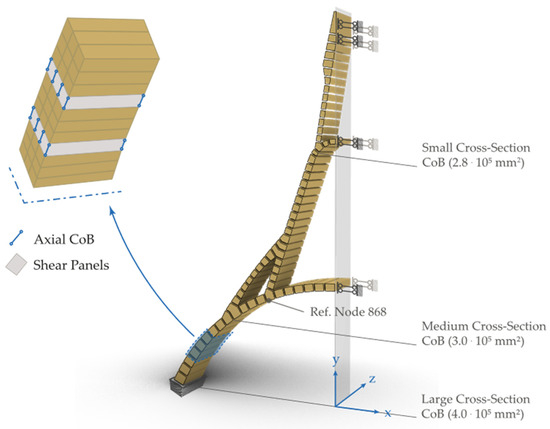
Figure 8.
Equivalent vault model of the GVP, with the boundary conditions applied. In addition, an enlargement details how the plate elements are connected by a joint of axial CoB and orthotropic elements (shear panels).
Pushdown analyses have been run to compare the effect of assigning either limited or infinite compressive strength and two different small values of tensile resistance (Table 1). The capacity curve for each case is then plotted. Moreover, a Thrust Line is also depicted at the maximum increment, to show the deformed configuration and the position of plastic hinges simply integrating axial forces in each CoB (the reader is referred to [46,47] for further information).
2.1.4. 2D Case: NLSA Results
The curves in Figure 9, resulting from a nonlinear static analysis under self-weight, enlighten the very low ultimate capacity of such a massive structure analysed with the same assumptions used for vaults (i.e., the Slicing Technique from Ungewitter [48] and assumed by Heyman, too [49]). Indeed, in this particular case, the load-carrying capacity is less than one, meaning that the structure would not even be capable of supporting its weight. In this case, the time taken by the solver for the analyses performed is compared in Table 3. Again, the shortest computational time is in the fc = inf. case.

Table 3.
Computational time for the NLSA on the 2D model of the GVP against various combinations of CoB mechanical properties.
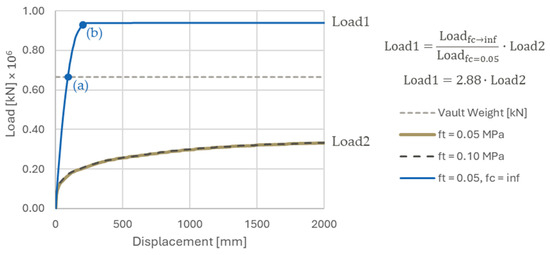
Figure 9.
Capacity curve of the GVP model analysed as its equivalent vault. Comparison between finite and infinite compressive strengths, and different small tensile strengths. The reference points (a) and (b) are related to the deformed shapes of Figure 10. The vault total weight (6.65·105 kN) matches that of the 3D model.
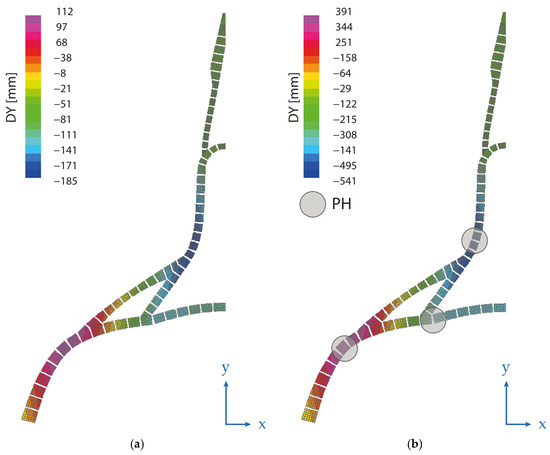
Figure 10.
Deformed shapes relative to the equivalent vault model, set with ft = 0.05, fc = inf. Load applied: (a) 21st step, self-weight: 6.65·103 kN and (b) 32nd step, 9.31·103 kN (1.4 times the self-weight).
The only way to have an acceptable 2D model is to consider the compressive resistance as infinite. A normal assumption for masonry structures is admissible for this kind of modelling, though in many cases unrealistic. A comparison between the capacity curves of the GVP under different assumptions is drawn in Figure 9, with the relative deformed shape in Figure 10. From the finite compression strength models, it can be stated that a change in the ft has no visible effects on the structural behaviour modelling. The curves refer to the node highlighted in Figure 8, chosen for the same reason explained in Section 2.1.2 and to draw meaningful comparisons with the 3D case. In the absence of hoop forces, the compression strength makes more difference.
In Figure 11, the thrust line is plotted on the deformed shape after having derived it from the axial stress resultants in the interface springs.
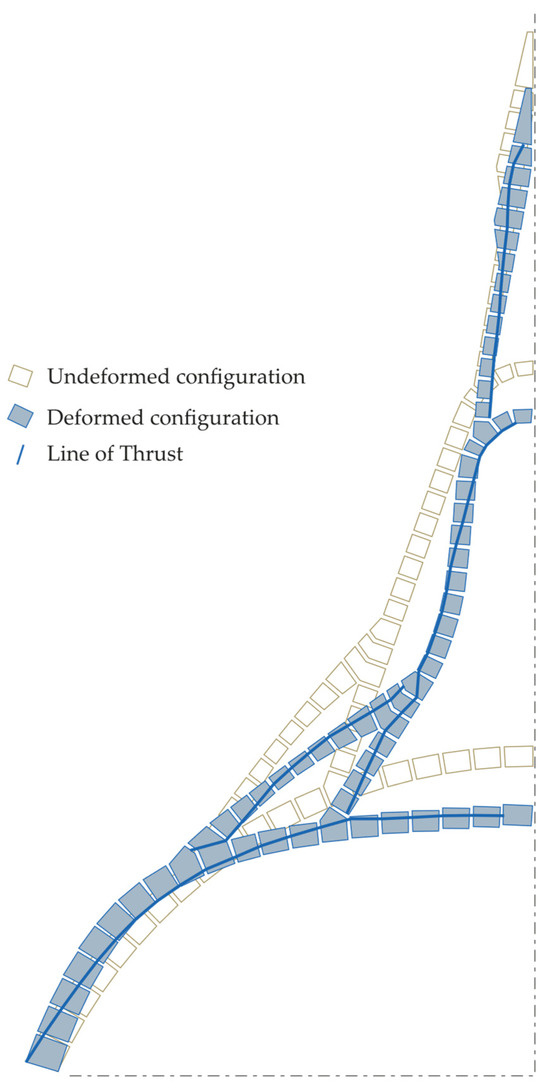
Figure 11.
Undeformed and deformed shape of the GVP equivalent vault with an indication of the line of thrust for ft = 0.05 MPa and infinite compressive strength.
2.2. Discussion
From the pushdown curves reported in the previous sections, the reader will figure out the considerable difference between the bi- and three-dimensional models. Moreover, the comparison between limited and infinite compression resistance is reported. As represented in the comparative chart in Figure 12, the 3D model shows a post-elastic capacity 1.75 times larger than that of the 2D model in the case of infinite compressive strength (D1 in the chart). For limited compressive strength, the 3D case is 3.25 times stronger than the 2D case.
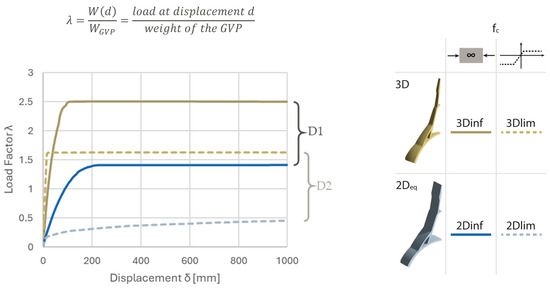
Figure 12.
Comparison between the curves of the 2D (blue) and 3D (golden) models of the GVP. The solid lines consider infinite compressive resistance assigned to the CoB, whereas the dashed ones are for a limited resistance.
The difference D1 is given mainly by the presence of hoop stresses.
It was highlighted previously that 2D models for domes (equivalent vault models) are suitable only if considering infinite compressive resistance—even though they are still conservative. This indeed provides the model for the stability of the missing hooping forces typical of the double curvatures. In any case, 2D models should be considered unsuitable because they are incapable of reproducing the actual static behaviour. From a different perspective, 2D modelling still gives conservative results and a too-simplified behaviour at collapse. In the literature, the importance of considering hoop stresses [32,50,51,52] and the expedience of modelling them by assigning tensile strength to meridian joints are highlighted [21,53].
Comparing this model with previous ones [33] is hard because of the differences in the initial assumptions and geometry, but still possible, as the results in Table 4 show briefly.

Table 4.
Comparison between the Fast Limit Analysis (LA) procedure and the present model.
3. Conclusions and Open Issues
The study of this paper demonstrated the influence of tensile and compressive strengths and the effect of their combination on parallel and meridian joints, benchmarking such considerations on a paradigmatic case study i.e., the Global Vipassana Pagoda (GVP). The difference between the collapse load of the structure modelled in 3D over the 2D model has been expounded in the discussion section, and it is due to the role played by strength assigned to the meridian joint CoBs.
The procedure is created to be simple, therefore insensible to the elastic properties of the material, in agreement with limit analysis assumptions. The effect of small changes in the tensile strength is hardly visible for such big structures (the reader may refer to the charts in Figure 5 and Figure 9). This characteristic is very useful in preliminary studies on historical buildings, when a low level of knowledge is available, and the mechanical properties can be cautiously derived from the standard ranges or using a no-tension material hypothesis.
The reader should note that the present study is just a first validation case, and a more thorough survey is needed before being able to conclude that the results are comparable to those obtained by limit analysis. In this regard, it should be also observed that the analysis proposed in the paper could be even more accurate than the limit analysis, because it could account for the actual interfaces within the masonry of the dome.
Future work will focus on three main issues: (i) damage induced by earthquakes in dome-type structures, (ii) the development of a more detailed model considering the equilibrium ensured by the buttressing mass, and (iii) thermal effects. For (i), the correct identification of the failure mechanism triggered is not an easy task, as shown in several numerical analyses already available in the literature [2,54,55]. Given the height, a combined effect with wind loads shall also be considered. As far as the second topic is concerned, it is worth noting that buttresses may affect both the computation of the collapse multiplier and the plot of the thrust line, already accounted for in [32,33]. Finally, for the third research stream, the benefits of modelling the thermal-induced displacements of the GVP by EBSM will be considered if any effect is detected in the long term, according to the structural health monitoring system already installed [56]. However, both (i) and (iii) require the entire 3D modelling of the structure.
Author Contributions
Conceptualisation, A.G., N.P. and G.M.; methodology, A.G., N.P. and G.M.; software, A.G., N.P. and G.M.; validation, A.G., N.P. and G.M.; formal analysis, A.G. and N.P.; investigation, A.G. and N.P.; resources, G.M.; data curation, A.G. and N.P.; writing—original draft preparation, A.G., N.P. and G.M.; writing—review and editing, A.G., N.P. and G.M.; visualisation, A.G.; supervision, N.P. and G.M.; project administration, G.M.; funding acquisition, G.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data available on request.
Acknowledgments
The study was developed within three research projects, gratefully acknowledged by the authors. An acknowledgment goes to the research project 2022–2024 MAECI, financed by the Italian Ministry of Foreign Affairs under the grant CUP D23C22000060006 and by the Department of Science and Technology (International Corporation Division), India under the research grant INT/Italy/P-29/2022. PIs were, for the Italian part, Gabriele Milani, and, for the Indian part, Siddhartha Ghosh. The study was also partially developed within the research activities carried out within the frame of the 2024–2026 ReLUIS Project—WP10 masonry structures (Coordinator—Guido Magenes), specifically by means of the research carried out in WP10.1.1 and WP10.2 Masonry Structures (Task Coordinators—respectively, Serena Cattari and Sergio Lagomarsino). The Italian Department of Civil Protection has funded such a project. Finally, the study was partially developed with the financial support of the Italian Ministry of Scientific Research MUR within the research project PRIN-2022 (https://www.dabc.polimi.it/en/progetto/advanced-mechanical-models-and-computational-methods-for-large-scale-3d-printing-of-innovative-concrete-structures/ accessed on 6 February 2025) titled “Advanced mechanical models and computational methods for large-scale 3D printing of innovative concrete structures (COM^3D-CREATE)” (National PI: Andrea Chiozzi, Local PI: Gabriele Milani). The aforementioned funding agencies are not responsible for the findings and conclusions reported in this paper. Note that the opinions and conclusions presented by the authors do not necessarily reflect those of the funding entities. ICT Service Software at Politecnico di Milano is gratefully acknowledged for having provided access to software facilities (Straus7 Academic License).
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Milani, E.; Milani, G.; Tralli, A. Limit Analysis of Masonry Vaults by Means of Curved Shell Finite Elements and Homogenization. Int. J. Solids Struct. 2008, 45, 5258–5288. [Google Scholar] [CrossRef]
- Grillanda, N.; Chiozzi, A.; Milani, G.; Tralli, A. Collapse Behavior of Masonry Domes under Seismic Loads: An Adaptive NURBS Kinematic Limit Analysis Approach. Eng. Struct. 2019, 200, 109517. [Google Scholar] [CrossRef]
- Dell’Endice, A.; DeJong, M.J.; Van Mele, T.; Block, P. Structural Analysis of Unreinforced Masonry Spiral Staircases Using Discrete Element Modelling. Structures 2022, 46, 214–232. [Google Scholar] [CrossRef]
- Işık, E.; Harirchian, E.; Arkan, E.; Avcil, F.; Günay, M. Structural Analysis of Five Historical Minarets in Bitlis (Turkey). Buildings 2022, 12, 159. [Google Scholar] [CrossRef]
- Milani, G.; Esquivel, Y.W.; Lourenço, P.B.; Riveiro, B.; Oliveira, D.V. Characterization of the Response of Quasi-Periodic Masonry: Geometrical Investigation, Homogenization and Application to the Guimarães Castle, Portugal. Eng. Struct. 2013, 56, 621–641. [Google Scholar] [CrossRef]
- Bilgin, H.; Ramadani, F. Numerical Study to Assess the Structural Behavior of the Bajrakli Mosque (Western Kosovo). Adv. Civ. Eng. 2021, 2021, 1–17. [Google Scholar] [CrossRef]
- Durand-Claye, A. Vérification de La Stabilité Des Voûtes et Des Arcs: Applications Aux Voûtes Sphériques. Ann. Ponts Chaussées 1880, 19, 416–440. [Google Scholar]
- Sharbaf, A.; Bemanian, M.; Daneshjoo, K.; Shakib, H. Masonry Dome Behavior under Gravity Loads Based on the Support Condition by Considering Variable Curves and Thicknesses. Buildings 2021, 11, 241. [Google Scholar] [CrossRef]
- O’Dwyer, D. Funicular Analysis of Masonry Vaults. Comput. Struct. 1999, 73, 187–197. [Google Scholar] [CrossRef]
- Block, P. Thrust Network Analysis. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2009. [Google Scholar]
- Cavicchi, A.; Gambarotta, L. Two-Dimensional Finite Element Upper Bound Limit Analysis of Masonry Bridges. Comput. Struct. 2006, 84, 2316–2328. [Google Scholar] [CrossRef]
- Milani, G. Upper Bound Sequential Linear Programming Mesh Adaptation Scheme for Collapse Analysis of Masonry Vaults. Adv. Eng. Softw. 2015, 79, 91–110. [Google Scholar] [CrossRef]
- Scacco, J.; Grillanda, N.; Milani, G.; Lourenço, P.B. Novel Non-Linear Static Numerical Model for Curved Masonry Structures Based on a Combined Adaptive Limit Analysis and Discrete FE Computations. Int. J. Solids Struct. 2022, 236–237, 111265. [Google Scholar] [CrossRef]
- Girardi, M.; Padovani, C.; Pellegrini, D. The NOSA-ITACA Code for the Safety Assessment of Ancient Constructions: A Case Study in Livorno. Adv. Eng. Softw. 2015, 89, 64–76. [Google Scholar] [CrossRef]
- Barsi, F.; Barsotti, R.; Bennati, S. Admissible Shell Internal Forces and Safety Assessment of Masonry Domes. Int. J. Solids Struct. 2023, 264, 112082. [Google Scholar] [CrossRef]
- Nodargi, N.A.; Bisegna, P. Collapse Capacity of Masonry Domes under Horizontal Loads: A Static Limit Analysis Approach. Int. J. Mech. Sci. 2021, 212, 106827. [Google Scholar] [CrossRef]
- Scacco, J.; Milani, G.; Lourenço, P.B. Automatic Mesh Generator for the Non-Linear Homogenized Analysis of Double Curvature Masonry Structures. Adv. Eng. Softw. 2020, 150, 102919. [Google Scholar] [CrossRef]
- Milani, G.; Valente, M.; Alessandri, C. The Narthex of the Church of the Nativity in Bethlehem: A Non-Linear Finite Element Approach to Predict the Structural Damage. Comput. Struct. 2018, 207, 3–18. [Google Scholar] [CrossRef]
- Öztürk, Ş.; Bayraktar, A.; Hökelekli, E.; Ashour, A. Nonlinear Structural Performance of a Historical Brick Masonry Inverted Dome. Int. J. Archit. Herit. 2020, 14, 1161–1179. [Google Scholar] [CrossRef]
- Jasieńko, J.; Raszczuk, K.; Kleszcz, K.; Frąckiewicz, P. Numerical Analysis of Historical Masonry Domes: A Study of St. Peter’s Basilica Dome. Structures 2021, 31, 80–86. [Google Scholar] [CrossRef]
- Gandolfi, A.; Pingaro, N.; Milani, G. Simple Non-Linear Numerical Modelling for Unreinforced and FRP-Reinforced Masonry Domes. Buildings 2024, 14, 166. [Google Scholar] [CrossRef]
- Lourenço, P.B. Construction Materials: Their Nature and Behaviour. Part VIII, 5th ed.; Domone, P., Soutsos, M., Eds.; CRC Press/Taylor & Francis Group: Boca Raton, FL, USA, 2017; ISBN 9781315164595. [Google Scholar]
- Page, A.W. The Biaxial Compressive Strength of Brick Masonry. Proc. Inst. Civ. Eng. (Lond.) Part 1—Des. Constr. 1981, 71, 893–906. [Google Scholar] [CrossRef]
- Xu, C.; Xiangli, C.; Bin, L. Modeling of Influence of Heterogeneity on Mechanical Performance of Unreinforced Masonry Shear Walls. Constr. Build. Mater. 2012, 26, 90–95. [Google Scholar] [CrossRef]
- Heyman, J. The Stone Skeleton. Int. J. Solids Struct. 1966, 2, 249–279. [Google Scholar] [CrossRef]
- Heyman, J. The Safety of Masonry Arches. Int. J. Mech. Sci. 1969, 11, 363–385. [Google Scholar] [CrossRef]
- Huerta, S. Mechanics of Masonry Vaults: The Equilibrium Approach. In Proceedings of the 3rd International Seminar in Historical Constructions, Guimarães, Portugal, 7–9 November 2001; pp. 47–70. [Google Scholar]
- Huerta, S. Block Models of the Masonry Arch and Vault; Birkhäuser: Basel, Switzerland, 2020; ISBN 9783433609613. [Google Scholar]
- Gandolfi, A.; Pingaro, N.; Milani, G. On the Nonlinear Behaviour of Domes Subjected to Point Loads on the Crown. In Proceedings of the Lecture Notes in Civil Engineering, ICSCES 2023; Springer: Berlin/Heidelberg, Germany, 2024; Volume 486 LNCE, pp. 191–201. [Google Scholar]
- Varma, N.R.; Jangid, R.S.; Ghosh, S.; Milani, G.; Cundari, G.A. Global Vipassana Pagoda: Main Features and History of Construction. In Proceedings of the 2023 IEEE International Workshop on Metrology for Living Environment (MetroLivEnv), Milano, Italy, 29–31 May 2023. [Google Scholar]
- Gandolfi, A.; Pingaro, N.; Ghosh, S.; Halani, B.; Milani, G. Nonlinear Static Analysis of Global Vipassana Pagoda by Means of a Novel FE-Based Method: Modelling Strategy. In Proceedings of the 2024 IEEE International Workshop on Metrology for Living Environment (MetroLivEnv), Chania, Greece, 13 June 2024. [Google Scholar]
- Varma, M.; Milani, G.; Jangid, R.S.; Cundari, G.A.; Ghosh, S.; Bakliwal, T.; Designers, N. Global Vipassana Pagoda: Finite Element Thrust Line FETLA Analyses. In Proceedings of the 2023 IEEE International Workshop on Metrology for Living Environment (MetroLivEnv), Milan, Italy, 29–31 May 2023; pp. 1–6. [Google Scholar]
- Aita, D.; Milani, G.; Taliercio, A. Fast Limit Analysis of Domes Belonging to the Architectural Heritage Under Different Hypotheses on Masonry Strength. Int. J. Archit. Herit. 2024, 1–33. [Google Scholar] [CrossRef]
- Aita, D.; Milani, G.; Taliercio, A. Limit Analysis of Masonry Domes with Oculus and Lantern: A Comparison between Different Approaches. Math. Mech. Solids 2025, 30, 6–28. [Google Scholar] [CrossRef]
- Aita, D.; Bruggi, M.; Taliercio, A. Thrust Network Analysis of Masonry Arches and Domes of Any Stereotomy with Finite Compressive Strength: Multi-Constrained Minimization Problem Versus Stability Area Method; Springer: Berlin/Heidelberg, Germany, 2024; Volume 437, ISBN 9783031443275. [Google Scholar]
- Amer, O.; Aita, D.; Mohamed, E.K.; Torky, A.; Shawky, A. Multi-leaf Stone Masonry Walls in Egypt: A Legend. Heritage 2021, 4, 2763–2791. [Google Scholar] [CrossRef]
- Tiberti, S.; Milani, G. 3D Homogenized Limit Analysis of Non-Periodic Multi-Leaf Masonry Walls. Comput. Struct. 2020, 234, 106253. [Google Scholar] [CrossRef]
- Tiberti, S.; Milani, G. 3D Voxel Homogenized Limit Analysis of Single-Leaf Non-Periodic Masonry. Comput. Struct. 2020, 229, 106186. [Google Scholar] [CrossRef]
- Kaur, G.; Ahuja, A.; Thakur, S.N.; Pandit, M.; Duraiswami, R.; Singh, A.; Kaur, P.; Saini, J.; Goswami, R.G.; Prakash, J.; et al. Jodhpur Sandstone: An Architectonic Heritage Stone from India. Geoheritage 2020, 12, 16. [Google Scholar] [CrossRef]
- Javed, U.; Khan, A.; Iqbal, M.; Arif, S.; Mueed Iqbal, A. Compressive Strength of Lime Mortars with Surkhi and Kankar as Pozzolans under Normal and Humid Conditions. Sci. Int. 2016, 28, 3889–3892. [Google Scholar]
- SP 7; National Building Code of India. Bureau of Indian Standards: New Delhi, India, 2016.
- IS 1905; Indian Standard Code of Practice for Structural Use of Unreinforced Masonry. Bureau of Indian Standards: New Delhi, India, 1987.
- Bathe, K.J.; Wilson, E.L. Numerical Methods in Finite Element Analysis; Prentice-Hall: Englewood Cliffs, NJ, USA, 1976. [Google Scholar]
- Wilson, E.L. Three Dimensional Static and Dynamic Analysis of Structures: A Physical Approach with Emphasis on Earthquake Engineering; Computers and Structures, Inc.: Berkeley, CA, USA, 2000; ISBN 0923907009. [Google Scholar]
- Gandolfi, A.; Pingaro, N.; Ghosh, S.; Halani, B.; Milani, G. Nonlinear Static Analysis of Global Vipassana Pagoda by Means of a Novel FE-Based Method: Results. In Proceedings of the 2024 IEEE International Workshop on Metrology for Living Environment (MetroLivEnv), Chania, Greece, 13 June 2024. [Google Scholar]
- Pingaro, N.; Milani, G. Simple Non-Linear Numerical Modelling of Masonry Arches Reinforced with SRG Using Elasto-Fragile and Elasto-Ductile Truss Finite Elements. Eng. Struct. 2023, 293, 116637. [Google Scholar] [CrossRef]
- Pingaro, N.; Buzzetti, M.; Milani, G. Advanced FE Nonlinear Numerical Modeling to Predict Historical Masonry Vaults Failure: Assessment of Risk Collapse for a Long Span Cloister Vault Heavily Loaded at the Crown by Means of a General-Purpose Numerical Protocol. Eng. Fail. Anal. 2025, 167, 109070. [Google Scholar] [CrossRef]
- Ungewitter, G.G.; Mohrmann, K. Lehrbuch der Gotischen Konstruktionen, 3rd ed.; Weigel: Leipzig, Germany, 1890. [Google Scholar]
- Heyman, J. The Stone Skeleton; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Varma, M.N.; Ghosh, S. Finite Element Thrust Line Analysis of Axisymmetric Masonry Domes. Int. J. Mason. Res. Innov. 2016, 1, 59–73. [Google Scholar] [CrossRef]
- Varma, M.; Milani, G.; Ghosh, S. Finite Element Thrust Line Analysis of Cracked Axisymmetric Masonry Domes Reinforced with Tension Rings. Int. J. Mason. Res. Innov. 2018, 3, 72–78. [Google Scholar] [CrossRef]
- Varma, M.N.; Jangid, R.S.; Achwal, V.G. Tension Ring in Masonry Domes; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1–8. [Google Scholar]
- Gandolfi, A.; Pingaro, N.; Milani, G. Efficacy of FRP Hooping in Masonry Domes: A Simple Numerical Approach. In Proceedings of the Engineering Proceedings, Virtual, 25–27 January 2024; Volume 53. [Google Scholar]
- Kocaman, İ. The Effect of the Kahramanmaraş Earthquakes (Mw 7.7 and Mw 7.6) on Historical Masonry Mosques and Minarets. Eng. Fail. Anal. 2023, 149, 107225. [Google Scholar] [CrossRef]
- Gandolfi, A.; Milani, G. Pushover Analysis of Masonry Double Curvature Structures Subjected to Horizontal Loads: The Anime Sante Dome. In Proceedings of the 9th European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS), Lisboa, Portugal, 6 June 2024. [Google Scholar]
- Ghosh, S.; Varma, M.; Milani, G.; Halani, B.; Cundari, G.A. Global Vipassana Pagoda: Medium Term IoT Based Structural Health Monitoring. In Proceedings of the 2023 IEEE International Workshop on Metrology for Living Environment (MetroLivEnv), Milan, Italy, 29–31 May 2023. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).