Effect of Photovoltaic Energy-Saving Window Factors on Building Heating Load Under Three Control Modes
Abstract
1. Introduction
2. Methodology
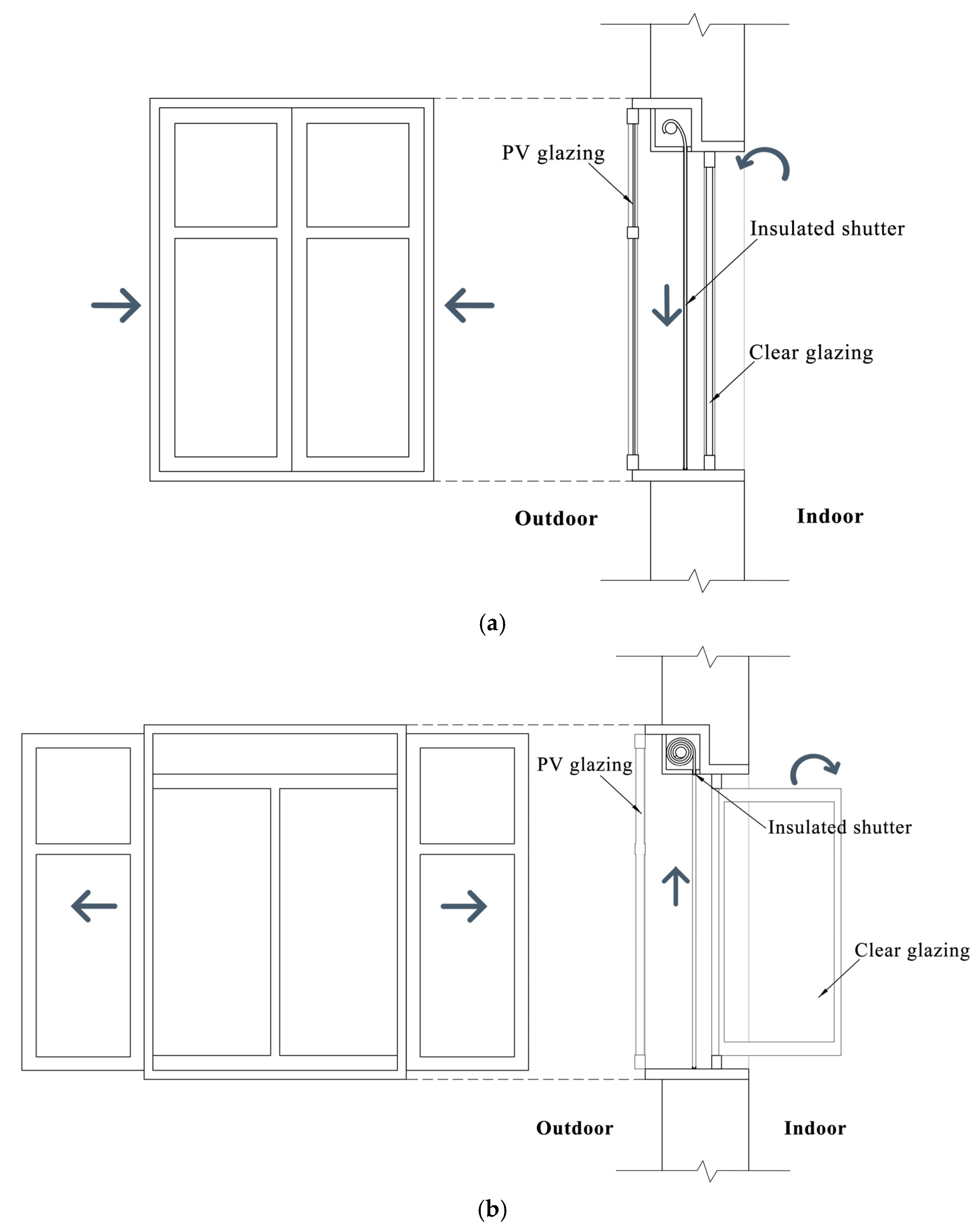
2.1. Window Design and Mathematical Model
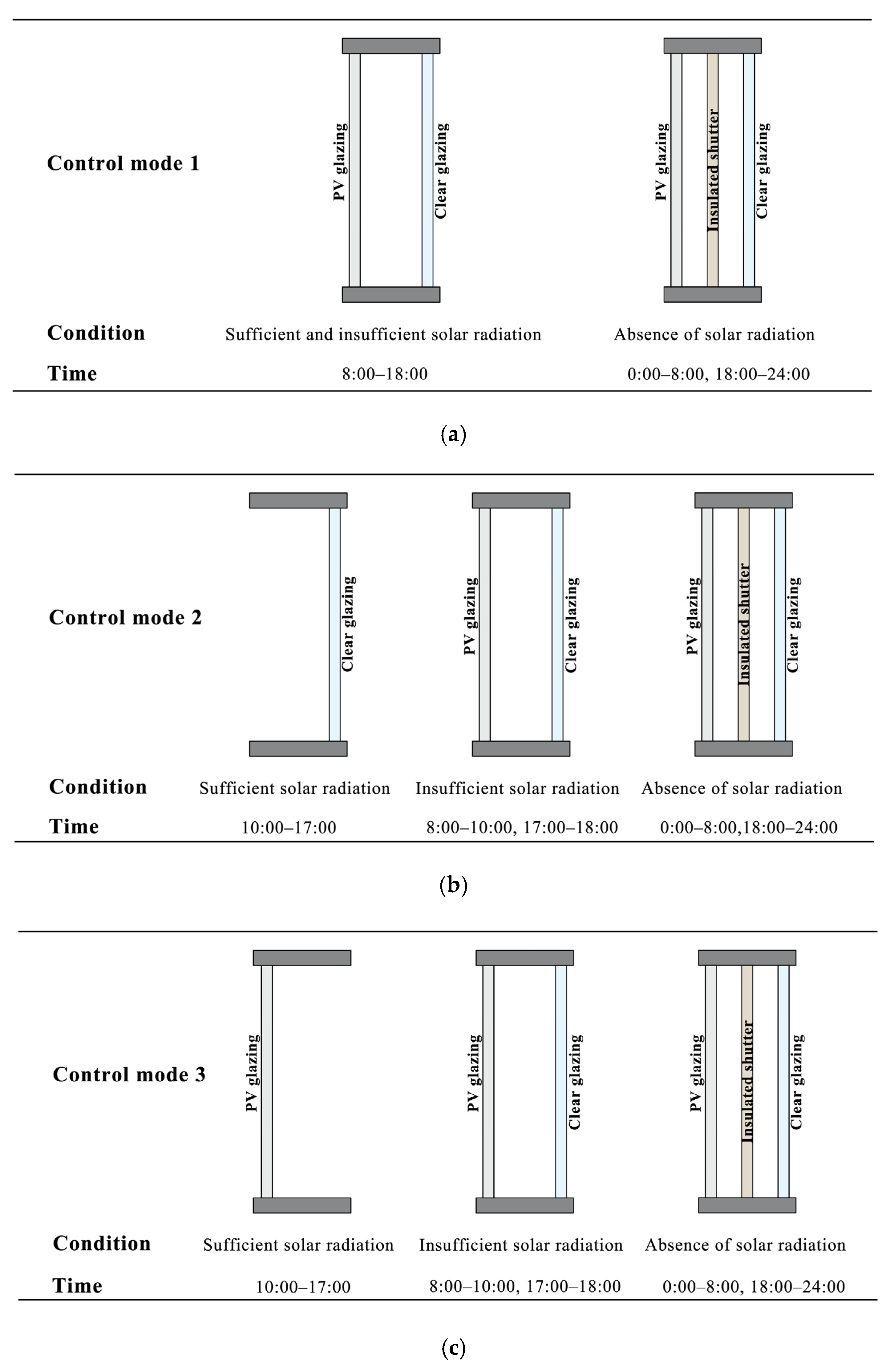
2.1.1. Window Structure and Three Control Modes
2.1.2. Mathematical Model
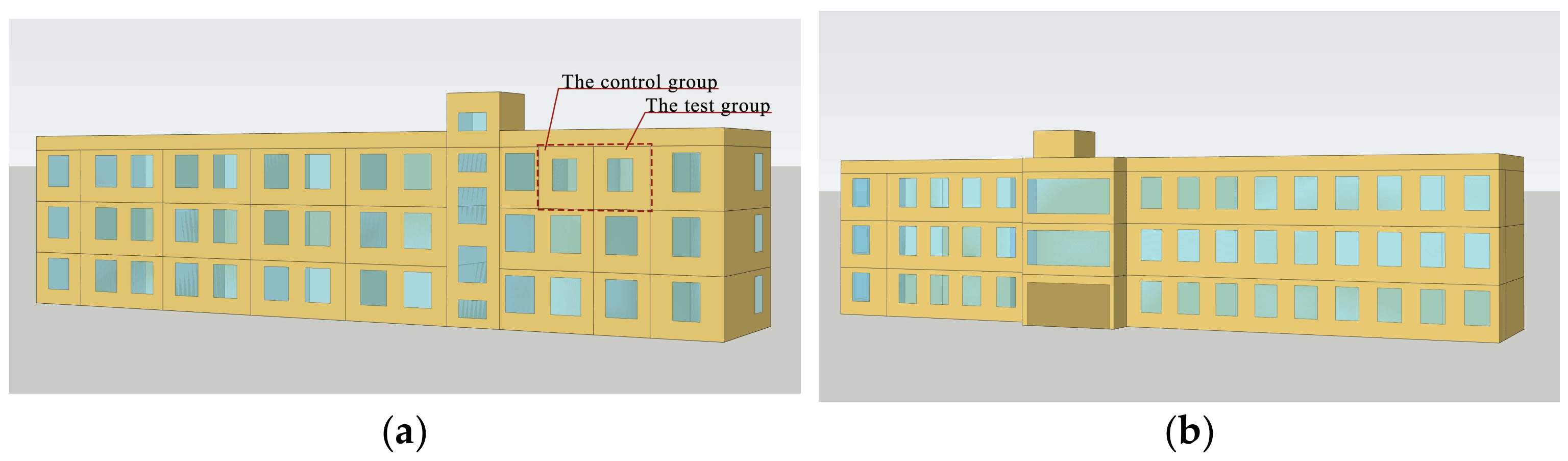
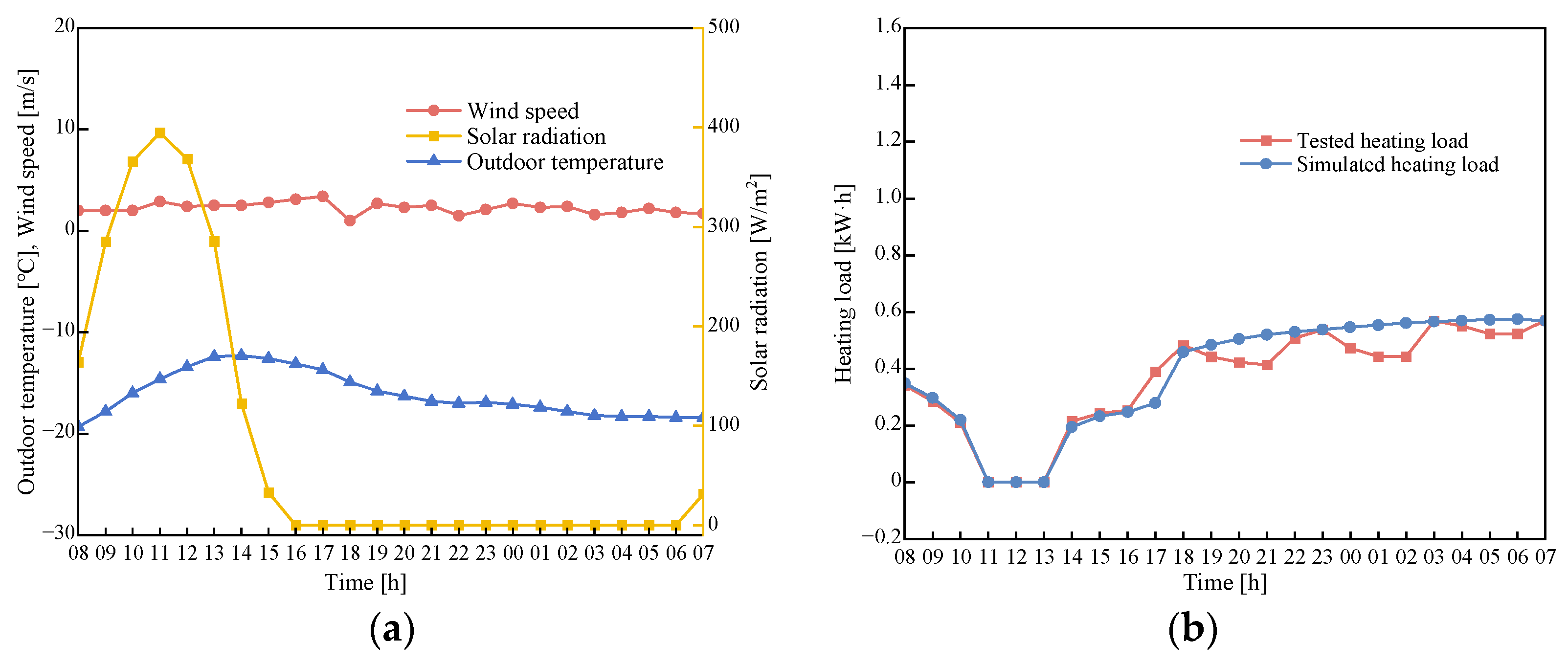
2.2. In Situ Test Setup and Energy-Saving Effect Confirmation
2.2.1. In Situ Test Setup
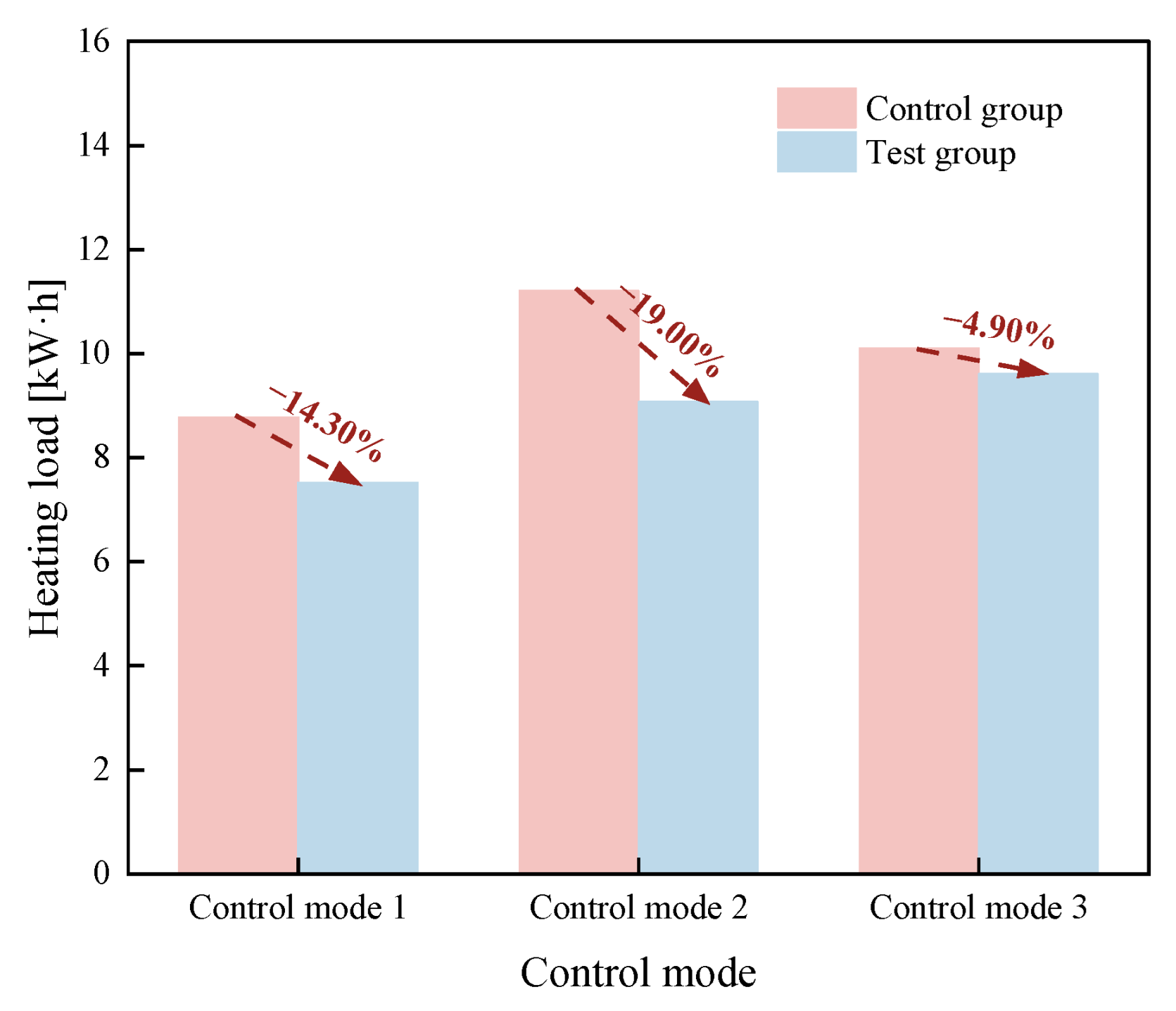
2.2.2. Confirmation of the Window Energy-Saving Effect
2.3. Numerical Experiment Setup and Model Validation
2.3.1. Numerical Experiment Setup
2.3.2. Model Validation
3. Results and Discussion
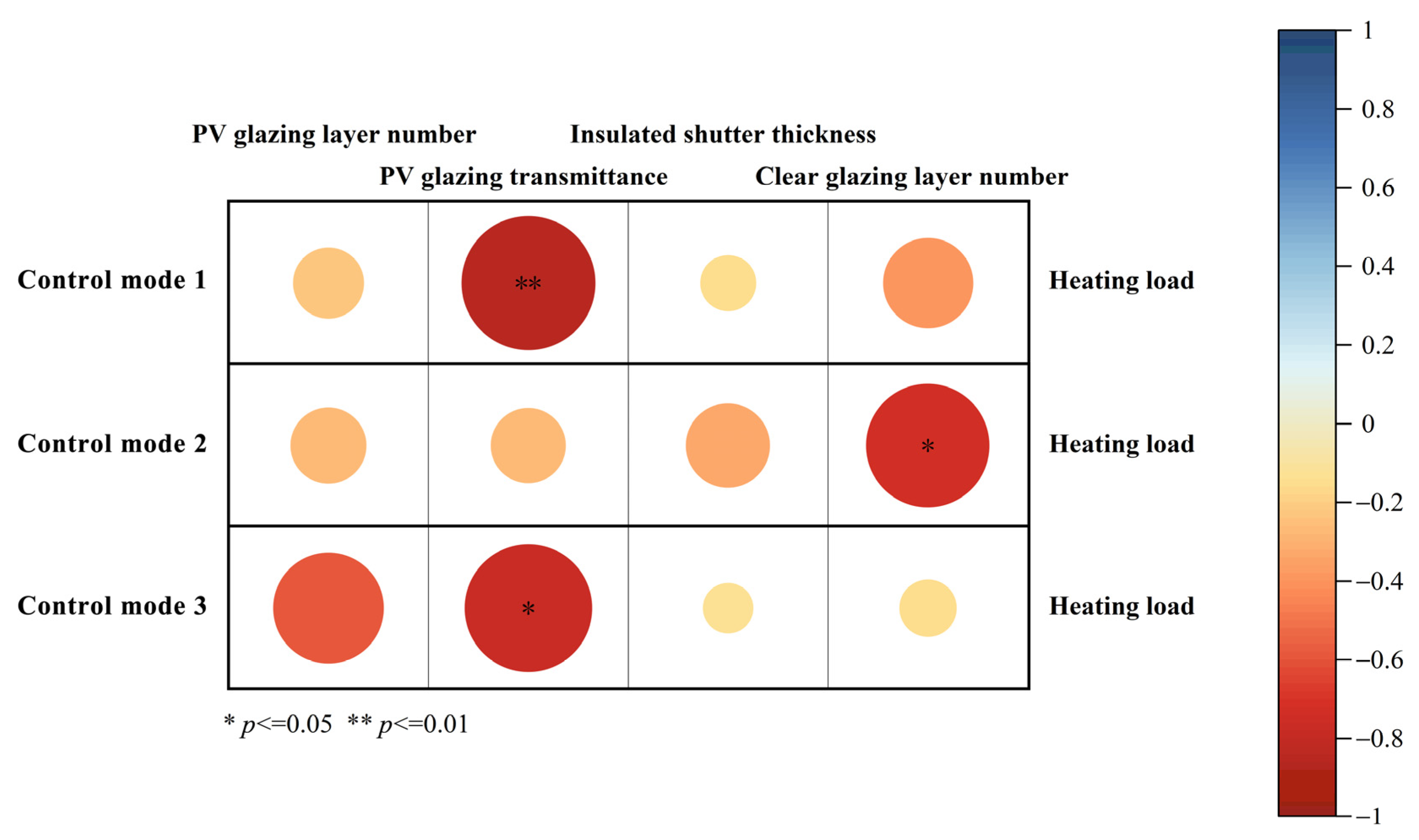
3.1. Correlation Analysis of Key Factors Influencing Building Heating Load
3.2. Effect of Key Factor Configurations on Building Heating Load
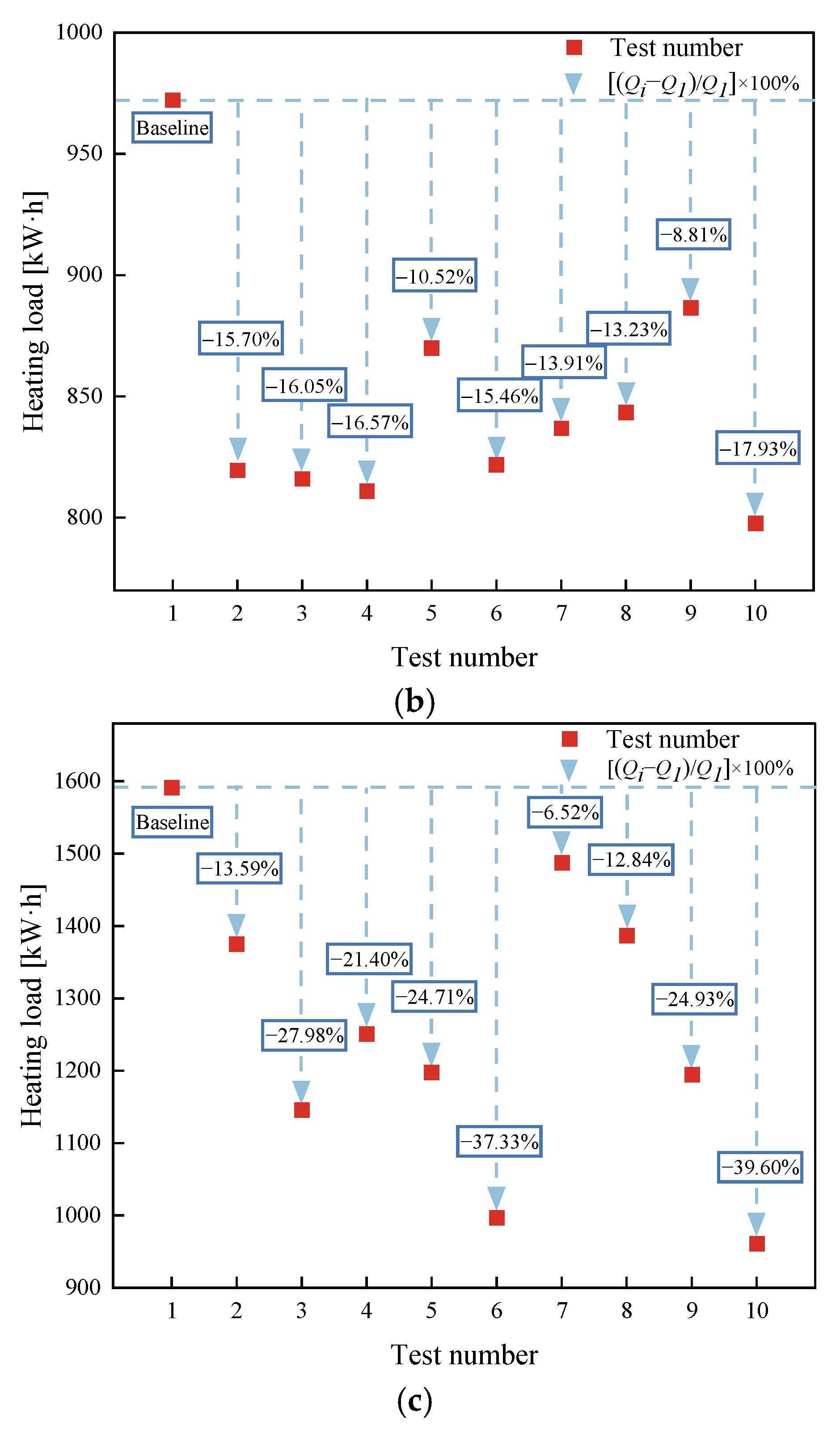
3.2.1. Comparison Within Control Modes
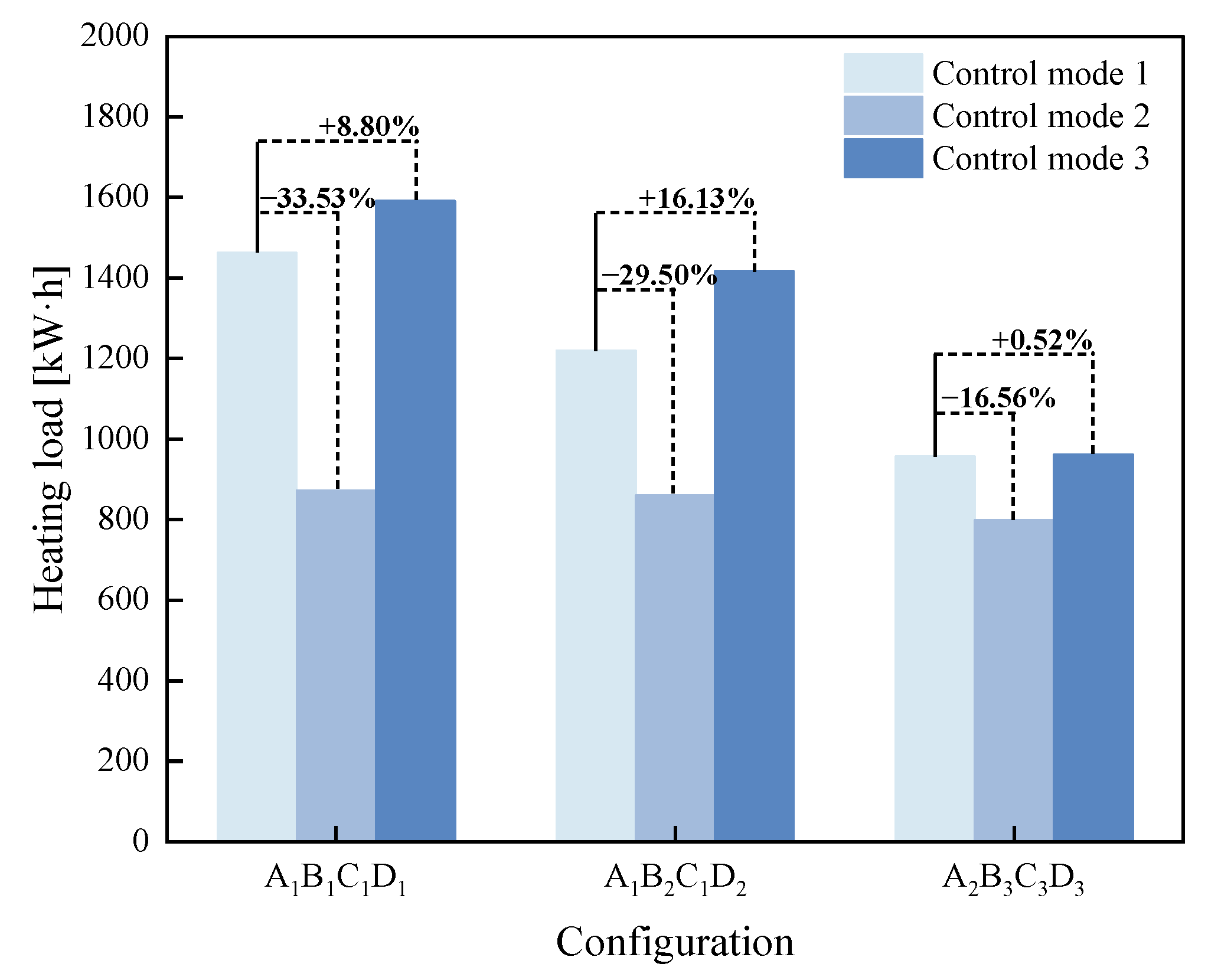
3.2.2. Comparison Between Control Modes
4. Conclusions
- (1)
- The degree of correlation between key factors and heating load is influenced by the control mode. When the PV glazing is not controlled and remains closed, transmittance is the most critical factor. However, in control mode 2, where PV glazing is controlled, the number of clear glazing layers proves to be the most influential factor on heating load.
- (2)
- Configurations under control modes 1 and 3 have a relatively greater impact on heating load, with reductions from the highest to the lowest heating load of 34.62% and 39.60%, respectively. In contrast, the reduction is smaller in control mode 2, with a decrease of 17.93% from the highest to the lowest heating load. This suggests that an appropriate control mode can reduce heating load differences caused by configuration variations.
- (3)
- Among the three control modes for PV energy-saving window, control mode 2 proves to be the most optimal. Even under the optimal configuration, the heating load in control mode 2 is reduced by 16.56% compared to control mode 1. These results confirm that position-controlled operation of the PV glazing is a viable approach for reducing heating load.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviation | |
| PV | photovoltaic |
| DSF | double-skin façade |
| SHGC | solar heat gain coefficient |
| BIPV | building-integrated photovoltaic |
| EPS | expanded polystyrene |
| CdTe | Cadmium Telluride |
| ECMWF | European Centre for Medium-Range Weather Forecasts |
| MAPE | Mean Absolute Percentage Error |
| RMSE | Root Mean Square Error |
| TMY | typical meteorological year |
| NVDPV | natural ventilated double photovoltaic |
| Symbol | |
| T | temperature [K] |
| τ | time |
| ρ | density [kg/m3] |
| C | specific heat capacity [J/(kg·K)] |
| λ | thermal conductivity [W/(m·K)] |
| heat generation from the internal heat source [W/m3] | |
| h | heat transfer coefficient [W/(m2·K)] |
| ε | emissivity |
| σ | Stefan–Boltzmann constant, 5.67 × 10−8 [W/(m2·K4)] |
| μ | dynamic viscosity [Pa·s] |
| A | the area [m2] |
| X | angle factor |
| D | thickness [m] |
| k | thermal conductivity [W/(m·K)] |
| I | solar radiation [W/m2] |
| ξ | absorbance |
| U | effective heat transfer coefficient [W/(m2·K)] |
| δ | PV coverage ratio |
| V | wind speed [m/s] |
| Q | heating load [kW·h] |
| Subscript | |
| f | air temperature |
| s | surface temperature |
| sur | environmental surface temperature |
| po | outer part glass of PV glazing |
| pi | inner part glass of PV glazing |
| pc | photovoltaic cells of PV glazing |
| c | convection heat transfer |
| r | radiative heat transfer |
| gnd | ground surface temperature |
References
- Boehle, L.; Callioni, F.; Loyant, H.; Camarasa, C.; Gask, C.; Henriot, P.; Klimovich, K.; Kauf, N.; Kaur, S.; Laera, S.; et al. Energy Efficiency 2023; International Energy Agency: Paris, France, 2023; Available online: https://www.iea.org/reports/energy-efficiency-2023 (accessed on 18 September 2024).
- Available online: https://www.clearvuepv.com/project/cfmeu-wellness-centre/?utm_medium=website&utm_source=archdaily.com (accessed on 26 September 2024).
- Wang, M.; Peng, J.Q.; Li, N.P.; Yang, H.X.; Wang, C.L.; Li, X.; Lu, T. Comparison of energy performance between PV double skin facades and PV insulating glass units. Appl. Energy 2017, 194, 148–160. [Google Scholar] [CrossRef]
- Wu, Z.H.; Zhang, L.; Su, X.S.; Wu, J.; Liu, Z.B. Experimental and numerical analysis of naturally ventilated PV-DSF in a humid subtropical climate. Renew. Energy 2022, 200, 633–646. [Google Scholar] [CrossRef]
- Peng, J.Q.; Curcija, D.C.; Lu, L.; Selkowitz, S.E.; Yang, H.X.; Zhang, W.L. Numerical investigation of the energy saving potential of a semi-transparent photovoltaic double-skin facade in a cool-summer Mediterranean climate. Appl. Energy 2016, 165, 345–356. [Google Scholar] [CrossRef]
- Guo, W.W.; Kong, L.; Chow, T.T.; Li, C.Y.; Zhu, Q.Z.; Qiu, Z.Z.; Li, L.; Wang, Y.L.; Riffat, S.B. Energy performance of photovoltaic (PV) windows under typical climates of China in terms of transmittance and orientation. Energy 2020, 213, 118794. [Google Scholar] [CrossRef]
- Wang, C.Y.; Uddin, M.M.; Ji, J.; Yu, B.D.; Wang, J. The performance analysis of a double-skin ventilated window integrated with CdTe cells in typical climate regions. Energy Build. 2021, 241, 110922. [Google Scholar] [CrossRef]
- Roberts, F.; Yang, S.L.; Du, H.; Yang, R. Effect of semi-transparent a-Si PV glazing within double-skin façades on visual and energy performances under the UK climate condition. Renew. Energy 2023, 207, 601–610. [Google Scholar] [CrossRef]
- Xu, C.W.; Shi, X.P.; Ni, Y.H.; Su, H.; Lei, X.Y.; Kong, D.F.; Han, F.; Zhu, C.S. Comparative study of dynamic thermal performance of photovoltaic double skin façades influenced by glass transmittance and natural ventilation. Energy Build. 2023, 294, 113220. [Google Scholar] [CrossRef]
- Lee, C.S.; Lee, H.M.; Choi, M.J.; Yoon, J.H. Design optimization and experimental evaluation of photovoltaic double skin facade. Energy Build. 2019, 202, 109314. [Google Scholar] [CrossRef]
- Ioannidis, Z.; Buonomano, A.; Athienitis, A.K.; Stathopoulos, T. Modeling of double skin facades integrating photovoltaic panels and automated roller shades: Analysis of the thermal and electrical performance. Energy Build. 2017, 154, 618–632. [Google Scholar] [CrossRef]
- Su, X.S.; Zhang, L.; Luo, Y.Q.; Liu, Z.B. Energy performance of a reversible window integrated with photovoltaic blinds in Harbin. Build. Environ. 2022, 213, 108861. [Google Scholar] [CrossRef]
- Su, X.S.; Zhang, L.; Luo, Y.Q.; Liu, Z.B.; Yang, H.X.; Wang, X.C. Conceptualization and preliminary analysis of a novel reversible photovoltaic window. Energy Conv. Manag. 2021, 250, 114925. [Google Scholar] [CrossRef]
- Luo, Y.Q.; Zhang, L.; Liu, Z.B.; Xie, L.; Wang, X.L.; Wu, J. Experimental study and performance evaluation of a PV-blind embedded double skin façade in winter season. Energy 2018, 165, 326–342. [Google Scholar] [CrossRef]
- Yang, S.L.; Cannavale, A.; Carlo, A.D.; Prasad, D.; Sproul, A.; Fiorito, F. Performance assessment of BIPV/T double-skin façade for various climate zones in Australia: Effects on energy consumption. Sol. Energy 2020, 199, 377–399. [Google Scholar] [CrossRef]
- Peng, J.Q.; Lu, L.; Yang, H.X.; Ma, T. Comparative study of the thermal and power performances of a semi-transparent photovoltaic façade under different ventilation modes. Appl. Energy 2015, 138, 572–583. [Google Scholar] [CrossRef]
- Liu, X.J.; Yang, H.T.; Wang, C.J.; Shen, C.; Bo, R.; Hinkle, L.; Wang, J.L. Semi-experimental investigation on the energy performance of photovoltaic double skin façade with different façade materials. Energy 2024, 295, 131049. [Google Scholar] [CrossRef]
- Liu, X.J.; Shen, C.; Bo, R.; Wang, J.L.; Ardabili, N.G. Experimental investigation on the operation performance of photovoltaic double skin façade in winter. Energy 2023, 283, 129040. [Google Scholar] [CrossRef]
- Yang, S.L.; Fiorito, F.; Prasad, D.; Sproul, A.; Cannavale, A. A sensitivity analysis of design parameters of BIPV/T-DSF in relation to building energy and thermal comfort performances. J. Build. Eng. 2021, 41, 102426. [Google Scholar] [CrossRef]
- Yang, S.L.; Cannavale, A.; Prasad, D.; Sproul, A.; Fiorito, F. Numerical simulation study of BIPV/T double-skin facade for various climate zones in Australia: Effects on indoor thermal comfort. Build. Simul. 2019, 12, 51–67. [Google Scholar] [CrossRef]
- Yang, S.L.; Fiorito, F.; Sproul, A.; Prasad, D. Optimising Design Parameters of a Building-Integrated Photovoltaic Double-Skin Facade in Different Climate Zones in Australia. Buildings 2023, 13, 1096. [Google Scholar] [CrossRef]
- Sharma, M.K.; Preet, S.; Mathur, J.; Chowdhury, A.; Mathur, S. Parametric analysis of factors affecting thermal performance of photovoltaic triple skin façade system (PV-TSF). J. Build. Eng. 2021, 40, 102344. [Google Scholar] [CrossRef]
- Wang, C.Y.; Ji, J.; Uddin, M.M.; Yu, B.D.; Song, Z.Y. The study of a double-skin ventilated window integrated with CdTe cells in a rural building. Energy 2021, 215, 119043. [Google Scholar] [CrossRef]
- Barman, S.; Chowdhury, A.; Mathur, S.; Mathur, J. Assessment of the efficiency of window integrated CdTe based semi-transparent photovoltaic module. Sustain. Cities Soc. 2018, 37, 250–262. [Google Scholar] [CrossRef]
- Preet, S.; Sharma, M.K.; Mathur, J.; Chowdhury, A.; Mathur, S. Performance evaluation of photovoltaic double-skin facade with forced ventilation in the composite climate. J. Build. Eng. 2020, 32, 101733. [Google Scholar] [CrossRef]
- Khalvati, F.; Omidvar, A. Summer study on thermal performance of an exhausting airflow window in evaporatively-cooled buildings. Appl. Therm. Eng. 2019, 153, 147–158. [Google Scholar] [CrossRef]
- European Centre for Medium-Range Weather Forecasts. Available online: https://www.ecmwf.int/ (accessed on 15 April 2024).
- EnergyPlus Weather Search. Available online: https://energyplus.net/weather-search/Changchun (accessed on 11 June 2024).
- Hwang, R.L.; Lin, T.P.; Liang, H.H.; Yang, K.H.; Yeh, T.C. Additive model for thermal comfort generated by matrix experiment using orthogonal array. Build. Environ. 2009, 44, 1730–1739. [Google Scholar] [CrossRef]
- Shao, N.; Zhang, J.L.; Ma, L.D. Analysis on indoor thermal environment and optimization on design parameters of rural Residence. J. Build. Eng. 2017, 12, 229–238. [Google Scholar] [CrossRef]
- Gong, G.C.; Xu, C.W.; Jiao, J.J.; Liu, Y.K.; Xie, S.N. Investigation of moisture condensation on papermaking plant envelopes in high humidity environment by orthogonal analysis and CFD simulation. Build. Environ. 2011, 46, 1639–1648. [Google Scholar] [CrossRef]
- Zhao, S.G.; Hai, G.; Zhang, X. An Analysis of the Influence of Cool Roof Thermal Parameters on Building Energy Consumption Based on Orthogonal Design. Buildings 2024, 14, 28. [Google Scholar] [CrossRef]





| Material | Density [kg/m3] | Thermal Conductivity [W/(m·K)] | Specific Heat [J/(kg·K)] |
|---|---|---|---|
| Brick | 1800 | 0.810 | 1050 |
| EPS | 20 | 0.039 | 1380 |
| Glass | 2500 | 1.000 | 840 |
| Parameters | Data |
|---|---|
| External layer: Cadmium Telluride (CdTe) PV glazing | |
| Glazing type | Single-pane |
| Visible transmittance | 20% |
| Thickness | 7 mm |
| Maximum power | 73.84 W |
| Voltage at the maximum power point (Vmp) | 86.37 V |
| Current at the maximum power point (Imp) | 0.85 A |
| Open Circuit Voltage (Voc) | 116.00 V |
| Short Circuit Current (Isc) | 0.97 A |
| Temperature coefficient | −0.214%/°C |
| Efficiency | 10.25% |
| Air cavity between PV glazing and shutter | |
| Thickness | 270 mm |
| Middle layer: insulated shutter | |
| Material | Polyurethane foam |
| Conductivity | 0.024 [W/(m·K)] |
| Thickness | 5 mm |
| Air cavity between clear glazing and shutter | |
| Thickness | 100 mm |
| Internal layer: clear glazing | |
| Glazing type | Double-pane |
| Thickness | 24 mm |
| Frame | plastic steel window frame |
| Window system frame | Wooden |
| Level | Factor A | Factor B [%] | Factor C [m] | Factor D |
|---|---|---|---|---|
| 1 | Single-pane | 10 | 0.005 | Single-pane |
| 2 | Double-pane | 20 | 0.025 | Double-pane |
| 3 | 40 | 0.045 | Triple-pane |
| Test Number | Factor A | Factor B | Factor C | Factor D | Heating Load of Control Mode 1 [kW·h] | Heating Load of Control Mode 2 [kW·h] | Heating Load of Control Mode 3 [kW·h] |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1462.62 | 972.18 | 1591.37 |
| 2 | 1 | 2 | 3 | 2 | 1178.88 | 819.58 | 1375.12 |
| 3 | 1 | 3 | 2 | 3 | 980.13 | 816.13 | 1146.05 |
| 4 | 2 | 1 | 3 | 3 | 1197.52 | 811.07 | 1250.79 |
| 5 | 2 | 2 | 2 | 1 | 1186.08 | 869.94 | 1198.07 |
| 6 | 2 | 3 | 1 | 2 | 988.07 | 821.88 | 997.26 |
| 7 | 1 | 1 | 2 | 2 | 1273.34 | 836.95 | 1487.61 |
| 8 | 1 | 2 | 1 | 3 | 1173.38 | 843.52 | 1387.05 |
| 9 | 1 | 3 | 3 | 1 | 1097.00 | 886.53 | 1194.69 |
| 10 (Optimal level) | 2 | 3 | 3 | 3 | 956.21 | 797.83 | 961.173 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Wu, J.; Xu, H. Effect of Photovoltaic Energy-Saving Window Factors on Building Heating Load Under Three Control Modes. Buildings 2025, 15, 238. https://doi.org/10.3390/buildings15020238
Li J, Wu J, Xu H. Effect of Photovoltaic Energy-Saving Window Factors on Building Heating Load Under Three Control Modes. Buildings. 2025; 15(2):238. https://doi.org/10.3390/buildings15020238
Chicago/Turabian StyleLi, Jiayi, Jianmei Wu, and Hongpeng Xu. 2025. "Effect of Photovoltaic Energy-Saving Window Factors on Building Heating Load Under Three Control Modes" Buildings 15, no. 2: 238. https://doi.org/10.3390/buildings15020238
APA StyleLi, J., Wu, J., & Xu, H. (2025). Effect of Photovoltaic Energy-Saving Window Factors on Building Heating Load Under Three Control Modes. Buildings, 15(2), 238. https://doi.org/10.3390/buildings15020238






