Seismic Response Estimation of Multi-Story Structures Equipped with a Cost-Effective Earthquake Protection System
Abstract
1. Introduction
2. Suppression of Residual Sliding Displacement and Estimation of Seismic Responses
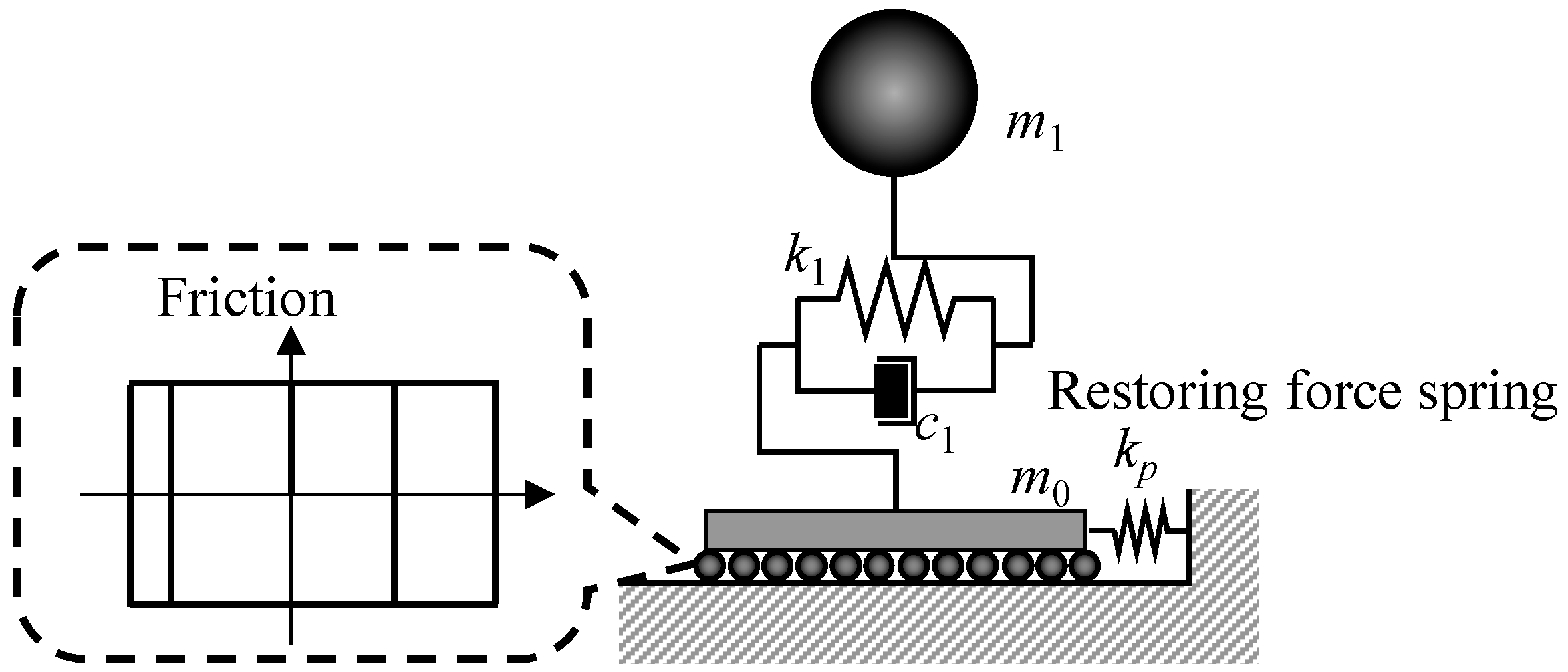
2.1. Response Estimation of a Single-Story Sliding Structure Equipped with a Restoring Force Mechanism
2.2. New Forms of β and γ
2.3. Response Estimation of a Multi-Story Sliding Structure Equipped with a Restoring Force Mechanism
- The multi-story superstructure is converted into a single story, as shown in Figure 3b, and is calculated from the converted structure.
- is distributed to each story of the superstructure, based on distribution factors.
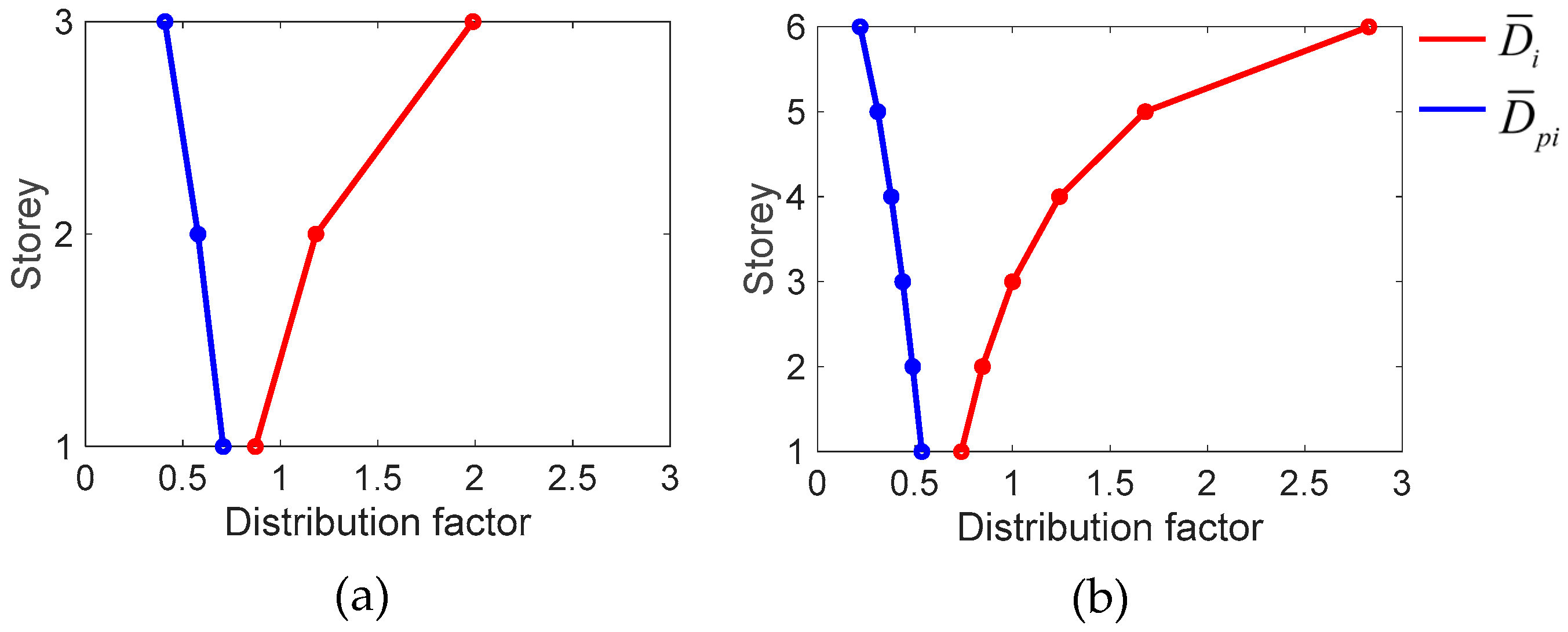
2.3.1. Distribution Factor
2.3.2. Distribution Factor
2.3.3. Examples of and
3. Numerical Simulations to Examine the Multi-Story Estimation
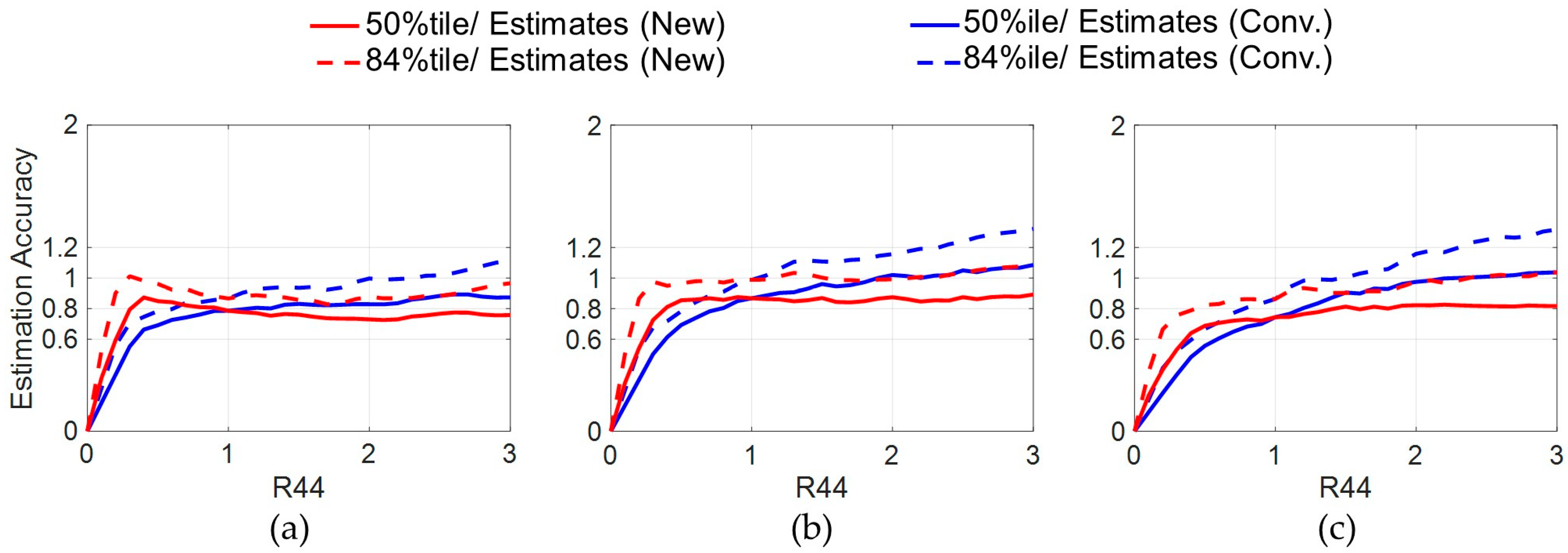
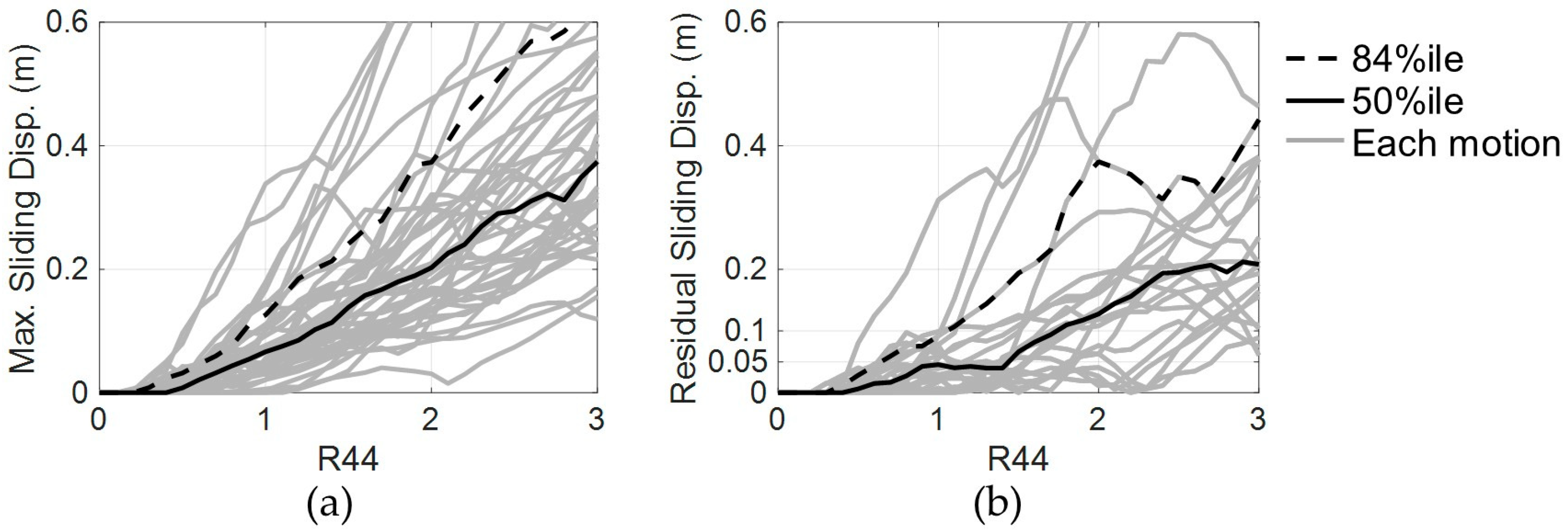
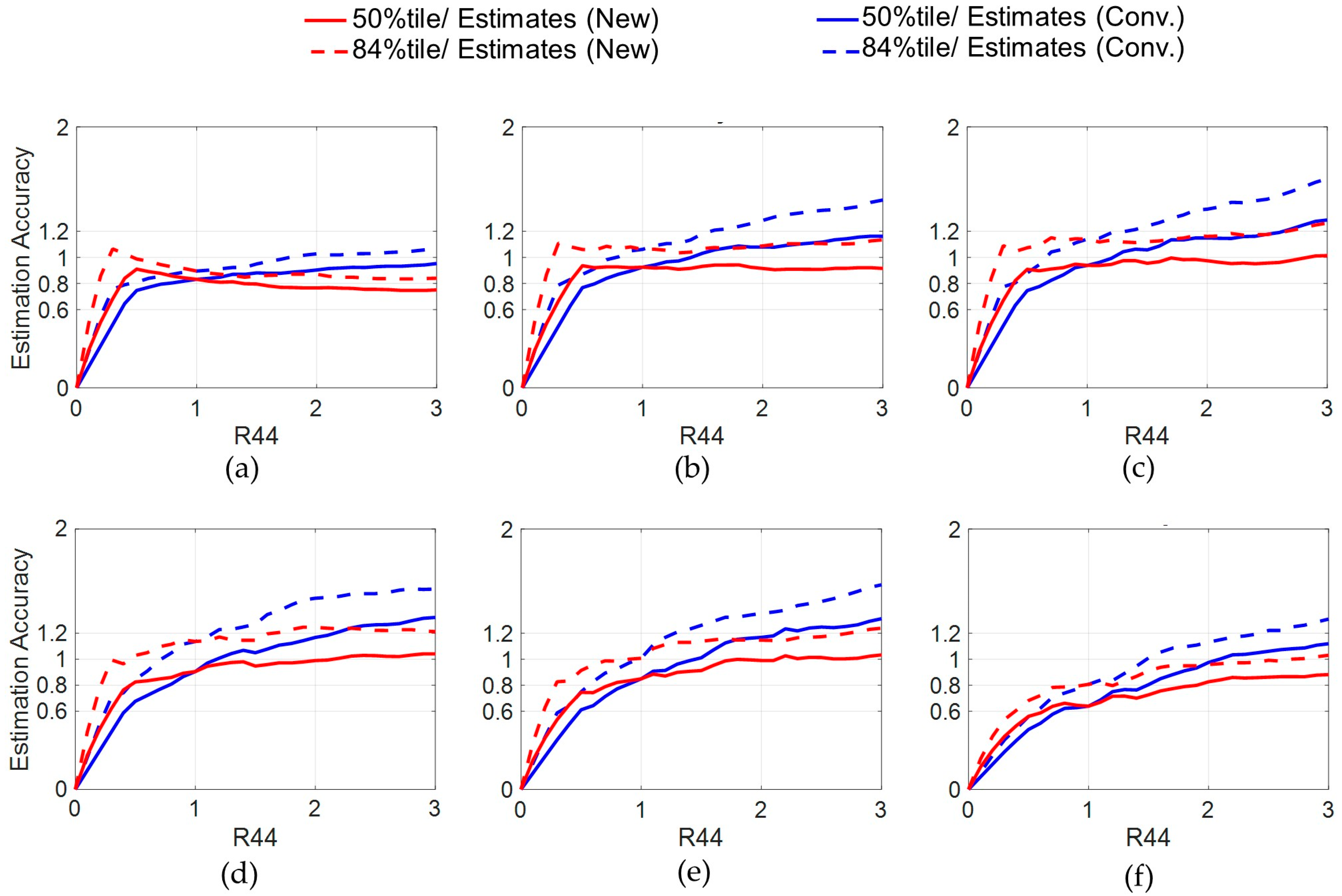
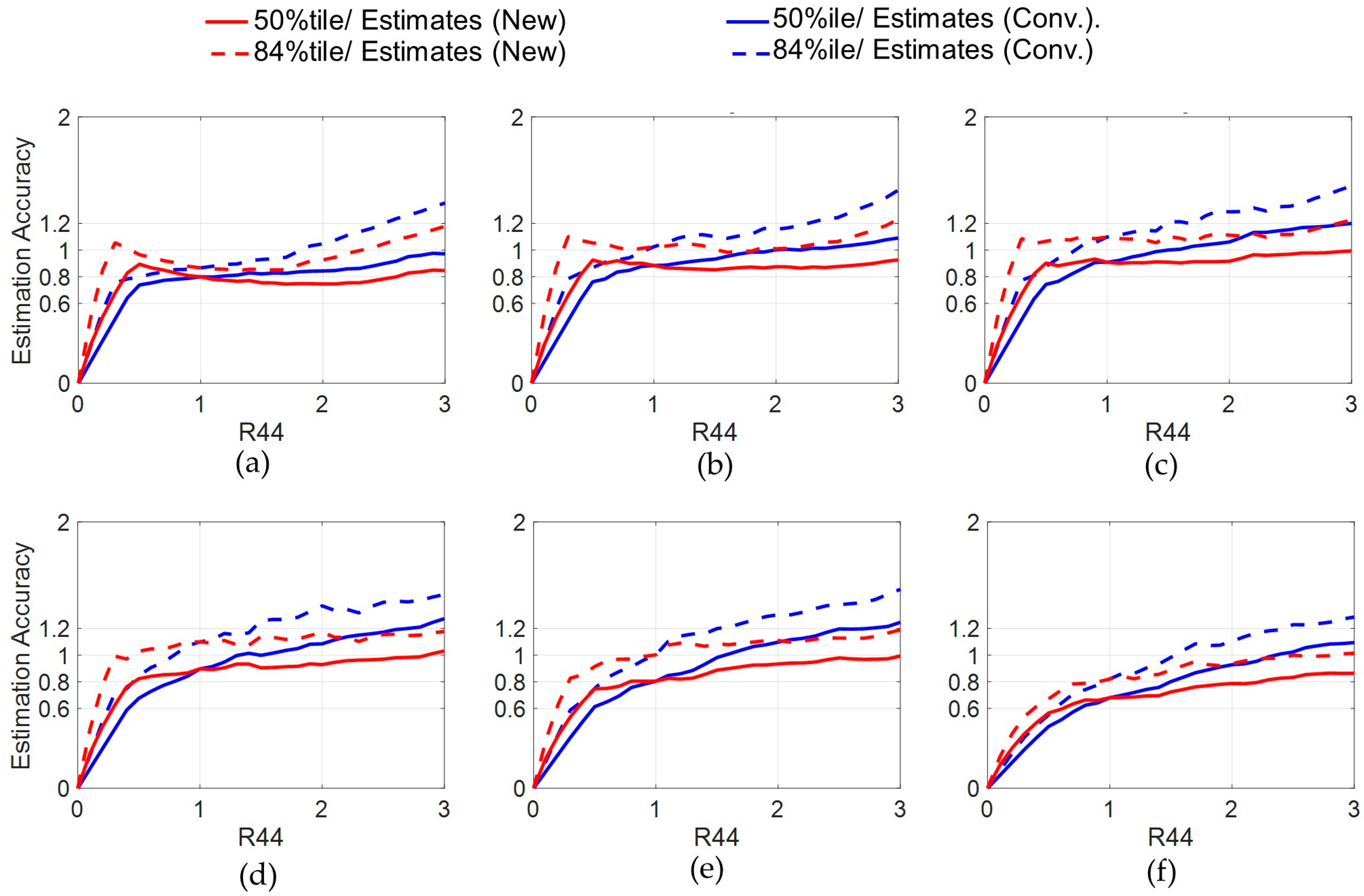
3.1. Incremental Dynamic Analysis and Indices for the Estimation Accuracy
3.2. Three-Story FSS Model
3.2.1. Numerical Model of a Three-Story FSS
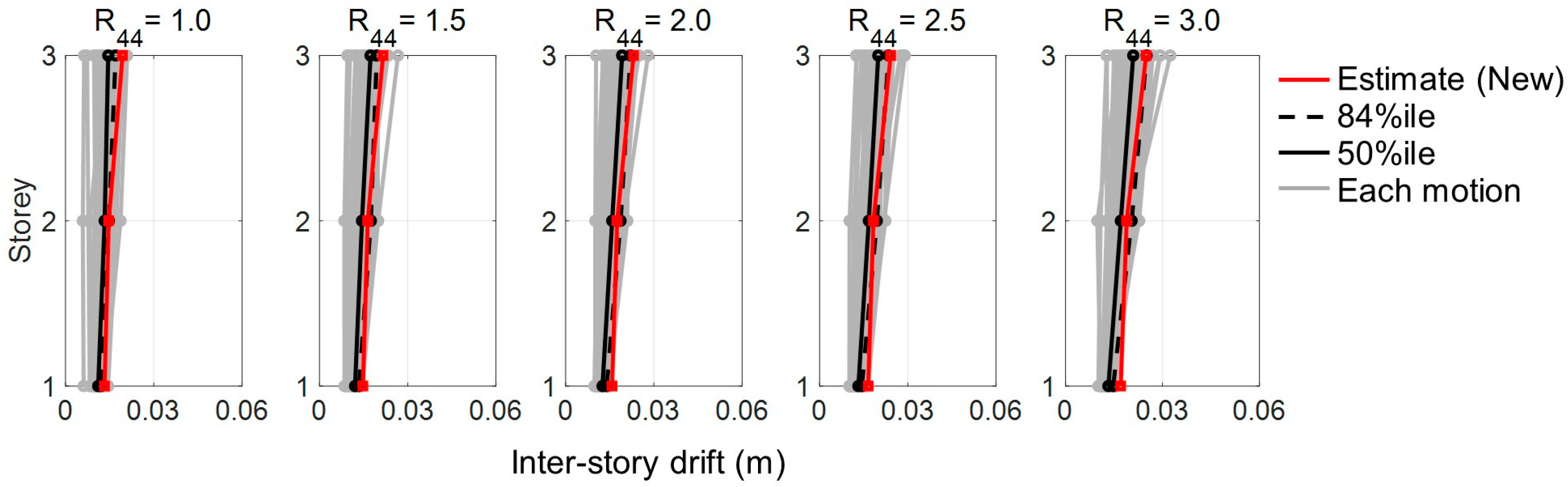
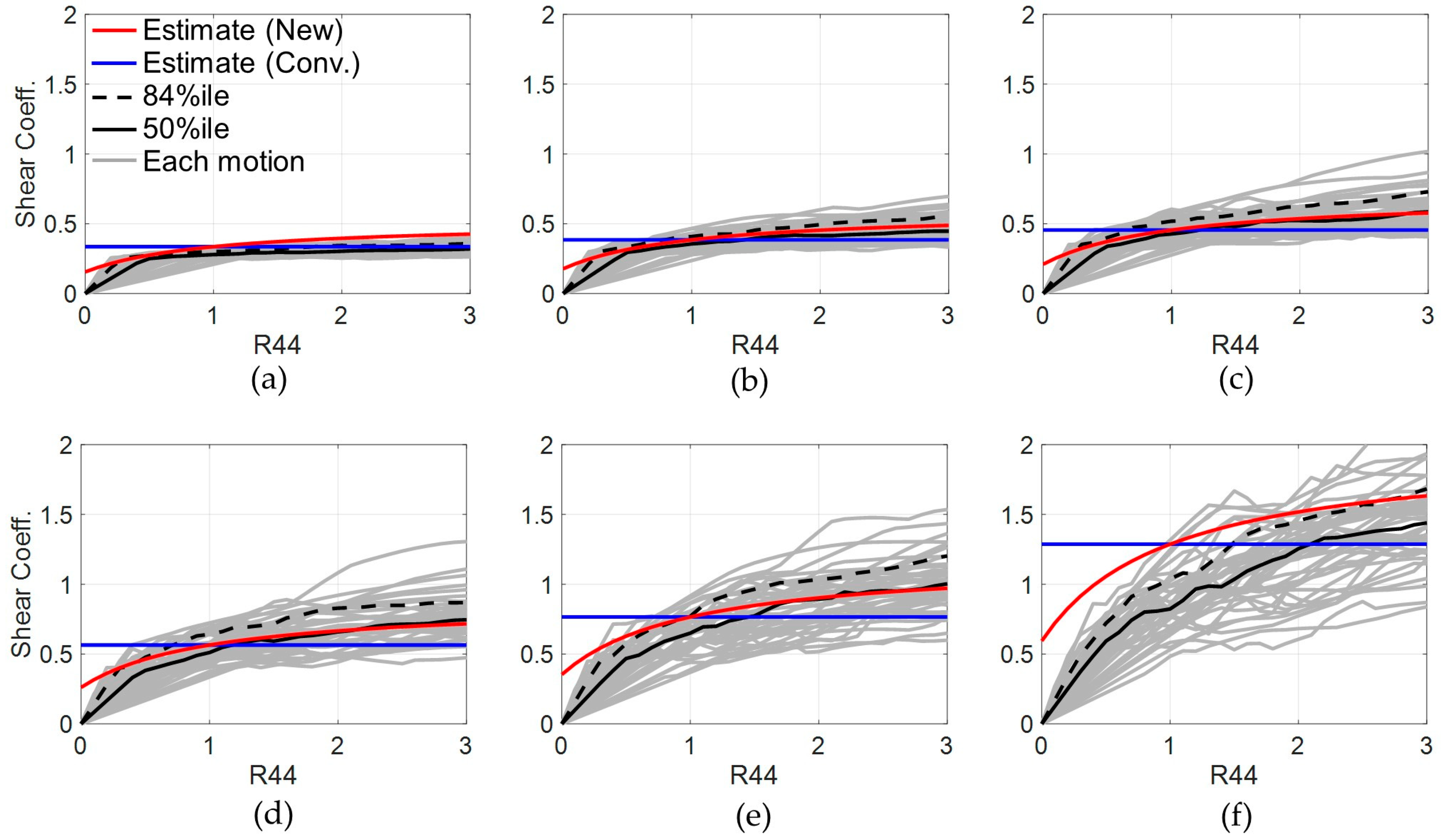
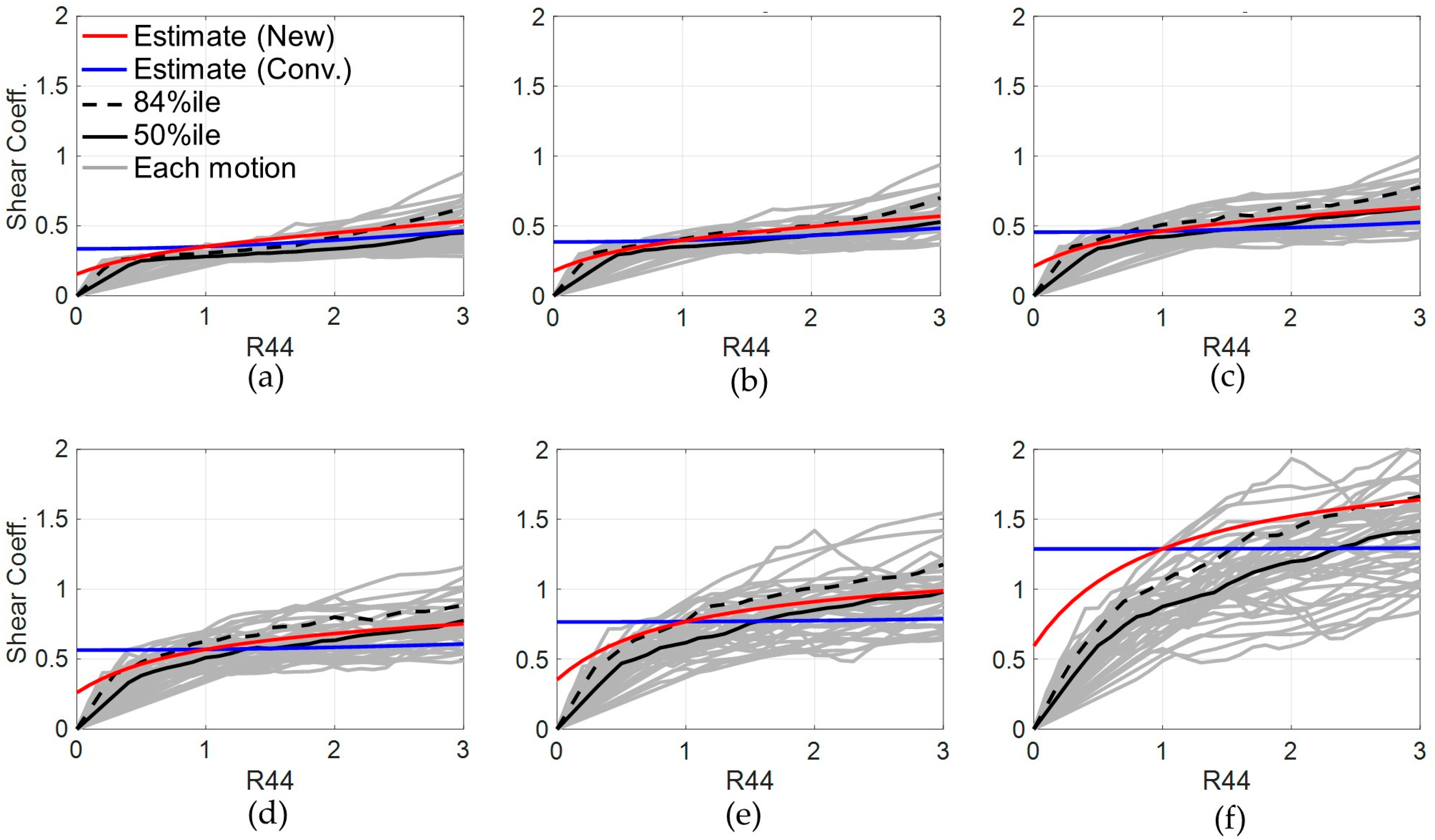
3.2.2. Three-Story FSS Model Without a Restoring Force Spring
3.2.3. Three-Story FSS Model with a Restoring Force Mechanism
3.3. Six-Story FSS Model
3.3.1. Numerical Model of a Six-Story FSS
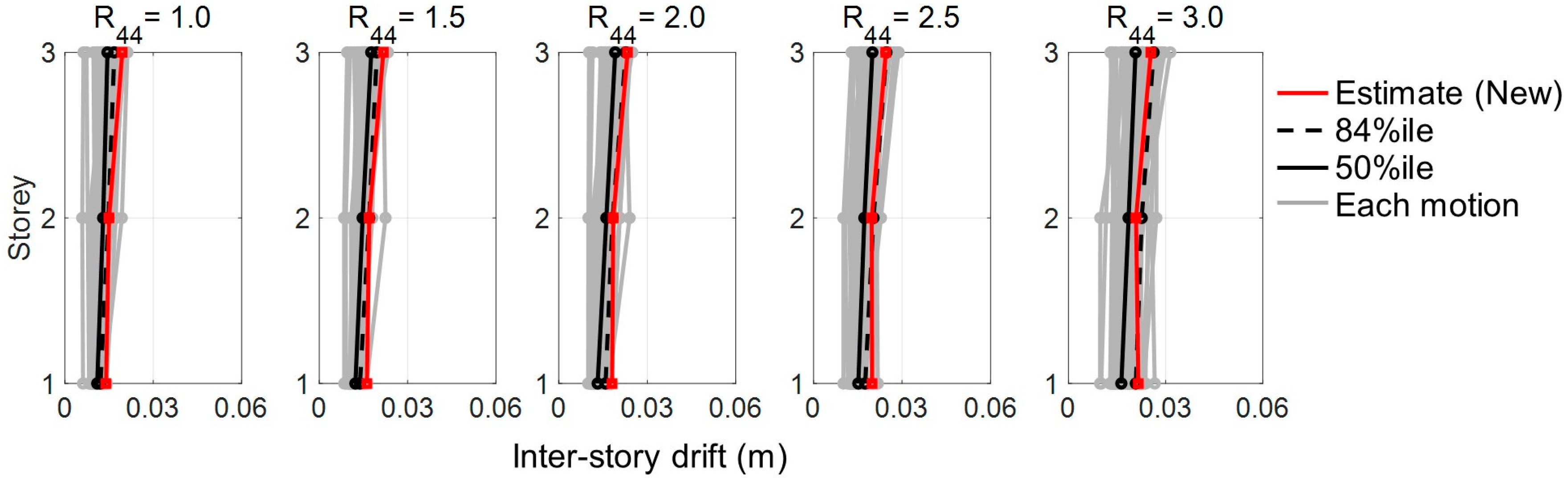
3.3.2. Six-Story FSS Model Without a Restoring Force Mechanism
3.3.3. Six-Story FSS Model with a Restoring Force Mechanism
4. Conclusions
- ✓
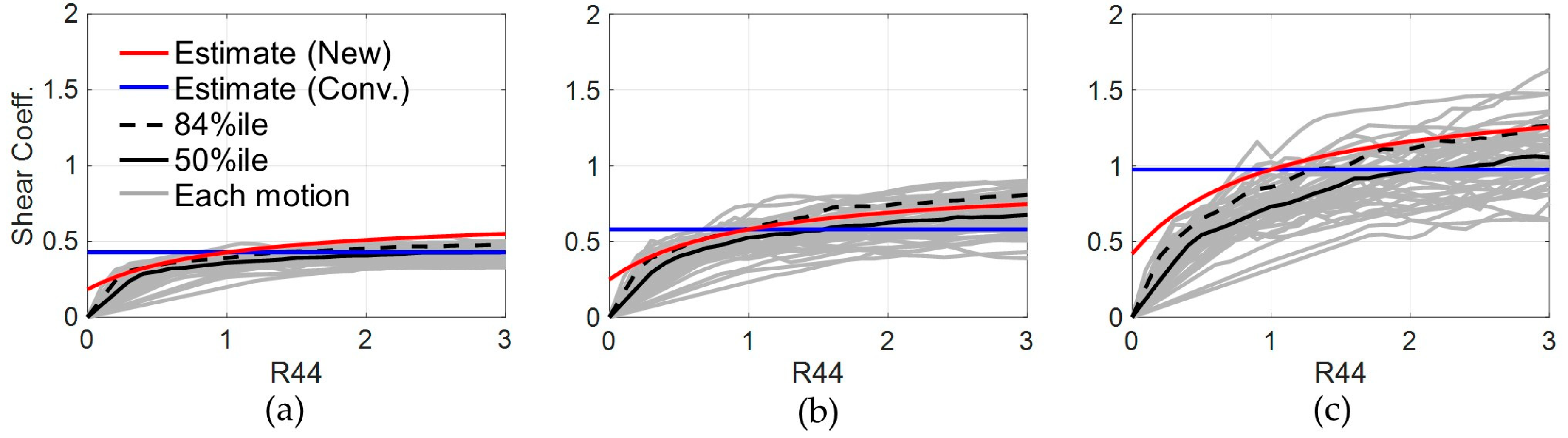
- The multi-story estimation was found to be sufficiently reliable and useful to estimate those seismic responses, as those estimates agreed well with the IDA results of these three/six-story FSS model, with high accuracies not exceeding the error range of ±20%. The new form was also found to be effective, as the estimates based on the form more reasonably matched with curvatures of the IDA results than the estimates of conventional one.
- ✓
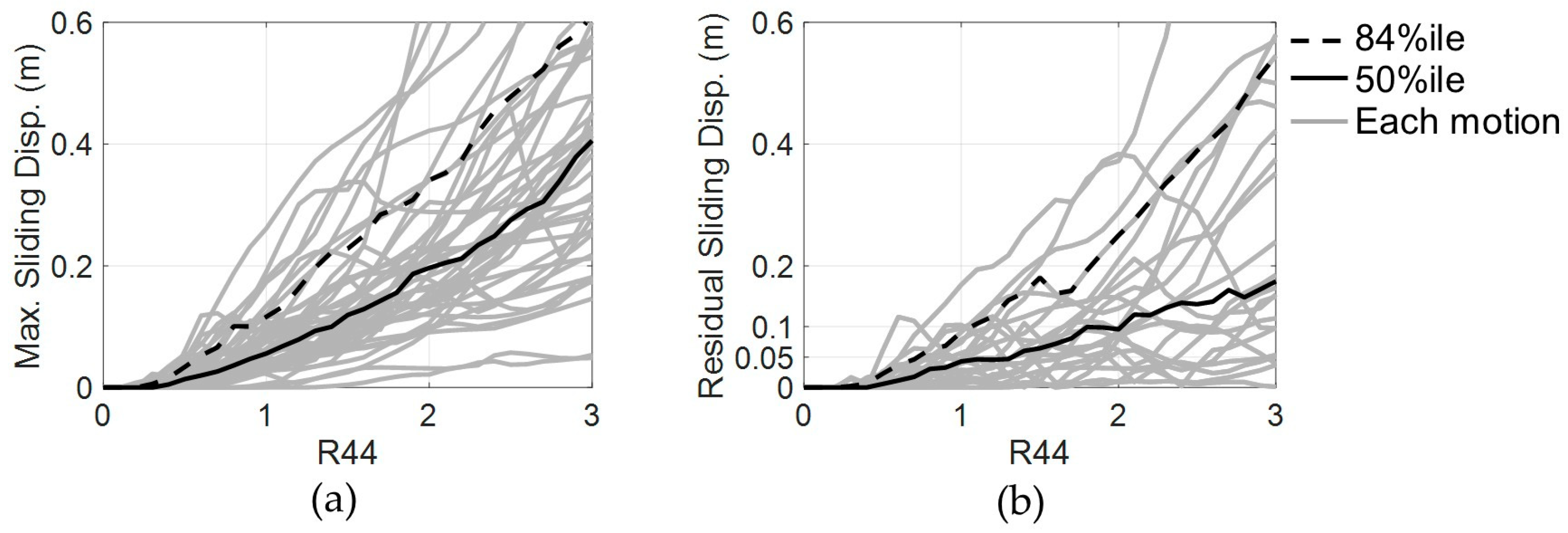
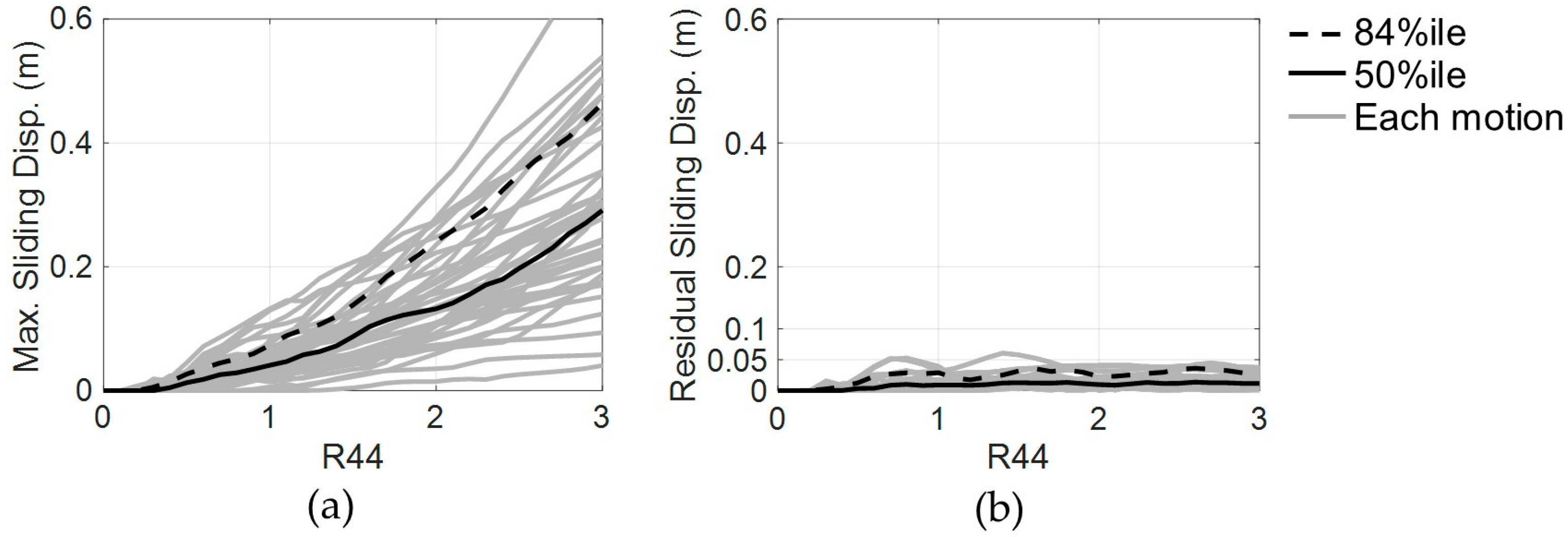
- The IDAs in this study supported that multi-story FSS models based on the friction coefficient around 0.2 are greatly effective in mitigating the seismic responses of the shear coefficient and inter-story drift. A reasonably designed restoring force mechanism is also effective in suppressing the residual sliding displacement without significantly accelerating the responses in the multi-story FSS model.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| IDA | Incremental dynamic analysis |
| FEMA | Federal Emergency Management Agency |
| FSS | Free-standing structure |
| PGV | Peak ground velocity |
| PGA | Peak ground acceleration |
| DOF | Degree-of-freedom |
References
- Kelly, J.M. Aseismic base isolation: Review and bibliography. Soil Dyn. Earthq. Eng. 1986, 5, 202–216. [Google Scholar] [CrossRef]
- Yenidogan, C. Earthquake-Resilient Design of Seismically Isolated Buildings: A Review of Technology. Vibration 2021, 4, 602–647. [Google Scholar] [CrossRef]
- Yenidogan, C.; Erdik, M. A comparative evaluation of design provisions for seismically isolated buildings. Soil Dyn. Earthq. Eng. 2016, 90, 265–286. [Google Scholar] [CrossRef]
- Yenidogan, C. Evaluation of Overall Seismic Performance of RC Structures and Effectiveness of Seismic Isolation Technology Under Extreme Events: February 6, 2023, Earthquakes. Buildings 2025, 15, 990. [Google Scholar] [CrossRef]
- Zayas, V.A.; Low, S.S.; Mahin, S.A. The FPS Earthquake Resisting System Experimental Report, Report No. UCB/EERC-87/01; Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 1987. [Google Scholar]
- Mokha, A.; Constantinou, M.C.; Reinhorn, A.M.; Zayas, V.A. Experimental Study of Friction-Pendulum Isolation System. J. Struct. Eng. 1991, 117, 1201–1217. [Google Scholar] [CrossRef]
- Fenz, D.M.; Constantinou, M.C. Behaviour of the double concave Friction Pendulum bearing. Earthq. Eng. Struct. Dyn. 2006, 35, 1403–1424. [Google Scholar] [CrossRef]
- Becker, T.C.; Mahin, S.A. Experimental and analytical study of the bi-directional behavior of the triple friction pendulum isolator. Earthq. Eng. Struct. Dyn. 2012, 41, 355–373. [Google Scholar] [CrossRef]
- Turer, A.; Özden, B. Seismic base isolation using low-cost Scrap Tire Pads (STP). Mater. Struct. 2008, 41, 891–908. [Google Scholar] [CrossRef]
- Spizzuoco, M.; Calabrese, A.; Serino, G. Innovative low-cost recycled rubber–fiber reinforced isolator: Experimental tests and Finite Element Analyses. Eng. Struct. 2014, 76, 99–111. [Google Scholar] [CrossRef]
- Calabrese, A.; Spizzuoco, M.; Serino, G.; Della Corte, G.; Maddaloni, G. Shaking table investigation of a novel, low-cost, base isolation technology using recycled rubber. Struct. Control. Heal. Monit. 2015, 22, 107–122. [Google Scholar] [CrossRef]
- Tsiavos, A.; Alexander, N.A.; Diambra, A.; Ibraim, E.; Vardanega, P.J.; Gonzalez-Buelga, A.; Sextos, A. A sand-rubber deformable granular layer as a low-cost seismic isolation strategy in developing countries: Experimental investigation. Soil Dyn. Earthq. Eng. 2019, 125, 105731. [Google Scholar] [CrossRef]
- Tsiavos, A.; Sextos, A.; Stavridis, A.; Dietz, M.; Dihoru, L.; Alexander, N.A. Experimental investigation of a highly efficient, low-cost PVC-Rollers Sandwich (PVC-RS) seismic isolation. Structures 2021, 33, 1590–1602. [Google Scholar] [CrossRef]
- Takagi, J.; Masui, T.; Araki, Y.; Ikago, K.; Pareek, S.; Lee, S.; Suzuki, Y.; Enokida, R.; Guo, J.; Shrestha, K.C.; et al. Development of low-cost rolling base isolation system for seismic protection of rubble stone masonry buildings in Himalayan Mountain range. Front. Built Environ. 2024, 10, 1495051. [Google Scholar] [CrossRef]
- Cilsalar, H.; Constantinou, M.C. Behavior of a spherical deformable rolling seismic isolator for lightweight residential construction. Bull. Earthq. Eng. 2019, 17, 4321–4345. [Google Scholar] [CrossRef]
- Nanda, R.P.; Shrikhande, M.; Agarwal, P. Low-Cost Base-Isolation System for Seismic Protection of Rural Buildings. Pract. Period. Struct. Des. Constr. 2016, 21, 04015001. [Google Scholar] [CrossRef]
- Campbell, W.E. Studies in boundary lubrication. Tran. ASME 1939, 61, 633–641. [Google Scholar]
- Tassios, T.P.; Vintzēleou, E.N. Concrete-to-Concrete Friction. J. Struct. Eng. 1987, 113, 832–849. [Google Scholar] [CrossRef]
- Rabbat, B.G.; Russell, H.G. Friction Coefficient of Steel on Concrete or Grout. J. Struct. Eng. 1985, 111, 505–515. [Google Scholar] [CrossRef]
- McCormick, J.; Nagae, T.; Ikenaga, M.; Zhang, P.-C.; Katsuo, M.; Nakashima, M. Investigation of the sliding behavior between steel and mortar for seismic applications in structures. Earthq. Eng. Struct. Dyn. 2009, 38, 1401–1419. [Google Scholar] [CrossRef]
- Bowden, F.P.; Tabor, D. The Friction and Lubrication of Solids Part II; Oxford University Press: New York, NY, USA, 1964. [Google Scholar]
- Lansdown, A.R. Lubrication, A Practical Guide to Lubricant Selection; Pergamon: Oxford, UK, 1982. [Google Scholar]
- Clauss, J.F. Solid Lubricants and Self-Lubricating Solids; Academic Press: New York, NY, USA; London, UK, 1972. [Google Scholar]
- Enokida, R.; Nagae, T. Seismic Damage Reduction of a Structural System based on Nontraditional Sliding Interfaces with Graphite Lubrication. J. Earthq. Eng. 2018, 22, 666–686. [Google Scholar] [CrossRef]
- Enokida, R.; Nagae, T.; Ikenaga, M.; Inami, M.; Nakashima, M. Application of graphite lubrication for column base in free standing steel structure. J. Struct. Constr. Eng. (Trans. AIJ) 2013, 78, 435–444. [Google Scholar] [CrossRef][Green Version]
- Barbagallo, F.; Hamashima, I.; Hu, H.; Kurata, M.; Nakashima, M. Base shear capping buildings with graphite-lubricated bases for collapse prevention in extreme earthquakes. Earthq. Eng. Struct. Dyn. 2017, 46, 1003–1021. [Google Scholar] [CrossRef]
- Enokida, R.; Ikago, K.; Guo, J.; Kajiwara, K. Nonlinear signal-based control for shake table experiments with sliding masses. Earthq. Eng. Struct. Dyn. 2023, 52, 1908–1931. [Google Scholar] [CrossRef]
- Enokida, R.; Ikago, K.; Guo, J.; Kajiwara, K. Performance Examination of Nonlinear Signal-Based Control in Shake Table Experiments with Sliding Structures. Struct. Control. Heal. Monit. 2023, 2023, 9526244. [Google Scholar] [CrossRef]
- Chung, Y.L.; Kuo, K.T.; Nagae, T.; Kajiwara, K. Seismic responses of a free-standing two-story steel moment frame equipped with a cast iron-mortar sliding base. Earthq. Struct. 2019, 17, 245–256. [Google Scholar] [CrossRef]
- Tosauchi, Y.; Sato, E.; Fukuyama, K.; Inoue, T.; Kajiwara, K.; Shiohara, H.; Nagae, T.; Fukuyama, H.; Kabeyasawa, T.; Mukai, T. Three-dimensional shaking table test of a ten story RC frame. J. Struct. Constr. Eng. (Trans. AIJ) 2015, 83, 1139–1149. (In Japanese) [Google Scholar] [CrossRef]
- Constantinou, M.C.; Mokha, A.S.; Reinhorn, A.M. Experimental and Analytical Study of Combined Sliding Disc Bearing and Helical Steel Spring Isolation System; Rep. NCEER-90-0019; National Center for Earthquake Engineering Research: Buffalo, NY, USA, 1990. [Google Scholar]
- Kawashima, K.; MacRae, G.A.; Hoshikuma, J.; Nagaya, K. Residual Displacement Response Spectrum. J. Struct. Eng. 1998, 124, 523–530. [Google Scholar] [CrossRef]
- Katsaras, C.P.; Panagiotakos, T.B.; Kolias, B. Restoring capability of bilinear hysteretic seismic isolation systems. Earthq. Eng. Struct. Dyn. 2008, 37, 557–575. [Google Scholar] [CrossRef]
- Cardone, D.; Gesualdi, G.; Brancato, P. Restoring capability of friction pendulum seismic isolation systems. Bull. Earthq. Eng. 2015, 13, 2449–2480. [Google Scholar] [CrossRef]
- Ponzo, F.C.; Di Cesare, A.; Leccese, G.; Nigro, D. Shake table testing on restoring capability of double concave friction pendulum seismic isolation systems. Earthq. Eng. Struct. Dyn. 2017, 46, 2337–2353. [Google Scholar] [CrossRef]
- AASHTO. Guide Specifications for Seismic Isolation Design; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2014. [Google Scholar]
- ASCE 7-16; Minimum Design Loads and Associated Criteria for Buildings and Other Structures. American Society of Civil Engineers: New York, NY, USA, 2016.
- EN 15129:2010; European Standard EN 15129:2010 for Anti-Seismic Devices. European Committee for Standardization: Brussels, Belgium, 2010.
- Calvi, P.M.; Calvi, G.M. Historical development of friction-based seismic isolation systems. Soil Dyn. Earthq. Eng. 2018, 106, 14–30. [Google Scholar] [CrossRef]
- Mostaghel, N.; Khodaverdian, M. Dynamics of resilient-friction base isolator (R-FBI). Earthq. Eng. Struct. Dyn. 1987, 15, 379–390. [Google Scholar] [CrossRef]
- Iemura, H.; Taghikhany, T.; Jain, S.K. Optimum design of resilient sliding isolation system for seismic protection of equipments. Bull. Earthq. Eng. 2007, 5, 85–103. [Google Scholar] [CrossRef]
- Sachdeva, G.; Chakraborty, S.; Ray-Chaudhuri, S. Seismic response control of a structure isolated by flat sliding bearing and nonlinear restoring spring: Experimental study for performance evaluation. Eng. Struct. 2018, 159, 1–13. [Google Scholar] [CrossRef]
- Naeem, A.; Kim, J. Seismic retrofit of structures using rotational friction dampers with restoring force. Adv. Struct. Eng. 2020, 23, 3525–3540. [Google Scholar] [CrossRef]
- Enokida, R. Suppression of residual sliding displacement of flat-sliding structures by cushion stoppers. Soil Dyn. Earthq. Eng. 2021, 150, 106905. [Google Scholar] [CrossRef]
- Kelly, J.M.; Beucke, K.E. A friction damped base isolation system with fail-safe characteristics. Earthq. Eng. Struct. Dyn. 1983, 11, 33–56. [Google Scholar] [CrossRef]
- Tsai, H.C. Dynamic analysis of base-isolated shear beams bumping against stops. Earthq. Eng. Struct. Dyn. 1997, 26, 515–528. [Google Scholar] [CrossRef]
- Matsagar, V.A.; Jangid, R.S. Seismic response of base-isolated structures during impact with adjacent structures. Eng. Struct. 2003, 25, 1311–1323. [Google Scholar] [CrossRef]
- Komodromos, P.; Polycarpou, P.C.; Papaloizou, L.; Phocas, M.C. Response of seismically isolated buildings considering poundings. Earthq. Eng. Struct. Dyn. 2007, 36, 1605–1622. [Google Scholar] [CrossRef]
- Masroor, A.; Mosqueda, G. Experimental simulation of base-isolated buildings pounding against moat wall and effects on superstructure response. Earthq. Eng. Struct. Dyn. 2012, 41, 2093–2109. [Google Scholar] [CrossRef]
- Mazza, F.; Labernarda, R. Internal Pounding between Structural Parts of Seismically Isolated Buildings. J. Earthq. Eng. 2021, 26, 5175–5203. [Google Scholar] [CrossRef]
- Enokida, R.; Tomoki, N.; Ikago, K. Experimental Examinations of Free-Standing Structures with/without Cushion Stoppers for the Suppression of the Residual Sliding Displacement. In World Conference on Seismic Isolation; Springer: Cham, Switzerland, 2024; Volume 533, pp. 400–409. [Google Scholar] [CrossRef]
- Vamvatsikos, D.; Cornell, C.A. Incremental dynamic analysis. Earthq. Eng. Struct. Dyn. 2002, 31, 491–514. [Google Scholar] [CrossRef]
- Vamvatsikos, D.; Cornell, C.A. Applied Incremental Dynamic Analysis. Earthq. Spectra. 2004, 20, 523–553. [Google Scholar] [CrossRef]
- Vamvatsikos, D.; Fragiadakis, M. Incremental dynamic analysis for estimating seismic performance sensitivity and uncertainty. Earthq. Eng. Struct. Dyn. 2010, 39, 141–163. [Google Scholar] [CrossRef]
- Castaldo, P.; Palazzo, B.; Ferrentino, T. Seismic reliability-based ductility demand evaluation for inelastic base-isolated structures with friction pendulum devices. Earthq. Eng. Struct. Dyn. 2017, 46, 1245–1266. [Google Scholar] [CrossRef]
- Castaldo, P.; Alfano, G. Seismic reliability-based design of hardening and softening structures isolated by double concave sliding devices. Soil Dyn. Earthq. Eng. 2020, 129, 105930. [Google Scholar] [CrossRef]
- Federal Emergency Management Agency. Quantification of Building Seismic Performance Factors; FEMA P695: Washington, DC, USA, 2009. [Google Scholar]
- Anagnostopoulos, S.A.; Spiliopoulos, K.V. An investigation of earthquake induced pounding between adjacent buildings. Earthq. Eng. Struct. Dyn. 1992, 21, 289–302. [Google Scholar] [CrossRef]
- Jankowski, R. Non-linear viscoelastic modelling of earthquake-induced structural pounding. Earthq. Eng. Struct. Dyn. 2005, 34, 595–611. [Google Scholar] [CrossRef]
- Jankowski, R. Analytical expression between the impact damping ratio and the coefficient of restitution in the non-linear viscoelastic model of structural pounding. Earthq. Eng. Struct. Dyn. 2006, 35, 517–524. [Google Scholar] [CrossRef]
- Faizian, M.; Ishiyama, Y. Comparison of seismic codes of 1981 Japan (BSLJ), 2000 USA (IBC) and 1999 Iran (ICS). In Proceedings of the 10th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. Paper No. 3168. [Google Scholar]
- Marino, E.M.; Nakashima, M.; Mosalam, K.M. Comparison of European and Japanese seismic design of steel building structures. Eng. Struct. 2005, 27, 827–840. [Google Scholar] [CrossRef]
- Lignos, D.G.; Hikino, T.; Matsuoka, Y.; Nakashima, M. Collapse Assessment of Steel Moment Frames Based on E-Defense Full-Scale Shake Table Collapse Tests. J. Struct. Eng. 2013, 139, 120–132. [Google Scholar] [CrossRef]
- Mizushima, Y.; Mukai, Y.; Namba, H.; Taga, K.; Saruwatari, T. Super-detailed FEM simulations for full-scale steel structure with fatal rupture at joints between members—Shaking-table test of full-scale steel frame structure to estimate influence of cumulative damage by multiple strong motion: Part 1. Jpn. Archit. Rev. 2018, 1, 96–108. [Google Scholar] [CrossRef]
- Ji, X.; Hikino, T.; Kasai, K.; Nakashima, M. Damping identification of a full-scale passively controlled five-story steel building structure. Earthq. Eng. Struct. Dyn. 2013, 42, 277–295. [Google Scholar] [CrossRef]
- Kurata, M.; Akazawa, M.; Aida, S.; Cho, K.; Kawamata, Y.; Saburi, K.; Ohtsuru, S. Seismic behavior of medical equipment in earthquake-resistant and seismically-isolated buildings at e-defense shaking table tests. J. Struct. Constr. Eng. (Trans. AIJ) 2023, 88, 1116–1123. (In Japanese) [Google Scholar] [CrossRef]
- Kato, S.; Yamaguchi, K.; Matsubayashi, T. Stick-Slip Motion of Machine Tool Slideway. J. Eng. Ind. 1974, 96, 557–566. [Google Scholar] [CrossRef]
- Constantinou, M.; Mokha, A.; Reinhorn, A. Teflon Bearings in Base Isolation II: Modeling. J. Struct. Eng. 1990, 116, 455–474. [Google Scholar] [CrossRef]








| ID No. | Earthquake | Site | PGAmax (g) | |||||
|---|---|---|---|---|---|---|---|---|
| Year | Name | M | Fault Type | Name | L (km) | Vs30 (m/sec) | ||
| 1 | 1994 | Northridge | 6.7 | Thrust | Beverly Hills-Mulhol | 13.3 | 356 | 0.52 |
| 2 | 1994 | Northridge | 6.7 | Thrust | Canyon Country-WLC | 26.5 | 309 | 0.48 |
| 3 | 1999 | Duzce, Turkey | 7.1 | Strike-slip | Bolu | 41.3 | 326 | 0.82 |
| 4 | 1999 | Hector Mine | 7.1 | Strike-slip | Hector | 26.5 | 685 | 0.34 |
| 5 | 1979 | Imperial Valley | 6.5 | Strike-slip | Delta | 33.7 | 275 | 0.35 |
| 6 | 1979 | Imperial Valley | 6.5 | Strike-slip | El Centro Array #11 | 29.4 | 196 | 0.38 |
| 7 | 1995 | Kobe, Japan | 6.9 | Strike-slip | Nishi-Akashi | 8.7 | 609 | 0.51 |
| 8 | 1995 | Kobe, Japan | 6.9 | Strike-slip | Shin-Osaka | 46 | 256 | 0.24 |
| 9 | 1999 | Kocaeli, Turkey | 7.5 | Strike-slip | Duzce | 98.2 | 276 | 0.36 |
| 10 | 1999 | Kocaeli, Turkey | 7.5 | Strike-slip | Arcelik | 53.7 | 523 | 0.22 |
| 11 | 1992 | Landers | 7.3 | Strike-slip | Yermo Fire Station | 86 | 354 | 0.24 |
| 12 | 1992 | Landers | 7.3 | Strike-slip | Coolwater | 82.1 | 271 | 0.42 |
| 13 | 1989 | Loma Prieta | 6.9 | Strike-slip | Capitola | 9.8 | 289 | 0.53 |
| 14 | 1989 | Loma Prieta | 6.9 | Strike-slip | Gilroy Array #3 | 31.4 | 350 | 0.56 |
| 15 | 1990 | Manjil, Iran | 7.4 | Strike-slip | Abbar | 40.4 | 724 | 0.51 |
| 16 | 1987 | Superstition Hills | 6.5 | Strike-slip | El Centro Imp. Co. | 35.8 | 192 | 0.36 |
| 17 | 1987 | Superstition Hills | 6.5 | Strike-slip | Poe Road (temp) | 11.2 | 208 | 0.45 |
| 18 | 1992 | Cape Mendocino | 7.0 | Thrust | Rio Dell Overpass | 22.7 | 312 | 0.55 |
| 19 | 1999 | Chi-Chi, Taiwan | 7.6 | Thrust | CHY101 | 32 | 259 | 0.44 |
| 20 | 1999 | Chi-Chi, Taiwan | 7.6 | Thrust | TCU045 | 77.5 | 705 | 0.51 |
| 21 | 1971 | San Fernando | 6.6 | Thrust | LA-Hollywood Stor | 39.5 | 316 | 0.21 |
| 22 | 1976 | Friuli, Italy | 6.5 | Thrust | Tolmezzo | 20.2 | 425 | 0.35 |
| Without the Restoring Force Spring | With the Restoring Force Spring | ||
|---|---|---|---|
| Superstructure: 2.0 Hz | Mass (kg) | m1 = m2 = m3 = M/4 (M = 600 × 103 kg) | |
| Stiffness (kN/mm) | k1 = 142.1, k2 = 115.9, k3 = 73.9 | ||
| Damping (kN·s/m) | c1 = 452.3, c2 = 368.8, c3 = 235.1 | ||
| Sliding part | Mass (kg) | m0 = M/4 | |
| Friction | Equation (10) (μmax = 0.21, μmin = 0.16 and ρ = 20 s/m) | ||
| Restoring force spring (kN/mm) | kp = 0.0 | kp = 5.69 (μe = 0.1 and vp = 0.5 m/s) | |
| Shear Coefficient [Inter-Story Drift (mm)] on Each Story | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| IDA Median Results | Estimates (New) | Estimates (Conv.) | ||||||||
| PGV (m/s) | 0.5 | 1.0 | 1.5 | 0.5 | 1.0 | 1.5 | 0.5 | 1.0 | 1.5 | |
| Story | 3rd | 0.73 [15] | 0.97 [19] | 1.05 [21] | 0.97 [19] | 1.16 [23] | 1.25 [25] | 0.97 [19] | ||
| 2nd | 0.53 [13] | 0.62 [15] | 0.67 [17] | 0.58 [15] | 0.69 [17] | 0.74 [19] | 0.58 [15] | |||
| 1st | 0.36 [11] | 0.41 [13] | 0.43 [13] | 0.43 [13] | 0.51 [15] | 0.55 [17] | 0.43 [13] | |||
| Shear Coefficient [Inter-Story Drift (mm)] on Each Story | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| IDA Median Results | Estimates (New) | Estimates (Conv.) | ||||||||
| PGV (m/s) | 0.5 | 1.0 | 1.5 | 0.5 | 1.0 | 1.5 | 0.5 | 1.0 | 1.5 | |
| Story | 3rd | 0.73 [14] | 0.96 [19] | 1.04 [21] | 0.98 [19] | 1.17 [23] | 1.28 [25] | 0.98 [19] | 0.99 [20] | 1.00 [20] |
| 2nd | 0.51 [13] | 0.64 [15] | 0.73 [19] | 0.59 [15] | 0.73 [18] | 0.82 [21] | 0.59 [15] | 0.62 [15] | 0.67 [17] | |
| 1st | 0.35 [11] | 0.42 [13] | 0.53 [15] | 0.45 [14] | 0.58 [18] | 0.69 [22] | 0.45 [14] | 0.51 [15] | 0.60 [19] | |
| Without the Restoring Force Mechanism | With the Restoring Force Mechanism | ||
|---|---|---|---|
| Superstructure: 1.5 Hz | Mass (kg) | m1 = m2 = m3 = m4 = m5 = m6 = M/7 (M = 600 × 103 kg) | |
| Stiffness (kN/mm) | k1 = 160.0, k2 = 148.8, k3 = 133.1, k4 = 112.5, k5 = 86.5, k6 = 53.7 | ||
| Damping (kN·s/m) | c1 = 678.9, c2 = 631.7, c3 = 564.9, c4 = 477.4, c5 = 367.0, c6 = 228.0 | ||
| Sliding part | Mass (kg) | m0 = M/7 | |
| Friction | Equation (10) (μmax = 0.21, μmin = 0.16 and ρ = 20 s/m) | ||
| Restoring force spring (kN/mm) | kp = 0.0 | kp = 5.69 (μe = 0.1 and vp = 0.5 m/s) | |
| Shear Coefficient [Inter-Story Drift (mm)] on Each Story | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| IDA Median Results | Estimates (New) | Estimates (Conv.) | ||||||||
| PGV (m/s) | 0.5 | 1.0 | 1.5 | 0.5 | 1.0 | 1.5 | 0.5 | 1.0 | 1.5 | |
| Story | 6th | 0.82 [13] | 1.25 [20] | 1.44 [22] | 1.29 [20] | 1.52 [24] | 1.63 [26] | 1.29 [20] | ||
| 3rd | 0.43 [11] | 0.52 [13] | 0.59 [15] | 0.46 [11] | 0.54 [14] | 0.58 [15] | 0.46 [11] | |||
| 1st | 0.28 [9] | 0.30 [9] | 0.32 [10] | 0.34 [11] | 0.40 [12] | 0.43 [13] | 0.34 [11] | |||
| Shear Coefficient [Inter-Story Drift (mm)] on Each Story | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| IDA Median Results | Estimates (New) | Estimates (Conv.) | ||||||||
| PGV (m/s) | 0.5 | 1.0 | 1.5 | 0.5 | 1.0 | 1.5 | 0.5 | 1.0 | 1.5 | |
| Story | 6th | 0.88 [14] | 1.20 [19] | 1.42 [22] | 1.29 [20] | 1.52 [24] | 1.64 [26] | 1.29 [20] | 1.29 [20] | 1.29 [20] |
| 3rd | 0.42 [11] | 0.52 [13] | 0.63 [15] | 0.46 [12] | 0.56 [14] | 0.63 [15] | 0.46 [12] | 0.49 [12] | 0.53 [13] | |
| 1st | 0.28 [9] | 0.34 [11] | 0.45 [14] | 0.35 [11] | 0.45 [14] | 0.53 [17] | 0.35 [11] | 0.40 [13] | 0.46 [15] | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Enokida, R.; Yenidogan, C. Seismic Response Estimation of Multi-Story Structures Equipped with a Cost-Effective Earthquake Protection System. Buildings 2025, 15, 3233. https://doi.org/10.3390/buildings15173233
Enokida R, Yenidogan C. Seismic Response Estimation of Multi-Story Structures Equipped with a Cost-Effective Earthquake Protection System. Buildings. 2025; 15(17):3233. https://doi.org/10.3390/buildings15173233
Chicago/Turabian StyleEnokida, Ryuta, and Cem Yenidogan. 2025. "Seismic Response Estimation of Multi-Story Structures Equipped with a Cost-Effective Earthquake Protection System" Buildings 15, no. 17: 3233. https://doi.org/10.3390/buildings15173233
APA StyleEnokida, R., & Yenidogan, C. (2025). Seismic Response Estimation of Multi-Story Structures Equipped with a Cost-Effective Earthquake Protection System. Buildings, 15(17), 3233. https://doi.org/10.3390/buildings15173233






