Abstract
By adjusting the two wall angles of the orthogonal hybrid honeycomb (OHH), the tunable Poisson’s ratio change from negative to positive values and the variation in stiffness can be achieved. To effectively analyze its static and dynamic characteristics, a two-dimensional equivalent Kirchhoff–Love model (2D-EKM) is established based on the variational asymptotic method (VAM).This model aids in effectively addressing the complexity arising from anisotropy. The obtained equivalent orthotropic properties are validated through unit-cell uniaxial compression tests and three-point bending experiments on 3D-printed specimens. The numerical simulation results suggest that the VAM-based 2D-EKM can predict the in-plane and out-of-plane static behaviors of OHH panels, with a maximum error below 10%. Particularly in the dynamic analysis of a four-sided fixed OHH panel, the analysis time required by 2D-EKM is only 0.37% of that needed for the 3D FE model. The OHH-ZPR panel exhibits exceptional resistance to deformation, with a maximum deformation under in-plane tension reaching only 27% of that in the OHH-PPR panel. Moreover, each 1% increase in the height–length ratio results in a respective increase of 275.62% and 281.93% in equivalent bending stiffness along both directions. This highlights that enhancing this ratio effectively boosts the fundamental frequency compared to the elastic modulus ratio, effectively prevents low-frequency resonance occurrences, and offers vital insights for the design and optimization of OHH panels.
1. Introduction
The incorporation of tailor-made metamaterials into the cellular structure enhances the potential for achieving superior strength, exceptional acoustic/electromagnetic/infrared stealth capabilities, improved vibration comfort, and enhanced resistance to explosive impacts [1]. Based on their transverse deformation responses to axial loading, metamaterials can be classified as having positive Poisson’s ratio (PPR), zero Poisson’s ratio (ZPR), or negative Poisson’s ratio (NPR) [2]. In the analysis of porous structures, the nominal Poisson’s ratio is utilized to describe the degree of transverse deformation [3,4]. In contrast to traditional PPR materials, NPR materials expand under tension and contract under compression, whereas ZPR materials exhibit minimal lateral deformation when subjected to uniaxial loading [5]. The NPR characteristic remains consistent regardless of scale, stemming from either the material’s overall behavior or its internal structure, embodying traits of both the material at a macroscopic level and its microscopic internal arrangement [6].
Auxetic materials are considered typical mechanical metamaterials [7]. Due to their unique mechanical properties, they offer significant advantages in shear resistance, indentation resistance, fracture toughness, surface curvature alignment, variable permeability, and energy absorption capabilities [8,9]. Currently, the application of auxetic materials has extended to various fields including artificial implants [10], textile materials, smart sensors [11], intelligent filters [12], molecular filters [13], protective pads [14], shock absorbers [15], and soundproofing devices [16]. However, the research into auxetic materials primarily focuses on the category of the negative Poisson’s ratio [17]. In fact, the deformation requirements in engineering applications are highly complex. Therefore, investigating the deformation modes of two-dimensional and even three-dimensional structures with a tunable Poisson’s ratio holds significant practical importance [18].
In aerospace, precision instruments, and civil engineering, accurate control of structural deformations is frequently essential. Traditional structures with a fixed positive or negative Poisson’s ratio face challenges in meeting the intricate requirements of engineering [19,20]. Thus, the exploration of structures with tunable positive/zero/negative Poisson’s ratios holds heightened practical importance [21]. Extensive research endeavors have resulted in a series of groundbreaking advancements in the investigation of tunable Poisson’s ratio structures, as showcased in Figure 1.
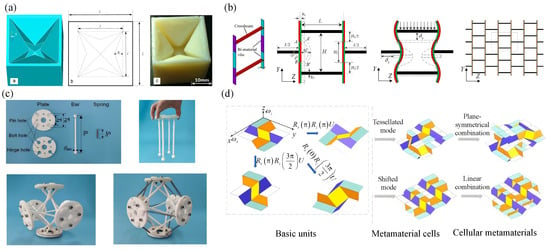
Figure 1.
Novel structures with tunable Poisson’s Ratio, (a) re-entrant unit-cell structures [22], (b) bi-material quadrilateral structure [23], (c) truncated regular structure [24], (d) origami-based structure [25].
Li et al. [22] introduced an innovative unit-cell design founded on the re-entrant framework capable of attaining a Poisson’s ratio ranging from −1 to −0.5, as illustrated in Figure 1a. They proposed a bi-material structure featuring a two-dimensional quadrilateral structure that can transition between concave and convex states through temperature modulation [23], facilitating the manipulation of positive and negative Poisson’s ratios shown in Figure 1b. Yin et al. [24] developed a mechanically tunable metamaterial based on a regular octahedron tensile structure in Figure 1c and constructed a theoretical model to forecast its mechanical characteristics.
By adjusting the structural prestress, initial twist angle, and string stiffness, a broad spectrum of adjustable Poisson’s ratios can be realized. Lyu et al. [25] developed a novel tunable Poisson’s ratio metamaterial by selecting a square twisted origami design with specific motion characteristics, as shown in Figure 1d. Pagliocca et al. [26] devised a set of adjustable Poisson’s ratio cylindrical structures. Their observations revealed that the structure with a low number of peripheral cells displays petal-like and polygonal deformation modes. Conversely, when the number of peripheral cells surpasses a critical threshold, the Poisson’s ratio approximates that of a two-dimensional planar structure.
In terms of the honeycomb panel’s vibration characteristics, Liu et al. [27] examined sandwich panels featuring isotropic panels and orthogonal anisotropic cores. They derived the governing partial differential equation using the variational principle and explored the impact of core layer density and plate thickness on vibration characteristics. Liu et al. [28] utilized the variational principle to analyze the vibration of sandwich panels with two identical isotropic panels and hexagonal element cores. Their research revealed a significant difference in horizontal shear modulus between the honeycomb panel and the core layer, indicating that horizontal shear deformation notably affects honeycomb panel vibration. Kant et al. [29] employed the generalized Jacobi method with a subspace iteration technique to compute the free vibration response, followed by using its mode to determine the dynamic response. Tanimoto et al. [30] investigated the influence of honeycomb core geometry and honeycomb panel thickness on characteristic frequency, showing that the geometry of the honeycomb core impacts the vibration characteristics of the honeycomb panel.
In the analysis of honeycomb structures, a key challenge lies in the substantial computational expenses linked to detailed multi-cell honeycomb FE modeling and analysis [31,32]. A prevalent and more pragmatic strategy involves employing an equivalent or homogenized two- or three-dimensional FE model to represent the honeycomb structure [33]. Sorohan et al. [34] introduced several general two- and three-dimensional FE models to accurately determine the equivalent in-plane orthotropic mechanical properties of honeycombs through the homogenization method. Saidi et al. [35] introduced a technique for generating three-dimensional models of sandwich structures using a two-dimensional equivalent plate-type model. Zhong and Yu [36] introduced a multiscale modeling technique for periodic composite structures leveraging the variational asymptotic method (VAM) [37]. Through the elimination of higher-order terms, a delicate balance between precision and efficiency in the minimization of approximation energy can be achieved [38,39].
This study extends the VAM to establish a two-dimensional equivalent Kirchhoff–Love model (2D-EKM) for the static and dynamic characteristics analyses of the orthogonal hybrid honeycomb panels (OHH panels). In comparison with the existing equivalent models, this work introduces novel contributions. Specifically, by employing variational asymptotic homogenization on the unit cell within the OHH panel, the equivalent constitutive parameters are determined to address the anisotropy complexities of OHH panels. Moreover, the tailorability of the unit cell proves to be a crucial and beneficial feature, greatly facilitating the parametric analysis of OHH panels.
The paper’s structure is outlined as follows: Section 2 provides a comprehensive description of the geometry of OHHs. In Section 3, the theoretical formulas and constitutive relationships of the 2D-EKM are developed using VAM. Section 4 validates the effectiveness and accuracy of the equivalent model through unit-cell uniaxial compression tests and three-point bending experiments using 3D-printed specimens, as well as in-plane and out-of-plane static behaviors, and dynamic analysis. In addition, Section 5 investigates the influence of geometric and material parameters on the Poisson’s ratio, equivalent properties, and structural responses of OHH panels. Finally, Section 6 provides a summary highlighting the key findings.
2. Geometry of the Orthogonal Hybrid Honeycomb
The unit cell of the OHH consists of horizontally and vertically arranged honeycombs in an orthogonal configuration. Its geometric features include length a, width b, height h, wall angles and , as well as wall thicknesses and . In conventional honeycombs, wall angle serves as a crucial geometric parameter. A wall angle below renders the re-entrant honeycomb, often displaying auxetic characteristics. As a result, present honeycombs are categorized into four classifications: negative Poisson’s ratio OHH (OHH-NPR, Figure 2b), zero Poisson’s ratio OHH (OHH-ZPR, Figure 2c), positive Poisson’s ratio OHH (OHH-PPR, Figure 2d), and semi-OHH (Figure 2e,f).
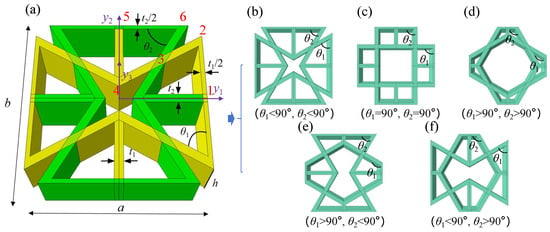
Figure 2.
Classifications of the orthogonal hybrid-honeycomb (OHH): (a) Dimensions and coordinates, (b) OHH with two orthogonal re-entrant honeycombs exhibiting negative Poisson’s ratio effect (OHH-NPR), (c) OHH with two orthogonal rectangular honeycombs demonstrating zero Poisson’s ratio effect (OHH-ZPR); (d) OHH with two orthogonal hexagonal honeycombs displaying positive Poisson’s ratio effect (OHH-PPR), (e,f) Semi-OHH structures combining re-entrant and hexagonal honeycombs.
The arrangement of honeycombs in an orthogonal configuration improves overall stability and robustness, offering excellent resistance to compression and bending. In addition, utilizing a honeycomb structure yields a lightweight design with a favorable strength-to-weight ratio, making it ideal for applications requiring reduced weight. The orthogonal intersections between horizontally and vertically oriented honeycombs efficiently absorb and disperse energy, demonstrating commendable energy absorption capabilities under impact conditions and enhancing structural protection.
According to the geometric relations of the OHH, the lengths of the inclined and non-inclined walls can be obtained as
where subscripts 1 to 7 represent the nodes of the walls, marked in red in Figure 2a, and the influence of the wall thickness is ignored.
To avoid geometric overlap, there exist certain constraint relationships, namely,
According to cell material theory, the equivalent density of the OHH can be obtained as
where represents the density of the base material.
3. VAM-Based Equivalent Plate Model for OHH Panel
The modeling challenge focuses on transforming the three-dimensional structural anisotropy of the OHH into the two-dimensional material anisotropy. As the thickness of the honeycomb panel is much smaller than the in-plane dimensions, it can be considered an equivalent plate-type model from an ESL (equivalent-single-layer) perspective [40]. This allows for a concise and efficient framework to express the virtual work and 3D Lagrangian of the honeycomb panel using representative kinematic variables, such as 2D generalized stresses.
The equivalent modeling of the OHH panel is illustrated in Figure 3. The displacement fields of the original OHH panel can be expressed as the displacement function defined on the - plane, and its partial derivative is [41].
where and () represent the macroscopic and microscopic coordinates, respectively, with the relationship between the two coordinates expressed by the small parameter .
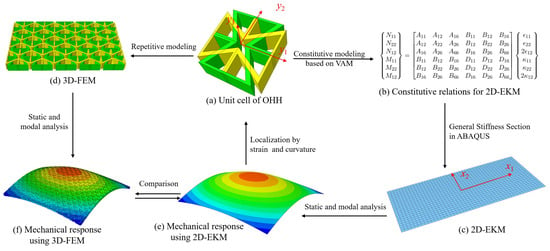
Figure 3.
Equivalent modeling of OHH panels, the global analysis (a) of the three-dimensional FE model (3D-FEM) (b) involves constitutive modeling at the unit-cell level (c) and global analysis (d) using the two-dimensional equivalent Kirchhoff–Love model (2D-EKM) (e) with constitutive relations of A, B, and D submatrix (f). The mechanical response of 2D-EKM (d) can be sent back into the unit cell (c) for local field recovery.
3.1. Kinematics of the OHH Panel
The first step is to define the displacement fields using the displacements of the 2D model and warping functions, such as
where represents warping functions utilized to characterize the through-the- thickness deformation.
The explicit expressions of can be derived from Equation (5),
where represents the average volume over the unit cell.
It can be inferred from Equation (6) that the displacements of the 2D-EKM are an average of those from the 3D-FEM, with each displacement offset by the warping-induced rotation. If the origin of is at the geometric center of the unit cell, and there are three constraints on the warping functions,
The corresponding strain field can be expressed as
where underlined and underbraced warping function terms are obtained from Equation (4), and the contribution of the underlined terms to the total energy can be neglected as they are higher-order terms resulting from the small parameter .
The 2D plate strains and in Equation (8) can be defined as
The following step is to express the variational principle of the original problem using the field variables from the equivalent model and unknown warping functions. The strain energy can be represented as
where represents the strain energy density; s represents the domain of the reference surface; and is the domain of a unit cell projected onto the – plane.
The explicit expression of is given by
where D is the 3D material matrix; denotes the local element coordinates, with the origin and directions adjusted according to the varying inclinations of the walls; the lengths of , , , and can be calculated using Equation (1) and are functions of and ; the subscripts 1 to 6 and A to C differentiate between various components within the hybrid honeycombs and overlap regions, respectively, as shown in Figure 4.
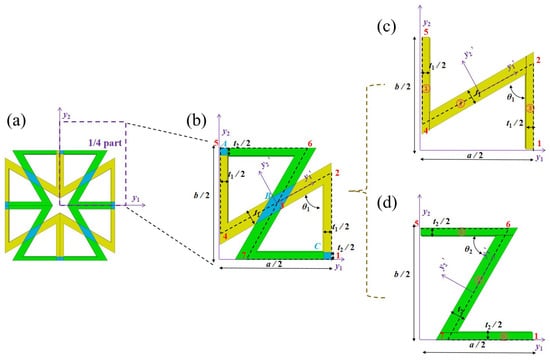
Figure 4.
Partition diagram for the strain energy of the OHH unit cell: (a) Unit-cell of OHH, (b) 1/4 part pf unit cell, (c) Quarter unit cell in the direction, and (d) Quarter unit cell in the direction.
The matrix form of 3D strain field is
where , , , and
Equation (10) can be expressed as
where , and are the corresponding sub-matrices of the 3D material matrix.
The load-induced virtual work can be expressed as
where represents the boundary curve; denotes the body force; and represent the tractions on the upper and lower surfaces of the panel, respectively; denotes the traction applied on the lateral surface. and denote the displacements on the lower and upper surfaces; the double angle brackets indicate integration along the thickness direction of the lateral surface.
By substituting the 3D displacement field in Equations (5) and (6) into Equation (15), one can obtain
where ,
and
where and represent the distribution of forces and moments on the reference surface, while and denote the forces and moments distributed along the boundary curve.
Based on the energy conservation, the kinetic energy () of the honeycomb panel should be the sum of the kinetic energy () of 2D-EKM and the difference between them, which corresponds to the remaining kinetic energy (), such as
where
where denotes the mass density of the panel, V and represent the absolute velocity and inertial angular velocity of a point in the deformed panel, respectively; , , and the notion represents the operation of transforming a vector into an antisymmetric matrix, using the permutation symbol ; , and are inertial constants used in plate dynamics and can be readily obtained through the integral operations as
The extended Hamilton principle is used to determine the elastodynamic behavior of OHH panels, such as
The traditional method to solve Equation (23) is to assume the unknown warping function and simplify the original 3D model into a 2D plate model. However, this assumption may not accurately capture the anisotropic complexities present in OHH panels. By considering the full 3D nature of OHH panels and applying variational principles to determine the warping function, variational asymptotic analysis provides a more efficient solution for addressing these anisotropy complexities, as detailed in the following section.
3.2. VAM-Based 2D-EKM for the OHH Panel
Before applying VAM, it is necessary to evaluate the order of each term in Equation (23), such as
where stands for the orders of the material properties, n represents the minimum strain required, and L indicates the length of the honeycomb panel.
The first approximation of the variational statement in Equation (23) can be achieved by removing the smaller terms and , such as
where can be derived from Equation (23) by eliminating the derivatives with respect to ,
By introducing Lagrange multipliers , one can obtain the corresponding Euler–Lagrange equation, such as
where .
The upper and lower surfaces of the OHH panel are considered free boundary conditions due to the periodicity being limited to only two in-plane directions, such as
where the superscript “+/−” indicates the items on the top and bottom facesheets of the panel.
Based on these conditions, one can obtain the solutions for and as
where
By substituting Equation (29) in Equation (26), the strain energy of 2D-EKM can be obtained as
where K is the 6 × 6 equivalent stiffness matrix, and
The constitutive relationship of 2D-EKM can be represented as
where , , and denote tensile, bending, and tensile–bending coupling stiffnesses, respectively.
Despite the developed model being similar to the classical Kirchhoff–Love model, its derivation process abstains from relying on a priori displacement-based assumptions, thereby guaranteeing the precision of the calculations. The 2D-EKM’s behavior is governed by the variational statement in Equation (25), which specifically considers the 2D field variables denoted by the macro-coordinates and . This enables the potential replacement of the original honeycomb panel with the 2D-EKM in finite element software (e.g., ABAQUS, version 6.14) for comprehensive global analyses, including static and dynamic analyses.
3.3. Local Field Recovery
A well-established equivalent model enables the evaluation of both global behavior and local fields. Enhancing the present equivalent model requires incorporating the recovery relationship for local displacement fields, such as
The local strain field can be recovered as
Based on the principle of general Hooke’s law, the local stress field can be determined as
4. Model Validation
4.1. Experimental Validation
Given the structural complexity, conventional molding processes face difficulties in manufacturing OHH; hence, this section employs 3D-printing (additive manufacturing) for fabricating the OHH specimens. The geometric parameters of the unit cell illustrated in Figure 2 are set as . According to the ASTM D638 standard, the mechanical properties of polylactic acid (PLA) plastic printed materials are determined through tensile tests utilizing a universal testing machine equipped with a 5 kN load cell. The specimens are subjected to tensile loads at a constant cross-head speed of 2 mm·min−1. The stress–strain curves of the PLA specimens are shown in Figure 5. Based on these curves, the mechanical properties of PLA were calculated to be , respectively.
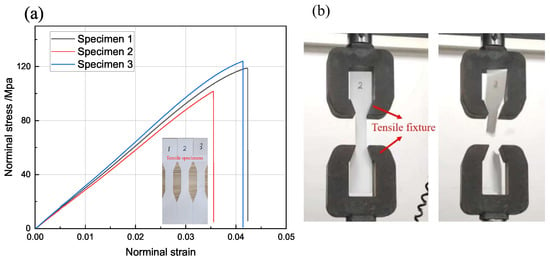
Figure 5.
(a) Stress–strain curve of PLA material and (b) setup for standard tensile test.
By adjusting the two wall angles and of the hybrid honeycombs within the OHH, it is possible to alter the equivalent Poisson’s ratio and equivalent stiffness. Prior to experimental validation, the Poisson’s ratio and equivalent stiffness of the OHH were determined using the 2D-EKM, which accounted for the variations in and . Figure 6a illustrates the variation in the equivalent Poisson’s ratio of OHH. It is evident that the Poisson’s ratio of OHH varies from −1 to 1 within the range of –, displaying an increasing trend as the angles rises. Furthermore, the equivalent density gradually decreases with increasing angles, as illustrated in Figure 6b.
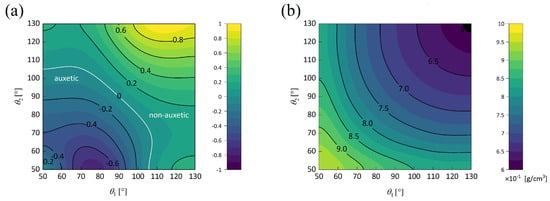
Figure 6.
Evaluation of (a) equivalent Poisson’s ratio and (b) equivalent density of the OHH as a function of the wall angles and .
Figure 7 illustrates the contour plots of equivalent stiffness obtained by the present model. Figure 7a,d demonstrate that the equivalent stiffness along the principal axis direction, denoted as and , reaches its peak when angles and approach 90 degrees. Deviation from these angles results in a gradual decrease in the equivalent stiffness along the principal axis. This phenomenon is attributed to the presence of inclined walls at non-90-degree angles. Under the application of identical external forces, an angular deviation exists between the wall and the force direction, leading to the decomposition of the force into components along and perpendicular to the wall axis. Only the axial component influences tensile stiffness, consequently diminishing the equivalent stiffness along the principal axis. As angles and increase, the Poisson effect induces a transition of and from negative to positive values, as illustrated in Figure 7b,e, prompting a redistribution of mass towards the unit cell’s periphery. This redistribution enhances the resistance of OHH to shear and torsion with increasing angles of and , consequently elevating the values of and , as illustrated in Figure 7c,f.
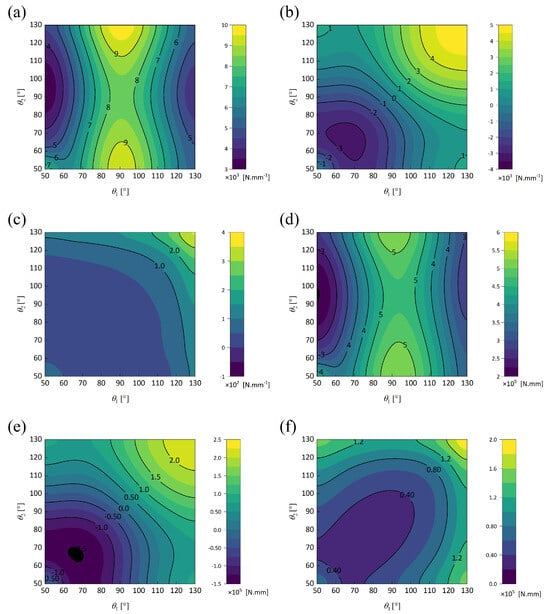
Figure 7.
Contour plots of (a) , (b) , (c) , (d) , (e) , and (f) of the OHH with changes in and .
4.1.1. Uniaxial Compression Test
To validate the accuracy of the equivalent properties and assess the compressive behaviors of the OHH with varying Poisson’s ratios, OHH-NPR, OHH-ZPR, and OHH-PPR cells in Figure 8b were fabricated via 3D printing for uniaxial compression tests at the unit-cell level, as illustrated in Figure 8a. A rigid steelhead was placed on top to compress the specimen into a quasi-static compression state. The compression speed of the testing apparatus was maintained at 0.5 mm/min along the 2-direction, with a maximum displacement of 5.6 mm (−0.07).
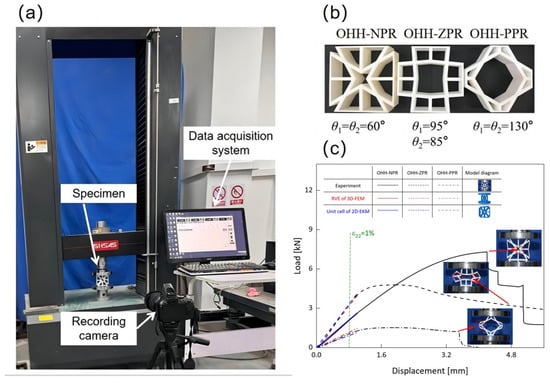
Figure 8.
Uniaxial compression test of OHH cells with different Poisson’s ratio at the unit-cell level, (a) test set-up, (b) specimens, and (c) load-displacement curves.
Figure 8c compares the load-displacement curves of OHH cells with different Poisson’s ratios obtained from representative volume element (RVE) of 3D-FEM, the 3D unit cell of 2D-EKM, and experiment. Notably, the data for the 3D unit cell of 2D-EKM were obtained through the local field recovery under . It is evident that the curve for the OHH-ZPR cell has the steepest slope, while the curve for the OHH-PPR cell is the smoothest, with the curve for the OHH-NPR cell falling in between. This disparity can be attributed to the OHH-ZPR cell having the highest equivalent stiffness of and , thereby demonstrating the greatest resistance to axial deformation. The OHH-NPR cell displays the highest ultimate bearing capacity, experiencing abrupt failure in the joint region between the inclined and horizontal walls in the 2-direction at a displacement of 4.2 mm (), resulting in a sudden decline in bearing capacity. Once displacements exceed 1.6 mm () for the OHH-ZPR and OHH-PPR cells, plastic hinges form in the joint area of the inclined and horizontal walls in the 2-direction, enabling slight rotation and entering a prolonged plastic deformation phase. Ultimately, OHH-PPR cell loses its bearing capacity at a displacement of 3.5 mm () due to left-side failure of the unit cell.
In Figure 8c, the loads recorded in experiments tend to be slightly lower compared to those obtained using RVE of 3D-FEM and 3D unit cell of 2D-EKM, possibly due to minimal discontinuities or defects between specimen layers in the 3D-printed specimens, resulting in a modest reduction in stiffness. Nonetheless, all three methods exhibit a strong alignment in their load-displacement curves throughout the elastic stage, suggesting that the VAM-based equivalent properties boast a commendable level of precision.
Table 1 compares the deformation characteristics of the OHH cells with varying Poisson’s ratios at an axial displacement of 0.8 mm ( = −0.01) along the 2-direction. It is apparent that under compressive loading, the OHH-NPR cell demonstrates a pronounced “auxetic effect” by reducing its lateral length by 0.559 mm. In contrast, the OHH-ZPR cell shows minimal lateral deformation, and the OHH-PPR cell experiences a lateral length expansion of 0.715 mm. Upon comparing the displacement contours of obtained from 3D-FEM and 2D-EKM, a close alignment is evident. Compared to the experimental results, the errors in Poisson’s ratios obtained from the 3D unit cell of the 2D-EKM are 5.7%, 2.5%, and 1.1% for three OHH cells, respectively. This underscores the high accuracy of the VAM-based local field recovery.

Table 1.
Comparison of deformations in OHH-NPR, OHH-ZPR, and OHH-PPR cells under an axial compression displacement of 0.8 mm in the 2-direction ( = −0.01).
4.1.2. Three-Point Bending Test
Three-point bending tests are crucial for assessing the out-of-plane performance of the OHH panel, aiding in the evaluation of design parameters and validation of numerical simulation results. This section examines the out-of-plane behavior of OHH panels with varying Poisson’s ratios via three-point bending tests. The wall angles and , as well as the material parameters, remain consistent with those outlined in Section 4.1.1. However, in this case, the dimensions are defined as follows: = 30 mm and = 2 mm for the unit cell.
Figure 9 illustrates the equivalent properties of three OHH panels with varying Poisson’s ratios obtained from 2D-EKM. It is evident that the OHH-ZPR panel shows pronounced anisotropy, with significantly higher stiffness along its principal axis compared to other directions; specifically, bending stiffness surpasses by a factor of 22.5. This disparity is due to its zero Poisson’s ratio trait, enhancing directional mechanical efficacy and reducing lateral deformations [42]. Conversely, the OHH-PPR panel demonstrates minimal variations in stiffness across different directions, rendering it inadequate for high performance in specific orientations.
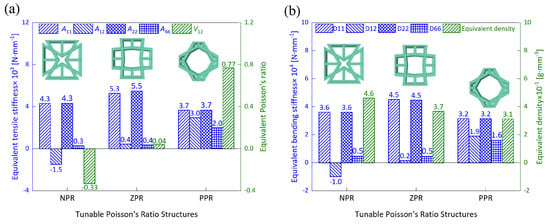
Figure 9.
Evaluation of (a) equivalent tensile stiffness and Poisson’s ratio, as well as (b) equivalent bending stiffness and density of three OHH panels with varying Poisson’s ratios predicted using 2D-EKM.
The equivalent properties of the OHH panels were utilized to create the 2D-EKM in the ABAQUS software (version 6.14). The 3D-FEM and 2D-EKM utilize C3D8R and S4R elements, with the number of elements being 25,621 and 625, respectively. Subsequently, the OHH panel specimen underwent a three-point bending test using the CMT-5205 (Xin Sansi Materials Testing Co., Ltd., Shenzhen, China) electronic universal testing machine. The specimen was placed on two lower supports that were 210 mm apart. Then, the indenter was lowered at a constant velocity of 1 mm/min to apply displacement loading and generate the load-displacement curve.
Figure 10 compares the load-displacement curves of three OHH panels obtained through three distinct methods. It is evident that the OHH-ZPR panel exhibits the steepest curve slope. Furthermore, it is the first to fail as the load escalates, with a maximum failure load of 445 N—surpassing the other honeycomb panels and indicating superior bending resistance. Upon examining the curves of the three panels, discrepancies in the elastic stage between the 2D-EKM, 3D-FEM, and experimental curves are minimal. This suggests that the VAM-based equivalent model adeptly predicts the bending behaviors of OHH panels with different Poisson’s ratios.
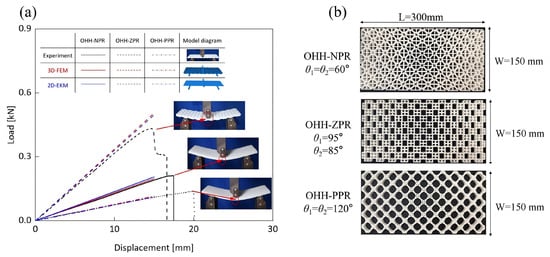
Figure 10.
Three-point bending test of OHH panels, (a) Load-displacement curves, (b) Dimensions of three OHH panel specimens.
4.2. Static and Modal Validation
4.2.1. Static Behavior Validation
This section aims to assess the accuracy of the 2D-EKM in predicting the static performance of the OHH panel, including in-plane tension and out-of-plane bending deformations. By utilizing the material and geometric parameters of the OHH unit cell outlined in Section 4.1, and to mitigate the impact of the height–length ratio, a square honeycomb panel with dimensions = 300 mm is employed as illustrated in Figure 11. In Case 1, the OHH panel is restricted at and subjected to a linear tensile load up to 50 kN at . Conversely, in Case 2, the OHH panel is clamped at the panel’s central point, with linear loads up to 100 N in the negative direction being applied at and , while the remaining two edges serve as free boundaries.
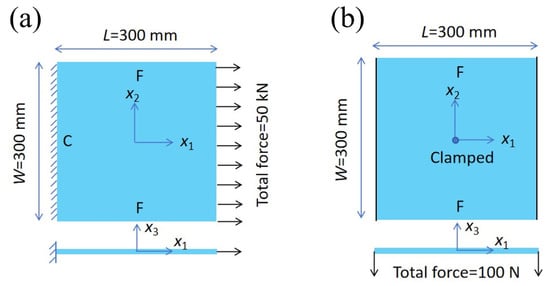
Figure 11.
Cases utilized in static behavior validation: (a) Case 1: in-plane tension, (b) Case 2: out-of-plane bending.
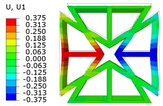
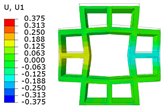
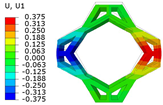
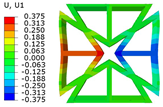
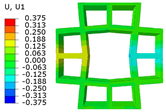
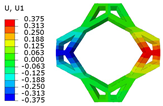
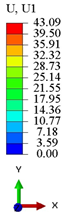
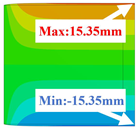
Table 2 compares the deformation contours of and for the three OHH panels under Case 1. It is evident that the OHH-ZPR panel demonstrates no lateral deformation of , whereas the OHH-NPR and OHH-PPR panels exhibit lateral expansion and contraction, respectively, showcasing a notable ’Poisson effect’. The deformations of along the loading direction for the OHH-NPR, OHH-ZPR, and OHH-PPR panels are 15.24 mm, 11.50 mm, and 43.09 mm, respectively. Notably, the deformation of the OHH-ZPR panel is merely 27% of that of the OHH-PPR panel, underscoring its superior resistance to axial deformation. This resistance can be attributed to the OHH-ZPR panel’s zero Poisson’s ratio and larger tensile stiffness , which prevent lateral deformations under external forces. This characteristic impedes lateral deformations and thus does not augment the structure’s elastic modulus in the deformation direction. The errors between 3D-FEM and 2D-EKM range from 1.87% to 8.73%, indicating the high accuracy of the VAM-based equivalent tensile stiffness for analyzing the in-plane behaviors of OHH panels, especially the in-plane auxetic behavior of the OHH-ZPR panel.

Table 2.
Comparison of deformation contours of and for the three OHH panels under Case 1, as predicted by 3D-FEM and 2D-EKM.
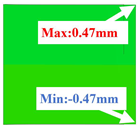
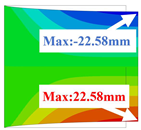
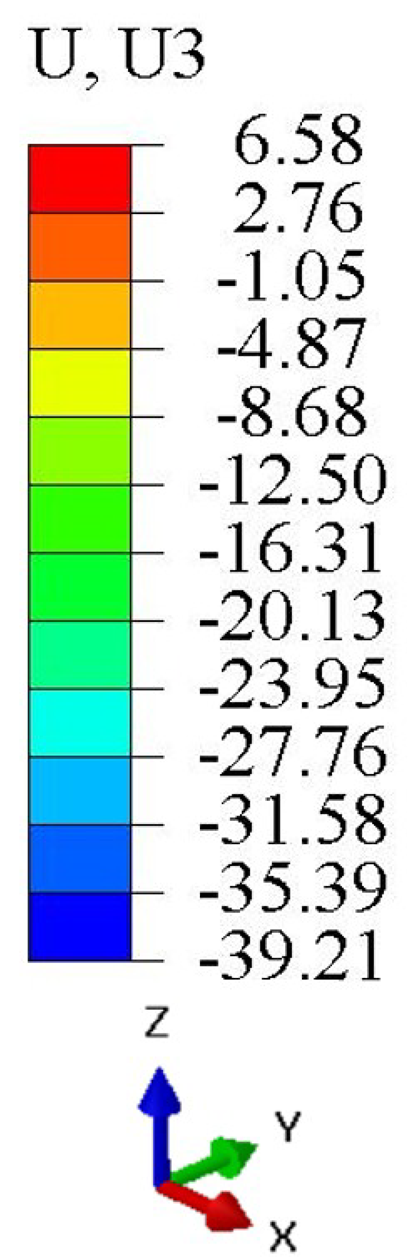
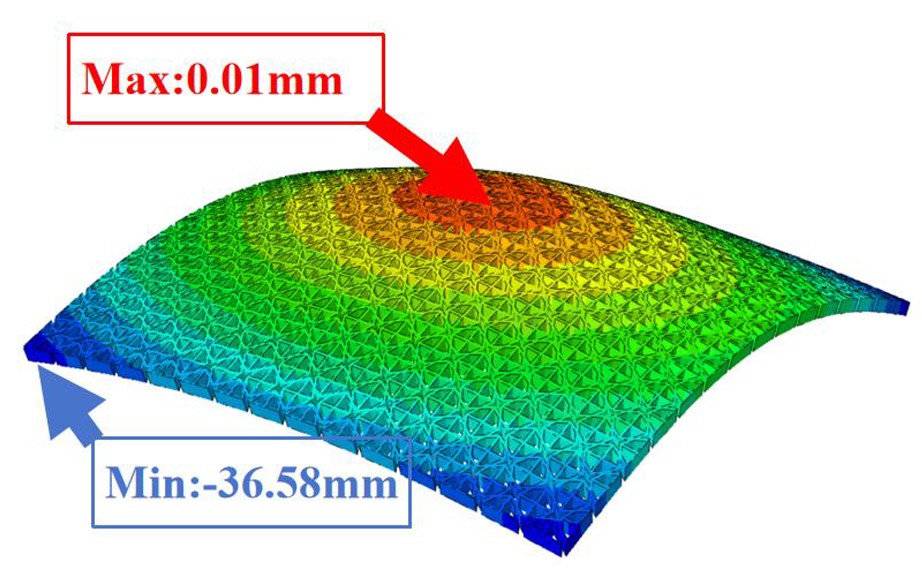
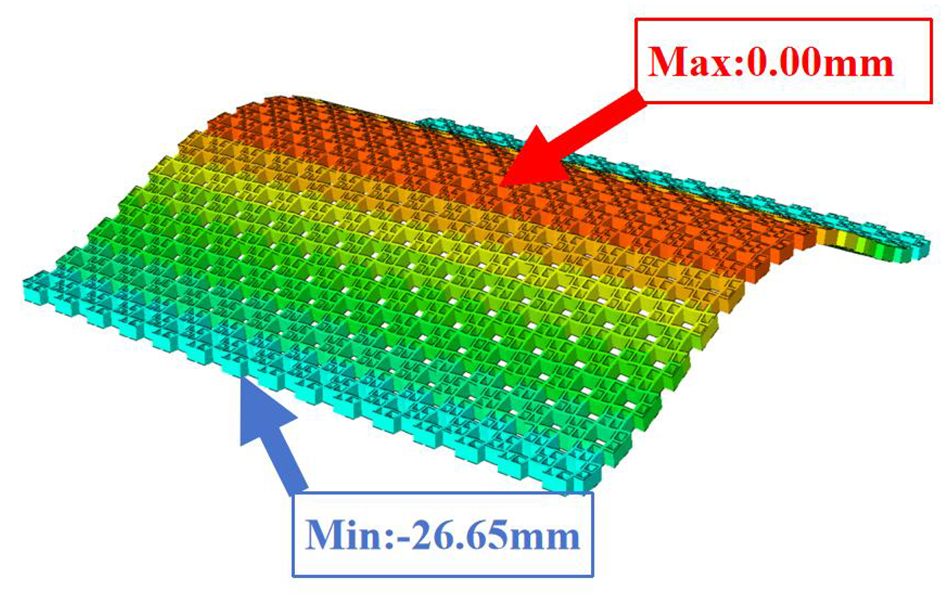
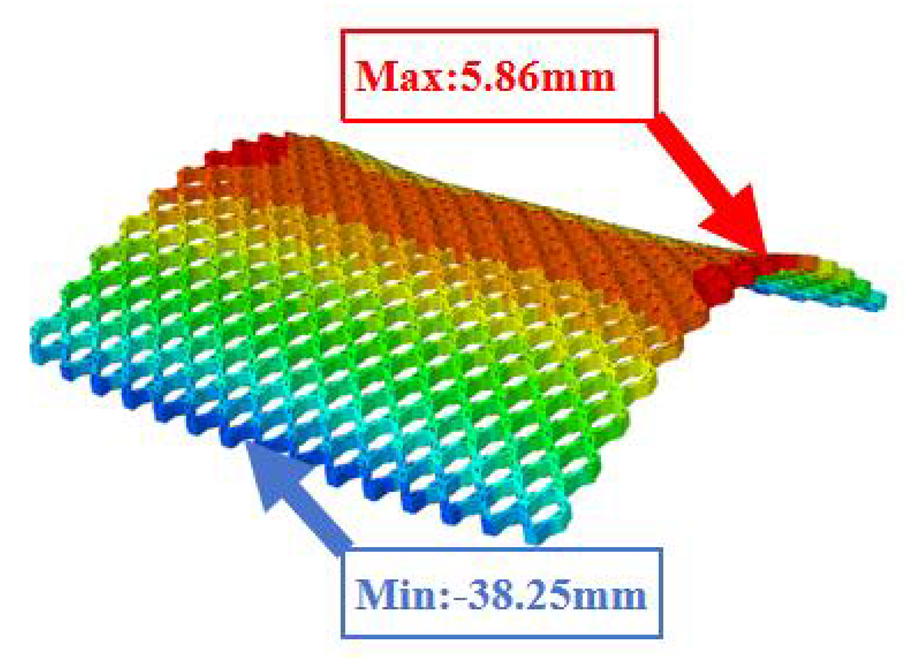
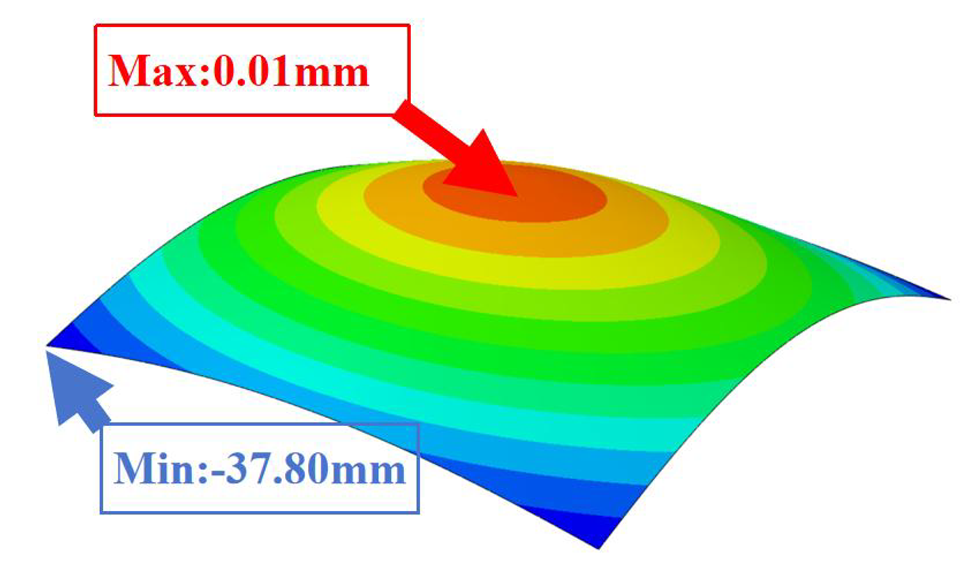
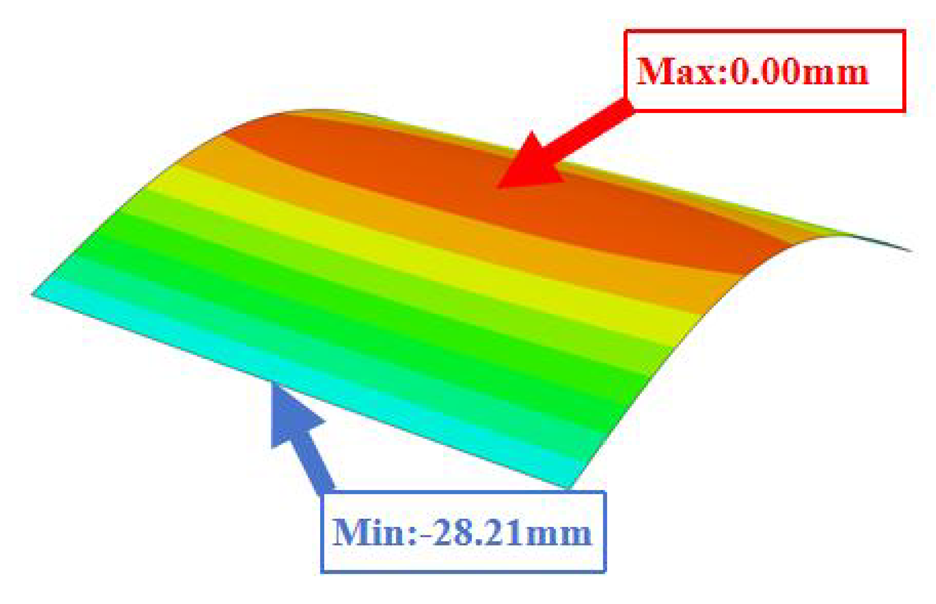
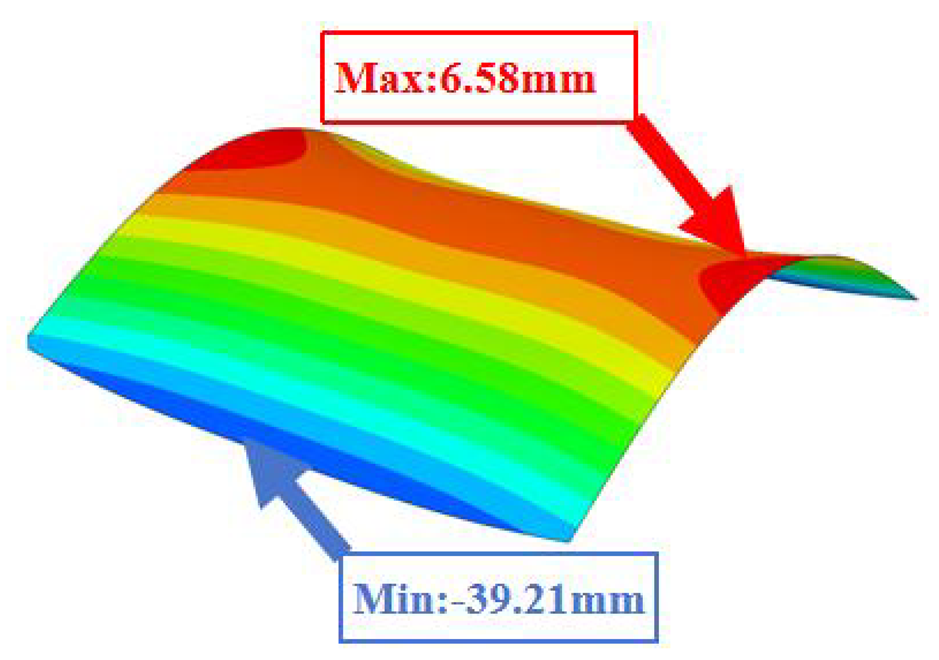
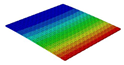
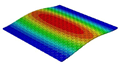
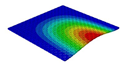
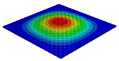
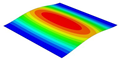
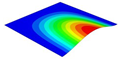
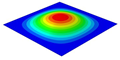
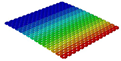
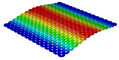
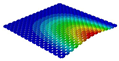
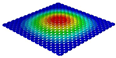
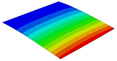
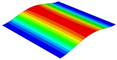
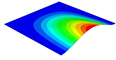
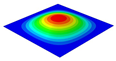
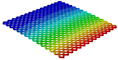
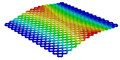
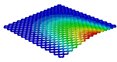
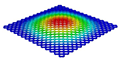
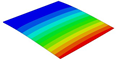
Table 3 compares the deformation contours of three OHH panels with varying Poisson’s ratios under Case 2. The out-of-plane deformations of the OHH-NPR, OHH-ZPR, and OHH-PPR panels exhibit dome-, cylinder-, and saddle-shaped surfaces, respectively. The displacements of the OHH-NPR and OHH-ZPR panels are negative, ranging from −36.58 mm to 0 mm, while the OHH-PPR panel shows a minimum displacement of −26.65 mm at the loaded edge and a maximum displacement of +5.86 mm due to the raised free edge. By adjusting the two wall angles and of the OHH, different in-plane and out-of-plane deformation shapes induced by tunable Poisson’s ratio can be obtained to meet various engineering requirements, as evidenced in both Cases 1 and 2.

Table 3.
Comparison of deformation contours of for the three OHH panels under Case 2, as predicted by 3D-FEM and 2D-EKM.
To elucidate the deformation mechanism of the OHH panels under bending loads and further validate the precision of 2D-EKM in predicting auxetic deformations, Figure 12 illustrates the path-displacement curves of the OHH panels along Paths 1 and 2 in Case 2. The starting and ending coordinates of Path 1 are (, 0) and (, 0), respectively, while those of Path 2 are (0, ) and (0, ). It is noted that all Path 1 displacement curves lie below = 0, whereas the Path 2 displacement curves of the OHH-NPR, OHH-ZPR, and OHH-PPR panels are positioned below, near, and above the = 0 axis, respectively. This indicates that the Path 1 and Path 2 deformation directions align in the OHH-NPR panel under bending loads, resulting in a dome-shaped surface. In contrast, the Path 2 deformation curvature for the OHH-ZPR panel is zero, leading to a cylindrical deformation, while the Path2-deformation direction of the OHH-PPR panel is opposite to that of Path 1, forming a saddle-shaped surface. A comparison of curves between 3D-FEM and 2D-EKM reveals significant consistency, suggesting that 2D-EKM provides high accuracy in predicting the bending behavior of OHH panels.
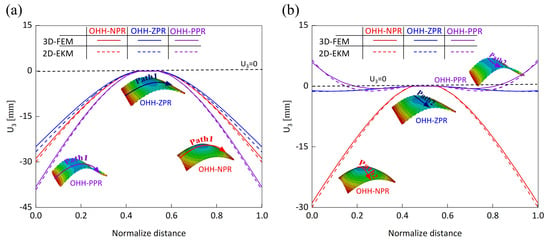
Figure 12.
Path-displacement curves of OHH panels with different Poisson’s ratios along (a) Path 1 and (b) Path 2 in Case 2.
4.2.2. Local Field Distribution Verification
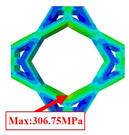
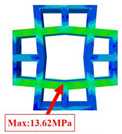
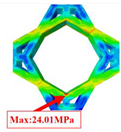
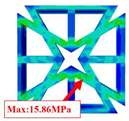
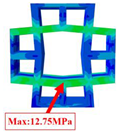
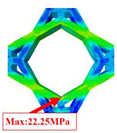
The mechanical performance of honeycomb structures is determined by the behavior of their fundamental unit—the unit cell. By examining the local stress and deformation within the unit cells, a more comprehensive insight into the mechanical behavior of the overall structure can be achieved. Table 4 compares the local stress fields within the unit cell in Case 1 (center of the panel) and Case 2 (midpoint of the free edge), as predicted by 2D-EKM and 3D-FEM. The analysis demonstrates a notable agreement between the two models, with a maximum stress error of 8.75%. This underscores the precision of the local fields reconstructed from the equivalent model, allowing for the precise prediction of the local stress characteristics.

Table 4.
Comparison of local stress field within the unit cell of three OHHs under Cases 1 and 2.
In Case 1, the maximum local stresses observed in the OHH-NPR, OHH-ZPR, and OHH-PPR cells are 120.85 MPa, 88.01 MPa, and 336.18 MPa, respectively. A significantly higher local stress is evident in the OHH-PPR cell compared to the OHH-NPR and OHH-ZPR cells, with a distinct stress concentration. This discrepancy can be attributed to the significant deformation experienced by the OHH-PPR cell under tensile loading, as detailed in Table 2, resulting in increased strain and subsequently the highest local stress among the three OHH cells. These findings imply that the OHH-PPR cell is more susceptible to fracture failure under in-plane tension.
In Case 2, the local stress of the OHH-ZPR cell is the lowest, with its maximum von Mises stress being 83.8% and 56.7% of the OHH-NPR and OHH-PPR cells, respectively. Moreover, the high local stress in the OHH-ZPR cell is predominantly situated at the outer connections of the two orthogonal honeycombs, whereas the high-stress areas in the OHH-NPR cell are mainly concentrated near the intersections of the orthogonal re-entrant honeycombs.
4.2.3. Dynamic Analysis
Determining the eigenfrequency of the honeycomb panel through dynamic analysis is essential to preclude resonance with external vibration sources, which may result in reduced structural integrity, along with fatigue-induced failures or prolonged stress accumulation. Figure 13 depicts the four types of boundary conditions utilized in dynamic analysis, with ‘C’ denoting a clamped boundary and ‘F’ signifying a free boundary. Table 5 details the associated eigenfrequencies and eigenmodes of OHH panels across the four boundary conditions.
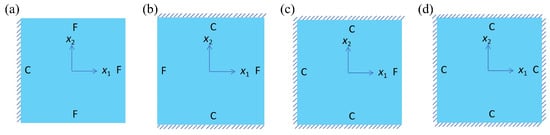
Figure 13.
Four types of boundary conditions utilized in dynamic analysis: (a) Case 3: CFFF, (b) Case 4: CCFF, (c) Case 5: CCCF, (d) Case 6: CCCC.

Table 5.
Comparison of natural frequencies and vibration modes of three OHH panels across the four boundary conditions, as predicted by 3D-FEM and 2D-EKM.
The dynamic analysis indicates that under four cases, the primary modes of the OHH panels involve bending deformations, with the OHH-ZPR panel exhibiting the highest equivalent bending stiffness of and , leading to its peak fundamental frequency. This suppresses resonance occurrences, thereby enhancing vibration performance and bolstering structural stability and reliability. An examination of the OHH panel’s fundamental frequencies under distinct boundary conditions reveals a proportional increase with the addition of fixed-support boundaries. Particularly noteworthy is the transition from CFFF to CCFF BCs, where the fundamental frequencies of the OHH-NPR, OHH-ZPR, and OHH-PPR panels surged by 5.62, 5.38, and 5.45 times, respectively. The imposition of heightened boundary constraints confines the panel’s free vibration, restricting eigenmodes to the structural core, diminishing effective structural mass, and consequently elevating the fundamental frequency.
Figure 14 illustrates the first eight eigenfrequencies of the OHH panels across four distinct cases. The eigenfrequencies systematically increase with higher mode orders, particularly the eighth eigenfrequencies for the OHH-NPR, OHH-ZPR, and OHH-PPR panels are 17.40, 17.99, and 18.62 times the fundamental frequency under the CFFF BCs, respectively. The amplification of higher-order eigenmodes results in localized vibrations, enhancing structural stiffness while reducing local mass, consequently elevating the OHH panel’s eigenfrequencies. In all cases, the eigenfrequency curves for the first eight modes of the OHH-NPR panel consistently lie below those of the OHH-ZPR and OHH-PPR panels. Figure 9b illustrates that the OHH-NPR panel exhibits the highest equivalent density, consequently enhancing its inertia and leading to a reduction in eigenfrequencies. The eigenfrequencies obtained from 2D-EKM and 3D-FEM closely align for the OHH panels, with the eigenmodes exhibiting strong correspondence, indicating that 2D-EKM can accurately analyze the modal characteristics of OHH panels.
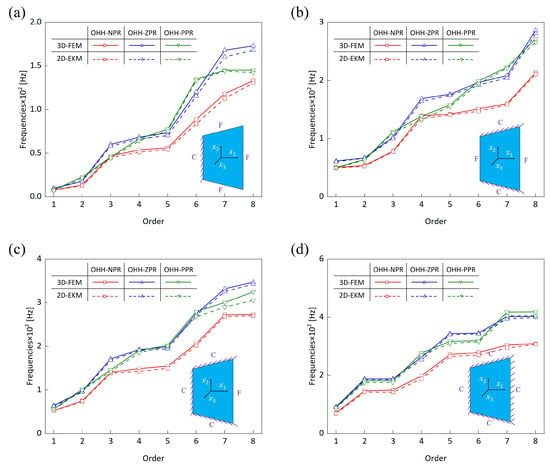
Figure 14.
Comparison of first eight eigenfrequencies of OHH panels across four distinct cases: (a) Case 3: CFFF, (b) Case 4: CCFF, (c) Case 5: CCCF, (d) Case 6: CCCC.
4.3. Efficiency Comparison
Figure 15a illustrates the mesh convergence of the OHH panels in Case 1. The 3D-FEM and 2D-EKM employ C3D10 and S4R elements, respectively. It is evident that as the element number rises, the maximum displacement of OHH panels under in-plane loading gradually converges. Remarkably, the mesh convergence in 2D-EKM (512 elements) is notably lower than that in 3D-FEM (256,325 elements). This disparity is a result of transforming the structural orthotropic properties of OHH panels into two-dimensional material orthotropy using the VAM, thereby reducing the model’s dimensionality. As a result, the necessity to capture intricate structural characteristics of the OHH panels is alleviated, leading to a substantial decrease in the required element number for convergence.
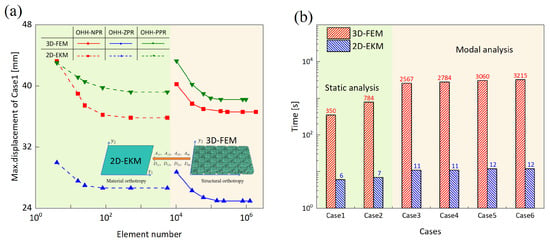
Figure 15.
Comparison of (a) mesh convergence of OHH panels in Case 1 and (b) time consumption for static and dynamic analysis in different models.
Figure 15b illustrates the time consumption for the static and dynamic analysis of OHH panels. It is evident that dynamic analysis requires more time than static analysis. This difference arises from the complexity of solving matrix eigenvalue problems in dynamic analysis to determine the panel’s eigenfrequencies and eigenmodes. The time required for 2D-EKM is significantly lower than that for 3D-FEM, with the former accounting for just 0.37% of the latter’s analysis time in Case 6. This discrepancy can be attributed to the reduced number of elements utilized in 2D-EKM, leading to a decrease in the degrees of freedom that need to be computed. As a result, this reduction in computational complexity alleviates the processing and memory requirements, consequently enhancing the overall computing efficiency.
5. Parameter Analysis
The hybrid honeycombs in two orthogonal directions of OHH have independent structural and material parameters. The previous studies in Section 4 have shown that the OHH-ZPR demonstrates optimal static and dynamic traits when and . Thus, this section examines the influence of geometric parameters such as wall thickness–height ratios (), height–length ratio (), and elastic modulus ratio of materials () on the equivalent properties and static–dynamic performance of the OHH-ZPR panel. Table 6 lists the range of variation in material and geometric parameters.

Table 6.
Range of variation in geometric and material parameters.
5.1. Wall Thickness–Height Ratio ()
Figure 16 illustrates the impact of the ratio on the equivalent properties, static deformations, and fundamental frequencies of the OHH-ZPR panel under different cases. It is evident that as the ratio increases, both the equivalent tensile and bending stiffness also increase. Specifically, the growth rates of and surpass significantly those of other equivalent properties. This effect is primarily due to the augmentation in the wall thickness of the hybrid honeycomb along the 1-direction (marked in yellow color) as the ratio escalates, resulting in a notable enhancement in the equivalent stiffness in that direction. The maximum deformations in Cases 1 and 2 gradually diminish with increasing , exhibiting reductions of 84% and 77%, respectively. This implies that augmenting can effectively bolster the resistance of OHH-ZPR against both in-plane and out-of-plane deformations.
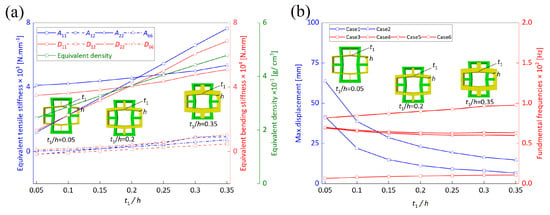
Figure 16.
Impact of the ratio on (a) equivalent stiffness and density, as well as (b) static deformations and fundamental frequencies of OHH-ZPR panel.
In dynamic analysis, the fundamental frequencies of Cases 3 to 5 remain relatively constant, while for Case 6 with CCCC boundary conditions, the fundamental frequency experiences a gradual rise. This behavior arises from the fact that for honeycomb panels with free edges, the boundary conditions may exert a more substantial influence on the eigenmodes than the increase in equivalent stiffness, leading to minimal alterations in the fundamental frequency. Conversely, in honeycomb panels constrained on all four sides, the rise in stiffness directly fortifies the overall vibration resistance of the panel, prompting an increase in the fundamental frequency.
5.2. Wall Thickness–Height Ratio ()
Figure 17 investigates the impact of the ratio on the equivalent properties, static deformations, and fundamental frequencies of the OHH-ZPR panel. The analysis reveals the significant anisotropy of OHH-ZPR, with the values of and being lower than those of and when the ratio is below 0.2. Conversely, when the ratio of exceeds 0.2, the opposite trend is observed. This phenomenon is attributed to the growth in the volume of the hybrid honeycomb in the 2-direction outpacing that of the 1-direction as the ratio increases, thereby enhancing the stiffness in the former direction.
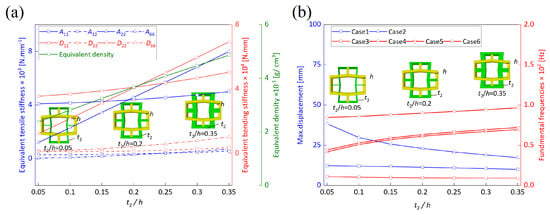
Figure 17.
Impact of the ratio on (a) equivalent stiffness and density, as well as (b) static deformations and fundamental frequencies of OHH-ZPR panel.
Considering that the boundaries of Cases 1 and 3 of OHH-ZPR are set as fixed at and other boundaries free (CFFF), changes in minimally affect and , resulting in slight alterations in the maximum deformation of Case 1 and the fundamental frequency of Case 3. As the ratio rises, the stiffnesses of and progressively increase, leading to a decrease in the maximum deformation of Case 2 and an elevation in the fundamental frequencies of Cases 4 to 6.
5.3. Height–Length Ratio ()
Figure 18 illustrates the impact of the ratio on the equivalent properties, static deformations, and fundamental frequencies of the OHH-ZPR panel. As the height–length ratio of OHH-ZPR increases, both its equivalent tensile and bending stiffness experience significant enhancement, with and showing linear growth, while and exhibit nonlinear growth. This behavior stems from the linear expansion of the cross-sectional area as a result of increased height h, leading to a proportional linear increase in tensile stiffness. Simultaneously, bending stiffness, dependent on the cross-sectional moment of inertia, displays nonlinear growth as a power function of the cross-section dimensions. The improved stiffness effectively enhances the OHH-ZPR panel’s resistance to deformation, resulting in a reduction in the maximum deformation of Cases 1 and 2 as increases, while the fundamental frequencies of Cases 3 to 6 increase accordingly. In particular, with escalating from 0.1 to 0.7, the maximum deformation of Case 2 decreases significantly by 97%, dropping from 98.5 to 2.62 mm.
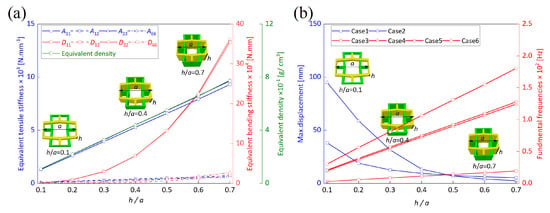
Figure 18.
Impact of the ratio on (a) equivalent stiffness and density, as well as (b) static deformations and fundamental frequencies of OHH-ZPR panel.
5.4. Elastic Modulus Ratio of Materials ()
Figure 19 examines the impact of varying material elastic modulus ratios on the equivalent properties, static deformation, and fundamental frequencies of OHH-ZPR panel. The study reveals that increasing the Young’s modulus of the hybrid honeycomb material in the 2-direction (marked in green) within the OHH-ZPR results in a linear augmentation of the equivalent tensile stiffness and bending stiffness in that specific direction, while maintaining other equivalent properties constant. For Cases 1 and 3, where the fixed boundaries are perpendicular to the 1-direction, fluctuations in have minimal effects on and , leading to little impact on their maximum deformation and fundamental frequencies. Conversely, Cases 2 to 6 exhibit higher sensitivity to stiffness variations in the 2-direction, resulting in decreased fundamental frequencies and reduced maximum deformations under the same loads.
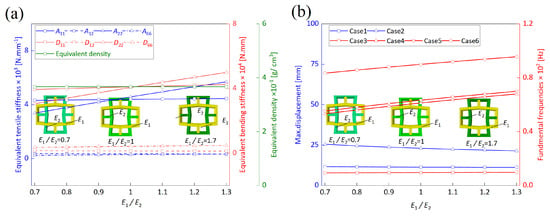
Figure 19.
Impact of the ratio on (a) equivalent stiffness and density, as well as (b) static deformations and fundamental frequencies of OHH-ZPR panel.
5.5. Summary of Parameter Analysis
To investigate the influence of various parameters on the equivalent properties and mechanical responses of the OHH-ZPR panel, a comparative analysis is conducted using dimensionless ratios (ratio of the variation in equivalent properties and mechanical response to the range of variation in each parameter), as illustrated in Figure 20. Specifically, increasing the ratios of four parameters enhances the equivalent properties of the OHH-ZPR panel. Moreover, the geometric parameters have a greater impact on the equivalent properties and mechanical responses of the OHH-ZPR panel compared to changes in the Young’s modulus ratio of materials. Particularly, the ratio makes a substantial contribution to the equivalent properties and mechanical responses of the OHH-ZPR panel, notably regarding the equivalent bending stiffness and . For each 1% increase in , and , respectively, increase by 275.62% and 281.93%.
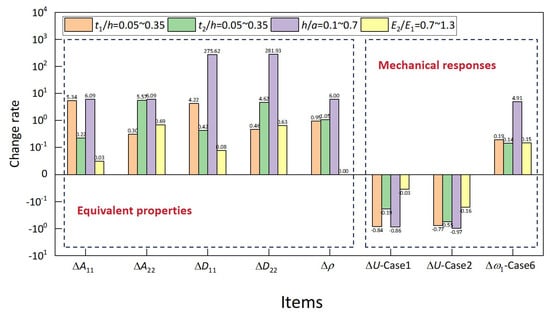
Figure 20.
Influence of various parameters on the equivalent properties and mechanical responses of OHH-ZPR panel.
In terms of the equivalent tensile stiffness and , augmenting the wall thickness of the hybrid honeycomb in the 1- and 2-directions effectively enhances the equivalent tensile stiffness in those directions, with a growth rate comparable to . Concerning mechanical responses, the increase in equivalent properties leads to reduced maximum deformations under in-plane tension in Case 1 and out-of-plane bending in Case 2, with the effects of and being the most significant. Notably, for the four-edge-supported OHH-ZPR panel in Case 6, increasing significantly elevates the fundamental frequency, effectively mitigating low-frequency resonance.
6. Conclusions
By utilizing the variational asymptotic method, a 2D equivalent Reissner–Mindlin model (2D-ERM) is developed to investigate the static characteristics of a sandwich panel with a three-dimensional orthogonal accordion structure (SP-3D-OAS). Through comparing the constructed 2D-ERM with the 3D FE model and conducting three-point bending tests on 3D-printed specimens, the accuracy of the developed 2D-ERM is validated. A parameter analysis is conducted to investigate the influence of different inclined angles on the equivalent stiffness of SP-3D-OAS. The key findings are as follows:
(1) The load-displacement curves of three-point bending confirm the accuracy of the 2D-ERM in predicting the out-of-plane behavior of SP-3D-OAS. By analyzing the in-plane and out-of-plane deformations of SP-3D-OAS under different boundary and loading conditions, the accuracy of 2D-ERM in analyzing the static characteristics of SP-3D-OAS is confirmed. The comparison between the computational efficiency of 3D-FEM and 2D-ERM indicates that excluding the pre- and post-processing stages, the computational time required for 2D-ERM is notably lower than that of 3D-FEM. This finding confirms the computational efficiency of the 2D-ERM.
(2) By adjusting the inclined angles and obtaining the contour plots of the equivalent stiffness, it is observed that except for the equivalent torsional stiffness, the other equivalent stiffnesses are minimized when all inclined angles are set to 90 degrees. Moreover, except for the equivalent torsional stiffness, all other equivalent stiffness values peak at the four corners of the contour plots. The adjustment of inclined angles has the most pronounced effect on the equivalent tensile and bending stiffness in the 1- and 2-directions.
(3) In comparing the stiffness of sandwich panels with different cellular core forms, the 3D-XYAS demonstrates the highest equivalent stiffness, followed by the 3D-OAS. However, upon examining specific stiffness values, it is revealed that the specific stiffness of the 3D-OAS is the highest. Furthermore, the SP-3D-OAS showcases relatively uniform local stress–strain distributions under different boundary and loading conditions.
Author Contributions
Individual contributions are as follows: conceptualization, Y.Z. (Yujie Zhou). Investigation and writing; analysis, Y.Z. (Yifeng Zhong) and Y.T. (Yuxin Tang) Revision, R.L. (Rong Liu) All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant Numbers, 51778088, 52073036).
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to subsequent analyses and publications.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chen, Y.; Zheng, B.B.; Fu, M.H. Doubly unusual 3D lattice honeycomb displaying simultaneous negative and zero Poisson’s ratio properties. Smart. Mater. Struct. 2018, 27, 045003. [Google Scholar] [CrossRef]
- Guo, M.F.; Yang, H.; Zhou, Y.M. Mechanical properties of 3D hybrid double arrow-head structure with tunable Poisson’s ratio. Aerosp. Sci. Technol. 2021, 119, 107177. [Google Scholar] [CrossRef]
- Fozdar, D.Y.; Soman, P.; Lee, J.W. Three-dimensional polymer constructs exhibiting a tunable negative Poisson’s ratio. Adv. Funct. Mater. 2011, 21, 2712–2720. [Google Scholar] [CrossRef]
- Lu, H.; Wang, X.; Chen, T. Design and quasi-static responses of a hierarchical negative Poisson’s ratio structure with three plateau stages and three-step deformation. Compos. Struct. 2022, 291, 115591. [Google Scholar] [CrossRef]
- Wang, F. Systematic design of 3D auxetic lattice materials with programmable Poisson’s ratio for finite strains. J. Mech. Phys. Solids. 2018, 114, 303–318. [Google Scholar] [CrossRef]
- Qiao, J.; Chen, C.Q. Analyses on the in-plane impact resistance of auxetic double arrowhead honeycombs. J. Appl. Mech. 2015, 82, 051007. [Google Scholar] [CrossRef]
- Ai, L.; Gao, X.L. Three-dimensional metamaterials with a negative Poisson’s ratio and a non-positive coefficient of thermal expansion. Int. J. Appl. Mech. 2018, 135, 101–113. [Google Scholar] [CrossRef]
- Kelkar, P.U.; Kim, H.S.; Cho, K.H. Cellular auxetic structures for mechanical metamaterials: A review. Sensors 2020, 20, 3132. [Google Scholar] [CrossRef] [PubMed]
- Du Plessis, A.; Razavi, N.; Benedetti, M. Properties and applications of additively manufactured metallic cellular materials: A review. Prog. Mater. Sci. 2022, 125, 100918. [Google Scholar] [CrossRef]
- Scarpa, F. Auxetic materials for bioprostheses. IEEE Signal Process. Mag. 2008, 25, 126–128. [Google Scholar] [CrossRef]
- Zhang, S.L.; Lai, Y.C.; He, X. Auxetic foam-based contact-mode triboelectric nanogenerator with highly sensitive self-powered strain sensing capabilities to monitor human body movement. Adv. Funct. Mater. 2017, 27, 1606695. [Google Scholar] [CrossRef]
- Alderson, A.; Rasburn, J.; Ameer-Beg, S. An auxetic filter: A tuneable filter displaying enhanced size selectivity or defouling properties. Ind. Eng. Chem. Res. 2000, 39, 654–665. [Google Scholar] [CrossRef]
- Grima, J.N.; Jackson, R.; Alderson, A. Do zeolites have negative Poisson’s ratios. Adv. Mater. 2000, 12, 1912–1918. [Google Scholar] [CrossRef]
- Wang, Y.C.; Lakes, R. Analytical parametric analysis of the contact problem of human buttocks and negative Poisson’s ratio foam cushions. Int. J. Solids Struct. 2002, 39, 4825–4838. [Google Scholar] [CrossRef]
- Ma, Y.; Scarpa, F.; Zhang, D. A nonlinear auxetic structural vibration damper with metal rubber particles. Smart Mater. Struct. 2013, 22, 084012. [Google Scholar] [CrossRef]
- Bertoldi, K.; Reis, P.M.; Willshaw, S. Negative Poisson’s ratio behavior induced by an elastic instability. Adv. Mater. 2010, 22, 361–366. [Google Scholar] [CrossRef]
- Cui, S.; Gong, B.; Ding, Q. Mechanical metamaterials foams with tunable negative poisson’s ratio for enhanced energy absorption and damage resistance. Materials 2018, 11, 1869. [Google Scholar] [CrossRef]
- Ai, L.; Gao, X.L. Metamaterials with negative Poisson’s ratio and non-positive thermal expansion. Compos. Struct. 2017, 162, 70–84. [Google Scholar] [CrossRef]
- Greaves, G.N.; Greer, A.L.; Lakes, R.S. Poisson’s ratio and modern materials. Nat. Mater. 2011, 10, 823–837. [Google Scholar] [CrossRef]
- Yu, X.; Zhou, J.; Liang, H. Mechanical metamaterials associated with stiffness, rigidity and compressibility: A brief review. Prog. Mater. Sci. 2018, 94, 114–173. [Google Scholar] [CrossRef]
- Huang, C.; Chen, L. Negative Poisson’s ratio in modern functional materials. Adv. Mater. 2016, 28, 8079–8096. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Dong, L.; Lakes, R. A unit cell structure with tunable Poisson’s ratio from positive to negative. Mater. Lett. 2016, 164, 456–459. [Google Scholar] [CrossRef]
- Li, D.; Ma, J.; Dong, L.; Lakes, R.S. A bi-material structure with Poisson’s ratio tunable from positive to negative via temperature control. Mater. Lett. 2016, 181, 285–288. [Google Scholar] [CrossRef]
- Yin, X.; Gao, Z.Y.; Zhang, S. Truncated regular octahedral tensegrity-based mechanical metamaterial with tunable and programmable Poisson’s ratio. Int. J. Mech. Sci. 2020, 167, 105285. [Google Scholar] [CrossRef]
- Lyu, S.N.; Qin, B.; Deng, H.C. Origami-based cellular mechanical metamaterials with tunable Poisson’s ratio: Construction and analysis. Int. J. Mech. Sci. 2021, 212, 106791. [Google Scholar] [CrossRef]
- Pagliocca, N.; Uddin, K.Z.; Anni, I.A. Flexible planar metamaterials with tunable Poisson’s ratios. Mater. Des. 2022, 215, 110446. [Google Scholar] [CrossRef]
- Liu, Q.; Zhao, Y. Prediction of natural frequencies of a sandwich panel using thick plate theory. J. Sandw. Struct. Mater. 2001, 3, 289–309. [Google Scholar] [CrossRef]
- Liu, Q.; Zhao, Y. Effect of soft honeycomb core on flexural vibration of sandwich panel using low order and high order shear deformation models. J. Sandw. Struct. Mater. 2007, 9, 95–108. [Google Scholar] [CrossRef]
- Kant, T.; Kommineni, J.R. Large amplitude free vibration analysis of cross-ply composite and sandwich laminates with a refined theory and C finite elements. Comput. Struct. 1994, 50, 123–134. [Google Scholar] [CrossRef]
- Tanimoto, Y.; Nishiwaki, T.; Shiomi, T. A numerical modeling for eigenvibration analysis of honeycomb sandwich panels. Compos. Interfaces 2001, 8, 393–402. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, J. Numerical and theoretical analysis of honeycomb structure filled with circular aluminum tubes subjected to axial compression. Compos. Part B Eng. 2019, 165, 626–635. [Google Scholar] [CrossRef]
- Kumar, A.; Muthu, N.; Narayanan, R.G. Equivalent orthotropic properties of periodic honeycomb structure: Strain-energy approach and homogenization. Compos. Part B Eng. 2023, 19, 137–163. [Google Scholar] [CrossRef]
- Saha, G.C.; Kalamkarov, A.L.; Georgiades, A.V. Effective elastic characteristics of honeycomb sandwich composite shells made of generally orthotropic materials. Compos. Part A Appl. Sci. Manuf. 2007, 38, 1533–1546. [Google Scholar] [CrossRef]
- Sorohan, Ş.; Sandu, M.; Sandu, A.; Constantinescu, D.M. Finite element models used to determine the equivalent in-plane properties of honeycombs. Mater. Today Proc. 2016, 3, 1161–1166. [Google Scholar] [CrossRef]
- Saidi, A.; Coorevits, P.; Guessasma, M. Homogenization of a sandwich structure and validity of the corresponding two-dimensional equivalent model. J. Sandw. Struct. Mater. 2005, 7, 7–30. [Google Scholar] [CrossRef]
- Zhong, Y.F.; Qin, W.; Yu, W. Variational asymptotic homogenization of magnetoelectro-elastic materials with coated fibers. Compos. Struct. 2015, 133, 300–311. [Google Scholar] [CrossRef]
- Cesnik, C.E.; Hodges, D.H. VABS: A new concept for composite rotor blade crosssectional modeling. J. Am. Helicopter Soc. 1997, 42, 27–38. [Google Scholar] [CrossRef]
- Peng, X.; Zhong, Y.F.; Shi, Z. Global buckling analysis of composite honeycomb sandwich plate with negative Poisson’s ratio (CSP-RHC) using variational asymptotic equivalent model. Compos. Stuct. 2021, 264, 113721. [Google Scholar]
- Peng, X.; Zhong, Y.F.; Shi, Z. Free flexural vibration analysis of composite sandwich plate with reentrant honeycomb cores using homogenized plate model. J. Sound Vib. 2022, 529, 116955. [Google Scholar] [CrossRef]
- Miao, S.Q.; Zhong, Y.F.; Zhou, Y.J. Equivalent single-layer model for hierarchical diamond honeycomb sandwich panels using variational asymptotic method. Compos. Struct. 2024, 339, 118149. [Google Scholar]
- Lee, C.Y.; Yu, W.B. Homogenization and dimensional reduction of composite plates with in-plane heterogeneity. Int. J. Solids Struct. 2011, 48, 1474–1484. [Google Scholar] [CrossRef]
- Grima, J.N.; Oliveri, L.; Attard, D. Hexagonal honeycombs with zero Poisson’s ratios and enhanced stiffness. Adv. Eng. Mater. 2010, 12, 855–862. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).