Next Article in Journal
Study on Strength Prediction and Material Scheme Optimization for Modified Red Mud Based on Artificial Neural Networks
Next Article in Special Issue
Accurate Dynamic Analysis Method of Cable-Damper System Based on Dynamic Stiffness Method
Previous Article in Journal
A Comprehensive Approach to Facade Design for Preventing Rainwater Penetration: Implementation in Spanish Regions
Previous Article in Special Issue
On-Site Measuring Robot Technology for Post-Construction Quality Assessment of Building Projects
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Buildings
Volume 14
Issue 11
10.3390/buildings14113543
buildings-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Study on Cubic Stiffness Nonlinear Energy Sink Controlling Dynamic Responses of Multi-Degree-of-Freedom Structure by Shake Table Tests

by
Qinhua Wang
1,2,*,
Xueshuang Yi
2,
Dongxu Yang
2 and
Yi Tang
1,3
1
State Key Laboratory of Building Safety and Built Environment, Beijing 100013, China
2
School of Civil Engineering and Architecture, Southwest University of Science and Technology, Mianyang 621010, China
3
China Academy of Building Research, Beijing 100013, China
*
Author to whom correspondence should be addressed.
Buildings 2024, 14(11), 3543; https://doi.org/10.3390/buildings14113543
Submission received: 2 October 2024 / Revised: 16 October 2024 / Accepted: 18 October 2024 / Published: 6 November 2024
(This article belongs to the Special Issue Advances and Applications in Structural Vibration Control)
Browse Figures
Versions Notes

Abstract

:
A nonlinear energy sink (NES) has such advantages as controlling broader band responses and better robustness than conventional control devices like tuned mass dampers (TMDs). In this research, a cubic stiffness NES mitigating the dynamic responses of a multi-degree-of-freedom structure under white noise, harmonic and seismic excitations was tested using a shake table, and the influences of the parameters of the NES on vibration mitigation effects were investigated. The test results indicate that the NES has the same vibration mitigation effects on the acceleration responses under the white noise and harmonic excitations as TMDs, even though the mass ratio of the NES is less than that of a TMD. The average control effects of the NES on the acceleration responses of the structure under the effect of 100 seismic waves are better than those of a TMD, which indicates that an NES has better robustness than a TMD.

1. Introduction

Various passive vibration control devices have been proposed to absorb vibration energy from a primary structure and mitigate the dynamic responses of the structure in the past decades [1]. In the civil engineering field, tuned mass dampers (TMDs) are widely applied for practical engineering around the world to control the dynamic responses of structures [2], such as the Hancock building (241 m) [3] in Boston, the Taibei 101 building (508 m high) [4], the Shanghai Center Tower (632 m high) [5] and the Ping-An Finance Center (600 m high) [6], due to their effectiveness in vibration mitigation and low maintenance costs. However, TMDs have a disadvantage because of their narrow tuning band; hence, their control robustness decreases as the primary structure is subjected to broadband excitations or the dynamic characteristics of the primary characteristics change. The nonlinear energy sink (NES) [7], composed of a nonlinear spring, damping element and auxiliary mass, may overcome the disadvantages of TMDs. The key difference between NESs and TMDs is the nonlinear stiffness aspect of NESs, which means their response varies in a complex manner. This nonlinear characteristic allows NESs to effectively engage with a wide range of frequencies, enabling them to resonate across a broad spectrum [8]. NESs require little mass to achieve excellent vibration mitigation, but they need a limited initial energy range to be effective [9,10]. A lot of research on the various types of NES, controlling the dynamic responses of structures, has been carried out using theoretical, numerical and test methods. Gourdon et al. [11] studied the vibration response of an eight-story structure with a fundamental frequency of 0.83 Hz controlled by an NES under seismic and stochastic excitations through numerical analysis. The numerical results show that the NES had excellent robustness. Nucera et al. [12,13] used an attached vibro-impact NES (VI NES) to control the vibration response of a three-story structure with the first natural frequency of 4.82 Hz. The results of the shaking table test and numerical simulation consistently verified that the VI NES showed good vibration control effects and excited higher structure modes under seismic excitations. Vaurigaud et al. [14] proposed a method to optimize the NES parameters. The feasibility of this method was verified experimentally and by the numerical simulation of a four-story structure controlled by two parallel NES structures under harmonic excitation. Wierschem et al. [15,16] used NES to control the vibration response of a nine-degree-of-freedom structure with a fundamental frequency of 1.74 Hz under impact loads. These studies show that NESs have excellent vibration mitigation effects and can quickly reduce the maximum response of a structure. Luo et al. [17] studied two types of NES mitigating the dynamic responses of a structure through numerical simulation and shaking table tests. Their investigation demonstrates that the combined use of two different NES systems has certain vibration mitigation effects on different earthquake excitations. Wierschem et al. [18] installed a type III NES on a six-degree-of-freedom structure subjected to impact forces and carried out tests by shaking table and numerical simulation. Their results show that the type III NES can reduce most of the vibration responses of the structure. Wang et al. [19] employed a track nonlinear energy sink (track NES) and a single-sided vibro-impact track nonlinear energy sink (SSVI track NES) to mitigate the vibration responses of a 32-story steel structure with a fundamental frequency of 0.24 Hz under the action of an earthquake. The numerical results from their study show that track NES and SSVI track NES show excellent seismic reduction effects and are suitable as control devices for high-rise buildings. Through experimental testing and numerical analysis, Wang et al. [20] evaluated the vibration mitigation performance of a two-story structure with a fundamental frequency of 1.63 Hz controlled by track nonlinear energy sink under seismic and pulse excitations. Analytical and numerical studies indicate that the vibration responses of the structure were reduced faster compared to when a conventional NES was used. Later, Wang et al. [21] proposed an asymmetric nonlinear energy sink (Asym NES) and applied it to control the vibration responses of a three-degree-of-freedom structure and a six-degree-of-freedom structure under seismic excitations. Their research shows that Asym NES has strong robustness to structural frequency changes. Following on their research, Wang et al. [22] used track bistable nonlinear energy sink (track BNES) to control the vibration response of this structure under impulse and earthquake excitations; the results show that track BNES shows better robustness than Asym NES when the frequency of the main structure changes. Yang et al. [23] carried out a shaking table test in order to study the vibration mitigation effects of an NES on the dynamic responses of a five-story concrete structure with a fundamental frequency of 5.0 Hz in the X direction and 4.75 Hz in the Y direction under earthquake action. The NES played a good role in reducing vibration responses and showed its robustness. Ndemanou et al. [24] studied the vibration response of super-high-rise buildings controlled by an NES under wind loads through numerical simulation. Their results demonstrate that the control rate of the NES on the top floor vibration response of the building was over 79%, which is better than that of a TMD. Wang et al. [25] analyzed the vibration responses of a 300-meter-high building controlled by a nonlinear energy sink inerter (NESI) under wind loads. Their numerical simulation results show that the vibration control effect and robustness of an NESI are better than that of a tuned mass damper inerter (TMDI).
However, most of the previous work focused on the NES controlling dynamic responses of structures under only one type of excitation. Some structures, like high-rise buildings, may be subjected to different types of loads, for instance, earthquake excitations, turbulent buffeting (a broadband stochastic process) and vortex-shedding aerodynamic forces (similarly, harmonic excitations) during their designed lifespan. In this research, an NES controlling a multi-degree-of-freedom structure under white noise, harmonic excitations and earthquake excitations was designed and tested by the shake table method. The effects of parameters of the NES on vibration mitigation effects of the structure under different types of excitations were investigated and compared with that of a TMD.

2. Test Introduction

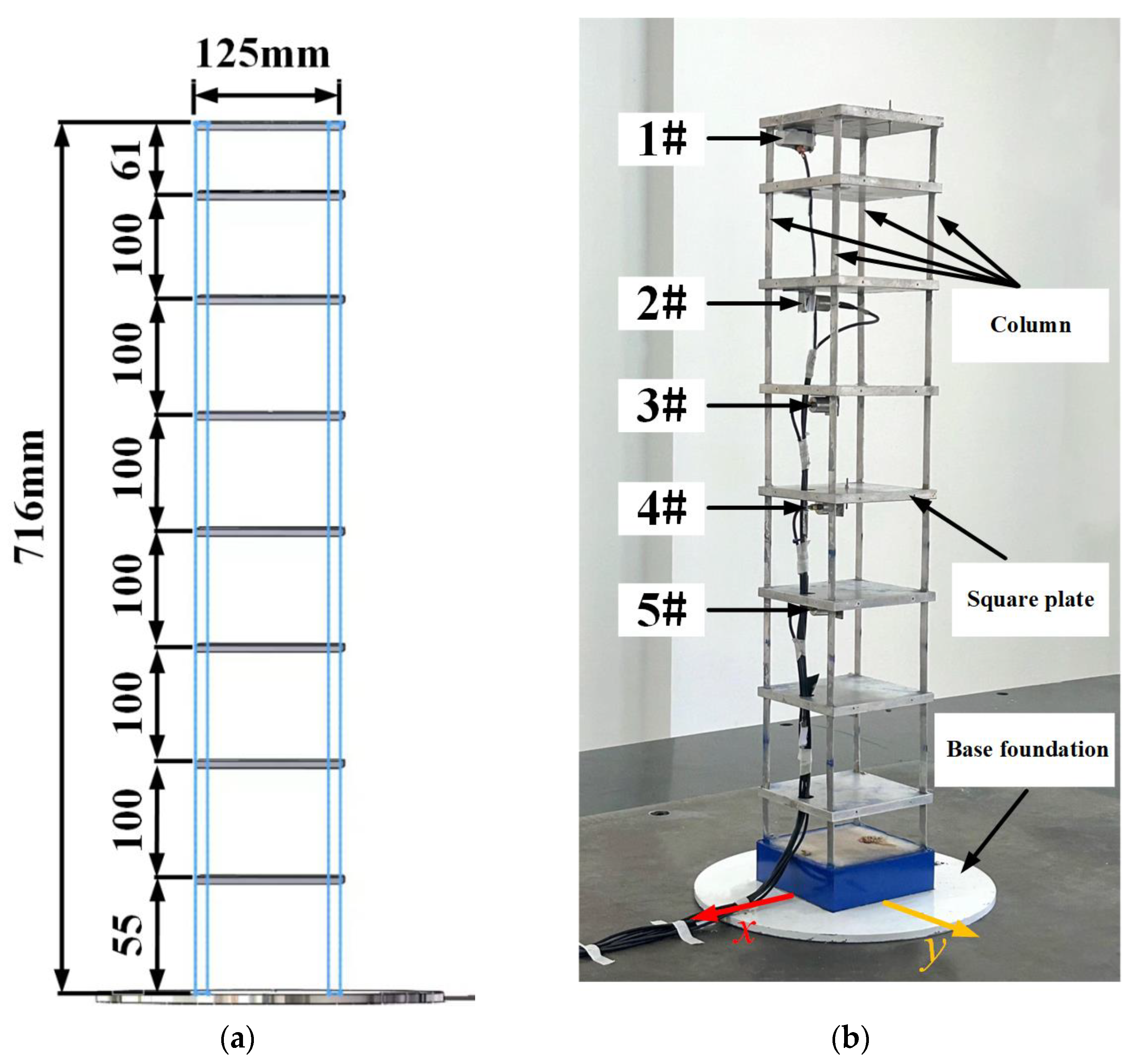
2.1. Introduction of Multi-Degree-of-Freedom Structure Model

As shown in Figure 1a, the multi-degree-of-freedom structure model is composed of eight rigid plates, four elastic columns with a rectangle cross-section, which simulated the stiffness of the structure, and a base foundation. The plates, columns and base foundation are joined by rigid connection. The model is 125 mm in width and 716 mm in height, as shown in Figure 1b. The total mass of the model is 3.29 kg. The stiffness of the model is larger at the y-axis direction than that at the x-axis, and the dynamic responses at the x-axis may be greater than the responses at the y-axis; hence, the NES is designed to control the dynamic responses of the model at the x-axis. The five sensors from 1# to 5# were distributed along the height of the model, as shown in Figure 1b, to measure acceleration responses at the x-axis of the model according to the standard [26]. The free vibration tests in Figure 2 indicate that the first natural frequency of the model is 5.88 Hz at the x-axis and the corresponding damping ratio is 0.4%.

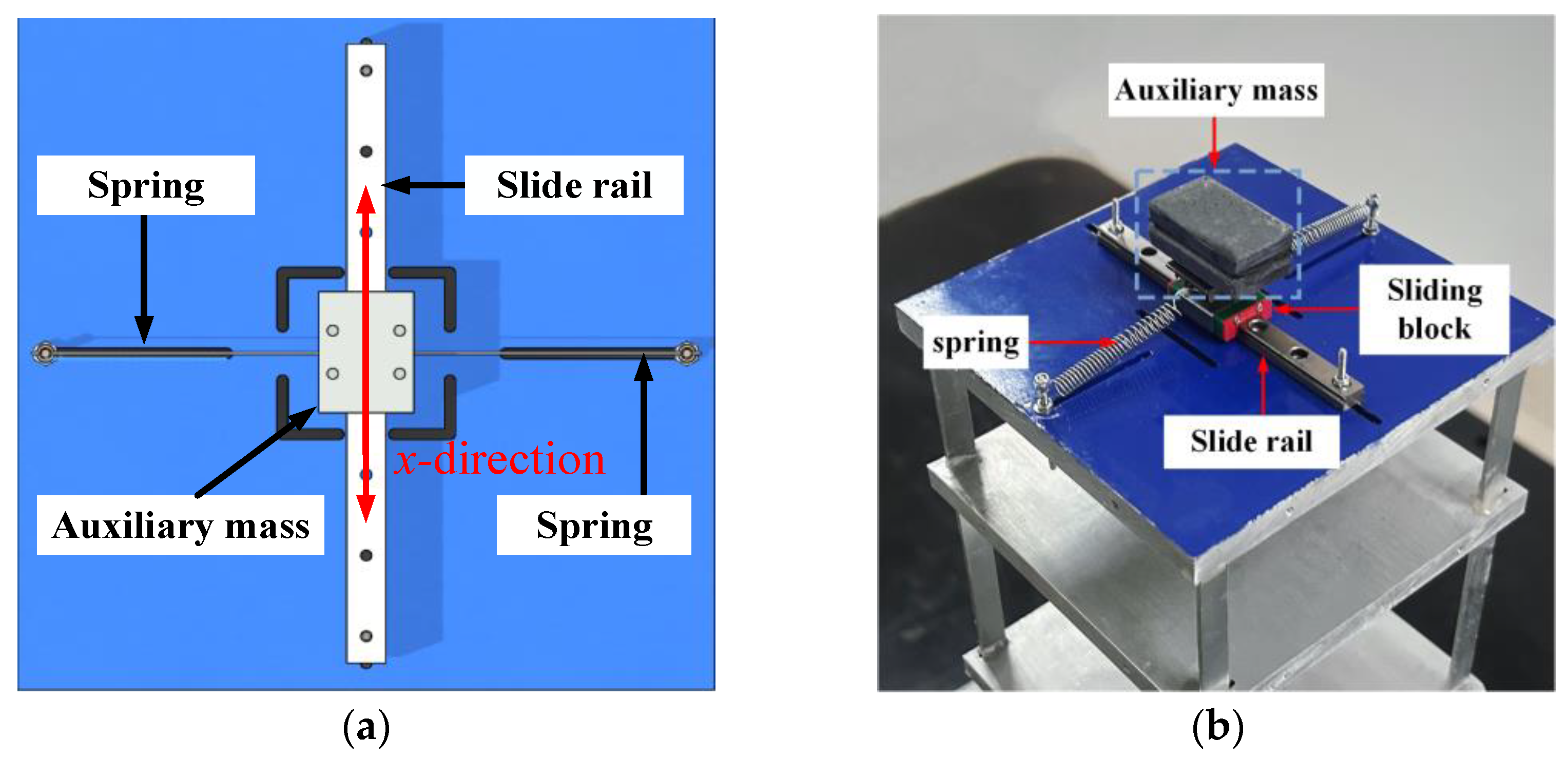
2.2. Model of NES Controlling Multi-Degree-of-Freedom Structure

As shown in Figure 3a, the NES comprises a sliding rail, a pair of springs and an auxiliary mass, which can freely move along the x-axis. The NES was installed on the top floor of the model by rigid connection. The stiffness of the spring and auxiliary mass in the NES can be changed to investigate the vibration mitigation effects of the different parameters of the NES on the dynamic responses of the model under different excitations. Three sets of auxiliary mass, e.g., 100 g, 150 g and 200 g, were adopted in this research. The corresponding mass ratio μ, which is the ratio of the auxiliary mass of the NES to the mass of the structure, was μ1 = 3.0%, μ2 = 4.5% and μ3 = 6.0%, respectively. The stiffness of the NES was set as k1 = 105.0 N/m and k2 = 330.0 N/m, respectively. The variation in auxiliary mass of the NES changes the natural frequency of the structure–NES system, when the NES is locked. Figure 4 shows the frequency response function of the structure–NES system when the NES is locked. It indicates that the natural frequencies are 5.71 Hz, 5.64 Hz and 5.57 Hz when μ1, μ2 and μ3 are equal to 3.0%, 4.5% and 6.0%, respectively. Table 1 gives the first three natural frequencies of the system when the NES locked. The first three natural frequencies are decreasing as the masses of the system are increasing.

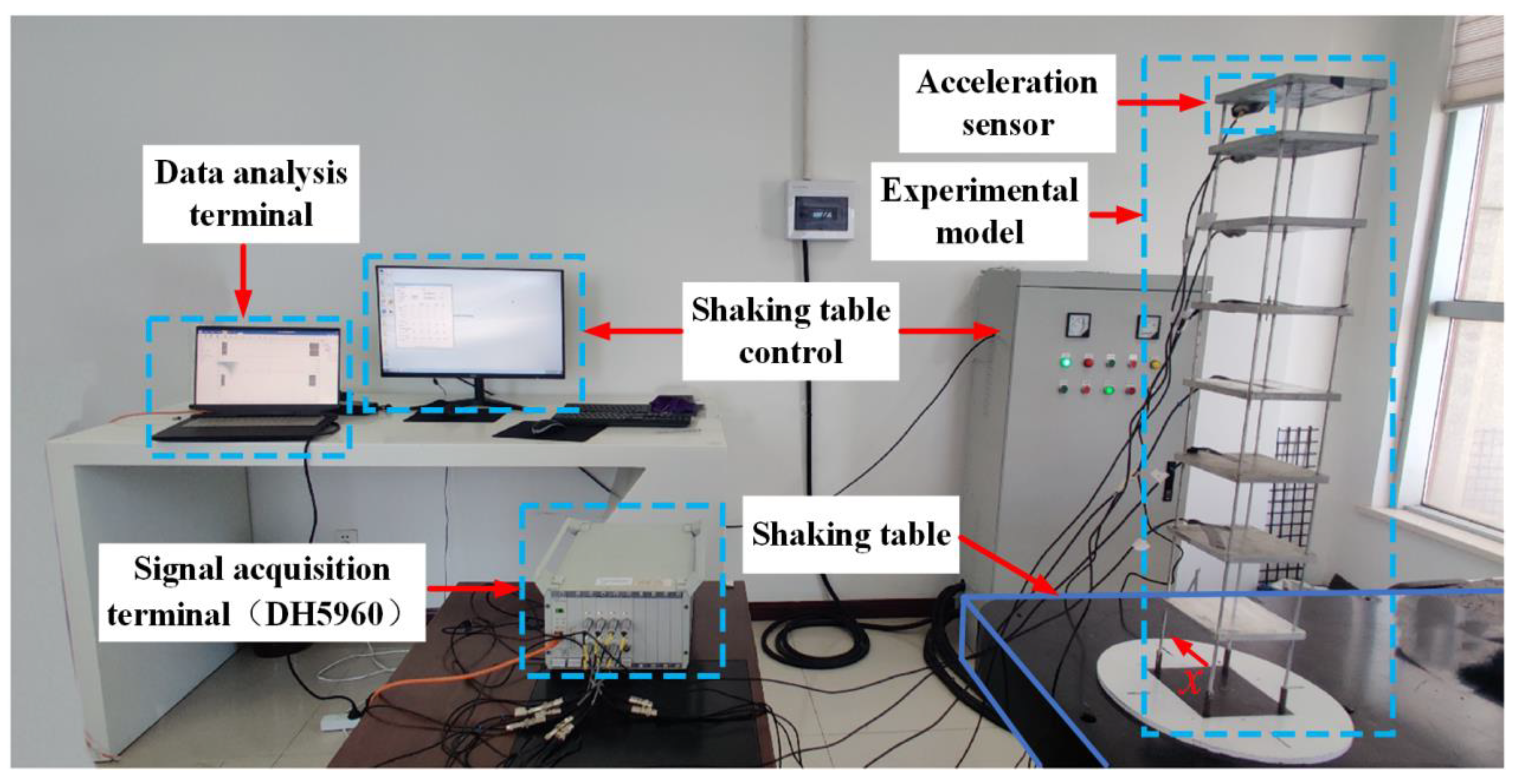
2.3. Shake Table Tests of NES Controlling MDOF Structure

The MDOF of the structural model was installed on a shake table, which was controlled by a computer terminal, and accelerometers on the model and data acquisition device were used to measure and collect the dynamic responses of the model, as shown in Figure 5. The shake table has six degrees of freedom, and the platform is 2.5 m in length and 1.5 m in width. The range of working frequencies of the shake table is from 0.0 Hz to 30.0 Hz, and the parameters of the shake table are shown in Table 2. The model was installed on the shake table as shown in Figure 6. The time histories of the dynamic responses were measured by the accelerometers at 1000.0 samples per second.
Tests of the NES with six sets of parameters controlling the dynamic responses of the structure were carried out to explore its optimal vibration mitigation effects. The corresponding tests of a TMD with optimal parameters were performed to compare its vibration mitigation effects with those of the NES. These test conditions are shown in Table 3. In Table 3, the mass ratios μ1, μ2 and μ3 are 3.0%, 4.5% and 6.0%, respectively. The stiffness values k1 and k2 are 105.0 N/m and 330.0 N/m. The frequency ratio f and the mass ratio of the TMD are 0.98 and 4.5%, respectively.

3. Results and Discussion

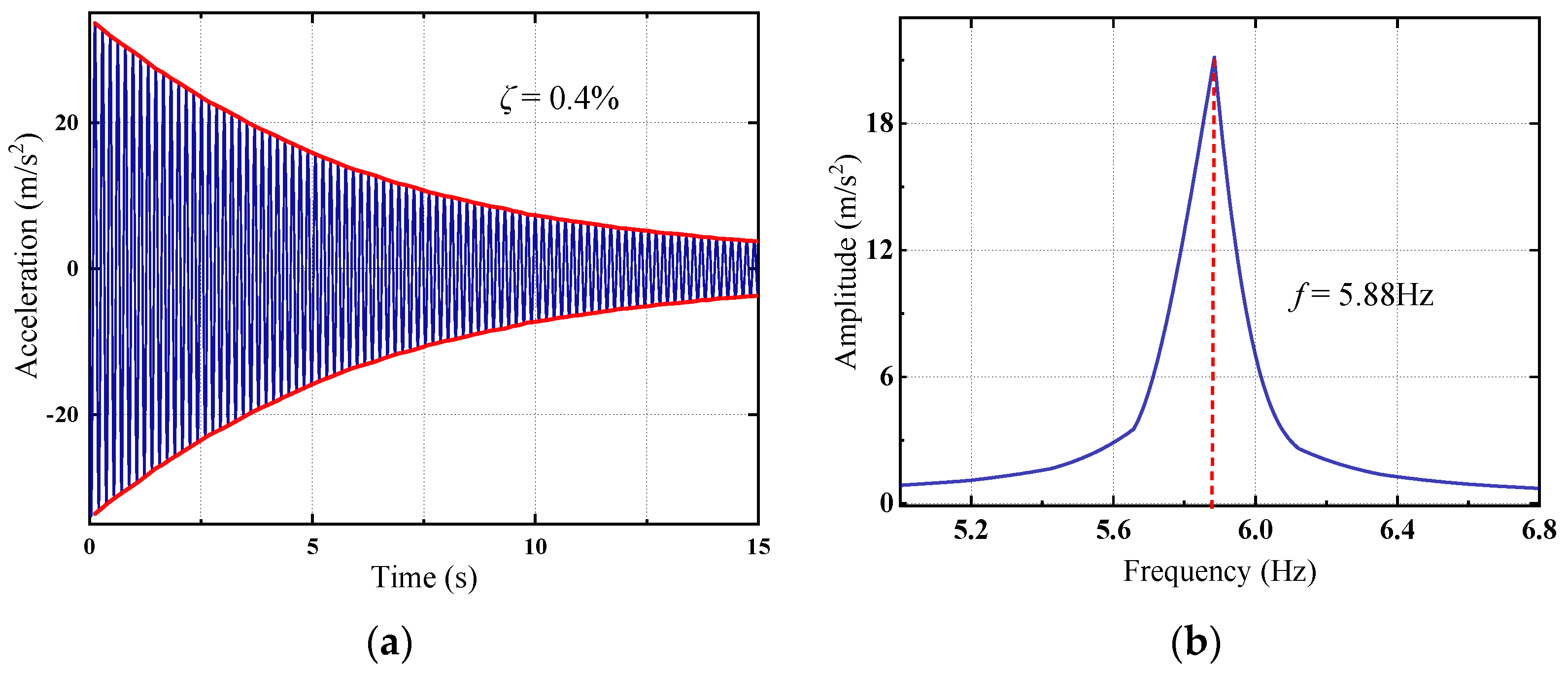
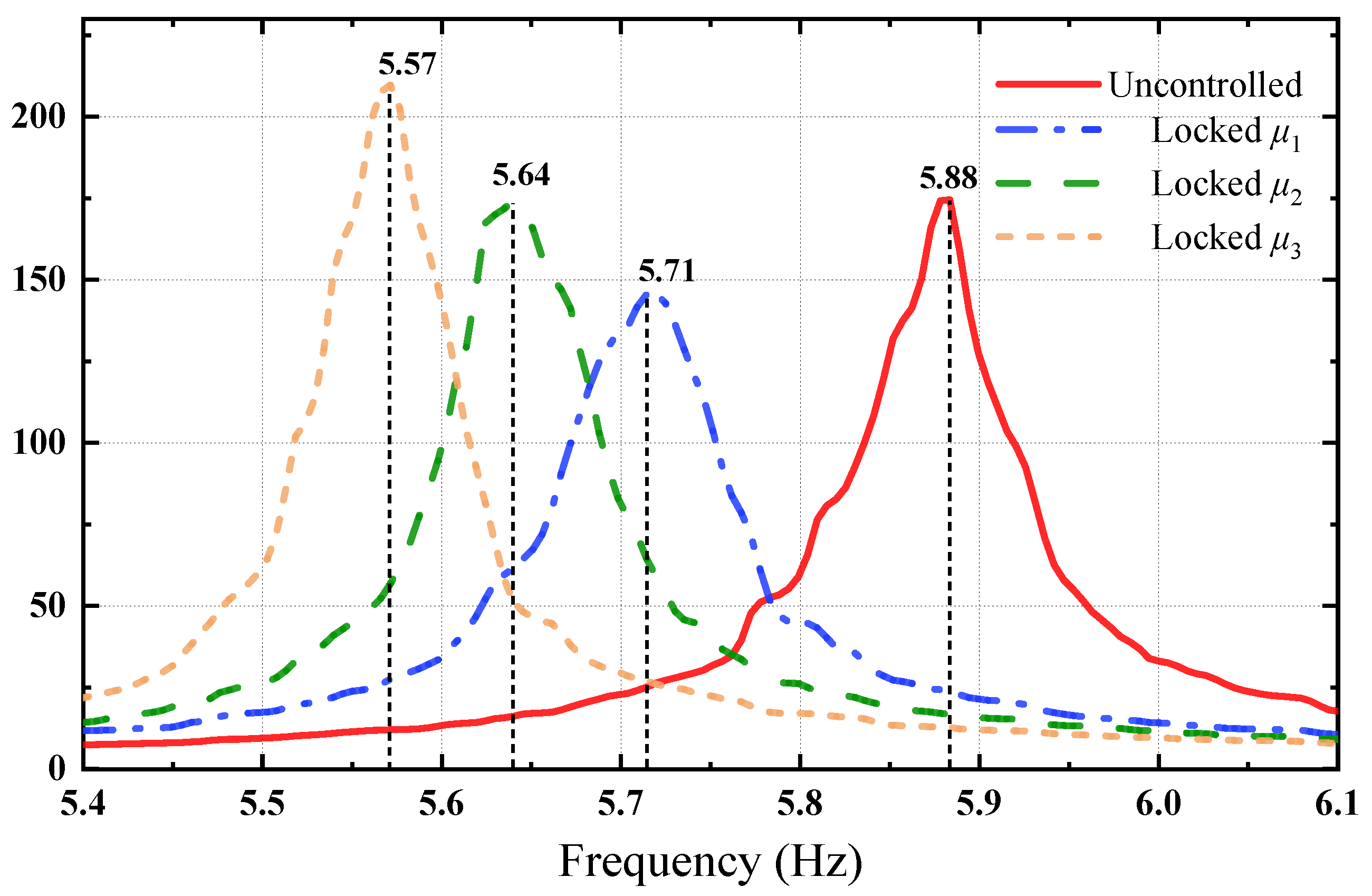
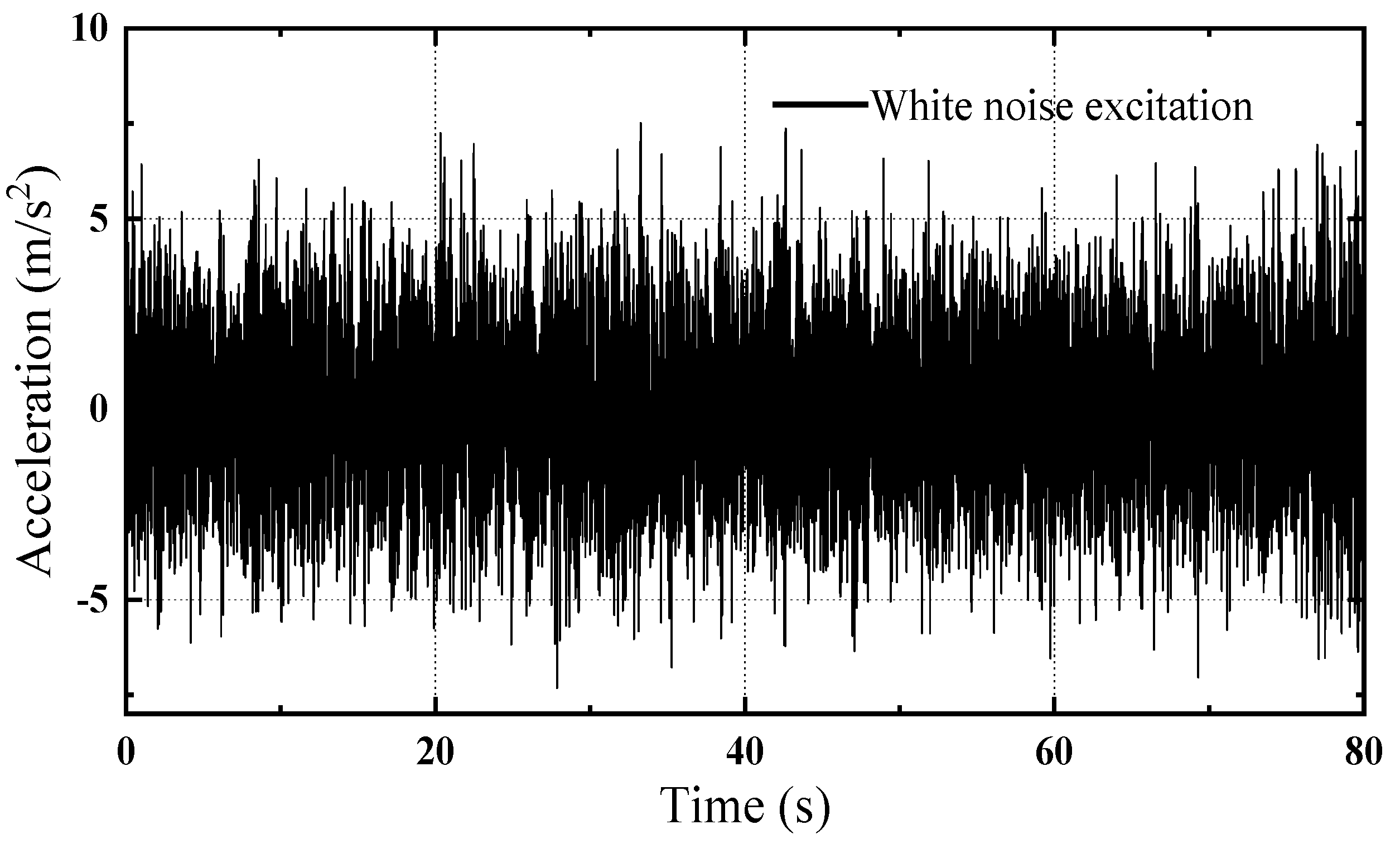
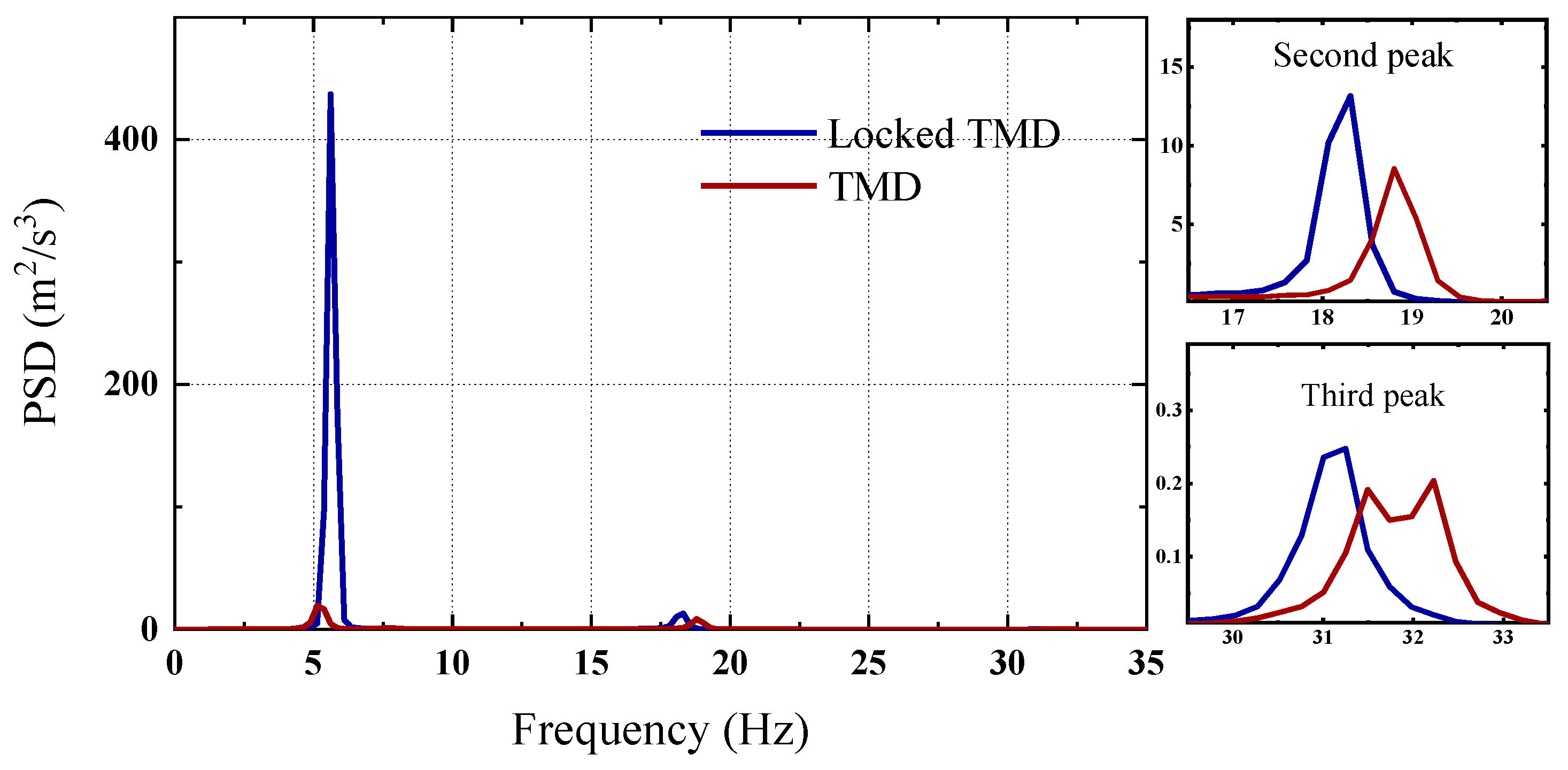
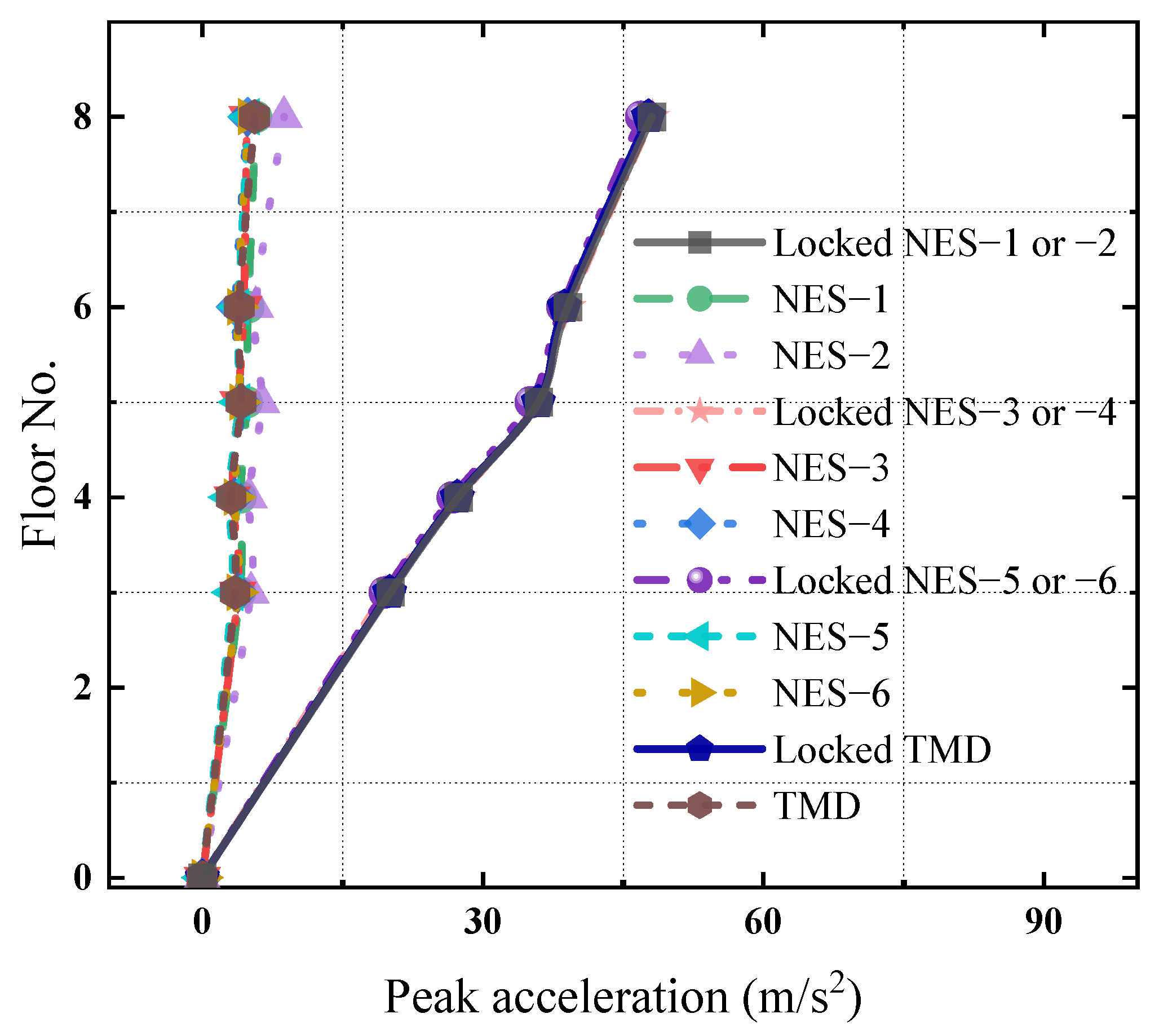
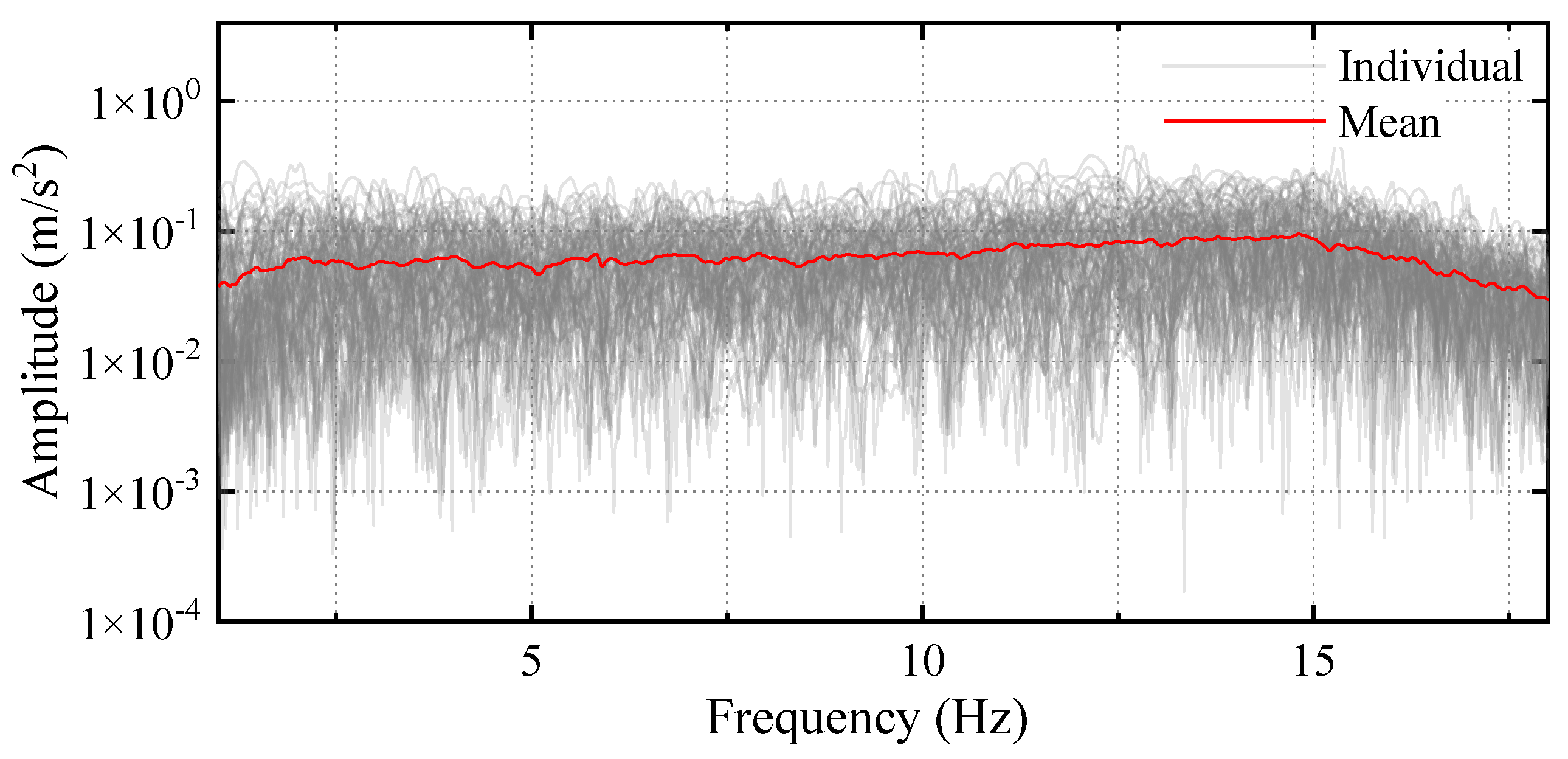
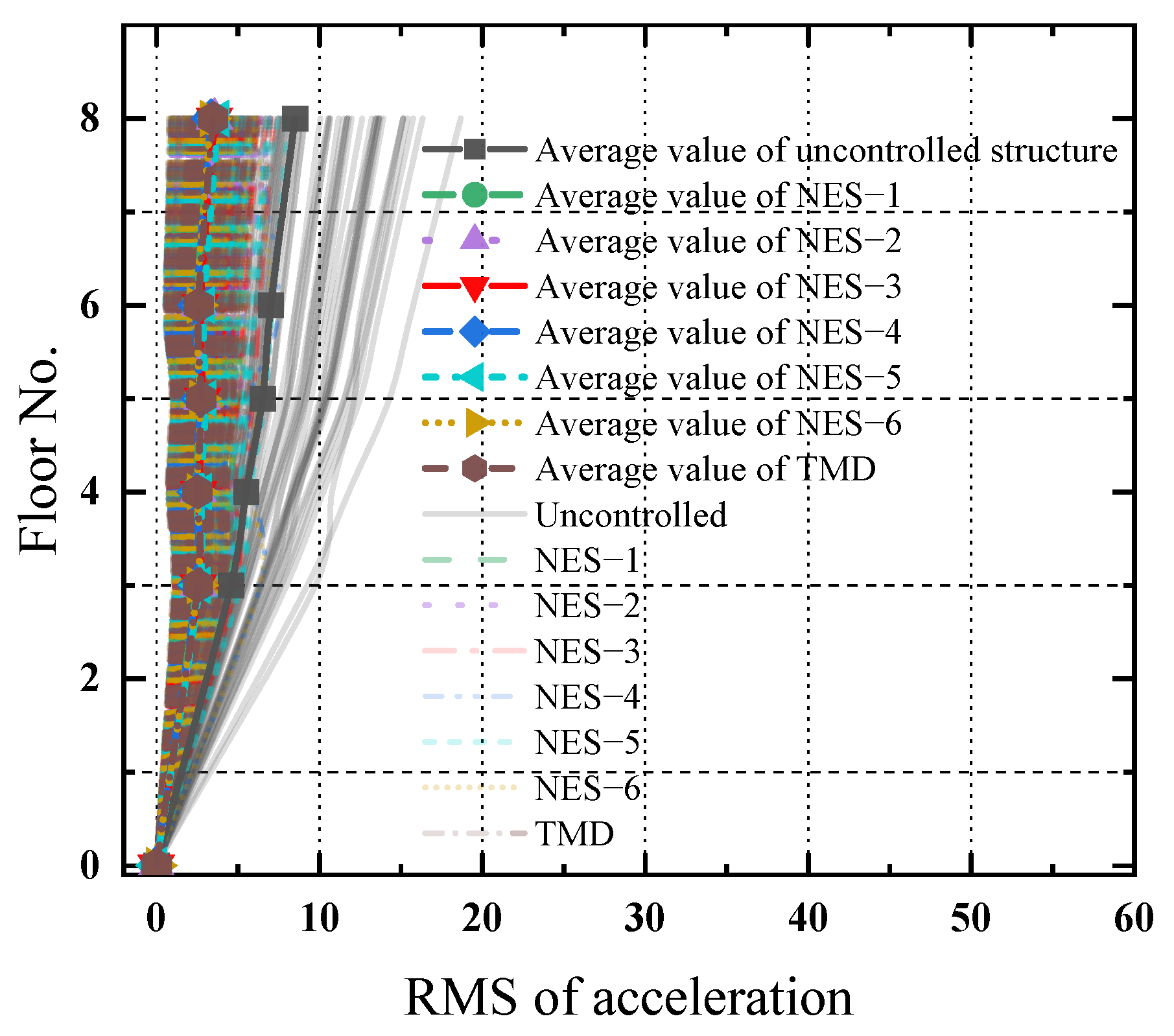
3.1. NES Mitigation Effects on Dynamic Responses of MDOF Structure Under White Noise Excitations

The NES and TMD controlling the dynamic responses of the MODF structure under the white noise excitations, with peak acceleration being 7.5 m/s2, as shown in Figure 7, were investigated in this section. Figure 8 presents the time history of acceleration responses on the top of the structure with and without NES or TMD installation under white noise excitations. Figure 8 indicates that the NES and TMD can dramatically decrease the acceleration responses of the structure compared with the uncontrolled structure.
The time histories of these acceleration responses of the structure with locked and unlocked TMD were analyzed in the frequency domain by power spectrum density (PSD), as shown in Figure 9. Figure 9 indicates that the TMD can control the dynamic responses corresponding to the first vibration mode and cannot decrease the responses of the higher vibration modes. Figure 10 presents the results of the NES controlling acceleration responses on the top of the structure in the frequency and time domain by wavelet transform. Figure 10 demonstrates that the energy of the dynamic responses of the structure comes entirely from the first vibration mode when the NES is locked. The energy of the dynamic responses corresponding to the first vibration mode were reduced and the dynamic responses corresponding to higher vibration modes appeared as the NES was working. Compared with the results in Figure 10b,c,e,f,h,i, the NES with parameters μ2 and k2 in Figure 10f has the best mitigation effects on the acceleration responses on the top of the structure. The maximum values of the acceleration responses were investigated based on the time histories of the responses measured by the acceleration sensors 1# to 5# shown in Figure 1b. Figure 11 shows the variation in the maximum values along the height of the structure, and that the NES and TMD can effectively mitigate the maximum values of the acceleration responses on different heights of the structure. With regard to the responses on the top in Figure 11, the vibration mitigation ratio of these control devices reaches about 50.0%; NES–4 has the best mitigation effects among these control devices, which is consistent with the result in Figure 10, and its vibration mitigation ratio is 56.1%.

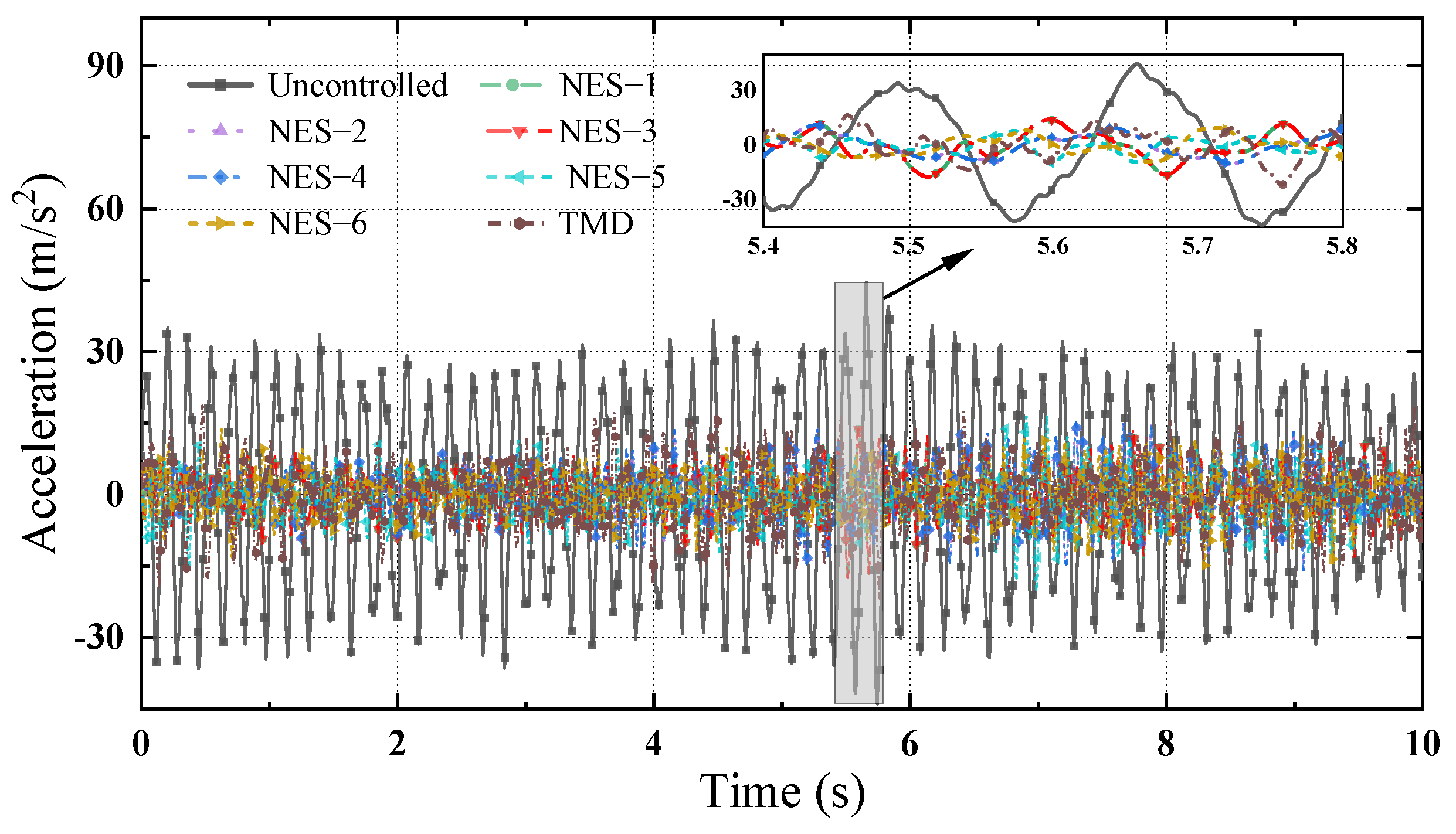
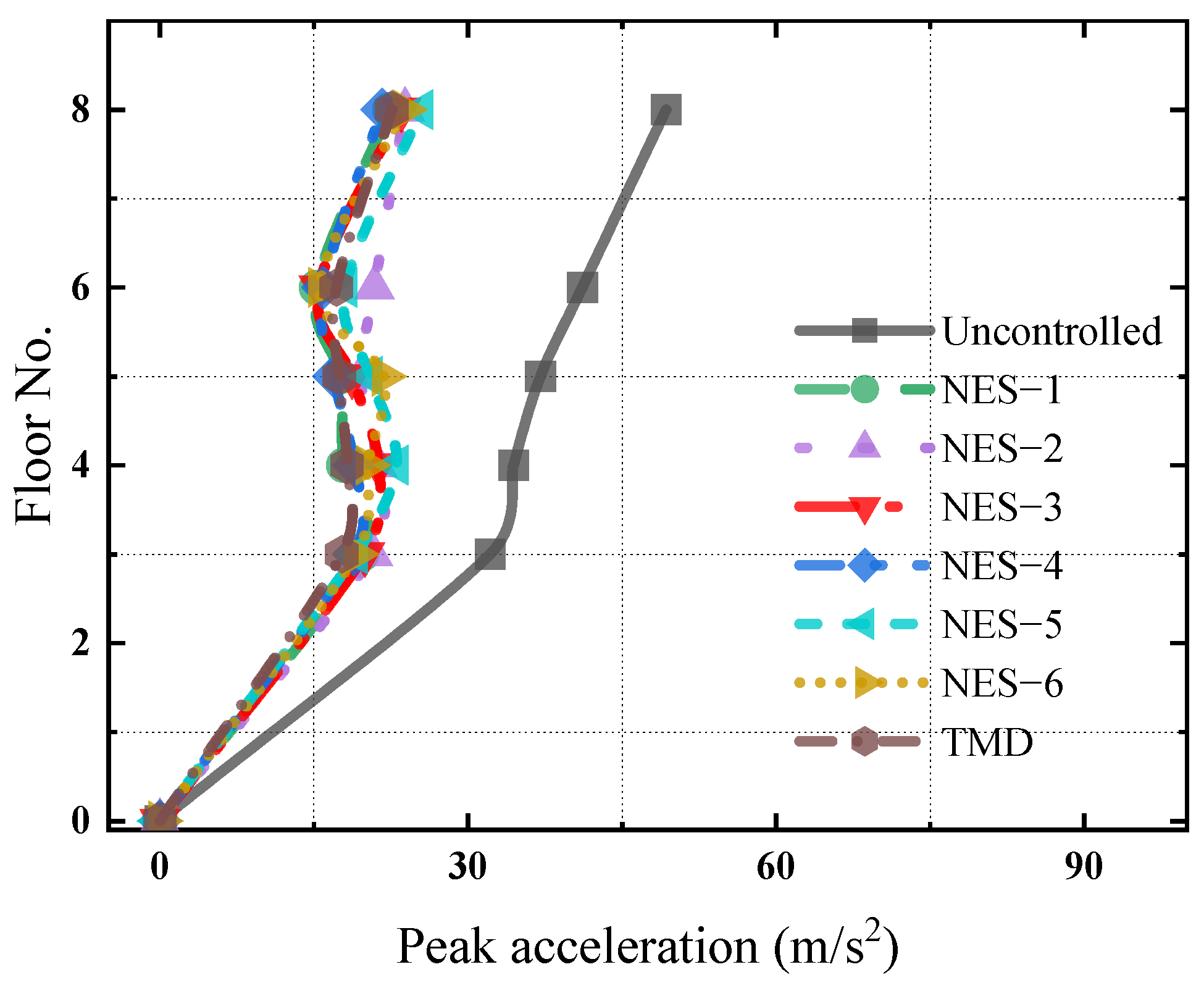
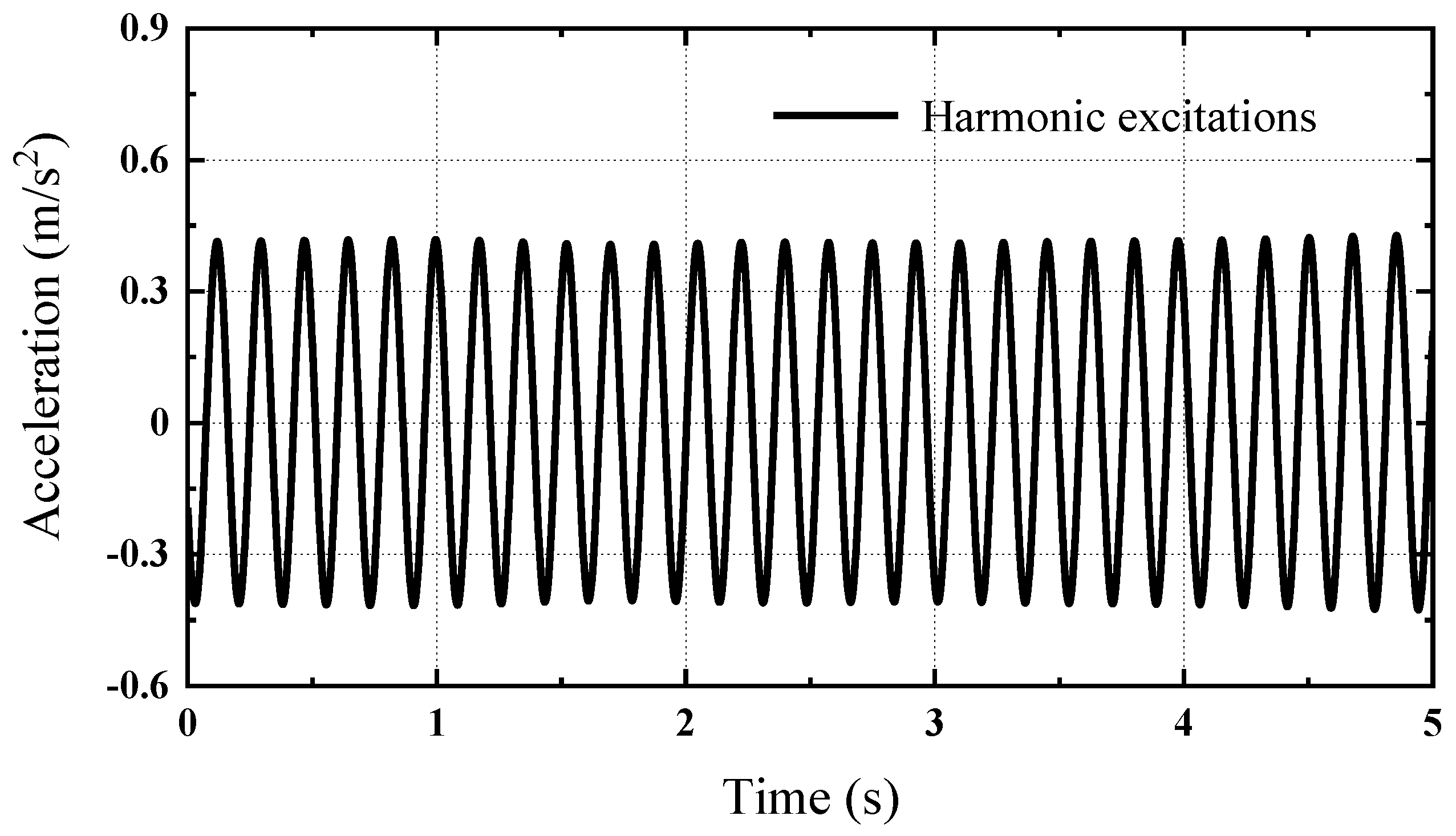
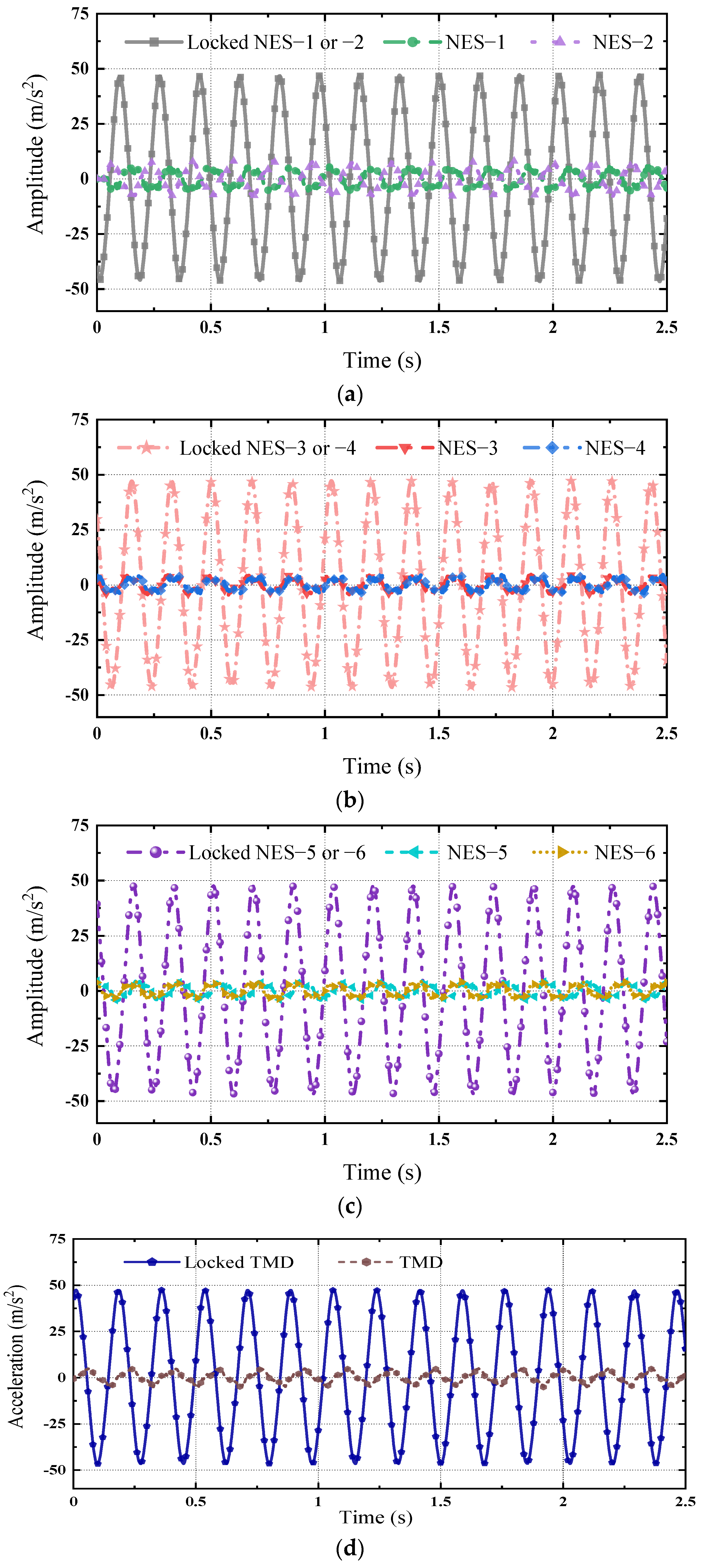
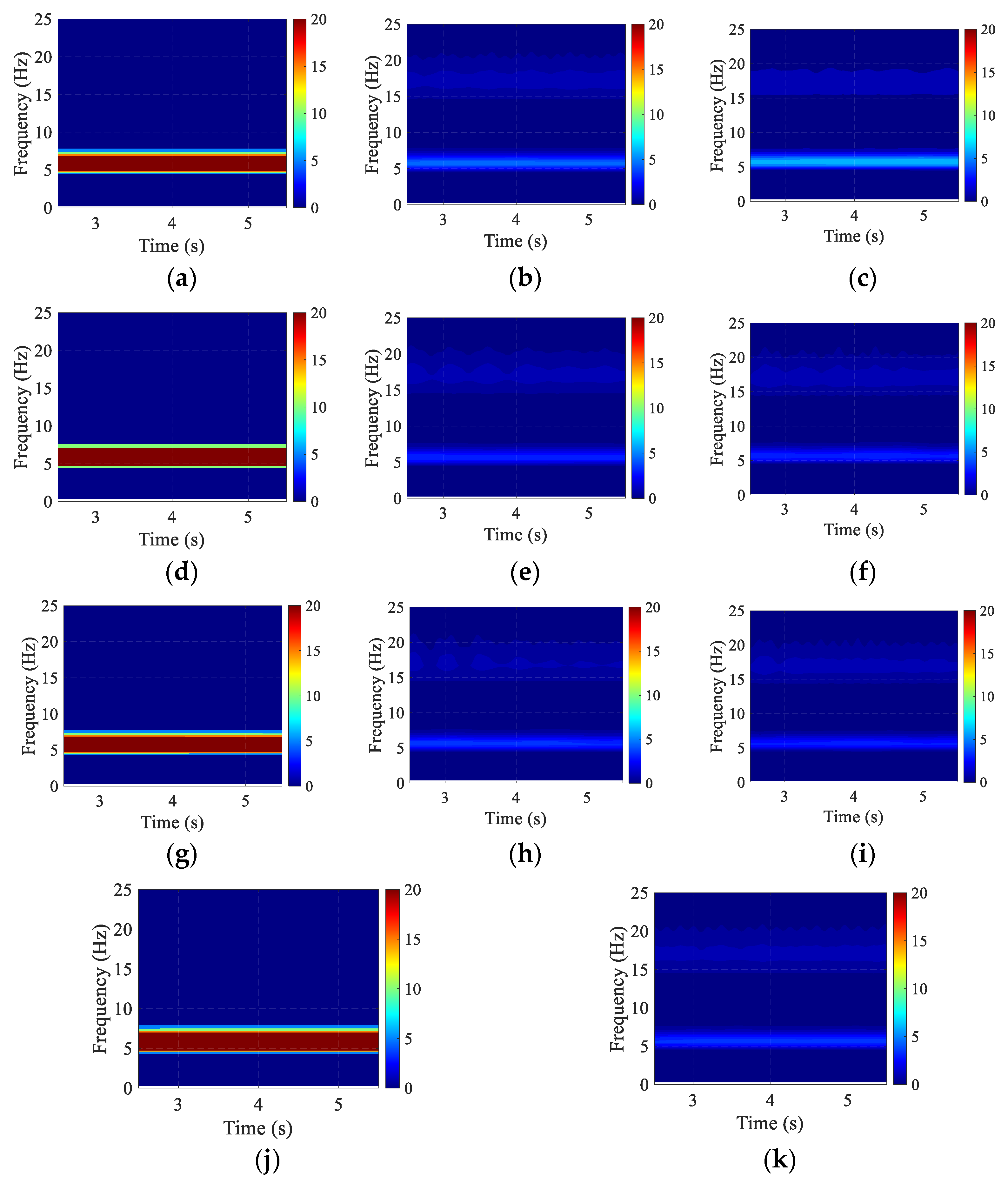
3.2. NES Mitigation Effects on the Dynamic Responses of the MDOF Structure Under Harmonic Excitations

The vibration mitigation effects of the NES on the dynamic responses of the structure under harmonic excitation, the frequency of which is equal to that of the structure with the NES installation, were investigated in this section, as shown in Figure 12. It is noted that the frequency of harmonic excitation varies along the structure with the NES having a different mass ratio μ, which can change the natural frequency of the structure–NES system. Figure 13a–d present the time histories of the acceleration responses on the top of the structure when the NES or TMD is locked or unlocked. Both NES and TMD can decrease the amplitude of the dynamic responses from 50.0 m/s2 to 5.0 m/s2. Figure 13a–d indicate that both the NES with different parameters such as mass ratio μ and stiffness k and the TMD have the same vibration mitigation effects on the acceleration responses, except for NES–2, even though the mass ratio of the NES is smaller than that of the TMD. Figure 13 indicates that NES–2 has the worst vibration mitigation effects on the acceleration responses of the structure under harmonic excitations among these control devices. Its vibration mitigation ratio is 81.84%, as shown in Figure 13a.
The time histories in Figure 13 can be transformed into the frequency and time domains by wavelet analysis to investigate the vibration mitigation effects, as shown in Figure 14. Figure 14a,d,g,j show that the energy of the structural dynamic responses entirely comes from the first vibration mode and does not vary with time, when the NES and TMD are locked. As shown in Figure 14b,c,e,f,h,i,k, when the NES and TMD work, the energy of the dynamic responses corresponding to the first vibration mode significantly decreases, while the higher vibration mode around 18.0 Hz begins to be involved in the vibration. Figure 14 demonstrates that the different NESs have the same vibration mitigation effects as that of the TMD except for NES–2, and the vibration mitigation effects of NES–2 are worse than those of the others. The variation in peak values of the time history in Figure 13 along the height of the structure can be calculated as shown in Figure 15. For the responses on the top of the structure in Figure 15, all control devices except for NES–2 achieved a vibration mitigation ratio of over 88%, and NES–3 and NES–4 exhibited the best mitigation effects at 90.1% and 90.0%, respectively, which is consistent with the results from Figure 13.

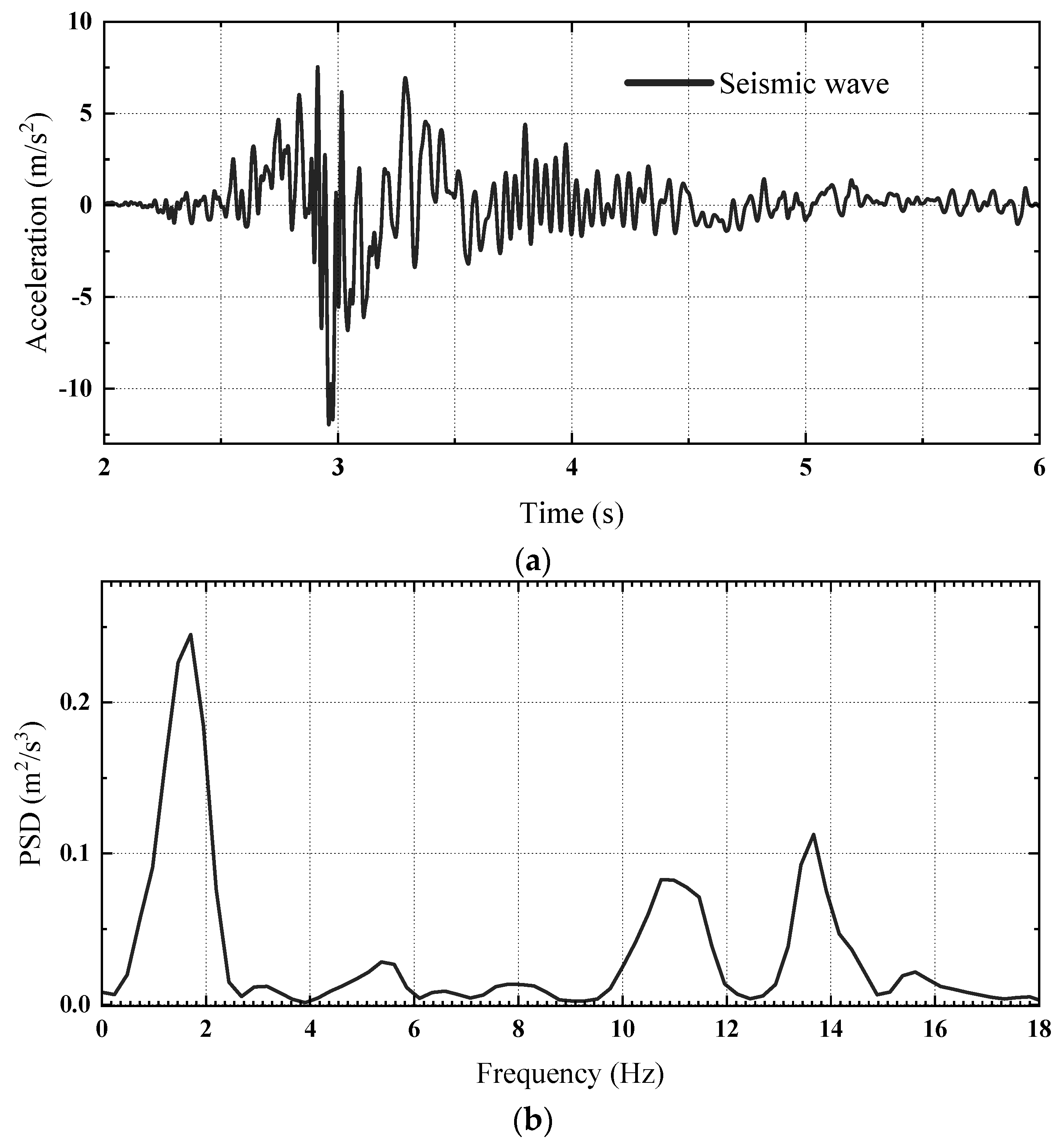
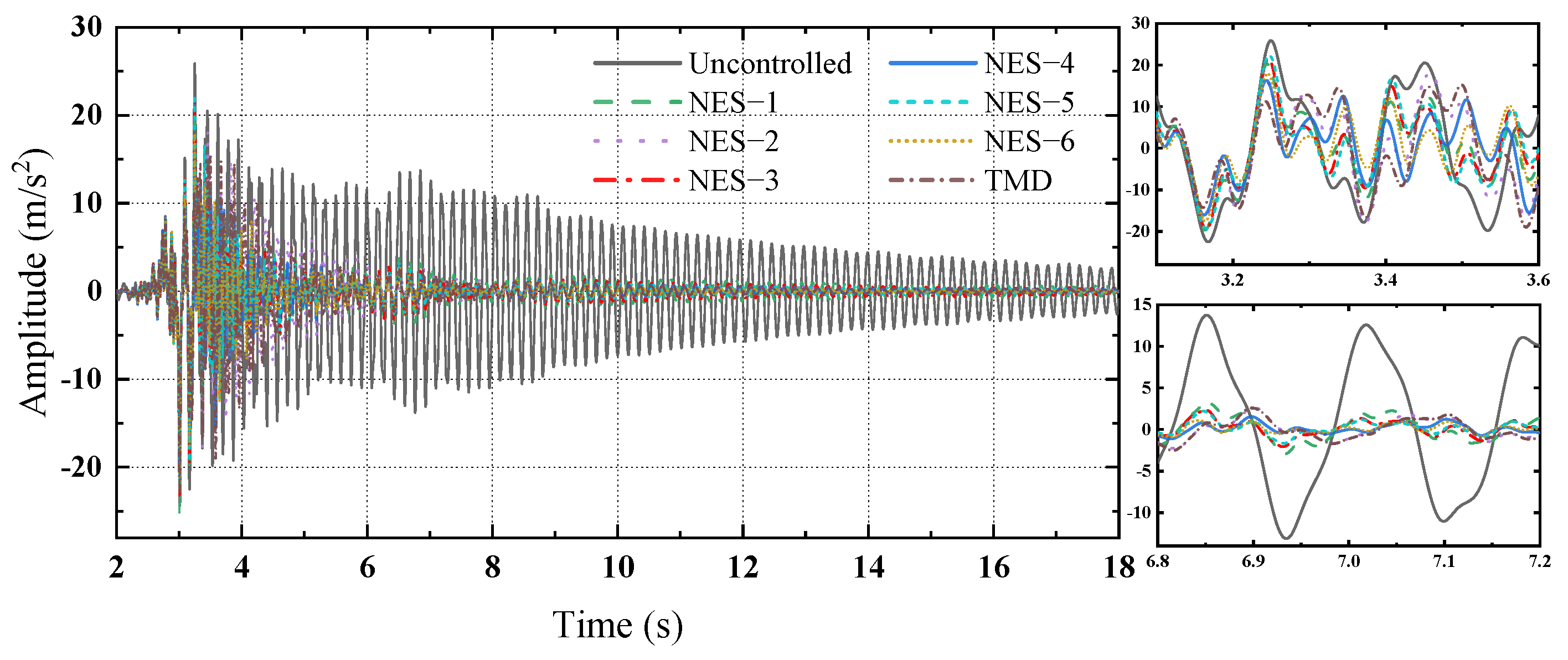
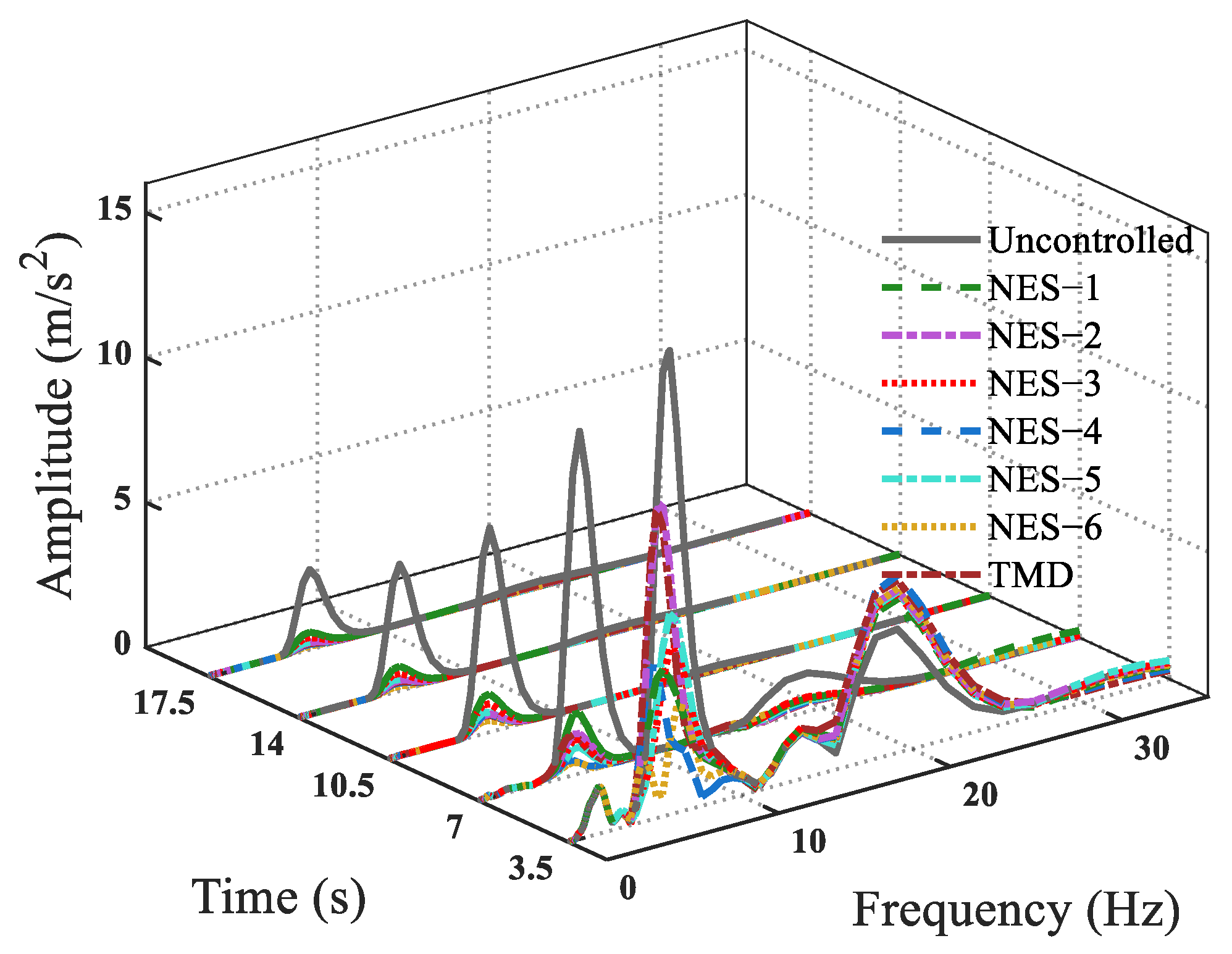
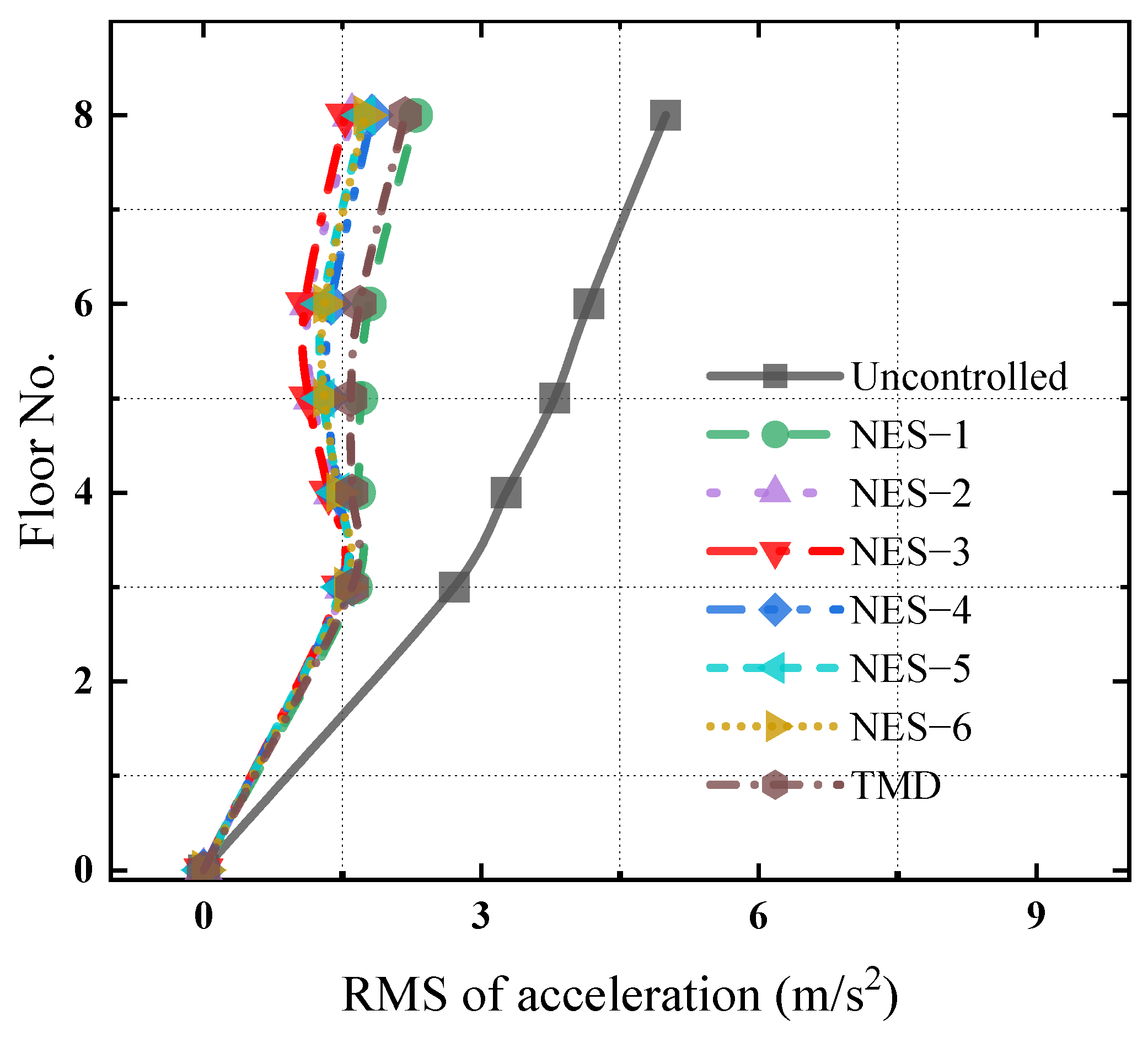
3.3. NES Mitigation Effects on the Dynamic Responses of the MDOF Structure Under Seismic Excitations

The NES controlling the dynamic responses of the MODF structure under stochastic excitations was examined in this section. Figure 16 shows the spectral analysis of 100 stochastic excitations.
Root mean square (RMS) values of the time history of the acceleration responses measured by the acceleration sensors, which were distributed on the structure, under 100 seismic waves were estimated by a statistic method, as shown in Figure 17. In Figure 17, the average value of the uncontrolled structure denotes the mean RMS value of these responses under 100 seismic excitations. Figure 17 shows that the average mitigation effects of the NES on the RMS values of the acceleration responses of the structure under 100 seismic waves are better than that of the TMD. This indicates that the robustness of the NES is better than that of the TMD.
One of the one hundred seismic waves was selected to show NES vibration mitigation effects on the dynamic responses of the structure under its excitation. Figure 18a displays the time history of the selected seismic wave. Figure 18b presents the PSD of the seismic waves, and indicates that its dominant frequency concentrates at the range of 1.3 Hz to 1.9 Hz.
The time histories of the acceleration responses on the top of the structure with and without NES or TMD installation under the seismic wave are shown in Figure 19. Figure 19 demonstrates that the NES and TMD have no considerable vibration mitigation effects on the acceleration responses of the structure under the seismic wave press before 3.5 s, and the vibration mitigation effects begin to become significant after this time. The acceleration response of the uncontrolled structure reaches 12.5 m/s2 at 7.0 s. At this time, the responses decrease to 1.8 m/s2, 0.54 m/s2, 1.2 m/s2, 0.3 m/s2, 1.13 m/s2, 0.15 m/s2 and 0.66 m/s2 corresponding to the control conditions of NES–1~NES–6 and TMD, respectively. Among them, NES–6 has the best vibration mitigation effects, and its mitigation ratio is 98.8%.
Through wavelet analysis, the time history in Figure 19 can be transformed into the frequency and time domain to investigate the vibration mitigation effects, as shown in Figure 20. Figure 20 shows that the dynamic responses mainly come from the first vibration mode, and the amplitude of dynamic responses corresponding to the first natural frequency around 5.88 Hz (the black line) decreases with time for the uncontrolled structure due to the values of stochastic excitations become smaller and smaller after 4.0 s, as shown in Figure 18a. It is clear that both NES and TMD can considerably decrease the structural dynamic responses corresponding to the first vibration mode, and do not affect the responses of the higher vibration modes, as shown in Figure 20.
The RMS values of the time history of the acceleration responses along the height of the structure under the seismic wave were estimated to evaluate the vibration mitigation effects of these control devices, as shown in Figure 21. Figure 21 manifests that these control devices can effectively alleviate the RMS values of the dynamic responses along the height of the structure. Among them, NES–3 has the best vibration reduction effects. The RMS value is 4.99 m/s2 at the top of the uncontrolled structure. NES–1~NES–6 and TMD reduce the values to 2.3 m/s2, 1.6 m/s2, 1.52 m/s2, 1.82 m/s2, 1.73 m/s2, 1.74 m/s2 and 2.18 m/s2, respectively, and the corresponding vibration mitigation ratios are 54.1%, 67.8%, 69.4%, 63.5%, 65.3%, 65.0% and 56.3%.

4. Conclusions

In this research, tests of the cubic stiffness NES controlling the dynamic responses of the MDOF structure under white noise, harmonic and seismic excitations were carried out using a shake table. The effects of the parameters of the NES on the vibration reduction ratios were explored. The main results and conclusions are summarized as follows.
(1) Under white noise excitations, these six NESs with different parameters and TMD have effective vibration mitigation effects, and their mitigation ratio of the acceleration responses at the top of the structure can reach about 50.0%. NES–4 has the best mitigation effects among these control devices.
(2) With regard to harmonic excitation, the NESs with different parameters and TMD almost have the same vibration mitigation effects on the acceleration responses except for NES–2, even though the mass ratio of the NES is less than that of the TMD. The vibration mitigation effects of NES–2 are worse than those of the other control devices under harmonic excitations. The control devices can achieve a vibration mitigation ratio of over 88.0% on the acceleration responses of the structure.
(3) One hundred seismic waves were inputted in the MODF structure using a shake table to investigate the vibration mitigation effects of the NES on the dynamic responses. The NES can alleviate the dynamic responses of the structure under the 100 seismic waves. The average mitigation effects of the NES on the RMS values of the acceleration responses of the structure under 100 seismic waves are better than that of the TMD. The robustness of the NES is better than that of the TMD.
To investigate the energy transmission from the structure to the NES under dynamic excitations, further shake table tests will be carried out to measure the responses of the structure as well as the dynamic responses of the NES.

Author Contributions

Conceptualization, Q.W. and Y.T.; methodology, Q.W. and Y.T.; software, X.Y. and D.Y.; validation, Y.T., X.Y. and Q.W.; formal analysis, X.Y. and D.Y.; investigation, Q.W., X.Y. and D.Y.; writing—original draft preparation, Q.W. and X.Y.; writing—review and editing, Q.W. and X.Y.; supervision, Q.W.; funding acquisition, Q.W. and Y.T. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Opening Funds of State Key Laboratory of Building Safety and Built Environment and the National Engineering Research Center of Building Technology (BSBE2021-11). This support is gratefully acknowledged.

Data Availability Statement

Data availability as required.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Housner, G.W.; Bergman, L.A.; Caughey, T.K.; Chassiakos, A.G.; Claus, R.O.; Masri, S.F.; Skelton, R.E.; Soong, T.T.; Spencer, B.F.; Yao, J.T.P. Structural Control: Past, Present, and Future. J. Eng. Mech. 1997, 123, 897–971. [Google Scholar] [CrossRef]
  2. Gutierrez Soto, M.; Adeli, H. Tuned Mass Dampers. Arch. Comput. Methods Eng. 2013, 20, 419–431. [Google Scholar] [CrossRef]
  3. Mahmoodi, P. Structural Dampers. J. Struct. Div. 1969, 95, 1661–1672. [Google Scholar] [CrossRef]
  4. Li, Q.S.; Zhi, L.-H.; Tuan, A.Y.; Kao, C.-S.; Su, S.-C.; Wu, C.-F. Dynamic Behavior of Taipei 101 Tower: Field Measurement and Numerical Analysis. J. Struct. Eng. 2011, 137, 143–155. [Google Scholar] [CrossRef]
  5. Lu, X.; Chen, J. Mitigation of wind-induced response of Shanghai Center Tower by tuned mass damper. Struct. Des. Tall Spec. Build. 2011, 20, 435–452. [Google Scholar] [CrossRef]
  6. Li, Q.; He, Y.; Zhou, K.; Han, X.; He, Y.; Shu, Z. Structural health monitoring for a 600 m high skyscraper. Struct. Des. Tall Spec. Build. 2018, 27, e1490. [Google Scholar] [CrossRef]
  7. Vakakis, A.F. Inducing Passive Nonlinear Energy Sinks in Vibrating Systems. J. Vib. Acoust. 2001, 123, 324–332. [Google Scholar] [CrossRef]
  8. Lee, Y.S.; Vakakis, A.F.; Bergman, L.A.; McFarland, D.M.; Kerschen, G.; Nucera, F.; Tsakirtzis, S.; Panagopoulos, P.N. Passive non-linear targeted energy transfer and its applications to vibration absorption: A review. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2008, 222, 77–134. [Google Scholar] [CrossRef]
  9. McFarland, D.M.; Kerschen, G.; Kowtko, J.J.; Lee, Y.S.; Bergman, L.A.; Vakakis, A.F. Experimental investigation of targeted energy transfers in strongly and nonlinearly coupled oscillators. J. Acoust. 2005, 118, 791–799. [Google Scholar] [CrossRef]
  10. Vakakis, A.F.; Bergman, L.A.; McFarland, D.M.; Gendelman, O.V.; Lee, G.K.Y.S. Nonlinear Targeted Energy Transfer in Mechanical and Structural Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
  11. Gourdon, E.; Lamarque, C.H. Energy Pumping with Various Nonlinear Structures: Numerical Evidences. Nonlinear Dyn. 2005, 40, 281–307. [Google Scholar] [CrossRef]
  12. Nucera, F.; Lo Iacono, F.; McFarland, D.M.; Bergman, L.A.; Vakakis, A.F. Application of broadband nonlinear targeted energy transfers for seismic mitigation of a shear frame: Experimental results. J. Sound Vib. 2008, 313, 57–76. [Google Scholar] [CrossRef]
  13. Nucera, F.; McFarland, D.M.; Bergman, L.A.; Vakakis, A.F. Application of broadband nonlinear targeted energy transfers for seismic mitigation of a shear frame: Computational results. J. Sound Vib. 2010, 329, 2973–2994. [Google Scholar] [CrossRef]
  14. Vaurigaud, B.; Savadkoohi, A.T.; Lamarque, C.H. Efficient Targeted Energy Transfer with Parallel Nonlinear Energy Sinks: Theory and Experiments. J. Comput. Nonlinear Dyn. 2011, 6, 041005. [Google Scholar] [CrossRef]
  15. Wierschem, N.E.; Hubbard, S.A.; Luo, J.; Fahnestock, L.A.; Spencer, B.F.; Quinn, D.D.; McFarland, D.M.; Vakakis, A.F.; Bergman, L.A. Experimental blast testing of a large 9-story structure equipped with a system of nonlinear energy sinks. In Proceedings of the ASME 2013 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Portland, OR, USA, 4–7 August 2013. [Google Scholar]
  16. Wierschem, N.E.; Hubbard, S.A.; Luo, J.; Fahnestock, L.A.; Spencer, B.F., Jr.; McFarland, D.M.; Quinn, D.D.; Vakakis, A.F.; Bergman, L.A. Response attenuation in a large-scale structure subjected to blast excitation utilizing a system of essentially nonlinear vibration absorbers. J. Sound Vib. 2017, 389, 52–72. [Google Scholar] [CrossRef]
  17. Luo, J.; Wierschem, N.E.; Hubbard, S.A.; Fahnestock, L.A.; Quinn, D.D.; McFarland, D.M.; Spencer, B.F.; Vakakis, A.F.; Bergman, L.A. Large-scale experimental evaluation and numerical simulation of a system of nonlinear energy sinks for seismic mitigation. J. Struct. Eng. 2014, 77, 34–48. [Google Scholar] [CrossRef]
  18. Wierschem, N.E.; Luo, J.; Al-Shudeifat, M.; Hubbard, S.; Ott, R.; Fahnestock, L.A.; Quinn, D.D.; McFarland, D.M.; Spencer, B.F.; Vakakis, A.; et al. Experimental Testing and Numerical Simulation of a Six-Story Structure Incorporating Two-Degree-of-Freedom Nonlinear Energy Sink. J. Struct. Eng. 2014, 140, 04014027. [Google Scholar] [CrossRef]
  19. Wang, J.J.; Wierschem, N.E.; Wang, B.; Spencer Jr, B.F. Multi-objective design and performance investigation of a high-rise building with track nonlinear energy sinks. Struct. Des. Tall Spec. Build. 2020, 29, e1692. [Google Scholar] [CrossRef]
  20. Wang, J.J.; Wierschem, N.; Spencer, B.F.; Lu, X. Experimental study of track nonlinear energy sinks for dynamic response reduction. Eng. Struct. 2015, 94, 9–15. [Google Scholar] [CrossRef]
  21. Wang, J.J.; Wang, B.; Liu, Z.B.; Zhang, C.; Li, H.B. Experimental and numerical studies of a novel asymmetric nonlinear mass damper for seismic response mitigation. Struct. Control Health Monit. 2020, 27, e2513. [Google Scholar] [CrossRef]
  22. Wang, J.J.; Zhang, C.; Li, H.; Liu, Z. Experimental and numerical studies of a novel track bistable nonlinear energy sink with improved energy robustness for structural response mitigation. Eng. Struct. 2021, 237, 112184. [Google Scholar] [CrossRef]
  23. Yang, H.X.; Li, Z.; Wang, H.B.; Zhang, M.H.; Ni, S.Y. Shaking table test study on seismic performance of RC frame structure with NES. Structures 2023, 47, 153–164. [Google Scholar] [CrossRef]
  24. Ndemanou, B.P.; Oumbé Tékam, G.T.; Kingni, S.T.; Nana Nbendjo, B.R. Energy sink outrigger control of a tall building under wind loads. Eng. Struct. 2023, 288, 116158. [Google Scholar] [CrossRef]
  25. Wang, Q.; Wu, H.; Qiao, H.; Yu, X.; Huang, P. Asymmetric and Cubic Nonlinear Energy Sink Inerters for Mitigating Wind-Induced Responses of High-Rise Buildings. Struct. Control Health Monit. 2023, 2023, 1150525. [Google Scholar] [CrossRef]
  26. ISO 5348:1998-05; Mechanical Vibration and Shock—Mechanical Mounting of Accelerometers. ISO: Geneva, Switzerland, 1998.
Buildings 14 03543 g001
Figure 1. Multi-degree-of-freedom structure model. (a) Elevation of the model. (b) Physical model.
Figure 1. Multi-degree-of-freedom structure model. (a) Elevation of the model. (b) Physical model.
Buildings 14 03543 g001
Buildings 14 03543 g002
Figure 2. Free vibration tests. (a) Time history of free vibration. (b) Acceleration response spectrum of the free vibration.
Figure 2. Free vibration tests. (a) Time history of free vibration. (b) Acceleration response spectrum of the free vibration.
Buildings 14 03543 g002
Buildings 14 03543 g003
Figure 3. NES model diagram. (a) NES top view. (b) Diagram of the NES installed on the model.
Figure 3. NES model diagram. (a) NES top view. (b) Diagram of the NES installed on the model.
Buildings 14 03543 g003
Buildings 14 03543 g004
Figure 4. The frequency response function when the NES is locked.
Figure 4. The frequency response function when the NES is locked.
Buildings 14 03543 g004
Buildings 14 03543 g005
Figure 5. Apparatus for the tests.
Figure 5. Apparatus for the tests.
Buildings 14 03543 g005
Buildings 14 03543 g006
Figure 6. The model installed on the shake table.
Figure 6. The model installed on the shake table.
Buildings 14 03543 g006
Buildings 14 03543 g007
Figure 7. Time history of white noise excitation.
Figure 7. Time history of white noise excitation.
Buildings 14 03543 g007
Buildings 14 03543 g008
Figure 8. Acceleration time history curve of the top of the structure.
Figure 8. Acceleration time history curve of the top of the structure.
Buildings 14 03543 g008
Buildings 14 03543 g009
Figure 9. Acceleration response spectrum of the TMD.
Figure 9. Acceleration response spectrum of the TMD.
Buildings 14 03543 g009
Buildings 14 03543 g010
Figure 10. Wavelet analysis of NES controlling dynamic responses under white noise excitation. (a) Locked NES–1 or –2, (b) NES–1, (c) NES–2, (d) locked NES–3 or –4, (e) NES–3, (f) NES–4, (g) locked NES–5 or –6, (h) NES–5, (i) NES–6.
Figure 10. Wavelet analysis of NES controlling dynamic responses under white noise excitation. (a) Locked NES–1 or –2, (b) NES–1, (c) NES–2, (d) locked NES–3 or –4, (e) NES–3, (f) NES–4, (g) locked NES–5 or –6, (h) NES–5, (i) NES–6.
Buildings 14 03543 g010
Buildings 14 03543 g011
Figure 11. Variation in the maximum responses along the height of the structure.
Figure 11. Variation in the maximum responses along the height of the structure.
Buildings 14 03543 g011
Buildings 14 03543 g012
Figure 12. Time history of harmonic excitations.
Figure 12. Time history of harmonic excitations.
Buildings 14 03543 g012
Buildings 14 03543 g013
Figure 13. Time history of acceleration responses on the top of the structure with control devices. (a) Vibration mitigation effects of NES–1 or NES–2 under 5.70 Hz harmonic excitation. (b) Vibration mitigation effects of NES–3 or NES–4 under 5.65 Hz harmonic excitation. (c) Vibration mitigation effects of NES–5 or NES–6 under 5.60 Hz harmonic excitation. (d) Vibration mitigation effects of TMD under 5.65 Hz harmonic excitation.
Figure 13. Time history of acceleration responses on the top of the structure with control devices. (a) Vibration mitigation effects of NES–1 or NES–2 under 5.70 Hz harmonic excitation. (b) Vibration mitigation effects of NES–3 or NES–4 under 5.65 Hz harmonic excitation. (c) Vibration mitigation effects of NES–5 or NES–6 under 5.60 Hz harmonic excitation. (d) Vibration mitigation effects of TMD under 5.65 Hz harmonic excitation.
Buildings 14 03543 g013
Buildings 14 03543 g014
Figure 14. Wavelet analysis of NES and TMD controlling dynamic response under harmonic excitation. (a) Locked NES–1 or –2, (b) NES–1, (c) NES–2, (d) locked NES–3 or –4, (e) NES–3, (f) NES–4, (g) locked NES–5 or –6, (h) NES–5, (i) NES–6, (j) locked TMD, (k) TMD.
Figure 14. Wavelet analysis of NES and TMD controlling dynamic response under harmonic excitation. (a) Locked NES–1 or –2, (b) NES–1, (c) NES–2, (d) locked NES–3 or –4, (e) NES–3, (f) NES–4, (g) locked NES–5 or –6, (h) NES–5, (i) NES–6, (j) locked TMD, (k) TMD.
Buildings 14 03543 g014
Buildings 14 03543 g015
Figure 15. Variation in the maximum responses along the height of the structure.
Figure 15. Variation in the maximum responses along the height of the structure.
Buildings 14 03543 g015
Buildings 14 03543 g016
Figure 16. Spectral analysis of 100 stochastic excitations.
Figure 16. Spectral analysis of 100 stochastic excitations.
Buildings 14 03543 g016
Buildings 14 03543 g017
Figure 17. RMS values of acceleration responses.
Figure 17. RMS values of acceleration responses.
Buildings 14 03543 g017
Buildings 14 03543 g018
Figure 18. Seismic waves: (a) time history of one seismic wave and (b) PSD of one seismic wave.
Figure 18. Seismic waves: (a) time history of one seismic wave and (b) PSD of one seismic wave.
Buildings 14 03543 g018
Buildings 14 03543 g019
Figure 19. Time history of acceleration responses on the top of the structure under the seismic wave.
Figure 19. Time history of acceleration responses on the top of the structure under the seismic wave.
Buildings 14 03543 g019
Buildings 14 03543 g020
Figure 20. Wavelet analysis of NES and TMD controlling dynamic responses under one seismic wave.
Figure 20. Wavelet analysis of NES and TMD controlling dynamic responses under one seismic wave.
Buildings 14 03543 g020
Buildings 14 03543 g021
Figure 21. Variation in RMS values along the height of the structure under the seismic wave.
Figure 21. Variation in RMS values along the height of the structure under the seismic wave.
Buildings 14 03543 g021
Table 1. The first three natural frequencies of the system when the NES is locked.
Table 1. The first three natural frequencies of the system when the NES is locked.
Mass Ratiof1 (Hz)f2 (Hz)f3 (Hz)
0.0 (no NES)5.8818.7531.50
μ1 = 3.0%5.7118.4031.17
μ2 = 4.5%5.6418.2630.90
μ3 = 6.0%5.5718.1430.65
Table 2. Parameters of the shaking table.
Table 2. Parameters of the shaking table.
DirectionRange of Displacement (mm)DirectionRange of Acceleration (g)
X(−185, 260)X(2, 2)
Y(−200, 200)Y(−2, 2)
Z(−111, 111)Z(−2, 2)
Table 3. Test conditions.
Table 3. Test conditions.
NumberTest ConditionsMass RatioStiffnessFrequency RatiosConditions of Control Device
1Uncontrolled--------
2NESμ1----Locked
3NES–1μ1k1--Unlocked
4NES–2μ1k2--Unlocked
5NES μ2----Locked
6NES–3μ2k1--Unlocked
7NES–4μ2k2--Unlocked
8NES μ3----Locked
9NES–5μ3k1--Unlocked
10NES–6μ3k2--Unlocked
11TMDμ2----Locked
12TMDμ2--fUnlocked
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Wang, Q.; Yi, X.; Yang, D.; Tang, Y. Study on Cubic Stiffness Nonlinear Energy Sink Controlling Dynamic Responses of Multi-Degree-of-Freedom Structure by Shake Table Tests. Buildings 2024, 14, 3543. https://doi.org/10.3390/buildings14113543

AMA Style

Wang Q, Yi X, Yang D, Tang Y. Study on Cubic Stiffness Nonlinear Energy Sink Controlling Dynamic Responses of Multi-Degree-of-Freedom Structure by Shake Table Tests. Buildings. 2024; 14(11):3543. https://doi.org/10.3390/buildings14113543

Chicago/Turabian Style

Wang, Qinhua, Xueshuang Yi, Dongxu Yang, and Yi Tang. 2024. "Study on Cubic Stiffness Nonlinear Energy Sink Controlling Dynamic Responses of Multi-Degree-of-Freedom Structure by Shake Table Tests" Buildings 14, no. 11: 3543. https://doi.org/10.3390/buildings14113543

APA Style

Wang, Q., Yi, X., Yang, D., & Tang, Y. (2024). Study on Cubic Stiffness Nonlinear Energy Sink Controlling Dynamic Responses of Multi-Degree-of-Freedom Structure by Shake Table Tests. Buildings, 14(11), 3543. https://doi.org/10.3390/buildings14113543

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop