Research on Quantitative Assessment and Dynamic Reasoning Method for Emergency Response Capability in Prefabricated Construction Safety
Abstract
:1. Introduction
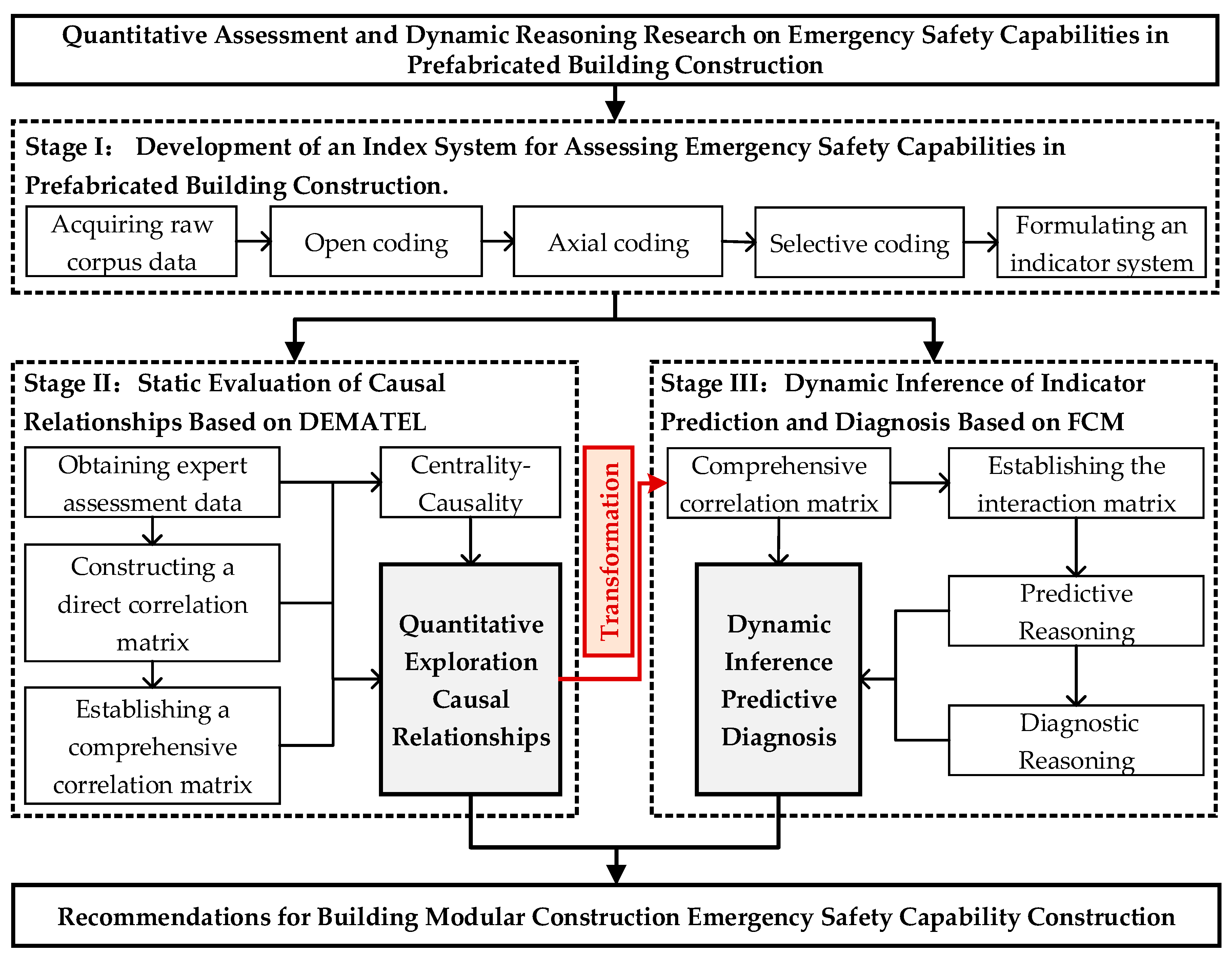
2. Methodology
2.1. DEMATEL
2.2. FCM
2.3. The Research Framework of the DEMATEL and FCM
3. Research Variables
3.1. Open Coding
3.2. Axial Coding
3.3. Selective Coding
4. Model Development
4.1. Quantifying Interrelationships Using DEMATEL Method
4.2. Predictive and Diagnostic Reasoning Using the FCM Model
5. Case Study
5.1. Empirical Cases
5.2. Data Collection and Preprocessing
6. Results and Discussion
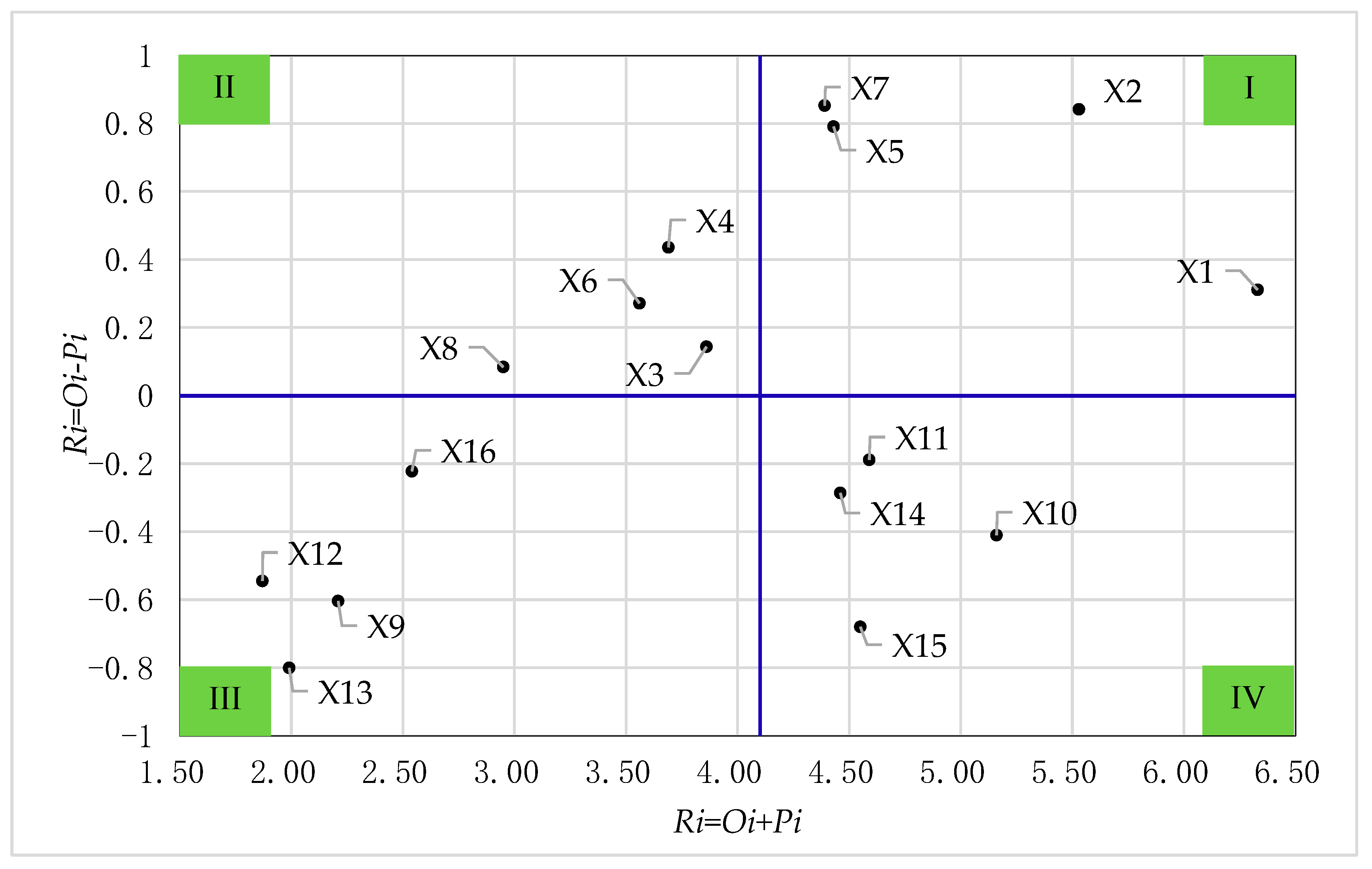
6.1. Static Evaluation of Causal Relationships
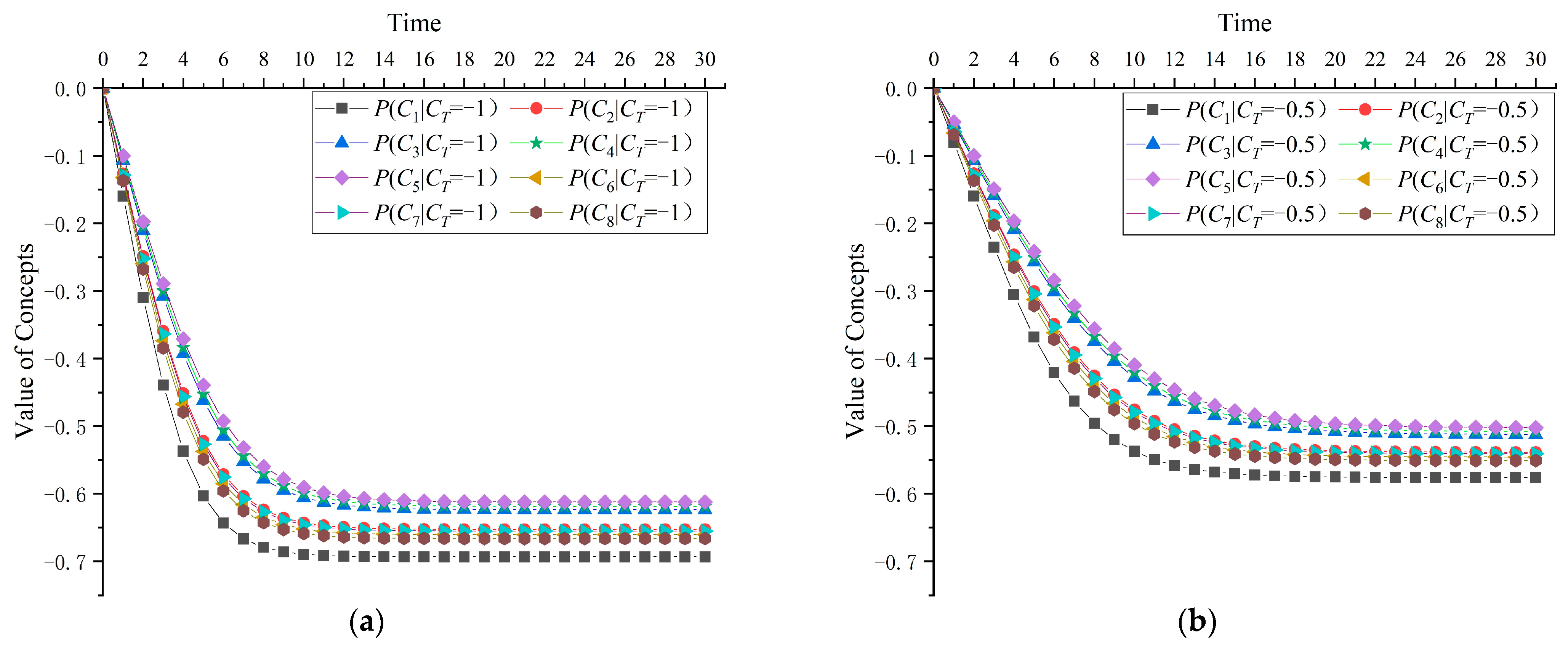
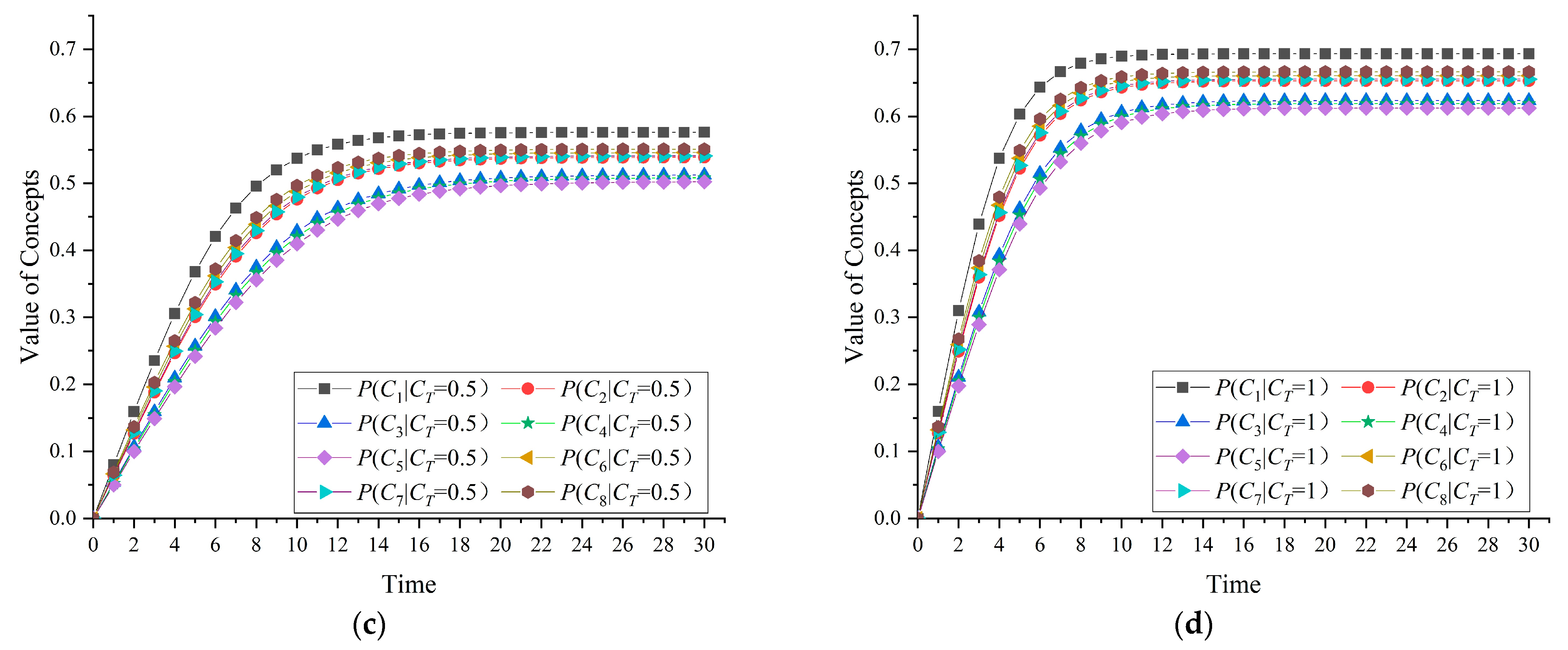
6.2. Dynamic Inference of Indicator Prediction and Diagnosis
- (1)
- Predictive Reasoning Analysis
- (2)
- Diagnostic Reasoning Analysis
6.3. Management Strategies and Recommendations
- (1)
- Organizational management: Establish a dedicated emergency management department and enhance communication and collaboration among various departments. Develop comprehensive emergency plans based on the challenges and safety risks of prefabricated projects. Clearly define emergency response procedures and establish a robust emergency management oversight mechanism.
- (2)
- Personnel qualifications: Conduct regular emergency training and educational activities to enhance the emergency awareness and skills of construction site personnel. Strengthen team collaboration capabilities and clarify emergency positions and responsibilities. Through training and practical exercises, improve the emergency response and crisis management abilities of dedicated personnel.
- (3)
- Technical measures: Establish a robust emergency communication system to ensure rapid and accurate information dissemination during emergencies. Utilize advanced monitoring and warning technologies to build emergency resource management systems, warning systems, and emergency decision support systems. These systems will enable real-time monitoring and early warning of safety conditions and risks on the construction site.
- (4)
- Emergency resources: Establish and strengthen emergency rescue forces to enhance response speed and capabilities. Adequately allocate emergency equipment and tools to effectively respond to various unexpected incidents on the construction site. Set up emergency resource reserves and support mechanisms to share and enhance comprehensive emergency capabilities.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Q.; Zhu, K.; Guo, P.; Guo, Z.; Zhang, B. Construction safety risk assessment of prefabricated building based on interaction matrix fuzzy cognitive map. J. Saf. Environ. 2023, 23, 2202–2211. [Google Scholar]
- Arashpour, M.; Abbasi, B.; Arashpour, M.; Hosseini, M.R.; Yang, R. Integrated management of on-site, coordination and off-site uncertainty: Theorizing risk analysis within a hybrid project setting. Int. J. Proj. Manag. 2017, 35, 647–655. [Google Scholar] [CrossRef]
- Xu, X.; Zou, P.X.W. Discovery of new safety knowledge from mining large injury dataset in construction. Saf. Sci. 2021, 144, 105481. [Google Scholar] [CrossRef]
- Ni, H.; Yao, X.; Chu, Y.; Shi, B. A pre evaluation model for emergency response effectiveness integrating “capability timeliness decision”. China Saf. Sci. J. 2020, 30, 148–156. [Google Scholar] [CrossRef]
- Cheng, J.; Yang, X.; Wang, H.; Li, H.; Lin, X.; Guo, Y. Evaluation of the emergency capability of subway shield construction based on cloud model. Sustainability 2022, 14, 13309. [Google Scholar] [CrossRef]
- Chen, W.; Qiao, Z.; Wang, W.; Zhang, K.; Niu, L.; Deng, C. SD model for emergency disposal of construction safety accident caused by rainstorm disaster. China Saf. Sci. J. 2017, 27, 169–174. [Google Scholar] [CrossRef]
- Luo, Z.; Guo, J.; Han, J.; Wang, Y. Research on the construction safety risk assessment of prefabricated subway stations in China. Eng. Constr. Archit. Manag. 2022. [Google Scholar] [CrossRef]
- Rakhi Vijayakumar, J.-H.C. Emerging trends of ergonomic risk assessment in construction safety management: A scientometric visualization analysis. Int. J. Environ. Res. Public Health 2022, 19, 16120. [Google Scholar] [CrossRef]
- Lima, C.B.D.C.; Aranha, P.E.; Castro, J.F.T.D.; Lima, G.B.A.; Hougaz, A.B.; Terra, F.D.S. Integrated risk management: A Petrobras application in offshore well construction safety to minimize critical emergency disconnections. Pet. Sci. 2018, 15, 421–431. [Google Scholar] [CrossRef]
- Wang, Q.; Zhu, K.; Wang, J.; Guo, P.; Shen, W. Bibliometric analysis of engineering project risk management literature. China Saf. Sci. J. 2021, 31, 15–23. [Google Scholar] [CrossRef]
- Nozari, M.A.; Ghadikolaei, A.S.; Govindan, K.; Akbari, V. Analysis of the sharing economy effect on sustainability in the transportation sector using fuzzy cognitive mapping. J. Clean. Prod. 2021, 311, 127331. [Google Scholar] [CrossRef]
- Kosko, B. Fuzzy cognitive maps. Int. J. Man. Mach. Stud. 1986, 24, 65–75. [Google Scholar] [CrossRef]
- Genc, T.O.; Ekici, A. A new lens to the understanding and reduction of household food waste: A fuzzy cognitive map approach. Sustain. Prod. Consum. 2022, 33, 389–411. [Google Scholar] [CrossRef]
- Ghaboulian Zare, S.; Alipour, M.; Hafezi, M.; Stewart, R.A.; Rahman, A. Examining wind energy deployment pathways in complex macro-economic and political settings using a fuzzy cognitive map-based method. Energy 2022, 238, 121673. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Q.; Dong, S.; Soares, C. Effectiveness assessment of ship navigation safety countermeasures using fuzzy cognitive maps. Saf. Sci. 2019, 117, 352–364. [Google Scholar] [CrossRef]
- Bas, E. An integrated OSH risk management approach to surgical flow disruptions in operating rooms. Saf. Sci. 2018, 109, 281–293. [Google Scholar] [CrossRef]
- Kuzu, A.C. Application of fuzzy DEMATEL approach in maritime transportation: A risk analysis of anchor loss. Ocean. Eng. 2023, 273, 113786. [Google Scholar] [CrossRef]
- Fontela, E.; Gabus, A. DEMATEL: Progress achieved. Futures 1974, 6, 361–363. [Google Scholar] [CrossRef]
- Bai, C.; Sarkis, J.; Dou, Y. Constructing a process model for low-carbon supply chain cooperation practices based on the DEMATEL and the NK model. Supply Chain. Manag. 2017, 22, 237–257. [Google Scholar] [CrossRef]
- Singh, P.K.; Sarkar, P. A framework based on fuzzy Delphi and DEMATEL for sustainable product development: A case of Indian automotive industry. J. Clean. Prod. 2020, 246, 118991. [Google Scholar] [CrossRef]
- Feng, C.; Ma, R. Identification of the factors that influence service innovation in manufacturing enterprises by using the fuzzy DEMATEL method. J. Clean. Prod. 2020, 253, 120002. [Google Scholar] [CrossRef]
- Khatun, M.; Wagner, F.; Jung, R.; Glaß, M. An application of DEMATEL and fuzzy DEMATEL to evaluate the interaction of safety management system and cybersecurity management system in automated vehicles. Eng. Appl. Artif. Intell. 2023, 124, 106566. [Google Scholar] [CrossRef]
- Du, Y.; Shen, X. Group hierarchical DEMATEL method for reaching consensus. Comput. Ind. Eng. 2023, 175, 108842. [Google Scholar] [CrossRef]
- Du, Y.; Li, X. Hierarchical DEMATEL method for complex systems. Expert Syst. Appl. 2021, 167, 113871. [Google Scholar] [CrossRef]
- Kosko, B. Hidden patterns in combined and adaptive knowledge networks. Int. J. Approx. Reason. 1988, 2, 377–393. [Google Scholar] [CrossRef]


| Method | Advantages | Disadvantages | Similarities | Combining |
|---|---|---|---|---|
| DEMATEL | 1. Reduced the composition of system elements and simplified the relationships between elements. 2. Quantified causal relationships, providing high credibility and reliability in decision-making and assessment. 3. Graphically intuitive and easy to understand, assisting analysts in better comprehending causal relationships and making decisions. | 1. Relies on experts’ experience and knowledge to address complex issues. 2. May not accurately reflect real-world situations when dealing with uncertain problems. 3. Overlapping causal relationships can occur, leading to less precise outcomes. | 1. Both can be used to deal with complex systems and uncertain information. 2. Both have graphical features, allowing for an intuitive representation of causal relationships and decision processes. 3. Both exhibit high flexibility and strong adaptability, making them applicable in various domains and scenarios | 1. The DEMATEL method provides accurate basic models and initial parameters for the FCM model, reducing the error of empirical parameter tuning in the FCM model. 2. The dynamic reasoning of the FCM model can handle uncertain information, making up for the shortcomings of the DEMATEL method in accurately reflecting the actual situation. |
| FCM | 1. Representing and analyzing causal relationships in complex systems. 2. Handling uncertainty and incomplete information. 3. Quantifying different scenarios and requirements by adjusting model weights. | 1. The FCM algorithm has a slow convergence rate and requires significant computational resources. 2. Parameter selection and adjustment in the FCM model often rely on trial and error and empirical knowledge. 3. FCM results may be influenced by various fuzzy logic operation methods, thus requiring improvement in result stability and repeatability. |
| Data Source | Excerpts from Original Statements | Open Coding—Labeling | |
|---|---|---|---|
| Literature Review | Literature 1 | …qualifications, skills, and experience, safety awareness and responsibilities, supervision plans and allocation of responsibilities, safety supervision inspections and records, safety education, training, and assessment, participation in safety plans, reasonableness of construction schemes, safety management systems and regulations… | KI111: Qualifications, skills, and experience KI112: Safety awareness and responsibility KI113: Safety education KI114: Reasonableness of construction schemes KI115: Safety management system |
| Literature 2 | …analyze the basic pattern of emergency response… action objectives, action modules, emergency resources… utilizing time-effectiveness assessment, broad priority relationships, organizational structure… combining to form an integrated “capability-time-effectiveness-decision” emergency response effectiveness pre-assessment model… | KI211: Basic modes of emergency response KI212: Action objectives KI213: Action modules KI214: Emergency resources KI215: Pre-evaluation model for emergency response effectiveness | |
| …… | …… | …… | |
| Policy Compilation | Policy 1 | The People’s Republic of China Building Law: …prepare safety technical measures plan… it is necessary to strengthen safety production publicity, education, and training, and enhance the safety skills and emergency response capabilities of employees… | KII111: Safety technical measures KII112: Safety production publicity, education, and training KII113: Safety skills and emergency response capabilities |
| Policy 2 | The People’s Republic of China Regulation on Safety Production in Construction Projects: …safety production measures and emergency rescue plans… taking into account the characteristics of different projects and the influence of different construction environments… adopting different safety production measures and emergency rescue measures… | KII211: Safety production measures KII212: Emergency rescue plans KII213: Engineering characteristics and different environments KII214: Emergency rescue measures | |
| …… | …… | …… | |
| Expert Interviews | Expert 1 | …establishing an effective inter-departmental coordination mechanism is crucial for enhancing emergency response capabilities… actively introducing modern technological means to promptly identify safety hazards and violations… the psychological state of personnel is equally important when responding to safety accidents… raising public awareness of safety and self-protection abilities… formulating relevant emergency measures tailored to the construction environment… | KIII111: Coordinating mechanism KIII112: Modern technological means KIII113: Psychological state of personnel KIII114: Public safety awareness and self-protection ability KIII115: Formulating relevant emergency measures for the construction environment |
| Expert 2 | …including safety training for all participants… emergency plans are essential… high-quality safety equipment and facilities are crucial for preventing and responding to safety accidents… regular safety drills and assessments are also highly important… a sound safety management system… | KIII211: Safety training KIII212: Emergency plan KIII213: Safety equipment and facilities KIII214: Safety drills and evaluations KIII215: Safety management system | |
| …… | …… | …… | |
| Open Coding—Labeling | Open Coding—Conceptualization | Axial Coding—Categorization |
|---|---|---|
| KI113 Safety Education KI114 Rationality of Construction Plan KI115 Safety Management System | H1 Emergency Plan System | X1 (Degree of Emergency Plan Adequacy) |
| KI211 Basic Model of Emergency Response KI215 Pre-Evaluation Model for Emergency Response Effectiveness | H2 Emergency Plan Procedures | |
| KII111 Safety Technical Measures KII211 Safety Production Measures KII214 Emergency Rescue Measures | H3 Emergency Plan Measures | |
| …… | …… | …… |
| Core Category | Main Category | Abbreviation |
|---|---|---|
| Organizational Management () | Emergency Plan Completeness | |
| Emergency Organizational Structure and Procedures | ||
| Emergency Coordination Capability | ||
| Frequency of Emergency Drills | ||
| Personnel Quality () | Level of Emergency Training | |
| Safety Awareness and Occupational Skills | ||
| Emergency Response Experience | ||
| Team Collaboration Ability | ||
| Technical Measures () | Adequacy of Emergency Facilities | |
| Emergency Technological Level | ||
| Emergency Response Efficiency | ||
| Completeness of Information Systems | ||
| Emergency Resources () | Emergency Equipment and Material Reserves | |
| Emergency Communication System | ||
| Emergency Rescue Capability | ||
| External Support and Collaboration Ability |
| Years of Service (Years) | Owner Unit (Person) | Design Unit (Person) | Supervision Unit (Person) | Construction Unit (Person) | Government Department (Person) | University (Person) |
|---|---|---|---|---|---|---|
| 10 ≤ Years < 15 | 1 | 1 | 1 | 1 | 2 | 1 |
| 15 ≤ Years < 20 | 1 | 1 | 1 | 1 | 1 | 2 |
| 20 ≤ Years | 1 | 0 | 1 | 1 | 1 | 2 |
| Total | 3 | 2 | 3 | 3 | 4 | 5 |
| Experts | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 4 | 3 | 2 | 4 | 2 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 2 | 0 | 4 | 4 | 2 | 2 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 3 | 3 | 4 | 4 |
| 3 | 0 | 4 | 4 | 2 | 2 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 3 | 3 | 4 | 4 |
| 4 | 0 | 4 | 3 | 2 | 3 | 3 | 3 | 4 | 3 | 3 | 4 | 3 | 4 | 4 | 3 | 4 |
| 5 | 0 | 3 | 3 | 2 | 3 | 3 | 4 | 4 | 3 | 3 | 4 | 3 | 4 | 4 | 3 | 4 |
| 6 | 0 | 3 | 3 | 2 | 3 | 3 | 4 | 4 | 3 | 4 | 4 | 3 | 4 | 4 | 3 | 4 |
| 7 | 0 | 4 | 3 | 2 | 3 | 3 | 4 | 4 | 3 | 4 | 3 | 3 | 3 | 3 | 4 | 4 |
| 8 | 0 | 4 | 3 | 2 | 3 | 3 | 4 | 4 | 3 | 4 | 3 | 4 | 3 | 3 | 4 | 4 |
| 9 | 0 | 3 | 2 | 2 | 4 | 3 | 4 | 3 | 3 | 4 | 4 | 4 | 3 | 4 | 4 | 4 |
| 10 | 0 | 3 | 2 | 2 | 4 | 3 | 4 | 3 | 4 | 4 | 4 | 4 | 3 | 4 | 4 | 4 |
| 11 | 0 | 3 | 2 | 2 | 4 | 3 | 4 | 3 | 4 | 3 | 4 | 4 | 4 | 4 | 4 | 4 |
| 12 | 0 | 4 | 3 | 2 | 4 | 3 | 4 | 3 | 4 | 3 | 4 | 3 | 4 | 4 | 4 | 3 |
| 13 | 0 | 4 | 3 | 2 | 4 | 3 | 3 | 3 | 4 | 3 | 4 | 3 | 4 | 4 | 4 | 3 |
| 14 | 0 | 4 | 3 | 2 | 4 | 2 | 3 | 3 | 4 | 3 | 4 | 2 | 4 | 4 | 4 | 4 |
| 15 | 0 | 4 | 3 | 2 | 4 | 2 | 3 | 3 | 4 | 4 | 4 | 2 | 4 | 4 | 4 | 4 |
| Q16 × 16 | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.1331 | 0.2420 | 0.1950 | 0.1492 | 0.2091 | 0.1795 | 0.2116 | 0.1909 | 0.2010 | 0.2602 | 0.2509 | 0.1831 | 0.1995 | 0.2469 | 0.2600 | 0.2102 | |
| 0.2819 | 0.1016 | 0.1965 | 0.1106 | 0.2295 | 0.1483 | 0.2278 | 0.1406 | 0.1783 | 0.2725 | 0.2536 | 0.1706 | 0.1765 | 0.2546 | 0.2650 | 0.1774 | |
| 0.2013 | 0.2193 | 0.0558 | 0.0861 | 0.1316 | 0.0870 | 0.1299 | 0.0830 | 0.0839 | 0.1572 | 0.2229 | 0.0397 | 0.0825 | 0.1851 | 0.1525 | 0.0828 | |
| 0.2036 | 0.1843 | 0.0963 | 0.0492 | 0.1719 | 0.1274 | 0.1705 | 0.0853 | 0.0456 | 0.1589 | 0.2254 | 0.0389 | 0.1214 | 0.1484 | 0.1542 | 0.0825 | |
| 0.2609 | 0.2004 | 0.1468 | 0.1364 | 0.0695 | 0.1756 | 0.2192 | 0.1330 | 0.0937 | 0.2155 | 0.2039 | 0.0860 | 0.1680 | 0.2016 | 0.2096 | 0.0924 | |
| 0.1596 | 0.1416 | 0.1304 | 0.0843 | 0.1668 | 0.0465 | 0.1654 | 0.1194 | 0.0804 | 0.1527 | 0.1826 | 0.0356 | 0.0405 | 0.1815 | 0.1478 | 0.0784 | |
| 0.2640 | 0.2412 | 0.2241 | 0.1744 | 0.1877 | 0.1411 | 0.0718 | 0.1728 | 0.1339 | 0.2539 | 0.2107 | 0.0504 | 0.0578 | 0.1698 | 0.2117 | 0.0572 | |
| 0.1404 | 0.0879 | 0.0784 | 0.0736 | 0.1163 | 0.1128 | 0.0774 | 0.0323 | 0.0705 | 0.1348 | 0.1662 | 0.0667 | 0.0699 | 0.1278 | 0.1319 | 0.0316 | |
| 0.1113 | 0.0662 | 0.0607 | 0.0568 | 0.0218 | 0.0195 | 0.0215 | 0.0174 | 0.0184 | 0.1088 | 0.0293 | 0.0181 | 0.0189 | 0.1051 | 0.1071 | 0.0204 | |
| 0.2489 | 0.1906 | 0.1388 | 0.1298 | 0.1008 | 0.1688 | 0.1358 | 0.1258 | 0.0880 | 0.0909 | 0.1938 | 0.1202 | 0.1243 | 0.1930 | 0.1999 | 0.1262 | |
| 0.2429 | 0.1486 | 0.1341 | 0.1638 | 0.1342 | 0.1283 | 0.0955 | 0.1226 | 0.1225 | 0.1984 | 0.0755 | 0.0798 | 0.0851 | 0.1886 | 0.1940 | 0.0856 | |
| 0.1046 | 0.0613 | 0.0187 | 0.0535 | 0.0193 | 0.0556 | 0.0191 | 0.0154 | 0.0152 | 0.1027 | 0.0248 | 0.0150 | 0.0153 | 0.0240 | 0.1019 | 0.0171 | |
| 0.1023 | 0.0593 | 0.0169 | 0.0522 | 0.0172 | 0.0155 | 0.0170 | 0.0138 | 0.0140 | 0.1005 | 0.0223 | 0.0143 | 0.0145 | 0.0216 | 0.0997 | 0.0160 | |
| 0.2368 | 0.1439 | 0.1299 | 0.1230 | 0.0904 | 0.0864 | 0.0894 | 0.0805 | 0.1190 | 0.2308 | 0.1447 | 0.1158 | 0.1193 | 0.0682 | 0.1892 | 0.1210 | |
| 0.1925 | 0.1381 | 0.1258 | 0.0817 | 0.1228 | 0.0826 | 0.0849 | 0.0765 | 0.1148 | 0.1873 | 0.1378 | 0.1497 | 0.0768 | 0.1395 | 0.0687 | 0.1542 | |
| 0.1266 | 0.1171 | 0.1089 | 0.1030 | 0.0325 | 0.0669 | 0.0324 | 0.0252 | 0.0254 | 0.1604 | 0.0435 | 0.0241 | 0.0265 | 0.1182 | 0.1201 | 0.0281 |
| Index | Rank | Rank | Rank | Factor Types | ||||
|---|---|---|---|---|---|---|---|---|
| 3.3222 | 1 | 3.0107 | 1 | 6.3329 | 1 | 0.3115 | Causal Factors | |
| 3.1854 | 2 | 2.3435 | 6 | 5.5289 | 2 | 0.8419 | Causal Factors | |
| 2.0007 | 9 | 1.8570 | 7 | 3.8576 | 9 | 0.1437 | Causal Factors | |
| 2.0640 | 8 | 1.6278 | 11 | 3.6918 | 10 | 0.4362 | Causal Factors | |
| 2.6125 | 4 | 1.8215 | 8 | 4.4341 | 7 | 0.7910 | Causal Factors | |
| 1.9135 | 11 | 1.6416 | 10 | 3.5551 | 11 | 0.2719 | Causal Factors | |
| 2.6224 | 3 | 1.7694 | 9 | 4.3918 | 8 | 0.8530 | Causal Factors | |
| 1.5186 | 12 | 1.4344 | 12 | 2.9530 | 12 | 0.0842 | Causal Factors | |
| 0.8012 | 14 | 1.4044 | 13 | 2.2056 | 14 | −0.6033 | Resultant Factors | |
| 2.3755 | 5 | 2.7855 | 2 | 5.1609 | 3 | −0.4100 | Resultant Factors | |
| 2.1993 | 6 | 2.3878 | 4 | 4.5871 | 4 | −0.1886 | Resultant Factors | |
| 0.6635 | 15 | 1.2081 | 16 | 1.8716 | 16 | −0.5446 | Resultant Factors | |
| 0.5972 | 16 | 1.3971 | 14 | 1.9943 | 15 | −0.7998 | Resultant Factors | |
| 2.0882 | 7 | 2.3740 | 5 | 4.4622 | 6 | −0.2858 | Resultant Factors | |
| 1.9338 | 10 | 2.6132 | 3 | 4.5470 | 5 | −0.6794 | Resultant Factors | |
| 1.1589 | 13 | 1.3810 | 15 | 2.5399 | 13 | −0.2221 | Resultant Factors |
| C′9×9 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.1331 | 0.2420 | 0.1950 | 0.2091 | 0.2116 | 0.2509 | 0.2469 | 0.2600 | 0.1552 | |
| 0.2819 | 0.1016 | 0.1965 | 0.2295 | 0.2278 | 0.2536 | 0.2546 | 0.2650 | 0.1607 | |
| 0.2013 | 0.2193 | 0.0558 | 0.1316 | 0.1299 | 0.2229 | 0.1851 | 0.1525 | 0.1153 | |
| 0.2609 | 0.2004 | 0.1468 | 0.0695 | 0.2192 | 0.2039 | 0.2016 | 0.2096 | 0.1342 | |
| 0.2640 | 0.2412 | 0.2241 | 0.1877 | 0.0718 | 0.2107 | 0.1698 | 0.2117 | 0.1403 | |
| 0.2429 | 0.1486 | 0.1341 | 0.1342 | 0.0955 | 0.0755 | 0.1886 | 0.1940 | 0.1077 | |
| 0.2368 | 0.1439 | 0.1299 | 0.0904 | 0.0894 | 0.1447 | 0.0682 | 0.1892 | 0.0970 | |
| 0.1925 | 0.1381 | 0.1258 | 0.1228 | 0.0849 | 0.1378 | 0.1395 | 0.0687 | 0.0897 | |
| 0.1610 | 0.1274 | 0.1072 | 0.1043 | 0.1003 | 0.1331 | 0.1291 | 0.1376 | 0.1760 |
| State | ||||||||
|---|---|---|---|---|---|---|---|---|
| −0.6869 | −0.6930 | −0.6357 | −0.6618 | −0.6695 | −0.6243 | −0.6067 | −0.5937 | |
| −0.5701 | −0.5758 | −0.5232 | −0.5469 | −0.5540 | −0.5127 | −0.4968 | −0.4850 | |
| 0.5701 | 0.5758 | 0.5232 | 0.5469 | 0.5540 | 0.5127 | 0.4968 | 0.4850 | |
| 0.6869 | 0.6930 | 0.6357 | 0.6618 | 0.6695 | 0.6243 | 0.6067 | 0.5937 |
| State | ||||
|---|---|---|---|---|
| −0.6933 | −0.5760 | 0.5760 | 0.6933 | |
| −0.6528 | −0.5387 | 0.5387 | 0.6528 | |
| −0.6235 | −0.5121 | 0.5121 | 0.6235 | |
| −0.6188 | −0.5078 | 0.5078 | 0.6188 | |
| −0.6123 | −0.5019 | 0.5019 | 0.6123 | |
| −0.6604 | −0.5457 | 0.5457 | 0.6604 | |
| −0.6551 | −0.5408 | 0.5408 | 0.6551 | |
| −0.6661 | −0.5509 | 0.5509 | 0.6661 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, S.; Zhu, K.; Guo, P. Research on Quantitative Assessment and Dynamic Reasoning Method for Emergency Response Capability in Prefabricated Construction Safety. Buildings 2023, 13, 2311. https://doi.org/10.3390/buildings13092311
Tang S, Zhu K, Guo P. Research on Quantitative Assessment and Dynamic Reasoning Method for Emergency Response Capability in Prefabricated Construction Safety. Buildings. 2023; 13(9):2311. https://doi.org/10.3390/buildings13092311
Chicago/Turabian StyleTang, Shanrong, Ke Zhu, and Peiwen Guo. 2023. "Research on Quantitative Assessment and Dynamic Reasoning Method for Emergency Response Capability in Prefabricated Construction Safety" Buildings 13, no. 9: 2311. https://doi.org/10.3390/buildings13092311
APA StyleTang, S., Zhu, K., & Guo, P. (2023). Research on Quantitative Assessment and Dynamic Reasoning Method for Emergency Response Capability in Prefabricated Construction Safety. Buildings, 13(9), 2311. https://doi.org/10.3390/buildings13092311








