Shear and Bending Performances of Reinforced Concrete Beams with Different Sizes of Circular Openings
Abstract
1. Introduction
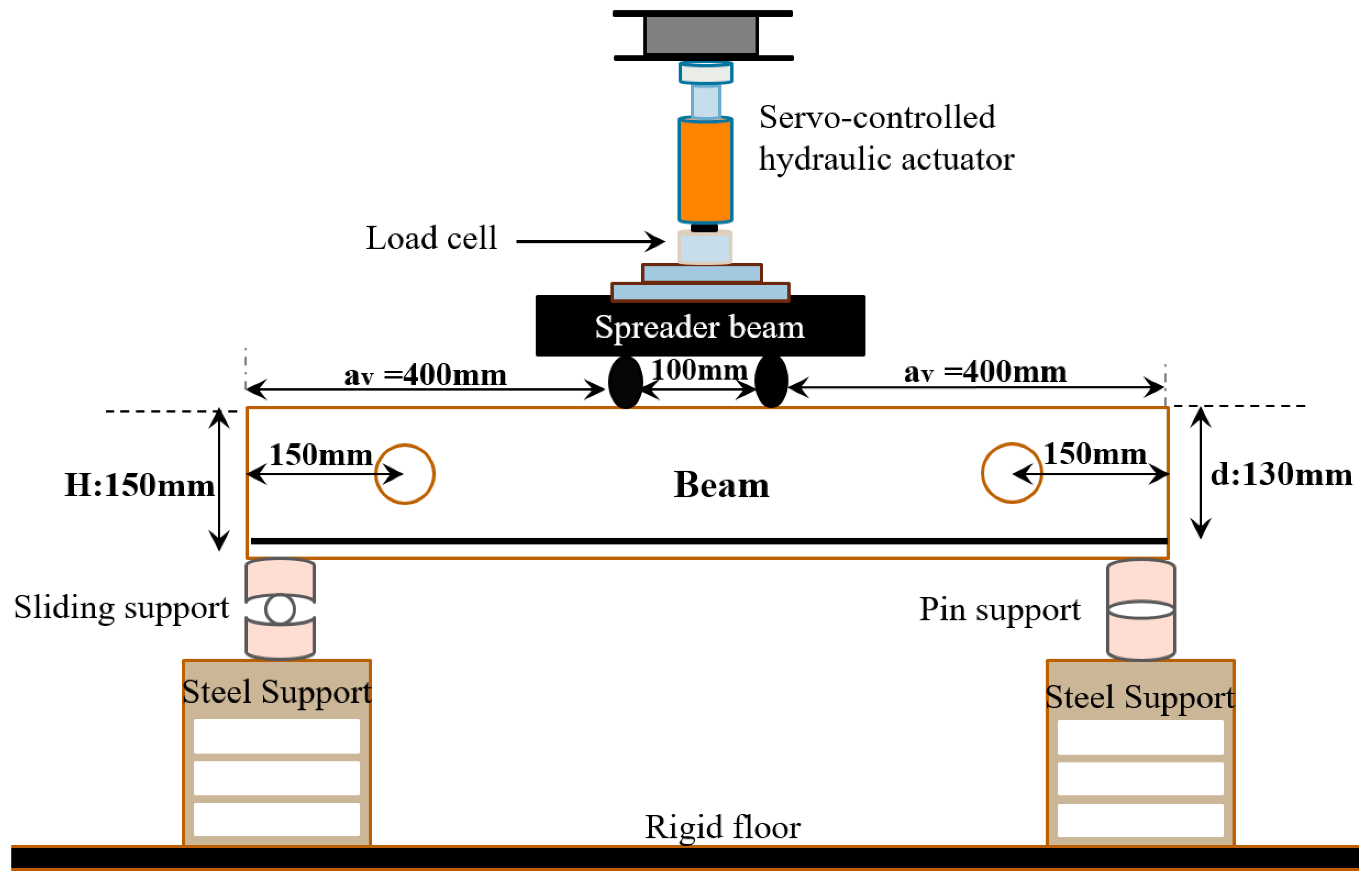
2. Materials and Method
2.1. Influence of D/H Ratio on Beam Behavior
2.1.1. First Group of Beams
2.1.2. Second Group of Beams
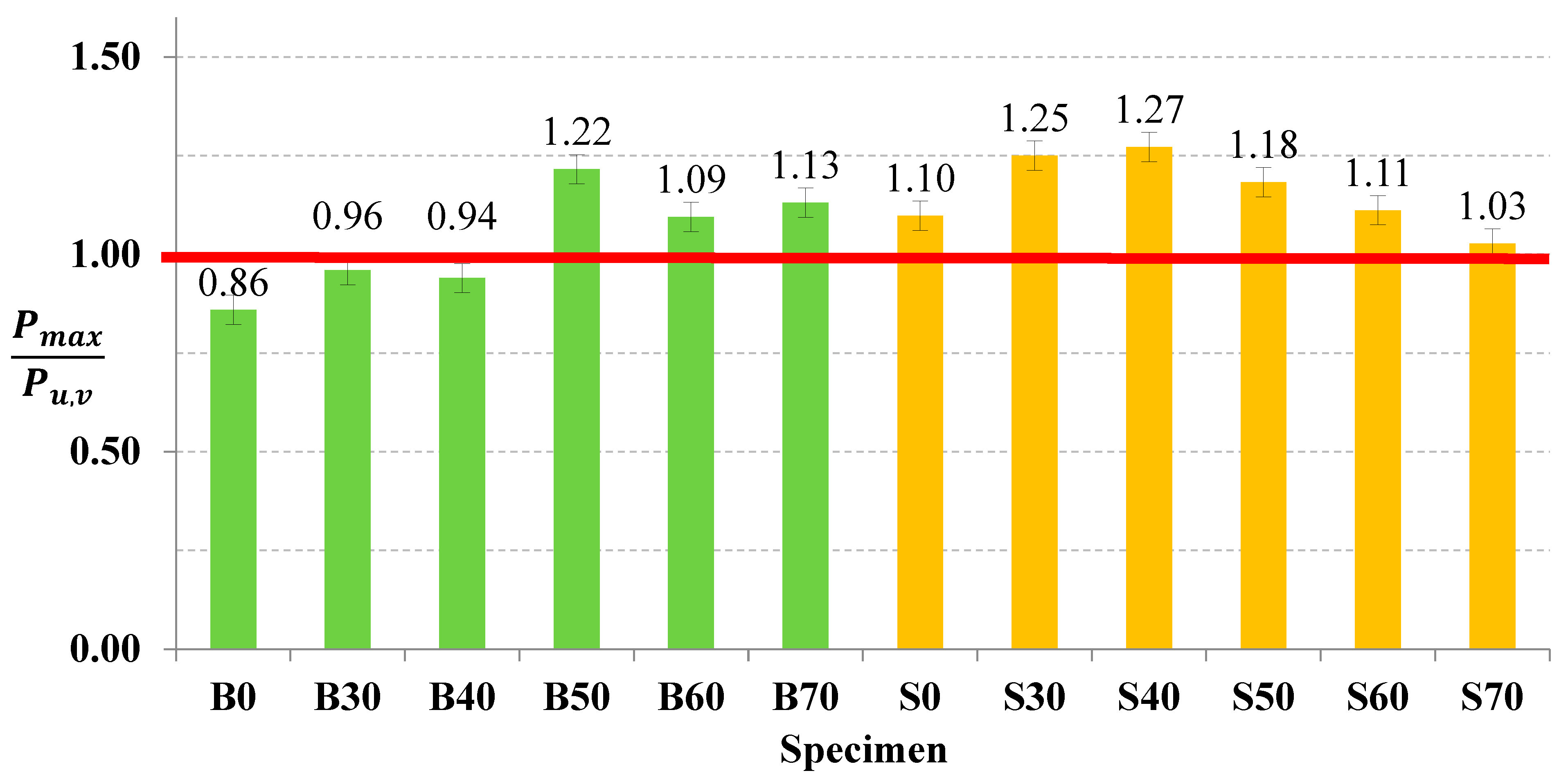
3. Analytical Ultimate Beam Capacity
4. Conclusions
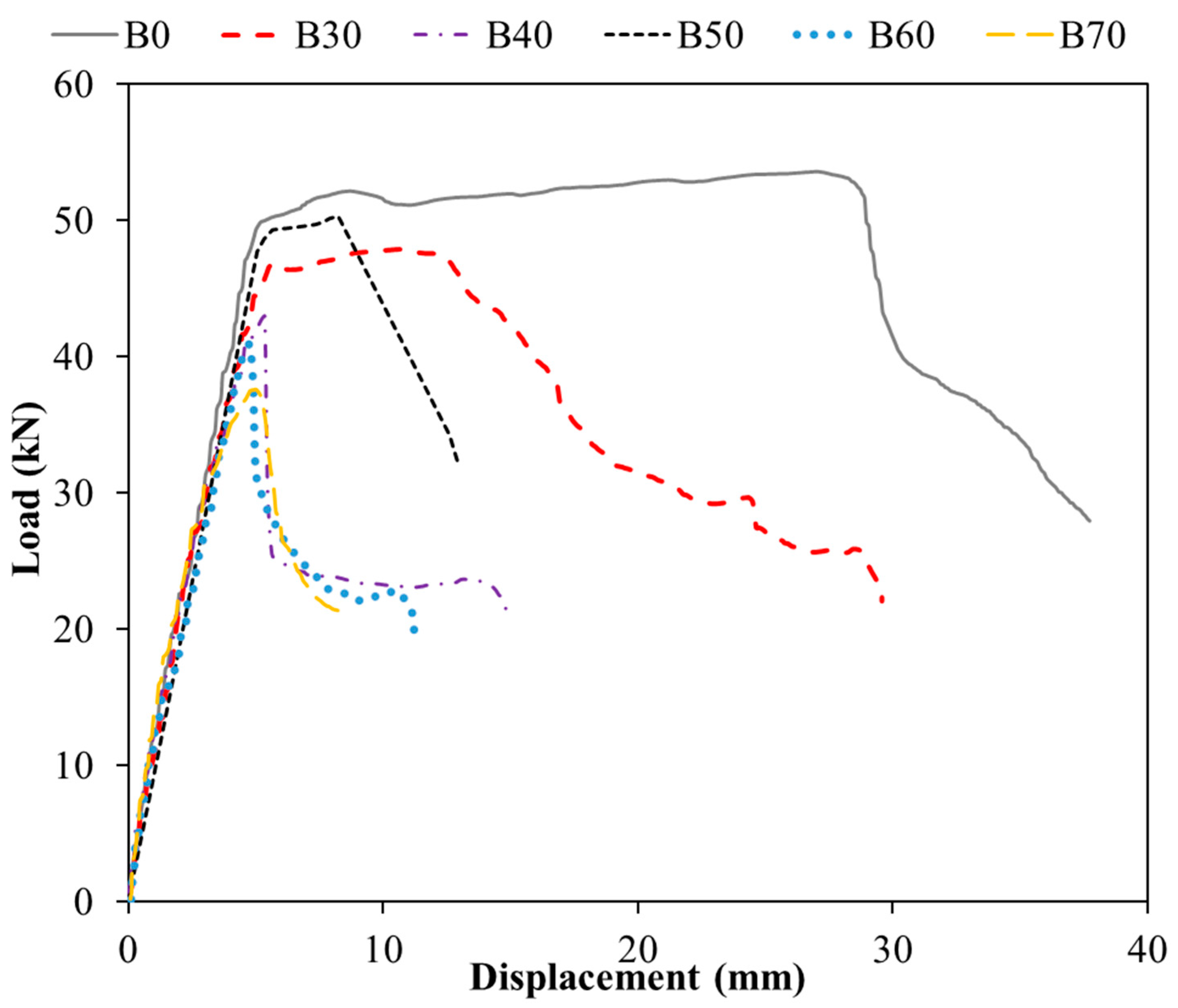
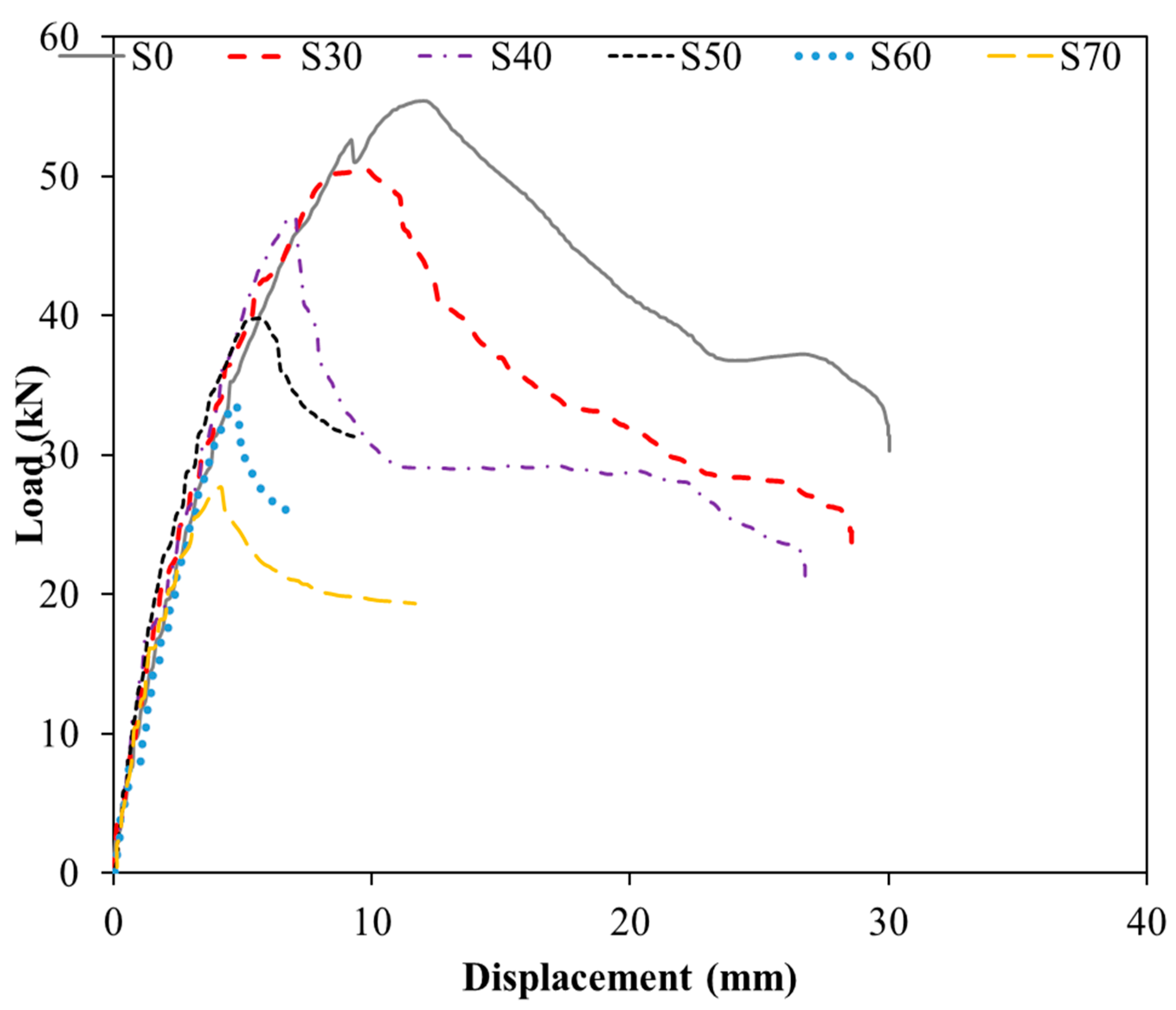
- The failure type of RC beams with adequate shear reinforcement turns from pure flexural failure to beam- or frame-type shear failure as the diameter of transverse openings in the beam increase. In cases of inadequate shear reinforcement, on the other hand, the reference beams without openings are subject to shear-tension or shear-compression failure, while the specimens with openings experience shear failures similar to the beams with adequate shear reinforcement.
- The tests indicated that the load-carrying capacities of RC beams with circular openings and the vertical deflections at the ultimate load decrease significantly with increasing opening diameter. Furthermore, the reduction in the load capacity increases with a decreasing transverse reinforcement ratio, i.e., increasing stirrup spacing, for identical opening diameters. Larger web openings result in greater reductions in the shear capacities of beams with more widely spaced stirrups, and therefore, RC beams with less shear reinforcement are affected to a greater extent by the introduction of transverse opening. As opposed to the finding about the load capacity, the decrease in the deflection at the ultimate load was found to decrease with a decreasing transverse reinforcement ratio for identical opening diameters.
- With an inadequate amount of shear reinforcement, energy absorption capacities in both elastic and plastic ranges of beam behavior decrease significantly with increasing opening diameter. On the contrary, the amount of energy dissipated in the elastic range decreases to a much lesser extent, while the total energy is reduced significantly in the presence of an adequate amount of shear reinforcement.
- The reductions in the ductilities of RC beams with increasing opening diameter are less pronounced if the beams are reinforced with smaller amounts of shear reinforcement. In both types of beams with adequate and inadequate amounts of shear reinforcement, the reduction trend in the beam ductility with increasing opening diameter is random rather than regular (steady).
- The theoretical shear strength values of the RC beams with circular openings were found to be in close agreement with the experimental values. The accuracy of the theoretical estimates was shown to increase with a decreasing amount of shear reinforcement in the beam. Accordingly, the shear strength formula, originally developed by Mansur and Tan (1999) and later adopted by various researchers, can be conservatively used for beams with circular openings. None of the beams of the present study failed prematurely at load levels smaller than the analytical estimate provided by this formula.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, H.; Li, M.; Yuan, Y.; Bai, H. Theoretical analysis on the lateral drift of precast concrete frame with replaceable artificial controllable plastic hinges. J. Build. Eng. 2022, 62, 105386. [Google Scholar] [CrossRef]
- Ghasemi, M.; Zhang, C.; Khorshidi, H.; Zhu, L.; Hsiao, P.-C. Seismic upgrading of existing RC frames with displacement-restraint cable bracing. Eng. Struct. 2023, 282, 115764. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, W.; Yang, J. Analysis of stochastic process to model safety risk in construction industry. J. Civ. Eng. Manag. 2021, 27, 87–99. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, W.; Liu, X. Assessment of diagonal macrocrack-induced debonding mechanisms in FRP-strengthened RC beams. J. Compos. Constr. 2022, 26, 04022056. [Google Scholar] [CrossRef]
- Özkılıç, Y.O.; Karalar, M.; Aksoylu, C.; Beskopylny, A.N.; Stel’makh, S.A.; Shcherban, E.M.; Qaidi, S.; da Sa Pereira, I.; Monteiro, S.N.; Azevedo, A.R.G. Shear Performance of Reinforced Expansive Concrete Beams Utilizing Aluminium Waste. J. Mater. Res. Technol. 2023, 24, 5433–5448. [Google Scholar] [CrossRef]
- Wang, M.; Yang, X.; Wang, W. Establishing a 3D aggregates database from X-ray CT scans of bulk concrete. Constr. Build. Mater. 2022, 315, 125740. [Google Scholar] [CrossRef]
- Shi, T.; Liu, Y.; Zhao, X.; Wang, J.; Zhao, Z.; Corr, D.J.; Shah, S.P. Study on mechanical properties of the interfacial transition zone in carbon nanofiber-reinforced cement mortar based on the PeakForce tapping mode of atomic force microscope. J. Build. Eng. 2022, 61, 105248. [Google Scholar] [CrossRef]
- Shi, T.; Liu, Y.; Hu, Z.; Cen, M.; Zeng, C.; Xu, J.; Zhao, Z. Deformation performance and fracture toughness of carbon nanofiber-modified cement-based materials. ACI Mater. J. 2022, 119, 119–128. [Google Scholar]
- Zhou, S.; Lu, C.; Zhu, X.; Li, F.J.E. Preparation and characterization of high-strength geopolymer based on BH-1 lunar soil simulant with low alkali content. Engineering 2021, 7, 1631–1645. [Google Scholar] [CrossRef]
- Fang, B.; Hu, Z.; Shi, T.; Liu, Y.; Wang, X.; Yang, D.; Zhu, K.; Zhao, X.; Zhao, Z. Research progress on the properties and applications of magnesium phosphate cement. Ceram. Int. 2022, 49, 4001–4016. [Google Scholar] [CrossRef]
- Mansur, M. Design of reinforced concrete beams with web openings. In Proceedings of the 6th Asia-Pacific structural engineering and construction conference (ASPEC 2006), Kuala Lumpur, Malaysia, 5–6 September 2006; pp. 5–6. [Google Scholar]
- Özkılıç, Y.O.; Aksoylu, C.; Gemi, L.; Arslan, M.H. Behavior of CFRP-strengthened RC BEAMS with Circular Web Openings in Shear Zones: Numerical Study. In Structures; Elsevier: Amsterdam, The Netherlands, 2022; pp. 1369–1389. [Google Scholar]
- Wojdak, R. Structural analysis of a failured RC beam with openings in a building under construction. Czas. Techniczne. Bud. 2013, 110, 157–168. [Google Scholar]
- Mansur, M.; Tan, K.-H. Concrete Beams with Openings: Analysis and Design; CRC Press: Boca Raton, FL, USA, 1999; Volume 20. [Google Scholar]
- El Maaddawy, T.; Sherif, S. FRP composites for shear strengthening of reinforced concrete deep beams with openings. Compos. Struct. 2009, 89, 60–69. [Google Scholar] [CrossRef]
- Chin, S.; Shafiq, N.; Nuruddin, M. Strengthening of RC beams with large openings in shear by CFRP laminates: Experiment and 2D nonlinear finite element analysis. Res. J. Appl. Sci. Eng. Technol. 2012, 4, 1172–1180. [Google Scholar]
- Ashour, A.F.; Rishi, G. Tests of reinforced concrete continuous deep beams with web openings. Struct. J. 2000, 97, 418–426. [Google Scholar]
- Mansur, M.A.; Tan, K.H.; Lee, S.-L. Collapse loads of R/C beams with large openings. J. Struct. Eng. 1984, 110, 2602–2618. [Google Scholar] [CrossRef]
- Osman, B.H.; Wu, E.; Ji, B.; Abdulhameed, S.S. Shear behavior of reinforced concrete (RC) beams with circular web openings without additional shear reinforcement. KSCE J. Civ. Eng. 2017, 21, 296–306. [Google Scholar] [CrossRef]
- Sayed, A.M. Numerical study using FE simulation on rectangular RC beams with vertical circular web openings in the shear zones. Eng. Struct. 2019, 198, 109471. [Google Scholar] [CrossRef]
- ACI Committee. Building Code Requirements for Structural Concrete (ACI 318-05) and Commentary (ACI 318R-05); American Concrete Institute: Farmington Hills, MI, USA, 2005. [Google Scholar]
- Yamada, Y. Shear Load Carrying Mechanisms of RC Beams Without Stirrups Strengthened by Multiple Holes. J. Jpn. Soc. Civ. Eng. Ser. E2 (Mater. Concr. Struct.) 2019, 75, 265–278. [Google Scholar] [CrossRef]
- Yamada, Y. An analytical study on interactions of artificial cracks and holes contributing to increases in the shear strengths of RC beams. J. Adv. Concr. Technol. 2019, 17, 579–591. [Google Scholar] [CrossRef]
- Yamada, Y. A study on construction of identifying method of hole positions contributing to change in shear strengths of RC beams without stirrups based on image analyses. J. Struct. Eng. JSCE 2020, 66, 675–683. [Google Scholar]
- Torunbalci, N. Behaviour and design of large rectangular openings in reinforced concrete beams. Archit. Sci. Rev. 2002, 45, 91–96. [Google Scholar] [CrossRef]
- Özkılıç, Y.O.; Aksoylu, C.; Arslan, M.H. Numerical evaluation of effects of shear span, stirrup spacing and angle of stirrup on reinforced concrete beam behaviour. Struct. Eng. Mech. Int’l J. 2021, 79, 309–326. [Google Scholar]
- Özkılıç, Y.O.; Aksoylu, C.; Arslan, M.H. Experimental and numerical investigations of steel fiber reinforced concrete dapped-end purlins. J. Build. Eng. 2021, 36, 102119. [Google Scholar] [CrossRef]
- Aksoylu, C.; Yazman, Ş.; Özkılıç, Y.O.; Gemi, L.; Arslan, M.H. Experimental analysis of reinforced concrete shear deficient beams with circular web openings strengthened by CFRP composite. Compos. Struct. 2020, 249, 112561. [Google Scholar] [CrossRef]
- Fu, L.; Wang, H.; Nakamura, H.; Wang, D. Mechanism of Improvement in the Shear Performance of RC Beams Due to Multiple Small Transverse Openings. In Structures; Elsevier: Amsterdam, The Netherlands, 2022; pp. 758–772. [Google Scholar]
- Amiri, S.; Masoudnia, R.; Pabarja, A.A. The study of the effects of web openings on the concrete beams. Aust. J. Basic Appl. Sci. 2011, 5, 547–556. [Google Scholar]
- Daniel, J.J. Experimental and Numerical Study on the CRACKING behavior and Flexural Strength of RC Shallow beams with Rectangular Opening And Varying Length. In Structures; Elsevier: Amsterdam, The Netherlands, 2022; pp. 460–468. [Google Scholar]
- Ali, S.R.M.; Saeed, J.A. Shear capacity and behavior of high-strength concrete beams with openings. Eng. Struct. 2022, 264, 114431. [Google Scholar] [CrossRef]
- Herrera, L.; Anacleto-Lupianez, S.; Lemnitzer, A. Experimental performance of RC moment frame beams with rectangular openings. Eng. Struct. 2017, 152, 149–167. [Google Scholar] [CrossRef]
- Morsya, A.; Barima, A.M. Behavior of RC Beams with Openings using Different Strengthening Techniques. Int. J. Sci. Basic Appl. Res. (IJSBAR) 2019, 46, 195–219. [Google Scholar]
- Al-Sheikh, S.A. Flexural behavior of RC beams with opening. Concr. Res. Lett. 2014, 5, 812–824. [Google Scholar]
- Ramadan, O.M.; Metwally, K.G.; Shaban, W.M. Proposed Recommendations for the Design of Reinforced Concrete Beams with Openings. In Proceedings of the World Congress on Advanced in Structural Engineering and Mechanics (NSEN15), Incheon, Republic of Korea, 25–29 August 2015. [Google Scholar]
- Elsanadedy, H.M.; Al-Salloum, Y.A.; Almusallam, T.H.; Alshenawy, A.O.; Abbas, H. Experimental and numerical study on FRP-upgraded RC beams with large rectangular web openings in shear zones. Constr. Build. Mater. 2019, 194, 322–343. [Google Scholar] [CrossRef]
- Liu, T.-J.; Chen, S.-W.; Feng, Z.-H.; Liu, H.-Y. Effect of web openings on flexural behaviour of underground metro station RC beams under static and cyclic loading. Adv. Civ. Eng. 2020, 2020, 1210485. [Google Scholar] [CrossRef]
- Ahmed, A.; Fayyadh, M.; Naganathan, S.; Nasharuddin, K. Reinforced concrete beams with web openings: A state of the art review. Mater. Des. 2012, 40, 90–102. [Google Scholar] [CrossRef]
- Osman, B.H.; Wu, E.; Ji, B.; S Abdelgader, A.M. A state of the art review on reinforced concrete beams with openings retrofitted with FRP. Int. J. Adv. Struct. Eng. 2016, 8, 253–267. [Google Scholar] [CrossRef]
- Vuggumudi, S. Experimental Study on Shear Strengthening of RC T-Beams with Web Openings Using FRP Composites. Ph.D. Thesis, NIT Rourkela, Rourkela, India, 2013. [Google Scholar]
- Amiri, J.V.; Alibygie, M.H. Effect of small circular opening on the shear and flexural behavior and ultimate strength of reinforced concrete beams using normal and high strength concrete. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Aykac, B.; Kalkan, I.; Aykac, S.; Egriboz, Y.E. Flexural behavior of RC beams with regular square or circular web openings. Eng. Struct. 2013, 56, 2165–2174. [Google Scholar] [CrossRef]
- Abdalla, H.; Torkey, A.; Haggag, H.; Abu-Amira, A. Design against cracking at openings in reinforced concrete beams strengthened with composite sheets. Compos. Struct. 2003, 60, 197–204. [Google Scholar] [CrossRef]
- Osman, B.H.; Wu, E.; Ji, B.; Abdulhameed, S.S. Repair of pre-cracked reinforced concrete (RC) Beams with openings strengthened using FRP sheets under sustained load. Int. J. Concr. Struct. Mater. 2017, 11, 171–183. [Google Scholar] [CrossRef]

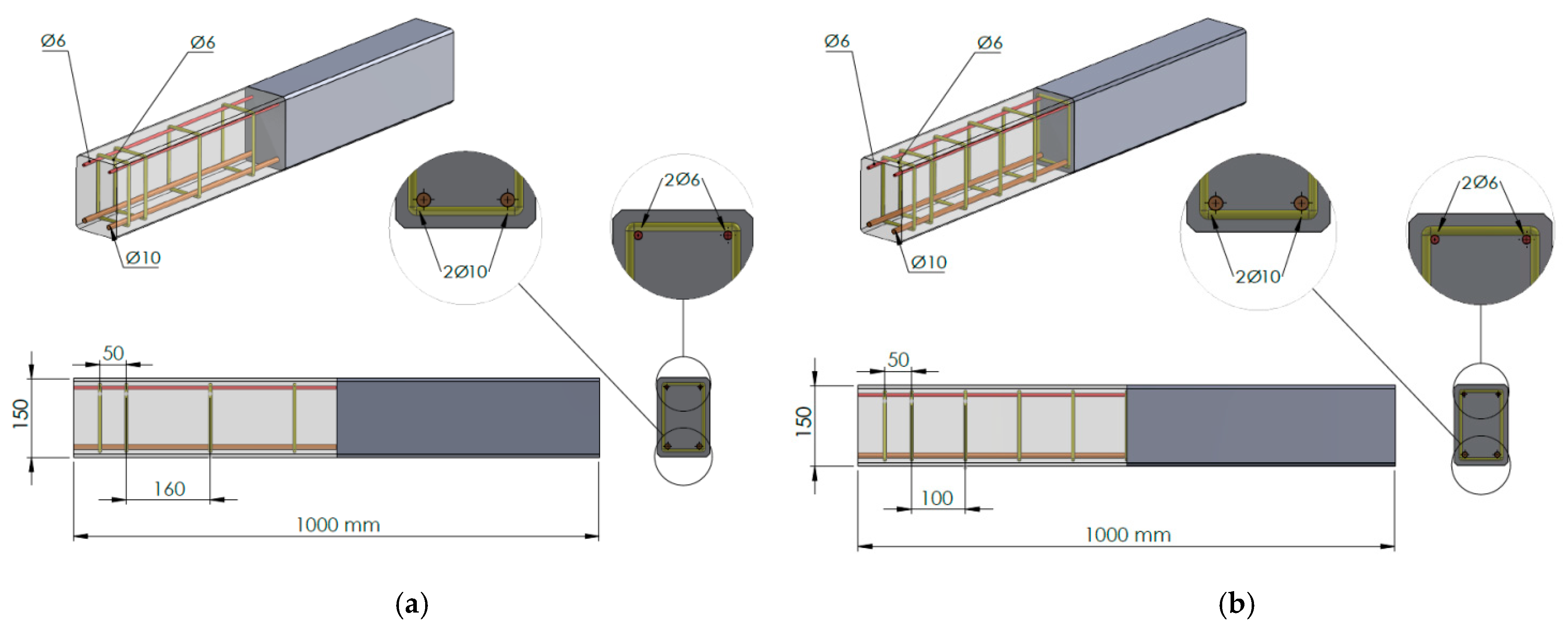


| Specimen Notation | Tensile Longitudinal Reinforcement | Compression Longitudinal Reinforcement | Stirrups (mm) | Opening Diameter (D) (mm) | D/H |
|---|---|---|---|---|---|
| B0 | 2ϕ10 | 2ϕ6 | ϕ6/100 | 0 | 0 |
| B30 | 30 | 0.20 | |||
| B40 | 40 | 0.27 | |||
| B50 | 50 | 0.33 | |||
| B60 | 60 | 0.40 | |||
| B70 | 70 | 0.47 |
| Specimen Name | Tensile Longitudinal Reinforcement | Compression Longitudinal Reinforcement | Stirrups (mm) | Opening Diameter (D) (mm) | D/H |
|---|---|---|---|---|---|
| S0 | 2ϕ10 | 2ϕ6 | ϕ6/160 | 0 | 0 |
| S30 | 30 | 0.20 | |||
| S40 | 40 | 0.27 | |||
| S50 | 50 | 0.33 | |||
| S60 | 60 | 0.40 | |||
| S70 | 70 | 0.47 |
| Test No. | Pmax (kN) | Decrease in Pmax (%) | δPmax (mm) | Decrease in δPmax (%) | SPmax (kN/mm) | Decrease in SPmax (%) | δy (mm) | δu (mm) | μ (mm/mm) | Decrease in μ (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| B0 | 53.58 | - | 26.95 | - | 1.98 | 0 | 4.50 | 29.44 | 6.53 | 0 |
| B30 | 47.88 | 11 | 10.64 | 60 | 4.49 | 127 | 4.42 | 15.69 | 3.54 | 46 |
| B40 | 42.96 | 20 | 5.36 | 80 | 8.01 | 305 | 4.05 | 5.41 | 1.33 | 80 |
| B50 | 50.51 | 6 | 8.24 | 69 | 6.10 | 208 | 4.54 | 10.29 | 2.26 | 65 |
| B60 | 40.94 | 24 | 4.77 | 82 | 8.56 | 332 | 3.80 | 4.94 | 1.30 | 80 |
| B70 | 37.59 | 30 | 5.02 | 81 | 7.48 | 278 | 3.44 | 5.57 | 1.61 | 75 |
| S0 | 55.39 | 0 | 11.97 | - | 4.62 | 0 | 7.57 | 16.71 | 2.20 | 0 |
| S30 | 50.44 | 8 | 9.75 | 18 | 5.17 | 12 | 6.07 | 12.29 | 2.02 | 8 |
| S40 | 47.06 | 15 | 6.91 | 42 | 6.81 | 47 | 5.00 | 7.61 | 1.52 | 31 |
| S50 | 39.78 | 28 | 5.53 | 53 | 7.18 | 55 | 3.70 | 7.22 | 1.95 | 11 |
| S60 | 33.65 | 39 | 4.65 | 61 | 7.23 | 56 | 3.55 | 5.49 | 1.54 | 30 |
| S70 | 27.64 | 50 | 4.17 | 65 | 6.61 | 43 | 2.91 | 5.42 | 1.86 | 15 |
| Test No. | δmax (mm) | EPmax (kj) | Ey (kj) | Decrease in Ey (%) | Ep (kj) | ET (kj) | Decrease in ET (%) | Failure Type | Ductility Level |
|---|---|---|---|---|---|---|---|---|---|
| B0 | 37.73 | 1.278 | 0.111 | 0 | 0.977 | 1.693 | 0 | FS | Sufficient |
| B30 | 29.57 | 0.393 | 0.100 | 10 | 0.928 | 1.029 | 39 | FS + S | Partially |
| B40 | 14.81 | 0.142 | 0.089 | 20 | 0.274 | 0.363 | 79 | S | Deficient |
| B50 | 12.93 | 0.277 | 0.120 | −8 | 0.353 | 0.473 | 72 | S | Deficient |
| B60 | 11.25 | 0.111 | 0.073 | 34 | 0.192 | 0.264 | 84 | S | Deficient |
| B70 | 8.56 | 0.126 | 0.068 | 39 | 0.144 | 0.213 | 87 | S | Deficient |
| S0 | 30.03 | 0.451 | 0.220 | 0 | 0.988 | 1.207 | 0 | S | Deficient |
| S30 | 28.57 | 0.340 | 0.163 | 26 | 0.812 | 0.975 | 19 | S | Deficient |
| S40 | 26.77 | 0.206 | 0.119 | 46 | 0.661 | 0.780 | 35 | S | Deficient |
| S50 | 9.51 | 0.147 | 0.078 | 65 | 0.200 | 0.278 | 77 | S | Deficient |
| S60 | 7.09 | 0.094 | 0.057 | 74 | 0.100 | 0.157 | 87 | S | Deficient |
| S70 | 11.67 | 0.078 | 0.044 | 80 | 0.185 | 0.230 | 81 | S | Deficient |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Özkılıç, Y.O.; Aksoylu, C.; Hakeem, I.Y.; Özdöner, N.; Kalkan, İ.; Karalar, M.; Stel’makh, S.A.; Shcherban’, E.M.; Beskopylny, A.N. Shear and Bending Performances of Reinforced Concrete Beams with Different Sizes of Circular Openings. Buildings 2023, 13, 1989. https://doi.org/10.3390/buildings13081989
Özkılıç YO, Aksoylu C, Hakeem IY, Özdöner N, Kalkan İ, Karalar M, Stel’makh SA, Shcherban’ EM, Beskopylny AN. Shear and Bending Performances of Reinforced Concrete Beams with Different Sizes of Circular Openings. Buildings. 2023; 13(8):1989. https://doi.org/10.3390/buildings13081989
Chicago/Turabian StyleÖzkılıç, Yasin Onuralp, Ceyhun Aksoylu, Ibrahim Y. Hakeem, Nebi Özdöner, İlker Kalkan, Memduh Karalar, Sergey A. Stel’makh, Evgenii M. Shcherban’, and Alexey N. Beskopylny. 2023. "Shear and Bending Performances of Reinforced Concrete Beams with Different Sizes of Circular Openings" Buildings 13, no. 8: 1989. https://doi.org/10.3390/buildings13081989
APA StyleÖzkılıç, Y. O., Aksoylu, C., Hakeem, I. Y., Özdöner, N., Kalkan, İ., Karalar, M., Stel’makh, S. A., Shcherban’, E. M., & Beskopylny, A. N. (2023). Shear and Bending Performances of Reinforced Concrete Beams with Different Sizes of Circular Openings. Buildings, 13(8), 1989. https://doi.org/10.3390/buildings13081989












