A Novel Response Factor-Based Method for In Situ Measurement of Wall Thermal Resistance
Abstract
1. Introduction
| Measurement Methods | The Calculation Formula for Wall Thermal Resistance |
|---|---|
| Average method [5] (Standard HFM method) | |
| Dynamic analysis method [5,19] | |
| Shi et al. [14] | |
| Rasooli et al. [15] | |
| Park et al. [17] | |
| Shen et al. [18] | |
| Laurenti et al. [19] | |
| Pentaur method from Flores Larsen et al. [20] |
| Ref. No. | Method | Estimation Errors (%) | Convergence Time (Days) | Test Condition | |||
|---|---|---|---|---|---|---|---|
| Period | Location | Wall Type | Data Source | ||||
| [14] | Average method with storage corrections (RHS-HFM) | 3.86 | 2 | 1/27–1/29 (2 days) | Hot summer and cold winter areas in China | Clay hollow brick with cement mortar and insulation. | In situ measurement |
| Double-side heat flow meter method (D-HFM) | 10.49 | >2 | |||||
| Average method (use inside heat flux) | 3.13 | 2 | |||||
| Average method (use outside heat flux) | 16.58 | >2 | |||||
| [15] | Double-side heat flux methods | 1.4 | 5 | 2018/04 (16 days) | Netherlands | Unknown but insulation inside the construction. | In situ measurement |
| Average method (use inside heat flux) | <5 | >16 | |||||
| Average method (use outside heat flux) | <5 | >16 | |||||
| [17] | Temperature based method (TBM) | 0.21–1.79 | NA | 2021/02–2021/04 | Korea | Concrete wall; insulated curtain wall structure with panel finishing. | In situ measurement |
| Average method | 0.20–1.82 | NA | |||||
| [19] | Proposed dynamic method | 0.1–4 | 1–12.5 | An entire year (24 datasets with 15 days for each set) | NA | Light, well-insulated wall; massive wall with insulation layers on both sides; moderately massive homogeneous wall. | Simulation |
| [20] | Average method | 15.0 | 20 | Four seasons with 30 days for each season | Salta, Argentina | Compound wall (solid brick and hollow brick wall with insulation). | Simulation |
| Average method with storage corrections | 5.0 | 6–18 | |||||
| Fourier method | >17.0 | 8–24 | |||||
| Pentaur method | <5.0 | 2 | |||||
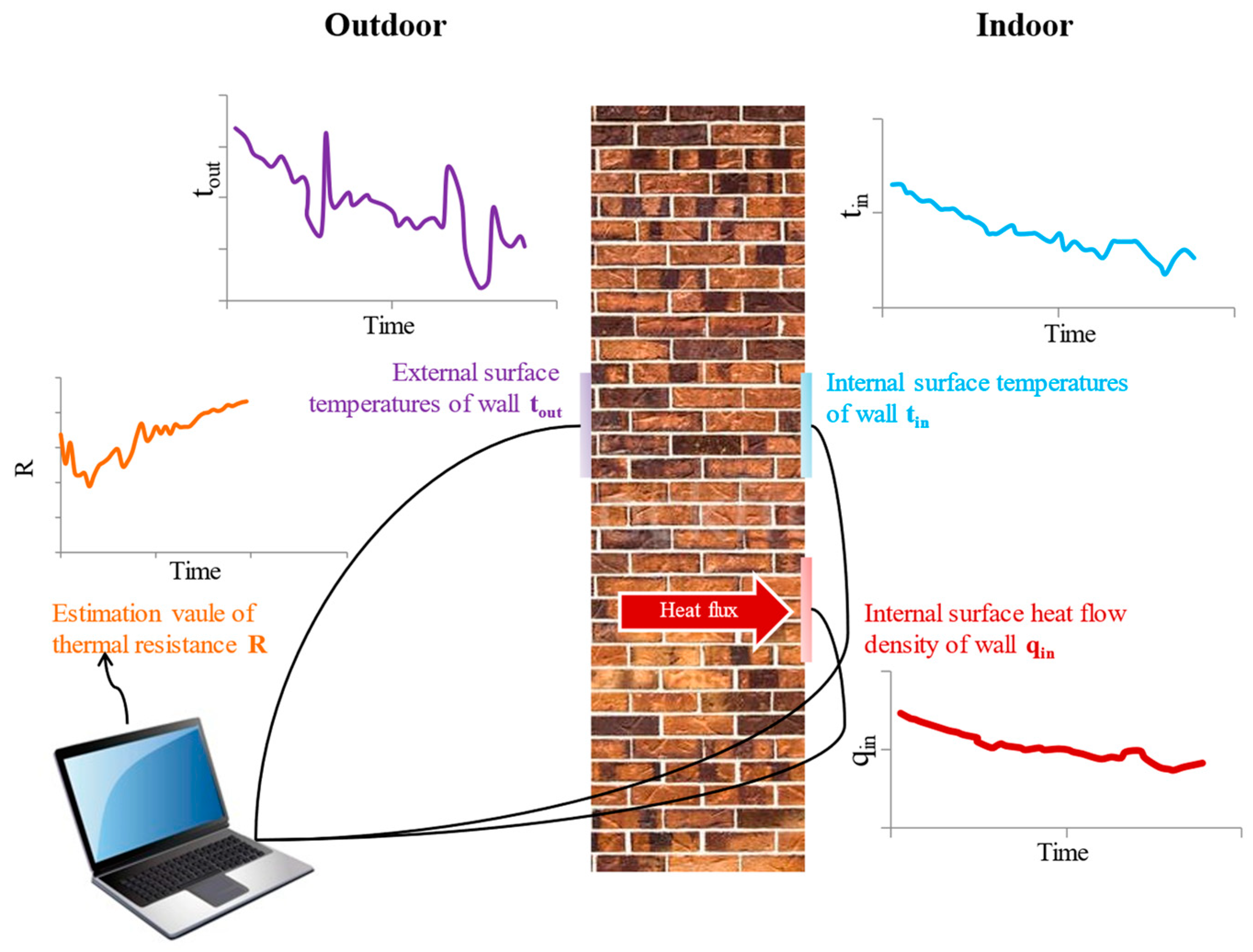
2. Methods
2.1. Fundamentals of Wall Heat Conduction Process
2.2. A Truncation Model for Wall Thermal Resistance Calculation
2.3. Convergence Criteria of In Situ Measurement
- Monotonicity: decreases with the increase of and , i.e., ;
- Tropism: the calculated value R approaches the true value when n and L tend to infinity, i.e., when and .
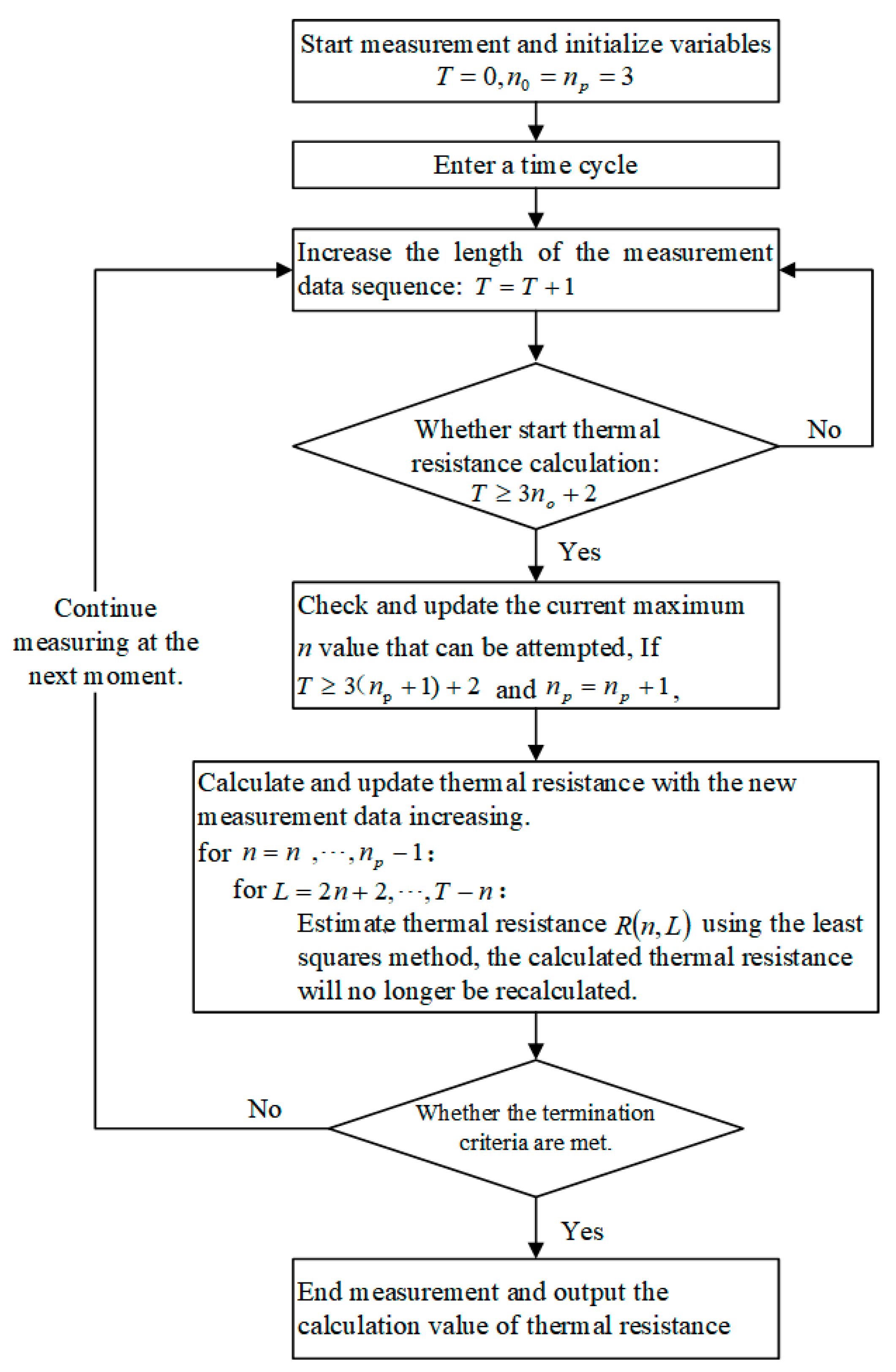
2.4. Implementation Process
- (1)
- Take the initial n value as 3 and the initial value as 8.
- (2)
- Start the initial estimation of wall thermal resistance when obtaining the length of the data .
- (3)
- With the increase in measurement time and data accumulation, try to increase the values of n and , and update the corresponding estimation of wall thermal resistance according to Equation (8).
- (4)
- When the criteria in the form of Equations (16)–(18) is met, output the estimated thermal resistance value at that time and end the measurement.
3. Theoretical Validation
3.1. Selection of Walls
3.2. Validation of Truncated Models
3.2.1. Truncation Error of Response Factors
3.2.2. Residual Error of Least Squares
4. Experiment Validation
4.1. Performance Indicators
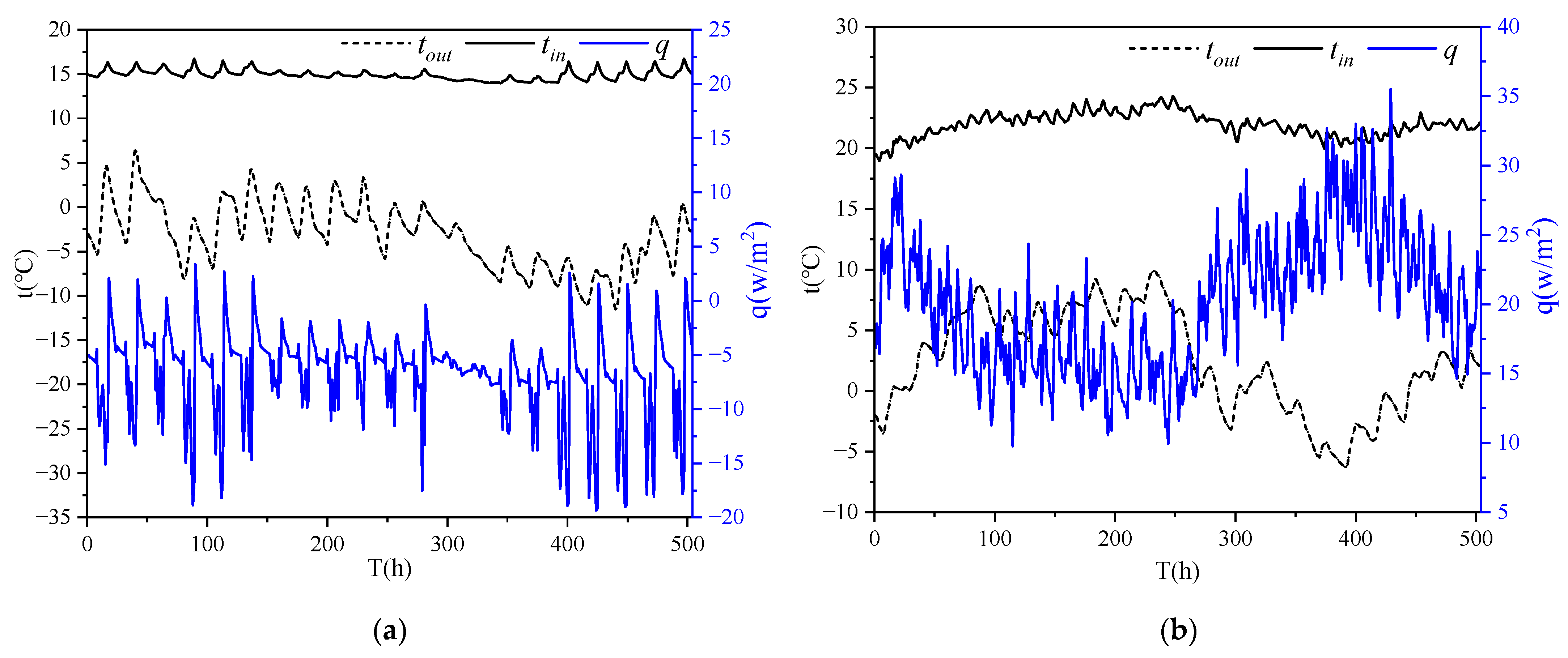
4.2. Simulation and Measurement Datasets
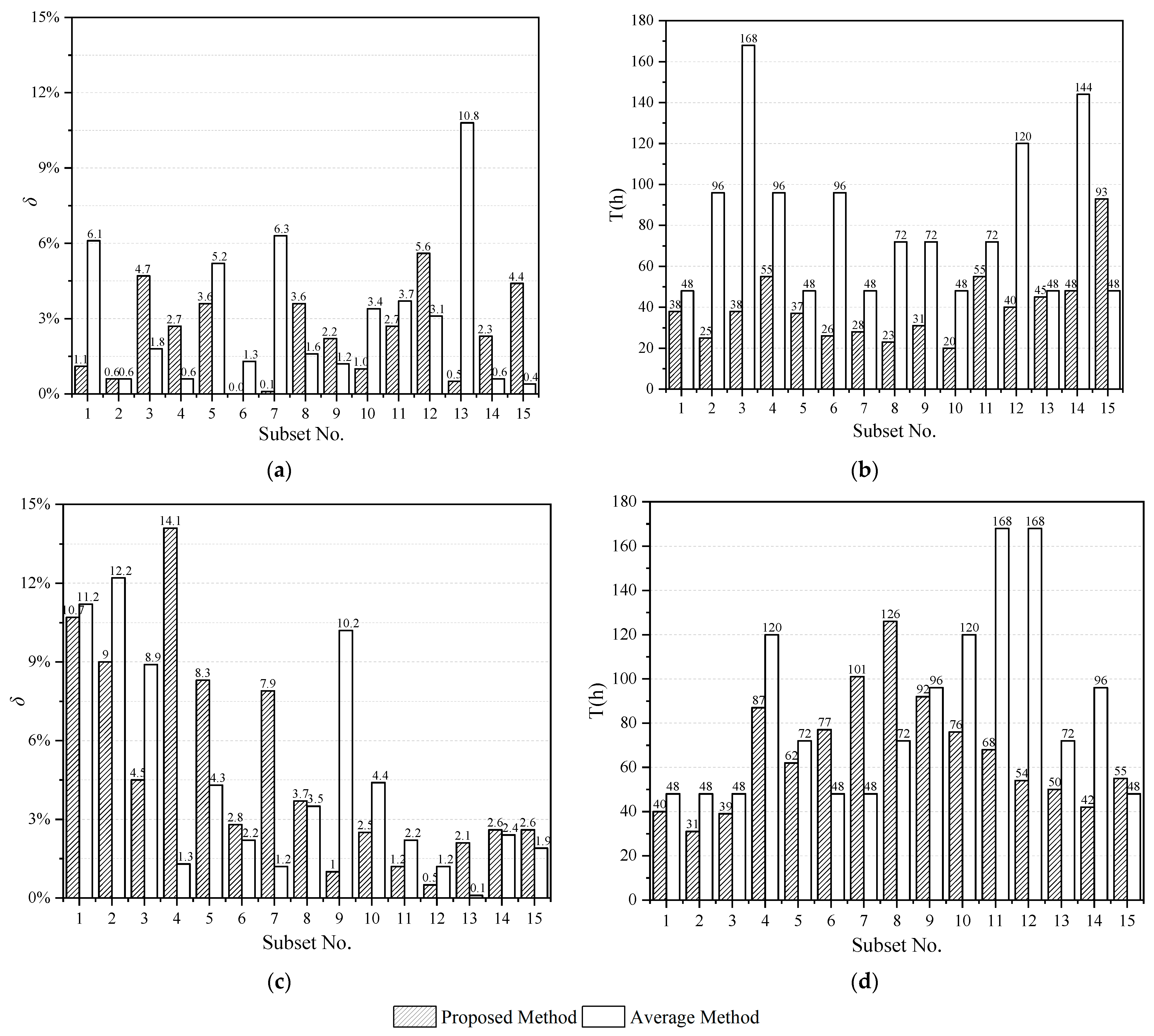
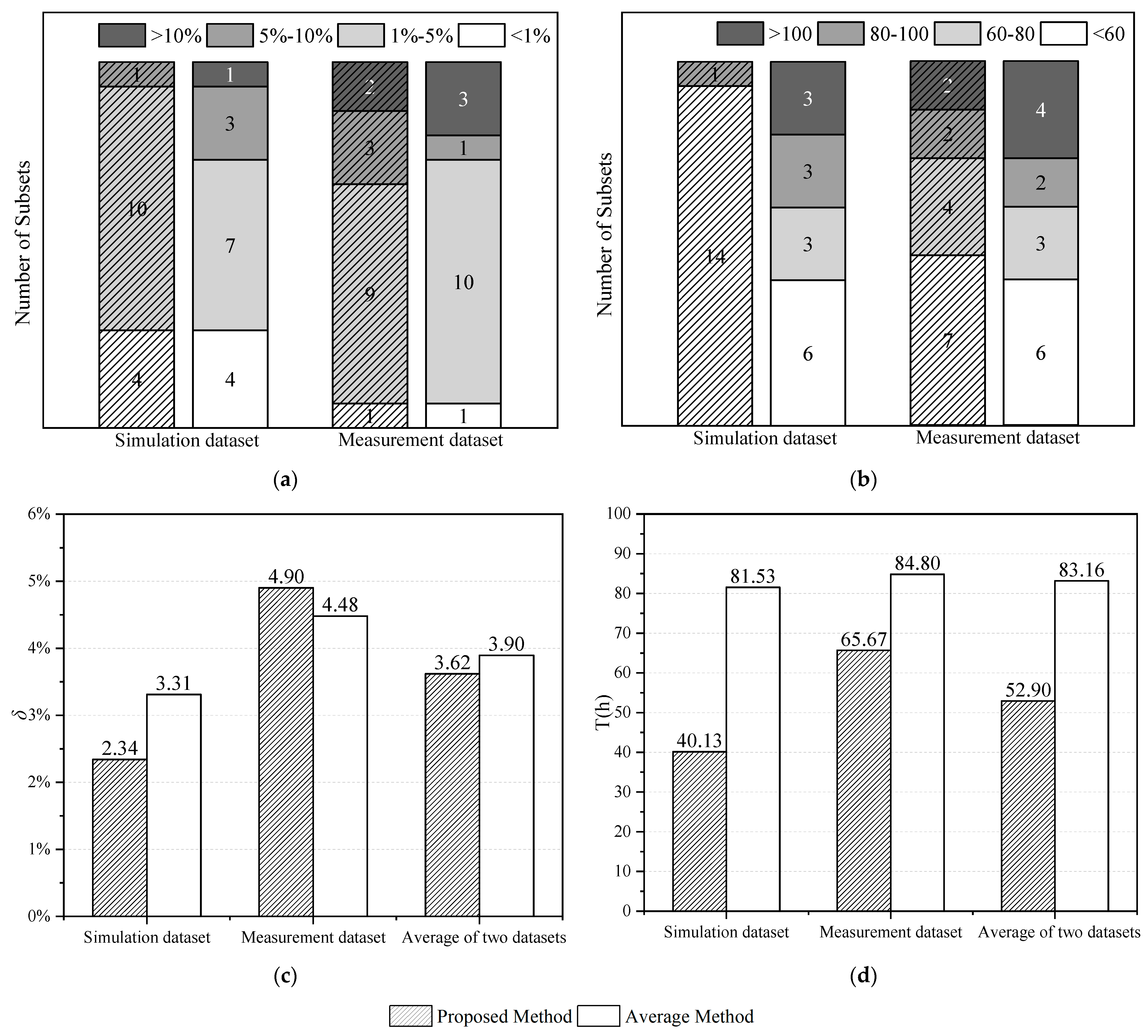
4.3. Results
5. Conclusions
- The data analysis method was established, including the truncation model for the wall thermal resistance calculation derived from the classical theory of wall thermal response factors, the convergence criteria based on theoretical and empirical analysis, and the implementation process for applying the method to the in situ measurement.
- The threshold value of 2 × 10−3 in the convergence criteria for determining if the measurement and calculation process converges is an empirical value obtained after many trials. It is a trade-off between the convergence time and the accuracy of wall thermal resistance estimations.
- The truncation model is theoretically validated from the perspectives of the truncation error of response factors and the residual error of least squares. Seven typical types of walls were selected based on Chinese building energy-saving standards. The results show that when the number of truncation terms, , is sufficient for different types of walls, a truncated form of wall response factors can replace the infinite form for wall thermal resistance calculation, and the truncation and residual errors can be ignored.
- The feasibility and accuracy of the proposed method are validated by one simulation dataset and one measurement dataset. The results show that the accuracy of the proposed method is similar to the standard average method and has a deviation of 3.86% on average. In terms of the convergence time, compared to the average method, the proposed method can effectively shorten the measurement period by about 36.4% on average.
- The preliminary validation results indicate that the proposed method and its convergence criteria apply to actual measurements while achieving a fast but accurate estimation result. Compared with other dynamic HFM methods, the proposed method has the significant advantages of simple principle and clear physical meaning.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tsinghua BERC. 2020 Annual Development Research Report on Building Energy Efficiency in China; China Architecture & Building Press: Beijing, China, 2020. (In Chinese) [Google Scholar]
- Hu, S.; Zhang, Y.; Yang, Z.; Yan, D.; Jiang, Y. Challenges and Opportunities for Carbon Neutrality in China’s Building Sector—Modelling and Data. Build. Simul. 2022, 15, 1899–1921. [Google Scholar] [CrossRef]
- GB 55015-2021; General Code for Energy Efficiency and Renewable Energy Application in Buildings. China Architecture & Building Press: Beijing, China, 2021. (In Chinese)
- Teni, M.; Krstić, H.; Kosiński, P. Review and Comparison of Current Experimental Approaches for In-Situ Measurements of Building Walls Thermal Transmittance. Energy Build. 2019, 203, 109417. [Google Scholar] [CrossRef]
- JGJT132-2009; Energy Efficiency Test Standard for Residential Buildings. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2010. (In Chinese)
- ISO 9869-1:2014; Thermal Insulation Building Elements In-Situ Measurement of Thermal Resistance and Thermal Transmittance—Part 1: Heat Flow Meter Method. ISO: Geneva, Switzerland, 2014.
- An-Heleen, D.; Staf, R. Comparison of Characterisation Methods Determining the Thermal Resistance of Building Components from Onsite Measurements. Energy Build. 2016, 130, 309–320. [Google Scholar] [CrossRef]
- Naveros, I.; Ghiaus, C.; Ruíz, D.P.; Castaño, S. Physical Parameters Identification of Walls Using ARX Models Obtained by Deduction. Energy Build. 2015, 108, 317–329. [Google Scholar] [CrossRef]
- François, A.; Ibos, L.; Feuillet, V.; Meulemans, J. Novel Active Method for the Estimation of a Building Wall Thermal Resistance. E3S Web Conf. 2020, 172, 14008. [Google Scholar] [CrossRef]
- Ke, R. Development of In-Situ Wall Thermal Resistance Test Instrument and Application of Double-Heat Flow Meter. Master’s Thesis, Donghua University, Shanghai, China, 2017. (In Chinese). [Google Scholar]
- Kou, F.; Wang, X.; Zou, Y.; Mo, J.; Wang, X.; Zuo, Y.; Mo, J. Simulation Study of Three-Dimensional Heat Transfer in the Wall Thermal Resistance Test. Build. Energy Effic. 2020, 48, 6–11+79. (In Chinese) [Google Scholar] [CrossRef]
- François, A.; Ibos, L.; Feuillet, V.; Meulemans, J. Estimation of the Thermal Resistance of a Building Wall with Inverse Techniques Based on Rapid Active in Situ Measurements and White-Box or ARX Black-Box Models. Energy Build. 2020, 226, 110346. [Google Scholar] [CrossRef]
- Rasooli, A.; Itard, L.; Ferreira, C.I. A Response Factor-Based Method for the Rapid in-Situ Determination of Wall’s Thermal Resistance in Existing Buildings. Energy Build. 2016, 119, 51–61. [Google Scholar] [CrossRef]
- Shi, X.; Gong, G.; Peng, P.; Liu, Y. Investigation of a New Kind of In-Situ Measurement Method of Thermal Resistance of Building Envelope. Energy Build. 2022, 258, 111803. [Google Scholar] [CrossRef]
- Rasooli, A.; Itard, L. In-Situ Characterization of Walls’thermal Resistance: An Extension to the ISO 9869 Standard Method. Energy Build. 2018, 179, 374–383. [Google Scholar] [CrossRef]
- Rasooli, A.; Itard, L. In-Situ Rapid Determination of Walls’ Thermal Conductivity, Volumetric Heat Capacity, and Thermal Resistance, Using Response Factors. Appl. Energy 2019, 253, 113539. [Google Scholar] [CrossRef]
- Park, S.; Song, D. In Situ Measurement Method of Thermal Transmittance of Opaque Building Elements under Small Indoor and Outdoor Temperature Differences. In Proceedings of the 12th International Symposium on Heating, Ventilation and Air Conditioning (ISHVAC 2021), Seoul, Republic of Korea, 24–26 November 2021; pp. 654–659. [Google Scholar]
- Shen, Q.; Liang, L.; Xia, J.; Liang, L.; Xia, J. On-Site Measuring Method of Heat Resistance of Wall by STLS. Build. Sci. 2015, 31, 47–53. (In Chinese) [Google Scholar] [CrossRef]
- Laurenti, L.; Marcotullio, F.; Monte, F. Determination of the Thermal Resistance of Walls through a Dynamic Analysis of In-Situ Data. Int. J. Therm. Sci. 2004, 43, 297–306. [Google Scholar] [CrossRef]
- Flores Larsen, S.; Silvana, M.; Castro, N.; González, S. Comparison of Four In-Situ Methods for the Determination of Walls Thermal Resistance in Free-Running Buildings with Alternating Heat Flux in Different Seasons. Constr. Build. Mater. 2019, 224, 455–473. [Google Scholar] [CrossRef]
- Iglesias, M.; Sawlan, Z.; Scavino, M.; Tempone, R.; Wood, C. Bayesian Inferences of the Thermal Properties of a Wall Using Temperature and Heat Flux Measurements. Int. J. Heat Mass Transf. 2018, 116, 417–431. [Google Scholar] [CrossRef]
- Beñat, A.; Roberto, G.-M.; Julen, A.; Juan, C.R. Monitoring and Thermal Performance Evaluation of Two Building Envelope Solutions in an Apartment Building. E3S Web Conf. 2020, 172, 25002. [Google Scholar] [CrossRef]
- Bienvenido-Huertas, D.; Pérez-Ordóñez, J.L.; Moyano, J.; Seara-Paz, S. Towards an In-Situ Evaluation Methodology of Thermal Resistance of Basement Walls in Buildings. Energy Build. 2020, 208, 109643. [Google Scholar] [CrossRef]
- Petojević, Z.; Gospavić, R.; Todorović, G. Estimation of Thermal Impulse Response of a Multi-Layer Building Wall through in-Situ Experimental Measurements in a Dynamic Regime with Applications. Appl. Energy 2018, 228, 468–486. [Google Scholar] [CrossRef]
- Yan, Q.; Zhao, Q. Building Thermal Process; China Architecture & Building Press: Beijing, China, 1986. [Google Scholar]
- Chen, Y.; Wang, S. A New Procedure for Calculating Periodic Response Factors Based on Frequency Domain Regression Method. Int. J. Therm. Sci. 2005, 44, 382–392. [Google Scholar] [CrossRef]
- Eunilkim, D.H. Wall-Response Factors to Estimate the Conduction Heat Gains with Time-Varying Thermal Coefficients. Energy 1991, 16, 933–939. [Google Scholar] [CrossRef]
- U.S. Department of Energy. EnergyPlusTM Version 9.0.1 Documentation; DOE: Washington, DC, USA, 2018. [Google Scholar]
- Cao, K.; Lesnic, D. Simultaneous Reconstruction of the Spatially-Distributed Reaction Coefficient, Initial Temperature and Heat Source from Temperature Measurements at Different Times. Comput. Math. Appl. 2019, 78, 3237–3249. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Introduction to Applied Linear Algebra; Cambridge University Press & Assessment: Cambridge, UK, 2018. [Google Scholar]
- JGJ26-2018; Design Standard for Energy Efficiency of Residential Buildings in Severe Cold and Cold Zones. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2018. (In Chinese)
- Kunze, O.; Fariborz, H. A Procedure for Calculating Thermal Response Factors of Multi-Layer Walls State Space Method. Build. Environ. 1991, 26, 173–177. [Google Scholar]
- Yan, D.; Xia, J.; Tang, W.; Song, F.; Zhang, X.; Jiang, Y. DeST—An Integrated Building Simulation Toolkit Part I: Fundamentals. Build. Simul. 2008, 1, 95–110. [Google Scholar] [CrossRef]
- Choi, D.S.; Ko, M.J. Analysis of Convergence Characteristics of Average Method Regulated by ISO 9869-1 for Evaluating In Situ Thermal Resistance and Thermal Transmittance of Opaque Exterior Walls. Energies 2019, 12, 1989. [Google Scholar] [CrossRef]



| No. | Wall Type | Material (From Inside to Outside) | Thickness [mm] | Theoretical Thermal Resistance [m2/(K·W)] |
|---|---|---|---|---|
| 1 | Brick wall | Cement mortar | 20 | 0.764 |
| Red clay brick | 310 | |||
| Cement mortar | 20 | |||
| 2 | Concrete wall with thin interior insulation | Cement mortar | 20 | 0.764 |
| Extruded polystyrene board (XPS) | 20 | |||
| Steel reinforced concrete | 200 | |||
| Cement mortar | 20 | |||
| 3 | Concrete wall with standard interior insulation | Cement mortar | 20 | 2.703 |
| XPS | 84 | |||
| Steel reinforced concrete | 200 | |||
| Cement mortar | 20 | |||
| 4 | Concrete wall with thick interior insulation | Cement mortar | 20 | 5.612 |
| XPS | 180 | |||
| Steel reinforced concrete | 200 | |||
| Cement mortar | 20 | |||
| 5 | Concrete wall with thin exterior insulation | Cement mortar | 20 | 0.764 |
| Steel reinforced concrete | 200 | |||
| XPS | 20 | |||
| Cement mortar | 20 | |||
| 6 | Concrete wall with standard exterior insulation | Cement mortar | 20 | 2.703 |
| Steel reinforced concrete | 200 | |||
| XPS | 84 | |||
| Cement mortar | 20 | |||
| 7 | Concrete wall with thick exterior insulation | Cement mortar | 20 | 5.612 |
| Steel reinforced concrete | 200 | |||
| XPS | 180 | |||
| Cement mortar | 20 |
| Material | Thermal Conductivity [w/(m·K)] | Density [kg/m3] | Specific Heat [J/(kg·k)] |
|---|---|---|---|
| Cement mortar | 0.93 | 1800 | 1050 |
| Red clay brick | 0.43 | 1668 | 754 |
| Extruded polystyrene board (XPS) | 0.033 | 29 | 1791.06 |
| Steel reinforced concrete | 1.74 | 2500 | 920 |
| Method | The Calculation Formula for Wall Thermal Resistance | Termination Criteria |
|---|---|---|
| Proposed method | Equations (6) and (8) | Equations (16)–(18). As the measurement period gradually increases, try increasing and to estimate the thermal resistance . The calculation stops at the first occurrence of that meets the above conditions. |
| Average method [6] | (1) The thermal resistance obtained at the time does not deviate by more than ±5% from the value obtained 24 h prior to it: (2) The thermal resistance obtained from the first INT(2 × DT/3) days does not deviate by more than ±5% from the values obtained from the last period of the same days, where DT is the measurement duration (in days) from the start, and INT is a rounding function for the integer part: |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Fu, X.; Tao, X.; Li, X.; An, J. A Novel Response Factor-Based Method for In Situ Measurement of Wall Thermal Resistance. Buildings 2023, 13, 1986. https://doi.org/10.3390/buildings13081986
Wang C, Fu X, Tao X, Li X, An J. A Novel Response Factor-Based Method for In Situ Measurement of Wall Thermal Resistance. Buildings. 2023; 13(8):1986. https://doi.org/10.3390/buildings13081986
Chicago/Turabian StyleWang, Chuang, Xiao Fu, Xiaoran Tao, Xiaoyan Li, and Jingjing An. 2023. "A Novel Response Factor-Based Method for In Situ Measurement of Wall Thermal Resistance" Buildings 13, no. 8: 1986. https://doi.org/10.3390/buildings13081986
APA StyleWang, C., Fu, X., Tao, X., Li, X., & An, J. (2023). A Novel Response Factor-Based Method for In Situ Measurement of Wall Thermal Resistance. Buildings, 13(8), 1986. https://doi.org/10.3390/buildings13081986







