Development of an IRMO-BPNN Based Single Pile Ultimate Axial Bearing Capacity Prediction Model
Abstract
1. Introduction
2. IRMO Algorithm and BPNN
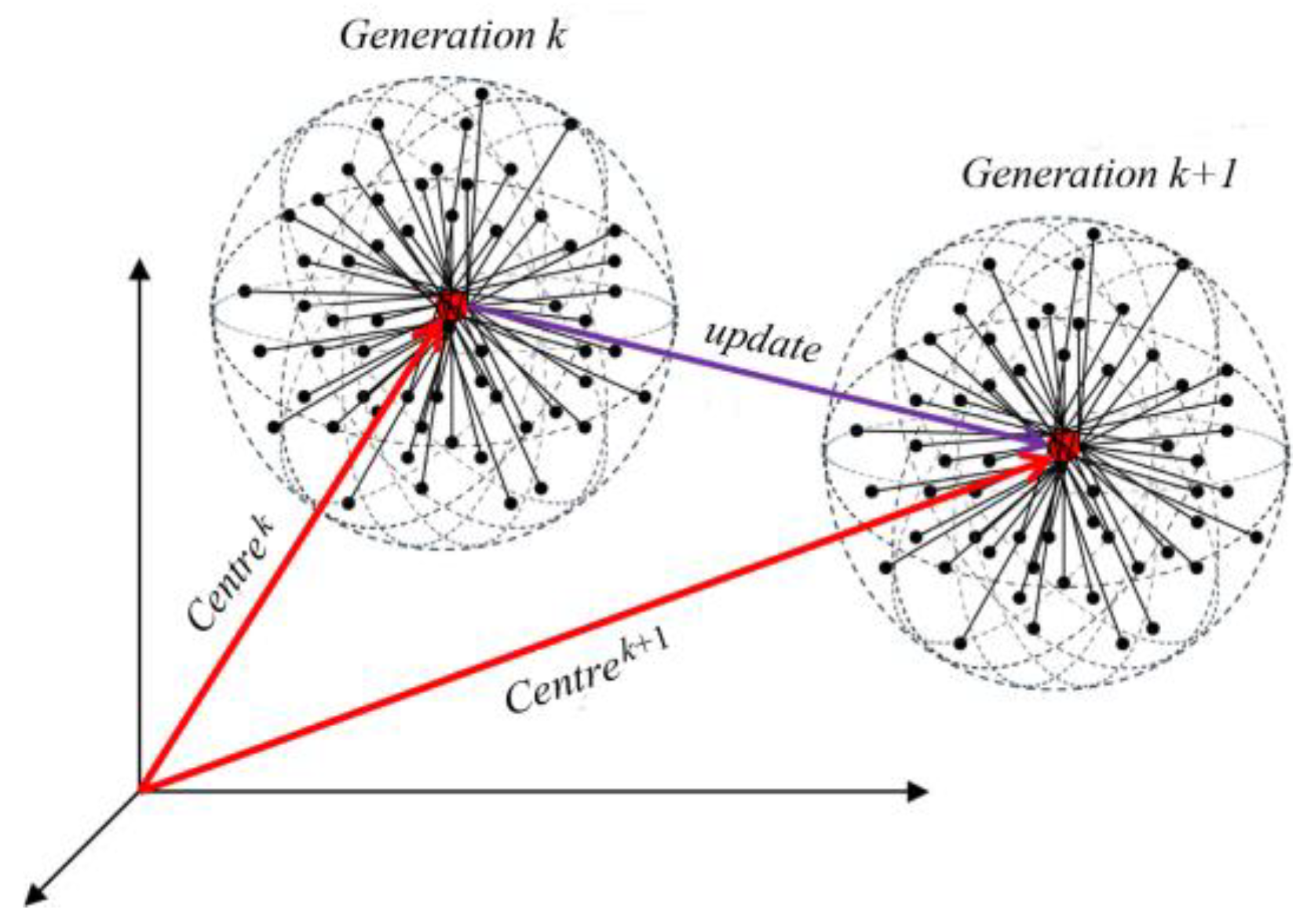
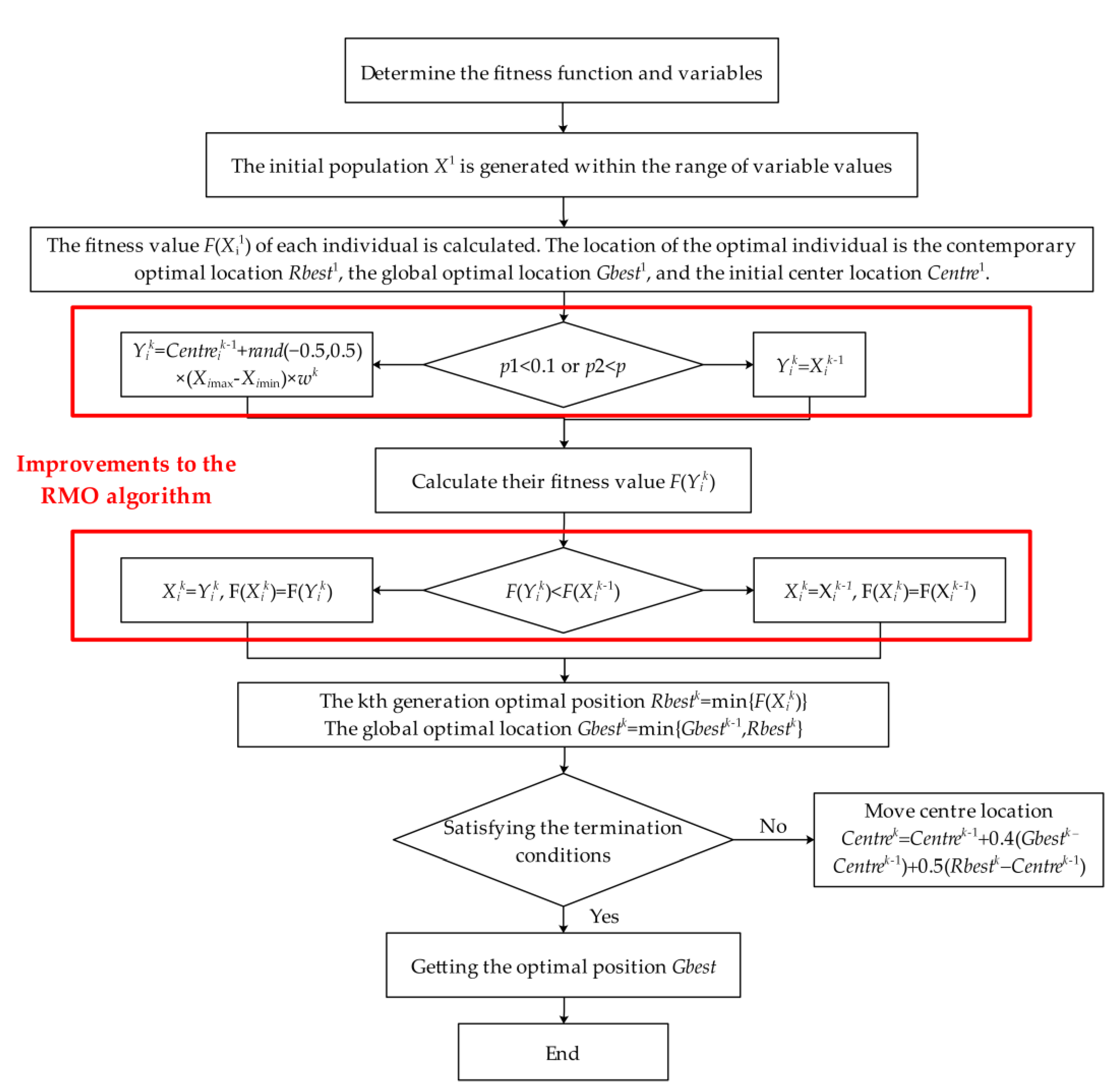
2.1. IRMO Algorithm
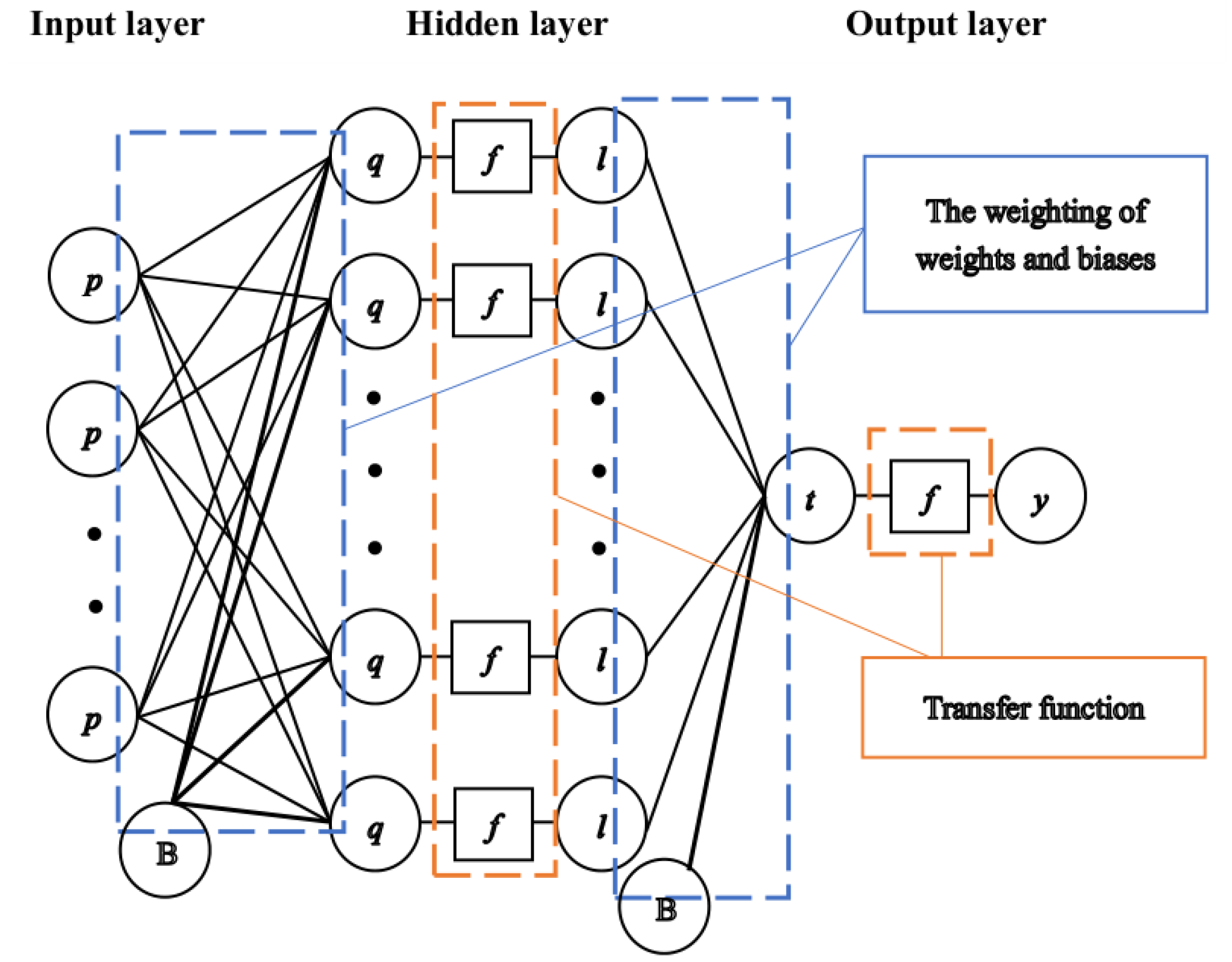
2.2. BPNN
3. IRMO-BPNN
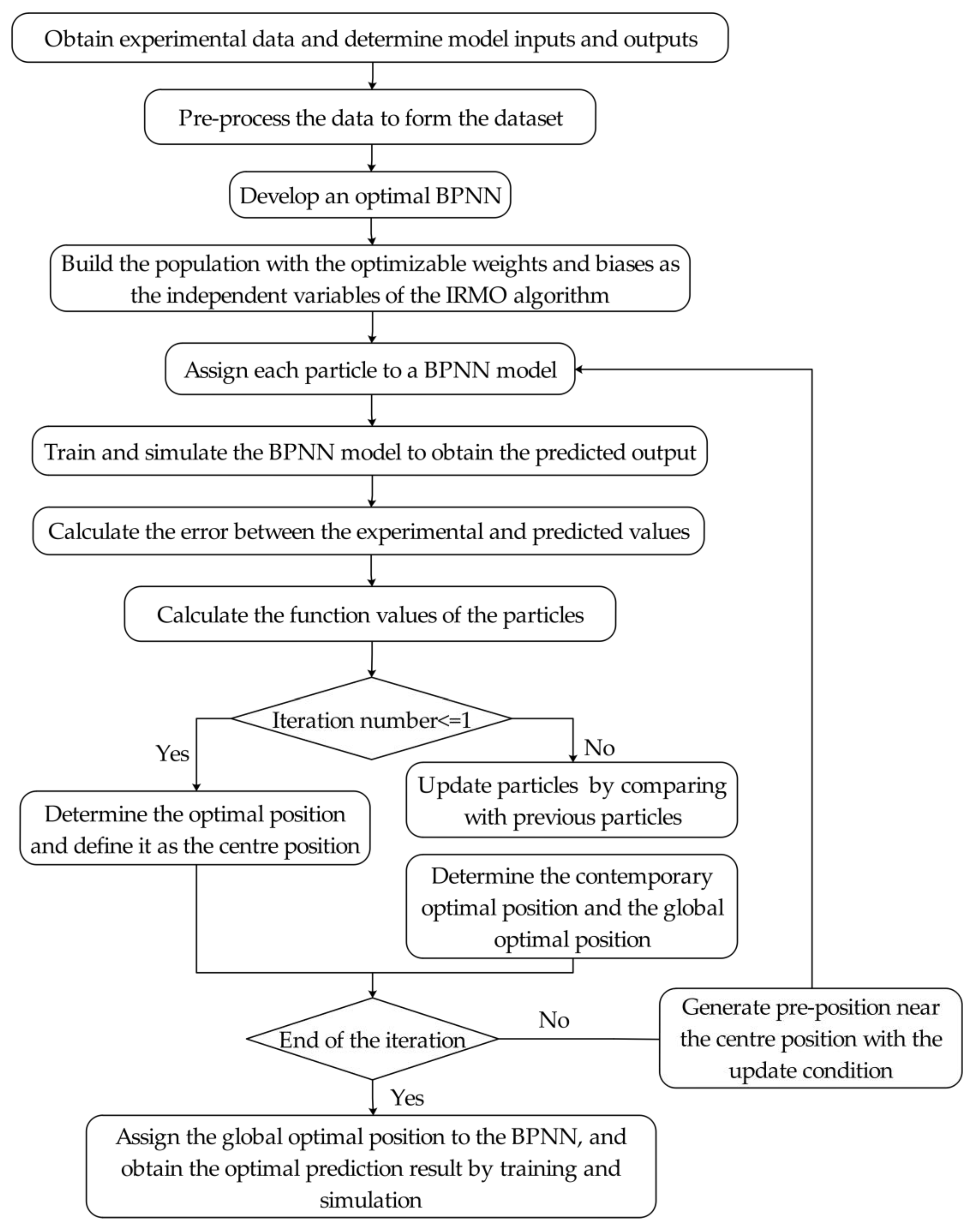
3.1. The Proposed IRMO-BPNN
3.2. Implementation Steps of the IRMO-BPNN
4. Development of an IRMO-BPNN Model
4.1. The Inputs and Outputs of the Model
4.2. Data Collection and Pre-Processing
4.2.1. Outlier Processing
4.2.2. Partition of Data Sets
4.2.3. Data Normalization
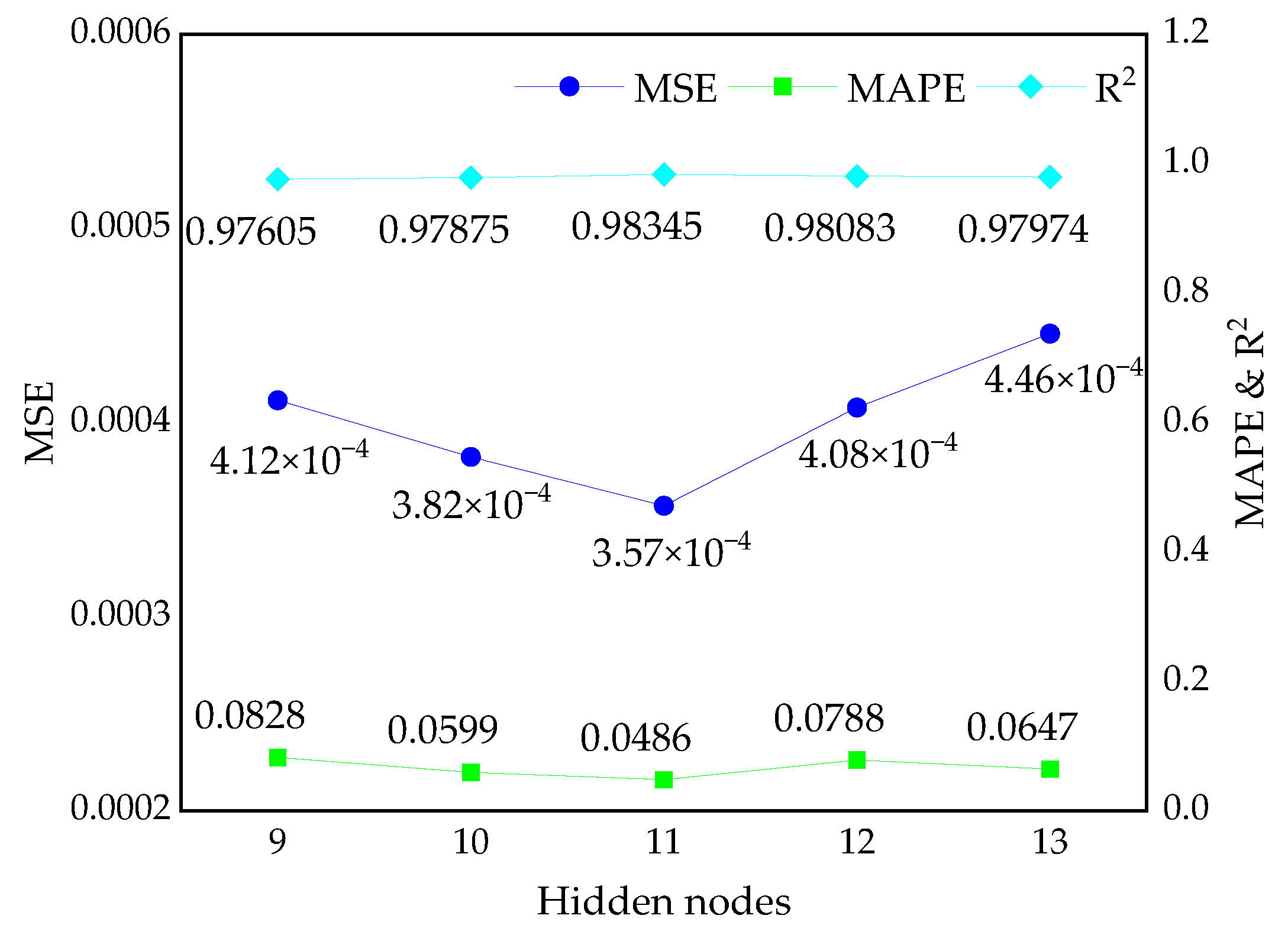
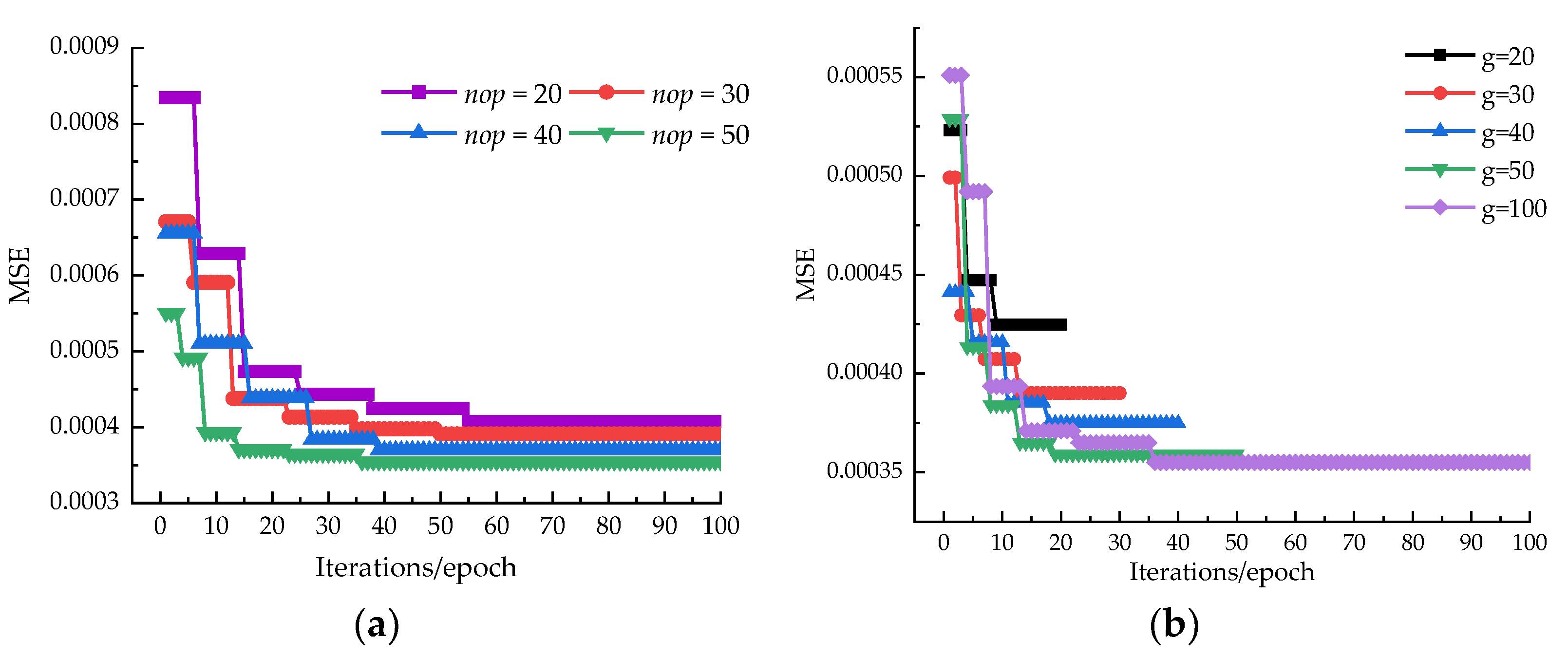
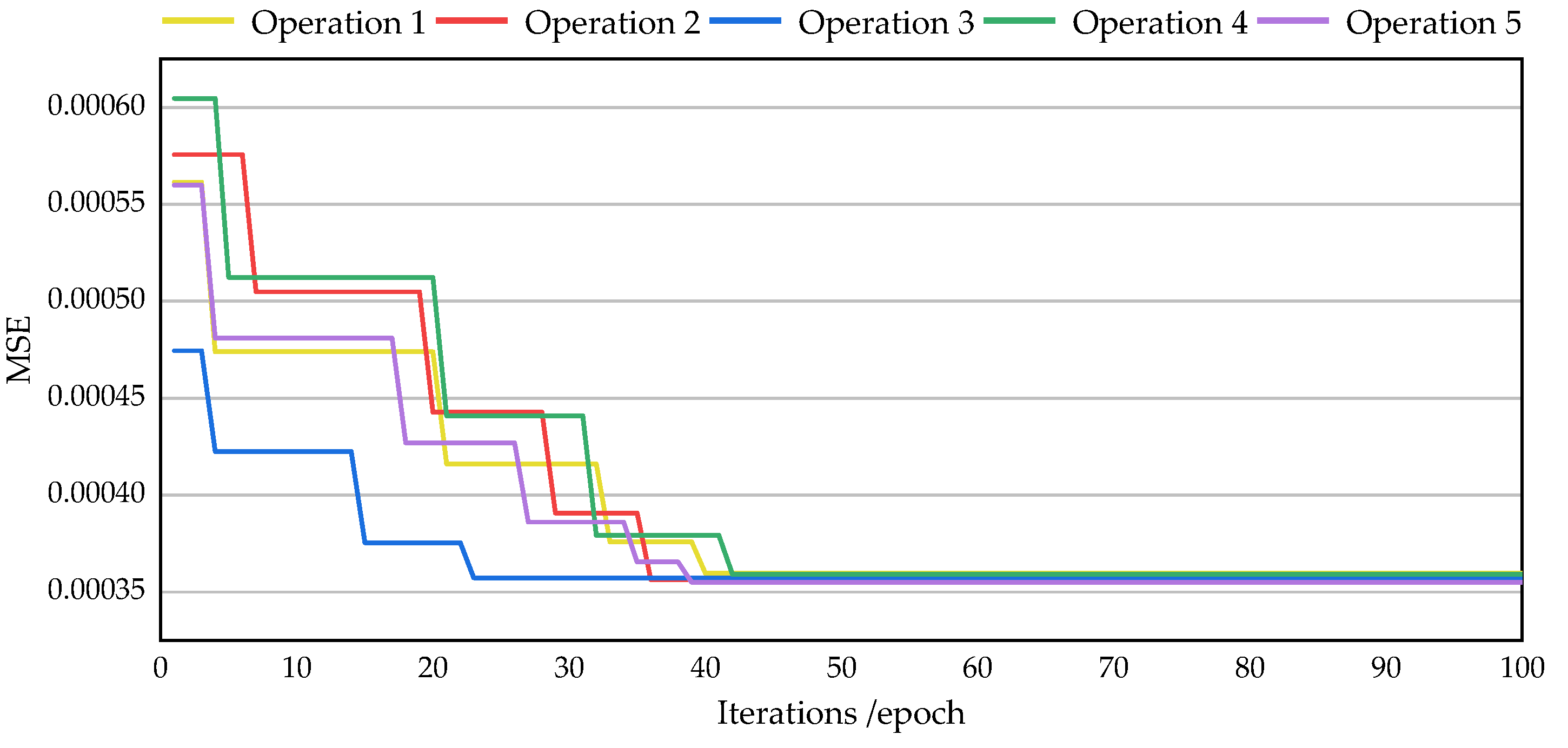
4.3. Parameter Optimization of the IRMO-BPNN Model
5. Comparison and Analysis
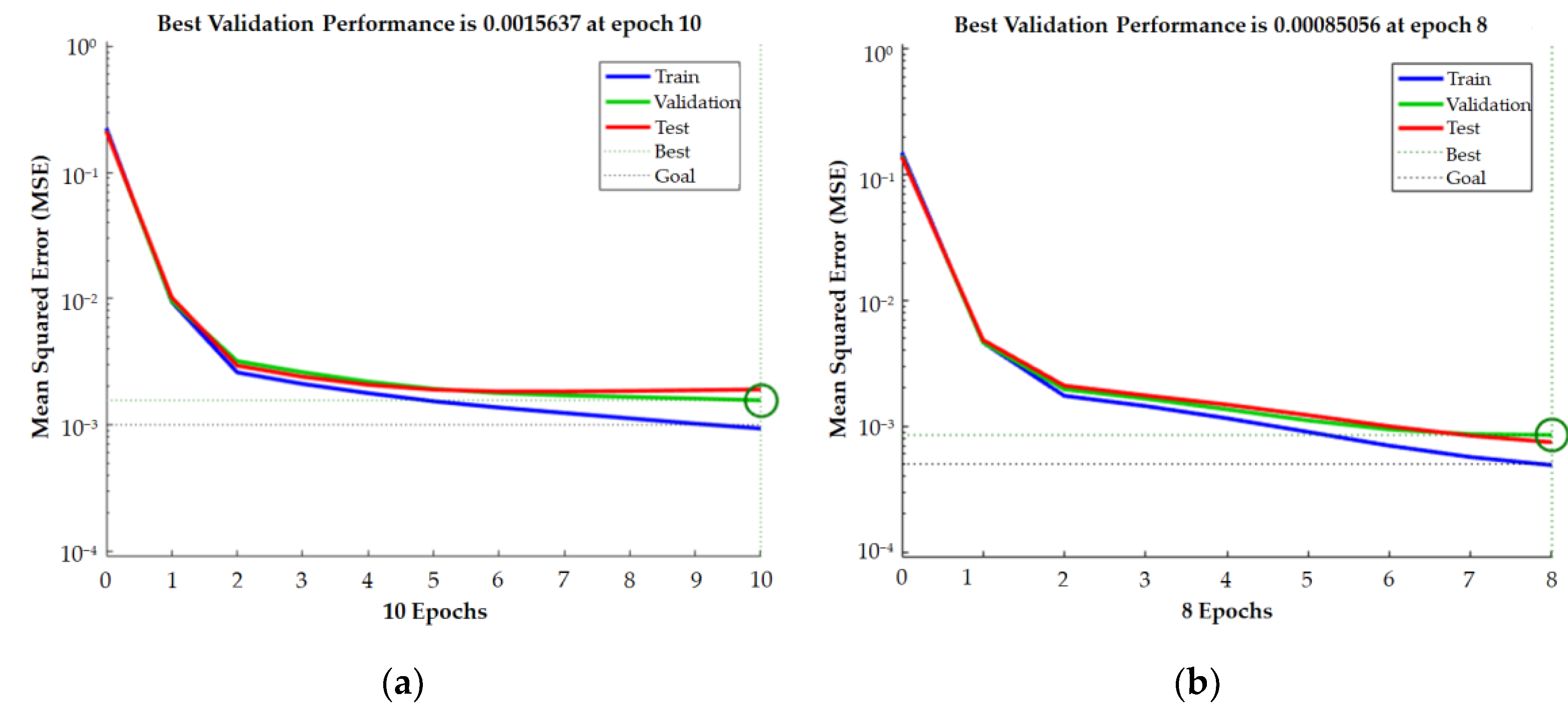
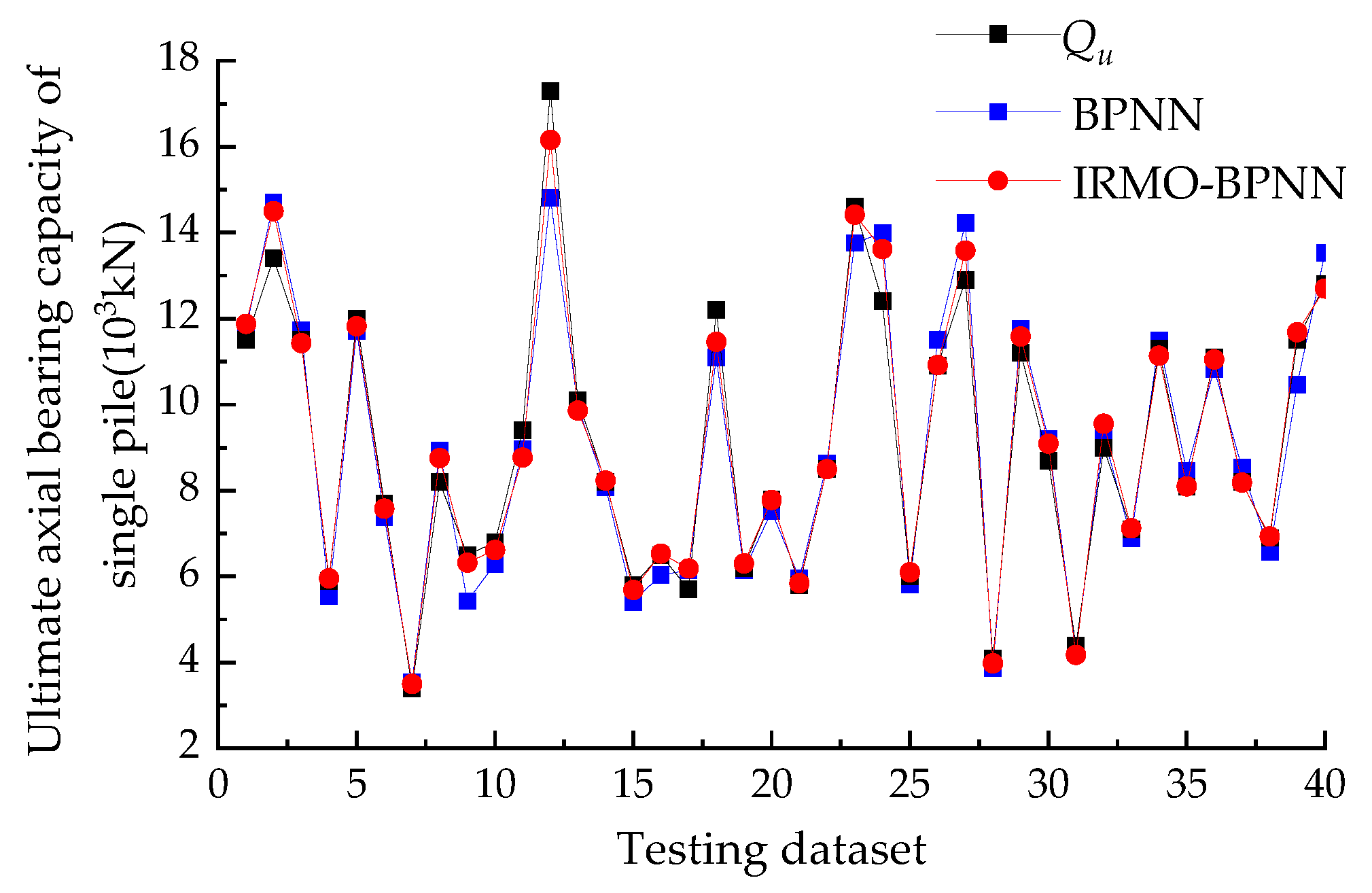
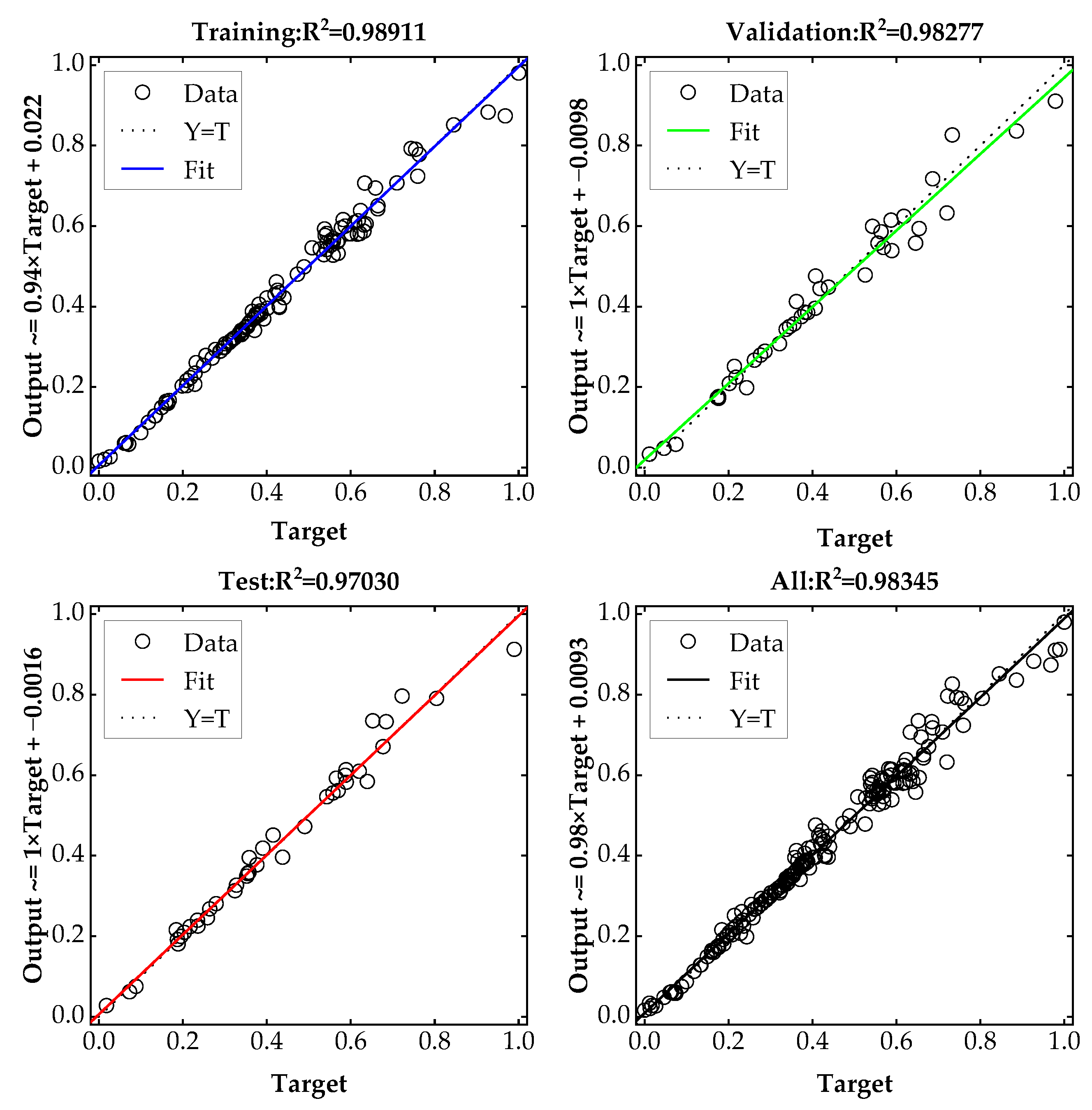
5.1. Performance of the IRMO-BPNN Model
5.2. Evaluation and Comparison
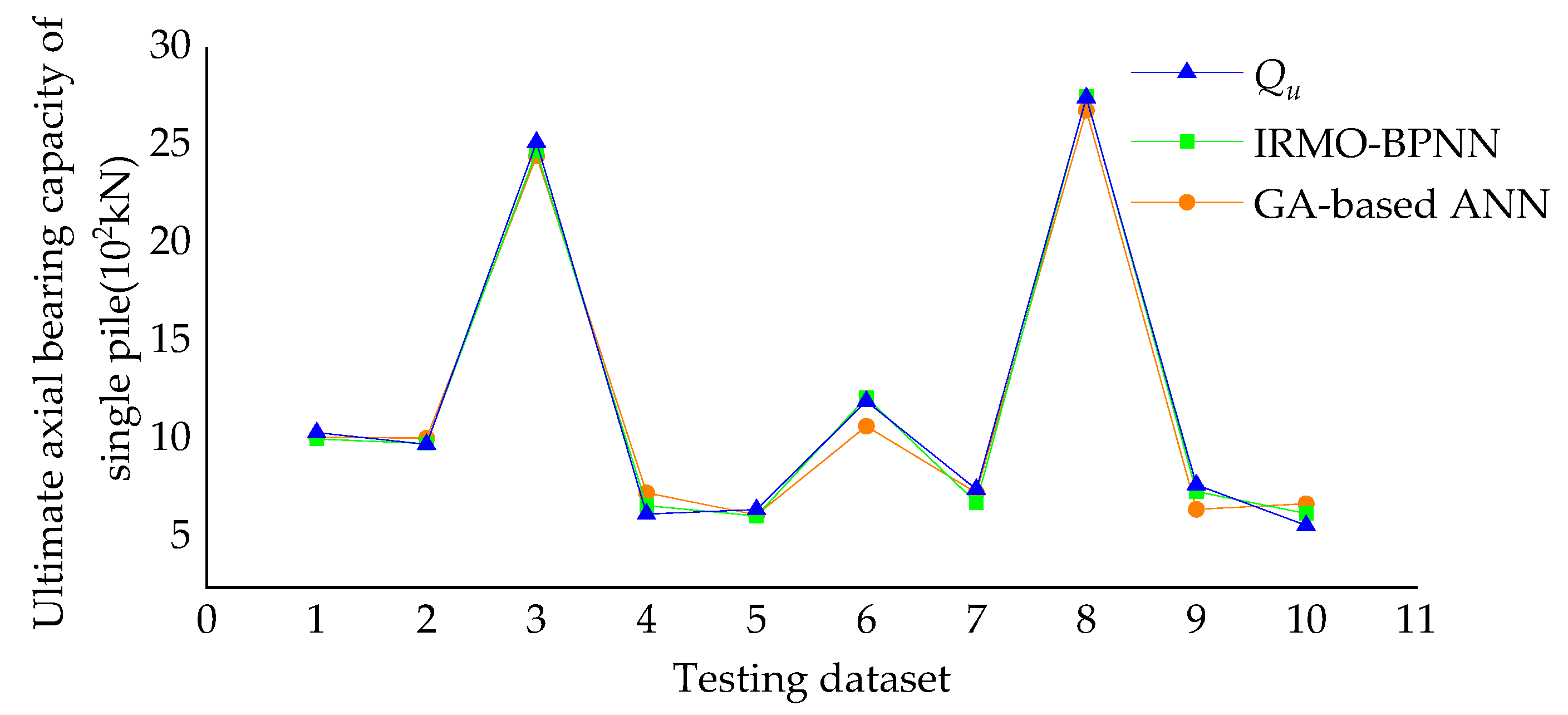
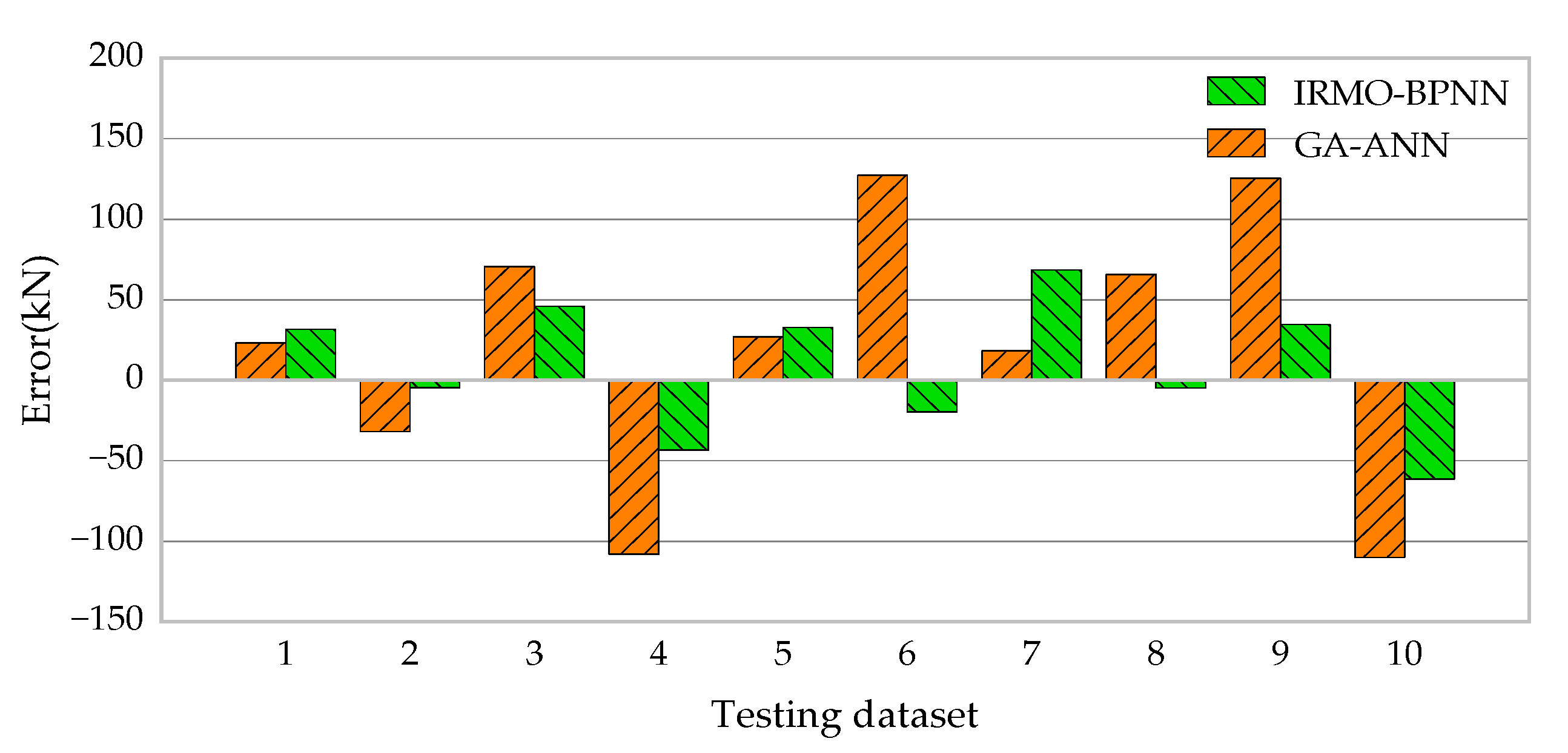
5.2.1. Comparison with GA-Based ANN Model
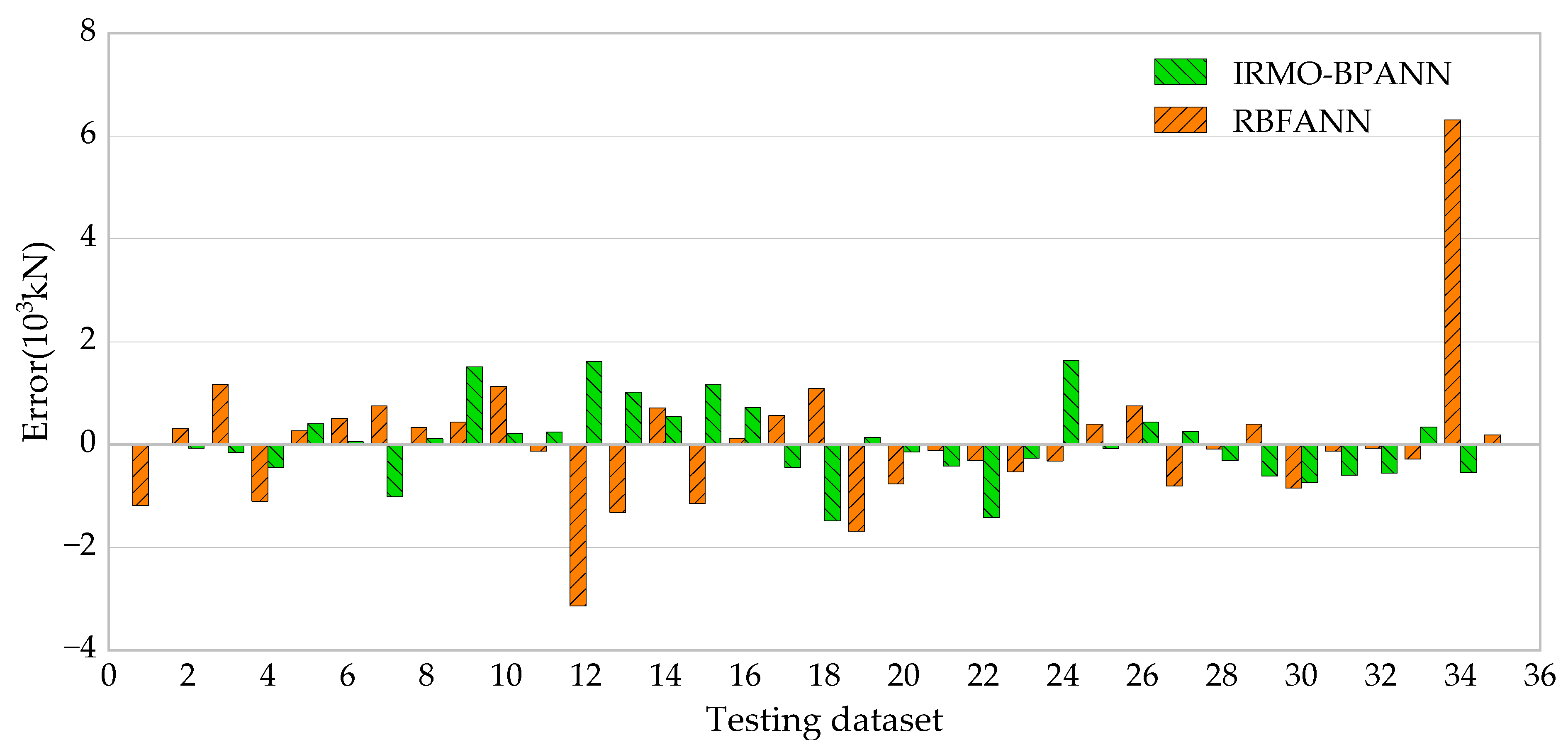
5.2.2. Comparison with the RBFANN Model
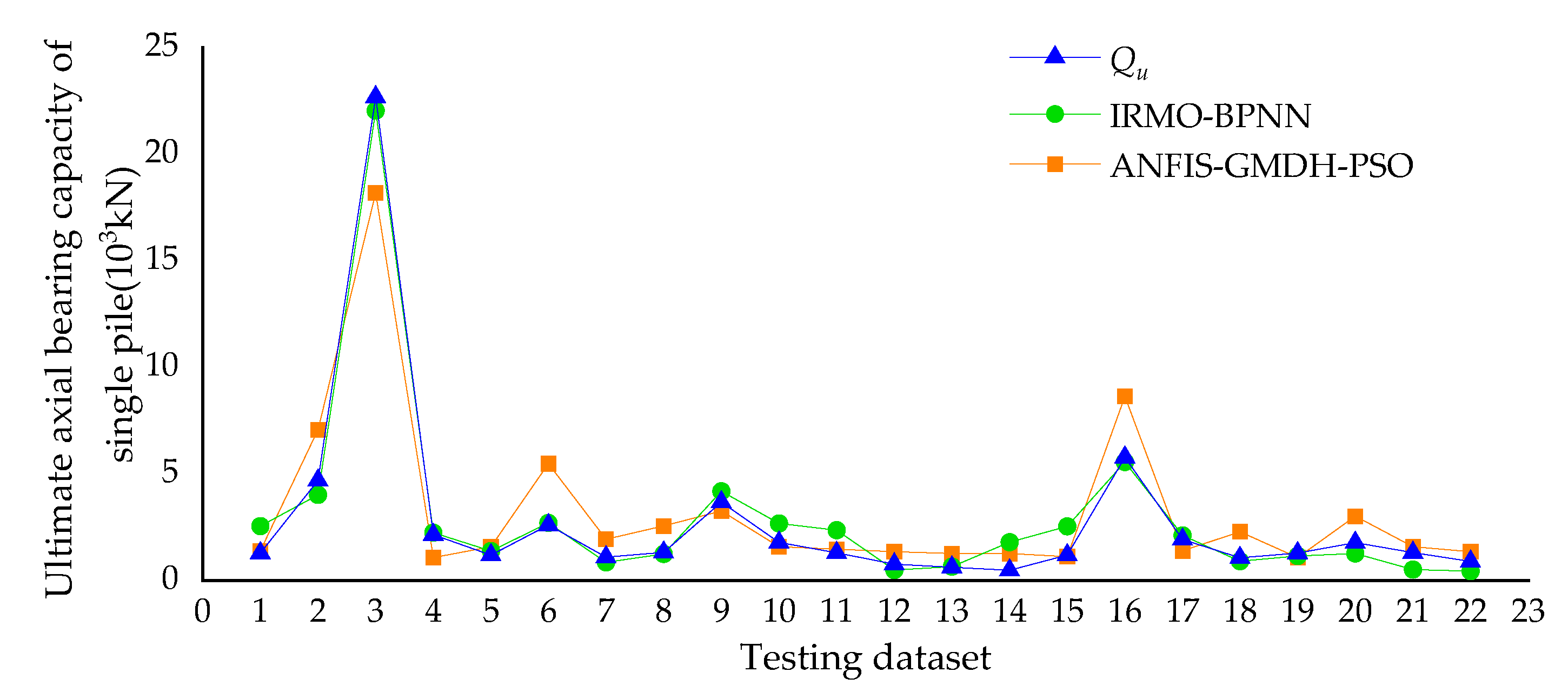
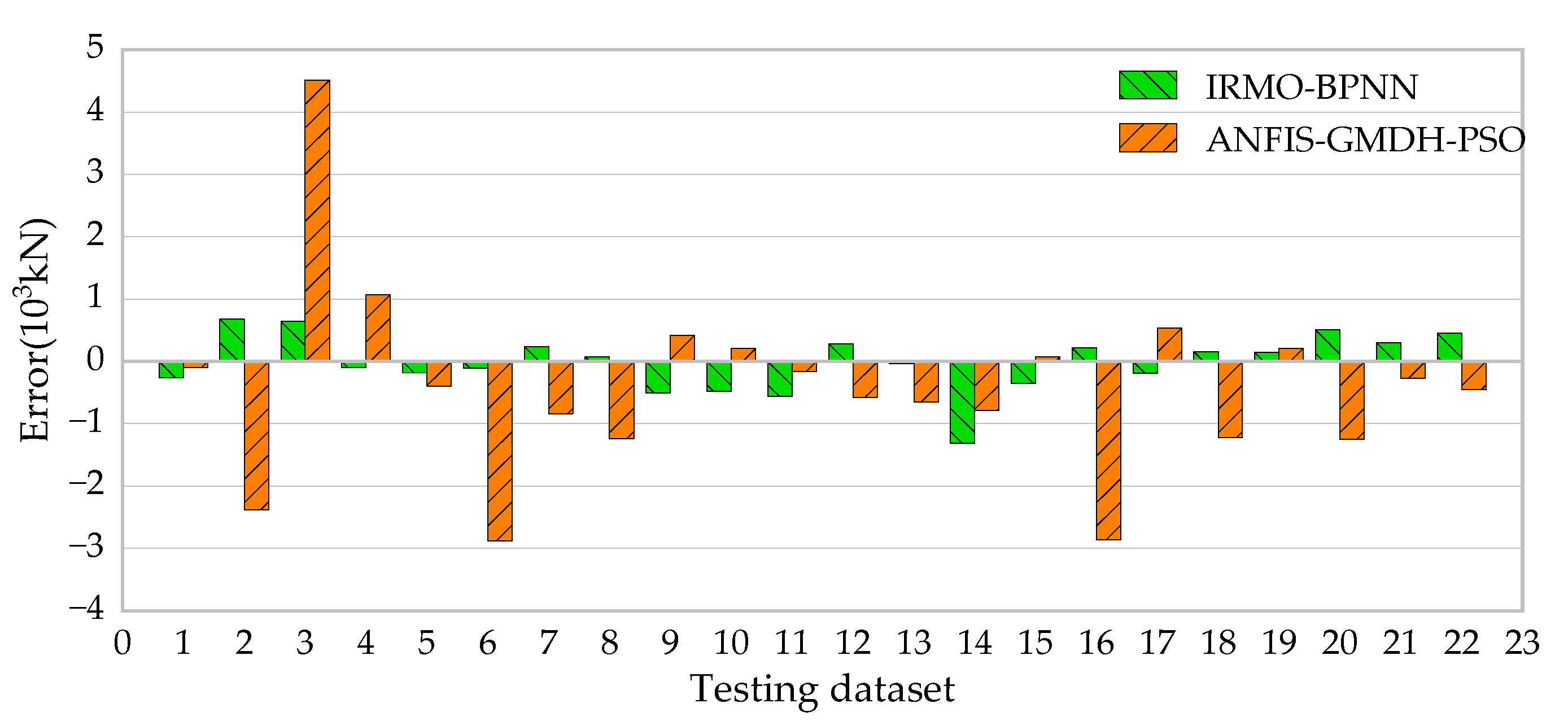
5.2.3. Comparison with the ANFIS-GMDH-PSO Model
6. Conclusions
- (1)
- Using a trial-and-error method, the optimal number of hidden nodes is 11 in this study. Hyper-parameters contribute to the IRMO-BPNN model being more accurate and with less prediction error as the population size and number of iterations grow. Additionally, increasing the model’s iterations is more effective in enhancing model performance.
- (2)
- The IRMO-BPNN model has good performance for predicting the UABC of a single pile. The model did not overfit in the iteration process, and the predicted value of the model is very close to the experimental value. The MAPE of the model is 4.86%, and the R2 of the training, verification, and testing sets are 0.98911, 0.98277, and 0.97030, respectively. During the iterative process, the MSE of the model decreases to stabilize gradually, and the results obtained from multiple runs are roughly the same, which indicates the great global optimization ability and search stability of the model.
- (3)
- The hybrid algorithm has been utilized to improve BPNN’s prediction performance. Compared to other hybrid algorithms, the IRMO-BPNN has a faster convergence rate, a higher prediction accuracy, and greater stability owing to its distinctive data structure.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kordjazi, A.; Pooya Nejad, F.; Jaksa, M.B. Prediction of ultimate axial load-carrying capacity of piles using a support vector machine based on CPT data. Comput. Geotech. 2014, 55, 91–102. [Google Scholar] [CrossRef]
- Meyerhof, G.G. The ultimate bearing capacity of foundations. Géotechnique 1951, 2, 301–302. [Google Scholar] [CrossRef]
- Meyerhof, G.G. Bearing Capacity and Settlement of Pile Foundations. J. Geotech. Eng. Div. 1976, 102, 197–228. [Google Scholar] [CrossRef]
- Titi, H.H.; Abu-Farsakh, M.Y. Evaluation of Bearing Capacity of Piles from Cone Penetration Test Data; Louisiana Transportation Research Center: Baton Rouge, LA, USA, 1999. [Google Scholar]
- Seed, H.B.; Reese, L.C. The action of soft clay along friction piles. Trans. Am. Soc. Civ. Eng. 1957, 122, 731–754. [Google Scholar] [CrossRef]
- Davis, E.H.; Poulos, H.G. The Settlement Behaviour of Single Axially Loaded Incompressible Piles and Piers. Géotechnique 1968, 18, 351–371. [Google Scholar] [CrossRef]
- Randolph, M.F.; Carter, J.; Wroth, C. Driven piles in clay—The effects of installation and subsequent consolidation. Geotechnique 1979, 29, 361–393. [Google Scholar] [CrossRef]
- Ellison, R.D.; D’Appolonia, E.; Thiers, G.R. Load-Deformation Mechanism for Bored Piles. J. Soil Mech. Found. Div. 1971, 97, 661–678. [Google Scholar] [CrossRef]
- Hamed, M.; Emirler, B.; Canakci, H.; Yildiz, A. 3D Numerical Modeling of a Single Pipe Pile Under Axial Compression Embedded in Organic Soil. Geotech. Geol. Eng. 2020, 38, 4423–4434. [Google Scholar] [CrossRef]
- Chan, W.T.; Chow, Y.K.; Liu, L.F. Neural network: An alternative to pile driving formulas. Comput. Geotech. 1995, 17, 135–156. [Google Scholar] [CrossRef]
- Lee, I.M.; Lee, J.H. Prediction of Pile Bearing Capacity Using Artificial Neural Networks. Comput. Geotech. 1996, 18, 189–200. [Google Scholar] [CrossRef]
- Goh, A.T.C. Pile Driving Records Reanalyzed Using Neural Networks. J. Geotech. Eng. 1996, 122, 492–495. [Google Scholar] [CrossRef]
- Benali, A.; Nechnech, A. Prediction of the pile capacity in purely coherent soils using the approach of the artificial neural networks. In Proceedings of the Second International Conference on the Innovation, Valorization and Construction INVACO2, Rabat, Morocco, 23–25 November 2011. [Google Scholar]
- Benali, A.; Boukhatem, B.; Hussien, M.N.; Nechnech, A.; Karray, M. Prediction of axial capacity of piles driven in non-cohesive soils based on neural networks approach. J. Civ. Eng. Manag. 2015, 23, 393–408. [Google Scholar] [CrossRef]
- Rezaei, H.; Nazir, R.; Momeni, E.; Engineering, F.O.; University, L. Bearing capacity of thin-walled shallow foundations: An experimental and artificial intelligence-based study. J. Zhejiang Univ.-Sci. (Appl. Phys. Eng.) 2016, 17, 273–285. [Google Scholar] [CrossRef]
- Moayedi, H.; Jahed Armaghani, D. Optimizing an ANN model with ICA for estimating bearing capacity of driven pile in cohesionless soil. Eng. Comput. 2017, 34, 347–356. [Google Scholar] [CrossRef]
- Momeni, E.; Nazir, R.; Jahed Armaghani, D.; Maizir, H. Prediction of pile bearing capacity using a hybrid genetic algorithm-based ANN. Measurement 2014, 57, 122–131. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Shoib, R.S.N.S.B.R.; Faizi, K.; Rashid, A.S.A. Developing a hybrid PSO–ANN model for estimating the ultimate bearing capacity of rock-socketed piles. Neural Comput. Appl. 2017, 28, 391–405. [Google Scholar] [CrossRef]
- Benali, A.; Hachama, M.; Bounif, A.; Nechnech, A.; Karray, M. A TLBO-optimized artificial neural network for modeling axial capacity of pile foundations. Eng. Comput. 2021, 37, 675–684. [Google Scholar] [CrossRef]
- Jin, L.X.; Feng, Q.X. Improved radial movement optimization to determine the critical failure surface for slope stability analysis. Environ. Earth Sci. 2018, 77, 564. [Google Scholar] [CrossRef]
- Jin, L.X.; Zhang, H.C.; Feng, Q.X. Ultimate bearing capacity of strip footing on sands under inclined loading based on improved radial movement optimization. Eng. Optimiz. 2021, 53, 277–299. [Google Scholar] [CrossRef]
- Rahmani, R.; Yusof, R. A new simple, fast and efficient algorithm for global optimization over continuous search-space problems: Radial Movement Optimization. Appl. Math. Comput. 2014, 248, 287–300. [Google Scholar] [CrossRef]
- Jin, L.X.; Feng, Y.W.; Zhang, H.C.; Feng, Q.X. The use of improved radial movement optimization to calculate the ultimate bearing capacity of a nonhomogeneous clay foundation adjacent to slopes. Comput. Geotech. 2020, 118, 103338. [Google Scholar] [CrossRef]
- Li, S.; Zhang, Q.; Zhang, Q.; Li, L. Field and theoretical study of the response of super-long bored pile subjected to compressive load. Mar. Georesources Geotechnol. 2016, 34, 71–78. [Google Scholar] [CrossRef]
- Gu, P.; Xiong, X.; Qian, W.; Zhao, J.; Lu, W. Grey relational analysis of influencing factors of bearing capacity for super-long bored piles. In Proceedings of the 2013 IEEE International Conference on Grey Systems and Intelligent Services (GSIS), Macau, China, 15–17 November 2013; pp. 57–61. [Google Scholar]
- Chen, Q.H.; Chen, G.Q.; Xie, R.B.; Zai, J.Z. Influence of the Penetration Depth into the Bearing Stratum on the Bearing Capacity of Single Pile. Chin. J. Geotech. Eng. 1981, 3, 16–27. [Google Scholar]
- JGJ 94-2008; Technical Code for Building Pile Foundations. China Building Industry Press: Beijing, China, 2008.
- Tabachnick, B.G.; Fidell, L.S. Using Multivariate Statistics, 6th ed.; Allyn and Bacon: Boston, MA, USA, 2013. [Google Scholar]
- Stone, M. Cross-validatory choice and assessment of statistical predictions. J. R. Stat. Soc. Ser. B (Methodol.) 1974, 36, 111–147. [Google Scholar] [CrossRef]
- Harandizadeh, H.; Toufigh, M.M.; Toufigh, V. Different neural networks and modal tree method for predicting ultimate bearing capacity of piles. Int. J. Optim. Civ. Eng. 2018, 8, 311–328. [Google Scholar]
- Harandizadeh, H.; Jahed Armaghani, D.; Khari, M. A new development of ANFIS–GMDH optimized by PSO to predict pile bearing capacity based on experimental datasets. Eng. Comput. 2021, 37, 685–700. [Google Scholar] [CrossRef]
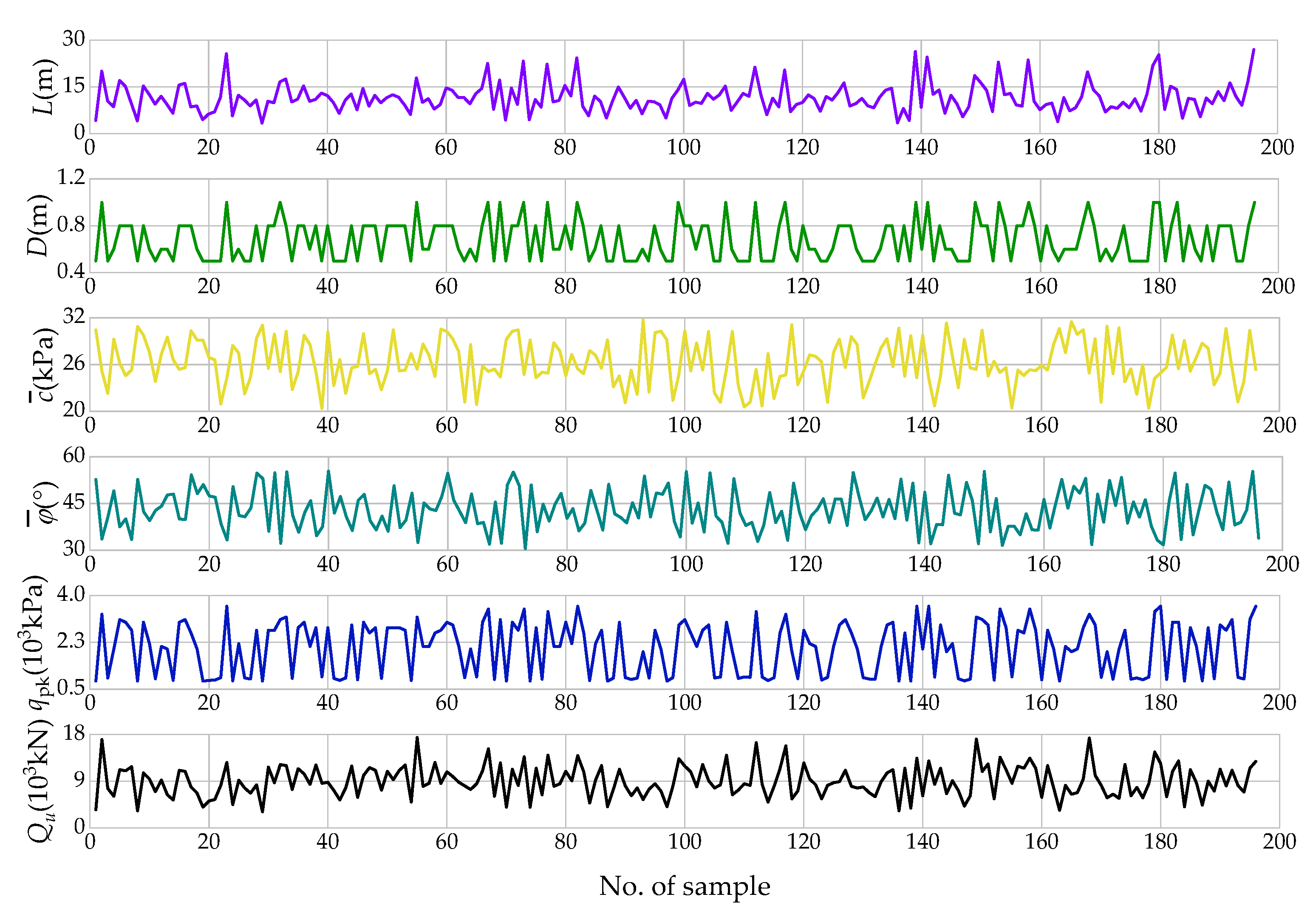


| Data Set | Statistics | Inputs | Output | ||||
|---|---|---|---|---|---|---|---|
| L (m) | D (m) | qpk (kPa) | Qu (kN) | ||||
| Train | Max | 25.6 | 1.0 | 55.36 | 31.72 | 3600 | 17,400 |
| Min | 3.4 | 0.5 | 30.54 | 20.38 | 800 | 3100 | |
| Average | 11.4 | 0.7 | 43.12 | 26.25 | 2029 | 8996 | |
| StD | 4.3 | 0.2 | 6.50 | 2.96 | 965 | 2990 | |
| Validation | Max | 26.4 | 1.0 | 55.26 | 31.35 | 3600 | 17,100 |
| Min | 3.5 | 0.5 | 31.52 | 20.45 | 800 | 3300 | |
| Average | 11.9 | 0.7 | 42.56 | 26.24 | 2054 | 9095 | |
| StD | 5.1 | 0.2 | 6.67 | 2.83 | 965 | 3189 | |
| Testing | Max | 26.9 | 1.0 | 55.25 | 31.50 | 3600 | 17,300 |
| Min | 3.9 | 0.5 | 31.72 | 20.43 | 800 | 3400 | |
| Average | 11.9 | 0.7 | 43.43 | 26.45 | 2047 | 9040 | |
| StD | 5.3 | 0.2 | 6.94 | 2.93 | 967 | 3139 | |
| All | Max | 26.9 | 1.0 | 55.36 | 31.72 | 3600 | 17,400 |
| Min | 3.4 | 0.5 | 30.54 | 2038 | 800 | 3100 | |
| Average | 11.6 | 0.7 | 43.07 | 26.29 | 2038 | 9025 | |
| StD | 4.7 | 0.2 | 6.63 | 2.93 | 965 | 3046 | |
| nop | g | MAPE | MSE | RMSE | R2 | VAF |
|---|---|---|---|---|---|---|
| 20 | 20 | 12.98% | 0.00047 | 0.0217 | 0.97680 | 98.91 |
| 30 | 12.63% | 0.00047 | 0.0217 | 0.97862 | 99.14 | |
| 40 | 10.46% | 0.00046 | 0.0214 | 0.97913 | 99.15 | |
| 50 | 9.49% | 0.00045 | 0.0212 | 0.97984 | 99.24 | |
| 100 | 7.91% | 0.00041 | 0.0202 | 0.98151 | 99.48 | |
| 30 | 20 | 12.51% | 0.00047 | 0.0217 | 0.97842 | 99.08 |
| 30 | 10.36% | 0.00046 | 0.0214 | 0.97941 | 99.21 | |
| 40 | 8.77% | 0.00043 | 0.0207 | 0.98048 | 99.27 | |
| 50 | 7.78% | 0.00040 | 0.0200 | 0.98107 | 99.31 | |
| 100 | 6.81% | 0.00039 | 0.0197 | 0.98166 | 99.52 | |
| 40 | 20 | 9.89% | 0.00045 | 0.0212 | 0.97875 | 99.15 |
| 30 | 8.64% | 0.00043 | 0.0207 | 0.98012 | 99.24 | |
| 40 | 7.04% | 0.00039 | 0.0197 | 0.98111 | 99.38 | |
| 50 | 6.30% | 0.00038 | 0.0195 | 0.98145 | 99.46 | |
| 100 | 5.69% | 0.00037 | 0.0192 | 0.98194 | 99.56 | |
| 50 | 20 | 8.44% | 0.00042 | 0.0205 | 0.97974 | 99.23 |
| 30 | 6.81% | 0.00039 | 0.0197 | 0.98060 | 99.28 | |
| 40 | 6.21% | 0.00037 | 0.0192 | 0.98123 | 99.46 | |
| 50 | 5.12% | 0.00036 | 0.0190 | 0.98159 | 99.50 | |
| 100 | 4.86% | 0.00036 | 0.0190 | 0.98345 | 99.73 |
| Data Set | Cases | ||
|---|---|---|---|
| Total | Training | Testing | |
| Data set 1 [17] | 50 | 40 | 10 |
| Data set 2 [30] | 100 | 65 | 35 |
| Data set 3 [31] | 72 | 50 | 22 |
| Model | Data Set | R2 | MSE | RMSE | VAF | Error Mean | Error StD |
|---|---|---|---|---|---|---|---|
| GA- based ANN | Training set | 0.9600 | 0.0115 | 0.1072 | - * | - * | - * |
| Testing set | 0.9900 | 0.0020 | 0.0447 | 98.88 | 21 | 84 | |
| IRMO-BPNN | Training set | 0.9948 | 0.0004 | 0.0207 | 99.83 | −2 | 68 |
| Testing set | 0.9896 | 0.0006 | 0.0236 | 99.72 | 8 | 81 |
| Model | Data Set | R2 | MSE | RMSE | VAF | Error Mean | Error StD |
|---|---|---|---|---|---|---|---|
| RBFANN | Training set | 0.9976 | 208444 | 457 | - * | 0 | 460 |
| Testing set | 0.9785 | 2045084 | 1430 | 97.89 | −9 | 1451 | |
| IRMO-BPNN | Training set | 0.9992 | 72546 | 269 | 99.91 | −29 | 270 |
| Testing set | 0.9940 | 553194 | 744 | 99.38 | 31 | 754 |
| Model | Data Set | R2 | MSE | RMSE | VAF | Error Mean | Error StD |
|---|---|---|---|---|---|---|---|
| ANFIS-GMDH-PSO | Training set | 0.8836 | 0.0020 | 0.0480 | - * | −0.0004 | 0.0480 |
| Testing set | 0.9216 | 0.0050 | 0.0690 | 89.48 | −0.0210 | 0.0670 | |
| IRMO-BPNN | Training set | 0.9868 | 0.0003 | 0.0162 | 98.68 | 0.0062 | 0.0151 |
| Testing set | 0.9801 | 0.0009 | 0.0298 | 97.96 | −0.0057 | 0.0299 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, L.; Ji, Y. Development of an IRMO-BPNN Based Single Pile Ultimate Axial Bearing Capacity Prediction Model. Buildings 2023, 13, 1297. https://doi.org/10.3390/buildings13051297
Jin L, Ji Y. Development of an IRMO-BPNN Based Single Pile Ultimate Axial Bearing Capacity Prediction Model. Buildings. 2023; 13(5):1297. https://doi.org/10.3390/buildings13051297
Chicago/Turabian StyleJin, Liangxing, and Yujie Ji. 2023. "Development of an IRMO-BPNN Based Single Pile Ultimate Axial Bearing Capacity Prediction Model" Buildings 13, no. 5: 1297. https://doi.org/10.3390/buildings13051297
APA StyleJin, L., & Ji, Y. (2023). Development of an IRMO-BPNN Based Single Pile Ultimate Axial Bearing Capacity Prediction Model. Buildings, 13(5), 1297. https://doi.org/10.3390/buildings13051297






