Analysis of the Seismic Response of Unequal-Span Metro Station in Saturated Site
Abstract
1. Introduction
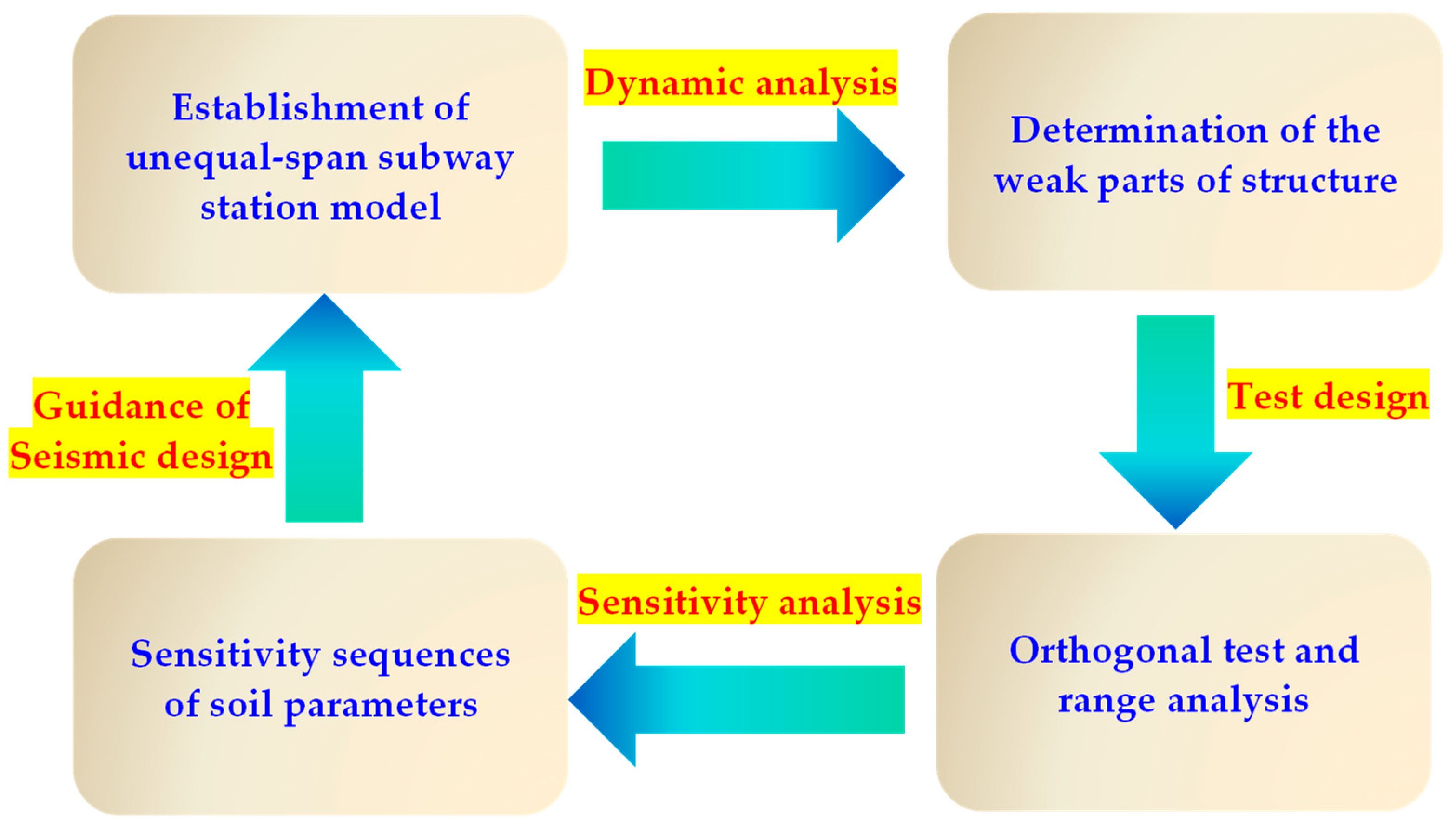
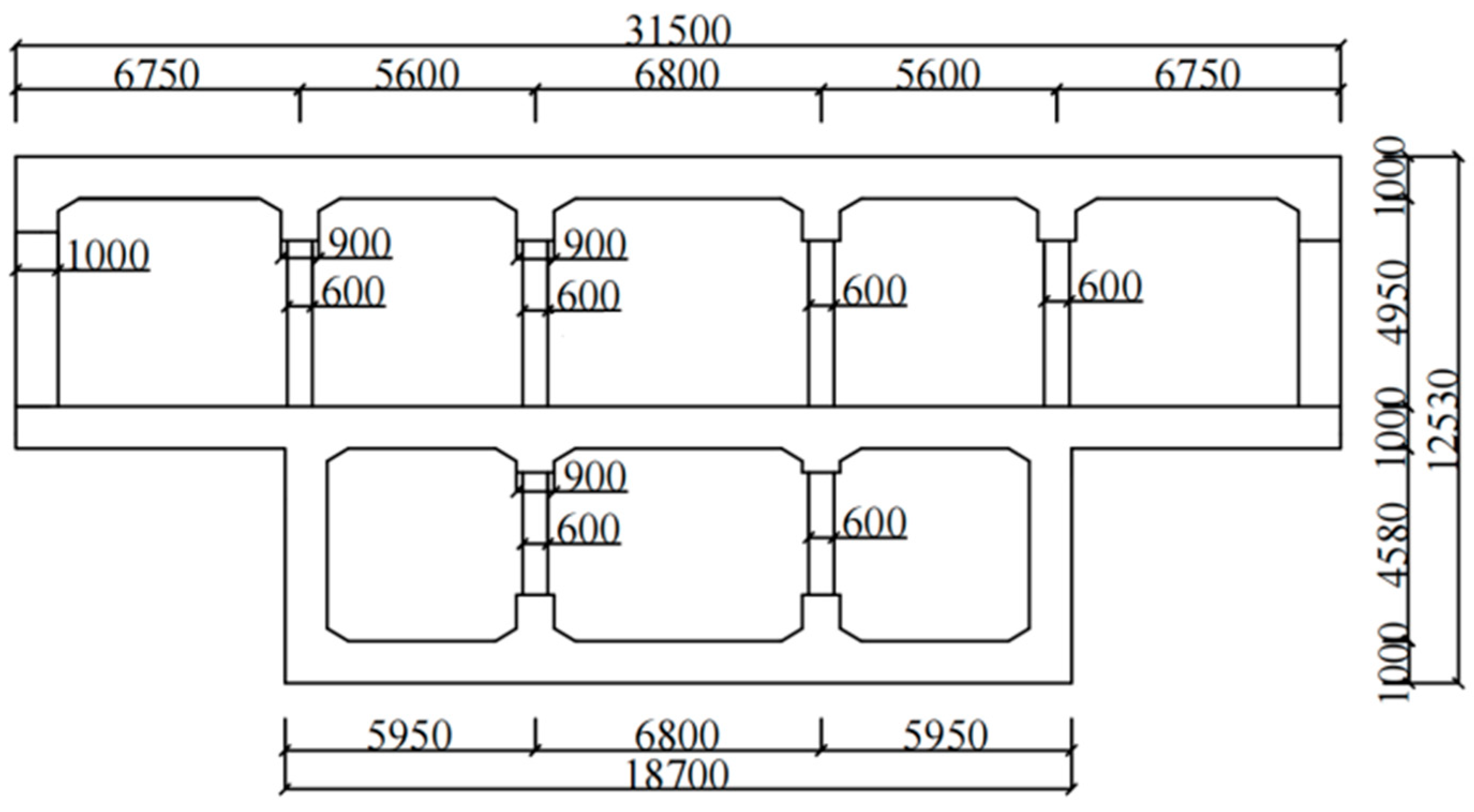
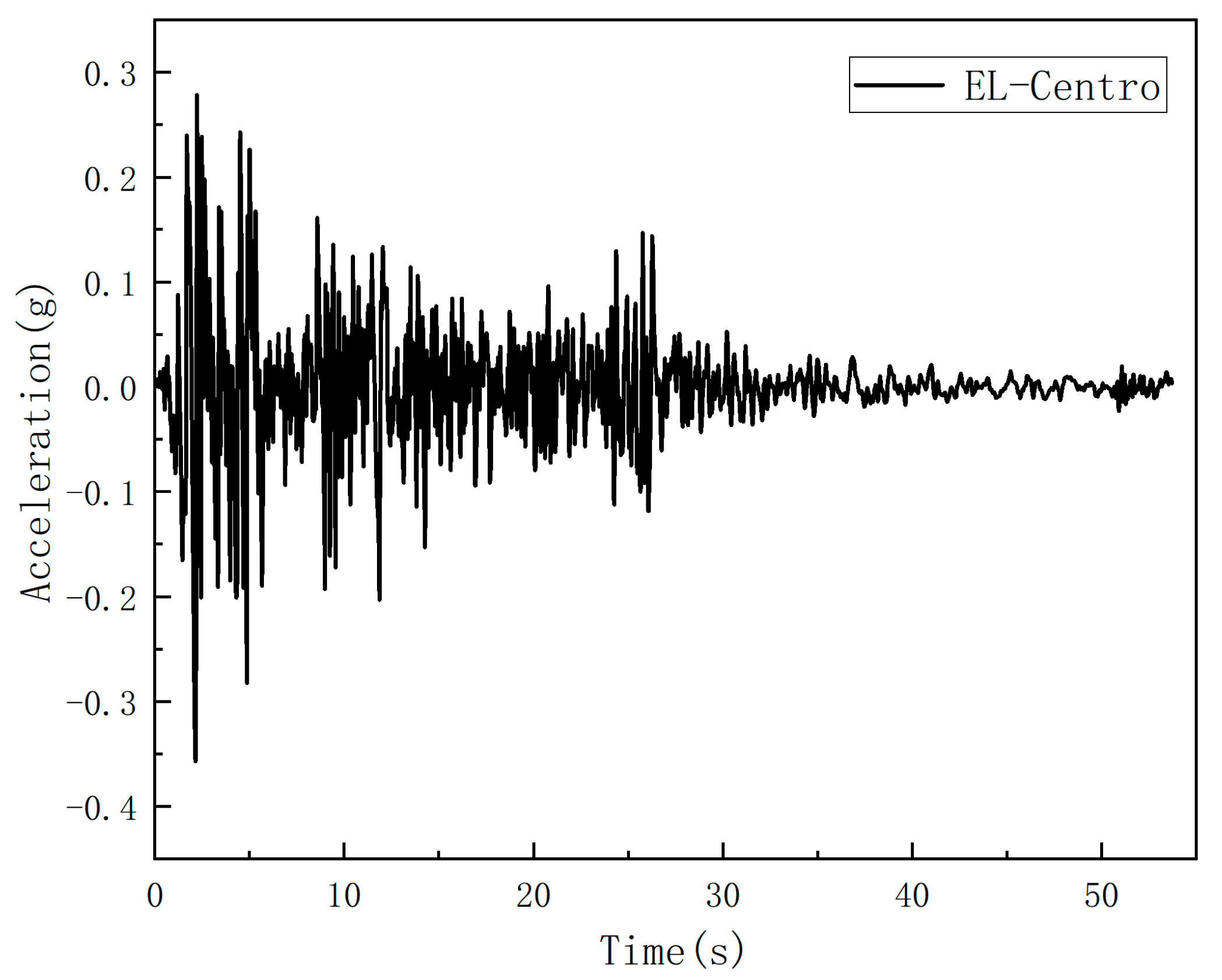
2. Numerical Model and Orthogonal Test Design
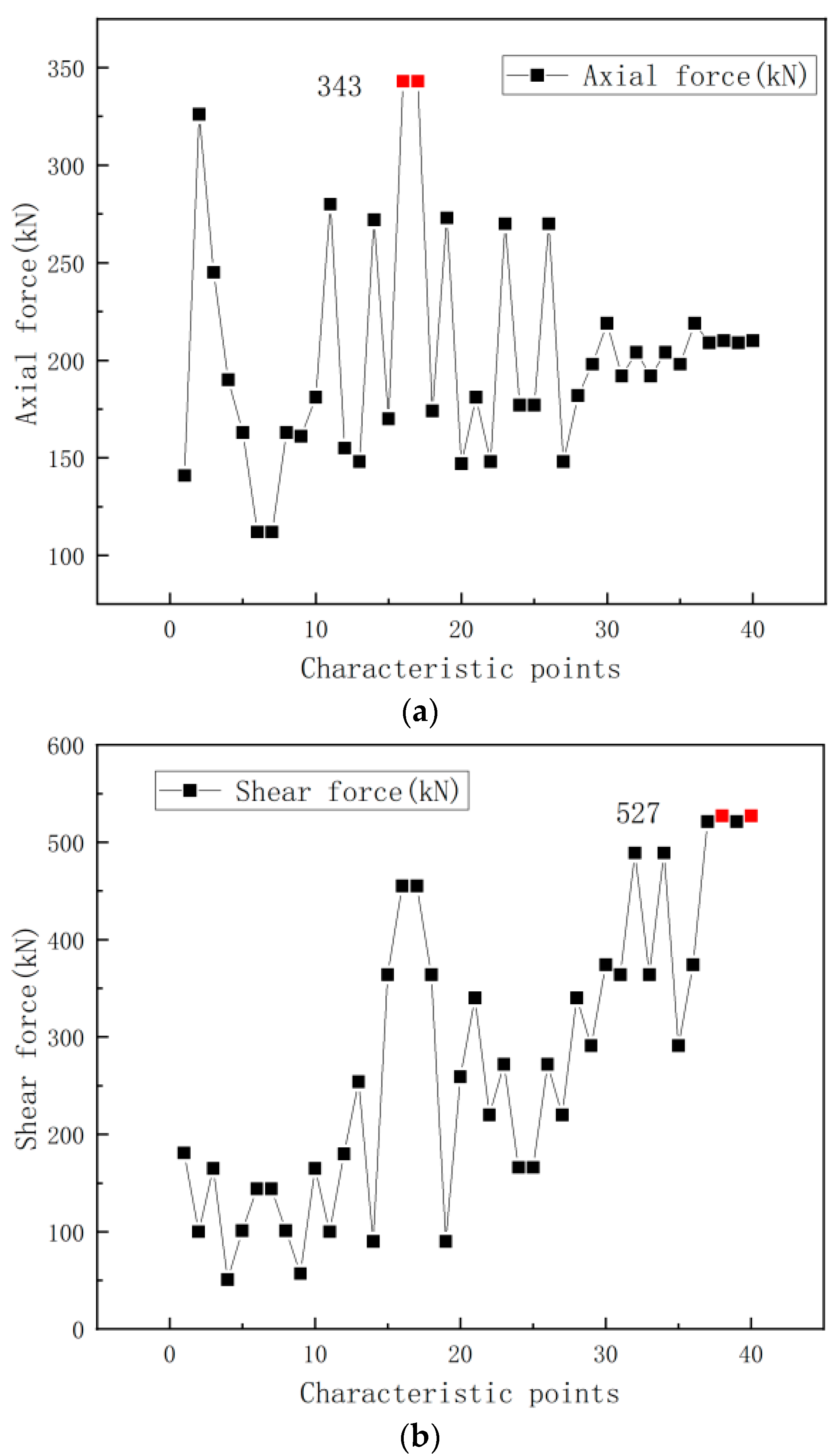
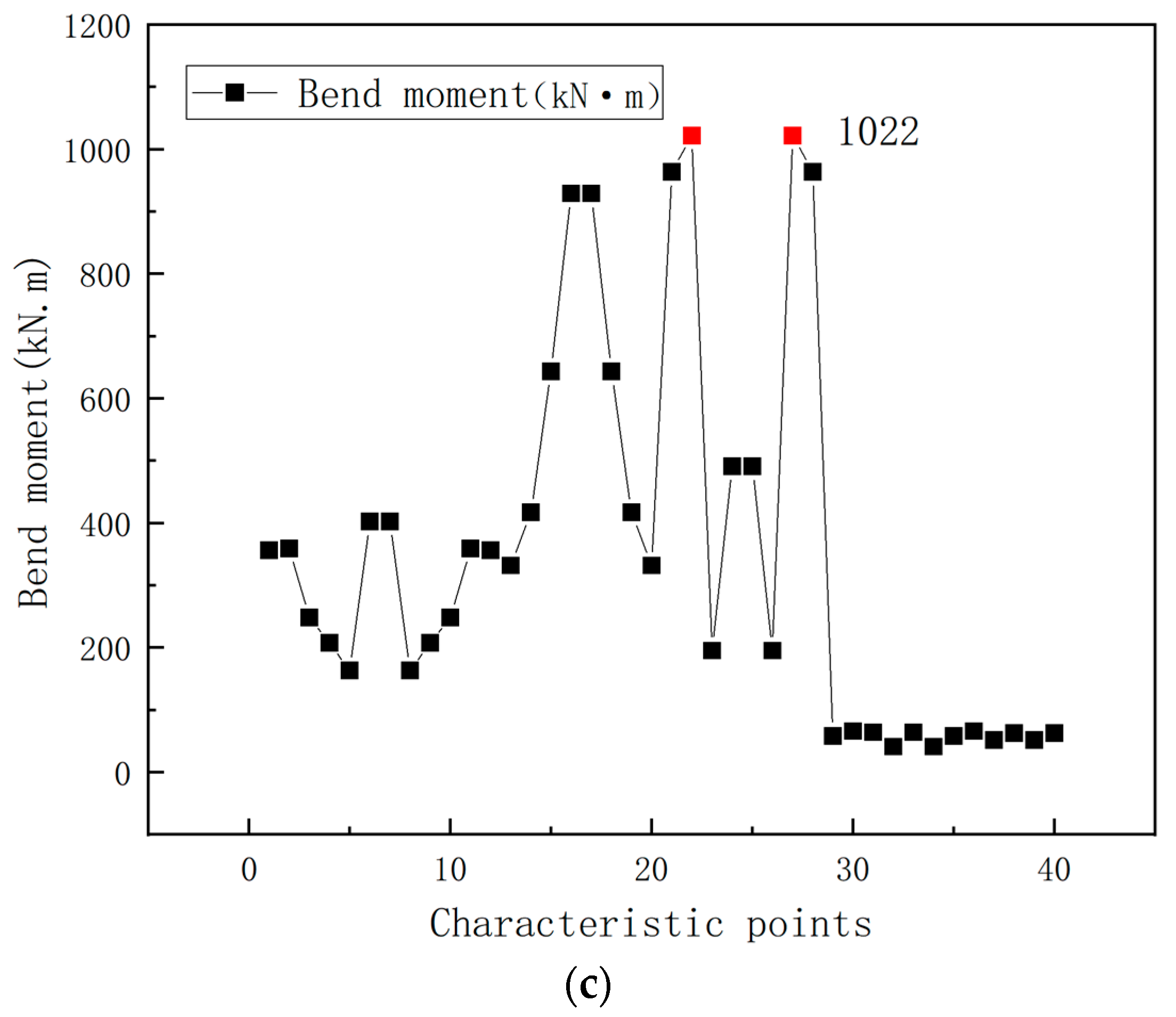
3. Seismic Dynamic Response Analysis of an Unequal-Span Subway Station Structure
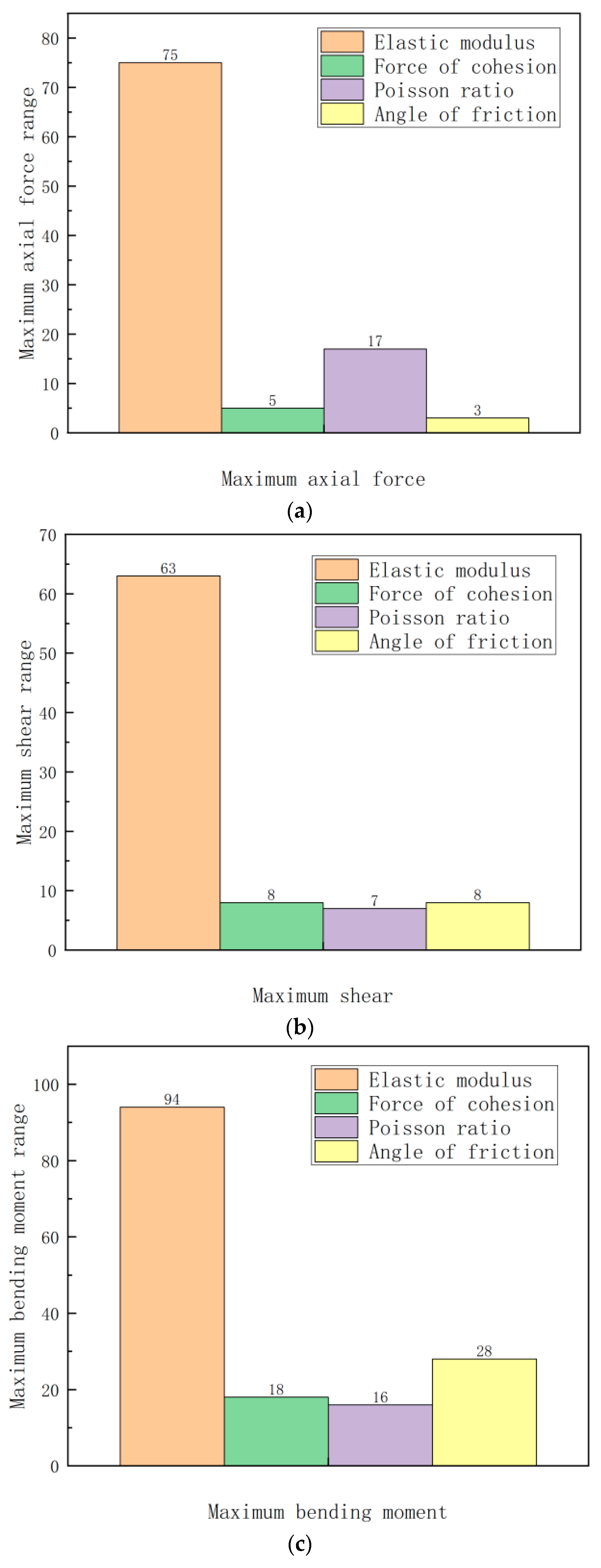
4. Parameter Sensitivity Analysis of the Seismic Dynamic Response Index of Unequal-Span Subway Station Structure
5. Conclusions
- (1)
- Under the action of an earthquake, the lower end of the shear wall and the vicinity of the cantilever span of the unequal-span subway station structure in the saturated site, are prone to bending failure, and the central columns of the station structure are prone to shear failure. All of them are weak components of the structure, with the accumulation of stress damage.
- (2)
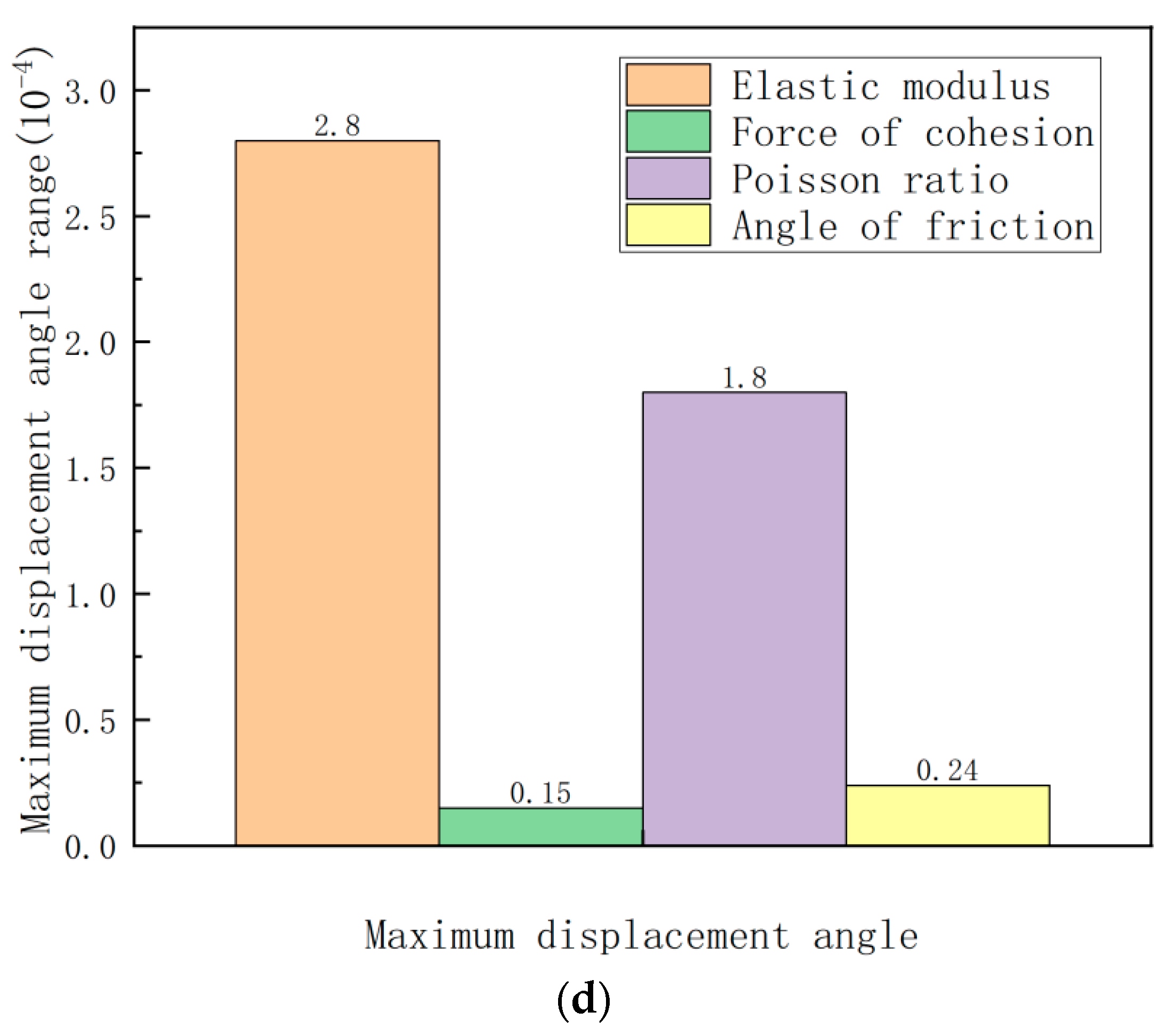
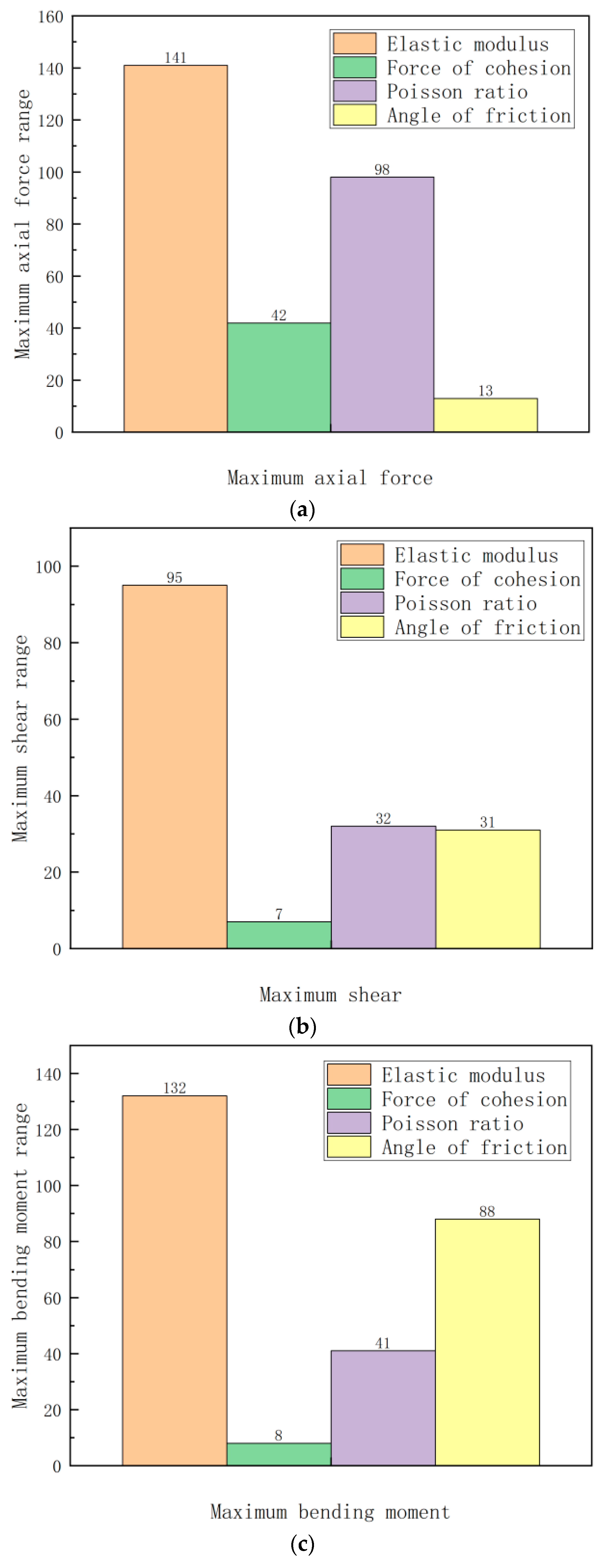
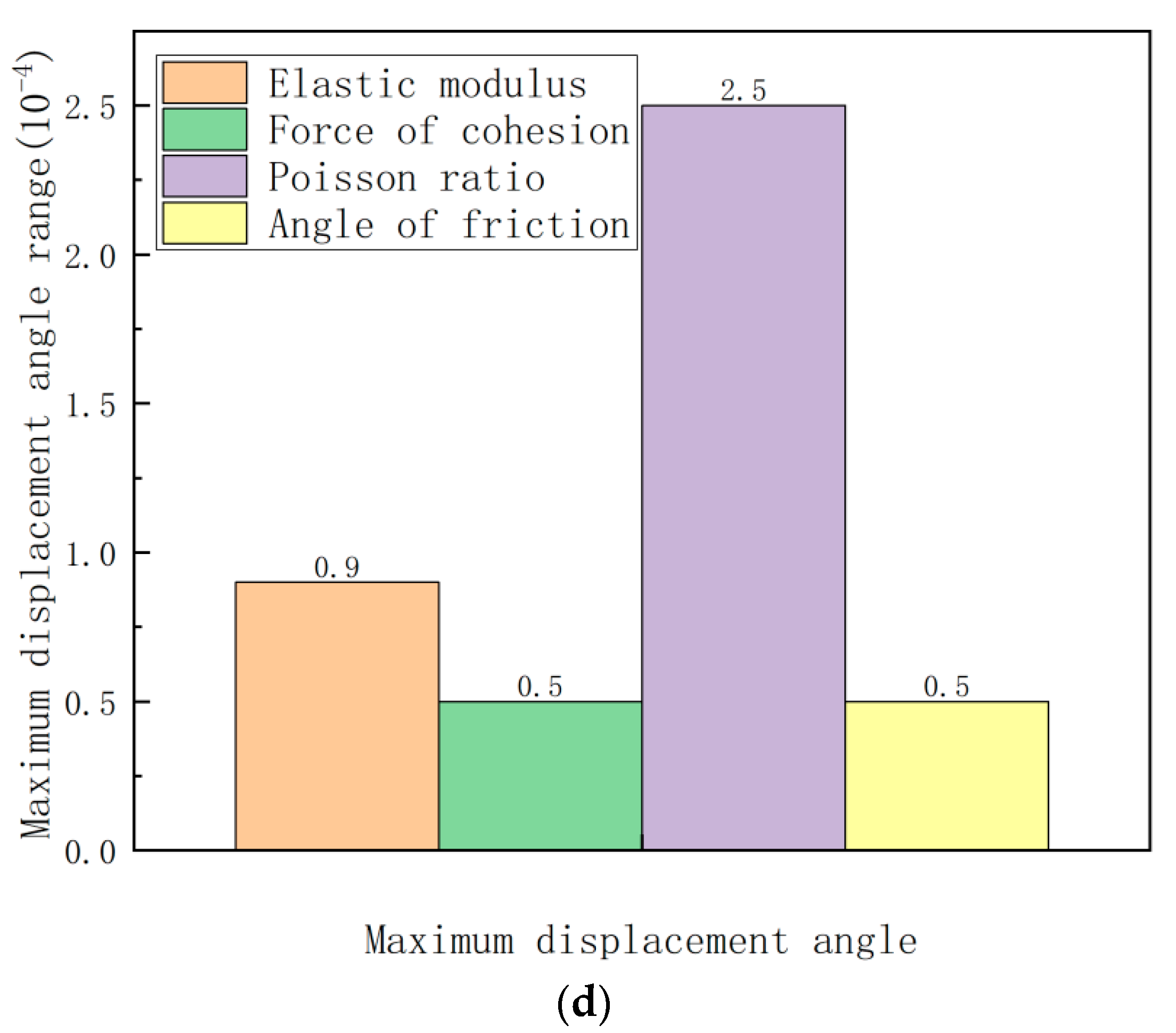
- Comparing the range of soil parameters on the dynamic response of the unequal-span subway station structure under the action of a single horizontal or combination of horizontal and vertical ground motions, it is clear that the elastic modulus has the greatest impact on the dynamic response of the unequal-span subway station structure, followed by the Poisson’s ratio and friction angle, and the sensitivity of cohesion has the least influence.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cui, C.; Xu, M.; Xu, C.; Zhang, P.; Zhao, J. An ontology-based probabilistic framework for comprehensive seismic risk evaluation of subway stations by combining Monte Carlo simulation. Tunn. Undergr. Space Technol. 2023, 135, 105055. [Google Scholar] [CrossRef]
- Yuan, B.; Li, Z.; Zhao, Z.; Ni, H.; Su, Z.; Li, Z. Experimental study of displacement field of layered soils surrounding laterally loaded pile based on transparent soil. J. Soils Sediments 2021, 21, 3072–3083. [Google Scholar] [CrossRef]
- Wang, J.; Ma, G.; Dou, Y.; Zhuang, H.; Fu, J. Performance levels and evaluation method for seismic behaviors of a large-scale underground subway station with unequal-span frame. J. Vib. Shock 2020, 39, 92–100. [Google Scholar] [CrossRef]
- Tang, X.; Fu, P.; Li, H.; Gong, J. Seismic simulation and analysis of the two-layer prestressed long-span subway station. J. Northeast. Univ. (Nat. Sci.) 2015, 36, 892–896. [Google Scholar] [CrossRef]
- Tao, L.; Liu, C.; Bian, J.; Wu, B.; Li, J.; Xu, Y. Seismic response of subway station with large span and Y shaped column. Chin. J. Theor. Appl. Mech. 2017, 49, 55–64. [Google Scholar] [CrossRef]
- Wang, J.; Dou, Y.; Zhuang, H.; Fu, J.; Ma, G. Seismic response of dynamic interaction system of soil-diaphragm wall-complicated unequal-span subway station. Chin. J. Geotech. Eng. 2019, 41, 1235–1243. [Google Scholar]
- Cui, C.; Liang, Z.; Xu, C.; Xin, Y.; Wang, B. Analytical solution for horizontal vibration of end-bearing single pile in radially heterogeneous saturated soil. Appl. Math. Model. 2023, 116, 65–83. [Google Scholar] [CrossRef]
- Meng, K.; Cui, C.; Liang, Z. A new approach for longitudinal vibration of a large-diameter floating pipe pile in visco-elastic soil considering the three-dimensional wave effects. Comput. Geotech. 2020, 128, 103840. [Google Scholar] [CrossRef]
- Zhong, Z.; Shen, Y.; Zhao, M.; Li, L.; Du, X.; Hao, H. Seismic fragility assessment of the Daikai subway station in layered soil. Soil Dyn. Earthq. Eng. 2020, 132, 106044. [Google Scholar] [CrossRef]
- Bu, X.; Ledesma, A.; Lopez-Almansa, F. Novel seismic design solution for underground structures: Case study of a 2-story 3-bay subway station. Soil Dyn. Earthq. Eng. 2021, 153, 107087. [Google Scholar] [CrossRef]
- Cui, C.; Meng, K.; Xu, C.; Wang, B.; Xin, Y. Vertical vibration of a floating pile considering the incomplete bonding effect of the pile-soil interface. Comput. Geotech. 2022, 150, 104894. [Google Scholar] [CrossRef]
- Yuan, B.; Chen, W.; Zhao, J.; Li, L.; Liu, F.; Guo, Y.; Zhang, B. Addition of alkaline solutions and fibers for the reinforcement of kaolinite-containing granite residual soil. Appl. Clay Sci. 2022, 228, 106644. [Google Scholar] [CrossRef]
- Lin, L.; Chen, J. Analysis of earthquake-resistant capacity of shallow-buried subway station structures in soft soil. J. Disaster Prev. Mitig. Eng. 2006, 26, 268–273. [Google Scholar] [CrossRef]
- Wang, G.; Yuan, M.; Miao, Y.; Wu, J.; Wang, Y. Experimental study on seismic response of underground tunnel-soil-surface structure interaction system. Tunn. Undergr. Space Technol. 2018, 76, 145–159. [Google Scholar] [CrossRef]
- Huan, Y.; Fang, Q.; Liu, J.; Chen, L.; Du, M. Theoretical and numerical investigations on enhancement of a seismic capability of metro stations. J. Vib. Shock 2011, 30, 252–257. [Google Scholar] [CrossRef]
- Han, X. Formation parameters sensitivity analysis of subway construction in loess region. Shanxi Sci. Technol. Commun. 2012, 4, 50–52+63. [Google Scholar]
- Cui, C.; Cheng, X.; Sun, Z.; Xu, C. Analysis of seismic response and parametric sensitivity of subway station surrounded by saturated soft soil. J. Railw. Eng. Soc. 2017, 34, 92–98. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Z. Seismic damage classifcation and risk assessment of mountain tunnels with a validation for the 2008 Wenchuan earthquake. Soil Dyn. Earthq. Eng. 2013, 45, 45–55. [Google Scholar] [CrossRef]
- Zhuang, H.; Chen, G.; Hu, Z.; Qi, C. Influence of soil liquefaction on the seismic response of a subway station in model tests. Bull. Eng. Geol. Environ. 2016, 75, 1169–1182. [Google Scholar] [CrossRef]
- Li, L.; Shi, P.; Du, X.; Jiao, H. Using numerical simulation to determine the seismic response of coastal underground structures in saturated soil deposits. J. Coast. Res. 2017, 33, 583–595. [Google Scholar] [CrossRef]
- Hu, J.; Liu, H. The uplift behavior of a subway station during different degree of soil liquefaction. Proc. Int. Sci. Conf. Transp. Geotech. Geoecol. 2017, 189, 18–24. [Google Scholar] [CrossRef]
- Xia, C.; Qi, C.; Zhao, B.; Qu, X. Seismic response of the subway station due to a specific active fault. Tunn. Undergr. Space Technol. 2019, 85, 12–20. [Google Scholar] [CrossRef]
- Song, Y.; Huang, M. Orthogonal numerical simulation experiment on structural parameter sensitivity of new type of primary support of metro tunnel. Tunn. Constr. 2019, 39, 163–168. [Google Scholar] [CrossRef]
- Xu, C.; Ma, J.; Meng, J.; Ge, Y. Sensitivity study on deformation influencing factors of metro tunnel underpass viaduct. Water Power 2019, 45, 29–32. [Google Scholar] [CrossRef]
- Wang, J.; Fu, J.; Zhuang, H.; Dou, Y.; Ma, G. Seismic response analysis of complex subway station structure with unequal-span in liquefiable foundation. J. Vib. Shock 2020, 39, 170–179. [Google Scholar] [CrossRef]
- Wang, J.; Ma, G.; Zhuang, H.; Dou, Y.; Fu, J. Seismic responses of a large unequal-span underground subway station in different classified sites. J. Basic Sci. Eng. 2021, 29, 324–336. [Google Scholar] [CrossRef]
- Xu, M.; Cui, C.; Wang, G.; Wang, Q.; Su, J. Parameter sensitivity analysis for seismic response of subway station embedded in saturated sand layers. J. Disaster Prev. Mitig. Eng. 2022, 42, 499–506. [Google Scholar] [CrossRef]
- He, Z.; Wang, P.; Wang, L.; Qiu, J. Influence of deep foundation pit construction on adjacent subway tunnel deformation and parameter sensitivity analysis. J. Chang. Univ. (Nat. Sci. Ed.) 2022, 42, 63–72. [Google Scholar] [CrossRef]
- Yang, X.; Xu, X.; Gu, Y.; Shi, W. Study on orthogonal sensitivity test of deep excavation above tunnel. Fly Ash Compr. Util. 2022, 38, 74–80. [Google Scholar] [CrossRef]
- Wu, C.; Lu, D.; El Naggar, M.; Ma, C.; Li, Q.; Du, X. Upgrading seismic performance of underground frame structures based on potential failure modes l Dynamics & Earthquake Engineering Soil Dynamics & Earthquake Engineering based on potential failure modes. Soil Dyn. Earthq. Eng. 2022, 153, 107116. [Google Scholar] [CrossRef]
- Wang, J.; Ma, G.; Zhuang, H.; Dou, Y.; Fu, J. Influence of diaphragm wall on seismic responses of large unequal-span subway station in liquefiable soils. Tunn. Undergr. Space Technol. 2019, 19, 102988. [Google Scholar] [CrossRef]
- Shatnawi, A.; Almasabha, G.; Tarawneh, B. Structural behavior of concrete box culverts under deep burial. J. Pipeline Syst. Eng. Pract. 2017, 8, 04017025. [Google Scholar] [CrossRef]
- Chen, Z.; Fan, Y.; Jia, P. Influence of buried depth on seismic capacity of underground subway stations through performance-based evaluation. Structures 2021, 32, 194–203. [Google Scholar] [CrossRef]
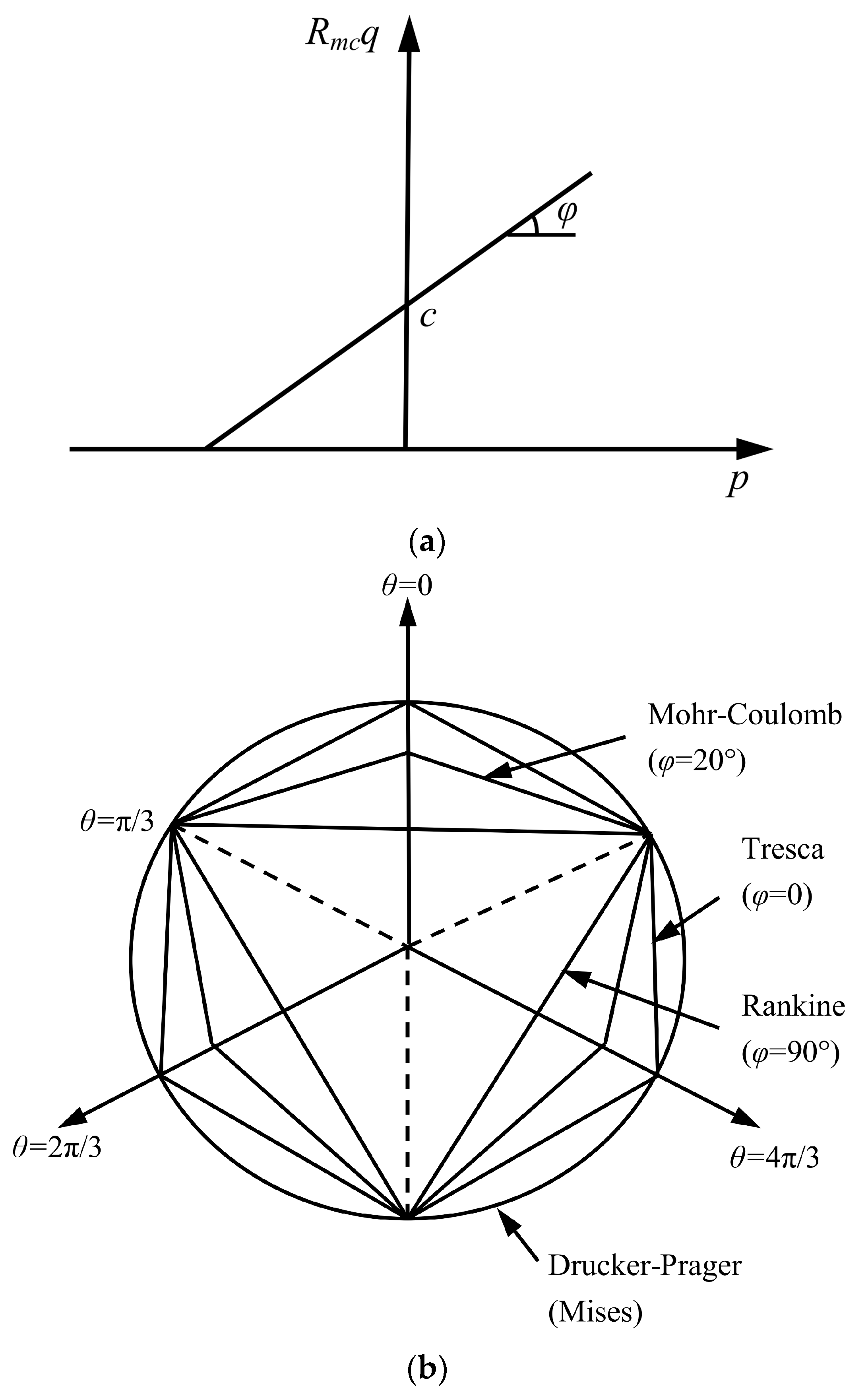
- David, M.; Antonio, M.; Ana, I. A state parameter-dependent constitutive model for sands based on the Mohr–Coulomb failure criterion. Comput. Geotech. 2022, 48, 104811. [Google Scholar] [CrossRef]
- Cheng, B.; Xu, T.; Tang, J. Reservoir brittleness prediction method based on the Mohr–Coulomb failure criterion and effective in situ stress principle. Rock Mech. Rock Eng. 2022, 55, 5933–5951. [Google Scholar] [CrossRef]
- Franeisco, J. Site Effects in Parkway Basin Comparison between Observations and 3-D Modeling. Appl. Geophys. 2003, 154, 633–646. [Google Scholar] [CrossRef]
- Zhou, Y.; Xiao, Y.; Gu, A.; Zhong, G.; Feng, S. Orthogonal experimental investigation of steel-PVA fiber-reinforced concrete and its uniaxial constitutive model. Constr. Build. Mater. 2019, 197, 615–625. [Google Scholar] [CrossRef]
- Chen, Q.; Hong, N.; Zhang, T.; Zhao, Z. Experiment-based performance evaluation framework for isolated structures in underground subway station–soil–aboveground structure interaction system under seismic excitations. J. Build. Eng. 2022, 56, 104790. [Google Scholar] [CrossRef]

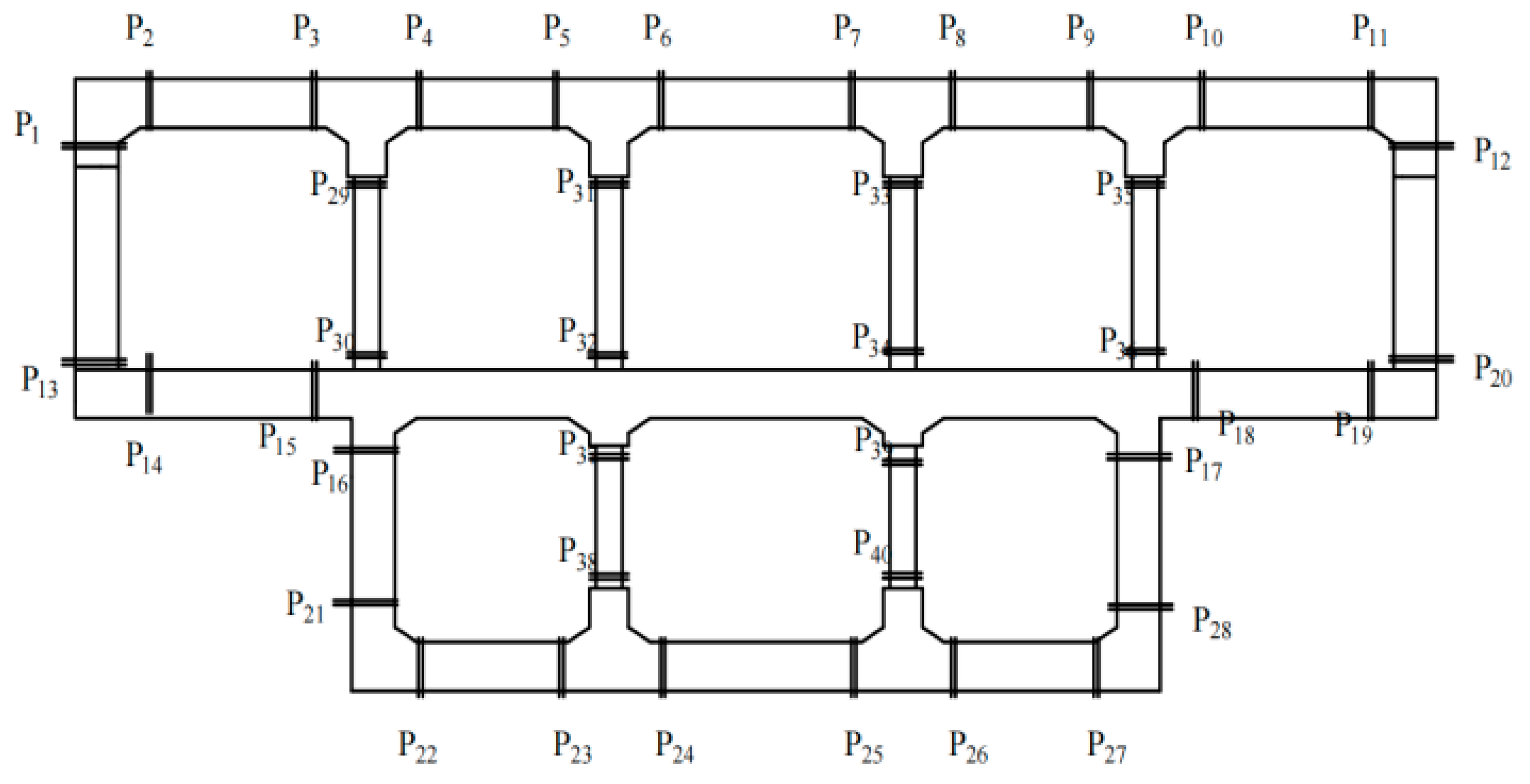
| Material | Elastic Modulus (kPa) | Gravity (kN/m3) | Poisson’s Ratio | Cohesion (kPa) | Friction Angle (°) |
|---|---|---|---|---|---|
| Clay | 19.404 | 0.3 | 18 | 20 | |
| Concrete | 25 | 0.2 | / | / |
| Level | Elastic Modulus/kPa | Cohesion/kPa | Poisson’s Ratio | Friction Angle/° |
|---|---|---|---|---|
| 1 | 18 | 0.3 | 20 | |
| 2 | 24 | 0.32 | 22 | |
| 3 | 30 | 0.35 | 25 |
| Number of Test | Elastic Modulus/kPa | Cohesion/kPa | Poisson’s Ratio | Friction Angle/° |
|---|---|---|---|---|
| 1 | 18 | 0.3 | 20 | |
| 2 | 24 | 0.32 | 22 | |
| 3 | 30 | 0.35 | 25 | |
| 4 | 18 | 0.32 | 25 | |
| 5 | 24 | 0.35 | 20 | |
| 6 | 30 | 0.3 | 22 | |
| 7 | 18 | 0.35 | 22 | |
| 8 | 24 | 0.3 | 25 | |
| 9 | 30 | 0.32 | 20 |
| Working Condition | Elastic Modulus | Cohesion | Poisson’s Ratio | Friction Angle | Maximum Axial Force | Maximum Shear | Maximum Bending Moment | Maximum Interstory Drift Ratio of Roof and Floor |
|---|---|---|---|---|---|---|---|---|
| kPa | kPa | ° | kN | kN | kN·m | rad | ||
| 1 | 18 | 0.3 | 20 | 343 | 527 | 1022 | 0.00136097 | |
| 2 | 24 | 0.32 | 22 | 351 | 531 | 1028 | 0.00127818 | |
| 3 | 30 | 0.35 | 25 | 363 | 541 | 1070 | 0.00114805 | |
| 4 | 18 | 0.32 | 25 | 294 | 469 | 954 | 0.00133839 | |
| 5 | 24 | 0.35 | 20 | 310 | 479 | 973 | 0.00124344 | |
| 6 | 30 | 0.3 | 22 | 287 | 463 | 942 | 0.00138669 | |
| 7 | 18 | 0.35 | 22 | 283 | 492 | 1034 | 0.00143551 | |
| 8 | 24 | 0.3 | 25 | 274 | 501 | 1064 | 0.00162570 | |
| 9 | 30 | 0.32 | 20 | 275 | 498 | 1053 | 0.00156752 |
| Working Condition | Elastic Modulus | Cohesion | Poisson’s Ratio | Friction Angle | Maximum Axial Force | Maximum Shear | Maximum Bending Moment | Maximum Interstory Drift Ratio of Roof and Floor |
|---|---|---|---|---|---|---|---|---|
| kPa | kPa | kN | kN | kN·m | rad | |||
| 1 | 18 | 0.3 | 20 | 1729 | 665 | 1593 | 0.00143746 | |
| 2 | 24 | 0.32 | 22 | 1716 | 670 | 1626 | 0.00134688 | |
| 3 | 30 | 0.35 | 25 | 1660 | 674 | 1576 | 0.00110069 | |
| 4 | 18 | 0.32 | 25 | 1653 | 592 | 1414 | 0.00135984 | |
| 5 | 24 | 0.35 | 20 | 1640 | 648 | 1494 | 0.00125037 | |
| 6 | 30 | 0.3 | 22 | 1714 | 639 | 1492 | 0.00142699 | |
| 7 | 18 | 0.35 | 22 | 1490 | 603 | 1621 | 0.00124805 | |
| 8 | 24 | 0.3 | 25 | 1643 | 554 | 1483 | 0.00150027 | |
| 9 | 30 | 0.32 | 20 | 1549 | 568 | 1545 | 0.00141977 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, J.; Xiao, W.; Xu, M.; Cui, C.; Zhao, J.; Ling, L. Analysis of the Seismic Response of Unequal-Span Metro Station in Saturated Site. Buildings 2023, 13, 953. https://doi.org/10.3390/buildings13040953
Su J, Xiao W, Xu M, Cui C, Zhao J, Ling L. Analysis of the Seismic Response of Unequal-Span Metro Station in Saturated Site. Buildings. 2023; 13(4):953. https://doi.org/10.3390/buildings13040953
Chicago/Turabian StyleSu, Jian, Wei Xiao, Minze Xu, Chunyi Cui, Jingtong Zhao, and Ling Ling. 2023. "Analysis of the Seismic Response of Unequal-Span Metro Station in Saturated Site" Buildings 13, no. 4: 953. https://doi.org/10.3390/buildings13040953
APA StyleSu, J., Xiao, W., Xu, M., Cui, C., Zhao, J., & Ling, L. (2023). Analysis of the Seismic Response of Unequal-Span Metro Station in Saturated Site. Buildings, 13(4), 953. https://doi.org/10.3390/buildings13040953





