Investigations into the Shear Load-Capacity of Strengthened Reinforced Concrete Structures with Carbon-Reinforced Concrete
Abstract
:1. Introduction
2. Shear Load Bearing Behavior of RC Structures
- Shear stresses in the uncracked compression zone (Vcz);
- Tensile stresses across cracks in the crack process zone (Vcr);
- Shear capacity of the shear reinforcement (Vs);
- Crack friction or crack interlocking (Vag);
- Anchorage effect of the longitudinal reinforcement (Vda);
- Load transfer in concrete through direct compressive strut/arching (Vsp).
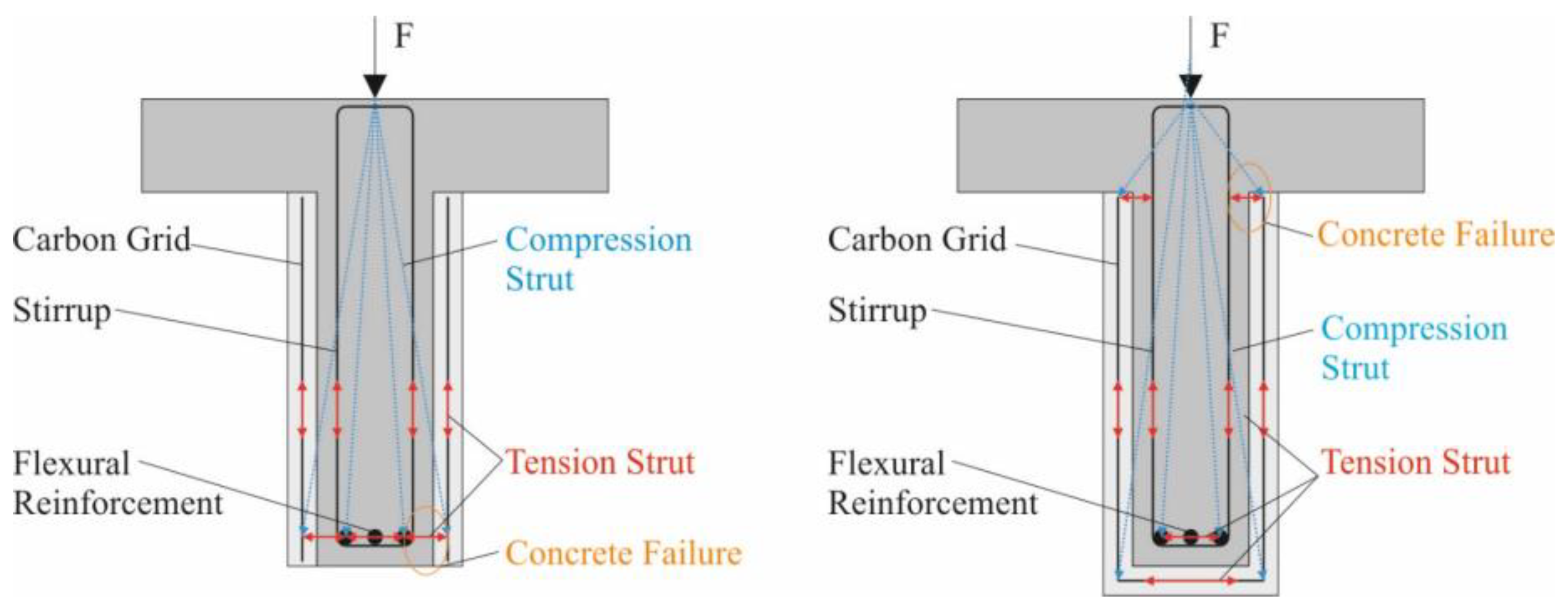
3. Shear Strengthening with Carbon-Reinforced Concrete
- Anchorage failure due to delamination within the plane of the carbon grid embedded in the fine concrete.
- Anchorage failure of the reinforcement by exceeding the tensile strength of the old concrete.
- Failure of the carbon grids when the tensile strength of the fiber strands is exceeded.
- Compressive strut failure of the old concrete.
4. Investigations
4.1. Extent of Testing
- Type of carbon grid. Two types of carbon grids were used.
- Geometry of the base component. Slim and compact T-beams were tested.
- Number of layers. The reinforced concrete beams were strengthened with one or two layers.
- Influence of an unreinforced fine concrete layer to assess the load-bearing contribution of the pure concrete layer in CRC-strengthening layers.
- Arrangement of the strengthening layer. The carbon grids were placed either on the sides (II) or on the sides and below (U) the web. Additionally, the fiber strands of the carbon grids were arranged parallel (0°/90°) and inclined to the stirrup reinforcement (45°/45° orientation) in the strengthening layer.
- Pre-damage of the base specimen before shear strengthening.
- Shear slenderness. Specimens with shear slenderness λ = 3.3 and 2.1 were examined.
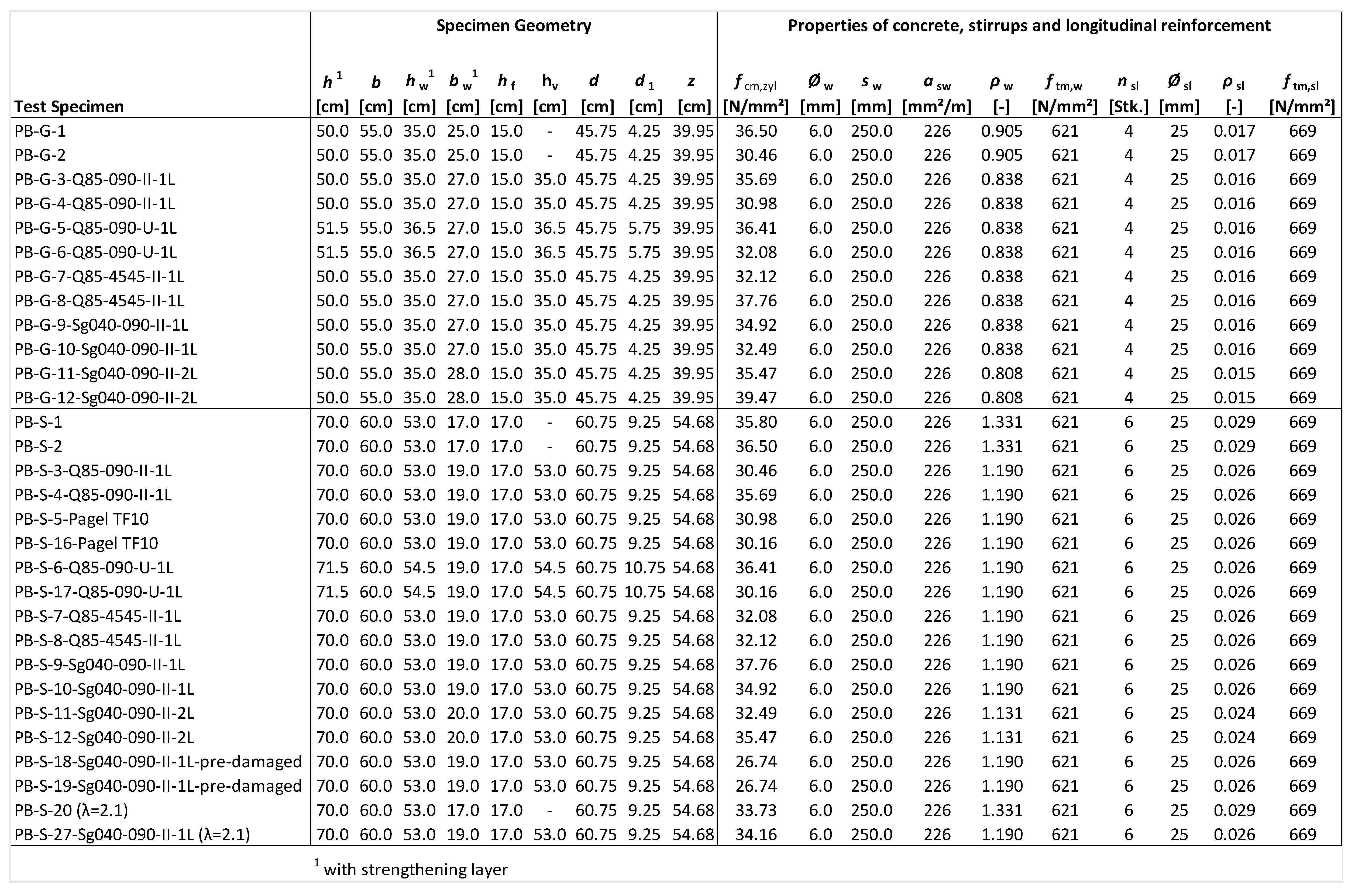
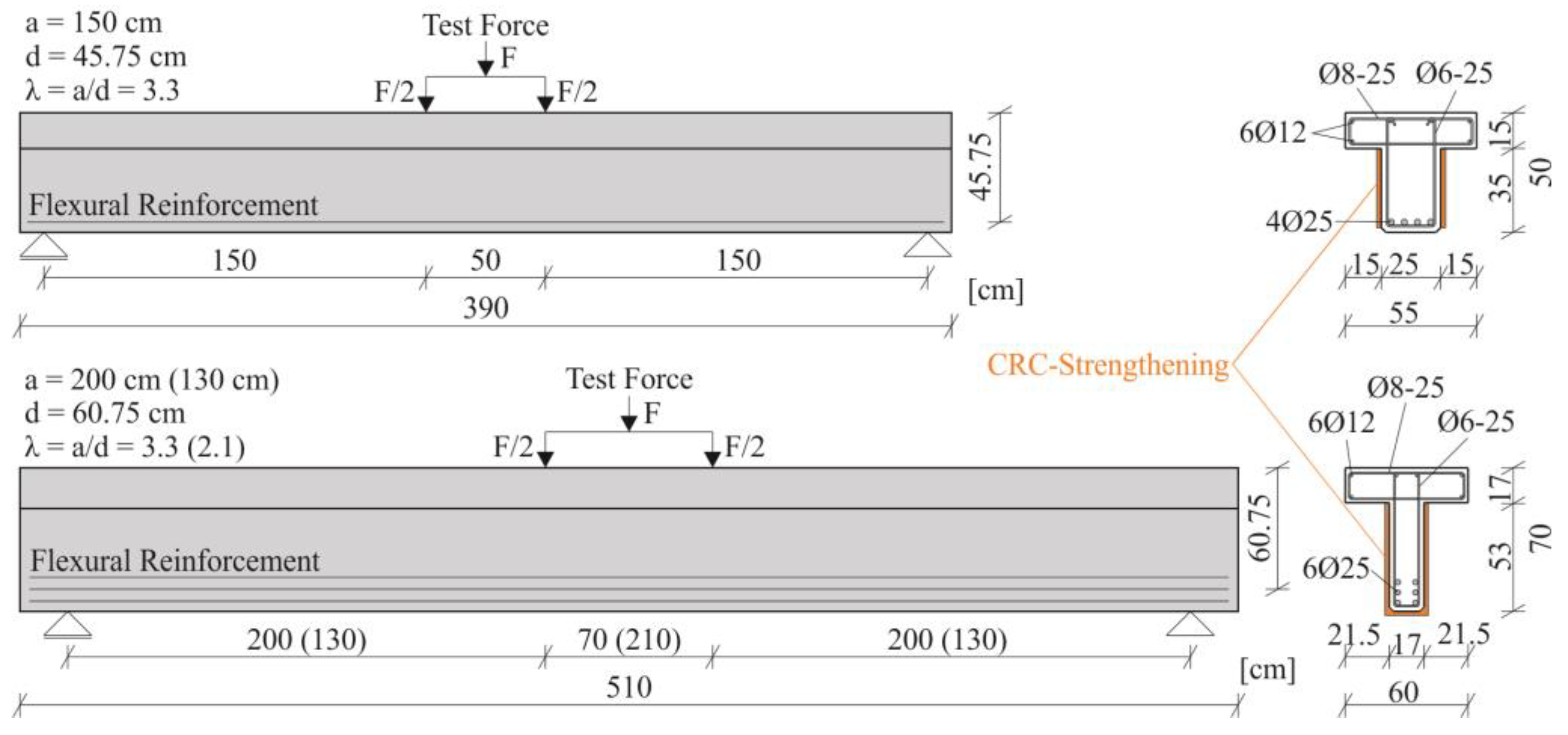
4.2. Test Specimens
4.3. Materials
Formularbeginn
4.4. Test Setup and Execution
4.5. Test Results
4.5.1. Overview
4.5.2. Unstrengthened Reference Beams
4.5.3. Influence of Unreinforced Fine Concrete Strengthening Layer
4.5.4. Strengthened Specimens—One-Layer SITgrid 040
4.5.5. Strengthened Specimens—Two-Layer SITgrid 040
4.5.6. Strengthened Specimens—One-Layer Solidian (0°/90°; II-Strengthening)
4.5.7. Strengthened Specimens—One-Layer Solidian (0°/90°; U-Strengthening)
4.5.8. Strengthened Specimens—One-Layer Solidian (45°/45°; II-Strengthening)
4.5.9. Strengthened Specimens—One-Layer SITgrid 040 (Pre-Damaged)
4.5.10. Specimens with Different Shear Slenderness
4.5.11. Comparison between Shear Stress and Concrete Tensile Strength
5. Experimental Verification
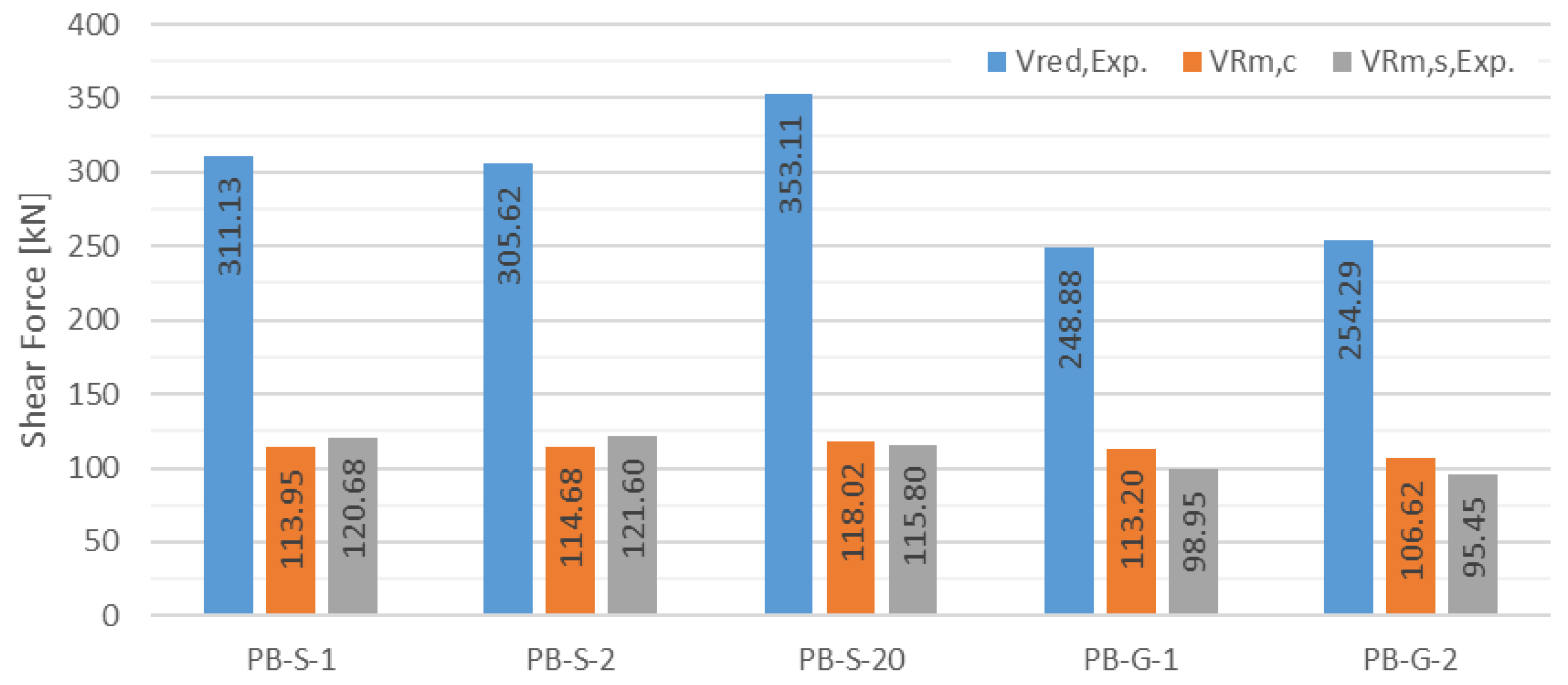
5.1. Unstrengthened Specimen with EC2
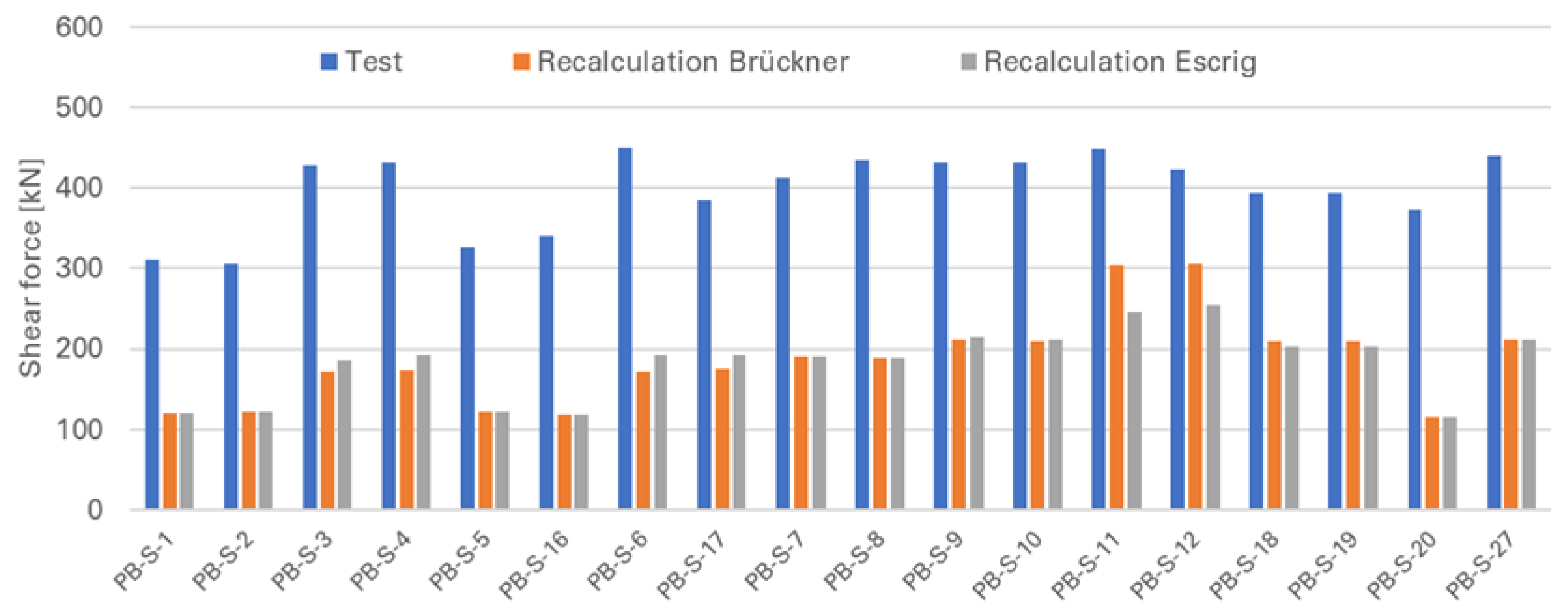
5.2. Strengthened Specimen with Brückner and Escrig
6. Summary and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Model of Escrig [34]
- Circumferentially closed strengthening: A = 0.035 B = 0.65
- Lateral or U-shaped strengthening: A = 0.020 B = 0.55
Appendix B. Recalculation with Brückner [11]

Appendix C. Recalculation with Escrig [34]

References
- Hegger, J.; Marzahn, G.; Teworte, F.; Herbrand, M. Principal tensile stress criterion for the shear assessmentof existing concrete bridges. Beton-Und Stahlbetonbau 2015, 110, 82–95. [Google Scholar] [CrossRef]
- Fischer, O.; Gehrlein, S.; Schram, N.; Nowak, M. Nachrechnungsdefizite bei Massivbrücken—Ein Problem der Tragfähigkeit oder [doch nur] der Modellvorstellung? In 29. Dresdner Brückenbausymposium—Planung, Bauausführung, Instandsetzung und Ertüchtigung von Brücken; Curbach, M., Ed.; Curbach: Dresden, Germany, 2019; pp. 129–146. [Google Scholar]
- Zilch, K.; Niedermeier, R.; Finckh, W. Praxisgerechte Bemessungsansätze für das wirtschaftliche Verstärken von Betonbauteilen mit geklebter Bewehrung—Querkrafttragfähigkeit. In Schriftenreihe des DAfStb, Heft 594; Deutscher Ausschuss für Stahlbeton, Ed.; Beuth Verlag: Berlin, Germany, 2012. [Google Scholar]
- Schnellenbach-Held, M.; Welsch, T.; Fickler, S.; Hegger, J.; Reißen, K. Verstärkungen Älterer Beton- und Spannbetonbrücken; Erfahrungssammlung Dokumentation, Projekt FE 15.0570/2012/NRB; Bundesanstalt für Straßenwesen (BASt): Bergisch Gladbach, Germany, 2016; 288p. [Google Scholar]
- Deutscher Ausschuss für Stahlbeton (Ed.) Richtlinie Verstärken von Betonbauteilen Mit Geklebter Bewehrung; Beuth Verlag: Berlin, Germany, 2012. [Google Scholar]
- CARBOCON GMBH: National Technical Approval (abZ) and General Construction Technique Permit (aBG) Z-31.10.-182: CARBOrefit®—Verfahren zur Verstärkung von Stahlbeton mit Carbonbeton; Printout; CARBOCON GMBH: Dresden, Germany, August 2023.
- Müller, E.; Schmidt, A.; Schumann, A.; May, S.; Curbach, M. Flexural strengthening with carbon reinforced concrete—Tests with new carbon reinforcements. Beton Und Stahlbetonbau 2020, 115, 758–767. [Google Scholar] [CrossRef]
- Hentschel, M.; Schumann, A.; Ulrich, H.; Jentzsch, S. Retrofitting of the Hyparshell in Magdeburg. Bautechnik 2019, 96, 25–30. [Google Scholar] [CrossRef]
- Scheerer, S.; Zobel, R.; Müller, E.; Senckpiel-Peters, T.; Schmidt, A.; Curbach, M. Flexural strengthening of RC structures with TRC—Experimental Observations, Design Approach and Application. Appl. Sci. 2019, 9, 1322. [Google Scholar] [CrossRef]
- Erhard, E.; Weiland, S.; Lorenz, E.; Schladitz, F.; Beckmann, B.; Curbach, M. Applications of textile reinforced concrete strengthening—Restoration and strengthening of built constructions with textile reinforced strengthening. Beton-Und Stahlbetonbau 2015, 110, 74–82. [Google Scholar] [CrossRef]
- Brückner, A. Shear Strengthening of Structural Members with Textile Reinforce Concrete. Ph.D. Thesis, TU Dresden, Dresden, Germany, 2011. [Google Scholar]
- Brückner, A.; Ortlepp, R.; Curbach, M. Textile reinforced concrete for strengthening in bending and shear. Mater. Struct. 2006, 39, 741–748. [Google Scholar] [CrossRef]
- Triantafillou, T.C.; Papanicolaou, C.G. Shear strengthening of reinforced concrete members with textile reinforced mortar (TRM) jackets. Mater. Struct. 2007, 39, 93–103. [Google Scholar] [CrossRef]
- Herbrand, M.; Adam, V.; Classen, M.; Kueres, D.; Hegger, J. Strengthening of Existing Bridge Structures for Shear and Bending with Carbon Textile-Reinforced Mortar. Materials 2017, 10, 1099. [Google Scholar] [CrossRef]
- Herbrand, M.; Classen, M.; Hegger, J. Shear tests on prestressed concrete beams strengthened with carbon textile reinforced spray mortar under cyclic loading. Beton-Und Stahlbetonbau 2016, 111, 576–587. [Google Scholar] [CrossRef]
- Brückner, A.; Wellner, S.; Ortlepp, R.; Scheerer, S.; Curbach, M. T-beams strengthened with TRC under non predominantly static loading. Beton-Und Stahlbetonbau 2013, 108, 169–178. [Google Scholar] [CrossRef]
- May, S.; Schumann, A.; Schütze, E.; Curbach, M. Querkraftverstärkung aus Carbonbeton unter zyklischer Beanspruchung. In Tagungsband zum 4. Brückenkolloquium—Fachtagung für Beurteilung, Planung, Bau, Instandhaltung und Betrieb von Brücken; Foster, F., Gilbert, R., Mendis, P., Al-Mahaidi, R., Millar, D., Eds.; Technischen Akademie Esslingen: Ostfildern, Germany, 2020; pp. 643–650. [Google Scholar]
- El Ghadioui, R.; Wagner, J.; Klein, J.; Proske, T.; Curbach, M.; Graubner, C. RC members with a flexural-strengthening layer of CFRP textile-reinforced concrete under monotonic and cyclic long-term loading. Struct. Concr. 2022, 23, 939–953. [Google Scholar] [CrossRef]
- Homepage Projekt C3—Carbon Concrete Composite: C3—Carbon Concrete Composite: C3–Carbon Concrete Composite–Carbonbeton–Die Zeit ist jetzt!–Neubau, Instandsetzung, Schulung, Zulassung rund um das Thema Carbonbeton. Available online: https://carbon-concrete.org (accessed on 6 October 2023).
- May, S.; Schumann, A.; Bergmann, S.; Curbach, M.; Hegger, J. Shear Strengthening of Reinforced Structures with Carbon Reinforced Concrete. In Proceedings of the Concrete—Innovations in Materials, Design and Structures, 2019 fib Symposium, Krakow, Poland, 27–29 May 2019; pp. 1563–1570. [Google Scholar]
- May, S.; Schumann, A.; Curbach, M. Shear strengthening of structures with carbon reinforced concrete. In Proceedings of the 12th fib International PhD Symposium in Civil Engineering, Prague, Czech Republic, 29–31 August 2018; pp. 879–885. [Google Scholar]
- Schumann, A.; Zobel, R.; Curbach, M. Finite element research of reinforced concrete structures strengthened with textile reinforced concrete (TRC). In Computational Modelling of Concrete Structures; Meschke, G., Pichler, B., Rots, J.G., Eds.; CRC Press: Boca Raton, FL, USA, 2018; pp. 829–837. [Google Scholar]
- Bergmann, S.; May, S.; Hegger, J.; Curbach, M. Shear strengthening of reinforced concrete T-beams using carbon reinforced concrete. Spec. Publ. 2020, 345, 169–184. [Google Scholar]
- Mazzuca, P.; Ombres, L.; Guglielmi, M.; Verre, S. Residual Mechanical Properties of PBO FRCM Composites after Elevated Temperature Exposure: Experimental and Comparative Analysis. J. Mater. Civ. Eng. 2023, 35, 04023383. [Google Scholar] [CrossRef]
- Holz, K.; Curbach, M. Carbon reinforced concrete exposed to high temperatures. Struct. Concr. 2023, 3178–3190. [Google Scholar] [CrossRef]
- Adam, V.; Herbrand, M.; Claßen, M. Experimental Investigations on the Influence of the Slab Width and the Moment-Shear-Ratio on the Shear Capacity of RC Slabs without Shear Reinforcement. Bauingenieur 2018, 93, 37–45. [Google Scholar] [CrossRef]
- Herbrand, M. Shear Strength Models for Reinforced and Prestressed Concrete Members. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 2017. [Google Scholar]
- Classen, M. Shear Crack Propagation Theory (SCPT)—The mechanical solution to the riddle of shear in RC members without shear reinforcement. Eng. Struct. 2020, 210, 110207. [Google Scholar] [CrossRef]
- Ruiz, M.F.; Muttoni, A.; Sagaseta, J. Shear strength of concrete members without transverse reinforcement: A mechanical approach to consistently account for size and strain effects. Eng. Struct. 2015, 99, 360–372. [Google Scholar] [CrossRef]
- Schacht, G. Experimental Evaluation of the Shear Bearing Safety. Ph.D. Thesis, TU Dresden, Dresden, Germany, 2014. [Google Scholar]
- Hegger, J.; Sherif, A.; Görtz, S. Shear Capacity of Beams made of High Performance Concrete. In Proceedings of the ACI’s 7th International Symposium on Utilization of High-Strength/High-Performance Concrete, Kassel, Germany, 13–15 September 2004. [Google Scholar]
- Huber, P.; Huber, T.; Kollegger, J. Investigation of the shear behavior of RC beams on the basis of measured crack kinematics. Eng. Struct. 2016, 113, 41–58. [Google Scholar] [CrossRef]
- Al-Salloum, Y.A.; Elsanadedy, H.M.; Alsayed, S.H.; Iqbal, R.A. Experimental and Numerical Study for the Shear Strengthening of Reinforced Concrete Beams Using Textile-Reinforced Mortar. J. Compos. Constr. 2012, 16, 74–90. [Google Scholar] [CrossRef]
- Escrig, C.; Gil, L.; Bernat-Maso, E.; Puigvert, F. Experimental and analytical study of reinforced concrete beams shear strengthened with different types of textile reinforced mortar. Constr. Build. Mater. 2015, 83, 248–260. [Google Scholar] [CrossRef]
- Müller, E.; Scheerer, S.; Curbach, M. Strengthening of existing concrete structures: Design models. In Textile Fibre Composites in Civil Engineering; Triantafillou, T.C., Ed.; Woodhead Publishing/Elsevier: Amsterdam, The Netherlands, 2016; pp. 323–359. [Google Scholar] [CrossRef]
- Gonzalez-Libreros, J.H.; Sneed, L.H.; D’Antino, T.; Pellegrino, C. Behaviour of RC beams strengthened in shear with FRP and FRCM composites. Eng. Struct. 2017, 150, 830–842. [Google Scholar] [CrossRef]
- Tetta, Z.C.; Koutas, L.; Bournas, D.A. Shear strengthening of concrete members with TRM jackets: Effect of shear span-to-depth ratio, material and amount of external reinforcement. Compos. Part B 2018, 137, 184–201. [Google Scholar] [CrossRef]
- Zilch, K.; Niedermeier, R.; Finckh, W. Strengthening of Concrete Structures with Adhesively Bonded Reinforcement; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- DIN EN 1992-1-1; Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings. German Version. Beuth Verlag: Berlin, Germany, 2011.
- Koutas, L.N.; Tetta, Z.; Bournas, D.A.; Triantafillou, T.C. Strengthening of Concrete Structures with Textile Reinforced Mortars: State-of-the-Art Review. J. Compos. Constr. 2019, 23, 03118001. [Google Scholar] [CrossRef]
- Kaufmann, N. The sand patch test. Straßenbautechnik 1971, 24, 131–135. [Google Scholar]
- DIN EN 206; Concrete—Specification, Performance, Production and Conformity. German Version. Deutsche Institut für Normung e.V.: Berlin, Germany, 2017.
- DIN 1045-2; Concrete, Reinforced and Prestressed Concrete Structures—Part 2: Concrete—Specification, Properties, Production and Conformity—Application Rules for DIN EN 206-1. Deutsche Institut für Normung e.V.: Berlin, Germany, 2008.
- DIN 488-1; Reinforcing Steels—Part 1: Grades, Properties, Marking. Deutsche Institut für Normung e.V.: Berlin, Germany, 2009.
- Solidian GmbH: Technisches Datenblatt: Solidian GRID 85/85_CCE-21. 1 February 2023. Available online: https://solidian.com/wp-content/uploads/solidian-GRID-Qxx-CCE-xx-Technical-Product-Data-Sheets-v2302.pdf (accessed on 13 October 2023).
- DIN EN ISO 15630-1; Steel for the Reinforcement and Prestressing of Concrete—Test Methods—Part 1: Reinforcing Bars, Rods and Wire (ISO 15630-1:2019). German Version. Deutsche Institut für Normung e.V.: Berlin, Germany, 2019.
- DIN EN 12390; Testing Hardened Concrete. German Version. Deutsche Institut für Normung e.V.: Berlin, Germany, 2012.
- DIN EN 196-1:2016; Methods of Testing Cement—Part 1: Determination of Strength. German Version. Deutsche Institut für Normung e.V.: Berlin, Germany, 2016.
- Schütze, E.; Bielak, J.; Scheerer, S.; Hegger, J.; Curbach, M. Uniaxial tensile test for carbon reinforced concrete with textile reinforcement. Beton-Und Stahlbetonbau 2018, 113, 33–47. [Google Scholar] [CrossRef]
- Wendler, J.; Hahn, L.; Farwig, K.; Nocke, A.; Scheerer, S.; Curbach, M.; Cherif, C. Analysis of the tensile mechanical characteristics of flexible carbon fibre strands and development of a novel test method. Bauingenieur 2020, 95, 325–334. [Google Scholar] [CrossRef]
- Brückner, A.; Ortlepp, R.; Curbach, M. Anchoring of shear strengthening for T-beams made of TRC. Mater. Struct. 2008, 41, 407–418. [Google Scholar] [CrossRef]
- Reineck, K.-H.; Kuchma, D.A.; Fitik, B. Erweiterte Datenbank zur Überprüfung der Querkraftbemessung für Konstruktionsbetonbauteile mit und ohne Bügel. In Schriftenreihe des DAfStb, Heft 597; Deutscher Ausschuss für Stahlbeton, Ed.; Beuth Verlag: Berlin, Germany, 2012. [Google Scholar]
- International Federation for Structural Concrete (Ed.) Fib MC 2010: Fib Model Code for Concrete Structures 2010; Structural Concrete: Lausanne, Switzerland, 2013. [Google Scholar]
- May, S. Experimental Investigations to the Shear Load-Bearing of Strengthen Reinforced Concrete Structures with Carbon Reinforced Concrete under Static and Dynamic Load. Ph.D. Thesis, TU Dresden, Dresden, Germany, 2023. submitted. [Google Scholar]







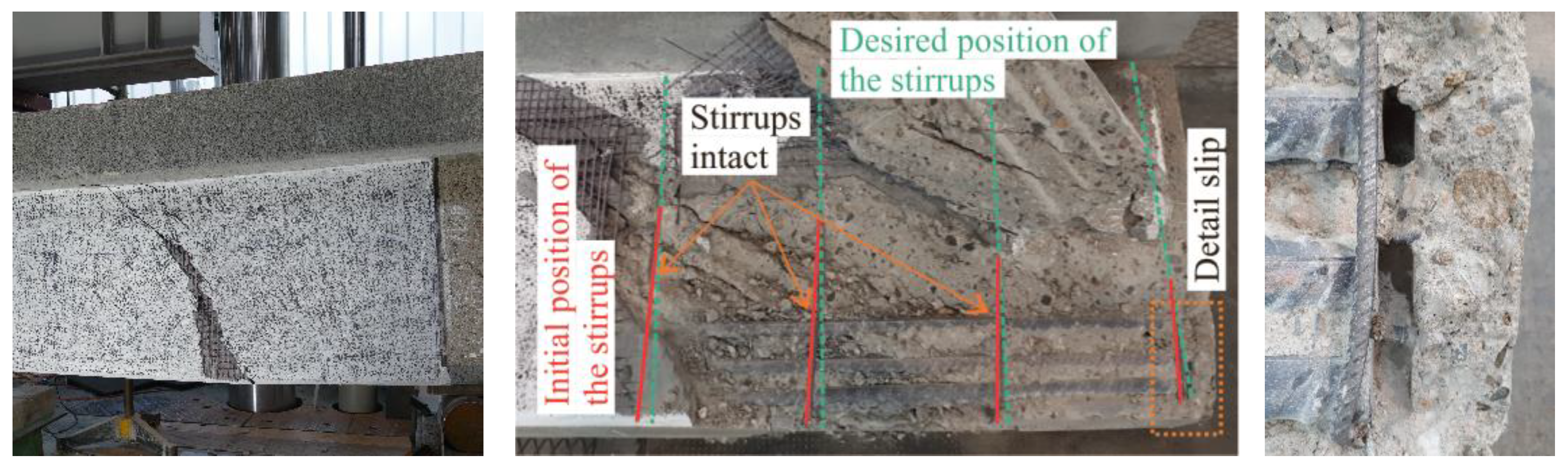


| Specimen Number | Strengthening | |||||
|---|---|---|---|---|---|---|
| Carbon Grids | Arrangement/ Number of Layers |  | Area at [mm2/m] | Angle α [°] | Thickness tm [mm] | |
| PB-G-1/-2 | - | - | - | - | - | |
| PB-G-3/-4 | solidian Q85 |  | 170 | 0/90 | 10 | |
| PB-G-5/-6 | solidian Q85 |  | 170 | 0/90 | 10 | |
| PB-G-7/-8 | solidian Q85 |  | 170 | 45/45 | 10 | |
| PB-G-9/-10 | SITgrid 040 |  | 282 | 0/90 | 10 | |
| PB-G-11/-12 | SITgrid 040 |  | 564 | 0/90 | 10 | |
| PB-S-1/-2 | - | - | - | - | - | |
| PB-S-3/-4 | solidian Q85 |  | 170 | 0/90 | 10 | |
| PB-S-5/-16 | Fine concrete |  | - | - | 10 | |
| PB-S-6/-17 | solidian Q85 |  | 170 | 0/90 | 10 | |
| PB-S-7/-8 | solidian Q85 |  | 170 | 45/45 | 10 | |
| PB-S-9/-10 | SITgrid 040 |  | 282 | 0/90 | 10 | |
| PB-S-11/-12 | SITgrid 040 |  | 564 | 0/90 | 15 | |
| PB-S-18/-19 a | SITgrid 040 |  | 282 | 0/90 | 10 | |
| PB-S-20 b | - | - | - | - | - | |
| PB-S-27 b | SITgrid 040 |  | 282 | 0/90 | 10 | |
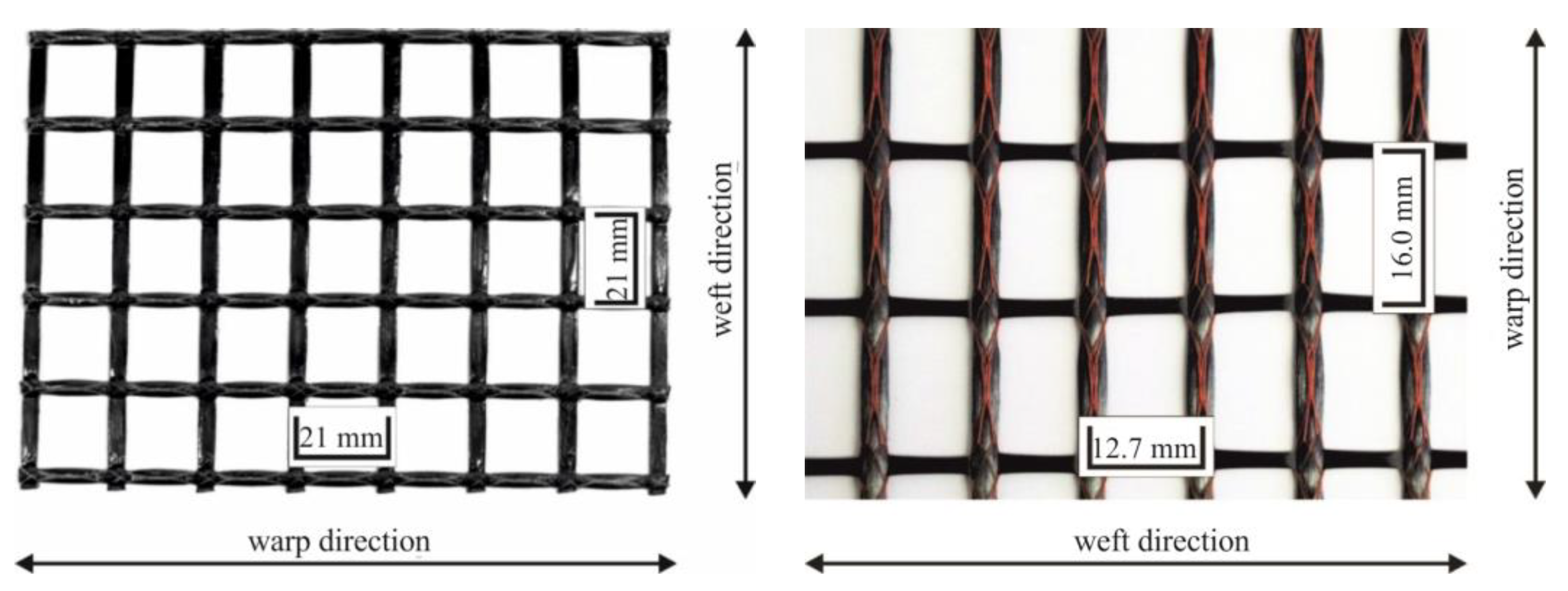
| Material | Property | Symbol | Unit | Value |
|---|---|---|---|---|
| solidian Q85 | Impregnation | - | - | Epoxy resin |
| Reinforcement area Warp/Weft direction | at | mm2/m | 85.0/85.0 | |
| Warp/Weft yarn spacing | st | mm | 21/21 | |
| Tensile strength | ftm,f a | N/mm2 | 3377 | |
| Strain at failure | εmf | ‰ | 13.9 | |
| Young’s-Modulus | Emf | N/mm2 | 243,259 | |
| SITgrid 040 | Impregnation | - | - | Polyacrylate |
| Reinforcement area Warp/Weft direction | at | mm2/m | 141.0/28.0 | |
| Warp/Weft yarn spacing | st | mm | 12.7/16 | |
| Tensile strength 1-/2-layer | ftm,f | N/mm2 | 3160/3340 | |
| Strain at failure 1-/2-layer | εmf | ‰ | 15.1/14.0 | |
| Young’s-Modulus 1-/2-layer | Emf | N/mm2 | 211,277/ 238,265 | |
| Fine concrete | Flexure strength | Rfm | N/mm2 | 5.82 |
| Compressive strength | Rcm | N/mm2 | 79.42 | |
| Reinforcement | Yield strength Ø6/8/12/25 | fym | N/mm2 | 513/529/542/551 |
| Tensile strength Ø6/8/12/25 | ftm | N/mm2 | 621/623/646/669 | |
| Young’s-Modulus Ø6/8/12/25 | Esm | N/mm2 | 188,299/187,916/ 185,152/208,475 |
| Specimen Number | Existing Concrete | |||||
|---|---|---|---|---|---|---|
| Cylinder Compressive Strength fcm,cyl | Young’s- Modulus Ecm | Split Tensile Strength fctm,sp | Max. Test Force F | Shear Force a VExp(d) | Shear Stress a τExp(d) | |
| [N/mm2] | [N/mm2] | [N/mm2] | [kN] | [kN] | [N/mm2] | |
| PB-G-1 | 36.5 | 28,217 | 1.91 | 487 | 249.0 | 2.18 |
| PB-G-2 | 30.5 | 28,775 | 2.39 | 498 | 254.5 | 2.23 |
| PB-G-3 | 35.7 | 31,340 | 2.18 | 689 | 350.0 | 2.83 |
| PB-G-4 | 31.0 | 28,283 | 2.09 | 612 | 311.5 | 2.52 |
| PB-G-5 | 36.4 | 27,682 | 2.61 | 673 | 342.0 | 2.77 |
| PB-G-6 | 32.1 | 27,832 | 1.72 | 680 | 345.5 | 2.80 |
| PB-G-7 | 32.1 | 28,995 | 2.13 | 615 | 313.0 | 2.53 |
| PB-G-8 | 37.8 | 28,512 | 2.69 | 623 | 317.0 | 2.57 |
| PB-G-9 | 34.9 | 27,417 | 1.74 | 615 | 313.0 | 2.53 |
| PB-G-10 | 32.5 | 30,818 | 2.48 | 612 | 311.5 | 2.52 |
| PB-G-11 | 35.5 | 28,062 | 2.03 | 633 | 322.0 | 2.51 |
| PB-G-12 | 39.5 | 29,425 | 2.11 | 613 | 312.0 | 2.44 |
| Specimen Number | Existing Concrete | |||||
|---|---|---|---|---|---|---|
| Cylinder Compressive Strength fcm,cyl | Young’s- Modulus Ecm | Split Tensile Strength fctm,sp | Max. Test Force F | Shear Force a VExp(d) | Shear Stress a τExp(d) | |
| [N/mm2] | [N/mm2] | [N/mm2] | [kN] | [kN] | [N/mm2] | |
| PB-S-1 | 35.8 | 26,618 | 2.46 | 606 | 311.4 | 3.01 |
| PB-S-2 | 36.5 | 28,217 | 1.91 | 595 | 305.9 | 2.96 |
| PB-S-3 | 30.5 | 28,775 | 2.39 | 839 | 428.0 | 3.71 |
| PB-S-4 | 35.7 | 31,340 | 2.18 | 847 | 432.0 | 3.74 |
| PB-S-5 | 31.0 | 28,283 | 2.09 | 637 | 327.0 | 2.83 |
| PB-S-6 | 36.4 | 27,682 | 2.61 | 885 | 451.0 | 3.91 |
| PB-S-7 | 32.1 | 27,832 | 1.72 | 807 | 412.0 | 3.57 |
| PB-S-8 | 32.1 | 28,995 | 2.13 | 852 | 434.5 | 3.76 |
| PB-S-9 | 37.8 | 28,512 | 2.69 | 845 | 431.0 | 3.73 |
| PB-S-10 | 34.9 | 27,417 | 1.74 | 847 | 432.0 | 3.74 |
| PB-S-11 | 32.5 | 30,818 | 2.48 | 881 | 449.0 | 3.70 |
| PB-S-12 | 35.5 | 28,062 | 2.03 | 828 | 422.5 | 3.48 |
| PB-S-16 | 30.2 | 29,834 | 1.48 | 664 | 340.5 | 2.95 |
| PB-S-17 | 30.2 | 29,834 | 1.48 | 752 | 384.5 | 3.33 |
| PB-S-18 | 26.7 | 26,747 | 1.97 | 771 | 394.0 | 3.41 |
| PB-S-19 | 26.7 | 26,747 | 1.97 | 771 | 394.0 | 3.41 |
| PB-S-20 | 33.7 | 28,564 | 1.86 | 728 | 372.5 | 3.23 |
| PB-S-27 | 34.2 | 25,669 | 1.62 | 1036 | 526.5 | 4.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
May, S.; Schumann, A. Investigations into the Shear Load-Capacity of Strengthened Reinforced Concrete Structures with Carbon-Reinforced Concrete. Buildings 2023, 13, 2765. https://doi.org/10.3390/buildings13112765
May S, Schumann A. Investigations into the Shear Load-Capacity of Strengthened Reinforced Concrete Structures with Carbon-Reinforced Concrete. Buildings. 2023; 13(11):2765. https://doi.org/10.3390/buildings13112765
Chicago/Turabian StyleMay, Sebastian, and Alexander Schumann. 2023. "Investigations into the Shear Load-Capacity of Strengthened Reinforced Concrete Structures with Carbon-Reinforced Concrete" Buildings 13, no. 11: 2765. https://doi.org/10.3390/buildings13112765
APA StyleMay, S., & Schumann, A. (2023). Investigations into the Shear Load-Capacity of Strengthened Reinforced Concrete Structures with Carbon-Reinforced Concrete. Buildings, 13(11), 2765. https://doi.org/10.3390/buildings13112765







