Constitutive Material Model for the Compressive Behaviour of Engineered Bamboo
Abstract
1. Introduction
2. Stress-Strain Behaviour of Bamboo and Engineered Bamboo
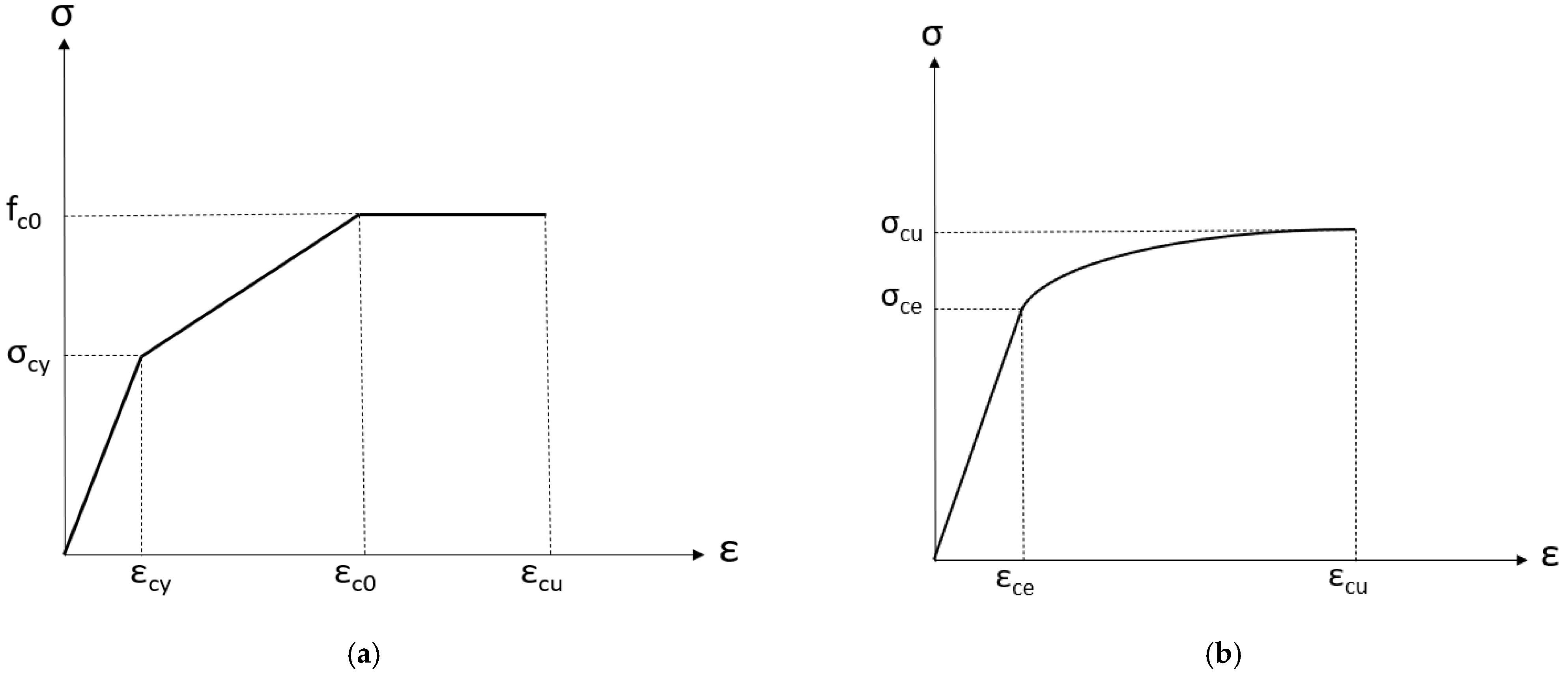
2.1. Natural Full Culm Bamboo
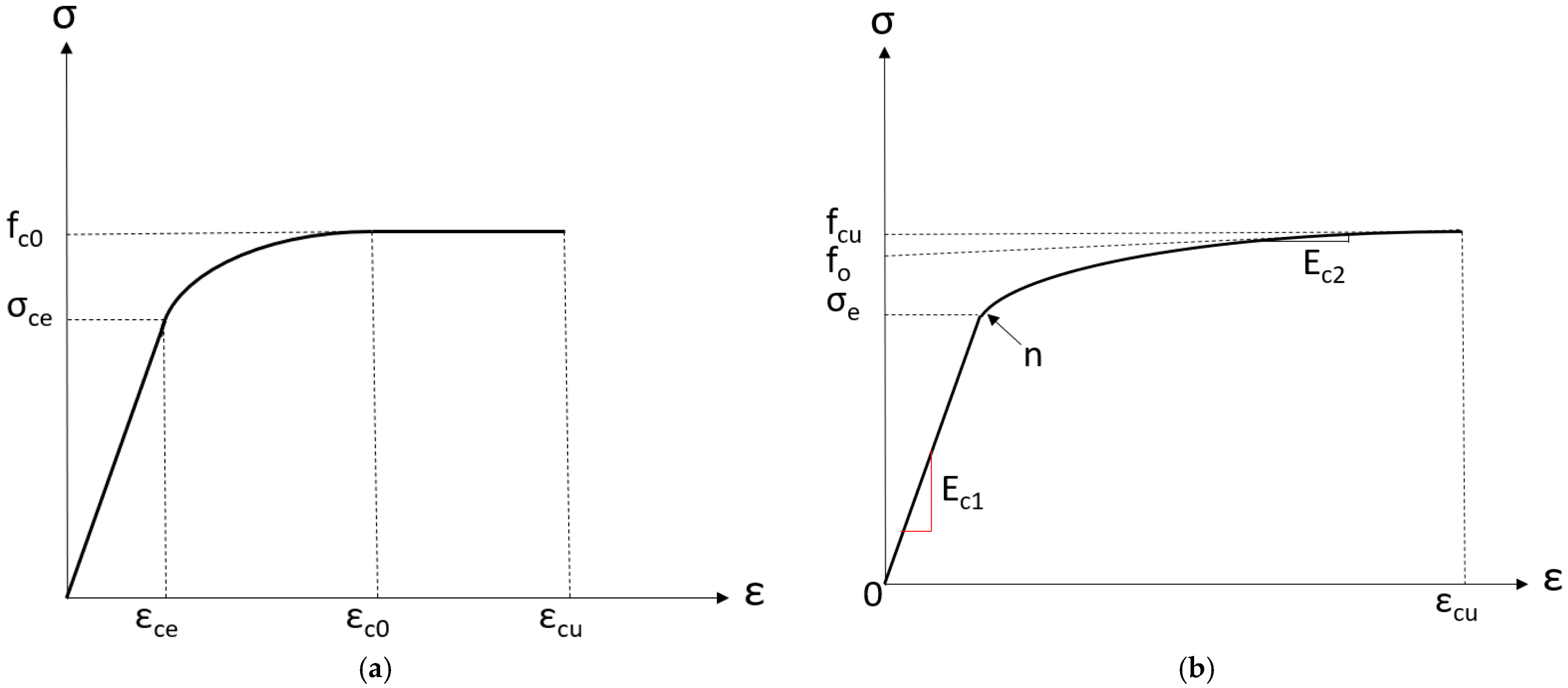
2.2. Engineered Bamboo
3. Existing Models for the Compression Behaviour of Engineered Bamboo
3.1. Empirical Models
3.1.1. Linear Model (LM) by Li et al. [48]
3.1.2. Quadratic Model (QM1) by Dongsheng et al. [45]
3.1.3. Quadratic Model (QM2) by Li et al. [19]
3.1.4. Cubic Model (CM) by Li et al. [48]
3.2. Modified Richard-Abbott (RA) Model by Wei et al. [46]
3.3. Limitations of the Existing Models
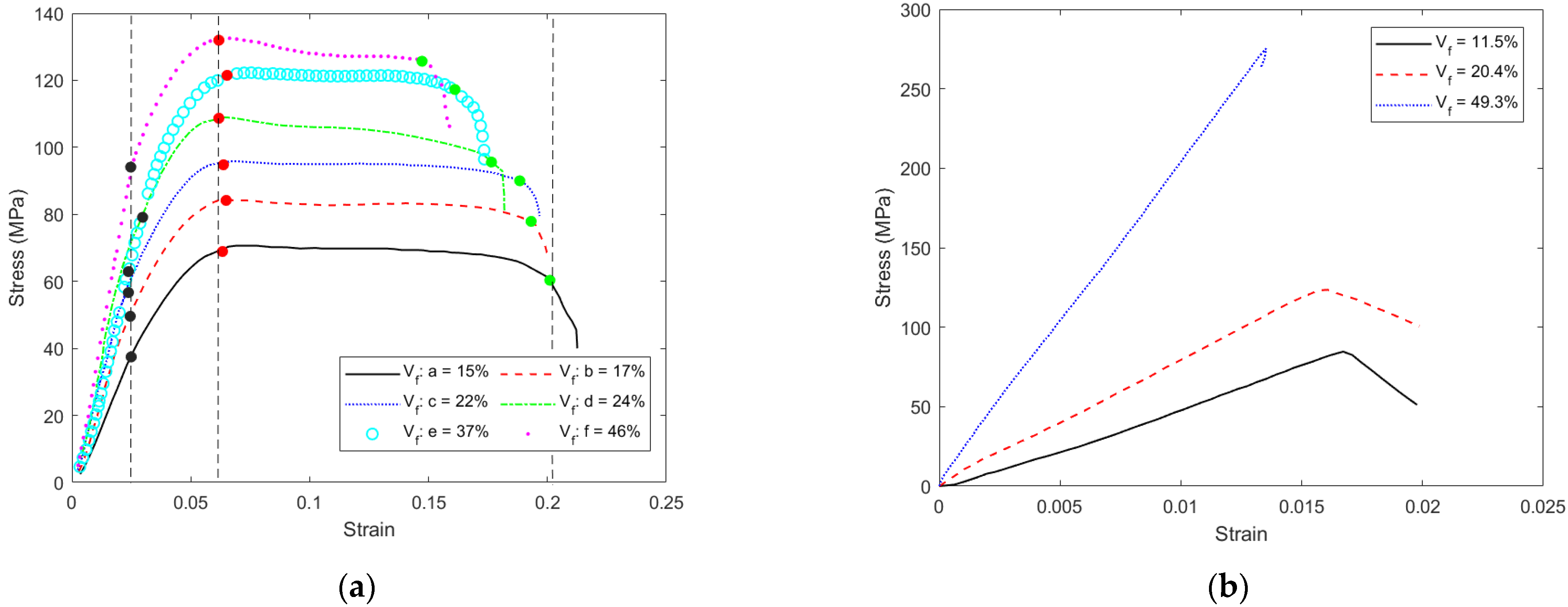
4. Material Properties of Bamboo Scrimber and LBL under Compression
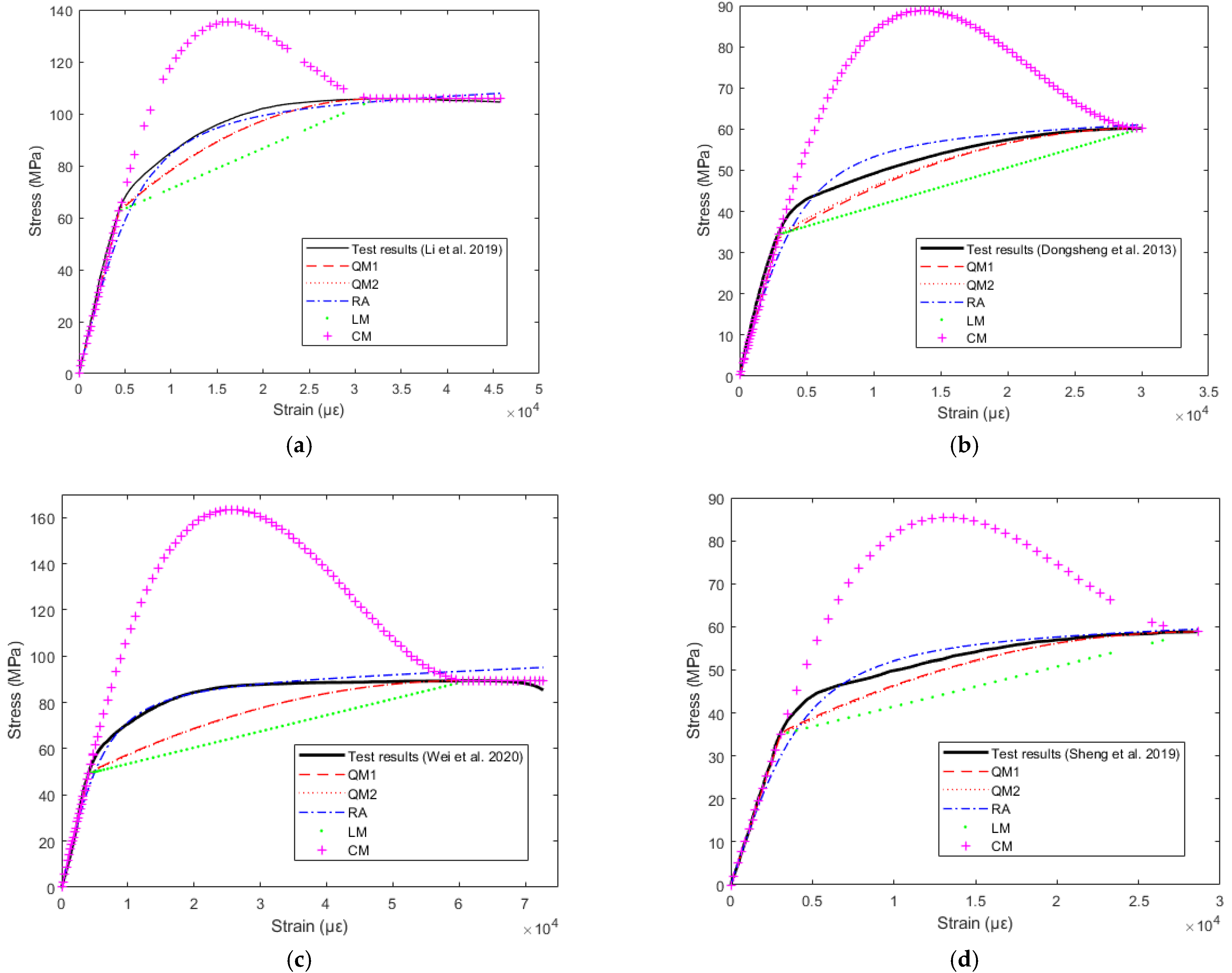
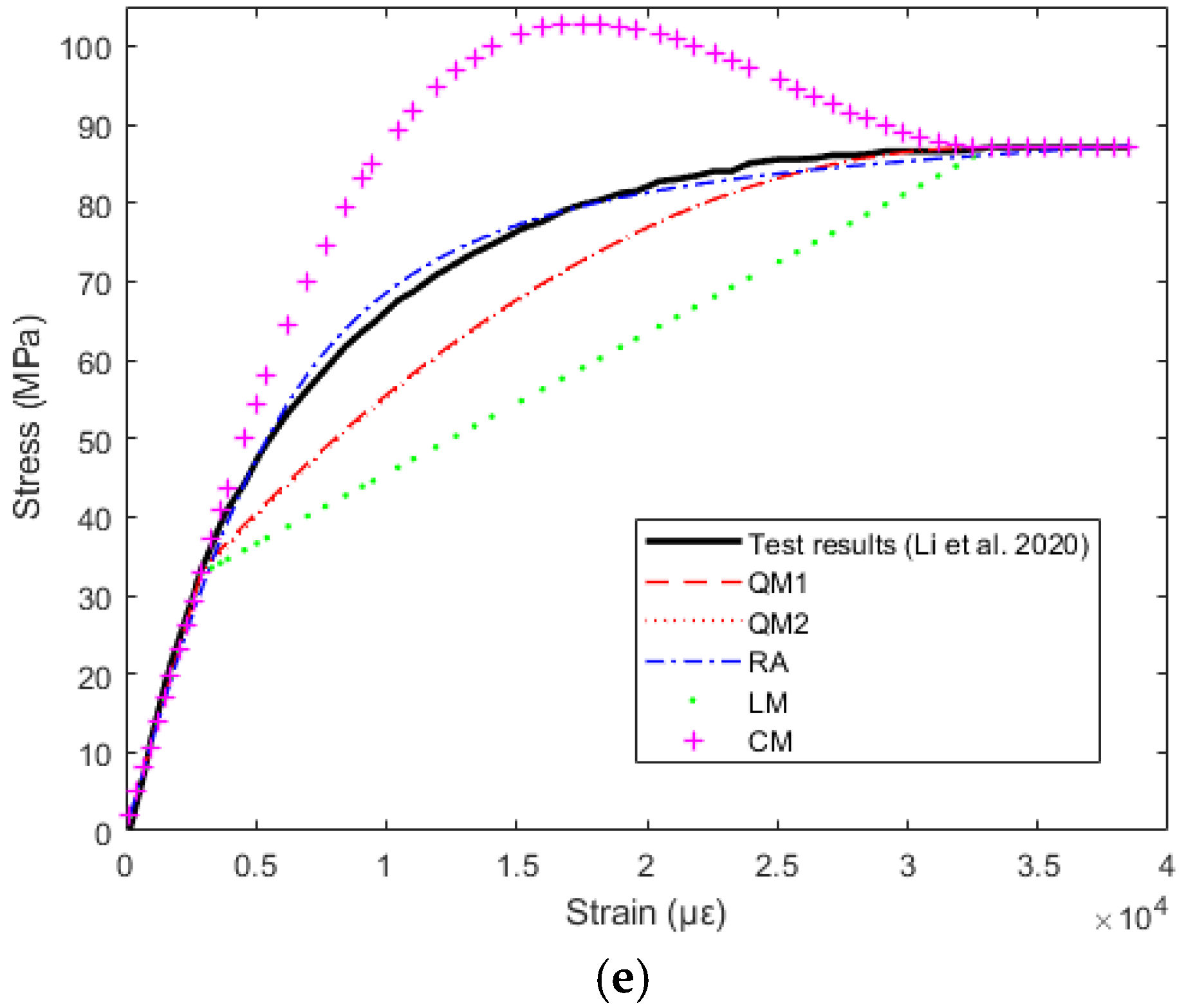
5. Performance of the Existing Models against All Test Results
6. Ramberg-Osgood Model for Engineered Bamboo
6.1. Ramberg-Osgood Material Model [37]
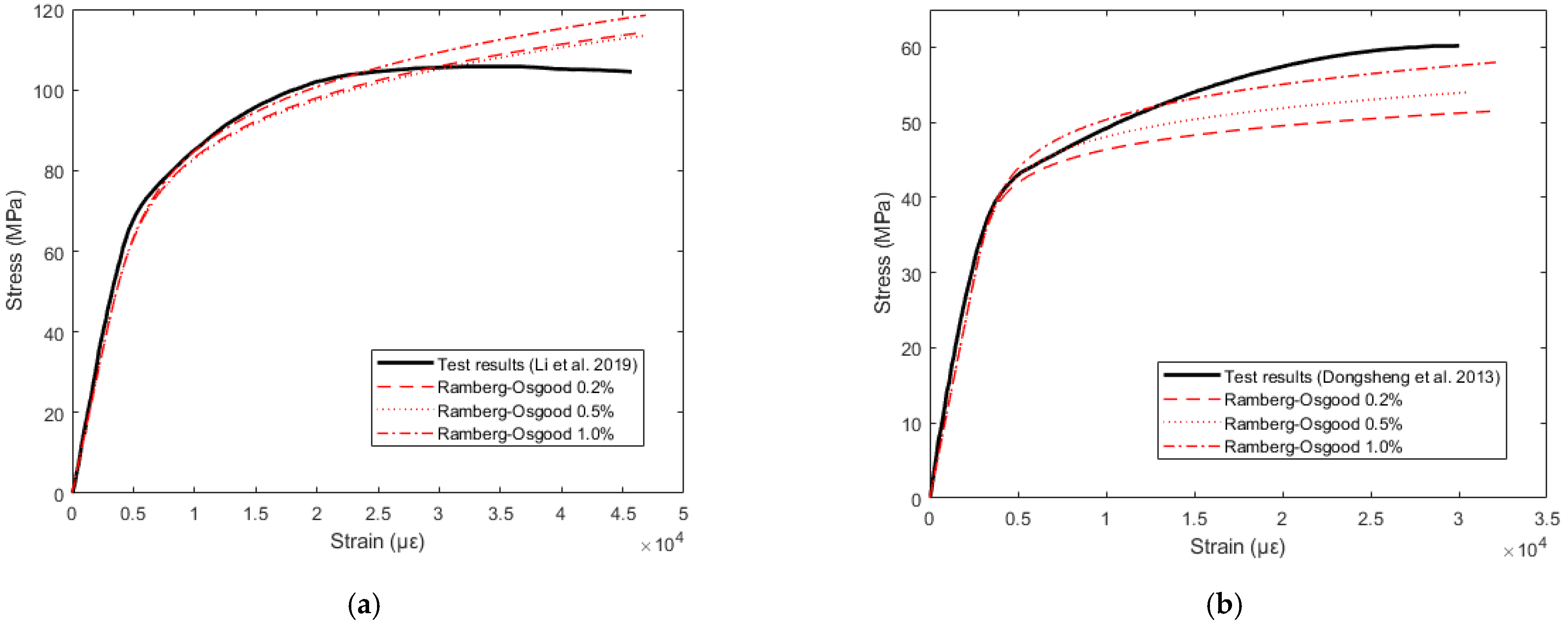
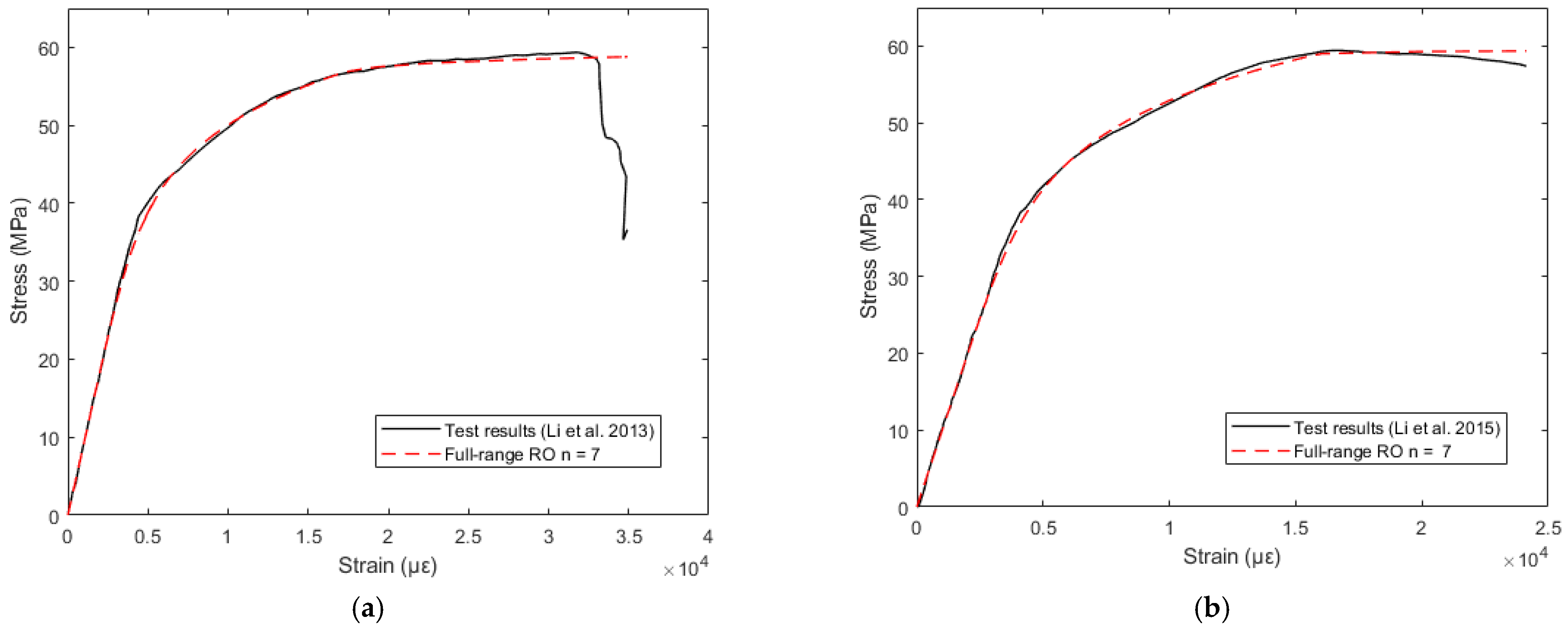
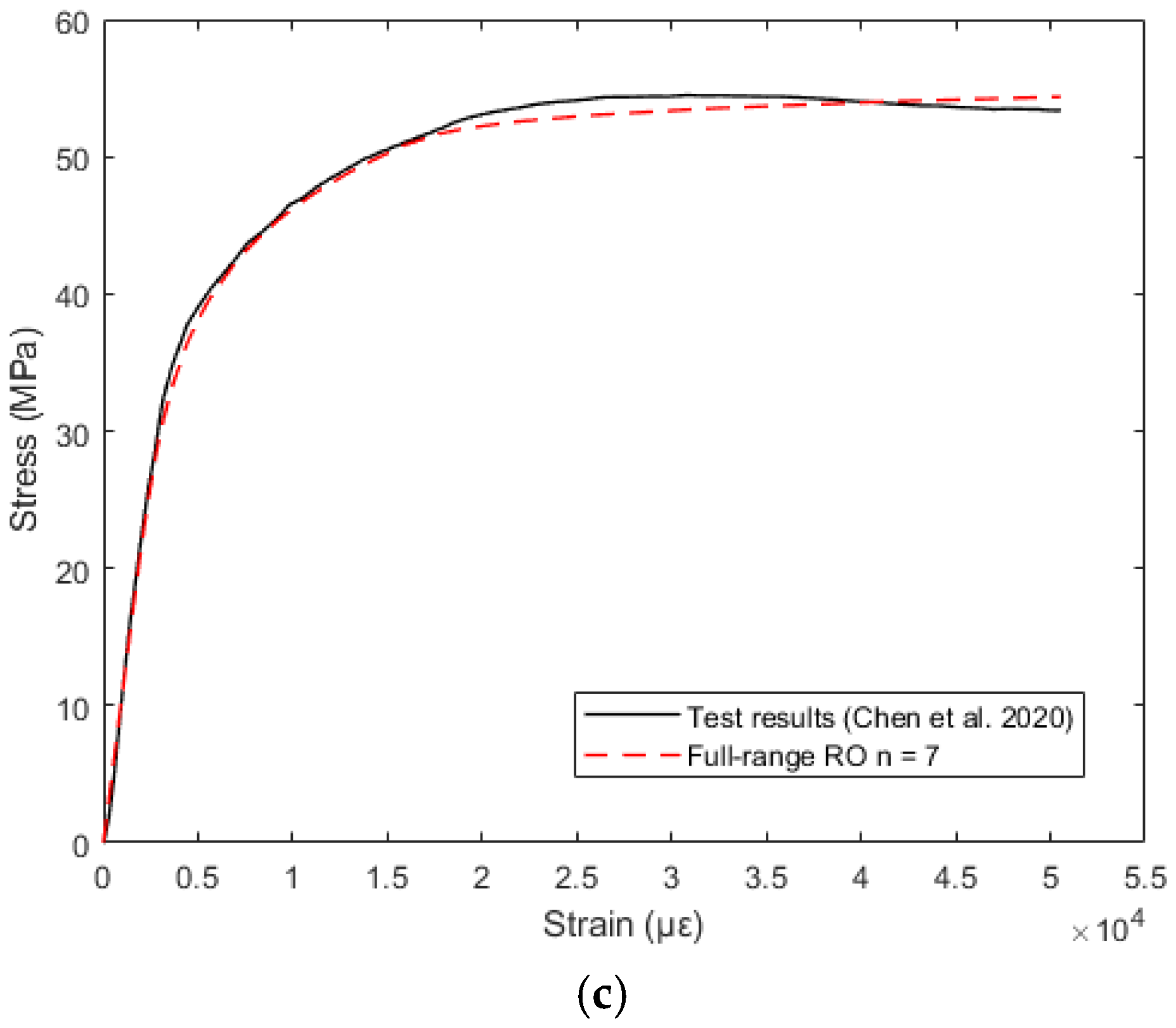
6.2. Full-Range Ramberg-Osgood Model
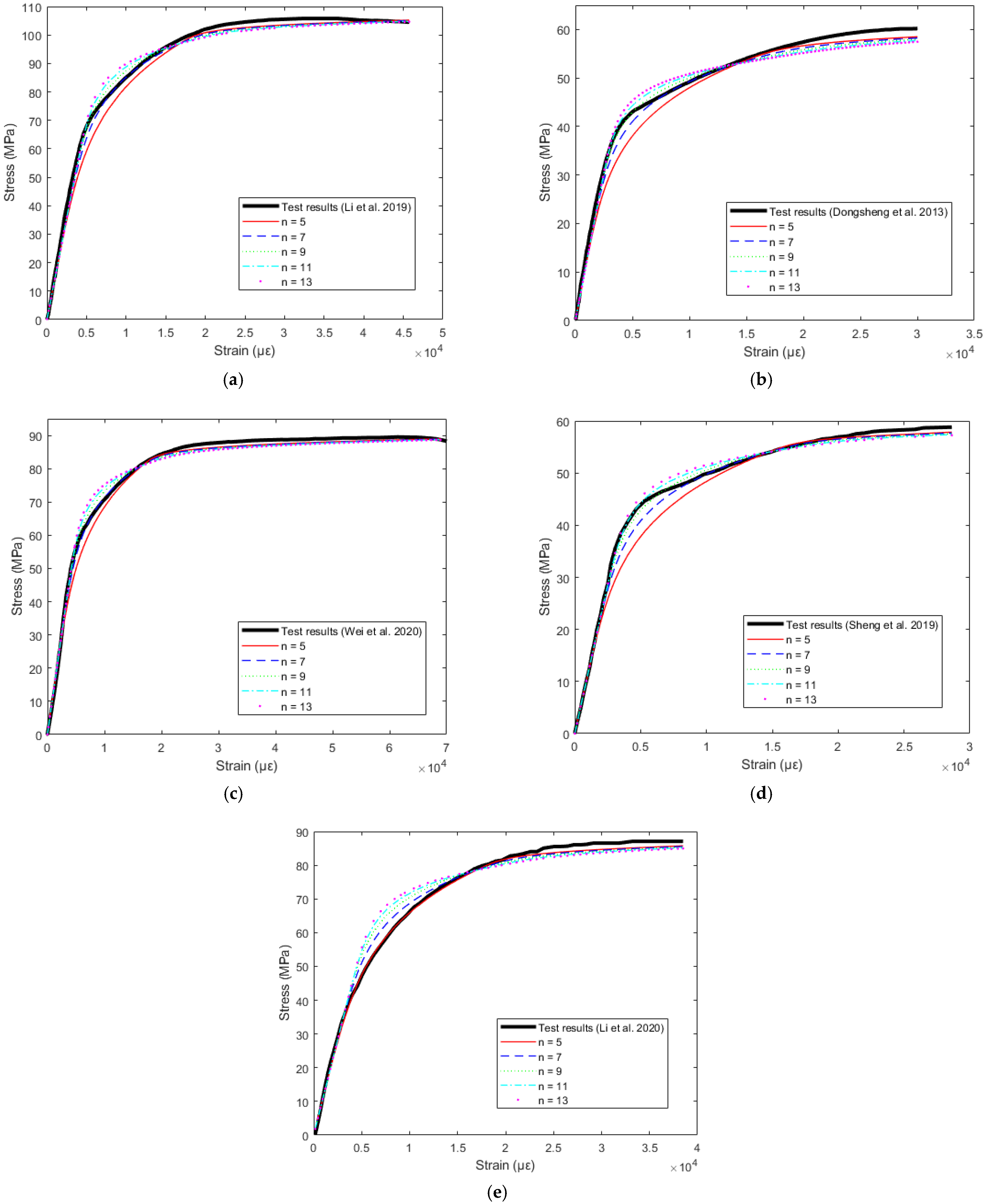
6.3. Sensitivity Analysis
7. Proposed Model for Laminated Bamboo Lumber
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Bansal, A.K.; Prasad, T.R.N. Manufacturing laminates from sympodial bamboos—An Indian experience. J. Bamboo Ratt. 2004, 3, 13–22. [Google Scholar] [CrossRef]
- Liese, W. Research on bamboo. Wood Sci. Technol. 1987, 21, 189–209. [Google Scholar] [CrossRef]
- Li, Z.; Liu, C.-P.; Yu, T. Laminate of Reformed Bamboo and Extruded Fiber-Reinforced Cementitious Plate. J. Mater. Civ. Eng. 2002, 14, 359–365. [Google Scholar] [CrossRef]
- Wong, K.M. The Bamboos of Peninsular Malaysia; Forest Research Institute Malaysia: Kuala Lumpur, Malaysia, 1995. [Google Scholar]
- Awalluddin, D.; Ariffin, M.A.M.; Osman, M.H.; Hussin, M.W.; Ismail, M.A.; Lee, H.-S.; Lim, N.H.A.S. Mechanical properties of different bamboo species. MATEC Web Conf. 2017, 138, 01024. [Google Scholar] [CrossRef]
- Naik, N.K. Mechanical and Physico-Chemical Properties of Bamboos; Indian Institute of Technology: Bombay, India, 2009. [Google Scholar]
- Molari, L.; Mentrasti, L.; Fabiani, M. Mechanical characterization of five species of Italian bamboo. Structures 2020, 24, 59–72. [Google Scholar] [CrossRef]
- Abdullah, A.; Karlina, N.; Rahmatiya, W.; Mudaim, S.; Fajrin, A. (Eds.) Physical and Mechanical Properties of Five Indonesian Bamboos; IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2017. [Google Scholar]
- Archila-Santos, H.F.; Ansell, M.P.; Walker, P. Low Carbon Construction Using Guadua Bamboo in Colombia. Key Eng. Mater. 2012, 517, 127–134. [Google Scholar] [CrossRef]
- Sharma, B.; Gatoo, A.; Bock, M.; Mulligan, H.; Ramage, M. Engineered bamboo: State of the art. Proc. Inst. Civ. Eng.-Constr. Mater. 2015, 168, 57–67. [Google Scholar] [CrossRef]
- Andy, W.C.L.; Xuesong, B.; Audimar, P.B. Selected Properties of Laboratory-Made Laminated-Bamboo Lumber. Holzforschung 1998, 52, 207–210. [Google Scholar]
- Nugroho, N.; Ando, N. Development of structural composite products made from bamboo I: Fundamental properties of bamboo zephyr board. J. Wood Sci. 2000, 46, 68–74. [Google Scholar] [CrossRef]
- Sulastiningsih, I.; Nurwati. Physical and mechanical properties of laminated bamboo board. J. Trop. For. Sci. 2009, 21, 246–251. [Google Scholar]
- Mahdavi, M.; Clouston, P.; Arwade, S. A low-technology approach toward fabrication of Laminated Bamboo Lumber. Constr. Build. Mater. 2012, 29, 257–262. [Google Scholar] [CrossRef]
- Chen, F.; Jiang, Z.; Deng, J.; Wang, G.; Zhang, D.; Zhao, Q.; Cai, L.; Shi, S.Q. Evaluation of the Uniformity of Density and Mechanical Properties of Bamboo-Bundle Laminated Veneer Lumber (BLVL). BioResources 2014, 9, 554–565. [Google Scholar] [CrossRef]
- Lugt, P. Design interventions for stimulating bamboo commercialization—Dutch design meets bamboo as a replicable model. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlans, 2008. [Google Scholar]
- Huang, Y.; Ji, Y.; Yu, W. Development of bamboo scrimber: A literature review. J. Wood Sci. 2019, 65, 25. [Google Scholar] [CrossRef]
- Li, H.-T.; Zhang, Q.-S.; Huang, D.-S.; Deeks, A.J. Compressive performance of laminated bamboo. Compos. Part B Eng. 2013, 54, 319–328. [Google Scholar] [CrossRef]
- Li, H.; Qiu, Z.; Wu, G.; Wei, D.; Lorenzo, R.; Yuan, C.; Zhang, H.; Liu, R. Compression Behaviors of Parallel Bamboo Strand Lumber Under Static Loading. J. Renew. Mater. 2019, 7, 583–600. [Google Scholar] [CrossRef]
- Zhao, P.; Zhang, X. Size effect of section on ultimate compressive strength parallel to grain of structural bamboo scrimber. Constr. Build. Mater. 2019, 200, 586–590. [Google Scholar] [CrossRef]
- Sharma, B.; Gatóo, A.; Ramage, M.H. Effect of processing methods on the mechanical properties of engineered bamboo. Constr. Build. Mater. 2015, 83, 95–101. [Google Scholar] [CrossRef]
- Penellum, M.; Sharma, B.; Shah, D.U.; Foster, R.M.; Ramage, M.H. Relationship of structure and stiffness in laminated bamboo composites. Constr. Build. Mater. 2018, 165, 241–246. [Google Scholar] [CrossRef]
- Qiu, Z.; Wang, J.; Fan, H.; Li, T. Anisotropic mechanical properties and composite model of parallel bamboo strand lumbers. Mater. Today Commun. 2020, 24, 101250. [Google Scholar] [CrossRef]
- Norris, C.; McKinnon, P. Compression, Tension, and Shear Tests on Yellow-Poplar Plywood Panels of Sizes that Do Not Buckle with Tests Made at Various Angles to the Face Grain; USDA. 1956. Available online: https://ir.library.oregonstate.edu/concern/defaults/4q77fw59k (accessed on 23 August 2022).
- Tsai, S.W.; Hahn, H.T. Introduction to Composite Materials; Routledge: London, UK, 2018. [Google Scholar]
- Li, X.; Ashraf, M.; Li, H.; Zheng, X.; Wang, H.; Al-Deen, S.; Hazell, P.J. An experimental investigation on Parallel Bamboo Strand Lumber specimens under quasi static and impact loading. Constr. Build. Mater. 2019, 228, 116724. [Google Scholar] [CrossRef]
- Li, X.; Ashraf, M.; Li, H.; Zheng, X.; Al-Deen, S.; Wang, H.; Hazell, P.J. Experimental study on the deformation and failure mechanism of parallel bamboo Strand Lumber under drop-weight penetration impact. Constr. Build. Mater. 2020, 242, 118135. [Google Scholar] [CrossRef]
- Li, H.; Su, J.; Xiong, Z.; Ashraf, M.; Corbi, I.; Corbi, O. Evaluation on the ultimate bearing capacity for laminated bamboo lumber columns under eccentric compression. Structures 2020, 28, 1572–1579. [Google Scholar] [CrossRef]
- Li, H.-T.; Chen, G.; Zhang, Q.; Ashraf, M.; Xu, B.; Li, Y. Mechanical properties of laminated bamboo lumber column under radial eccentric compression. Constr. Build. Mater. 2016, 121, 644–652. [Google Scholar] [CrossRef]
- Li, H.-T.; Wu, G.; Zhang, Q.-S.; Su, J.-W. Mechanical evaluation for laminated bamboo lumber along two eccentric compression di-rections. J. Wood Sci. 2016, 62, 503–517. [Google Scholar] [CrossRef]
- Su, J.-W.; Deeks, A.; Zhang, Q.-S.; Wei, D.D.; Yuan, C.G. Eccentric Compression Performance of Parallel Bamboo Strand Lumber Columns. Bioresources 2015, 10, 7065–7080. [Google Scholar]
- Tan, C.; Li, H.; Wei, D.; Lorenzo, R.; Yuan, C. Mechanical performance of parallel bamboo strand lumber columns under axial compression: Experimental and numerical investigation. Constr. Build. Mater. 2020, 231, 117168. [Google Scholar] [CrossRef]
- Tan, C.; Li, H.; Ashraf, M.; Corbi, I.; Corbi, O.; Lorenzo, R. Evaluation of axial capacity of engineered bamboo columns. J. Build. Eng. 2021, 34, 102039. [Google Scholar] [CrossRef]
- Li, H.-T.; Su, J.-W.; Zhang, Q.-S.; Deeks, A.J.; Hui, D. Mechanical performance of laminated bamboo column under axial compression. Compos. Part B Eng. 2015, 79, 374–382. [Google Scholar] [CrossRef]
- IT. ISO 22156; 2021 Bamboo Structures—Bamboo Culms—Structural Design. BSI Standards Limited: London, UK, 2021.
- Harries, K.A.; Sharma, B.; Richard, M. Structural Use of Full Culm Bamboo: The Path to Standardization. Int. J. Arch. Eng. Constr. 2012, 1, 66–75. [Google Scholar] [CrossRef]
- Ramberg, W.; Osgood, W.R. Description of Stress-Strain Curves by Three Parameters; NASA Scientific and Technical Information: Washington, DC, USA, 1943. [Google Scholar]
- Ochi, S. Mechanical Properties of Uni-Directional Long Bamboo Fiber/Bamboo Powder Composite Materials. Mater. Sci. Appl. 2014, 05, 1011–1019. [Google Scholar] [CrossRef]
- Xie, J.; Qi, J.; Hu, T.; De Hoop, C.F.; Hse, C.Y.; Shupe, T.F. Effect of fabricated density and bamboo species on physical–mechanical properties of bamboo fiber bundle reinforced composites. J. Mater. Sci. 2016, 51, 7480–7490. [Google Scholar] [CrossRef]
- Zhang, X.; Li, J.; Yu, Z.; Yu, Y.; Wang, H. Compressive failure mechanism and buckling analysis of the graded hierarchical bamboo structure. J. Mater. Sci. 2017, 52, 6999–7007. [Google Scholar] [CrossRef]
- Shao, Z.-P.; Fang, C.-H.; Huang, S.-X.; Tian, G.-L. Tensile properties of Moso bamboo (Phyllostachys pubescens) and its components with respect to its fiber-reinforced composite structure. Wood Sci. Technol. 2010, 44, 655–666. [Google Scholar] [CrossRef]
- Li, X. Physical, Chemical, and Mechanical Properties of Bamboo and Its Utilization Potential for Fiberboard Manufacturing. Master’s Thesis, Louisiana State University, Baton Rouge, LA, USA, 2004. [Google Scholar] [CrossRef]
- Sanchez, L. Bamboo as a Sustainable Engineering Material: Mechanical Properties, Safety Factors, and Experimental Testing; University of South Florida: Tampa, FL, USA, 2019. [Google Scholar]
- Chung, K.; Yu, W. Mechanical properties of structural bamboo for bamboo scaffoldings. Eng. Struct. 2002, 24, 429–442. [Google Scholar] [CrossRef]
- Dongsheng, H.; Aiping, Z.; Yuling, B. Experimental and analytical study on the nonlinear bending of parallel strand bamboo beams. Constr. Build. Mater. 2013, 44, 585–592. [Google Scholar] [CrossRef]
- Wei, Y.; Zhou, M.; Zhao, K.; Zhao, K.; Li, G. Stress–strain relationship model of glulam bamboo under axial loading. Adv. Compos. Lett. 2020, 29, 2633366X20958726. [Google Scholar] [CrossRef]
- Sheng, B.; Bian, Y.; Liu, Y.; Chui, Y.-H. Experimental Study of the Uniaxial Stress-strain Relationships of Parallel Strand Bamboo in the Longitudinal Direction. BioResources 2019, 14, 13. [Google Scholar]
- Li, H.; Zhang, H.; Qiu, Z.; Su, J.; Wei, D.; Lorenzo, R.; Yuan, C.; Liu, H.; Zhou, C. Mechanical Properties and Stress Strain Relationship Models for Bamboo Scrimber. J. Renew. Mater. 2020, 8, 13–27. [Google Scholar] [CrossRef]
- Chen, G.; Yu, Y.; Li, X.; He, B. Mechanical behavior of laminated bamboo lumber for structural application: An experimental investigation. Eur. J. Wood Wood Prod. 2020, 78, 53–63. [Google Scholar] [CrossRef]
- ASTM International. Standard Test Methods of Static Tests of Lumber in Structural Sizes; ASTM DASTM International: West Conshohocken, PA, USA, 2009. [Google Scholar]
- Gardner, L.; Ashraf, M. Structural design for non-linear metallic materials. Eng. Struct. 2006, 28, 926–934. [Google Scholar] [CrossRef]
- Richard, R.M.; Abbott, B.J. Versatile Elastic-Plastic Stress-Strain Formula. J. Eng. Mech. Div. 1975, 101, 511–515. [Google Scholar] [CrossRef]
- Rohatgi, A. WebPlotDigitizer; Austin, Texas, USA. 2017. Available online: https://automeris.io/WebPlotDigitizer/ (accessed on 23 August 2022).
- Ashraf, M.; Gardner, L.; Nethercot, D.A. Structural Stainless Steel Design: Resistance Based on Deformation Capacity. J. Struct. Eng. 2008, 134, 402–411. [Google Scholar] [CrossRef]
- Zhou, K.; Li, H.; Hong, C.; Ashraf, M.; Sayed, U.; Lorenzo, R.; Corbi, I.; Corbi, O.; Yang, D.; Zuo, Y. Mechanical properties of large-scale parallel bamboo strand lumber under local compression. Constr. Build. Mater. 2020, 271, 121572. [Google Scholar] [CrossRef]
- Zhu, W.; Qiu, Z.; Zhou, J.; Jin, F.; Fan, H. Size design and nonlinear stress-strain relationship of parallel bamboo strand lumbers in tension and compression. Eng. Fail. Anal. 2022, 140, 106587. [Google Scholar] [CrossRef]
- Mirambell, E.; Real, E. On the calculation of deflections in structural stainless steel beams: An experimental and numerical investigation. J. Constr. Steel Res. 2000, 54, 109–133. [Google Scholar] [CrossRef]
- Rasmussen, K.J. Full-range stress–strain curves for stainless steel alloys. J. Constr. Steel Res. 2003, 59, 47–61. [Google Scholar] [CrossRef]





| Ref. | Species | Age (Years) | Growth-Height | Laminate Method | Thermal Treatment | Resin | Resin Content (%) | Density (kg/m3) | Final MC (%) |
|---|---|---|---|---|---|---|---|---|---|
| Li et al. [19] | Phyllostachys pubescens | 3–4 | Upper | Hot-pressed | SST | PF | - | 1250 | - |
| Dongsheng et al. [45] | - | 5 | Upper | Hot-pressed | - | - | - | ||
| Wei et al. [46] | - | - | - | Cold-pressed /heat curing | - | PF | - | ||
| Sheng et al. [47] | Phyllostachys pubescens | 5 | - | - | - | - | - | ||
| Li et al. [48] | Phyllostachys pubescens | 3–4 | - | Hot-pressed | SST | PF | - | 1254 | 8.2 |
| Ref. | Species | Age (Years) | Growth-Height | Strip Dimensions (mm) | Resin | Density (kg/m3) | Final MC (%) | |
|---|---|---|---|---|---|---|---|---|
| Width | Thickness | |||||||
| Li et al. [18] | Phyllostachys pubescens | 3–4 | Upper | 17 | 4 | PF | 647 | 8.3 |
| Li et al. [34] | Phyllostachys pubescens | 3–4 | Lower | 21 | 8 | PF | 635 | 7.6 |
| Chen et al. [49] | Phyllostachys pubescens | 4 | All three heights | - | - | PF | 780 | 10.6 |
| Product Type | Experimental Study | Ec (MPa) | εcy (µε) | εc0 (µε) | fcy (MPa) | fc0 (MPa) | Selection Criteria for Representative Stress-Strain Response |
|---|---|---|---|---|---|---|---|
| Bamboo scrimber | Li et al. [19] | 14,275 | 4380 | 32,320 | 62.94 | 105.79 | A sample was chosen with the lowest slenderness ratio which is optimal for failure by compression. |
| Dongsheng et al. [45] | 11,600 | 2690 | 30,010 | 33.04 | 60.20 | This curve pertains to a sample which lies well within the upper and lower curve of all samples examined. | |
| Wei et al. [46] | 12,100 | 4074 | 61,352 | 49.71 | 89.52 | The average curve of the five samples was taken. | |
| Sheng et al. [47] | 11,440 | 3060 | 28,620 | 35.46 | 58.81 | The average curve of the compressive samples was taken. | |
| Li et al. [48] | 11,320 | 2900 | 33,210 | 33.29 | 87.08 | A stress-strain curve that was well within the upper and lower curves was chosen. | |
| LBL | Li et al. [18] | 9200 | 4220 | 31,820 | 36.66 | 59.36 | A sample with the upper growth portion was selected. |
| Li et al. [34] | 9930 | 3860 | 16,760 | 36.77 | 59.43 | A sample was chosen with the lowest slenderness ratio which is optimal for failure by compression. | |
| Chen et al. [49] | 10,880 | 3140 | 32,500 | 32.24 | 54.48 | The source has not specified which test result was taken in the results comparison, however 20 samples were tested. |
| Experimental Study | QM 1 | QM 2 | RA | LM | CM |
|---|---|---|---|---|---|
| Li et al. [19] | 0.0591 | 0.0603 | 0.0697 | 0.1040 | 0.1728 |
| Dongsheng et al. [45] | 0.0750 | 0.0698 | 0.0855 | 0.1273 | 0.3211 |
| Wei et al. [46] | 0.1093 | 0.1110 | 0.0626 | 0.1669 | 0.4034 |
| Sheng et al. [47] | 0.0389 | 0.0414 | 0.0420 | 0.0976 | 0.2860 |
| Li et al. [48] | 0.0678 | 0.0700 | 0.0302 | 0.1491 | 0.1397 |
| σ0.01 (MPa) | σ0.2 (MPa) | σ0.5 (MPa) | σ1.0 (MPa) | e | n | m | E0 (GPa) | σu (MPa) | εp | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.2% | 0.5% | 1.0% | 0.2% | 0.5% | 1.0% | 0.2% | 0.5% | 1.0% | ||||||||
| Li et al. [19] | 49 | 75 | 85 | 97 | 0.00468 | 0.00530 | 0.00605 | 7.04 | 7.10 | 6.74 | 3.48 | 3.81 | 4.21 | 14.28 | 105.79 | 0.03231 |
| Dongsheng et al. [45] | 35 | 43 | 47.5 | 53 | 0.00317 | 0.00350 | 0.00390 | 14.55 | 12.81 | 11.10 | 3.50 | 3.76 | 4.08 | 11.60 | 60.20 | 0.03001 |
| Wei et al. [46] | 49 | 63 | 71 | 81 | 0.00492 | 0.00555 | 0.00633 | 11.92 | 10.55 | 9.16 | 3.51 | 3.82 | 4.22 | 12.10 | 89.52 | 0.03082 |
| Sheng et al. [47] | 37 | 45.5 | 49 | 54 | 0.00389 | 0.00420 | 0.00463 | 14.49 | 13.93 | 12.18 | 3.71 | 3.92 | 4.21 | 11.44 | 58.81 | 0.02862 |
| Li et al. [48] | 33 | 55 | 68 | 78.5 | 0.00453 | 0.00560 | 0.00647 | 5.86 | 5.41 | 5.31 | 3.21 | 3.73 | 4.16 | 11.32 | 87.08 | 0.03321 |
| ‘n’ for Full-Range RO with 1.0% Proof Stress | Existing Models | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 7 | 9 | 11 | 13 | QM 1 | QM 2 | RA | LM | CM | |
| Li et al. [19] | 0.0519 | 0.0385 | 0.0369 | 0.0394 | 0.0420 | 0.0591 | 0.0603 | 0.0697 | 0.1040 | 0.1728 |
| Dongsheng et al. [45] | 0.0702 | 0.0531 | 0.0506 | 0.0546 | 0.0604 | 0.0750 | 0.0698 | 0.0855 | 0.1273 | 0.3211 |
| Wei et al. [46] | 0.0556 | 0.0459 | 0.0462 | 0.0496 | 0.0529 | 0.1093 | 0.1110 | 0.0626 | 0.1669 | 0.4034 |
| Sheng et al. [47] | 0.0429 | 0.0227 | 0.0175 | 0.0185 | 0.0227 | 0.0389 | 0.0414 | 0.0420 | 0.0976 | 0.2860 |
| Li et al. [48] | 0.0248 | 0.0353 | 0.0450 | 0.0518 | 0.0570 | 0.0678 | 0.0700 | 0.0302 | 0.1491 | 0.1397 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goonewardena, J.; Ashraf, M.; Reiner, J.; Kafle, B.; Subhani, M. Constitutive Material Model for the Compressive Behaviour of Engineered Bamboo. Buildings 2022, 12, 1490. https://doi.org/10.3390/buildings12091490
Goonewardena J, Ashraf M, Reiner J, Kafle B, Subhani M. Constitutive Material Model for the Compressive Behaviour of Engineered Bamboo. Buildings. 2022; 12(9):1490. https://doi.org/10.3390/buildings12091490
Chicago/Turabian StyleGoonewardena, Janeshka, Mahmud Ashraf, Johannes Reiner, Bidur Kafle, and Mahbube Subhani. 2022. "Constitutive Material Model for the Compressive Behaviour of Engineered Bamboo" Buildings 12, no. 9: 1490. https://doi.org/10.3390/buildings12091490
APA StyleGoonewardena, J., Ashraf, M., Reiner, J., Kafle, B., & Subhani, M. (2022). Constitutive Material Model for the Compressive Behaviour of Engineered Bamboo. Buildings, 12(9), 1490. https://doi.org/10.3390/buildings12091490