Abstract
This study aims to develop the optimal artificial neural networks (ANNs) capable of estimating the seismic damage of reinforced concrete (RC)-framed structures by considering several seismic intensity parameters based on the Hilbert–Huang Transform (HHT) analysis. The selected architecture of ANN is the multi-layer feedforward perceptron (MFP) network. The values of the HHT-based parameters were calculated for a set of seismic excitations, and a combination of five to twenty parameters was performed to develop input datasets. The output data were the structural damage expressed by the Park and Ang overall damage index (DIPA,global). The potential contribution of nine training algorithms to developing the most effective MFP was also investigated. The results confirm that the evolved MFP networks, utilizing the employed parameters, provide an accurate estimation of the target output of DIPA,global. As a result, the developed MFPs can constitute a reliable computational intelligence approach for determining the seismic damage induced on structures and, thus, a powerful tool for the scientific community for the performance-based design of buildings.
1. Introduction
The fast, comprehensive, and accurate coverage of existing and planned structures’ seismic hazards is a central task in earthquake engineering. The results of the seismic hazard estimation serve as a basis for preparing disaster plans and as a tool for determining premiums in the insurance industry and the damage forecast. It is well known that seismic intensity parameters have been widely used to express the damage potential of earthquakes [1,2]. Furthermore, structural damage indices have been used to express the postseismic damage status of buildings [1,2,3,4,5,6,7,8,9,10,11]. Several studies verified the correlation between seismic intensity parameters and seismic damage [1,2,6,7,8,9]. However, no explicit formula or algorithm exists for directly evaluating damage indices from seismic intensity parameters. Therefore, knowing the seismic intensity parameters, statistical and artificial intelligence techniques have been used to estimate the postseismic damage status of buildings, expressed by structural damage indices. Such established techniques in earthquake engineering are multilinear regression analysis and artificial intelligence procedures, such as ANNs [3,4,5,6,9,12,13,14,15,16]. Additionally, damage indices are essential quantities in performance-based design [17,18,19,20,21].
On the other hand, the HHT procedure is appropriate for processing nonlinear and nonstationary signals such as seismic excitation records [22,23,24,25,26]. Thus, new HHT-based seismic intensity parameters have been developed recently, considering the frequency-time history of seismic accelerograms. This study uses the multi-layer feedforward perceptron (MFP) ANN framework to evaluate the structural damage index used in recently developed HHT-based seismic intensity quantities for the first time [10,11]. The result values of the used structural damage index provided by the ANNs are compared with the corresponding results provided by nonlinear dynamic analyses, which have been considered exact results. The quality of the ANNs’ results is confirmed by the performance evaluation parameters mean squared error (MSE) and R correlation coefficient.
The seismic intensity measures can be classified into peak, spectral, and energy parameters. Generally, these conventional parameters ignore the frequency-time history of the seismic excitation, which is their main disadvantage in this context. The HHT is a procedure for processing nonlinear and nonstationary signals, such as seismic excitation records, which provide the frequency-time history of the seismic time histories [22,23,24,25,26]. HHT-based parameters overcome the disadvantage of the conventional intensity parameters mentioned above. In contrast to a large number of conventional seismic intensity parameters, only a relatively small number of HHT-based parameters have been defined and applied in seismic engineering. The present study covers this gap; thus, 40 HHT-based recently defined seismic intensity parameters have been considered [10,11].
The 40 HHT-based, recently developed seismic intensity parameters [10,11] used in this study have not yet been investigated in combination with ANNs. However, these parameters provided promising results in combination with statistical methods (correlation studies, multilinear regression analysis) [10,11]. The 40 used seismic intensity parameters are investigated in this study for the first time combined with ANNs procedures to determine their effectiveness in predicting the postseismic damage status of a building in terms of a structural damage index.
2. Methods
2.1. Hilbert-Huang Transform (HHT) Analysis
The Hilbert–Huang transform (HHT) is an innovative signal processing technique suitable for nonstationary and nonlinear signals [22]. HHT uses an adaptive basis derived from the data collected as the natural phenomenon unfolds over time. In contrast to other standard techniques for analyzing signals (e.g., wavelet analysis, Fourier transform), it assumes that signals are stationary, within the time window of observation at least, and are associated with no adaptive bases.
The HHT technique is a combination of two stages, namely, empirical mode decomposition (EMD) and Hilbert analysis (HA):
The empirical mode decomposition (EMD) decomposes complex signal data assuming that, at any given time, the signal consists of coexisting simple oscillatory modes of notably different frequencies, one superimposed on the other. In the end, the EMD algorithm manages to separate the data into locally non-overlapping time scale components, the intrinsic mode functions (IMF) with physical meaning, which follow specific conditions.
Hence, the initial signal X(t) was decomposed into a sum of n IMFs and a residual rn which was either a monotonic function or a constant
After extracting the IMFs of a signal, the Hilbert transform yj(t) was applied to each of them, as described in the following equation
where P denotes the Cauchy principal value of the integral.
The IMF cj(t) and the Hilbert transform yj(t) form an analytical signal zj(t) as follows:
from which the amplitude aj(t) and the phase function θj(t) were defined.
Furthermore, the instantaneous frequency was calculated from the phase function’s first derivative.
Knowing the instantaneous frequencies and amplitudes of the IMFs, a frequency-time distribution of amplitude (energy) was designated as the “Hilbert Spectrum” (HS) and defined below as:
The calculation procedure of the two-step HHT algorithm is illustrated in Figure 1. The left-hand side of Figure 1 shows the procedure for using the empirical mode decomposition (sifting process) to define the IMFs, while the right-hand side shows the procedure to construct the Hilbert spectrum.
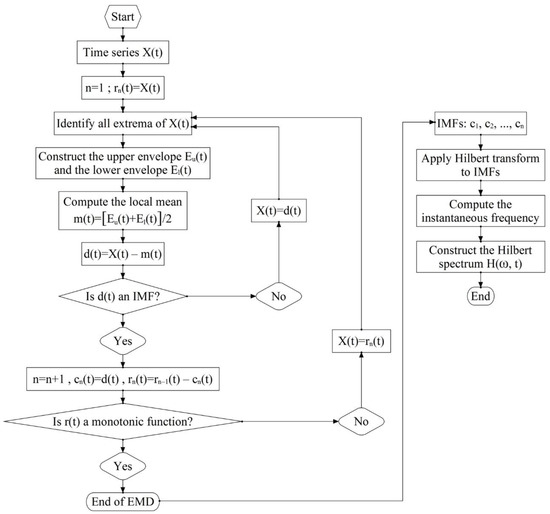
Figure 1.
Flowchart of Hilbert–Huang Transform (HHT) Analysis.
2.2. HHT-Based Seismic Parameters
The study, through Hilbert spectra, of the inherent features of signals and their differences as the difference between their frequency content and the amplitude fluctuations across the time range, has led to the development of a number of new seismic intensity parameters, which have already been presented in the scientific literature [10,11].
After the evaluation of Hilbert spectra and their graphical representation, the connection between their geometrical features with the characteristics of the signals, the following forty seismic parameters were extracted and calculated for this research.
The first parameter was the volume V1(HHT) occupied by each spectrum, which represents the released energy during a seismic excitation and was calculated as
where a(f,t) denotes the instantaneous amplitude, which corresponds to the instantaneous frequency f at a time equal to t, while fmax and tmax are the maximum instantaneous frequency calculated by the analytical signal and the total duration of the signal, respectively.
The upper surface of the defined volume V1(HHT) obtained from every Hilbert spectrum was the second seismic parameter and was described as
From the values of the instantaneous amplitude α(f,t) obtained from the analytical signal, the maximum, the mean values, and their difference were distinguished and considered additional parameters, which were described as
Identifying that the magnitude and quantity of the maximum amplitude values of every signal are related to the destructive potential of excitation, a first limitation of the Hilbert spectrum was realized. Therefore, a parallel layer to the time-frequency one, which intersects the z-axis (axis of α amplitudes) of the Hilbert spectrum at the point of the A1(mean,HHT) value, was set (Figure 2). For the bounded Hilbert spectrum, the new volume V1(Pos,HHT), the volume over the parallel layer, and the new upper surface S1(Pos,HHT) of the spectrum were defined as two more parameters.
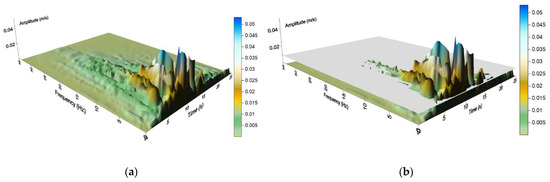
Figure 2.
(a) Hilbert spectrum (HS) for a seismic excitation; (b) bounded HS with the layer that crosses the amplitude-axis of HS at Amean,HHT.
The volumes V1(HHT) and V1(Pos,HHT) were divided by the corresponding values of surfaces S1(HHT) and S1(Pos,HHT), respectively, and so, the parameters A1(HHT) and A1(Pos,HHT) were calculated.
The seismic parameters VA1(max,HHT), VA1(mean,HHT), and VA1(dif,HHT) were set by the multiplication of the volume V1(HHT) with the maximum, minimum values of amplitude and their difference correspondingly.
Moreover, comparing the frequency content of a seismic excitation with the fundamental frequency of a structure is helpful in identifying possible resonance phenomena between the structure and soil vibration, which result in maximum values of the response forces. For this reason, a new limitation of the Hilbert spectrum on the band of frequencies encompassed in the zone limited by the following equation
0.90 ⋅ f0 ≤ f ≤ 1.10 ⋅ f0
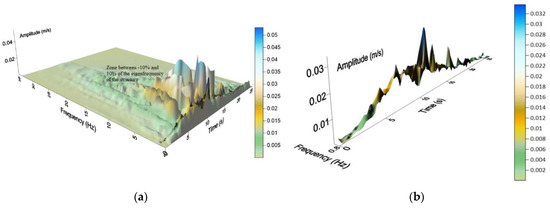
Figure 3.
(a) Limitation of the HS on the band of frequencies encompassed in the zone between 0.90 and 1.10 of the fundamental frequency f0; (b) enlargement of the characteristic zone of HS.
All the above parameters were defined for the new limitation of the Hilbert spectrum and, correspondingly, were assigned as V2(HHT), S2(HHT), A2(max,HHT), A2(mean,HHT), A2(dif,HHT), V2(Pos,HHT) and S2(Pos,HHT), VA2(max,HHT), VA2(mean,HHT), VA2(dif,HHT), A2(HHT), and A2(Pos,HHT).
Additionally, the released energy from every excitation at the frequency equal to the fundamental frequency (f0) value of a structure is presented by the calculation of the area SEF(HHT) of the amplitude-time section that intersects the Hilbert spectrum frequency-axis at the frequency value (f0) (Figure 3) and defined by Equation (9).
This Hilbert spectrum section’s maximum and mean amplitude values were selected and designated as A3(max,HHT) and A3(mean,HHT) parameters, respectively.
The following additional seismic intensity parameters were evaluated from the combination of the above parameters, as presented in Equation (12).
In the end, the ratio of A1(mean,HHT), A2(mean,HHT), and A3(mean,HHT) to A1(max,HHT), A2(max,HHT), and A3(max,HHT) resulted in the A1(Ratio,HHT), A2(Ratio,HHT) and A3(Ratio,HHT) HHT-based seismic intensity parameters respectively.
As is obvious, the computational effort for evaluating the HHT-based seismic intensity parameters is generally more extensive than the conventional ones. However, the HHT procedure provides an insight into the frequency-time history of the seismic accelerograms, which is enclosed in the HHT-based quantities.
2.3. Global Damage Index of Park and Ang
Park and Ang is a cumulative damage model [27,28] reflecting the effects of repeated cycling under seismic loading. It is the most utilized damage index (DIPA,global) to date, mainly due to its general applicability and the precise definition of different damage states. Its most used modification is the one proposed by Kunnath et al. [29,30], and it is described by the equation
where θm is the maximum rotation in loading history, θu is the ultimate rotation capacity, My is the yield moment, dEh is the incremental absorbed hysteretic energy, and β is a non-negative parameter representing the effect of cyclic loading on structural damage.
A value of DIPA,global over 0.80 signifies total damage or complete collapse of the structure, while a value equal to zero signifies that the structure is under elastic response. According to the values of DIPA,global, classification of the structural damage is presented in Table 1.

Table 1.
Structural damage grade classification according to DIPA,global.
3. Application
A number of 100 earthquake excitations were employed for the needs of this paper. The employed excitations were applied to a seven-story reinforced concrete (RC) frame structure with a total height of 22 m, as shown in Figure 4. The structure was designed in agreement with the rules of the recent Eurocodes EC8 [31] for antiseismic structures and EC2 [32] for structural concrete. The cross-section of the beams were T-shapes with 60 cm total height, 30 cm width, and 20 cm plate thickness. The effective plate width was 1.15 m at the end bays and 1.80 m at the middle bay. The distance between frames in the three-dimensional structure was 6 m. The building was considered an “importance class ΙΙ”, “subsoil of type B”, and “ductility class Medium”. The dead weight and the seismic loading, snow, wind, and live loads were also considered. The fundamental period of the frame was equal to 0.95 s.
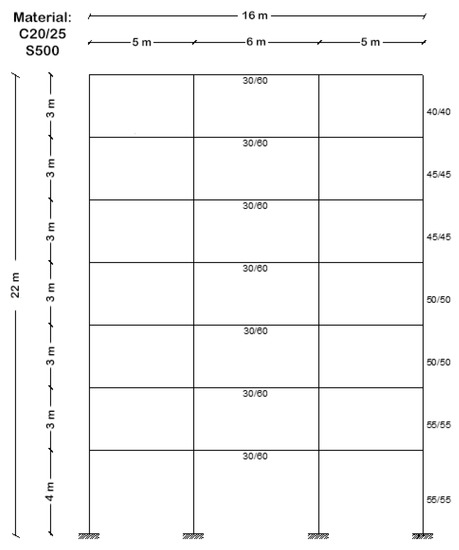
Figure 4.
Reinforced concrete frame.
After applying the employed seismic acceleration time histories, nonlinear dynamic analysis of the RC frame was conducted to evaluate the structural seismic response. The hysteretic behavior of beams and columns was specified at both ends using a three-parameter Park model. Every dynamic analysis was realized using the computer software IDARC2D [33].
This model incorporates strength deterioration, stiffness degradation, slip-lock, non-symmetric response, and a trilinear monotonic envelope. The values of the above degrading parameters have been chosen from the experimental results of cyclic force-deformation characteristics of typical components of the studied structure [28,34].
From the derived results of the response evaluation performing the nonlinear dynamic analysis of the structure, this article concentrates on Park and Ang’s overall structural damage index (DIPA,global). The evaluated overall structural damage indices of Park and Ang for every seismic vibration cover a broad spectrum of damage (low, medium, large, and total) for statistical reasons, as presented in Figure 5.
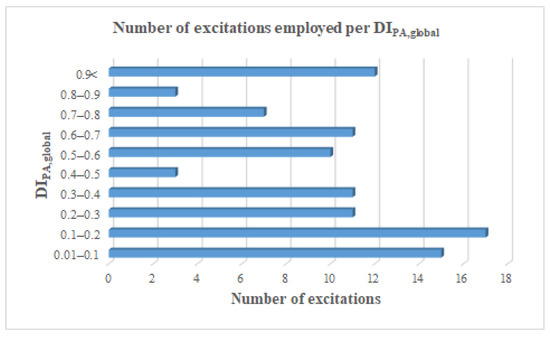
Figure 5.
The number of excitations employed per DIPA,global range.
4. Results
4.1. Evaluation of the HHT-Based Seismic Intensity Parameters
Using the velocity time histories generated by the earthquake accelerograms, all the HHT-based seismic intensity parameters, as described above, were evaluated separately, and their elementary statistical values are presented in Table 2.

Table 2.
T Statistical results of HHT-based seismic parameters.
4.2. Problem Formulation and ANN Framework Selection
Artificial neural networks (ANNs) refer to complex algorithms capable of imitating behaviors of biological neural systems, and they are able to learn the applied knowledge gained from experience and solve new problems in new environments. Like the structure of the human brain, they connect a number of neurons in a complex and nonlinear form. Weighted links achieve the connection between the neurons. The multi-layer feedforward perceptron (MFP) artificial neural networks have been chosen in this study. MFPs are based on a supervised learning procedure, where a number of vectors are used as input data to obtain the optimal combination of neurons’ connection weights with a backpropagation algorithm for training. The ultimate target is the estimation of a set of predefined target outputs. Once the network has fit the input-output data, it forms a generalization of their relationship, and it can be used to generate output for input it was not trained on.
Artificial neural networks have been utilized in civil engineering, and many researchers have investigated their advantages in structural engineering [14,15,16]. In the present research, the constructed MFPs aim to model the examined parameters’ ability to estimate the structures’ damage potential after an earthquake. The problem in the study was approached as a function approximation problem (FA). Thus, MFP artificial neural networks were trained on a set of inputs in order to produce a set of target outputs. A large number of ANNs have evolved by trying all the potential combinations of every data set of the input HHT-based seismic parameters, and every one of them was trained with nine deferent algorithms only one time. No retraining procedure was followed for every configured ANN so that over-training models would be avoided. Over-trained models are prone to memorization, and they present extremely limited ability for generalization. In addition, all the structural damage grades (low, medium, large, and total) were considered during the ANN training. Finally, the use of the “trial and error” approach confirms the reliability of a large number of the developed MFPs, which are capable of perfectly serving the estimation of the seismic vulnerability.
The proposed procedure is an open methodology. Thus, alternative conventional and HHT-based seismic intensity parameters can be used. Additionally, alternative damage indices can be used. Finally, the proposed procedure can be applied to other structural materials and structural types (such as bridges, towers, and silos). In the latter case, appropriate damage indices must be considered.
4.3. Configuration of ANNs
The development of the MFPs requires the determination of the input and the output datasets, the choice of the optimal learning algorithm, the determination of the number of hidden layers/neurons, and the selection of the activation functions. The schematic diagram of the developed MFPs is displayed in Figure 6 and analysed below.
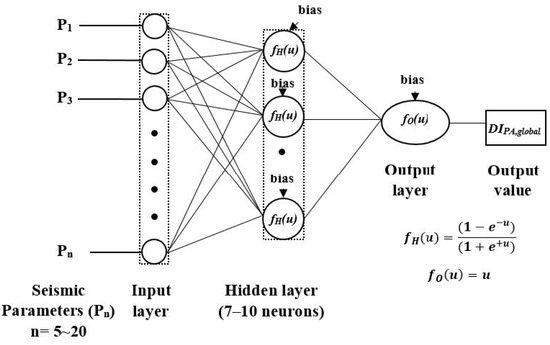
Figure 6.
Schematic diagram of the developed MFPs.
The input data sets for the constructed MFP networks comprise the forty HHT-based seismic parameters, separated into two groups of twenty parameters. The division of parameters into two groups was implemented to make the calculations of ANNs with the available computational systems feasible. A separate analysis was performed following the “trial and error” approach to obtain the best network for each group. Hence, a huge number of potential input datasets that emerged by combinations of every group’s parameters were tested. Each combination is comprised of at least 5 parameters. An input vector’s maximum number of features was twenty as the maximum number of parameters in every group.
As target output of the formulated ANNs considered the structural damage as expressed by the overall damage index of Park and Ang (DIPA,global). The DIPA,global values were derived from nonlinear dynamic analyses of the structure after applying every employed seismic accelerogram. Thus, the output layer of the MFPs consisted of one neuron presenting the value of DIPA,global.
All the evolved MFP networks had one hidden layer to keep their architecture as simple as possible. This choice was based on the ability of feedforward perceptron networks with one hidden layer to precisely approach functions f(x): Rn→R1, as well as on their already proven efficiency by numerous relevant investigations [12,13]. The number of neurons in the hidden layer was also investigated. ANN models with 7 to 10 hidden neurons were tested. This range was chosen based on the number of available excitations (100) in the source data as training vectors. As a result, four additional networks were calculated for every produced ANN by combining the examined seismic parameters of every group.
At last, as presented in Table 3, nine different training backpropagation algorithms were utilized in the formulation of the multilinear feedforward networks. Moreover, a sigmoid, precisely the tangent hyperbolic (TanH) transfer function fH, was employed for the hidden layer, while the choice of linear activation function was made for the output layer.

Table 3.
Backpropagation training algorithms of the developed ANNs.
4.4. Calculation of ANNs
The MATLAB 2019a [35] software program was used to develop and evaluate the formulated artificial networks according to the flowchart in Figure 7. Due to the extensive number of developed networks with training algorithms that are not always GPU capable, a parallelized environment of ten virtual instances of the program MATLAB was utilized.
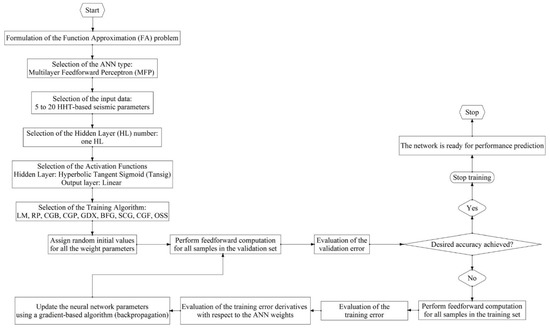
Figure 7.
Flowchart of ANN computational procedures.
Additionally, each instance was equipped with two MATLAB workers and had access to 12 GB of memory and 8 i9-9900k threads.
An appropriate MATLAB script was developed so all the ANNs could be formulated and trained with the employed training algorithms with the best use of the available resources. The performance evaluation parameters R correlation coefficient and the mean squared error (MSE) were adopted and calculated to compare the MFP networks. From the total employed seismic excitations, a 70% was used as the training set, 15% was used as the testing set, and 15% was used as the validation set.
In statistics, the R coefficient between two variables reflects the strength and the direction of a linear relationship and takes values between −1 (total negative linear correlation and +1 (total positive linear correlation). The MSE is an average of the absolute difference between the target values, calculated by nonlinear dynamic analysis values of DIPA,global, and the corresponding ones evaluated by the constructed ANNs.
The basic statistics of R and MSE values and their classification for the constructed ANNs are presented in the following Tables. Specifically, Table 4, Table 5, Table 6 and Table 7 present the minimum (min), maximum (max), mean, and standard deviation (st.dev.) of the evaluated R and MSE values. The values are presented for every training algorithm and every investigated number of neurons in the hidden layer for both groups of input data. In addition, Table 8, Table 9, Table 10 and Table 11 present the classification of MFPs according to an R absolute value equal to or greater than 0.90 and their classification according to MSE values. As displayed in Table 8, Table 9, Table 10 and Table 11, the calculated MFPs for both coefficients (R, MSE) are categorized into three classes.

Table 4.
Statistics of R—ANNs with input parameters of Group 1.

Table 5.
Statistics of MSE—ANNs with input parameters of Group 1.

Table 6.
Statistics of R—ANNs with input parameters of Group 2.

Table 7.
T Statistics of MSE—ANNs with input parameters of Group 2.

Table 8.
Classification of R—ANNs with input parameters of Group 1.

Table 9.
Classification of MSE—ANNs with input parameters of Group 1.

Table 10.
Classification of R—ANNs with input parameters of Group 2.

Table 11.
Classification of MSE—ANNs with input parameters of Group 2.
5. Discussion
The investigation of the results reveals that all the training algorithms present a number of configured ANNs whose performance in the estimation of the structural damage through the examined parameters is described with a very high R correlation coefficient (R > 0.95) and very small MSE (MSE < 0.02). However, observing Table 4, Table 5, Table 6 and Table 7, it becomes obvious that the most efficient training algorithm is the Levenberg–Marquardt (LM) algorithm for the first group of input data preventing the most significant configured MFP networks with mean correlation coefficient ranging from 0.9008 to 0.9042 and with mean MSE ranging from 0.0183 to 0.0192. Additionally, the best MFP model was trained by the LM algorithm for input datasets of the first group of parameters with an absolute maximum value of R equal to 0.9882 and a minimum MSE value equal to 0.0023 for 8 neurons in the hidden layer.
Furthermore, depending on the number of neurons in the hidden layer, ANN cases trained with the LM algorithm present R > 0.90 with a percentage up to 66.30% for the first group of parameters and up to 37.04% for the second group of parameters. Likewise, most ANN cases trained with the same algorithm are able to predict the DIPA,global damage index with MSE less than 0. Similarly, depending on the number of neurons in the hidden layer, up to 73.85% for the group 1 parameters and up to 50.92% for the group 2 can predict the DIPA,global damage index with MSE less than 0.02. This means that at least 66.30% of the first group and 37.04% for the second group of parameters are able to develop ANNs with excellent predictive accuracy (with R > 0.90 και MSE < 0.02 simultaneously).
Concluding, the very high correlation coefficient R combined with a very small mean squared error (MSE) are effective quality indicators of the results. This fact confirms that the proposed methodology provides satisfactory results in predicting the utilized damage index and is an efficient tool using artificial intelligence procedures.
One possible application of the proposed methodology is to use the trained ANN to predict the damage indicator of a building for the early identification of its structural damage immediately after a seismic event, under the condition that all the required seismic intensity parameters have been evaluated instantly after the event by processing regional seismic record data.
6. Conclusions
This research designates the performance of forty HHT-based seismic intensity parameters, calculated for an RC-framed structure, to predict seismic damage through artificial neural network models. A number of 75,051,360 MFPs were developed, and their investigation revealed the increased ability of the examined parameters to predict the structural damage proving their interrelation with the overall structural damage index of Park and Ang. For this reason, the structure of the MFP artificial network with one hidden layer was chosen. The calculation of the configured MFPs led to the development of high-performance mathematical models which are able to express the probability that a structure will experience a damage situation, as expressed by DIPA,global, with high accuracy.
For the calculation of the MFPs, nine training algorithms were utilized, which led to a significant percentage of ANNs with a very high coefficient correlation (R > 0.90) and low MSE (MSE < 0.02). The most efficient of them turned out to be the LM algorithm. A number of 8.339.040 ANNs were configured with the LM algorithm from two groups of twenty parameters. These seismic parameters created MFP networks of a high explanation of variance of DIPA,global (with R > 0.90) and a very low MSE (MSE < 0.02), simultaneously with a percentage up to 66.30% for the first group and up to 37.04% for the second group of parameters. According to the classification table of the DIPA,global, an MSE coefficient with values lower than 0.02 cannot essentially change the class of structural damage caused by a seismic excitation.
The numerical results reveal that the 40 examined HHT-based seismic intensity parameters provided adequate results, evaluating the used damage index with sufficient accuracy, justified by many seismic excitations with very high correlation coefficient R and a very small mean squared error. Thus, the proposed methodology is a valuable complement to existing artificial intelligence procedures.
Additionally, it is observed that the best performance of all the investigated statistical coefficients was displayed among the ANNs with nine neurons in the hidden layer, which used the LM algorithm. In particular, the MFPs with nine neurons in the hidden layer for the input datasets of Group 1 accomplished an estimation of damage with an R correlation coefficient value upon the value of 0.9883 and a value of MSE that can be reduced until the values of 0.0023.
The conditions that must be considered for applying the proposed procedure are first that the number of the used seismic intensity parameters and accelerograms is sufficiently large for the appropriate training of the ANN. In addition, the numerical values of the utilized damage index must be considered to cover all the structural damage grades (low, medium, large, and total) during the ANN training.
It is obvious that all the above outcomes confirm the capability of the examined seismic intensity parameters to predict the induced seismic damage to the RC-framed structures. In addition, the investigated HHT-based seismic parameters are presented as effective descriptors of the seismic damage potential and, thus, are able to stand as helpful tools for a performance-based design of framed structures. Consequently, the developed ANN models using HHT-based seismic parameters can be considered an essential method for the early identification of structural vulnerability.
Author Contributions
Conceptualization, M.T. and A.E.; methodology, M.T., A.E., I.A. and L.V.; software, M.T., A.E., I.A. and L.V.; validation, I.A. and L.V.; formal analysis, M.T., A.E., I.A. and L.V.; investigation, M.T., A.E., I.A. and L.V.; resources, M.T., A.E., I.A. and L.V.; data curation, M.T., A.E., I.A. and L.V.; writing—original draft preparation, M.T. and A.E.; writing—review and editing, A.E.; visualization, M.T., A.E., I.A. and L.V.; supervision, A.E.; project administration, A.E.; funding acquisition, N/A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
The study did not require ethical approval.
Informed Consent Statement
Not applicable.
Data Availability Statement
The study did not report any data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Elenas, A. Correlation between seismic acceleration parameters and overall structural damage indices of buildings. Soil Dyn. Earthq. Eng. 2000, 20, 93–100. [Google Scholar] [CrossRef]
- Elenas, A.; Meskouris, K. Correlation study between seismic acceleration parameters and damage indices of structures. Eng. Struct. 2001, 23, 698–704. [Google Scholar] [CrossRef]
- Alvanitopoulos, P.F.; Andreadis, I.; Elenas, A. A genetic algorithm for the classification of earthquake damages in buildings. In Proceedings of the 5th IFIP Conference on Artificial Intelligence Applications & Innovations, Thessaloniki, Greece, 23–25 April 2009; pp. 341–346. [Google Scholar]
- Alvanitopoulos, P.F.; Andreadis, I.; Elenas, A. A New Algorithm for the Classification of Earthquake Damages in Structures. In Proceedings of the 5th IASTED Conference on Signal Processing, Pattern Recognition and Applications, Innsbruck, Austria, 13–15 February 2008; pp. 151–156. [Google Scholar]
- Alvanitopoulos, P.F.; Andreadis, I.; Elenas, A. Neuro-fuzzy techniques for the classification of earthquake damages in buildings. Measurement 2010, 43, 797–809. [Google Scholar] [CrossRef]
- Elenas, A. Seismic-Parameter-Based Statistical Procedure for the Approximate Assessment of Structural Damage. Math. Probl. Eng. 2014, 2014, 916820. [Google Scholar] [CrossRef]
- Elenas, A. Interdependency between seismic acceleration parameters and the behavior of structures. Soil Dyn. Earthq. Eng. 1997, 16, 317–322. [Google Scholar] [CrossRef]
- Nanos, N.; Elenas, A.; Ponterosso, P. Correlation of different strong motion duration parameters and damage indicators of reinforced concrete structures. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Kostinakis, K.; Athanatopoulou, A.; Morfidis, K. Correlation between ground motion intensity measures and seismic damage of 3D R/C buildings. Eng. Struct. 2015, 82, 151–167. [Google Scholar] [CrossRef]
- Tyrtaiou, M.; Elenas, A. Seismic Damage Potential Described by Intensity Parameters Based on Hilbert-Huang Transform Analysis and Fundamental Frequency of Structures. Earthq. Struct. 2020, 18, 507–517. [Google Scholar]
- Tyrtaiou, M.; Elenas, A. Novel Hilbert spectrum-based seismic intensity parameters interrelated with structural damage. Earthq. Struct. 2019, 16, 197–208. [Google Scholar]
- Lautour, O.R.; Omenzetter, P. Prediction of seismic-induced structural damage using artificial neural networks. Eng. Struct. 2009, 31, 600–606. [Google Scholar] [CrossRef]
- Morfidis, K.; Kostinakis, K. Approaches to the rapid seismic damage prediction of r/c buildings using artificial neural networks. Eng. Struct. 2018, 165, 120–141. [Google Scholar] [CrossRef]
- Tsou, P.; Shen, M.H. Structural Damage Detection and Identification Using Neural Network. In Proceedings of the 34thAIAA/ASME/ASCEAHS/ASC, Structural, Structural Dynamics and Materials Conference, AIAA/ASME Adaptive Structural Forum, La Jolla, CA, USA, 19–22 April 1993. [Google Scholar]
- Wu, X.; Ghaboussi, J.; Garrett, J. Use of Neural Network in Detection of Structural Damage. Comput. Struct. 1992, 42, 649–659. [Google Scholar] [CrossRef]
- Zhao, J.; Ivan, J.N.; DeWold, J.T. Structural Damage Detection Using Artificial Neural Networks. J. Infrastructural Syst. 1998, 13, 182–189. [Google Scholar] [CrossRef]
- Zameeruddin, M.; Sangle, K.K. Damage assessment of reinforced concrete moment resisting frames using performance-based seismic evaluation procedure. J. King Saud Univ. Eng. Sci. 2021, 33, 227–239. [Google Scholar] [CrossRef]
- Zameeruddin, M.; Sangle, K.K. Review on Recent developments in the performance-based seismic design of reinforced concrete structures. Structures 2016, 6, 119–133. [Google Scholar] [CrossRef]
- Loh, C.H.; Chao, S.H. The Use of Damage Function in Performanced-Based Seismic Design of Structures. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Gholizadeh, S.; Fattahi, F. Damage-controlled performance-based design optimization of steel moment frames. Struct. Des. Tall Spec. Build. 2018, 27, e1498. [Google Scholar] [CrossRef]
- Jiang, H.J.; Chen, L.Z.; Chen, Q. Seismic Damage Assessment and Performance Levels of Reinforced Concrete Members. In Proceedings of the 12th East Asia-Pacific Conference on Structural Engineering and Construction, Hong Kong, China, 26–28 January 2011. [Google Scholar]
- Huang, N.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Huang, N.; Shen, Z.; Long, S.R. A new view of nonlinear water waves: The Hilbert spectrum. Annu. Rev. Fluid Mech. 1999, 31, 417–457. [Google Scholar] [CrossRef]
- Huang, N.; Wu, M.L.; Qu, W.; Long, S.; Shen, S. Applications of Hilbert–Huang transform to non-stationary financial time series analysis applied stochastic models in business and industry. Appl. Stoch. Models Bus. Ind. 2003, 19, 245–268. [Google Scholar] [CrossRef]
- Yu, M.; Erlei, Y.; Bin, R.; Haiyang, Z.; Xiaohong, L. Improved Hilbert spectral representation method and its application to seismic analysis of shield tunnel subjected to spatially correlated ground motions. Soil Dyn. Earthq. Eng. 2018, 111, 119–130. [Google Scholar]
- Zhang, R.R.; Ma, S.; Safak, E.; Hartzell, S. Hilbert–Huang transform analysis of dynamic and earthquake motion recordings. ASCE J. Eng. Mech. 2003, 129, 861–875. [Google Scholar] [CrossRef]
- Park, Y.J.; Ang, A.H.-S. Mechanistic seismic damage model for reinforced concrete. J. Struct. Eng. 1985, 111, 722–739. [Google Scholar] [CrossRef]
- Park, Y.J.; Ang, A.H.-S.; Wen, Y.K. Damage-limiting aseismic design of buildings. Earthq. Spectra 1987, 3, 1–26. [Google Scholar] [CrossRef]
- Kunnath, S.K.; Reinhorn, A.M.; Abel, J.F. A Computational Tool for Seismic Performance of Reinforced Concrete Building. Comput. Struct. 1992, 41, 157–173. [Google Scholar] [CrossRef]
- Kunnath, S.K.; Reinhorn, A.M.; Lobo, R.F. IDARC Version 3.0: A Program for the Inelastic Damage Analysis of Reinforced Concrete Structures, Report No. NCEER-92-0022; National Center for Earthquake Engineering Research; University at Buffalo: Buffalo, NY, USA, 1992. [Google Scholar]
- Eurocode 8. Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions, and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- Eurocode 2. Design of Concrete Structures—Part 1: General Rules and Rules for Building; European Committee for Standardization: Brussels, Belgium, 2000. [Google Scholar]
- Reinhorn, A.M.; Roh, H.; Sivaselvan, M.; Kunnath, S.K.; Valles, R.E.; Madan, A.; Li, C.; Lobo, R.; Park, Y.J. IDARC2D Version 7.0: A Program for the Inelastic Damage Analysis of Structures; Tech. Rep. MCEER-09-0006; MCEER, State University of New York at Buffalo: Buffalo, NY, USA, 2009. [Google Scholar]
- Gholamreza, G.A.; Elham, R. Maximum damage prediction for regular reinforced concrete frames under consecutive earthquakes. Earthq. Struct. 2018, 14, 129–142. [Google Scholar]
- The Math Works Inc. MATLAB and Statistics Toolbox Release 2016b; The Math Works Inc.: Natick, MA, USA, 2016. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).