Experimental Investigation and Numerical Simulation of C-Shape Thin-Walled Steel Profile Joints

Abstract

The versatility of steel, its high resistance in relation to its low mass, as well as the easily accessible technology in the context of using recyclable materials and the low negative impact on the environment represent important arguments in using thin-walled steel profiles to make structures for buildings with a low height regime. This paper presents the results of an experimental program that investigated the behavior of three types of joints in a T-shape form made of thin-walled steel profiles to make shear wall panels or truss beam floors. Due to the small dimensions of the C-profiles of 89 × 41 × 12 × 1 mm, and of the technology of their joining, manufacturers prefer the hinged connections of elements with self-drilling screws. The purpose of the research presented in this paper is to assess the maximum capacity of the joints, the elastic and post-elastic behavior until failure, and also the mechanisms failure. The types of joints analyzed are commonly used in the production of structural systems for houses. The experimental program, which consisted of testing 5 specimens for each type of joint in tension (shear on screws), showed different behavior in terms of load-displacement. The experimental, tested models were analyzed by finite element simulations in an ANSYS nonlinear static structure with 3D solid models. The materials were defined by a bilinear true stress–strain curve obtained after some experimental tensile tests of the steel. The results of the experimental tests showed that the main failure mechanism is a yielding of the holes where the screws were mounted and a shearing of the profile walls. Adding an additional screw on each side increases the capacity of the joints, but not until a yield loss is obtained. In conclusion, it is shown that the solution is suitable for a low level of loading in a static manner; however, additional studies are necessary in order to develop and verify other solutions, thus improving the strength of the connection.

1. Introduction

Since the introduction of steel as a building material in the field of construction, it has constantly evolved in terms of increasing the performance of the material by obtaining alloys with very high strengths and a ductile behavior. This was done to ensure the sufficient deformation capacity required for structural elements. Construction steel products that can be hot-rolled or cold-formed from thin sheets have also evolved through the development of multiple cross-sectional shapes.

Cold-formed profiles began to be used in 1850, but their use as structural elements was accepted only after 1925. The first design standards for hot-rolled steel appeared after 1930, but they could not be applied to cold-formed profiles. In the United States, the first edition of the design rules for cold-formed lightweight profiles was based on research conducted at Cornell University and published in 1946 [1]. Several countries use the American code, and those in the European Union use Eurocode 3 [2,3,4,5]. During the past two decades, the structures made of thin-walled profiles have become more and more popular. The numerous advantages compared to other construction materials, coupled with an increase in the number of technological solutions for the production of these profiles, have led to the adoption of these structural solutions for residential buildings, including those located in active seismic areas.

Today, technology and industrial machines have facilitated the emergence of various entrepreneurs producing custom profiles. Some proposed structural systems for buildings, as shown in Figure 1, are made of wall panels stiffened by a system of diagonals at the ends. Sometimes profiles with larger sections and a sheet thickness of 3–5 mm are required in cases of bordering the gaps for windows or doors. Different research programs have been carried out regarding the overall behavior of cold-formed steel profile beams or their connections [6,7,8,9].

Figure 1. Example of structure for housing made of spatial frames and trusses from thin-walled C-shaped steel profiles, Germany 2018 (authors’ collection).

The floor system for roofs can also be made of truss beams spaced, for example, at 60 cm apart. Figure 2 presents an example of such an adopted solution in the case of a roof for a residential complex building located in Cluj-Napoca city, Romania.

Figure 2. Example of a floor system for a roof made of truss beams with thin-walled steel profiles Cluj-Napoca, Romania 2019 (authors’ collection).

Apart from the realization and obtainment of cold-formed profiles from thin steel sheets up to 1 mm used for the purpose of creating structural elements for buildings, there still remains the very important issue of joining these profiles. There are numerous studies in the scientific literature presenting a variety of connecting solutions such as welding, riveting, screws, self-tapping screws, bolting, blind rivets, self-drilling screws, fired pins, arc-welding, imprint holes or a combination of these [8,10,11,12,13,14,15,16,17,18,19,20,21].

For example, on spot welded specimens tested experimentally [6], a good capacity and ductility was observed, but in comparison with self-drilling screws the ductility was smaller.

Given the large number of alternatives to conceive the joints of cold-formed thin-walled elements, there is still a need for further investigations in order to completely understand the behavior under various loading scenarios. This article presents the results of an experimental and numerical study carried out on a system of profiles and joints used by a Romanian manufacturer [22]. The fully equipped manufacturing facility can produce a large number of geometrical configurations for trusses as load bearing subsystems for roofs, floors (Figure 2) or wall panels (Figure 1). Unlike previously proposed solutions [6,23,24,25,26], in the case of these new systems, the structural concept is based on the truss beams and panels for walls. The joints are based on self-drilling and self-tapping screws with holes prepared in advance.

The joints between the profiles are made by drilling and stamping the sheets during the formation of the profiles on the rolling line. The parts are labeled with bar codes which, according to the sketches, are mounted later with self-drilling screws of Ø 4.8 × 19 mm or Ø 4.8 × 22 mm. The assembly of the structural elements are positioned according to the structural drawings and are connected to each other with the same types of self-drilling screws. Over these elements are added 18 mm thick OSB boards with fasteners at a distance of 20 cm on the outer faces, with plasterboards mounted on the inside. The thermal insulation layer of basalt wool is then added between these boards.

According to the current design practice, the numerical model used during the design stage of such structural systems considers the connection between the component elements as joints. Moreover, the contribution to the strength and rigidity of the OSB or gypsum board is neglected. In the case of seismic actions, the structures are subjected to cyclic axial forces, which makes the compressed elements vulnerable to the loss of stability and the tensioned ones prone to being torn from the joints. Additionally, the overloaded floor elements above the design limit may exhibit a fragile behavior, which was observed in a previous study by experimental testing of some floor elements [27]. Some details from the tested system are presented in Figure 3 and Figure 4. At a maximum load capacity, the failure mechanism was brittle, but the maximum displacement before collapse for a 5 m opening around 60 kN/sqm was 4 cm, two times bigger than the maximum admissible one.

Figure 3. Detail of a floor truss system with the 5 m opening gravitationally tested.

Figure 4. The floor truss system after the experimental test with the detail of the failure mechanism.

In this context, an experimental investigation and numerical validation was necessary to understand the behavior of joints and correctly assess the load transfer mechanisms. Experimental and numerical investigations of the overall strength and rigidity of a new type of joint consisting of a drawn-socket can offer insightful information on the behavior of the joint, as well as the structural element the joint was extracted from. Moreover, the load-displacement graphs may provide information that can be used in the design process of such types of joints as the ones presented in the paper.

Additionally, the numerical simulations of joints consisting of 1d-elements may not be so accurate, overestimating the real strength and stiffness capacity of the joint, if it was not for the use of joints with a limited predefined axial rigidity expressed by polynomial functions derived from load–displacement curves. Further research should be conducted in this direction for the numerical models to be improved in order to be able to capture the complex phenomena taking place in such a joint. This could represent the first step in introducing new design procedures to accommodate the large number of joint types with different geometries used in the market.

2. Materials and Methods

The main objective was to check the maximum load capacity of 3 distinct sets of joints with self-drilling and self-tapping screws. A total of 5 specimens were prepared for each considered set, amounting to 15 specimens in all. The 3 types of joints and the test layout are presented in Figure 5. In this context, it is important to experimentally investigate and assess the mechanical properties of the steel from which the profiles were made. This information is of significant importance from the point of view of the subsequent numerical simulations that needed validation and calibration from a material behavior point of view. The geometry of the joints is the simplest one in a T form. Figure 5 presents the schematic geometry and loading process, as well as the 3 types of joints (A, B, C).

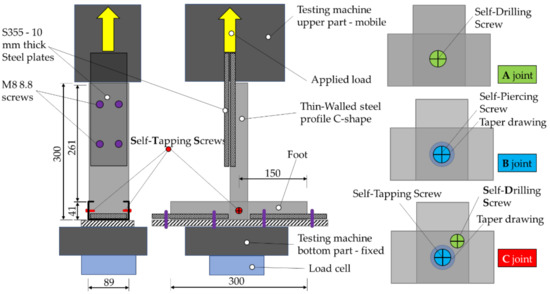
Figure 5. Geometry of the joints and the loading schema.

The details of the components that make up the joints are shown in Figure 6. The C-profiles made of DX51D+Z steel sheet with a thickness of 1 mm were placed at a 90 degrees angle in the shape of the letter T. The C-shape section dimensions are presented in Figure 6. The horizontal profile at the bottom of the joint was fixed in the testing machine by means of thick metal plates attached to the thin-walled cold-formed element by M8 screws. The vertical profile was also fastened with thick metal plates and screws to the top of the testing machine. As already mentioned, 3 types of joint layouts were considered. In the A-type joint, yellow galvanized 4.8 × 19 mm self-drilling screws were used (Figure 7), whereas in the type B joint, gray galvanized 4.8 × 22 mm self-tapping screws were positioned in a tapper drawing on each side (Figure 8).

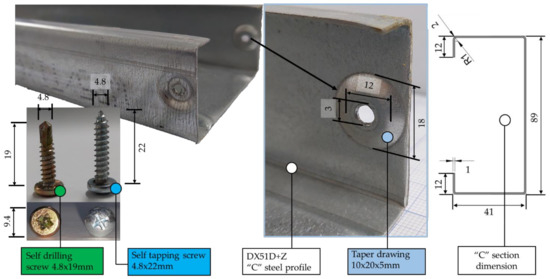
Figure 6. Types of screws and tapper drawing used for the joints.

Figure 7. Specimens for A joint.

Figure 8. Specimens for B joint.

The investigated joints belong to scaled-down models of shear walls and trusses used in flooring systems. The use of DX51D+Z steel for structural applications is not, in general, a good choice compared to their better counterparts S280G+Z and S350GD+Z steel. Taking into account its lower yield strength (120 MPa) and lower ultimate strength (250 MPa) compared to the other types of steel, but its higher ductility, it was intended to investigate whether this type of steel was suitable for structural applications, in the sense of representing the lower limit of the strength interval.

Sometimes, the ability to undergo large deformations before collapse, in case of certain loading scenarios, may prove a viable solution in comparison to a more brittle failure mode. Therefore, an investigation of deformation and load bearing capacities offers useful data related to the possible application of these types of steel in structural elements subjected to static loads. Additionally, the use of this type of steel in structures built in highly seismic areas should be avoided.

The type C joint (Figure 9) is a combination between A and B, with the self-drilling screw being additionally added to the type B joint.

Figure 9. Specimens for C joint.

In order to determine the tensile strength and modulus of elasticity of the material the elements were made of, 5 specimens with the dimensions and shape shown in Figure 10 were cut from the web of the profiles and tested in direct tension. These were tested according to ISO 6892-1: 2019 [28]. The secant modulus of elasticity was automatically assessed by means of the TestXpert II v3.5 software as part of the control unit for the Zwick/Roell SP 1000 universal test machine. The test speed was based on a stress rate of 30 MP/s for the dog-bone specimens (Figure 10). After the tests, 2 specimens were invalidated because of abnormal values. The specimens made of DX51D+Z are shown before and after the tests in Figure 10 and Figure 11. An external extensometer connected to the machine software interface was used for measuring the axial strains.

Figure 10. Tensile test specimen prepared and Zwick/Roell SP1000 machine testing.

Figure 11. Specimens mounted with extensometer during the tests and specimens tested.

The material properties of the steel, experimentally determined, and for the screws, as supplied by the manufacturer, are summarized in Table 1.

Table 1. Materials properties.

Component	Type	Elastic Modulus (GPa)	Tensile Strength (MPa)	Shear Strength (MPa)
Profile steel sheet	DX51D+Z	210	250	-
Self-drilling screw—SDR	4.8 × 19 mm [29]	210	1531	1313
Self-tapping screw—STR	4.8 × 22 mm [30]	210	1000	500

The T joints were subjected to a tensile force applied along the centerline of the vertical element, as shown in Figure 12 and video recorded available on-line with links presented in Section: Supplementary Materials at the end of the paper. In order to prevent local crushing or tearing of the steel profile, a 10 mm steel sheet was attached to the vertical element, as schematically represented in Figure 5, and then fixed in the upper grip of the testing equipment (Figure 12). The horizontal element was attached via M8 screws to a rigid T-shaped steel component that was fixed in the lower grips of the universal testing machine. The loading of the specimens was performed at a constant speed of 50 N/s.

Figure 12. Universal Testing Machine Zwick/Roell SP 1000 and the tested joints A, B, C.

3. Experimental Results

The test results are presented in a graphical manner as a stress–strain curve. For each set of the results, the average curve was calculated and a comparison between the three considered joint configurations was made. The results presented below are discussed in the next chapter.

3.1. Sheet DX51D+Z Results

The stress–strain curves obtained from the three validated specimens are shown in Figure 13a. The averaged stress–strain curve, termed as the “experimental engineering” curve in Figure 13b, was transformed into a true stress–strain curve, used in the numerical analyses as a bilinear curve, for the nonlinear definition of the material behavior [31,32,33]. The yielding stress was 120 MPa with a corresponding axial strain of 0.36%. The maximum tensile stress was 250 MPa, and the maximum strain at the end of the test was 21.39%.

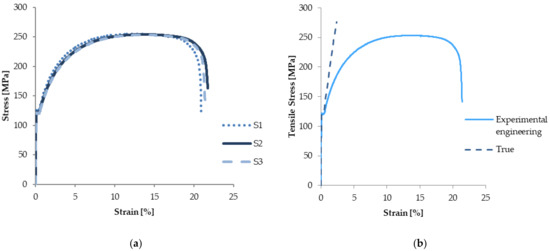
Figure 13. Engineering Stress-Strain curve of the DX51D+Z steel sheet; (a) experimental; (b) averaged experimental vs. True.

The engineered stress–strain curve was converted into a true stress–strain curve using the relations:

$${\epsilon }_{true}=ln\left(1+{\epsilon }_{nom}\right);$$

(1)

$${\sigma }_{true}={\sigma }_{nom}\left(1+{\sigma }_{nom}\right);$$

(2)

3.2. Joint Results

The load–displacement curves for joint A and B are presented in Figure 14a,b, respectively. For joint A, the maximum load as an averaged value was 8.7 kN, with a corresponding 7 mm displacement. From the graph it can be observed that the elastic behavior of the joint is between 0 and 2 kN. In the case of joint B, the maximum averaged load was 9.8 kN, for which a 5 mm displacement was recorded. The failure is initiated due to stress concentrations occurring at the edges of the steel sheet in the area of the holes where the contact between the steel profile and the self-drilling screw is present. These stress concentrations favor the occurrence of stress values larger than the yield strength of the steel in the C-profile.

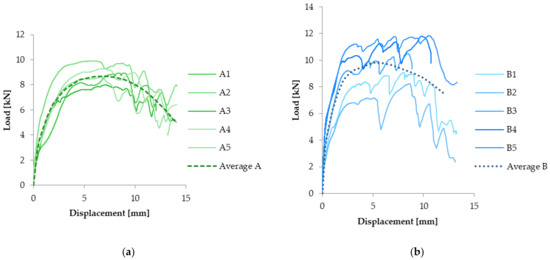
Figure 14. Load-displacement curves: (a) joint A; (b) joint B.

The T-joints were fixed in the grips of the universal testing machine by means of additional thick steel plates connected to the T-joint by means of screws. This introduced additional deformations and increased the chance of supplementary slips in the connecting areas. Moreover, the estimation of the load-displacement behavior is accurate only in the linear-elastic range of material behavior. A soon as the yield limit of the steel in the thin-walled cold-formed elements was reached, additional deformations were recorded. The jumps in the load-displacement graph were produced by the passing of the steel profile in the connecting area (the hole area) over each twist on the shank of the self-drilling bolts. This behavior was caused by the fact that the screws tilted upwards due to the applied load.

Figure 15a presents the load–displacement curves for the C joint. One of the tested samples, C5, failed at a load approximately 40% lower than the average value of the other 4. Therefore, the load–displacement curve was removed from the calculation procedure. In the case of this joint, two specimens were invalidated due to some abnormal failure. The maximum load for this joint was 15.1 kN at a 9 mm vertical displacement. A comparison between the experimental load–displacement curves of the joints is shown in Figure 15b.

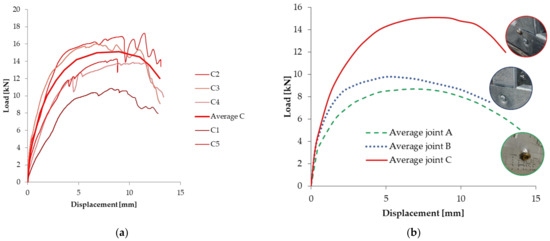
Figure 15. Load–displacement curves: (a) joint C; (b) Comparison of Average A, B, C.

The aspects of the tested specimens are presented in Figure 16, Figure 17 and Figure 18. It can be observed that 3 of 5 specimens were pulled-out in case of joint A. The failure was preceded by tilting of the screw, followed by lateral deformations of the flanges in the horizontal element. This resulted in a loss of grip between the elements of the joint and the vertical element was pulled-out.

Figure 16. Joint A tested specimens.

Figure 17. Joint B tested specimens.

Figure 18. Joint C tested specimens.

In the case of joint B and C, there are large, visible deformations and a failure mechanism which is similar to joint A. One of the specimens, C3, failed with shearing the entire section of the edge of the profile.

4. Finite Element Modelling

4.1. Nonlinear Analysis of the DX51D+Z Sheet Tensile Specimen

In order to calibrate the nonlinear behavior of the material, some numerical simulations were carried out. The material was defined in ANSYS as a nonlinear with bilinear stress–strain curve, a yield stress of 120 MPa, maximum strength of 250 MPa, elastic modulus of 210 GPa and tangent modulus of 6750 MPa. Figure 19a,b present the environment of the structural analysis. The bottom of the specimen was fixed, and the upper part had a 2 mm displacement defined in an X direction, the longitudinal axis of the specimen. The discretization of the solid model is presented in Figure 19b with an element quality map distribution. The total number of nodes was 11,548, and the total number of elements was 5525. The elements are defined with nonlinear behavior. Below are presented some characteristics of the analysis:

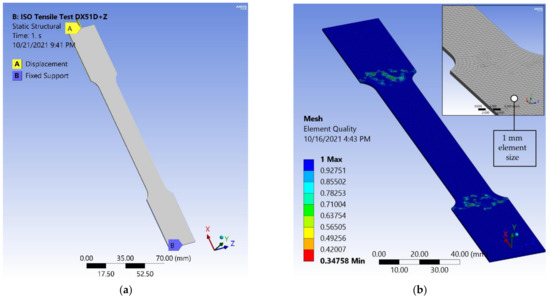
Figure 19. Finite Element Model for tensile stress–strain test calibration: (a) loading schema; (b) mesh element quality discretization and detail.

• Problem dimensionality: 3-d;
• Degrees of freedom: ux, uy, uz;
• Analysis type: static (steady-state);
• Offset temperature from absolute zero: 273.15;
• Nonlinear geometric effects: on;
• Equation solver option: sparse;
• Plastic material properties included: yes;
• Newton-Raphson option: program chosen;
• Globally assembled matrix: symmetric.

4.2. Results on Tensile Simulation Test

Figure 20a presents a map distribution of equivalent (von Mises) stress, which shows the yielding value of the material at 0.1 mm displacement of the upper end. Figure 20b shows the map of equivalent plastic strain at same value of displacement. It can be observed that the maximum values of the equivalent plastic strain occur in the reduction area of the section and also the apparition in the central area of the plastic strain.

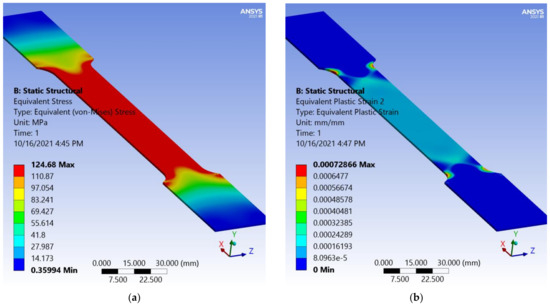
Figure 20. Results at 0.1 mm displacement: (a) equivalent von Mises stress; (b) equivalent plastic strain.

The results representing the nonlinear behavior of the model are confirmed by the graph presented in Figure 21. The stress–strain curves for the material, considered as a true stress–strain bilinear curve, coincide with the stress–strain results curve at the central node, named a node of interest, positioned in the center of the model.

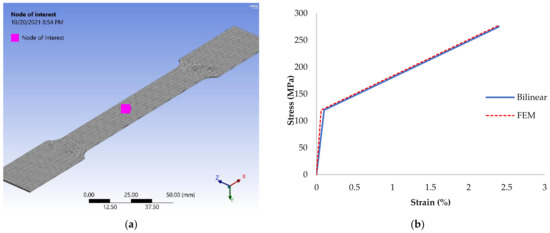
Figure 21. Stress–strain curve: (a) node of interest central position; (b) stress–strain curves for material definition bilinear and finite element model in node of interest.

4.3. Joint A Modelling and Results

Figure 22 presents joint A’s geometry and environment of the model, with a close detail of some hidden parts and a screw description. The screw was shaped considering the two ribs of the thread located between the layers of the profiles. The contacts of the bodies were assumed to be bonded. The mesh discretization and the quality of the finite elements are presented in Figure 23a,b. A SOLID186 brick-type element was used for the thin-walled cold-formed steel profiles, with a maximum grid size of 4 mm. The finite element size decreased to approximately 0.5 mm near the holes and for the screws. Only one layer of the SOLID186 element was considered over the thickness of the steel profile. The screws were modeled by means of tetrahedron SOLID187 element, and three layers were used.

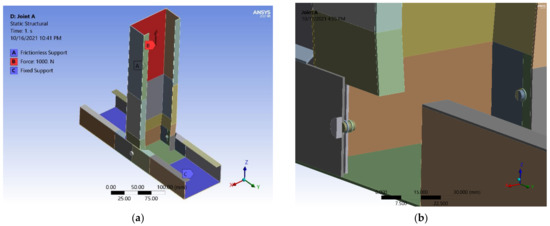
Figure 22. Joint A geometry: (a) Static schema; (b) detail of screws with hidden body parts.

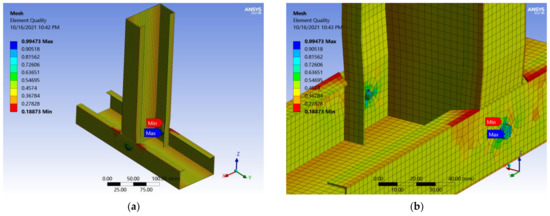
Figure 23. Joint A mesh: (a) element quality mesh; (b) detail of screw connection area.

The shear locking phenomenon was not considered at this stage of the research, with this being identified as the main source for such discrepancies between the experimental and numerical simulation results. Taking into account the raw processing power required for such numerical analyses, coupled with the need for finer mesh discretization as well as the required, at this stage, level of accuracy, the solution presented in the paper was deemed as being the most efficient. It should be pointed out that, for the time being, only a calibration of the model was intended, and a not an optimization process.

The results presented in Figure 24 represent a map distribution of the equivalent von Mises stress with the detail near the holes in profiles at a 2 kN load. The maximum stress value occurred in the screws. Furthermore, at this value of loading it can be seen that the value of the yield stress was exceeded at the points located on the outside part of the vertical element wall, near the circular hole for the screw. In Figure 24b the value of the stress marked is 141 MPa at 2 kN tensile load. Regarding the strain, a map distribution for the equivalent elastic strain at the same value of loading is presented in Figure 25a. The map distribution for plastic strain and those values are presented in detail in Figure 25b. Figure 26a,b present a comparison in terms of deformations in the real experiment and the numerical simulation. It can be seen that the screws are tilting, while the steel sheet of the profiles exhibit local pressure in the area of the screw holes.

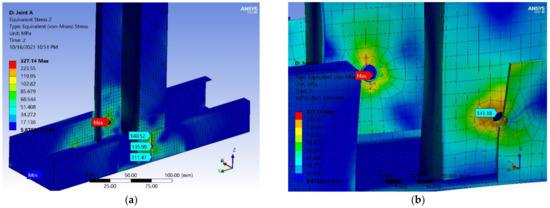
Figure 24. Equivalent stress von Mises joint A: (a) map distribution; (b)detail near hole and screws area.

Figure 25. Equivalent strain distribution joint A: (a) overall equivalent elastic strain; (b) detail near hole and screws area of equivalent plastic strain.

Figure 26. Comparison of displacement joint A: (a) experimental; (b) numerical model.

4.4. Joint B Modelling and Results

Figure 27 presents joint B’s geometry and the environment of the model with a close detail of some hidden parts with a screw and tapper drawing description. The screw was shaped while considering two ribs of the thread located between the layers of the sheet steel of the profiles. The contacts of the bodies were assumed to be bonded. The mesh discretization and the quality of the finite elements are presented in Figure 28a,b. Finite elements were the parallelepipedal solids type, with a maximum size of 4 mm. The screws were modelled with tetrahedron elements.

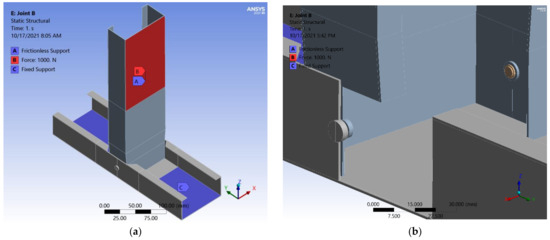
Figure 27. Geometry joint B: (a) overall; (b) detail.

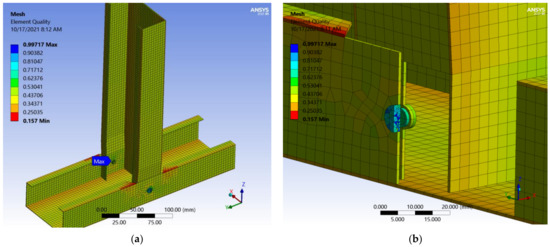
Figure 28. Mesh element quality joint B: (a) overall; (b) detail.

Figure 29 presents the map distribution of the equivalent von Mises stress. It can be seen that at a same 2 kN load, the values are distributed around the holes and tapper drawings. These values are smaller than those for joint A by up to 10%. In Figure 30a, the map distribution of the equivalent total strain (elastic and plastic) can be seen, while Figure 30b shows a close detail with the plastic deformation on the upper edge of the screw hole.

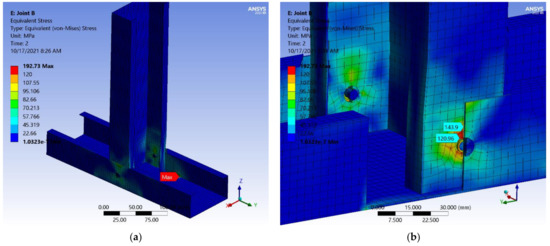
Figure 29. Joint B equivalent stress von Mises: (a) map distribution; (b) detail near holes and screw area.

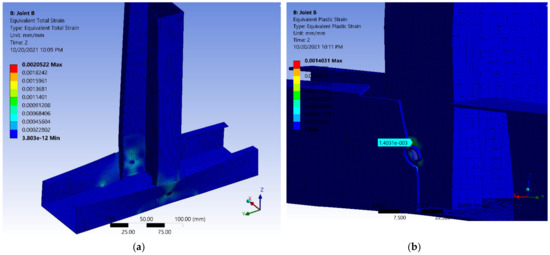
Figure 30. Equivalent strain in joint B at 2 kN—deformed shape: (a) overall map total (elastic + plastic) strain; (b) detail with plastic strain.

A close detail of tested specimen joint B is shown in Figure 31a. It can be seen that the screw tilted, and the tapper drawings exhibited bearing deformation. The vertical profile failed due to a shearing of the bottom edge of the holes. In the numerical simulation, the deformed model at a maximum load showed similarities with the experimental ones. However, keeping in mind that bonded contacts were considered on the tapper drawing area between the elements, this leads to a better distribution of the stress and a decreased local deformation near the holes. Nevertheless, the values obtained in the experiments and numerical simulation regarding the load and displacements are close as it will shown in subsequent sections Figure 31b.

Figure 31. Displacements of joint B—deformed shape: (a) experimental; (b) numerical model.

4.5. Joint C Modelling and Results

Figure 32 presents joint C’s geometry and the environment of the model with a close detail of some hidden parts with a description of the screws and tapper drawings. The screws were shaped considering two ribs of the thread located between the layers of the sheet steel of the profiles. The contacts of the bodies were initially assumed to be bonded. The mesh discretization and the quality of the finite elements are presented in Figure 33a,b. Finite elements were the parallelepipedal solids type, with a maximum size of 4 mm. The structural steel elements, including the screw, were modelled using three-dimensional solid finite elements SOLID186 and SOLID187, respectively. The contact surfaces between the screw head and shank and the steel sheet, as well as the contact between the finite elements in the two steel profiles, were modeled by means of Conta174 and Targe170 elements. The assumption of perfect bond was applied.

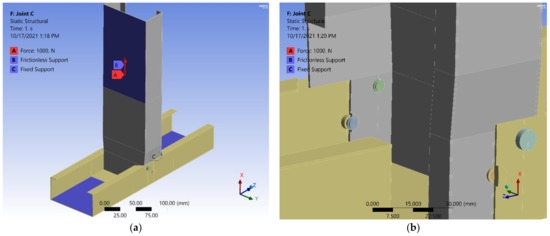
Figure 32. Joint C: (a) overall; (b) details of screws with hidden parts.

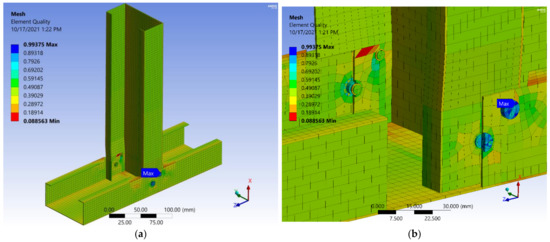
Figure 33. Joint C mesh: (a) overall; (b) details of screws with hidden parts.

This type of contact is, however, acceptable only for joint types A and B. For joint type C, the influence of the type of contact considered in the numerical model on the overall behavior of the joint was more pronounced compared to the other two. Based on the reviewer’s suggestions, the authors conducted additional numerical simulations and concluded that a FRICTIONAL type of contact, available in ANSYS, was a better approach. A comparative load–displacement curve is introduced in this paper to render evident the influence of the type of contact on the overall behavior of the joint. A detailed parametric analysis is considered in the form of a future research stage.

Figure 34 presents the map distribution of the equivalent von Mises stress. It can be seen that at a same 2 kN load, the values are distributed around the holes and tapper drawings, with a concentration in the upper holes. These values are 5% smaller than those obtained for joints A and B. In Figure 35a, the map distribution of the equivalent elastic strain can be seen, while Figure 30b shows a close detail with the plastic deformation on the upper edge of the first screw hole in the upper part.

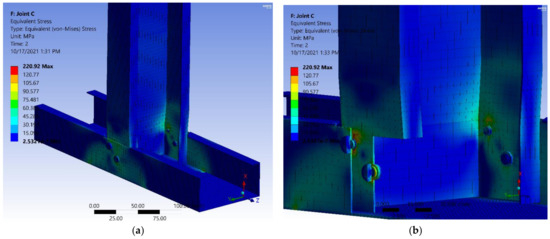
Figure 34. Joint C Equivalent stress: (a) overall; (b) details of screws with hidden parts.

Figure 35. Equivalent strain distribution joint C: (a) overall map distribution of equivalent elastic strain; (b) detail near hole area of equivalent plastic strain.

In Figure 36a, there is a close detail of the tested specimen joint C, where it can be seen that the screw tilted and the tapper drawings had a bearing deformation. The vertical profile failed due to shearing of the bottom edge of the holes. In the numerical simulation, the deformed model at a maximum load showed similarities with the experimental ones. Considering that the contacts bonded on the tapper drawing area between elements, this leads to a better distribution of stresses and smaller local deformations near the holes. However, the values obtained in the experiments and numerical simulation regarding the load and displacements were much lower compared to the previous two joint types, with joint C being almost two times stiffer (the bonded contact in comparative load-displacement graphs). Comparing the results between the experimental and numerical, we can see, in the case of joint A and joint B, a small influence of contacts definition, while in the case of joint C, the influence is greater, making the model stiffer than the experimented one.

Figure 36. Joint C deformed shape: (a) experimental; (b) FE model.

Figure 37a,b and Figure 38a present the comparative load–displacement curves for joints A, B and C, respectively. It can be observed that there is a good agreement between the numerical simulations and the experimental results in terms of ultimate loads and corresponding displacements. The numerical models exhibited higher initial stiffness compared to the experiment, mainly due to the assumption of perfect bond between the constitutive parts of the joint. This is very visible, especially for joint type C. The additional models with frictional contacts, which are presented in comparison, show that they are more accurate and closer to the experimental data obtained.

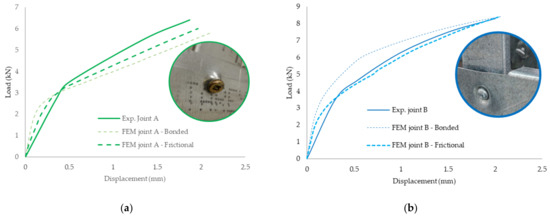
Figure 37. Comparative load–displacement curves: (a) joint A; (b) joint B.

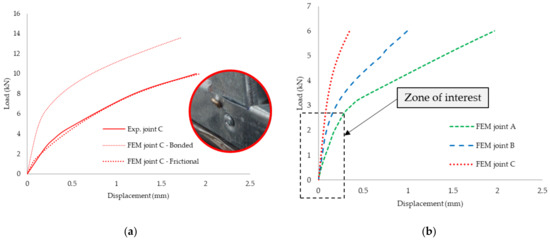
Figure 38. Comparative load–displacement curves: (a) Joint C; (b) FE models.

The elastic-plastic range, identified on the load-displacement graphs as starting from the point where the graph changes slope, was quite accurately identified in the numerical model and matched the experimental results.

Comparing the values obtained for each type of joint in Figure 38b on the finite element models, there is clearly an increase in the load carrying capacity at the same displacement. The yielding process occurred in joint A sooner than for joints B and C. In Figure 39, the comparative displacements at same value of load at 6 kN show that joint C was 50% stiffer than joint A, and joint B was 41% stiffer than joint A. Comparing joints B and C, it can be observed that adding a supplementary self-drilling screw on each side increased the overall stiffness and the overall load capacity.

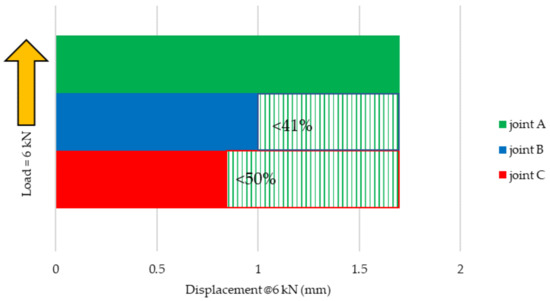
Figure 39. Comparative displacements @ same Load = 6 kN.

4.6. Design Resistance of Joint A, According to EN 1993-1-3

The assessment of the load carrying capacity of a joint, following the recommendations of EN1993-1-3 presented in Table 2, could represent a valuable benchmark for joint type A (Figure 40). Taking into account the fact that the EN1993-1-3 code only gives information on the load carrying capacity of simple joints using self-drilling screws and does not provide any information on the overall rigidity of these joints, the present study brings its contribution to broadening knowledge in the case of joints consisting of drawn-sockets to the deformation capacity of the joint itself.

Table 2. Joint A design according to EN 1993-1-3.

Basic Data
Nominal diameter of the screw	$d=4.8 \mathrm{mm}$	(3)
Total number of screws	$n_f=2$	(4)
End and edge distance for screw	$e_1=20.5 \mathrm{mm}; e_2=20.5 \mathrm{mm}$	(5)
The dimensions of the stud cross-section:
Total height	$h_1=89 \mathrm{mm}$	(6)
Total width of flange	$b_1=41 \mathrm{mm}$	(7)
Total width of edge fold	$c_1=12 \mathrm{mm}$	(8)
Nominal thickness	$t_{1,nom}=1 \mathrm{mm}$	(9)
Steel core thickness	$t_1=0.96 \mathrm{mm}$	(10)
Gross area of the studied cross-section	$A_1=185 {\mathrm{mm}}^2$	(11)
The dimensions of the rail cross-section:
Total height	$h=89 \mathrm{mm}$	(12)
Total width of flange	$b=41 \mathrm{mm}$	(13)
Nominal thickness	$t_{nom}=1 \mathrm{mm}$	(14)
Steel core thickness	$t=0.96 \mathrm{mm}$	(15)
The materials properties are:
Basic yield strength	$f_{yb}=125 \raisebox{1ex}{$\mathrm{N}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{mm}}^2$}\right.$	(16)
Ultimate strength	$f_u=420 \raisebox{1ex}{$\mathrm{N}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{mm}}^2$}\right.$	(17)
Modulus of elasticity	$E=210,000 \raisebox{1ex}{$\mathrm{N}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{mm}}^2$}\right.$	(18)
Poisson’s ratio	$\nu =0.3$	(19)
Shear modulus	$G=\frac{E}{2\left(1+\nu \right)}=81,000 \raisebox{1ex}{$\mathrm{N}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{mm}}^2$}\right.$	(20)
Partial factor	$\gamma =1.25$	(21)
The design force on the connection	$N_{Ed}=2 \mathrm{kN}$	(22)
The design shear force per screw in the ultimate limit state is:	$F_{v, Ed}=\frac{N_{Ed}}{n_f}=\frac{2}{2}=1\mathrm{kN}$	(23)
Check the range of validity for design resistance formulas
The following conditions should be satisfied:
$e_1\ge 3d; p_1\ge 3d; e_2\ge 1.5d; 3 \mathrm{mm}\le 8 \mathrm{mm}$		(24)
$e_1=20.5 \mathrm{mm}>3d=3\times 4.8=14.4 \mathrm{mm}$	OK	(25)
$e_2=20.5 \mathrm{mm}>1.5d=1.5\times 4.8=7.2 \mathrm{mm}$	OK	(26)
$3 \mathrm{mm}<d=4.8 \mathrm{mm}<8 \mathrm{mm}$	OK	(27)
Resistance check for self-tapping screws loaded in shear
Bearing resistance	$F_{b,Rd}=\frac{\propto f_{u}dt}{{\gamma }_{M2}}$	(28)
$\mathrm{for}{t}_1=t=1 \mathrm{mm}$	$\propto =3.2\sqrt{\raisebox{1ex}{$t$}\!\left/ \!\raisebox{-1ex}{$d$}\right.}=3.2\times \sqrt{\raisebox{1ex}{$0.96$}\!\left/ \!\raisebox{-1ex}{$4.8$}\right.}=1.43$	(29)
The bearing resistance of one screw is:	$$\begin{gathered} F_{b,Rd}=\frac{\alpha f_{u}dt}{{\gamma }_{M2}}=\frac{1.43\times 250\times 4.8\times 1}{1.25}=1373\mathrm{N} \\ =1.373 \mathrm{kN} \end{gathered}$$	(30)
Net-section resistance	$F_{n,Rd}=\frac{A_{net}{f}_u}{{\gamma }_{M2}}$	(31)
	$$\begin{gathered} \mathrm{Where}\mathrm{the}\mathrm{net}\mathrm{cross}-\mathrm{sectional}\mathrm{area}\mathrm{is}\text{:} \\ {A}_{net}=A_1-2d{t}_1=185-2\times 4.8\times 0.96=175.8 {\mathrm{mm}}^2 \end{gathered}$$	(32)
The net-section resistance is:	$F_{n,Rd}=\frac{A_{net}{f}_u}{{\gamma }_{M2}}=\frac{175.8\times 250}{1.25}=35,160\mathrm{N}=35.16 \mathrm{kN}$	(33)
Shear resistance	$F_{v,Rd}=\frac{F_{v,Rk}}{{\gamma }_{M2}}$	(34)
$F_{v,Rk}=9050 \mathrm{N}=9.05 \mathrm{kN} \mathrm{according}\mathrm{to}\mathrm{manufacturer}\mathrm{catalogue}$
	$F_{v,Rd}=\frac{9050}{1.25}=7240 \mathrm{N}=7.24 \mathrm{kN}$	(35)
The resistance of a fastener in shear may be verified using
$\frac{F_{v,Ed}}{\min (F_{b,Rd}; \raisebox{1ex}{$F_{n,Rd}$}\!\left/ \!\raisebox{-1ex}{$n_f$}\right.; F_{v,Rd}}\le 1$		(36)
$\frac{1}{\min \left(1.373; 17.58; 7.24\right)}=\frac{1}{1.373}=0.72<1$		(37)

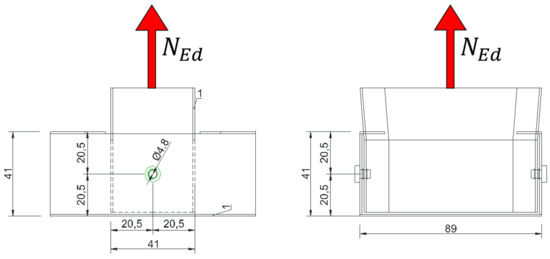
Figure 40. Joint A geometric schema.

5. Discussion

All the experimental tested specimens revealed that the main failure mechanism was caused by the exceeding of the strength of the sheet profile on edge holes. After the yielding of the material in the steel profiles, the screws tilted, and this caused a secondary mechanism of bearing deformations in the flanges due to the screw head.

For DX51D+Z steel, a very ductile material, permanent plastic deformations were produced in every case on the hole’s edge in the first stage of the loading. Hence, even though higher strength steel could be used, in excess of 250 MPa, the yield strength would be the one controlling the maximum bearing capacity for the design rules. A simple joint with one self-drilling screw on each side of the profile could be loaded with a maximum load of 1.5 kN before the upper limit of the linear-elastic range was attained.

Adding a tapper drawing and a self-tapping screw increased the stiffness of the joint by almost 15% in the elastic zone, and by almost 41% in terms of maximum load. The presence of the tapper drawing had, as a direct effect, the occurrence of an additional friction force, and the contact between the two profiles of the joint could be assumed, at least at the beginning of the loading process, to be perfectly bonded. This resulted in an improved behavior of the joint.

For a stiffer and strengthened joint, two screws on each side of the profile and a tapper drawing were deemed suitable and appropriate for connecting elements in truss beams or wall panels. The maximum loading in the elastic zone could be considered 4 kN.

The simulation results also showed that the failure mechanisms were similar to the real experimented specimens, with a combination of two failure mechanisms: the tilting of the screw and the bearing deformation in the flanges of the cold-formed thin-walled profiles.

The load–displacement curves of the joints obtained by the finite element analyses were similar in behavior and values with those obtained experimentally.

In a comparison between the assessment procedures put forward in Eurocode 3, it can be observed that, up to a value of the load of 2 kN, the considered joint is assumed to be safe, according to the norm. On the other hand, the ultimate strength of the steel considered in Eurocode 3 could lead to an overestimation of the bearing capacity of the joint. A better solution could be to consider the yield strength of the material for the assessment stage. Exceeding the yield strength could lead to the occurrence of plastic deformations that can endanger the safety of the occupants.

For the two remaining cases, joint types B and C, the presence of the drawn-socket is not covered in Eurocode 3. This study could be considered as the starting point for the formulations of design equations for joints with different configurations.

6. Conclusions

This paper presented a detailed study on thin-walled steel profile joints based on two types of screws: self-drilling and self-tapping, in addition to a tapper drawing. The experiments on tension loading showed that the simple self-drilling screws, with one at each side of the profiles, have an elastic behavior until around 1.5 kN; after that, plastic deformation appears on the hole’s edge, and the failure mechanism is revealed by a tilting of the screw and bearing deformation of the sheet steel.

Adding a tapper drawing and a self-tapping screw increased the friction between profiles and screw making a stiffer joint. Adding two screws on each side of the profiles with a tapper drawing resulted in a suitable connection for truss element connections or wall panels. When comparing these results with other solutions, such as riveted joints or welded joints, from a technological and strength point of view, it can be said that even if the strengthening is 50% weaker, it is a more practical and accessible technologically for mounting elements on sites. Rivets are also suitable and appropriate, but require holes and a higher precision of positioning of the rivets and holes, which is time consuming on mounting elements.