Predicting Maximum and Cumulative Response of A Base-isolated Building Using Pushover Analysis
Abstract
1. Introduction
2. Description of the Proposed Procedure
2.1. Basis Procedure
- The considered base-isolated building predominantly oscillates in the first mode.
- The superstructure behavior is linearly elastic, while nonlinear behavior is assumed only in the isolated layer.
- The local response (e.g., floor displacement and acceleration) can be approximated by a combination of the first and second modal responses.
- The cumulative response in the isolated layer (e.g., the cumulative strain energy of the damper) can be approximated by the first modal contribution.
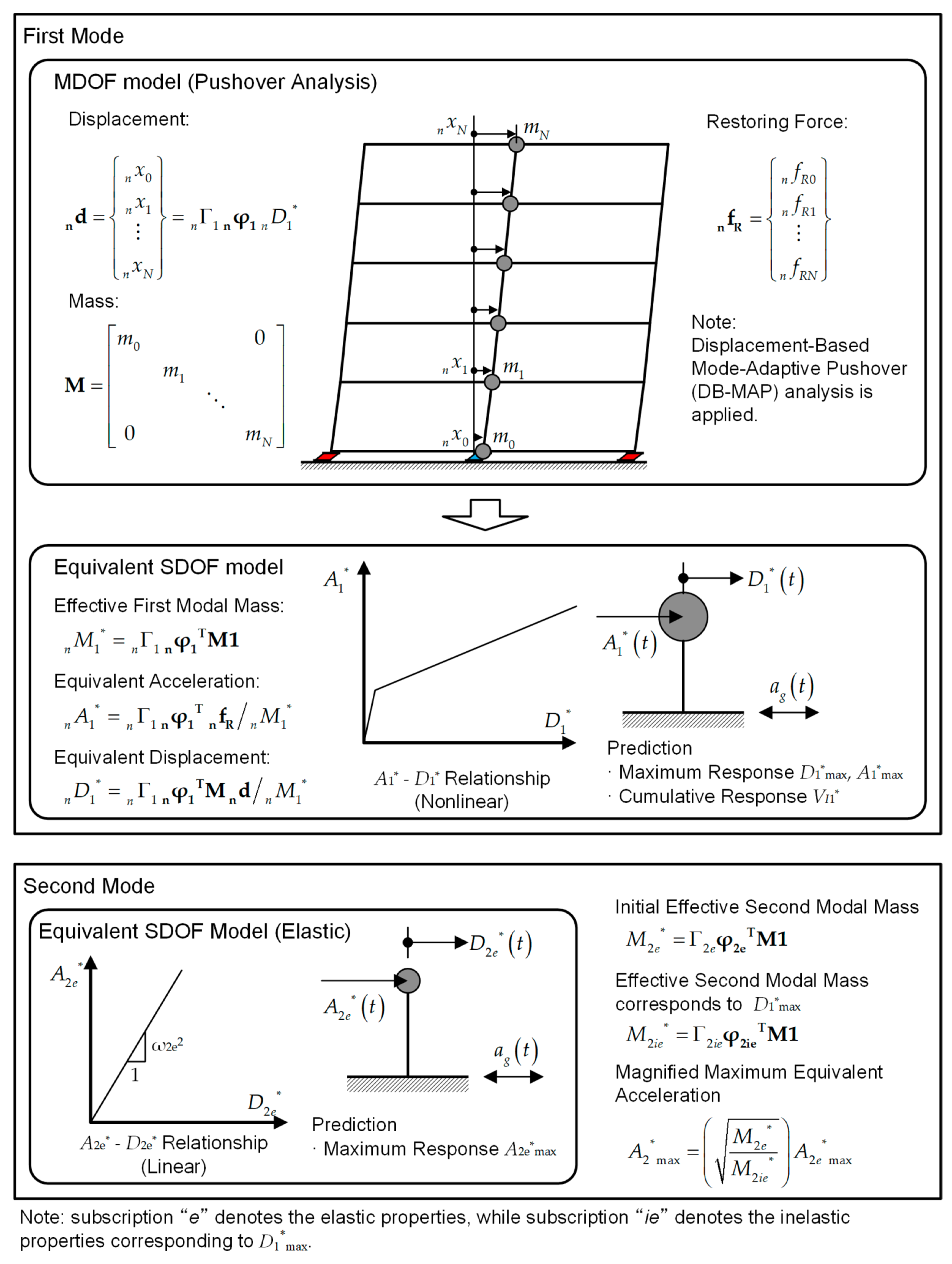
2.2. Outline of the Procedure
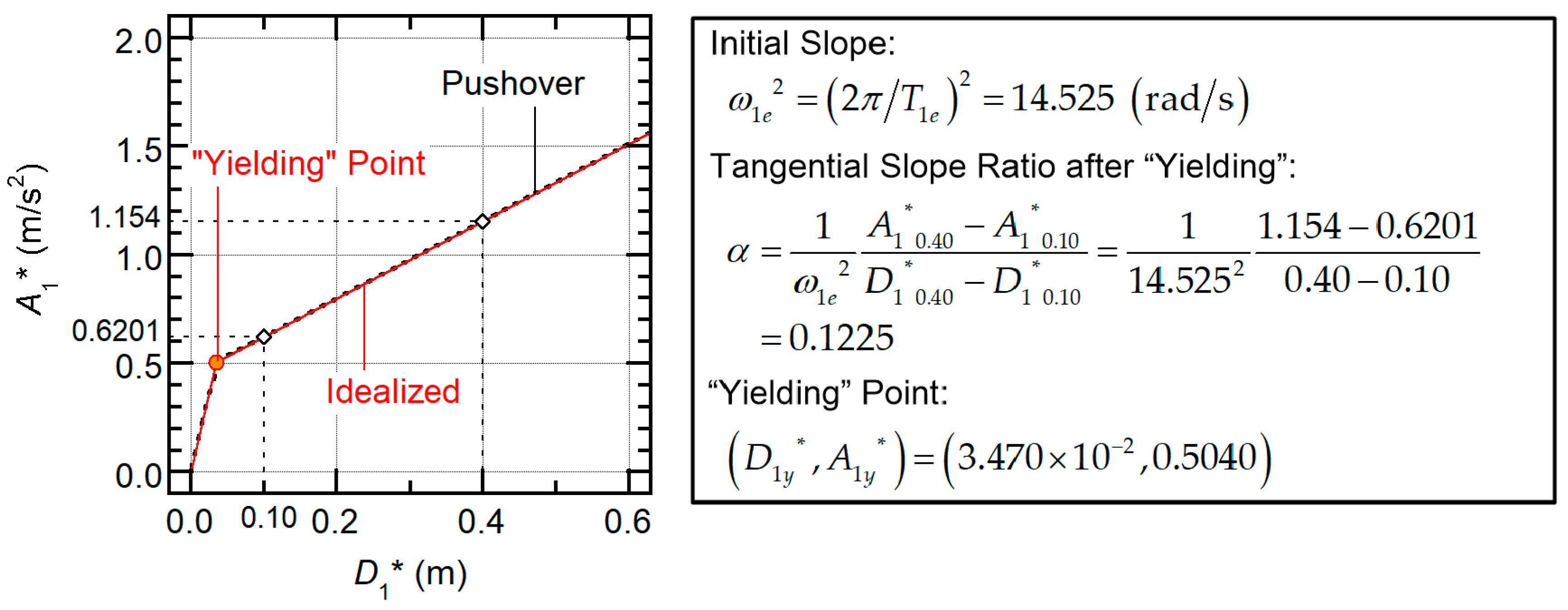
2.2.1. Step 1: Pushover Analysis of the Building Model (First Mode)
2.2.2. Step 2: Nonlinear Analysis of the Equivalent SDOF Model (First Mode)
2.2.3. Step 3: Prediction of Local Cumulative Response from First Mode
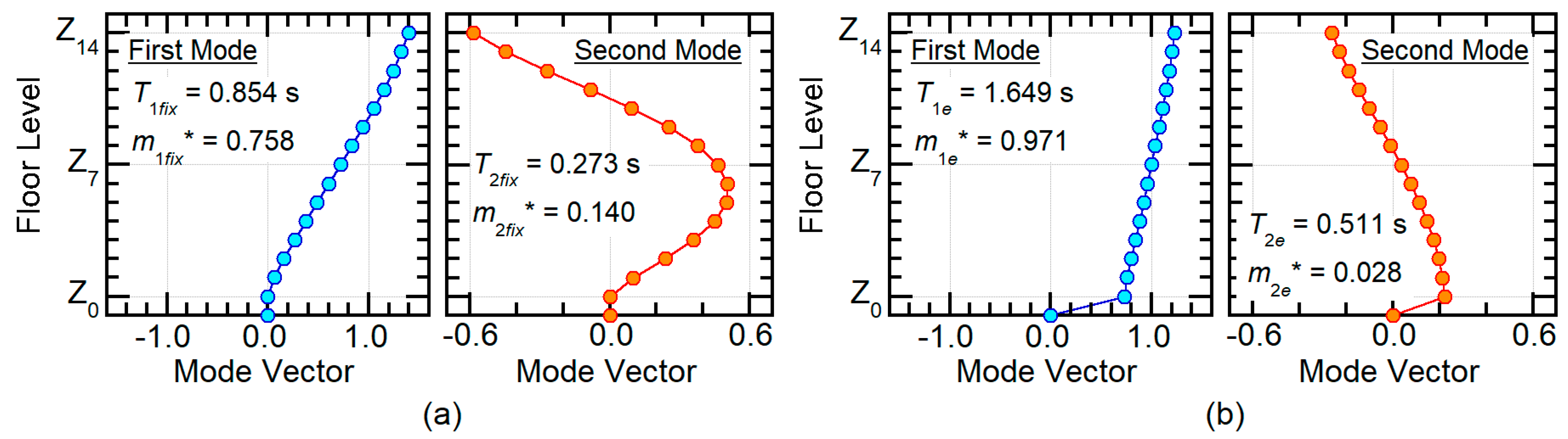
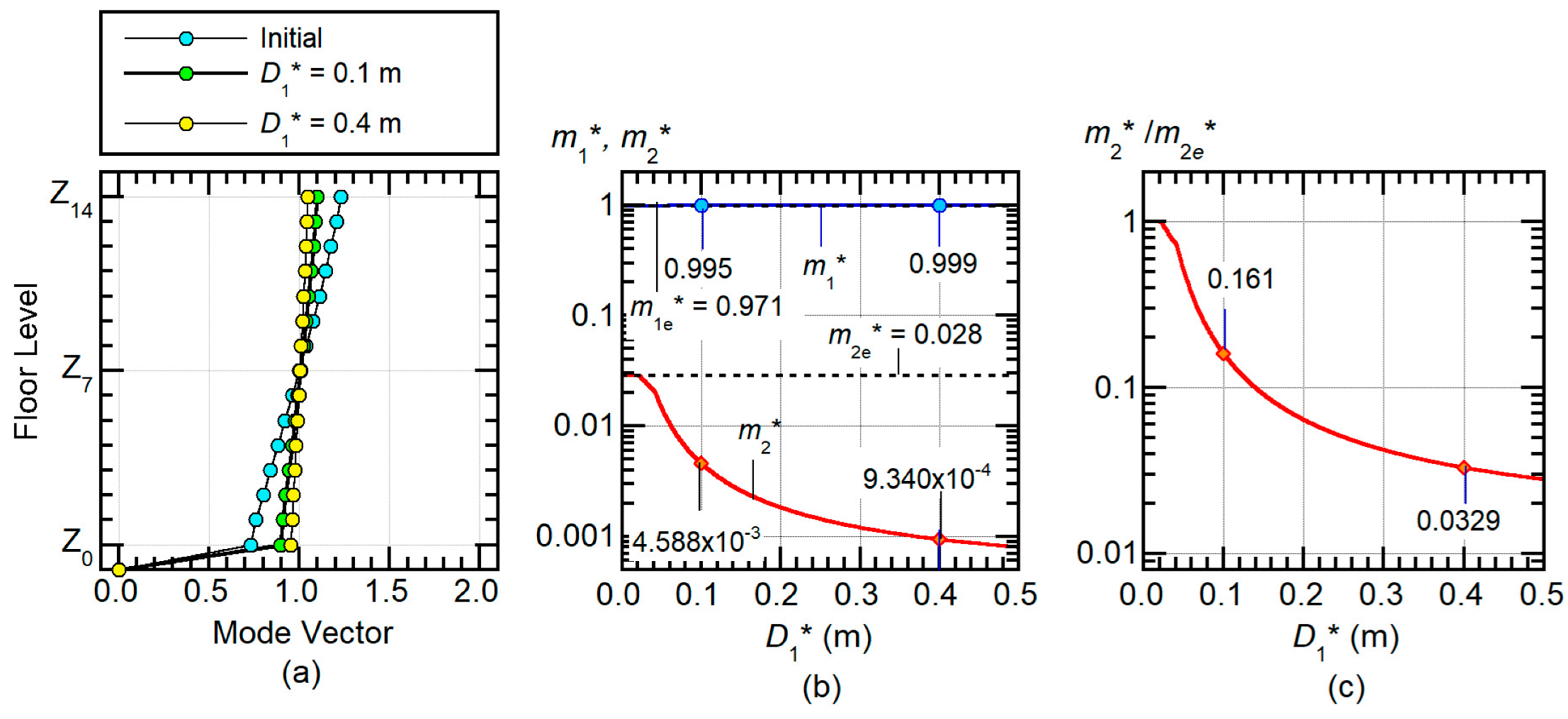
2.2.4. Step 4: Calculation of Equivalent SDOF Model Properties (Second Mode)
2.2.5. Step 5: Linear Analysis of Equivalent SDOF Model (Second Mode)
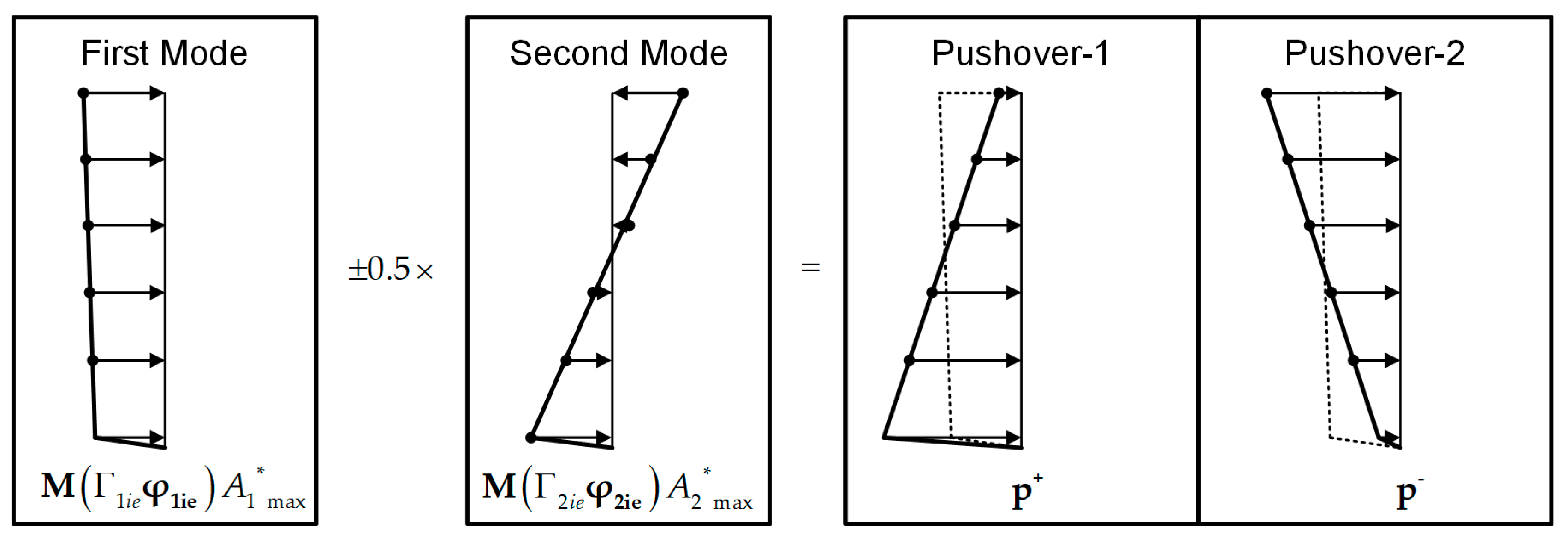
2.2.6. Step 6: Prediction of Local Maximum Response Considering the Contribution of the Second Mode
3. Building and Ground Motion Data
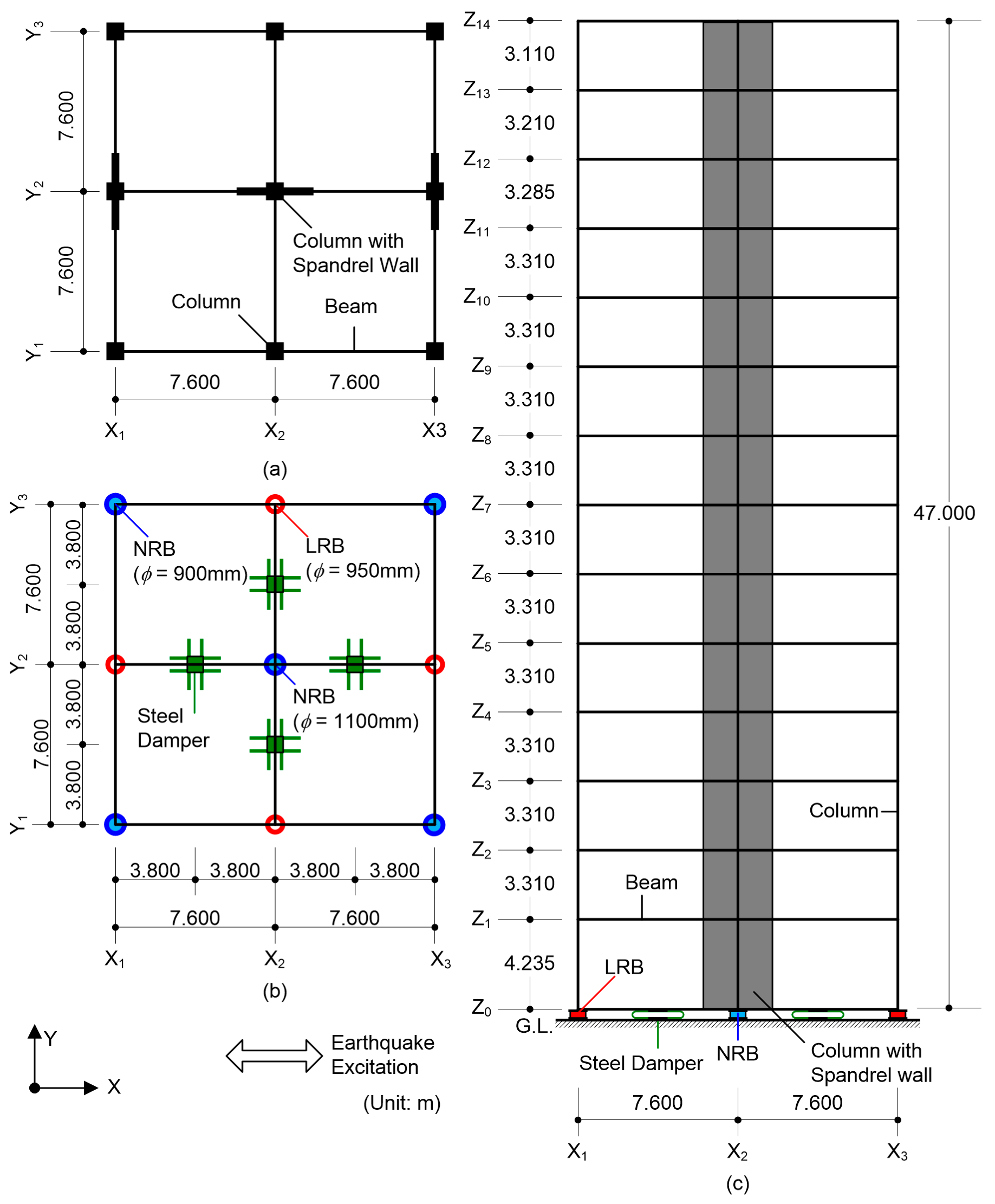
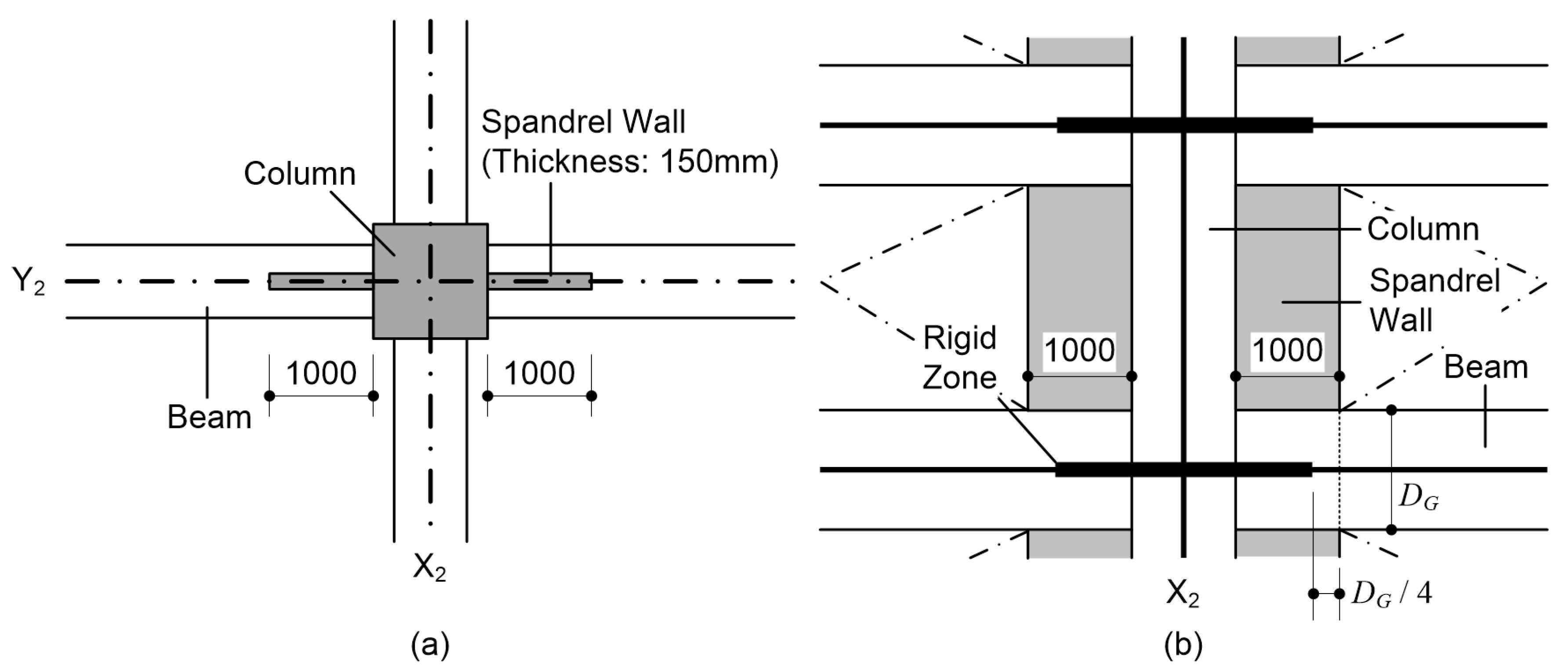
3.1. Building Data
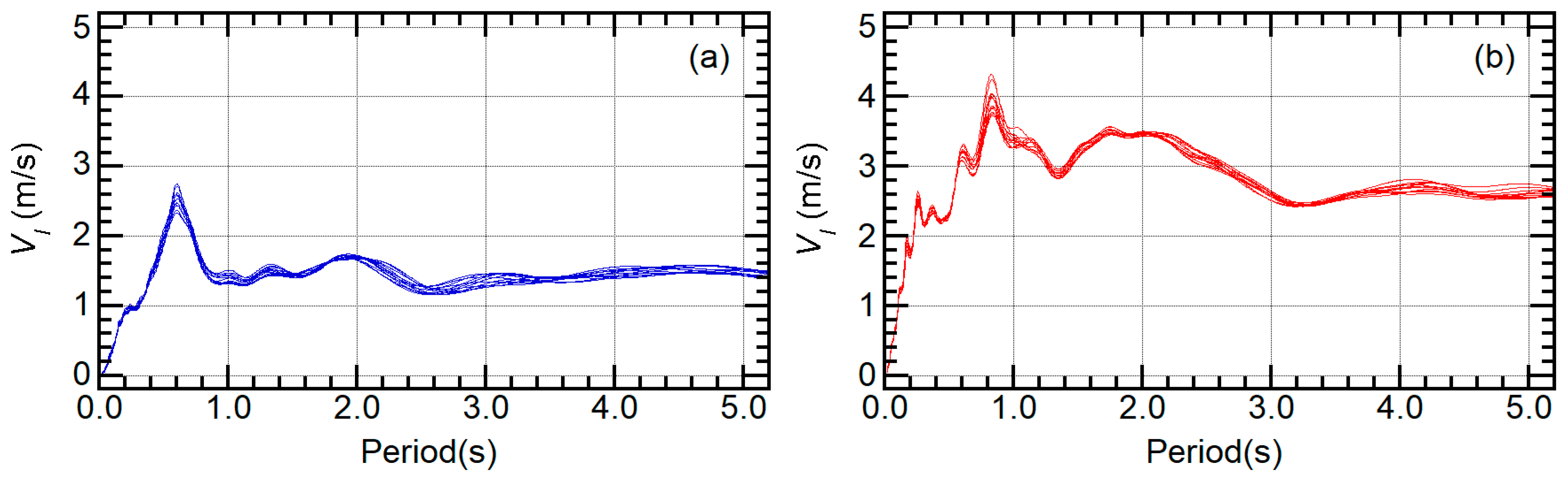
3.2. Ground Motion Data
3.3. Nonlinear Time-History Analysis Cases
4. Analysis Results
4.1. Pushover Analysis Results
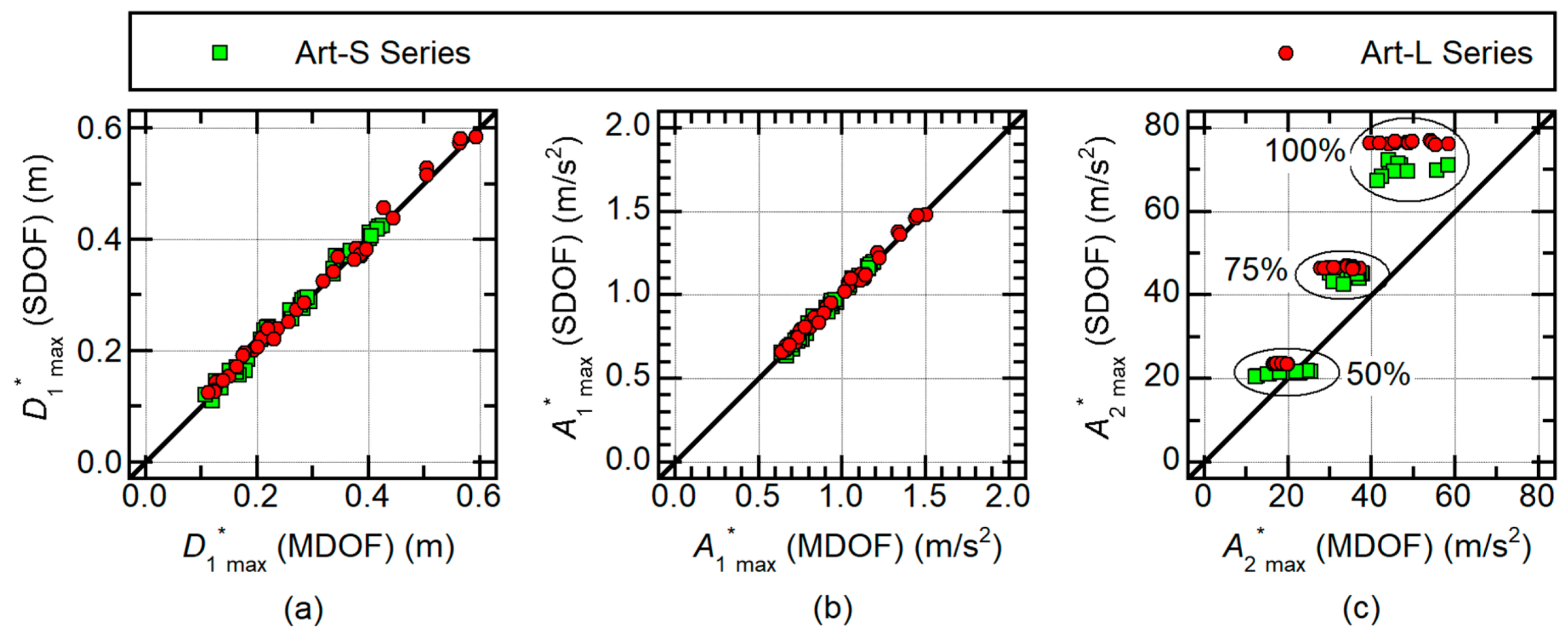
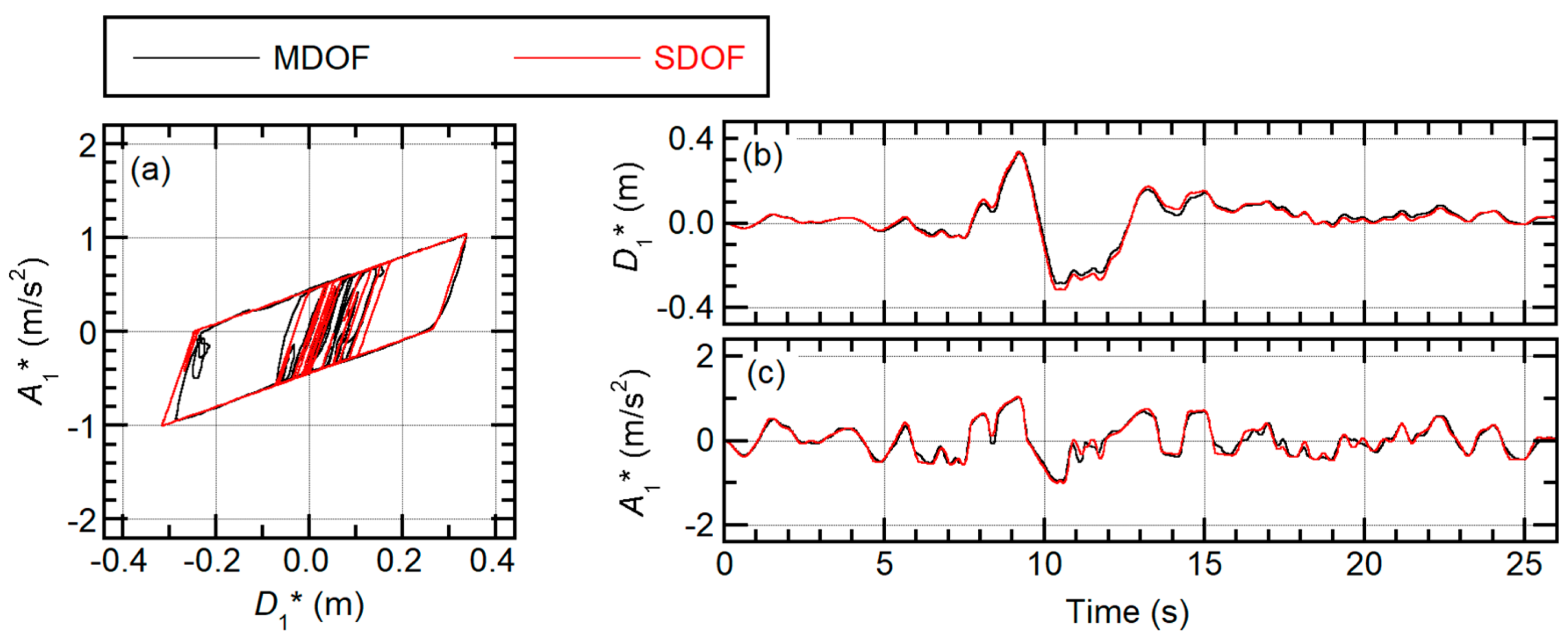
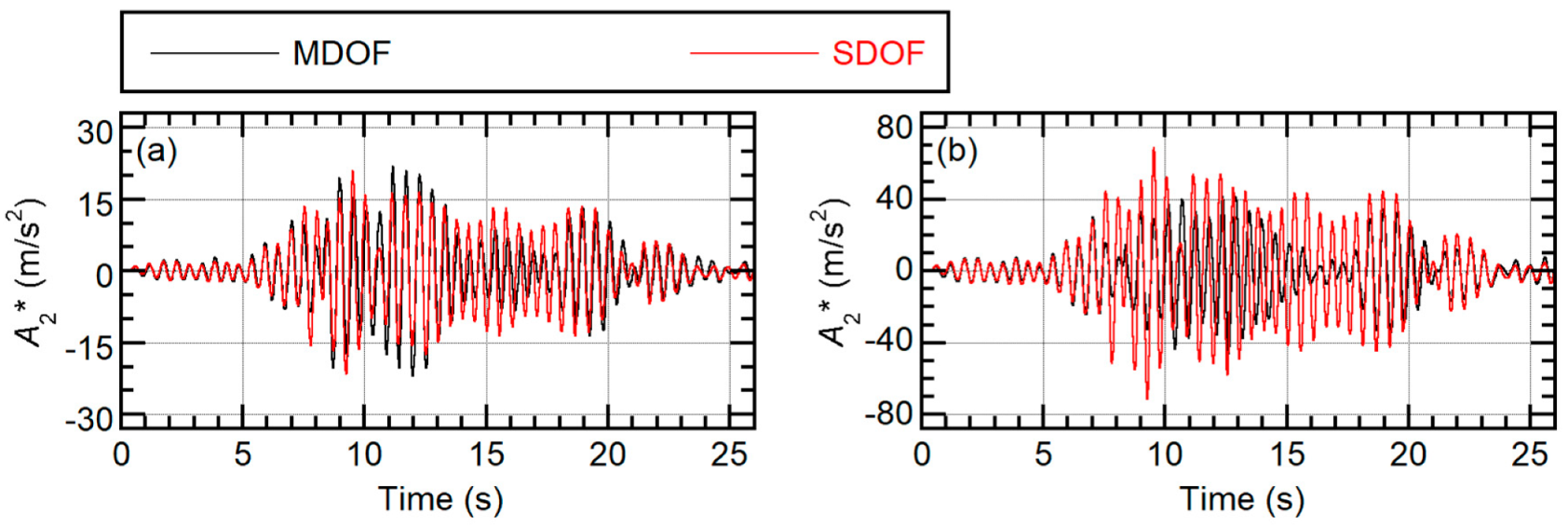
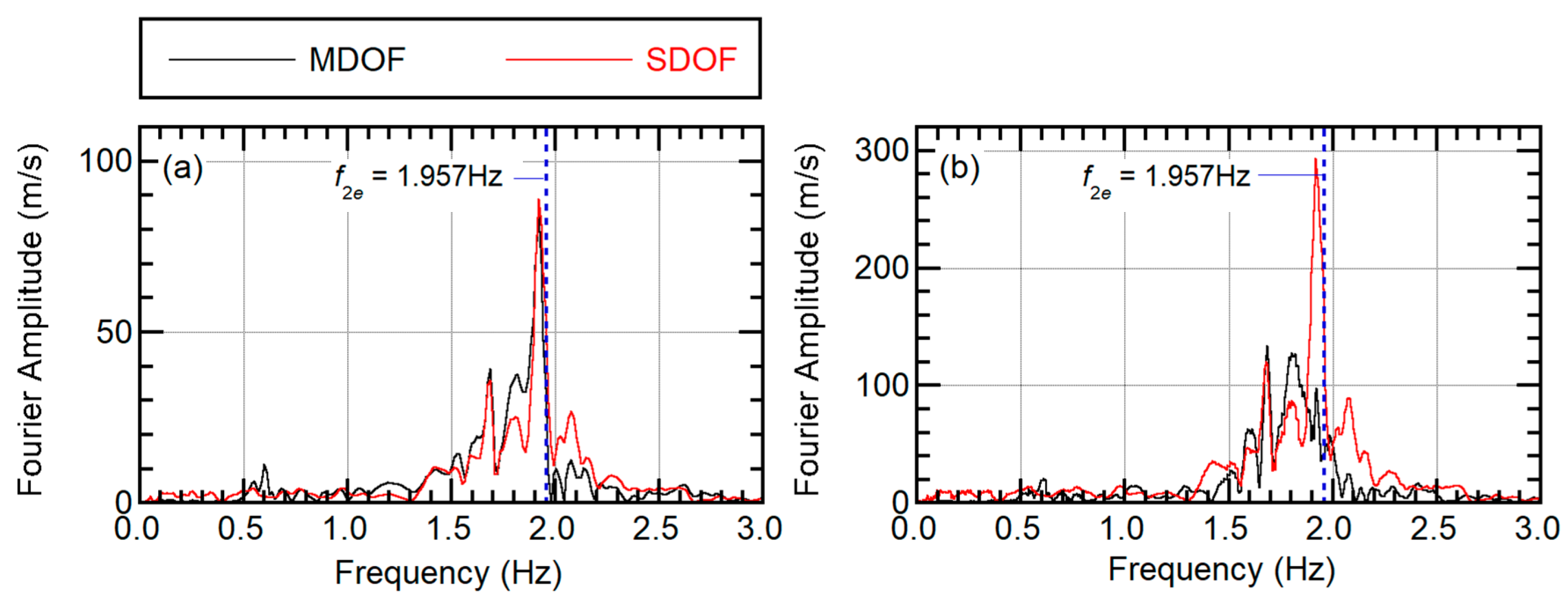
4.2. Validation of the Predicted Results
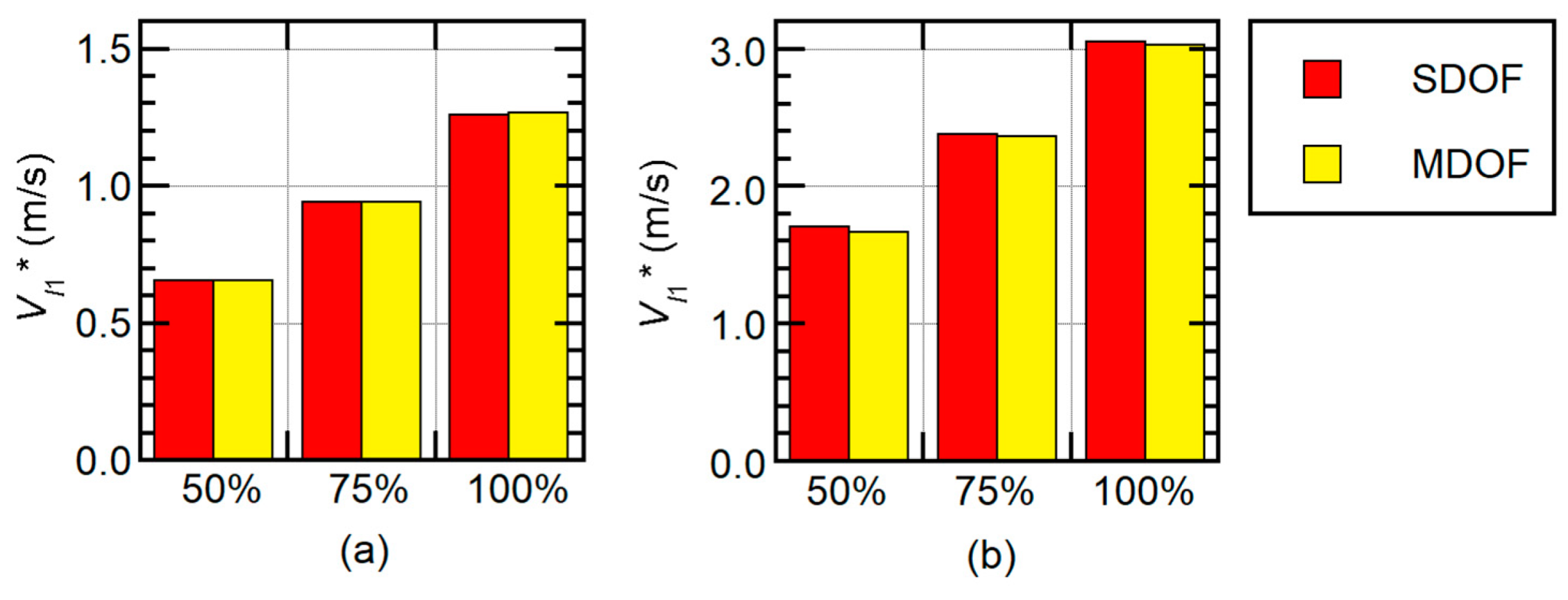
4.2.1. Maximum Floor Response
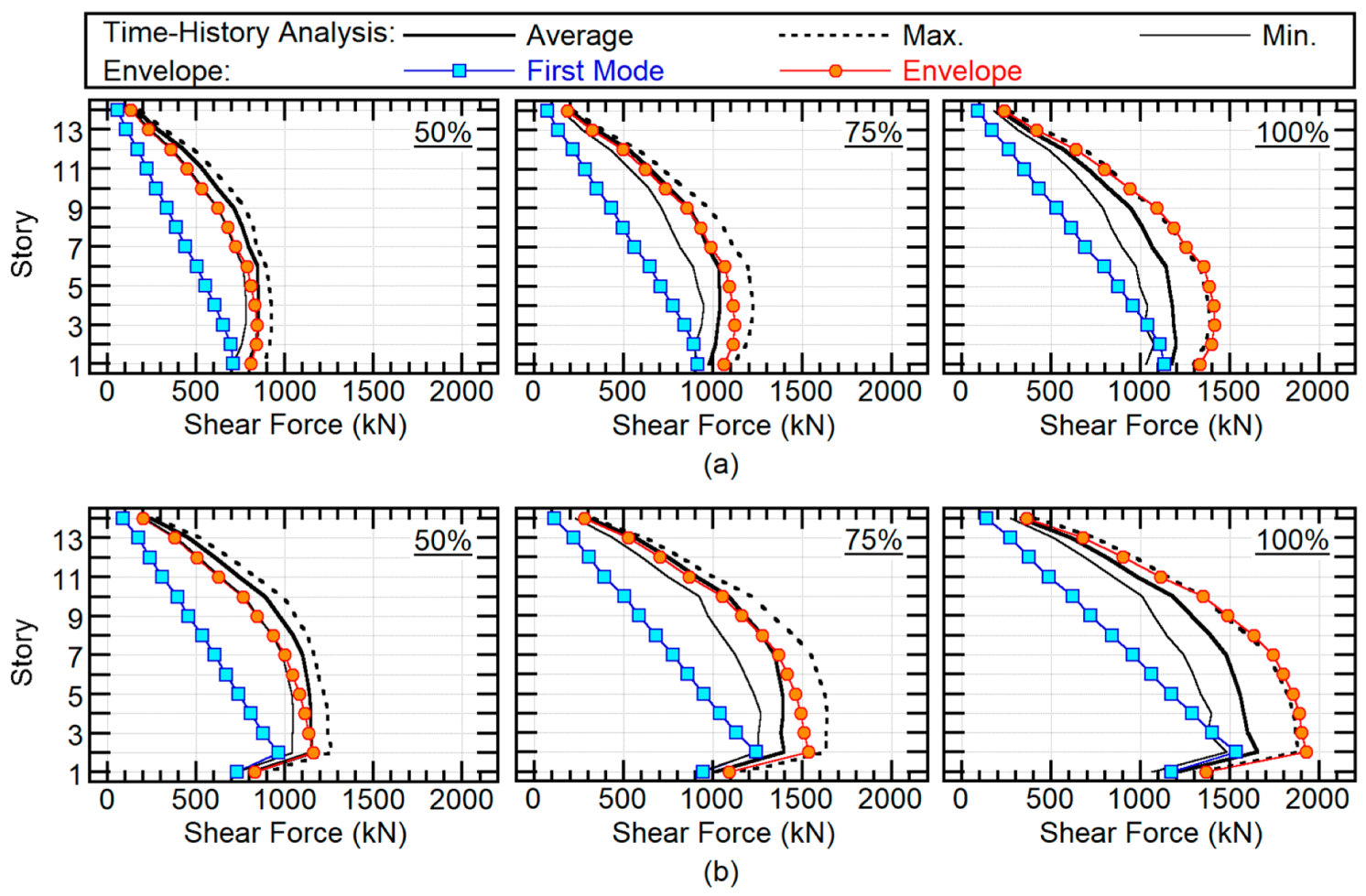
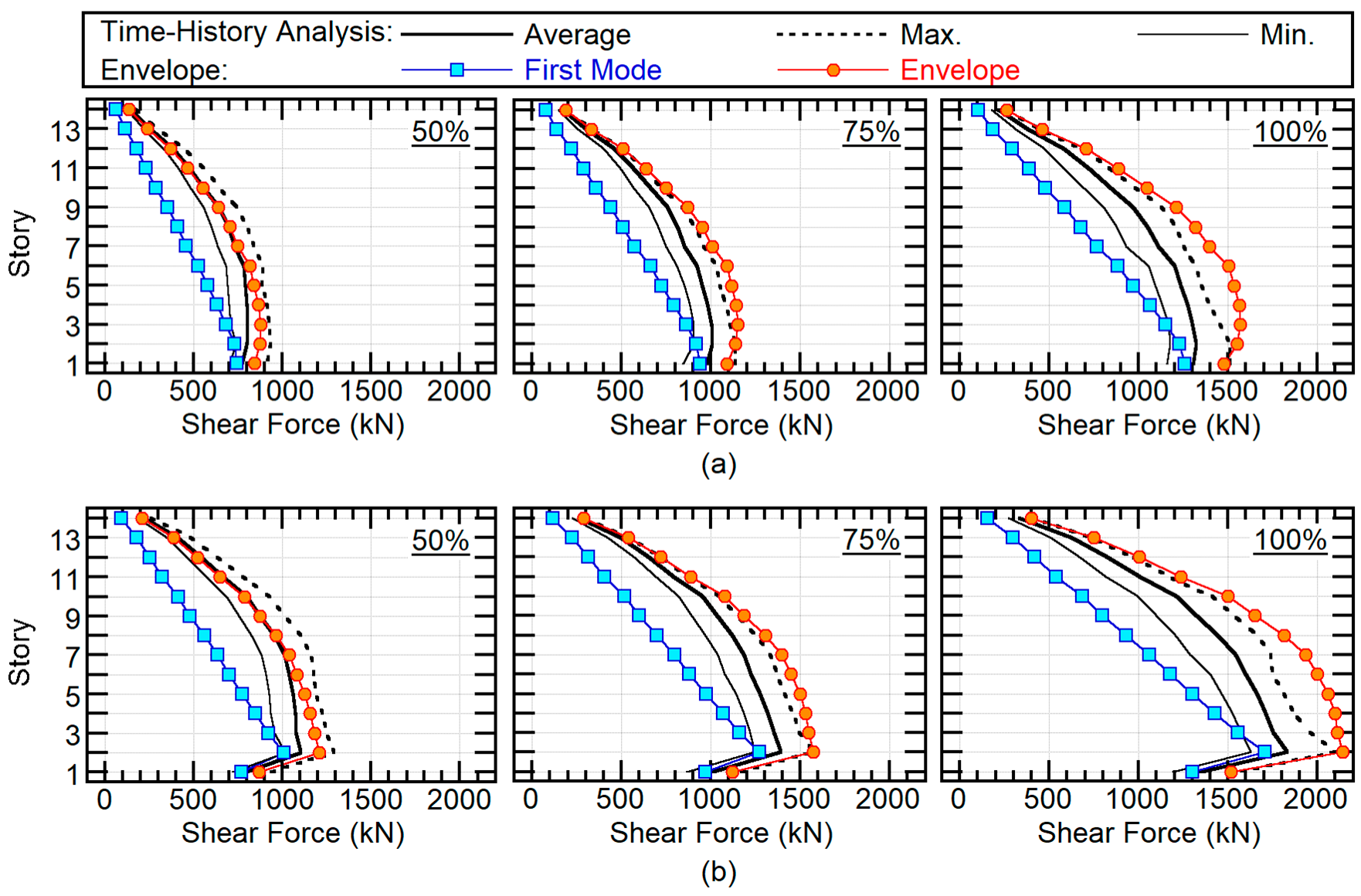
4.2.2. Maximum Shear Forces of Vertical Members
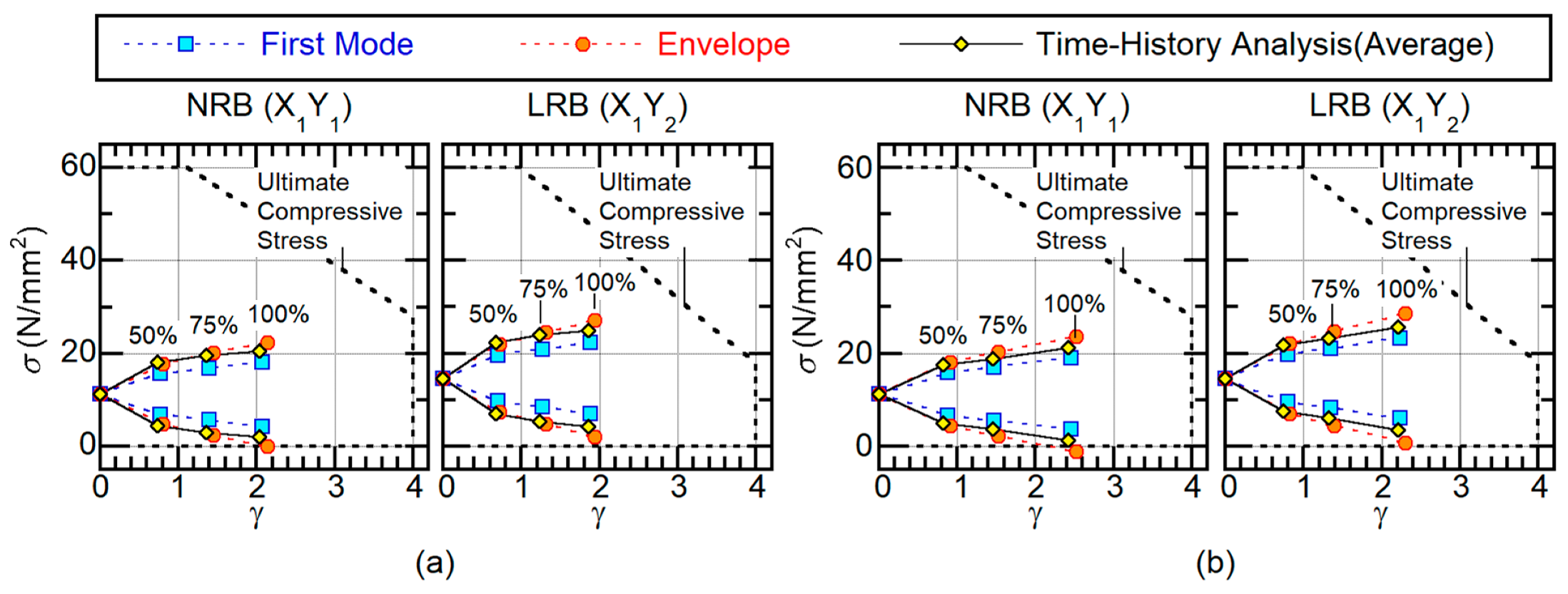
4.2.3. Maximum Response of Isolators
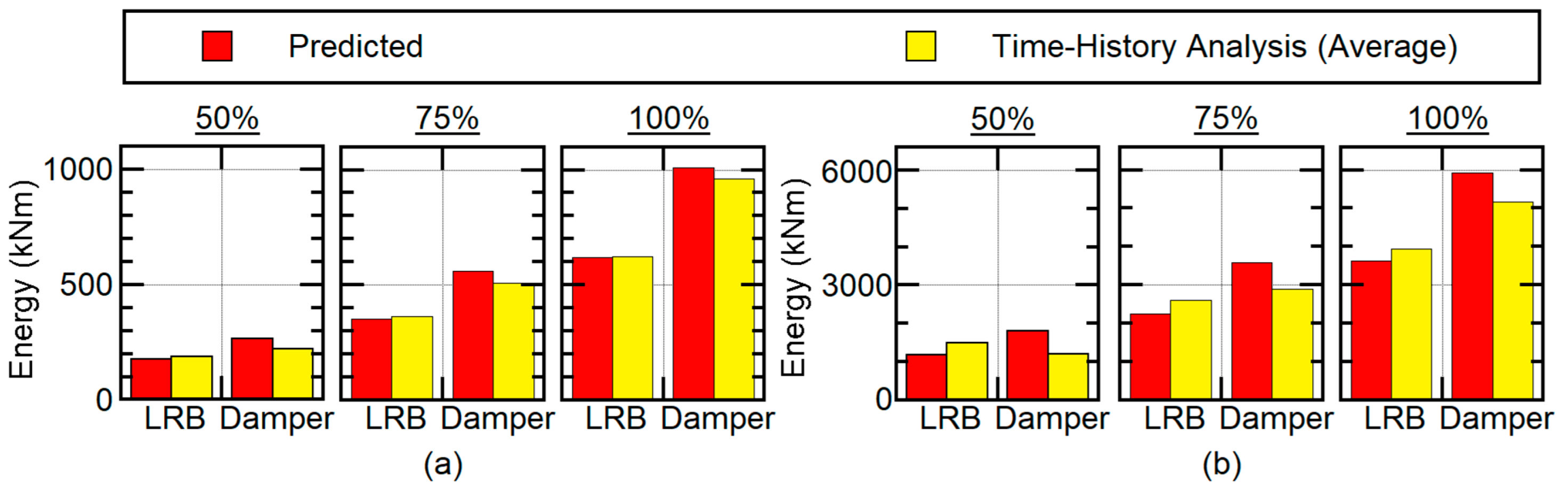
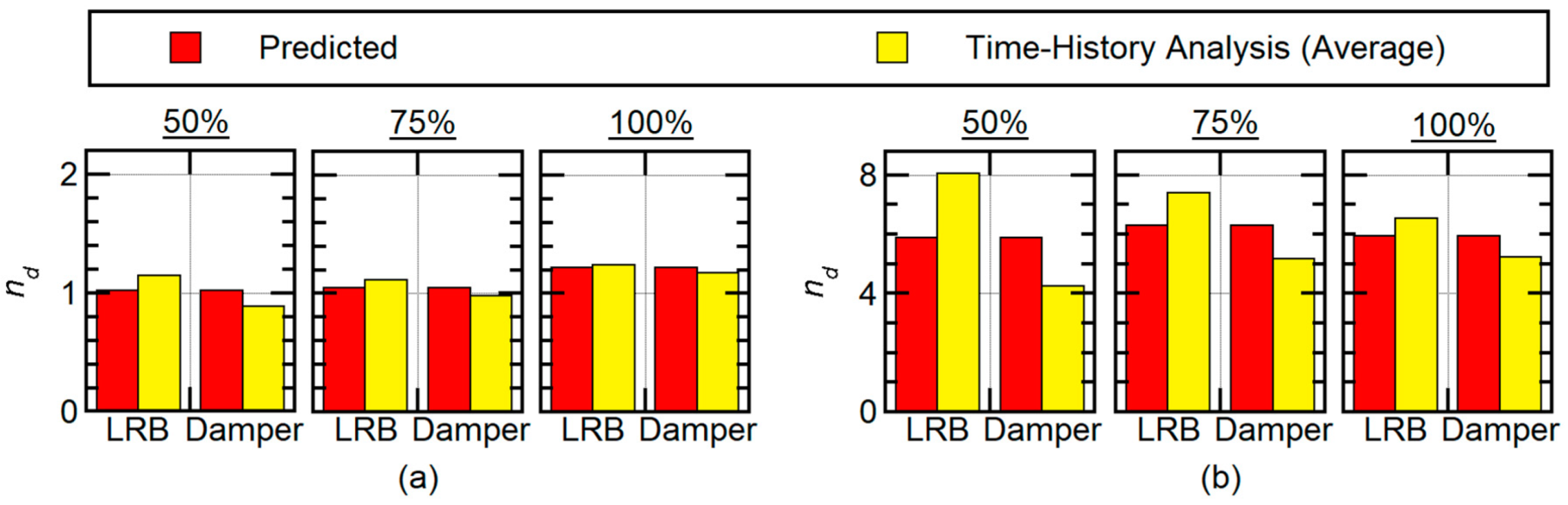
4.2.4. Cumulative Strain Energy of Isolators and Dampers
5. Discussion
5.1. Accuracy in Predicting Maximum Modal Responses
5.2. Accuracy in Predicting Cumulative Responses
6. Conclusions
- The consideration of the second modal response’s contribution is important to better predict the maximum floor acceleration and maximum shear forces of the vertical members in the superstructure. The predicted maximum response obtained by the proposed procedure is in good agreement with the nonlinear time-history analysis results.
- The cumulative strain energy of the isolators (LRBs) and dampers in the isolation layer can be satisfactorily predicted by considering only the first modal response. The reason for this is that the effective first modal mass is approximately 100% of the total mass.
- The maximum and cumulative response of the first mode is satisfactorily predicted using the equivalent SDOF model.
- The maximum equivalent acceleration of the second modal response is conservatively predicted by magnifying the linear analysis results of the equivalent SDOF model and considering the change in the equivalent second modal mass.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Magnification Factor for Equivalent Second Modal Acceleration
References
- Charleson, A.; Guisasola, A. Seismic Isolation for Architects; Routledge: London, UK; New York, NY, USA, 2017. [Google Scholar]
- Warn, G.P.; Ryan, K.L. A Review of seismic isolation for buildings: Historical development and research needs. Buildings 2012, 2, 300–325. [Google Scholar] [CrossRef]
- Kobayashi, M.; Koh, T. Modal coupling effects of mid-story isolated buildings. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Anajafi, H.; Medina, R.A. Comparison of the seismic performance of a partial mass isolation technique with conventional TMD and base-isolation systems under broad-band and narrow-band excitations. Eng. Struct. 2018, 158, 110–123. [Google Scholar] [CrossRef]
- Hashimoto, T.; Fujita, K.; Tsuji, M.; Takewaki, I. Innovative base-isolated building with large mass-ratio TMD at basement for greater earthquake resilience. Future Cities Environ. 2015, 1, 9. [Google Scholar] [CrossRef]
- Ordoñez, D.; Foti, D.; Bozzo, L. Comparative study of the inelastic response of base isolated buildings. Earthq. Eng. Struct. Dyn. 2003, 32, 151–164. [Google Scholar] [CrossRef]
- Kikuchi, M.; Black, C.J.; Aiken, I.D. On the response of yielding seismically isolated structures. Earthq. Eng. Struct. Dyn. 2008, 37, 659–679. [Google Scholar] [CrossRef]
- Cardone, D.; Flora, A.; Gesualdi, G. Inelastic response of RC frame buildings with seismic isolation. Earthq. Eng. Struct. Dyn. 2013, 42, 871–889. [Google Scholar] [CrossRef]
- Architectural Institute of JAPAN (AIJ). Design Recommendations for Seismically Isolated Buildings; Architectural Institute of Japan: Tokyo, Japan, 2016. [Google Scholar]
- Calvi, P.M.; Ruggiero, D.M. Earthquake-induced floor accelerations in base isolated structures. In Proceedings of the 16th World Conference on Earthquake Engineering, Santiago, Chile, 9–13 January 2017. [Google Scholar]
- Architectural Institute of JAPAN (AIJ). Structural Response and Performance for Long Period Seismic Ground Motion; Architectural Institute of Japan: Tokyo, Japan, 2007. (In Japanese) [Google Scholar]
- Takaoka, E.; Takenaka, Y.; Kondo, A.; Hikita, M.; Kitamura, H. Heat-mechanics interaction behavior of laminated rubber bearings under large and cyclic lateral deformation. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Konishi, Y.; Kawamura, N.; Terashima, M.; Kishiki, S.; Yamada, S.; Aiken, I.; Black, C.; Murakami, K.; Someya, T. Evaluation of the fatigue life and behavior characteristics of U-shaped steel dampers after extreme earthquake loading. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012. [Google Scholar]
- Kilar, V.; Koren, D. Usage of simplified N2 method for analysis of base isolated structures. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Kilar, V.; Koren, D. Simplified inelastic seismic analysis of base-isolated structures using N2 method. Earthq. Eng. Struct. Dyn. 2010, 39, 967–989. [Google Scholar] [CrossRef]
- Kilar, V.; Koren, D. Seismic behaviour of asymmetric base isolated structures with various distributions of isolators. Eng. Struct. 2009, 31, 910–921. [Google Scholar] [CrossRef]
- Koren, D.; Kilar, V. The applicability of the N2 method to the estimation of torsional effects in asymmetric base-isolated buildings. Earthq. Eng. Struct. Dyn. 2011, 40, 867–886. [Google Scholar] [CrossRef]
- Providakis, C.P. Pushover analysis of base-isolated steel–concrete composite structures under near-fault excitations. Soil Dyn. Earthq. Eng. 2008, 28, 293–304. [Google Scholar] [CrossRef]
- Faal, H.N.; Poursha, M. Applicability of the N2, extended N2 and modal pushover analysis methods for the seismic evaluation of base-isolated building frames with lead rubber bearings (LRBs). Soil Dyn. Earthq. Eng. 2017, 98, 84–100. [Google Scholar] [CrossRef]
- Bhandari, M.; Bharti, S.D.; Shrimali, M.K.; Datta, T.K. Assessment of proposed lateral load patterns in pushover analysis for base-isolated frames. Eng. Struct. 2018, 175, 531–548. [Google Scholar]
- Bhandari, M.; Bharti, S.D.; Shrimali, M.K.; Datta, T.K. Applicability of capacity spectrum method for base-isolated building frames at different performance points. J. Eqrthq. Eng. 2018, 1–30. Available online: www.tandfonline.com (accessed on 30 June 2019). [CrossRef]
- Fajfar, P. A nonlinear analysis method for performance-based seismic design. Earthq. Spectra 2000, 16, 573–592. [Google Scholar] [CrossRef]
- Kreslin, M.; Fajfar, P. The extended N2 method considering higher mode effects in both plan and elevation. Bull. Earthq. Eng. 2002, 10, 561–582. [Google Scholar] [CrossRef]
- Chopra, A.K.; Goel, R.K. A modal pushover analysis procedure for estimating seismic demands for buildings. Earthq. Eng. Struct. Dyn. 2002, 31, 561–582. [Google Scholar] [CrossRef]
- Chopra, A.K.; Goel, R.K.; Chintanapakdee, C. Evaluation of a modified MPA procedure assuming higher modes as elastic to estimate seismic demands. Earthq. Spectra 2004, 20, 757–778. [Google Scholar] [CrossRef]
- Fujii, K. Prediction of the maximum seismic member force in a superstructure of a base-isolated frame building by using pushover analysis. Buildings 2019, 9, 201. [Google Scholar] [CrossRef]
- Fujii, K. Prediction of the largest peak nonlinear seismic response of asymmetric buildings under bidirectional excitation using pushover analyses. Bull. Earthq. Eng. 2014, 12, 909–938. [Google Scholar] [CrossRef]
- Fujii, K. Pushover-based seismic capacity evaluation of Uto city hall damaged by the 2016 Kumamoto earthquake. Buildings 2019, 9, 140. [Google Scholar] [CrossRef]
- Akiyama, H. Earthquake–Resistant Limit–State Design for Buildings; University of Tokyo Press: Tokyo, Japan, 1985. [Google Scholar]
- Building Research Institute (BRI). BRI Strong Motion Network, Strong Motion Report, 2011/03/11 14:46 Off Sanriku (M = 9.0, h = 24 km). Available online: http://smo.kenken.go.jp/index.php/report/201103111446 (accessed on 4 August 2019).
- Bridgestone Corporation. Seismic Isolation Product Line-Up Version 2017 Vol. 1. Available online: https://www.bridgestone.com/products/diversified/antiseismic_rubber/pdf/catalog_201710.pdf (accessed on 3 August 2019).





© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fujii, K.; Mogi, Y.; Noguchi, T. Predicting Maximum and Cumulative Response of A Base-isolated Building Using Pushover Analysis. Buildings 2020, 10, 91. https://doi.org/10.3390/buildings10050091
Fujii K, Mogi Y, Noguchi T. Predicting Maximum and Cumulative Response of A Base-isolated Building Using Pushover Analysis. Buildings. 2020; 10(5):91. https://doi.org/10.3390/buildings10050091
Chicago/Turabian StyleFujii, Kenji, Yoshiyuki Mogi, and Takumi Noguchi. 2020. "Predicting Maximum and Cumulative Response of A Base-isolated Building Using Pushover Analysis" Buildings 10, no. 5: 91. https://doi.org/10.3390/buildings10050091
APA StyleFujii, K., Mogi, Y., & Noguchi, T. (2020). Predicting Maximum and Cumulative Response of A Base-isolated Building Using Pushover Analysis. Buildings, 10(5), 91. https://doi.org/10.3390/buildings10050091




