A New Proposal for the Shear Strength Prediction of Beams Longitudinally Reinforced with Fiber-Reinforced Polymer Bars
Abstract
1. Introduction
2. Available Models and Design Recommendations
3. Experimental Database
4. Verification of the Available Models and Design Recommendations
5. Proposed Model for Estimating the Shear Capacity of Support Zones Reinforced Longitudinally with FRP Bars without Shear Reinforcement
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bywalski, C.; Drzazga, M.; Kamiński, M.; Kaźmierowski, M. Analysis of calculation methods for bending concrete elements reinforced with FRP bars. Arch. Civ. Mech. Eng. 2016, 16, 901–912. [Google Scholar] [CrossRef]
- Li, G.; Zhao, J.; Wang, Z. Fatigue Behavior of Glass Fiber-Reinforced Polymer Bars after Elevated Temperatures Exposure. Materials 2018, 11, 1028. [Google Scholar] [CrossRef] [PubMed]
- Hoła, J.; Bień, J.; Sadowski, L.; Schabowicz, K. Non-destructive and semi-destructive diagnostics of concrete structures in assessment of their durability. Bull. Pol. Acad. Sci. Tech. Sci. 2015, 63, 87–96. [Google Scholar] [CrossRef]
- Nikoo, M.; Sadowski, Ł.; Nikoo, M. Prediction of the corrosion current density in reinforced concrete using a self-organizing feature map. Coatings 2017, 7, 160. [Google Scholar] [CrossRef]
- ACI Committee 440. ACI 440.1R-15—Guide for the Design and Construction of Structural Concrete Reinforced with Fiber-Reinforced Polymer (FRP) Bars; American Concrete Institute: Farmington Hills, MI, USA, 2015; ISBN 978-1-942727-10-1. [Google Scholar]
- Kosior-Kazberuk, M.; Wasilczyk, R. Ugięcia i zarysowanie betonowych belek zbrojonych prętami HFRP (Deflections and cracking of concrete beams reinforced with HFRP bars). Przegląd Bud. 2019, 1, 24–28. (In Polish) [Google Scholar]
- FIB Task Group 9.3. FRP: Reinforcement for Concrete Structures. FRP Reinforcement in RC Structures; Technical Report, Bulletin 40; International Federation for Structural Concrete (FIB): Lausanne, Switzerland, 2007; ISBN 978-2-88394-080-2. [Google Scholar]
- Canadian Standards Association. CAN/CSA S806-12—Design and Construction of Building Components with Fiber Reinforced Polymers; Canadian Standards Association: Toronto, ON, Canada, 2012; ISBN 978-1-554919-31-4. [Google Scholar]
- Japan Society of Civil Engineering (JSCE). Recommendation for Design and Construction of Concrete Structures Using Continuous Fiber Reinforcing Materials; Japan Society of Civil Engineering: Tokyo, Japan, 1997. [Google Scholar]
- National Research Council. Guide for the Design and Construction of Concrete Structures Reinforced with Fiber-Reinforced Polymer Bars—CNR-DT 206/2006; National Research Council: Rome, Italy, 2007. [Google Scholar]
- Drzazga, M. Stany graniczne betonowych belek zbrojonych na ścinanie prętami z włókien szklanych, poddanych działaniu obciążeń doraźnych (The Limit States of Concrete Beams Reinforced with Glass Fiber Reinforced Polymer Shear Reinforcement, Subject to Short Term Load). Ph.D. Thesis, Wrocław University of Science and Technology, Wrocław, Poland, July 2019. (In Polish). [Google Scholar]
- Kosior-Kazberuk, M.; Krassowska, J. Failure mode in shear of steel fiber reinforced concrete beams. In Proceedings of the MATBUD’2018—8th Scientific-Technical Conference on Material Problems in Civil Engineering, June 2018, Cracow, Poland, 25–27 June 2018. [Google Scholar] [CrossRef]
- Yang, K.H.; Mun, J.H. Cyclic Flexural and Shear Performances of Beam Elements with Longitudinal Glass Fiber Reinforced Polymer (GFRP) Bars in Exterior Beam-Column Connections. Appl. Sci. 2018, 8, 2353. [Google Scholar] [CrossRef]
- Bywalski, C.; Drzazga, M.; Kamiński, M.; Kaźmierowski, M. Shear Behavior of Concrete Beams Reinforced With A New Type of Glass Fiber Reinforced Polymer Reinforcement: Experimental Study. Materials 2020, 13, 1159. [Google Scholar] [CrossRef] [PubMed]
- Tottori, S.; Wakui, H. Shear capacity of RC and PC beams using FRP reinforcement. ACI Spec. Publ. 1993, 138, 615–632. [Google Scholar] [CrossRef]
- Michaluk, C.R.; Rizkalla, S.H.; Tadros, G.; Benmokrane, B. Flexural behaviour of one-way slabs reinforced by fibre reinforced plastic reinforcement. ACI Struct. J. 1998, 95, 353–365. [Google Scholar] [CrossRef]
- Deitz, D.H.; Harik, I.E.; Gersund, H. One-way slabs reinforced with Glass Fiber Reinforced Polymer reinforcing bars. In Proceedings of the 4th International Symposium Fiber-Reinforced Polymer (FRP) Reinforcement for Concrete Structures, Michigen, MI, USA, 31 October–5 November 1999. [Google Scholar]
- El-Sayed, A.; El-Salakawy, E.; Benmokrane, B. Shear strength of concrete beams reinforced with FRP bars: Design method. In Proceedings of the 7th International Symposium on Fiber Reinforced Polymer Reinforcement for Concrete Structures, Kansas City, MS, USA, 6–9 November 2005. [Google Scholar]
- Wegian, F.M.; Abdalla, H.A. Shear capacity of concrete beams reinforced with fiber reinforced polymers. Compos. Struct. 2005, 71, 130–138. [Google Scholar] [CrossRef]
- Nehdi, M.; El Chabi, H.; Aly Said, A. Proposed shear design equations for FRP reinforced concrete beams based on genetic algorithms approach. J. Mater. Civ. Eng. 2007, 19, 1033–1042. [Google Scholar] [CrossRef]
- Hoult, N.A.; Sherwood, E.G.; Bentz, E.C.; Collins, M.P. Does the use of FRP reinforcement change the one-way shear behavior of reinforced concrete slabs? J. Compos. Constr. 2008, 12, 125–133. [Google Scholar] [CrossRef]
- Razaqpur, A.G.; Spadea, S. Shear strength of reinforced concrete elements brackets with FRP. In Proceedings of the AIAS, 39th National Congress of Italian Association of Stress Analysis, Calabria, Italy, 7–10 September 2010. [Google Scholar]
- Alam, M.S. Influence of different parameters on shear strength of FRP reinforced concrete beams without web reinforcement. Ph.D. Thesis, University of Newfoundland, St. John’s, NL, Canada, June 2010. [Google Scholar]
- Kara, I.F. Prediction of shear strength of FRP-reinforced concrete beams without stirrups based on genetic programming. Adv. Eng. Softw. 2011, 42, 295–304. [Google Scholar] [CrossRef]
- Kurth, M. Zum Querkrafttragverhalten von Betonbauteilen mit Faserverbundkunststoff-Bewehrung (Shear Behaviour of Concrete Members with Fibre Reinforced Polymers as Internal Reinforcement). Ph.D. Thesis, Rheinisch-Westfälische Technische Hochschule Aachen, Aachen, Germany, December 2012. (In German). [Google Scholar]
- Jang, H.S.; Kim, C.H. Concrete shear strength of normal and lightweight concrete beams reinforced with FRP bars. J. Compos. Constr. 2014, 18, 483–492. [Google Scholar] [CrossRef]
- Lignola, G.P.; Nardone, F.; Prota, A.; Manfredi, G. Assessment of design equation for the shear capacity of FRP-RC members. In Proceedings of the 6th International Conference on Fiber Reinforced Polymer (FRP) Composites in Civil Engineering, Rome, Italy, 5 September 2015. [Google Scholar]
- Valivonis, J.; Budvytis, B.; Atutis, M.; Atutis, E.; Juknevičius, L. Study of shear resistance of fiber-reinforced polymer-reinforced concrete beams. Adv. Mech. Eng. 2015, 7, 1–17. [Google Scholar] [CrossRef]
- Thomas, J.; Ramadass, S. Design for shear strength of concrete beams longitudinally reinforced with GFRP bars. Struct. Eng. Mech. 2015, 53, 41–55. [Google Scholar] [CrossRef]
- Hamid, N.A.A.; Thamrin, R.; Ibrahim, A.; Hamid, H.A.; Salleh, N.; Jamellodin, Z.; Majid, M.A.; Khalid, N.H.A.K. Shear strength prediction for concrete beams reinforced with GFRP bars. In Proceedings of the International Symposium on Civil and Environmental Engineering 2016, Wuhan, China, 20–21 December 2016. [Google Scholar]
- European Committee for Standardization. Eurocode 2—Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings; EN 1992-1-1:2004; European Standard: Brussels, Belgium, 2004. [Google Scholar]
| Algorithm | Shear Strength of Member without Shear Reinforcement | |
|---|---|---|
| Tottori et al. [15] | (1) | |
| JSCE-97 [9] | (2) | |
| Michaluk et al. [16] | (3) | |
| Deitz et al. [17] | (4) | |
| El-Sayed et al. [18] | (5) | |
| Wegian et al. [19] | (6) | |
| CNR DT 203/2006 [10] | ; ; | (7) |
| Nehdi et al. [20] | (8) | |
| Hoult et al. [21] | ; ; | (9) |
| Razaqpur et al. [22] | ; ; | (10) |
| Alam [23] | (11) | |
| Kara [24] | (12) | |
| CSA S806-12 [8] | ; ; ; ; ; ; | (13) |
| Kurth [25] | ; ; in (mm) | (14) |
| Jang et al. [26] | (15) | |
| Lignola et al. [27] | ; in (mm); | (16) |
| ACI 440.1R-15 [5] | (17) | |
| Valivonis et al. [28] | ; | (18) |
| Thomas et al. [29] | (19) | |
| Hamid et al. [30] | (20) | |
| Number of Support Zones | 310 | ||||
|---|---|---|---|---|---|
| Properties | Min | Max | Average | COV1 (%) | |
| bw | (mm) | 89 | 1000 | 251 | 68 |
| h | (mm) | 100 | 1000 | 318 | 51 |
| d | (mm) | 73 | 937 | 270 | 54 |
| a | (mm) | 200 | 3055 | 907 | 53 |
| a/d | (–) | 0.8 | 12.5 | 3.7 | 43 |
| fc | (MPa) | 20 | 93 | 44 | 39 |
| ρf | (%) | 0.12 | 11.57 | 1.35 | 134 |
| Efl | (MPa) | 29,400 | 192,000 | 73,408 | 59 |
| Longitudinal reinforcement material | (–) | AFRP, BFRP, CFRP, GFRP | |||
| Vtest | (N) | 9000 | 291,300 | 62,490 | 85 |
| ACI 440.1R-15 [5] | CSA S806-12 [8] | |
| Arithmetic mean | 2.20 | 1.18 |
| Parameter X (inverse of regression curve slope) | 2.20 | 1.47 |
| Coefficient of variation (COV) (%) | 63.38 | 43.18 |
| Mean absolute percentage error (MAPE) (%) | 45.88 | 20.61 |
| Percentage of beams with overestimated strength (%) | 0.97 | 39.03 |
| Theoretical concrete shear strength versus experimental concrete shear strength | 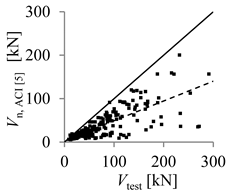 | 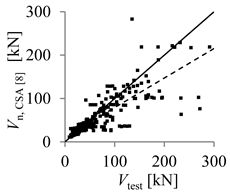 |
| JSCE-97 [9] | CNR-DT 203/2006 [10] | |
| Arithmetic mean | 1.61 | 0.89 |
| Parameter X (inverse of regression curve slope) | 2.03 | 1.38 |
| Coefficient of variation (COV) (%) | 62.86 | 62.39 |
| Mean absolute percentage error (MAPE) (%) | 28.29 | 56.32 |
| Percentage of beams with overestimated strength (%) | 10.32 | 77.74 |
| Theoretical concrete shear strength versus experimental concrete shear strength | 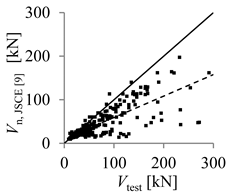 | 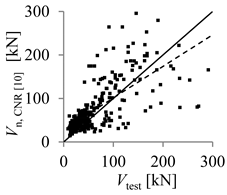 |
| Tottori et al. [15] | Michaluk et al. [16] | |
| Arithmetic mean | 1.20 | 3.26 |
| Parameter X (inverse of regression curve slope) | 1.57 | 3.87 |
| Coefficient of variation (COV) (%) | 36.98 | 73.26 |
| Mean absolute percentage error (MAPE) (%) | 19.38 | 59.09 |
| Percentage of beams with overestimated strength (%) | 30.00 | 10.97 |
| Theoretical concrete shear strength versus experimental concrete shear strength |  | 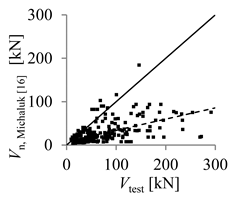 |
| Deitz et al. [17] | El-Sayed et al. [18] | |
| Arithmetic mean | 1.09 | 0.97 |
| Parameter X (inverse of regression curve slope) | 1.29 | 1.09 |
| Coefficient of variation (COV) (%) | 73.26 | 72.67 |
| Mean absolute percentage error (MAPE) (%) | 64.15 | 49.49 |
| Percentage of beams with overestimated strength (%) | 51.29 | 75.48 |
| Theoretical concrete shear strength versus experimental concrete shear strength | 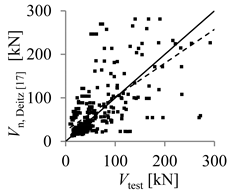 | 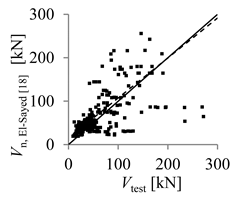 |
| Wegian et al. [19] | Nehdi et al. [20] | |
| Arithmetic mean | 1.44 | 1.12 |
| Parameter X (inverse of regression curve slope) | 1.52 | 1.13 |
| Coefficient of variation (COV) (%) | 43.55 | 25.50 |
| Mean absolute percentage error (MAPE) (%) | 26.32 | 18.96 |
| Percentage of beams with overestimated strength (%) | 12.58 | 34.52 |
| Theoretical concrete shear strength versus experimental concrete shear strength | 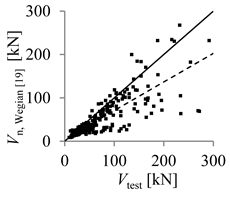 | 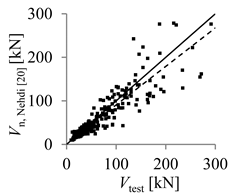 |
| Hoult et al. [21] | Razaqpur et al. [22]. | |
| Arithmetic mean | 1.88 | 1.09 |
| Parameter X (inverse of regression curve slope) | 2.21 | 1.04 |
| Coefficient of variation (COV) (%) | 91.29 | 24.59 |
| Mean absolute percentage error (MAPE) (%) | 34.15 | 18.97 |
| Percentage of beams with overestimated strength (%) | 13.23 | 39.97 |
| Theoretical concrete shear strength versus experimental concrete shear strength | 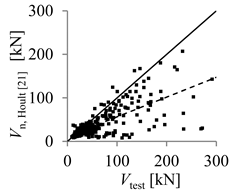 | 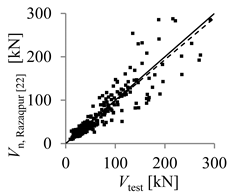 |
| Alam [23] | Kara [24] | |
| Arithmetic mean | 1.25 | 1.20 |
| Parameter X (inverse of regression curve slope) | 1.70 | 1.27 |
| Coefficient of variation (COV) (%) | 40.54 | 56.75 |
| Mean absolute percentage error (MAPE) (%) | 21.89 | 22.05 |
| Percentage of beams with overestimated strength (%) | 28.39 | 50.00 |
| Theoretical concrete shear strength versus experimental concrete shear strength | 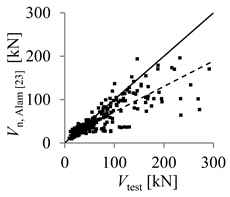 | 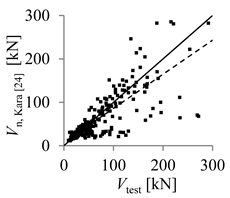 |
| Kurth [25] | Jang et al. [26] | |
| Arithmetic mean | 1.03 | 1.25 |
| Parameter X (inverse of regression curve slope) | 1.26 | 1.13 |
| Coefficient of variation (COV) (%) | 27.11 | 57.86 |
| Mean absolute percentage error (MAPE) (%) | 19.09 | 33.80 |
| Percentage of beams with overestimated strength (%) | 54.52 | 46.45 |
| Theoretical concrete shear strength versus experimental concrete shear strength | 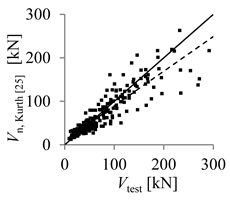 | 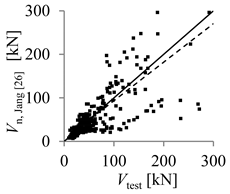 |
| Lignola et al. [27] | Valivonis et al. [28] | |
| Arithmetic mean | 1.07 | 0.98 |
| Parameter X (inverse of regression curve slope) | 1.37 | 1.08 |
| Coefficient of variation (COV) (%) | 64.64 | 39.97 |
| Mean absolute percentage error (MAPE) (%) | 31.91 | 32.81 |
| Percentage of beams with overestimated strength (%) | 64.84 | 65.48 |
| Theoretical concrete shear strength versus experimental concrete shear strength | 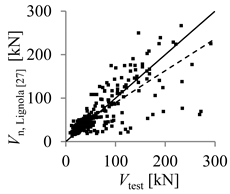 | 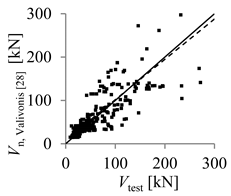 |
| Thomas et al. [29] | Hamid et al. [30] | |
| Arithmetic mean | 1.06 | 1.38 |
| Parameter X (inverse of regression curve slope) | 1.42 | 1.52 |
| Coefficient of variation (COV) (%) | 33.86 | 40.66 |
| Mean absolute percentage error (MAPE) (%) | 55.16 | 27.87 |
| Percentage of beams with overestimated strength (%) | 21.18 | 23.87 |
| Theoretical concrete shear strength versus experimental concrete shear strength | 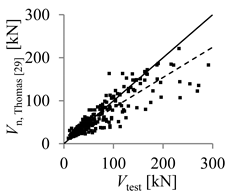 |  |
| Proposed Model (21) | |
|---|---|
| Arithmetic mean | 1.00 |
| Parameter X (inverse of regression curve slope) | 1.03 (R2 = 0.87) |
| Coefficient of variation (COV) (%) | 22.50 |
| Mean absolute percentage error (MAPE) (%) | 18.62 |
| Percentage of beams with overestimated strength (%) | 52.90 |
| Theoretical concrete shear strength versus experimental concrete shear strength | 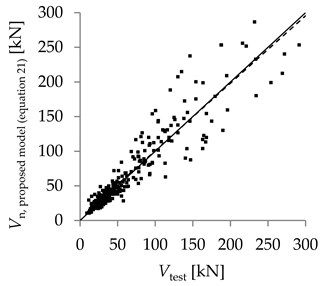 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bywalski, C.; Drzazga, M.; Kamiński, M.; Kaźmierowski, M. A New Proposal for the Shear Strength Prediction of Beams Longitudinally Reinforced with Fiber-Reinforced Polymer Bars. Buildings 2020, 10, 86. https://doi.org/10.3390/buildings10050086
Bywalski C, Drzazga M, Kamiński M, Kaźmierowski M. A New Proposal for the Shear Strength Prediction of Beams Longitudinally Reinforced with Fiber-Reinforced Polymer Bars. Buildings. 2020; 10(5):86. https://doi.org/10.3390/buildings10050086
Chicago/Turabian StyleBywalski, Czesław, Michał Drzazga, Mieczysław Kamiński, and Maciej Kaźmierowski. 2020. "A New Proposal for the Shear Strength Prediction of Beams Longitudinally Reinforced with Fiber-Reinforced Polymer Bars" Buildings 10, no. 5: 86. https://doi.org/10.3390/buildings10050086
APA StyleBywalski, C., Drzazga, M., Kamiński, M., & Kaźmierowski, M. (2020). A New Proposal for the Shear Strength Prediction of Beams Longitudinally Reinforced with Fiber-Reinforced Polymer Bars. Buildings, 10(5), 86. https://doi.org/10.3390/buildings10050086





