1. Introduction
The application of mathematics to architecture is very likely as old as architecture itself [
1]. From the use of arithmetic to measure lengths, to the calculation of squares and angles, to the complex analysis of structural loading capacities, mathematics has served architecture as an essential toolset to improve quality and performance. The improvements sought have not only been in construction soundness and utility—famously termed by the Roman architect Vitruvius as “firmitas” and “utilitas”—but also in aesthetic character, or what Vitruvius called “venustas” or beauty. Over many centuries, scores of theories have been developed and applied in search of the most beautiful (judged by most people) proportions, scales, patterns and relationships [
2]. In this discussion, the topic of symmetry has also been a core interest [
1].
In the modern era, when aesthetics has come to be seen as relatively plastic and subjective, the role of mathematics in architecture has shifted to producing more sheer varieties of aesthetic expression, with a notable emphasis on artistic novelty [
3]. This dominance has come at the expense of improving the desirable aesthetic quality and performance of a building as seen by most users (whether incorporating novelty or not). Indeed, even the possibility of “improving” aesthetics is often regarded by many architects and planners as merely a matter of subjective taste, or a matter that is merely conditional on one’s own individual and highly variable aesthetic goals [
4].
However, as this paper will discuss further below, a different perspective is coming from the social and medical sciences, where the impacts of varying environmental characteristics have begun to be measured, including psychological impacts (e.g., calmness, pleasure, excitement, fear, etc.) and even medical impacts (e.g., stress levels, restorative health effects, speed of recovery from surgery, etc.) It seems the geometric properties of environments do indeed carry predictable and largely shared impacts for those who experience a given environmental structure [
5].
At the same time, there is an important gap in the literature that still needs to be addressed. While there is ample evidence for the strong preference of a large majority of people for natural environments over built environments, especially contemporary ones [
6,
7], and ample evidence for the relationship between this preference and the psychological and physical health benefits of these environments [
5,
8], there is only weak evidence for the precise geometric characteristics that produce these benefits, or conversely, the relatively negative impacts of built environments. Such an understanding could guide researchers and practitioners to identify the specific factors that produce these beneficial effects within natural environments. In turn they might be better positioned to incorporate more of these factors into built environments, thereby producing greater beneficial effects for their users.
There have indeed been preliminary efforts to connect the specific geometries of natural environments with their beneficial characteristics. Dosen, Ostwald and Dawes [
9] investigate the hypothesis “that certain spatial and formal features may not only influence psychological wellbeing but also our aesthetic preference for environments” and go on to seek “a mathematical basis for the analysis of human perceptual responses to space.” Hagerhall, Purcell and Taylor [
10] examine the fractal geometry of natural environments as a predictor of their preference by subjects, and find “that there is a relationship between preference and the fractal dimension, which in turn gives rise to the hypothesis that the fractal dimension could provide part of the explanation to the well-documented connection between preference and naturalness.”
Yet the age-old topic of symmetry in architecture, curiously, has been overlooked as a fertile subject of research in bridging this gap [
11]. The purpose of this paper, then, is to explore the literature, to assess the potential for new research, and to outline a new research agenda. The methodology will be to conduct a literature review, drawing conclusions for further research. The paper will begin with a review of the concept of symmetry, proceeding to examine its history in architecture, to examine more recent research findings in biology, medicine, psychology and other fields, and then turn to new frontiers, before proposing tentative conclusions and hypotheses for further research.
2. Definition and Background
Before undertaking this research survey, the first task is to clarify the working definition of “symmetry.” While many people focus almost exclusively on so-called reflectional or “mirror” symmetry, wherein one side of an object is a mirror copy of the other, the concept is vastly broader. Most readers will be well aware that the word originates with the Greek
sym (together) +
metron (measure), and thus refers to a correspondence between different forms with similar measurements or shapes. In geometry, the “symmetrical” form in question is said to be invariant under a given transformation, which may include reflection, rotation, translation, scale changes, or other changes. When the transformed form is compared to the original form, the correspondence is said to be a symmetry [
12].
Symmetry is also an important concept in other forms of mathematics, where similar transformations can occur in non-geometric elements, and symmetries can be described more broadly as structural invariances through transformation [
13]. In a fundamental sense, an “equation” is nothing other than an expression of a symmetry between the two formulae being equated.
More recently, the concept of symmetry has also played an important role in information theory [
14]. What is called “information” could also be thought of as nothing other than a symmetrical relationship between any two structures in the world that are of interest to us; all that is required is that one structure is capable of transforming into the other while preserving some symmetrical aspect, e.g., in the transformation of a sound wave into its digital representation, whose measurement preserves a symmetrical relationship to the original wave [
15]. While one thinks of information as symmetry that is of interest to human beings, it can be applied more broadly to phenomena in nature, such as the “information” contained in DNA [
16]. Once again, the symmetrical structure is an invariance through transformation, and in the case of DNA, the invariance is in the pattern of proteins that is expressed by the transformations of a given sequence of DNA, repeated (with perhaps some natural variation) by symmetrical copies of the DNA sequence in other cells.
Some theorists have proposed that “information”—understood in this way as symmetrically related structure—is the fundamental structure of the Universe [
17]. That is, the structures of the Universe transform and differentiate from one another, but preserve some symmetric relationships in combination with various forms of “symmetry-breaking,” or differentiation into other structures with new symmetries. In a sense, this is the “really real” structure of things, without which the Universe would be an undifferentiated homogeneous field. Indeed, some propose that it may have been precisely so prior to the initial “symmetry-breaking event” of the Big Bang, and subsequent differentiation processes [
18].
This broader perspective helps to set the context for the exploration of symmetry as a phenomenon of both process and product. Here, however, the narrower focus is upon the role of symmetry within the human environment, including buildings, and in their specific geometric properties as well as the transformations that generate them.
3. Classes of Symmetry
As a preface, this section includes, for the unfamiliar reader, a brief review of the classes of symmetry as applied later to the human environment, from the most straightforward to the most complex, and the most concrete to the most abstract [
12,
19].
Perhaps the most familiar class of symmetry is
reflectional (
Figure 1a and
Figure 2a), in which one geometric configuration is reflected across an axis. For example, in many Classical buildings, the axis is the centreline of the building, and the façade as it appears on one side of the axis is exactly reproduced on the other in a matching progression (identical geometries moving to left as moving to right). It is common to say that one side is the “mirror image” of the other. In nature, a reflection in a body of water has a vertical reflectional symmetry with the scene above it, across the axis of the horizon.
Another familiar class of symmetry is
rotational (
Figure 1b and
Figure 2b), in which a configuration is symmetrical as it rotates about a point. A perfect circle has a rotational symmetry about the centre point of the circle. Many structures in nature have rotational symmetry at least in part: planetary bodies, the iris of the human eye, an inflated balloon (except where its nozzle distorts the shape) and so on. In the case of the inflated balloon, the symmetry of its shape is a product of the symmetry of the pressures radiating outward from within the balloon.
A
translational symmetry (
Figure 1c and
Figure 2c) is a correspondence between different shapes that may not be otherwise symmetrical about an axis. For example, a repeated figure has a translational symmetry with itself. In architecture, one part of a repeated motif has a translational symmetry with another part. A child’s blue eyes can be said to express a translational symmetry with its parents’ identical blue eyes (and the child may have partial translational symmetries in other respects, e.g., shape of the face, etc.)
A
scaling symmetry (
Figure 1d and
Figure 2d) is similar to a translational symmetry, but instead of symmetry across positions, the symmetry occurs also across sizes. The most familiar example is the so-called fractal pattern, in which the same geometry is visible at multiple scales.
Symmetry breaking, though not strictly speaking a class of symmetry in its own right, is an important process of symmetry formation and transformation, and therefore it is included as an important element in this list. When existing symmetries are perturbed or “broken,” they often produce new symmetries at smaller scales, or new compound structures combining smaller symmetries and partial asymmetries (
Figure 3). For example, a tubular structure, which is symmetrical about its axis, may break at some point along the axis, producing a new form of mirror symmetry. It is now understood that many classes of biological morphogenesis rely on broken symmetries to generate new compound symmetries, and importantly, complex body geometries as well as functionalities in organisms [
20]. Symmetry breaking also plays a large role in recent theories of physics and cosmology [
21,
22]. It may be that symmetry, together with the process of its breaking and recombining into new complex forms, is a fundamental aspect of the evolving structure of the Universe at many different scales.
An
information symmetry is a symmetry that is not per se between geometric forms, but has some other more abstract correspondence. At its most fundamental level, mathematics is a representation of symmetries, or preserved correspondences, in the transformation of mathematical constructs [
23]. The familiar “equal” sign in a formula expresses just such a symmetry. As forms of information, these constructs can therefore be described as a major class of “information symmetry.” One can also describe an “information symmetry” between the pattern of a DNA sequence and the complex protein that it generates, which in turn allows the “information” to be further transmitted, e.g., through inheritance. In the realm of human technology, one could describe an information symmetry between the pattern of grooves in a vinyl audio recording and the changes in air pressure at the microphone or speaker, corresponding to the sounds that are made or heard (
Figure 4). Any language or code can be said to contain information symmetries as well, for example, the symmetries between a symbol and its referent, or a map and its territory. In the case of literature, information symmetries can take the form of analogies or metaphors. In the case of the built environment, they can take the form of literal signs or symbols.
Compound symmetries, which combine other kinds of symmetry into more complex forms, are what is experienced most commonly in natural and human environments. Many classic tile patterns and motifs combine reflectional and translational symmetry, in what is known as a glide reflection (
Figure 5): a figure is repeated, then reflected across a glide axis [
24]. The three basic plane symmetries, plus their 14 possible combinations, form 17 symmetry groups in two dimensions (called “wallpaper groups”). The familiar kaleidoscope pattern is also a compound symmetry in two dimensions (
Figure 6).
Three-dimensional symmetries are even more complex, and are common in human experience. For example, a sunset on the water may combine a radial symmetry of the Sun, a reflectional symmetry of the sun as reflected in the water, translational symmetries in the ripples of the water, and scaling symmetries in the self-similar patterns of clouds (
Figure 7).
Broken symmetries are often seen compounded with other symmetries in the irregularities of our world, which embody the complex processes of their breaking. For example, a street grid which breaks in response to terrain can help to reveal the pattern of the terrain in a way which is aesthetically pleasing. This is because the resulting pattern is not more disorderly, but perhaps paradoxically, more orderly. It reveals a deeper level of compound, complex order in the human environment. Finally, one can see many information symmetries in the symbols and metaphors of art, particularly in its most abstract aspects.
Many daily experiences involve exceedingly complex forms of these compound and broken symmetries, which nonetheless help reveal important overall structural characteristics within human environments. This “deep symmetry” helps one to understand, navigate, and interact with one’s world, with important implications for health and well-being, as subsequent sections of the paper will further examine.
4. Theories of Symmetry in History
The pursuit of symmetry in human structures stretches back to antiquity, and even deep into prehistory [
25]. As Salvadori [
1] has documented, there is ample evidence of complex forms of symmetry in ancient Chinese, Indian, and American pre-Columbian architectures. The symmetric proportions and geometries of ancient Egyptian structures, including the Pyramids of Giza, have also been described at length [
26], although there is considerable debate over the degree to which the Egyptians were consciously aware of the mathematics involved. Perhaps the earliest explicit and written theory of symmetry in mathematics, as it is known today, came from Pythagoras roughly 2500 years ago, and his familiar “Pythagorean theorem” [
27]. The influence of his ideas played a major role in the thinking of later Greeks, including Plato, about the importance of symmetry in the world [
28].
Perhaps the most influential Western thinker on symmetry in architecture was the Roman Marcus Vitruvius Pollio, known more commonly as Vitruvius. In his writings of about 2000 years ago, his “symmetry” was a fundamental concept. However, it was less focused upon the more common reflectional or rotational classes of symmetry, and more focused upon translational and scalar symmetries, and to some extent, information symmetries, or correspondences under transformation. He defined symmetry as:
“…a proper agreement between the members of the work itself, and relation between the different parts and the whole general scheme, in accordance with a certain part selected as standard. Thus, in the human body there is a kind of symmetrical harmony … and so it is with perfect buildings.”
Thus, a “certain part selected as standard” may be transformed through a change in size (scalar symmetry) or repetitive position (translational symmetry), or through the formation of new proportional groups (informational symmetry). Once again, one can see the importance of compound symmetries in the human environment, and moreover, a proposal for their application as a normative standard.
It was not until after the seminal Renaissance architect and writer Alberti (1404–1472) that reflectional symmetry began to dominate theories of architectural design. Alberti’s own theory of symmetry was much more nuanced, and in fact the Latin phrase used by Alberti was “ita ut mutuo ad speciem correspondeant,” or “so as to correspond to one another as a species,” which only later came to be understood as (reflectional) symmetry [
30]. For Alberti, symmetry was moreover an inter-relationship of parts and wholes, or a kind of harmony (which he termed “concinnitas”). In this respect, Alberti continued to echo Vitruvius’ and Pythagoras’ broader concept of symmetry.
Indeed, Alberti’s writings on this topic reflect a rather modern view of the complex interplay of part-whole relations:
“Beauty is a kind of concord and mutual interplay of the parts of a thing. This concord is realized in a particular number, proportion, and arrangement demanded by harmony, which is the fundamental principle of nature… There are three basic things which contain everything that we seek: number, what I have called proportion, and arrangement (numerus, finitio, collocatio). But besides these there is something else which originates from the linking and mutual relationship of these things, and which makes the surface of beauty glisten with a marvelous brilliance; this thing we call harmony (concinnitas).”
[
31] (Book 9, Section 5, pp. 337–340)
5. Modern Developments
As noted previously, symmetry (in its varied forms) plays a major role in the contemporary history of mathematics and physics. In a number of notable cases, these lessons were applied to aesthetics. For example, the mathematician George Birkhoff [
32] developed a proposed mathematical measure for the aesthetics of an art object, expressed as M = f (O/C), where O stands for order and C for complexity. For Birkhoff, order “O” was intimately related to symmetry, as when an object “is characterised by a certain harmony, symmetry, or order (O), more or less concealed, which seems necessary to aesthetic effect” [
32] (pp. 3–4).
Several years later, Eysenck [
33] proposed a major modification to Birkhoff’s theory, arguing that O/C (order divided by complexity) should be replace by O × C (order times complexity). In other words, the complexity of a structure magnifies its perceived order. This revised formula seems to better capture the increased attractiveness of compound symmetries.
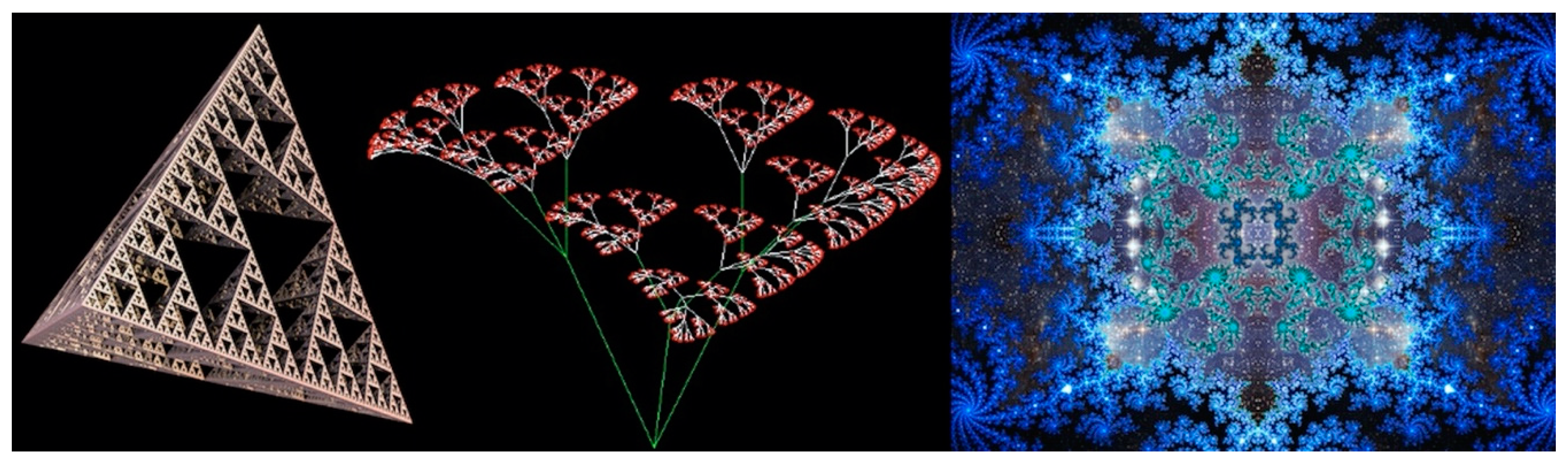
More recently, Mandelbrot [
34] described scalar symmetries in self-similar objects in Euclidean space, which he termed “fractals”. These recursive patterns can be quite beautiful (
Figure 8). These self-similar objects at a variety of scales have been described as expanding symmetry or unfolding symmetry. It is now understood that many structures in nature have this “fractal” form of scalar symmetry, including clouds, landscapes, plants, and other structures. In fact, fractal mathematics has been used in a powerful form of image compression and regeneration, even producing quite convincing synthetic images [
35].
6. The Role of Symmetry in Biology
One of the most common occurrences of symmetry in nature is in biological structures, and in particular, the forms of plants and animals. Everyone is familiar with the reflectional, rotational, translational, and scaling symmetries in beautiful flower patterns, for example. There is some evidence that the symmetrical patterns of flowers serve as innate attraction signals for pollinator insects [
36] and that the specific configuration of flower symmetries guides specific insect pollinator behaviour such as landing [
37].
The symmetries of flowers and other organisms are not only devices to attract insects, of course, but have their roots in the morphogenetic processes of growth, including folding, rotating, replicating, and so on [
38,
39]. Once again, one can see the essential relationship between process and product, allowing the transmission of information about the potential benefits of biological structures.
More broadly, symmetry has been advanced as a form of biological signalling, conveying the signaller’s health and genetic quality [
40]. There is also evidence that the ability to perceive characteristics of symmetry regardless of orientation enhances object recognition and is strongly related to aesthetic preference [
41]. It may be that the ability to perceive symmetry aids in the ability to “read” the structures of the environment and their likely impacts on the health and well-being of the organism.
Here too, “broken symmetry” plays an important role in biological morphogenesis, as noted previously [
20]. However, a broken symmetry in the environment is not a mysterious form of disorder if its breaking can be perceived—for example, if a mainly symmetrical animal is lounging on an irregular surface, causing its apparently symmetrical parts to present asymmetrically. The work of Enquist and Arak [
41] suggests that the ability to perceive both unbroken and broken symmetries is key to object recognition.
7. The Role of Symmetry in Human Biology
A related hypothesis has been advanced about the human body, and in particular the perceived attractiveness of the human face (
Figure 9). Males and females find each other more attractive in the presence of higher degrees of facial symmetry [
42]. They also find more symmetrical features more desirable when considering the suitability of a life partner [
43].
The evidence presented by Enquist and Arak [
41] that the ability to perceive symmetry aids in structural legibility also applies to humans, they note. This heightened structural legibility appears to apply not only to biological structures but to other forms of environmental structure, which need to be made legible in order to assess their capacity to support human well-being. They suggest that the pleasurable experience of this legibility may well be an important component in what is experienced as “beauty.” Indeed, functional MRI studies have found evidence to support this view [
44].
Thus, a growing body of recent evidence is clarifying the role of symmetry (in its many forms, both broken and unbroken) as an essential biological attribute for sensing and seeking the conditions of health and well-being. Importantly, one can see that the ability to perceive symmetries conveys otherwise hidden information to an organism about both the morphology and morphogenesis (that is, product and process) of the structures it encounters, both biological and non-biological. When it comes to an organism’s interest in the impact of a structure on its well-being—whether it be finding food, choosing a mate or settling in a salubrious environment—this information is invaluable.
8. Evidence for the Health Impacts of Symmetry and Its Absence
Evidence has been growing in the literature that the presence of natural forms and geometries, including their fractal and symmetrical properties, have remarkably positive effects on human health and well-being. Ulrich [
45] showed a positive relationship between recovery from surgery, including reduced morbidity and length of hospitalization, and the ability to view a natural environment. Other investigators have since shown similar properties, which have come to be referred to as “biophilia” [
46]. Further work has shown that not only natural environments, but buildings and other built environments, can confer important benefits to users through biophilic geometries and related characteristics [
47].
The specific geometric characteristics of beneficial natural environments, particularly their characteristics of symmetry, have also been recognised. As noted previously, Hagerhall, Purcell and Taylor [
10] investigated the fractal dimension of landscapes—a form of scalar symmetry—as a factor in human preferences, and found a correlation. The previous discussion has also illustrated that natural environments typically contain abundant forms of symmetry, strongly suggesting that symmetry is a factor in both environmental preference and in the benefits of natural environments. As this paper has already noted, more research is needed on this topic. However, already there is tantalizing research evidence emerging from a number of fields.
At the same time, evidence has been accumulating that a deficit in the experience of natural environments and their forms can be harmful, especially to children. The journalist Richard Louv [
48], citing this evidence, coined the term “nature deficit disorder” to describe the adverse impact upon children who are deprived of regular contact with natural environments. Grinde and Patil [
49] also found negative impacts on health and quality of life from environments devoid of nature, while Kellert [
50] surveyed the literature and found evidence that “children’s emotional, intellectual, and values-related development, especially during middle childhood and early adolescence, is greatly enhanced by varied, recurrent, and ongoing contact with relatively familiar natural settings and processes” [
50] (p. 146).
Here it must be noted, however, that not all built environments must be assumed to be uniformly deleterious. Stamps [
6] noted that, just as natural environments are preferred over built ones, old buildings are typically preferred over new ones. These structures, and the urban environments they comprise, often possess explicit characteristics of natural environments, including literal plant forms, but also geometric characteristics like reflectional, translational, and scaling symmetry (
Figure 10).
Zeki [
51] surveyed neurological research (including his own) and concluded that “mathematical principles of symmetry, harmony and proportion… are part of the cognitive apparatus of all brains” and that these principles “have to be respected” in order for a structure such as a human face to be perceived as beautiful [
51] (p. 19).
Moreover, the experience of beauty is a neurological requirement of healthy brains: “In our daily activity, we search for and seek to satisfy that quality; in simpler terms, we seek the beautiful to nourish the emotional brain since, from a neurobiological point of view, all areas of the brain must be continually nourished in a way that corresponds to their specific functions… Hence, whatever other demands go into architectural design, beauty must be a central element. Its experience adds to the health of its individuals and thus to society’s wellbeing. It is not a luxury, but an essential ingredient in nourishing the emotional brain” [
51] (p. 19).
There is also an important distinction to be made between “artifactual” and “biological” perceptions of beauty, according to Zeki et al. [
52]. While the former are highly variable between people based upon their different life experiences (for example, professionals with specialised training), the latter are more dependent upon inherited responses to invariant mathematical relationships that are widely shared among populations. Even though these relationships are a form of information which may be manipulated as constructs within art, their roots are in innate and shared ways of experiencing the world. In that sense, the innate and the constructed are not opposites, but exist within an overlapping continuum of the artifactual and the biological—the world of art, and the world of life.
9. Applications of Symmetry to Built Environments: Art in Service to Life
Echoing the distinction made by Zeki and his colleagues, the urbanist Jane Jacobs [
53] famously pointed out that although art and life are interwoven and overlapping, they are not the same thing. Confusion between these two realms of experience causes immense problems for city planning and design, she argued, resulting in neither art nor life, but what she called “taxidermy”—a result that is lifeless: “All this is a life-killing (and art-killing) misuse of art. The results impoverish life instead of enriching it… Instead of attempting to substitute art for life, city designers should return to a strategy ennobling both to art and to life: a strategy of illuminating and clarifying life and helping to explain to us its meanings and order—in this case, helping to illuminate, clarify and explain the order of cities” [
48] (pp. 373–375).
Thus, the “artefactual” has its place, but it is to serve the meaning and order of life, and of the “biological.” Using the language of symmetry outlined herein, the construction of artificial information symmetries can indeed enrich life and well-being—but only if they are serving to engage and enrich the natural symmetries of the physical and biological world.
The mathematician and design theorist Nikos Salingaros [
54] has assessed evidence that human perception relies upon combined symmetries to reduce information overload and to group architectural elements into larger wholes. These perceptions of symmetry have their roots in what is biologically useful, Salingaros has noted, and what is inherent in the structure of matter and life itself. Drawing on the work of Christopher Alexander [
55], Salingaros concluded that symmetry conveys a “structural meaning, rooted in our biological selves and in the natural world” [
54] (p. 233).
For Salingaros, these symmetries can be generated in methodical ways. Citing Alexander, Salingaros proposed “tools to organize complexity, including,
The critical factor, according to Salingaros, is adaptation. Even asymmetry is pleasant when users are able to perceive its adaptive origins: “When asymmetry arises from adaptation… the configuration may be surprising but it is ‘comfortable’ to our perceptual system” [
24].
The aforementioned Christopher Alexander, an architect with previous training in physics and mathematics, also proposed an extensive theory of geometric properties of “order,” in Birkhoff’s sense, in his four-volume work
The Nature of Order [
55]. In the first volume, Alexander reported his observation of “fifteen properties” (
Figure 11) which he found repeatedly in his own surveys of many structures in human history. Alexander proposed that all structures with characteristics of life have these properties in them—not only literal organisms, but what he referred to as “living structure” with the characteristics of “wholeness” [
55] (p. 80).
In this work, Alexander drew on insights of modern philosophers like Alfred North Whitehead [
57,
58] who argued for the primordial nature of life as an inherent structural potential of nature. Yet there was also a strong echo of the ideas of Pythagoras, Vitruvius and Alberti about the importance of interrelatedness, correspondence, harmony, and indeed, symmetry in the broader sense.
Alexander’s fifteen properties are geometric configurations of space, as seen in
Figure 11:
Levels of Scale (similar figures at a range of scales)
Strong Centers (prominent geometrical zones in between others)
Boundaries (geometrical zones that bound others, e.g., centers)
Alternating Repetition (patterns that repeat with some alternating variation)
Positive Space (a geometric region that does not have excessively acute sub-regions)
Good Shape (a geometric region that is coherent and interrelated)
Local Symmetries (groups of regions that are internally symmetrical but may not be externally symmetrical)
Deep Interlock and Ambiguity (patterns that inter-relate in complex ways)
Contrast (adjacent figures that are starkly different from one another)
Gradients (figures whose characteristics gradually transition)
Roughness (figures with many small-scale asymmetrical characteristics)
Echoes (figures that repeat some aspect from other figures)
The Void (areas where few or no figures are present)
Simplicity and Inner Calm (overall figures that are highly unified and harmonious)
Not-separateness (connectedness of all figures to one another and to the viewer)
Following the earlier discussion of classes of symmetry, one can also describe each of Alexander’s fifteen properties as some class or combination of symmetry, as follows:
Levels of Scale (scaling symmetries)
Strong Centers (rotational, reflectional symmetries)
Boundaries (rotational, reflectional symmetries)
Alternating Repetition (compound symmetries)
Positive Space (net convex symmetrical spaces)
Good Shape (coherent symmetrical shapes)
Local Symmetries (reflectional symmetries within symmetry breaking)
Deep Interlock and Ambiguity (translational symmetries)
Contrast (reflectional symmetries)
Gradients (translational symmetries)
Roughness (translational symmetries)
Echoes (deep translational symmetries)
The Void (symmetry void)
Simplicity and Inner Calm (symmetry simplicity ratio)
Not-separateness (ultimate symmetry, with symmetry breaking, of all things)
These fifteen properties (symmetries) also have their counterparts in the physical processes by which they are generated, through what Alexander called “wholeness-extending transformations.” The symmetries of experience arise as the result of coherent processes of formation. Human beings, with their highly evolved capacities of perception, can detect these symmetries, and sense the biologically relevant characteristics of the processes that formed them (healthy, beneficial, dangerous, etc). Once again it is clear that the perception of symmetry is biologically useful.
Alexander’s work also reinforces the conclusion that the world is shot through with symmetry and its transformations, in many different forms and deep combinations. One can tease out these symmetric properties, understand and work with them, and in the act of design, create more of them. In a basic sense, this is what the act of design must do: create and shape symmetries, in effect weaving them together in a way that is most beneficial for human beings.
Alexander argued that these symmetric properties are abundant in high-quality human environments. Conversely, he argued, in those environments where the properties are not abundant, there is a negative impact upon human well-being. Here, there is a normative implication for practice: the designer has a professional duty to create more of the symmetric structures characteristic of the left-hand image in
Figure 10, and fewer places like that of the right-hand image.
Elsewhere in
The Nature of Order, Alexander also drew upon the work of Salingaros [
59], building upon the earlier work of Birkhoff [
32] and Eysenck [
33] to propose a mathematical theory of beauty. However, rather than using the term “beauty,” Alexander and Salingaros referred to “life,” or “living structure,” described extensively throughout Alexander’s 2002 book:
“…life, as I have defined it, is mathematical. By this I mean that it arises because of the mathematics of space itself. Since living structures arise primarily as symmetries and structures of symmetries, their presence and their density can, in principle, be calculated for any given configuration.”
For Alexander, living structure produced an experience of beauty, but was not itself an experience. Rather, it was a physical structure in the world, with mathematical properties that could even be expressed (or at least approximated) in a formula.
Salingaros proposed the formula L = T × H, where L is “life” in the Alexandrian definition, T is “temperature,” which “estimates the density of occurrence” of Alexander’s properties (which as can be seen are classes of symmetry), and H is what Salingaros called “harmony,” described by Alexander as “the number of local symmetries present in a configuration” [
55] (p. 469). Salingaros then applied the formula to a number of famous buildings, generating results that Alexander found to be rough but promising approximations of what could be observed. He concluded that “Salingaros’ work opens the door to a rich field of study” [
55] (p. 472).
10. A Basic Distinction
From this discussion it can readily be seen, then, that symmetry permeates the structures of the world, and also the structures of experience and thought—indeed, of brains and their patterns of activity [
44,
52]. But these different realms of symmetry should not be confused. Drawing on Zeki, Jacobs, Salingaros and Alexander, one can now make a fundamental distinction between three overlapping but separate phenomena:
The immense structures of the physical world, with their vastly complex geometric properties;
One’s innate experiences of these structures, which are conditioned by humans’ evolution as complex neurological organisms; and
One’s own synthetic mental constructs, which sometimes interact with these physical symmetries and one’s experiences of them, and sometimes go into other directions, creating linguistic or artistic symbols, metaphors, allegories, artworks, and other constructions.
The first two categories are widely shared between individuals and across cultures, whereas, as research has shown [
52], the third category can vary widely between individuals, depending upon their language, culture, life experience, and other factors.
One should note that the synthetic mental constructs of the third category also often have their own physical counterparts, but these are often incidental to the expression of the mental constructs. For example, a work of literature may also exist as a physical pattern of printed marks on pages bound in a printed volume. However, the work of “literature” as such is in the realm of concepts, not the realm of the printed marks on the pages. (At the same time, the printed volume may itself be widely experienced as beautiful, perhaps containing many compound forms of symmetry.)
This distinction between the conceptual and the physical is fundamentally important. It must be recognised that while there is a relationship between the two (and between the abstract and the concrete, or the urban and the artistic) they are distinct, and it is dangerous to confuse the two.
To be able to clearly identify these two realms, one may refer herein to symmetries in the physical world using the Latin term “structura naturalis”—that is, the immense range of concrete, physical, and natural structures that surrounds us in daily life.
However, when one thinks about these structures, or form abstractions, or uses language to describe them, one is generating a “structura mentis”—a mental structure—with powerful capacities to extend and compare these and other structures of the world. Indeed, these great capacities are a defining trait of the human species, extending its further capacities of language, art, and culture.
As Jacobs pointed out, each of these is a vital component of human experience. Indeed, many important aspects of literature and other arts occur in the domain of structura mentis, including symbolism, metaphor, and allegory. These structures also go on to produce structura naturalis, in the form of the structures of the world. But planners and designers in particular must be clear about the relation of the two, and the coherence—or less happily, the discord—between them.
11. Tentative Conclusions and Hypotheses for a New Research Agenda
It is clear from the literature that symmetry is a central component of human perception and understanding, and one with its roots in the biological need to apprehend the structure and meaning of the world. From these insights, one may now formulate a series of tentative conclusions or hypotheses, already tentatively supported by evidence, that can be further tested and evaluated through a new research agenda.
The hypotheses are:
Hypothesis 1. Symmetry, particularly compound symmetry, is an essential attribute of human environments that helps one to comprehend, navigate within, and interact successfully with one’s world, including fostering aesthetic enjoyment and well-being.
Evidence is mounting that people find structures with high levels of symmetry, especially compound symmetry, preferable to those with low levels of symmetry. Nor is this merely a matter of preference, as evidence shows it is tied to mental and physical health. It may also be tied to other forms of social and economic interaction (for example, the willingness of people to walk and encounter one another within public spaces) which in turn are related to health and well-being.
Hypothesis 2. The origin of this aesthetic enjoyment and well-being—of the craving for deep symmetry—lies in these biological roots.
Humans are order-seeking or “ordophilic” creatures, whose well-being depends on their ability to detect the complex forms of order represented by nourishing food, suitable mates, salubrious environments, and other beneficial structures that they encounter or create. Symmetry, in its many forms, is an expression and a manifestation of this order. In particular, humans crave highly complex forms of compound symmetries with deep coherent inter-linkages, or what one may call “deep symmetry.”
Hypothesis 3. There is an important distinction between symmetries within structures in the physical world, and symmetries between the mental structures of human beings, sometimes expressed symbolically or metaphorically through structures in the physical world.
These different forms of symmetry are themselves related through structural symmetries—that is, language and art bear a symmetrical relation—but not an identical one—to the physical world. This view of the relation of language to reality suggests a kind of “symmetric structuralism” [
60].
Hypothesis 4. To confuse these realms, and to allow mental symmetries to supplant physical ones, can be damaging to human well-being.
The evidence for this proposition is growing, as the research discussed here has described. One likely reason that many people judge contemporary structures to be disordered and unattractive (and therefore degrading to their enjoyment and, as research shows, even harmful to their well-being) is that architects are over-focused upon their own, often private, mental symmetries, and have diminished the importance of the more shareable physical symmetries. There is abundant research to describe this divergence in aesthetic judgment between architects and non-architects (Gifford et al., 2000), with implications for the failure of architects to understand and respond adequately to user needs. Some of the most compelling research substantiating the biological basis of this need comes from neuroscience [
52,
61].
Hypothesis 5. The cause of the prominence of this confusion in the modern era can be understood as a fateful consequence of multiple historical forces.
Zeki [
51] described “other considerations to which beauty becomes hostage, such as social or financial constraints, or the projection of power in the design.” To those one could add functional requirements of transportation including automobiles, the short-term dictates of capital, technological imperatives and constraints, and other consequences of the exploitation of “economies of scale and standardization” at the expense of “economies of place and differentiation” [
3].
At the same time, architects and planners are hardly free of responsibility. It has been alleged that architects in particular became complicit in a kind of marketing or commodification regime [
62]. The allure of their fine art—their
structura mentis—together with the pedigree of the fine universities at which they endlessly discussed these abstractions with connoisseurs and critics, served as a kind of “product packaging” over what were, it now seems, toxic industrial products. This was a fateful combination of architects’ cognitive biases with the dictates of a relatively primitive technological era.
Hypothesis 6. There is an important implication for professional practice and policy: today’s built environments may be damaging human health and well-being through a “symmetry-deficit disorder”.
Following Richard Louv’s “nature-deficit disorder,” one can now postulate (sufficient for further research) a related disorder that evidence suggests is produced by a deficiency of symmetry in the human environment—one manifestation of which is a lack of contact with nature and its complex symmetries. This deep symmetry, and the experience of beauty that it produces, is nothing less than “an essential ingredient in nourishing the emotional brain” [
51]. Yet too often it is displaced by what one may call “shallow symmetry”—few or disordered forms of symmetry—often left as a residual by-product from displaced attention to the deep symmetry of
structura mentis.
12. Discussion
Clearly there is, and should be, no constraint on structura mentis as a matter of free expression (except perhaps as has been decided by courts on various grounds of public safety, i.e., the proverbial shouting fire in a crowded theater, and so on). Clearly, too, structura mentis is a potentially infinite domain of creative expression and culture, and should be celebrated as such. Structura naturalis is, however, a much more concrete structure, with more specific and predictable human effects and consequences. It follows that, whatever other forms of structura mentis they may employ, architects and planners have a primary duty to support the emotional and physical well-being of users with a sufficient level of deep symmetry in the human environment (structura naturalis). What that level is and how it can be ascertained is another, larger subject for further research; but as of now, the basic conclusion stands.
Some architects will protest here that their role as artists supersedes their professional responsibility to ensure the enjoyment and well-being of users. After all, is it not the case that some of the greatest art shocks and disturbs? In a gallery or private residence, such an argument has merit. However, in the public realm, where users are forced to experience the work of architects, there is a matter of professional responsibility to promote public health and well-being.
Few architects would question their basic professional duty to serve the needs of their clients and users. After all, the profession does maintain clear professional responsibilities, with penalties (even criminal ones) for malpractice. This is clearly understood in the case of Vitruvius’ firmitas and utilitas (firmness and commodity). What remains insufficiently examined (particularly in light of evidence discussed herein) is the question of venustas: that is, do the impacts on health and well-being of a structura naturalis imply the need for a normative theory as well? As the evidence indicates, it appears they do.
This is true not only of clients and users of a building, but of the general public who are impacted by a building’s exterior and its contribution to shaping the public realm. In particular, architects have a duty not to impose their constructs of structura mentis where they have the capacity to be harmful, in place of beneficial forms of structura naturalis. As discussed previously, while the two are naturally related and supportive aspects of a continuum, they are not the same, and the tendency to impose the latter onto the former—especially by specialists whose mental symmetries have become divorced from the symmetries experienced by most people—may well be the cause of negative impacts on the human experience and well-being of a majority of the population.
There are many aspects of this issue that are beyond the scope of this paper, but several warrant a mention. One is the implication of “construal level theory” [
63], which describes the potentially negative impacts of psychological distance from the actual experiences of those to whom professionals are responsible. In place of effective responses, professionals often insert their own “construals”—which in this case become forms of
structura mentis. A related phenomenon is the occurrence of “geometrical fundamentalism” by architects, described by Mehaffy and Salingaros [
64]. The strong and simple mental symmetries they admire come from relatively primitive geometric characteristics, which result in denuded, low-symmetry structures in place of the symmetry-rich environments that promote enjoyment and well-being for the vast majority of the public.
In architects’ partial defence, this is often not a wilful act. Mehaffy and Salingaros [
65] describe the divergence between architects’ and laypersons’ judgments as “architectural myopia”—that is, architects literally cannot see what non-architects see in the physical world, because their mental associations, symbols, metaphors, fondness for geometrical fundamentalism—their
structura mentis—dominates their view. What is needed, then, is something like a set of “corrective lenses”—new forms of normative guidance, provided and supported by a maturing body of research.
13. Conclusions
A key gap has been identified in the research, namely in understanding the geometric factors that influence environmental preference and well-being in architectural and urban environments. This survey research has assessed the evidence, and explored a hypothesis that the characteristics of symmetry do have significant impacts on users. This hypothesis, if further validated, will help to account for the divergence in preference for natural versus contemporary built environments, and secondly, the divergence in judgment between professionals and users as to desirable environmental characteristics. That in turn will carry normative weight regarding important but unmet obligations of professionals toward users’ well-being.
None of this discussion is meant to suggest that the theoretical and normative framework of deep symmetry outlined here is the only important factor in the human experience of built environments. On the contrary, there are surely many other important factors that support well-being and delight, among them novelty, contrast, drama, and the many deep mental symmetries within artistic structures and others—some of which can be experienced by broad sections of the public too—that is referred to above as structura mentis. Rather, the argument made here is merely that physical symmetry in the environment—structura naturalis—has been overlooked and diminished, with fateful consequences for human well-being.
To assist in rectifying the problem, a new agenda is needed for research. It must have the normative aim of guiding a reformed professional practice—exactly as Alberti, Vitruvius, Pythagoras, and innumerable other scholars have sought to do over for many centuries, with manifest benefits to public welfare and city life. Such an agenda might include the following key elements:
A clarified understanding of the ways that people are impacted by buildings and urban environments containing varying forms of symmetry under varying circumstances, and the lessons to draw about likely shared reactions and evaluations.
A clarified understanding of the measurable impacts of symmetry on different aspects of human health and well-being, and the conditions under which these impacts occur.
A clarified understanding of the role that symmetry might play in achieving other urban goals, including walkability, active public space, social capital, urban resilience, low-carbon living, and mitigation of loneliness.
A better articulated understanding of the different forms and combinations of symmetry, including “deep symmetry” (as initially outlined herein), and how they combine and interact to produce human impacts.
New methods for defining and measuring these forms of symmetry, building on the work of Alexander, Salingaros, and others, and providing useful diagnostic and design guidance tools.
Articulation of the philosophical framework of “symmetric structuralism” described herein, in order to provide a comprehensible and useful model of the relationships between these issues.
Finally, and perhaps most controversially—but supported by evidence—new normative and practical guidance for inclusion of these geometric characteristics in building design so as to enhance positive user impacts and attenuate negative ones, as part of responsible professional practice.
In the end, such a research agenda must have a practical aim, to aid practitioners (and secondarily, policymakers and educators) to produce environments that users find more satisfying, more beautiful, and more salubrious. The aid must include specific guidance on the weaving together of more coherent patterns and spaces—including especially public spaces—that are better able to support human flourishing.
To accomplish this exceedingly ambitious goal, such a research agenda must reflect and build upon the very forefront of findings in environmental psychology, neuroscience, healthcare, biology, mathematics, and other related fields. As the research surveyed herein suggests, it must be more firmly rooted also in the evolutionary history of humanity, its biology, and the nature of the physical universe itself.