Abstract
Aluminium alloys form many important structural components, and the addition of alloying elements contributes to the improvement of properties and characteristics. The objective of this work is to study the influence of thermal variables on the microstructure, present phases, microhardness, dynamic modulus of elasticity, and damping frequency in unidirectional solidification experiments, which were performed in situ during the manufacturing of Al–0.8 Nb and Al–1.2 Nb (wt.%) alloys. Experimental laws for the primary (λ1) and secondary (λ2) dendritic spacings for each alloy were given as a function of thermal variables. For Al–0.8%wt Nb, λ1 = 600.1()−1.85 and λ2 = 186.1(VL)−3.62; and for Al–1.2%wt Nb, λ1 = 133.6()−1.85 and λ2 = 55.6(VL)−3.62. Moreover, experimental growth laws that correlate the dendritic spacings are proposed. An increase in dendritic spacing influences the solidification kinetics observed, indicating that metal/mold interface distance or an increase in Nb content lowers the liquidus isotherm velocity (VL) and the cooling rate (Ṫ). There is also a small increase in the microhardness, dynamic modulus of elasticity, and damping frequency in relation to the composition of the alloy and the microstructure.
1. Introduction
Materials engineering still faces major challenges in the modern world. There are a great variety of metal alloys, many of which are used due to their excellent properties. The importance of metallurgy field is evident, all metals, except for sintered parts, undergo a process of phase transformation and solidification during manufacturing, whether they are cast into shaped molds or produced into ingots. Alloys are studied with the aim to reduce weight, improve the combinations of mechanical properties, and predict their mechanical behaviour, such as damping capacity. Damping has practical engineering importance in limiting the amplitude of vibration at resonance conditions, and thereby reducing the probability of fatigue failure or it is capable to increase fatigue lives. Turbine blades, crankshafts, and overhead conductors are the typical applications where knowledge about damping capacity is crucial [1,2,3,4,5,6].
Nowadays, Nb applications in aluminum alloys continuously increase, with about 10% growth per year in the energy, automotive, and construction sectors [7]. The alloys contained in their Nb composition attract interest because of the potential to resist different types of corrosive media, from marine atmospheres to oxidizing atmospheres [8,9,10].
Brazil has the largest niobium reserves in the world, with 98.53% of the world total [7]. Alloys with Nb addition show that they may be a promise in the substitution of Ni-based alloys. Al–Nb known system properties are desirable in order to show where its application will be better. The literature review indicates that information on the subject is limited such as, microstructural and mechanical properties, dynamic properties, thermal properties, intermetallic formed, among others [11,12].
When it comes to non-ferrous alloys, such as Ni–Ti–Nb–Al, recent studies have shown that the casting of aluminium promotes the diffusion of Nb. Thus, the high-temperature mechanical properties of alloys with structural Nb additions can be altered and possibly improved by rapid solidification under supercooled conditions. The process can be used to obtain finer and more homogeneous microstructures, as well as to change the path of solidification and reduce the formation of fragile phases. Hutchinson et al. observed that the addition of a small amount of Nb (<0.1 wt.%) to Al alloys causes significant variations in the mechanical properties [13,14,15,16].
However, the Al–Nb binary system attracts interest, although there is limited information on the thermodynamic properties and some phases still without complete identification [4,12,17]. Hu et al. [11] in their review of the Al–Nb system, show that one of the most important information in the experimental phase diagram comes from the work of Jorda et al. [18]. In this context, recent studies propose that the solubility limits of Al3Nb, AlNb3, and AlNb2 phases are higher than the values accepted in the literature [12,17,19].
New solid phase emergence characterizes the beginning of solidification. The emergence and subsequent growth of solid particles characterizes the microstructure formation in metals and metal alloys at successive moments, such that kinetics, thermal, chemical, and thermodynamic aspects are strongly related [20].
Molten metals have a common structural form, which is dendritic growth and dendrites cooling degree, by interfering with the size and shape of the structure, which directly influences the mechanical properties, corrosion resistance, and subsequent heat treatments of the molten products. These structures are formed with solute content very different from the average of the alloy. This difference in solute concentration from the center of the dendrites to the interdendritic region is caused by the difference in solubility between the liquid and solid phases [21].
The determination of thermal parameters that act during solidification—such as temperature gradient (GL), liquidus isotherm velocity (VL), and cooling rate (Ṫ)—is important due to the growth of cellular structures at slow cooling rates. If the GL is smaller and the VL is increasing, the supercooled region is extended and the cellular structures begin to transform into dendritic structures [22,23,24]. In the solidification process, one of the paramount parameters is the dendritic spacing, λ. This affects both the microsegregation and the development of secondary phases within the interdendritic regions, and thus influences the mechanical properties of the structure [25]. Under some processing conditions, substantial heat extraction occurs that leads to a change in dendritic morphology, resulting in grain nucleation or lateral growth (giving primary (λ1) and secondary (λ2) dendritic arms). During solidification, the microstructural formation depends on the local thermal field, specifically the thermal gradient and the rate of solidification. With the local thermal conditions, the solidification morphology is generally characterized as planar, cellular, or dendritic [26].
This study evaluates the in situ production of two alloys, Al–0.8 Nb and Al–1.2 Nb (wt.%), which were solidified in an ascending unidirectional solidification device to obtain a consistent microstructure. The fusion, present phases, and the correlation with the thermal parameters were evaluated, and the dynamic elastic modulus, damping frequency, and microhardness were analyzed as a function of the microstructure.
2. Experimental Procedure
Experiments were carried out with Al–0.8 Nb and Al–1.2 Nb (wt.%) alloys. The alloys were prepared with commercially pure metals; the bulk percentages of the major elements, obtained by X-ray fluorescence spectrometry (Shimadzu EDX 720 HS, Kyoto, Japan), are shown in Table 1. The composition of the two alloys was designed by stoichiometric calculation, and all elements were weighed by an analytical balance with a precision of 0.01g. Then, the metals were melted in an electric furnace for dissolution of the components and homogenization of the alloys.

Table 1.
Chemical composition (wt.%) of the metals used to prepare the alloys.
A schematic representation of the unidirectional solidifying device is shown in Figure 1. It is constituted by a cooling system (1, 2, and 3), a mold plate (4), and an ingot (5). The ingot is made of 314 stainless steel and has a square cross-section of 65 mm and a length of 100 mm and a 3 mm wall thickness. The mold plate was manufactured using a 1020 steel plate with 3 mm thickness. The cooling system is coupled to the mold plate to keep the temperature constant (at 23 °C) during the experiment. This device was kept inside a furnace capable of reaching a temperature of 1200 °C by means of two independently controlled zones of electrical resistance. The ingot was instrumented with seven type K thermocouples, positioned at 8, 10, 14, 18, 22, 27, and 35 mm from the refrigerated mold plate, which were connected to a data logger interface with a computer and the temperature data were acquired. Thermal data acquired in the casting were monitored during solidification with a frequency of 1 Hz.
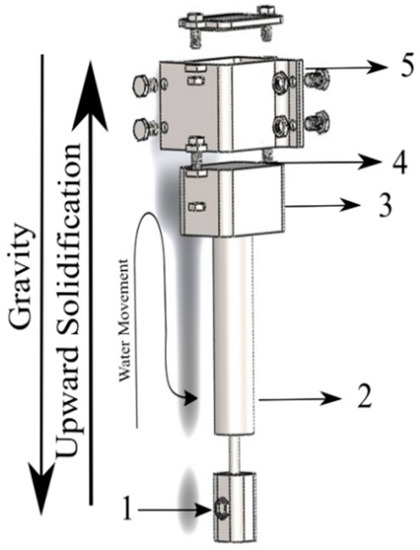
Figure 1.
Schematic drawing of the unidirectional solidification device. 1—Water inlet, 2—water outlet, 3—cooling chamber, 4—plate mold, 5—ingot.
The alloy was previously prepared in a muffle furnace, where the liquidus temperature (TL) was measured, and subsequently poured into the mold in the liquid state. For the experiment, the alloy was remelted inside the experimental furnace, avoiding the convection caused by the initial leak. The cooling system was triggered when the temperature of the first thermocouple reached a value 5% higher than the measured TL, ensuring that the whole alloy was in the liquid state, thus promoting solidification in a vertical and ascending manner. The mold plates were polished to ensure the same contact surface with the solidified metal for both alloys. In this way, the procedures and analyses performed resemble and corroborate with the recent solidification studies found in the literature [27,28,29,30,31,32,33,34,35,36].
In order to examined the macro and microstructures, metallographic techniques were used according to ASTM E3-11 [37]. The ingots were sectioned on a midplane, grinded, polished, and etched with a Flick solution (10 mL HF, 15 mL HCL, and 10 mL H2O) for macroscopy examination. The evaluated microstructures were taken from the center of the ingot to ensure directionality for the measurement of dendritic spacings by the method proposed by Gunduz and Çadirli [38]. Transverse sections, perpendicular to the growth direction, from the directionally solidified specimens at different positions along the ingot length were polished and etched with Keller solution (2 mL HF, 3 mL HCL, 5 mL HON3, and 190 mL H2O) for measurement of primary dendritic spacings and longitudinal section for measurement of secondary dendritic spacings. The image processing was carried out using the Olympus LEXT OLS 4000 confocal laser microscope (Shinjuku, Japan). At least 40 measurements were performed for each selected position for l1 and 50 measurements for l2, for both alloys. For the determination of the dynamic elastic modulus and damping frequency, the impulse excitation technique was used (Sonelastic, ATCP Physical Engineering) following ASTM E1876-09 [39]. For the microhardness test, 20 random indentations were performed on each sample with 50 gf load with an EmcoTest microdurometer (model DuraScan 20) according to the norm ASTM E384-08 [40]. X-ray diffraction (XRD, Bruker Smart Apex) was carried out over a wide range of diffraction angles (2θ = 20° to 120°), with an angular pitch of 0.05° and a counting time per point equal to 2.4 s.
3. Results and Discussions
3.1. Thermal Variables
Figure 2a,b shows the typical cooling curves acquired during the upward directional solidification for alloys Al–0.8 Nb and Al–1.2 Nb (wt.%) and the liquidus temperature (TL) measured for alloys were 645.8° and 653.39° (Celsius), respectively. It can be observed that the Al–0.8 wt.% Nb alloy solidifies more quickly than Al–1.2 wt.% Nb, probably as a function of thermal diffusivity and solute redistribution. The experimental cooling curves refer to thermocouples located at specific distances (P in mm) from the cooled metal/mold interface.
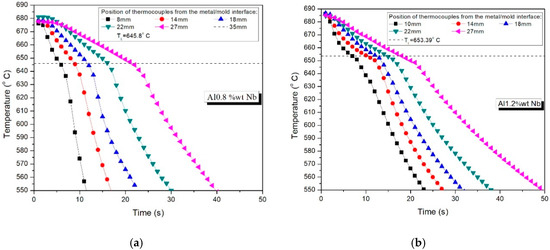
Figure 2.
Experimental cooling curves for (a) Al–0.8 Nb and (b) Al–1.2 Nb (wt.%) alloys during unsteady-state directional solidification.
By plotting the time at which the liquidus isotherm passes through a certain position against the height of the corresponding thermocouple, velocity curves of the liquidus isotherm were obtained as a function of position, as shown in Figure 3. The cooling rate (Ṫ) was obtained by dividing the temperature difference by the time difference (Ṫ = ΔT/Δt) of the two points as the liquidus isotherm passed their positions [41] according to Figure 4.
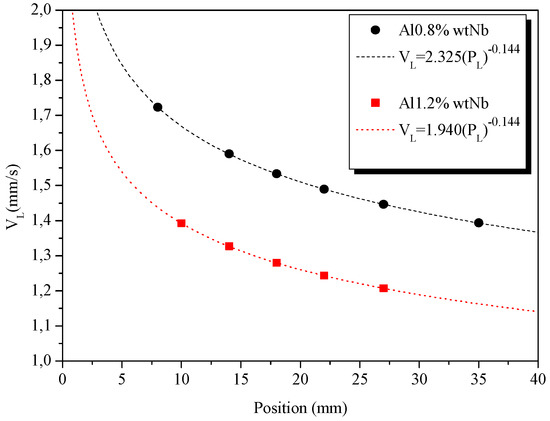
Figure 3.
Speed of the liquidus isotherm.
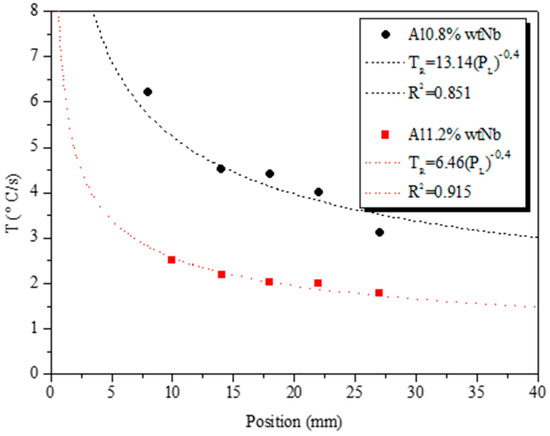
Figure 4.
Cooling rate as a function of position from the metal/mold interface.
The curves of the thermal variables VL and Ṫ (Figure 4 and Figure 5) have a decreasing profile from the moment they move away from the metal/mold interface. This phenomenon occurs as the solidified layer creates a solid/liquid interface, thereby increasing the thermal resistance of the solid, making it difficult for heat to travel toward the mold. The thermal gradient at the front of the solid/liquid interface indicates how the temperature is distributed per unit length, as shown in Figure 5.
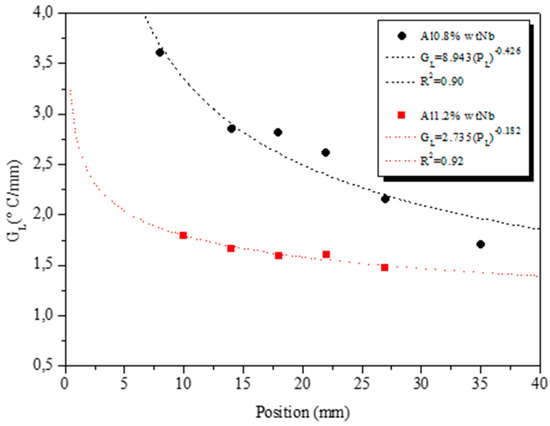
Figure 5.
Thermal gradient as a function of position from the metal/mold interface.
To ensure sequential solidification along the ingot and to prevent the growth of equiaxial grains in areas of constitutional sub-cooling within the molten liquid, a high thermal gradient is needed during the solidification process [42]. This gradient also reduces segregation and allows the materials to be used at higher operating temperatures [43].
3.2. Macrostructure
Figure 6 shows the solidification macrostructure of alloys Al–0.8%wt Nb and Al–1.2%wt Nb. The macrostructure is composed of columnar grains. This directionality is due to the flow of heat extraction, which confirms the unidirectional solidification. The amount of Nb studied does not seem to be enough to cause grain refinement under the solidification conditions of the experiments.

Figure 6.
Typical directionally solidified macrostructures for alloys Al–0.8 Nb and Al–1.2 Nb (wt.%).
3.3. Microstructure
Figure 7 shows the optical images of the longitudinal and transverse microstructures of the alloys Al–0.8%wt Nb and Al–1.2%wt Nb. The images are associated with thermal parameters such as, VL and Ṫ, and the dendritic spacings λ1 and λ2. The higher the velocities and cooling rates, the nearer the plate mold gives a refinement of the microstructure. Once the thermal resistance increases due to the formation of the solidified layer, the dendritic formation profile increases. As such, the primary and secondary dendritic spacings increase along the ingot; however, it is possible to identify that although the alloy with 1.2%wt Nb presents lower rates and velocities this also has smaller spacings, which leads to believe that Nb may have influenced this parameter.
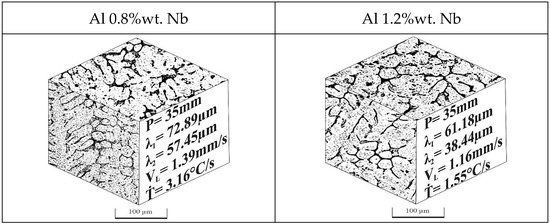
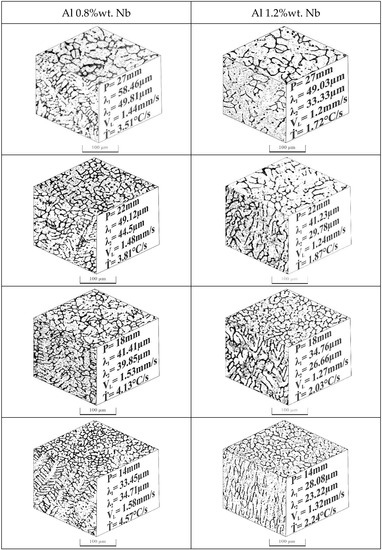
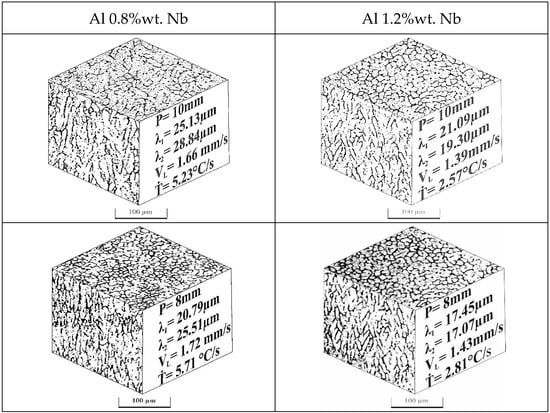
Figure 7.
Typical solidification microstructures along the transverse (λ1) and longitudinal sections (λ2) of Al–0.8 Nb and Al–1.2 Nb (wt.%) alloys at the metal/mold interface 35 and 27 mm.
Figure 8 and Figure 9 show the values of the experimental laws of the primary and secondary dendritic spacing for alloys Al–0.8%wt Nb and Al–1.2 Nb as a function of the distance from the plate mold. The error bar is related to the standard deviation obtained from 50 measurements for each position.
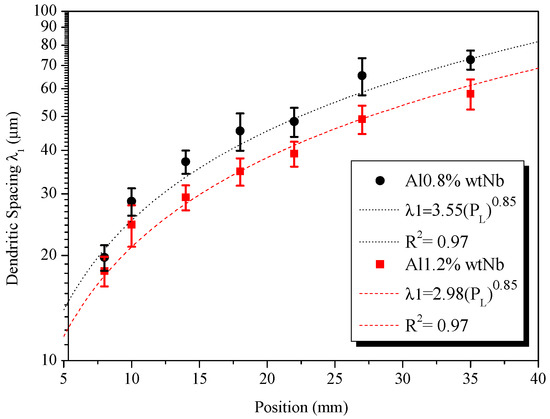
Figure 8.
Experimental equations of the primary dendritic spacing as a function of the distance to the metal/mold interface, for alloys Al–0.8%wt Nb and Al–1.2 Nb.
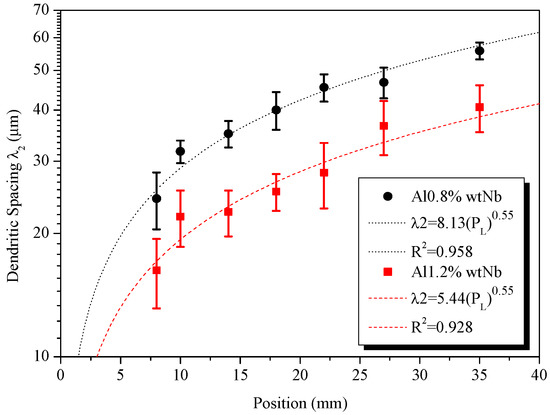
Figure 9.
Experimental equations of the secondary dendritic spacing as a function of the metal/mold interface, for alloys Al–0.8%wt Nb and Al–1.2%wt Nb.
Figure 10 and Figure 11 show the correlation of the thermal parameters with the experimental values of the primary dendritic spacing (λ1) for alloys Al–0.8%wt Nb and Al–1.2 Nb as a function of the cooling rate. The figure indicates that with more refined spacings, there is an increase in the values of these thermal parameters. It can be observed from Figure 10 and Figure 11 that there is a high correlation coefficient (R2 > 0.9) between the points and the plotted curve.
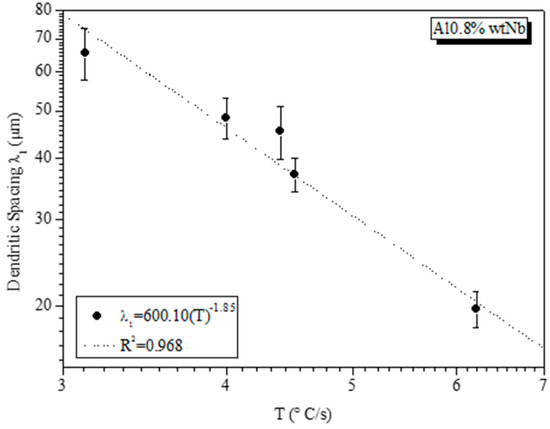
Figure 10.
Experimental equation of the primary dendritic spacing as a function of the cooling rate for Al–0.8 Nb (wt.%).
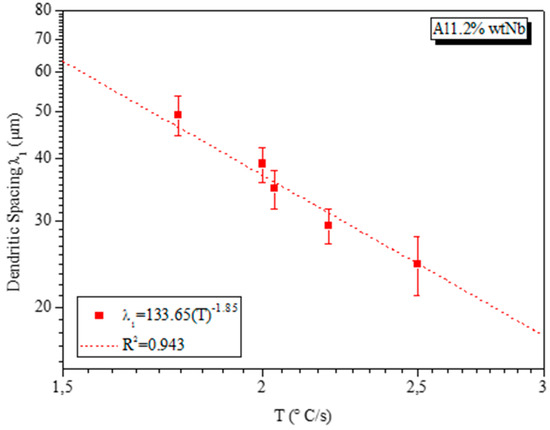
Figure 11.
Experimental equation of the primary dendritic spacing as a function of the cooling rate for Al–1.2 Nb (wt.%).
Figure 12 and Figure 13 show the experimental values of the secondary dendritic spacing (λ2) for alloys Al–0.8 Nb and Al–1.2 Nb (wt.%) as a function of the liquidus isotherm velocity. The functions obtained for the experimental law of growth’s spacing λ2 characterize potential functions, where there is a high coefficient of correlation (R2 > 0.9) between the points and the plotted curve.
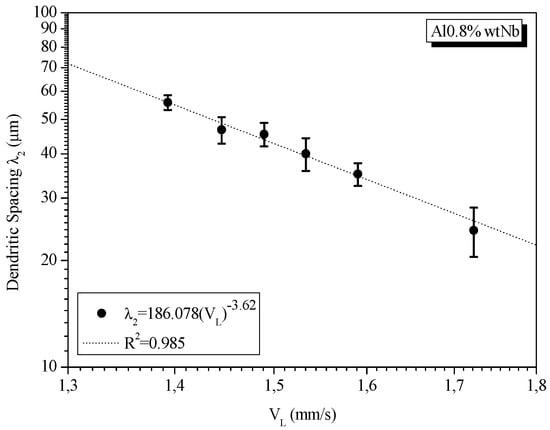
Figure 12.
Experimental equation of the secondary dendritic spacing as a function of liquidus isotherm velocity for Al–0.8 Nb (wt.%).
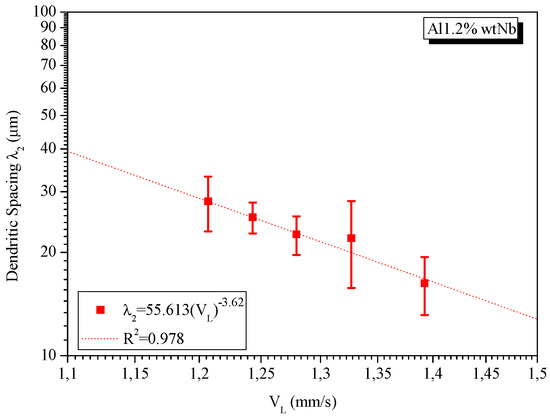
Figure 13.
Experimental equation of the secondary dendritic spacing as a function of liquidus isotherm velocity for Al–1.2 Nb (wt.%).
3.4. Characterisation: Microhardness, Dynamic Modulus of Elasticity, Damping Frequency, and XRD
Figure 14 shows the obtained microhardness values for alloys Al–0.8 Nb and Al–1.2 Nb (wt.%) as a function of the primary dendritic spacing. The microhardness measurements along the ingot did not show significant changes with the change in microstructure, remaining at an average value of 42.7 HV for Al–0.8%wt Nb alloy and 44 HV for Al–1.2%wt Nb alloy. There is no difference in the microhardness values as the volumetric amount of the intermetallic is insufficient to strengthen the microstructure.
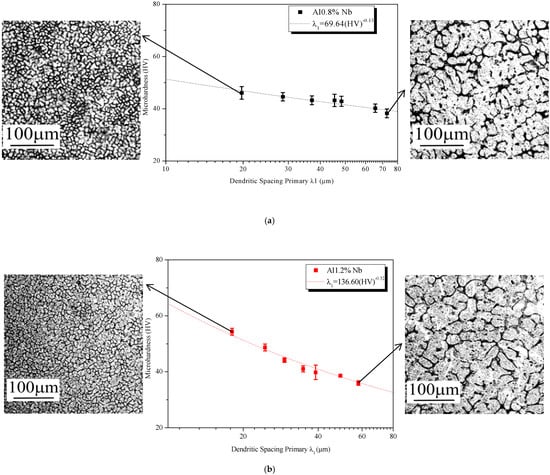
Figure 14.
Microhardness as a function of the primary dendritic spacing. (a) Al–0.8 Nb and (b) Al–1.2 Nb (wt.%).
Figure 15 shows the experimental values obtained by the impulse excitation test for the (a) modulus of elasticity, (b) the damping frequency, and (c) damping, in relation to the position of the metal/mold interface. Both the internal and external variables are directly dependent on the rate of heating and cooling, frequency, grain size, and the presence of precipitates [44,45,46]. The addition of Nb provided an approximately 70% increase in Al–1.2 wt.% Nb alloy’s damping (Figure 15c) forming a larger number of Al3Nb as shown by XRD. It indicates that the precipitate can be the reason of this increase.
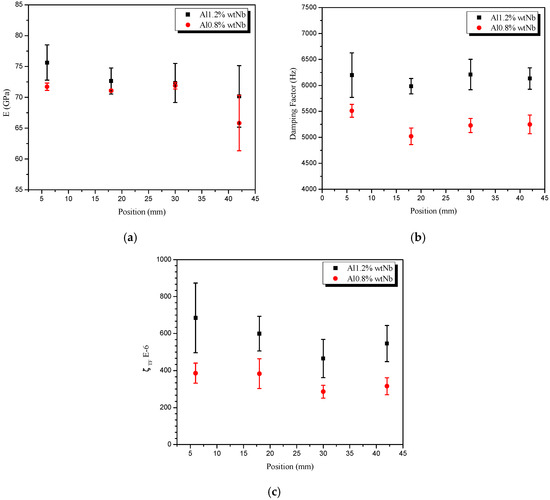
Figure 15.
(a) The modulus of elasticity, (b) the damping frequency, and (c) damping, in relation to the position of the metal/mold interface.
The XRD analyses presented in Figure 16 were performed with the objective of characterising the crystalline phases present in the microstructure of the alloys. According to the Elliott [47] diagram, the intermetallic phase identified using XRD was Al3Nb, as shown in Figure 16. The intensity of the Al3Nb peaks in the studied alloys confirms that the Al–0.8 wt.% Nb alloy has a smaller volumetric fraction of the Al3Nb solid solution. Thus, the damping seems to be influenced by the quantity of this volumetric fraction. Furthermore, Figure 14a–c suggests that it may also influence the microhardness. However, there was no significant change in the modulus of elasticity, as shown in Figure 15a.
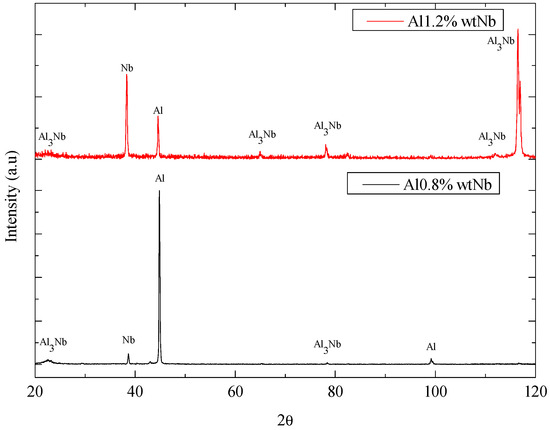
Figure 16.
X-ray diffraction (XRD) of the alloys Al–0.8 Nb and Al–1.2 Nb (wt.%).
4. Conclusions
The Nb content in the alloy influenced the characteristics related to the solidification kinetics, indicating that with the Nb addition, the spacings were more refined with the decrease in the values of the thermal parameters ( and VL). The primary dendritic growth of the alloys Al–0.8 Nb and Al–1.2 Nb (% wt), solidified in the upward unidirectional solidification device, can be represented by the experimental laws: λ1 = 600.1()−1.85 and λ1 = 133.6()−1.85, respectively. The experimental laws obtained for secondary dendritic growth: λ2 = 186.1(VL)−3.62 and λ2 = 55.6(VL)−3.62, respectively for 0.8%wt Nb and 1.2%wt Nb.
The Nb content and the thermal variables had tiny influence on the microhardness values, with average values of 42.7 HV and 44 HV, respectively for alloys with 0.8%wt Nb and 1.2%wt Nb.
The increase in the volumetric fraction of Al3Nb seems to influence the damping frequency and the damping, with increases of 18% and 70%, respectively. However, no significant differences were observed in the elastic modulus (71.07 GPa and 72.16 GPa, respectively for 0.8%wt Nb and 1.2%wt Nb) indicating that further studies are needed to clarify the influence of Al3Nb on the Al–Nb alloy properties.
Author Contributions
Conceptualization, D.M.R.; methodology, M.M.C. and D.M.R.; validation, M.M.C., T.P.S.; formal analysis, J.I.S.S. and M.M.C.; investigation, J.I.S.S., M.M.C., and T.P.S.; resources, M.M.C., T.P.S., and D.M.R.; writing—original draft preparation, M.M.C. and T.P.S.; writing—review and editing, D.M.R.; supervision, D.M.R.
Acknowledgments
The authors acknowledge financial support provided by CAPES (Coordination of Improvement of Higher-Level Personnel) and National Council for Scientific and Technological Development (CNPq).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, J.; Cui, C.; Han, M.; Chen, J.; Xu, N.; Liu, L.; Fu, H. Microstructure and property of Czochralski-grown Si–TaSi2 eutectic in situ composite for field emission. J. Cryst. Growth 2005, 276, 92–96. [Google Scholar] [CrossRef]
- Shafii, M.B.; Dehkordi, E.A.; Moghadam, M.E.; Koochesfahani, M.M. Koochesfahani. Using nucleators to control freckles in unidirectional solidification. Exp. Therm. Fluid Sci. 2009, 33, 1209–1215. [Google Scholar] [CrossRef]
- Bergeon, N.; Trivedi, R.; Billia, B.; Echebarria, B.; Karma, A.; Liu, S.; Weiss, C.; Mangelinck, N. Necessity of investigating microstructure formation during directional solidification of transparent alloys in 3D. Adv. Sp. Res. 2005, 36, 80–85. [Google Scholar] [CrossRef]
- Fadel, A.A.; Rosa, D.; Murça, L.B.; Fereira, J.L.A.; Araújo, J.A. Effect of high mean tensile stress on the fretting fatigue life of an Ibis steel reinforced aluminium conductor. Int. J. Fatigue 2012, 42, 24–34. [Google Scholar] [CrossRef]
- Cesnik, M. Uninterrupted and accelerated vibrational fatigue testing with simultaneous monitoring of the natural frequency and damping. J. Sound Vib. 2012, 331, 5370–5382. [Google Scholar] [CrossRef]
- Dieter, G.E. Mechanical metallurgy, 1st ed.; Mehl, R.F., Bver, M., Eds.; McGraw—Hill Book Company: New York City, NY, USA, 1961; ISBN 07-016890-3. [Google Scholar]
- Alves, A.R.; Coutinho, A.D.R. The evolution of the niobium production in Brazil. Mater. Res. 2015, 18, 106–112. [Google Scholar] [CrossRef]
- Heisterkamp, F.; Carneiro, T. Niobium: Future Possibilities–Technology and the Market Place. In Proceedings of the International Symposium, Niobium, Orlando, FL, USA, 2–5 December 2001; Science & Tecnology; pp. 1109–1160. [Google Scholar]
- Li, C.Y.; Huang, J.F.; Lu, J.; Cao, L.Y.; Fei, J. Effect of Nb coating on oxidation behavior of C/C composites. Corros. Sci. 2012, 63, 182–186. [Google Scholar] [CrossRef]
- Car, T.; Salamon, K.; Radić, N.; Ivkov, J. Elastic Energy Fraction as the Phenomenological Connection Between Electrical, Mechanical and Thermal Properties of the Al–(Nb, Mo, Ta, W) Amorphous Thin Films. Met. Mater. Int. 2019, 1–8. [Google Scholar] [CrossRef]
- Zhu, Z.; Du, Y.; Zhang, L.; Chen, H.; Xu, H.; Tang, C. Experimental identification of the degenerated equilibrium and thermodynamic modeling in the Al-Nb system. J. Alloy. Compd. 2008, 460, 632–638. [Google Scholar] [CrossRef]
- Pisch, A.; Pasturel, A. On the partial enthalpy of mixing of Nb in liquid Al. Thermochim. Acta 2019, 671, 103–109. [Google Scholar] [CrossRef]
- Hutchinson, C.R.; Fan, X.; Pennycook, S.J.; Shiflet, G.J. On the origin of the high coarsening resistance of Ω plates in Al-Cu-Mg-Ag alloys. Acta Mater. 2001, 49, 2827–2841. [Google Scholar] [CrossRef]
- Wang, C.; Gao, Q.; Yuan, Y.; Zhang, H.; Zhang, J.; Wang, Q.; Qu, F. Microstructure evolutions of Ni-Ti-Nb-Al alloys with different Al addition. J. Alloy. Compd. 2017, 695, 2923–2929. [Google Scholar] [CrossRef]
- Takeyama, M.B.; Noya, A. Application of Al–Nb alloy film to metal capping layer on Cu Application of Al–Nb alloy fi lm to metal capping layer on Cu. Jpn. J. Appl. Phys. 2016, 55, 02BC22. [Google Scholar] [CrossRef]
- Munitz, A.; Gokhale, A.B.; Abbaschian, R. Effect of supercooling on the microstructure of Al-Nb alloys. J. Mater. Sci. 2000, 35, 2263–2271. [Google Scholar] [CrossRef]
- Koutná, N.; Erdely, P.; Zöhrer, S.; Franz, R.; Du, Y.; Liu, S.; Mayrhofer, P.H.; Holec, D. Experimental Chemistry and Structural Stability of AlNb 3 Enabled by Antisite Defects Formation. Materials 2019, 12, 1104. [Google Scholar] [CrossRef] [PubMed]
- Jorda, J.L.; Flükiger, R.; Muller, J. A new metallurgical aluminium system investigation of the niobium. J. Less Common Met. 1980, 75, 227–239. [Google Scholar] [CrossRef]
- He, C.; Stein, F.; Palm, M. Thermodynamic description of the systems Co-Nb, Al-Nb and Co-Al-Nb. J. Alloy. Compd. 2015, 637, 361–375. [Google Scholar] [CrossRef]
- Wang, X.L.; Zhang, K.F. Mechanical alloying, microstructure and properties of Nb-16Si alloy. J. Alloy. Compd. 2010, 490, 677–683. [Google Scholar] [CrossRef]
- Stefan-Kharicha, M.; Kharicha, A.; Wu, M.; Ludwig, A. Observation of flow regimes and transitions during a columnar solidification experiment. Fluid Dyn. Res. 2014, 46, 4. [Google Scholar] [CrossRef]
- Rosa, D.M.; Spinelli, J.E.; Ferreira, I.L.; Garcia, A. Cellular/dendritic transition and microstructure evolution during transient directional solidification of Pb-Sb alloys. Metall. Mater. Trans. A 2008, 39, 2161–2174. [Google Scholar] [CrossRef]
- Yu, L.; Ding, G.L.; Reye, J.; Tewari, S.N.; Ojha, S.N. Cellular/dendritic array tip morphology during directional solidification of Pb-5.8 Wt Pct Sb alloy. Metall. Mater. Trans. A 1999, 30, 2463–2472. [Google Scholar] [CrossRef]
- Ding, G.L.; Huang, W.D.; Huang, X.; Lin, X.; Zhou, Y.H. On primary dendritic spacing during unidirectional solidification. Acta Mater. 1996, 44, 3705–3709. [Google Scholar] [CrossRef]
- Spinelli, J.E.; Rosa, D.M.; Ferreira, I.L.; Garcia, A. Influence of melt convection on dendritic spacings of downward unsteady-state directionally solidified Al-Cu alloys. Mater. Sci. Eng. A 2004, 383, 271–282. [Google Scholar] [CrossRef]
- Miller, J.D.; Pollock, T.M. Stability of dendrite growth during directional solidification in the presence of a non-axial thermal field. Acta Mater. 2014, 78, 23–36. [Google Scholar] [CrossRef]
- Bertelli, F.; Freitas, E.S.; Cheung, N.; Arenas, M.A.; Conde, A.; de Damborenea, J.; Garcia, A. Microstructure, tensile properties and wear resistance correlations on directionally solidified Al-Sn-(Cu; Si) alloys. J. Alloy. Compd. 2016, 695, 3621–3631. [Google Scholar] [CrossRef]
- Vida, T.A.; Conde, A.; Freitas, E.S.; Arenas, M.A.; Cheung, N.; Brito, C.; de Damborenea, J.; Garcia, A. Directionally solidified dilute Zn-Mg alloys: Correlation between microstructure and corrosion properties. J. Alloy. Compd. 2017, 723, 536–547. [Google Scholar] [CrossRef]
- Reis, B.P.; França, R.P.; Spim, J.A.; Garcia, A.; Costa, E.M.; Santos, C.A. The effects of dendritic arm spacing (as-cast) and aging time (solution heat-treated) of Al–Cu alloy on hardness. J. Alloy. Compd. 2013, 549, 324–335. [Google Scholar] [CrossRef]
- Reis, B.P.; Lopes, M.M.; Garcia, A.; Santos, C.A. The correlation of microstructure features, dry sliding wear behavior, hardness and tensile properties of Al-2wt%Mg-Zn alloys. J. Alloy. Compd. 2018, 764, 267–278. [Google Scholar] [CrossRef]
- Kakitani, R.; Reyes, R.V.; Garcia, A.; Spinelli, J.E.; Cheung, N. Relationship between spacing of eutectic colonies and tensile properties of transient directionally solidified Al-Ni eutectic alloy. J. Alloy. Compd. 2018, 733, 59–68. [Google Scholar] [CrossRef]
- Xavier, M.G.; Cruz, C.B.; Kakitani, R.; Silva, B.L.; Garcia, A.; Cheung, N.; Spinelli, J.E. Directional solidification of a Sn-0.2Ni solder alloy in water-cooled copper and steel molds: Related effects on the matrix micromorphology, nature of intermetallics and tensile properties. J. Alloy. Compd. 2017, 723, 1039–1052. [Google Scholar] [CrossRef]
- Garcia, A. The effects of Zn segregation and microstructure length scale on the corrosion behavior of a directionally solidi fi ed Mg-25 wt.% Zn alloy. J. Alloy. Compd A 2017, 723, 649–660. [Google Scholar] [CrossRef]
- Quaresma, M.V. The effect of solidification thermal variables on surface quality of Al–Cu ingots. J. Alloy. Compd. 2007, 428, 130–138. [Google Scholar] [CrossRef]
- Silva, B.L.; Garcia, A.; Spinelli, J.E. Complex eutectic growth and Bi precipitation in ternary Sn-Bi-Cu and Sn-Bi-Ag alloys. J. Alloy. Compd. 2016, 691, 600–605. [Google Scholar] [CrossRef]
- Santos, C.A.; Garcia, A. Determination of transient interfacial heat transfer coefficients in chill mold. Castings 2001, 319, 174–186. [Google Scholar] [CrossRef]
- ASTM E3-11. Standard Guide for Preparation of Metallographic Specimens 1; ASTM International: West Conshohocken, PA, USA, 2011; pp. 1–12. [Google Scholar] [CrossRef]
- Gündüz, M.; Çadirli, E. Directional solidification of aluminium-copper alloys. Mater. Sci. Eng. A 2002, 327, 167–185. [Google Scholar] [CrossRef]
- ASTM E1876-15. Standard Test Method for Dynamic Young’s Modulus, Shear Modulus, and Poisson’s Ratio by Impulse Excitation of Vibration; ASTM International: West Conshohocken, PA, USA, 2015. [Google Scholar] [CrossRef]
- ASTM International. ASTM E384: Standard Test Method for Knoop and Vickers Hardness of Materials; ASTM International: West Conshohocken, PA, USA, 2012; pp. 1–43. [Google Scholar] [CrossRef]
- Okamoto, T.; Kishitake, K. Dendritic structure in unidirectionally solidified aluminum, tin, and zinc base binary alloys. J. Cryst. Growth 1975, 29, 137–146. [Google Scholar] [CrossRef]
- Wang, F.; Ma, D.X.; Zhang, J.; Bogner, S.; Bührig-Polaczek, A. A high thermal gradient directional solidification method for growing superalloy single crystals. J. Mater. Process. Technol. 2014, 214, 3112–3121. [Google Scholar] [CrossRef]
- Brundidge, C.L.; Miller, J.D.; Pollock, T.M. Development of dendritic structure in the liquid-metal-cooled, directional-solidification process. Metall. Mater. Trans. A 2011, 42, 2723–2732. [Google Scholar] [CrossRef]
- Cai, W.; Lu, X.L.; Zhao, L.C. Damping behavior of TiNi-based shape memory alloys. Mater. Sci. Eng. A 2005, 394, 78–82. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.C.; Liu, S.W.; Rong, L.J.; Zhao, X.Q. Damping capacity of TiNi-based shape memory alloys. J. Alloy. Compd. 2009, 482, 151–154. [Google Scholar] [CrossRef]
- Van Humbeeck, J. Damping capacity of thermoelastic martensite in shape memory alloys. J. Alloy. Compd. 2003, 355, 58–64. [Google Scholar] [CrossRef]
- Elliott, R.; Shunk, F. The Al-Nb system (Aluminium-Niobium). Bull. Alloy Ph. Diagr. 1981, 2, 75–81. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).