Cyclic Indentation of Iron: A Comparison of Experimental and Atomistic Simulations
Abstract
1. Introduction
2. Materials and Experimental Method
3. Simulation Method
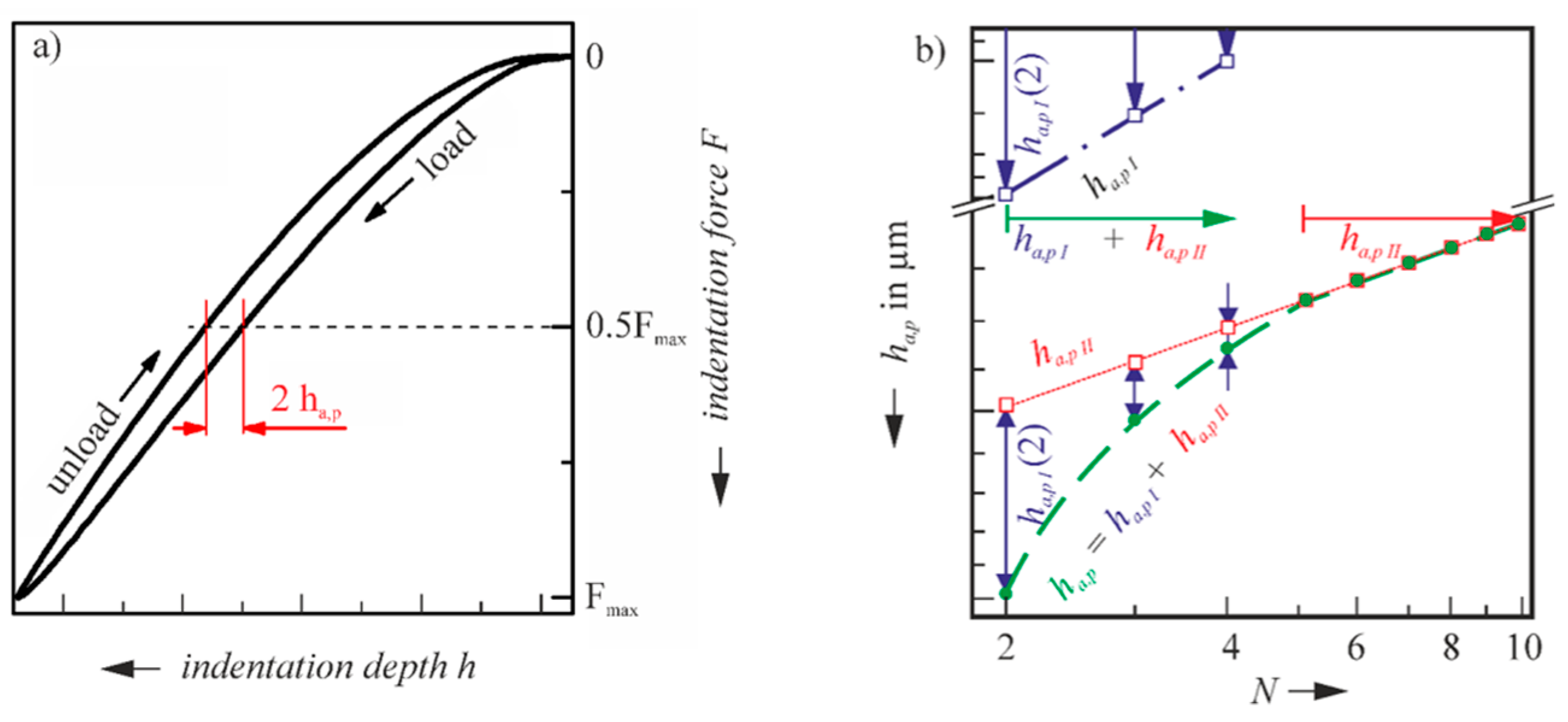
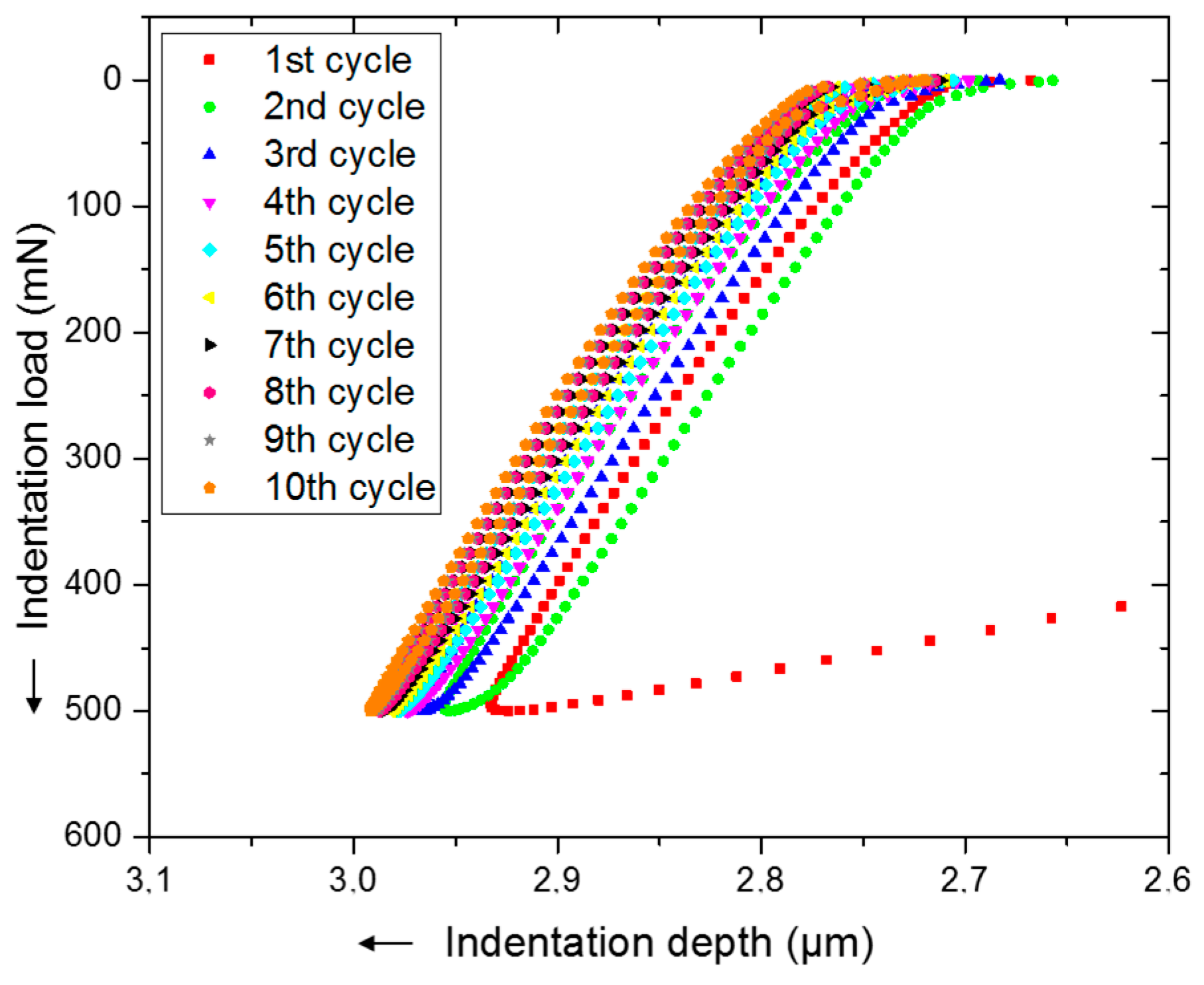
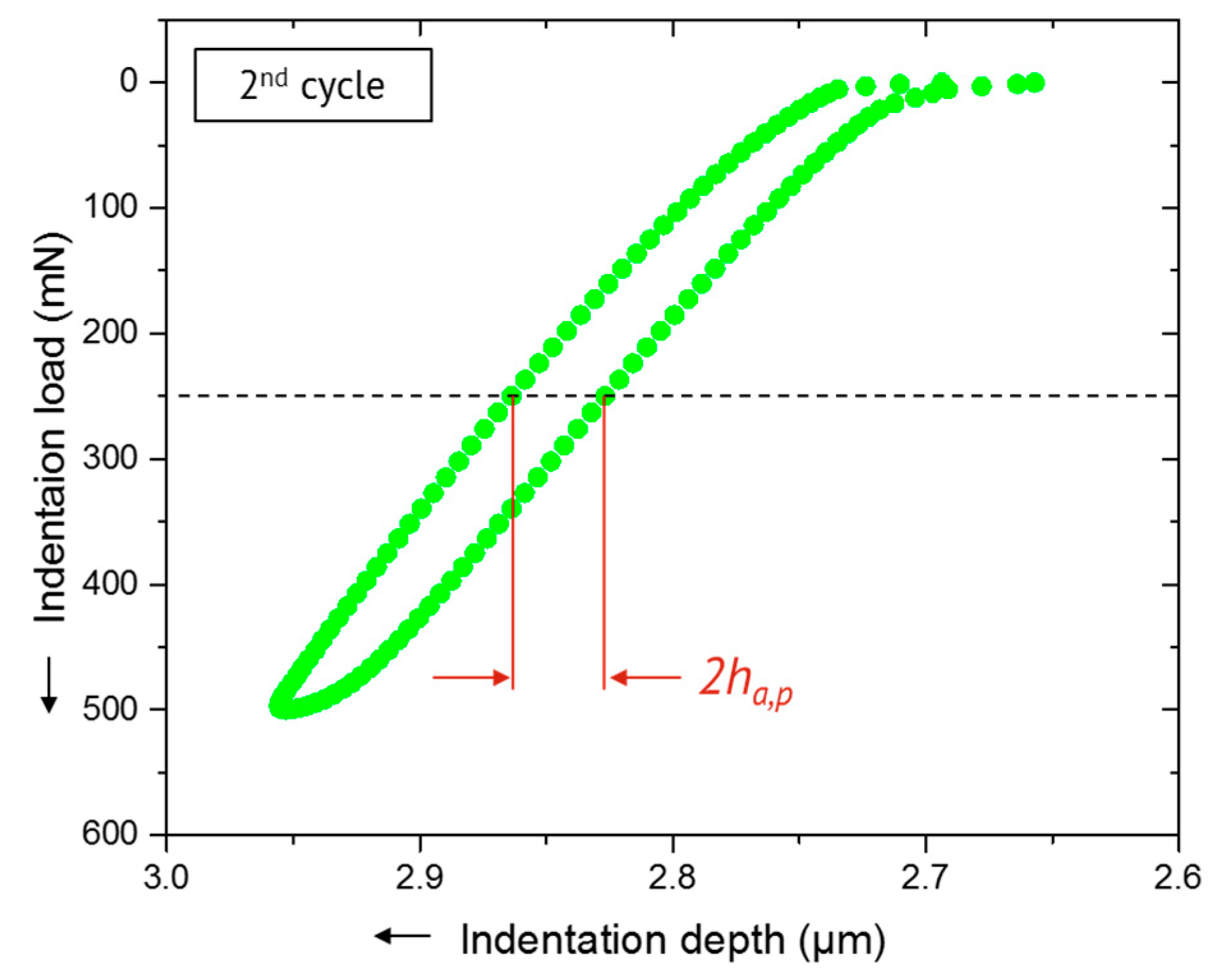
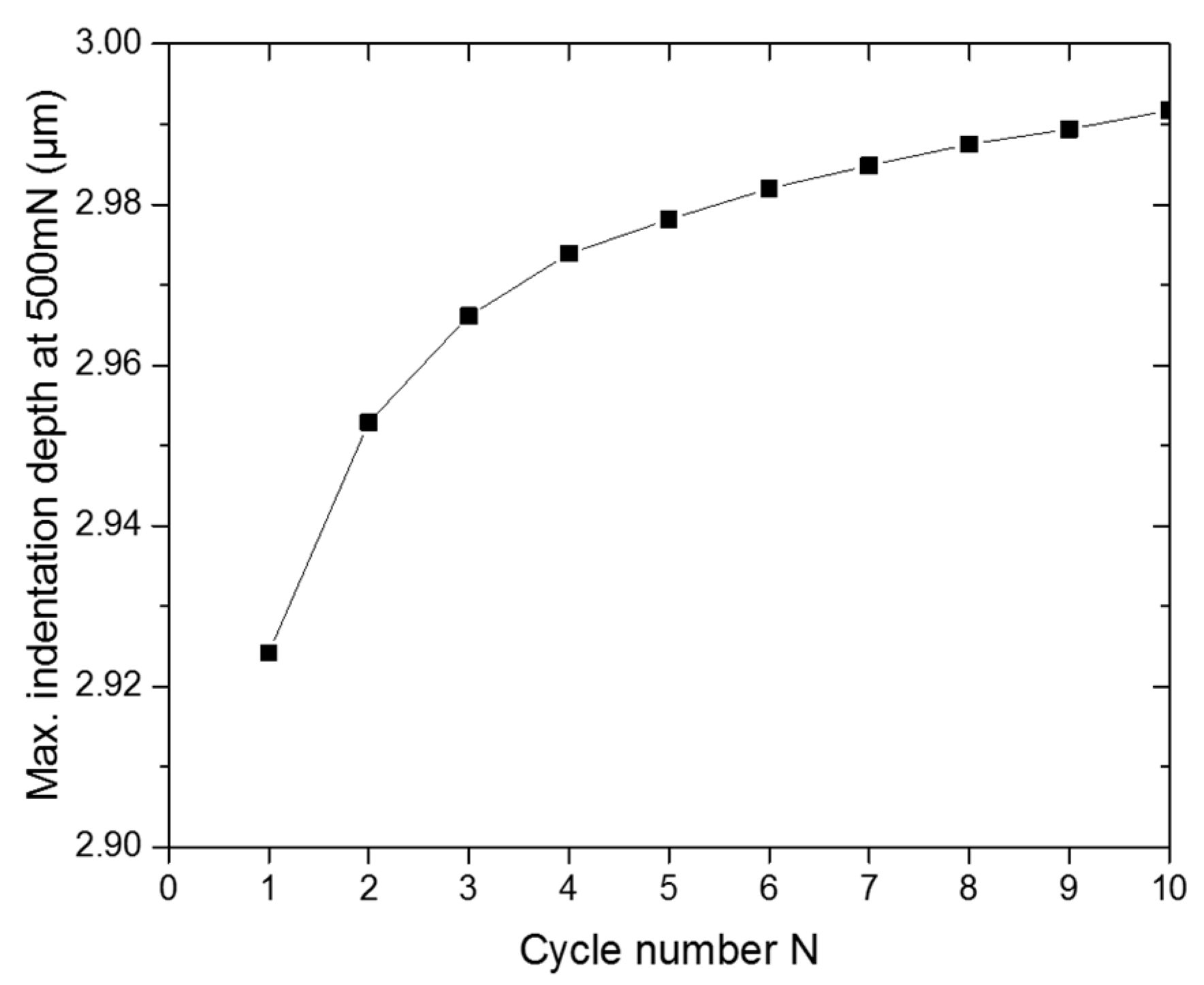
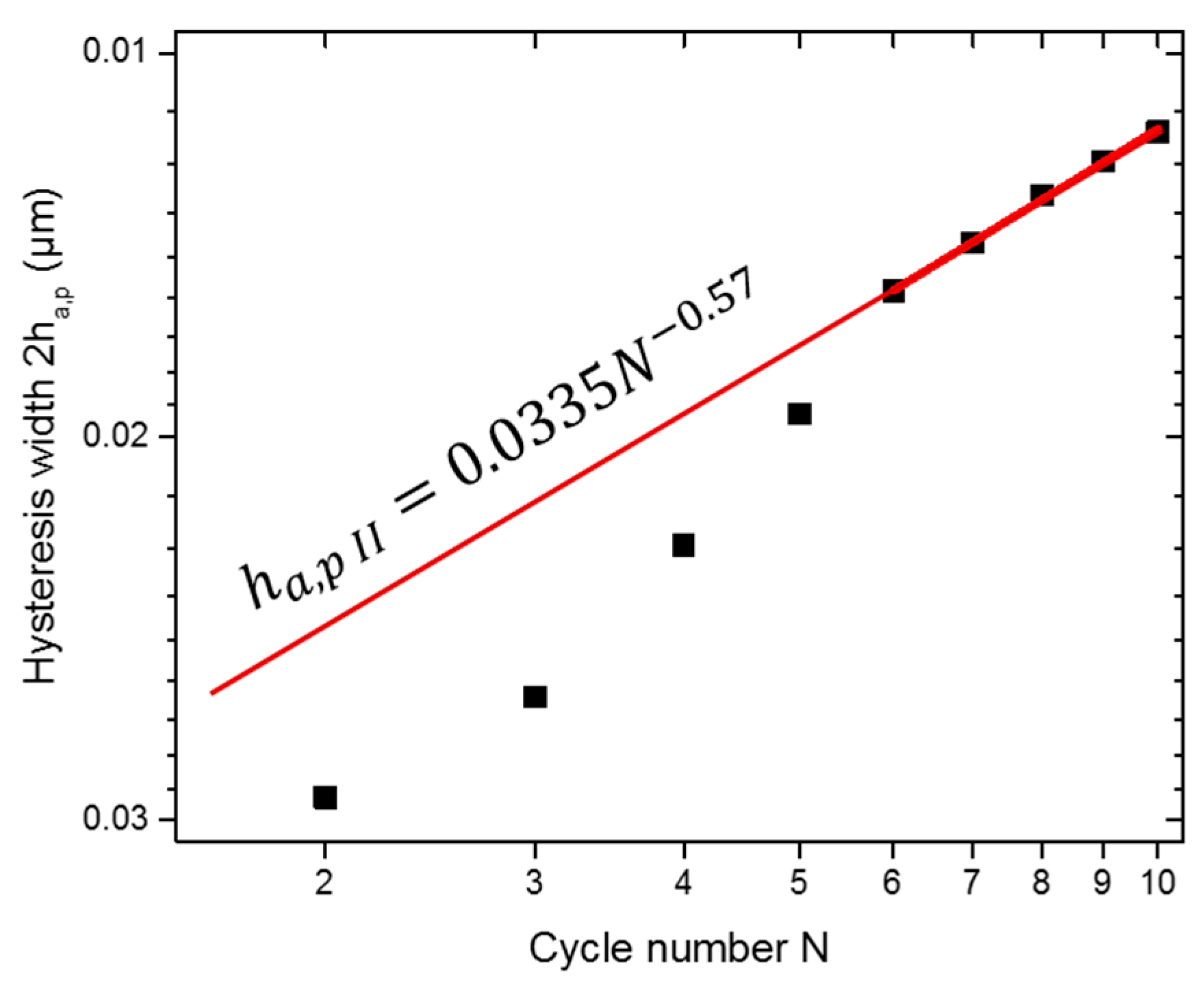
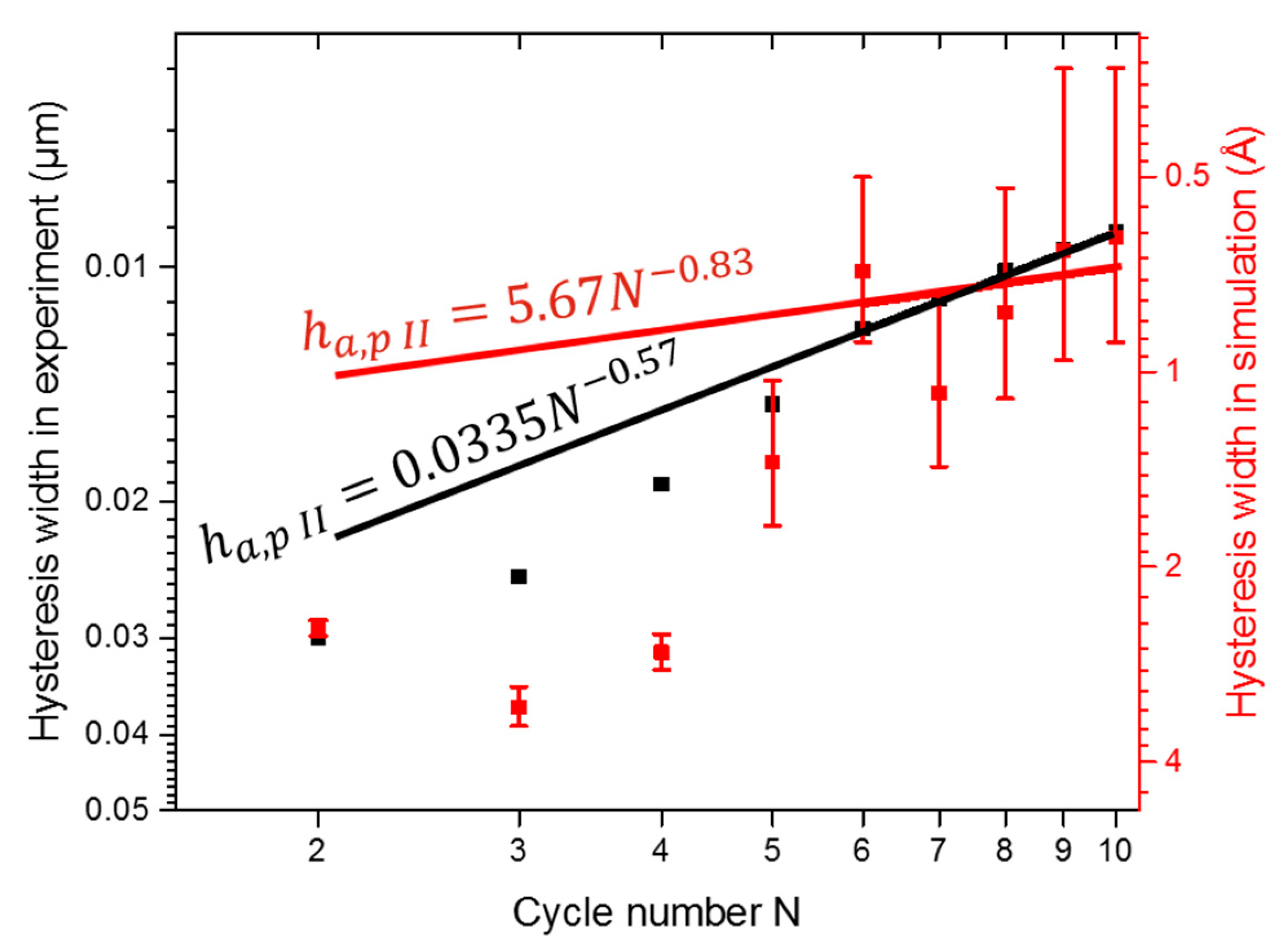
4. Experimental Results
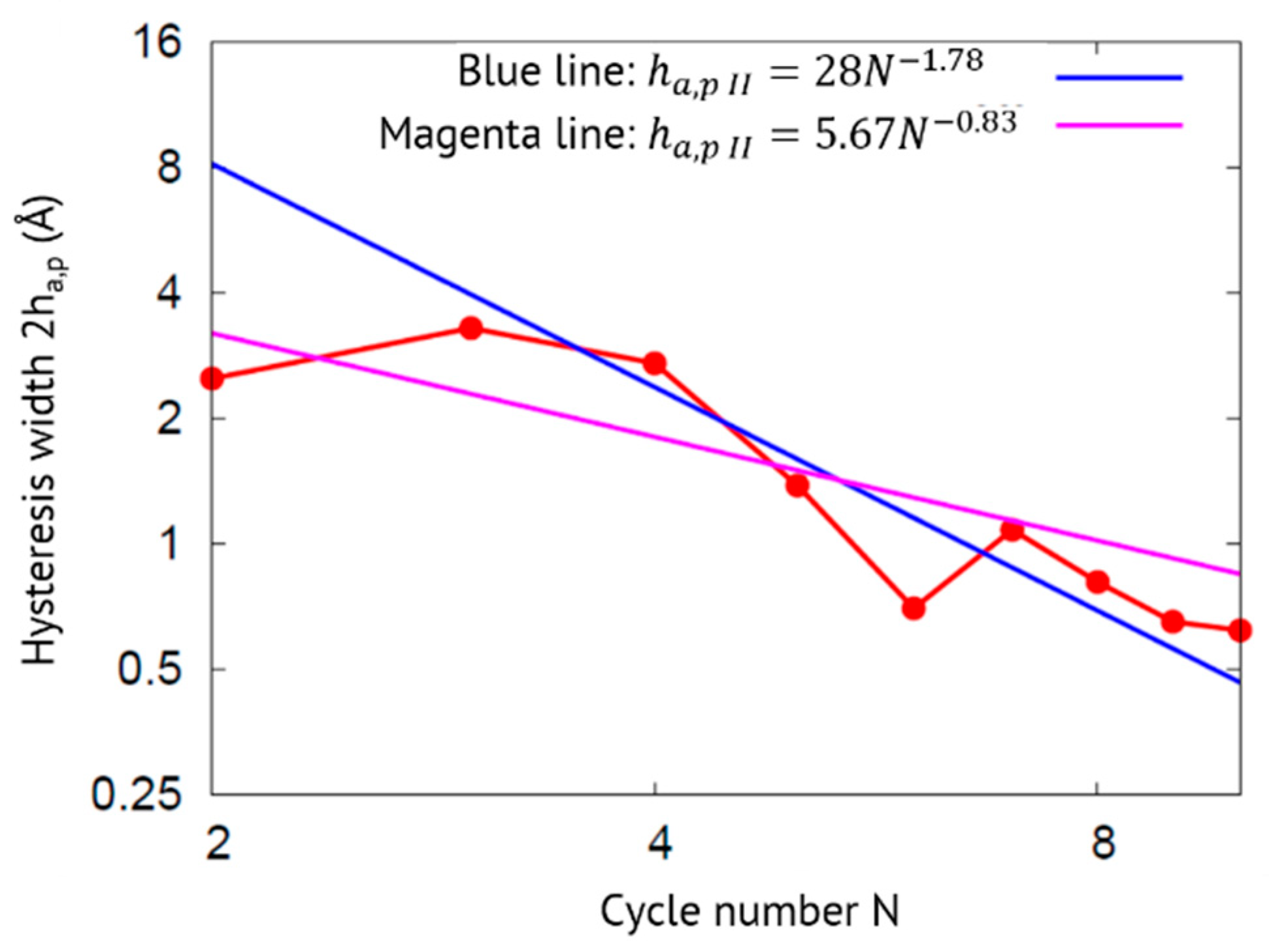
5. Simulation Results
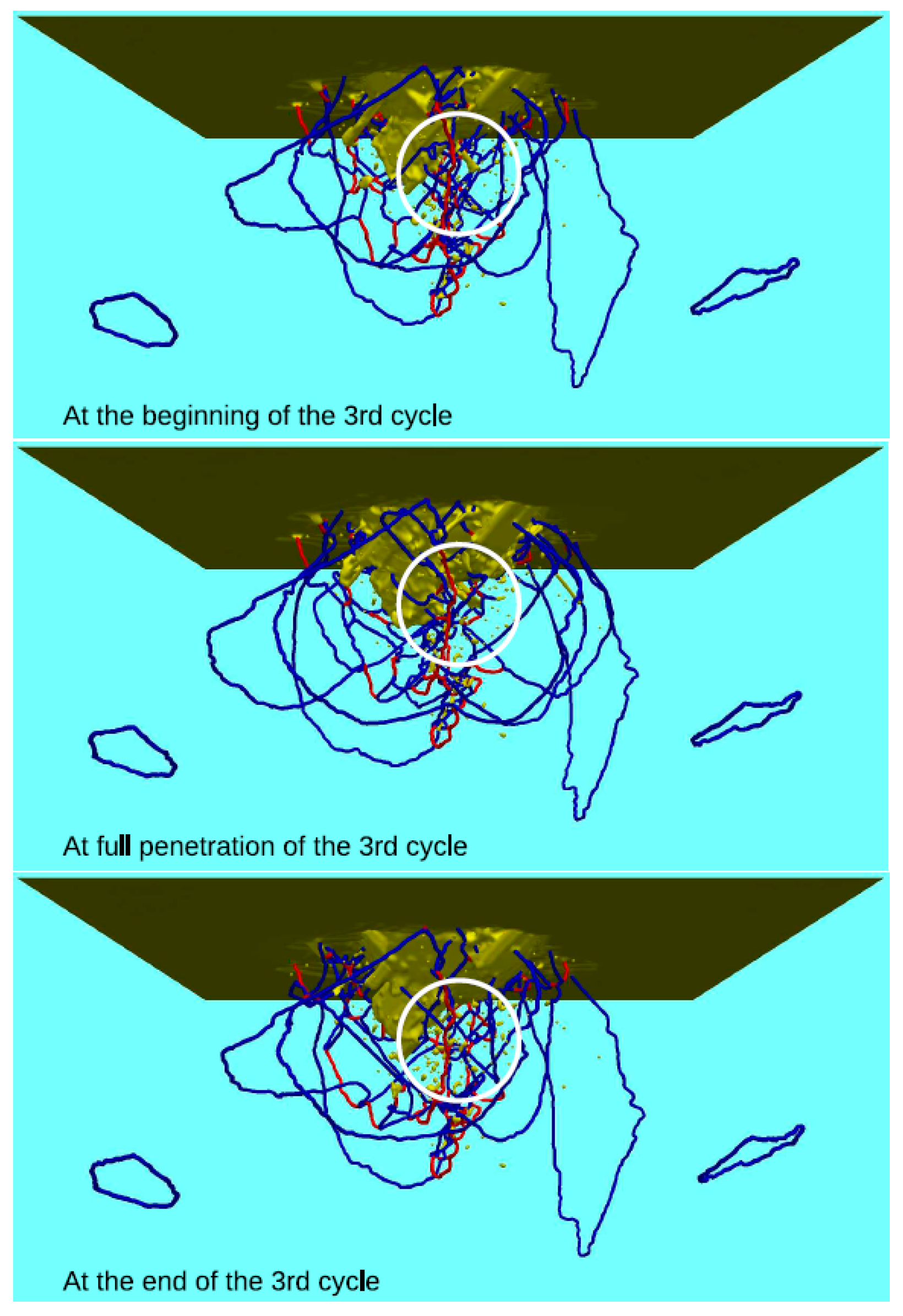
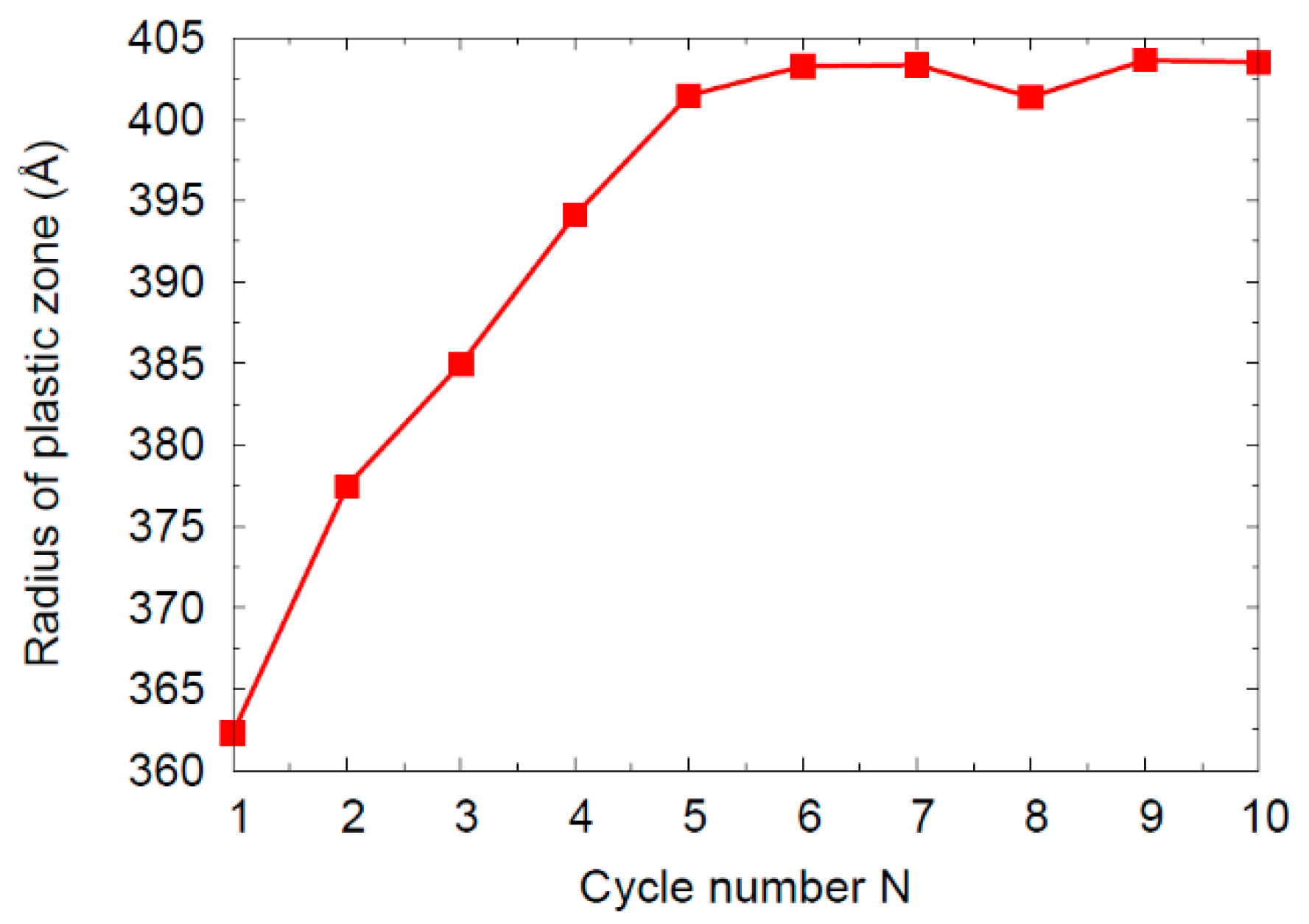
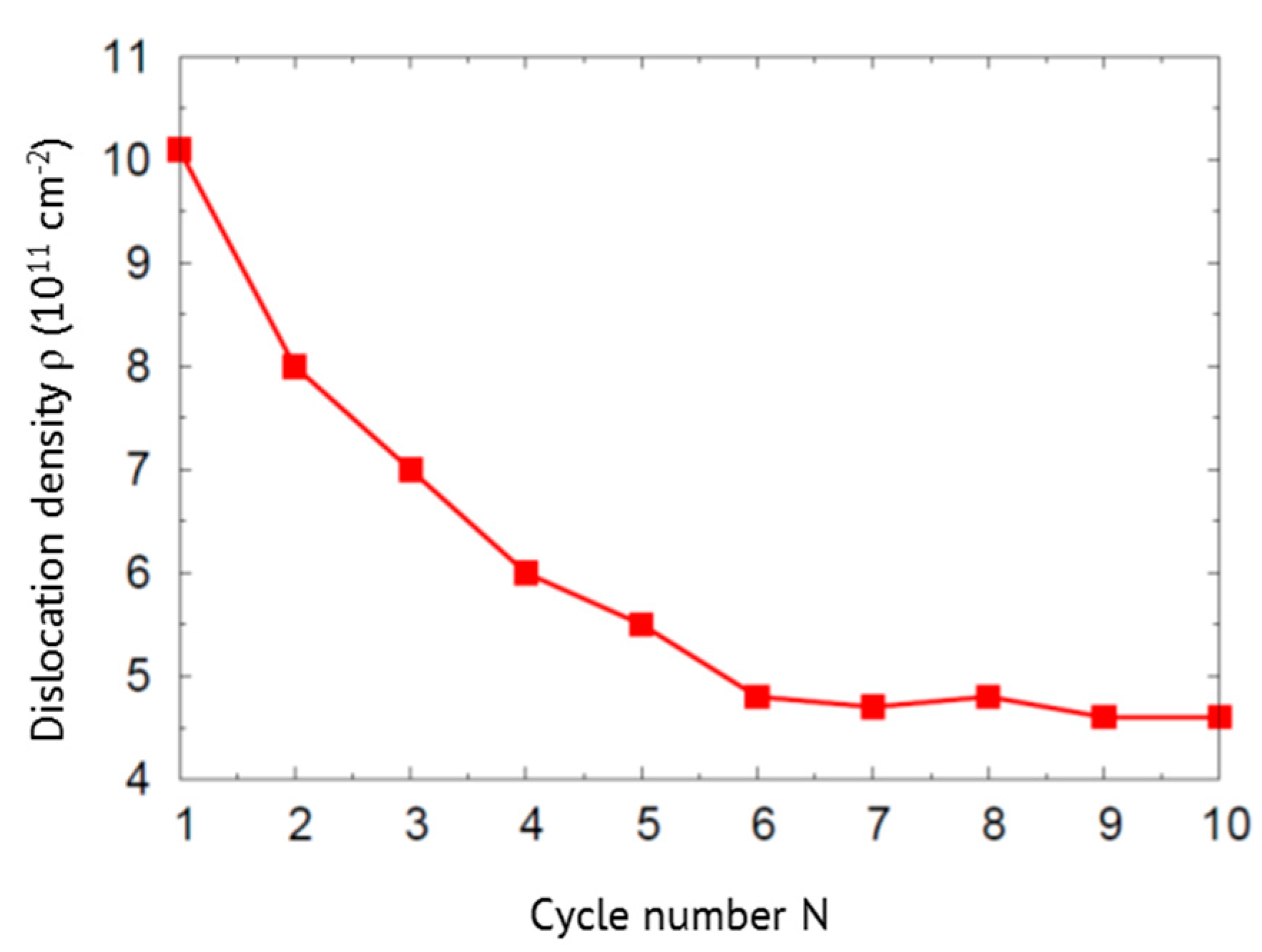
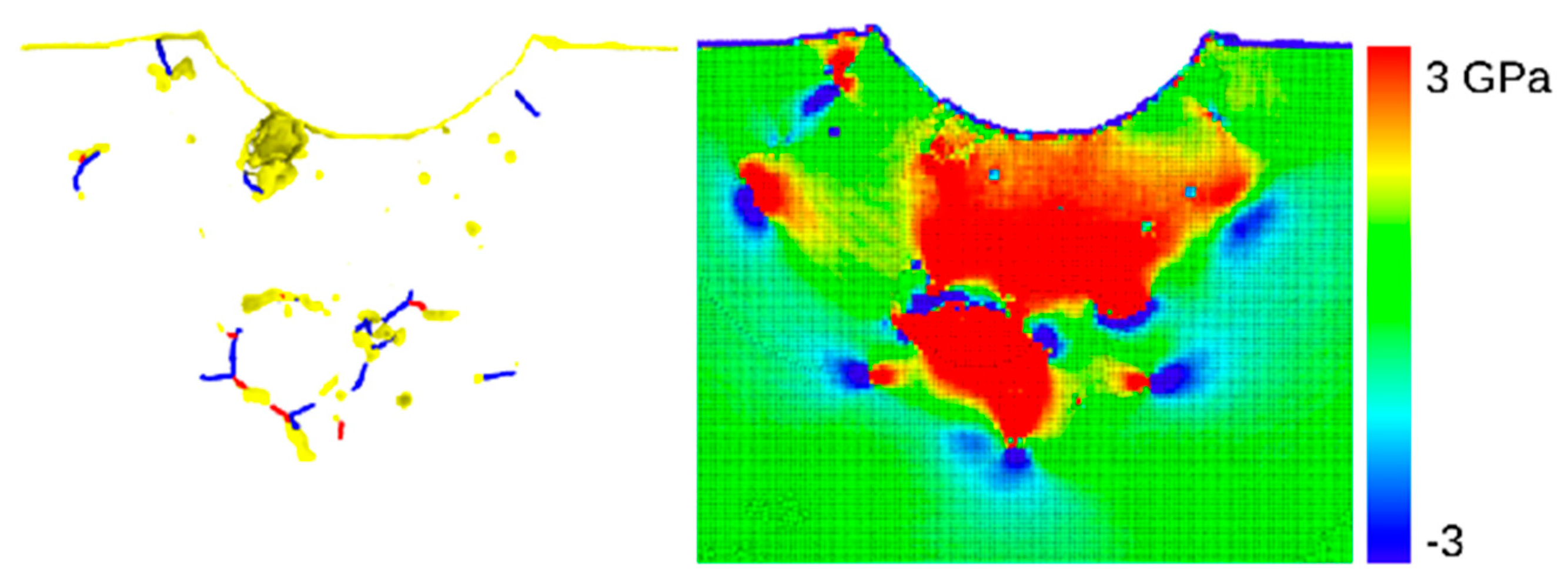
5.1. Plasticity
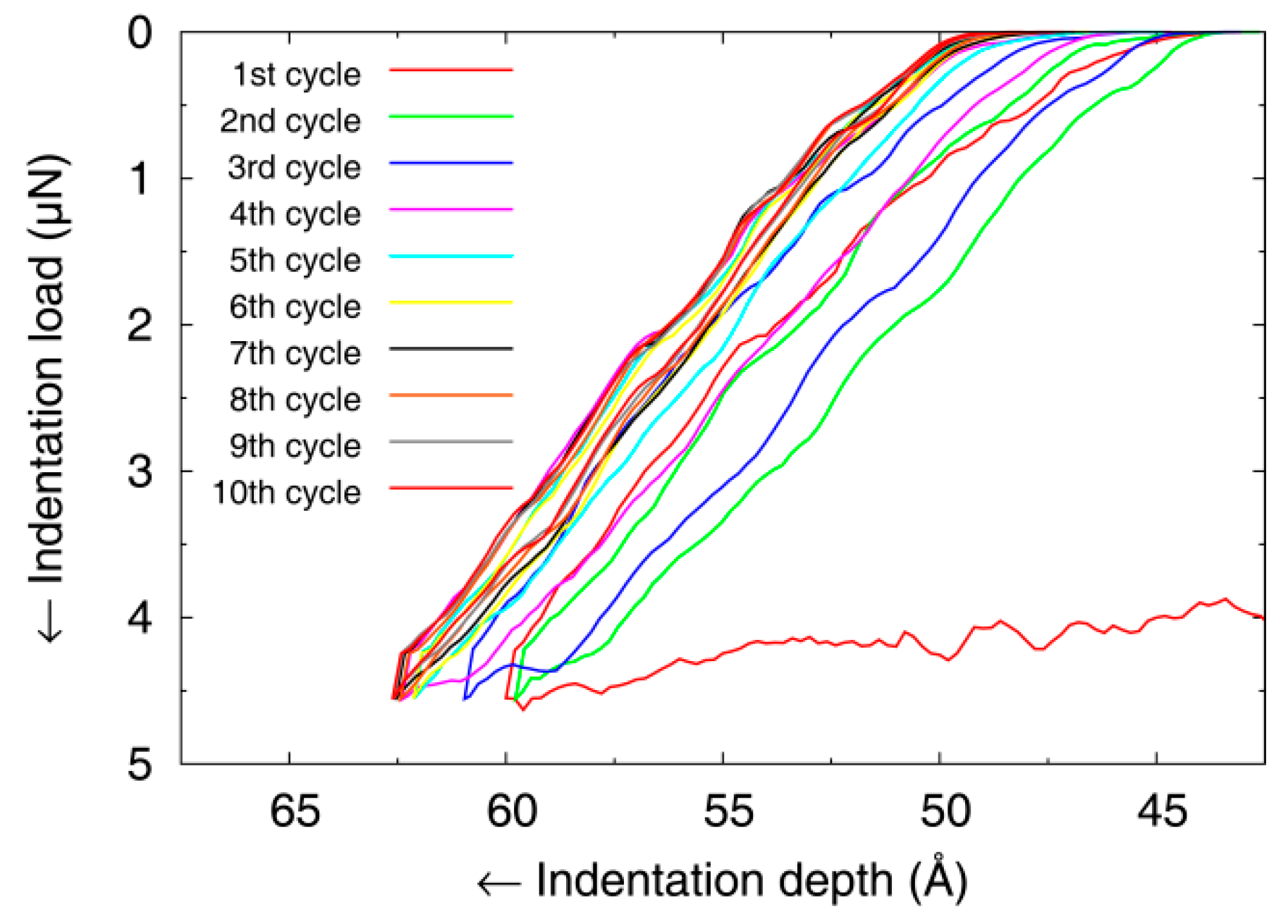
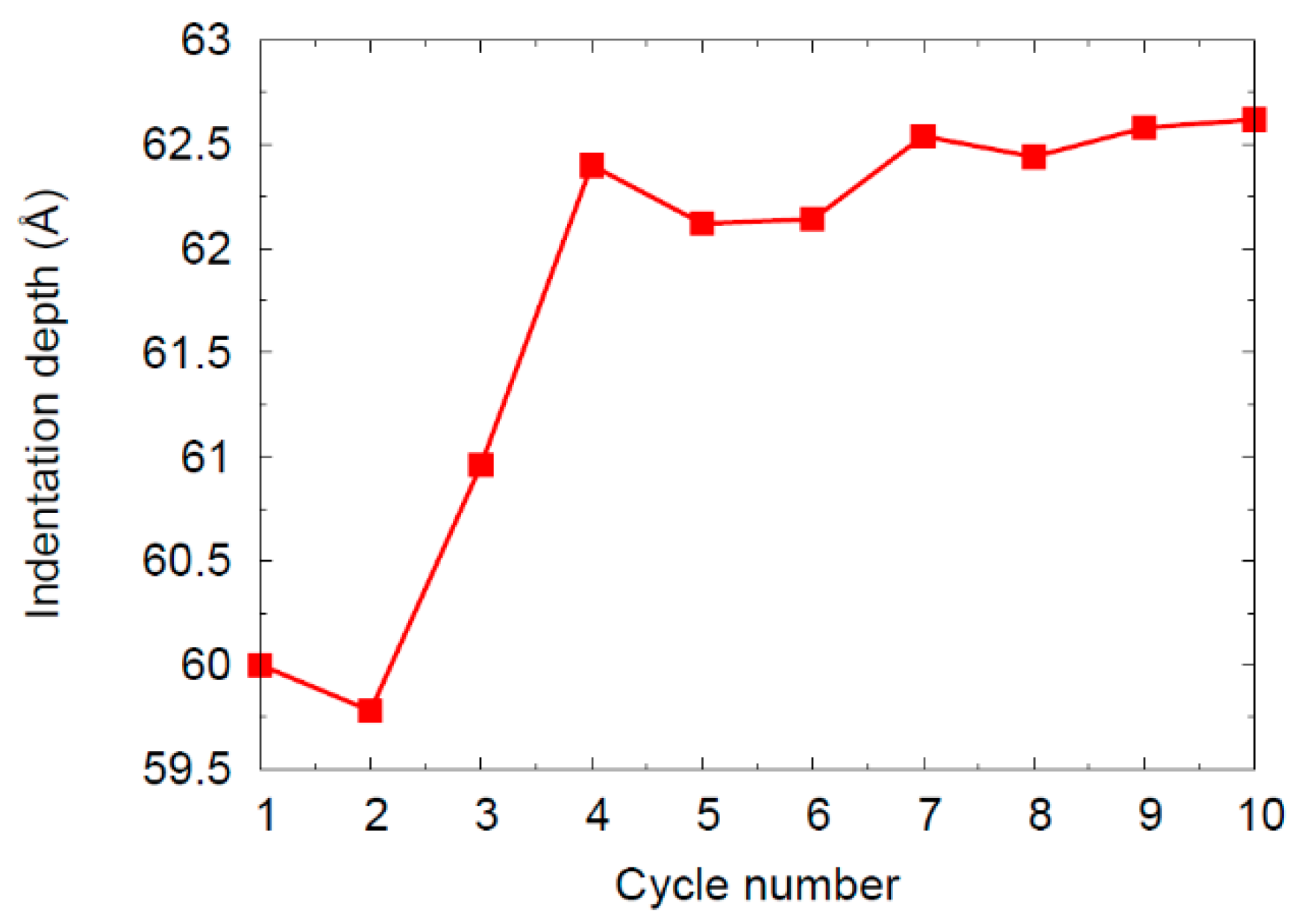
5.2. Load-Depth Curves
6. Conclusions
- Under subsequent indentations: (i) the dislocation network widens slightly, since the stress gradients exerted by the indenter move the farthest shear loops further out; (ii) the network simplifies in the vicinity of the indent pit, since the highly non-equilibrium dislocation structure generated in the first indentation is subject to dislocation reactions when dislocations move in the stress fields of the subsequent indentation cycles.
- Both effects lower the dislocation density. We thus observe in the atomistic simulations effectively a softening under cyclic indentation.
- As a consequence, the indentation depth increases slightly under constant load.
- As the changes in the dislocation network become more and more negligible, so do the changes in the indentation depth and hysteresis width.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schwarm, S.C.; Kolli, R.P.; Aydogan, E.; Mburu, S.; Ankem, S. Characterization of phase properties and deformation in ferritic-austenitic duplex stainless steels by nanoindentation and finite element method. Mater. Sci. Eng. A 2017, 680, 359–367. [Google Scholar] [CrossRef]
- Basan, R.; Franulović, M.; Smokvina Hanza, S. Estimation of cyclic stress-strain curves for low-alloy steel from hardness. Metalurgija 2010, 49, 83–86. [Google Scholar]
- Chicot, D.; Roudet, F.; Zaoui, A.; Louis, G.; Lepingle, V. Influence of visco-elasto-plastic properties of magnetite on the elastic modulus: Multicyclic indentation and theoretical studies. Mater. Chem. Phys. 2010, 119, 75–81. [Google Scholar] [CrossRef]
- Roessle, M.L.; Fatemi, A. Strain-controlled fatigue properties of steels and some simple approximations. Int. J. Fatigue 2000, 22, 495–511. [Google Scholar] [CrossRef]
- Blada, C.B.; Shen, Y.-L. Cyclic indentation behavior of layered nanocomposites: viscoplastic numerical study. J. Nanomech. Micromech. 2014, 4, 4013001. [Google Scholar] [CrossRef]
- Faisal, N.H.; Prathuru, A.K.; Goed, S.; Ahmed, R.; Droubi, M.G.; Baeke, B.D.; Fu, Y.Q. Cyclic nanoindentation and nano-impact fatigue mechanisms of functionally graded TiN/TiNi film. Shap. Mem. Superelasticity 2017, 3, 149–167. [Google Scholar] [CrossRef]
- Leng, Y.; Yang, G.; Hu, Y.; Zheng, L. Computer experiments on nano-indentation: A molecular dynamics approach to the elasto-plastic contact of metal copper. J. Mater. Sci. 2000, 35, 2061–2067. [Google Scholar] [CrossRef]
- Ruestes, C.J.; Alabd Alhafez, I.; Urbassek, H.M. Atomistic studies of nanoindentation—A review of recent advances. Crystals 2017, 7, 293. [Google Scholar] [CrossRef]
- Fischer-Cripps, A.C. Nanoindentation, 2nd ed.; Springer: New York, NY, USA, 2004. [Google Scholar]
- Cui, Y.-Y.; Jia, Y.-F.; Xuan, F.-Z. Micro-deformation evolutions of the constituent phases in duplex stainless steel during cyclic nanoindentation. Sci. Rep. 2018, 8, 6199. [Google Scholar] [CrossRef]
- Kramer, H.S.; Starke, P.; Klein, M.; Eifler, D. Cyclic hardness test PHYBALCHT – Short-time procedure to evaluate fatigue properties of metallic materials. Int. J. Fatigue 2014, 63, 78–84. [Google Scholar] [CrossRef]
- Blinn, B.; Görzen, D.; Klein, M.; Eifler, D.; Beck, T. PhyBaLCHT – Influence of indentation force on the results of cyclic hardness tests and investigations of comparability to uniaxial fatigue loading. Int. J. Fatigue 2019, 119, 78–88. [Google Scholar] [CrossRef]
- Deldar, S.; Smaga, M.; Beck, B. Investigating the fatigue behavior of grain-oriented Fe-3%Si steel sheets using magnet-optical Kerr microscopy and micromagnetic multiparameter, microstructure and stress analysis. MATEC Web Conf. 2018, 165, 06006. [Google Scholar] [CrossRef]
- Bambach, M.D.; Bleck, W.; Kramer, H.S.; Klein, M.; Eifler, D.; Beck, T.; Surm, H.; Zoch, H.-W.; Hoffmann, F.; Radulescu, A. Tailoring the hardening behavior of 18CrNiMo7-6 via Cu alloying. Steel Res. Int. 2016, 87, 550–561. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Ruestes, C.J.; Bringa, E.M.; Gao, Y.; Urbassek, H.M. Molecular dynamics modeling of nanoindentation. In Applied Nanoindentation in Advanced Materials; Tiwari, A., Natarajan, S., Eds.; Wiley: Chichester, UK, 2017; pp. 313–345. [Google Scholar]
- Klechner, C.L.; Plimpton, S.J.; Hamilton, J.C. Dislocation nucleation and defect structure during surface indentation. Phys. Rev. B 1998, 58, 11085–11088. [Google Scholar] [CrossRef]
- Ziegenhain, G.; Hartmaier, A.; Urbassek, H.M. Pair vs. many-body potentials: Influence on elastic and plastic behavior in nanoindentation of fcc metals. J. Mech. Phys. Sol. 2009, 57, 1514–1526. [Google Scholar] [CrossRef]
- Mendelev, M.I.; Han, S.; Srolovitz, D.J.; Ackland, G.J.; Sun, D.Y.; Asta, M. Development of new interatomic potentials appropriate for crystalline and liquid iron. Philos. Mag. 2003, 83, 3977–3994. [Google Scholar] [CrossRef]
- Stukowski, A.; Albe, K. Extracting dislocations and non-dislocation crystal defects from atomistic simulation data. Model. Silul. Mater. Sci. Eng. 2010, 18, 085001. [Google Scholar] [CrossRef]
- Henderson, A. Paraview Guide, a Parallel Visualization Application; Kitware Inc.: Clifton Park, NY, USA, 2007; Available online: http://www.paraview.org (accessed on 9 May 2019).
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Modell. Simul. Mater. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Remington, T.P.; Ruestes, C.J.; Bringa, E.M.; Remington, B.A.; Lu, C.H.; Kad, B.; Meyers, M.A. Plastic deformation in nanoindentation of tantalum: A new mechanism for prismatic loop formation. Acta Mater. 2014, 78, 378–393. [Google Scholar] [CrossRef]
- De Guzman, M.S.; Neubauer, G.; Flinn, P.; Nix, W.D. The role of indentation depth on the measured hardness of materials. Mater. Res. Soc. Symp. Proc. 1993, 308, 613–618. [Google Scholar] [CrossRef]
- Nix, W.D.; Gao, H. Indentation size effects in crystalline materials: A law for strain gradient plasticity. J. Mech. Phys. Sol. 1998, 46, 411–425. [Google Scholar] [CrossRef]
- Swadener, J.G.; George, E.P.; Pharr, G.M. The correlation of the indentation size effect measured with indenters of various shapes. J. Mech. Phys. Sol. 2002, 50, 681–694. [Google Scholar] [CrossRef]
- Cotterill, R.M.J. Does dislocation density have a natural limit? Phys. Lett. A 1977, 60, 61–62. [Google Scholar] [CrossRef]
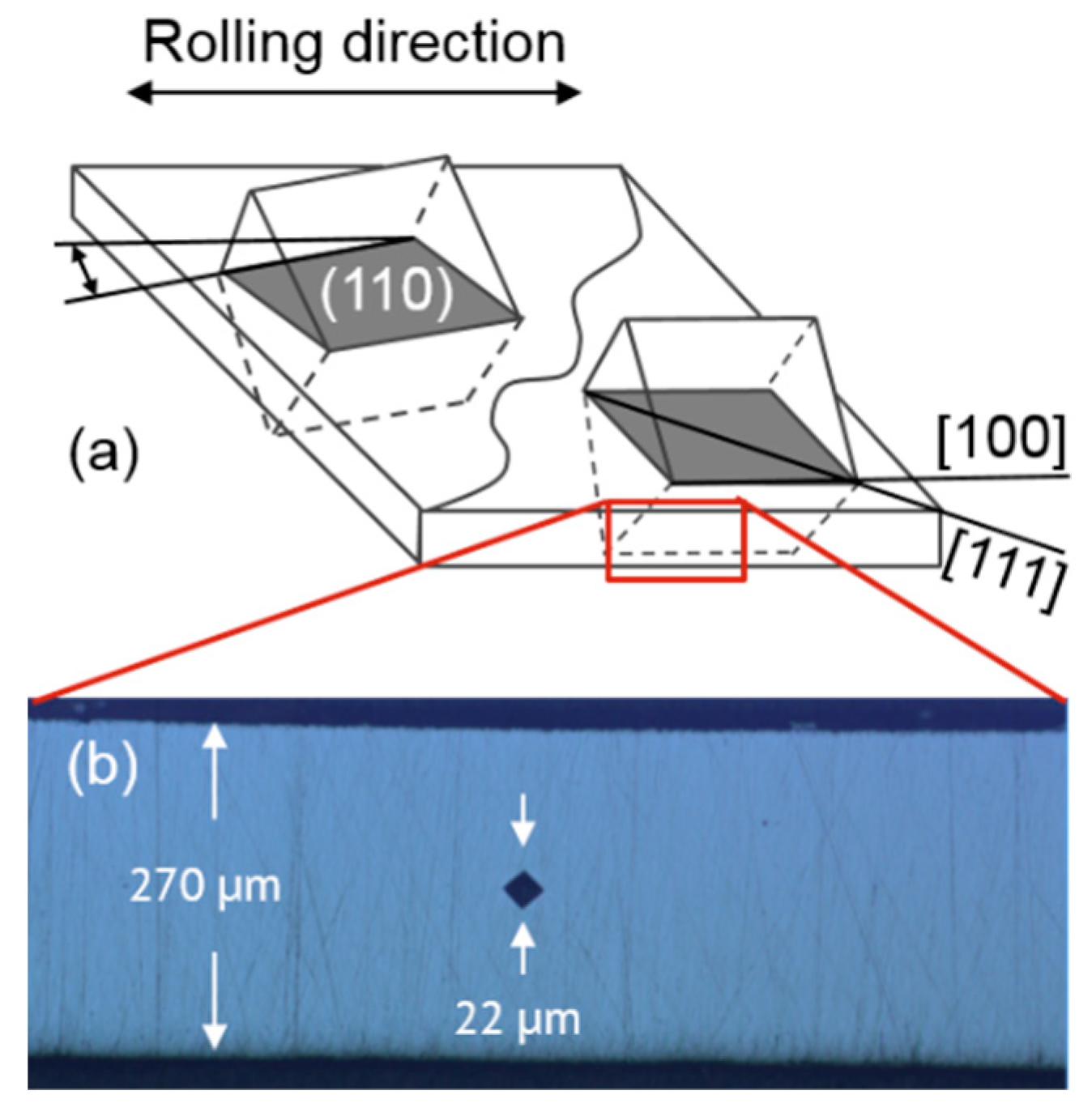


| Chemical Composition | C | Mn | Si | Fe |
|---|---|---|---|---|
| In wt% | 0.007 | 0.080 | 3.230 | Bal. |
| In at% | 0.03 | 0.76 | 6.22 | Bal. |
| Description | Value |
|---|---|
| Elastic modulus | 110 ± 10 GPa |
| Yield stress | 320 ± 5 MPa |
| Tensile strength | 325 ± 2 MPa |
| Hardness | 180 ± 5 HV0.1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deldar, S.; Alabd Alhafez, I.; Smaga, M.; Beck, T.; Urbassek, H.M. Cyclic Indentation of Iron: A Comparison of Experimental and Atomistic Simulations. Metals 2019, 9, 541. https://doi.org/10.3390/met9050541
Deldar S, Alabd Alhafez I, Smaga M, Beck T, Urbassek HM. Cyclic Indentation of Iron: A Comparison of Experimental and Atomistic Simulations. Metals. 2019; 9(5):541. https://doi.org/10.3390/met9050541
Chicago/Turabian StyleDeldar, Shayan, Iyad Alabd Alhafez, Marek Smaga, Tilmann Beck, and Herbert M. Urbassek. 2019. "Cyclic Indentation of Iron: A Comparison of Experimental and Atomistic Simulations" Metals 9, no. 5: 541. https://doi.org/10.3390/met9050541
APA StyleDeldar, S., Alabd Alhafez, I., Smaga, M., Beck, T., & Urbassek, H. M. (2019). Cyclic Indentation of Iron: A Comparison of Experimental and Atomistic Simulations. Metals, 9(5), 541. https://doi.org/10.3390/met9050541







