Research and Application of a Rolling Gap Prediction Model in Continuous Casting
Abstract
1. Introduction
Motivation
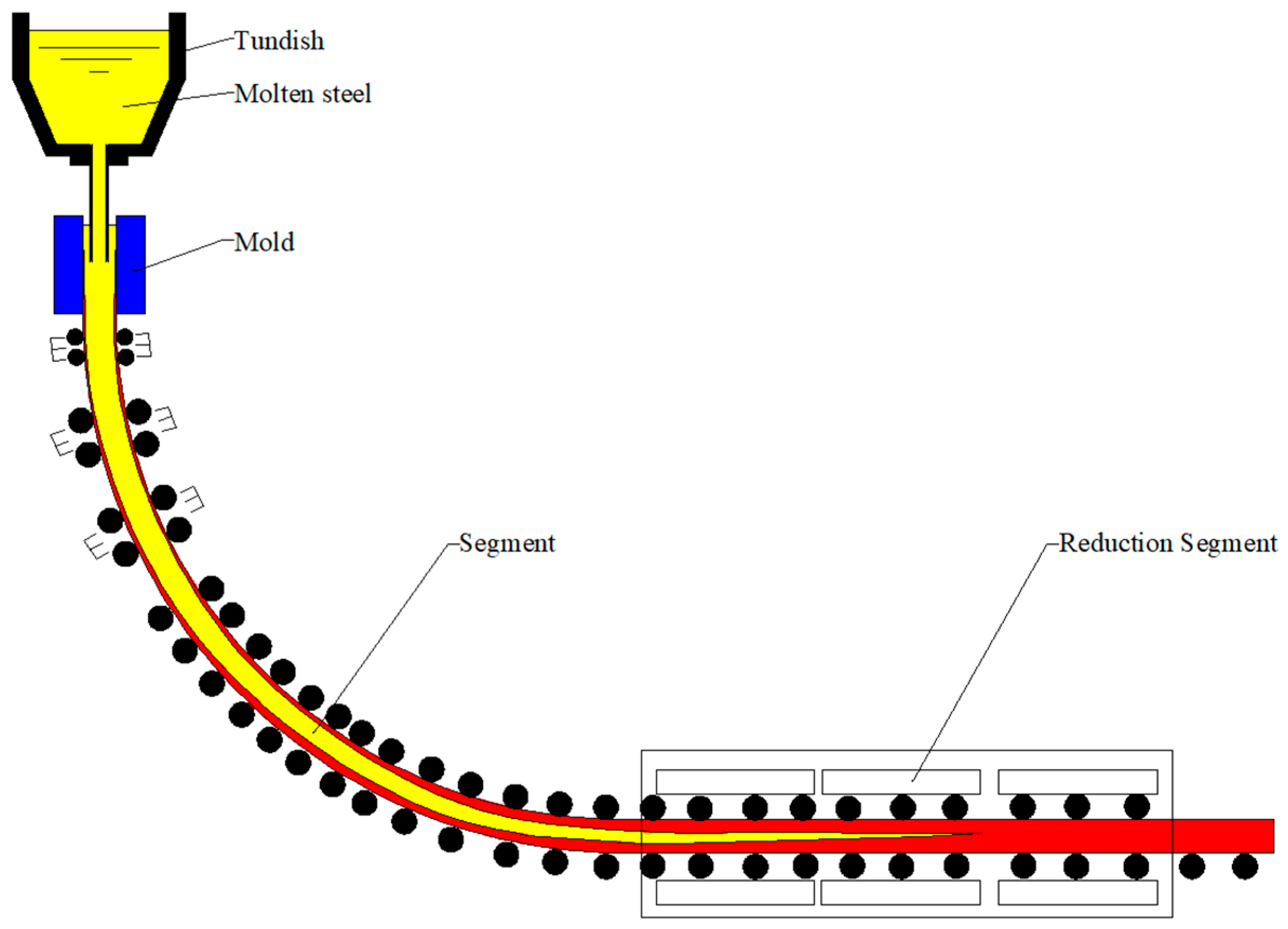
2. Continuous Casting Process Parameters
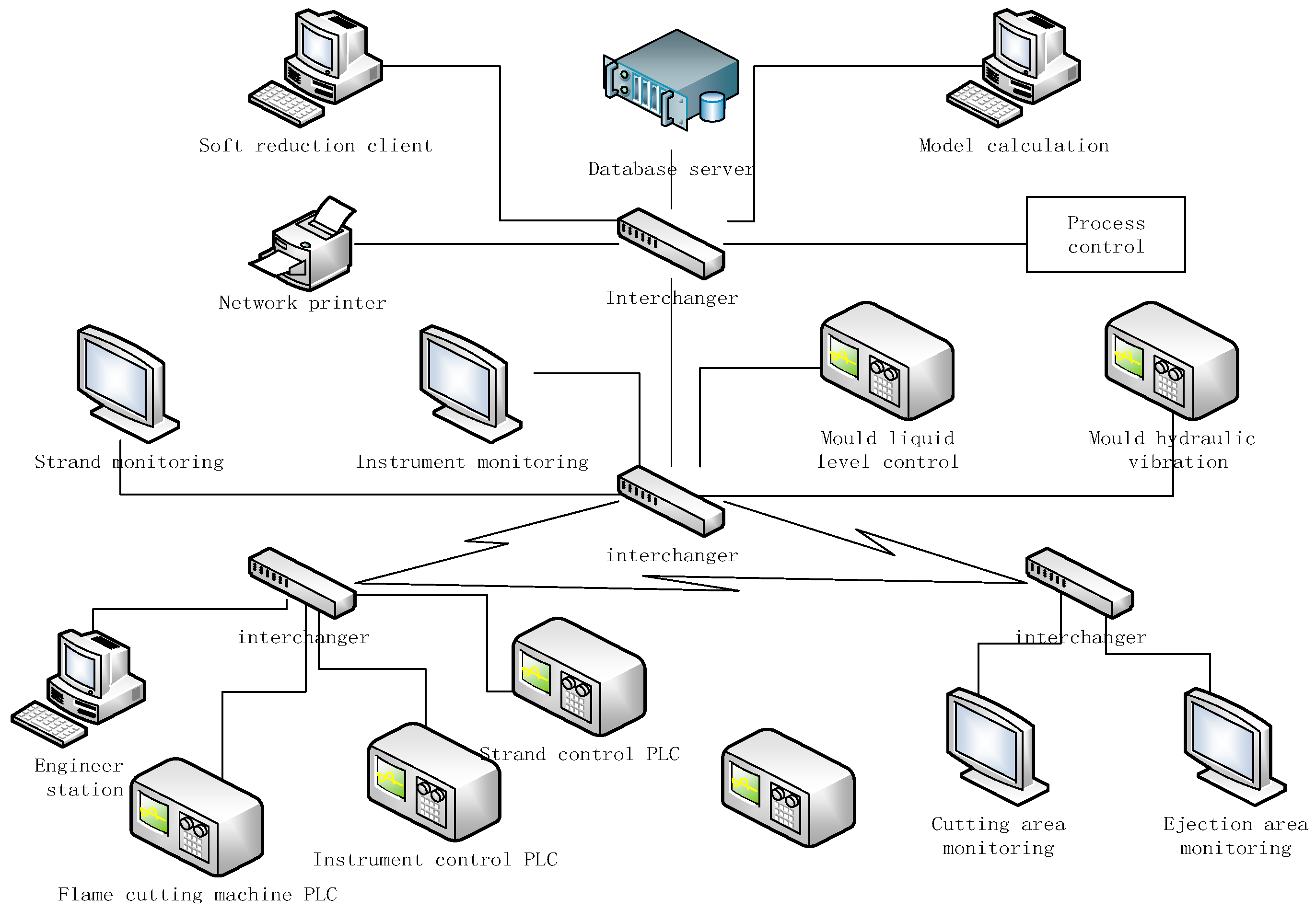
2.1. Acquisition of Continuous Casting Process Parameters
2.2. Data Pre-Processing
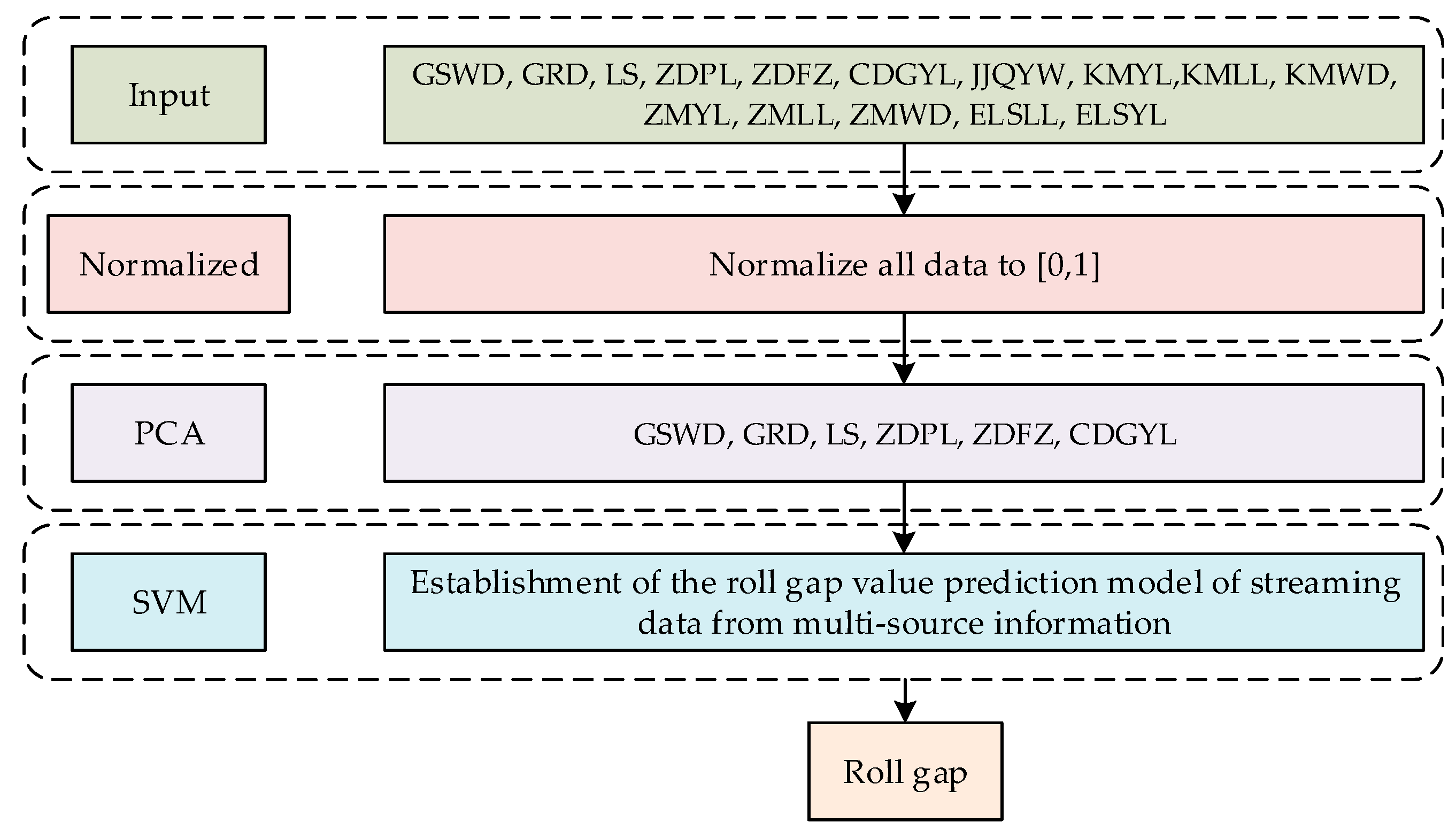
3. Dimension Reduction of Streaming Data from Multi-Source Information
3.1. Standardization of Continuous Casting Process Parameters
3.2. Dimension Reduction of Continuous Casting Process Parameters
4. Establishing a Roll Gap Value Prediction Model from Multi-Source Information
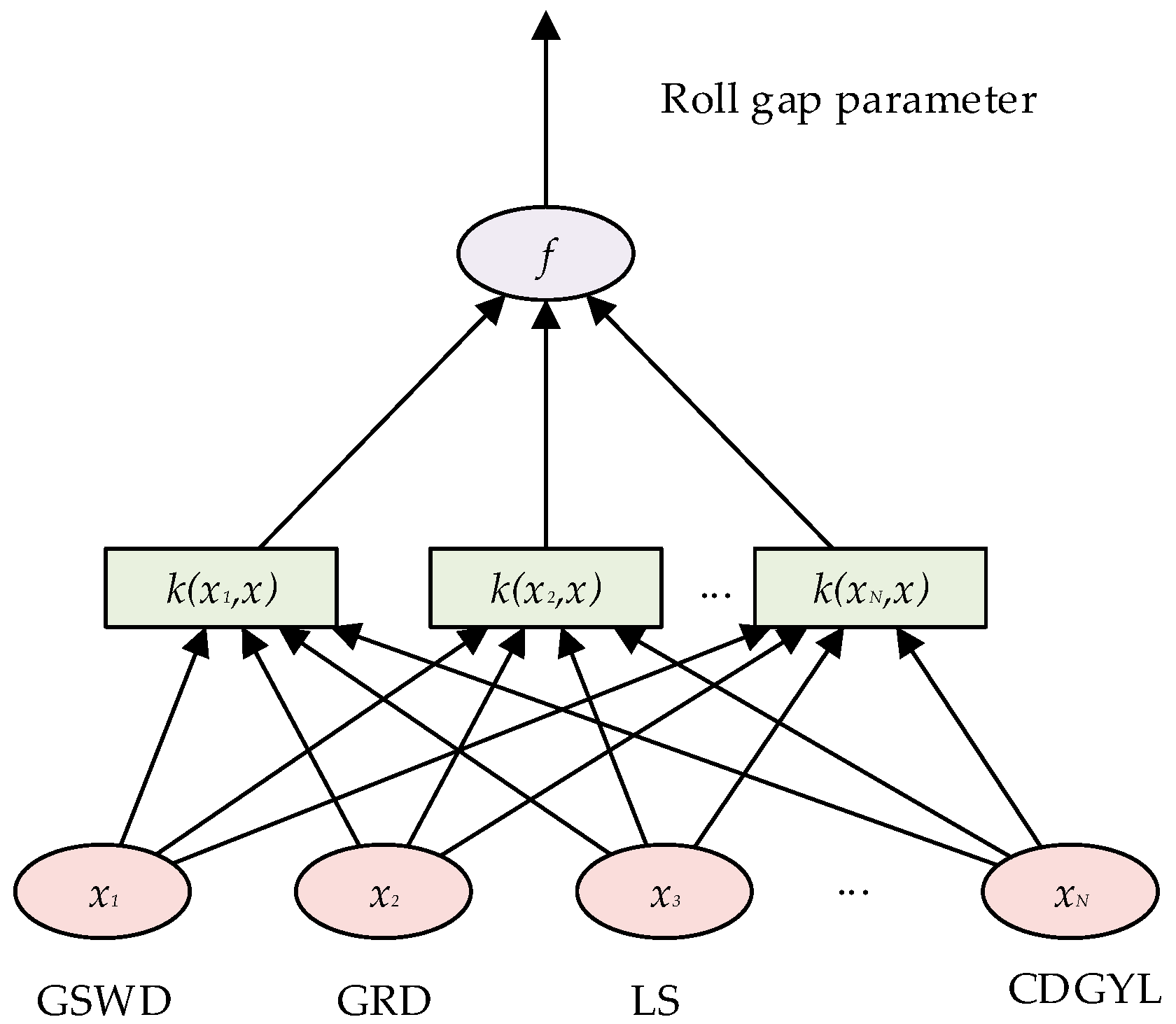
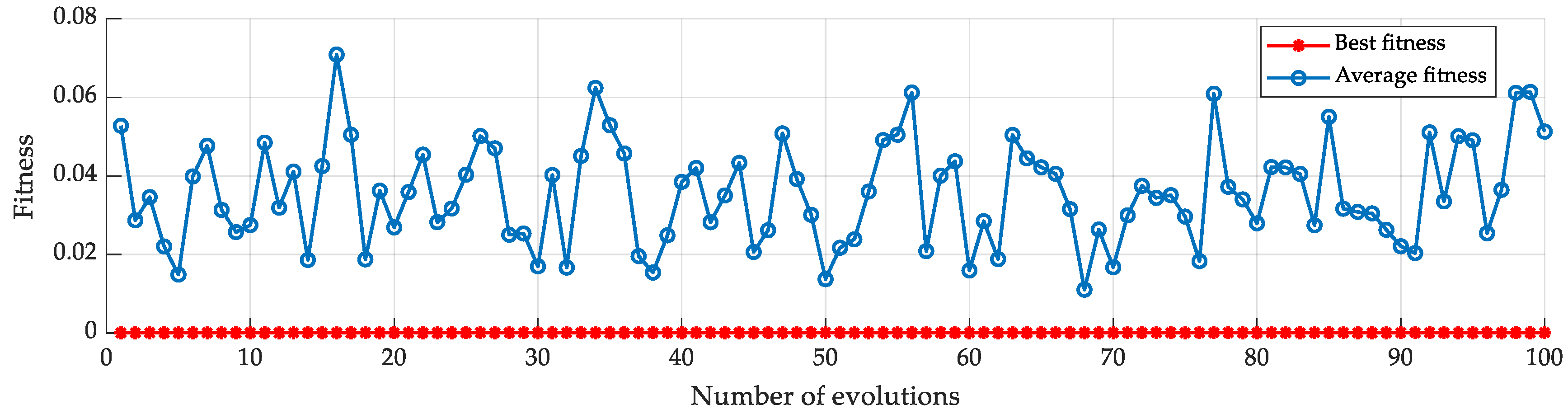
4.1. PSO-SVM Model
4.2. Establishing the PSO-Roll Gap Value Prediction
5. Experiments and Results
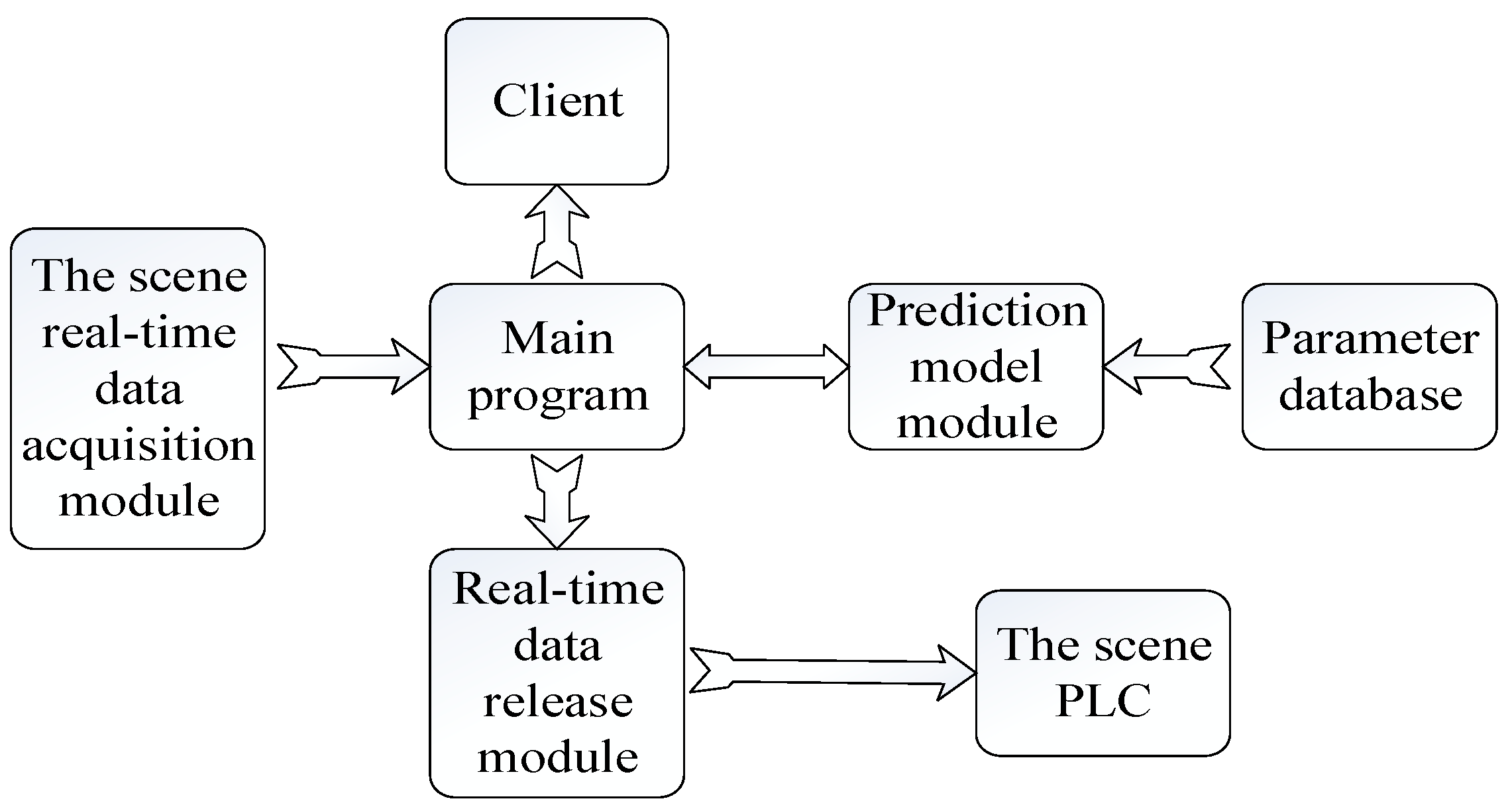
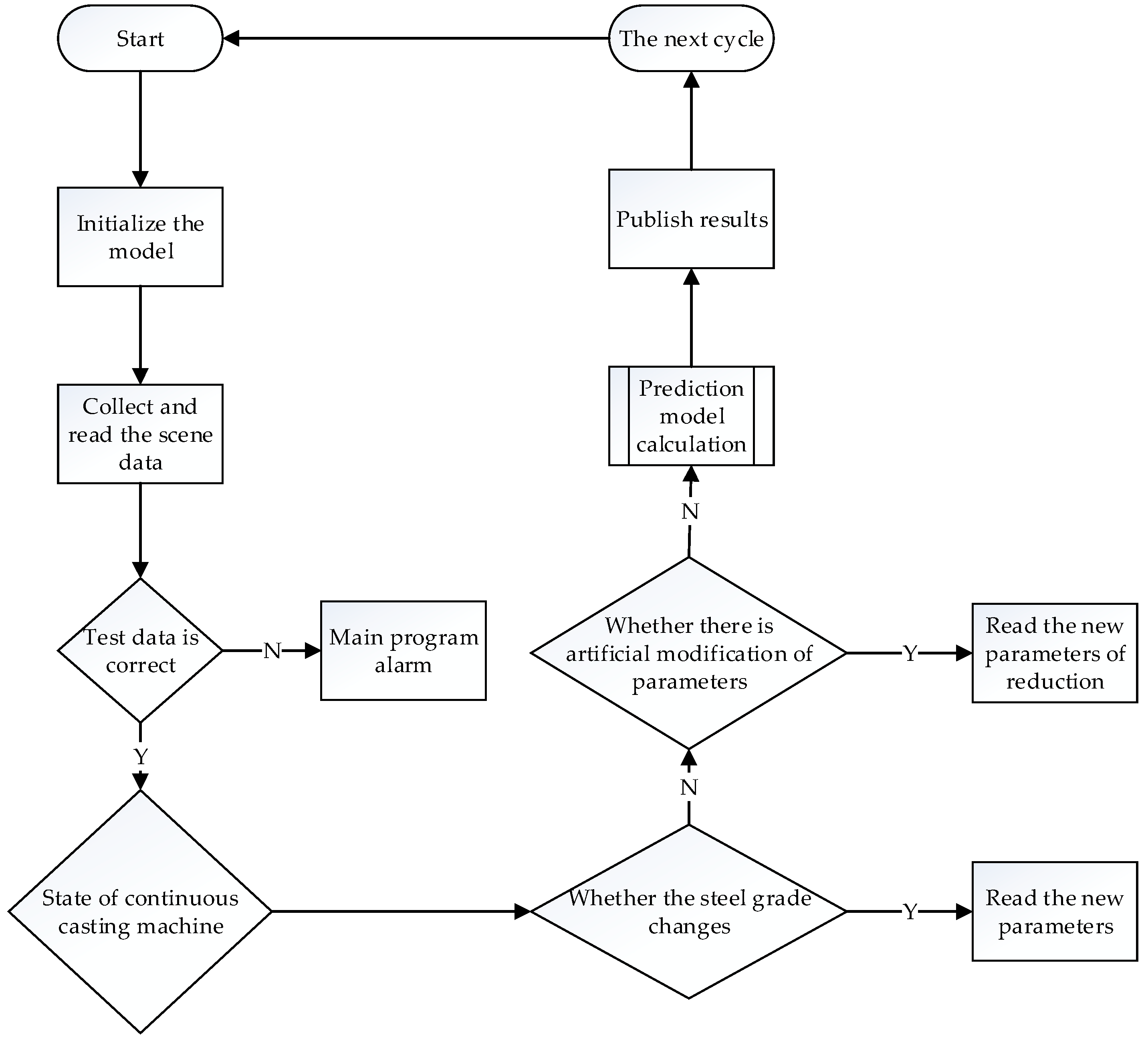
6. Industrial Application
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ataka, M. Rolling technology and theory for the last 100 years: The contribution of theory to innovation in strip rolling technology. ISIJ Inter. 2015, 55, 89–102. [Google Scholar] [CrossRef]
- Ge, S.; Isac, M.; Guthrie, R.I.L. Progress of strip casting technology for steel; historical developments. ISIJ Inter. 2012, 52, 2109–2122. [Google Scholar] [CrossRef]
- Tacke, K.H.; Schwinn, V. Recent developments on heavy plate steels. Stahl Eisen 2005, 125, 55. [Google Scholar]
- Wolf, M.M. History of Continuous Casting. In Proceedings of the 75th Steelmaking Conference, Toronto, ON, Canada, 5–8 April 1992; pp. 47–101. [Google Scholar]
- Lait, J. Mathematical modelling of heat flow in the continuous casting of steel. Ironmak. Steelmak. 1974, 1, 90–97. [Google Scholar]
- Rappaz, M. Modeling of microstructure formation in solidification processes. Int. Mater. Rev. 1989, 34, 93–123. [Google Scholar] [CrossRef]
- Choudhary, S.K.; Ganguly, S. Morphology and segregation in continuously cast high carbon steel billets. ISIJ Inter. 2007, 47, 1759–1766. [Google Scholar] [CrossRef]
- Koric, S.; Hibbeler, L.C.; Liu, R.; Thomas, B.G. Multiphysics model of metal solidification on the continuum level. Numer. Heat Transfer, Part B-Fundam. 2010, 58, 371–392. [Google Scholar] [CrossRef]
- Nilsson, N.J. Principles of Artificial Intelligence; Morgan Kaufmann Publishers: Burlington, MA, USA, 2014. [Google Scholar]
- Yang, Y.; Cai, Y.D.; Lu, Q.; Zhang, Y.; Koric, S.; Shao, C. High-Performance Computing Based Big Data Analytics for Smart Manufacturing. In Proceedings of the ASME 2018, the 13th International Manufacturing Science and Engineering Conference, College Station, TX, USA, 18–22 June 2018. [Google Scholar]
- Hore, S.; Das, S.K.; Banerjee, S.; Mukherjee, S. An adaptive neuro-fuzzy inference system-based modelling to predict mechanical properties of hot-rolled TRIP steel. Ironmak. Steelmak. 2016, 44, 656–665. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, Z. Enhanced just-in-time modelling for online quality prediction in BF ironmaking. Ironmak. Steelmak. 2015, 42, 321–330. [Google Scholar] [CrossRef]
- Mahmoodkhani, Y.; Wells, M.A.; Song, G. Prediction of roll force in skin pass rolling using numerical and artificial neural network methods. Ironmak. Steelmak. 2016, 44, 281–286. [Google Scholar] [CrossRef]
- Tiensuu, H.; Tamminen, S.; Pikkuaho, A.; Röning, J. Improving the yield of steel plates by updating the slab design with statistical models. Ironmak. Steelmak. 2016, 44, 577–586. [Google Scholar] [CrossRef]
- Zhang, L.; Li, Y.; Wang, Q.; Yan, C. Prediction model for steel/slag interfacial instability in continuous casting process. Ironmak. Steelmak. 2015, 42, 705–713. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A New Optimizer Using Particle Swarm Theory. In Proceedings of the MHS’95, the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar] [CrossRef]
- Valvano, S.; Orlando, C.; Alaimo, A. Design of a noise reduction passive control system based on viscoelastic multilayered plate using PDSO. Mech. Syst. Sig. Process. 2019, 123, 153–173. [Google Scholar] [CrossRef]
- Zhang, M.; Yuan, H. The Pauta criterion and rejecting the abnormal value. J. Zhengzhou Univ. Tech. 1997, 1, 84–88. [Google Scholar]
- Martinez, A.M.; Kak, A.C. PCA versus LDA. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 228–233. [Google Scholar] [CrossRef]
- Cervantes, J.; Garcia-Lamont, F.; Rodriguez-Mazahua, L.; Lopez, A.; Ruiz-Castilla, J.; Trueba, A. PSO-based method for SVM classification on skewed data sets. Neurocomputing 2017, 228, 187–197. [Google Scholar] [CrossRef]
- Chiang, J.H.; Hao, P.Y. A new kernel-based fuzzy clustering approach: Support vector clustering with cell growing. IEEE Trans. Fuzzy Syst. 2003, 11, 518–527. [Google Scholar] [CrossRef]
- Fang, Y.; Hu, C.; Liu, L.; Zhang, X. Breakout prediction classifier for continuous casting based on active learning GA-SVM. China Mech. Eng. 2016, 27, 1609–1614. [Google Scholar] [CrossRef]
- Gaudioso, M.; Gorgone, E.; Labbe, M.; Rodriguez-Chia, A.M. Lagrangian relaxation for SVM feature selection. Comput. Oper. Res. 2017, 87, 137–145. [Google Scholar] [CrossRef]
- Zhang, G.Z.; Sun, J. Application of fuzzy control on the caster segment’s gap control of slab continuous casting machine. Electr. Drive 2009, 39, 51–53. [Google Scholar]
- Jain, A.K.; Duin, R.P.W.; Mao, J. Statistical pattern recognition: A review. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 4–37. [Google Scholar] [CrossRef]
- Muscat, R.; Mahfouf, M.; Zughrat, A.; Yang, Y.Y.; Thornton, S.; Khondabi, A.V.; Sortanos, S. Hierarchical fuzzy support vector machine (SVM) for rail data classification. IFAC Papersonline 2014, 47, 10652–10657. [Google Scholar] [CrossRef]
- Refan, M.H.; Dameshghi, A.; Kamarzarrin, M. Improving RTDGPS accuracy using hybrid PSOSVM prediction model. Aerosp. Sci. Technol. 2014, 37, 55–69. [Google Scholar] [CrossRef]
- Wang, J.-S.; Chiang, J.-C. A cluster validity measure with Outlier detection for support vector clustering. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2008, 38, 78–89. [Google Scholar] [CrossRef] [PubMed]
- Wei, J.; Zhang, R.; Yu, Z.; Hu, R.; Tang, J.; Gui, C.; Yuan, Y. A BPSO-SVM algorithm based on memory renewal and enhanced mutation mechanisms for feature selection. Appl. Soft Comput. 2017, 58, 176–192. [Google Scholar] [CrossRef]



| Name | Process Parameter | Name | Process Parameter |
|---|---|---|---|
| GSWD | Temperature of tundish molten steel | KMLL | Water flow of mold width surface |
| GRD | Overheating of molten steel | KMWD | Outlet temperature of mold width surface |
| LS | Pulling rate | ZMYL | Water pressure of mold narrow surface |
| ZDPL | Vibration frequency of mold | ZMLL | Water flow of mold narrow surface |
| ZDFZ | Vibration amplitude of mold | ZMWD | Outlet temperature of mold narrow surface |
| CDGYL | Average pressure of 18 drive rollers | ELSLL | Average flow of 18 second cold water loops |
| JJQYW | Mold liquid level | ELSYL | Average pressure of 18 second cold water loops |
| KMYL | Water pressure of mold width surface | - | - |
| NO. | Feature | Variance Contribution Ratio (%) | Summation Variance Contribution Ratio (%) |
|---|---|---|---|
| 1 | 4.79 | 36.97 | 36.97 |
| 2 | 3.43 | 32.85 | 69.82 |
| 3 | 1.76 | 14.74 | 84.56 |
| 4 | 1.24 | 5.25 | 89.81 |
| 5 | 1.01 | 4.74 | 93.55 |
| 6 | 0.903 | 3.02 | 96.57 |
| 7 | 0.605 | 1.92 | 98.49 |
| 8 | 0.455 | 0.43 | 98.92 |
| 9 | 0.350 | 0.32 | 99.24 |
| 10 | 0.203 | 0.21 | 99.45 |
| 11 | 0.113 | 0.15 | 99.6 |
| 12 | 0.058 | 0.12 | 99.72 |
| 13 | 0.044 | 0.1 | 99.82 |
| 14 | 0.030 | 0.09 | 99.91 |
| 15 | 0.008 | 0.09 | 100.00 |
| Parameter Optimization Results | Training Time | Mean Square Deviation |
|---|---|---|
| C = 0.1; g = 0.1 | 304.8 s | 97.5% |
| Serial Number | Section Size (mm × mm) | Centre Segregation | Centre Porosity | Intermediate Cracks | Triangle Area Cracks |
|---|---|---|---|---|---|
| Without proposed model | 230 × 1350 | B1.0 | 2.0 | 1.5 | 1.5 |
| Proposed model | 230 × 1350 | C0.5 | 1.0 | 1.0 | 0.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, Z.; Su, W. Research and Application of a Rolling Gap Prediction Model in Continuous Casting. Metals 2019, 9, 380. https://doi.org/10.3390/met9030380
Lei Z, Su W. Research and Application of a Rolling Gap Prediction Model in Continuous Casting. Metals. 2019; 9(3):380. https://doi.org/10.3390/met9030380
Chicago/Turabian StyleLei, Zhufeng, and Wenbin Su. 2019. "Research and Application of a Rolling Gap Prediction Model in Continuous Casting" Metals 9, no. 3: 380. https://doi.org/10.3390/met9030380
APA StyleLei, Z., & Su, W. (2019). Research and Application of a Rolling Gap Prediction Model in Continuous Casting. Metals, 9(3), 380. https://doi.org/10.3390/met9030380





