Ab Initio Study of the Combined Effects of Alloying Elements and H on Grain Boundary Cohesion in Ferritic Steels
Abstract
:1. Introduction
2. Methodology
2.1. Technical Details
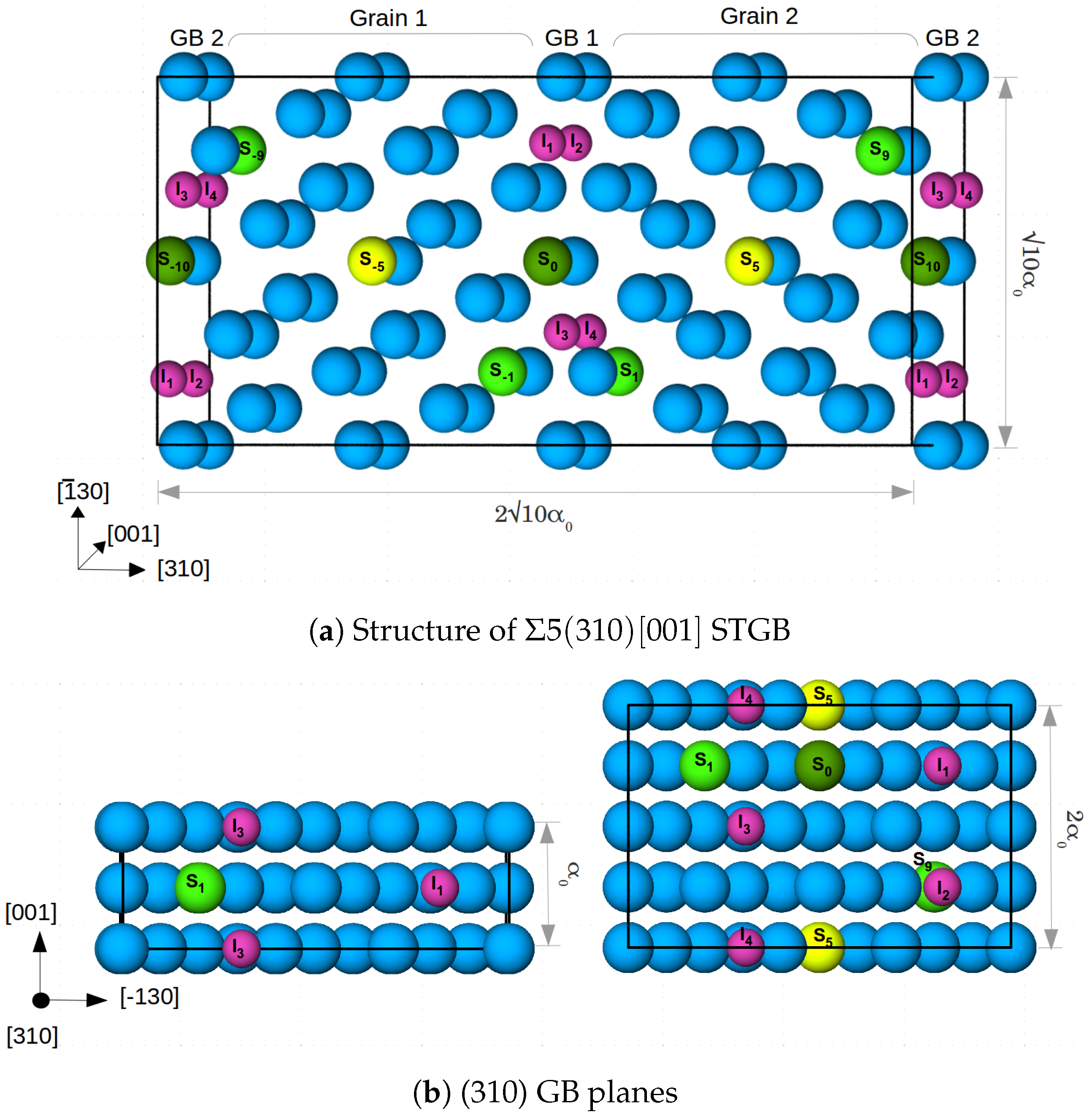
2.2. Simulation Cell
2.3. Grain Boundary and Segregation Energies
2.4. Work of Separation and Theoretical Strength
3. Results
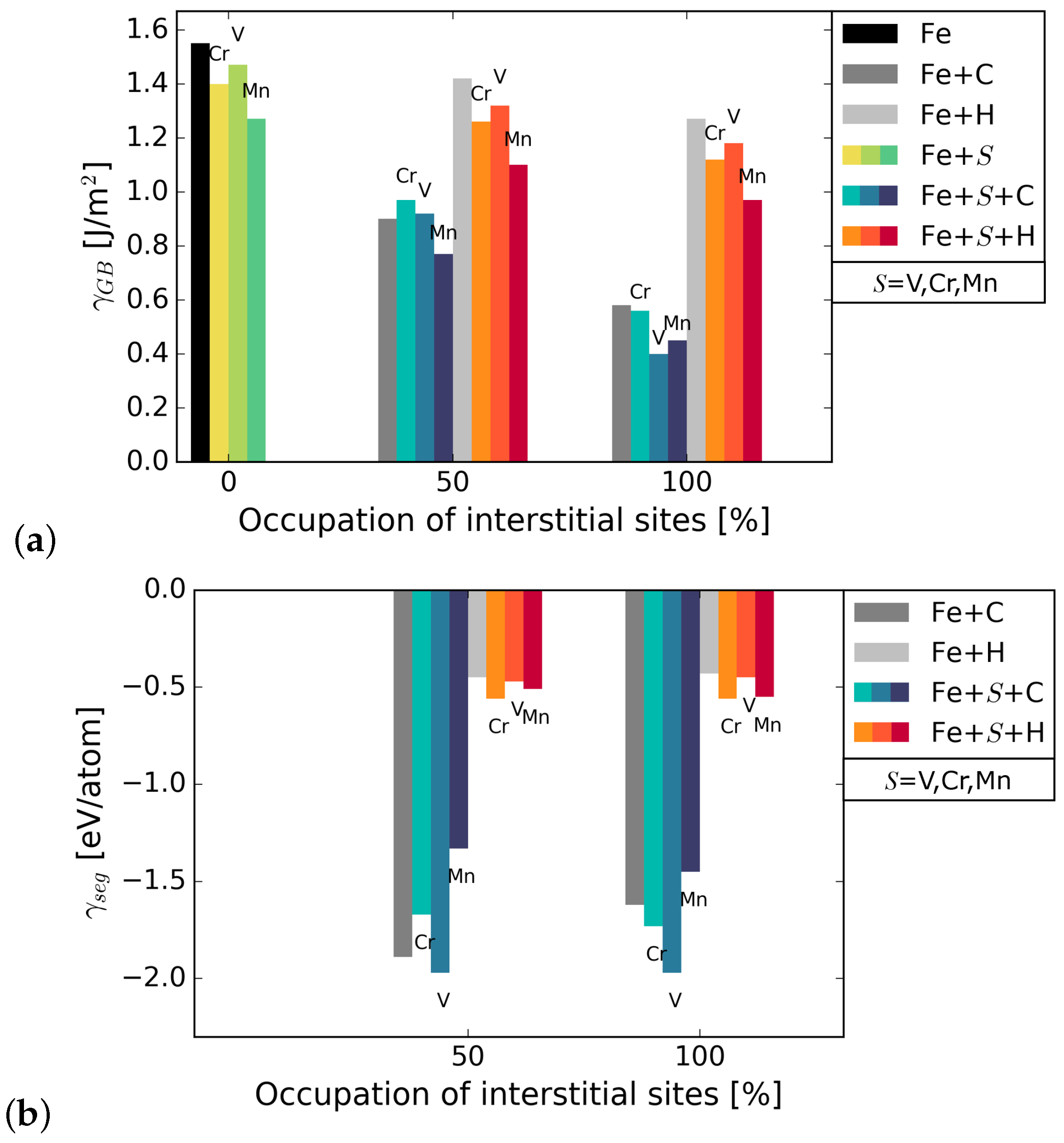
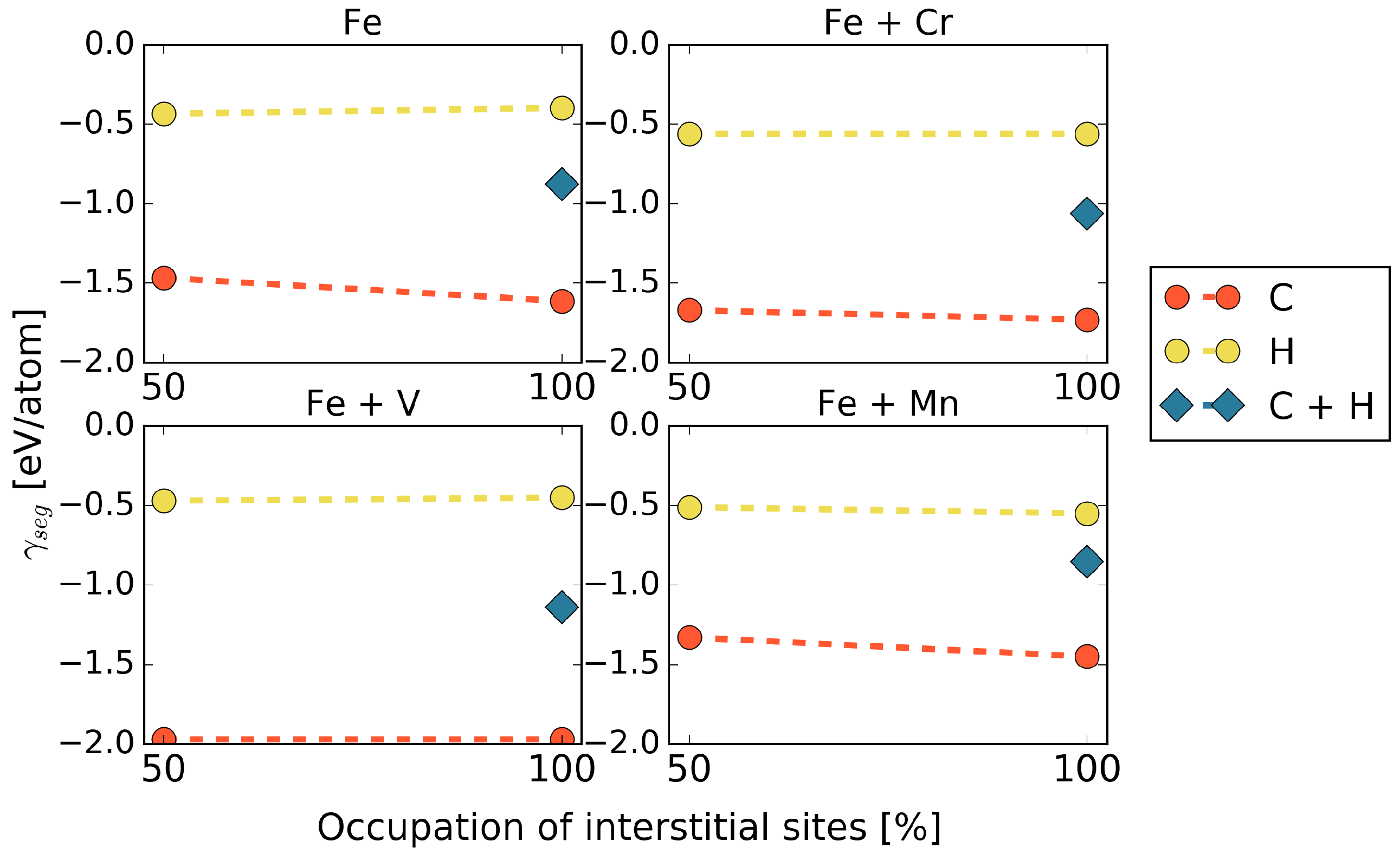
3.1. Segregation
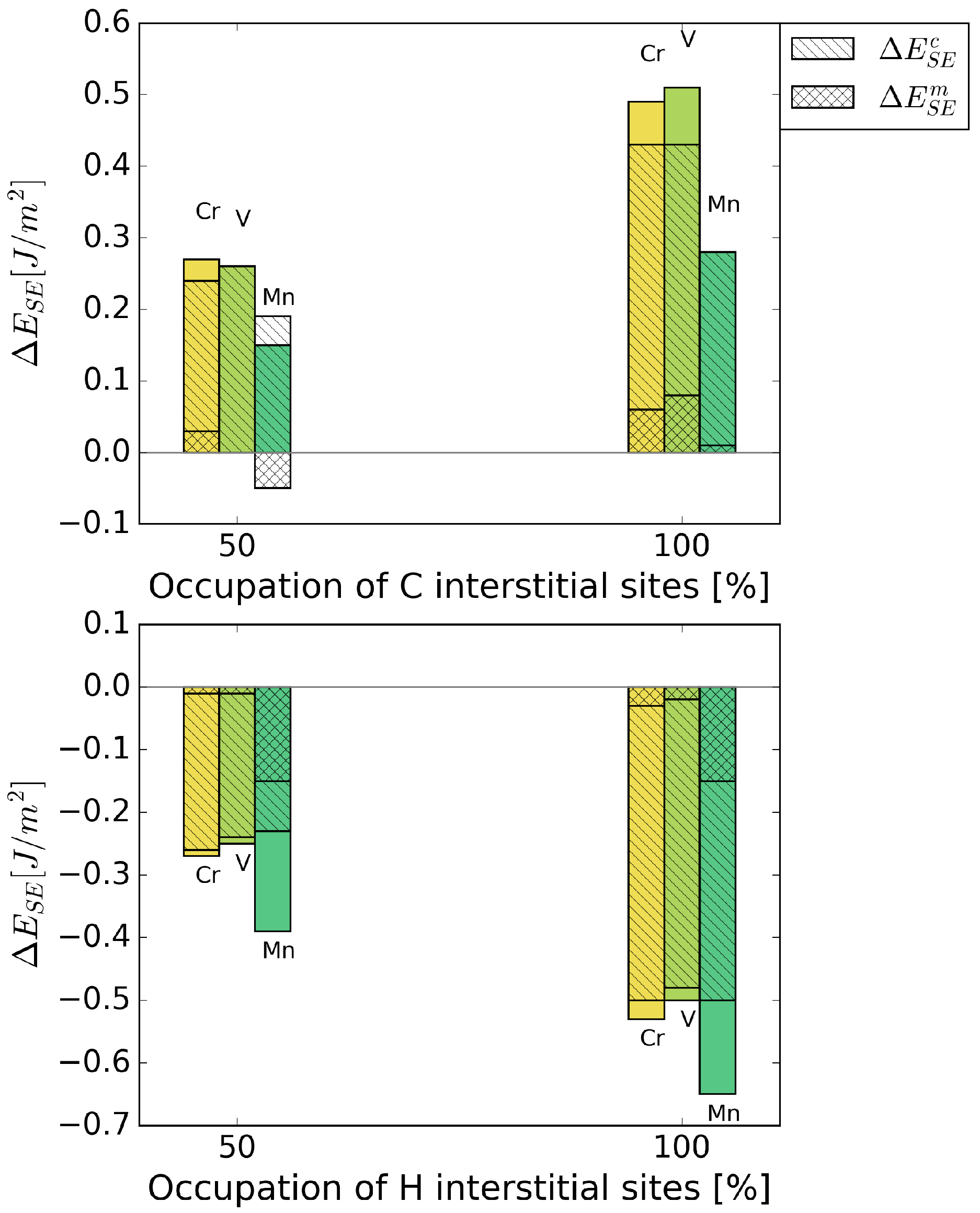
3.1.1. Segregation of V, Cr, and Mn to the GB
3.1.2. Segregation of C and H to the GB Segregated with V, Cr, and Mn
3.1.3. Co-Segregation of C and H
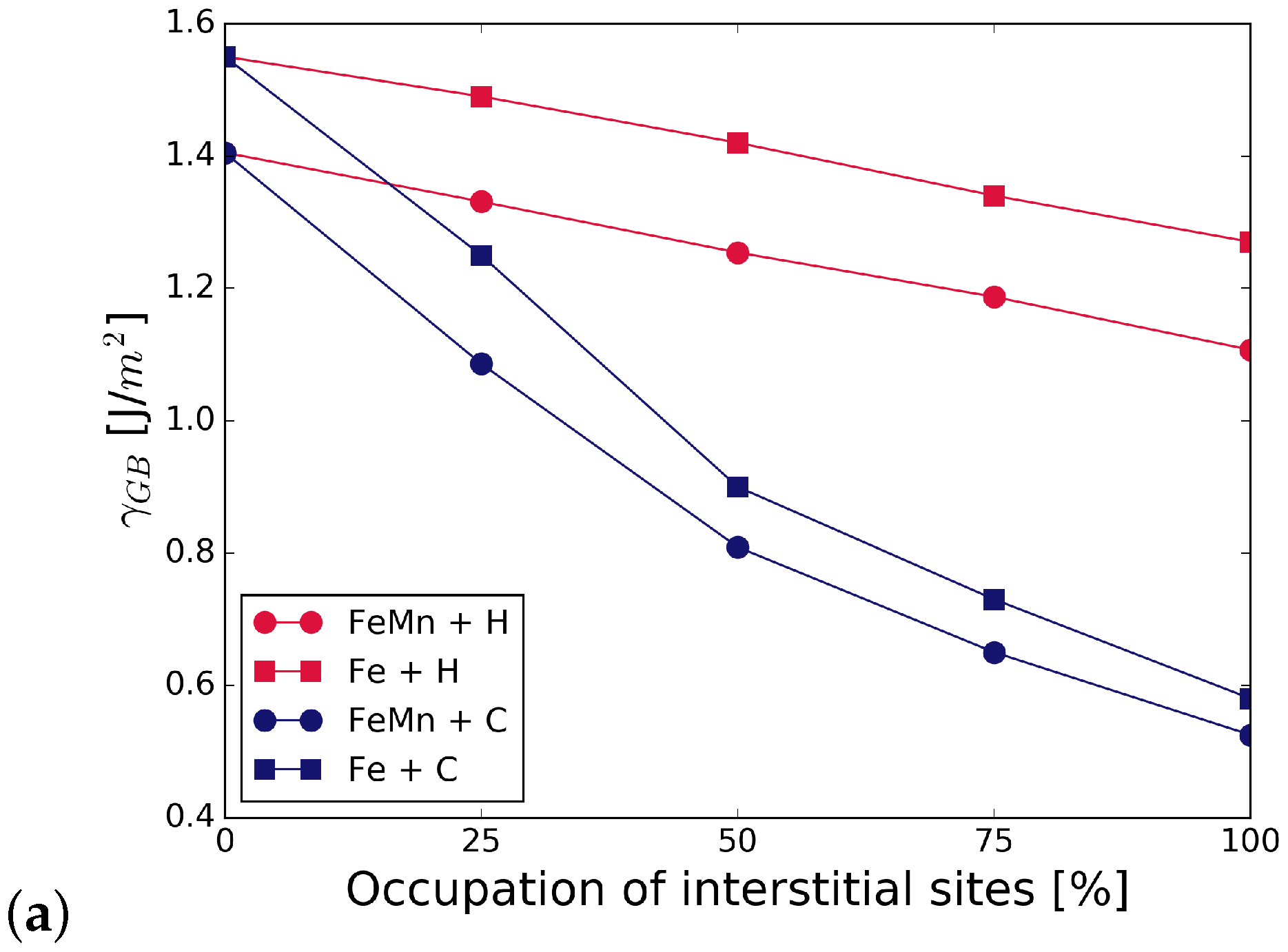
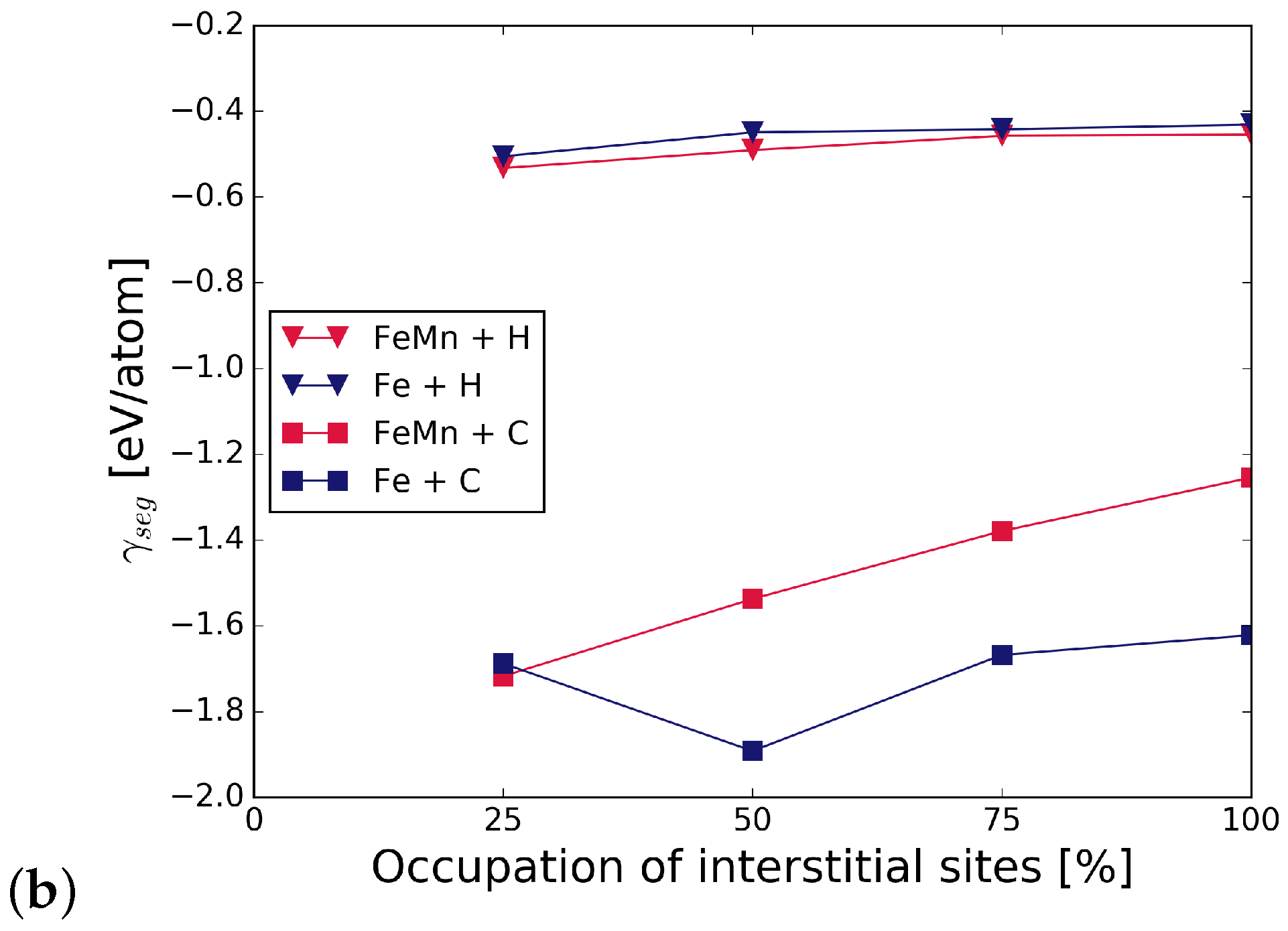
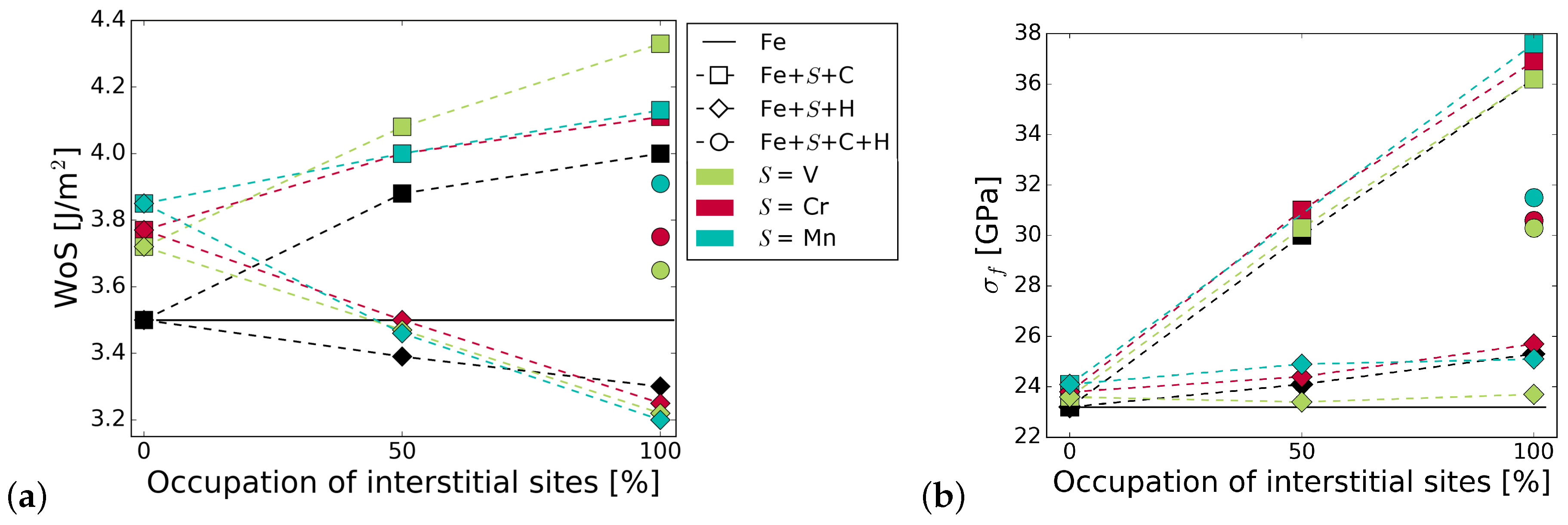
3.2. Mechanical Properties: Work of Separation and Fracture Stress
3.2.1. Influence of Substitutional Alloying Elements
3.2.2. Influence of C and H on Grain Boundary Cohesion
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Segregation of Interstitial Elements
| S | Segregation Site | Occupation Interstitial Sites [%] | Fe + S + C | Fe + S + C | ||
|---|---|---|---|---|---|---|
| [J/m] | [eV/Atom] | [J/m] | [eV/Atom] | |||
| V | S | 50 | 0.92 | −1.97 | 1.33 | −0.44 |
| 100 | 0.40 | −1.97 | 1.23 | −0.41 | ||
| S | 50 | 0.98 | −1.89 | 1.32 | −0.47 | |
| 100 | 0.50 | −1.89 | 1.18 | −0.45 | ||
| Cr | S | 50 | 0.93 | −1.67 | 1.33 | −0.54 |
| 100 | 0.53 | −1.73 | 1.27 | −0.49 | ||
| S | 50 | 0.98 | −1.59 | 1.26 | −0.56 | |
| 100 | 0.53 | −1.73 | 1.12 | −0.56 | ||
| Mn (cell) | S | 50 | 0.77 | −1.33 | 1.10 | −0.51 |
| 100 | 0.45 | −1.45 | 0.97 | −0.55 | ||
| Mn 2.5 at.% (cell) | S | 25 | 1.09 | −1.72 | 1.33 | −0.53 |
| 50 | 0.81 | −1.54 | 1.25 | −0.49 | ||
| 75 | 0.65 | −1.38 | 1.19 | −0.46 | ||
| 100 | 0.52 | −1.25 | 1.10 | −0.45 | ||
| Mn 5 at.% (cell) | S | 25 | 0.89 | −1.66 | 1.13 | −0.57 |
| 100 | 0.49 | −1.08 | 0.91 | −0.46 | ||
References
- Johnson, W. On some remarkable changes produced in iron and steel by the action of hydrogen and acids. Proc. R. Soc. Lond. 1875, 23, 168–179. [Google Scholar] [CrossRef]
- Bhadeshia, H.K.D.H. Prevention of hydrogen embrittlement in steels. ISIJ Int. 2016, 56, 24–36. [Google Scholar] [CrossRef]
- Du, Y.A.; Ismer, L.; Rogal, J.; Hickel, T.; Neugebauer, J.; Drautz, R. First-principles study on the interaction of H interstitials with grain boundaries in α- and γ-Fe. Phys. Rev. B 2011, 84, 144121. [Google Scholar] [CrossRef]
- Du, Y.A.; Rogal, J.; Drautz, R. Diffusion of hydrogen within idealized grains of bcc Fe: A kinetic Monte Carlo study. Phys. Rev. B 2012, 86, 174110. [Google Scholar] [CrossRef]
- Yamaguchi, M.; Ebihara, K.I.; Itakura, M.; Kadoyoshi, T.; Suzudo, T.; Kaburaki, H. First-principles study on the grain boundary embrittlement of metals by solute segregation: Part II. metal (Fe, Al, Cu)-hydrogen (H) systems. Metall. Mater. Trans. A 2011, 42, 330–339. [Google Scholar] [CrossRef]
- Tahir, A.; Janisch, R.; Hartmaier, A. Hydrogen embrittlement of a carbon segregated Σ5(310)[001] symmetrical tilt grain boundary in α-Fe. Mater. Sci. Eng. A 2014, 612, 462–467. [Google Scholar] [CrossRef]
- Yuasa, M.; Hakamada, M.; Chino, Y.; Mabuchi, M. First-principles study of hydrogen-induced embrittlement in Fe grain boundary with Cr segregation. ISIJ Int. 2015, 55, 1131–1134. [Google Scholar] [CrossRef]
- Hristova, E.; Janisch, R.; Drautz, R.; Hartmaier, A. Solubility of carbon in α-iron under volumetric strain and close to the Σ5(310)[001] grain boundary: Comparison of DFT and empirical potential methods. Comput. Mater. Sci. 2011, 50, 1088–1096. [Google Scholar] [CrossRef]
- Wang, J.; Janisch, R.; Madsen, G.K.; Drautz, R. First-principles study of carbon segregation in bcc iron symmetrical tilt grain boundaries. Acta Mater. 2016, 115, 259–268. [Google Scholar] [CrossRef]
- Kurishita, H.; Oishi, A.; Kubo, H.; Yoshinaga, H. Grain boundary fracture in molybdenum bicrystals with various <110> symmetric tilt boundaries. Trans. Jpn. Inst. Met. 1985, 26, 341–352. [Google Scholar] [CrossRef]
- Wu, R.; Freeman, A.J.; Olson, G.B. Effects of carbon on Fe-grain-boundary cohesion: First-principles determination. Phys. Rev. B 1996, 53, 7504–7509. [Google Scholar] [CrossRef]
- Wachowicz, E.; Ossowski, T.; Kiejna, A. Cohesive and magnetic properties of grain boundaries in bcc Fe with Cr additions. Phys. Rev. B 2010, 81, 094104. [Google Scholar] [CrossRef]
- Shang, J.X.; Zhao, X.D.; Wang, F.H.; Wang, C.Y.; Xu, H.B. Effects of Co and Cr on bcc Fe grain boundaries cohesion from first-principles study. Comput. Mater. Sci. 2006, 38, 217–222. [Google Scholar] [CrossRef]
- He, B.; Xiao, W.; Hao, W.; Tian, Z. First-principles investigation into the effect of Cr on the segregation of multi-H at the Fe Σ3 (111) grain boundary. J. Nucl. Mater. 2013, 441, 301–305. [Google Scholar] [CrossRef]
- Yang, R.; Wang, Y.M.; Ye, H.Q.; Wang, C.Y. Effects of Cr, Mn on the cohesion of the γ-iron grain boundary. J. Phys. Condens. Matter 2001, 13, 4485–4493. [Google Scholar] [CrossRef]
- Yang, R.; Huang, R.Z.; Wang, Y.M.; Ye, H.Q.; Wang, C.Y. The effects of 3d alloying elements on grain boundary cohesion in gamma-iron: A first principles study on interface embrittlement due to the segregation. J. Phys. Condens. Matter 2003, 15, 8339–8349. [Google Scholar] [CrossRef]
- Shang, J.X.; Wang, C.Y.; Zhao, D.L. First-principles investigation of the effect of alloying elements Ti, V on grain boundary cohesion of FCC Fe. Comput. Mater. Sci. 2001, 22, 193–199. [Google Scholar] [CrossRef]
- Shang, J.X.; Wang, C.Y. Electronic effects of alloying elements Nb and V on body-centred-cubic Fe grain boundary cohesion. J. Phys. Condens. Matter 2001, 13, 9635–9644. [Google Scholar] [CrossRef]
- Tian, Z.X.; Yan, J.X.; Hao, W.; Xiao, W. Effect of alloying additions on the hydrogen-induced grain boundary embrittlement in iron. J. Phys. Condens. Matter 2011, 23, 015501. [Google Scholar] [CrossRef] [PubMed]
- Zhong, L.; Wu, R.; Freeman, A.J.; Olson, G.B. Effects of Mn additions on the P embrittlement of the Fe grain boundary. Phys. Rev. B 1997, 55, 11133–11137. [Google Scholar] [CrossRef]
- Ismer, L.; Hickel, T.; Neugebauer, J. Ab initio study of the solubility and kinetics of hydrogen in austenitic high Mn steels. Phys. Rev. B 2010, 81, 094111. [Google Scholar] [CrossRef]
- von Appen, J.; Dronskowski, R.; Chakrabarty, A.; Hi ckel, T.; Spatschek, R.; Neugebauer, J. Impact of Mn on the solution enthalpy of hydrogen in austenitic Fe-Mn a lloys: A first-principles study. J. Comput. Chem. 2014, 35, 2239–2244. [Google Scholar] [CrossRef] [PubMed]
- Counts, W.; Wolverton, C.; Gibala, R. First-principles energetics of hydrogen traps in α-Fe: Point defects. Acta Mater. 2010, 58, 4730–4741. [Google Scholar] [CrossRef]
- Medvedeva, N.I.; Van Aken, D.C.; Medvedeva, J.E. The effect of carbon distribution on the manganese magnetic moment in bcc Fe–Mn alloy. J. Phys. Condens. Matter 2011, 23, 326003. [Google Scholar] [CrossRef] [PubMed]
- Wicaksono, A.T.; Militzer, M. Interaction of C and Mn in a Σ3 grain boundary of bcc iron. IOP Conf. Ser. Mater. Sci. Eng. 2017, 219, 012044. [Google Scholar] [CrossRef]
- Enomoto, M.; White, C.L.; Aaronson, H.I. Evaluation of the effects of segregation on austenite grain-boundary energy in Fe-C-X alloys. Metall. Mater. Trans. A 1988, 19, 1807–1818. [Google Scholar] [CrossRef]
- Scheiber, D.; Romaner, L.; Fischer, F.; Svoboda, J. Kinetics of grain boundary segregation in multicomponent systems—The example of a Mo-C-B-O system. Scr. Mater. 2018, 150, 110–114. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [Green Version]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Methfessel, M.; Paxton, A.T. High-precision sampling for Brillouin-zone integration in metals. Phys. Rev. B 1989, 40, 3616–3621. [Google Scholar] [CrossRef]
- Rice, J.R.; Wang, J.S. Embrittlement of interfaces by solute segregation. Mater. Sci. Eng. A 1989, 107, 23–40. [Google Scholar] [CrossRef]
- Geng, W.T.; Freeman, A.J.; Wu, R.; Geller, C.B.; Raynolds, J.E. Embrittling and strengthening effects of hydrogen, boron, and phosphorus on a Σ5 nickel grain boundary. Phys. Rev. B 1999, 60, 7149–7155. [Google Scholar] [CrossRef]
- Janisch, R.; Elsässer, C. Segregated light elements at grain boundaries in niobium and molybdenum. Phys. Rev. B 2003, 67, 224101. [Google Scholar] [CrossRef]
- Möller, J.J.; Bitzek, E.; Janisch, R.; ul Hassan, H.; Hartmaier, A. Fracture ab initio: A force-based scaling law for atomistically informed continuum models. J. Mater. Res. 2018, 33, 3750–3761. [Google Scholar] [CrossRef]
- Rose, J.H.; Smith, J.R.; Guinea, F.; Ferrante, J. Universal features of the equation of state of metals. Phys. Rev. B 1984, 29, 2963–2969. [Google Scholar] [CrossRef]
- Janisch, R.; Ahmed, N.; Hartmaier, A. Ab initio tensile tests of Al bulk crystals and grain boundaries: Universality of mechanical behavior. Phys. Rev. B 2010, 81, 184108. [Google Scholar] [CrossRef]
- Tahir, A.M.; Janisch, R.; Hartmaier, A. Ab initio calculation of traction separation laws for a grain boundary in molybdenum with segregated C impurites. Model. Simul. Mater. Sci. Eng. 2013, 21, 075005. [Google Scholar] [CrossRef] [Green Version]
| System | Segregation Sites | Excess Length [Å] | Shift [Å] | [] | [eV/Atom] |
|---|---|---|---|---|---|
| Fe | - | 0.31 | 0.43 | 1.55 | - |
| Fe + V | S | +0.08 | +0.12 | 1.47 | −0.16 |
| S | +0.06 | +0.01 | 1.47 | −0.15 | |
| Fe + Cr | S | +0.09 | +0.10 | 1.45 | −0.18 |
| S | +0.05 | −0.03 | 1.40 | −0.27 | |
| Fe + Mn (cell) | S | +0.11 | −0.02 | 1.36 | −0.33 |
| S | +0.09 | −0.25 | 1.27 | −0.48 | |
| Fe + Mn (cell) | S | +0.00 | +0.00 | 1.59 | 0.12 |
| S | +0.09 | −0.07 | 1.40 | −0.48 | |
| S, S | +0.07 | −0.32 | 1.21 | −0.55 |
| Structure | Occupation of SUs | Segregation Sites | [eV/Atom] | |
|---|---|---|---|---|
| C | H | |||
| cell 2.5 at.% Mn | 75% | I | I, I | −1.18 |
| I − I | - | −1.38 | ||
| - | I, I, I | −0.46 | ||
| 100% | I, I | I, I | −1.18 | |
| I − I | - | −1.25 | ||
| - | I − I | −0.45 | ||
| cell 5.0 at.% Mn | 100% | I, I | I, I | −1.36 |
| I − I | - | −1.08 | ||
| - | I − I | −0.46 | ||
| cell 5.0 at.% Mn | 100% | I | I | −0.85 |
| I, I | - | −1.45 | ||
| - | I, I | −0.55 | ||
| System | Segregation Sites | WoS | ||||
|---|---|---|---|---|---|---|
| [J/m] | [J/m] | [J/m] | [J/m] | [GPa] | ||
| Fe | 3.48 | |||||
| Fe + V | S | 3.82 | 0.34 | 0.34 | 0.00 | 24.7 |
| S | 3.72 | 0.24 | 0.25 | −0.01 | 23.6 | |
| Fe + Cr | S | 3.75 | 0.27 | 0.27 | 0.00 | 24.2 |
| S | 3.77 | 0.29 | 0.30 | −0.01 | 23.8 | |
| Fe + Mn (cell) | S | 3.72 | 0.24 | −0.06 | 0.30 | 23.7 |
| S | 3.85 | 0.37 | 0.10 | 0.27 | 24.1 | |
| Fe + Mn (cell) | S | 3.61 | 0.13 | −0.20 | 0.33 | 24.6 |
| S, S | 3.82 | 0.34 | 0.09 | 0.25 | 26.1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
P. A. Subramanyam, A.; Azócar Guzmán, A.; Vincent, S.; Hartmaier, A.; Janisch, R. Ab Initio Study of the Combined Effects of Alloying Elements and H on Grain Boundary Cohesion in Ferritic Steels. Metals 2019, 9, 291. https://doi.org/10.3390/met9030291
P. A. Subramanyam A, Azócar Guzmán A, Vincent S, Hartmaier A, Janisch R. Ab Initio Study of the Combined Effects of Alloying Elements and H on Grain Boundary Cohesion in Ferritic Steels. Metals. 2019; 9(3):291. https://doi.org/10.3390/met9030291
Chicago/Turabian StyleP. A. Subramanyam, Aparna, Abril Azócar Guzmán, Smobin Vincent, Alexander Hartmaier, and Rebecca Janisch. 2019. "Ab Initio Study of the Combined Effects of Alloying Elements and H on Grain Boundary Cohesion in Ferritic Steels" Metals 9, no. 3: 291. https://doi.org/10.3390/met9030291
APA StyleP. A. Subramanyam, A., Azócar Guzmán, A., Vincent, S., Hartmaier, A., & Janisch, R. (2019). Ab Initio Study of the Combined Effects of Alloying Elements and H on Grain Boundary Cohesion in Ferritic Steels. Metals, 9(3), 291. https://doi.org/10.3390/met9030291






