Electronic Structure Calculations of Oxygen Atom Transport Energetics in the Presence of Screw Dislocations in Tungsten
Abstract
1. Introduction
2. Computational Details
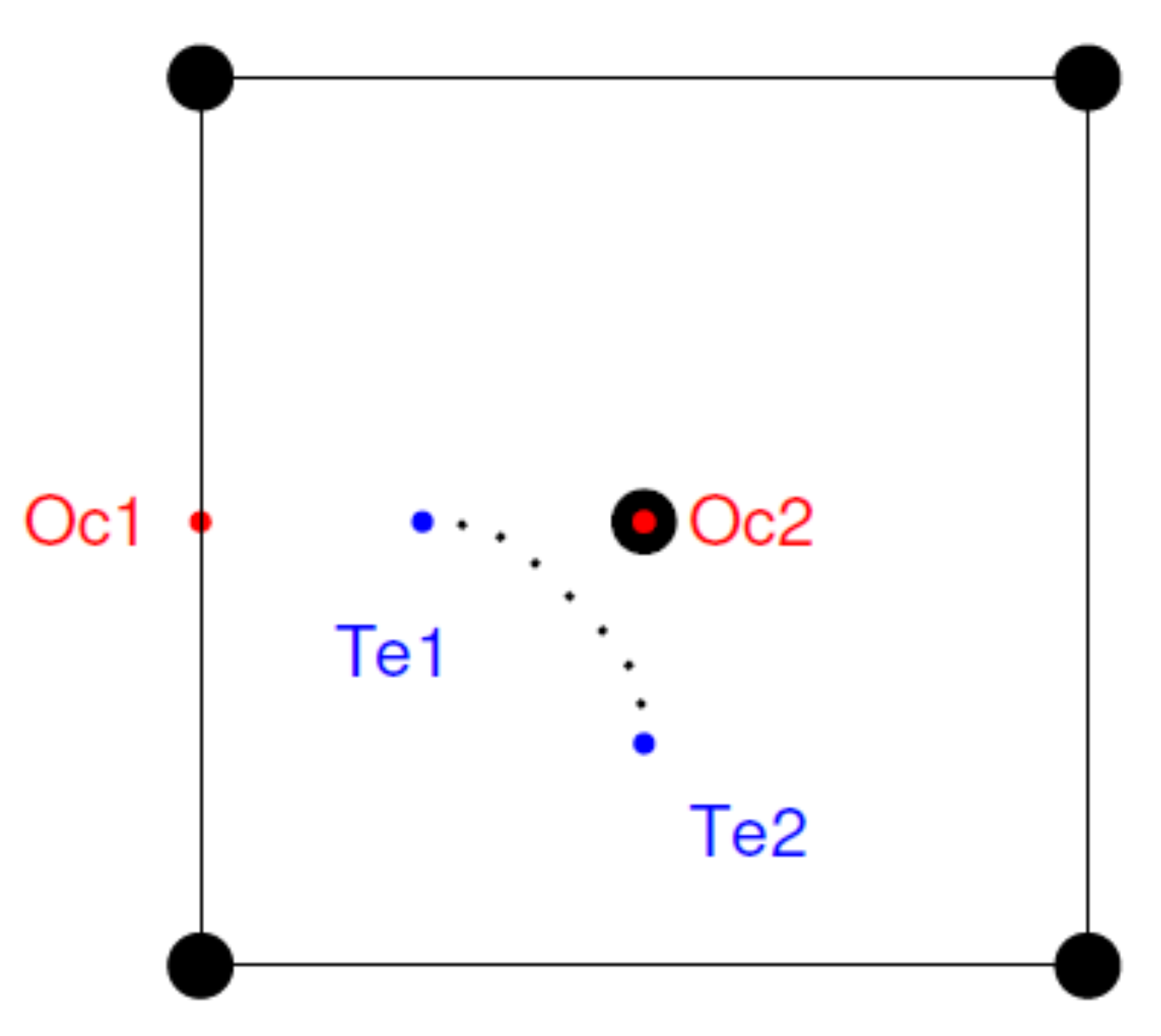
2.1. O Solution and Migration Energies under Strain
- (i)
- Hydrostatic strain:
- (ii)
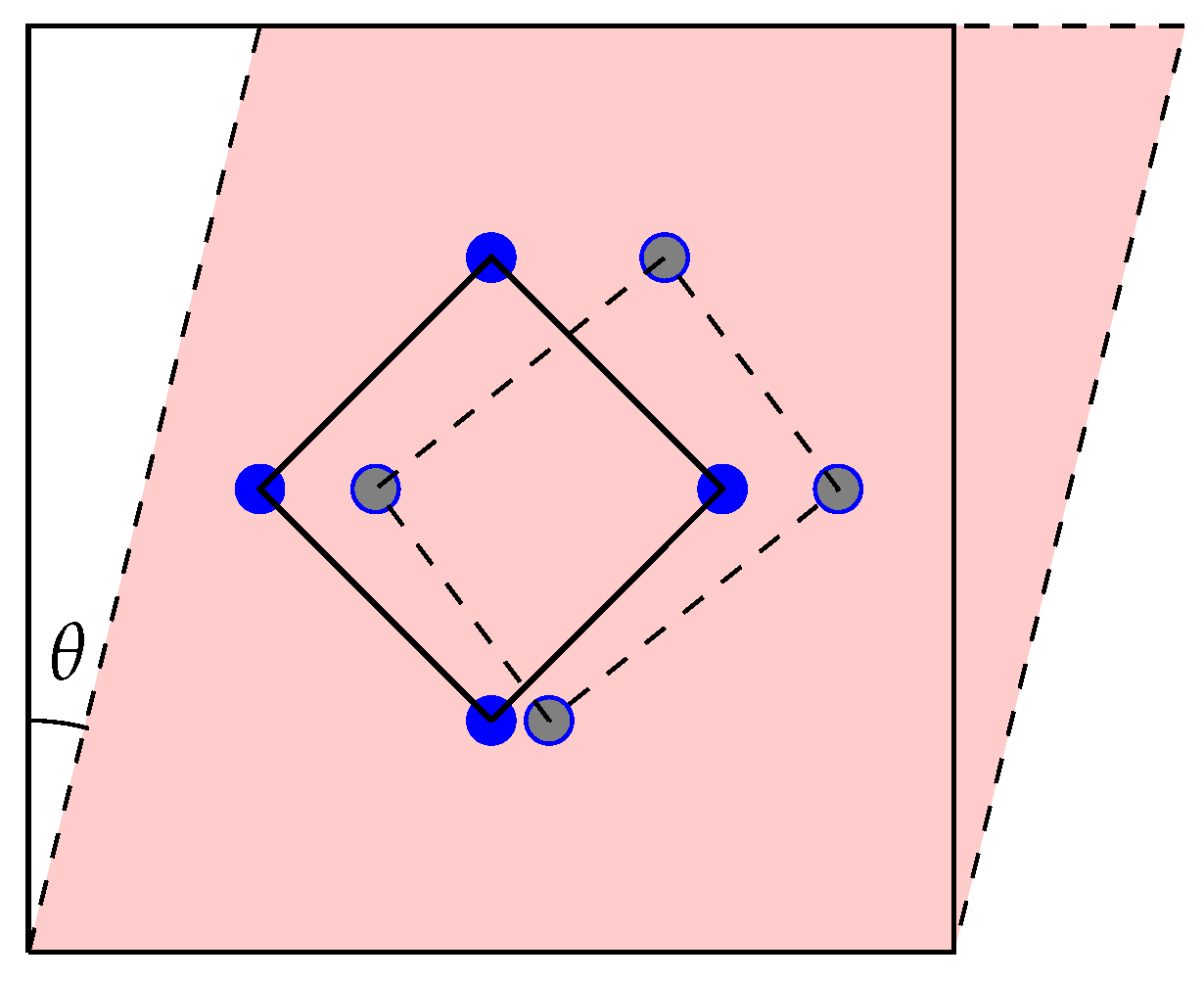
- Volume-conserving shear:where and are the applied dilatational and shear strains, respectively. Positive values of are taken to represent tensile distortions. Note that in the limit of small deformations, (i) the volumetric strain and (ii) , with the shear angle as defined in Figure 1. Note that shear deformation turns a symmetric cubic cell into a monoclinic one, which results in a shortening of certain tetrahedral→tetrahedral paths and in the extension of others, as illustrated in the figure. This is equivalent to applying negative shear strain, and consequently, we have investigated both reaction paths when calculating O migration in sheared bcc W. We used 10 NEB images in the majority of the cases considered here, the only exceptions being and , where seven images where used.
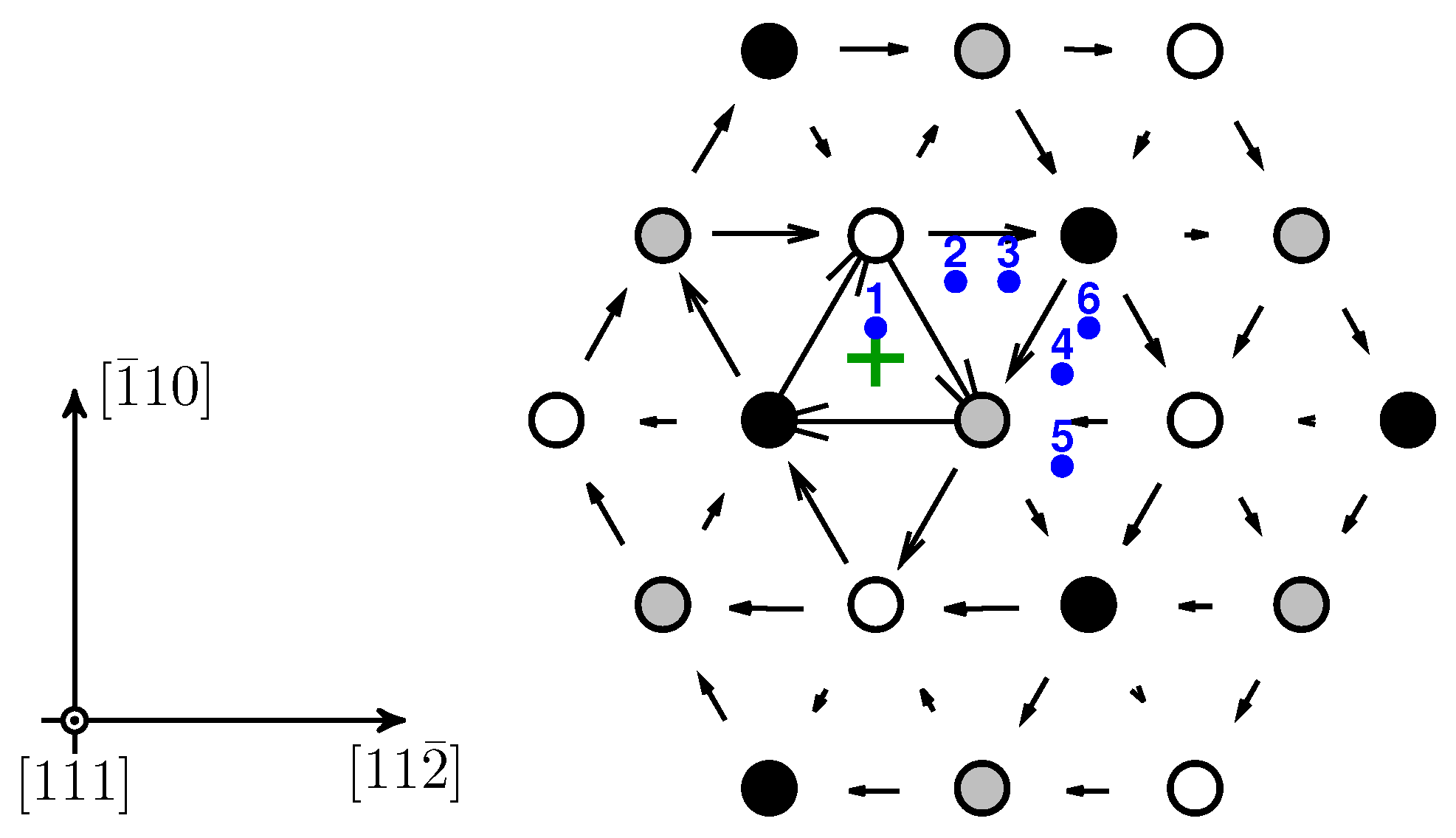
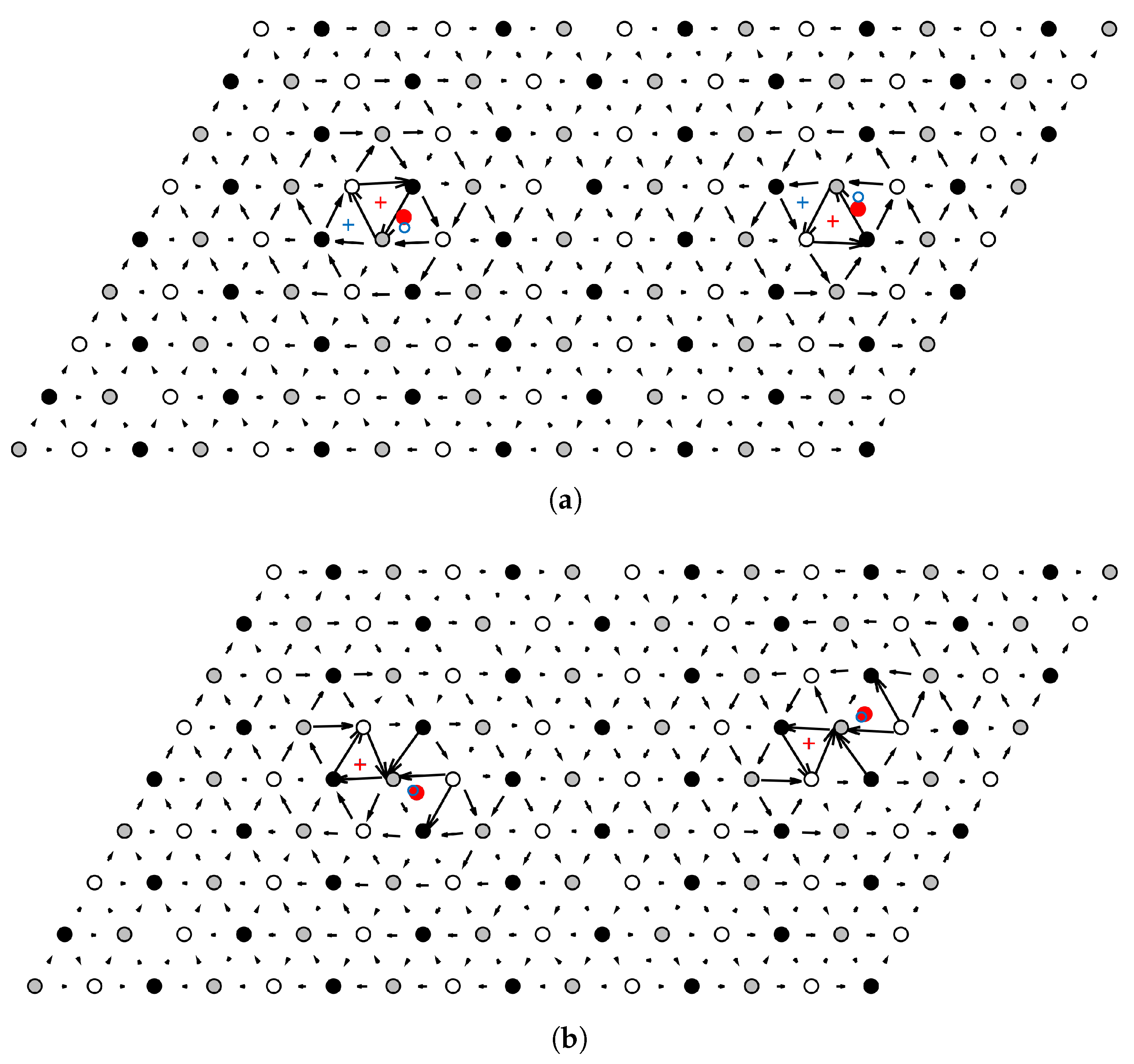
2.2. Screw Dislocation–O Interaction
3. Results
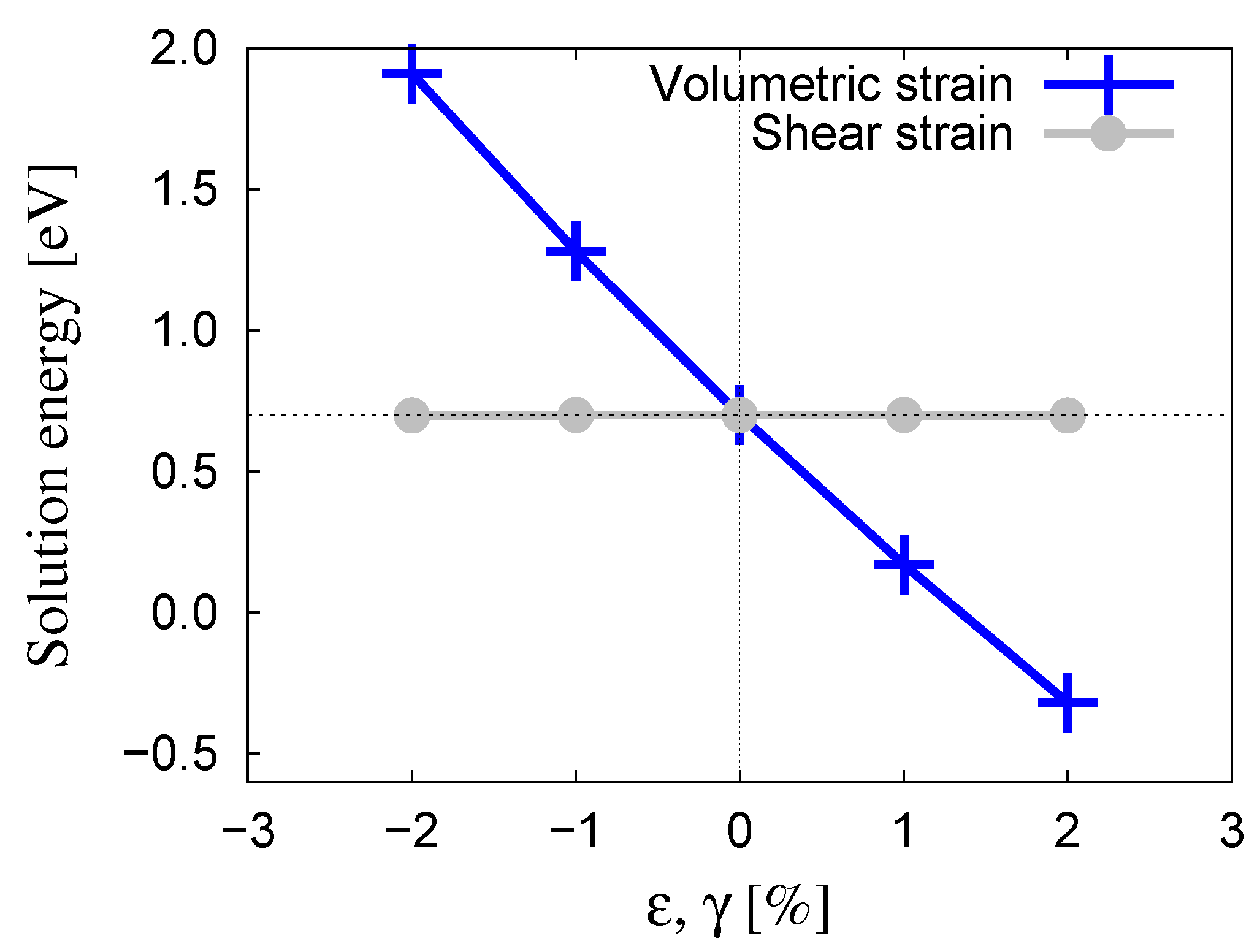
3.1. Oxygen Atom Stability in Bulk Tungsten
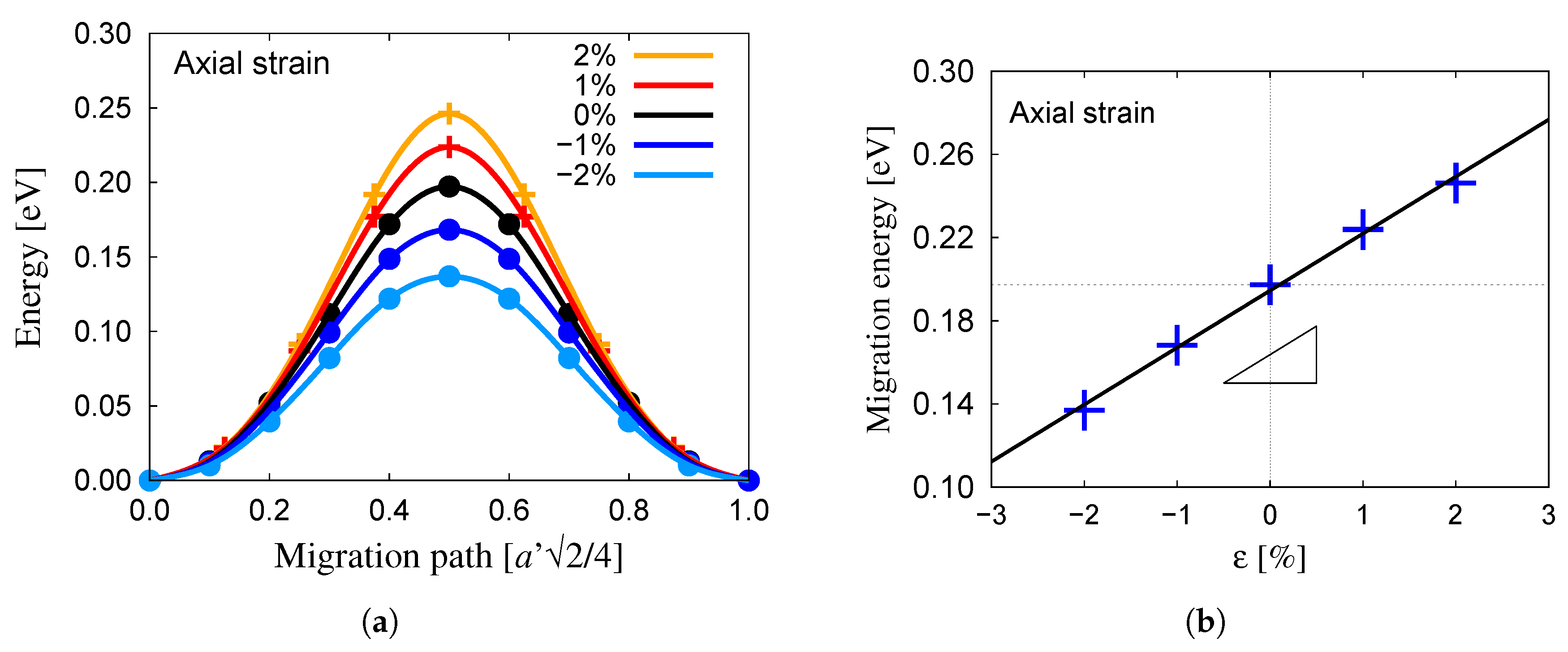
3.2. Oxygen Migration in Bulk Tungsten
3.3. Screw Dislocation–Oxygen Interaction in Tungsten
4. Discussion
5. Conclusions
- We have conducted electronic structure calculations of the fundamental energetics of oxygen atoms in tungsten, including the heat of solution, migration energies, activation volumes, and interaction energy with screw dislocation cores.
- Oxygen atoms are preferentially found in tetrahedral lattice sites, with solution energies of eV. The substitutional heat of solution (an O atom associated with a vacant site) was found to be eV.
- The migration energy for the tetrahedral→tetrahedral transition in the bulk is 0.20 eV. This energy is modified by stress according to activation volumes of and for volumetric and shear deformations, respectively.
- The interaction energy between a screw dislocation core and an O atom depends on the relative position of the oxygen, but it is found to be either 1.20 or 1.83 eV, depending on the final configuration. We find that this is due to the accommodation of the large local distortions induced by the O atom in the lattice, which is seen to lead to a core reconstruction from an easy core configuration to a hard core one when O atoms are present.
- In most cases, once absorbed at a screw dislocation core, O atoms are seen to induce a dislocation core transformation from an easy core configuration to a hard core one.
- These calculations will serve to parameterize mesoscale models of material deformation by dislocation slip.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Compilation of DFT Results for Dislocation Core–Oxygen Atom Interaction Energy Calculations
| O-Atom | Distance between | Distance between | Final Core | Uncorrected | Corrected | |||
|---|---|---|---|---|---|---|---|---|
| Location (NN) | Cores () | Oxygen Atoms () | Configuration | (eV) | (eV) | |||
| initial | final | initial | final | initial | final | |||
| 1 | 2 | 7.5 | 7.5 | 7.5 | 6.5 | hard | ||
| 2 | 2 | 7.5 | 8.5 | 7.5 | 7.5 | hard | ||
| 3 | 2/5 | 7.5 | 7.5 | 7.5 | 7.5 | hard/ext.easy | ||
| 4 | 2 | 7.5 | 7.5 | 7.5 | 7.5 | hard | ||
| 5 | 5 | 7.5 | 7.5 | 7.5 | 7.5 | ext. easy | ||
| 6 | 2 | 7.5 | 7.5 | 7.5 | 7.5 | hard | ||
References
- Tietz, T.E.; Wilson, J.W. Behavior and Properties of Refractory Metals; Stanford University Press: Stanford, CA, USA, 1965. [Google Scholar]
- Davis, J.R. Alloying: Understanding the Basics; ASM International: Materials Park, OH, USA, 2001. [Google Scholar]
- Lassner, E.; Schubert, W.D. Tungsten alloys. In Tungsten; Springer: Berlin/Heidelberg, Germany, 1999; pp. 255–282. [Google Scholar]
- Lassner, E.; Schubert, W.D. Properties, Chemistry, Technology of the Element, Alloys, and Chemical Compounds; Vienna University of Technology: Vienna, Austria, 1999; pp. 124–125. [Google Scholar]
- Stephens, J.R. Effects of Interstitial Impurities on the Low-Temperature Tensile Properties of Tungsten; Technical Report; National Aeronautics and Space Administration Cleveland OH Lewis Research Center: Cleveland, OH, USA, 1964. [Google Scholar]
- Ulitchny, M.; Gibala, R. The effects of interstitial solute additions on the mechanical properties of niobium and tantalum single crystals. J. Less Common Met. 1973, 33, 105–116. [Google Scholar] [CrossRef]
- Stein, D.; Low, J., Jr. Effects of orientation and carbon on the mechanical properties of iron single crystals. Acta Metall. 1966, 14, 1183–1194. [Google Scholar] [CrossRef]
- Smialek, R.; Mitchell, T. Interstitial solution hardening in tantalum single crystals. Philos. Mag. 1970, 22, 1105–1127. [Google Scholar] [CrossRef]
- Baird, J. The effects of strain-ageing due to interstitial solutes on the mechanical properties of metals. Metall. Rev. 1971, 16, 1–18. [Google Scholar]
- Das, J.; Sankaranarayana, M.; Nandy, T. Serrated flow behavior in tungsten heavy alloy. Mater. Sci. Eng. A 2015, 646, 75–81. [Google Scholar] [CrossRef]
- Wells, A.F. Structural Inorganic Chemistry; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Stephens, J.R. Effect of Oxygen on Mechanical Properties of Tungsten; Technical Report; National Aeronautics and Space Administration Cleveland OH Lewis Research Center: Cleveland, OH, USA, 1963. [Google Scholar]
- Cottrell, A.H.; Bilby, B. Dislocation theory of yielding and strain ageing of iron. Proc. Phys. Soc. Sect. A 1949, 62, 49. [Google Scholar] [CrossRef]
- Vitek, V.; Perrin, R.; Bowen, D. The core structure of 1/2 (111) screw dislocations in bcc crystals. Philos. Mag. 1970, 21, 1049–1073. [Google Scholar] [CrossRef]
- Clouet, E.; Garruchet, S.; Nguyen, H.; Perez, M.; Becquart, C.S. Dislocation interaction with C in α-Fe: A comparison between atomic simulations and elasticity theory. Acta Mater. 2008, 56, 3450–3460. [Google Scholar] [CrossRef]
- Trinkle, D.R.; Woodward, C. The chemistry of deformation: How solutes soften pure metals. Science 2005, 310, 1665–1667. [Google Scholar] [CrossRef]
- Medvedeva, N.; Gornostyrev, Y.N.; Freeman, A. Solid solution softening and hardening in the group-V and group-VI bcc transition metals alloys: First principles calculations and atomistic modeling. Phys. Rev. B Condens. Matter 2007, 76, 212104. [Google Scholar] [CrossRef]
- Romaner, L.; Ambrosch-Draxl, C.; Pippan, R. Effect of rhenium on the dislocation core structure in tungsten. Phys. Rev. Lett. 2010, 104, 195503. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Lu, G. QM/MM study of dislocation—Hydrogen/helium interactions in α-Fe. Model. Simul. Mater. Sci. Eng. 2011, 19, 065004. [Google Scholar] [CrossRef]
- Li, H.; Wurster, S.; Motz, C.; Romaner, L.; Ambrosch-Draxl, C.; Pippan, R. Dislocation-core symmetry and slip planes in tungsten alloys: Ab initio calculations and microcantilever bending experiments. Acta Mater. 2012, 60, 748–758. [Google Scholar] [CrossRef]
- Itakura, M.; Kaburaki, H.; Yamaguchi, M.; Okita, T. The effect of hydrogen atoms on the screw dislocation mobility in bcc iron: A first-principles study. Acta Mater. 2013, 61, 6857–6867. [Google Scholar] [CrossRef]
- Samolyuk, G.D.; Osetsky, Y.; Stoller, R. The influence of transition metal solutes on the dislocation core structure and values of the Peierls stress and barrier in tungsten. J. Phys. Condens. Matter 2012, 25, 025403. [Google Scholar] [CrossRef] [PubMed]
- Romaner, L.; Razumovskiy, V.; Pippan, R. Core polarity of screw dislocations in Fe–Co alloys. Philos. Mag. Lett. 2014, 94, 334–341. [Google Scholar] [CrossRef]
- Ventelon, L.; Lüthi, B.; Clouet, E.; Proville, L.; Legrand, B.; Rodney, D.; Willaime, F. Dislocation core reconstruction induced by carbon segregation in bcc iron. Phys. Rev. B Condens. Matter 2015, 91, 220102. [Google Scholar] [CrossRef]
- Rodney, D.; Ventelon, L.; Clouet, E.; Pizzagalli, L.; Willaime, F. Ab initio modeling of dislocation core properties in metals and semiconductors. Acta Mater. 2017, 124, 633–659. [Google Scholar] [CrossRef]
- Lüthi, B.; Ventelon, L.; Rodney, D.; Willaime, F. Attractive interaction between interstitial solutes and screw dislocations in bcc iron from first principles. Comput. Mater. Sci. 2018, 148, 21–26. [Google Scholar] [CrossRef]
- Lüthi, B.; Ventelon, L.; Elsässer, C.; Rodney, D.; Willaime, F. First principles investigation of carbon-screw dislocation interactions in body-centered cubic metals. Model. Simul. Mater. Sci. Eng. 2017, 25, 084001. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B Condens. Matter 1993, 47, 558. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B Condens. Matter 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B Condens. Matter 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Clouet, E.; Ventelon, L.; Willaime, F. Dislocation core energies and core fields from first principles. Phys. Rev. Lett. 2009, 102, 055502. [Google Scholar] [CrossRef]
- Ventelon, L.; Willaime, F.; Clouet, E.; Rodney, D. Ab initio investigation of the Peierls potential of screw dislocations in bcc Fe and W. Acta Mater. 2013, 61, 3973–3985. [Google Scholar] [CrossRef]
- Dezerald, L.; Ventelon, L.; Clouet, E.; Denoual, C.; Rodney, D.; Willaime, F. Ab initio modeling of the two-dimensional energy landscape of screw dislocations in bcc transition metals. Phys. Rev. B Condens. Matter 2014, 89, 024104. [Google Scholar] [CrossRef]
- Ventelon, L.; Willaime, F. Generalized stacking-faults and screw-dislocation core-structure in bcc iron: A comparison between ab initio calculations and empirical potentials. Philos. Mag. 2010, 90, 1063–1074. [Google Scholar] [CrossRef]
- Itakura, M.; Kaburaki, H.; Yamaguchi, M. First-principles study on the mobility of screw dislocations in bcc iron. Acta Mater. 2012, 60, 3698–3710. [Google Scholar] [CrossRef]
- Hossain, M.; Marian, J. Stress-dependent solute energetics in W–Re alloys from first-principles calculations. Acta Mater. 2014, 80, 107–117. [Google Scholar] [CrossRef]
- Weinberger, C.R.; Tucker, G.J.; Foiles, S.M. Peierls potential of screw dislocations in bcc transition metals: Predictions from density functional theory. Phys. Rev. B Condens. Matter 2013, 87, 054114. [Google Scholar] [CrossRef]
- Duesbery, M.; Vitek, V.; Bowen, D.K. The effect of shear stress on the screw dislocation core structure in body-centred cubic lattices. Proc. R. Soc. Lond. A 1973, 332, 85–111. [Google Scholar] [CrossRef]
- Vitek, V. Structure of dislocation cores in metallic materials and its impact on their plastic behaviour. Prog. Mater. Sci. 1992, 36, 1–27. [Google Scholar] [CrossRef]
- Jiang, D.E.; Carter, E.A. Diffusion of interstitial hydrogen into and through bcc Fe from first principles. Phys. Rev. B 2004, 70, 064102. [Google Scholar] [CrossRef]
- Alkhamees, A.; Liu, Y.L.; Zhou, H.B.; Jin, S.; Zhang, Y.; Lu, G.H. First-principles investigation on dissolution and diffusion of oxygen in tungsten. J. Nucl. Mater. 2009, 393, 508–512. [Google Scholar] [CrossRef]
- Nguyen-Manh, D. Ab-Initio Modelling of Point Defect-Impurity Interaction in Tungsten and other BCC Transition Metals. Adv. Mater. Res. 2009, 59, 253–256. [Google Scholar] [CrossRef]
- Barouh, C.; Schuler, T.; Fu, C.C.; Jourdan, T. Predicting vacancy-mediated diffusion of interstitial solutes in α-Fe. Phys. Rev. B 2015, 92, 104102. [Google Scholar] [CrossRef]
- Shang, S.; Fang, H.; Wang, J.; Guo, C.; Wang, Y.; Jablonski, P.; Du, Y.; Liu, Z. Vacancy mechanism of oxygen diffusivity in bcc Fe: A first-principles study. Corros. Sci. 2014, 83, 94–102. [Google Scholar] [CrossRef]
- Frank, W.; Engell, H.; Seeger, A. Migration energy and solubility of oxygen in body centered cubic iron. Z. Metallkd. 1967, 58, 452–455. [Google Scholar]
- Li, R.; Zhang, P.; Li, X.; Zhang, C.; Zhao, J. First-principles study of the behavior of O, N and C impurities in vanadium solids. J. Nucl. Mater. 2013, 435, 71–76. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO—The Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
- Jacobs, A.J. Diffusion of Oxygen in Tungsten and some other Transition Metals. Nature 1963, 200, 1310. [Google Scholar] [CrossRef]
- Lee, C.H. Oxygen Diffusion in Tungsten. Nature 1964, 203, 1163. [Google Scholar] [CrossRef]
- Rapperport, E.; Nerses, V.; Smith, M. Diffusion in Refractory Metals; Technical Report; Defense Technical Information Center: Fort Belvoir, VA, USA, 1964. [Google Scholar]
- Butz, R.; Wagner, H. Diffusion of oxygen on tungsten (110). Surf. Sci. 1977, 63, 448–459. [Google Scholar] [CrossRef]
- Sikka, V.; Rosa, C. The oxidation kinetics of tungsten and the determination of oxygen diffusion coefficient in tungsten trioxide. Corros. Sci. 1980, 20, 1201–1219. [Google Scholar] [CrossRef]
- Lu, G.H.; Zhou, H.B.; Becquart, C.S. A review of modelling and simulation of hydrogen behaviour in tungsten at different scales. Nucl. Fusion 2014, 54, 086001. [Google Scholar] [CrossRef]
- Bakaev, A.; Terentyev, D.; Grigorev, P.; Posselt, M.; Zhurkin, E.E. Ab initio study of interaction of helium with edge and screw dislocations in tungsten. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2017, 393, 150–154. [Google Scholar] [CrossRef]
- Wang, G.; Ramesh, N.; Hsu, A.; Chu, D.; Chen, R. Density functional theory study of the adsorption of oxygen molecule on iron phthalocyanine and cobalt phthalocyanine. Mol. Simul. 2008, 34, 1051–1056. [Google Scholar] [CrossRef]
- Zhao, B.; Shang, C.; Qi, N.; Chen, Z.; Chen, Z. Stability of defects in monolayer MoS2 and their interaction with O2 molecule: A first-principles study. Appl. Surf. Sci. 2017, 412, 385–393. [Google Scholar] [CrossRef]
- Xu, W.; Moriarty, J. Atomistic simulation of ideal shear strength, point defects, and screw dislocations in bcc transition metals: Mo as a prototype. Phys. Rev. B 1996, 54, 6941. [Google Scholar] [CrossRef]
- Zhao, Y.; Marian, J. Direct prediction of the solute softening-to-hardening transition in W–Re alloys using stochastic simulations of screw dislocation motion. Modell. Simul. Mater. Sci. Eng. 2018, 26, 045002. [Google Scholar] [CrossRef]


| Å) | (eV) | (eV) |
|---|---|---|
| 1.23 (O) | ||
| 2.76 () | ||
| 5.52 () |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Dezerald, L.; Marian, J. Electronic Structure Calculations of Oxygen Atom Transport Energetics in the Presence of Screw Dislocations in Tungsten. Metals 2019, 9, 252. https://doi.org/10.3390/met9020252
Zhao Y, Dezerald L, Marian J. Electronic Structure Calculations of Oxygen Atom Transport Energetics in the Presence of Screw Dislocations in Tungsten. Metals. 2019; 9(2):252. https://doi.org/10.3390/met9020252
Chicago/Turabian StyleZhao, Yue, Lucile Dezerald, and Jaime Marian. 2019. "Electronic Structure Calculations of Oxygen Atom Transport Energetics in the Presence of Screw Dislocations in Tungsten" Metals 9, no. 2: 252. https://doi.org/10.3390/met9020252
APA StyleZhao, Y., Dezerald, L., & Marian, J. (2019). Electronic Structure Calculations of Oxygen Atom Transport Energetics in the Presence of Screw Dislocations in Tungsten. Metals, 9(2), 252. https://doi.org/10.3390/met9020252





