Analysis of the Influence of Segmented Rollers on Slab Bulge Deformation
Abstract
:1. Introduction
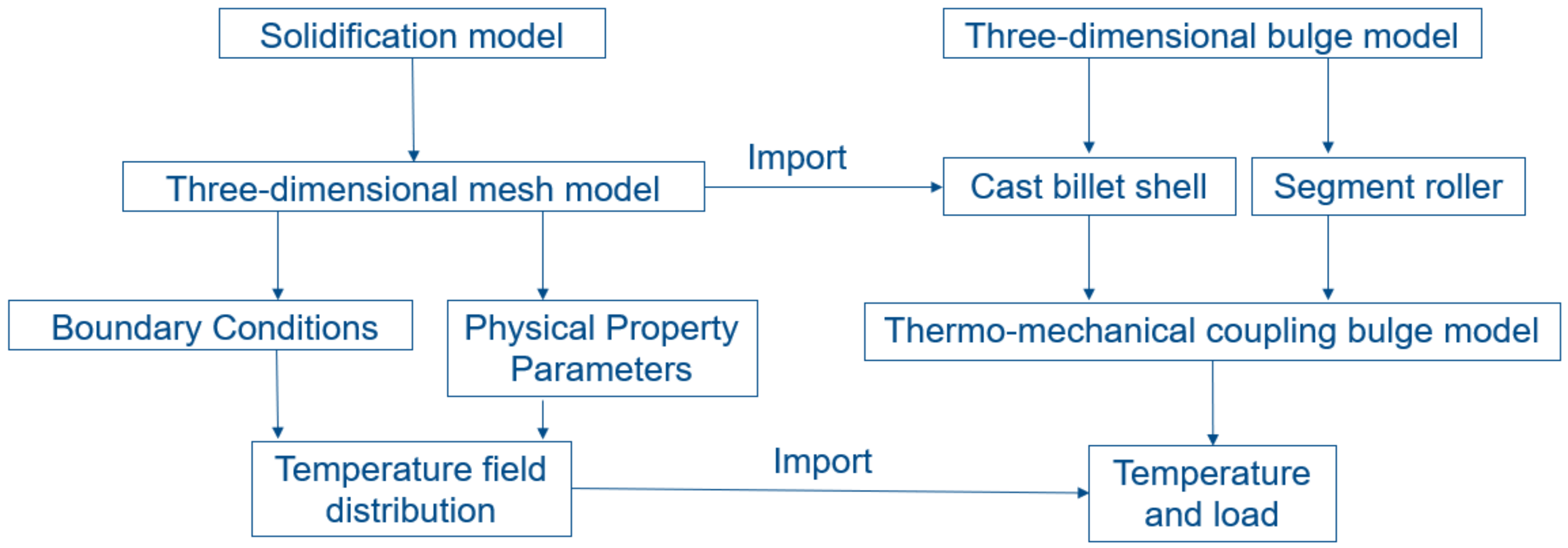
2. 3D Solidification Model Description
2.1. 3D Solidification Finite Element Model
- is the density (),
- is the specific heat capacity under constant pressure (),
- is the temperature (),
- is time (),
- is the internal heat source (),
- is the thermal conductivity (), and
- is the casting speed, ().
- is the thermal conductivity of the solid phase zone (), and
- is the thermal conductivity of the liquid phase zone ().
- is latent heat of solidification under the action of various metals (),
- is the liquidus temperature (K), and
- is the solidus temperature (K).
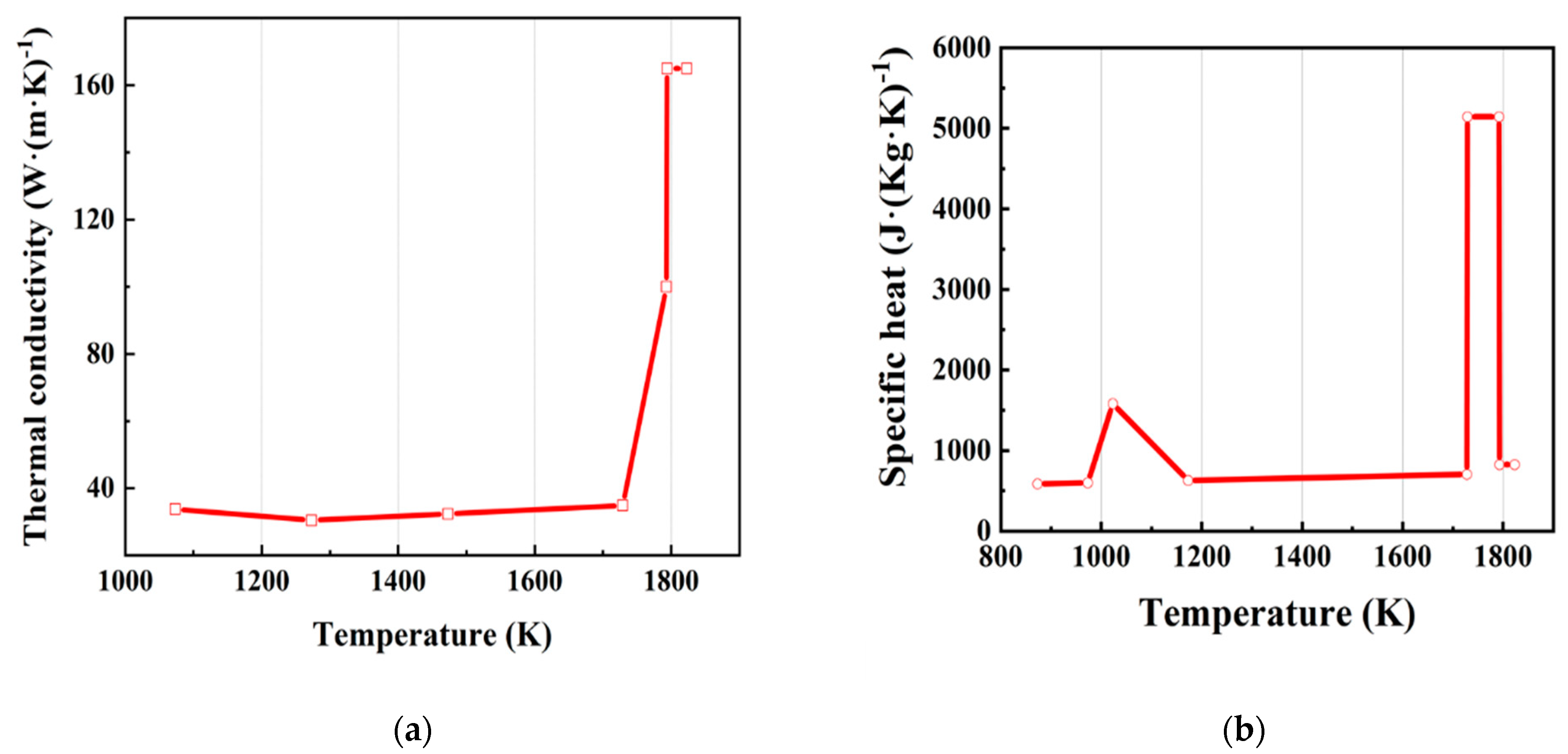
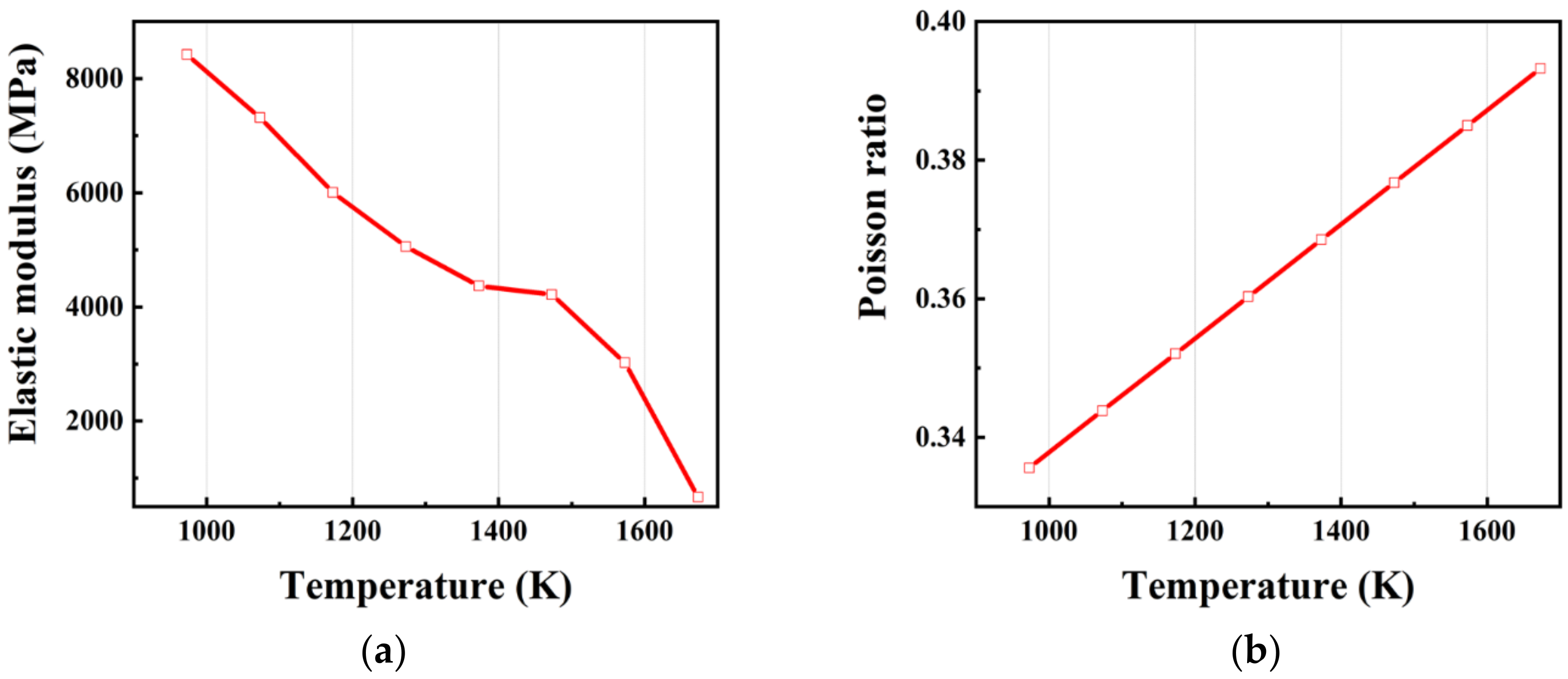
2.2. Physical Property Parameters
2.3. Boundary Conditions
- is determined by the actual heat balance calculation,
- is the crystallizer length (m), and
- is the casting speed ().
- is the heat flux (),
- is the heat transfer coefficient (),
- is the slab surface temperature (), and
- is the cooling water temperature ().
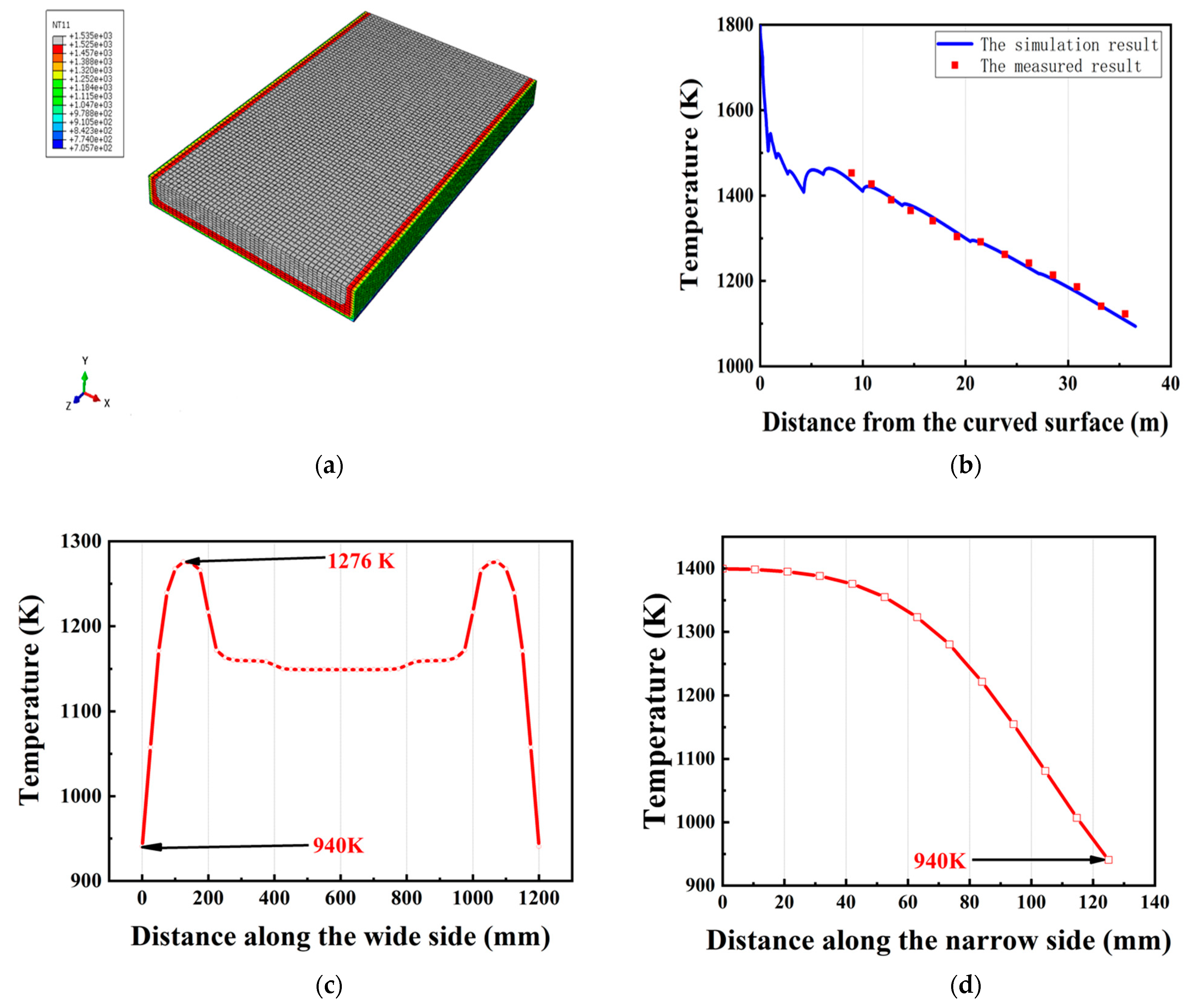
2.4. Results and Discussion
3. The Establishment of the Bulge Deformation Model
3.1. Physical Property Parameters
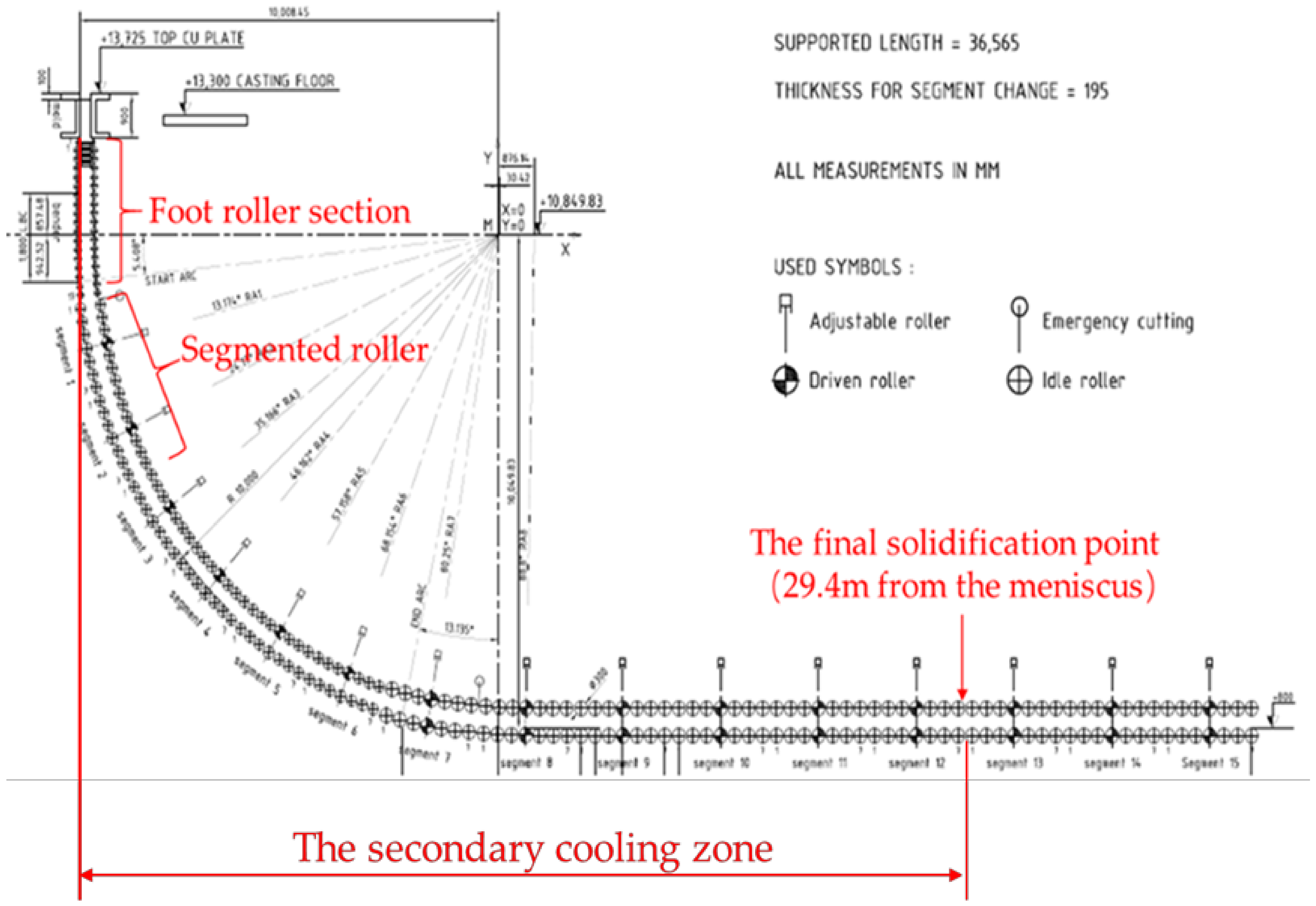
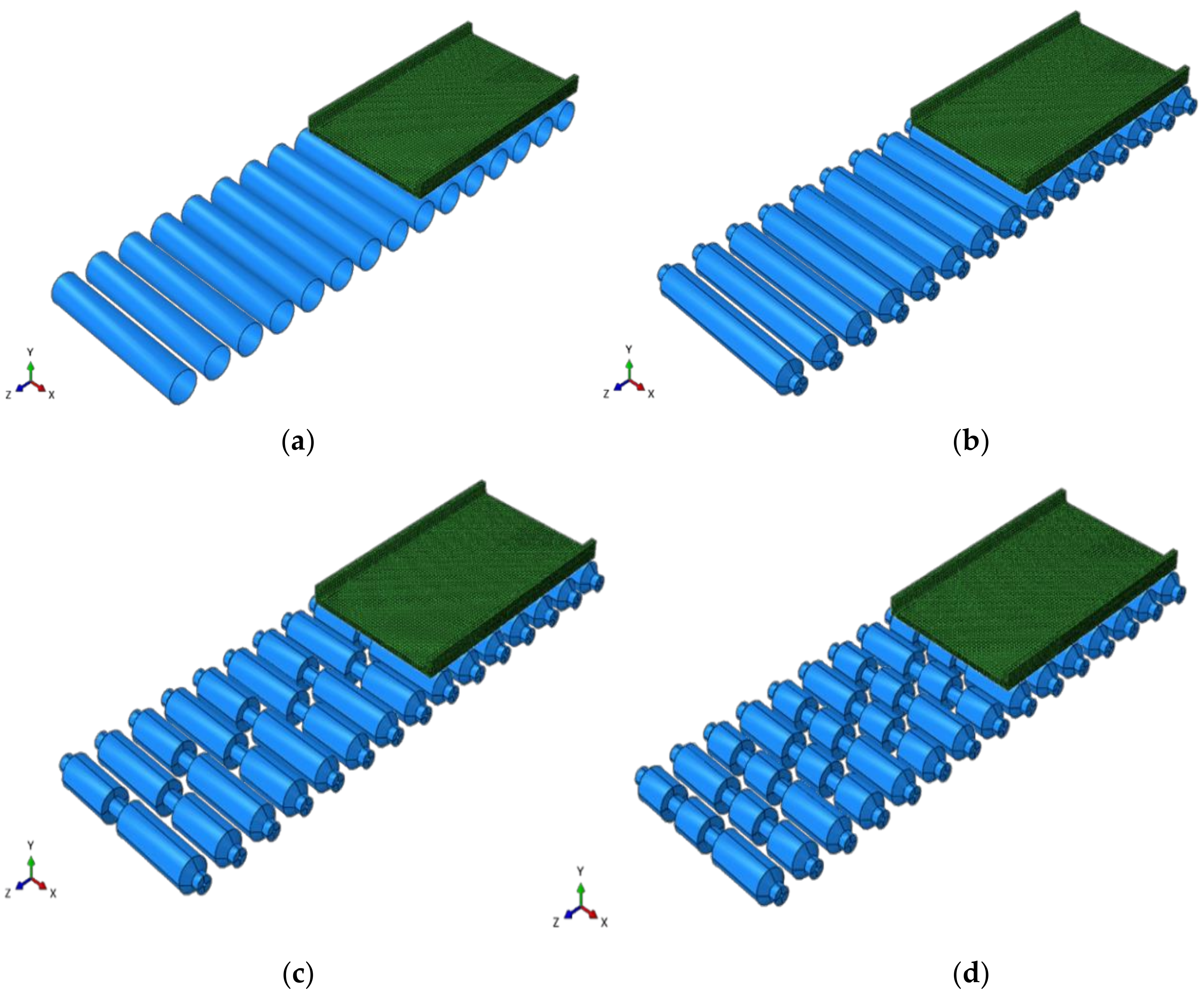
3.2. Geometric Model with Various Segmented Casting Rollers
3.3. Boundary Conditions and Contact Definition
3.4. Creep Model
- ,
- ,
- ,
- ,
- is the creep strain rate (),
- is the influence parameter of carbon content (),
- is the stress (MPa),
- is the deformation energy constant (),
- is the temperature (),
- is the time (),
- is the temperature-dependent time influence index, and
- is the temperature-dependent comprehensive stress influence index.
3.5. Predefined Temperature Field
4. Comparisons of Slab Bulge Deformations with Different Segment Rollers
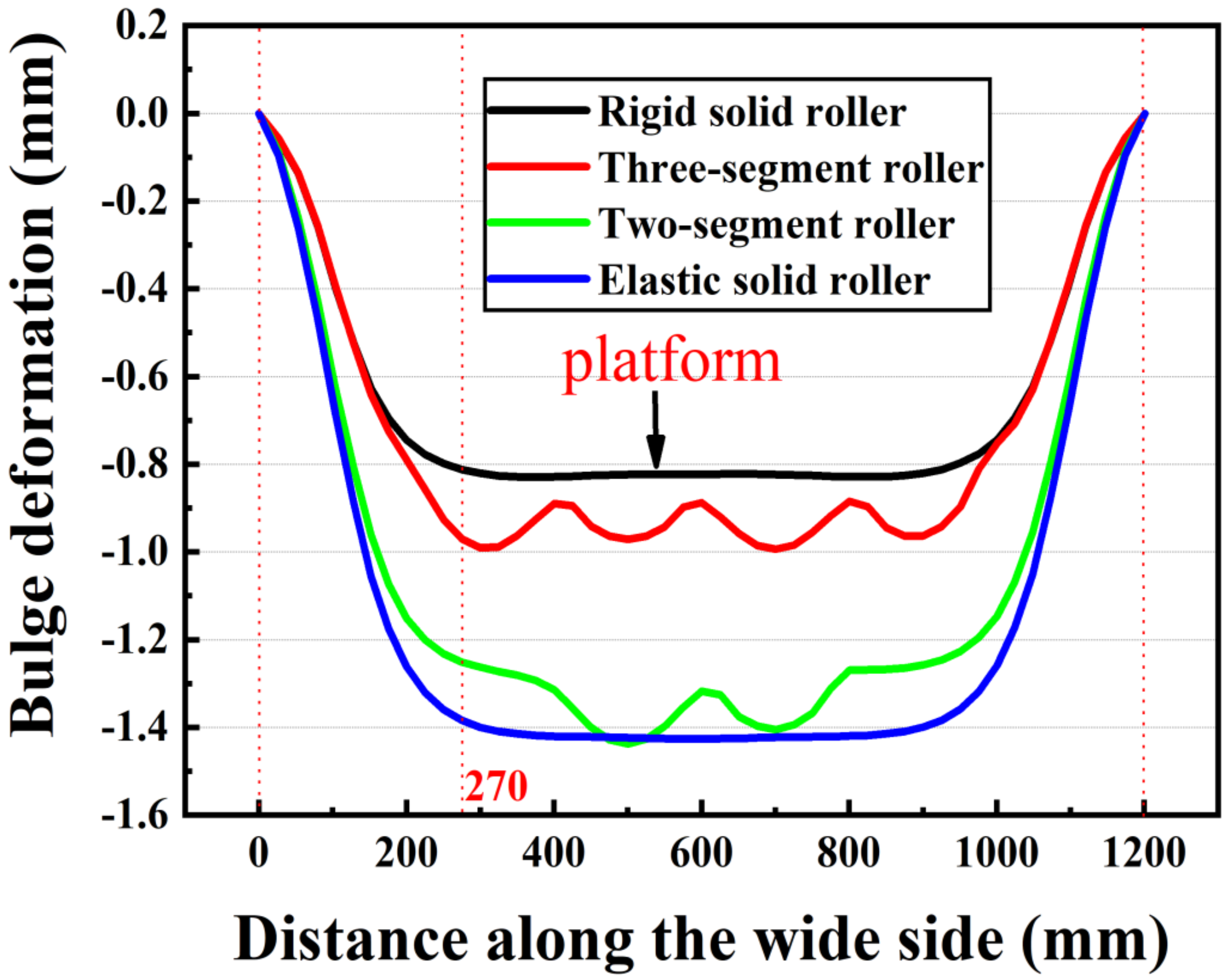
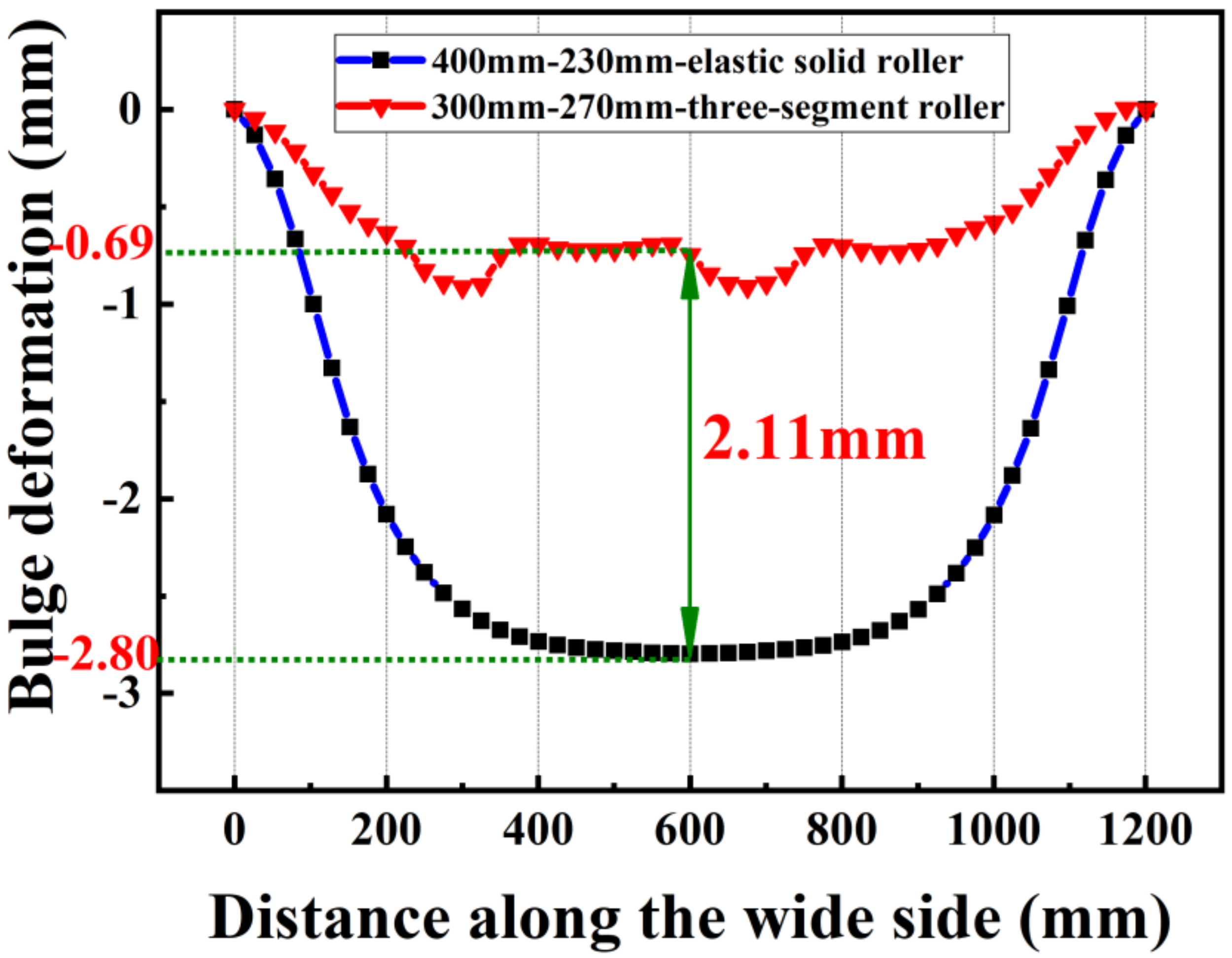
4.1. Bulge Deformation on the Wide Side
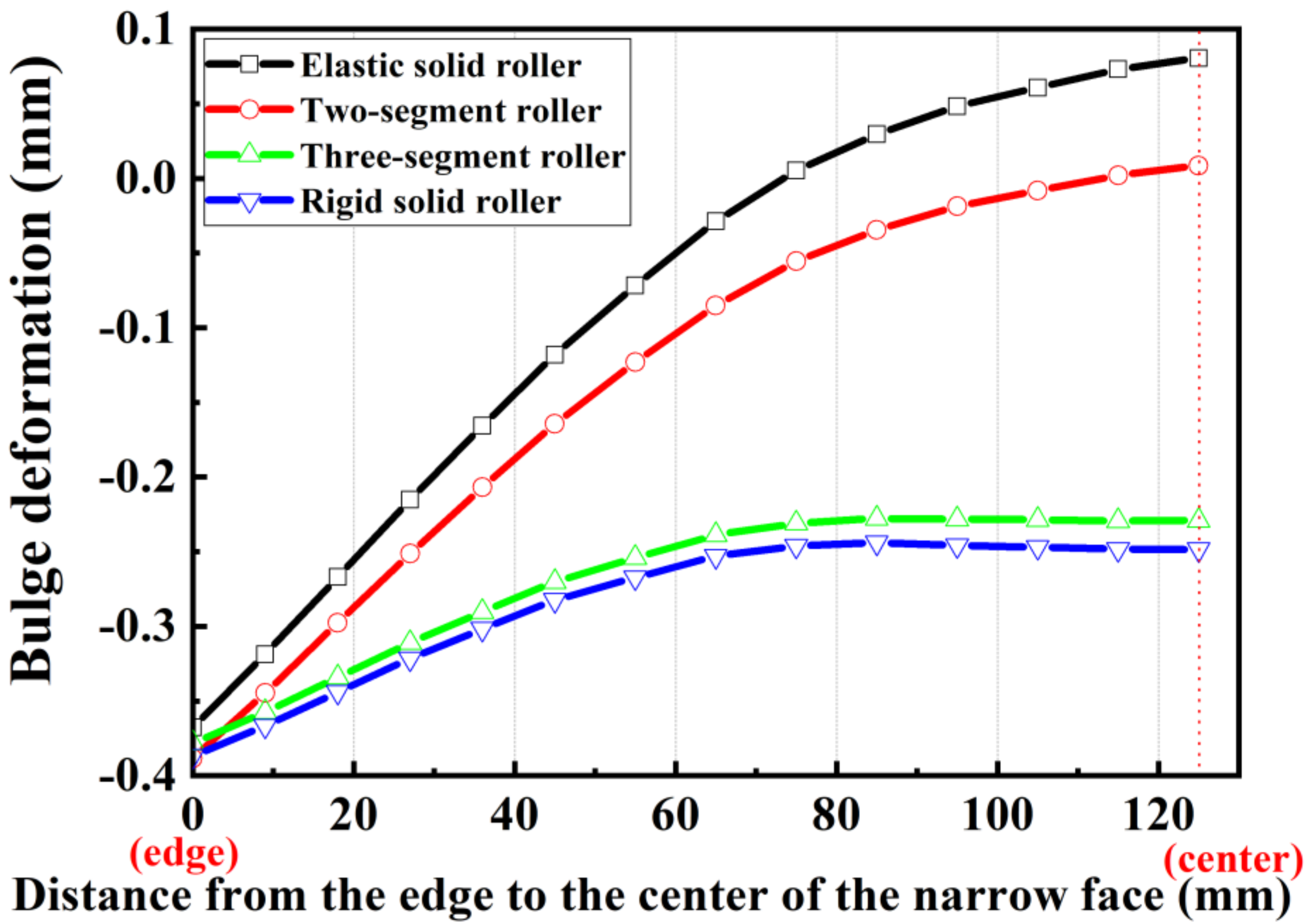
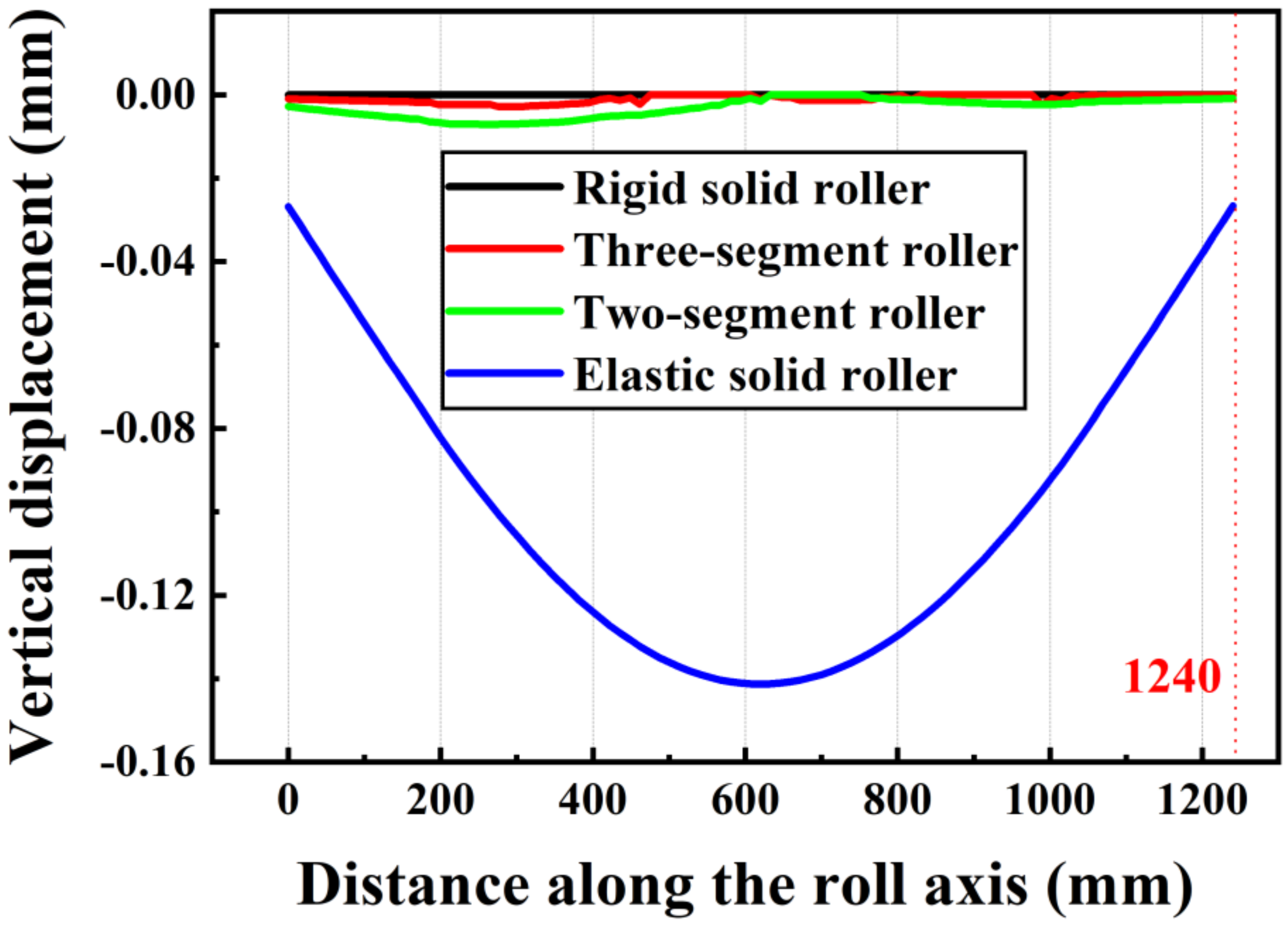
4.2. Bulge Deformation on the Narrow Side
4.3. Analysis of Segmented Roller’s Stiffness
5. Influences of Roller Spacing and Roller Diameter on Slab Bulge Deformation
5.1. Establishment of Deformation Model with Different Roller Spacings and Diameters
5.2. Results and Conclusions
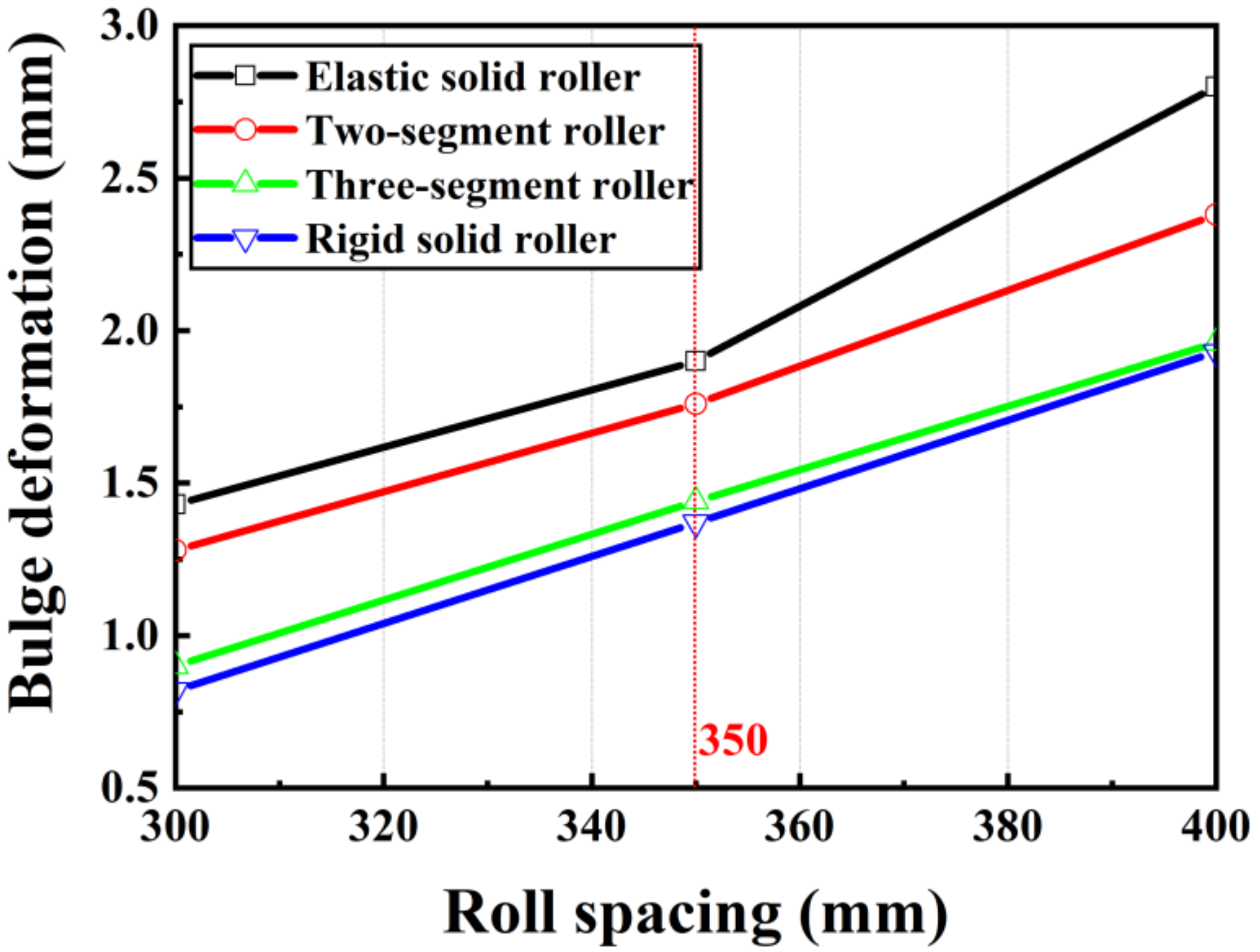
5.2.1. Influences of Roller Spacing on Bulge Deformation
5.2.2. Influences of Roller Diameter on Bulge Deformation
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Janik, M.; Dyja, H.; Berski, S.; Banaszek, G. Two-dimensional thermomechanical analysis of continuous casting process. J. Mater. Process. Technol. 2004, 153, 578–582. [Google Scholar] [CrossRef]
- Ji, C.; Luo, S.; Zhu, M.; Sahai, Y. Uneven solidification during wide-thick slab continuous casting process and its influence on soft reduction zone. ISIJ Int. 2014, 54, 103–111. [Google Scholar] [CrossRef]
- Dong, Q.; Zhang, J.; Yin, Y.; Wang, B. Three-dimensional numerical modeling of macrosegregation in continuously cast billets. Metals 2017, 7, 209. [Google Scholar] [CrossRef]
- Long, M.; Chen, H.; Chen, D.; Yu, S.; Liang, B.; Duan, H. A combined hybrid 3-D/2-D model for flow and solidification prediction during slab continuous casting. Metals 2018, 8, 182. [Google Scholar] [CrossRef]
- Yoshii, A.; Kihara, S. Analysis of bulging in continuously cast slabs by bending theory of continuous beam. Trans. Iron Steel Inst. Jpn. 1986, 26, 891–894. [Google Scholar] [CrossRef]
- Liu, W.; Dai, Y. Study on the deformation of the liquid core continuous casting shell. Heavy Mach. 1994, 10–16. [Google Scholar] [CrossRef]
- Sun, J.; Sheng, Y.; Zhang, X. Analysis of bulging deformation and stress in continuous cast slabs. J. Iron Steel Res. 1996, 11–15. [Google Scholar] [CrossRef]
- Xu, R. Behavior analysis of bulging deformation in slab casting process. Heavy Mach. 2012, 17–21. [Google Scholar] [CrossRef]
- Toishi, K.; Miki, Y. Generation mechanism of unsteady bulging in continuous casting-2-fem simulation for generation mechanism of unsteady bulging. ISIJ Int. 2016, 56, 1764–1769. [Google Scholar] [CrossRef]
- Ha, J.; Cho, J.; Lee, B.; Ha, M. Numerical analysis of secondary cooling and bulging in the continuous casting of slabs. J. Mater. Process. Technol. 2001, 113, 257–261. [Google Scholar] [CrossRef]
- Zhang, Y. Analysis of solidification heat transfer and bulging in the cast slab. Master’s Thesis, Yanshan University, Hebei, China, 2011. [Google Scholar]
- Okamura, K.; Kawashima, H. Three-dimensional elasto-plastic and creep analysis of bulging in continuously cast slabs. Tetsu-to-Hagane 1989, 75, 1905–1912. [Google Scholar] [CrossRef]
- Ning, Z.; Wu, D.; Qin, Q.; Zang, Y. Three-dimensional emulation research on the bulging deformation during continuously casting slab. Metall. Equip. 2007, 2. [Google Scholar]
- Qin, Q.; Shang, S.; Wu, D.; Zang, Y. Comparative analysis of bulge deformation between 2D and 3D finite element models. Adv. Mech. Eng. 2014, 6, 942719. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, X.; Qian, L. 3D Finite element calculation of creep bulging system development and application. Contin. Cast. 2015, 40, 54–58. [Google Scholar]
- Camporredondo, J.E.; Acosta, F.A.; Castillejos, A.H.; Gutierrez, E.P.; De la Gonzalez, R. Analysis of thin-slab casting by the compact-strip process: Part II. Effect of operating and design parameters on solidification and bulging. Metall. Mater. Trans. B 2004, 35, 561–573. [Google Scholar] [CrossRef]
- Zhang, J.; Shen, H.F.; Huang, T.Y. Finite element thermal-mechanical coupled analysis of strand bulging deformation in continuous casting. Adv. Mater. Res. 2011, 154–155, 1456–1461. [Google Scholar] [CrossRef]
- Qin, Q.; Yang, Z. Finite element simulation of bulge deformation for slab continuous casting. Int. J. Adv. Manuf. Technol. 2017, 93, 4357–4370. [Google Scholar] [CrossRef]
- Triolet, N.; Bobadilla, M.; Bellet, M.; Avedian, L.; Mabelly, P. A thermomechanical modelling of continuous casting to master steel slabs internal soundness and surface quality. Rev. De Métallurgie–Int. J. Metall. 2005, 102, 343–353. [Google Scholar] [CrossRef]
- Fu, J.-X.; Hwang, W.-S. Numerical simulation of slab broadening in continuous casting of steel. In Numerical Simulation-From Theory to Industry; InTech: Rijeka, Croatia, 2012. [Google Scholar]
- Li, B. Study about the High-temperature creep property of q460e steel and its bulging in continuous casting process. Master’s Thesis, Yan Shan University, Hebei, China, 2015. [Google Scholar]
- Han, P.; Ren, T.; Jin, X. Influence of roll misalignment on bulging of continuous casting slab. Iron Steel 2016, 51, 53–58. [Google Scholar]
- Ohno, H.; Miki, Y.; Nishizawa, Y. Generation mechanism of unsteady bulging in continuous casting-1-development of method for measurement of unsteady bulging in continuous casting. ISIJ Int. 2016, 56, 1758–1763. [Google Scholar] [CrossRef]
- Verma, R.; Girase, N. Comparison of different caster designs based on bulging, bending and misalignment strains in solidifying strand. Ironmak. Steelmak. 2006, 33, 471–476. [Google Scholar] [CrossRef]
- Yu, Y.; Duan, L.; Cui, X. Brief introduction of slab caster segment rollers. Metall. Equip. 2016, 45–48. [Google Scholar] [CrossRef]
- Li, S.; Shen, B. Roller type selection of sector of WISCO three steelmaking continuous casting machine. Metall. Equip. 1992, 14, 51–52. [Google Scholar]
- Shi, J. The advantages and theoretical argument of caster segment sub-section roller. In Proceedings of the 8th (2011) China Steel Annual Meeting, Beijing, China, 26 October 2011; p. 6. [Google Scholar]
- Liu, W.; Wang, W. Analysis on the stiffness of segmented baeking guide roll of slab continuous caster. Bao Steel Technol. 1994, 12, 58–63. [Google Scholar]
- Liu, W.; Wang, W. The influence of structure and classified number of backup guide rolls in CCM on the deformation of slab bulge. Shanghai Metals 1995, 17, 25–30. [Google Scholar]
- Qin, Q.; Wu, D. Thermal and Mechanical Behavior of Continuous Casting Equipment; Metallurgical Industry Press: Beijing, China, 2013. [Google Scholar]
- Mizikar, E.A. Mathematical heat transfer model for solidification of continuously cast steel slabs. Trans. Metall. Soc. AIME 1967, 239, 1747–1753. [Google Scholar]
- Cheng, J. Continuous Casting Steel Manual; Metallurgical Industry Press: Beijing, China, 1991. [Google Scholar]
- Feng, K.; Chen, D.; Xu, C.; Wen, L.; Dong, L. Effect of main thermo-physical parameters of steel Q 235 on accuracy of concasting transport model. Special Steel 2004, 25, 28–31. [Google Scholar]
- Mills, K.C.; Su, Y.; Li, Z.; Brooks, R.F. Equations for the calculation of the thermo-physical properties of stainless steel. ISIJ Int. 2004, 44, 1661–1668. [Google Scholar] [CrossRef]
- Fu, J.; Li, J.; Wang, C.; Zhu, J. Research of Young’s modulus of elasticity of steel Q235. Mater. Rev. 2009, 23, 68–70. [Google Scholar]
- Uehara, M. Mathematical modelling of the unbending of continuously cast steel slabs. Master’s Thesis, University of British Columbia, Vancouver, BC, Canada, 1983. [Google Scholar]
- Kozlowski, P.F.; Thomas, B.G.; Azzi, J.A.; Wang, H. Simple constitutive equations for steel at high temperature. Metall. Trans. A 1992, 23, 903. [Google Scholar] [CrossRef]
| Chemical Element | C | Si | Mn | P | S |
|---|---|---|---|---|---|
| Content (%) | 0.18 | 0.20 | 0.40 | ≤0.025 | ≤0.022 |
| Chemical Element | C | Si | Mn | P | S | Al | Cr | Cu | Ni |
|---|---|---|---|---|---|---|---|---|---|
| Content (%) | 0.157 | 0.2489 | 1.4143 | 0.0162 | 0.0044 | 0.0289 | 0.0375 | 0.0284 | 0.0177 |
| Parameters | Values |
|---|---|
| Mold width | 1200 mm |
| Half slab thickness | 125 mm |
| Mold length | 2000 mm |
| Casting speed | 1.5 m∙min−1 |
| Water temperature | 303 K |
| Inlet temperature | 1808 K |
| Liquidus temperature | 1793 K |
| Solidus temperature | 1732 K |
| Specific heat capacity of the solid phase zone () | 706 |
| Specific heat capacity of the liquid phase zone () | 825 |
| Thermal conductivity of the solid phase zone () | 34.83 |
| Thermal conductivity of the liquid phase zone () | 165 |
| Latent heat of solidification under various metals () | 284 |
| Density | 7400 kg∙m−3 |
| Parameters | Values |
|---|---|
| Thickness of the solidified slab on the wide side | 42.5 mm |
| Thickness of the solidified slab on the narrow side | 41 mm |
| Number of rollers | 15 |
| Roller spacing | 300 mm |
| Radius of roller | 115 mm |
| Length of roller | 1240 mm |
| Casting speed | 1.5 m∙min−1 |
| Roller Spacing | Rigid Roller | Elastic Roller | Two-Segment Roller | Three-Segment Roller |
|---|---|---|---|---|
| Roller Diameter | ||||
| 300 mm | 230 mm | 230 mm | 230 mm | 230 mm |
| 250 mm | 250 mm | 250 mm | 250 mm | |
| 270 mm | 270 mm | 270 mm | 270 mm | |
| 350 mm | 230 mm | 230 mm | 230 mm | 230 mm |
| 400 mm | 230 mm | 230 mm | 230 mm | 230 mm |
| Roller Spacing | Rigid Roller | Elastic Roller | Two-Segment Roller | Three-Segment Roller |
|---|---|---|---|---|
| 300 mm | 0.82 mm | 1.43 mm | 1.28 mm | 0.90 mm |
| 350 mm | 1.37 mm | 1.90 mm | 1.76 mm | 1.44 mm |
| 400 mm | 1.93 mm | 2.80 mm | 2.38 mm | 1.96 mm |
| Roller Diameter | Rigid Solid Roller | Elastic Solid Roller | Elastic Two-Segment Roller | Elastic Three-Segment Roller |
|---|---|---|---|---|
| 230 mm | 0.82 mm | 1.43 mm | 1.28 mm | 0.90 mm |
| 250 mm | 0.80 mm | 1.37 mm | 1.10 mm | 0.80 mm |
| 270 mm | 0.80 mm | 1.25 mm | 0.86 mm | 0.69 mm |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, Q.; Li, M.; Huang, J. Analysis of the Influence of Segmented Rollers on Slab Bulge Deformation. Metals 2019, 9, 231. https://doi.org/10.3390/met9020231
Qin Q, Li M, Huang J. Analysis of the Influence of Segmented Rollers on Slab Bulge Deformation. Metals. 2019; 9(2):231. https://doi.org/10.3390/met9020231
Chicago/Turabian StyleQin, Qin, Ming Li, and Jianlin Huang. 2019. "Analysis of the Influence of Segmented Rollers on Slab Bulge Deformation" Metals 9, no. 2: 231. https://doi.org/10.3390/met9020231
APA StyleQin, Q., Li, M., & Huang, J. (2019). Analysis of the Influence of Segmented Rollers on Slab Bulge Deformation. Metals, 9(2), 231. https://doi.org/10.3390/met9020231





