3. Tribology of Metal Rolling and Geometry Relationship
The phenomena of contact between rolling dies and slab can be explained in terms of the friction hypothesis which examines the origin of the resistance to relative motion in terms of slid or stick between the two contacting surfaces. The hypothesis, presented in [
15], which is credited to the French scientist Desaguliers, explains the origin of resistance to motion in terms of adhesive bonds. The hypothesis states that the surface of engineering materials are generally never completely smooth, and they contain asperities and valleys when viewed under suitable magnification. In metal rolling, friction is responsible for drawing the slab into the rolling gap.
Friction is a phenomenon of shearing stress when it acts in a tangential way to the rolling dies at any section along the arc of contact with the slab. However, the direction of shearing stress reverses at the neutral point [
16,
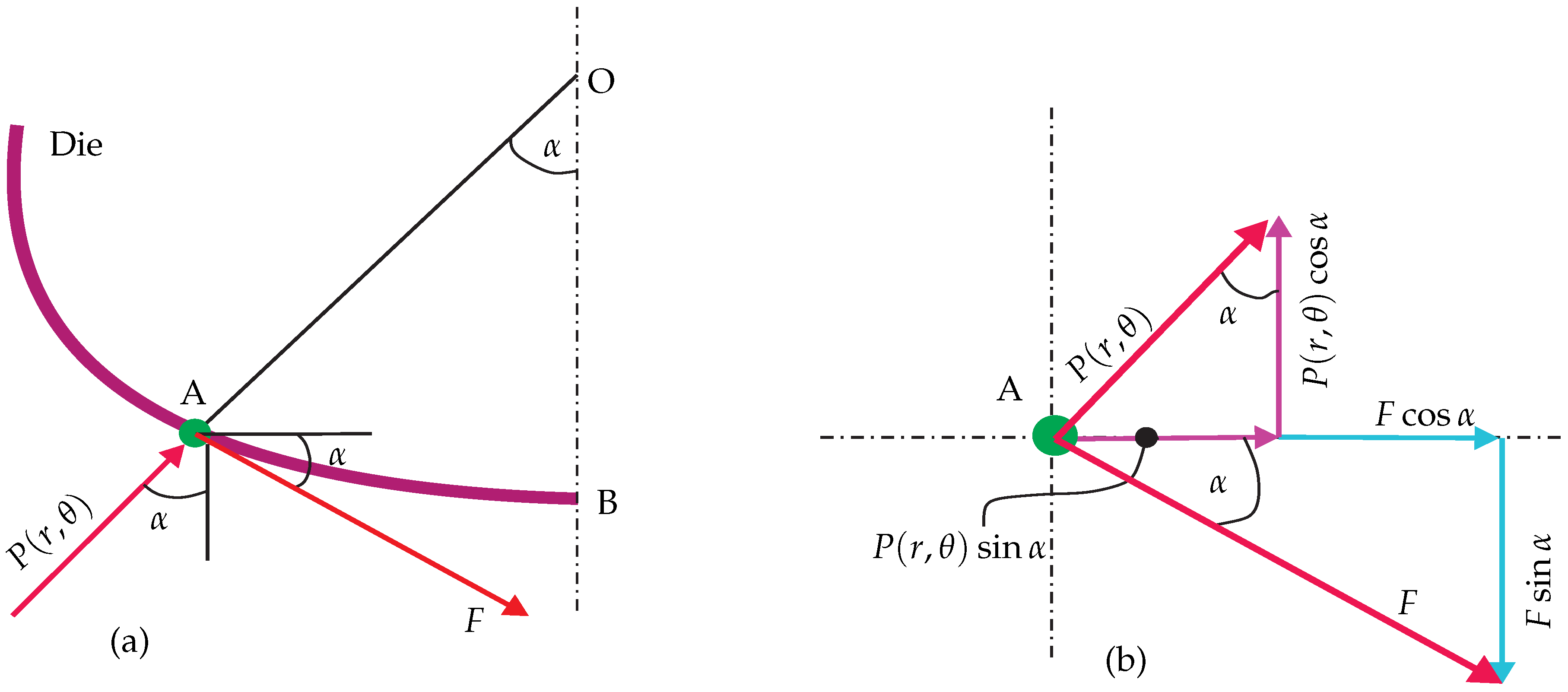
17]. Between the entry section of the rolling gap and the neutral section, the direction of friction is the same as the direction of motion of the slab. Therefore, the friction aids in pulling the slab into the rolling gap as part of the travel. The direction of friction reverses after the neutral point when the velocity of the slab is higher than the velocity of the rolling die. Friction force opposes the forward motion of the slab in beyond the neutral point. In the same way, rolling die pull forward (see
Figure 4). This interpretation, magnitude of the friction acting ahead of neutral point is greater than that beyond the neutral point. Therefore, the net friction is acting along the direction of the slab movement, thereby aiding the pulling of the slab forward.
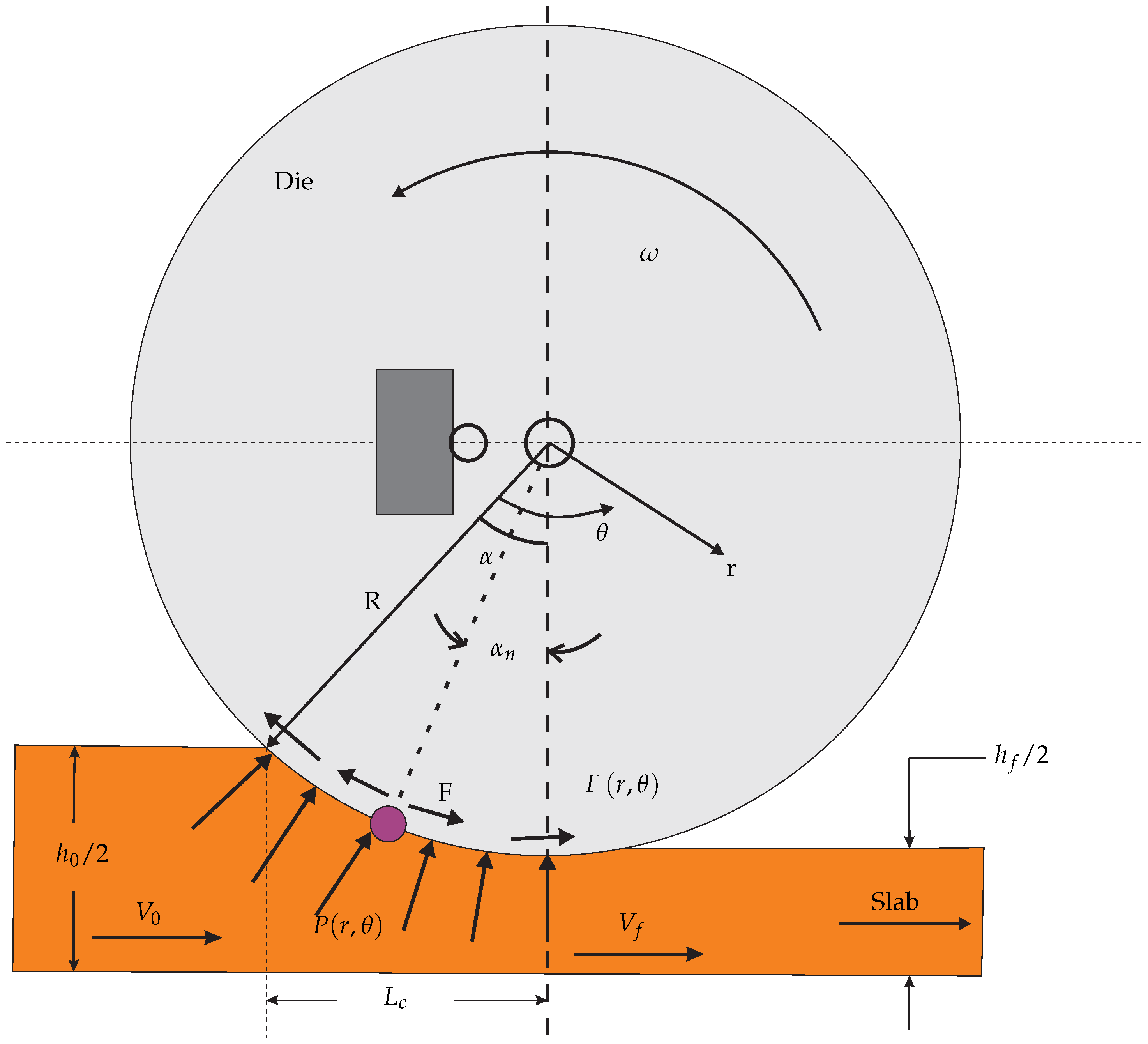
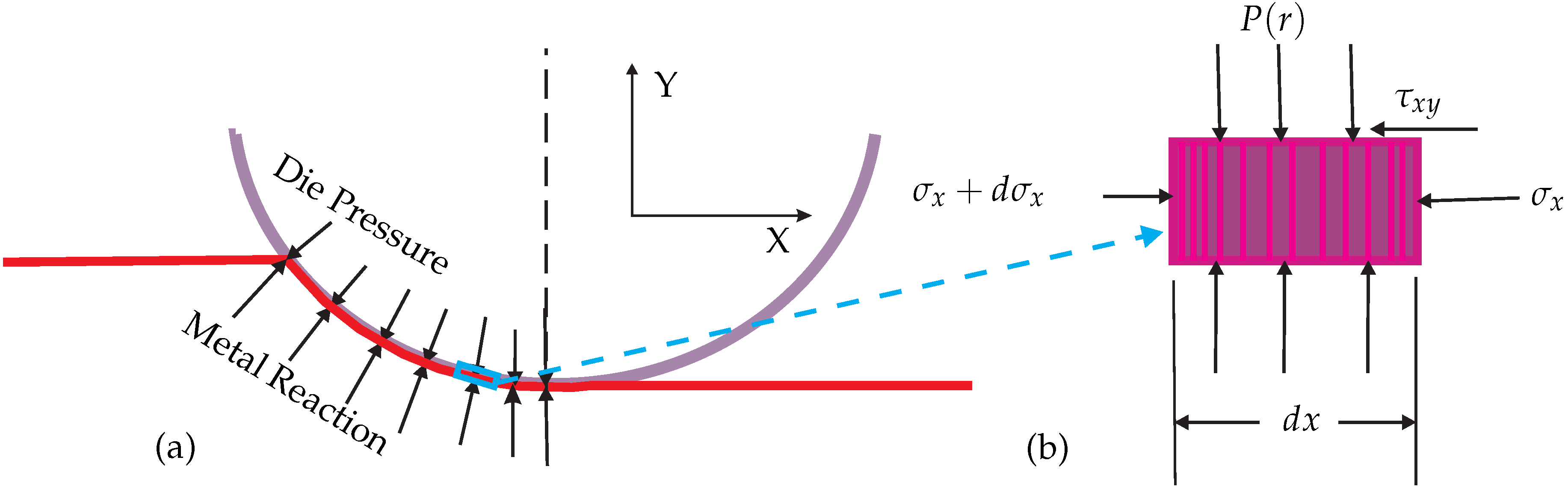
Rolling die exerts a normal pressure on the slab which is imagined to be the pressure exerted by the slab on the dies to separate them. Frictional shear stress is induced due to friction force in the tangential direction
F in the rolling gap. This relationship is shown in
Figure 5 with rolling die pressure distribution
and is mathematically expressed as follows
where
is coefficient of friction,
P is a function of variables
r and
. In this case,
r and
are the coordinates in a die (cylindrical) system. In the other word,
r and
are indicates the direction of the loads in the radial and/or circumferential direction, respectively. Based on the variations in application conditions, the slip coefficient friction is considered between the rolling die and slab. At the entry section, i.e., if the forces acting on the slab are balanced, Equation (
10) can be formulated
The slab is pulled into rolling at entry section without considering that the slab bulges out in the transversal direction. Such a problem may even happen in continuous casting at an early strand of deformation. For the slab to be drawn into the rolling gap, the following condition should be satisfied
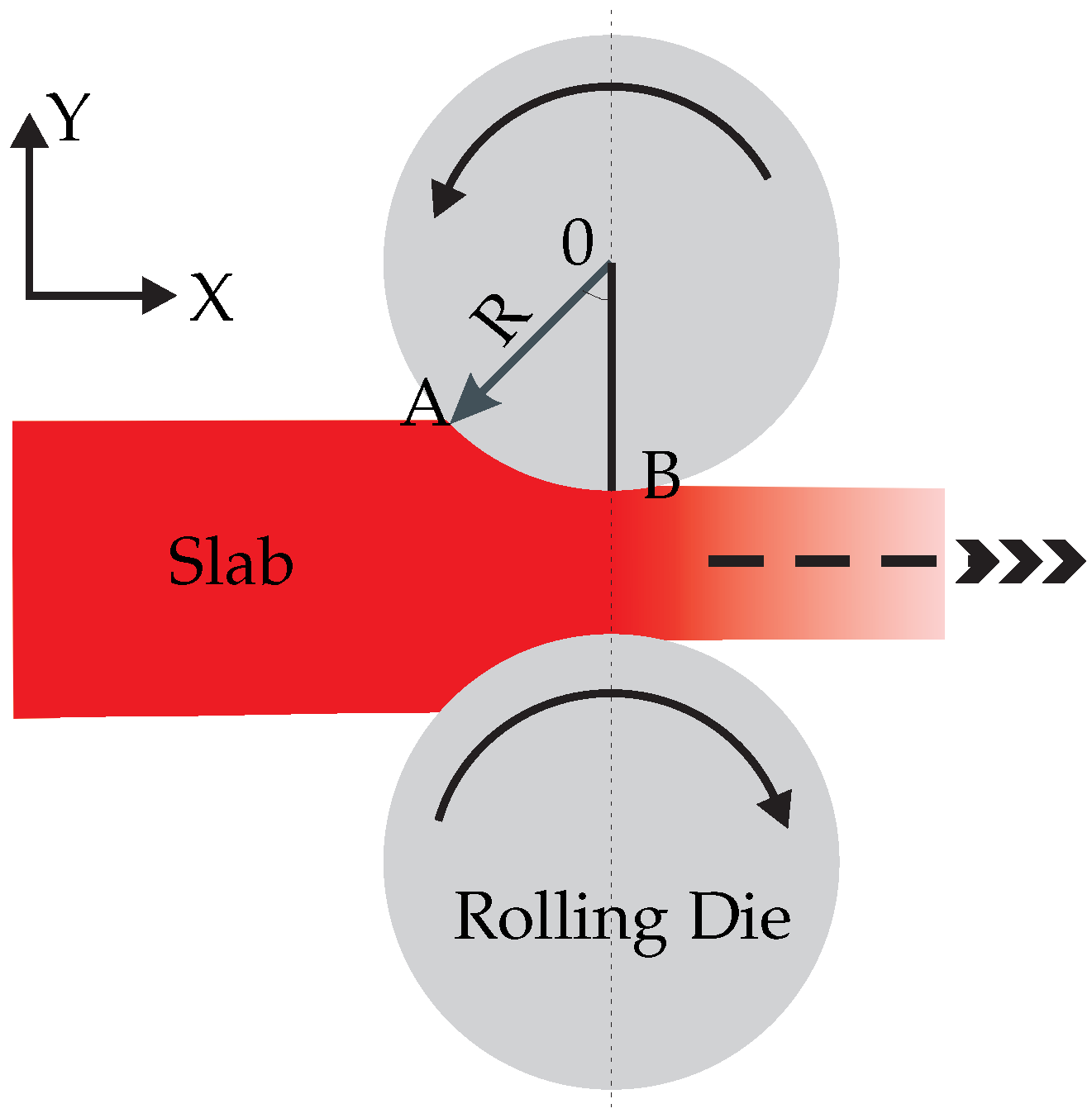
In other words, if the tangent of the angle of bite exceeds the coefficient of friction, the slab will not be drawn into the rolling gap. The detailed mathematical expression can be derived by considering the necessary conditions. i.e., angle of bite or angle of contact, slip direction in arc contact and neutral point, as shown in
Figure 4.
Before proceeding to determine the relationship between force and geometry in rolling contact, first let us consider the plastic deformation of the slab direction. According the condition given in Equations (
12) and (
13) the result of incremental width is zero. Thus, the vertical compression of the metal is translated into an elongation in the rolling direction. As the slab is dragged by the dies into the rolling gap, it decreases in thickness while passing from the entrance to the exit. From the volume metal conservation law, one can write the following equation
where
w is the width of deformed slab,
V is velocity at any thickness and
h is intermediate between initial thickness
and final thickness
. At the mean time slab, velocity gradually increases from
at the entrance to
at the exit. In order that vertical elements in the metal remain undistorted, Equation (
14) requires that the exit velocity
must be greater than the entrance velocity
. Due to the variation in the velocities of die surface and slab surface, there will be relative motion between them. The relative motion between the die and the slab is referred to as a slip. Slip takes place at the front and the back of the rolling dies in the rolling gap. There is a point where the velocity of
equal to
, which is called neutral point. It is indicated in
Figure 4 by angle
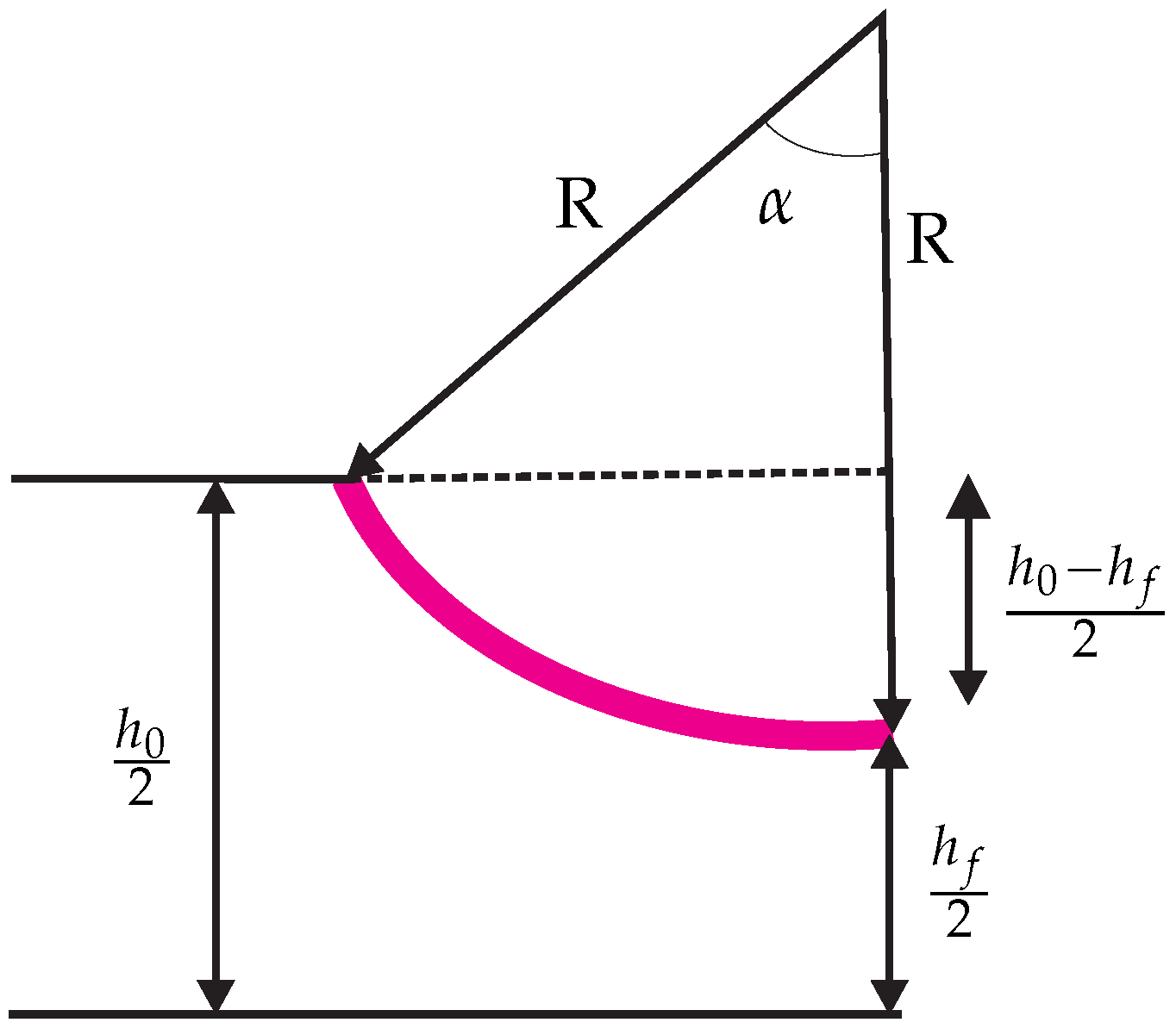
. Before determining the neutral point, let us find angle of contact
. The angle
between the entrance plane and the centerline of the rolling die as shown in
Figure 6. From the definition of circular segment and using Taylor’s series expansion
can be derived
where,
.
The position of the neutral angle (the pseudo independent parameter) is also determined as one of independent function parameters from
Figure 4 and rearranging the equation that was developed in [
18] and considering hot rolling conditions as well as other analyses based in [
19]. The rest of the analytical treatment is presented in this section with symmetry assumption. Top and bottom are mirrored around the plane of symmetry. So, the pressure distribution and the position of the neutral point are identical for the top and bottom or left and right side. Taking the above justification into account, the location of the neutral point is calculated by
where,
.
In the same way, flattening neutral point due to rolling die flattening radius
can be given
where
is determined from Hitchcock’s equation [
20]
where,
,
is pressure distribution with flattened die and
is young’s modulus of the die material.
4. Pressure Distribution in Contact Area
The shape of the die–slab contact surface is not known at the exact point. Computation and analysis of pressure distribution must be combined with the deformed slab and rolling die by suitable equation. A number of theories and equations were attempted in earlier studies, but there are no rationalized differences between them or no model has been found which is repeatable, and gives better predictions than the others. For instance, Bland and Ford’s model [
21], Sims’ model [
22], Alexander’s model [
23], refinement of the Orowan models [
24] and new cold-rolling theory [
25]. However, most of the approaches offered some unique advantage and also had deficiencies of one sort or another. On the other hand, the choice of those models is based on the knowledge of researchers and professionals on the specific domain.
Hot-rolling has no advance to the state of knowledge that exists for cold-rolling due to the problem of inhomogeneous deformation and less well defined friction conditions. In hot-working conditions, the flow stress is also a function of temperature and speed of rolling die. With the above-mentioned plasticity/elastic deformations and other relative issues after considered, pressure distribution equation between rolling die and slab is proposed. For this approach the following assumptions are considered, that is the same state of stress exists at all points of the plane
x,
y and
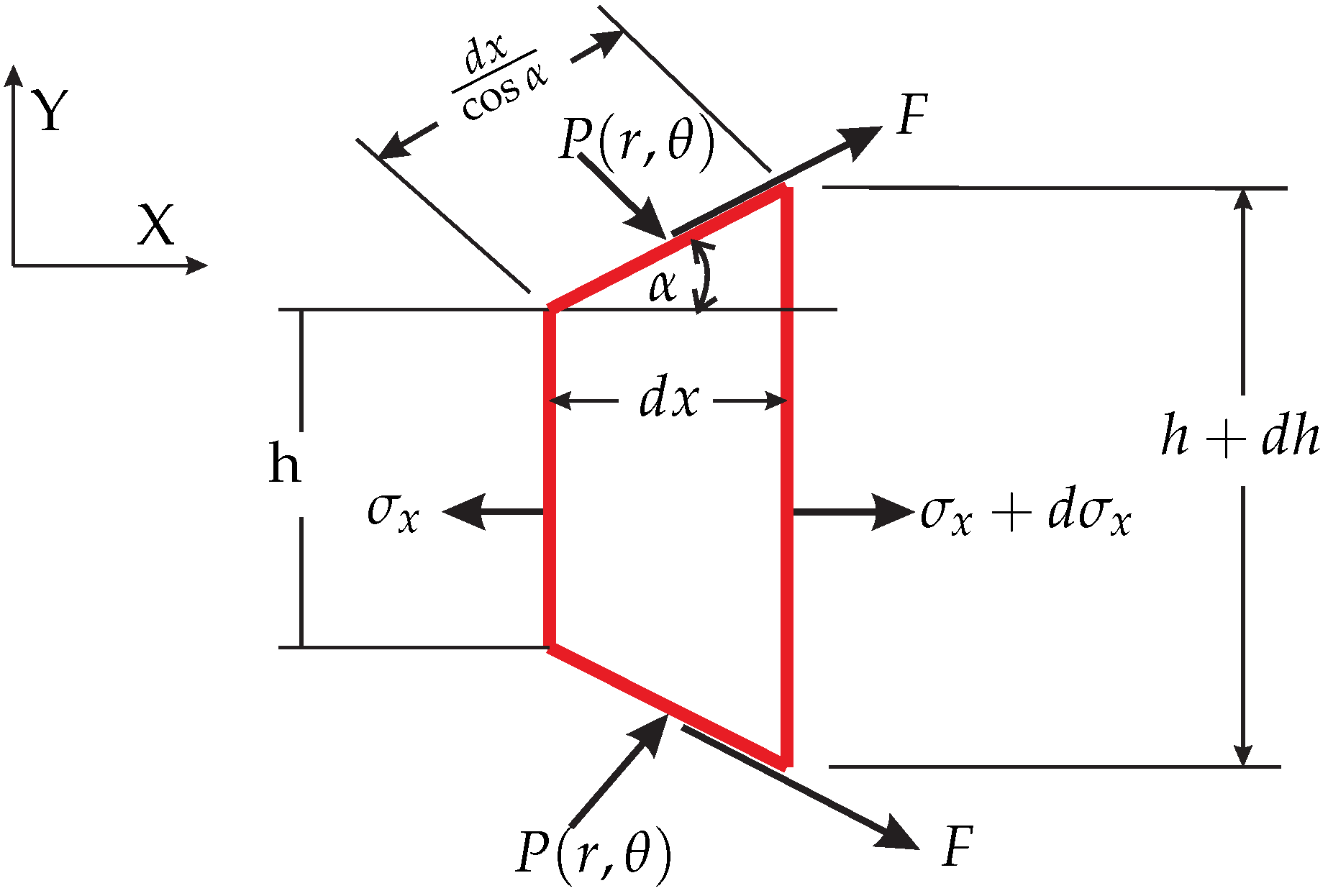
z directions. In the same way, considering a volume element of unit width having the instantaneous thickness change
and length
(see
Figure 7). Furthermore, assume that the longitudinal stress
, which is constant over a plane normal to the
x direction, and the pressure
acting on rolling die interface, are the two principal stresses which are acting. In this case,
is a pressure distribution in radial direction (in
Y-axis direction) as shown in
Figure 7. As a result of these assumptions, a slab is deformed in the plane.
Taking the equilibrium of forces in the vertical direction results in a relationship between the normal pressure and the radial pressure. The relationship between the normal pressure and the horizontal compressive stress
is given by the distortion energy criterion of yielding in plane strain. Because of symmetry, the metal flows away from the center plane in both directions, and it will be sufficient to analyze the conditions for half side. By introducing the shearing stresses,
acting on the surface, the equilibrium of the
x component of the forces acting on a volume element is expressed by
The distortion-energy condition of plasticity is expressed, in the case of plane strain, by the relationship
where
is yield strength and
is deviatory stress. Substitute Equation (
20) into the Equation (
19)
Introducing the parameter
, which is defined by the equation
Following the procedure of Equation (
15)
Its derivative with respect to the parameter
is
Substituting the expressions from Equations (
25) and (
26) into Equation (
23) and introducing the the constant
One has differential equation and multiplying both sides by
At the end, rearranging and then integrating:
where
is constant of integration. According to relation given in Ref. [
26], the integral appearing in this equation can be calculated with sufficient approximation by putting
, then
The general solution of this equation
At the boundary condition of entry side (just at outside of entry point),
, and
C can be obtained from Equation (
32) with this condition. And then, furnish the above expression with all situations, the pressure distribution on the entrance side of the neutral point can be given as
The pressure distribution on the exit side of the neutral point is expressed as follows
where
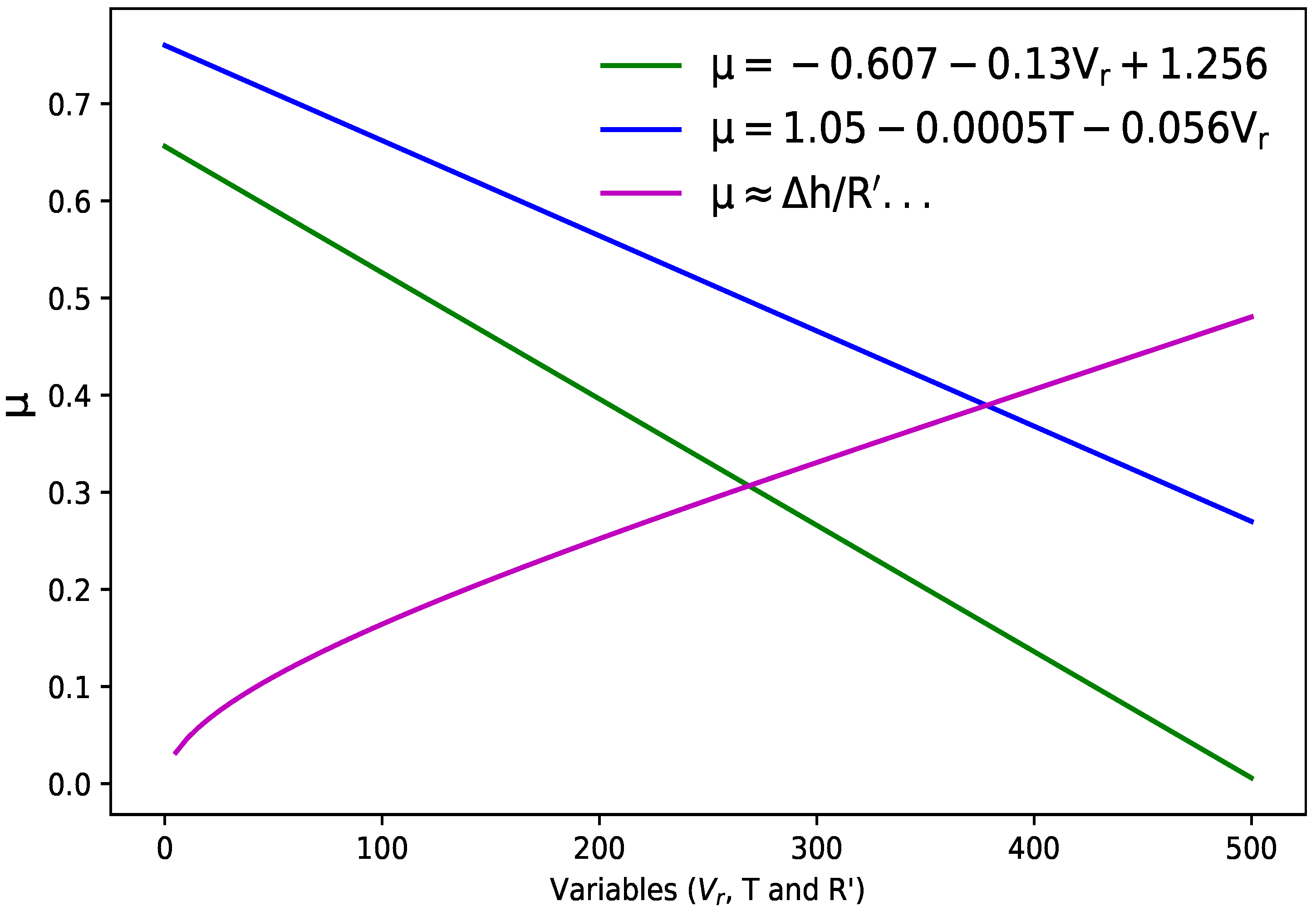
The magnitude of the coefficient of friction at the die–slab interface has been commonly characterized in two ways. The first method of characterizing interface friction by the use of a constant coefficient of friction (Coulomb friction). The second method of calculating interface coefficient of friction assumes that the interface zone may be represented by material constant, in which friction factor is constant in the rolling gap. However, the phenomena of hot metal-rolling includes the frictional events like heat transfer and other related parameters. In other words, the frictional stress instantly changes direction at the neutral point, which is identified based on an initial guess for the velocity field. From this justification, the following equations are considered from the literature
where
T is the temperature, given here in
and
is given in
. For steel rolling, the relevant formula for
in Equation (
36) is developed by Geleji in [
27] and even cited by different researchers. In the same way, Equations (
38) and (
37) are given in [
28] and [
29], respectively. Where the
depends on the surface velocity of the rolling die, reduction and temperature is shown in
Figure 8. The result shows that
decreases with increasing rolling die speed and temperature, at the same time, it is affected by reduction ratio.
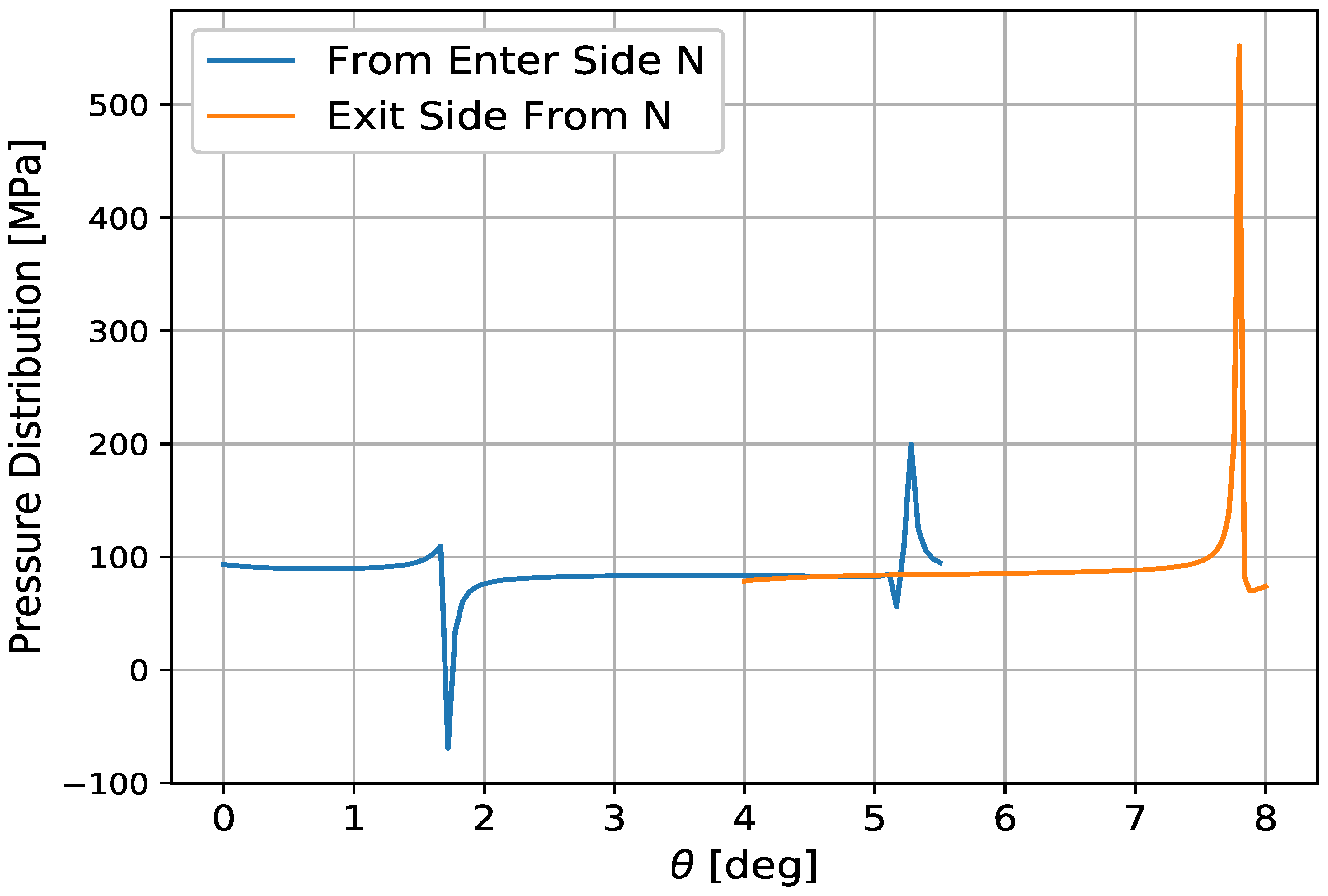
In
Figure 9, two lines are intersected at the neutral point due to the action of compression and tension force where the model is derived from Equations (
33) and (
34). For this method,
mm,
mm,
and
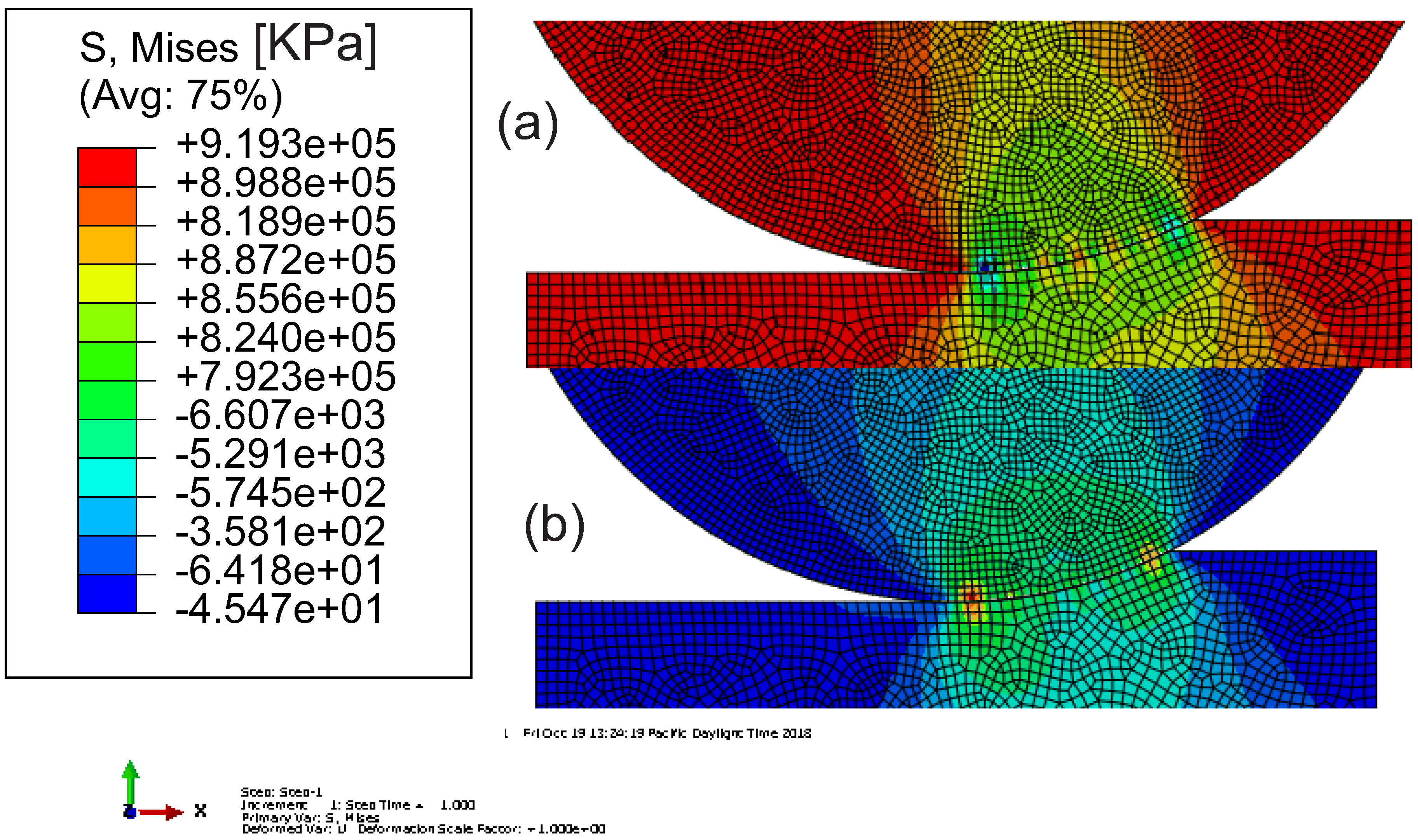
m/s are considered, the result indicates that tension force is greater than the compressive load, which means maximum stress is exerted on the rolling die from exited side rather than the entry side of neutral point. In the same way, FORTRAN program was developed with PYTHON script to simulate this phenomena in ABAQUS 6.14 (ABAQUS Inc., Palo Alto, CA, USA), as depicted in
Figure 10, where the following steps are considered:
Figure 9 shows analytical results of maximum stress distribution, which is induced in rolling die at the entry and exit sides. On the other hand, finite element simulation agree with the numerical computation that are implemented in python along the arc of contact when plasticity deformation is performed. However, the numerical model shows exaggerated stress at the specific point which means maximum tension stress developed due to the maximum velocity of slab from exit side being high. Finally, the result suggests that tension load exerted on rolling die is different from the entry side to exit side in magnitude and direction.
To get a unified equation, let us find the mean rolling die pressure at interface through integration. Considering a volume element of unit width and having a thickness
with length
(see
Figure 11).
Which is obtained by substituting Equation (
20) in the Equation (
39), and then separating the variables. In addition, it is known that the relationship of Coulomb’s law in slide friction is given by,
Integrating both sides
where
is a new integration constant to be determined from the boundary condition at
,
and consequently
, then obtain
After substitution, the mean pressure is
where,
and
is the length of contact between the slab and rolling die as shown in the
Figure 4. In
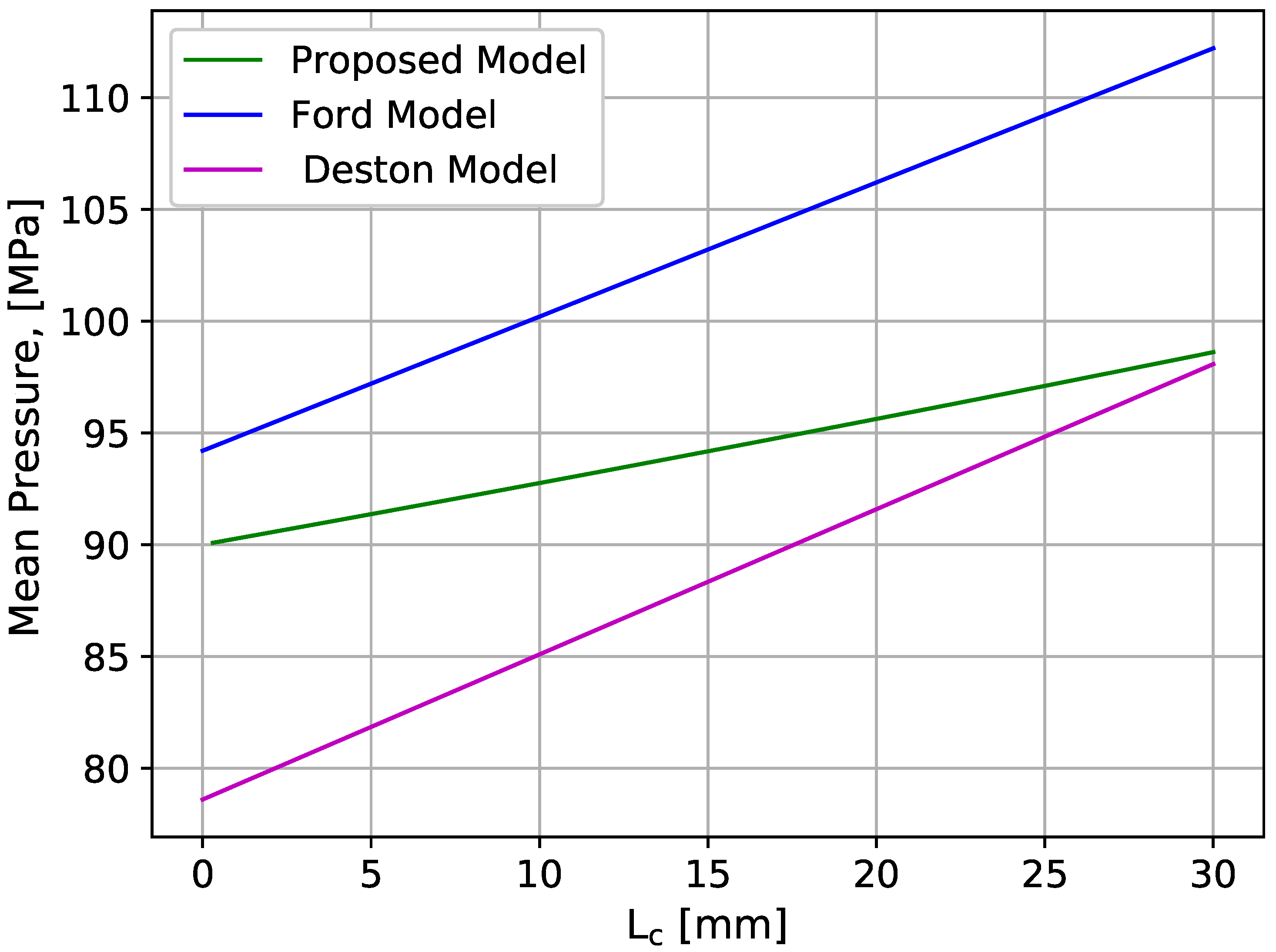
Figure 12 computational result of mean pressure is compared with the Equations (
44) and (
45), which is purposely developed for hot working condition in [
33] and [
34], respectively
In
Figure 12, where reduction ratio and roll diameter are constant, the angle contact length is the relative distance along
x. The same basic equation for hot-rolling with important condition which were given for determining the effective pressure in rolling gap. Upon comparison, the difference between the models appeared as per the authors’ concern. Accordingly, the Ford model shows maximum mean pressure in rolling gap, whereas the Deston model shows minimum pressure load. In the same way, the model proposed in this work is relatively the average of the two models. In the continuous casting process, the proposed model is fair enough because its main objective is supporting highly heated metal for further subsequent strands rather than breaking down the casting ingot into slab/bloom under single strand. However, for given
, an increasing coefficient of friction easily leads to more deformation pressure. The role of
in raising pressure distribution should be clear from the above calculation. Note also that the role of
becomes particularly important at large values of
.
5. The Deformation of the Rolling Die and Constitutive Equation
The review of Robert in [
16] concerning the Hitchcock’s formula that is given in [
20] to calculate the radius of the flattened is not accepted, as mentioned in
Section 3. Rolling die deformation modeling is the core model of this section which can determine stress behavior under rolling contact for a number of cyclic loads
n. Numerical modeling is a hotspot of research aiming to tackle experimentally tedious tasks and expenses. Thus, analysis and modeling play a vital role in metal-forming and tool design industries.
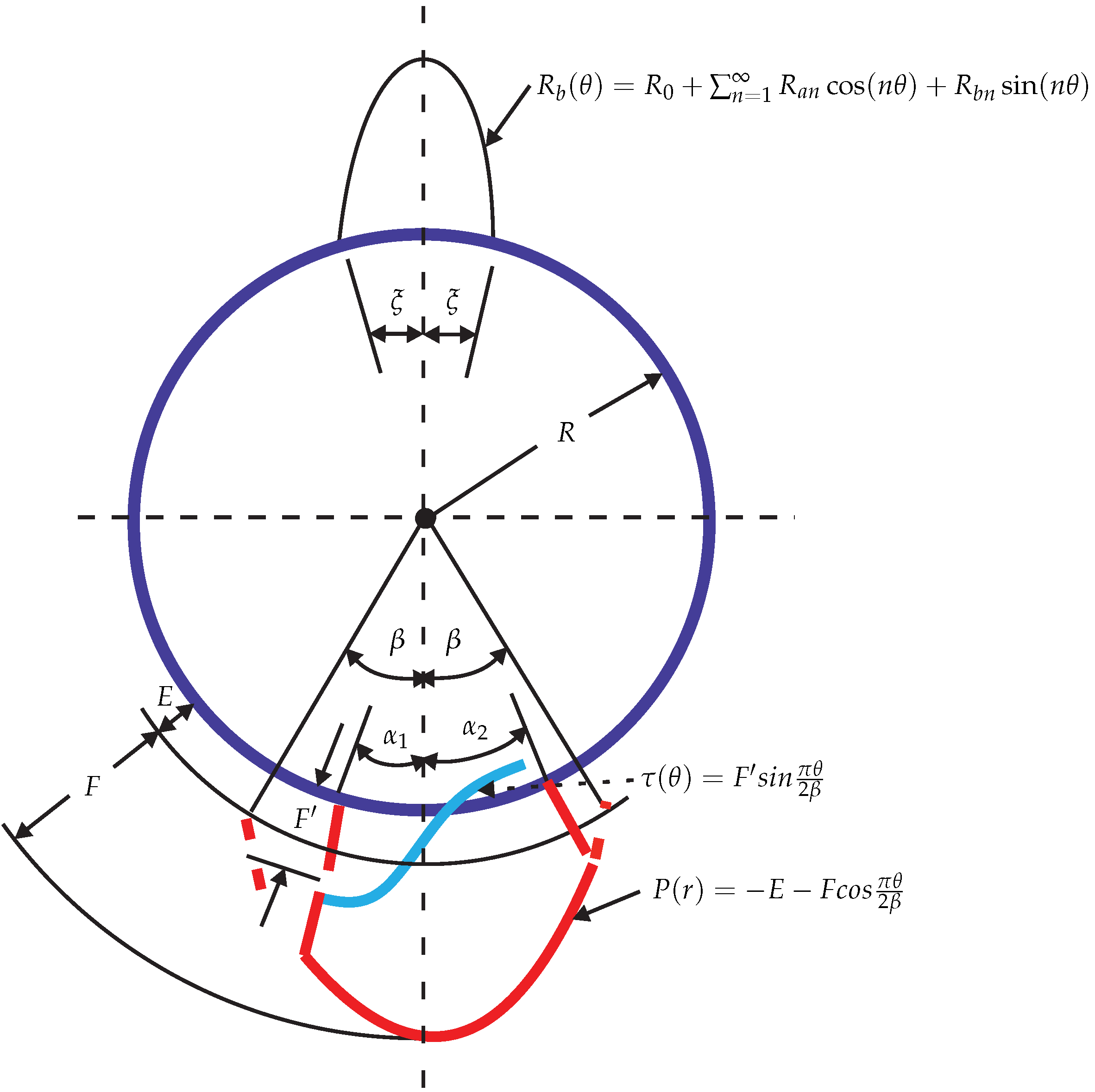
The problem of the deformation of the rolling die is treated here by assuming that a solid cylinder is subjected to non-symmetrical loads. The schematic loading diagram of a rolling die is shown in
Figure 13. The loading consists of the radial stress and the interfacial shear stress, where the radial stress is designated by
and the interface shear stress by
. These loads must be balanced by a statically equivalent force system, the location of which would depend on the type of mill considered. For four-high mills or six-high mills, the backup rolls would supply the necessary balance, while for two-high mills the reaction forces would be applied through the bearings of the rolling die journals. The present analysis is concerned with a two-dimensional treatment of the rolling die of a two-high mill (usually used in continuous casting) and die bending being neglected. The balancing loads are taken to be distributed over the dies with
, where
is the extent of the pressure distribution of the now imaginary back-up roll instead of journal bearings. This condition ensures that the mid planes of the rolling die remain undeformed and stationary.
The stress distribution in any problem of linear elasticity should satisfy the biharmonic equation, which in
cylindrical coordinates is
where the coefficients of terms singular at the origin were taken to equal zero. The radial and shear stresses are then obtained terms of the Airy stress function
and
Following the procedure of [
35], the stress and strain distributions in the rolling die in a state of plane strain may be calculated from a stress function by using biharmonic functions
where the constants
,
,
,
,
,
and
need to be determined such that the stress boundary conditions at
are satisfied. They are determined next by representing the normal and shear loading on the rolling die’s surface
Normal and shear loading on the rolling die’s surface in terms of fourier series
and
where the coefficients are obtained from the Euler formula. For the normal pressure distribution, then
and
And for the shear stress distribution
and
where the values of
and
depends on the neutral point and amplitude of the reaction force, as shown in
Figure 13. The rolling die pressure distribution in the roll gap can also expressed as a cosine function using optimization methods
where
E and
F are constants. The function
in Equations (
53)–(
55) represents the reactions required to keep the rolling die in equilibrium. This can be calculated by expressing the reactions using Fourier series.
where the coefficients are obtained by the Euler formula
In the above equations,
is the angle between the resultant reaction force and the vertical axis,
is the amplitude of the reaction force and
represents half of the angle over which reaction
is distributed. It is noted that, beyond two mills, the value of
may be determined from the Hertz contact stresses. However, as was mentioned above, for a two-high mill, the reactions are represented by letting
which in fact indicates the distribution of those forces across a diametral plane of the rolling die. In Equation (
52) the shear stress distribution can be is represented by
To determine the strain components one can use the plane strain form of hook’s law
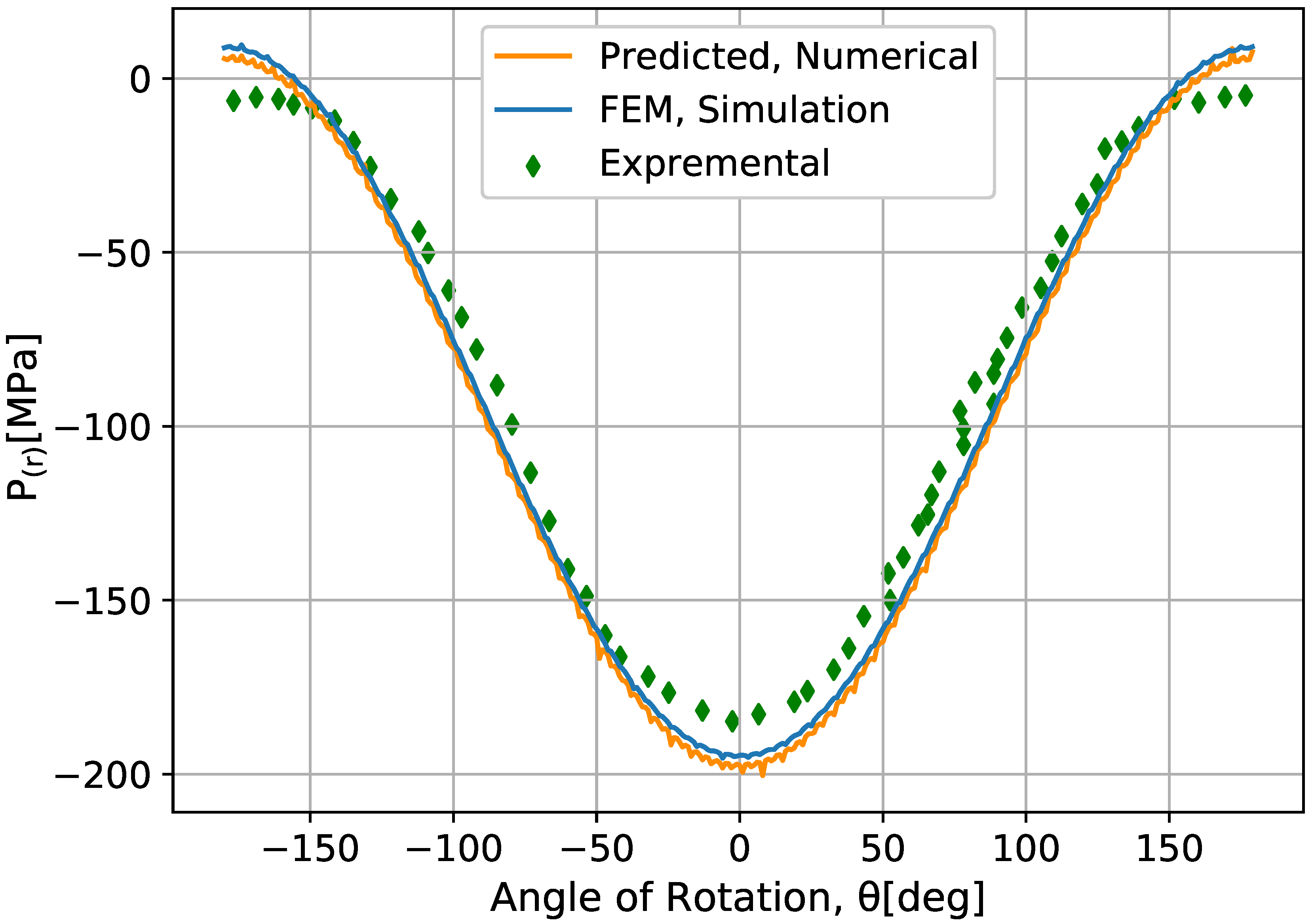
The comparison between the numeric and finite element simulation result with experimental data is presented in
Figure 14. In the same way, finite element computation is modeled as shown in
Figure 15 with following the steps that explained in the
Section 4. Where the initial load 90 MPa is considered for numeric and FEM computation, the result shows good overlapping. At the same time, both computational results are compared with experimental data, where the result shows good agreements as depicted in
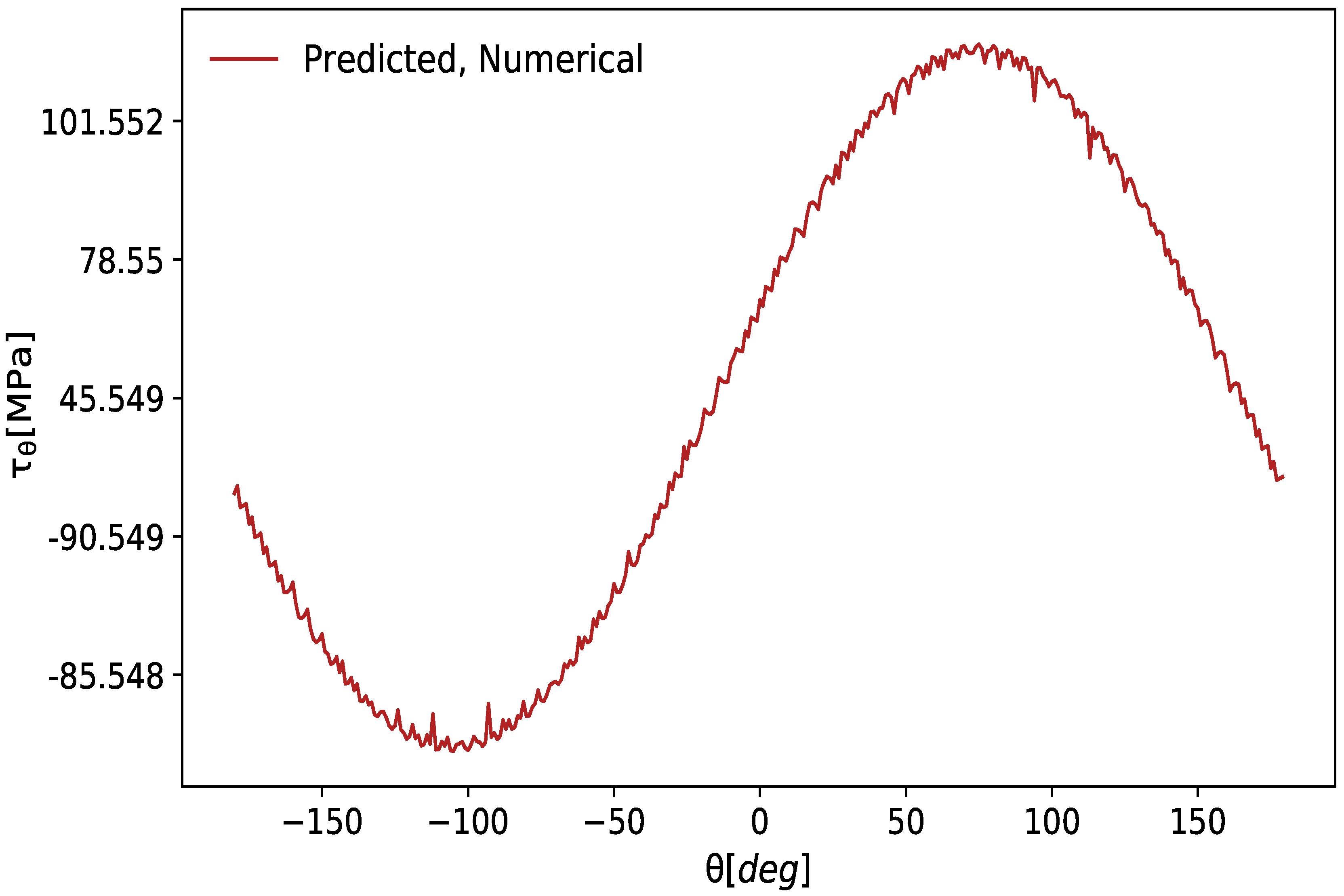
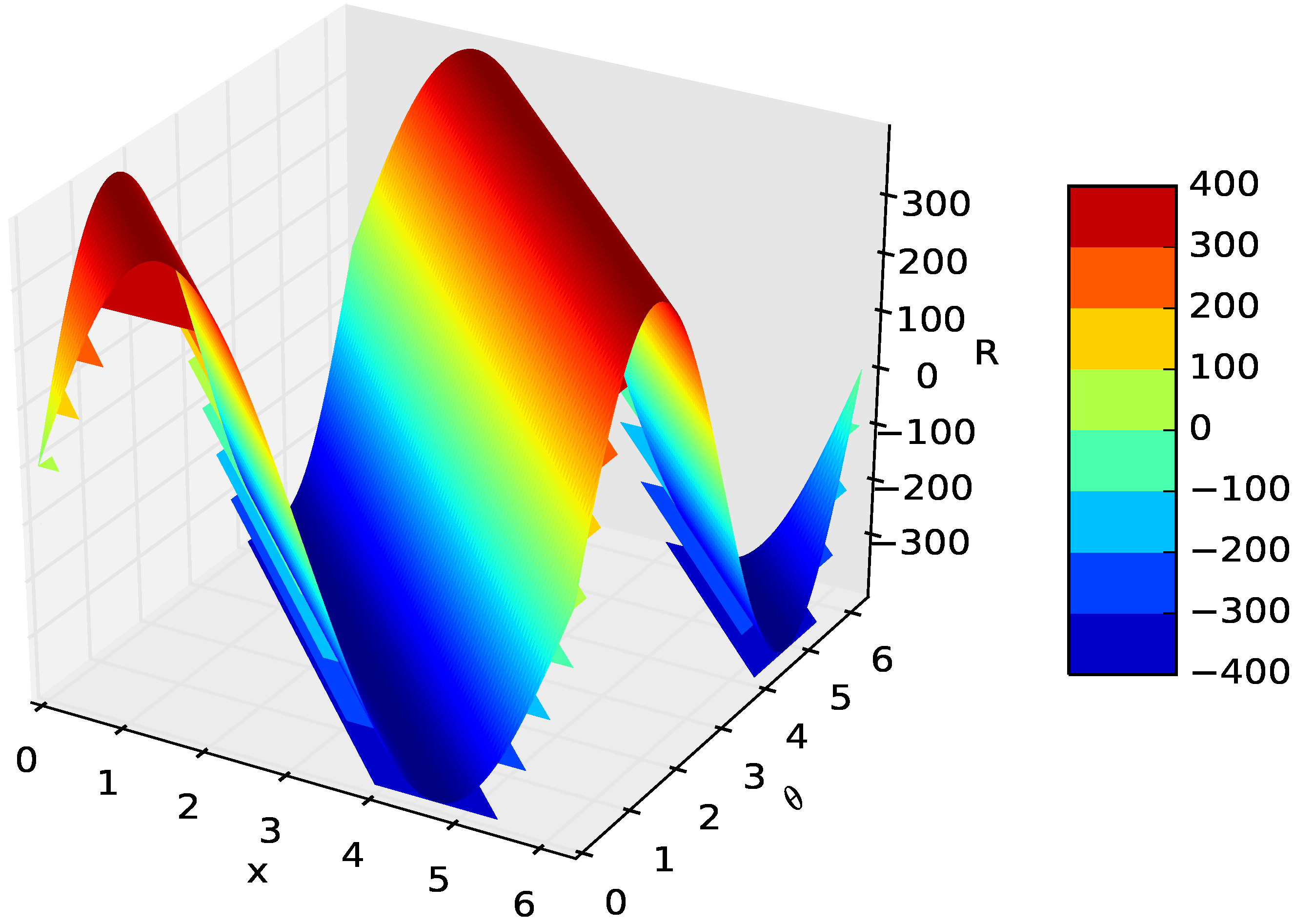
Figure 14. Meanwhile, a computer program is written to compute the system of Equation (
52) for various values of the input parameters, including 3D modeling for surface folding due to tension and compressive loads on the surface of the rolling die as shown in
Figure 16 and
Figure 17, respectively. At the end, overall radial and tangential stress for a number cyclic loads in rolling gap is modeled and the result is shown in
Figure 18.
A critical issue of this analysis consists of the accurate selection of all parameters as input for the numerical simulation and finite simulation which are often difficult under this circumstance. This work simplified the approach to compute mechanical stresses in rolling die of hot milling, based on a plane strain subjected on its surface to mechanical loads for number of cyclic loads. The presented approach is obviously a preliminary investigation, in which the contribution is more methodological than quantitative. The model can be used as a tool in the most challenging aspects of hot rolling activities, concerning the identification of the elasticity damage mechanisms in rolling die. Actually, this approach looks quite promising, since it avoids analyzing the slab behavior in rolling gap, which is able to catch the relevant phenomena induced by rolling contact and identifies the radial and tangential stress behavior of the rolling die material.
ABAQUS offers many capabilities that enable stresses and failure modeling. Especially, Dynamic Explicit is designed for continuous and singularity-free problems, such as its application in damage evolution. A representative result of FEM analyses that is shown in
Figure 15 is a progressive damage in which damage initiation and evolution are characterized by the accumulated inelastic stress energy per stabilized cycle. The capability uses a combination of Fourier series and time integration is fruitful to obtain the stabilized response of material structure. In short, the results agree with expectations and indicates the successful implementation of the constitutive model in ABAQUS.