Experimental and Numerical Study of an Automotive Component Produced with Innovative Ceramic Core in High Pressure Die Casting (HPDC)
Abstract
:1. Introduction
2. Materials and Methods
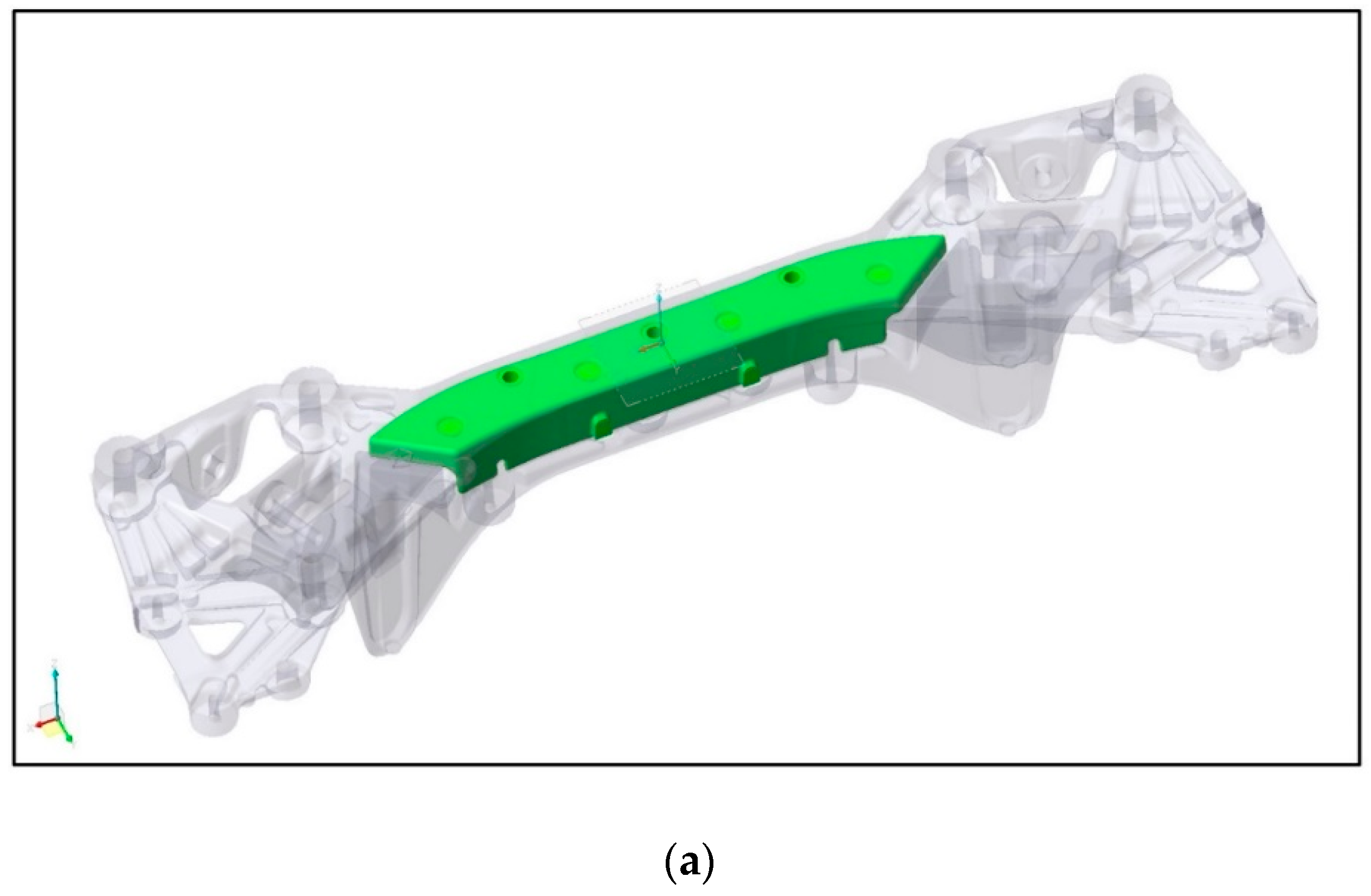
2.1. Description of the Automotive Component Structure and Materials
2.1.1. Geometric Description
2.1.2. Material Properties
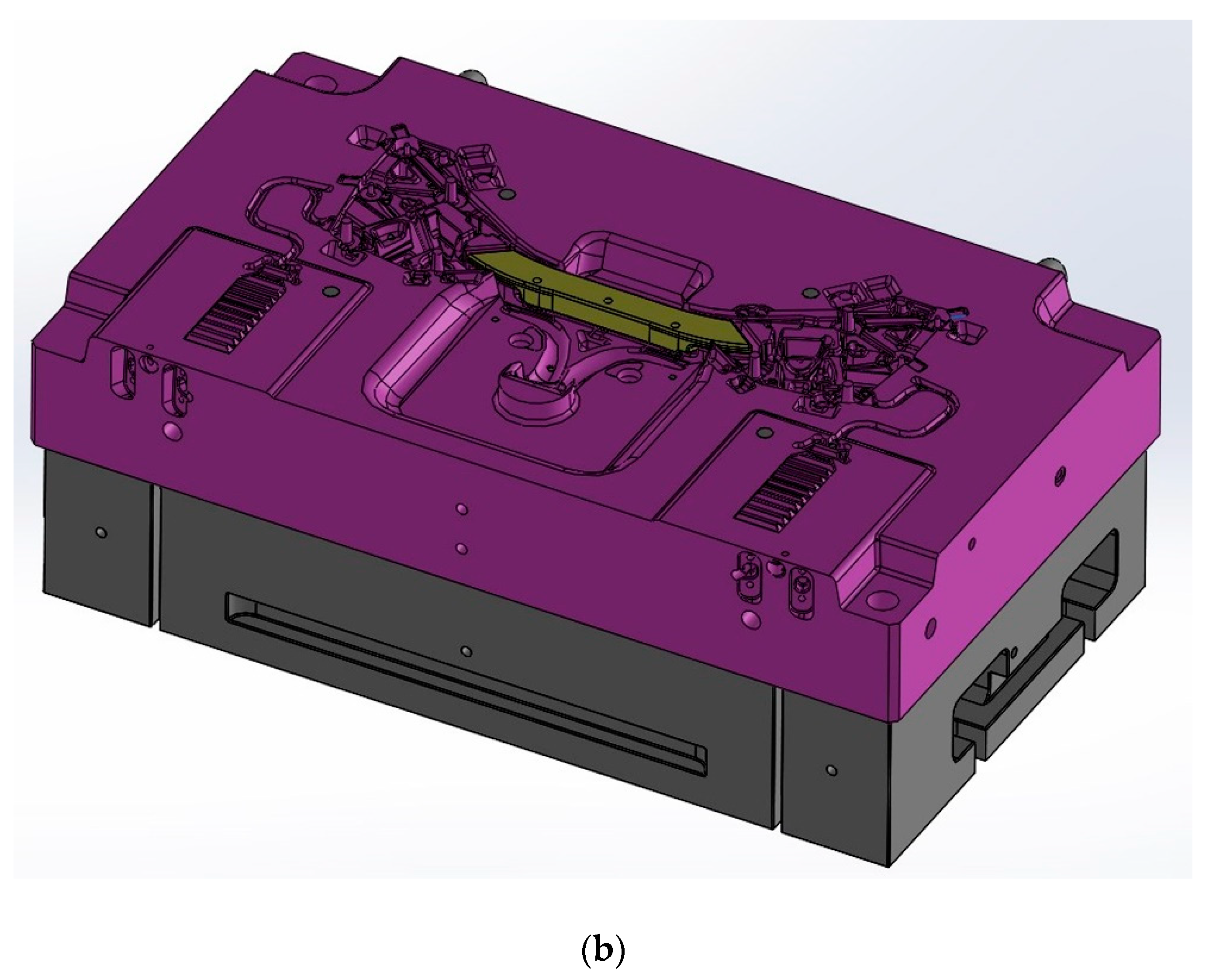
2.2. Experimental and Numerical Setups
2.2.1. FEA
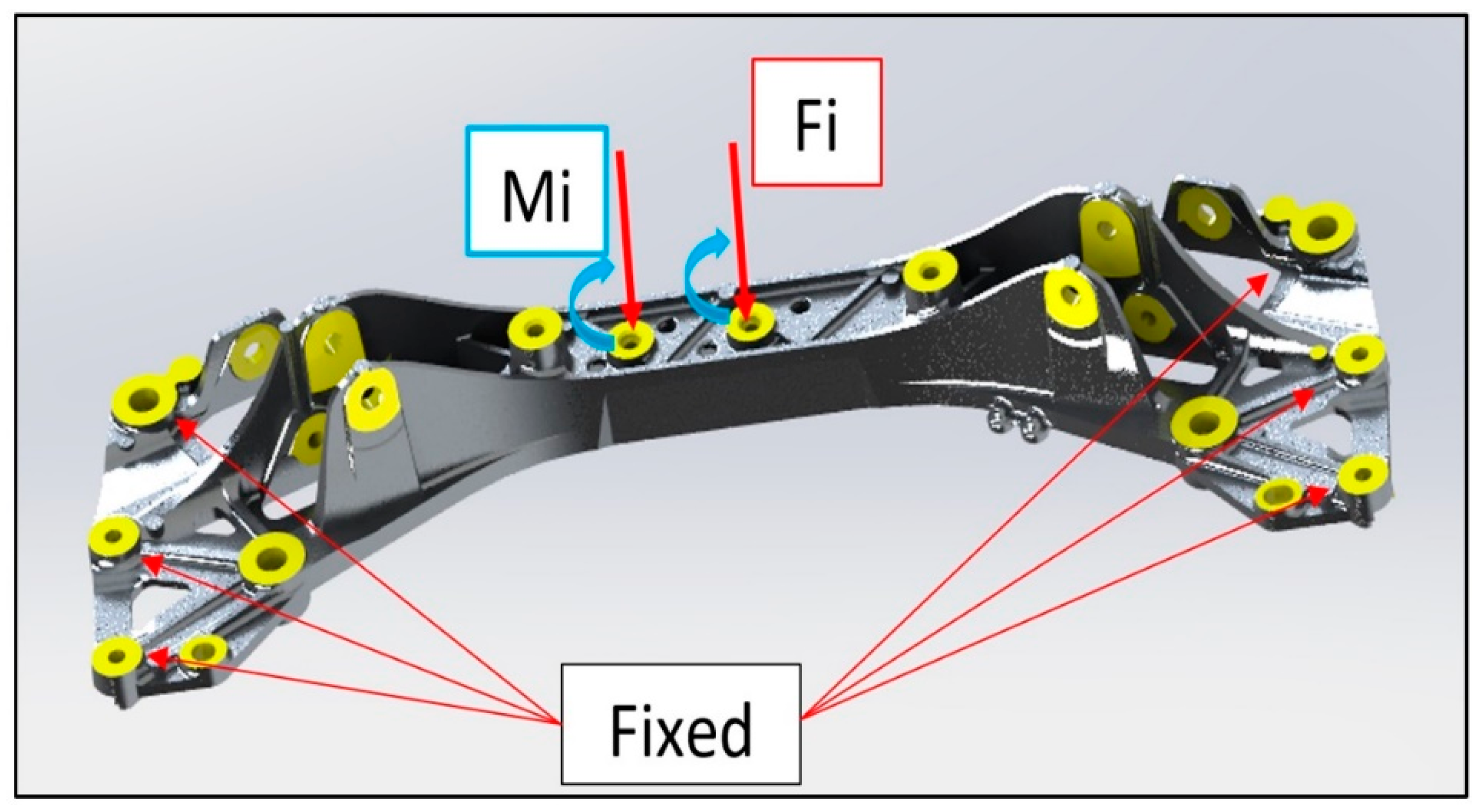
Structural Simulation
Process Simulation
2.2.2. Material Characterization
Ceramic Samples
3. Results and Discussion
3.1. FEA Results
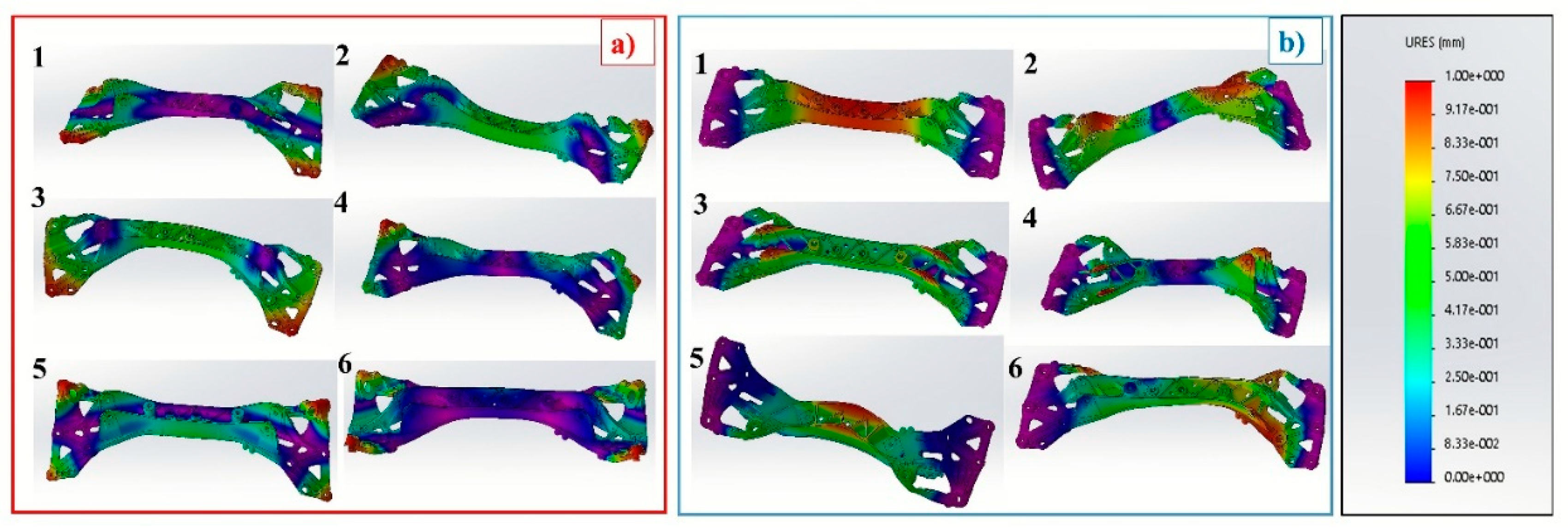
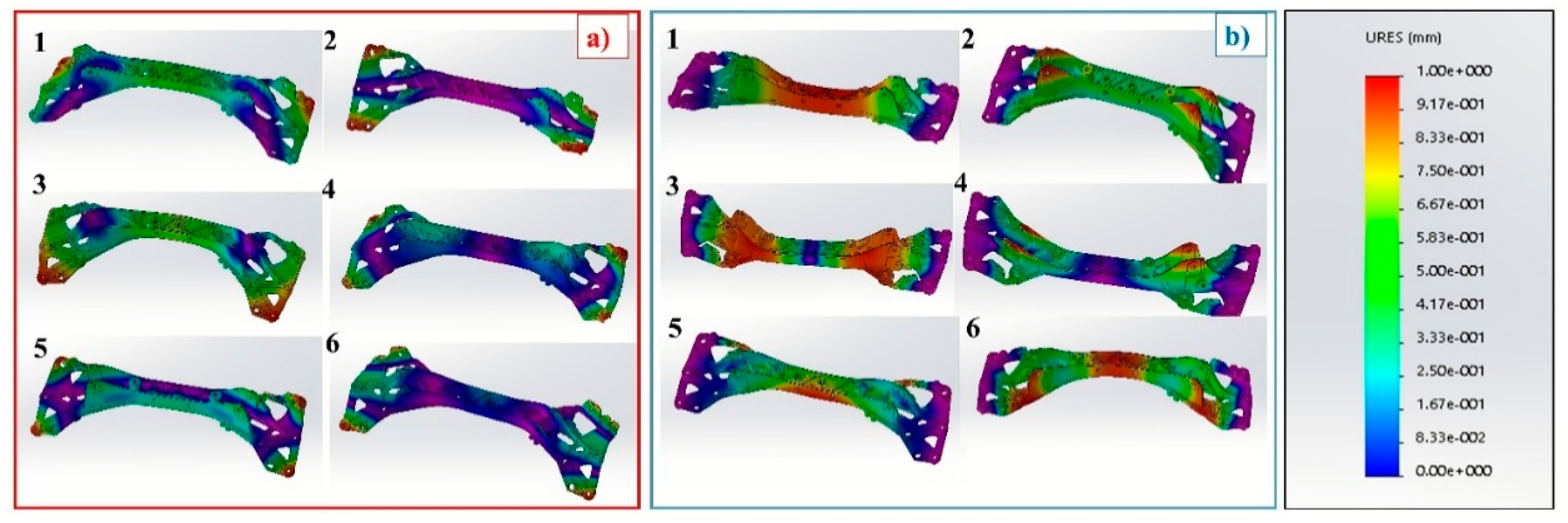
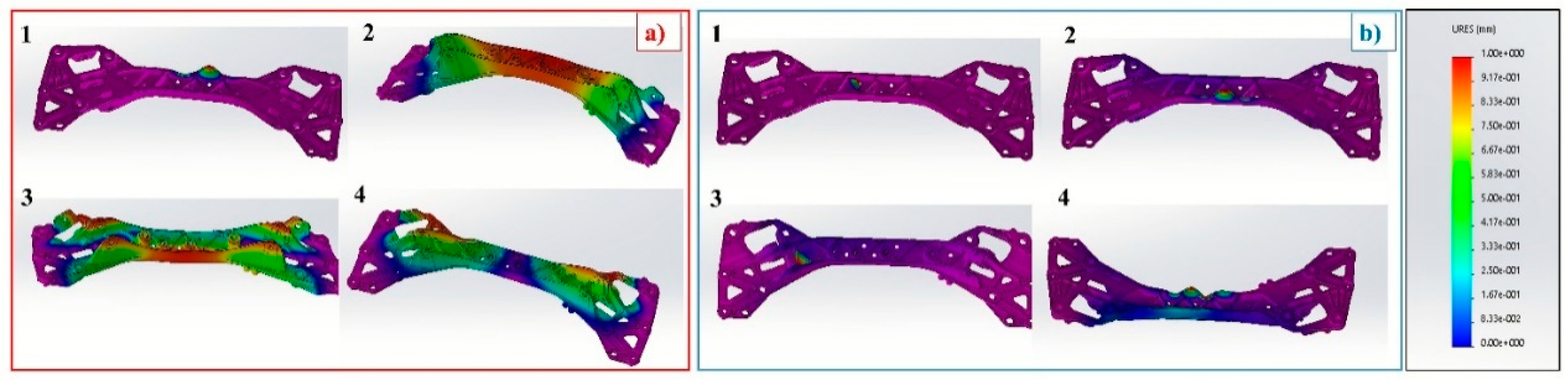
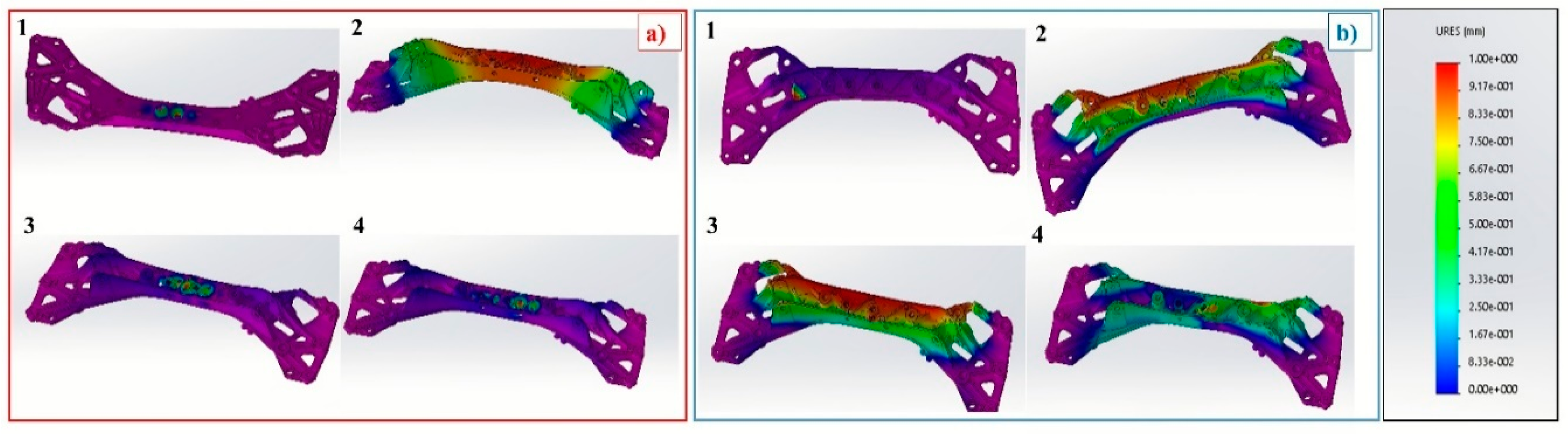
3.1.1. Mechanical Behaviour Simulation
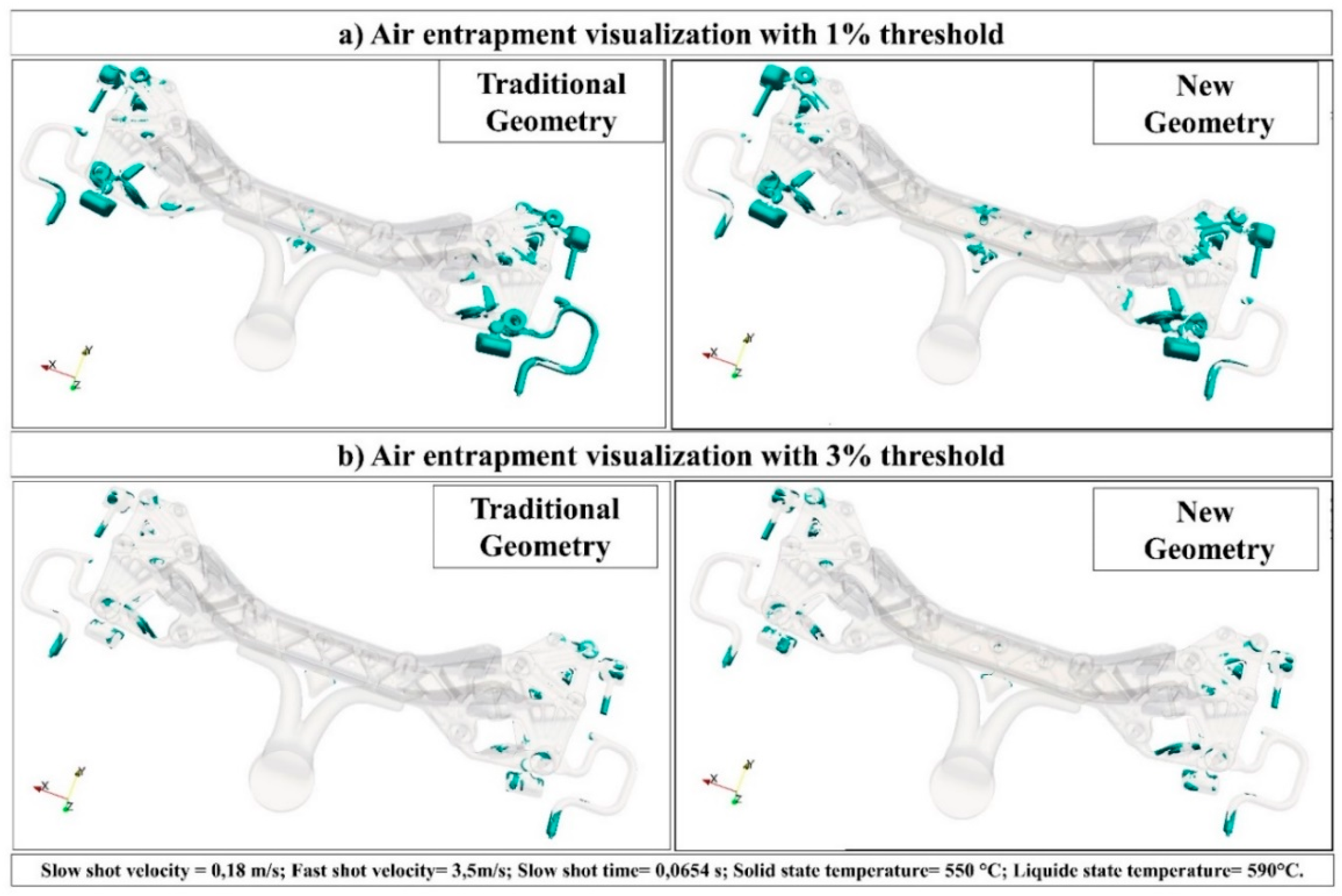
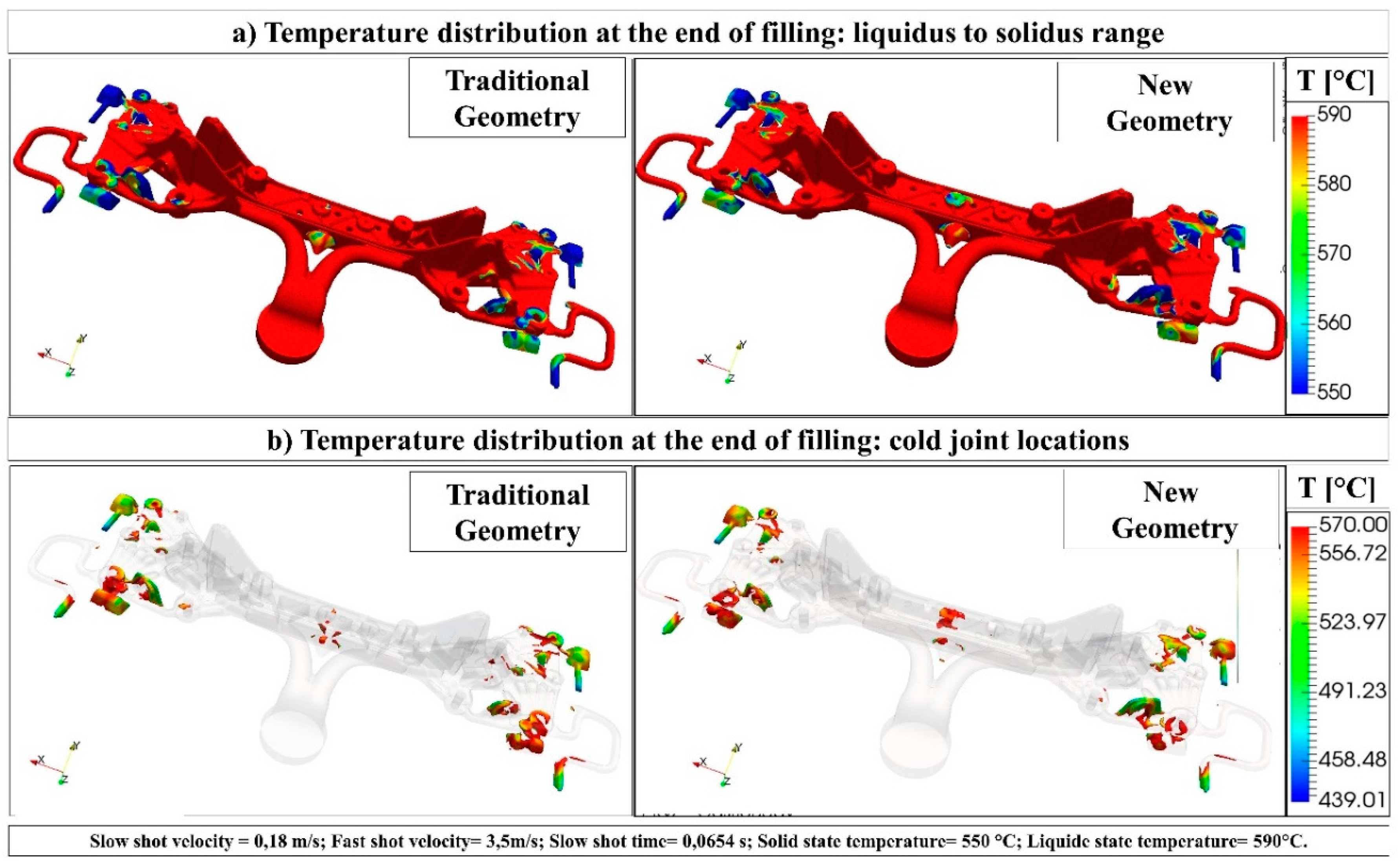
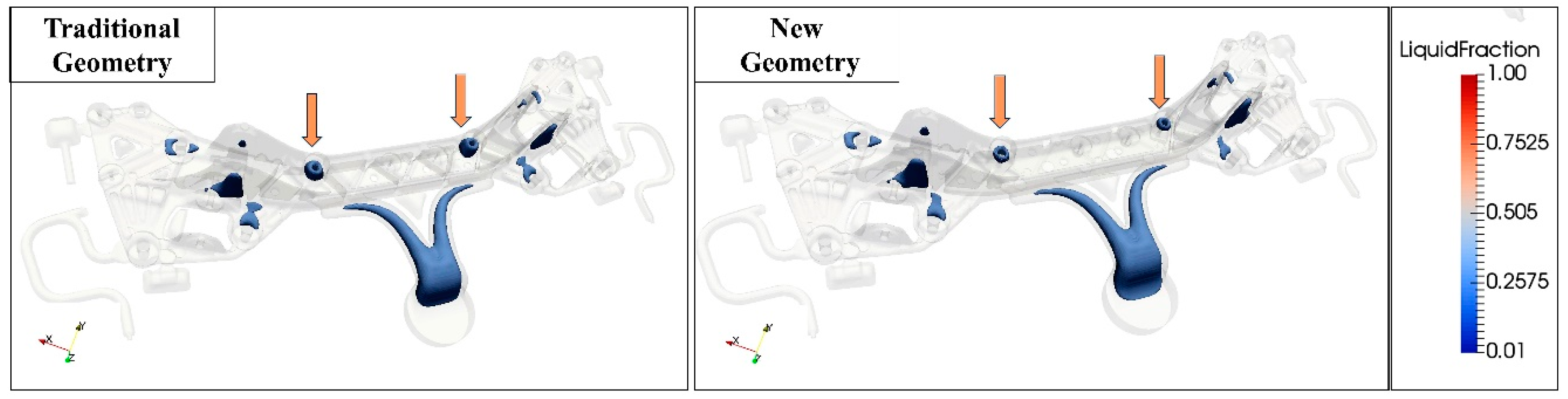
3.1.2. Process Simulation
3.2. Material Characterization Results
3.2.1. Ceramic Samples
Density
Ceramic Decoring
3.2.2. Hollowed Aluminum High Pressure Die Casting Component
Microstructure
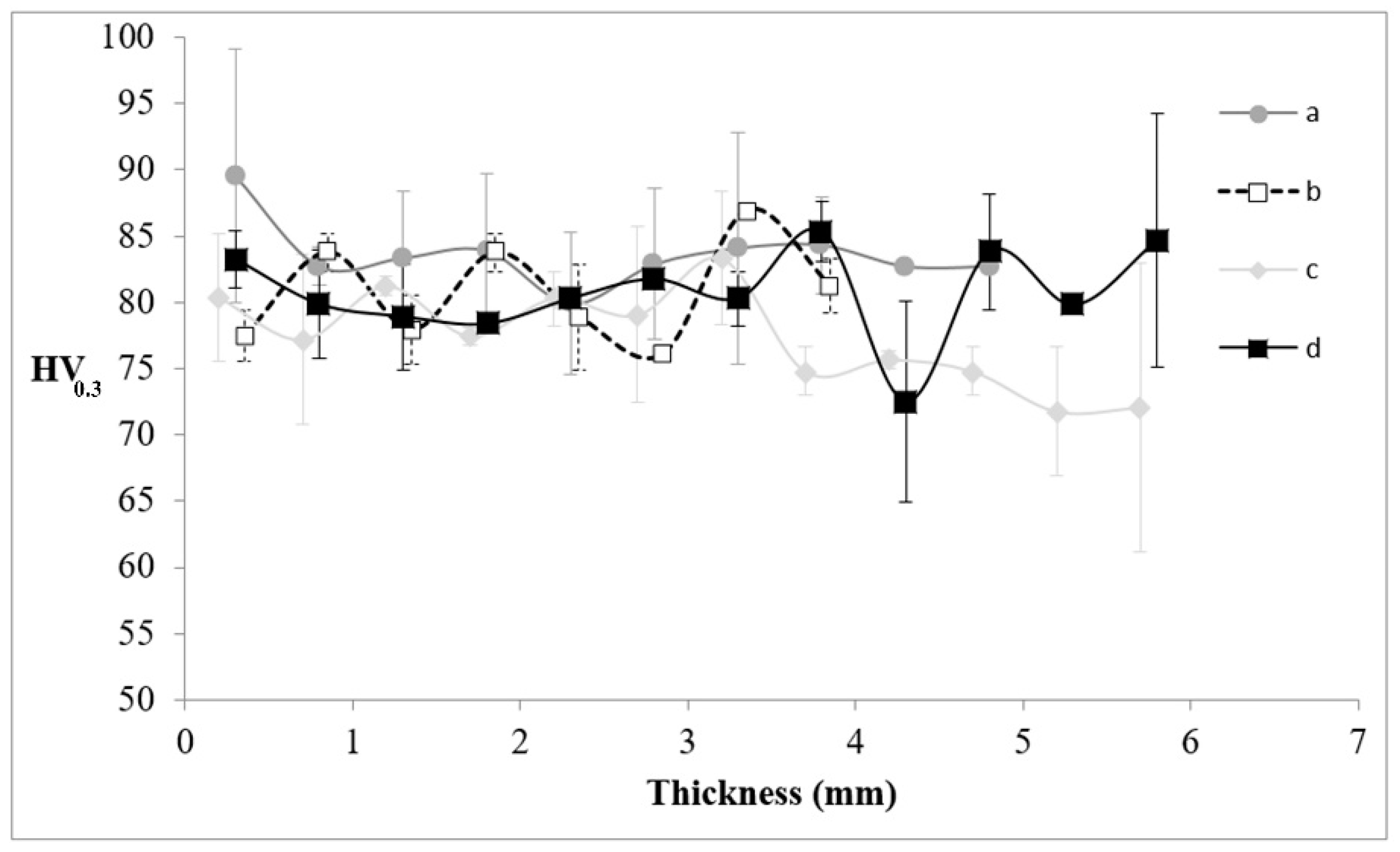
Vickers Hardness HV
4. Conclusions
- Despite the thinness of the original component, a slight decrease in weight was achieved thanks to the design modifications applied to the new boxed part.
- The modal analysis results pointed out that the frequencies of the new geometry were higher than those of the original geometry. From the numerical buckling analyses, it is clear that these values are significantly higher in the new solution compared with the original one. Therefore, the new geometry has much higher performance than the original solution, as regards both the dynamic behavior of the component and the external loads that act on the component through the vehicle’s chassis.
- The process simulations confirmed that the new HPDC with ceramic core solution is feasible and able to produce complex components with a quality very similar to the traditional process.
- The results of the ceramic experimental characterization allowed for selection of the best match of mechanical properties for the ceramic cores. Approximately 100 hollowed crossbeam prototypes were produced, and the as-cast condition was characterized by means of metallurgical analyses and hardness tests. The results confirm that the actual case study has properties and a microstructure very similar to the component produced with the traditional HPDC technology (without ceramic core). A trace of cermet compound was observed in some areas at the interface between aluminum and ceramic core which is not an issue in this component.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chindamo, D.; Gadola, M. Reproduction of real-world road profiles on a four-poster rig for indoor vehicle chassis and suspension durability testing. Adv. Mech. Eng. 2017, 9, 1–10. [Google Scholar] [CrossRef]
- Chiaberge, M. New Trends and Developments in Automotive Industry; InTech: London, UK, 2011; ISBN 978-953-307-999-8. [Google Scholar] [CrossRef]
- Tempelman, E. Multi-Parametric study of the effect of materials substitution on life cycle energy use and waste generation of passenger car structures. Transp. Res. Part D Transp. Environ. 2011, 16, 479–485. [Google Scholar] [CrossRef]
- Cecchel, S.; Chindamo, D.; Turrini, E.; Carnevale, C.; Cornacchia, G.; Gadola, M.; Panvini, A.; Volta, M.; Ferrario, D.; Golimbioschi, R. Impact of reduced mass of light commercial vehicles on fuel consumption, CO2 emissions, air quality, and socio-economic costs. Sci. Total Environ. 2018, 613–614, 409–417. [Google Scholar] [CrossRef] [PubMed]
- Cecchel, S.; Ferrario, D.; Panvini, A.; Cornacchia, G. Lightweight of a cross beam for commercial vehicles: Development, testing and validation. Mater. Des. 2018, 149, 122–134. [Google Scholar] [CrossRef]
- Cecchel, S.; Ferrario, D. Numerical and experimental analysis of a high pressure die casting Aluminum suspension cross beam for light commercial vehicles. La Metallurgia Italiana 2016, 6, 41–44. [Google Scholar]
- Morello, L.; Rosti Rossini, L.; Pia, G.; Tonoli, A. The Automotive Body: Volume I: Components Design; Springer: New York, NY, USA, 2001; ISBN 978-94-007-0513-5. [Google Scholar]
- Cecchel, S.; Cornacchia, G.; Panvini, A. Cradle-to-Gate Impact Assessment of a High-Pressure Die-Casting Safety-Relevant Automotive Component. JOM 2016, 8, 2443–2448. [Google Scholar] [CrossRef]
- Cecchel, S.; Chindamo, D.; Collotta, M.; Cornacchia, G.; Panvini, A.; Tomasoni, G.; Gadola, M. Lightweighting in light commercial vehicles: Cradle-to-grave life cycle assessment of a safety relevant component. Int. J. Life Cycle Assess. 2018, 23, 1–12. [Google Scholar] [CrossRef]
- Cecchel, S.; Collotta, M.; Cornacchia, G.; Panvini, A.; Tomasoni, G. A comparative cradle-to gate impact assessment: Primary and secondary aluminum automotive components case. La Metallurgia Italiana 2018, 2, 46–55. [Google Scholar]
- Cecchel, S.; Cornacchia, G.; Gelfi, M. Corrosion behavior of primary and secondary AlSi High Pressure Die Casting alloys. Mater. Corros. 2017, 68, 961–969. [Google Scholar] [CrossRef]
- Solazzi, L. Applied research for Weight Reduction of an industrial Trailer. FME Trans. 2012, 40, 57–62. [Google Scholar]
- Solazzi, L. Wheel rims for industrial vehicles: Comparative and experimental analyses. Int. J. Heavy Veh. Syst. 2011, 18, 214–225. [Google Scholar] [CrossRef]
- Hirsch, J. Aluminium in Innovative Light-Weight Car Design. Mater. Trans. 2011, 52, 818–824. [Google Scholar] [CrossRef]
- Chindamo, D.; Lenzo, B.; Gadola, M. On the vehicle sideslip angle estimation: A literature review of methods, models and innovations. Appl. Sci. 2018, 8, 355. [Google Scholar] [CrossRef]
- Henriksson, F.; Johansen, K. On Material Substitution in Automotive BIWs – From Steel to Aluminum Body Sides. Procedia CIRP 2016, 50, 683–688. [Google Scholar] [CrossRef]
- Kelkar, A.; Roth, R.; Clark, J. Automobile Bodies: Can Aluminum Be an Economical Alternative To Steel? JOM 2001, 53, 28–32. [Google Scholar]
- Zhoua, J.; Wana, X.; Lia, Y. Advanced aluminium products and manufacturing technologies applied on vehicles at the EuroCarBody conference. Mater. Proc. 2015, 2, 5015–5022. [Google Scholar] [CrossRef]
- Fridlyander, I.N.; Sister, V.G.; Grushko, O.E.; Berstenev, V.V.; Sheveleva, L.M.; Ivanova, L.A. Aluminum alloys: Promising materials in the automotive industry. Met. Sci. Heat Treat. 2002, 44, 365–370. [Google Scholar] [CrossRef]
- Dioni, D.; Cecchel, S.; Cornacchia, G.; Faccoli, M.; Panvini, A. Effects of artificial aging conditions on mechanical properties of gravity cast B356 aluminum alloy. Trans. Nonferrous Met. Soc. China 2015, 25, 1035–1042. [Google Scholar] [CrossRef]
- Faccoli, M.; Dioni, D.; Cecchel, S.; Cornacchia, G.; Panvini, A. Optimization of heat treatment of gravity cast Sr-modified B356 aluminum alloy. Trans. Nonferrous Met. Soc. China 2017, 27, 1698–1706. [Google Scholar] [CrossRef]
- Haracopos, B.; Fisher, T.P. The Technology of Gravity Die Casting; Hart Pub. Co.: Oxford, UK, 1968. [Google Scholar]
- ASM. Metals Handbook, 10th ed.; ASM-Metals Park: Geauga, OH, USA, 1990. [Google Scholar]
- Campbell, J.; Harding, R.A. Casting Technology; TALAT 2.0 [CD-ROM]; EAA: Bruxelles, Belgium, 2000. [Google Scholar]
- Schleg, S.; Kamicki, D.P. Guide to casting and moulding processes. Engineered casting solutions; Technical Articles; 2000. [Google Scholar]
- Brown, J.R. Foseco Non-Ferrous Foundryman’s Handbook; Elsevier: Oxford, UK, 1999; ISBN 9780080531878. [Google Scholar]
- Street, A.C. The Diecasting Book, 2nd ed.; Portcullis Press: London, UK, 1990. [Google Scholar]
- Nagendra Parashar, S.; Mittal, R.K. Elements of Manufacturing Processes; PHI learning Pvt. Ltd.: New Delhi, India, 2006. [Google Scholar]
- Vinarcik, E.J. High Integrity Die Casting Processes; John Wiley & Sons: Hoboken, NJ, USA, 2002; ISBN 978-0-471-20131-1. [Google Scholar]
- Andresen, W. Die Cast Engineering: A Hydraulic, Thermal, and Mechanical Process; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Jelínek, P.; Adámková, E.; Mikšovský, F.; Beňo, J. Advances in technology of soluble cores for die castings. Arch. Foundry Eng. 2015, 15, 29–34. [Google Scholar] [CrossRef]
- Pierri, D. Lost Core: New Perspectives in Die Casting. Available online: https://www.buhlergroup.com/northamerica/en/industry-solutions/die-casting/latest-news/details-7797.htm?title= (accessed on 9 February 2019).
- Czerwinski, F.; Birsan, G.; Benkel, F.; Kasprzak, W.; Walker, M.J.; Smith, J.; Trinowski, D.; Musalem, I. Developing strong core technology for high pressure die casting. Automot. Mater. 2017, 8, 1–11. [Google Scholar]
- Rupp, S.; Heppes, F. La rivoluzione nella pressofusione. Tecnico-Industria Fusoria 2017, 4, 72–76. [Google Scholar]
- Donahue, R.J.; Degler, M.T. Congruent Melting Salt Alloys for Use as Salt Cores in High Pressure Die Casting. U.S Patent US9527131B1, 25 August 2014. [Google Scholar]
- Radadiya, V.A.; Dave, K.G.; Patel, K.R. Design and analysis of salt core for a casting of alluminium alloys. Int. J. Adv. Eng. Res. Dev. 2015, 2, 344–348. [Google Scholar]
- Jelinek, P.; Miksovsky, F.; Beoo, J.; Adamkova, E. Development of foundry cores based on inorganic salts. MTAEC9 2013, 47, 689–693. [Google Scholar]
- Jelínek, P.; Adámková, E. Lost cores for high-pressure die casting. Arch. Foundry Eng. 2014, 14, 101–104. [Google Scholar] [CrossRef]
- Yaokawa, J.; Miura, D.; Anzai, K.; Yamada, Y.; Yoshii, H. Strength of salt core composed of alkali carbonate and alkali chloride mixtures made by casting technique. Mater. Trans. 2007, 8, 1034–1041. [Google Scholar] [CrossRef]
- Yaokawa, J.; Koichi, A.; Yamada, Y.; Yoshii, H. Strength of salt core for die casting. In Proceedings of the International Conference CastExpo ’05 NADCA, St. Louis, MO, USA, 16–19 April 2005; NADCA: St. Louis, MO, USA, 2005. [Google Scholar]
- Fuchs, B.; Eibisch, H.; Körner, C. Core viability simulation for salt core technology in high-pressure die casting. Int. J. Metalcast. 2013, 7, 39–45. [Google Scholar] [CrossRef]
- Fuchs, B.; Körner, C. Mesh resolution consideration for the viability prediction of lost salt cores in the high pressure die casting process. Prog. Comput. Fluid Dyn. 2014, 14, 24–30. [Google Scholar] [CrossRef]
- Mizukusa, Y. Casting Apparatus and Casting Method for Producing Cylinder Block. U.S. Patent 5,690,159, 27 August 1996. [Google Scholar]
- Ackerman, A.D.; Aula, H.A. Method of Making a Cast Aluminum Based Engine Block. U.S. Patent 4,446,906, 8 May 1984. [Google Scholar]
- Brown, W.N.; Robinson, P.M. Soluble Metal Casting Cores Comprising a Water Soluble Salt and a Synthetic Resin. U.S. Patent 364,549, 22 July 1969. [Google Scholar]
- Gibbons, W.A. Core or Filler of Fusible Material for Hollow Vulcanizable Articles. U.S. Patent 1,523,519, 20 January 1925. [Google Scholar]
- Foreman, R.W. Mixture and Method for Preparing Casting Cores and Cores Prepared Thereby. U.S. Patent 4,840,219, 20 June 1989. [Google Scholar]
- Sakoda, T. Water Soluble Core for Pressure Die Casting and Process for Making the Same. U.S. Patent 3,963,818, 15 June 1976. [Google Scholar]
- Molina, R.; Moschini, R. Production of hollow components in high pressure die casting through the use of ceramic lost cores. In Proceedings of the International Conference High Tech Die Casting 2012, Vicenza, Italy, 9–10 April 2012. [Google Scholar]
- Moschini, R.; Calzolaro, A.L. Method for Manufacturing Monolithic Hollow Bodies by Means of a Casting or Injection Moulding Process. Patent International Publication No WO 2011/061593 A1, 26 May 2011. [Google Scholar]
- Solazzi, L. Innovative Bolted junction with high ductility for circular tubular element. J. Constr. Steel Res. 2015, 112, 175–182. [Google Scholar] [CrossRef]
- Mats, G.; Larson, F.B. The Finite Element Method: Theory, Implementation and Applications; Springer: Berlin, Germany, 2010; ISBN 978-3-642-33286-9. [Google Scholar]
- Dimitrios, G. Pavlou Essentials of Finite Element Method for Mechanical and Industrial Engineers; Elsevier: Amsterdam, The Netherlands, 2015; ISBN 978-0-12-802386-0. [Google Scholar]
- Panvini, A.; Molin, D.; Gislon, C. Dual phase simulation for high pressure die casting: Overview and validation of its capabilities. In Proceedings of the HTDC Conference 2016, AIM, Venice, Italy, 22–23 June 2016. [Google Scholar]
- Panvini, A.; Gislon, C. Air entrapment prediction in diecasting through dual phase simulation. In Proceedings of the Die Casting Congress Tabletop 2013, Louisville, KY, USA, 16–18 September 2013. [Google Scholar]
- Miller, A. PQ2 and Gating Manual; NADCA: Arlington Heights, IL, USA, 2016. [Google Scholar]
- UNI EN 843-1:2007. Advanced Technical Ceramics—Mechanical Properties of Monolithic Ceramics at Room Temperature—Part 1: Determination of Flexural Strength; NSAI: Dublin, Ireland, 2007. [Google Scholar]
- UNI EN 843-2:2007. Advanced Technical Ceramics—Mechanical Properties of Monolithic Ceramics at Room Temperature—Part 2: Determination of Young’s Modulus, Shear Modulus and Poisson’s Ratio; NSAI: Dublin, Ireland, 2007. [Google Scholar]
- Smith, J.H. An Introduction to Modern Vehicle Design; Elsevier: Oxford, UK, 2002; ISBN 07506 5044 3. [Google Scholar]
- Pacejka, H.B. Tyre and Vehicle Dynamics, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2006; ISBN 0-7506-6918-7. [Google Scholar]
- Franke, R.; Dragulin, D.; Zovi, A.; Casarotto, F. Progress in ductile aluminium high pressure die casting alloys for the automotive industry. La Metallurgia Italiana 2007, 5, 21–26. [Google Scholar]
- Tinklepaugh, J.R.; James, R. Cermets; Reinhold Publishing Corporation: New York, NY, USA, 1960; ASIN B0007E6FO4. [Google Scholar]
- Hanaor, D.A.H.; Hu, L.; Kan, W.H.; Proust, G.; Foley, M.; Karaman, I.; Radovic, M. Compressive performance and crack propagation in Al alloy/Ti2AlC composites. Mater. Sci. Eng. 2016, 72, 247–256. [Google Scholar] [CrossRef]
- Bhattacharya, A.K.; Petrovic, J.J. Ductile phase toughening and R-curve behaviour in a B4C-AI cermet. J. Mater. Sci. 1992, 27, 2205–2210. [Google Scholar] [CrossRef]
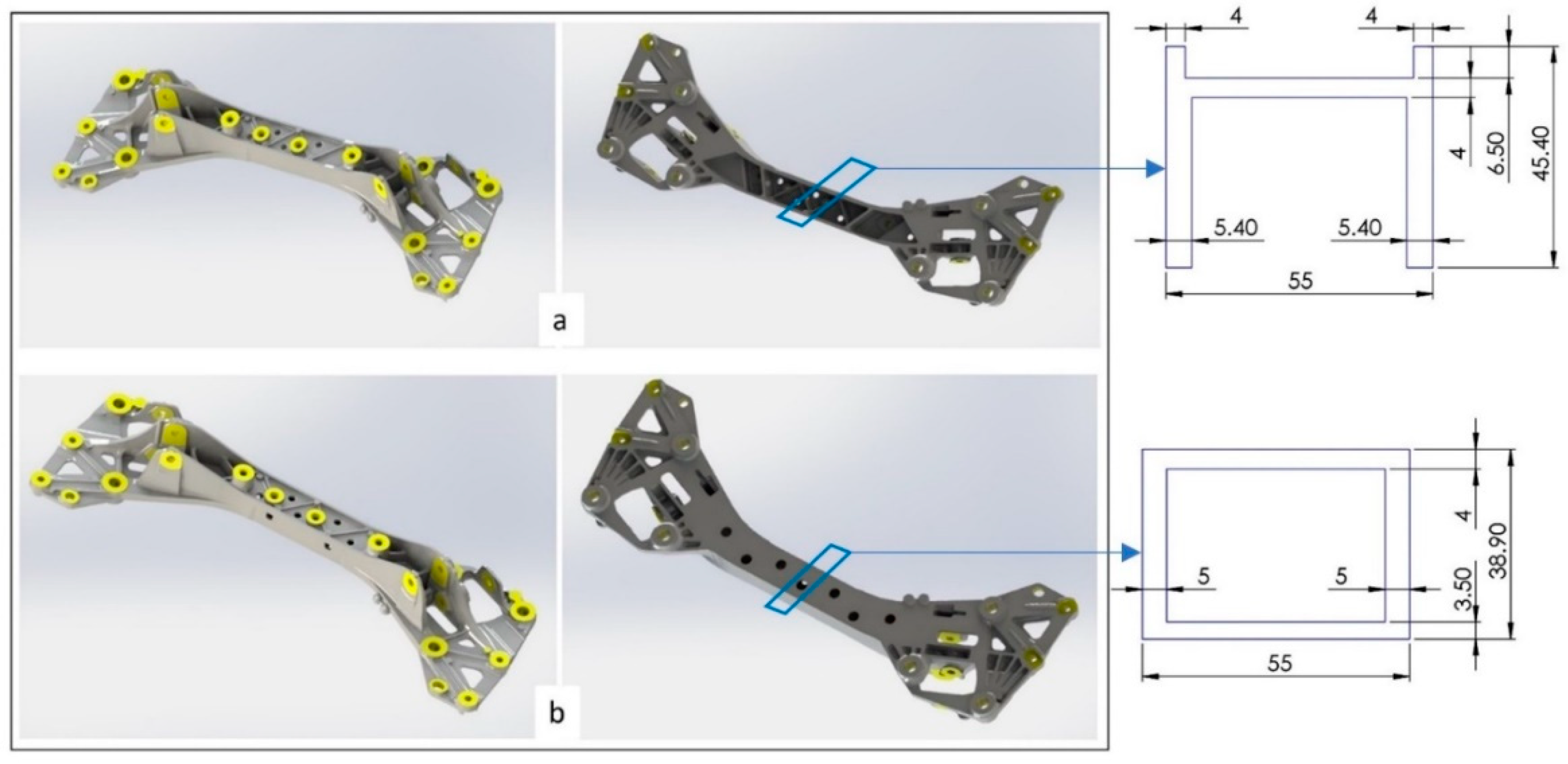
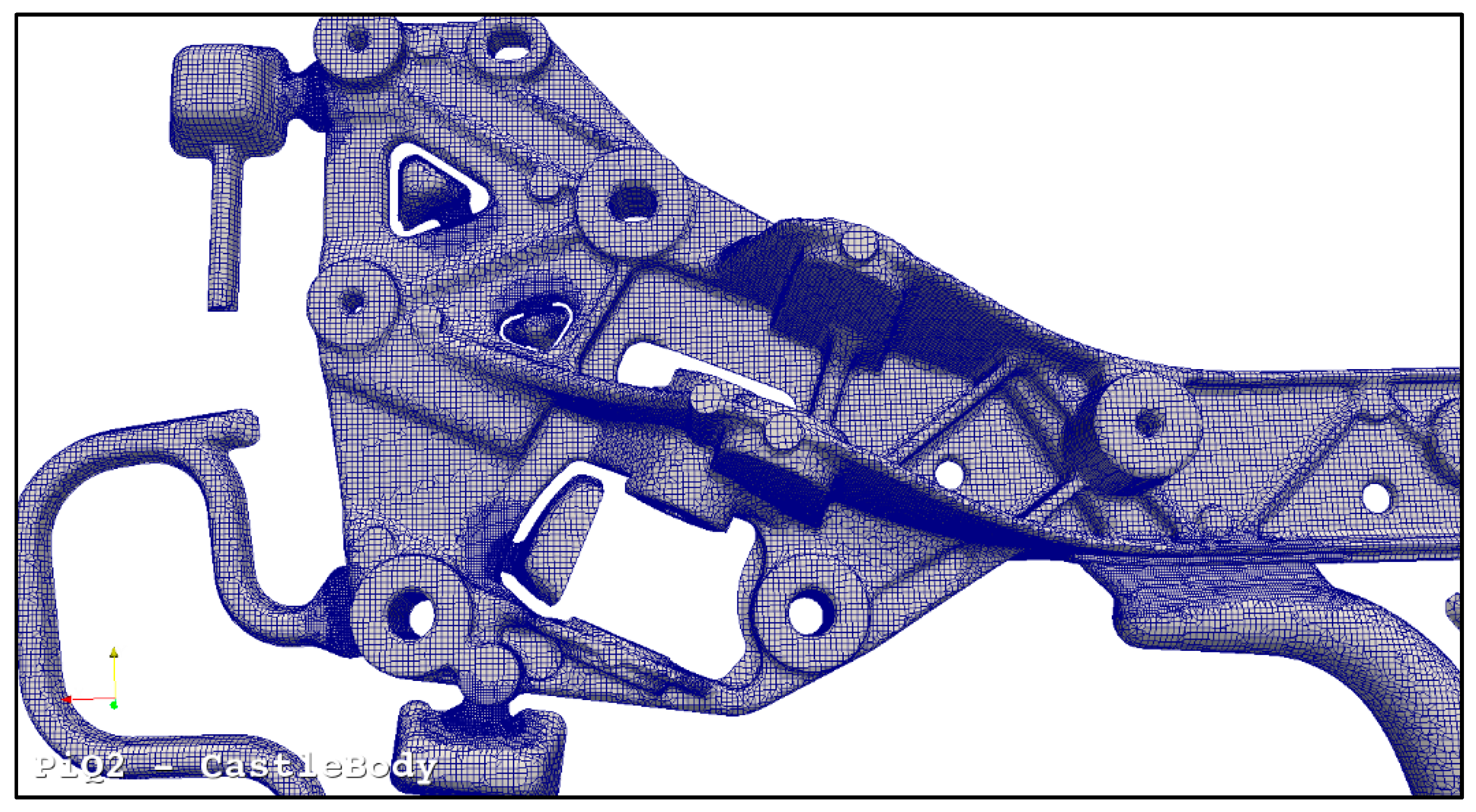




| Chemical Elements | Si | Fe | Cu | Mn | Mg | Ni | Zn | Sn | Ti |
|---|---|---|---|---|---|---|---|---|---|
| EN AC-43500 | 9.5–11.5 | 0.15 | 0.03 | 0.5–0.8 | 0.1–0.5 | - | 0.07 | - | 0.15 |
| E (Young Modulus) (N/mm2) | ν (Poisson Coefficient) | G (Tangential Modulus) (N/mm2) | ρ (Density) (kg/dm3) |
|---|---|---|---|
| 70,000 | 0.3 | 30,000 | 2.7 |
| Ceramic insert | |||
| Thermal Conductivity (W/m/K) | Specific Heat (m2/s2/K) | Density (kg/m3) | Initial Temperature (°C) |
| 0.336 | 818.3 | 1920 | 100 |
| H11 W1.2343 Steel Die | |||
| Thermal Conductivity (W/m/K) | Specific Heat (m2/s2/K) | Density (kg/m3) | Initial Temperature (°C) |
| 28.6 | 460 | 7780 | 230 |
| Pouring temperature of liquid alloy | 690 °C |
| Ceramic insert preheating temperature | 100 °C |
| Initial temperature of the die | 230 °C |
| Heat transfer coefficient between liquid Al and mold during filling | 4000 W/m2/K |
| Heat transfer coefficient between liquid Al and mold during solidification | 1200 W/m2/K |
| Slow shot plunger speed | 0.18 m/s |
| Fast shot plunger speed | 3.5 m/s |
| Third phase intensified pressure on metal | 90 MPa |
| Shotsleeve active length | 0.860 m |
| Fast shot start stroke | 0.563 m |
| First Six Natural Frequencies | Original Geometry | New Geometry | ||
|---|---|---|---|---|
| N° | Free-Free (Hz) | Fixed (Hz) | Free-Free (Hz) | Fixed (Hz) |
| 1 | 226.2 | 251.1 | 330.1 | 264.5 |
| 2 | 278.1 | 603.2 | 349.2 | 625.3 |
| 3 | 412.1 | 620.3 | 408.2 | 653.5 |
| 4 | 632.6 | 810.1 | 677.3 | 905.6 |
| 5 | 733.3 | 1044.4 | 745.5 | 1128.1 |
| 6 | 882.4 | 1250.4 | 899.3 | 1282.9 |
| Buckling Coefficients | Original Geometry | New Geometry | ||
|---|---|---|---|---|
| N° | Buckling Factors for Load Case 1 (F) | Buckling Factors for Load Case 2 (M) | Buckling Factors for Load Case 1 (F) | Buckling Factors for Load Case 2 (M) |
| 1 | −1.415 | −0.881 | −1.515 | −1.539 |
| 2 | 1.107 | 1.200 | 1.508 | 1.565 |
| 3 | 1.742 | 1.254 | 1.706 | 1.931 |
| 4 | 1.832 | 1.358 | 1.951 | 1.991 |
| Type of Ceramic Decoring Tested | HF | HNO3 | C6H8O7 | CH3COOH | C6H8O7/CH3COOH (1:1) | |||
|---|---|---|---|---|---|---|---|---|
| Acid amount (water solution) | 5% | 10% | 65% | 50% | 50% | 50% | 100% | |
| Immersion with ultrasound | no | no | no | yes | yes | yes | yes | yes |
| a | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| b | N/A | N/A | N/A | N/A | ✗ | ✗ | ✗ | ✗ |
| c | N/A | N/A | N/A | N/A | ✗ | ✗ | ✗ | ✗ |
| Aluminum | Burned-out | No effect | No effect | No effect | No effect | |||
| Samples | Sintering T (°C) | E (GPa) | σf (MPa) | ||
|---|---|---|---|---|---|
| Avg. | ± | Avg. | ± | ||
| a | 892 | 13.26 | 0.96 | 14.13 | 1.7 |
| 900 | 13.59 | 1.72 | 14.07 | 1.43 | |
| 908 | 15.45 | 0.83 | 16.28 | 1.91 | |
| b | 1075 | 9.2 | 0.76 | 13.02 | 0.92 |
| 1110 | 10.14 | 0.33 | 13.41 | 0.52 | |
| c | 1075 | 12.12 | 1.35 | 17.56 | 1.82 |
| 1110 | 13.97 | 0.97 | 19.41 | 0.56 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cornacchia, G.; Dioni, D.; Faccoli, M.; Gislon, C.; Solazzi, L.; Panvini, A.; Cecchel, S. Experimental and Numerical Study of an Automotive Component Produced with Innovative Ceramic Core in High Pressure Die Casting (HPDC). Metals 2019, 9, 217. https://doi.org/10.3390/met9020217
Cornacchia G, Dioni D, Faccoli M, Gislon C, Solazzi L, Panvini A, Cecchel S. Experimental and Numerical Study of an Automotive Component Produced with Innovative Ceramic Core in High Pressure Die Casting (HPDC). Metals. 2019; 9(2):217. https://doi.org/10.3390/met9020217
Chicago/Turabian StyleCornacchia, Giovanna, Daniele Dioni, Michela Faccoli, Claudio Gislon, Luigi Solazzi, Andrea Panvini, and Silvia Cecchel. 2019. "Experimental and Numerical Study of an Automotive Component Produced with Innovative Ceramic Core in High Pressure Die Casting (HPDC)" Metals 9, no. 2: 217. https://doi.org/10.3390/met9020217
APA StyleCornacchia, G., Dioni, D., Faccoli, M., Gislon, C., Solazzi, L., Panvini, A., & Cecchel, S. (2019). Experimental and Numerical Study of an Automotive Component Produced with Innovative Ceramic Core in High Pressure Die Casting (HPDC). Metals, 9(2), 217. https://doi.org/10.3390/met9020217







