Multiparametric Investigation of Welding Techniques on Toe Radius of High Strength Steel at Low-Temperature Levels Using 3D-Scanning Techniques
Abstract
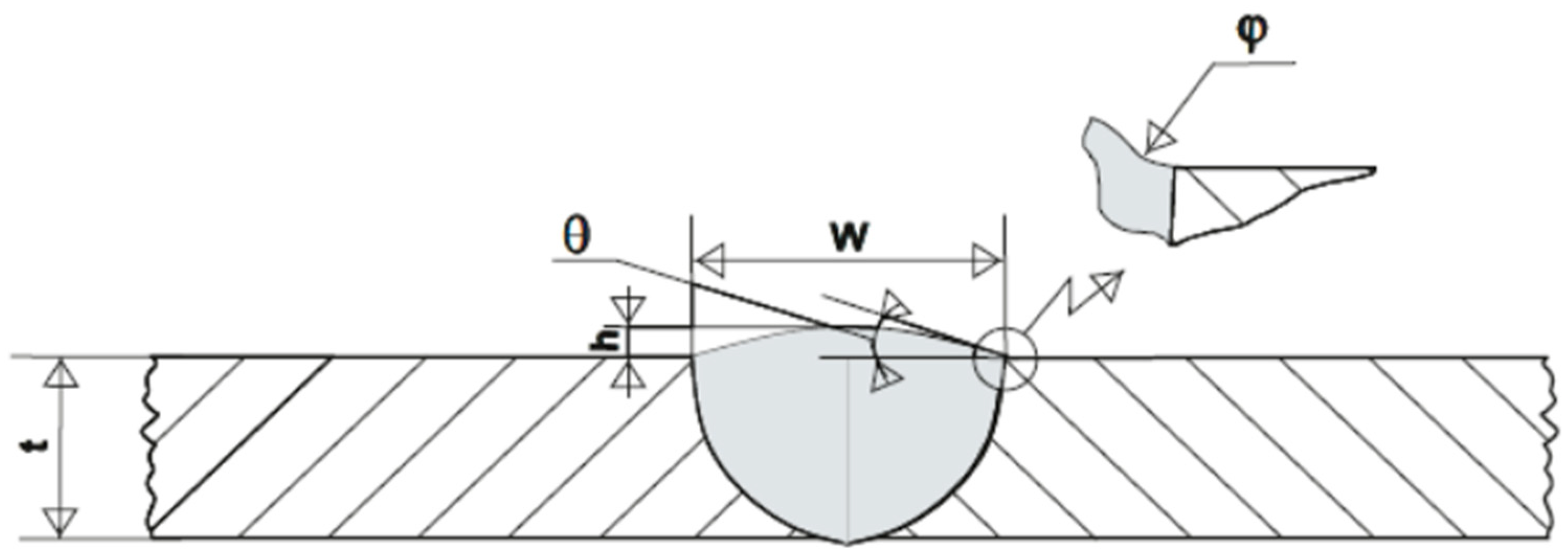
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Varying Welding Techniques
- torch angle;
- number of cover passes;
- the length of electrode stick-out;
- the shielding gas.
2.2.1. Torch Angle
2.2.2. Number of Cover Passes
2.2.3. Length of Electrode Stick-Out
2.2.4. Shielding Gas
3. Results
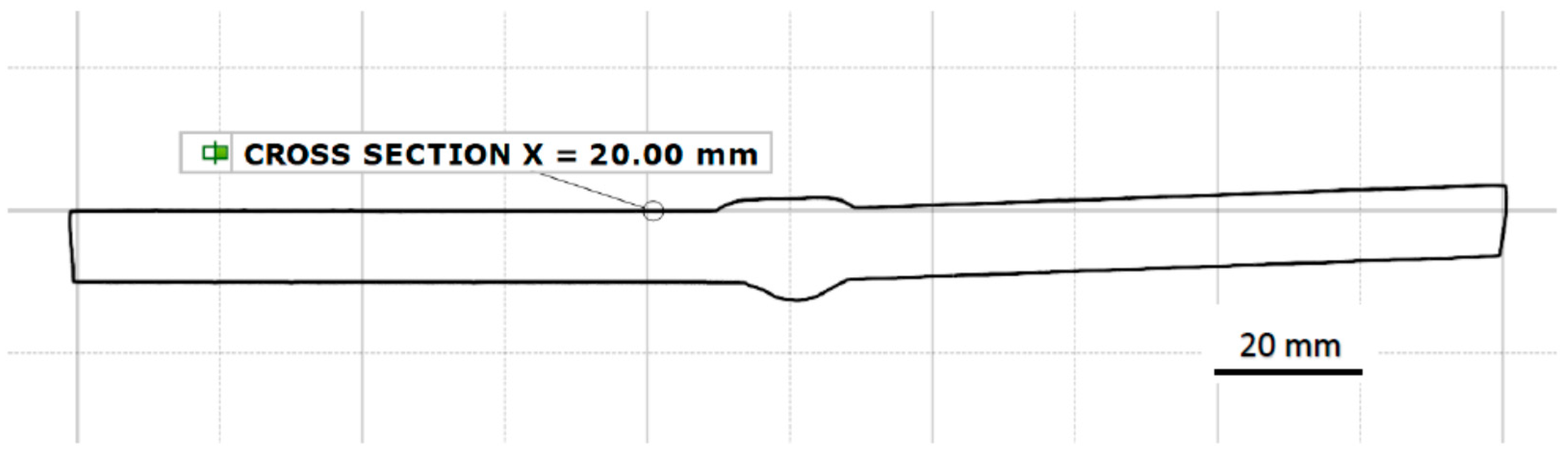
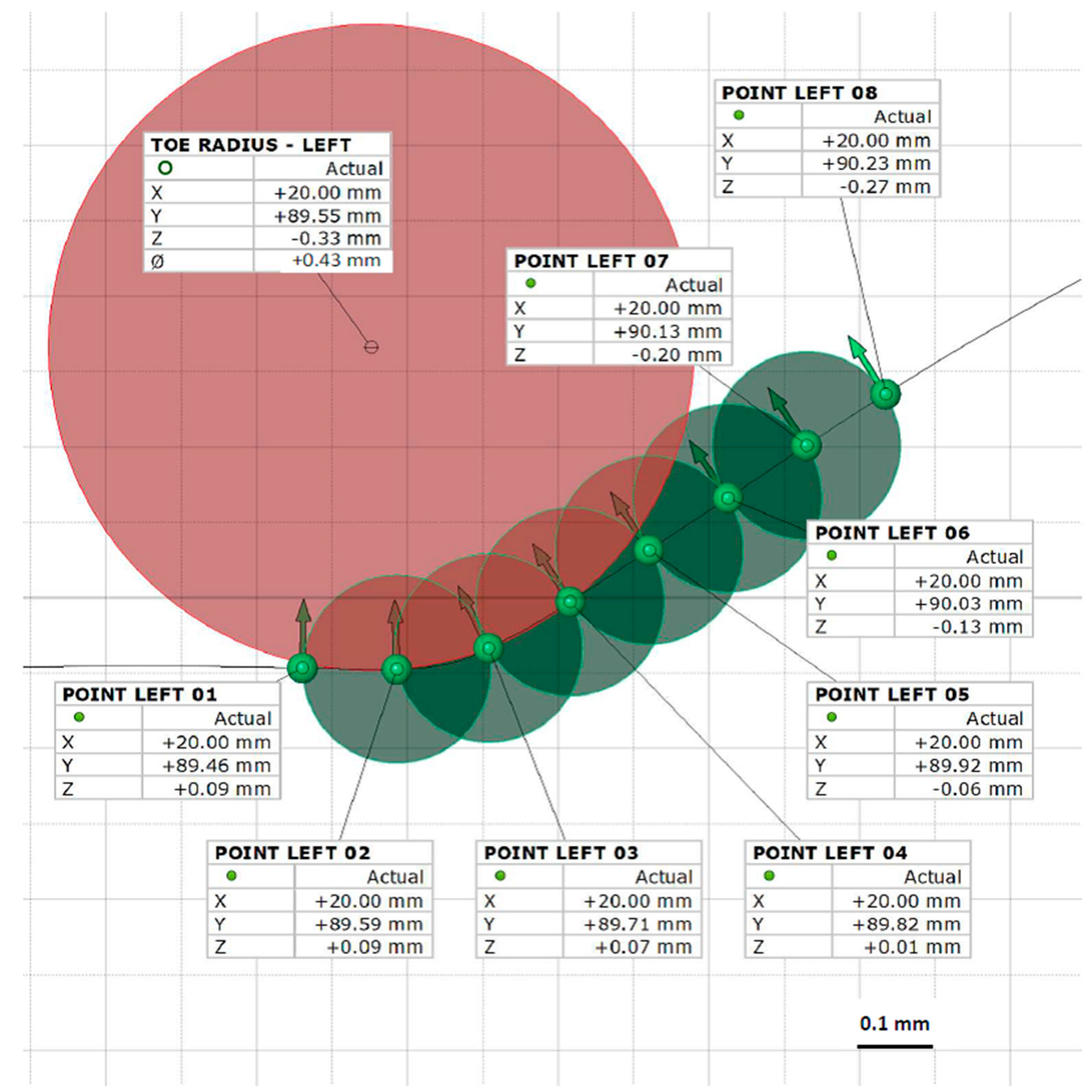
3.1. D-Scanning and Methodology
3.2. Measurement of Geometries of the Welded Joint Cross-Section With the GOM Inspect Computational Software
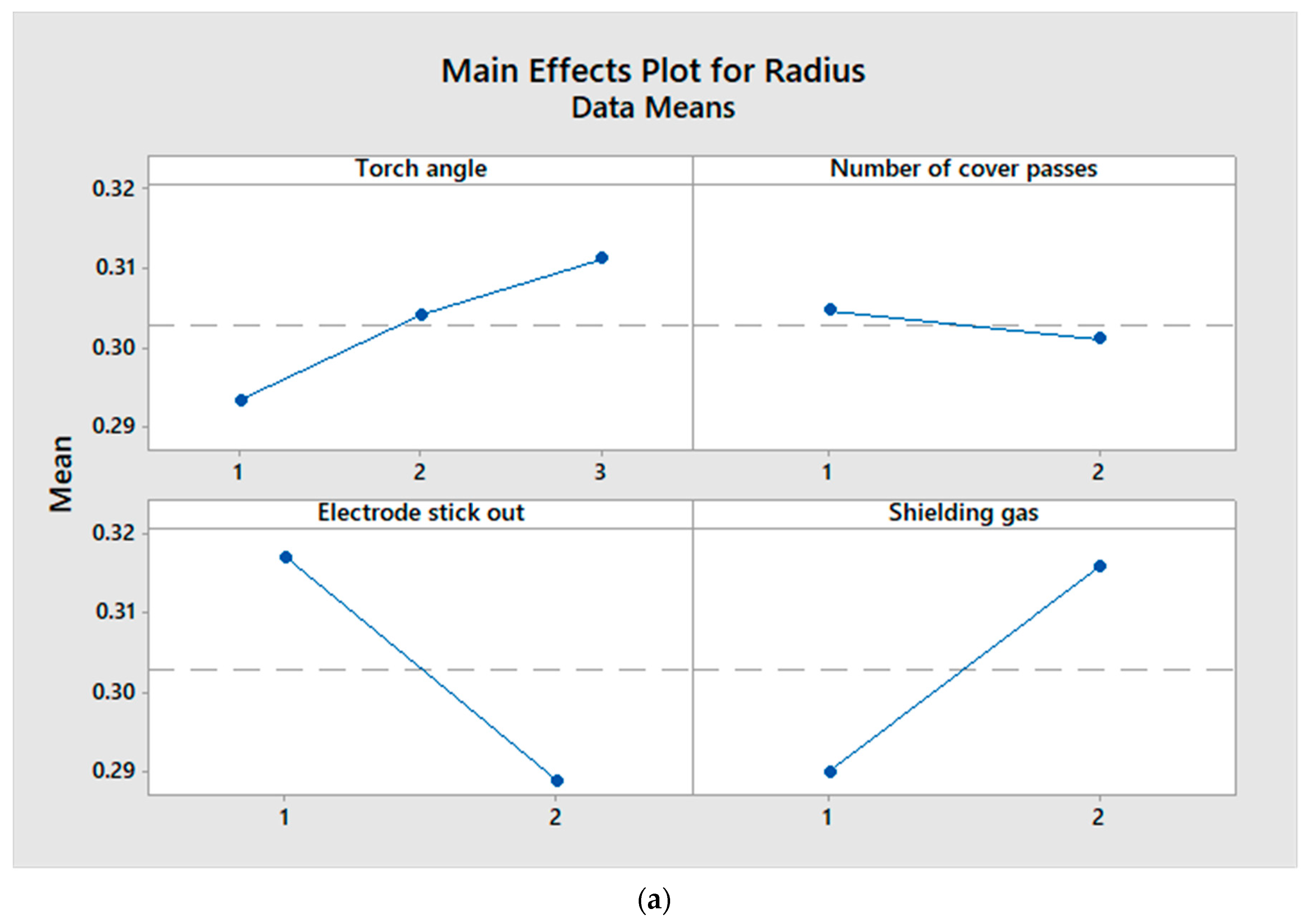
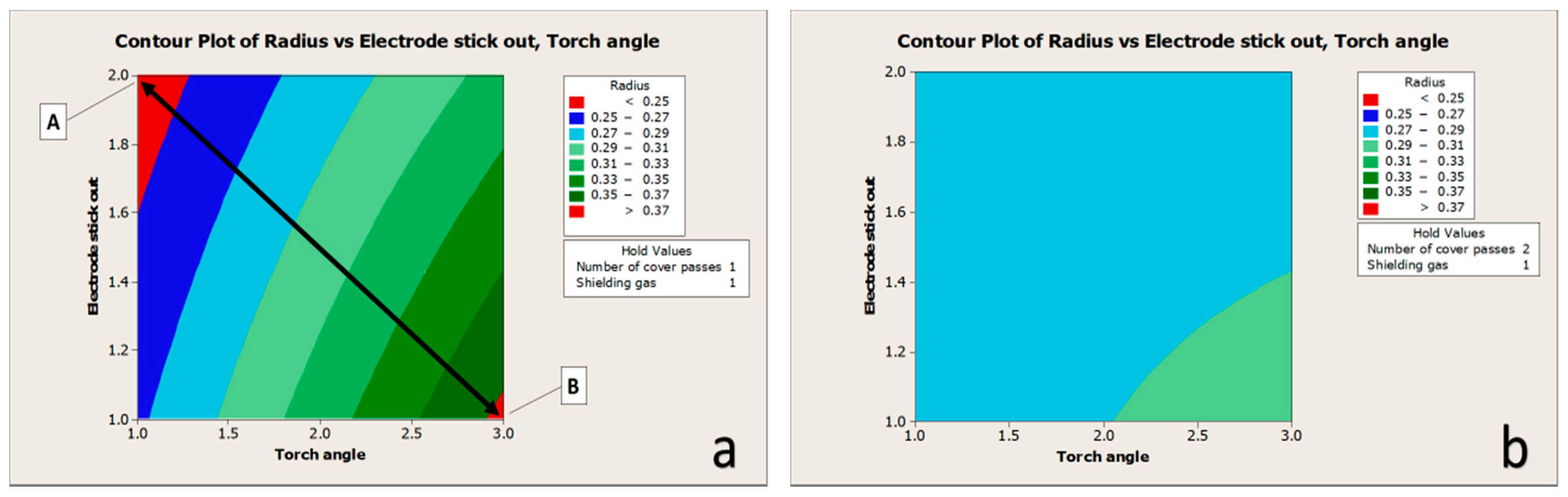
4. Discussion
- (1)
- a new state-of-the-art method for scanning a welded joint surface and measuring the seam edge radius with a 3D scanner have been presented;
- (2)
- by analyzing the radius of the seam edge with a 3D scanner, new welding parameters were obtained which significantly affect the surface shape of the welded joint, thus preventing the initiation of surface cracks;
- (3)
- welding parameters have been obtained which should definitely be avoided during welding because if used, there is a high probability of surface cracks.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
The Sensitivity Analysis of Expression for Calculation of Stress Concentration Factor in Butt Welding Joints
| Geometric Quantity | Values in which the Sensitivity was Analyzed |
|---|---|
| Thickness of the base metal | 6, 10, and 20 mm |
| Weld toe angle | 5°, 10°, 20°, and 50° |
| Toe radius | 0,1, 0.5, 1, and 3 mm |
| Reinforcement height | 1, 2, and 4 mm |
| Weld width | 20, 25, and 30 mm |
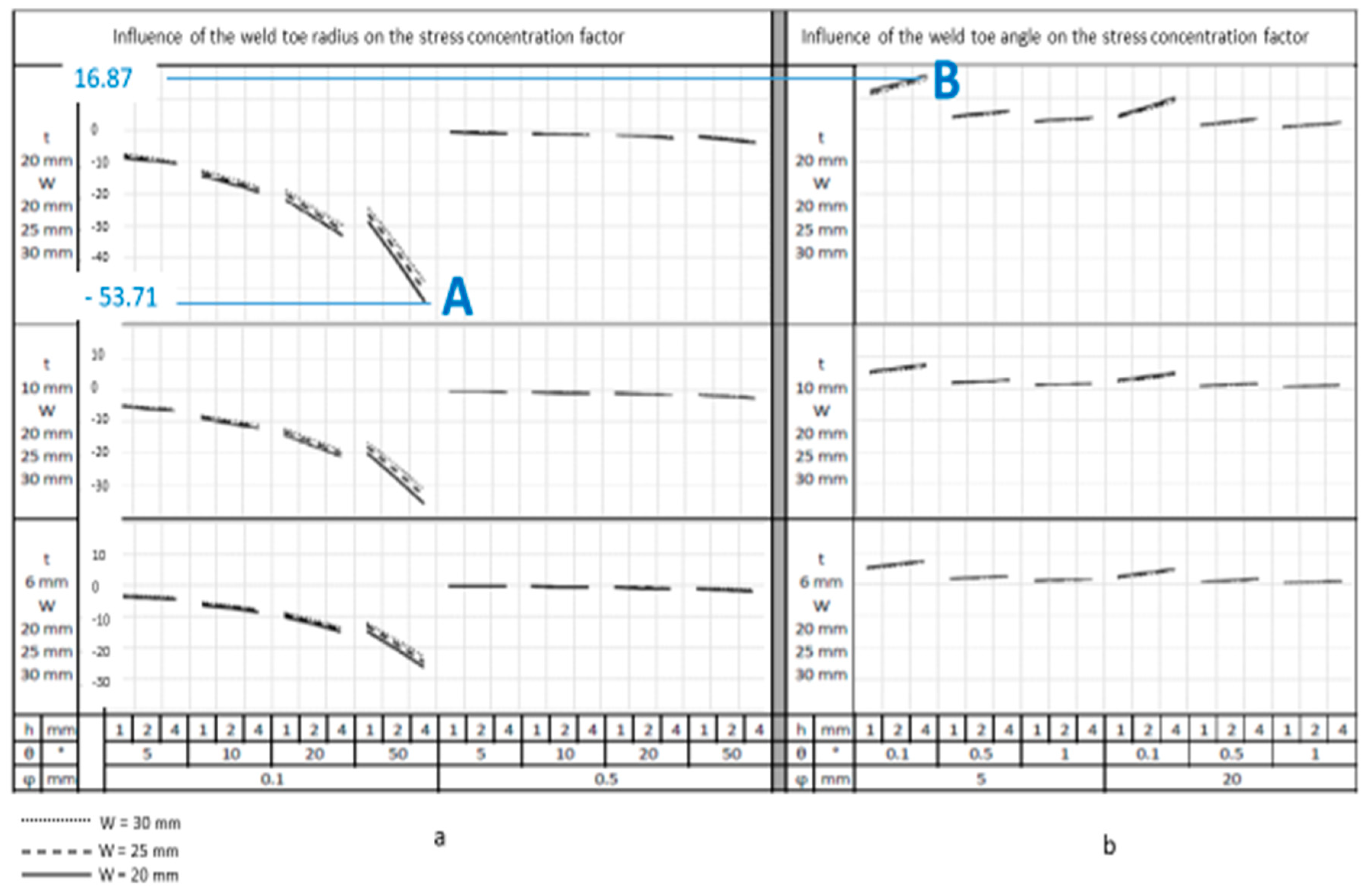
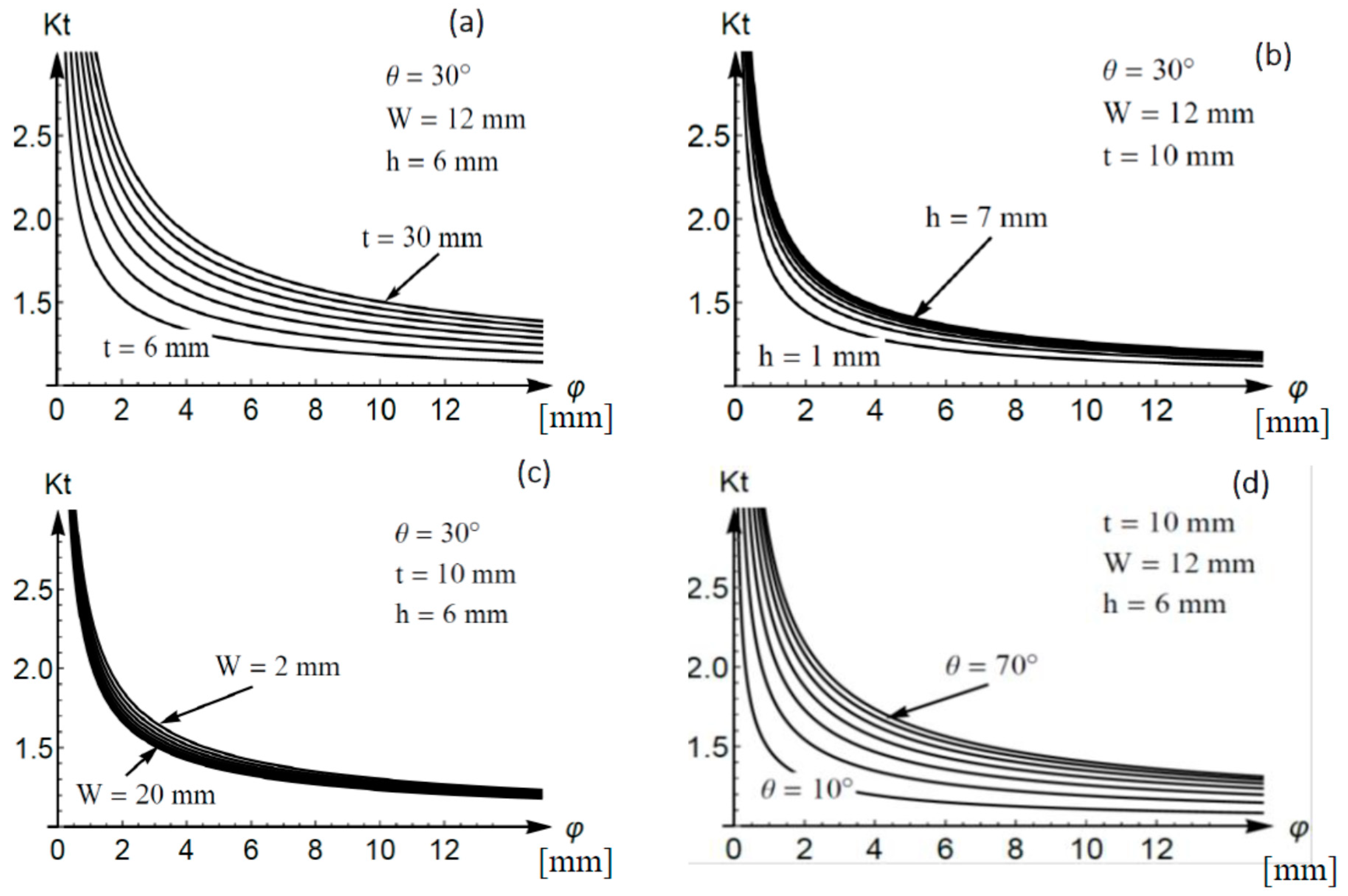
- weld width
- base metal thickness;
- reinforcement height;
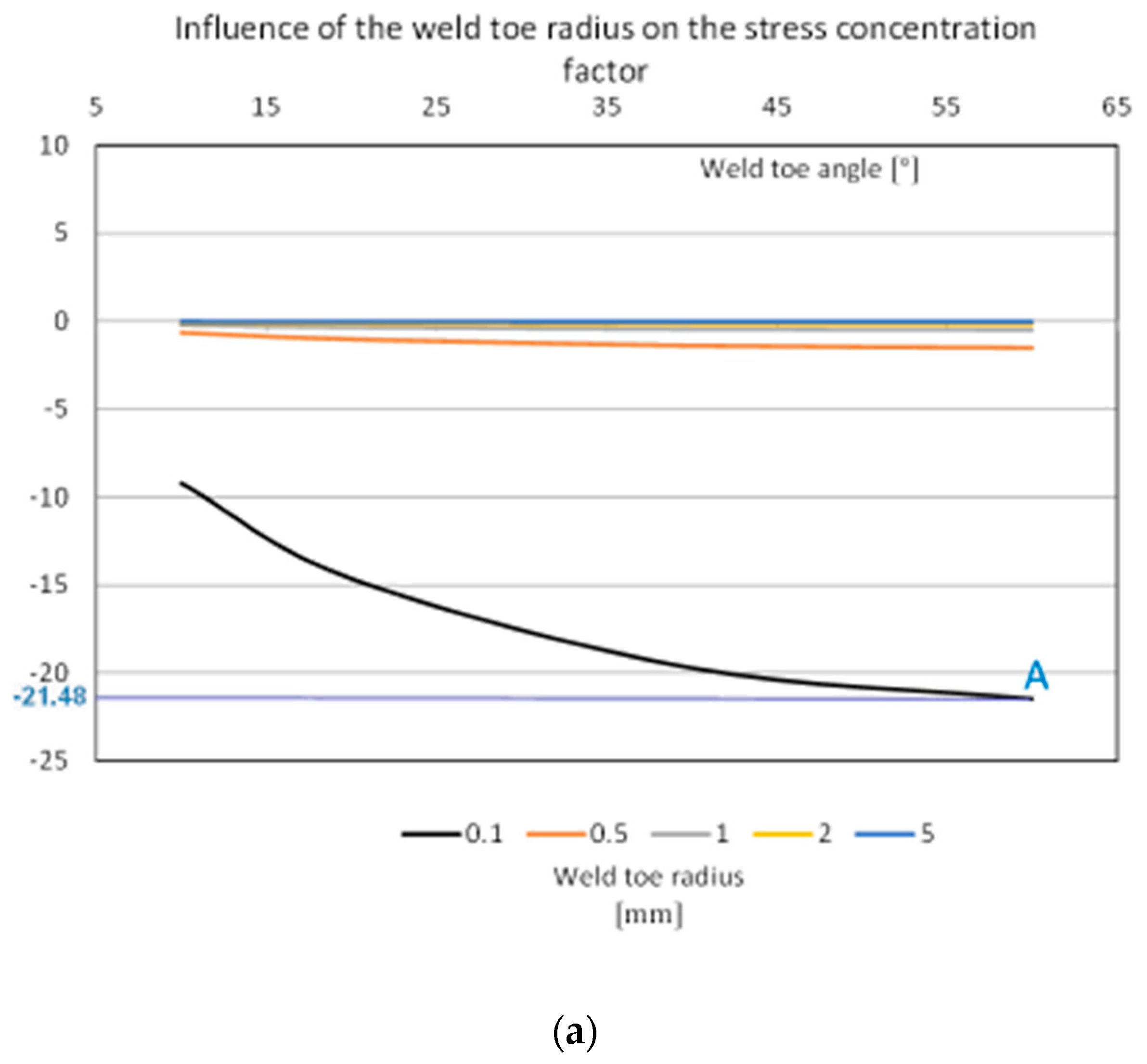
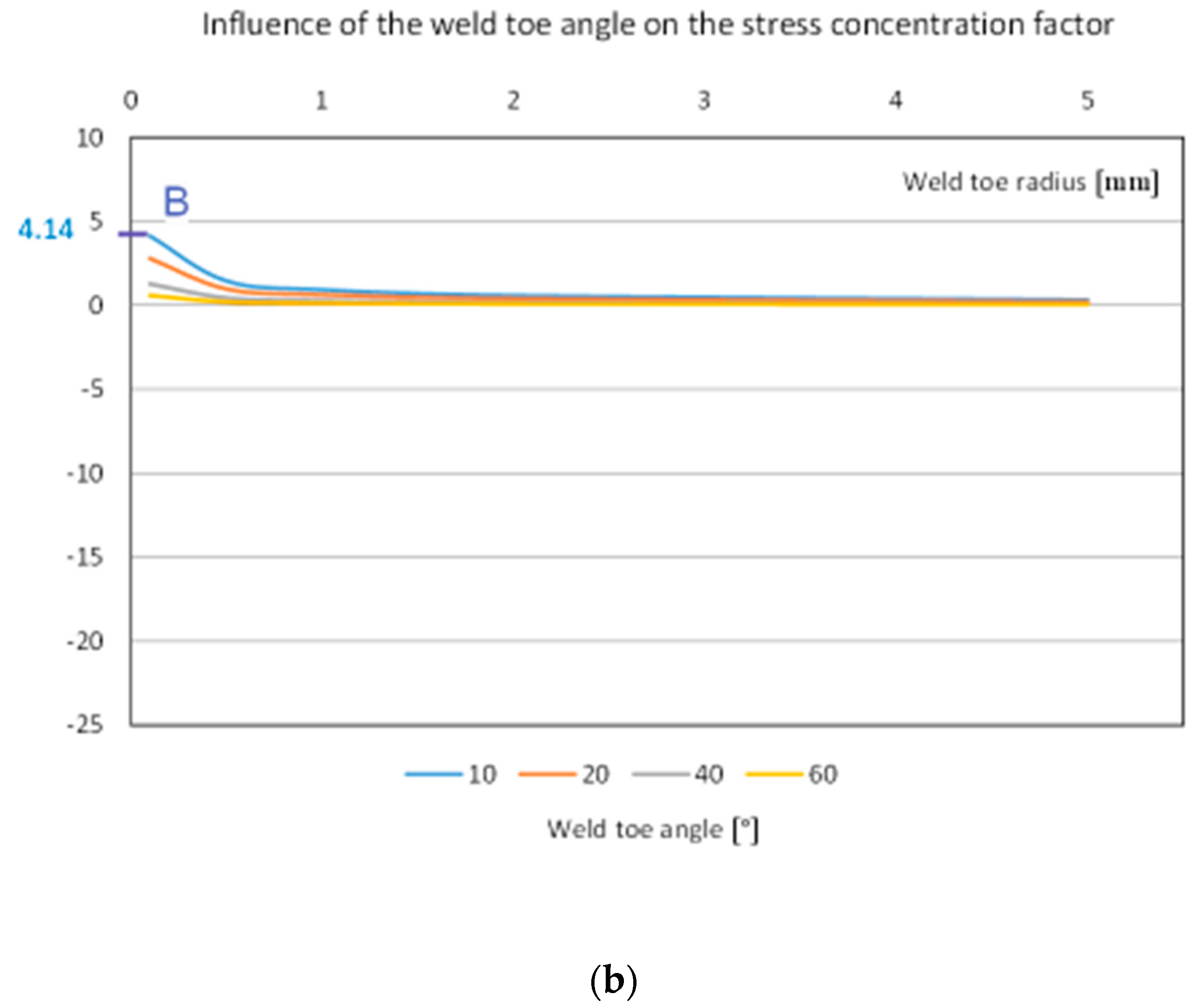
- weld toe angle with the toe radius bigger than 1 mm;
- toe radius with the radius bigger than 1 mm;
- weld toe angle with the toe radius of up to 1 mm;
- toe radius with the radius from 0.5 mm to 1 mm;
- Area of great influence:
- toe radius with the radius of up to 0.5 mm.
References
- Lawrence, F.V.; Mattos, R.J.; Higashida, Y. Estimating the Fatigue Crack Initiation Life of Welds; American Society for Testing and Materials: Toronto, CA, USA, 1978. [Google Scholar]
- Telsang, M.T.; Patil, R.M. Fatigue analysis of butt welded joint using LEFM–experimental investigation. Int. J. Eng. Res. Technol. 2013, 2, 2278–2283. [Google Scholar]
- Hadjoui, F.; Benachour, M.; Benguediab, M. Fatigue crack growth on double butt weld with toe crack of pipelines steel. Mater. Sci. Appl. 2012, 3, 596–599. [Google Scholar] [CrossRef]
- Dvornik, J.; Dvornik, S. Ship Construction; Faculty of Maritime Studies: Split, Croatia, 2013. [Google Scholar]
- Moore, P.L. The importance of welding quality in ship construction. In Proceedings of the 2nd International Conference on Marine Structures-Analysis and design of Marine Structures (MARSTRUCT 2009), Lisbon, Portugal, 16–18 March 2009. [Google Scholar]
- Teng, T.L.; Fung, C.P.; Chang, P.H. Effect of weld geometry and residual stresses on fatigue in butt welded joints. Int. J. Press. Ves. Pip. 2002, 79, 467–482. [Google Scholar] [CrossRef]
- Chattopadhyay, A.; Glinka, G.; El-Zein, M.; Qian, J.; Formas, R. Stress analysis and fatigue of welded structures. Weld World 2011, 55, 2–21. [Google Scholar] [CrossRef]
- Lawrence, F.V.; Ho, N.J.; Mazumdar, P.K. Predicting the fatigue resistance of welds. Ann. Rev. Mater. Sci. 1981, 11, 401–425. [Google Scholar] [CrossRef]
- Jonsson, B.; Dobmann, G.; Hobbacher, A.F.; Kassner, M. IIW Guidelines on Well Quality in Relationship to Fatigue Strength; International Institute of Welding: Paris, France, 2016. [Google Scholar]
- Ilda, K.; Uemura, T. Stress concentration factor formulae widely used in Japan. Fatigue Fract. Eng. Mater. Struct. 1996, 19, 779–786. [Google Scholar]
- Kirkhope, K.J.; Bell, R.; Caron, L.; Basu, R.I.; Ma, K.T. Weld detail fatigue life improvement techniques. Part 1: Review. Mar. Struct. 1999, 12, 447–474. [Google Scholar] [CrossRef]
- Lechner, C.; Bleicher, F.; Habersohn, C. The use of machine hammer peening technology for smoothening and structuring of surfaces. In Proceedings of the 23rd DAAAM Symposium, Vienna, Austria, 24–27 October 2012; Volume 23. [Google Scholar]
- Cozzolino, L.D.; Coules, H.E.; Colegrove, P.A.; Wen, S.W. Investigation of post-weld rolling methods to reduce residual stress and distortion. J. Mater. Process. Technol. 2017, 247, 243–256. [Google Scholar] [CrossRef]
- Haagensen, P.J.; Maddox, S.J. IIW Recommendations on Post Weld Improvement of Steel and Aluminium Structures; The International Institute of Welding: Villepinte, France, 2001. [Google Scholar]
- Radaj, D.; Sonsino, C.M.; Fricke, W. Fatigue Assessment of Welded Joints by Local Approaches; Woodhead Publishing Ltd.: Cambridge, UK, 2006. [Google Scholar]
- Den Ouden, G.; Hermans, M. Welding Technology; VSSD: Delft, The Netherlands, 2009. [Google Scholar]
- Jeffus, L. Welding Principles and Applications, 17th ed.; Delmar: New York, NY, USA, 2012. [Google Scholar]
- Bytyqi, B.; Osmani, H.; Idrizi, F. Influence of welding parameters on seam welded quality with MAG welding. In Proceedings of the 4th International Research and Expert Conference, Fojnica, Bosnian, 9–12 November 2005. [Google Scholar]
- Kasuya, T.; Yurioka, N. Effects of ambient temperature on steel weldability. Weld Int. 1992, 6, 145–150. [Google Scholar] [CrossRef]
- Nouri, M.; Abdollah-zadehy, A.; Ghaini, F.M. Effect of welding parameters on dilution and weld bead geometry in cladding. J. Mater. Sci. Technol. 2007, 23, 817–822. [Google Scholar]
- Tewari, S.P.; Gupta, A.; Prakash, J. Effect of welding parameters on the weldability of materials. Int. J. Eng. Sci. Technol. 2010, 2, 512–516. [Google Scholar]
- Williams, H.E.; Ottsen, H.; Lawrence, F.V.; Munse, W.H. The Effects of Weld Geometry on the Fatigue Behavior of Welded Connections; University of Illinois: Urbana, IL, USA, 1970. [Google Scholar]
- Robakowski, T. Effect of height of reinforcement bead on fatigue strengths of butt joints with internal defects. Weld Int. 1989, 3, 301–304. [Google Scholar] [CrossRef]
- Berge, S. On the effect of plate thickness in fatigue of welds. Eng. Fract. Mech. 1985, 21, 423–435. [Google Scholar] [CrossRef]
- Cerit, M.; Kokumer, O.; Genel, K. Stress concentration effects of undercut defect and reinforcement metal in butt welded joint. Eng. Fail. Anal. 2010, 17, 571–578. [Google Scholar] [CrossRef]
- Kim, I.S.; Kwon, W.H.; Park, C.E. The effect of welding process parameters on weld bead width in GMAW processes. Korea Weld Soc. 1996, 14, 204–213. [Google Scholar]
- Pilkey, W.D.; Pilkey, D.F. Peterson’s Stress Concentration Factors, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Ushirokawa, O.; Nakayama, E. Stress Concentration Factor at Welded Joints; Technical Report; Ishikawajima-Harima Gihou: Tokyo, Japan, 1983. (In Japanese) [Google Scholar]
- Karaoğlu, S.; Seçgin, A. Sensitivity analysis of submerged arc welding process parameters. J. Mater. Proc. Technol. 2008, 202, 500–507. [Google Scholar] [CrossRef]
- Ferretti, F.; Saltelli, A.; Tarantola, S. Trends in sensitivity analysis practice in the last decade. Sci. Total. Environ. 2016, 568, 666–670. [Google Scholar] [CrossRef] [PubMed]
- Det Norske Veritas Germanischer Lloyd. Rules for Classification: Ships. Part 2 Materials and Welding, Chapter 2 Metallic Materials; DNVGL: Hovik, Norway, 2015. [Google Scholar]
- Dalmont Limited. Welding Procedures Specification, Nos D014 & D015; Dalmont: Rijeka, Croatia, 10 May 2016. [Google Scholar]
- Vitkovice Steel Limited. Inspection Certificate 3.2; Vitkovice Steel: Vitkovice, Czech Republic, 2011. [Google Scholar]
- Randić, M.; Pavletić, D.; Turkalj, G. The measurement of weld surface geometry. In Proceedings of the 17th International Congress of the International Maritime Association of the Mediterranean, Lisbon, Portugal, 9–11 October 2017. [Google Scholar]
- GOM GmbH. Acquisition Basic; GOM Software: Braunschweig, Germany, 2016. [Google Scholar]
- Hinkelmann, K.; Kempthorne, O. Design and Analyses of Experiments, 2nd ed.; Wiley & Sons: New York, NY, USA, 2008; Volume 1. [Google Scholar]
- Rowlands, H.; Antony, J. Application of design of experiments to a spot welding process. Assem. Autom. 2003, 23, 273–279. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Runger, G.C. Applied Statistic and Probability for Engineers, 3rd ed.; John Wiley & Sons: New York, NY, USA, 2003. [Google Scholar]
- Niemi, E.; Fricke, W.; Maddox, S.J. Fatigue Analysis of Welded Components; Woodhead Publishing Ltd.: Cambridge, UK, 2006. [Google Scholar]





| Welding Techniques | Level | ||
|---|---|---|---|
| Lower (Mark “−“) | Middle (Mark “0”) | Higher (Mark “+”) | |
| Torch angle (A) | Forehand technique Group 1 | Vertical technique Group 2 | Backhand technique Group 3 |
| Number of cover passes (B) | 1 pass | 3 passes | |
| Length of electrode stick-out (C) | 5 mm | 15 mm | |
| Shielding gas (D) | 82% Ar + 18% CO2 | 100% CO2 | |
| Input Factor | The Experiment Group and Label Level of Input Factor | |||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1-1 | 1-2 | 1-3 | 1-4 | 1-5 | 1-6 | 1-7 | 1-8 | 2-1 | 2-2 | 2-3 | 2-4 | 2-5 | 2-6 | 2-7 | 2-8 | 3-1 | 3-2 | 3-3 | 3-4 | 3-5 | 3-6 | 3-7 | 3-8 | |
| Group 1 | Group 2 | Group 3 | ||||||||||||||||||||||
| Torch angle | − | − | − | − | − | − | − | − | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | + | + | + | + | + | + | + | + |
| Number of cover passes | − | − | − | − | + | + | + | + | − | − | − | − | + | + | + | + | − | − | − | − | + | + | + | + |
| Length of electrode stick-out | − | − | + | + | − | − | + | + | − | − | + | + | − | − | + | + | − | − | + | + | − | − | + | + |
| Shielding gas | − | + | − | + | − | + | − | + | − | + | − | + | − | + | − | + | - | + | − | + | − | + | − | + |
| Chemical Element (%) | C | Si | Mn | P | S | Cr | Mo | Ni | Al | Cu | Nb |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Required (according to DNV GL Rules) [31] | ≤0.18 | ≤0.50 | 0.90–1.60 | ≤0.035 | ≤0035 | ≤0.20 | ≤0.08 | ≤0.40 | ≥0.020 | ≤0.35 | 0.02–0.05 |
| Actual (according to factory certificate) [33] | 0.176 | 0.34 | 1.42 | 0.014 | 0.001 | 0.050 | 0.003 | 0.020 | 0.024 | 0.020 | 0.026 |
| Sample | 1-1 | 1-2 | 1-3 | 1-4 | 1-5 | 1-6 | 1-7 | 1-8 | 2-1 | 2-2 | 2-3 | 2-4 |
| Band A | 0.22 | 0.27 | 0.27 | 0.30 | 0.20 | 0.43 | 0.22 | 0.36 | 0.29 | 0.27 | 0.33 | 0.29 |
| Band B | 0.21 | 0.41 | 0.29 | 0.30 | 0.29 | 0.39 | 0.26 | 0.31 | 0.27 | 0.40 | 0.26 | 0.26 |
| Band C | 0.23 | 0.30 | 0.26 | 0.23 | 0.29 | 0.29 | 0.26 | 0.45 | 0.41 | 0.40 | 0.28 | 0.24 |
| Sample | 2-5 | 2-6 | 2-7 | 2-8 | 3-1 | 3-2 | 3-3 | 3-4 | 3-5 | 3-6 | 3-7 | 3-8 |
| Band A | 0.39 | 0.28 | 0.27 | 0.26 | 0.48 | 0.38 | 0.37 | 0.30 | 0.28 | 0.31 | 0.26 | 0.35 |
| Band B | 0.39 | 0.24 | 0.28 | 0.33 | 0.29 | 0.33 | 0.25 | 0.29 | 0.27 | 0.29 | 0.21 | 0.25 |
| Band C | 0.37 | 0.25 | 0.25 | 0.29 | 0.37 | 0.33 | 0.32 | 0.28 | 0.25 | 0.35 | 0.31 | 0.36 |
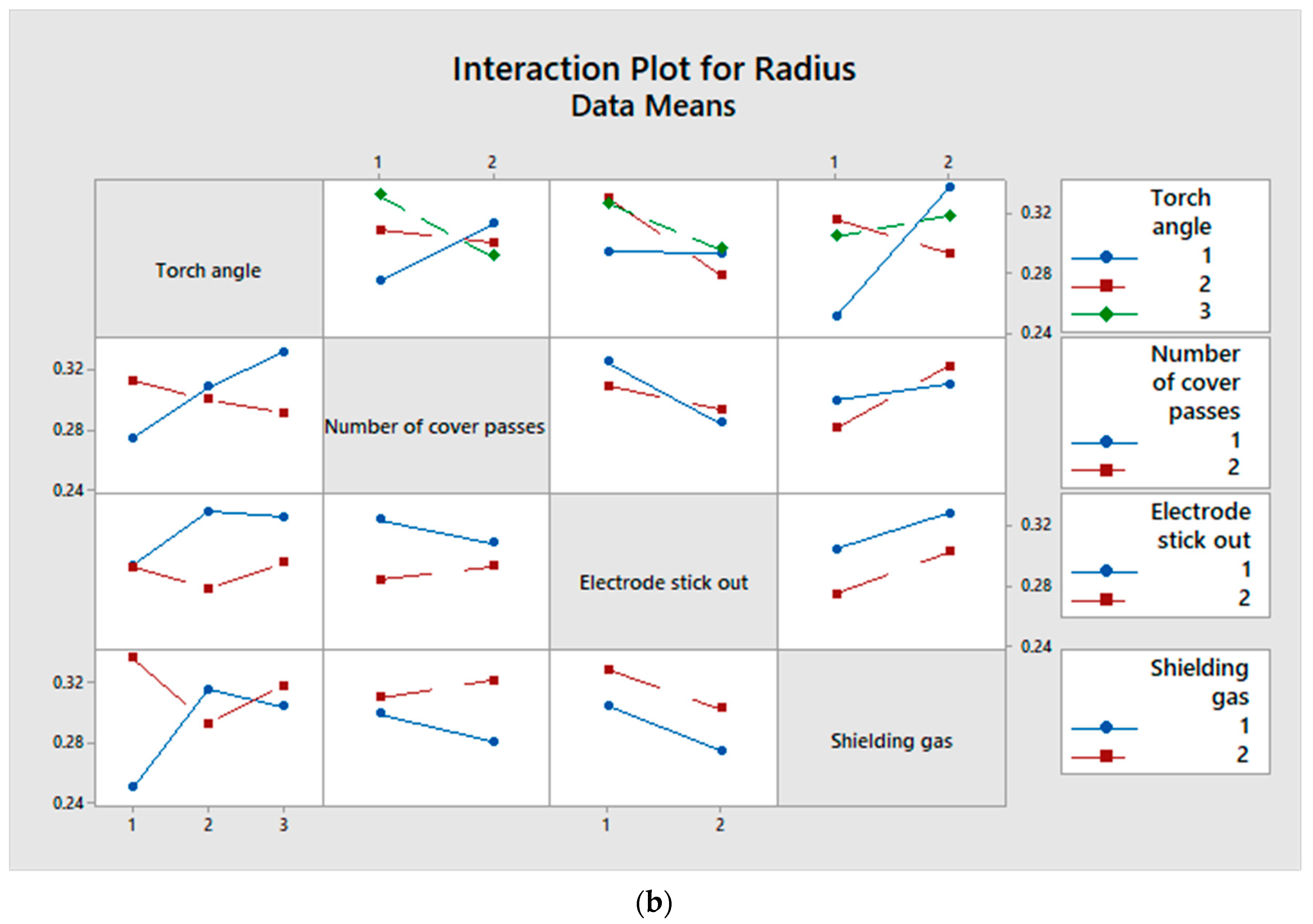
| Main Effects and Interactions | p-Value | |
|---|---|---|
| A | Torch angle | 0.267 |
| B | Number of cover passes | 0.783 |
| C | Electrode stick-out | 0.036 |
| D | Shielding gas | 0.053 |
| AB | Torch angle—Number of cover passes | 0.016 |
| AC | Torch angle—Length of electrode stick-out | 0.366 |
| AD | Torch angle—Shielding gas | 0.027 |
| BC | Number of cover passes—Length of electrode stick-out | 0.342 |
| BD | Number of cover passes—Shielding gas | 0.247 |
| CD | Length of electrode stick-out—Shielding gas | 0.882 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Randić, M.; Pavletić, D.; Turkalj, G. Multiparametric Investigation of Welding Techniques on Toe Radius of High Strength Steel at Low-Temperature Levels Using 3D-Scanning Techniques. Metals 2019, 9, 1355. https://doi.org/10.3390/met9121355
Randić M, Pavletić D, Turkalj G. Multiparametric Investigation of Welding Techniques on Toe Radius of High Strength Steel at Low-Temperature Levels Using 3D-Scanning Techniques. Metals. 2019; 9(12):1355. https://doi.org/10.3390/met9121355
Chicago/Turabian StyleRandić, Miroslav, Duško Pavletić, and Goran Turkalj. 2019. "Multiparametric Investigation of Welding Techniques on Toe Radius of High Strength Steel at Low-Temperature Levels Using 3D-Scanning Techniques" Metals 9, no. 12: 1355. https://doi.org/10.3390/met9121355
APA StyleRandić, M., Pavletić, D., & Turkalj, G. (2019). Multiparametric Investigation of Welding Techniques on Toe Radius of High Strength Steel at Low-Temperature Levels Using 3D-Scanning Techniques. Metals, 9(12), 1355. https://doi.org/10.3390/met9121355






