Construction of Cellular Substructure in Laser Powder Bed Fusion
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
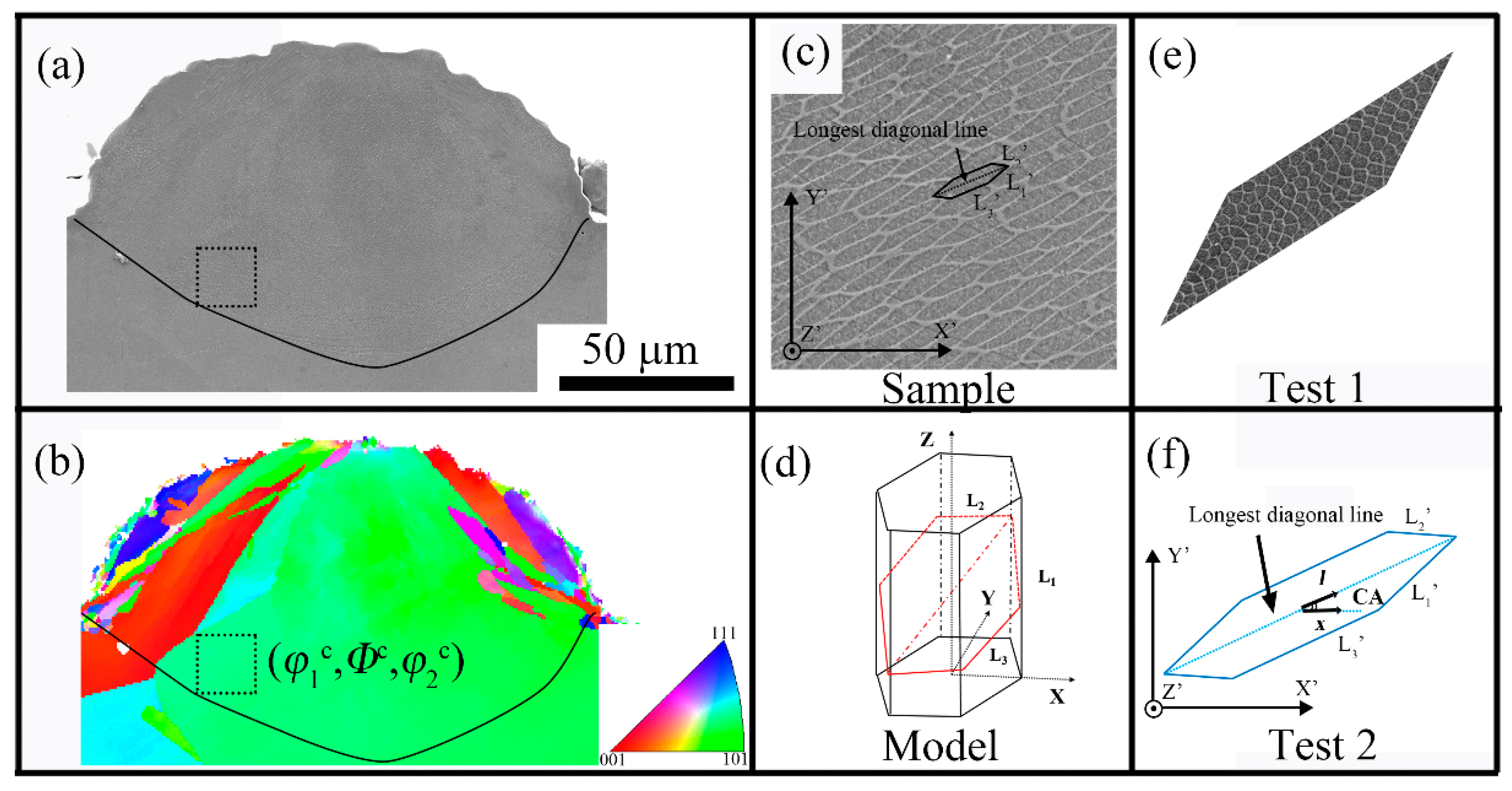
3.1. 3D Morphology of the Substructure
3.2. Model of the Substructure
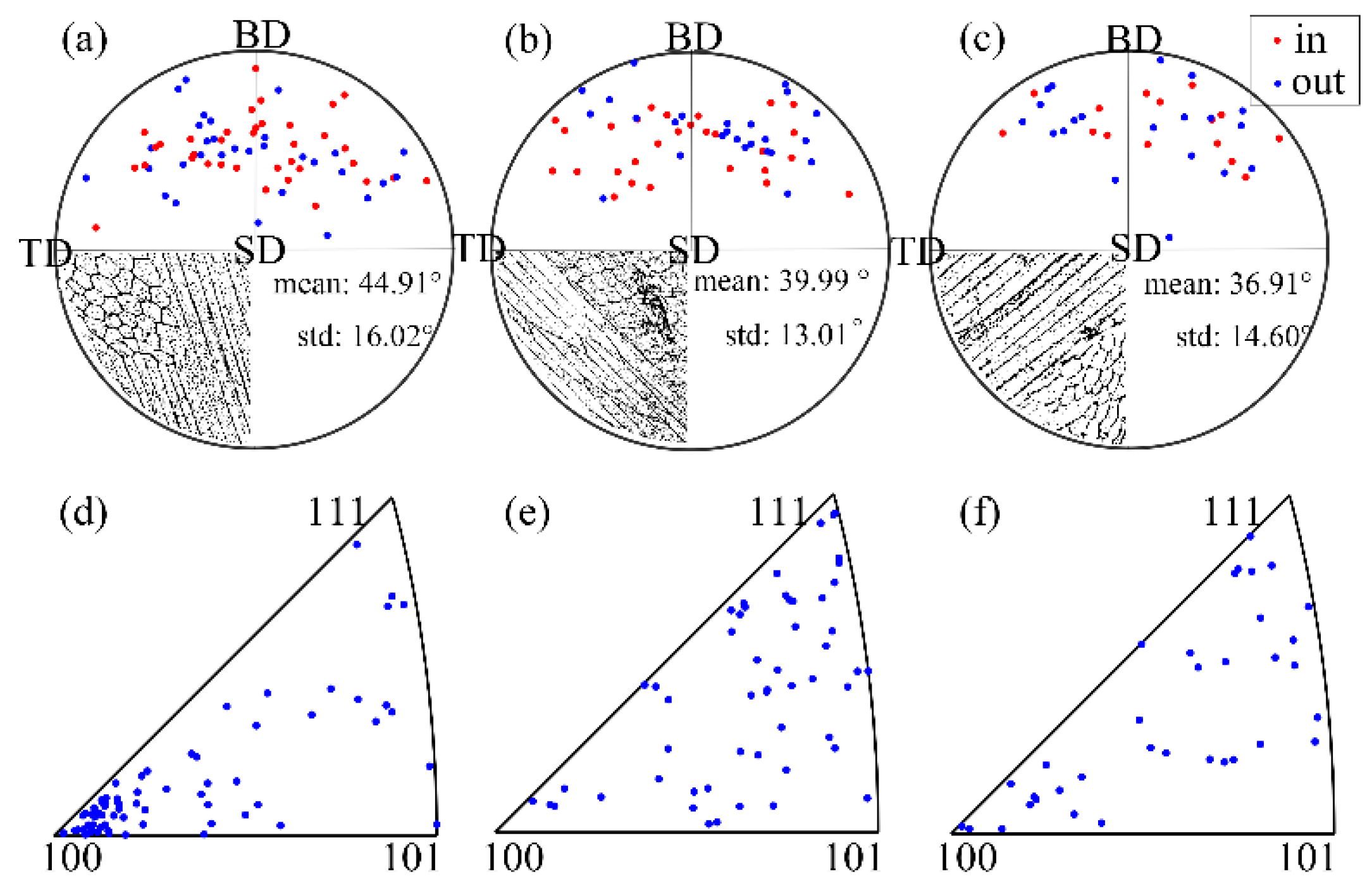
3.3. Application of the Model
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Over, C.; Meiners, W.; Wissenbach, K.; Lindemann, M.; Hammann, G. Selective laser melting: A new approach for the direct manufacturing of metal parts and tools. In Proceedings of the International Conferences on LANE 2001, Erlangen, Germany, 28–31 August 2001; 2001; pp. 391–398. [Google Scholar]
- Wang, Y.M.; Voisin, T.; McKeown, J.T.; Ye, J.; Calta, N.P.; Li, Z.; Zeng, Z.; Zhang, Y.; Chen, W.; Roehling, T.T.; et al. Additively manufactured hierarchical stainless steels with high strength and ductility. Nat. Mater. 2017, 17, 63. [Google Scholar] [CrossRef] [PubMed]
- Prashanth, K.G.; Eckert, J. Formation of metastable cellular microstructures in selective laser melted alloys. J. Alloys Compd. 2017, 707, 27–34. [Google Scholar] [CrossRef]
- Zhong, Y.; Liu, L.; Wikman, S.; Cui, D.; Shen, Z. Intragranular cellular segregation network structure strengthening 316L stainless steel prepared by selective laser melting. J. Nucl. Mater. 2016, 470, 170–178. [Google Scholar] [CrossRef]
- Saeidi, K.; Gao, X.; Zhong, Y.; Shen, Z.J. Hardened austenite steel with columnar sub-grain structure formed by laser melting. Mater. Sci. Eng. A 2015, 625, 221–229. [Google Scholar] [CrossRef]
- Tao, P.; Li, H.; Huang, B.; Hu, Q.; Gong, S.; Xu, Q. The crystal growth, intercellular spacing and microsegregation of selective laser melted Inconel 718 superalloy. Vacuum 2019, 159, 382–390. [Google Scholar] [CrossRef]
- Chen, Z.W.; Phan, M.A.L.; Darvish, K. Grain growth during selective laser melting of a Co–Cr–Mo alloy. J. Mater. Sci. 2017, 52, 7415–7427. [Google Scholar] [CrossRef]
- Arısoy, Y.M.; Criales, L.E.; Özel, T.; Lane, B.; Moylan, S.; Donmez, A. Influence of scan strategy and process parameters on microstructure and its optimization in additively manufactured nickel alloy 625 via laser powder bed fusion. Int. J. Adv. Manuf. Technol. 2017, 90, 1393–1417. [Google Scholar] [CrossRef]
- Rutter, J.W.; Chalmers, B. A prismatic substructure formed during solidification of metals. Can. J. Phys. 1953, 31, 15–39. [Google Scholar] [CrossRef]
- Wang, X.; Muñiz-Lerma, J.A.; Sánchez-Mata, O.; Attarian Shandiz, M.; Brochu, M. Microstructure and mechanical properties of stainless steel 316L vertical struts manufactured by laser powder bed fusion process. Mater. Sci. Eng. A 2018, 736, 27–40. [Google Scholar] [CrossRef]
- Sun, S.-H.; Hagihara, K.; Nakano, T. Effect of scanning strategy on texture formation in Ni-25at %Mo alloys fabricated by selective laser melting. Mater. Des. 2018, 140, 307–316. [Google Scholar] [CrossRef]
- Bunge, H.-J. Texture Analysis in Materials Science: Mathematical Methods; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Kurz, W.; Fisher, D.J. Fundamentals of Solidification; Trans Tech Publications: Aedermannsdorf, Switzerland, 1986; Volume 1. [Google Scholar]
- Boettinger, W.J.; Shechtman, D.; Schaefer, R.J.; Biancaniello, F.S. The effect of rapid solidification velocity on the microstructure of Ag-Cu alloys. Metall. Trans. A 1984, 15, 55–66. [Google Scholar] [CrossRef]
- Gremaud, M.; Carrard, M.; Kurz, W. The microstructure of rapidly solidified Al-Fe alloys subjected to laser surface treatment. Acta Metall. Mater. 1990, 38, 2587–2599. [Google Scholar] [CrossRef]
- Gill, S.C.; Kurz, W. Rapidly solidified Al-Cu alloys—I. experimental determination of the microstructure selection map. Acta Metall. Mater. 1993, 41, 3563–3573. [Google Scholar] [CrossRef]
- Yadroitsev, I.; Krakhmalev, P.; Yadroitsava, I.; Johansson, S.; Smurov, I. Energy input effect on morphology and microstructure of selective laser melting single track from metallic powder. J. Mater. Process. Technol. 2013, 213, 606–613. [Google Scholar] [CrossRef]
- Yadroitsev, I.; Smurov, I. Selective laser melting technology: From the single laser melted track stability to 3D parts of complex shape. Phys. Procedia 2010, 5, 551–560. [Google Scholar] [CrossRef]
- Yadroitsev, I.; Gusarov, A.; Yadroitsava, I.; Smurov, I. Single track formation in selective laser melting of metal powders. J. Mater. Process. Technol. 2010, 210, 1624–1631. [Google Scholar] [CrossRef]
- Krakhmalev, P.; Fredriksson, G.; Svensson, K.; Yadroitsev, I.; Yadroitsava, I.; Thuvander, M.; Peng, R. Microstructure, solidification texture, and thermal stability of 316 L stainless steel manufactured by laser powder bed fusion. Metals 2018, 8, 643. [Google Scholar] [CrossRef]
- Hunt, J.D.; McCartney, D.G. Numerical finite difference model for steady state cellular array growth. Acta Metall. 1987, 35, 89–99. [Google Scholar] [CrossRef]
- Liu, J.; To, A.C. Quantitative texture prediction of epitaxial columnar grains in additive manufacturing using selective laser melting. Addit. Manuf. 2017, 16, 58–64. [Google Scholar] [CrossRef]
- Kurz, W.; Giovanola, B.; Trivedi, R. Theory of microstructural development during rapid solidification. Acta Metall. 1986, 34, 823–830. [Google Scholar] [CrossRef]
- Esaka, H.; Daimon, H.; Natsume, Y.; Ohsasa, K.; Tamura, M. Growth direction of cellular and dendritic interface in a constrained growth condition. Mater. Trans. 2002, 43, 1312–1317. [Google Scholar] [CrossRef][Green Version]
- Trivedi, R.; Seetharaman, V.; Eshelman, M.A. The effects of interface kinetics anisotropy on the growth direction of cellular microstructures. Metall. Trans. A 1991, 22, 585–593. [Google Scholar] [CrossRef]
- Trivedi, R.; Sekhar, J.A.; Seetharaman, V. Solidification microstructures near the limit of absolute stability. Metall. Trans. A 1989, 20, 769–777. [Google Scholar] [CrossRef]
- Khorasani, A.M.; Gibson, I.; Ghasemi, A.; Ghaderi, A. A comprehensive study on variability of relative density in selective laser melting of Ti-6Al-4V. Virtual Phys. Prototyp. 2019, 14, 1–11. [Google Scholar] [CrossRef]
- Sing, S.L.; Wiria, F.E.; Yeong, W.Y. Selective laser melting of titanium alloy with 50wt% tantalum: Effect of laser process parameters on part quality. Int. J. Refract. Met. Hard Mater. 2018, 77, 120–127. [Google Scholar] [CrossRef]

| Element | Fe | Cr | Ni | Mo | Mn | Si | N | O | P | C | S |
| wt pct | balance | 16 to 18 | 10 to 14 | 2 to 3 | 2 | 1 | 0.1 | 0.1 | 0.045 | 0.03 | 0.03 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhang, C.; Yu, C.; Xing, L.; Li, K.; Chen, J.; Ma, J.; Liu, W.; Shen, Z. Construction of Cellular Substructure in Laser Powder Bed Fusion. Metals 2019, 9, 1231. https://doi.org/10.3390/met9111231
Wang Y, Zhang C, Yu C, Xing L, Li K, Chen J, Ma J, Liu W, Shen Z. Construction of Cellular Substructure in Laser Powder Bed Fusion. Metals. 2019; 9(11):1231. https://doi.org/10.3390/met9111231
Chicago/Turabian StyleWang, Yafei, Chenglu Zhang, Chenfan Yu, Leilei Xing, Kailun Li, Jinhan Chen, Jing Ma, Wei Liu, and Zhijian Shen. 2019. "Construction of Cellular Substructure in Laser Powder Bed Fusion" Metals 9, no. 11: 1231. https://doi.org/10.3390/met9111231
APA StyleWang, Y., Zhang, C., Yu, C., Xing, L., Li, K., Chen, J., Ma, J., Liu, W., & Shen, Z. (2019). Construction of Cellular Substructure in Laser Powder Bed Fusion. Metals, 9(11), 1231. https://doi.org/10.3390/met9111231




