Influence of Vibrational Loading on Deformation Behavior of Metallic Glass: A Molecular Dynamics Study
Abstract
1. Introduction
2. Methods
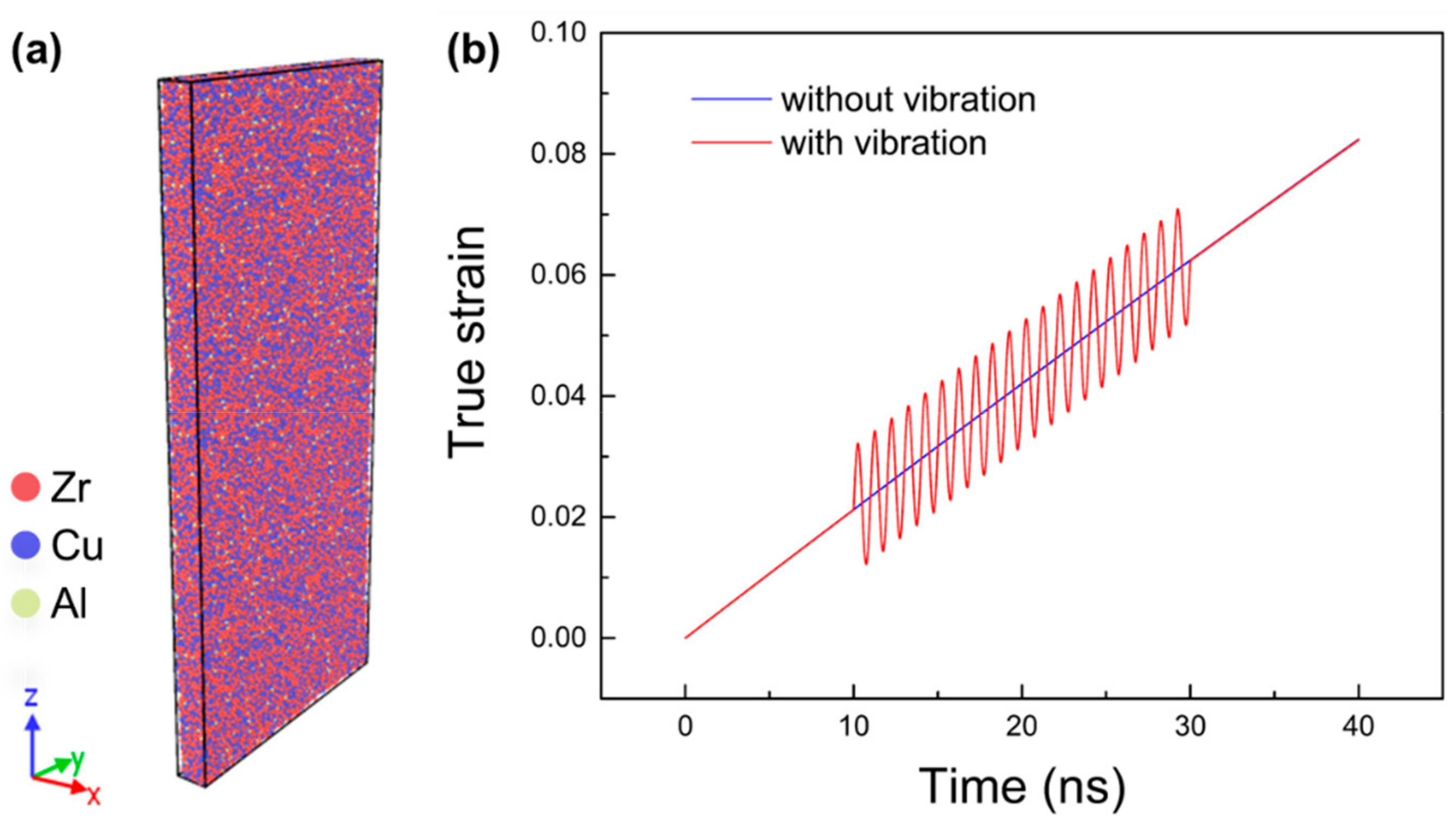
2.1. Model Establishment
2.2. Vibration-Assisted Tension
3. Results and Discussion
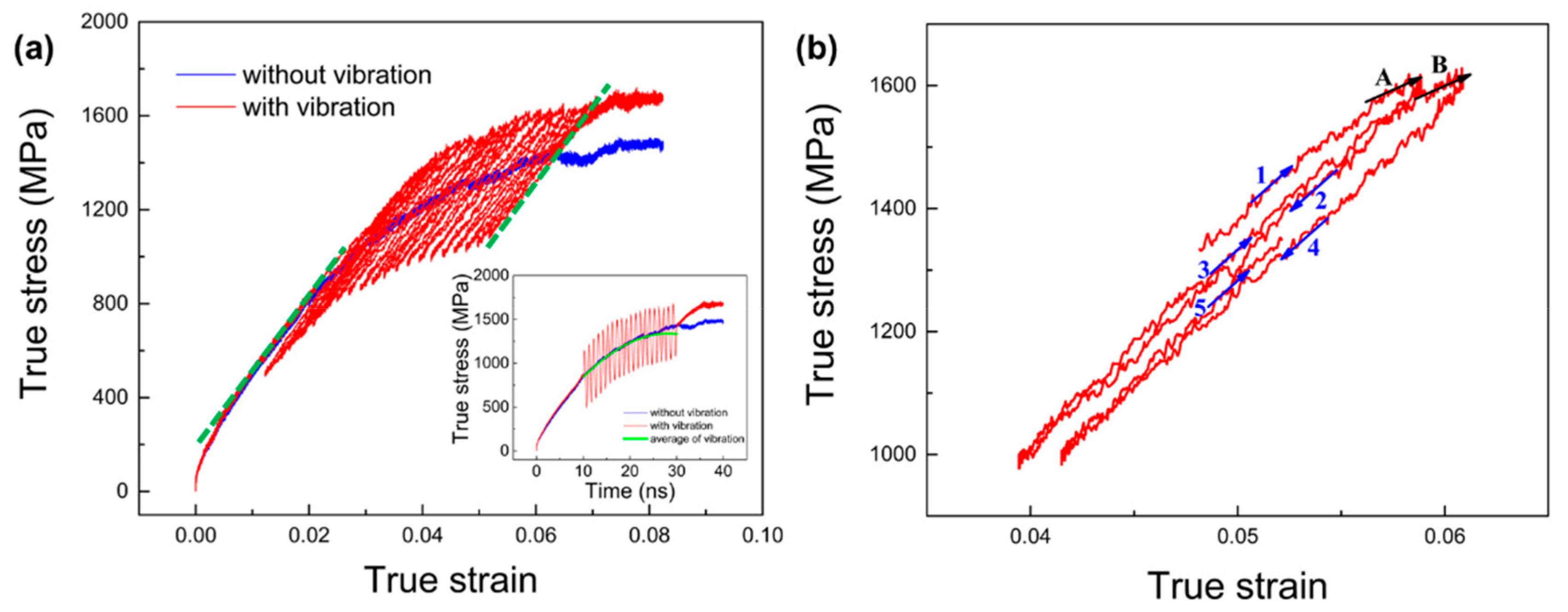
3.1. Mechanical Response
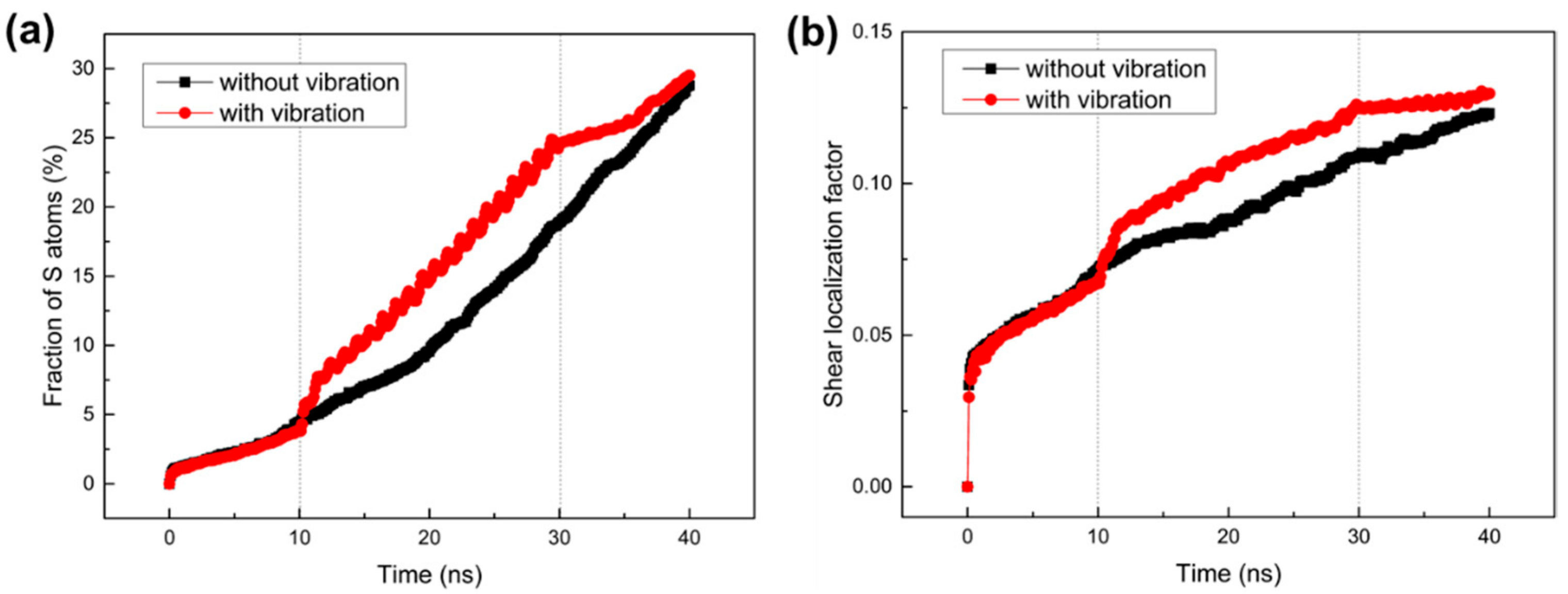
3.2. Strain Distribution
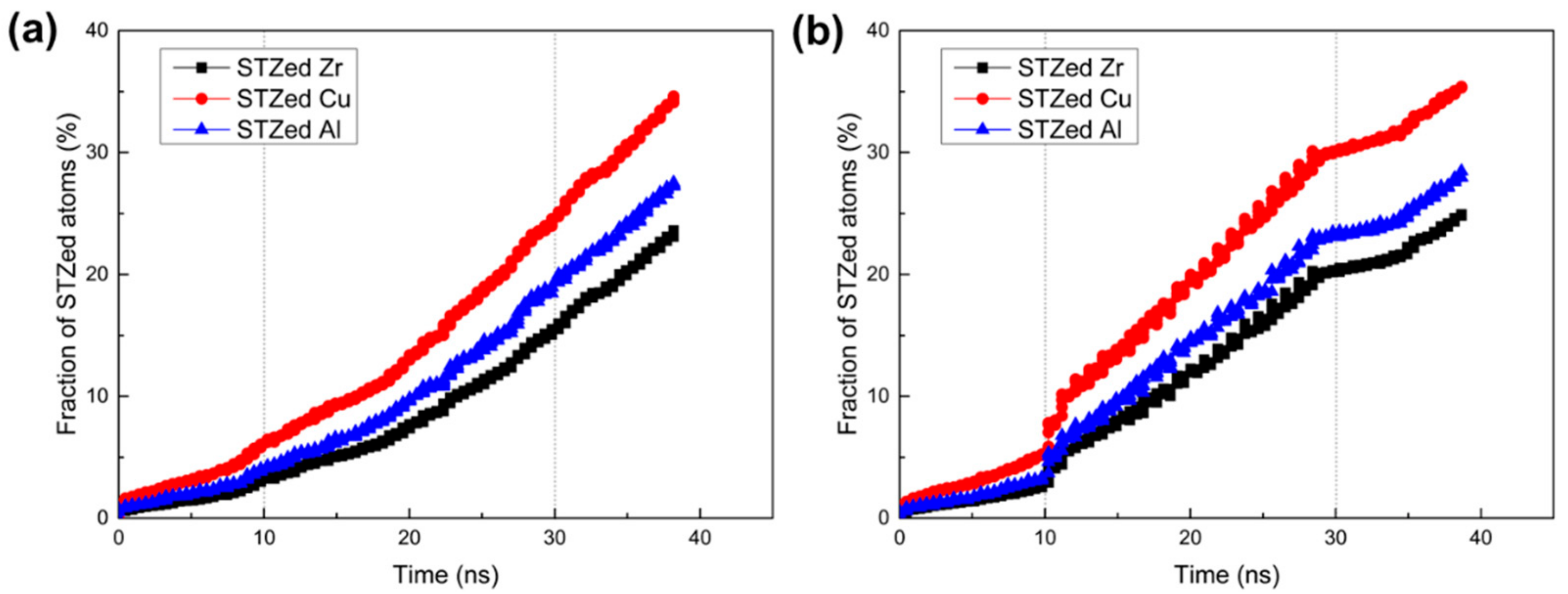
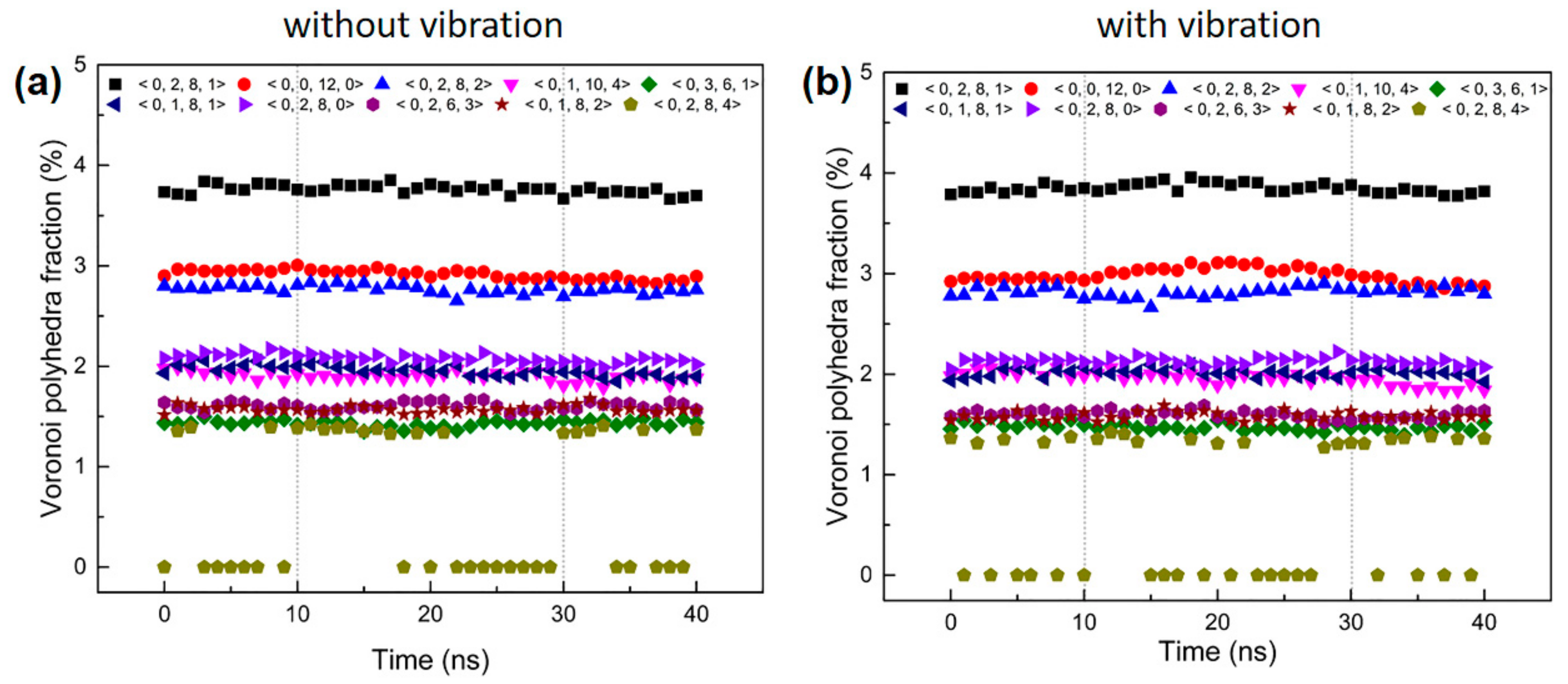
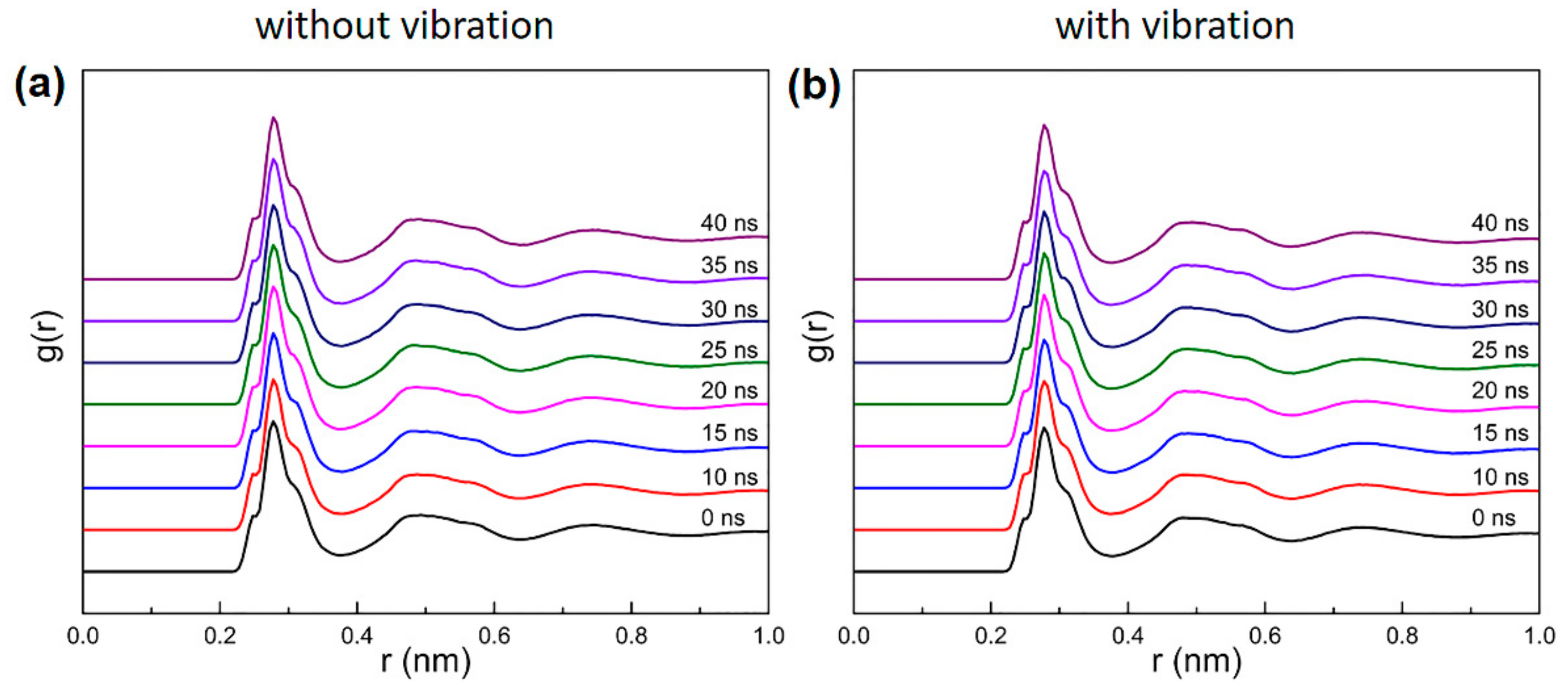
3.3. Local Microstructural Evolution
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Miller, M.; Liaw, P. Bulk Metallic Glasses: An Overview; Springer: New York, NY, USA, 2008. [Google Scholar]
- Suryanarayana, C.; Inoue, A. Bulk Metallic Glasses; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Wang, W.H.; Dong, C.; Shek, C.H. Bulk metallic glasses. Mater. Sci. Eng. R Rep. 2004, 44, 45–89. [Google Scholar] [CrossRef]
- Schroers, J. The superplastic forming of bulk metallic glasses. JOM 2005, 57, 35–39. [Google Scholar] [CrossRef]
- Zhang, M.; Yao, D.; Wang, X.; Deng, L. Air oxidation of a Zr55Cu30Al10Ni5 bulk metallic glass at its super cooled liquid state. Corros. Sci. 2014, 82, 410–419. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, M.; Deng, L. Oxidation behavior of Zr55Cu30Al10Ni5 BMG under static loading. J. Non Cryst Solids 2017, 469, 7–13. [Google Scholar] [CrossRef]
- Zhang, M.; Yao, D.; Cao, Z.; Li, P.; Zhou, P.; Wang, X. Influence of oxidation on the performance of Zr55Cu30Al10Ni5 BMG. Intermetallics 2016, 79, 20–27. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, J.; Deng, L.; Li, Q.; Jin, J.; Wang, X. Microstructure evolution of bulk metallic glass during thermal oxidation under plastic strain. Corros. Sci. 2019, 147, 192–200. [Google Scholar] [CrossRef]
- Deng, L.; Li, P.; Wang, X.; Zhang, M.; Li, J. Influence of low-frequency vibrations on the compression behavior and microstructure of T2 copper. Mater. Sci. Eng. A 2018, 710, 129–135. [Google Scholar] [CrossRef]
- Li, N.; Liu, Z.; Wang, X.; Zhang, M. Vibration-accelerated activation of flow units in a Pd-based bulk metallic glass. Mater. Sci. Eng. A 2017, 692, 62–66. [Google Scholar] [CrossRef]
- Bai, Y.; Yang, M. The influence of superimposed ultrasonic vibration on surface asperities deformation. J. Mater. Process. Technol. 2016, 229, 367–374. [Google Scholar] [CrossRef]
- Han, G.; Li, K.; Peng, Z.; Jin, J.; Sun, M.; Wang, X. A new porous block sonotrode for ultrasonic assisted micro plastic forming. Int. J. Adv. Manuf. Technol. 2017, 89, 2193–2202. [Google Scholar] [CrossRef]
- Zhang, M.; Li, P.; Yao, D.; Deng, L.; Jin, J.S.; Wang, X.Y. Investigation on upsetting assisted by low-frequency vibration. In Proceedings of the International Conference on New Forming Technology, Scotland, UK, 6–8 August 2015; EDP Sciences: Les Ulis, France, 2015. [Google Scholar]
- Li, N.; Xu, X.; Zheng, Z.; Liu, L. Enhanced formability of a Zr-based bulk metallic glass in a supercooled liquid state by vibrational loading. Acta Mater. 2014, 65, 400–411. [Google Scholar] [CrossRef]
- Ma, J.; Liang, X.; Wu, X.; Liu, Z.; Gong, F. Sub-second thermoplastic forming of bulk metallic glasses by ultrasonic beating. Sci. Rep. 2015, 5, 17844. [Google Scholar] [CrossRef] [PubMed]
- Hirel, P. Atomsk: A tool for manipulating and converting atomic data files. Comput. Phys. Commun. 2015, 197, 212–219. [Google Scholar] [CrossRef]
- Cheng, Y.Q.; Ma, E.; Sheng, H.W. Atomic level structure in multicomponent bulk metallic glass. Phys. Rev. Lett. 2009, 102, 245501. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Alexander, S. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Modell. Simul. Mater. Sci. Eng. 2010, 18, 15012. [Google Scholar]
- Khan, A.; Giraud-Audine, C.; Bigot, R.; Abba, G.; Abideen, M.Z. An alternative explanation of forming force reduction for forming process submitted to vibration: Influence of the waveform in the viscoplastic domain. J. Mater. Process. Technol. 2016, 230, 288–299. [Google Scholar] [CrossRef]
- Yao, Z.; Kim, G.; Faidley, L.; Zou, Q.; Mei, D.; Chen, Z. Acoustic softening and hardening of aluminum in high-frequency vibration-assisted micro/meso forming. Mater. Manuf. Process. 2013, 28, 584–588. [Google Scholar] [CrossRef]
- Sha, Z.D.; Qu, S.X.; Liu, Z.S.; Wang, T.J.; Gao, H. Cyclic deformation in metallic glasses. Nano Lett. 2015, 15, 7010–7015. [Google Scholar] [CrossRef]
- Zhang, M.; Li, Q.; Zhang, J.; Zheng, G.; Wang, X. The prominent combination of ultrahigh strength and superior tensile plasticity in Cu–Zr nanoglass connected by oxide interfaces: A molecular dynamics study. J. Alloys Compd. 2019, 801, 318–326. [Google Scholar] [CrossRef]
- Yang, M.H.; Li, J.H.; Liu, B.X. Comparatively studying the local atomic structures of metallic glasses upon cyclic-loading by computer simulations. RSC Adv. 2017, 7, 18358–18365. [Google Scholar] [CrossRef]
- Adibi, S.; Sha, Z.; Branicio, P.S.; Joshi, S.P.; Liu, Z.; Zhang, Y. A transition from localized shear banding to homogeneous superplastic flow in nanoglass. Appl. Phys. Lett. 2013, 103, 211905. [Google Scholar] [CrossRef]
- Mattern, N.; Schoeps, A.; Kuehn, U.; Acker, J.; Khvostikova, O.; Eckert, J. Structural behavior of CuxZr100−x metallic glass (x = 35−70). J. Non Cryst. Solids 2008, 354, 1054–1060. [Google Scholar] [CrossRef]
- Packard, C.E.; Homer, E.R.; Al-Aqeeli, N.; Schuh, C.A. Cyclic hardening of metallic glasses under Hertzian contacts: Experiments and STZ dynamics simulations. Philos. Mag. 2010, 90, 1373–1390. [Google Scholar] [CrossRef]
- Packard, C.E.; Witmer, L.M.; Schuh, C.A. Hardening of a metallic glass during cyclic loading in the elastic range. Appl. Phys. Lett. 2008, 92, 171911. [Google Scholar] [CrossRef]
- Zhou, Z.; Peng, H.; Yu, H. Structural origin for vibration-induced accelerated aging and rejuvenation in metallic glasses. J. Chem. Phys. 2019, 150, 204507. [Google Scholar] [CrossRef]
- Qiao, J.C.; Pelletier, J.M. Dynamic mechanical relaxation in bulk metallic glasses: A review. J. Mater. Sci. Technol. 2014, 30, 523–545. [Google Scholar] [CrossRef]
- Wang, W.H. The elastic properties, elastic models and elastic perspectives of metallic. Prog. Mater. Sci. 2012, 57, 487–656. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Li, Q.; Zhang, J.; Wang, X.; Jin, J.; Gong, P.; Deng, L. Influence of Vibrational Loading on Deformation Behavior of Metallic Glass: A Molecular Dynamics Study. Metals 2019, 9, 1197. https://doi.org/10.3390/met9111197
Zhang M, Li Q, Zhang J, Wang X, Jin J, Gong P, Deng L. Influence of Vibrational Loading on Deformation Behavior of Metallic Glass: A Molecular Dynamics Study. Metals. 2019; 9(11):1197. https://doi.org/10.3390/met9111197
Chicago/Turabian StyleZhang, Mao, Qiaomin Li, Jiacheng Zhang, Xinyun Wang, Junsong Jin, Pan Gong, and Lei Deng. 2019. "Influence of Vibrational Loading on Deformation Behavior of Metallic Glass: A Molecular Dynamics Study" Metals 9, no. 11: 1197. https://doi.org/10.3390/met9111197
APA StyleZhang, M., Li, Q., Zhang, J., Wang, X., Jin, J., Gong, P., & Deng, L. (2019). Influence of Vibrational Loading on Deformation Behavior of Metallic Glass: A Molecular Dynamics Study. Metals, 9(11), 1197. https://doi.org/10.3390/met9111197






