Determination of Directional Residual Stresses by the Contour Method
Abstract
:1. Introduction
2. Materials and Methods
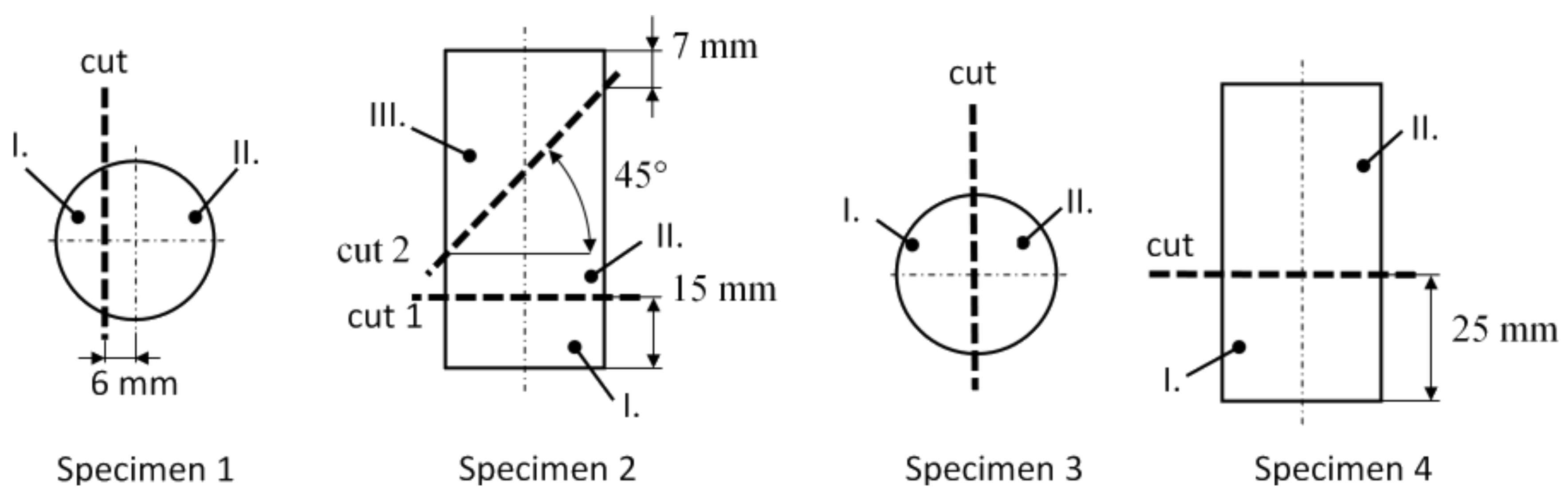
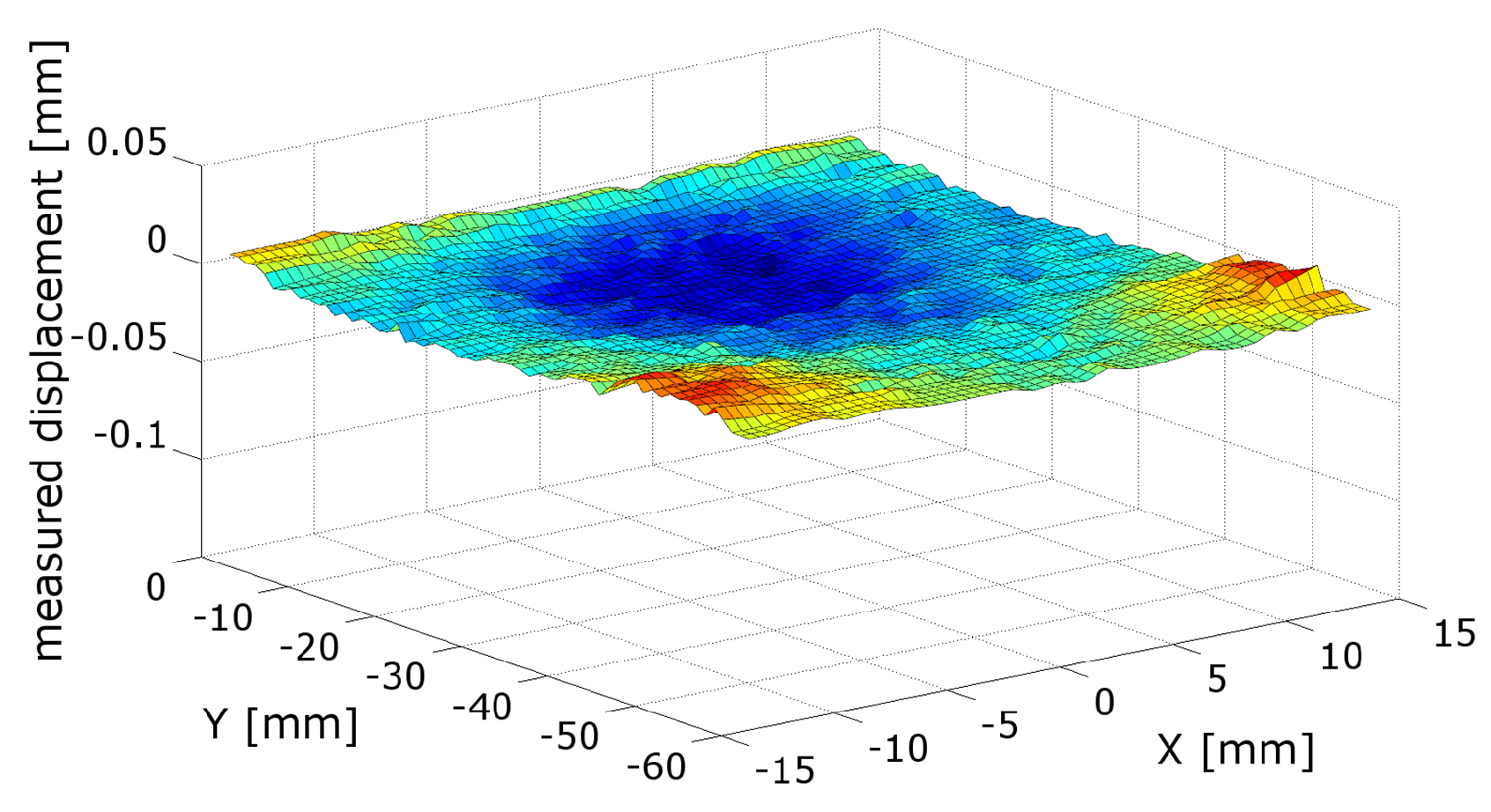
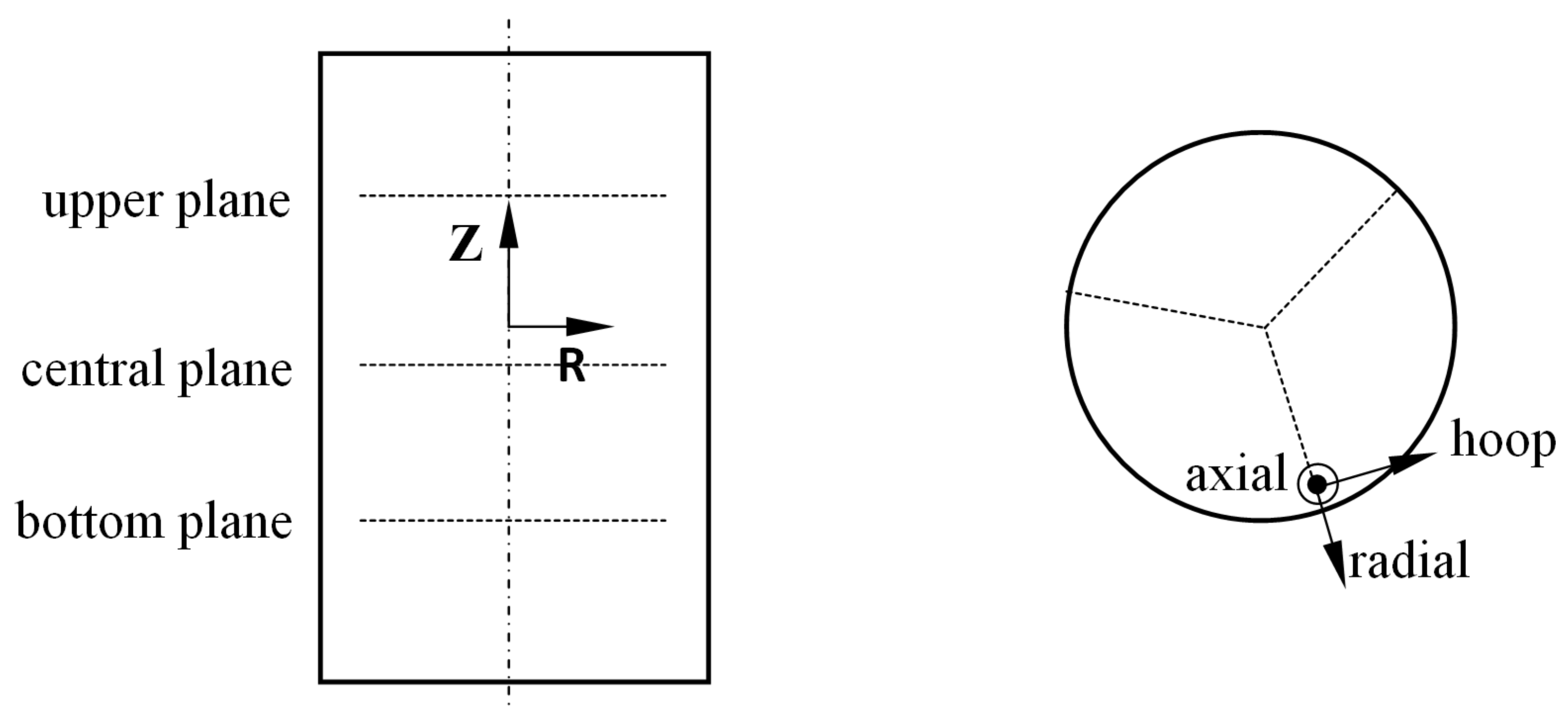
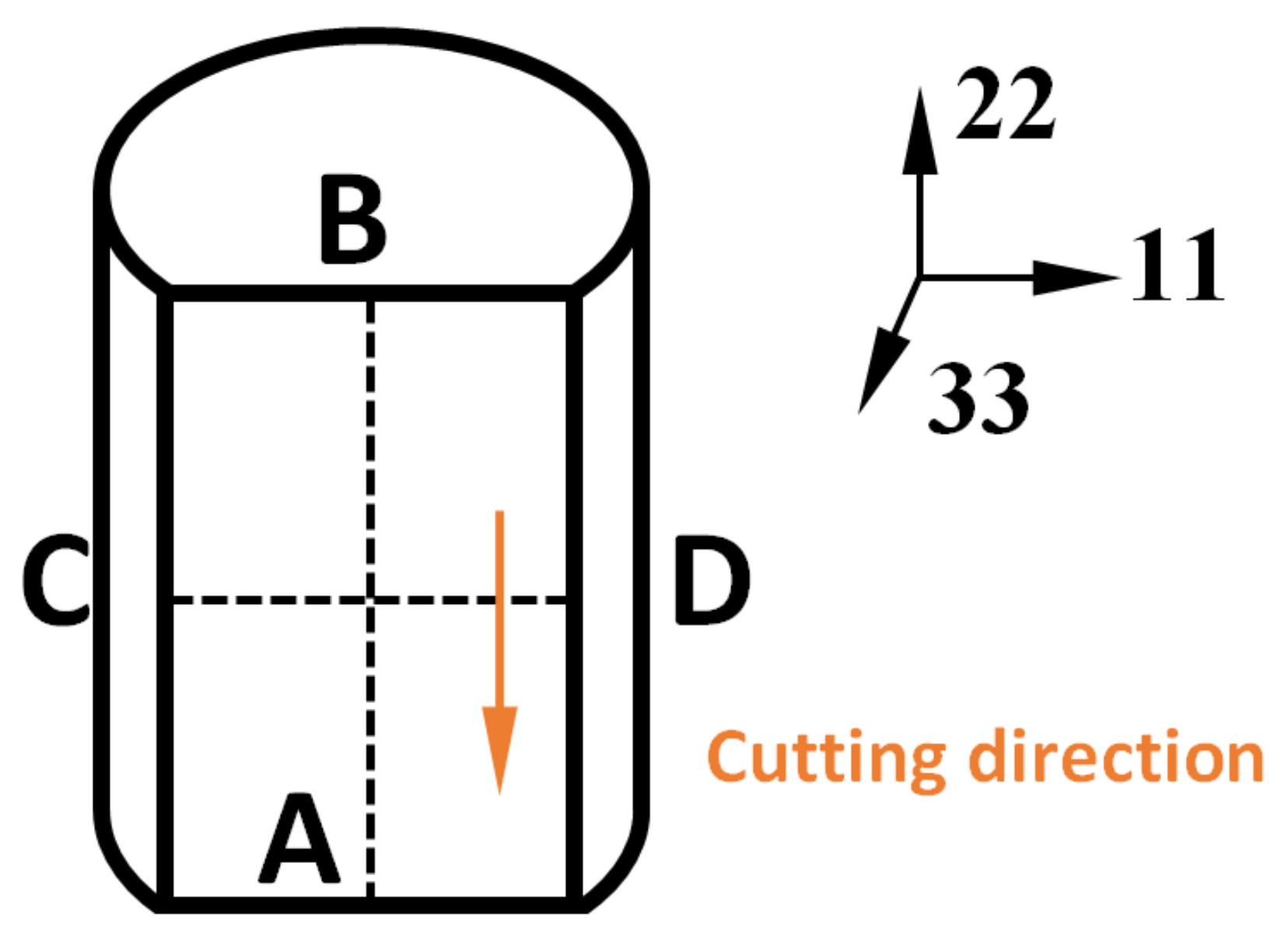
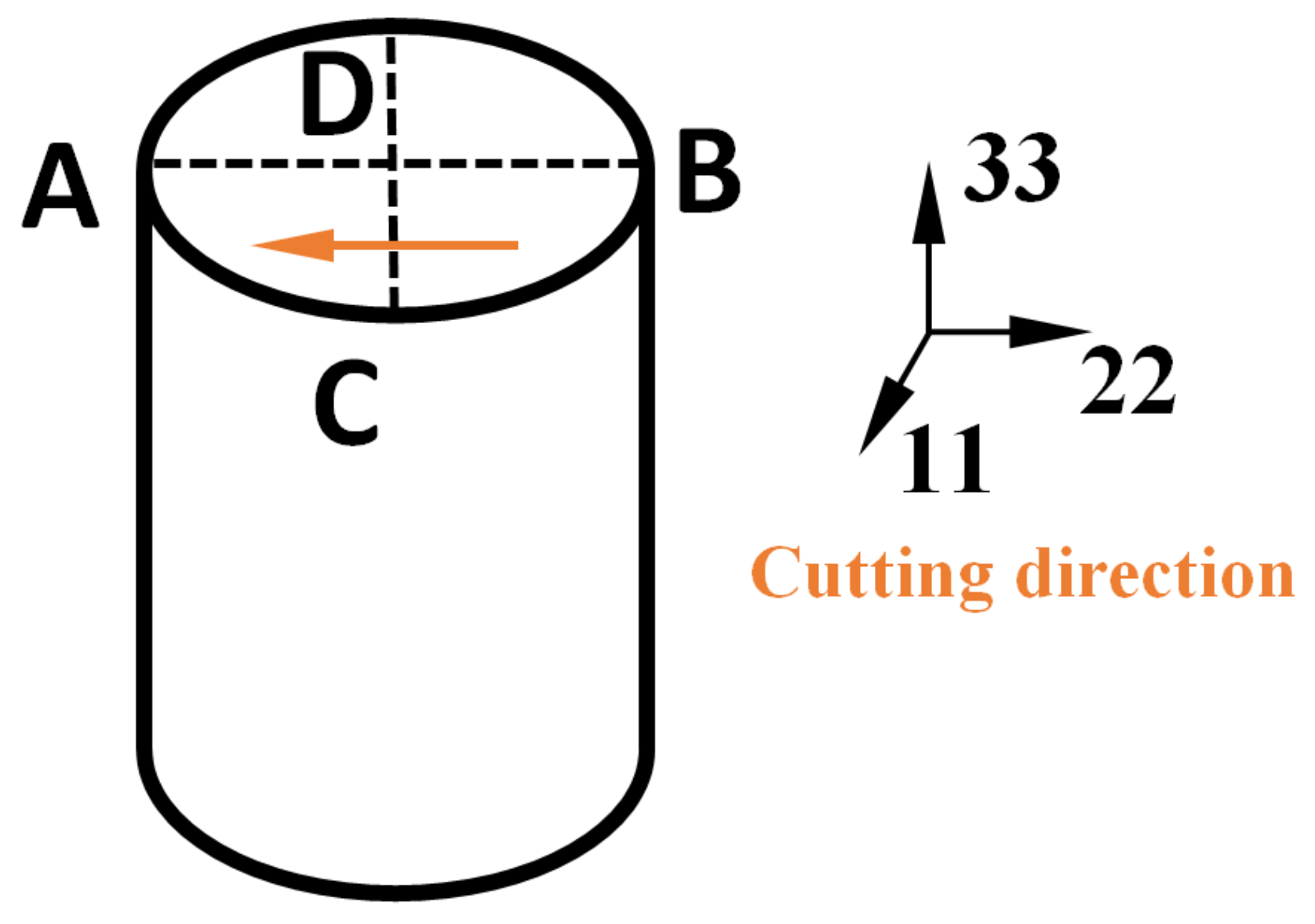
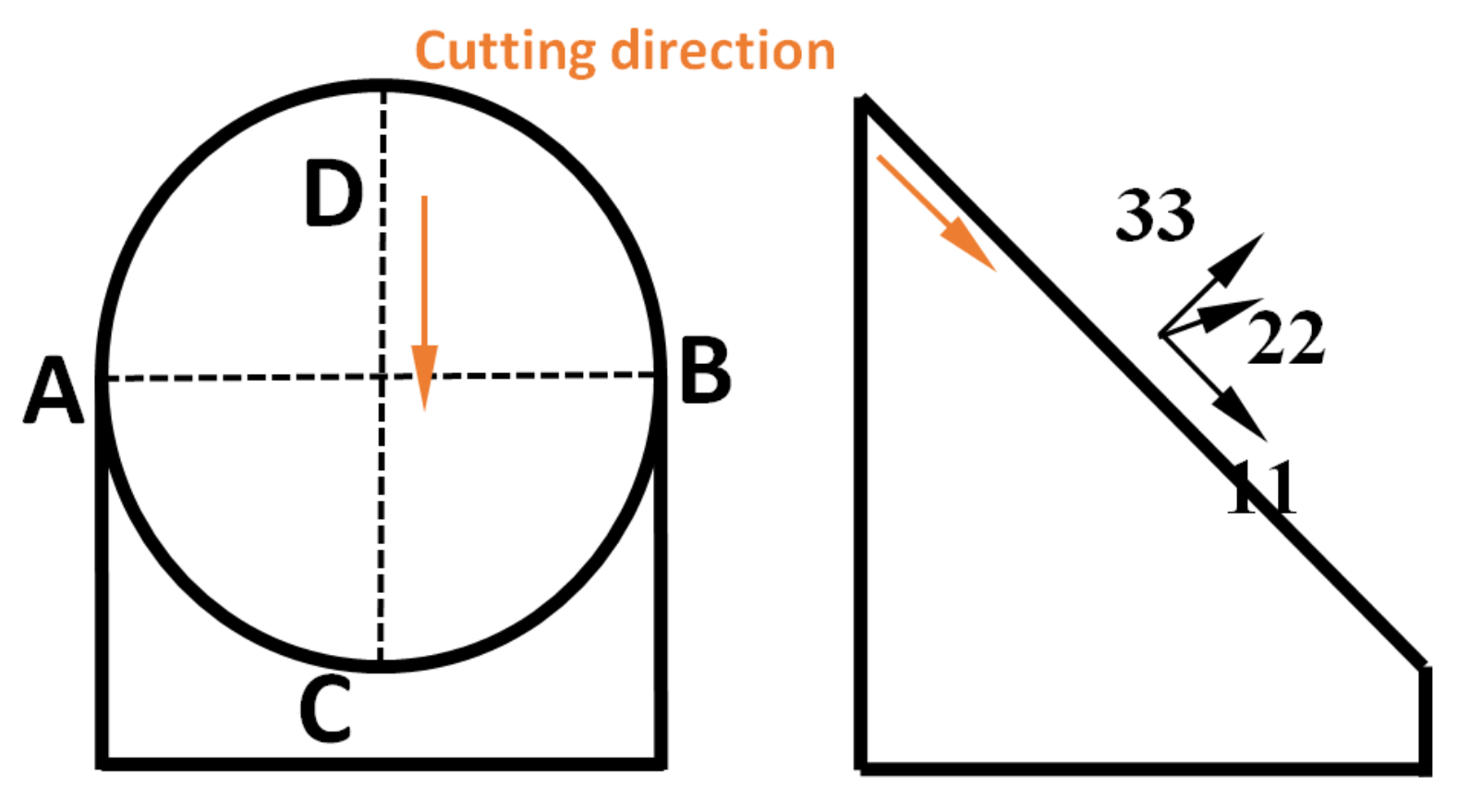
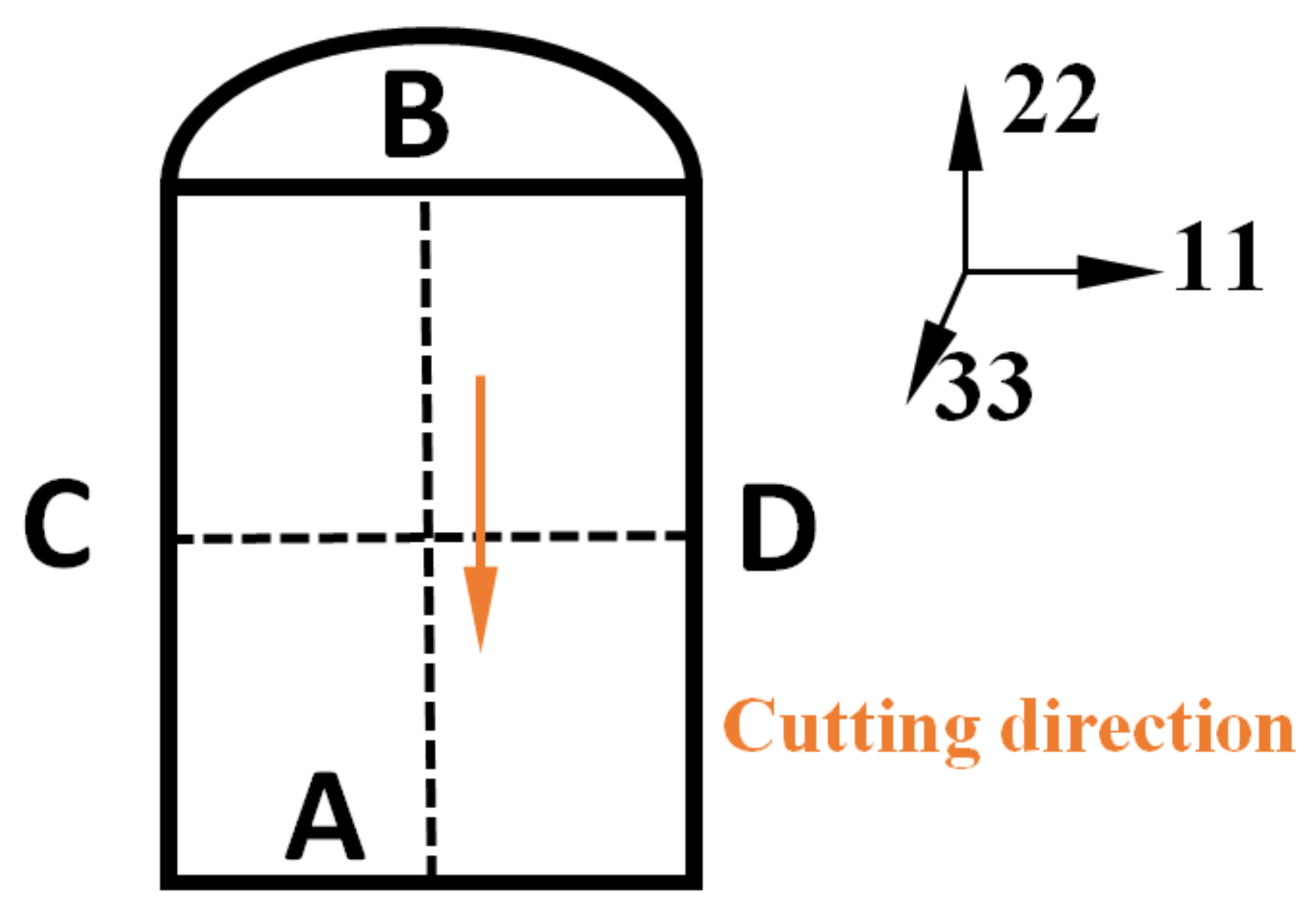
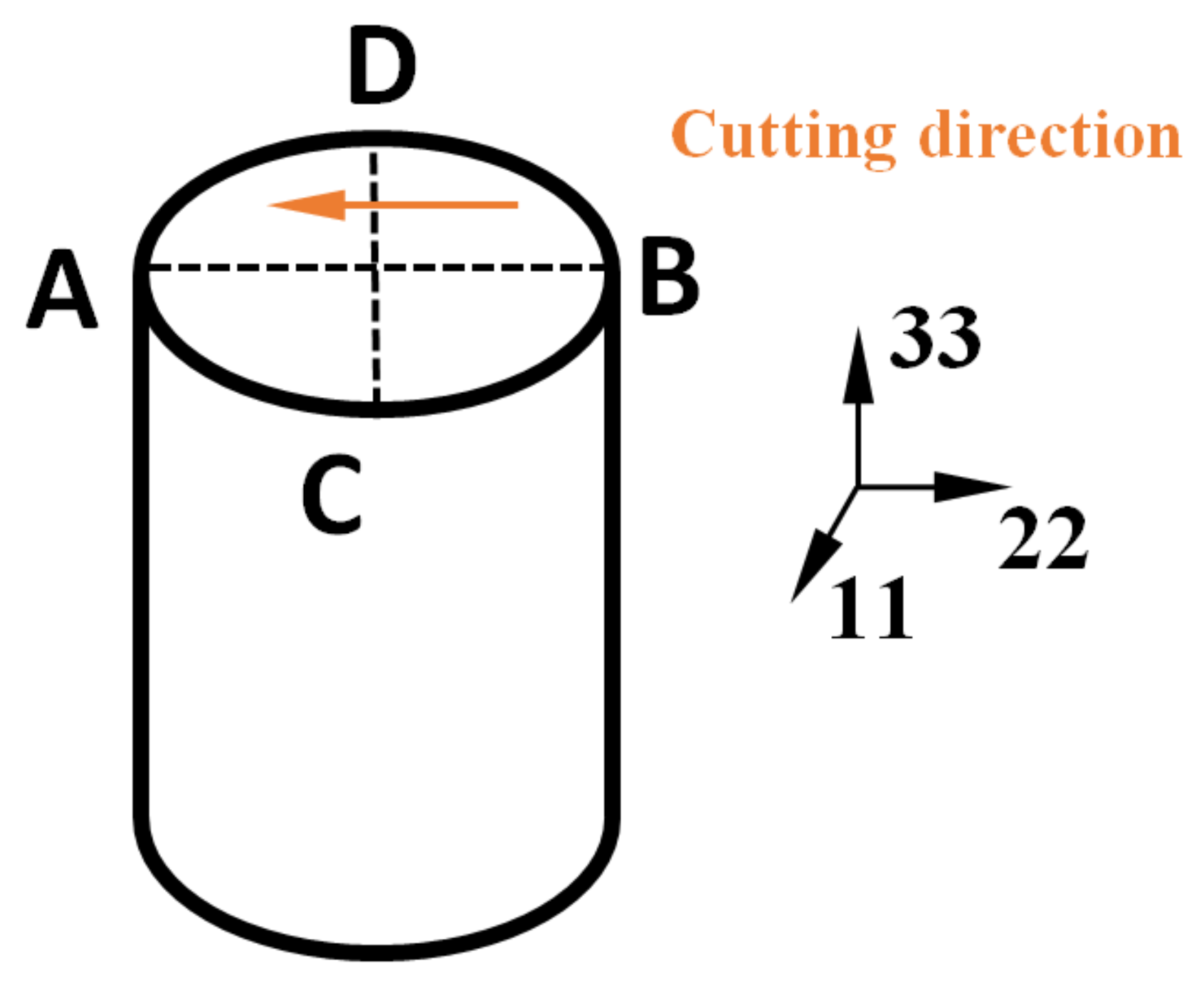
2.1. Specimen Preparation and Contour Method
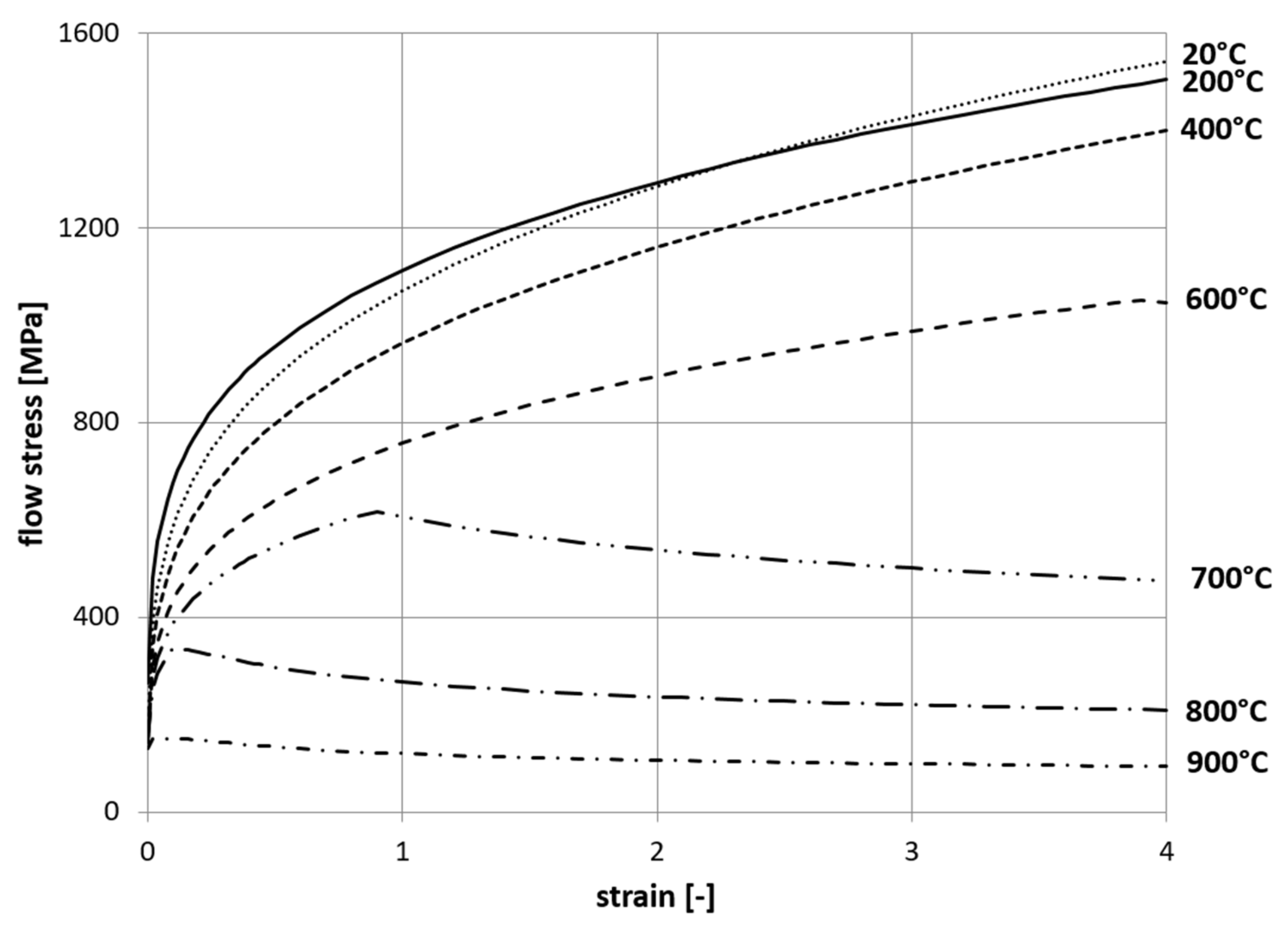
2.2. Determination of Thermo-Physical Properties
2.3. Finite-Element Model for the Contour Method
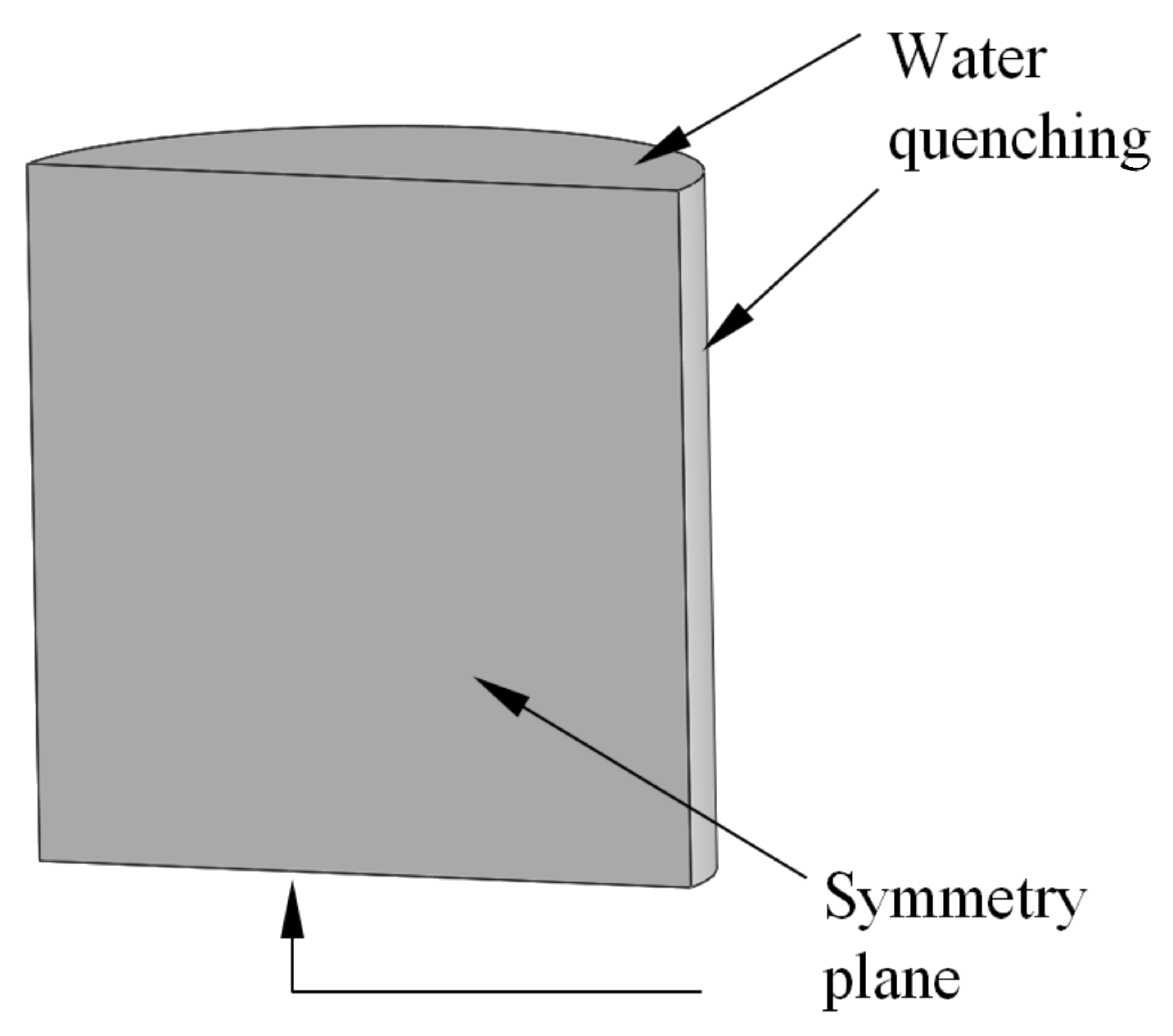
2.4. Finite-Element Model of Heat Treatment
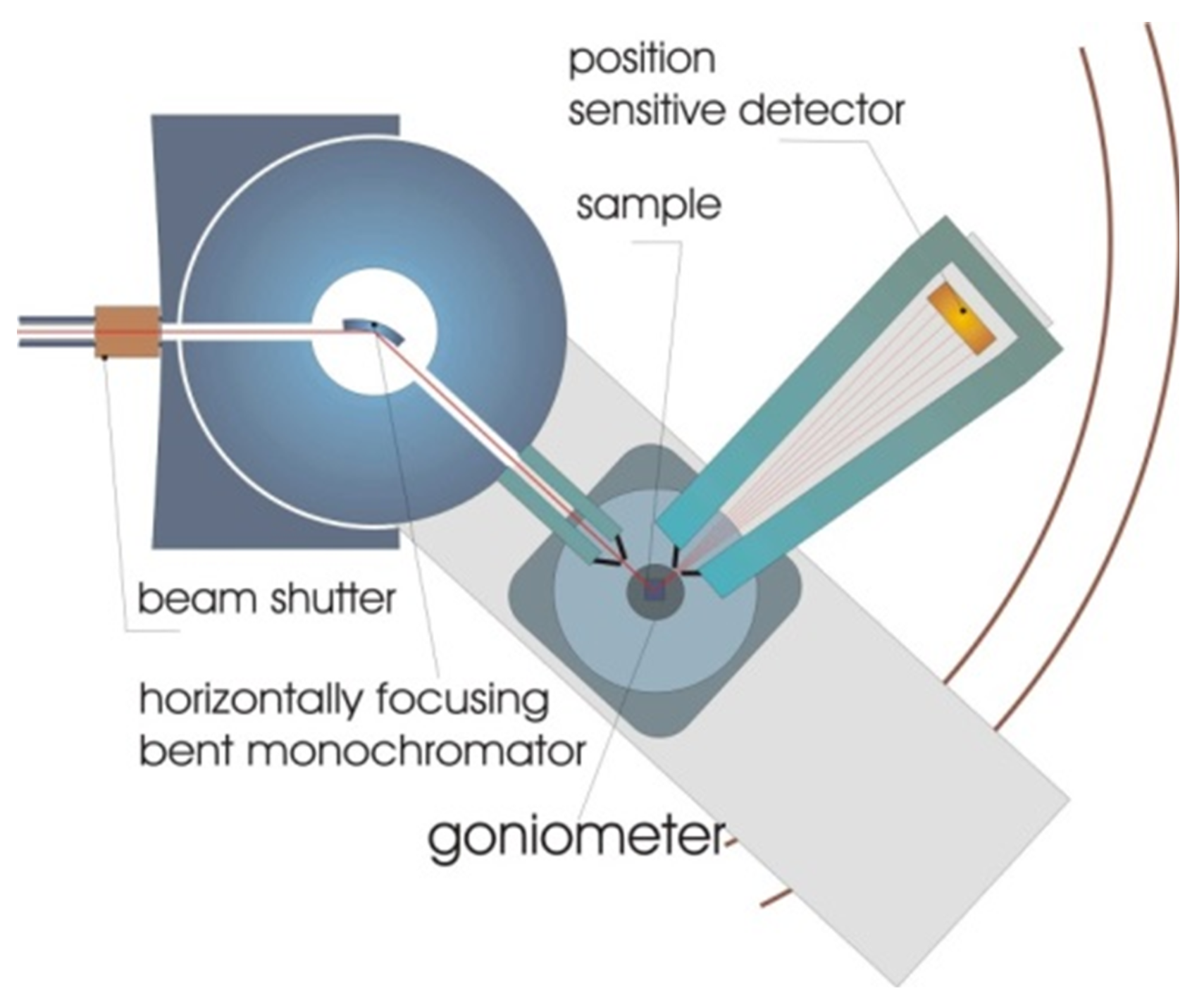
2.5. Neutron-Diffraction Measurement of Residual Stresses
2.6. Comparison of Residual Stresses Computed from Neutron-Diffraction Measurements and Residual Stresses from the FE Model of Heat Treatment
2.7. FE Simulation of the Contour Cut Method
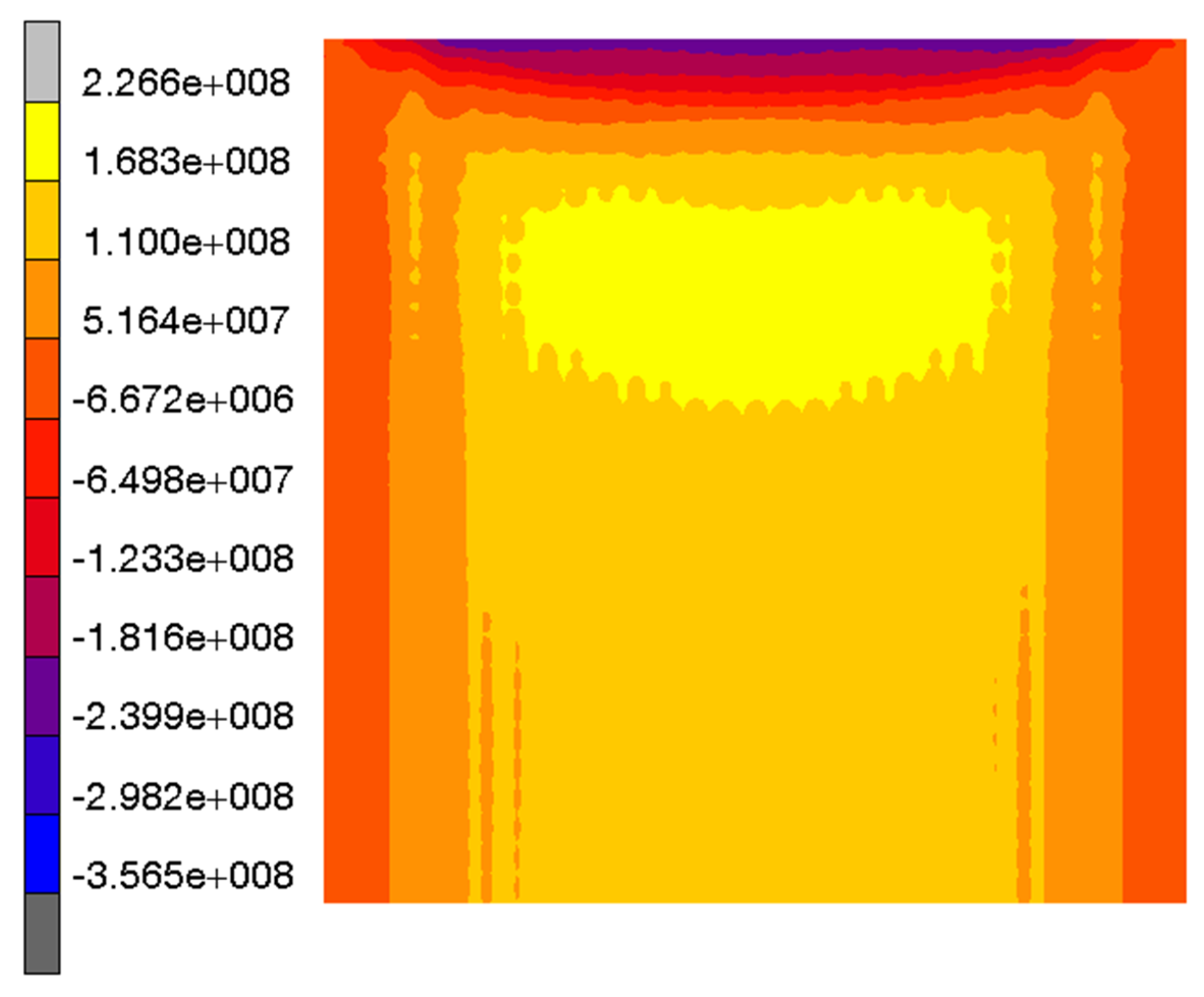
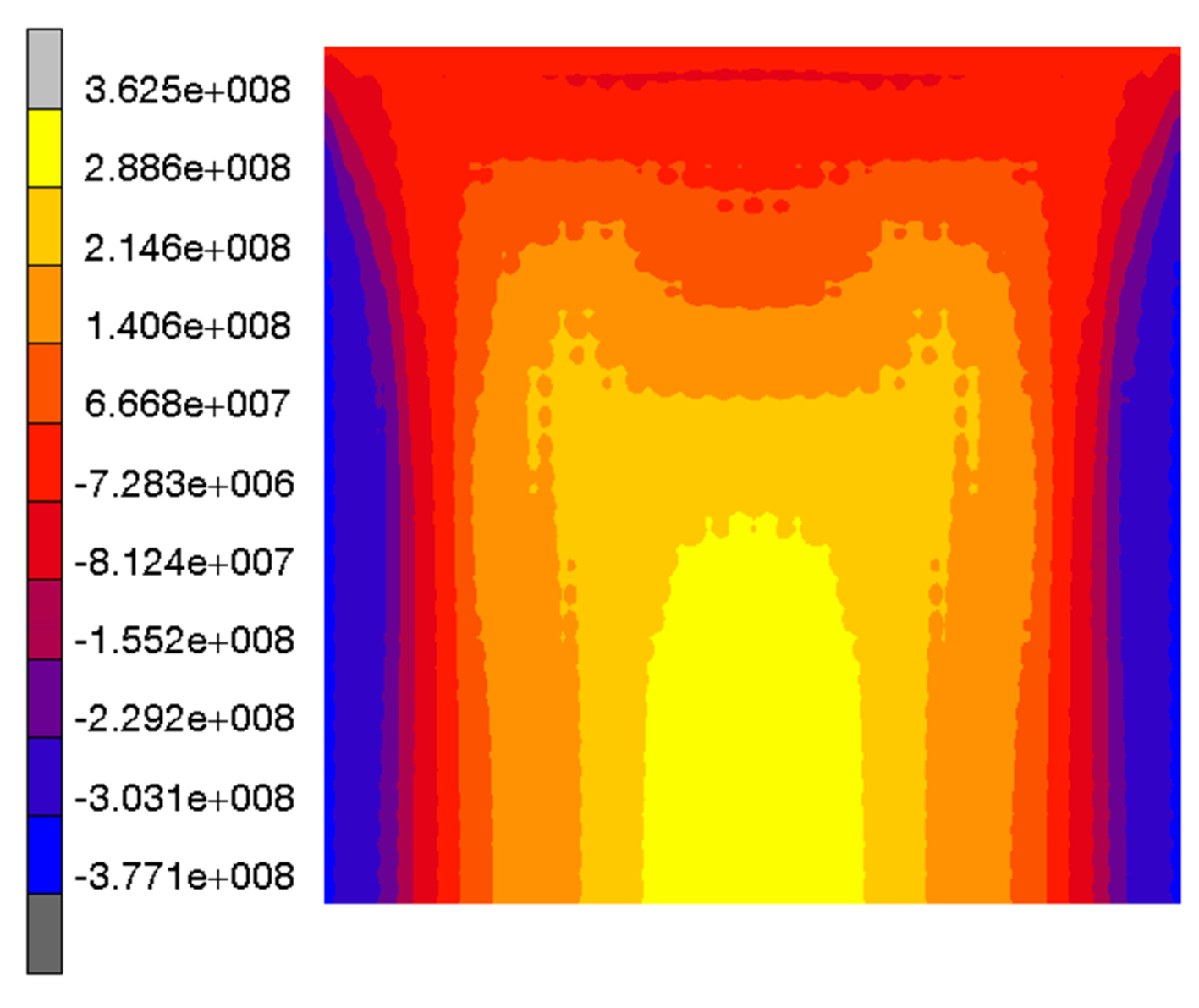
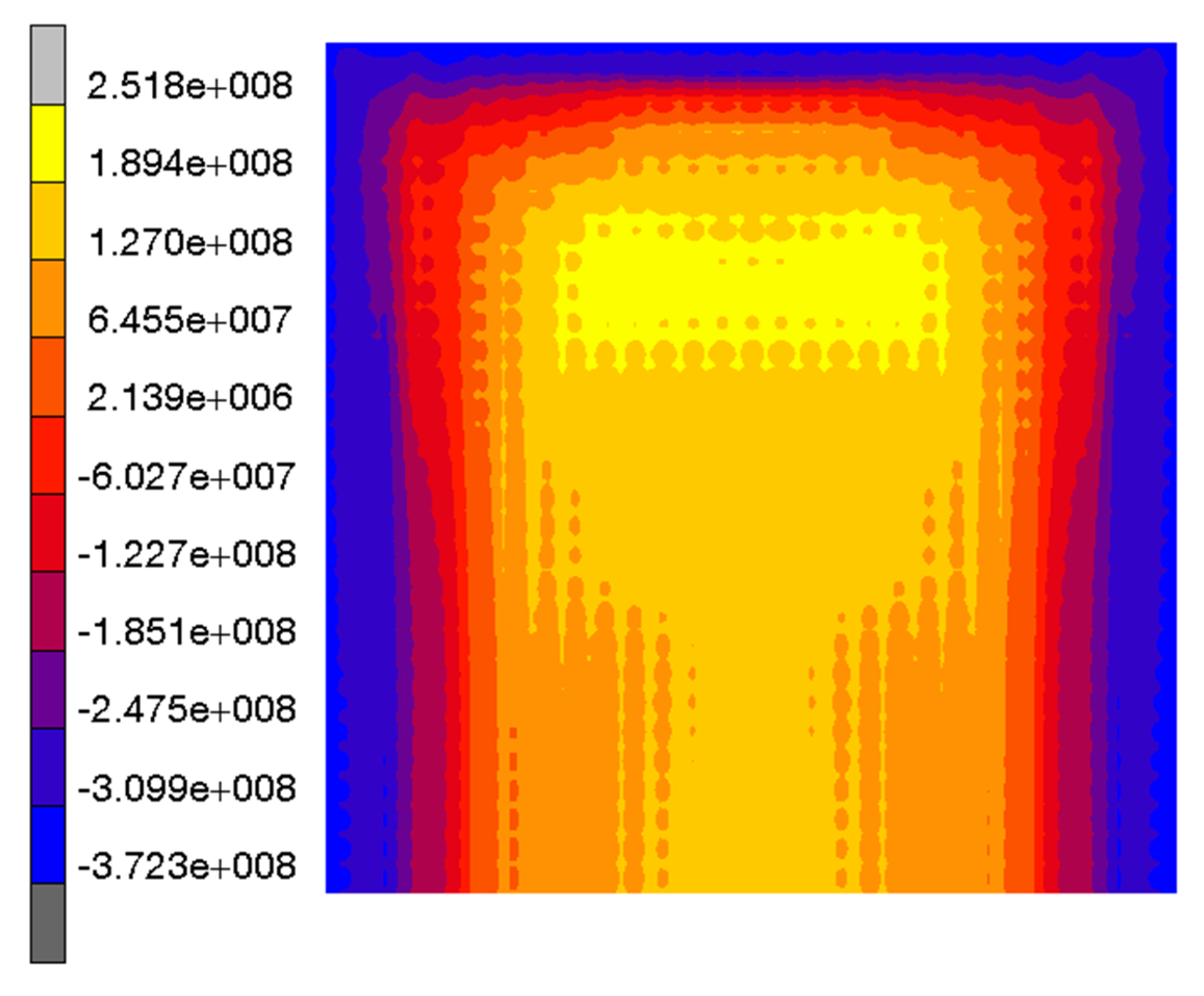
3. Results and Discussion
3.1. Comparison of Residual Stresses Determined Using the Contour Method (CM) and Residual Stresses Found by FE Analysis of Heat Treatment (FEM)
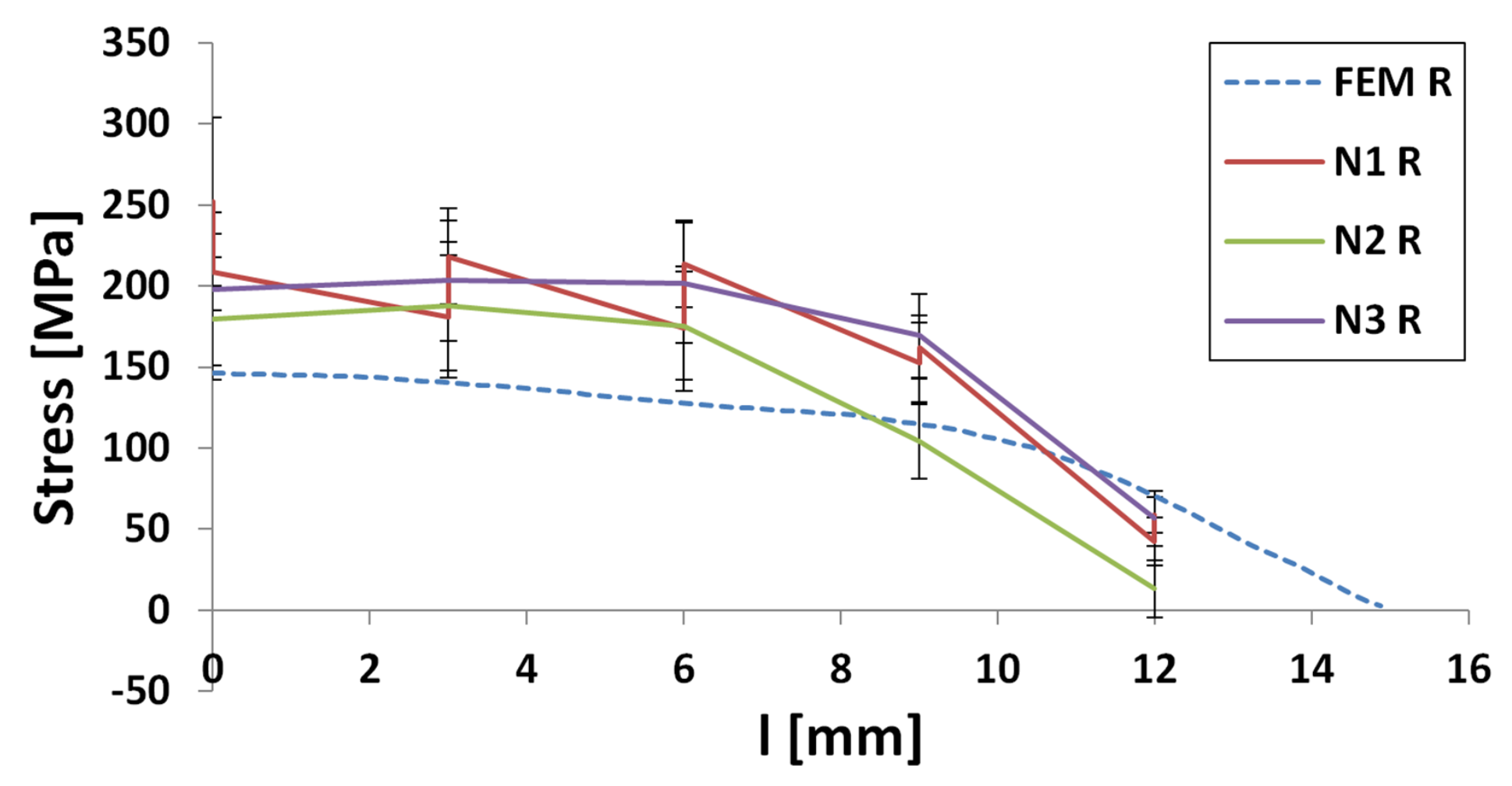
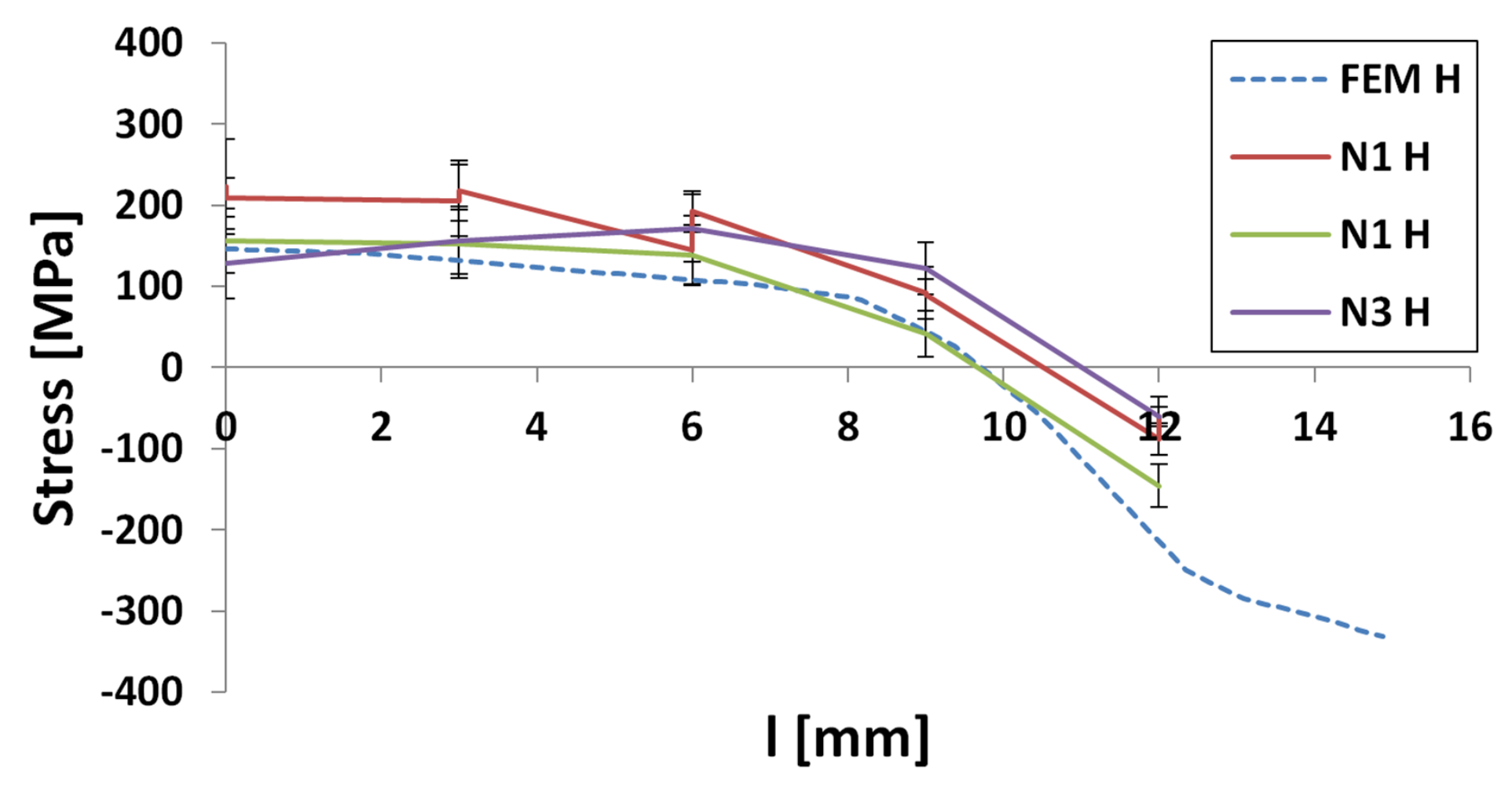
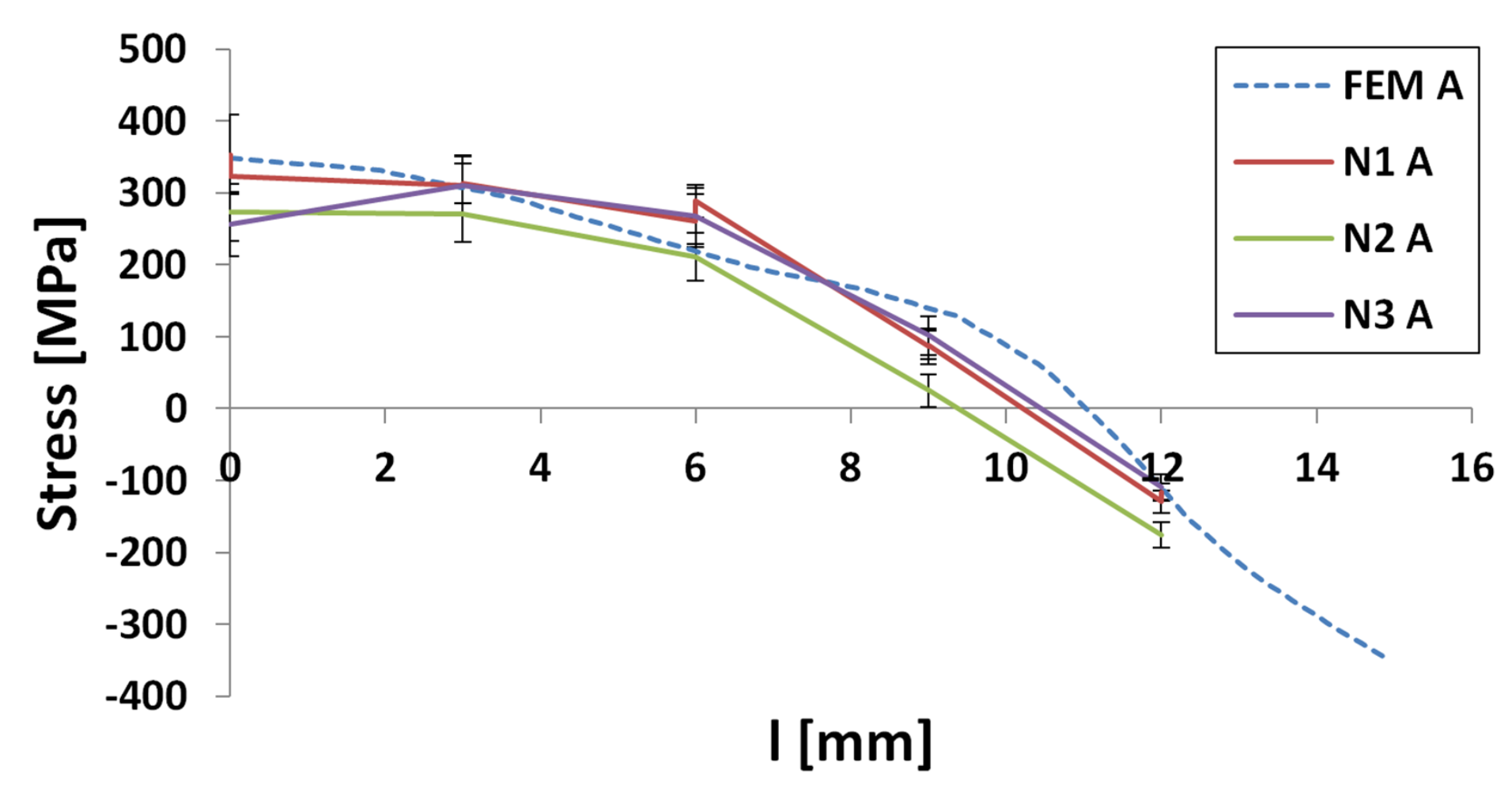
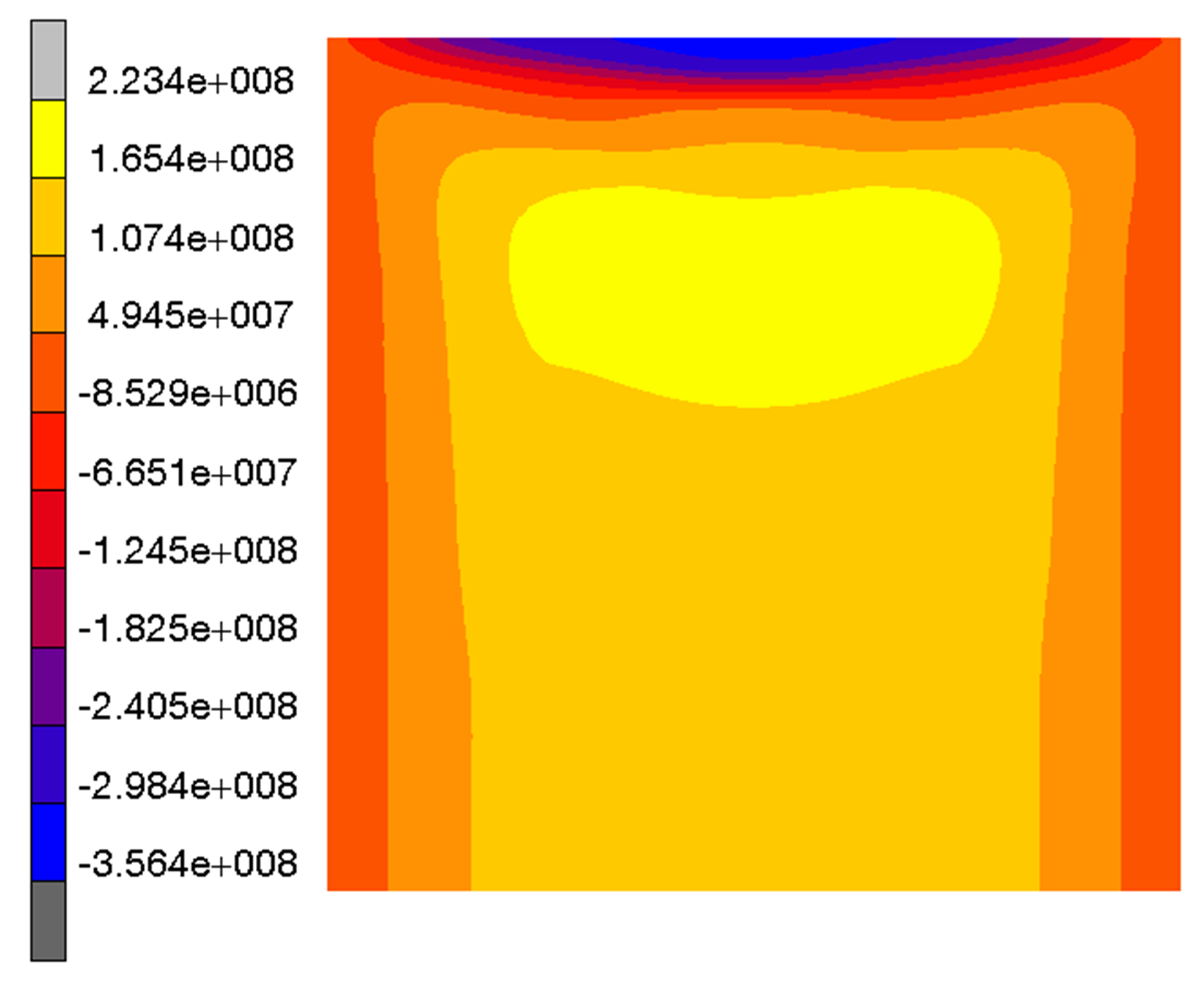
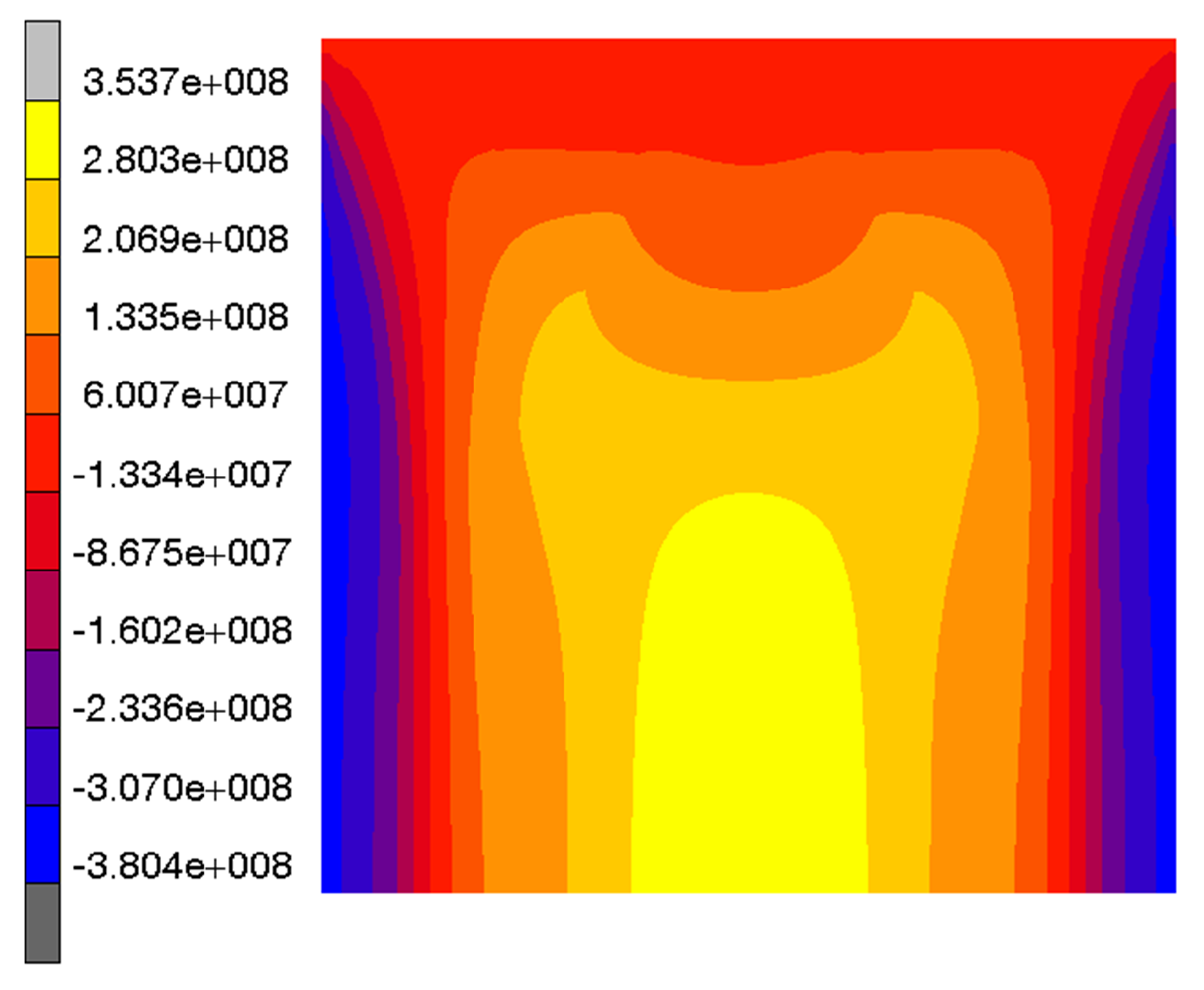
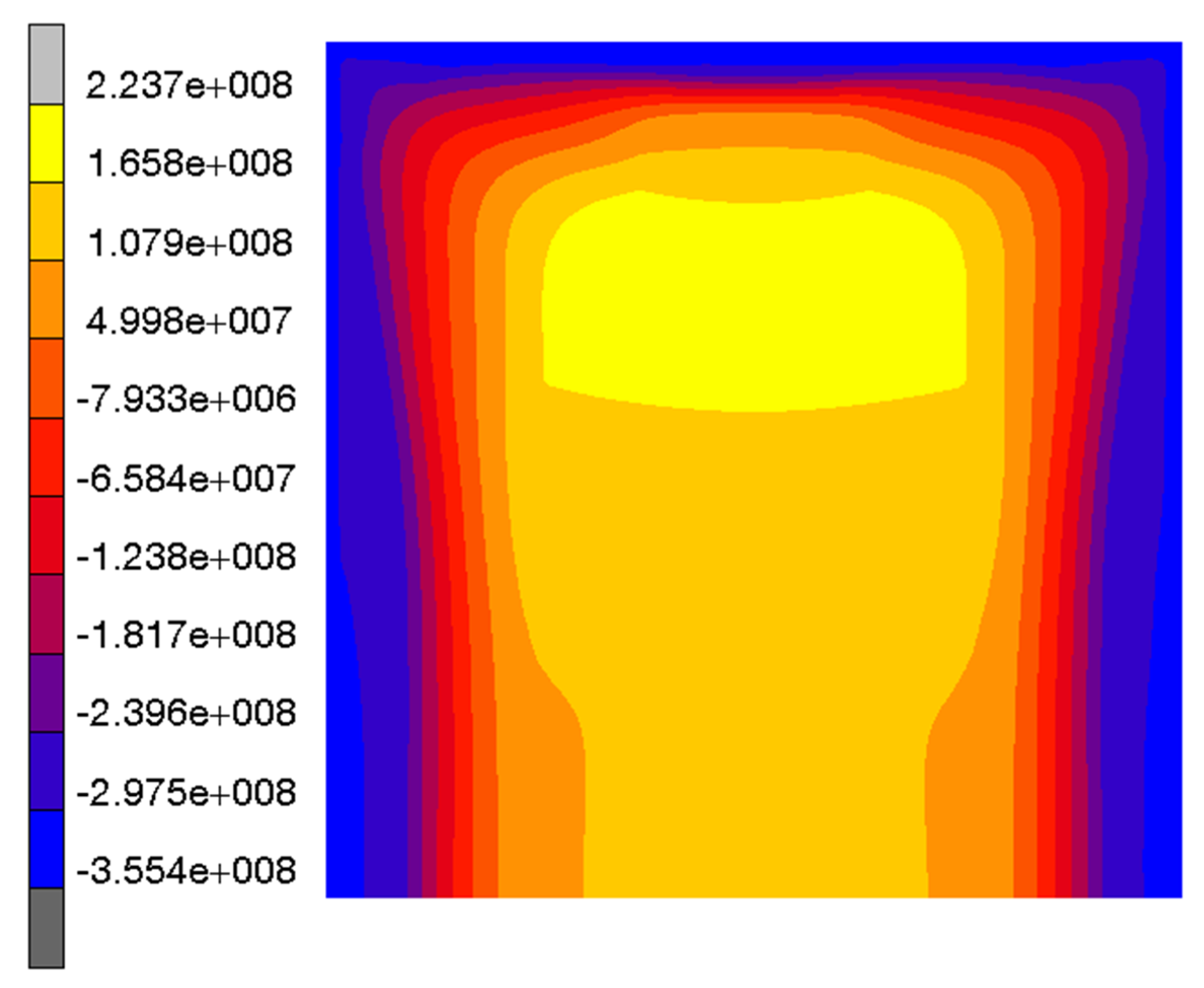
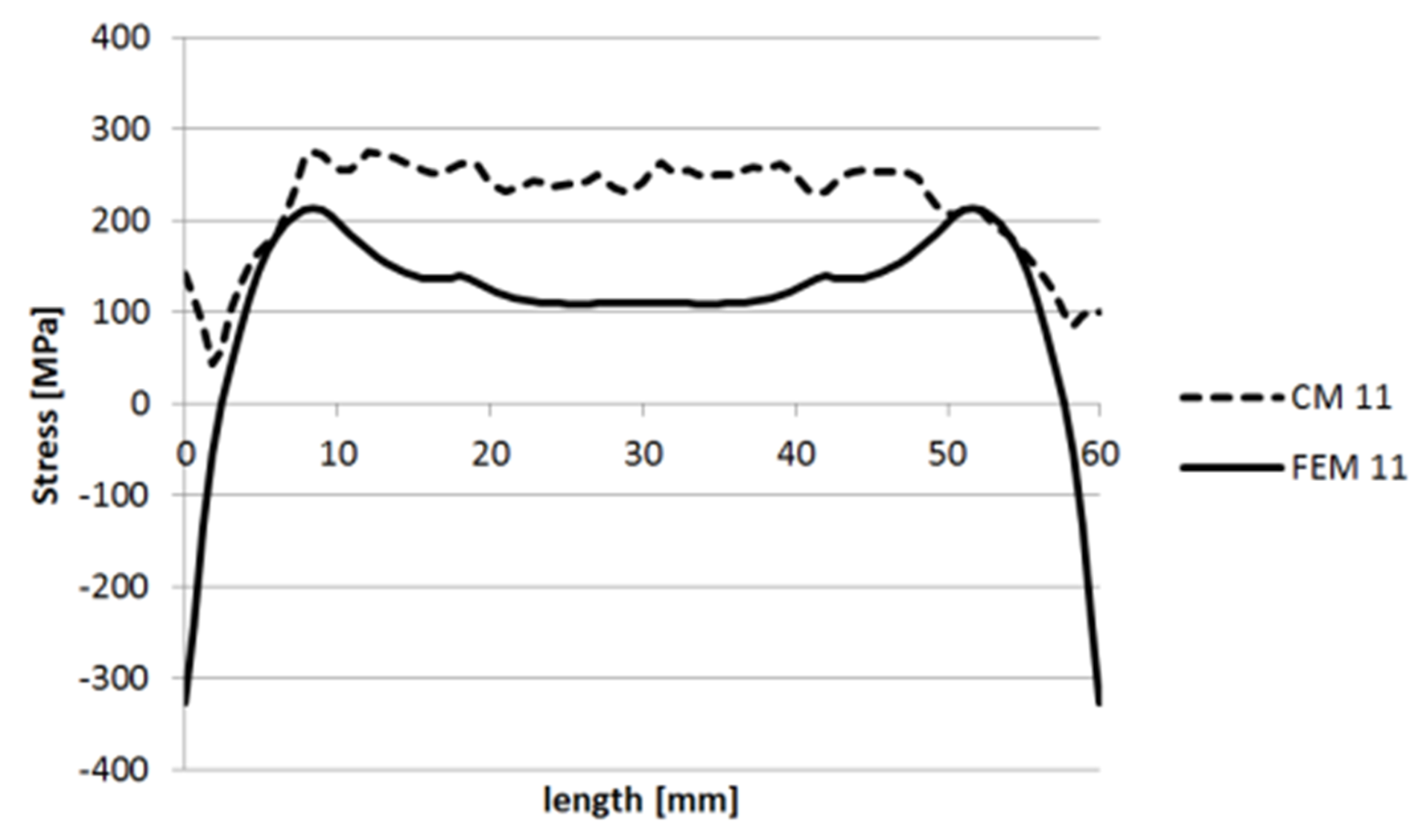
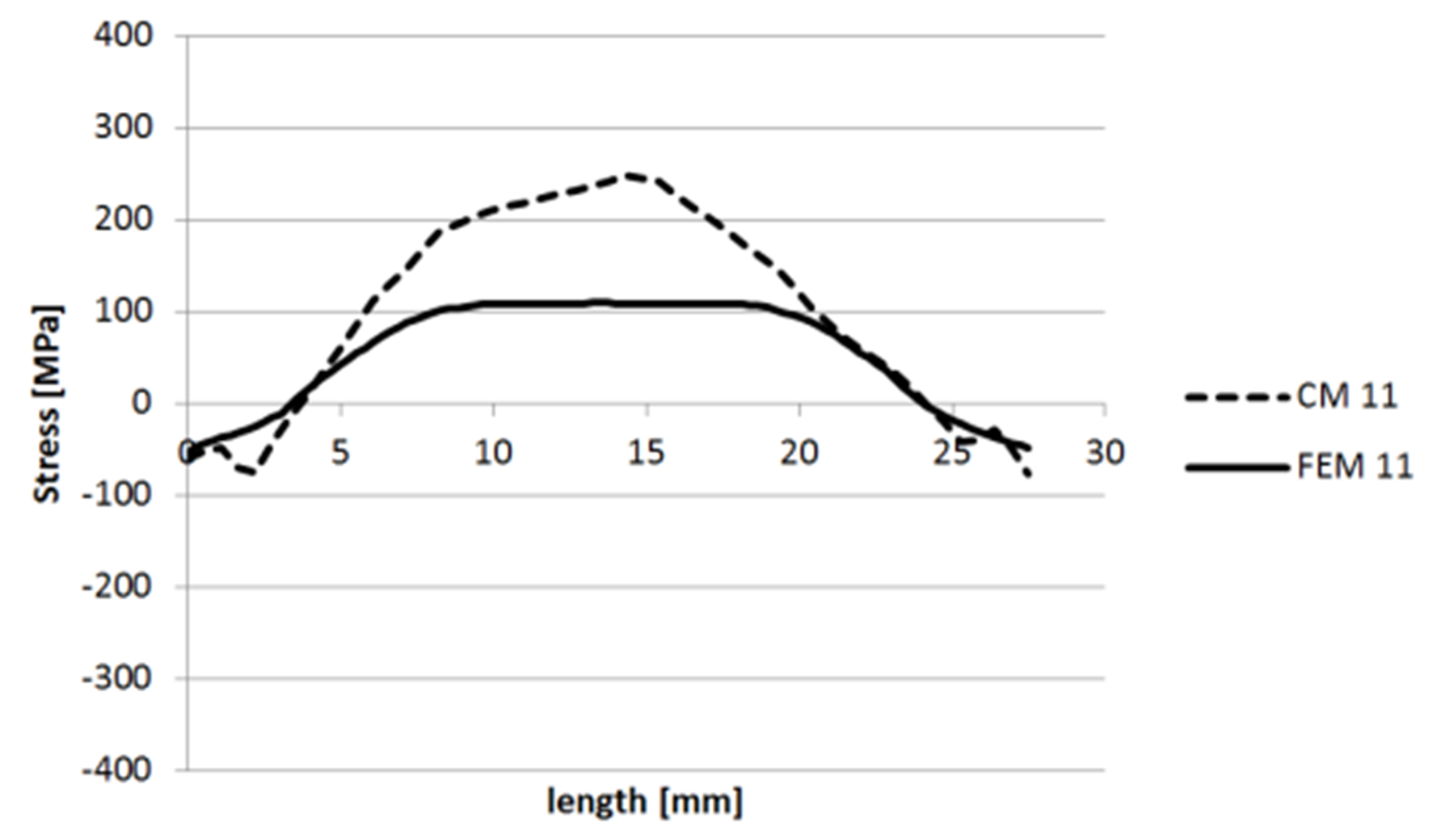
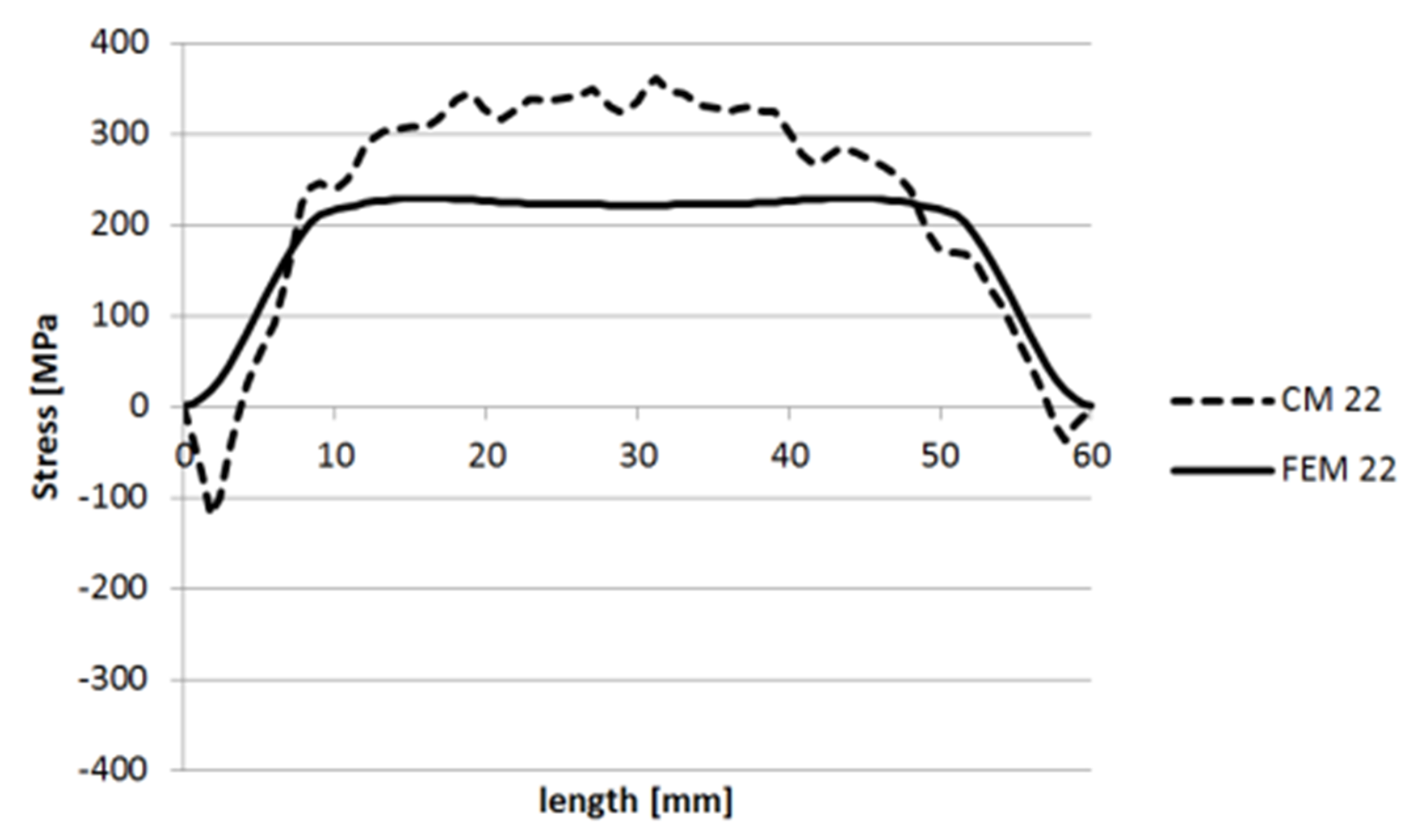
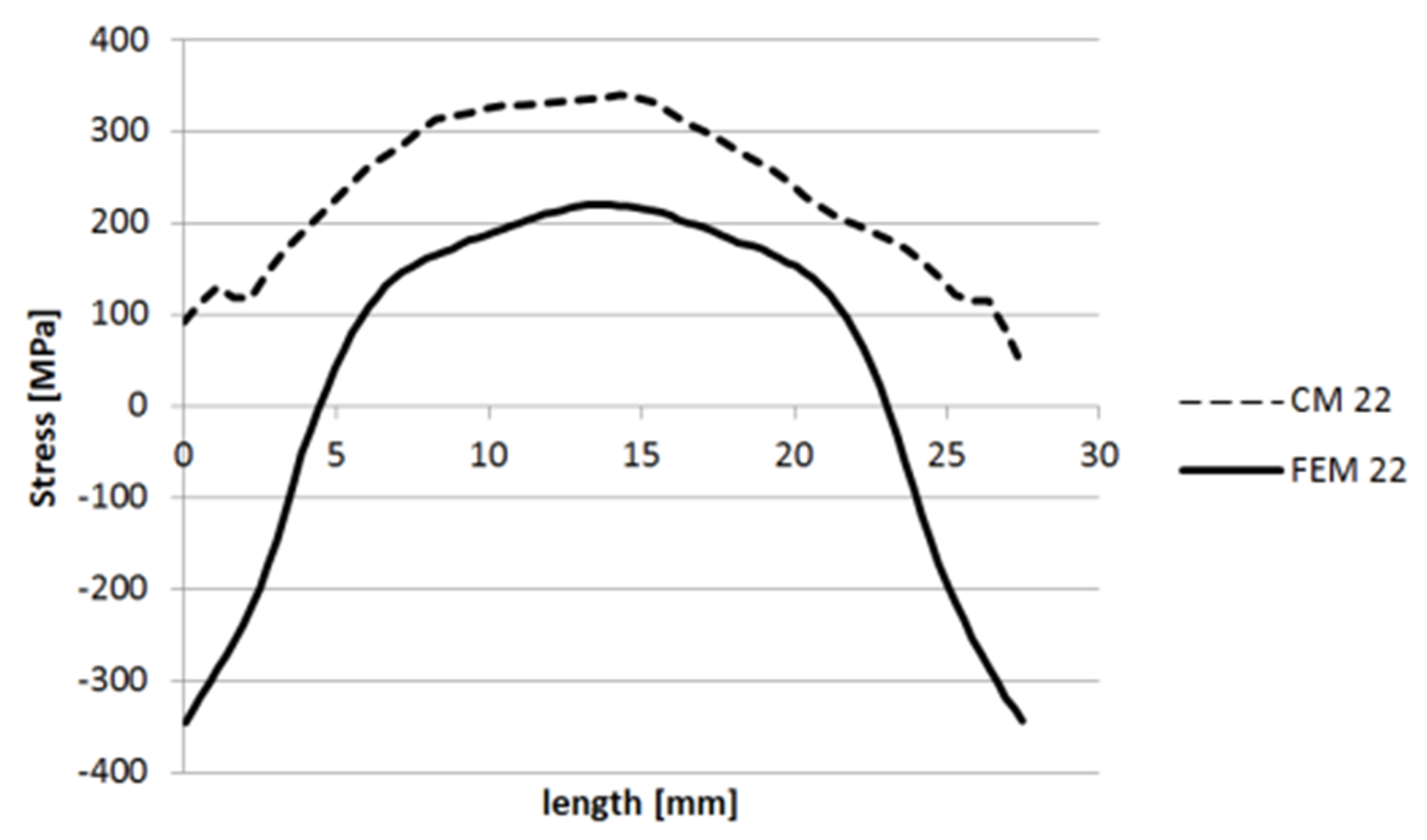
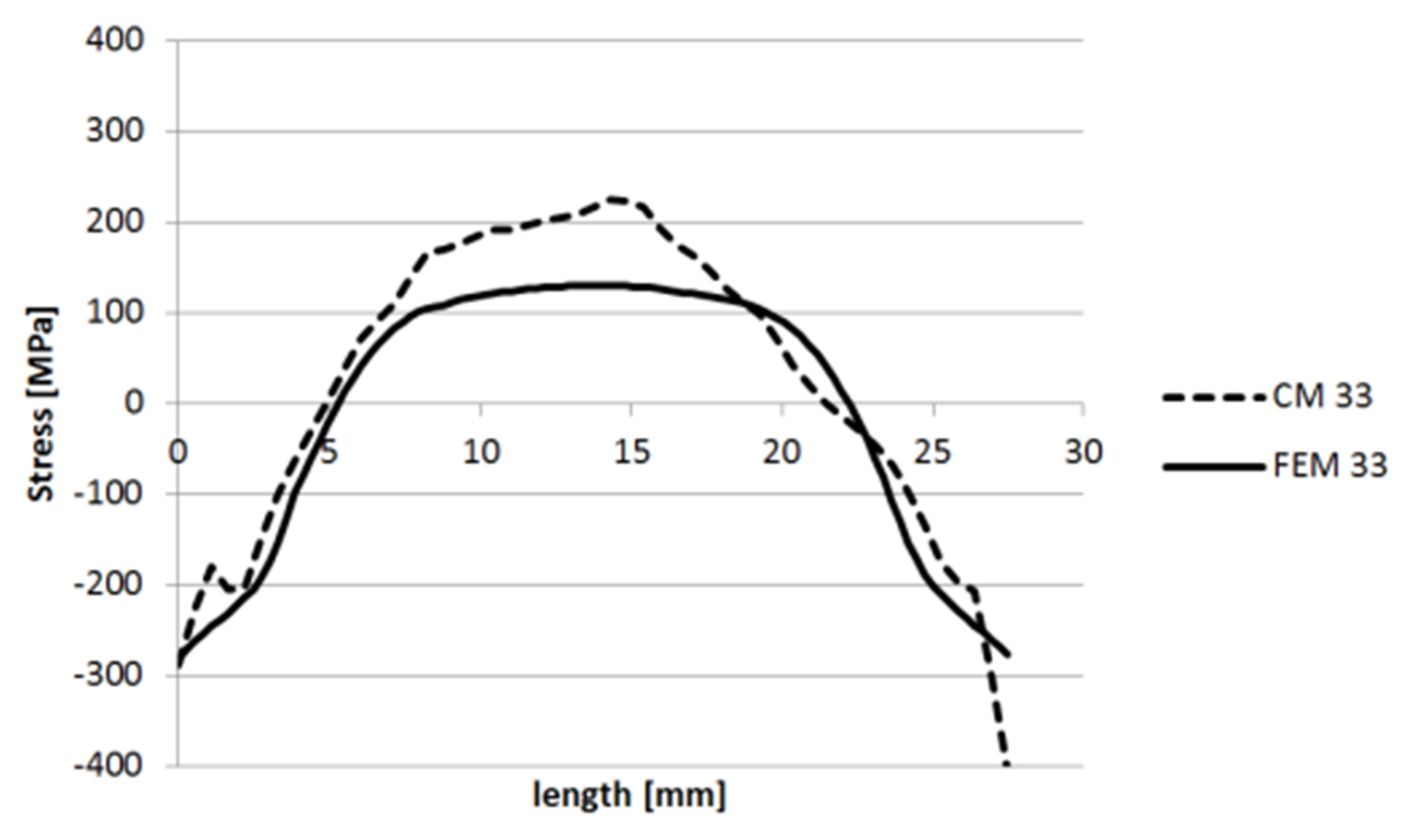
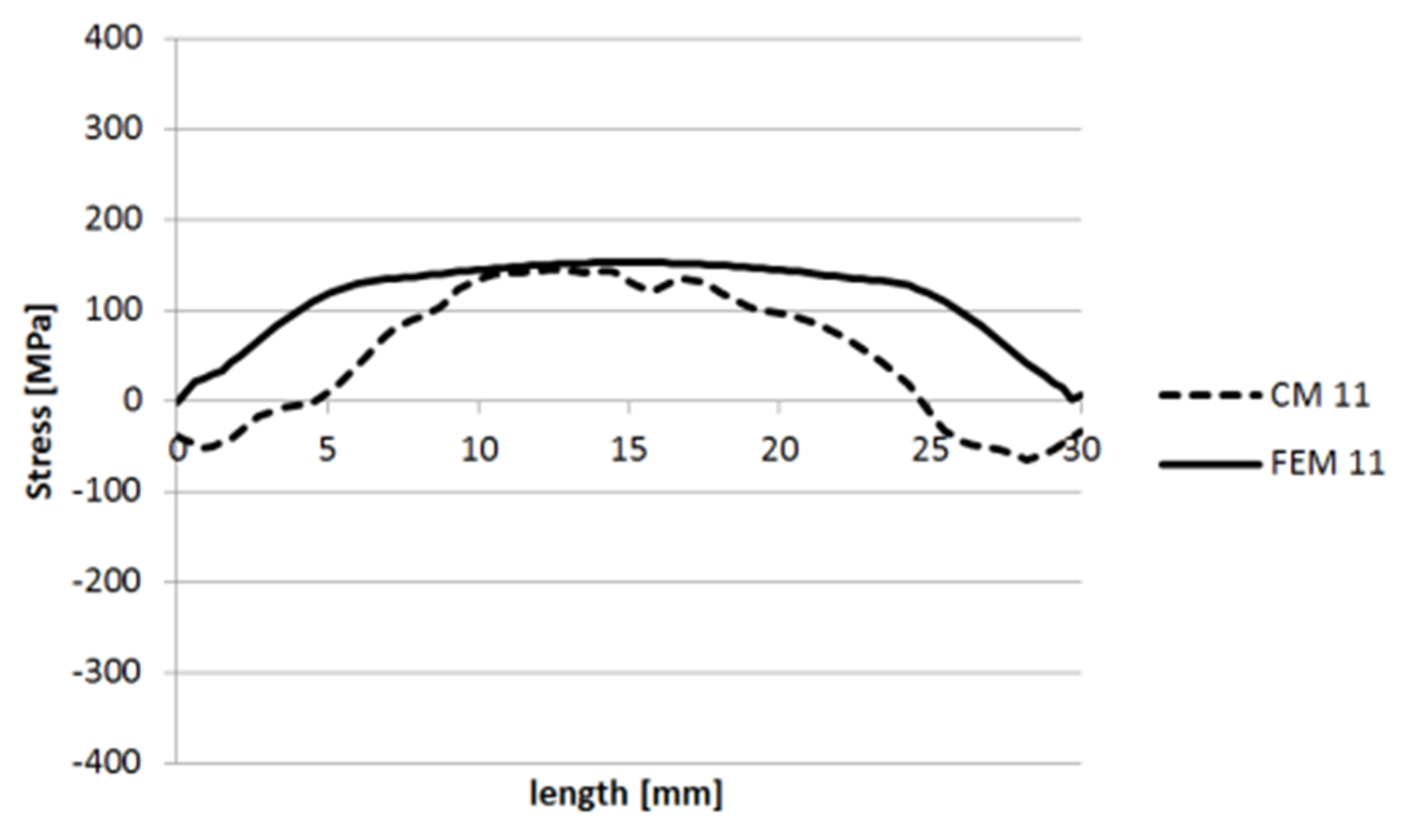
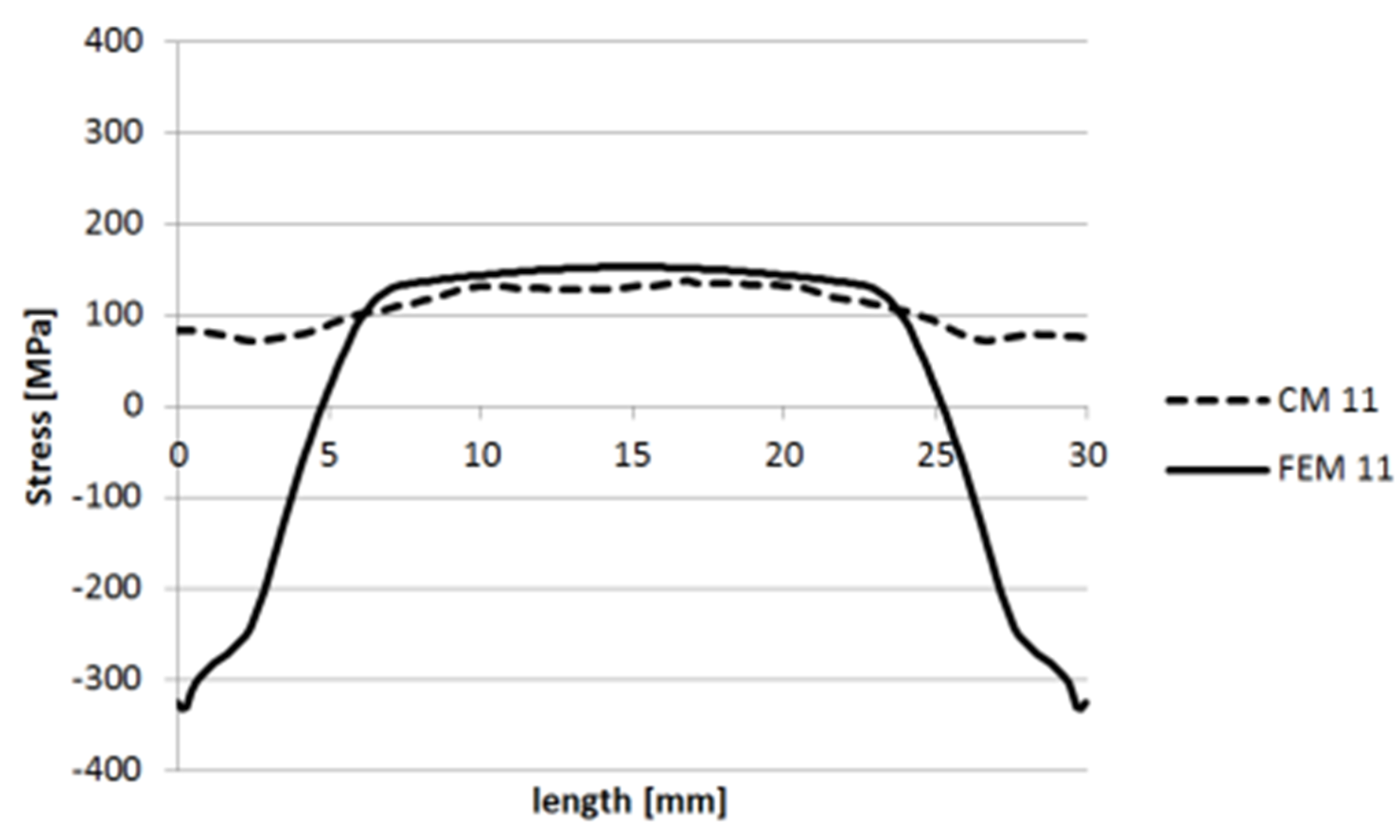
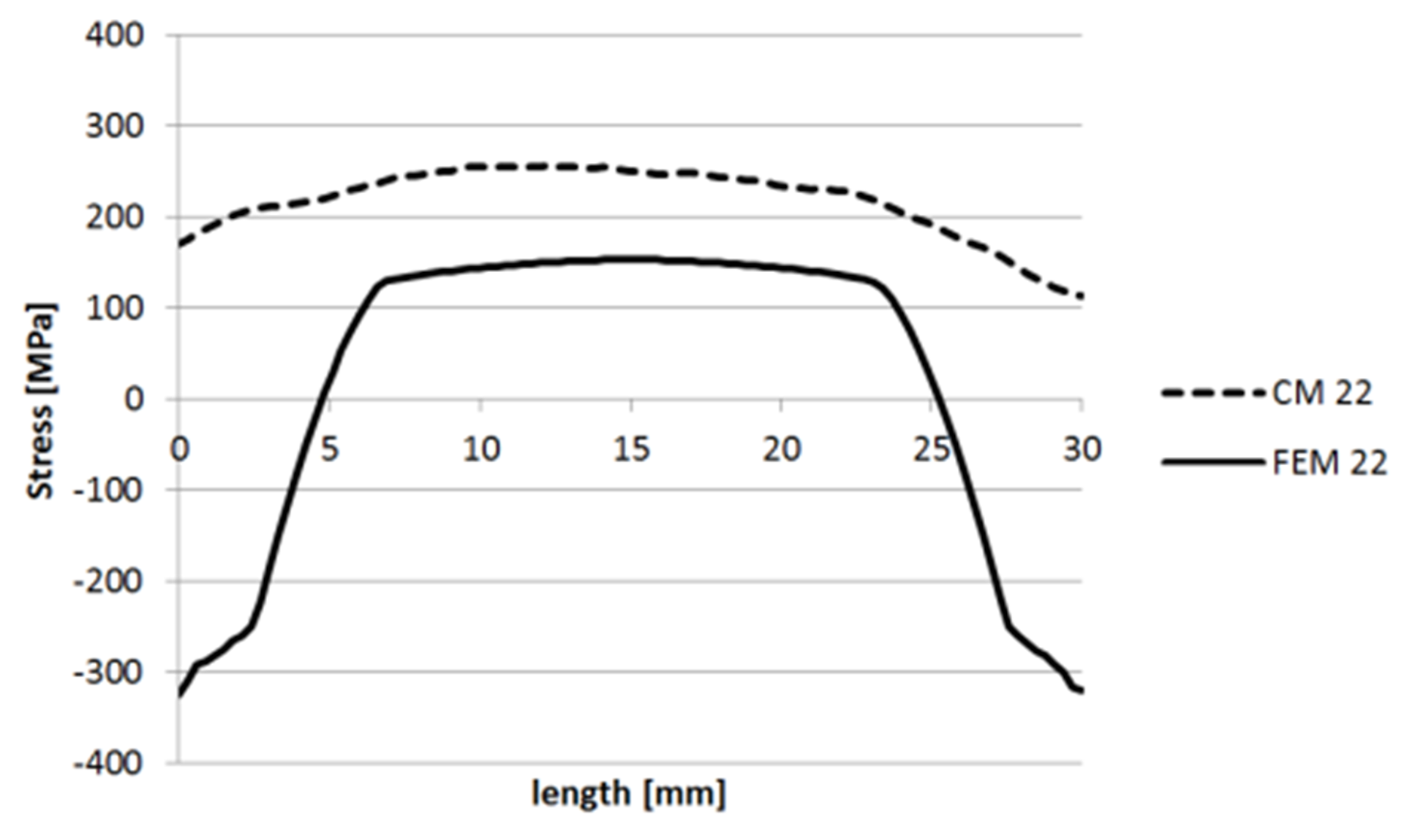
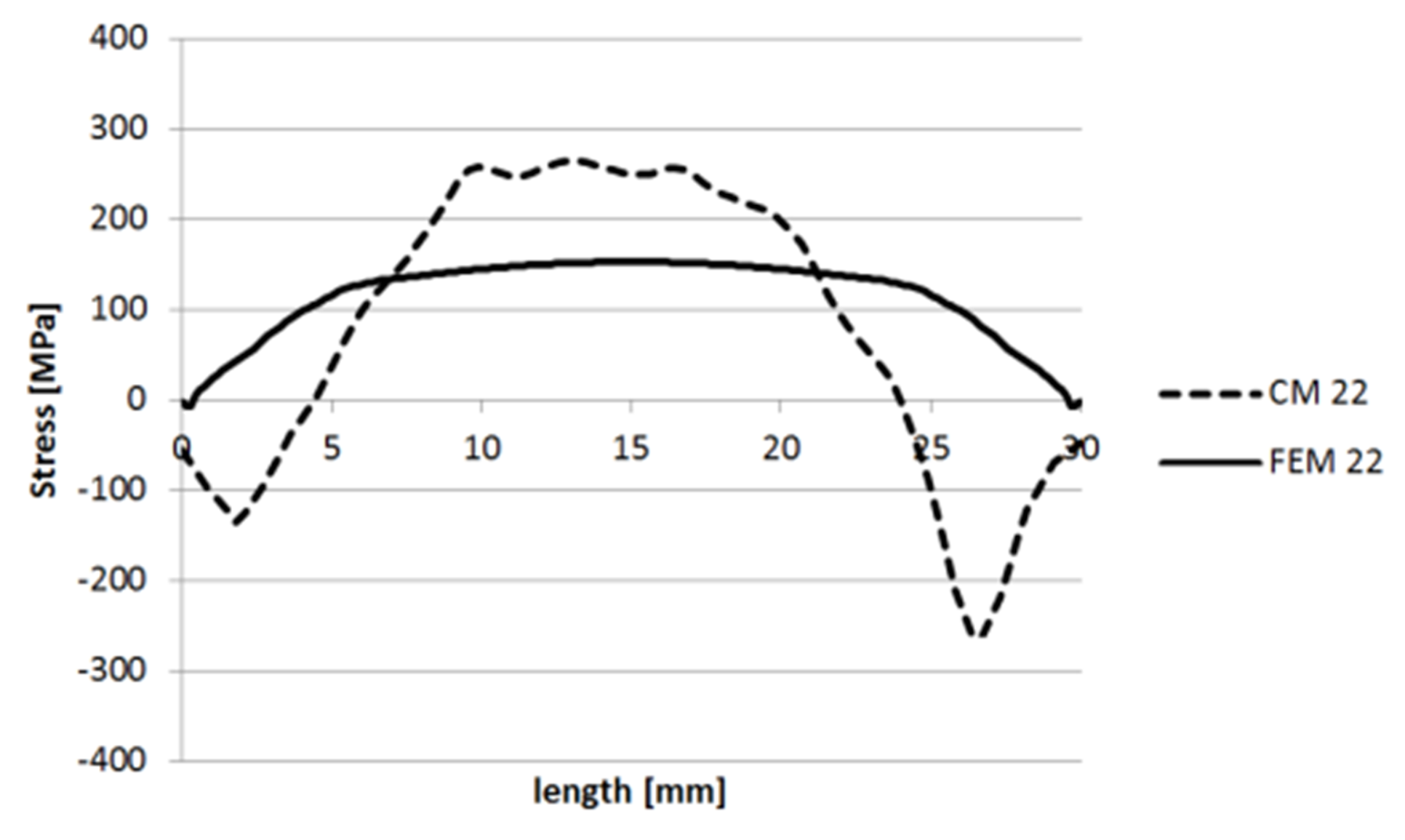
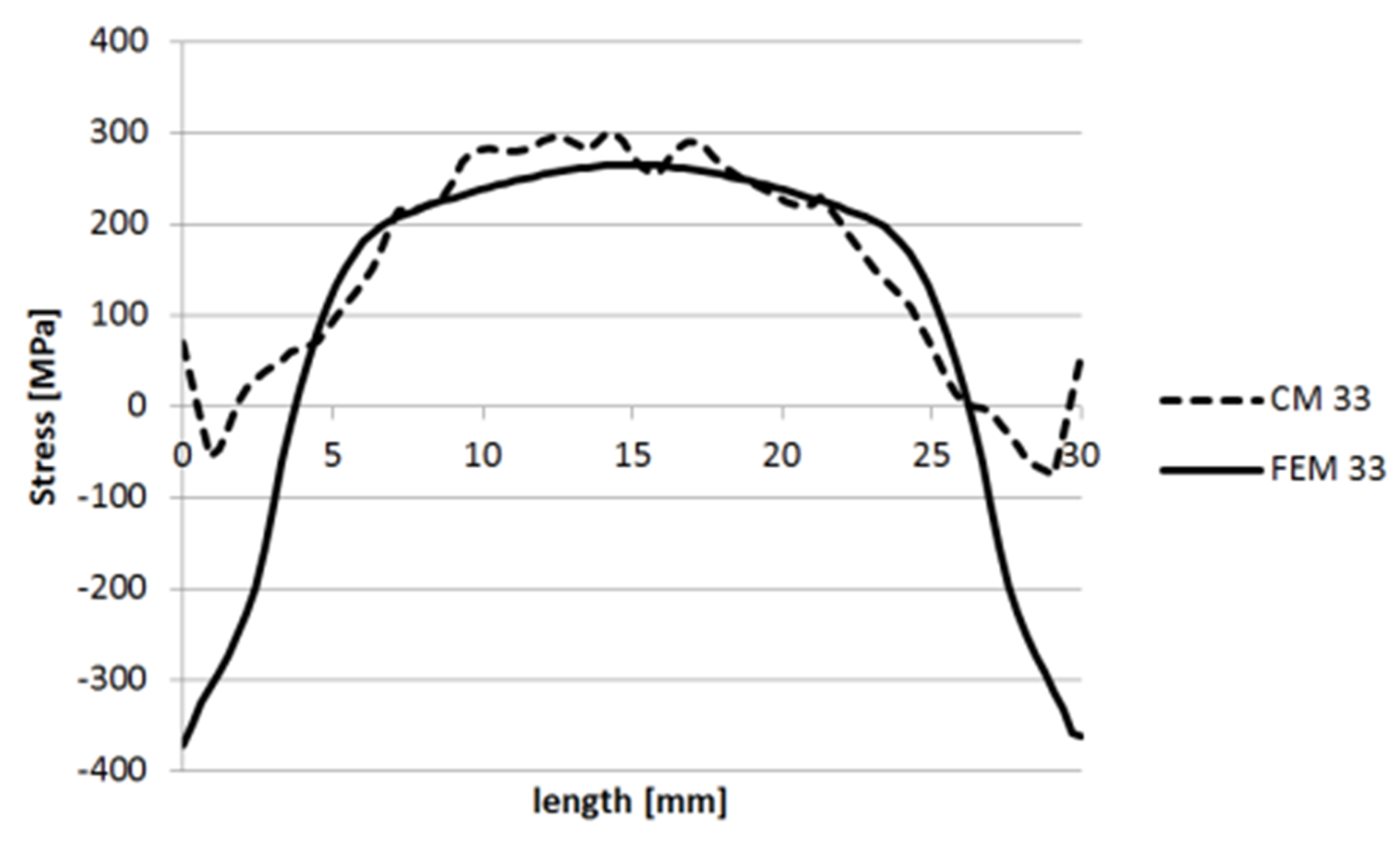
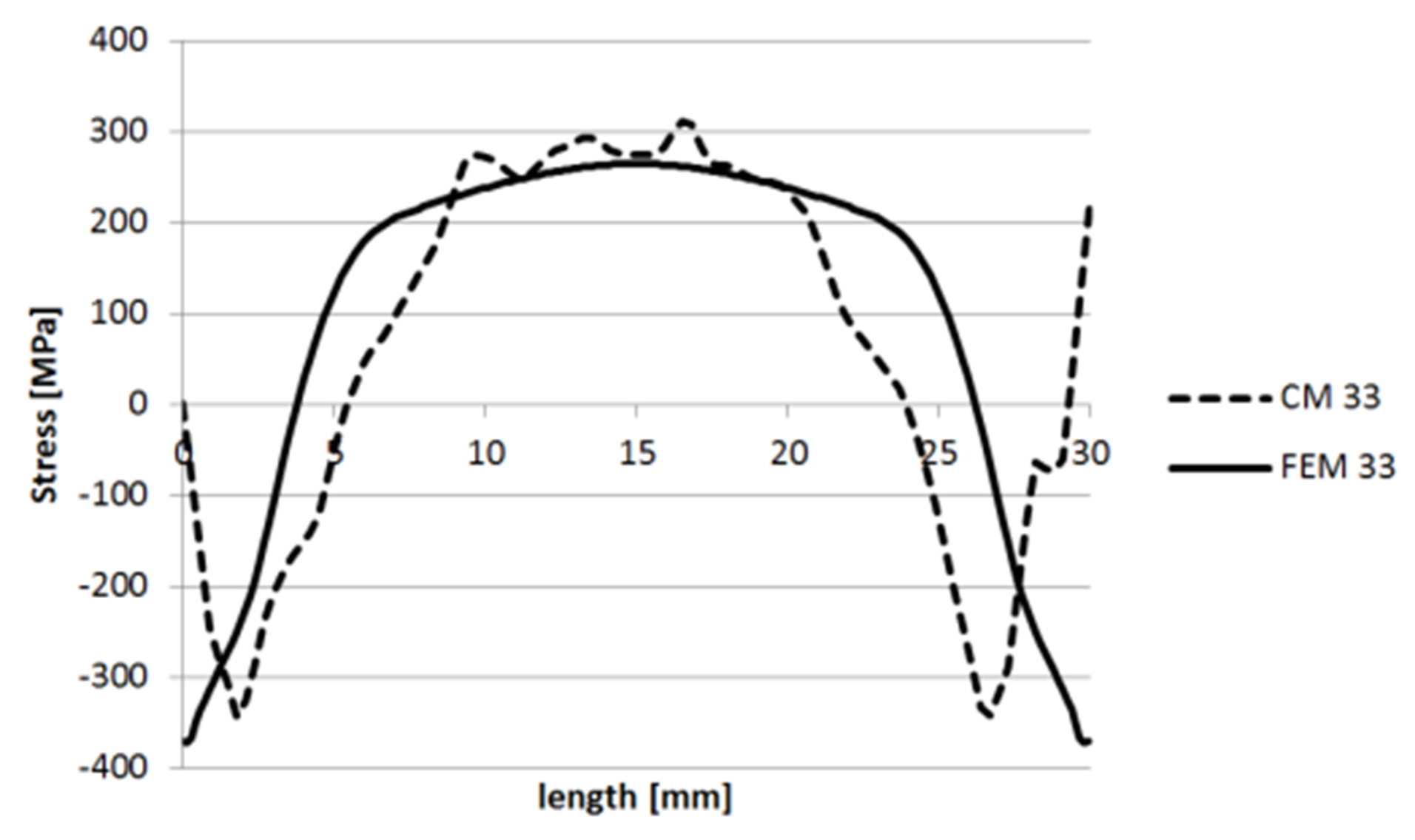
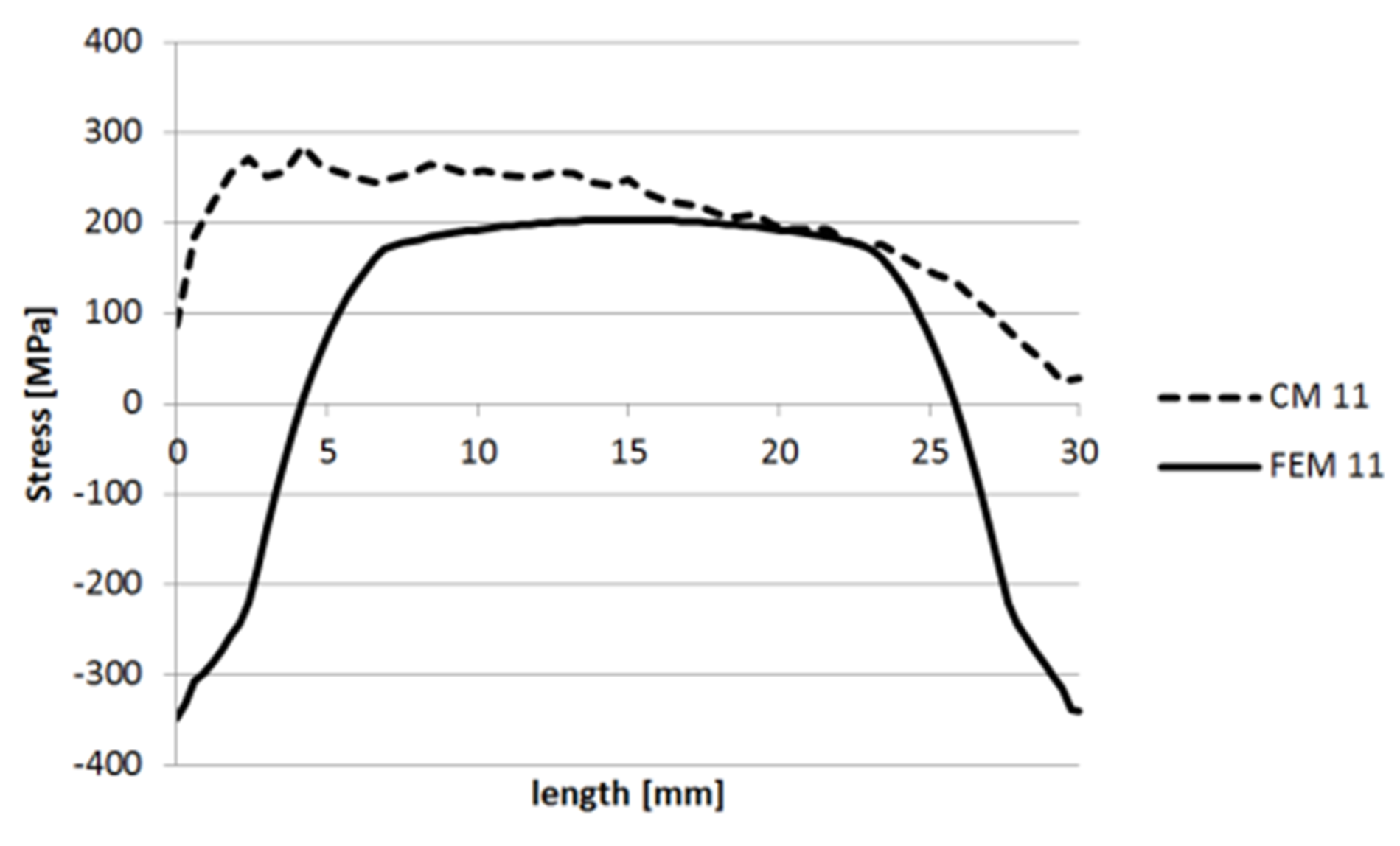
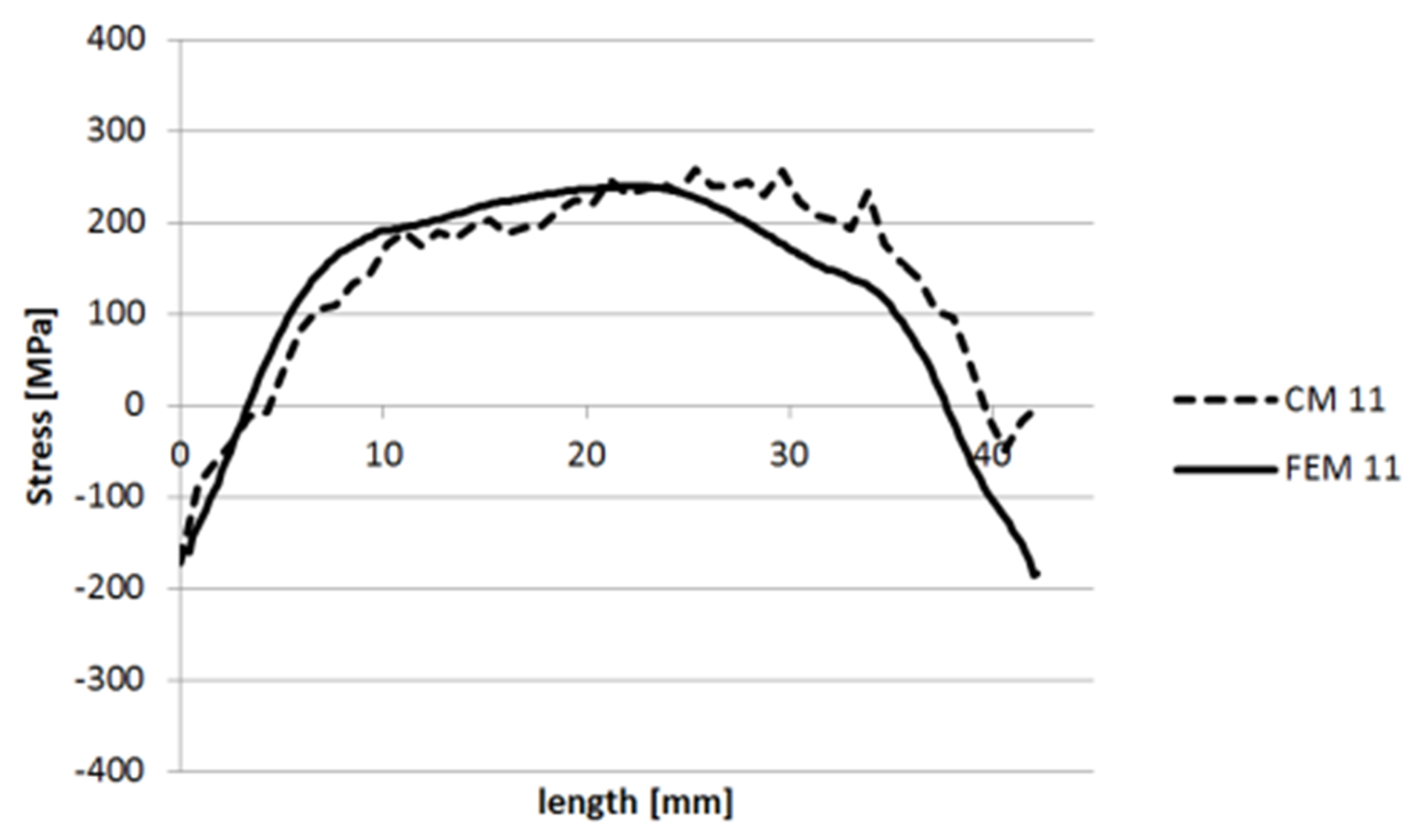
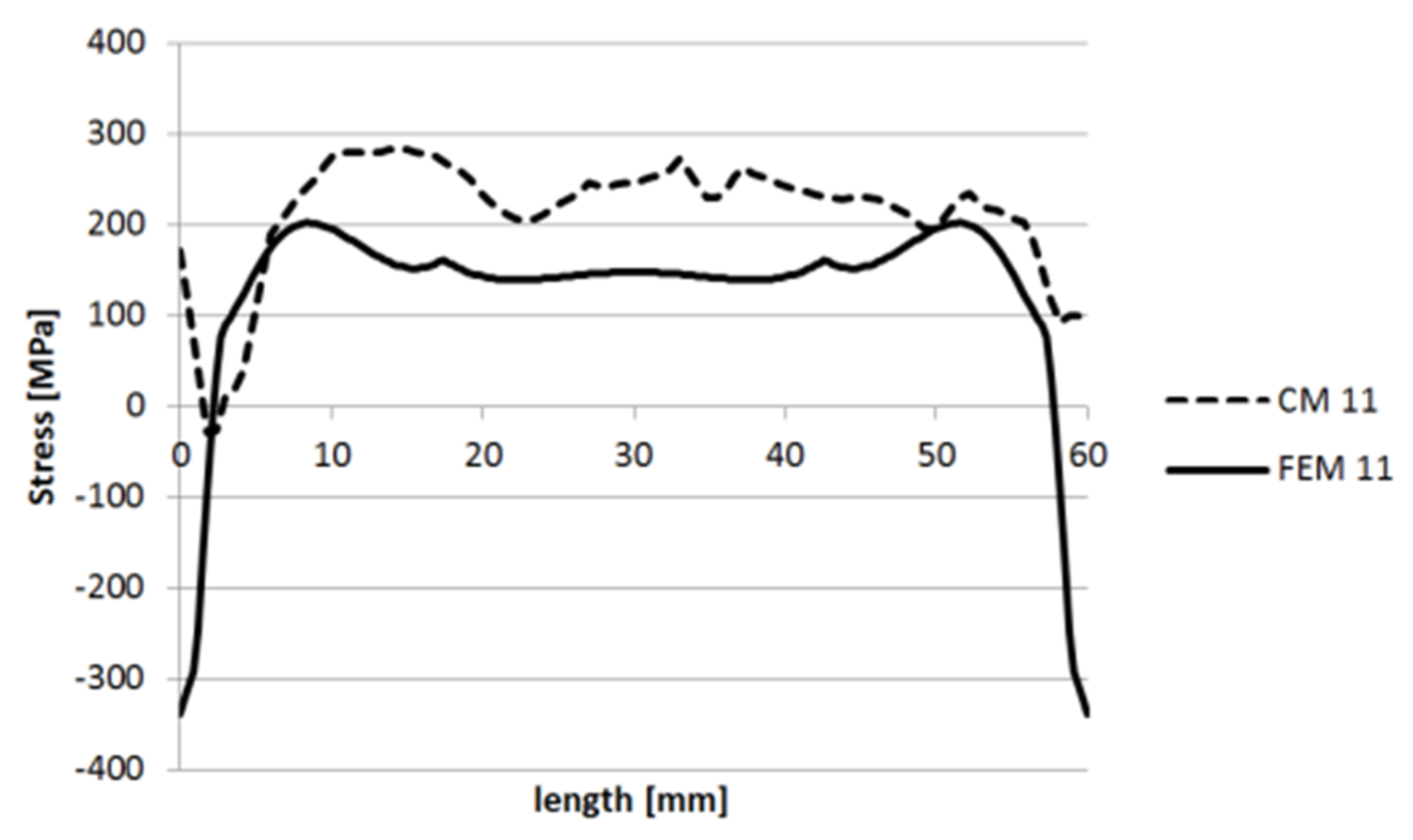
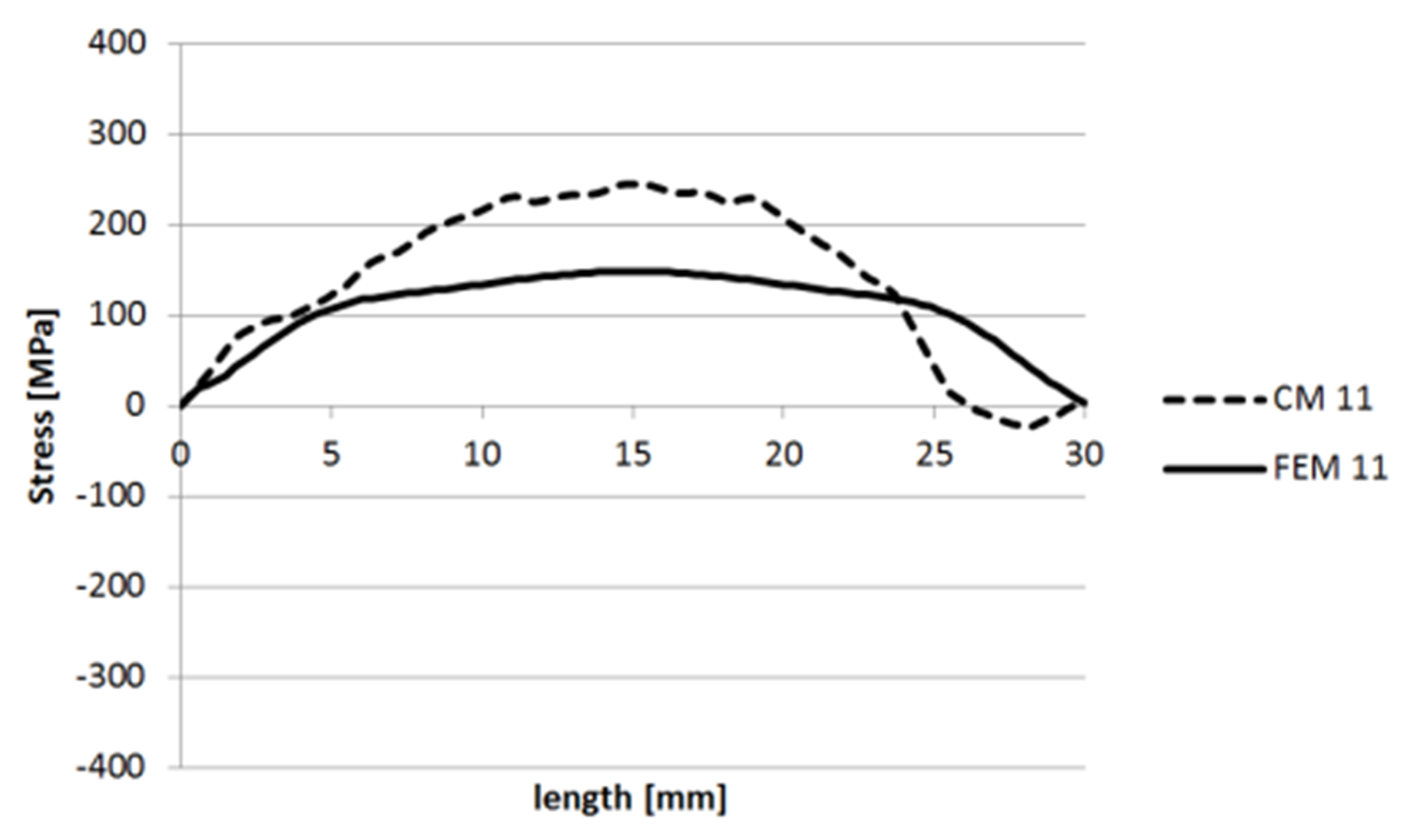
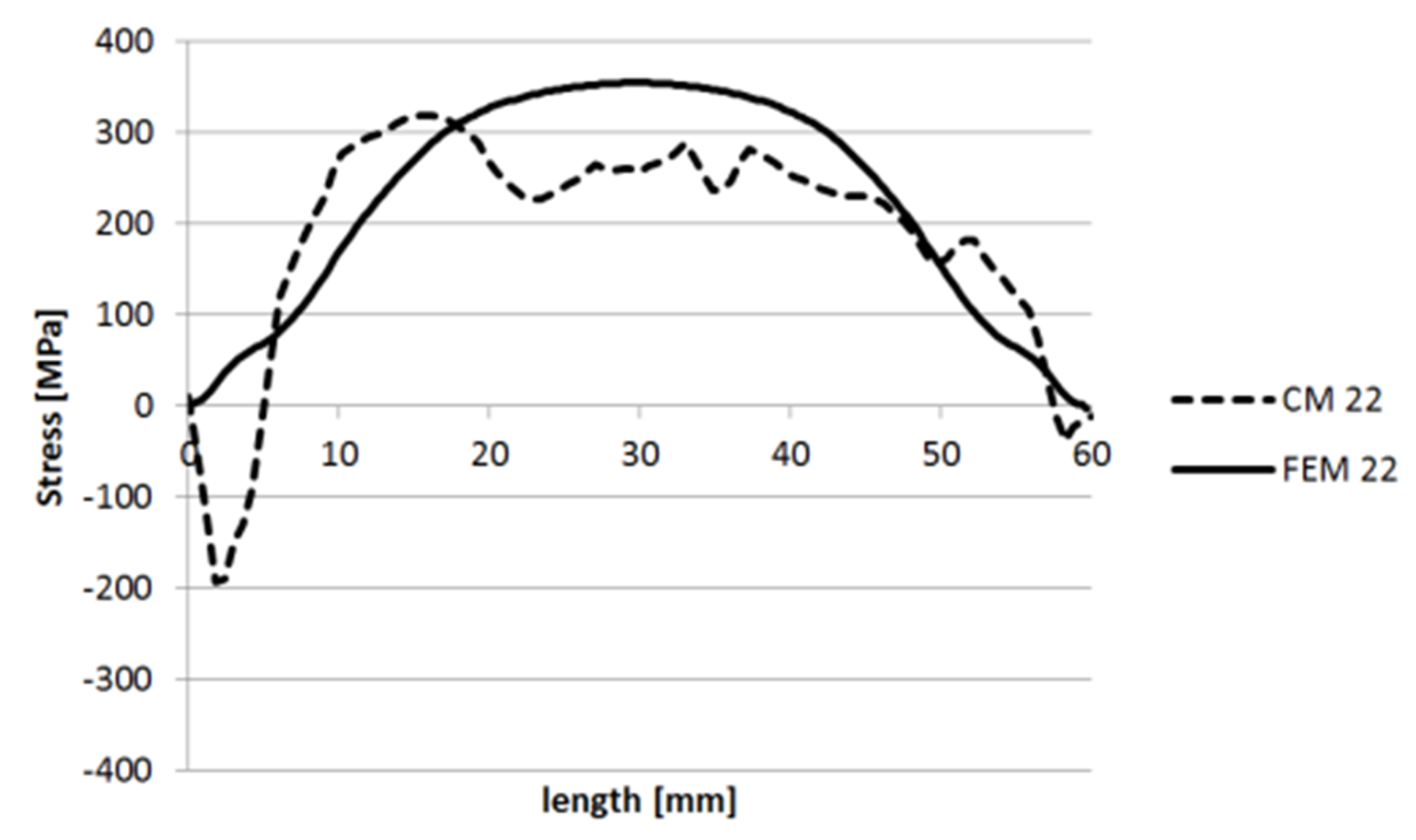
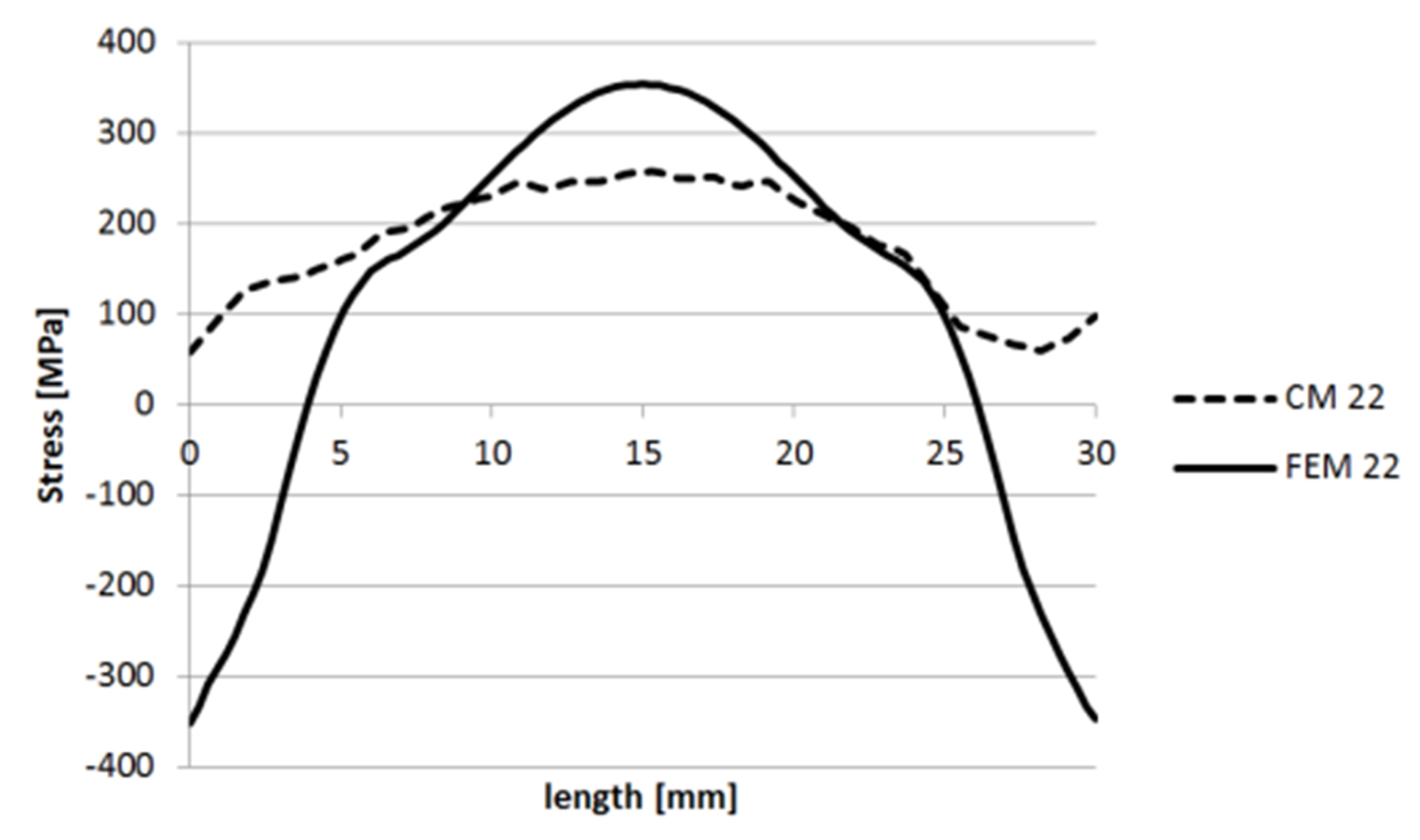
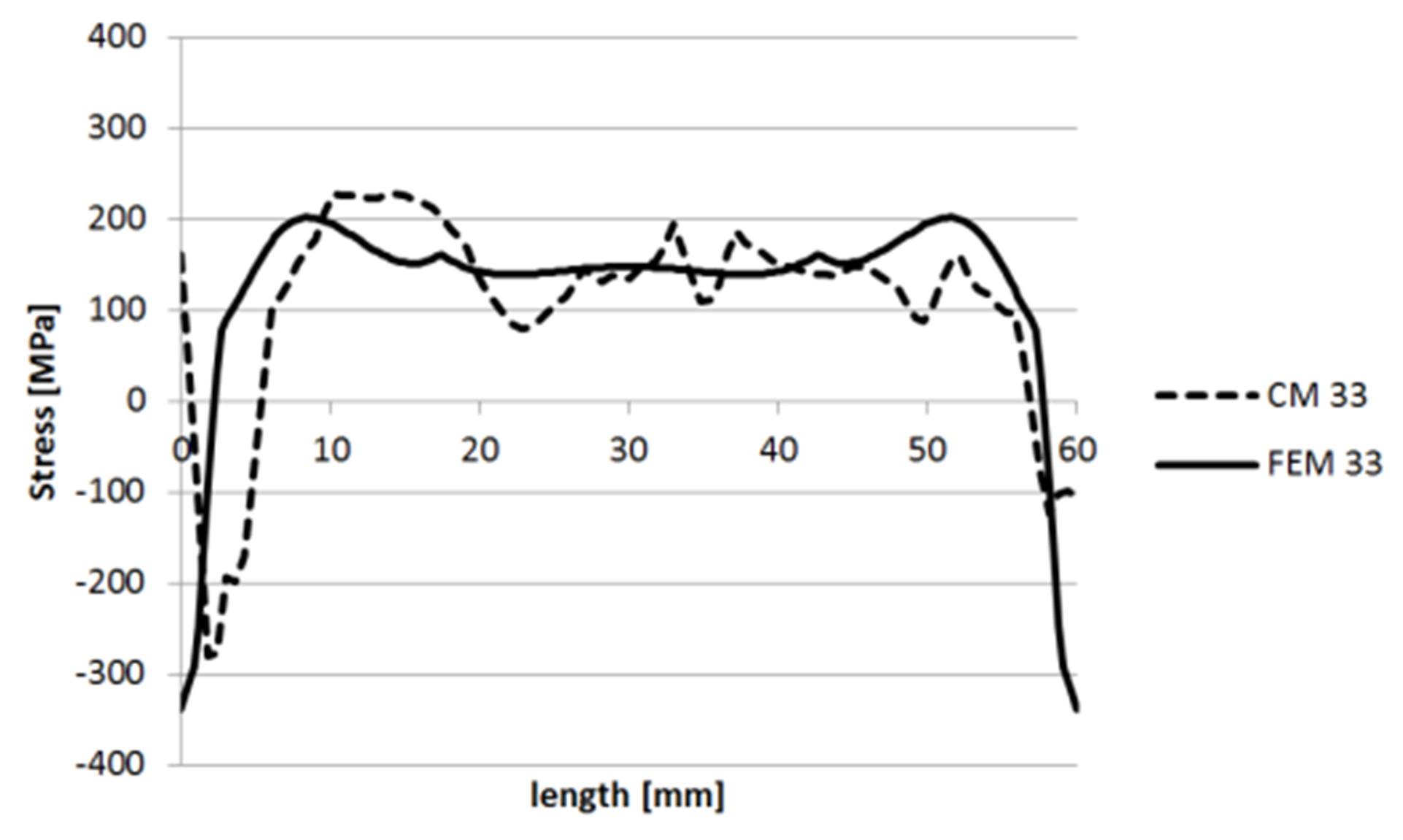
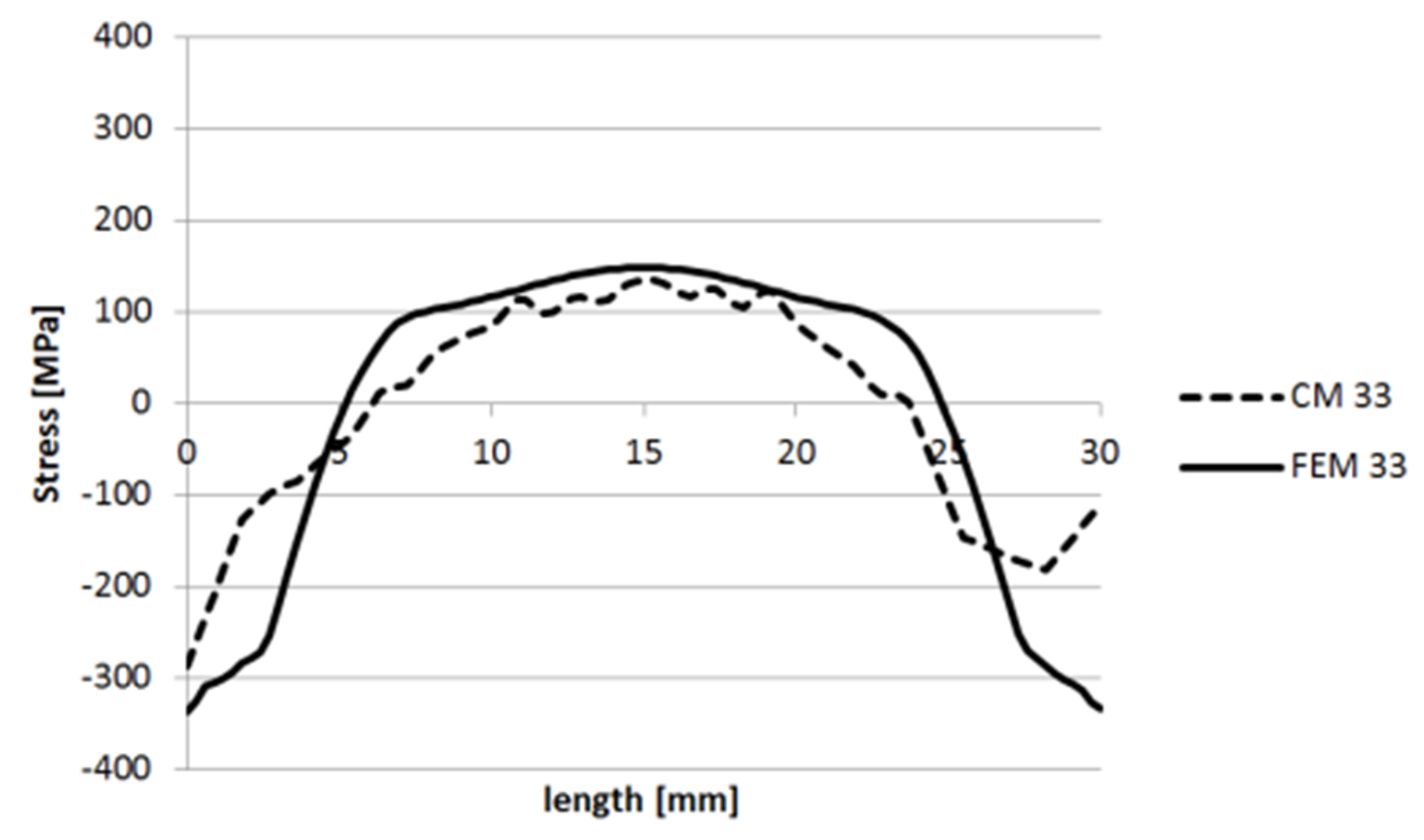
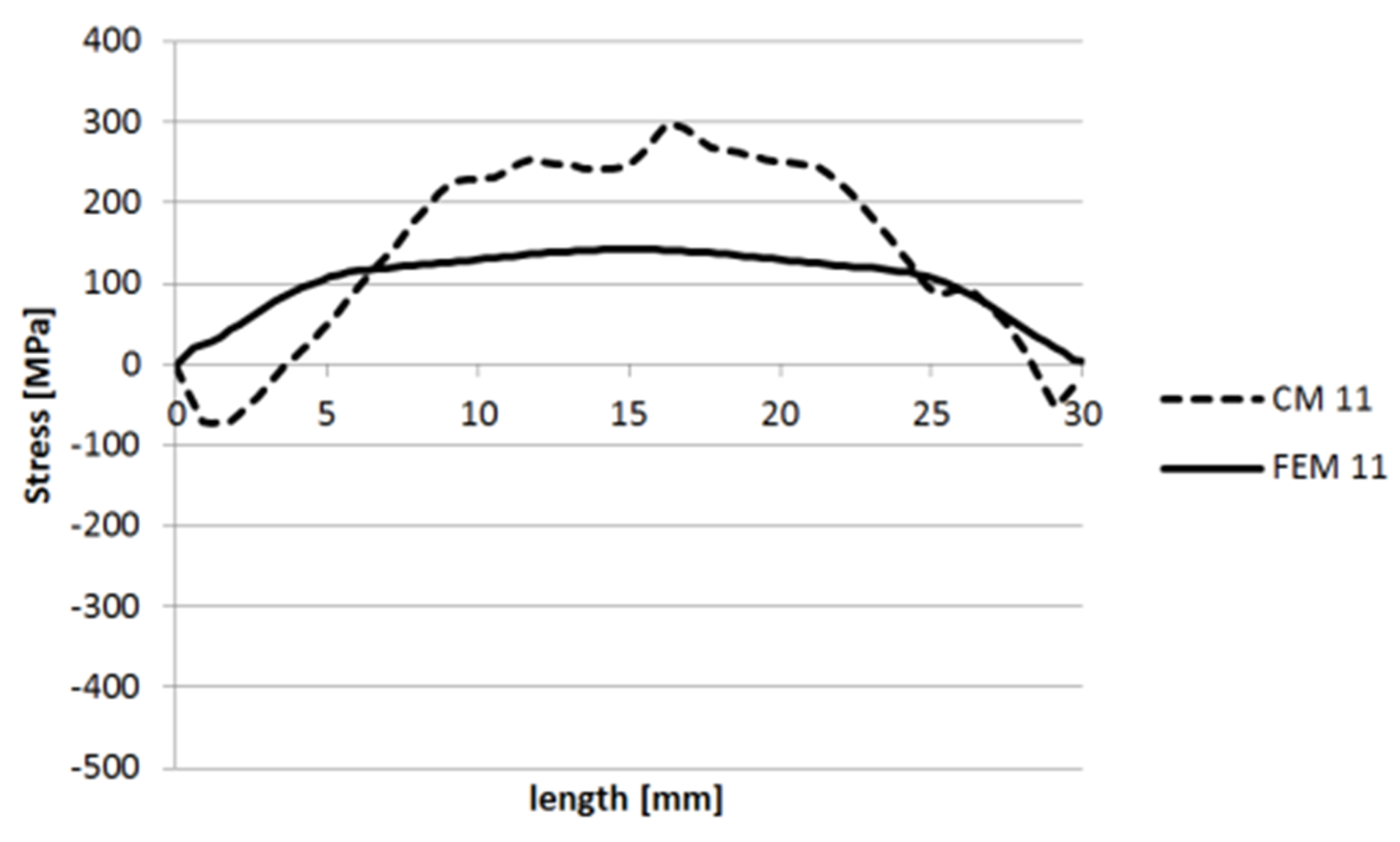
3.1.1. Specimen 1
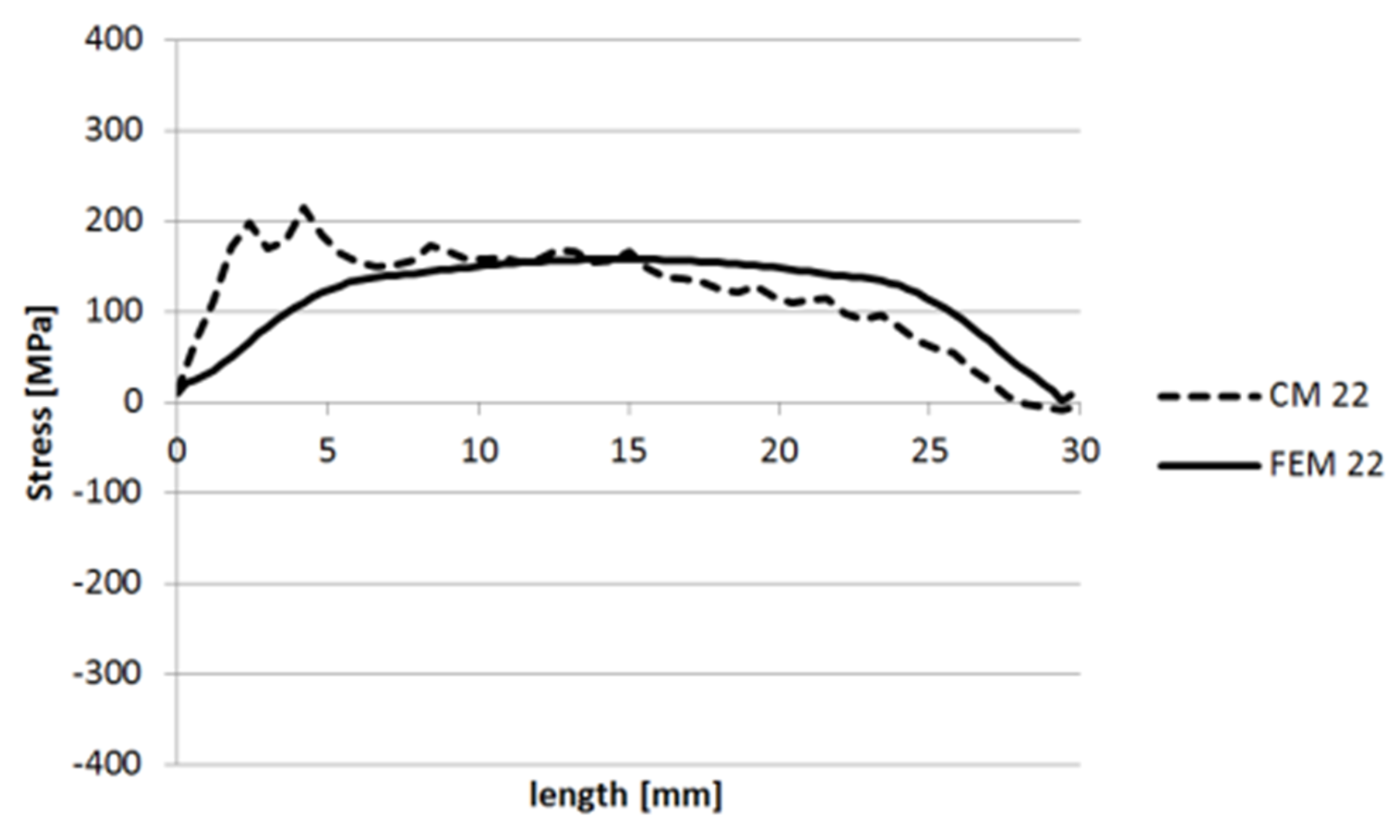
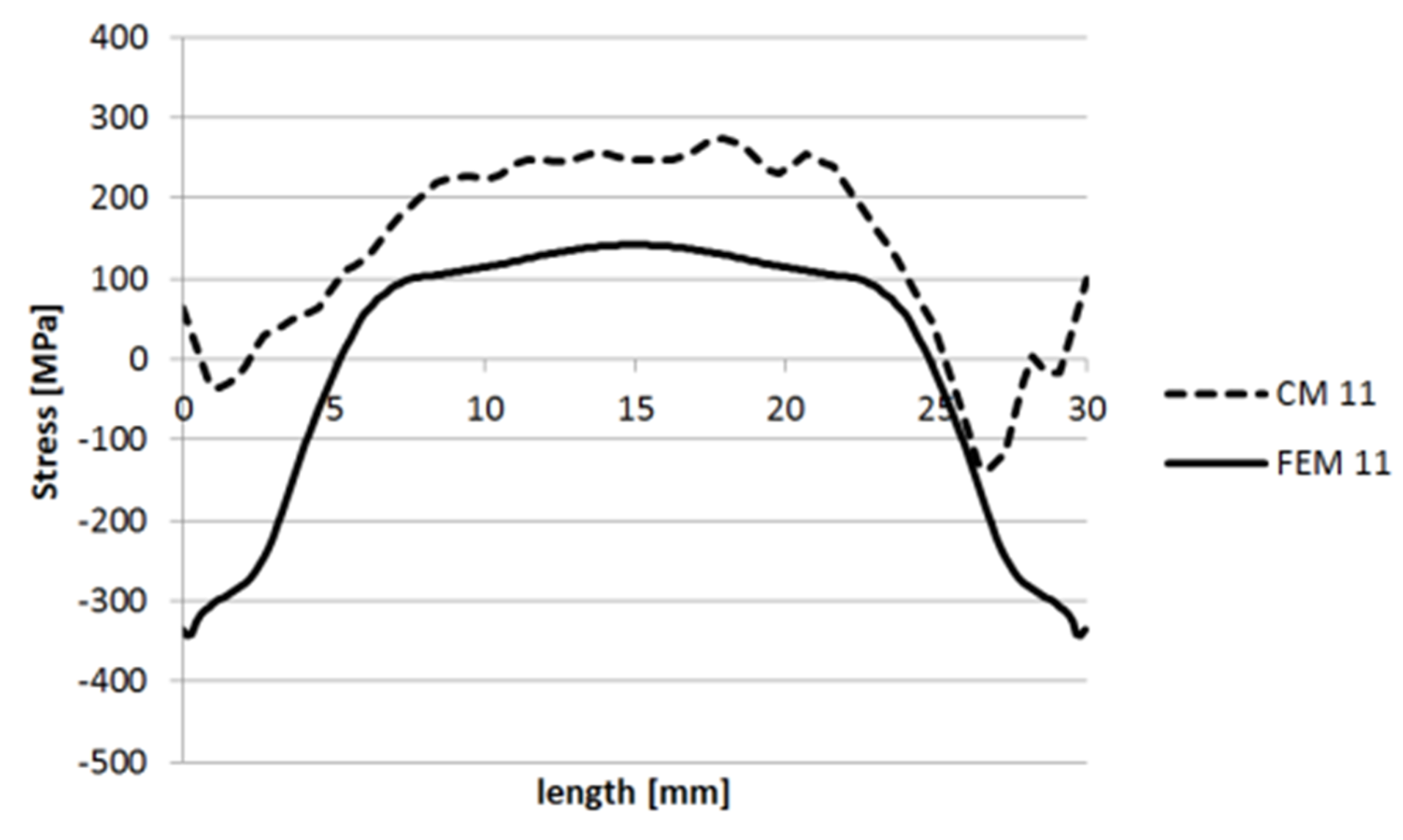
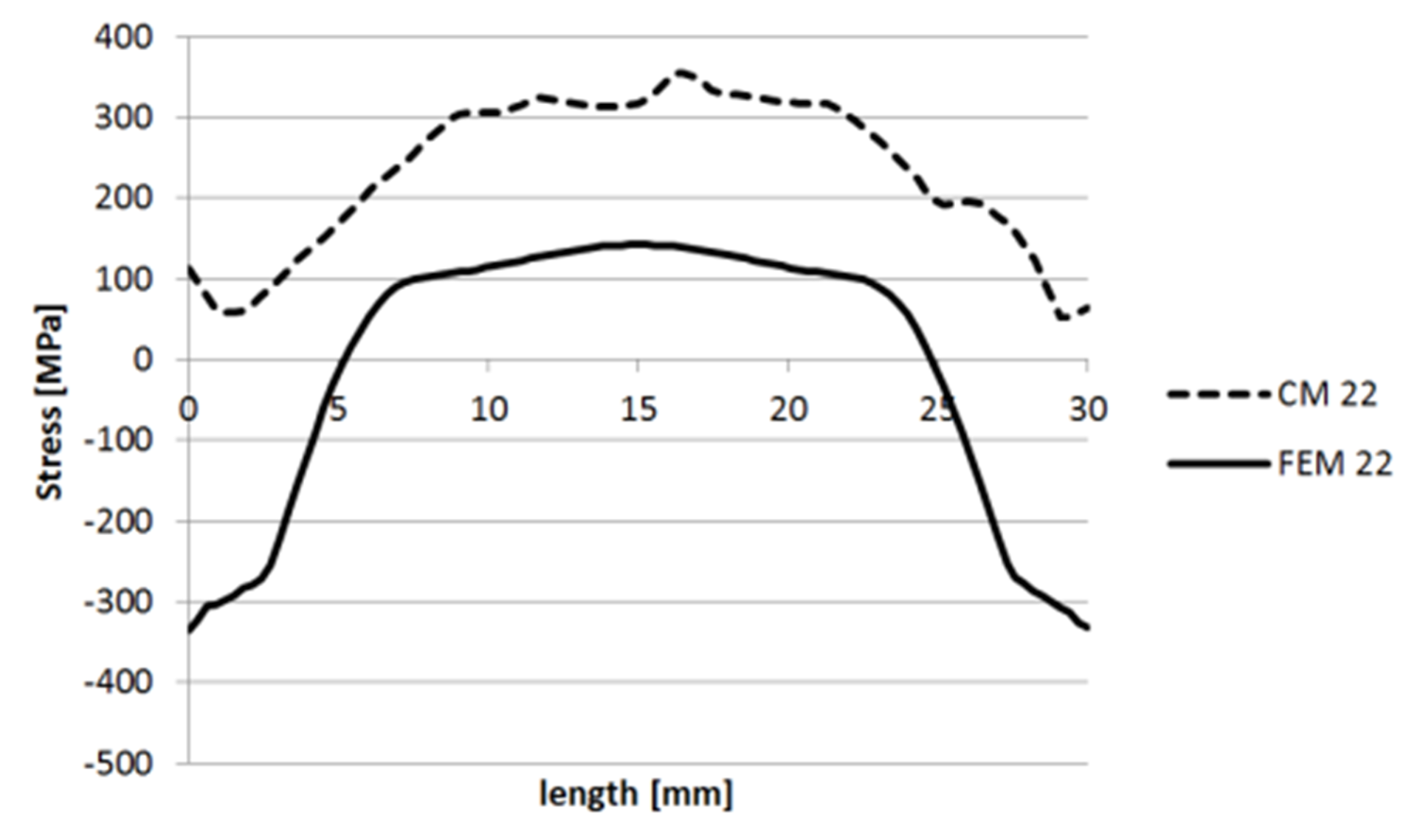
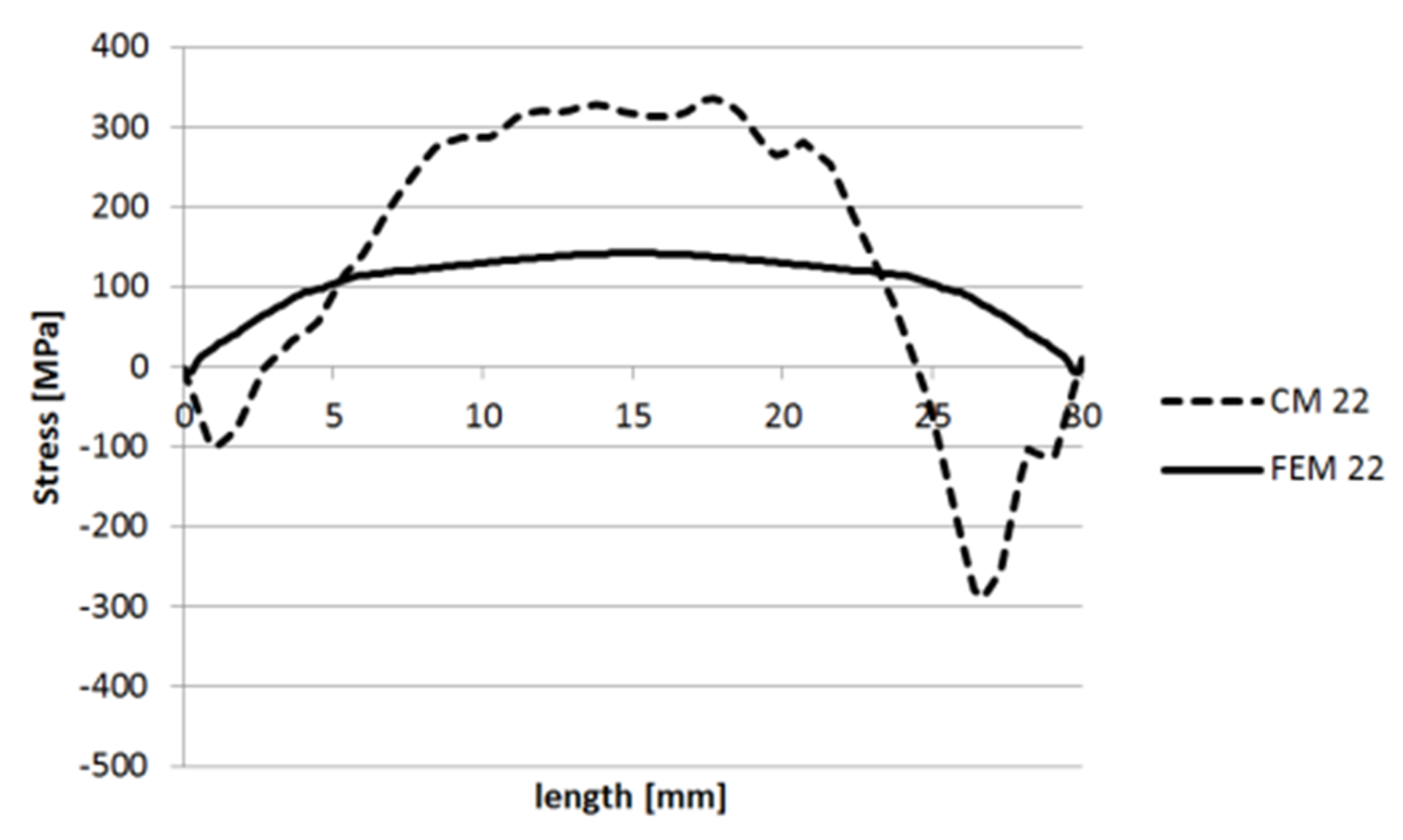
3.1.2. Specimen 2—Cut 1
3.1.3. Specimen 2—Cut 2
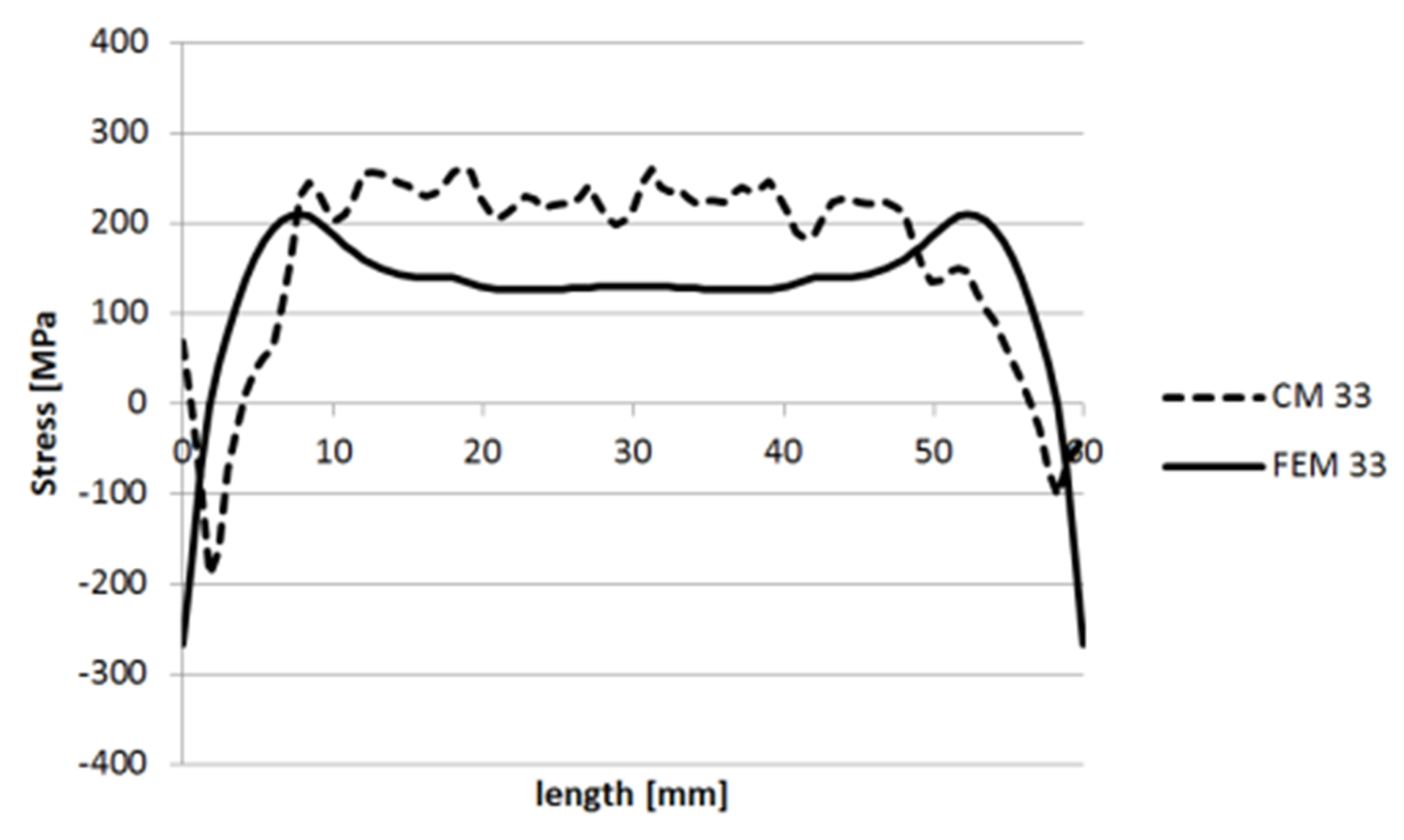
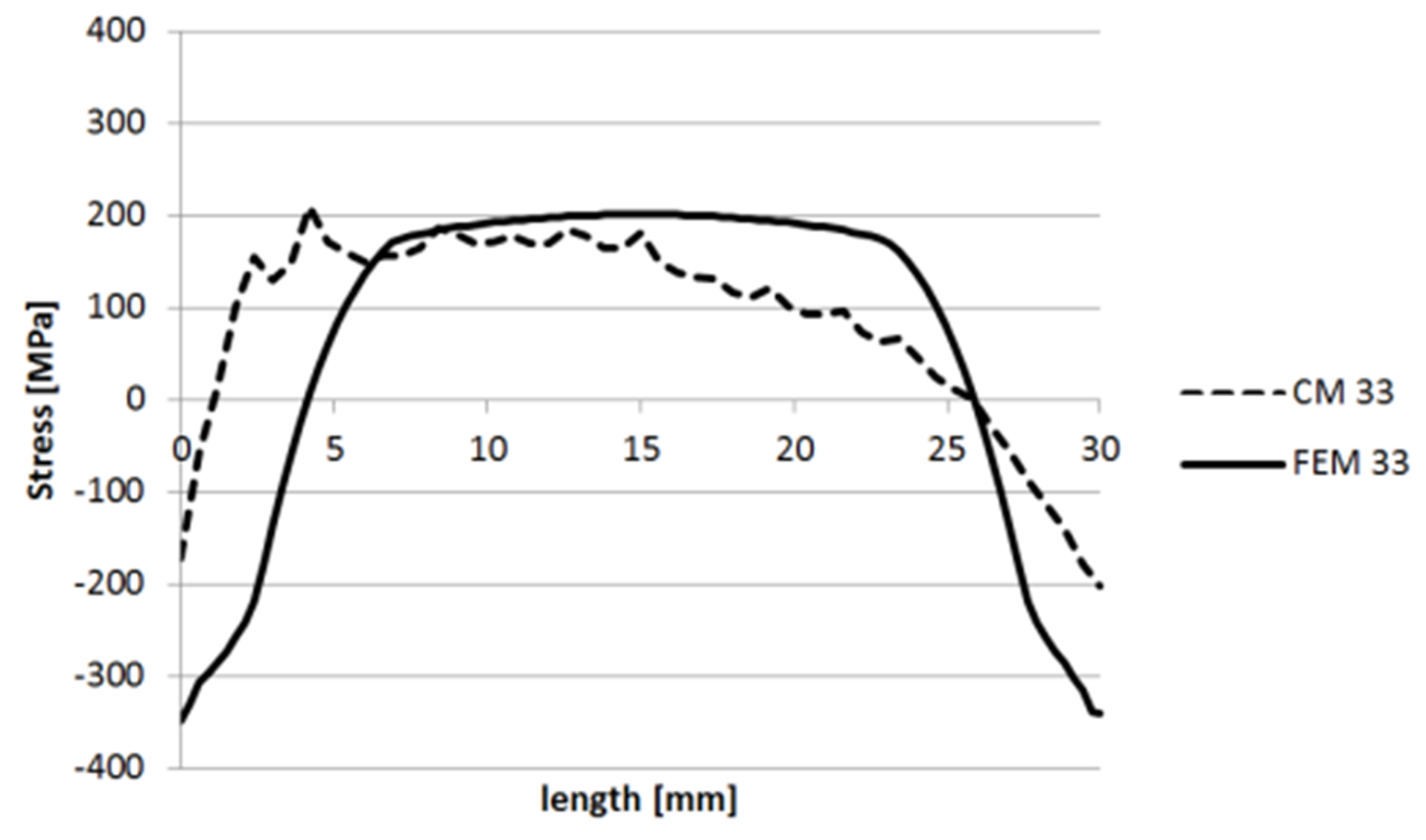
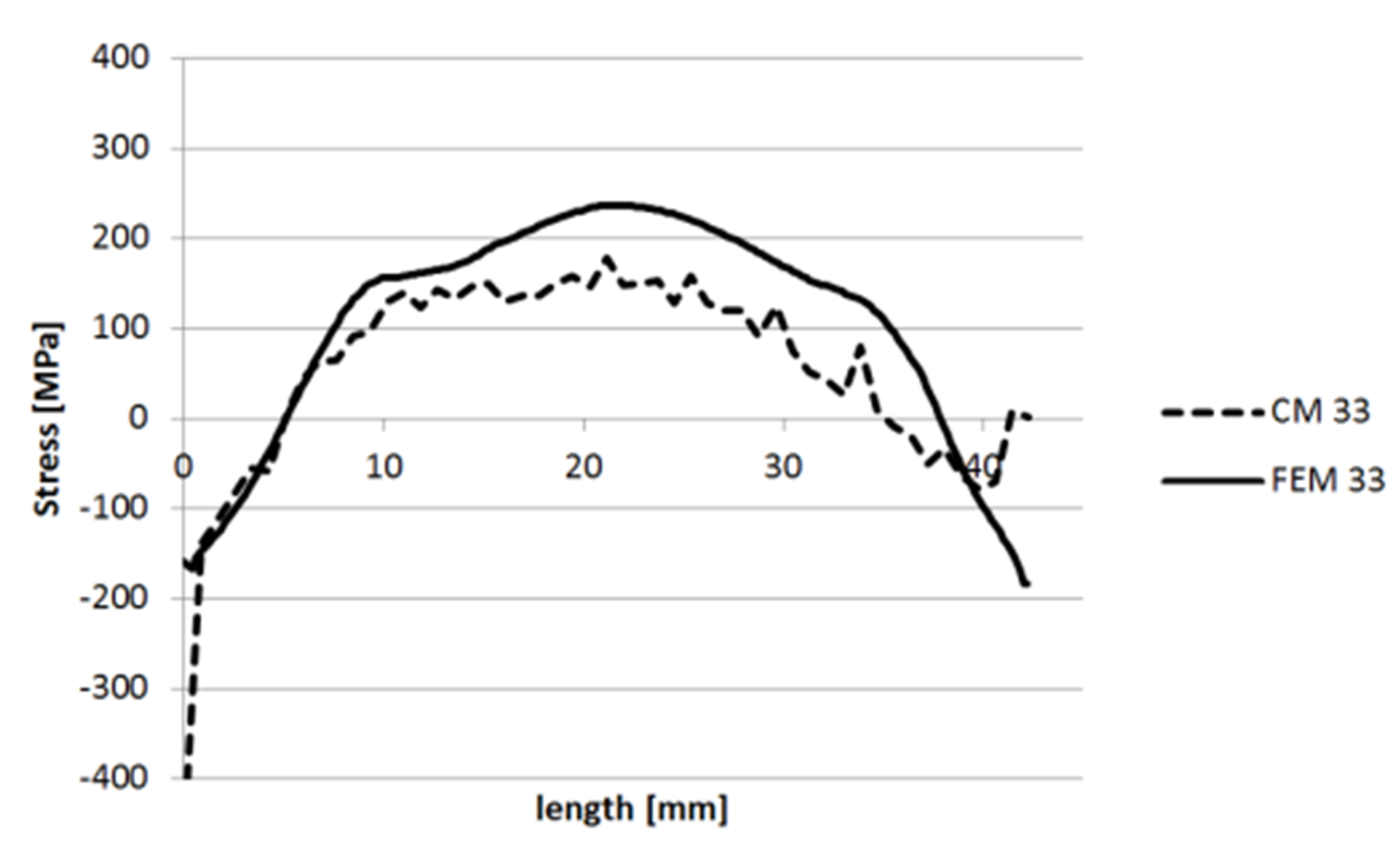
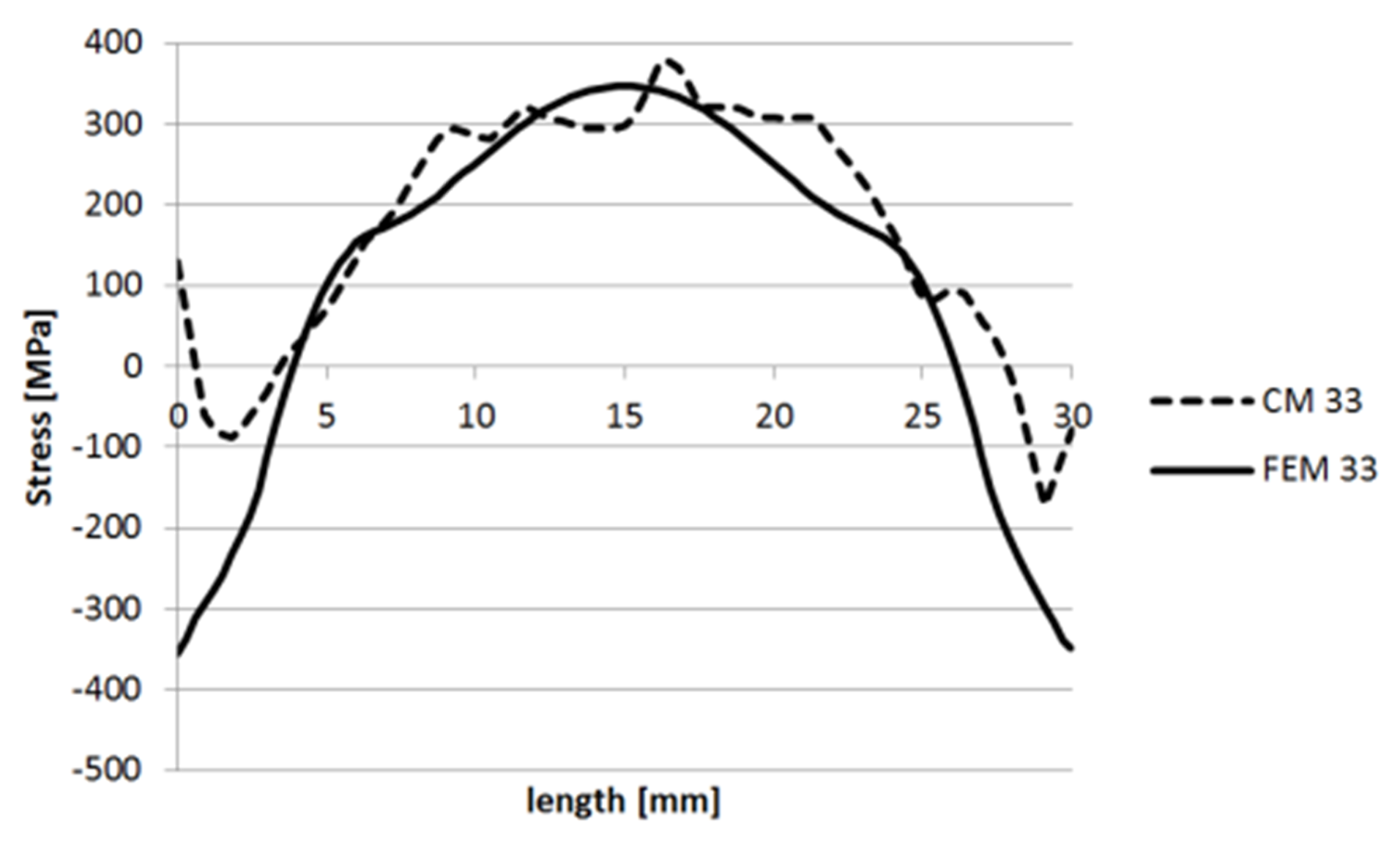
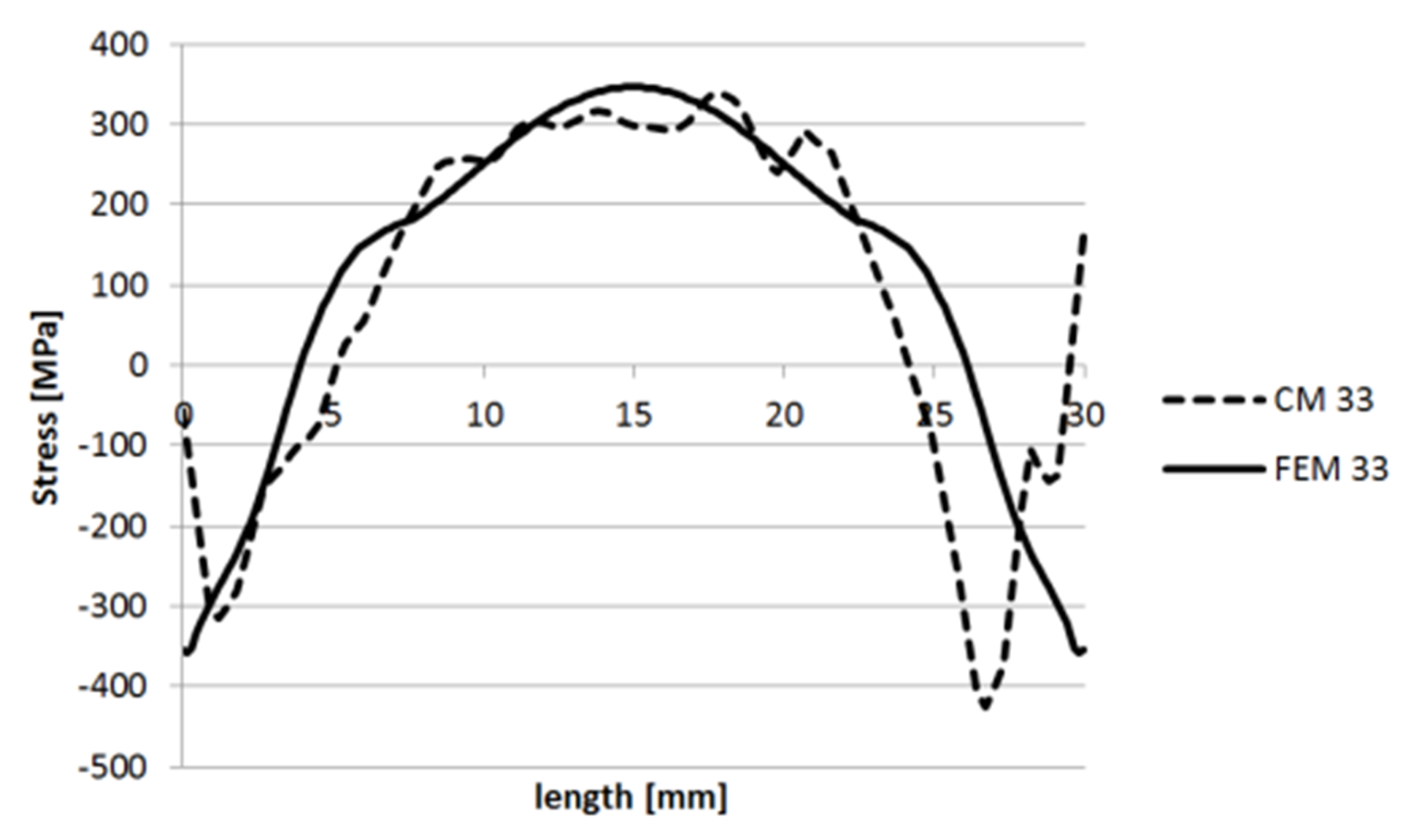
3.1.4. Specimen 3
3.1.5. Specimen 5
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Withers, P.J. Recent advances in residual stress measurement. Int. J. Press. Vessel. Pip. 2008, 85, 118–127. [Google Scholar] [CrossRef]
- Rendler, N.J.; Vigness, I. Hole-drilling strain-gage method of measuring residual stresses. Exp. Mech. 1966, 6, 577–586. [Google Scholar] [CrossRef]
- Hodek, J.; Zemko, M.; Shykula, P. Finite Element Model of Gear Induction Hardening. In Proceedings of the 8th International Conference on Electromagnetic Processing of Materials, Cannes, France, 12–16 October 2015. [Google Scholar]
- Schajer, G.S. (Ed.) Practical Residual Stress Measurement Methods; Wiley: Chichester, UK, 2013; Chapter 5; pp. 109–138. [Google Scholar]
- Hosseinzadeh, F.; Kowal, J.; Bouchard, P.J. Towards good practice guidelines for the contour method of residual stress measurement. J. Eng. 2014, 2014, 453–468. [Google Scholar] [CrossRef]
- Johnson, G. Residual Stress Measurements Using the Contour Method. Ph.D. Thesis, University of Manchester, Manchester, UK, 2008. [Google Scholar]
- Džugan, J.; Spaniel, M.; Prantl, A.; Konopík, P.; Růžička, J.; Kuzelka, J. Identification of ductile damage parameters for pressure vessel steel. Nucl. Eng. Des. 2018, 372–380. [Google Scholar] [CrossRef]
- AchouriI, A.; Bouchard, P.J.; Kabra, S.; Hosseinzadeh, F. Asymmetric cuts in the contour method for residual stress measurement. In Proceedings of the 7th International Conference on Mechanics and Materials in Design, Albufeira, Portugal, 11–15 June 2017. [Google Scholar]
- Prime, M.B.; Kastengren, A.L. The contour method cutting assumption: Error minimization and correction. In Experimental and Applied Mechanics; Springer: New York, NY, USA, 2011; Volume 6, pp. 233–250. [Google Scholar]
- Sun, Y.L.; Roy, M.; Vasileiou, A.; Smith, M.; Francis, J.; Hosseinzadeh, F. Evaluation of errors associated with cutting-induced plasticity in residual stress measurements using the contour method. Exp. Mech. 2017, 57, 719–734. [Google Scholar] [CrossRef] [PubMed]
- Hutchings, M.T.; Withers, P.J.; Holden, T.M.; Lorentzen, T. Introduction to the Characterization of Residual Stress by Neutron Diffraction; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- GNU OCTAVE, Version 4.0.0. Available online: https://octave.org/doc/interpreter/ (accessed on 20 October 2017).
- JMatPro, Version 10. Available online: https://www.sentesoftware.co.uk/ (accessed on 20 October 2017).
- Poláková, I.; Kubina, T. Flow stress determination methods for numerical modelling. In Proceedings of the 22nd International Conference on Metallurgy and materials, Brno, Czech Republic, 15–17 May 2013; p. 17. [Google Scholar]
- MARC MENTAT, Version 2017.1.0. Available online: http://www.mscsoftware.com/product/marc (accessed on 20 October 2017).
- Mikula, P.; Strunz, P. The Use of Thermal Neutron Beams at Medium Power Reactor LWR-15 in Řež for Competetive Neutron Research. In Proceedings of the International Conference on Research Reactors: Safe Management and Effective Utilization, Vienna, Austria, 16–20 November 2015; p. 35. [Google Scholar]
- Pagliaro, P.; Prime, M.B.; Robinson, J.S.; Clausen, B.; Swenson, H.; Steinzig, M.; Zuccarello, B. Measuring inaccessible residual stresses using multiple methods and superposition. Exp. Mech. 2011, 51, 1123–1134. [Google Scholar] [CrossRef]
- Kartal, M.E.; Liljedahl, C.; Gungor, S.; Edwards, L.; Fitzpatrick, M. Determination of the complete residual stress tensor in VPPA weld using the multi-axial contour method. Acta Mater. 2008, 56, 4417–4428. [Google Scholar] [CrossRef]
- Navalho, D.; Deus, A.M.; Infante, V. Residual Stresses Due to Quenching in Aluminum Forging Parts for Aerospace Applications: Finite Element Analysis and Contour Method Measurement. In Proceedings of the 6th International Quenching and Control of Distortion Conference American Society for Metals, Chicago, IL, USA, 9–13 September 2012. [Google Scholar]









| C | Si | Mn | Cr | Mo | Ni | Cu | Fe |
|---|---|---|---|---|---|---|---|
| 0.021 | 0.534 | 1.335 | 16.66 | 2.003 | 10.447 | 0.489 | Bal. |
| Temperature [C] | 25 | 100 | 300 | 600 | 900 |
|---|---|---|---|---|---|
| Property | |||||
| Thermal conductivity [W/mK] | 14.57 | 15.58 | 18.24 | 22.20 | 26.14 |
| Specific heat [J/kgK] | 455.37 | 475.11 | 508.96 | 549.63 | 621.17 |
| Poisson’s ratio [-] | 0.298 | 0.301 | 0.31 | 0.324 | 0.338 |
| Young’s modulus [MPa] | 192.96 | 187.74 | 173.39 | 150.78 | 126.69 |
| Thermal expansivity 10-5 [1/K] | 1.78 | 1.80 | 1.84 | 1.91 | 1.99 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hodek, J.; Prantl, A.; Džugan, J.; Strunz, P. Determination of Directional Residual Stresses by the Contour Method. Metals 2019, 9, 1104. https://doi.org/10.3390/met9101104
Hodek J, Prantl A, Džugan J, Strunz P. Determination of Directional Residual Stresses by the Contour Method. Metals. 2019; 9(10):1104. https://doi.org/10.3390/met9101104
Chicago/Turabian StyleHodek, Josef, Antonín Prantl, Jan Džugan, and Pavel Strunz. 2019. "Determination of Directional Residual Stresses by the Contour Method" Metals 9, no. 10: 1104. https://doi.org/10.3390/met9101104
APA StyleHodek, J., Prantl, A., Džugan, J., & Strunz, P. (2019). Determination of Directional Residual Stresses by the Contour Method. Metals, 9(10), 1104. https://doi.org/10.3390/met9101104






