On Phenomenological Failure Loci of Metals under Constant Stress States of Combined Tension and Shear: Issues of Coaxiality and Non-Uniqueness
Abstract
1. Introduction
2. Review of the Methodology for Failure Characterization using Stress Invariants and the Equivalent Stress or Strain
2.1. Characterization of the Stress State
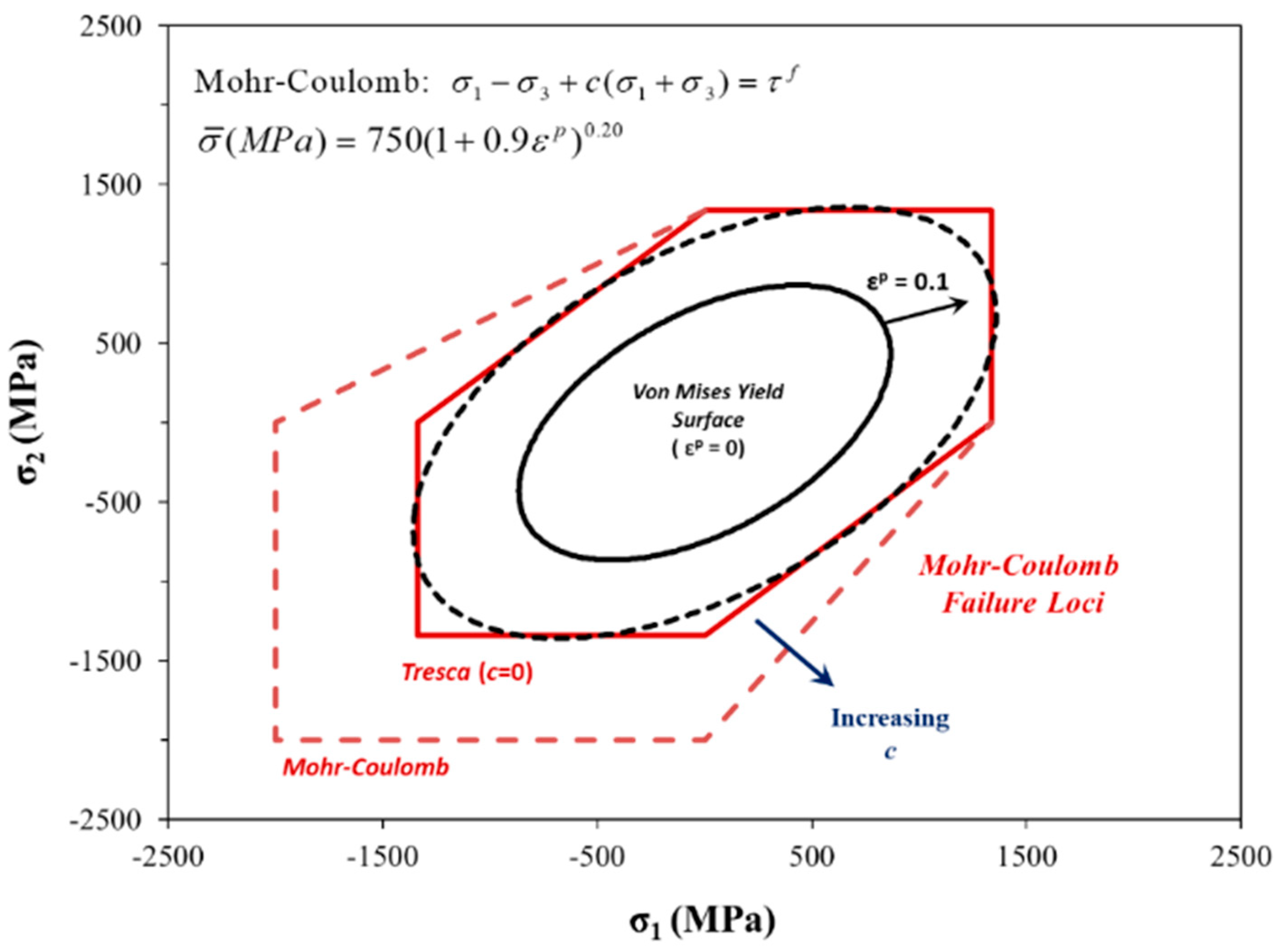
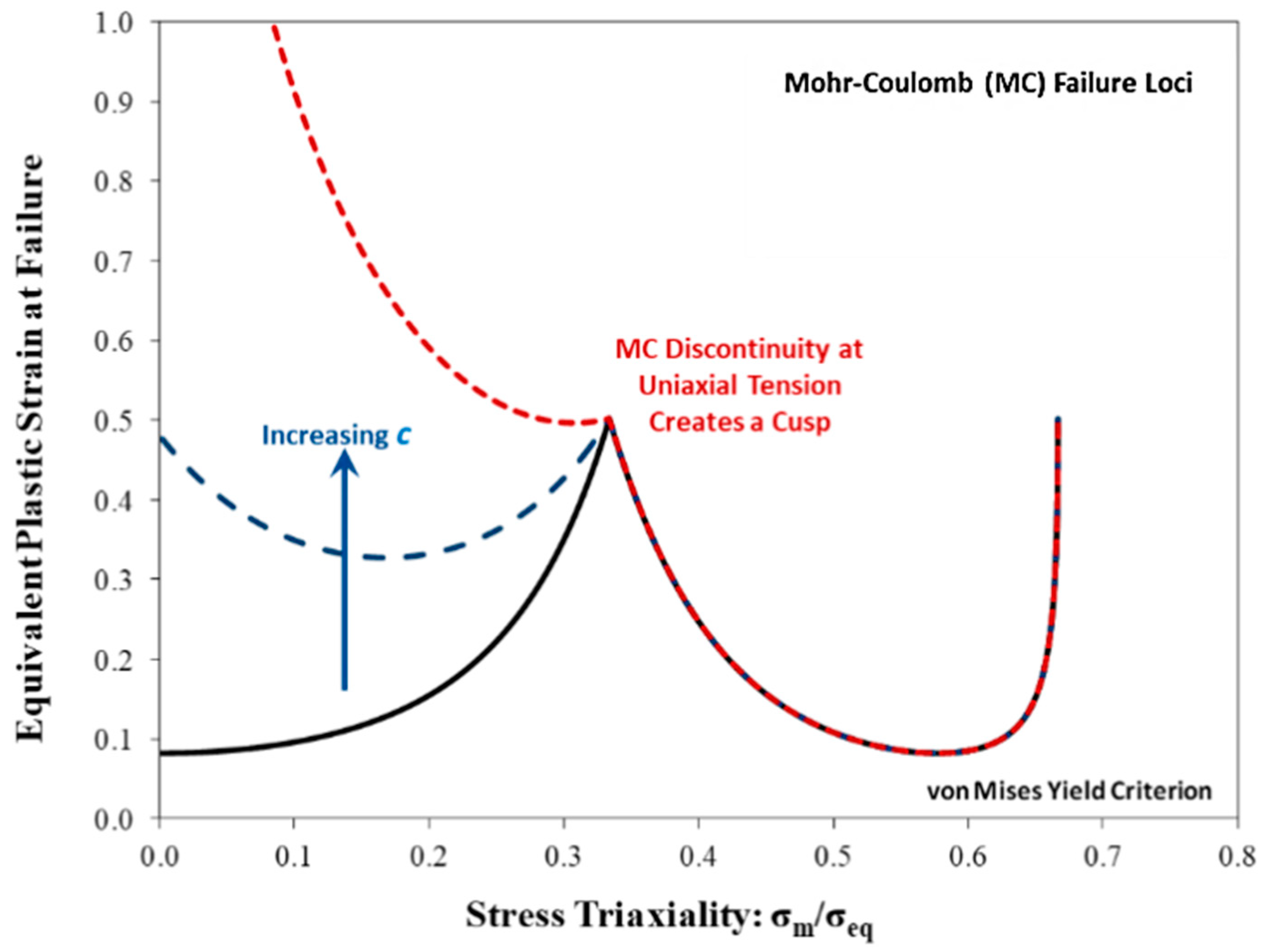
2.2. Phenomenological Descriptions of the Failure Locus
2.3. MMC Failure Criterion and Assumptions of Proportional Loading
3. Proportional Loading: Coaxial and Non-Coaxial Deformation
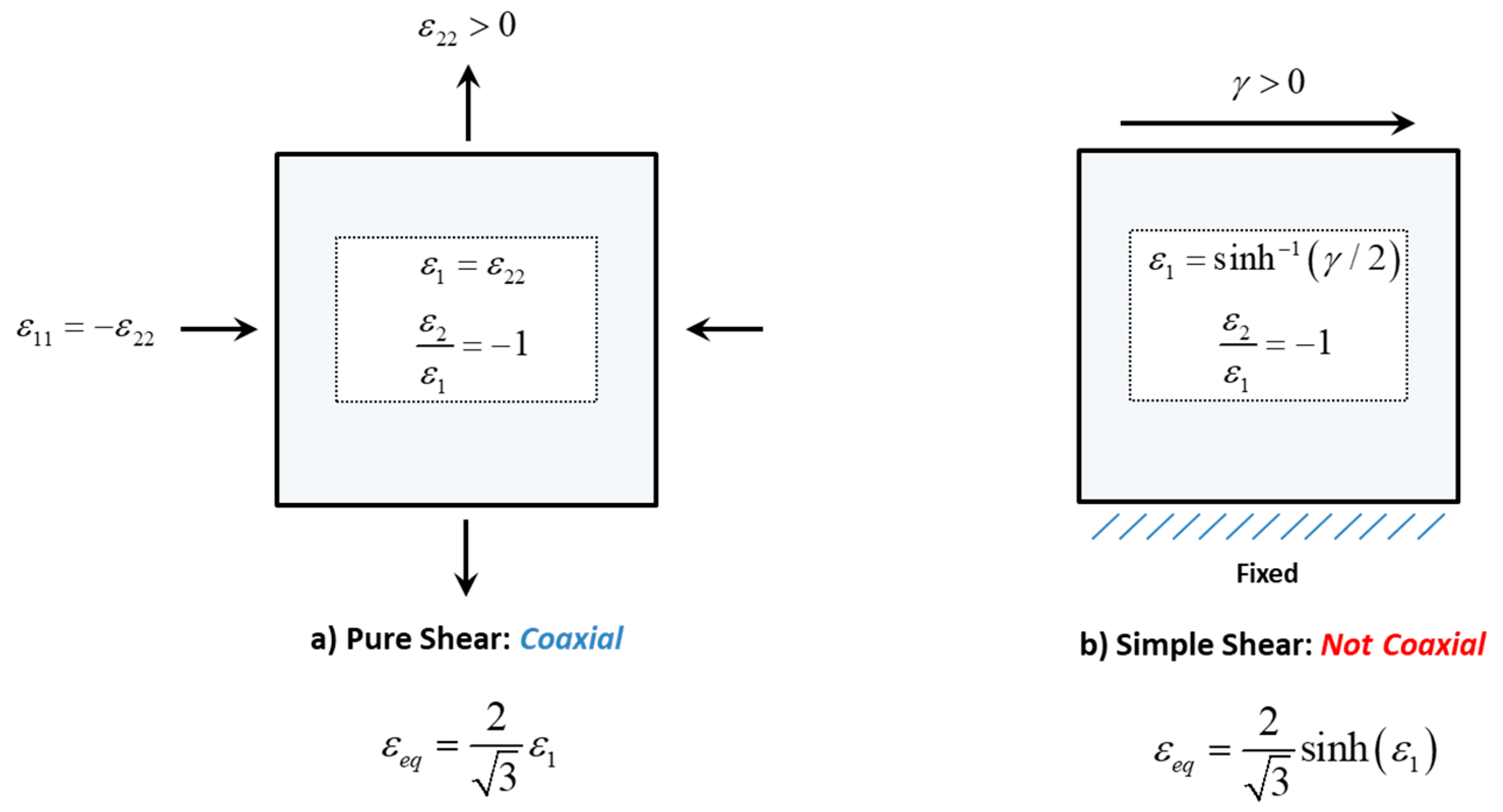
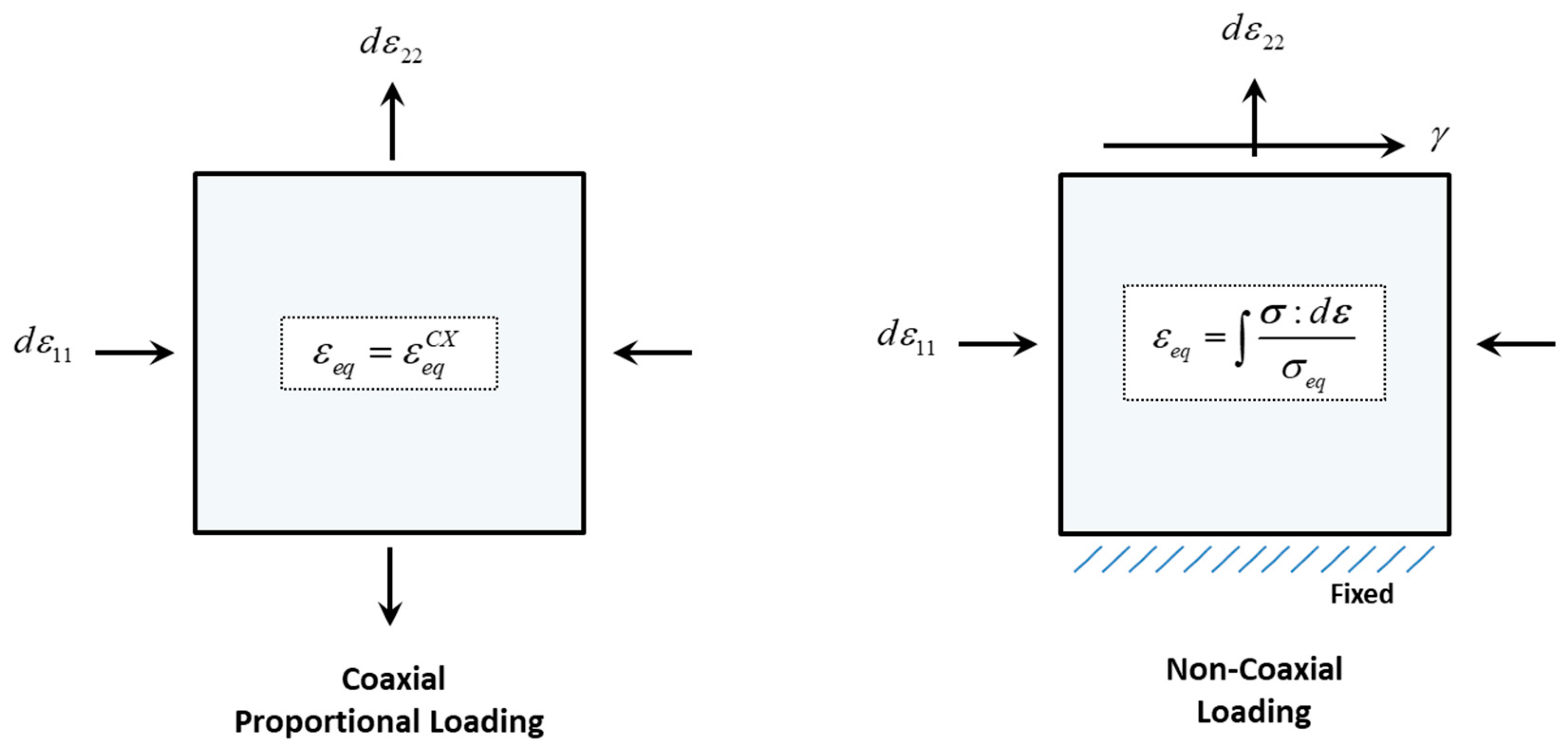
3.1. Definition of Proportional Coaxial Loading and Equivalent Strain
- Monotonic loading is applied in the same direction(s) for the duration of the test.
- The components of the stress and cumulative strain tensors can be expressed as constant ratios of one another. Consequently, the equivalent plastic strain is proportional to the principal plastic strain.
- The axes of the principal stress and the cumulative principal strains are aligned (coaxial). The incremental principal strain and the principal stresses are always aligned.
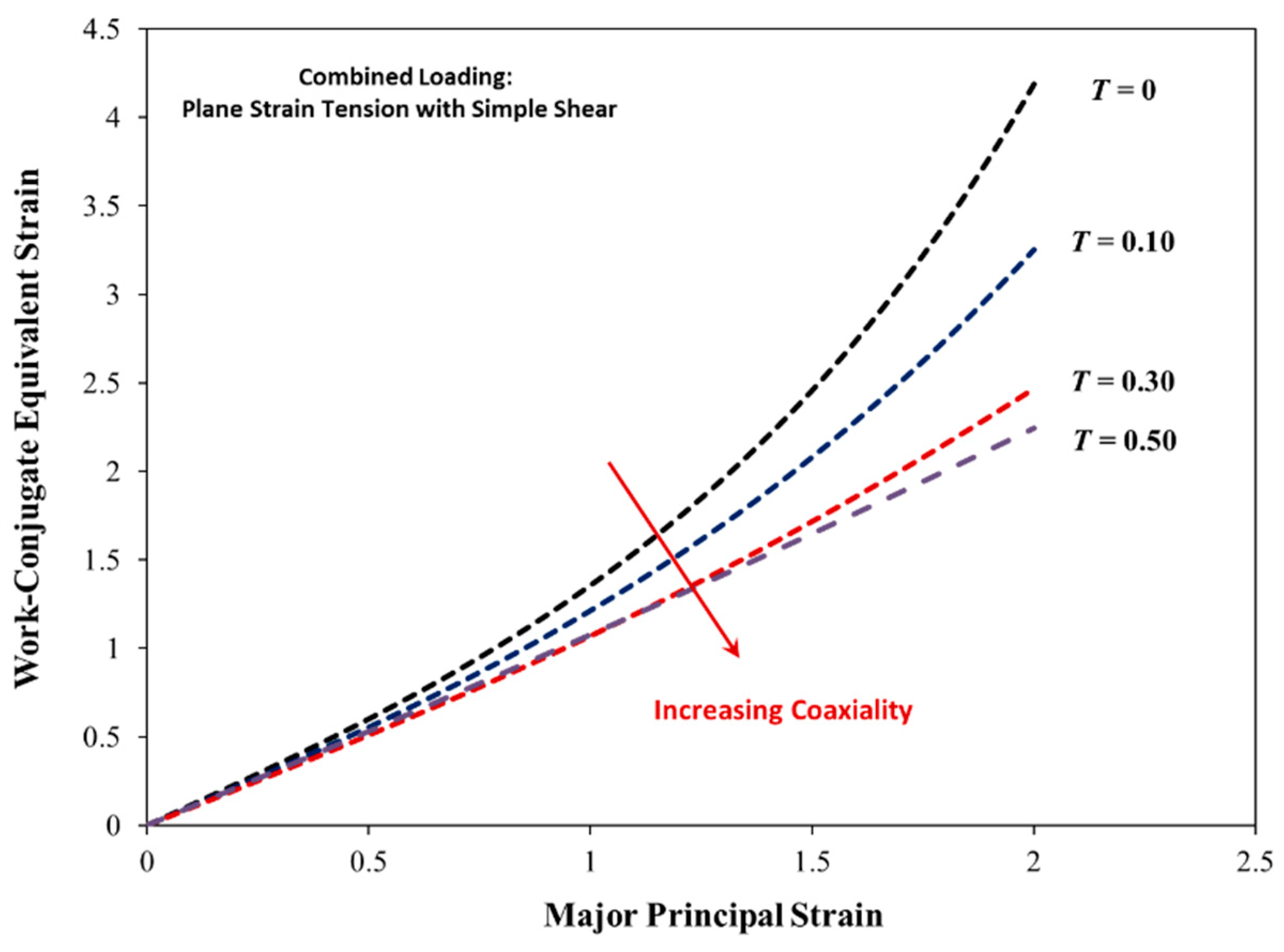
3.2. Shear Loading: Equivalent Stress States with Different Work-Conjugate Equivalent Strains
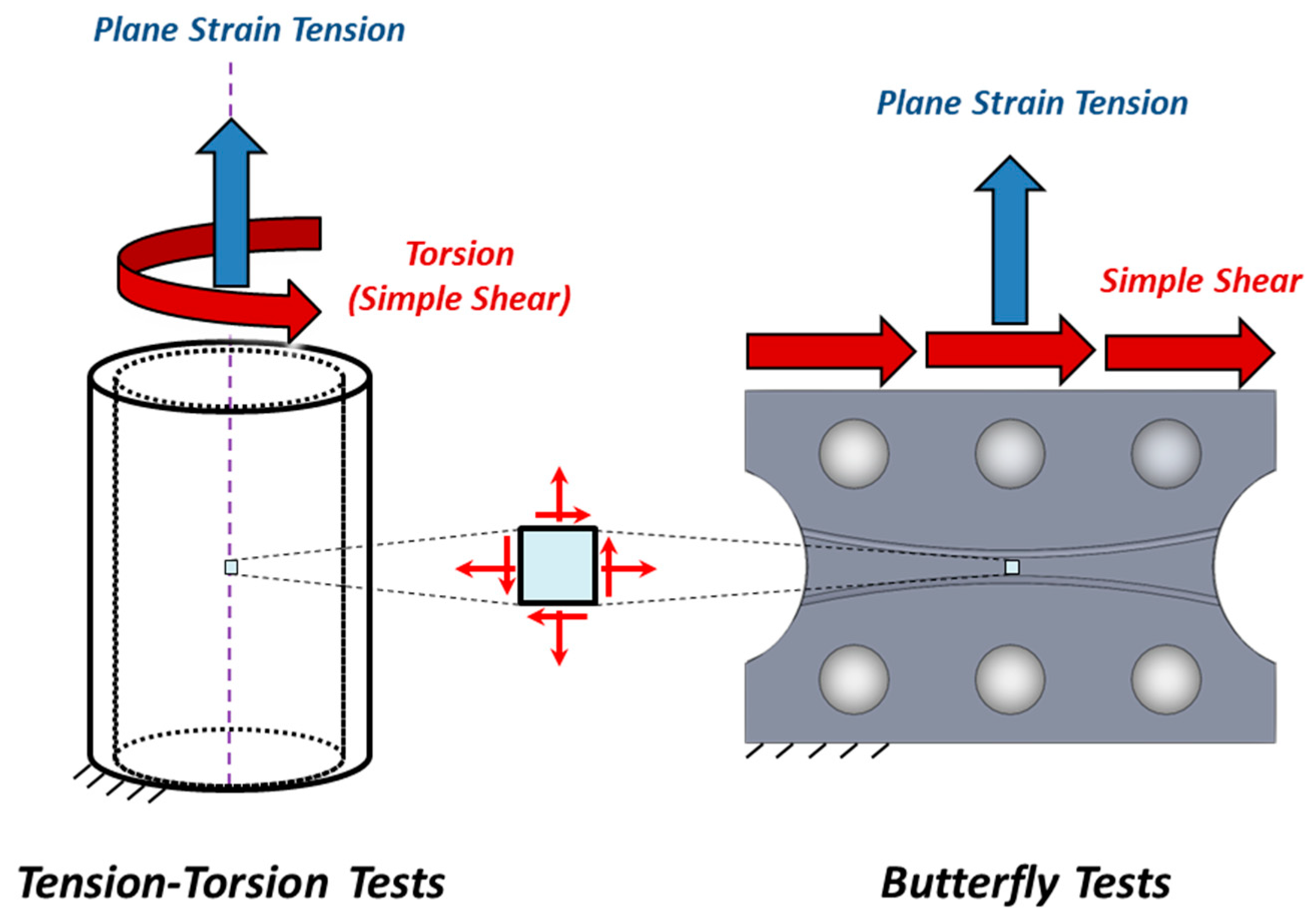
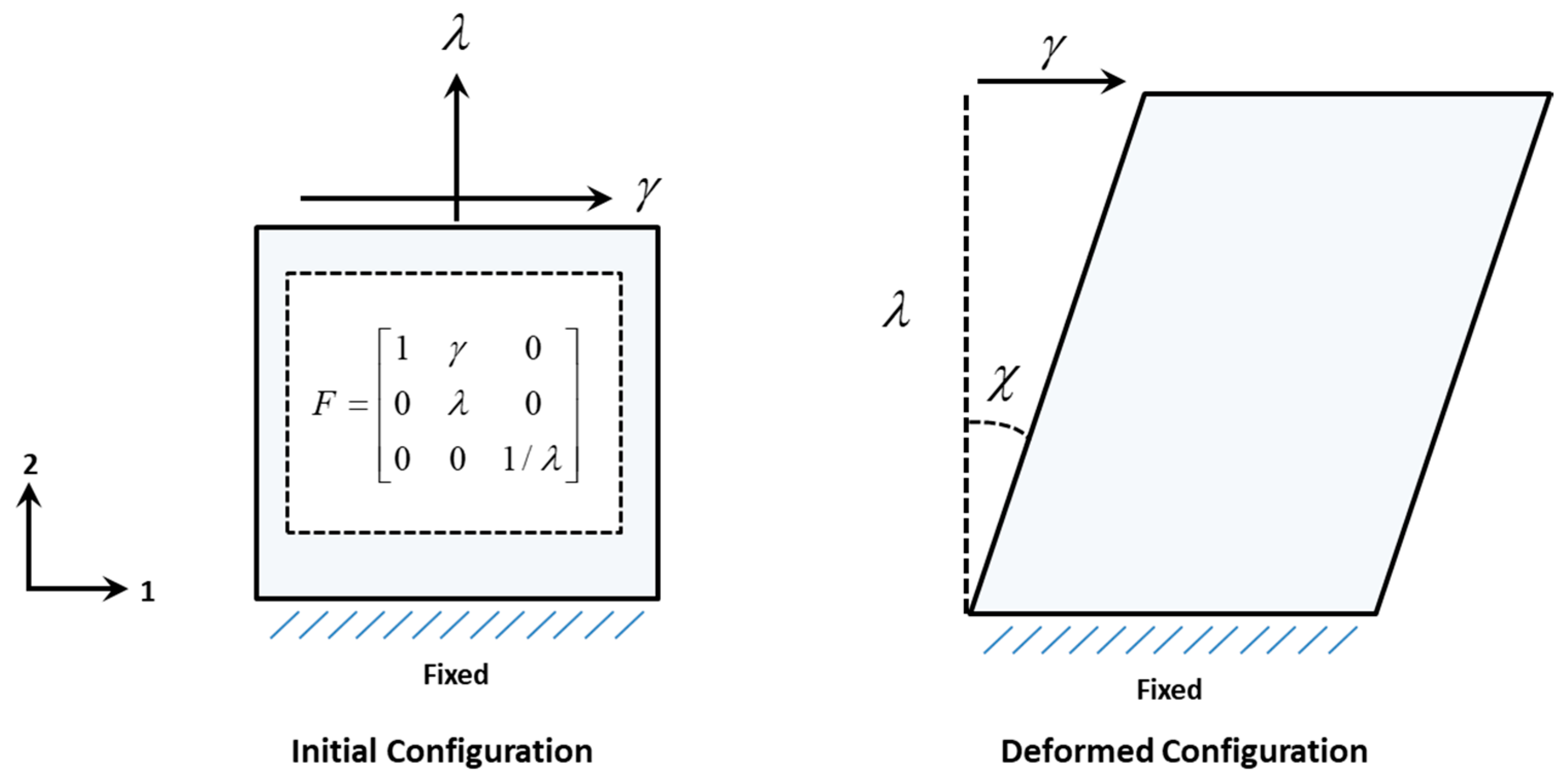
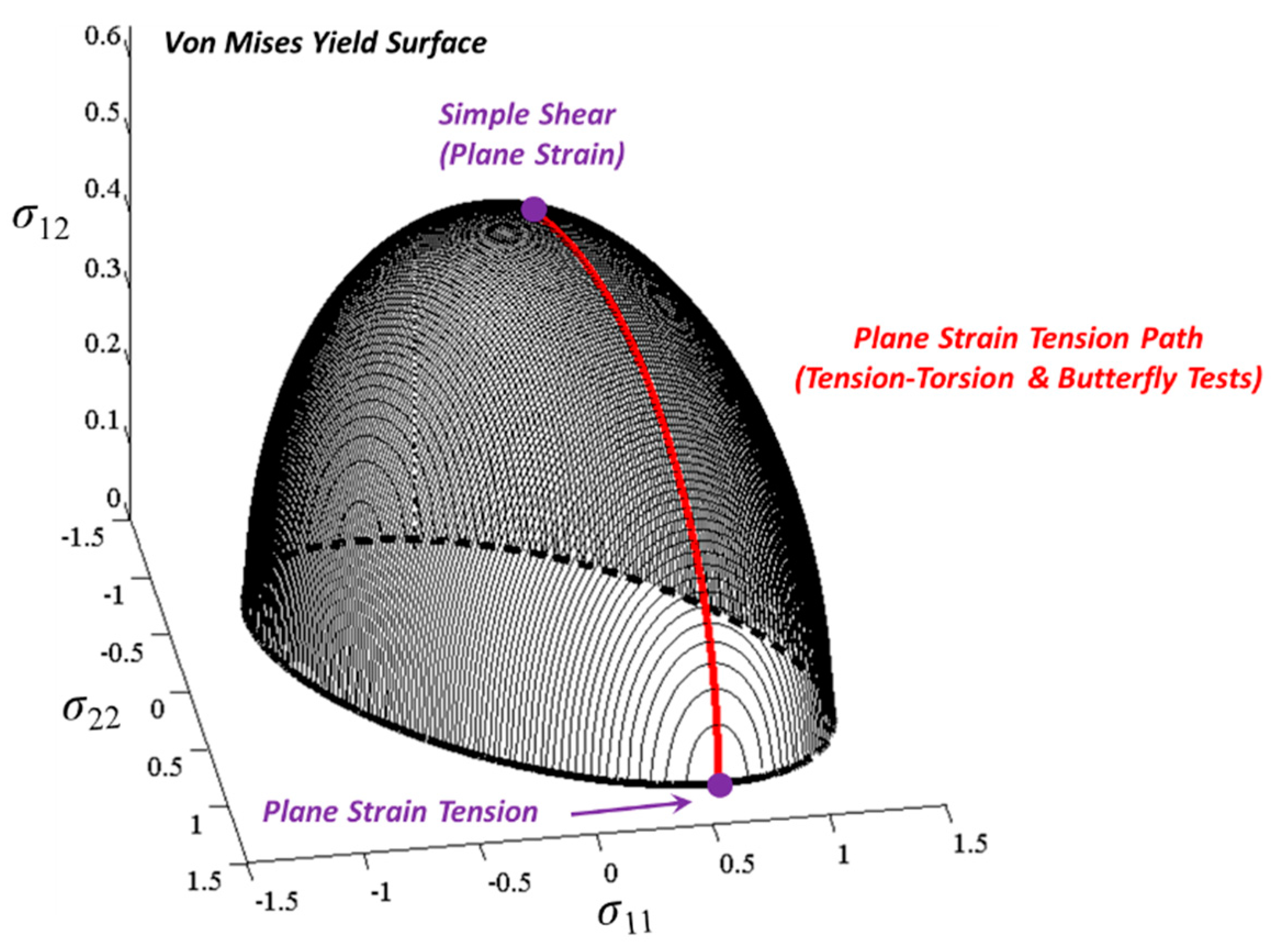
3.3. Mechanics of Combined Plane Strain Tension and Simple Shear in Plane Stress
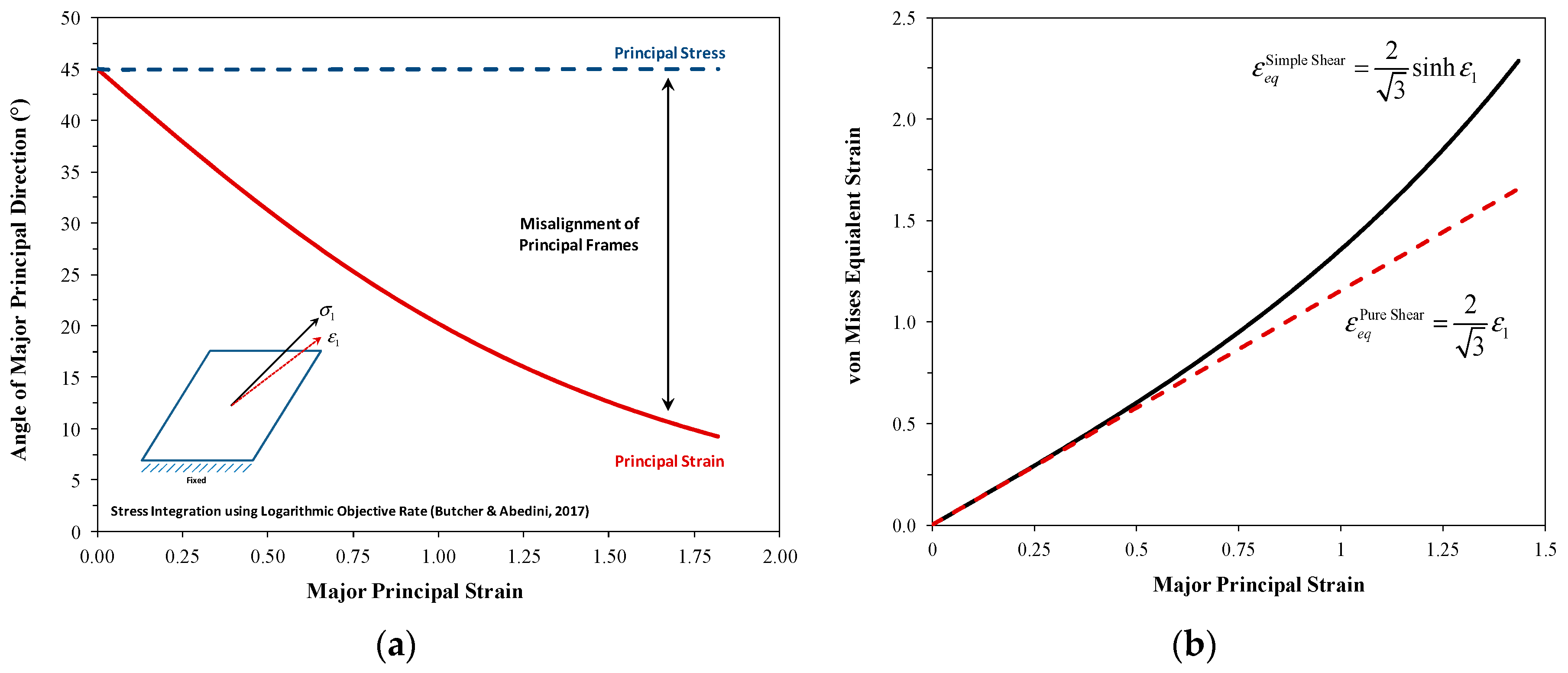
3.4. Application of Non-Coaxial Equivalent Strain to the Tension–Torsion Results of Haltom et al. (2013) and Scales et al. (2016) for AA6061-T6
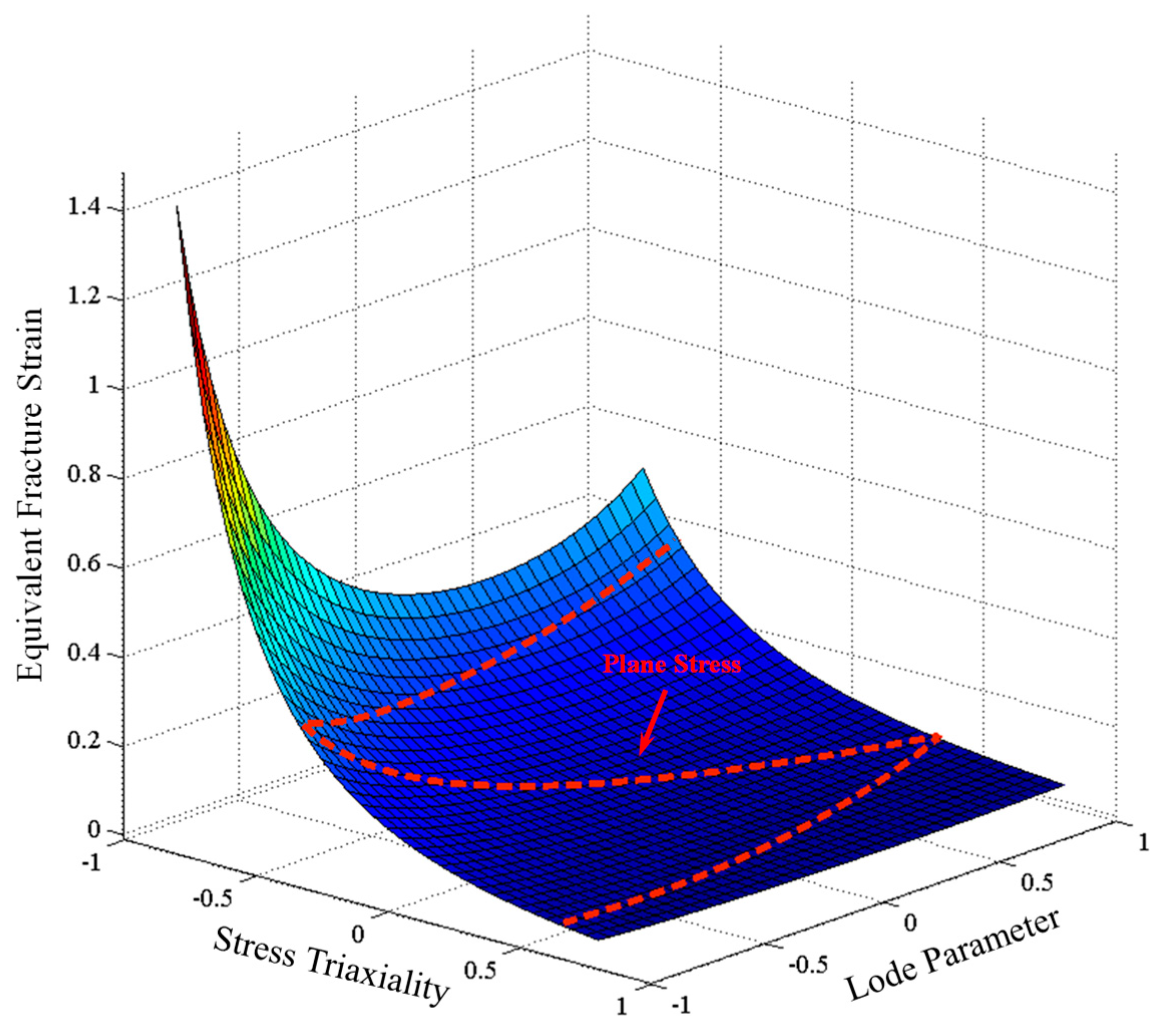
4. Dependence of Failure Loci on the Characterization Tests
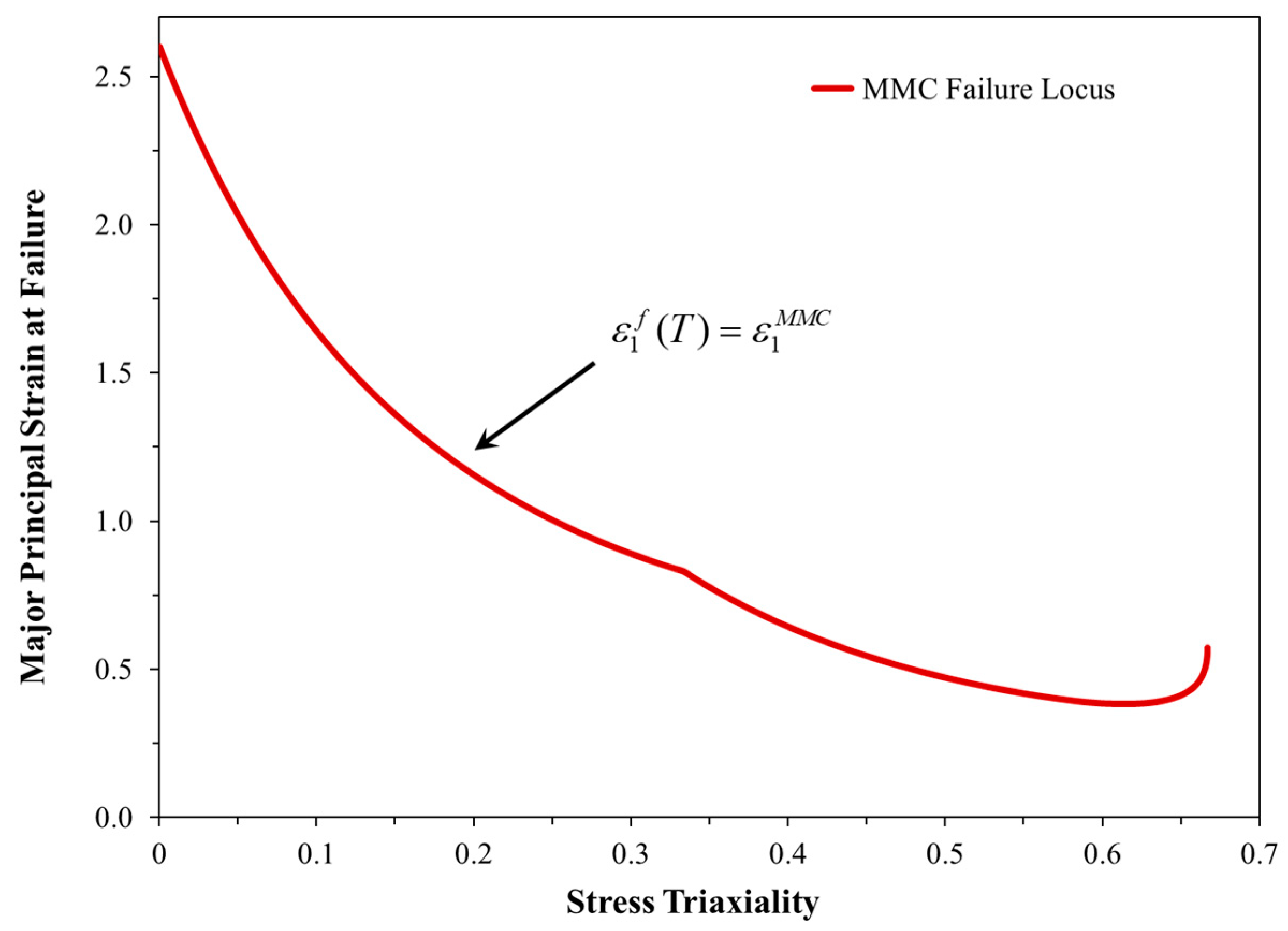
4.1. Construction of a Coaxial Failure Locus Based Upon the Major Principal Strain
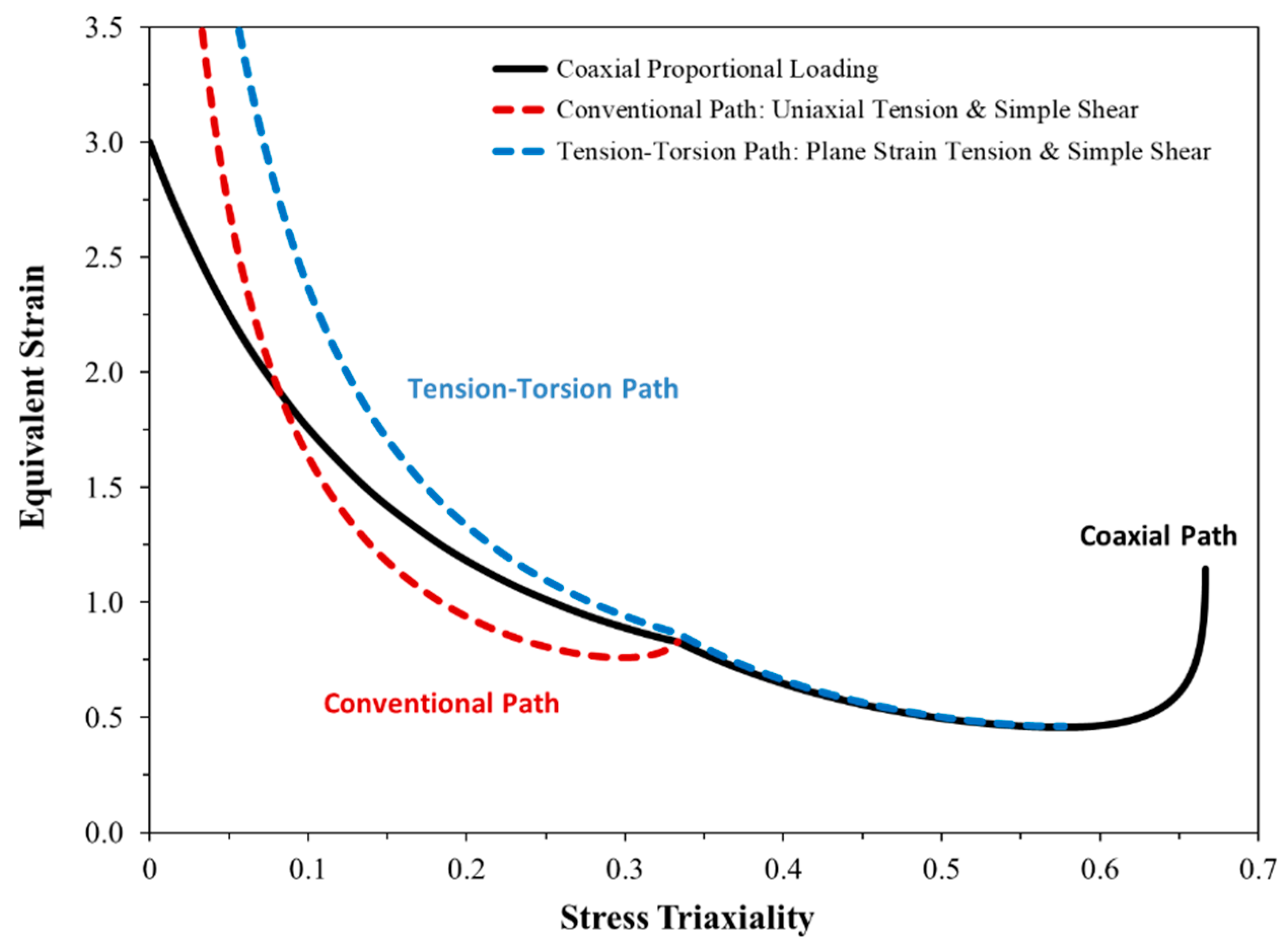
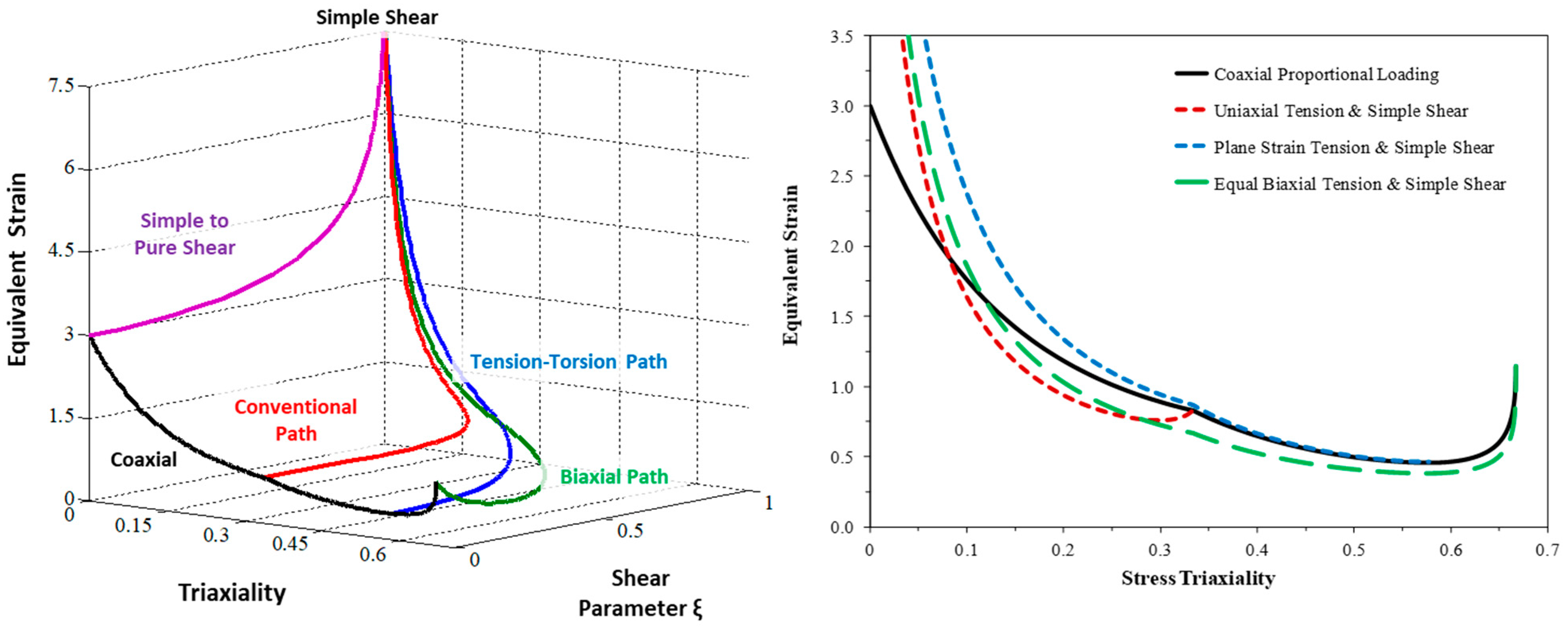
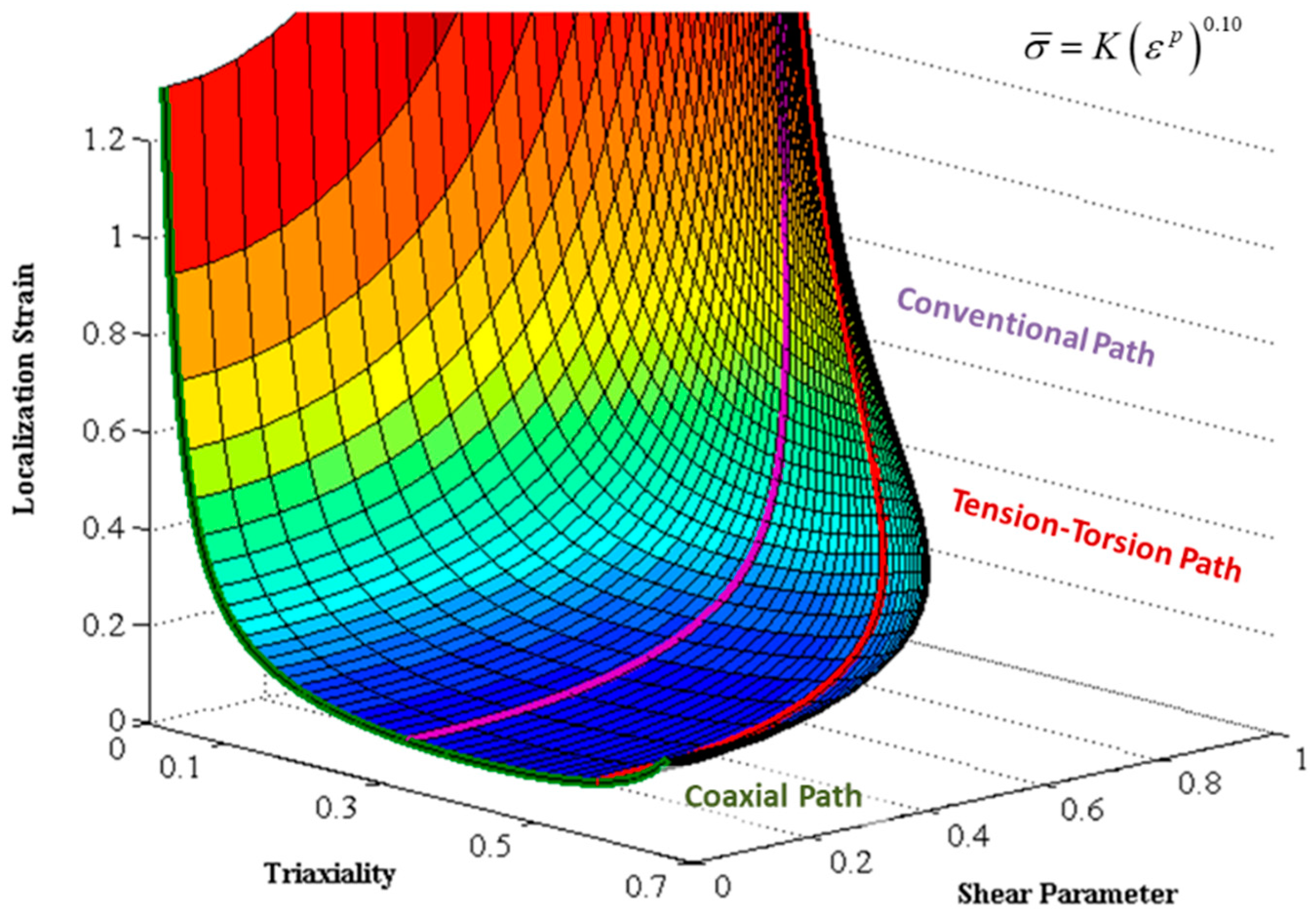
4.2. Generation of Failure Loci Based Upon the Equivalent Plastic Strain
- 1
- Coaxial path from pure shear to equal biaxial tension;
- 2
- Conventional path from simple shear to uniaxial tension and then equal biaxial tension;
- 3
- Tension–torsion path from simple shear to plane strain tension and then equal biaxial tension;
- 4
- Biaxial path from simple shear to equal biaxial tension; and
- 5
- Shear path from pure shear to simple shear where the stress triaxiality remains zero.
4.3. Characterization of the Plane Stress State for Coaxial and Non-Coaxial Proportional Loading
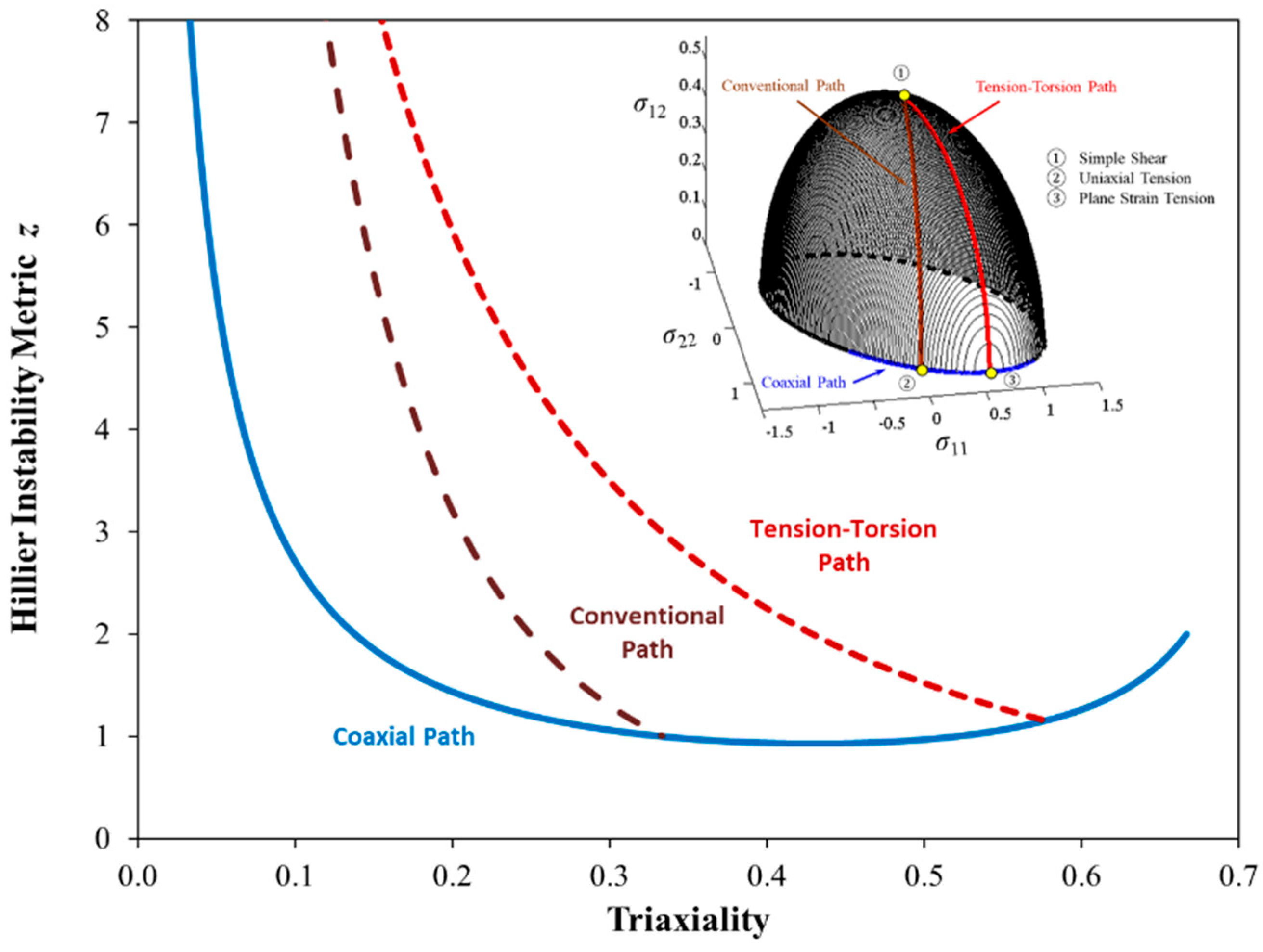
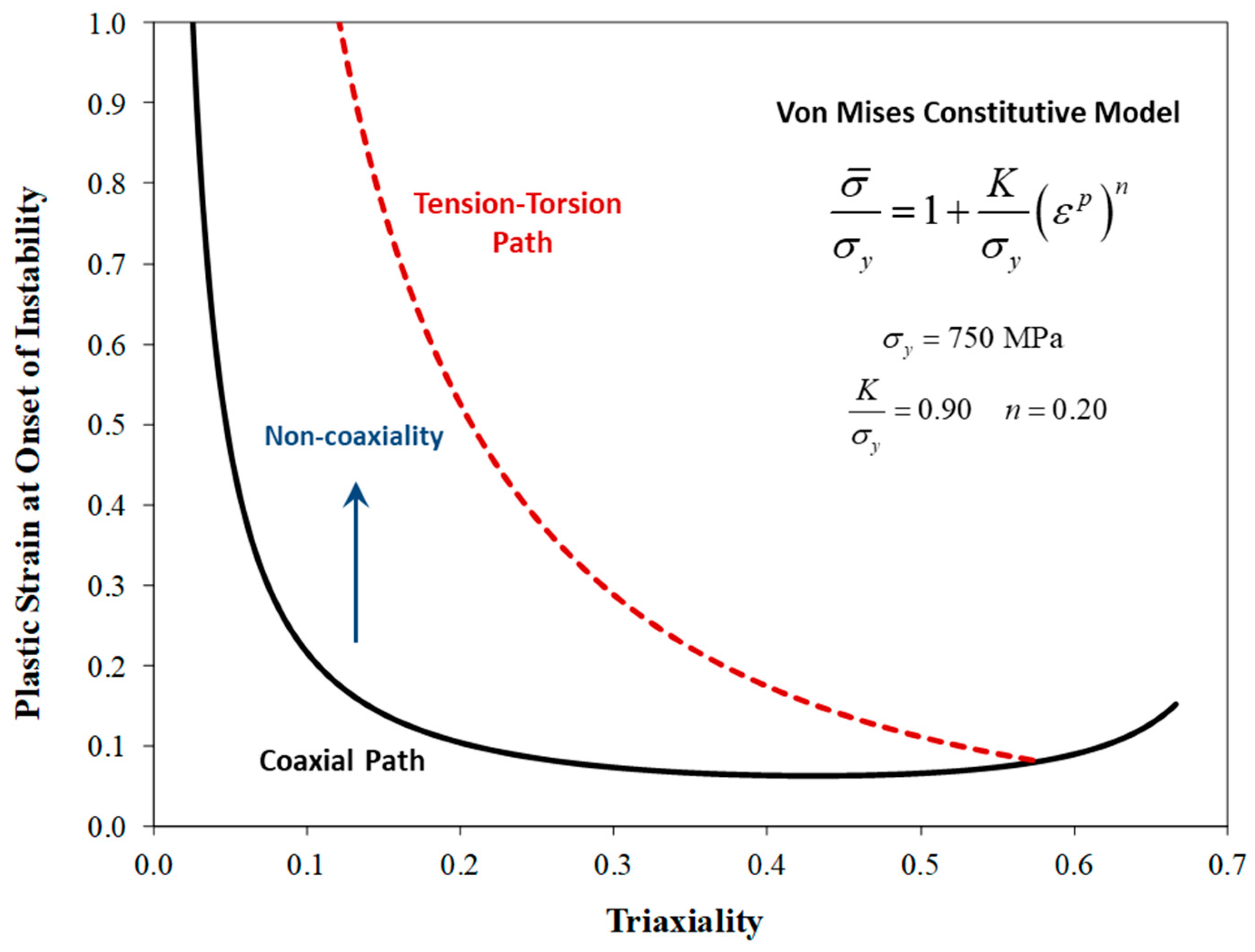
5. Onset of Diffuse Necking in Combined Tensile and Shear Stress States
6. Discussion and Implications on Phenomenological Fracture Characterization
7. Conclusions
- Stress states composed of a simple shear and superimposed tension, such as constant tension–torsion and butterfly tests, provide a constant stress state in terms of the stress invariants but are not strictly proportional. A constant stress state where the equivalent strain is not proportional to the cumulative principal strains due to the presence of a simple shear component has been denoted as non-coaxial. The presence of normal tensile stress with pure shear (no spin) is coaxial and proportional.
- It is recommended to differentiate between pure and simple shear since only pure shear is proportional and coaxial, which can be important for fracture since the microstructure will evolve differently. For plastic yielding, this distinction may not be as important.
- The failure loci in terms of the equivalent strain and stress triaxiality may depend upon the choice of characterization tests and if non-coaxial or coaxial test data was used in the calibration.
- General loading conditions for failure characterization cannot be uniquely defined by the stress triaxiality and Lode parameters. Thus, the current MMC-type framework may only be unique for coaxial proportional stress states, which appears to exclude the use of simple shear and non-coaxial characterization tests. This is an inconsistency with the fracture characterization tests used to calibrate the models.
- The analytical solution of Hillier [47] for the onset of a tensile instability in a constant tension–torsion test predicts that the onset of localization is delayed or suppressed in combined shear and tensile stress states in comparison with a tensile stress state with the same triaxiality. This is in general agreement with the observations of Scales et al. [26] where the failure strains in CTT tests were significantly higher than those from in-plane tests for the same alloy and no cusp is observed at the triaxiality for uniaxial tension.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Logarithmic (true) strain tensor | |
| Principal strains in descending order | |
| Ratio of the incremental normal strain components | |
| Ratio of shear stress to normal stress in the applied stress direction | |
| Angle of the principal strain directions | |
| Work-conjugate Equivalent plastic strain | |
| Coaxial equivalent strain or Effective strain computed using cumulative strains | |
| Equivalent plastic strain at failure | |
| Maximum principal strain at failure | |
| True (Cauchy) stress tensor | |
| Ratio of the normal stress components | |
| Ratio of shear stress to normal stress in the applied stress direction | |
| , | Angles to define the normalized shear and normal stress in polar coordinates |
| Parameter for the severity of shear loading under plane stress | |
| Principal stresses in descending order | |
| Maximum principal stress at failure | |
| Hydrostatic stress | |
| Von mises equivalent stress | |
| First invariant of the stress tensor | |
| Three invariants of the deviatoric stress tensor | |
| Lode parameter: General parameter as there are multiple definitions | |
| Lode parameter computed from the deviatoric stress invariants | |
| Stress triaxiality | |
| Lode parameter computed by normalizing the Lode angle | |
| Angle of principal stress directions in plane stress | |
| Maximum shear stress | |
| Maximum shear stress at fracture |
| Flow stress | |
| Parameter in the Mohr-Coulomb yield function | |
| Parameters in failure locus of Bai and Wierzbicki (2010) | |
| Damage parameter | |
| Strength coefficient and hardening exponent in the Holloman hardening model | |
| Critical sub-tangent for onset of instability |
| F | Deformation gradient tensor |
| V | Left stretch tensor |
| R | Rotation tensor |
| B | Left Cauchy-Green stretch tensor |
| L | Velocity gradient tensor |
| W | Vorticity tensor |
| D | Rate of deformation tensor or logarithmic strain rate |
| Logarithmic spin tensor | |
| Applied shear deformation in deformation gradient | |
| Applied extensional stretch in deformation gradient | |
| Ratio of the applied shear deformation to the extensional stretch | |
| Ratio of the incremental applied shear deformation to the incremental stretch |
| CTT | Constant Tension Torsion tests |
| MMC | Modified Mohr Coulomb |
| FEA | Finite-element analysis |
Appendix A: Mechanics of Coaxial and Non-Coaxial Strain Paths in Proportional Loading
Appendix A.1. Proportional Loading from Simple Shear to Pure Shear
Appendix A.2. Proportional Loading from Simple Shear to Uniaxial Tension
Appendix A.3. Proportional Loading from Simple Shear to Equal Biaxial Tension
References
- Bao, Y.; Wierzbicki, T. On the fracture locus in the equivalent strain and stress triaxiality space. Int. J. Mech. Sci. 2004, 46, 81–98. [Google Scholar] [CrossRef]
- Bai, Y. Effect of Loading History in Necking and Fracture. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2008. [Google Scholar]
- Bai, Y.; Wierzbicki, T. A new model of metal plasticity and fracture with pressure and lode dependence. Int. J. Plast. 2008, 24, 1071–1096. [Google Scholar] [CrossRef]
- Bai, Y.; Wierzbicki, T. Application of extended Mohr-Coulomb criterion to ductile fracture. Int. J. Fract. 2010, 161, 1–20. [Google Scholar] [CrossRef]
- Dunand, M.; Mohr, D. Hybrid experimental-numerical analysis of basic fracture experiments for sheet metals. Int. J. Solids Struct. 2010, 47, 1130–1143. [Google Scholar] [CrossRef]
- Dunand, M.; Mohr, D. Optimized butterfly specimen for the fracture testing of sheet materials under combined normal and shear loading. Eng. Fract. Mech. 2011, 78, 2919–2934. [Google Scholar] [CrossRef]
- Dunand, M.; Mohr, D. Effect of Lode parameter on plastic flow localization after proportional loading at low stress triaxialities. J. Mech. Phys. Solids 2014, 66, 133–153. [Google Scholar] [CrossRef]
- Gu, G.; Mohr, D. Anisotropic Hosford-Coulomb fracture initiation model: Theory and application. Eng. Fract. Mech. 2015, 147, 480–497. [Google Scholar] [CrossRef]
- Mohr, D.; Henn, S. Calibration of stress-triaxiality dependent crack formation criteria: A new hybrid experimental-numerical method. Exp. Mech. 2007, 47, 805–820. [Google Scholar] [CrossRef]
- Mohr, D.; Marcadet, S.J. Micromechanically-motivated phenomenological Hosford-Coulomb model for predicting ductile fracture initiation at low stress triaxialities. Int. J. Solids Struct. 2015, 67–68, 40–55. [Google Scholar] [CrossRef]
- Papasidero, J.; Doquet, V.; Mohr, D. Determination of the Effect of Stress State on the Onset of Ductile Fracture through Tension–torsion Experiments. Exp. Mech. 2013, 54, 137–151. [Google Scholar] [CrossRef]
- Papasidero, J.; Doquet, V.; Mohr, D. Ductile fracture of aluminum 2024-T351 under proportional and non-proportional multi-axial loading: Bao-Wierzbicki results revisited. Int. J. Solids Struct. 2015, 69–70, 459–474. [Google Scholar] [CrossRef]
- Roth, C.C.; Mohr, D. Ductile fracture experiments with locally proportional loading histories. Int. J. Plast. 2016, 79, 328–354. [Google Scholar] [CrossRef]
- Abedini, A.; Butcher, C.; Worswick, M.J. Fracture characterization of rolled sheet alloys in shear loading: Studies of specimen geometries, anisotropy, and rate sensitivity. Exp. Mech. 2017, 57, 75–88. [Google Scholar] [CrossRef]
- Peirs, J.; Verleysen, P.; Degrieck, J. Novel technique for static and dynamic shear testing of Ti6Al4V sheet. Exp. Mech. 2012, 52, 729–741. [Google Scholar] [CrossRef]
- Rahmaan, T.; Abedini, A.; Butcher, C.; Pathak, N.; Worswick, M.J. Experimental investigation of strain rate effect on fracture characteristics of DP600 and AA5182-O sheet metal alloys under shear loading. Int. J. Impact Eng. 2017, 108, 303–321. [Google Scholar] [CrossRef]
- Butcher, C.; Abedini, A. Shear Confusion: Identification of the Appropriate Equivalent Strain in Simple Shear using the Logarithmic Strain Measure. Int. J. Mech. Sci. 2017, 273–283. [Google Scholar] [CrossRef]
- Cheong, K.; Omer, K.; Butcher, C.; George, R.; Dykeman, J. Evaluation of the VDA 238-100 Tight Radius Bending Test using Digital Image Correlation Strain Measurement, Proceedings of 36th International Conference of the International Deep Drawing Research Group (IDDRG 2017). J. Phys. Conf. Ser. 2017, 896, 012075. [Google Scholar] [CrossRef]
- Butcher, C.; Anderson, D.; Worswick, M. Predicting failure during sheared edge stretching using a damage-based model for the shear-affected zone. Int. J. Mater. Manuf. 2013, 6, 304–312. [Google Scholar] [CrossRef]
- Pathak, N.; Butcher, C.; Worswick, M.J.; Bellhouse, E.; Gao, J. Damage evolution in complex-phase and dual-phase steels during edge stretching. Materials 2017, 10, 346. [Google Scholar] [CrossRef]
- Anderson, D.; Butcher, C.; Pathak, N.; Worswick, M.J. Failure parameter identification and validation for a dual-phase 780 steel sheet. Int. J. Solids Struct. 2017, 124, 89–107. [Google Scholar] [CrossRef]
- Gruben, G.; Fagerholt, E.; Hopperstad, O.; Borvik, T. Fracture Characteristics of a Cold-Rolled Dual-Phase Steel. Eur. J. Mech. A Solids 2011, 30, 204–218. [Google Scholar] [CrossRef]
- Barsoum, I.; Faleskog, J. Rupture mechanisms in combined tension and shear—Experiments. Int. J. Solids Struct. 2007, 44, 1768–1786. [Google Scholar] [CrossRef]
- Barsoum, I.; Faleskog, J. Rupture mechanisms in combined tension and shear—Micromechanics. Int. J. Solids Struct. 2007, 44, 5481–5498. [Google Scholar] [CrossRef]
- Haltom, S.S.; Kyriakides, S.; Ravi-Chandar, K. Ductile fracture under combined shear and tension. Int. J. Solids Struct. 2013, 50, 1507–1522. [Google Scholar] [CrossRef]
- Scales, M.; Tardif, N.; Kyriakides, S. Ductile failure of aluminum alloy tubes under combined torsion and tension. Int. J. Solids Struct. 2016, 97–98, 116–128. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 21–48. [Google Scholar] [CrossRef]
- Hooputra, H.; Gese, H.; Dell, H.; Werner, H. A comprehensive failure model for crashworthiness simulation of aluminum extrusions. Int. J. Crashworthiness 2004, 9, 449–463. [Google Scholar] [CrossRef]
- Lou, Y.; Huh, H.; Lim, S.; Pack, K. New Ductile Fracture Criterion for Prediction of Fracture Forming Limit Diagrams of Sheet Metals. Int. J. Solids Struct. 2012, 49, 3605–3615. [Google Scholar] [CrossRef]
- Lou, Y.; Huh, H. Extension of a Shear-Controlled Ductile Fracture Model Considering the Stress Triaxiality and the Lode Parameter. Int. J. Solids Struct. 2013, 50, 447–455. [Google Scholar] [CrossRef]
- Lou, Y.; Chena, L.; Clausmeyer, T.; Tekkayaa, E.; Yoon, J.W. Modeling of ductile fracture from shear to balanced biaxial tension for sheet metals. Int. J. Solids Struct. 2017, 112, 169–184. [Google Scholar] [CrossRef]
- Park, N.; Huh, H.; Lim, S.J.; Lou, Y.; Kang, Y.S.; Seo, M.H. Fracture-based forming limit criteria for anisotropic materials in sheet metal forming. Int. J. Plast. 2017, 96, 1–35. [Google Scholar] [CrossRef]
- Li, Y.; Luo, M.; Gerlach, J.; Wierzbicki, T. Prediction of shear-induced fracture in sheet metal forming. J. Mater. Process. Technol. 2010, 210, 1858–1869. [Google Scholar] [CrossRef]
- Luo, M.; Wierzbicki, T. Numerical failure analysis of a stretch-bending test on dual phase steel sheet using a phenomenological fracture model. Int. J. Solids Struct. 2010, 47, 3084–3102. [Google Scholar] [CrossRef]
- Malcher, L.; Andrade Pires, F.M.; Cesar de Sa, J.M.A. An assessment of isotropic constitutive models for ductile fracture under high and low stress triaxiality. Int. J. Plast. 2012, 30, 81–115. [Google Scholar] [CrossRef]
- Gurben, G.; Hopperstad, O.S.; Borvik, T. Evaluation of uncoupled ductile fracture criteria for dial-phase steel Docol 600DL. Int. J. Mech. Sci. 2012, 62, 133–146. [Google Scholar] [CrossRef]
- Cao, T.S.; Gaillac, A.; Montmitonnet, P.; Bouchard, P.O. Identification methodology and comparison of phenomenological ductile damage models via hybrid numerical-experimental analysis of fracture experiments conducted on a zirconium alloy. Int. J. Solids Struct. 2013, 24, 3984–3999. [Google Scholar] [CrossRef]
- Kofiani, K.; Nonn, A.; Wierzbicki, T. New Calibration method for high and low triaxiality and validation on SENT specimens of API X70. Int. J. Press. Vessel. Pip. 2013, 111–112, 187–201. [Google Scholar] [CrossRef]
- Lian, J.; Sharaf, M.; Archie, F.; Munstermann, S. A hybrid approach for modelling of plasticity and failure behaviour of advanced high-strength steel sheets. Int. J. Damage Mech. 2013, 22, 188–218. [Google Scholar] [CrossRef]
- Rousselier, G.; Lou, M. A fully coupled void damage and Mohr-Coulomb based ductile fracture model in the framework of a reduced texture methodology. Int. J. Plast. 2014, 55, 1–24. [Google Scholar] [CrossRef]
- Neukamm, F.; Feucht, M.; Haufe, A. Consistent Damage Modelling in the Process Chain of Forming to Crashworthiness Simulations. In Proceedings of the 7th LS-DYNA Anwenderforum, Bamberg, Germany, 30 September–1 October 2008. [Google Scholar]
- Basaran, M.; Wolkerling, S.D.; Feucht, M.; Neukamm, F.; Weichert, D. An Extension of the GISSMO Damage Model Based on Lode Angle Dependence. In Proceedings of the 9th LS-DYNA Anwenderforum, Bamberg, Germany, 12–13 October 2010. [Google Scholar]
- Benzerga, A.A.; Surovik, D.; Keralavarma, S.M. On the path-dependence of the fracture locus in ductile materials—Analysis. Int. J. Plast. 2012, 37, 157–170. [Google Scholar] [CrossRef]
- Thomas, N.; Basu, S.; Benzerga, A.A. On fracture loci of ductile materials under non-proportional loading. Int. J. Mech. Sci. 2016, 117, 135–151. [Google Scholar] [CrossRef]
- Jia, Y.; Bai, Y. Ductile fracture prediction for metal sheets using all-strain-based anisotropic eMMC model. Int. J. Mech. Sci. 2016, 115–116, 516–531. [Google Scholar] [CrossRef]
- Beese, A.M.; Luo, M.; Li, Y.; Bai, Y.; Wierzbicki, T. Partially coupled anisotropic fracture model for aluminum sheets. Eng. Fract. Mech. 2010, 77, 1128–1152. [Google Scholar] [CrossRef]
- Hillier, M.J. Tensile Plastic Instability Under Complex Stress. Int. J. Mech. Sci. 1963, 5, 57–67. [Google Scholar] [CrossRef]
- Lode, W. Versuche über den Einfluss der mittleren Hauptspannung auf das Fliessen der Metalle Eisen, Kupfer, und Nickel. Z. Phys. 1926, 36, 913–939. [Google Scholar] [CrossRef]
- Cockcroft, M.G.; Latham, D.J. Ductility and the workability of metals. J. Inst. Met. 1968, 96, 33–39. [Google Scholar]
- Oyane, M.; Sato, T.; Okimoto, K.; Shima, S. Criteria for ductile fracture and their applications. J. Mech. Work. Technol. 1980, 4, 65–81. [Google Scholar] [CrossRef]
- Clift, S.E.; Hartley, P.; Sturgess, C.E.N.; Rowe, G.W. Fracture prediction in plastic deformation processes. Int. J. Mech. Sci. 1990, 32, 1–17. [Google Scholar] [CrossRef]
- Wierzbicki, T.; Bao, Y.B.; Lee, Y.-W.; Bai, Y.L. Calibration and evaluation of seven fracture models. Int. J. Mech. Sci. 2005, 47, 719–743. [Google Scholar] [CrossRef]
- Omer, K.; ten Kortenaar, L.; Butcher, C.; Worswick, M.J.; Detwiler, D.; Malcolm, S. Testing of a Hot Stamped Axial Crush Member with Tailored Properties—Experiments and Models. Int. J. Impact Eng. 2017, 103, 12–28. [Google Scholar] [CrossRef]
- Stoughton, S.; Yoon, J.W. Path independent forming limits in strain and stress spaces. Int. J. Solids Struct. 2012, 49, 3616–3625. [Google Scholar] [CrossRef]
- Abedini, A.; Butcher, C.; Nemcko, M.J.; Kurukuri, S.; Worswick, M.J. Constitutive characterization of a rare-earth magnesium alloy sheet (ZEK100-O) in shear loading: Studies of anisotropy and rate sensitivity. Int. J. Mech. Sci. 2017, 128–129, 54–69. [Google Scholar] [CrossRef]
- Abedini, A.; Butcher, C.; Rahmaan, T.; Worswick, M.J. Evaluation and calibration of anisotropic yield criteria in shear loading: Constraints to eliminate numerical artefacts. Int. J. Solids Struct. 2017. [Google Scholar] [CrossRef]
- Butcher, C.; Abedini, A. On anisotropic plasticity models using linear transformations on the deviatoric stress: Physical constraints on plastic flow in generalized plane strain. Int. J. Mech. Sci. 2019, 161–162, 105044. [Google Scholar] [CrossRef]
- Gorji, M.; Berisha, B.; Hora, P.; Barlat, F. Modeling of localization and fracture phenomena in strain and stress space for sheet metal forming. Int. J. Mater. Form. 2016, 9, 573–584. [Google Scholar] [CrossRef]
- Reinhardt, W.D.; Dubey, R.N. Application of Objective Rates in Mechanical Modeling of Solids. J. Appl. Mech. 1996, 118, 692–698. [Google Scholar] [CrossRef]
- Xiao, H.; Bruhns, O.T.; Meyers, A. Logarithmic strain, logarithmic spin and logarithmic rate. Acta Mech. 1997, 124, 89–105. [Google Scholar] [CrossRef]
- Bruhns, O.T.; Xiao, H.; Meyers, A. Self-consistent Eulerian rate type elasto-plasticity models based upon the logarithmic stress rate. Int. J. Plast. 1999, 15, 479–520. [Google Scholar] [CrossRef]
- Ghahremaninezhad, A.; Ravi-Chandar, K. Ductile failure behavior of polycrystalline Al 6061-T6 under shear dominant loading. Int. J. Fract. 2013, 180, 23–39. [Google Scholar] [CrossRef]
- Gruben, G.; Morin, D.; Langseth, M.; Hopperstad, O.S. Strain localization and ductile fracture in advanced high-strength steel sheets. Eur. J. Mech. A Solids 2017, 61, 315–329. [Google Scholar] [CrossRef]
- Considère, A. L’Emploi du Fer et de L’Acier dans les Constructions. Ann. Ponts Chaussees 1968, 9, 574. [Google Scholar]
- Swift, H.W. Plastic instability under plane stress. J. Mech. Phys. Solids 1952, 1, 1–16. [Google Scholar] [CrossRef]
- Zener, C.; Hollomon, J.H. Effect of strain rate upon plastic flow of steel. J. Appl. Phys. 1944, 15, 22–32. [Google Scholar] [CrossRef]
- Scheyvaerts, F.; Onck, P.R.; Tekoglu, C.; Pardoen, T. The growth and coalescence of ellipsoidal voids in plane strain under combined shear and tension. J. Mech. Phys. Solids 2011, 59, 373–397. [Google Scholar] [CrossRef]
- Tvergaard, V. Shear deformation of voids with contact modelled by internal pressure. Int. J. Mech. Sci. 2008, 50, 1459–1465. [Google Scholar] [CrossRef]
- Tvergaard, V. Behavior of voids in a shear field. Int. J. Fract. 2009, 158, 41–49. [Google Scholar] [CrossRef]
- Tvergaard, V. Effect of stress-state and spacing on voids in a shear field. Int. J. Solids Struct. 2012, 49, 3047–3054. [Google Scholar] [CrossRef]
- Tvergaard, V. Behavior of porous ductile solids at low stress triaxiality in different modes of deformation. Int. J. Solids Struct. 2015, 60–61, 28–34. [Google Scholar] [CrossRef]
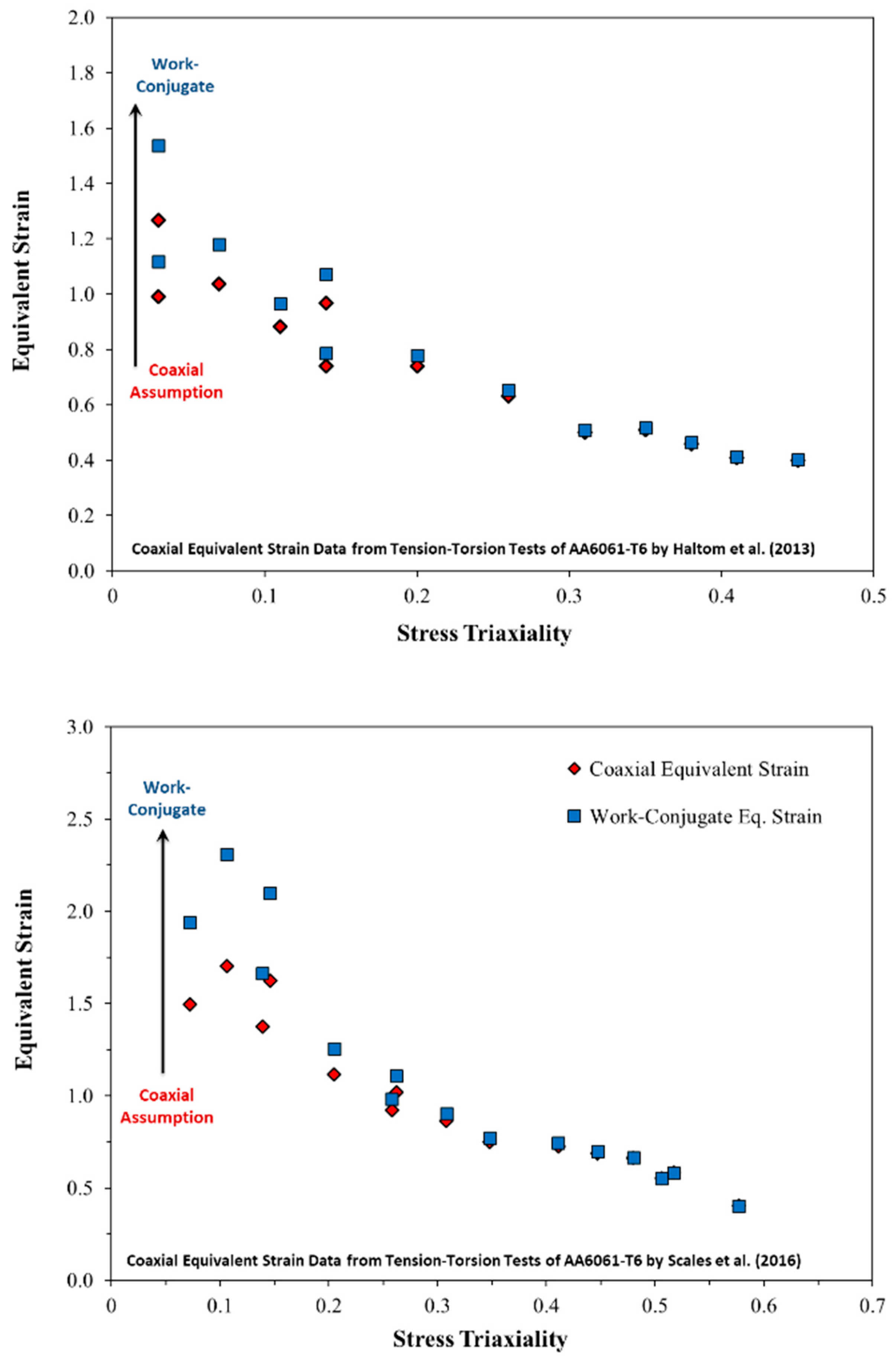


| Experiment Data of Scales et al. (2016) | Finite Strain Combined Plane Strain & Simple Shear | |||
|---|---|---|---|---|
| Triaxiality | Coaxial von Mises Eq. Strain (DIC max.) | Major True Strain | Minor True Strain | Von Mises Work Conjugate Eq. Strain |
| 0.072 | 1.50 | 1.39 | −1.18 | 1.94 |
| 0.106 | 1.70 | 1.62 | −1.25 | 2.31 |
| 0.139 | 1.37 | 1.32 | −0.97 | 1.66 |
| 0.146 | 1.62 | 1.58 | −1.12 | 2.10 |
| 0.205 | 1.12 | 1.10 | −0.72 | 1.26 |
| 0.258 | 0.92 | 0.92 | −0.53 | 0.98 |
| 0.262 | 1.02 | 1.02 | −0.58 | 1.11 |
| 0.308 | 0.86 | 0.86 | −0.44 | 0.90 |
| 0.348 | 0.75 | 0.75 | −0.35 | 0.77 |
| 0.411 | 0.73 | 0.72 | −0.26 | 0.74 |
| 0.447 | 0.69 | 0.67 | −0.20 | 0.70 |
| 0.48 | 0.66 | 0.63 | −0.15 | 0.67 |
| 0.506 | 0.55 | 0.52 | −0.10 | 0.55 |
| 0.517 | 0.58 | 0.54 | −0.09 | 0.58 |
| 0.577 | 0.40 | 0.35 | 0.00 | 0.40 |
| Loading Condition | Normal Strain Ratio | Normal Stress Ratio | Shear Stress Ratio | Shear Strain Ratio | Equivalent Strain Ratio |
| Pure & Simple Shear | −1 | −1 | |||
| Uniaxial Tension & Simple Shear | −0.5 | 0 | |||
| Plane Strain Tension & Simple Shear | 0 | 1/2 | |||
| Biaxial Tension & Simple Shear | 1 | 1 | |||
| Coaxial Loading | 0 | 0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Butcher, C.; Abedini, A. On Phenomenological Failure Loci of Metals under Constant Stress States of Combined Tension and Shear: Issues of Coaxiality and Non-Uniqueness. Metals 2019, 9, 1052. https://doi.org/10.3390/met9101052
Butcher C, Abedini A. On Phenomenological Failure Loci of Metals under Constant Stress States of Combined Tension and Shear: Issues of Coaxiality and Non-Uniqueness. Metals. 2019; 9(10):1052. https://doi.org/10.3390/met9101052
Chicago/Turabian StyleButcher, Cliff, and Armin Abedini. 2019. "On Phenomenological Failure Loci of Metals under Constant Stress States of Combined Tension and Shear: Issues of Coaxiality and Non-Uniqueness" Metals 9, no. 10: 1052. https://doi.org/10.3390/met9101052
APA StyleButcher, C., & Abedini, A. (2019). On Phenomenological Failure Loci of Metals under Constant Stress States of Combined Tension and Shear: Issues of Coaxiality and Non-Uniqueness. Metals, 9(10), 1052. https://doi.org/10.3390/met9101052




