1. Introduction
Complicated components are widely used in the fields of aeroengine blade, turbine rotor, pressure bended-pipe and spherical head, etc., which usually suffer from local plastic deformations when subjected to an external mechanical load or temperature change. The plastic deformation-induced residual stress, or internal stress, is one of the main reasons for micro-crack initiation and growth in components. Thus, monitoring of the residual stress could be used to evaluate the safety of the in-service components. For instance, the aeroengine blades generally undergo high centrifugal loads or foreign object impacts at a high risk, which lead to local micro elastoplasticity and then cause residual stress concentration. It is reported that the fatigue or plastic-deformed status can be assessed by inspecting the residual stress of blade surface, and the safety assessment of the aeroengine blade can be solved [
1]. In addition, the knowledge of residual stresses allows us to estimate more accurately the safety factor and remaining life for components in fabrication condition or in the service [
2]. Thus, the characterization of residual stress, as an important indicator of early-damage prediction and assessment, has received wide attention.
Several methods of residual stress measurement are available for securing the reliability of in-service components, which include destructive, semi-destructive and non-destructive methods [
3]. Destructive/semi-destructive techniques, such as slitting and hole-drilling, are based on measuring elastic deformation generated from relieving residual stress by removing a sample from a component or drilling small holes into the component surface [
4]. Although some destructive methods are widely used in engineering practice, their application is limited because of the additional damage introduced in the process. Currently, non-destructive techniques like X-ray diffraction (XRD) and ultrasonic testing methods are often considered for periodic routine inspection. These techniques calculate residual stress by measuring parameters affected by it, requiring less measuring time and costs [
4,
5,
6,
7,
8]. Since fatigue and stress-corrosion-cracking failures are surface-sensitive phenomena, it is often accepted that evaluation of surface residual stress is adequate to assess these deformations. XRD is now considered a reliable method to measure surface or subsurface residual stresses and is often used to verify other measurement methods [
4,
8]. Note that neutron diffraction technique was recently considered to measure the residual stress in self-piercing riveting joints [
9,
10], where the incident beam was a monochromatic beam of thermal neutrons with a wavelength of 1.67 Å and a 2D position sensitive 3He detector recorded the diffraction peak. Residual stress can be calculated based on the strain, the reference lattice, and the measured one.
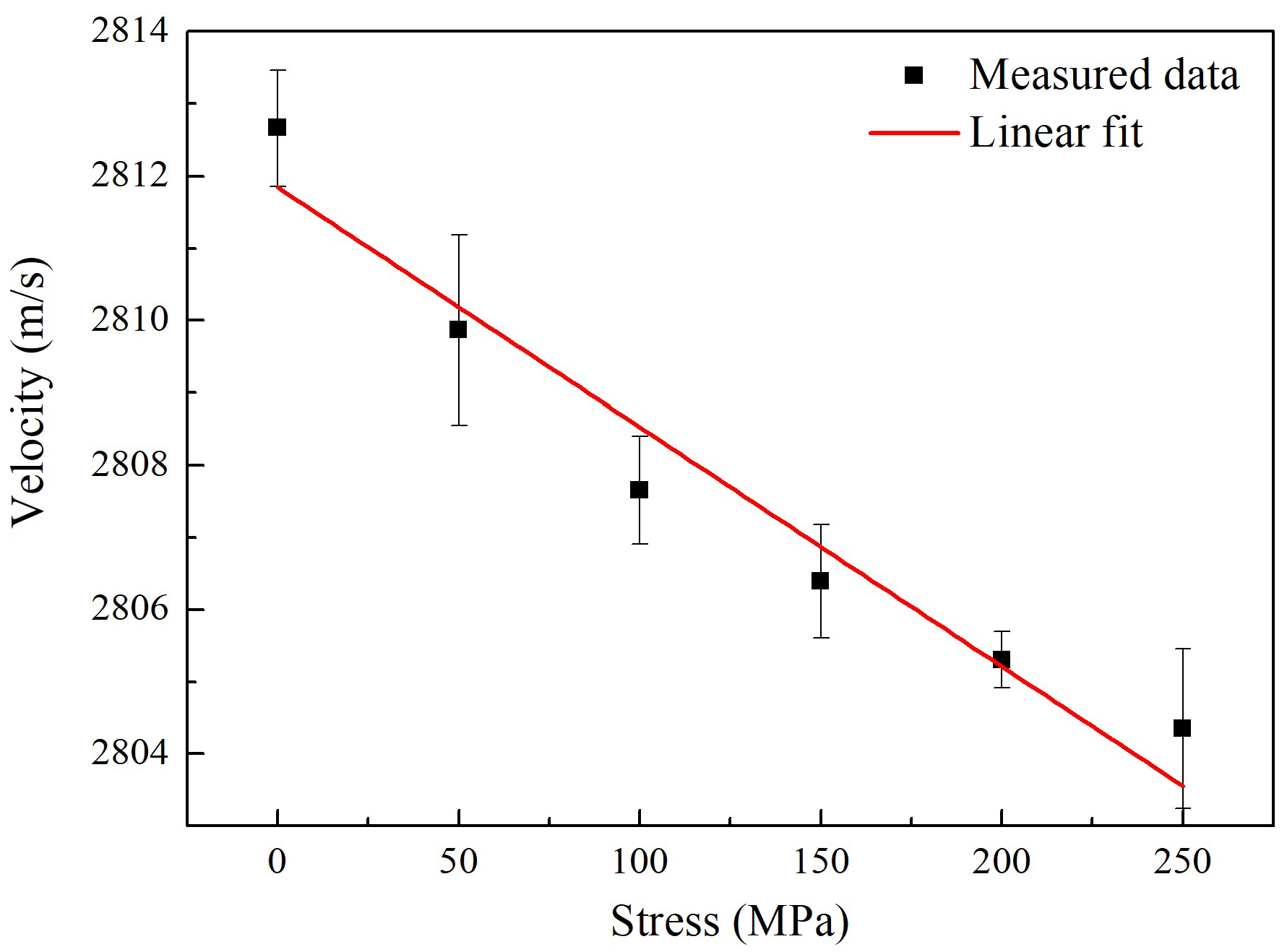
One of the most promising methods for non-destructive residual stress measurements is the application of ultrasound, which is based on the effect of acoustoelasticity that is a relationship between the velocity of ultrasonic wave and the internal/applied stress and is described by Hughes and Kelly [
11]. The ultrasonic technique for measuring residual stresses was given in 1967 by Crecraft [
12]. He described the acoustic birefringence phenomenon, which is analogous to optical birefringence observed in photo-elastic strain analysis. The velocity of shear waves polarized in one principal direction depends on the stress level applied in that direction. Recently, the longitudinal critically refracted (LCR) wave, known for its easy excitation and high sensitivity to residual stress, was used to evaluate surface residual stress in steel plates, bars and welds [
13,
14]. Bray and Junghans employed the evaluation of residual stress in steel plates after post-weld heat treatment by LCR ultrasonic method [
13]. The LCR travel-time measurements can not only distinguish between residual stress states in the plate, but also offer information on their distribution and magnitude. Javadi et al. recently carried out a lot of work on LCR ultrasonic measurements and simulations of residual stresses [
3,
7,
15,
16]. They reported that LCR waves are able to penetrate at different depths and measure the through-thickness stresses of stainless steel plates by four different testing frequencies of the transducers [
15]. They also compared the ultrasonic measurement results with those obtained from the finite element simulation of weldings. The LCR wave was also applied to evaluate residual stresses in carbon steel weld joint fabricated using the manual metal arc welding process with marginally different heat inputs [
2].
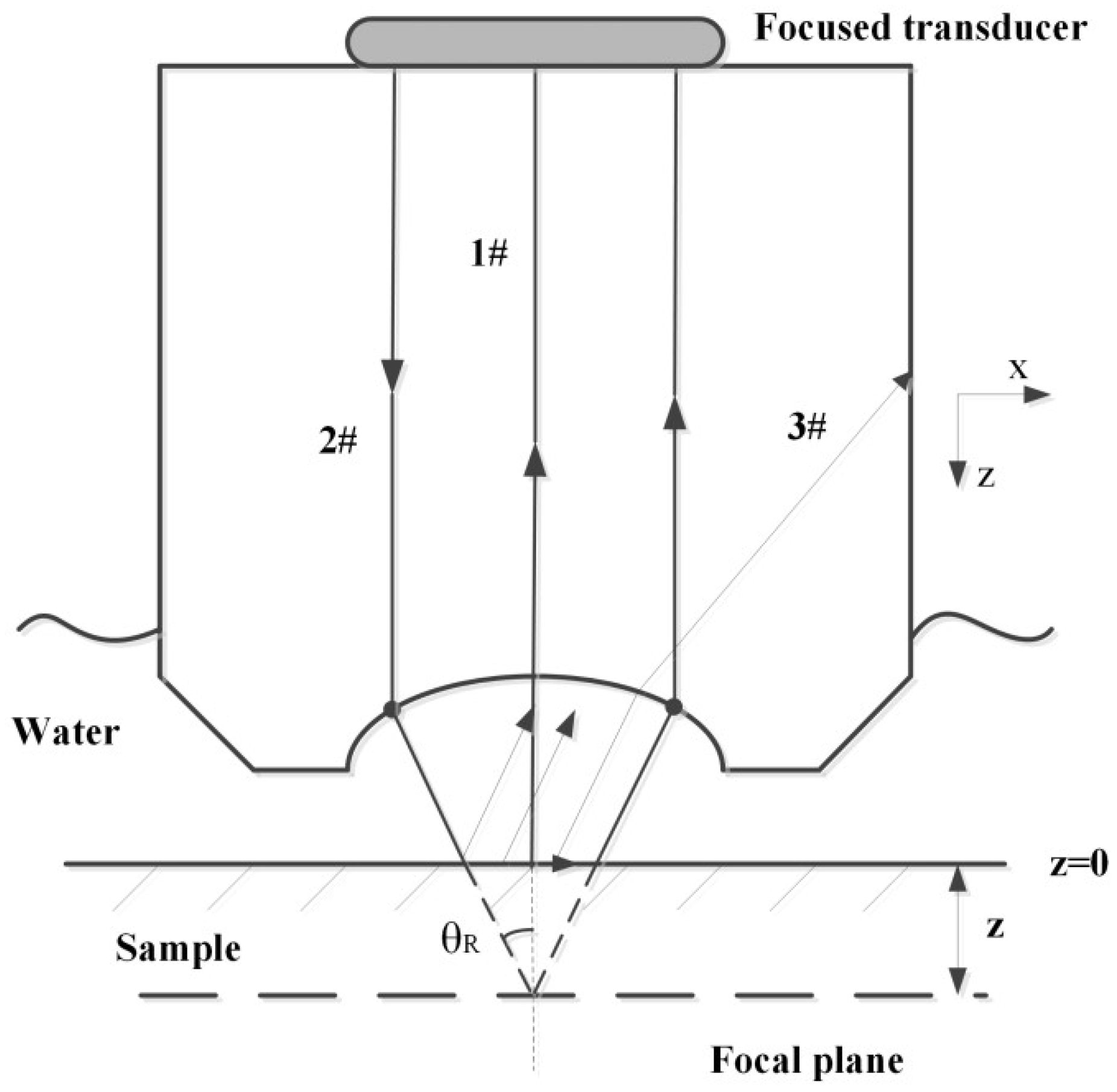
LCR waves are usually used to assess the residual stresses distributed in components with planar or cylindrical shapes due to their sensitivity to stresses and capability of indicating stress gradients. However, there are a few applications of LCR waves for residual stress evaluations in complicated components or curved surfaces, such as aeroengine blade, turbine rotor, pressure bended-pipe, etc. Generally, in order to improve the measurement resolution of stress, the LCR method should sacrifice the space resolution for a bulk measurement over whole volume with a couple of millimeters between two receivers, if a set-up of one transmitter and two receivers is considered [
3,
4]. To find a general solution to evaluate residual stresses in complicated components with a space resolution of 1–2 mm, just like X-ray diffraction method, here a
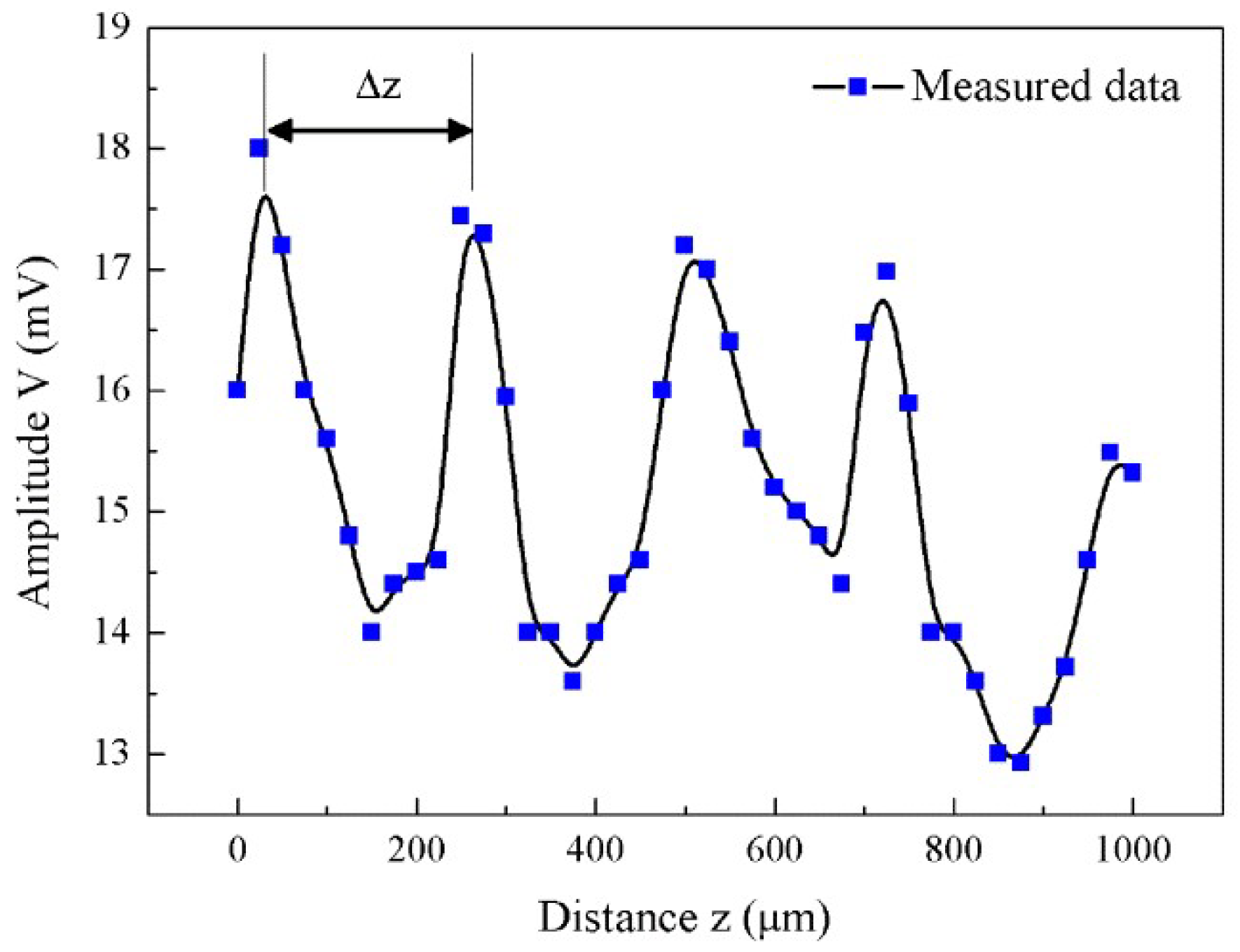
V(
z) curve method based on Rayleigh surface wave is proposed; it measures residual stresses at a point-like region in complicated components. Due to the using of leaky Rayleigh wave, a liquid-immersed experimental set-up with a focused ultrasonic transducer is generally considered in experiments. When the focused transducer is defocused towards the specimen to be tested, the receiving signal/voltage of the leaky Rayleigh wave displays a periodical change because of the interference effect of waves. The plot of the periodical changes is the so-called
V(
z) curve [
17], representing a relationship between the output voltage of ultrasonic signal and the transducer lifting location, which can be used with leaky Rayleigh wave to measure the residual stresses on curved surface. The periodicity of
V(
z) curve was verified by Weglin in 1979; the relationship between oscillation interval of
V(
z) curve and leaky Rayleigh wave velocity was observed as well [
18]. In recent years, some research were conducted to characterize stresses at surface or sub-surface of materials by the
V(
z) curve method of scanning acoustic microscopy at a high frequency, even up to 400 MHz [
19,
20,
21,
22]. However, the characterization of residual stresses on the surface of complicated components by
V(
z) curve technique at a normal ultrasonic frequency such as less than 20 MHz has not been fully addressed before, which could be a practical way for measuring the residual stress at a point-like region with a space resolution of 1–2 mm in engineering metallic components.
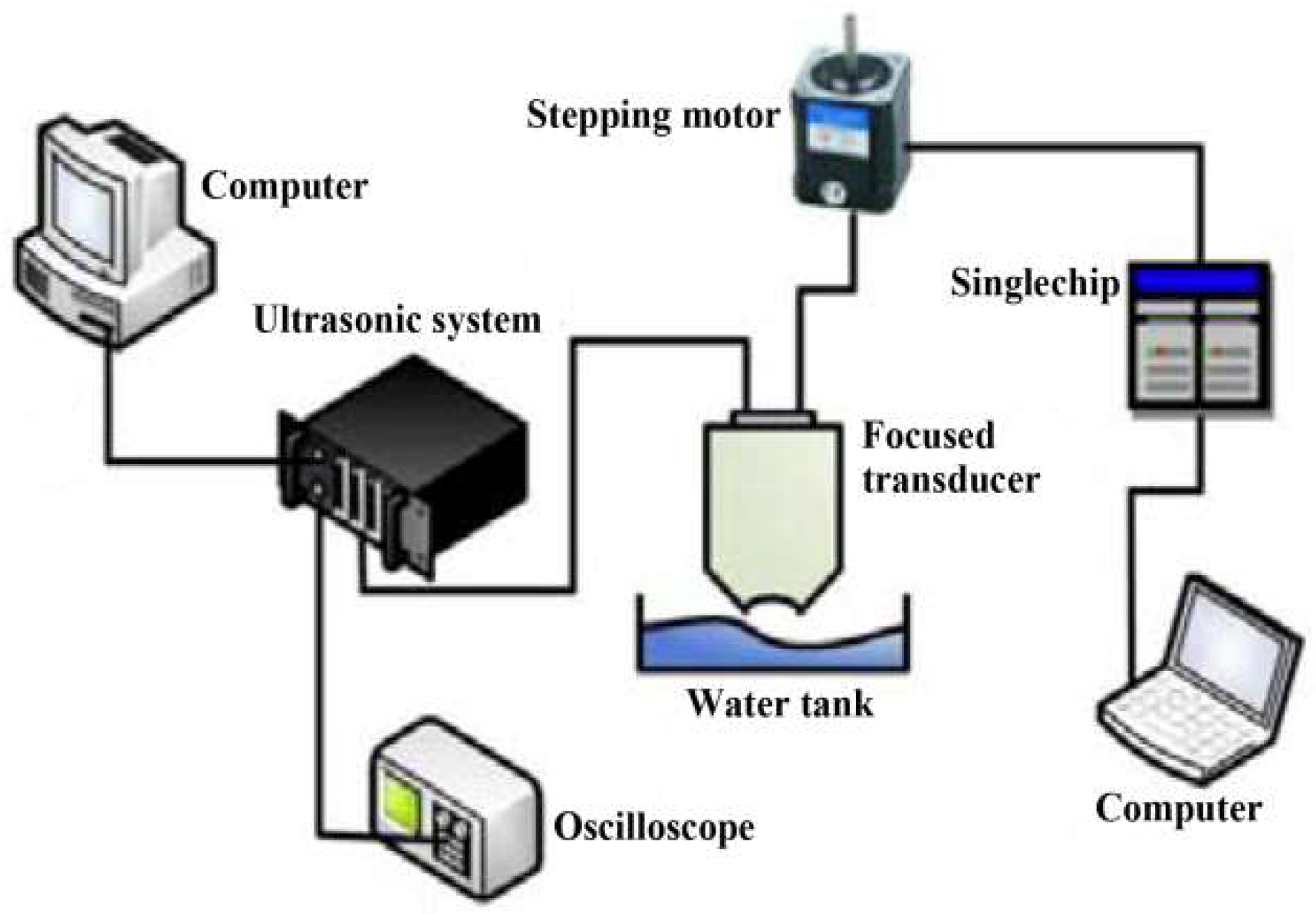
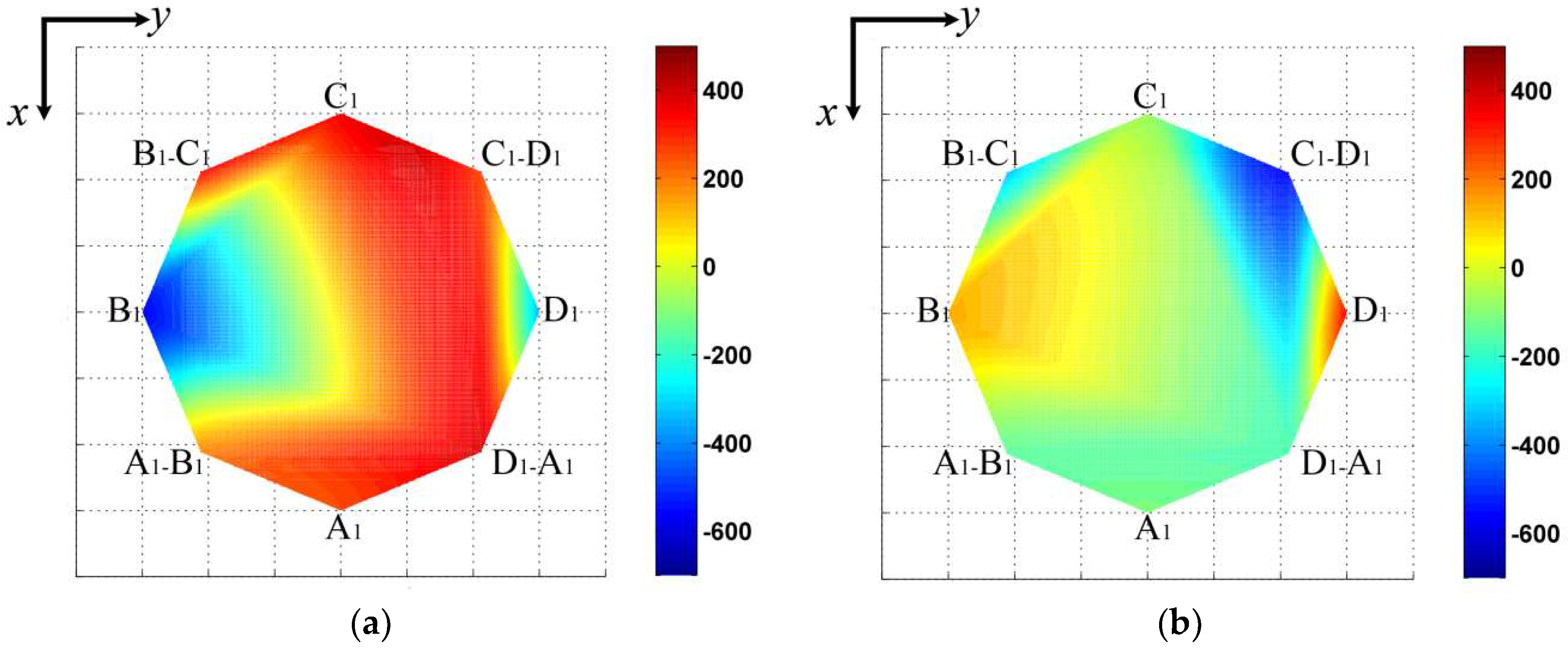
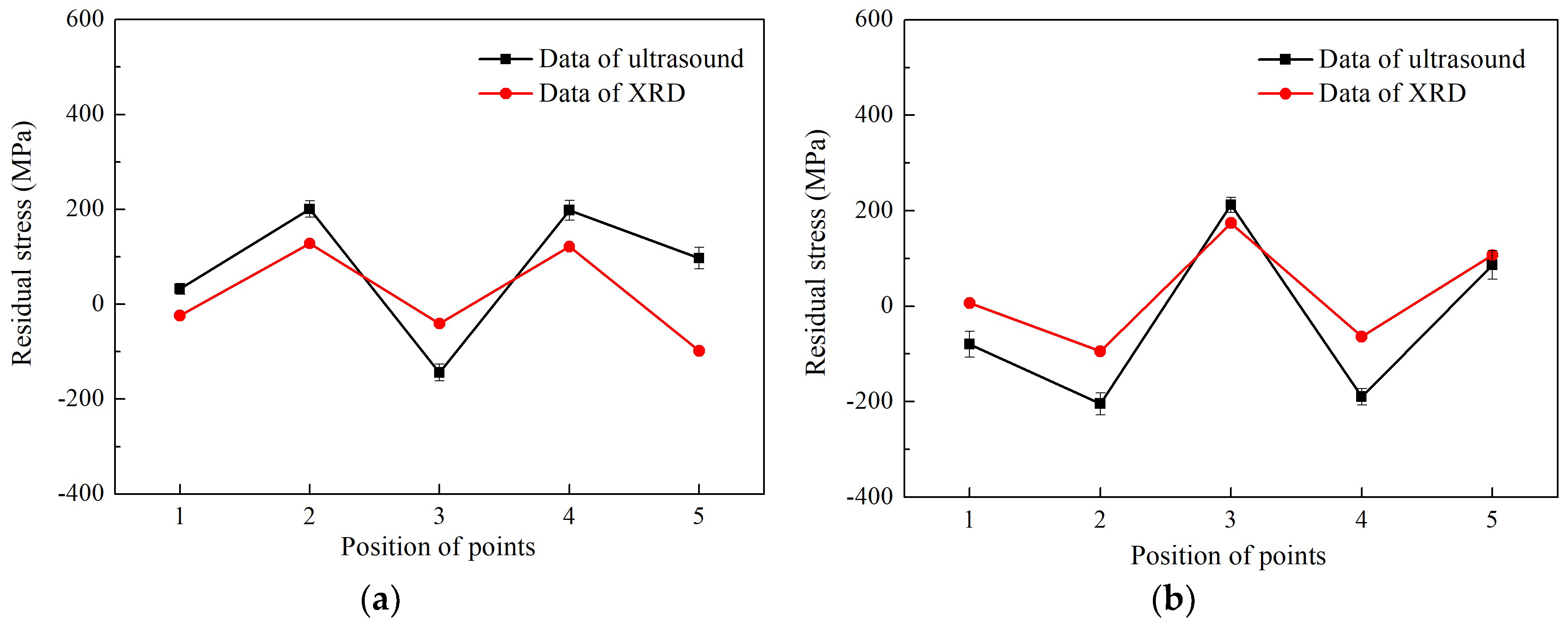
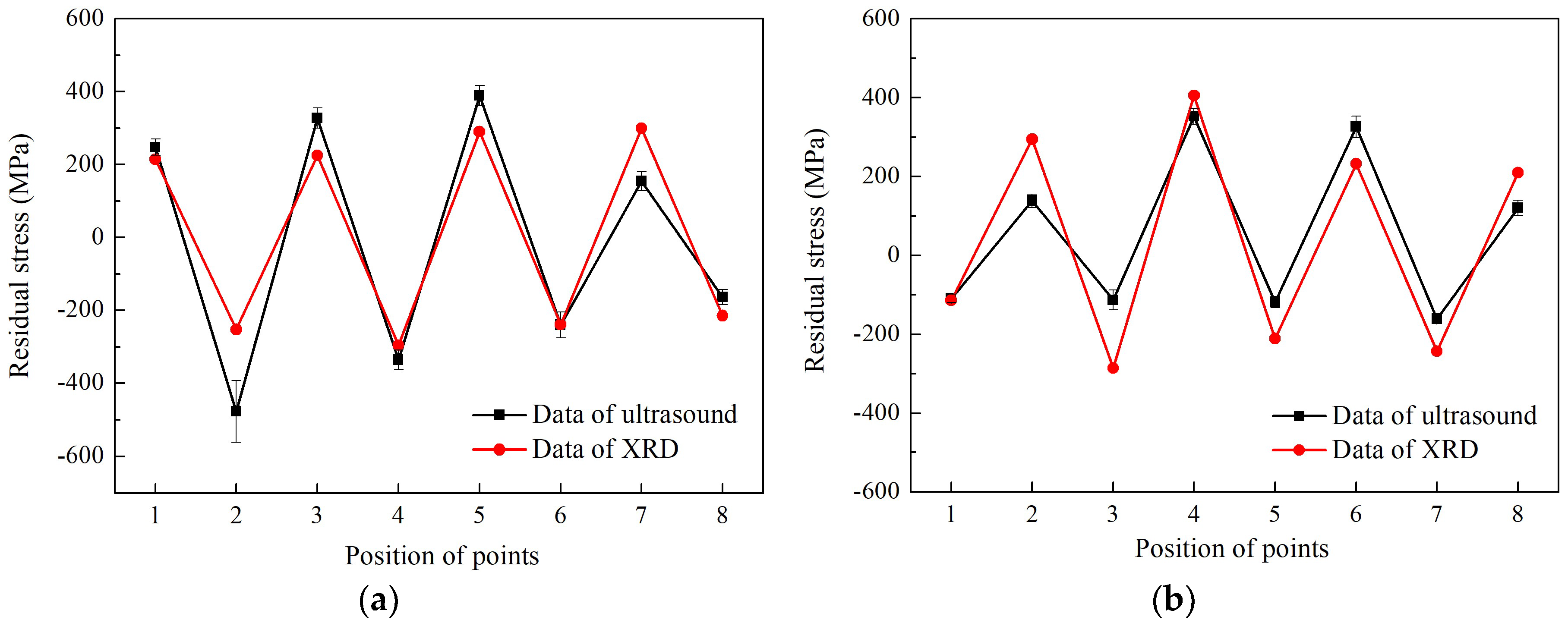
The Rayleigh surface wave-based V(z) curve method is adopted in this work to evaluate the distribution of residual stresses in aeroengine blades, in which the residual stresses were artificially made by shot of steel balls. The experimental measurements are divided into two parts, one is a determination of the acoustoelastic coefficients of titanium alloy Ti-6Al-4V, and the other is measurement of the V(z) curve for the velocity calculation of Rayleigh surface wave. The data acquisition based on the motor driving system is designed to measure the amplitudes of the output ultrasonic signal. The distribution of residual stresses in pre-fabricated aeroengine blades was measured by the proposed set-up and verified by the XRD method.
Author Contributions
Conceptualization, Y.X. and M.D.; Methodology, Y.L.; Software, D.T.; Validation, C.L. and F.X.; Formal Analysis, Y.X.; Investigation, Y.X.; Resources, M.D. and F.X.; Data Curation, Y.L. and D.T.; Writing–Original Draft Preparation, Y.X.; Writing–Review & Editing, F.X.; Visualization, Y.X.; Supervision, F.X.; Project Administration, F.X.; Funding Acquisition, F.X.
Funding
This research was funded by the National Natural Science Foundation of China (11622430, 11774090 and 11474361), the National Key Research and Development Program of China (2016YFC0801903), and the Fundamental Research Funds for the Central Universities (222201717005 and 222201718005).
Acknowledgments
The authors would like to thank Ying Li (AECC Commercial Aircraft Engine Co., Ltd.) for his help of making Ti-6Al-4V samples.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, J.; Wei, D.; Liu, C.; Yang, J. Surface residual stress test for aero-engine blade and its safety assessment. Sci. Technol. Eng. 2009, 11, 006. (In Chinese) [Google Scholar]
- Joseph, A.; Palanichamy, P.; Jayakumar, T. Evaluation of residual stresses in carbon steel weld joints by ultrasonic LCR wave technique. J. Nondestr. Eval. 2015, 34, 266. [Google Scholar] [CrossRef]
- Javadi, Y.; Azari, K.; Ghalehbandi, S.M.; Roy, M.J. Comparison between using longitudinal and shear waves in ultrasonic stress measurement to investigate the effect of post-weld heat-treatment on welding residual stresses. Res. Nondestr. Eval. 2017, 28, 101–122. [Google Scholar] [CrossRef]
- Rossini, N.S.; Dassisti, M.; Benyounis, K.Y.; Olabi, A.G. Methods of measuring residual stresses in components. Mater. Design. 2012, 35, 572–588. [Google Scholar] [CrossRef] [Green Version]
- Ceretti, M.; Braham, C.; Lebrun, J.L.; Bonnafe, J.P.; Perrin, M.; Lodini, A. Residual stress analysis by neutron and X-ray diffraction applied to the study of two phase materials: Metal matrix composites. Exp. Tech. 1996, 20, 14–18. [Google Scholar] [CrossRef]
- Zhu, Z.; Post, M.A.; Meguid, S.A. The potential of ultrasonic non-destructive measurement of residual stresses by modal frequency spacing using leaky lamb waves. Exp. Mech. 2012, 52, 1329–1339. [Google Scholar] [CrossRef]
- DsdSadeghi, S.; Najafabadi, M.A.; Javadi, Y.; Mohammadisefat, M. Using ultrasonic waves and finite element method to evaluate through-thickness residual stresses distribution in the friction stir welding of aluminum plates. Mater. Design. 2013, 52, 870–880. [Google Scholar] [CrossRef]
- Moussaoui, K.; Segonds, S.; Rubio, W.; Mousseigne, M. Studying the measurement by X-ray diffraction of residual stresses in Ti-6Al-4V titanium alloy. Mater. Sci. Eng. A 2016, 667, 340–348. [Google Scholar] [CrossRef]
- Haque, R.; Wong, Y.C.; Paradowska, A.; Blacket, S.; Durandet, Y. SPR characteristics curve and distribution of residual stress in self-piercing riveted joints of steel sheets. Adv. Mater. Sci. Eng. 2017, 2017, 5824171. [Google Scholar] [CrossRef]
- Haque, R. Residual stress in self-piercing riveting (SPR) joints—A review. Mater. Perform. Charact. 2018, 7, 20170109. [Google Scholar] [CrossRef]
- Hughes, D.S.; Kelly, J.L. Second-order elastic deformation of solids. Phys. Rev. 1953, 92, 1145. [Google Scholar] [CrossRef]
- Crecraft, D.I. The measurement of applied and residual stresses in metals using ultrasonic waves. J. Sound Vib. 1967, 5, 173–192. [Google Scholar] [CrossRef]
- Bray, D.E.; Junghans, P. Application of the LCR ultrasonic technique for evaluation of post-weld heat treatment in steel plates. NDT E Int. 1995, 28, 235–242. [Google Scholar] [CrossRef]
- Bray, D.E.; Tang, W. Subsurface stress evaluation in steel plates and bars using the LCR ultrasonic wave. Nucl. Eng. Design. 2001, 207, 231–240. [Google Scholar] [CrossRef]
- Javadi, Y.; Hasani, M.; Sadeghi, S. Investigation of clamping effect on the welding sub-surface residual stress and deformation by using the ultrasonic stress measurement and finite element method. J. Nondestr. Eval. 2015, 34, 3. [Google Scholar] [CrossRef]
- Javadi, Y.; Pirzaman, H.S.; Raeisi, M.H.; Najafabadi, M.A. Ultrasonic inspection of a welded stainless steel pipe to evaluate residual stresses through thickness. Mater. Design. 2013, 49, 591–601. [Google Scholar] [CrossRef]
- Atalar, A.; Quate, C.F.; Wickramasinghe, H.K. Phase imaging in reflection with the acoustic microscope. Appl. Phys. Lett. 1977, 31, 791–793. [Google Scholar] [CrossRef]
- Weglein, R.D. A model for predicting acoustic material signatures. Appl. Phys. Lett. 1979, 34, 179–181. [Google Scholar] [CrossRef]
- Obata, M.; Shimada, H.; Mihara, T. Stress dependence of leaky surface wave on PMMA by line-focus-beam acoustic microscope. Exp. Mech. 1990, 30, 34–39. [Google Scholar] [CrossRef]
- SdsadLee, Y.C.; Kim, J.O.; Achenbach, J.D. Measurement of stresses by line-focus acoustic microscopy. Ultrasonics 1994, 32, 359–365. [Google Scholar] [CrossRef]
- Sathish, S.; Moran, T.J.; Martin, R.W.; Reibel, R. Residual stress measurement with focused acoustic waves and direct comparison with X-ray diffraction stress measurements. Mater. Sci. Eng. A 2005, 399, 84–91. [Google Scholar] [CrossRef]
- Miyasaka, C.; Tittmann, B.R.; Tanaka, S.I. Characterization of stress at a ceramic/metal joined interface by the V(z) technique of scanning acoustic microscopy. J. Press. Vessel Technol. 2002, 124, 336–342. [Google Scholar] [CrossRef]
- Li, Y.; Liu, C.; Xiang, Y.; Li, Y. Characterization of local residual stress on curved blades by ultrasound. In Proceedings of the 2016 IEEE International Ultrasonics Symposium (IUS), Tours, France, 18–21 September 2016. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).